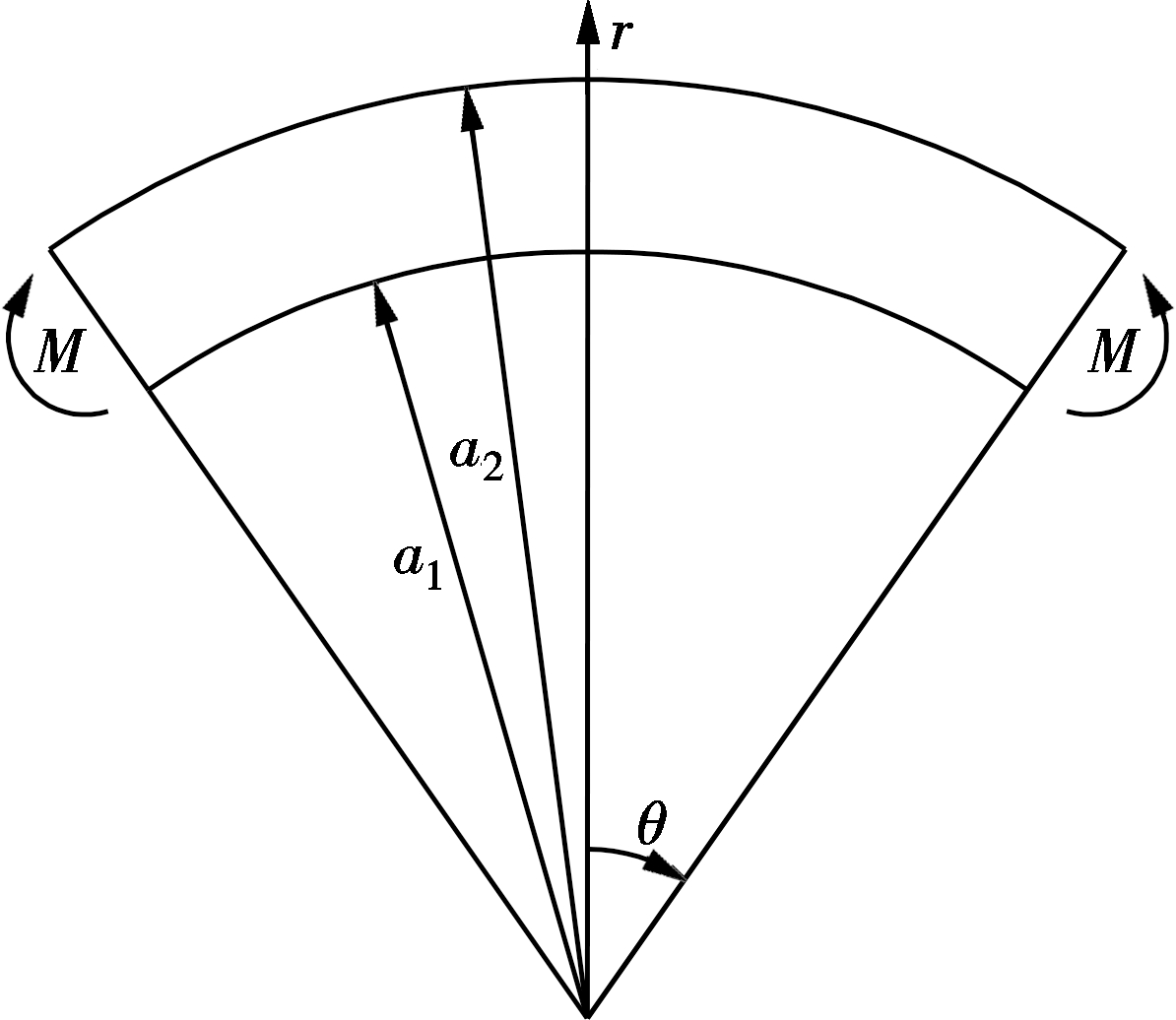
Fig.1 Geometry of the curved beam
Abstract：The analysis of plane strain elastic-plastic bending of a linear strain hardening curved beam with a narrow rectangular cross section subjected to couples at its end is conducted based on a unified yield criterion. The solutions for the mechanical properties of plane strain bending are derived, which are adapted for various kinds of non-strength differential materials and can be degenerated to those based on the Tresca, von Mises, and twin-shear yield criteria. The dependences of the two critical bending moments, the radii of the interfaces between the elastic and plastic regions and the radial displacements of the points at the symmetrical plane on different yield criteria and Poisson’s ratios are discussed. The results show that the influences of different yield criteria and Poisson’s ratio on the two critical bending moments, the radii of the interfaces between the elastic and plastic regions and the radial displacements of the points at the symmetrical plane of the curved beam are significant. Once the value ofb is obtained by experiments, the yield criterion and the corresponding solution for the materials of interest are then determined.
Key words：curved beam; plane strain; strain hardening; elastic-plastic bending; unified yield criterion
It is known that curved beams are widely applied in engineering practice, such as aerospace engineering, civil engineering, and mechanical engineering, etc. Consequently, the investigation of mechanical properties of a curved beam is of great necessity to make full use of the load-carrying capacity of the materials and ensure the safety of the curved beam in practical applications. There exist a large number of studies on elastic-plastic bending of a curved beam. A comprehensive research on the curved beam which is in the state of being completely elastic was presented by Timoshenko and Goodier[1]. Under the plane strain assumption, Shaffer and House[2-4] discussed the mechanical properties for pure bending of the wide curved bar. The theory for plane strain bending for rigid-perfectly plastic and work hardening materials was formulated by Hill[5] and Dadras et al.[6], respectively. In Ref.[7], the solutions of plane strain elasto-plastic pure bending of a linear strain-hardening curved beam were derived. A concise analytical treatment of elastic-plastic bending of a strain hardening curved beam was developed by Eraslan and Arslan[8], and their theory was further extended to nonlinearly hardening materials[9-10].
It is noted that the studies mentioned above were developed for one or several specific materials and thus have their own limitations in application. For this reason, this paper conducts the plane strain bending analysis of curved beams on the basis of the unified yield criterion (UYC)[11-13]. The solutions for the mechanical properties of plane strain bending of the curved beam consisting of non-SD (strength difference in tension and compression) materials such that many ductile metallic materials are derived, which can be adapted for a wide variety of materials.
In this paper, a wide curved beam with a narrow rectangular cross section is taken into consideration. The curved beam is subjected to a couple of moments at its end sections. The geometry of the beam, the coordinate system and the loading of the beam are shown in Fig.1. It is assumed that the beam is fixed at point r=a1 and θ=0 during the deformation. In the process of elasto-plastic deformation, the plastic deformation begins at r=a1, and with the increase in the couple moment, the plastic region
Fig.1 Geometry of the curved beam
expands into the beam.When the moment approaches a critical value, another plastic region appears at r=a2. At this time, the beam consists of three parts: an inner plastic region, a middle elastic region, and an outer plastic region. With the increase in the couple moment, the two plastic regions will go on expanding.
When the curved beam is purely under bending, the stresses and strains are the only function of r, and the shear stress τrθ=0. Thus, the strain-displacement relationships can be expressed as
(1)
(2)
where u and v denote the radial and tangential components of displacement; r and θ denote the radial and tangential coordinates; εr and εθ denote the radial and tangential normal strain components; and γrθ is the shear strain. Due to τrθ=0, the equation of equilibrium can be obtained by
(3)
where σr and σθ are the radial and tangential normal stress components, respectively. In addition, the compatibility relationship is
(4)
and the equations of the generalized Hook’s law are
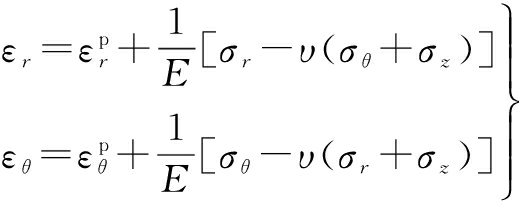
(5)
where 
and 
denotes the radial and tangential plastic strain components; E is the modulus of elasticity; and υ represents the Poisson’s ratio which satisfies 0<υ≤0.5.
Eraslan and Arslan[8] derived the radial and tangential components of displacement, which are expressed as
v(r,θ)=Crθ+Asinθ, u(r,θ)=rεθ-Cr-Acosθ (6)
where C and A are integration constants, and
(7)
It follows from Eqs.(3), (5) and (7) that[8]
(8)
This is the differential equation that governs the curved beam’s partially plastic response under pure bending, and it is applicable to the case of plane strain.
For the case of plane strain and in the stage of purely elastic deformation, we have[8]
(9)
(10)
where the four integration constants B1, B2, C, and A can be obtained by
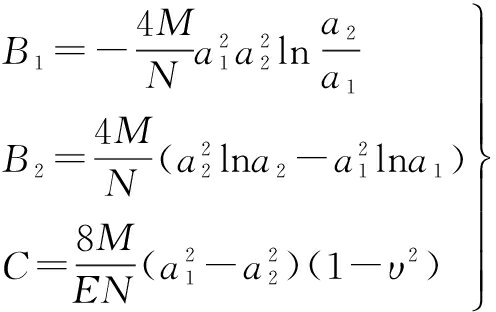
(11)
(12)
n.
In the plastic region, the stress state is σθ>σz>σr[8]. As τrθ=0, σr, σθ, and σz are three principal stresses. Thus, we have σθ=σ1, σz=σ2, and σr=σ3. For the UYC, its principal stress is expressed as[11-13]
(13a)
(13b)
where σ1, σ2 and σ3 represent the principal stresses, satisfying σ1≥σ2≥σ3, and σy is the material’s tensile yield stress. It should be noted that parameter b plays an important role in the UYC. It reflects the influence of the intermediate principal stress on the failure of a material. On the other hand, it builds a bridge among different yield criteria. It is the parameter that distinguishes one criterion from another. Hence, the UYC is not a single yield criterion but a theoretical system including a series of regular yield criteria, and it can be applied to various types of non-SD materials. With different choices of parameter b, the UYC can be simplified to the Tresca yield criterion (b=0), the linear approximations of Mises yield criterion 
, the twin-shear yield criterion (TS) (b=1)[14] and a series of new yield criteria. In practice, when basic material parameters are obtained by experiments, the value of b can be determined by
(14)
where φ stands for the ratio of the shear yield stress to the tensile yield stress, i.e. φ=τs/σy, and 0≤b≤1 for convex yield criteria.
For the plane strain situation, we have
σz=υ(σθ+σr)
(15)
Thus, the UYC takes the form of Eq. (13a). By combining Eq.(13a) with Eq.(15), we have
(16)
P=1+b-υb, Q=1+υb
(17)
For a linearly hardening material, the relationship between the yield stress and equivalent plastic strain can be expressed as
σy=σ0(1+ηεEQ)
(18)
where σ0 is the initial yield stress; η represents the material hardening parameter; and εEQ the equivalent plastic strain.
The associated flow rule of the UYC gives
(19)
and from the equivalence of the increment of plastic work, we have
(20)
with R=(1+b)/P. The combination of Eqs.(16), (18), (19) and (20) gives the tangential plastic strain component
(21)
Substituting Eqs.(3), (15), (19) and (21) into Eq.(8), the differential equation for the first plastic region can be obtained as
(23)
in which H is a normalized hardening parameter expressed as H=ησ0/E.
The solution of Eq.(22) can be given by
(24)
(25)
Accordingly, the tangential stress, plastic strains, and radial displacement can be obtained as
σθ= -WB3r-1-W+WB4r-1+W+
(26)
(27)
Acosθ
(28)
where B3 and B4 are integration constants.
For the case of b=0, it can be obtained from Eqs.(24) to (28) that
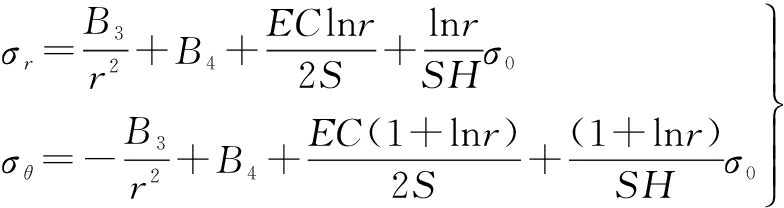
(29)
Acosθ
(31)
.
It is found from Eqs.(29) to (31) that the expressions for σr, σθ, , 
, and u are identical to those obtained by Eraslan and Arslan[8].
In the plastic region, the stress state is σr>σz>σθ[8]. Thus, the UYC takes the form of Eq.(13a), and we have
(32)
Based on the associated flow rule of the UYC and the equivalence of the increment of plastic work, we can obtain
(33)
The relationship between the yield stress and equivalent plastic strain for linear hardening material is
σt=σ0(1+ηεEQ)
(34)
Thus, the radial plastic strain component becomes
(35)
The differential equation for the second plastic region can be obtained as
where
(37)
The solution of Eq.(36) is
(38)
where
(39)
As a consequence, it can be found that
σθ= -WB5r-1-W′+WB6r-1+W′-
(40)
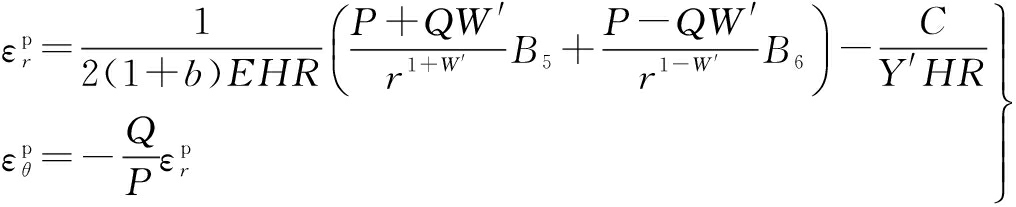
(41)
(42)
where B5 and B6 are integration constants.
For the case of b=0, it can be obtained from Eqs.(38) to (42) that
(43)
Acosθ
(45)
It is found from Eqs.
.
5.1 The first stage of elastic-plastic deformation
In this stage, the curved beam consists of two regions, a plastic region (a1<r<r1) and an elastic region (r1<r<a2), where r1 is the border radius of the plastic and elastic regions. There are seven unknowns which are A, B1, B2, B3, B4, C, and r1 in the expressions. In order to determine these unknowns, seven unrelated boundary conditions are available, and they are listed as follows:
upⅠ(a1,0)=0
(46)
(47)
(48)
upⅠ(r1,θ)=ue(r1,θ)
(49)
(50)
(51)
(52)
where superscript pⅠ and e represent the first plastic region and the elastic region, respectively, and a function defined as f(x)=x2(lnx+1/2)/2 is used to make the expression more concise.
5.2 The second stage of plastic-elastic deformation
In this stage, the curved beam consists of three regions, a plastic region (a1<r<r1), an elastic region (r1<r<r2) and another plastic region (r2<r<a2), where r1 and r2 is the border radius of the plastic and elastic regions. There are ten unknowns in the expressions, and they are A, B1, B2, B3, B4, B5, B6, C, r1, and r2. In order to determine these unknowns, we need to add five conditions on the basis of section 5.1, and they are listed as follows:
(53)
(54)
ue(r2,θ)=upⅡ(r2,θ)
(55)
(56)
(57)
where superscript pⅡ represents the second plastic region. By using Eqs.(46) to (50) and (53) to (57), the ten unknowns can be obtained.
With these unknowns determined, the stress, strain and displacement of the beam can be obtained from the corresponding expressions.
In this section, a curved beam of a2/a1=1.3 is considered. The dimensionless form and normalized variables are used for the presentation of the results and they are defined as
The values of material parameters used in the following analysis are: E=200 GPa, σ0=250 GPa, H=0.2.
In the process of elastic-plastic deformation of the curved beam, there are two critical states. One is when the plastic deformation commences at the inner surface (r=a1) and the other is when the plastic deformation commences at the outer surface (r=a2). Obviously, there are two elasto-plastic critical moments 
Ⅰ and Ⅱ representing these two critical states, and Ⅰ is also the elastic limit load. When 
Ⅰ, the beam is completely in an elastic state. With the increase in load, when Ⅰ
Ⅱ, the beam consists of an inner plastic region and an outer elastic region. Finally, when 
Ⅱ, the beam consists of an inner plastic region, a middle elastic region, and an outer plastic region. It is assumed that 
1 denotes the radius of the boundary between the inner plastic and middle elastic regions, and 2 represents the radius of the boundary between the middle elastic and outer plastic regions.
Figs.2 and 3 show the variation of the two critical loads Ⅰ and Ⅱ with parameter b and Poisson’s ratio υ. It is revealed from these two figures that parameter b has significant influences on the two critical loads Ⅰ and Ⅱ. The values of Ⅰ and Ⅱ increase with the increase in parameter b. The significant dependence of the two critical loads on parameter b implies the considerable influences of different yield criteria on the two critical loads as b is a parameter determining the specific expression of the yield criterion. It is seen that the TS-based predictions of the two critical loads provide upper bounds to the critical loads due to the full consideration of the influence of the intermediate principal stress (b=1), while the Tresca-based predictions give lower bounds owing to the ignorance of the effect of the intermediate principal stress (b=0). Consequently, the selection of parameter b becomes much more important. In practice, when basic material parameters σy and τs are obtained by experiments, the value of b can be determined by Eq.(14). Whenever parameter b is obtained, the two critical loads for a curved beam consisting of this sort of material can be obtained.
In addition, it is observed from Figs.2 and 3 that the two
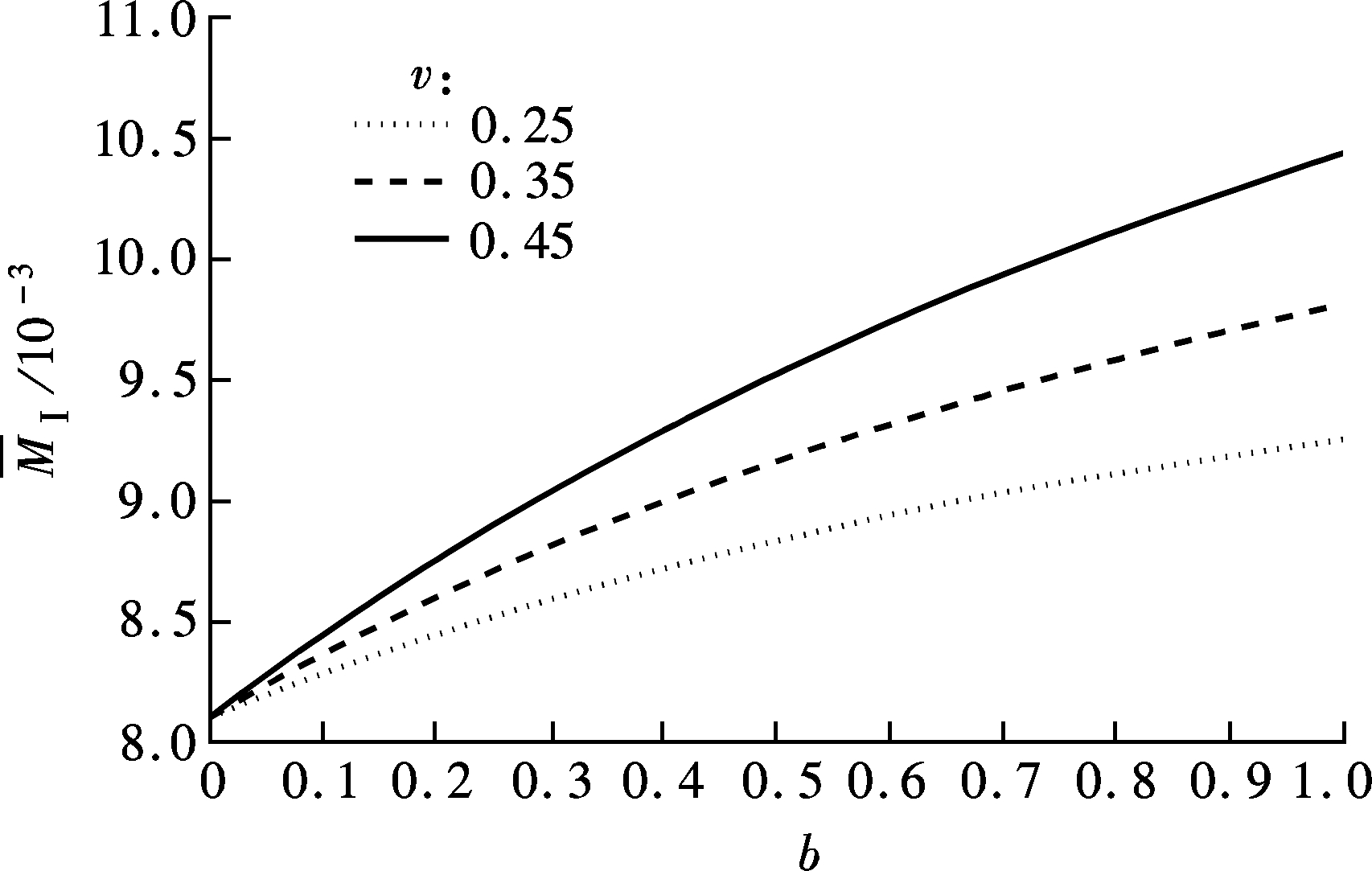
Fig.2 Effect of parameter b on the critical load 
Ⅰ with various Poisson’s ratios
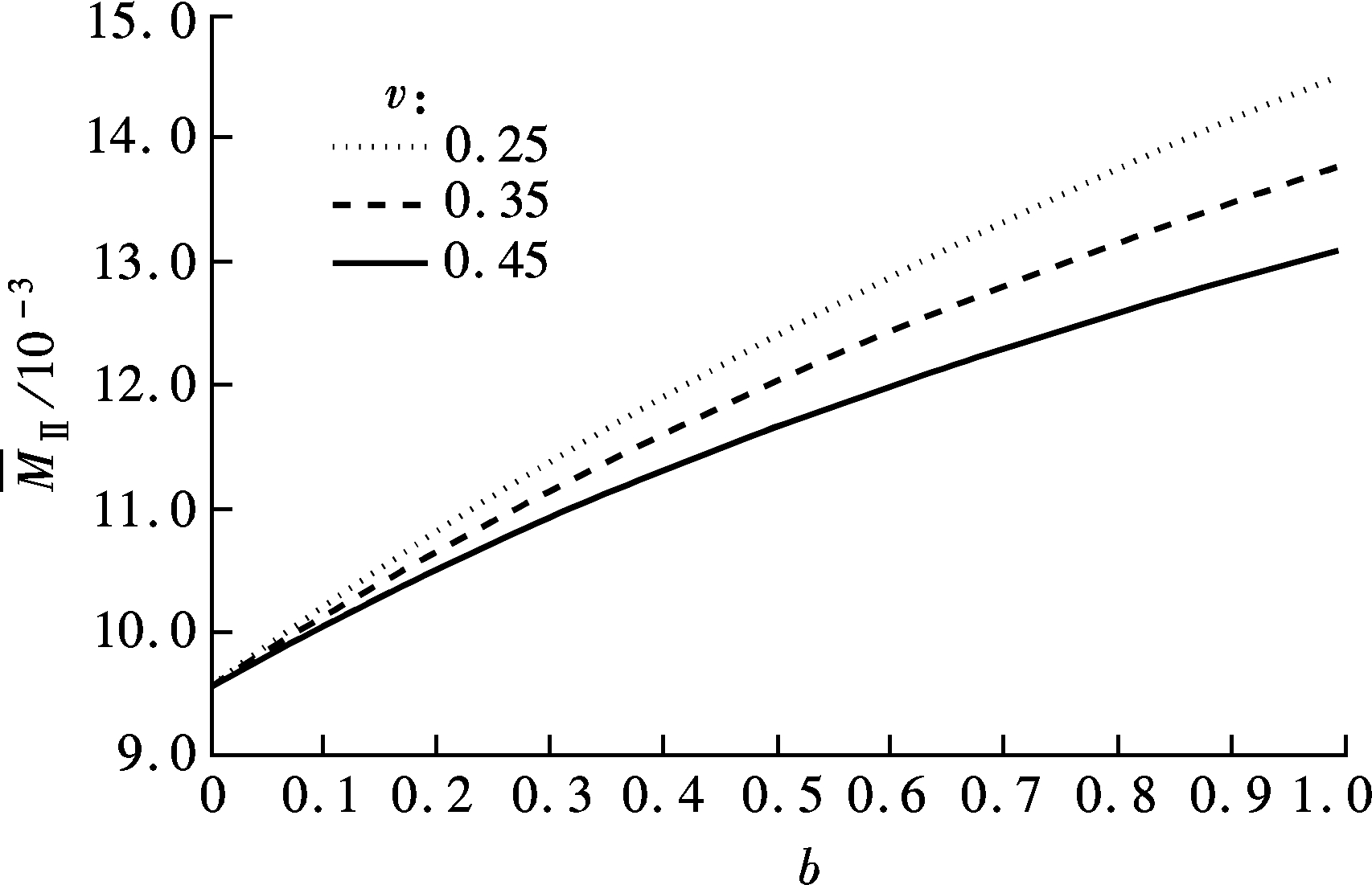
Fig.3 Effect of parameter b on the critical load 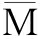Ⅱ with various Poisson’s ratios
critical loads 
Ⅰ and Ⅱ are dependent upon Poisson’s ratio υ as 0<b≤1, whereas they have nothing to do with Poisson’s ratio when b=0. When 0<b≤1, the critical load Ⅰ becomes larger with the increase of the value of Poisson’s ratio υ, whereas the critical load Ⅱ becomes smaller with the increase of the value of Poisson’s ratio υ. The extent of influence of Poisson’s ratio on the two critical loads becomes more significant with the increase in the value of parameter b.
As is known, when the subjected bending moment is larger than the critical load MⅡ, the curved beam consists of an inner plastic region, an elastic region and an outer plastic region. Figs.4 and 5 show the variations of radii 
1 and 2 with parameters b and υ. As can be seen, the radii 1 and 2 are dependent upon parameters b and υ. It is observed from Fig.4 that radius 1 becomes larger with the increase of Poisson’s ratio υ when the value of parameter b is very small. However, with the further increase of parameter b, radius 1 becomes smaller with the increase of Poisson’s ratio υ.
Fig.4 Variations of 
1 with parameter b for the case of =0.016
Fig.5 Variations of 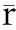2 with parameter b for the case of 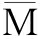=0.016
From Fig.5, it is found that radius 
2 decreases with the increase in Poisson’s ratio υ. Additionally, it is seen from Figs.4 and 5 that radius 1 diminishes with the augmentation of b, whereas radius 2 becomes larger with increasing b. Thus, it can be concluded that the influences of different yield criteria and Poisson’s ratios cannot be overlooked in the predictions of the values of radii 1 and 2.
Figs.6 and 7 show the influences of parameter b and Poisson’s ratio υ on the radial displacements for those points at the plane of symmetry of the curved beam. As can be seen, the radial displacements are greatly dependent upon parameter b and Poisson’s ratio υ. For instance, it can be found from Fig.8 that the radial displacement 
at the plane of symmetry is negative. The absolute value of the radial displacement 
(1.15a1,0) diminishes with the augmentation of the value of parameter b, but it becomes larger with the increase of Poisson’s ratio υ. The great dependences of the radial displacements on parameter b imply the significant effects of different yield criteria on the radial displacements.
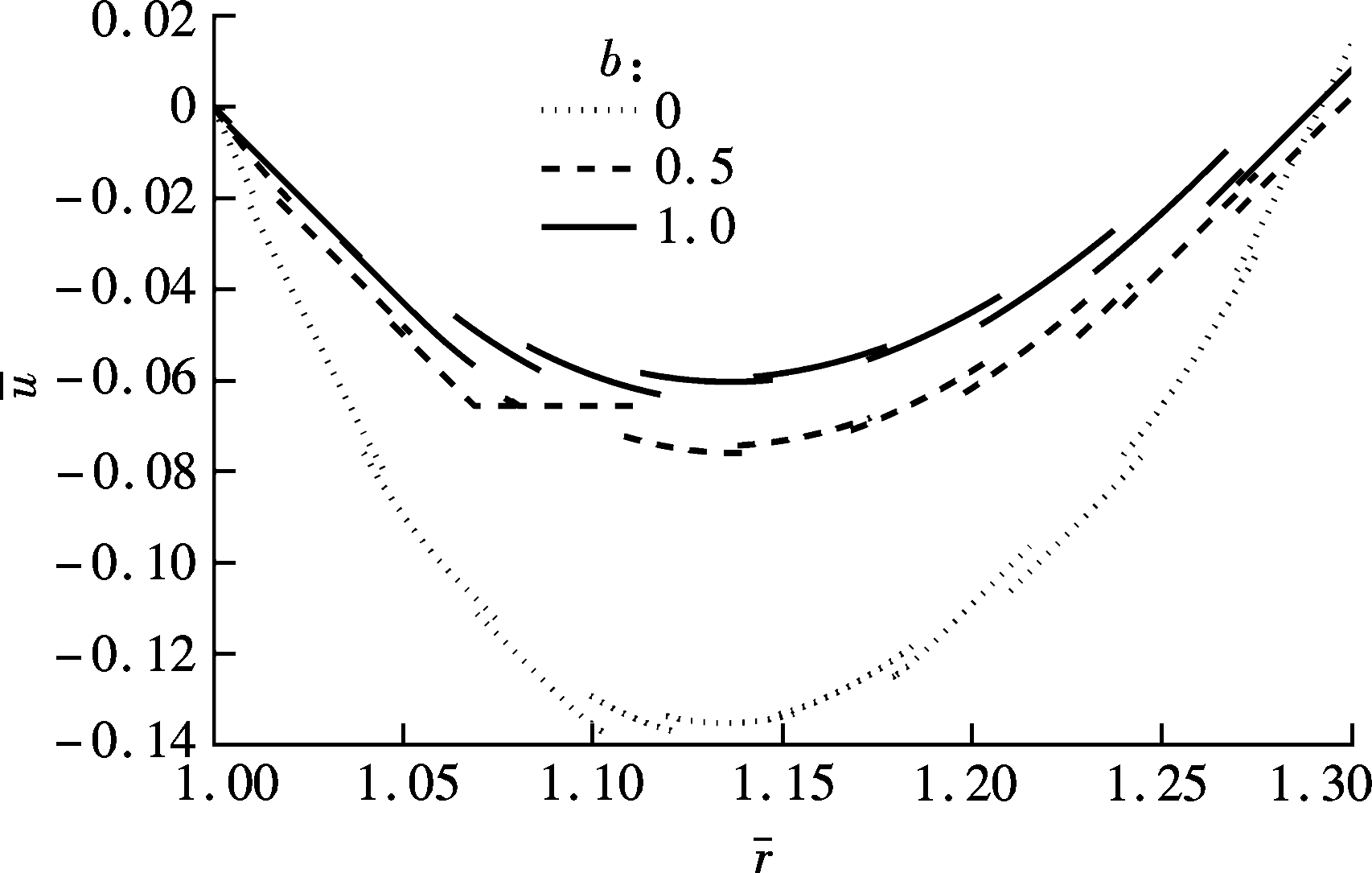
Fig.6 Dependence of radial displacements of the points at the plane of symmetry on parameter b with 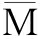=0.016 and υ=0.35
Fig.7 Dependence of radial displacements of the points at the plane of symmetry on Poisson’s ratio with 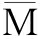=0.016 and b=0
Fig.8 Effect of parameter b on the displacement 
(1.15a1,0) with =0.016
Based on the unified yield criterion, the analysis of plane strain elastic-plastic bending of a linear strain hardening curved beam is carried out. The solutions for the mechanical properties of plane strain bending are derived. The solutions are adapted for various kinds of non-SD materials. With a specific value of b, the solutions can be simplified to those based on the Tresca, von Mises, and TS criteria. It is concluded that proper choice of yield criteria is of great importance for the analysis of properties of plane strain bending of the curved beam. In engineering practice, when basic material parameters are obtained by experiments, the value of b can be determined. With parameter b, the yield criteria and the corresponding solution suitable for the material of interest are then available.
References：
[1]Timoshenko S P, Goodier J N. Theory of elasticity[M]. New York: McGraw-Hill, 1970.
[2]Shaffer B W, House Jr R N. The elasto-plastic stress distribution within a wide curved bar subjected to pure bending[J]. Journal of Applied Mechanics, 1955, 22: 305-310.
[3]Shaffer B W, House Jr R N. The significance of zero shear stress in the pure bending of a wide curved bar[J]. Journal of the Aeronautical Sciences, 1957, 24: 307-308.
[4]Shaffer B W, House Jr R N. Displacements in a wide curved bar subjected to pure elasto-plastic bending[J]. Journal of Applied Mechanics, 1957, 24: 447-452.
[5]Hill R. The mathematical theory of plasticity[M]. London: Oxford University Press, 1967.
[6]Dadras P, Majlessi S A. Plastic bending of working hardening materials[J]. Journal of Engineering for Industry, 1982, 104(3): 224-230. DOI:10.1115/1.3185823.
[7]Dadras P. Plane strain elastic-plastic bending of a strain-hardening curved beam[J]. International Journal of Mechanical Sciences, 2001, 43: 39-56. DOI:10.1016/s0020-7403(99)00102-2.
[8]Eraslan A N, Arslan E. A concise analytical treatment of elastic-plastic bending of a strain hardening curved beam[J]. Zeitschrift für Angewandte Mathematik und Mechanik, 2008, 88: 600-616. DOI:10.1002/zamm.200600037.
[9]Arslan E, Eraslan A N. Analytical solution to the bending of a nonlinearly hardening wide curved bar[J]. Acta Mechanica, 2010, 210(1): 71-84. DOI:10.1007/s00707-009-0195-y.
[10]Eraslan A N, Arslan E. A computational study on the nonlinear hardening curved beam problem[J]. International Journal of Pure Applied Mathematics, 2008, 43: 129-143.
[11]Yu M H, He L N. A new model and theory on yield and failure of materials under complex stress state[C]//Mechanical Behaviours of Materials VI. Oxford: Pergamon Press, 1992: 841-846.
[12]Fan S C, Yu M H, Yang S Y. On the unification of yield criteria[J]. Journal of Applied Mechanics, 2001, 68(2): 341-343. DOI:10.1115/1.1320451.
[13]Yu M H. Advance in strength theory of material and complex stress state in the 20th century[J]. Applied Mechanics Reviews, 2002, 55(3): 169-218. DOI:10.1115/1.1472455.
[14]Yu M H. Twin shear stress yield criterion[J]. International Journal of Mechanical Sciences, 1983, 25(1): 71-74. DOI:10.1016/0020-7403(83)90088-7.
Citation：Fu Jun, Pang Miao, Song Guangyuan, et al. Analysis of plane strain bending of a strain hardening curved beam based on unified yield criterion[J].Journal of Southeast University (English Edition),2016,32(3):339-345.DOI:10.3969/j.issn.1003-7985.2016.03.014.
DOI：10.3969/j.issn.1003-7985.2016.03.014
摘要：在统一屈服准则的基础上,研究了两端力偶作用下具有窄矩形截面线性应变硬化曲梁的平面应变弹塑性弯曲问题.获得的平面应变弯曲解答适用于各类非强度差材料,并可以退化到基于Tresca, von Mises和广义双剪屈服(TS)准则的解答.讨论了2个临界弯矩、弹塑性区界面的半径及对称面上点的径向位移与不同屈服准则和泊松比之间的相关性.结果表明,不同屈服准则和泊松比对曲梁的2个临界弯矩、弹塑性区界面的半径及对称面上点的径向位移有显著的影响.当材料的参数b通过实验得到后,便可确定对应的屈服准则及相应解答.
关键词：曲梁;平面应变;应变硬化;弹塑性弯曲;统一屈服准则
中图分类号：O343
Received：2015-12-18.
Foundation item：The Project of the Ministry of Housing and Urban-Rural Development (No.2014-K4-010).
Biographies：Fu Jun (1970—), male, doctor, associate professor,fujun@zstu.edu.cn; Pang Miao (1972—), male, doctor, associate professor, pm@zju.edu.cn.