Abstract：To study the influence of original defects on the dynamic stability of the columns under periodic transient loadings, the approximate solution method and the Fourier method of the stable periodic solution are adopted while considering the influence of original defects on columns.The dynamic stability of the columns under periodic transient loadings is analyzed theoretically.Through the study of different deflections, the dynamic instability of the columns is obtained by Maple software. The results of theoretical analysis show that the larger the original defects, the greater the unstable area, the stable solution amplitude of columns and the risk of instability caused by parametric resonance will be. The damping of columns is a vital factor in reducing dynamic instability at the same original defects. On the basis of the Mathieu-Hill equation, the relationship between the original defects and deflection is deduced, and the dynamic instability region of the columns under different original defects is obtained. Therefore, reducing the original defects of columns can further enhance the dynamic stability of the compressed columns in practical engineering.
Key words：periodic transient loading;parametric resonance;original defect;dynamic stability
The parametric vibration of columns under axial-periodic loadings has received considerable attention in the literature. Lyapunov[1-2]took the lead in explaining, in an exact manner, the definition of dynamic stability, and thus the general definition of dynamic stability came into being in mathematics. Bolotin[3] systematically studied structural stability under the influence of periodic loads, the essence of which was a study on the influence of frequency changes of harmonic loads on the solution of equation by representing the systematic dynamics as the Mathieu-Hill equation.Even today, there are numerous studies and documents on the Mathieu-Hill equation domestically and internationally[4-6].
However, the prerequisite of the Mathieu-Hill equation is that there are no original defects on columns. However, original defects are unavoidable due to the asymmetry of structural materials, the bending of structural materials caused by self weight and the influence of construction, which is a major threat to dynamic stability. In recent years, the influence of original defects on structural dynamic stability has been studied by many scholars in China, but a few of them have analyzed how great the influence of original defects is on the dynamic unstable region of columns[7-8].
The purpose herein is to determine the maximum transient lateral response for an initially curved column. With the influence of original defects on the dynamic stability of columns under consideration, the dynamic stability of columns with original defects is studied by further theoretical derivation, and the impact of original defects on the dynamic unstable region is found to provide a reference for practical engineering construction in this paper.
The research on the Mathieu-Hill equation is correct only if there is no original curvature and original bending. If the column is originally bent, the dynamic equation cannot be represented as the Mathieu-Hill equation. Considering the deflection caused by defects of the column as v0(x), its overall deflection will be a function of coordinates and time, represented as v1(x,t).The rotational inertial force of the transverse surface of the column around the axis is not considered in this paper as its impact is rather small if the transverse dimension is not similar to the vertical dimension, which is often the case. The differential equation of the column’s dynamic deflection curve can be expressed as [9-10]
(1)
where EI is the bending rigidity; m is the mass per unit length; P is the dynamic load.
If the two ends of the column are hinges, the deflection v1and v0 are rather small when compared with the length l. Therefore, an approximate elastic curve is adopted, supposing
(2)
where f0 is the deflection caused by defects and f the overall deflection, in other words, the function of time. Substituting Eq.(2) into Eq.(1) yields the following ordinary differential equation after transformation and iteration:
(3)
where Pcr is Euler load, and it is a non-dimensional parameter, Pcr=π2EI/l2.
The fundamental frequency of the column is 
. Introducing a non-dimensional time parameter
(4)
then Eq.(3) can be expressed as
(5)
In this section, the dynamic stability of columns is studied by utilizing Eq.(5). Consider that the frequency of the acting force is θ and 
is the semi-period of the change of force. The force of the column is shown in Fig.1 and Fig.2. The change of vibration in terms of speed and deflection within one cycle is studied in this section. When P>Pcr,the deflection caused by loads is always on the rise. Therefore, the prerequisite of this section is P<Pcr. From the second cycle, the starting deflection of the column, which is not zero, is the stable
Fig.1 Force model of columns with original defects
Fig.2 P-t figure of columns with original defects
solution produced at the end of last cycle. Then by applying the approximate solution, the dynamic unstable region becomes available. Under the influence of transient loadings, the column will vibrate. If the vibration decreases, the starting condition of the column is dynamically stable. Within this period, if the vibration is periodic or nearly periodic, the starting condition is dynamic criticality. Assuming that after the end of every vibrating cycle, the amplitude is sf0. If the coefficient s is greater than 1, the vibration at the end of every cycle will continue to rise because the deflection caused by repeated loads always increases[11].Therefore, the starting condition of the column is unstable. However, if the coefficient s=1, the range of the dynamic unstable region can be obtained. Substitution of the boundary condition of the equation yields the following stable solution of the first cycle:
f1=A2sintω+A1costω+f0
(6)
Therefore, the starting deflection of every cycle is related to time. Assuming that fε is the starting deflection of the cycle and the cycle studied at this time is the first one, then in the first half of the cycle (0≤t≤T/2), the deflection will be
(7)
The general solution of Eq.(7) is
(8)
(9)
where Ωk is the natural frequency of the column under the impact of longitudinal forces and 
.η2 is the ratio of natural frequency under the impact of longitudinal forces and the basic frequency.
Assuming that when tw=0 and the starting deflection is fε, its results will depend on cycle T. Before the load of this cycle operates and with a starting speed of 
, then
(10)
At the second half of the cycle (T/2≤t≤T) and with the external force P=0, the dynamic equation can be expressed as
(11)
The general solution of Eq.(11) is
f(tk)=D2sintω+D1costω+fε
(12)
At the end of a whole cycle, the parameter 
, and the variation of deflection and speed is sfε and 
ε,respectively. Then
(13)
At the end of the first half, when tw=πω/θ, the results produced by Eqs. (8) and (12), with deflection and speed as the substitution, respectively, should be equal.
(14)
(15)
Substituting Eqs.(10) and (13) into Eqs.(14) and (15) yields
(16)
where
To ensure fε≠0, 
ε≠0,the prerequisite should be
(17)
After arrangement, we have
s2-sA+B=0
(18)
where
A=
(19)
B=
(20)
According to the assumption above, the vibration of the column is the critical value when s=1, and then
(21)
If A2<4B, the expression of s is plural. Therefore, the starting assumption that deflection and speed increase imultaneously s times cannot be satisfied. Through the fit of Maple, the dynamic unstable region can be expressed as shown in Fig.3.
Fig.3 The approximate solution of the dynamic unstable region of the column with original defects
In the theoretical derivation above, the approximate solution of the dynamic unstable region is acquired while the initial defects are ignored. When the load is less than the critical Euler load, a similar vibration will also occur. The amplitudes will increase by a large amount as time passes and there will be consecutive stimulating areas. Compared with the work of MaKushen[3], the unstable region produced here may have ignored a few vibration parameters since there is no comparison addressing initial defects. Therefore, this approximate method may not be exact.
The cyclical transient load is expressed as
(22)
According to the Fourier transformation[12],
Ptk=0 k=2,4,6,…
(23)
By utilizing the Fourier transformation, it is clear that Eq.(3) is logical only when k is an odd number. If k is an even number, the excitation coefficient will be zero, which is obviously illogical. Based on the research of Bolotin on columns without original defects, there is the assumption:
(24)
The vibration of the column can be expressed as a linear differential equation[13]:
f ″+2εf 
(25)
where ε is the damping coefficient and μk the excitation coefficient of k.
(26)
The stable solution is
f=a+bsin(kθt)+ccos(kθt)
(27)
where
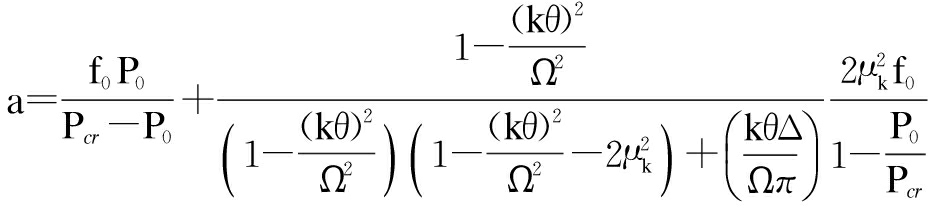
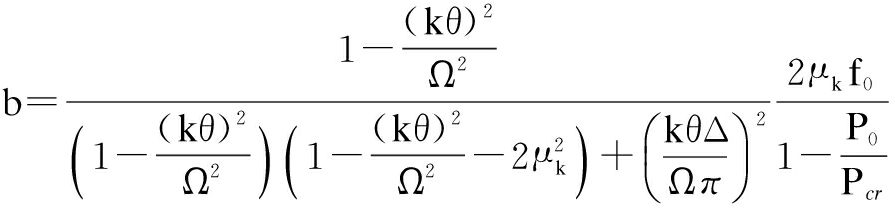
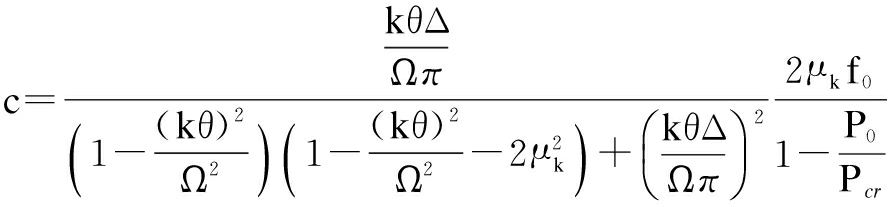
(28)
where 
, representing the fixed vibration damping ratio under the influence of longitudinal force.
The largest amplitude of the stable solution is
(29)
Without the consideration of damping,
A=
(30)
To ensure that the amplitude is the largest, the denominator of Eq.(30) is zero. In other words,
(31)
Assume that[14]
2k=t
(32)
where t is a positive integer and represents the unstable region. After substituting Eq.(32) into Eq.(31), we obtain
(33)
When the excitation coefficient μk is relatively small,
(34)
The stable solution now matches the unstable region and is proved to a large extent. When the perturbed frequency and the transient natural frequency form a steady ratio, parametric resonance will occur. If μk is ignored, it is clear that every unstable region depends on the corresponding simple harmonic waves, which share great commonalities with the research of Крылов[3]. The premier objective is to find the connection among the excitation coefficient, the original bending and the maximal value of the lateral amplitude. Assume that
(35)
where M is the ratio of the largest amplitude of the stable solution and the original midspan deflection.
Under a great excitation coefficient, the ratio of the excited frequency and natural frequency cannot satisfy the conditions of parametric resonance. Therefore, only a small excitation coefficient is studied in this paper. Fig.4 gives the highest amplitude under a small excitation coefficient when the column is stable. Generally speaking, the highest amplitude is settled after 100 cycles. It is clear that the figure of amplitude is similar to that of the forced vibration. When P0/Pcr=0.2, ε=0, the parametric resonance occurs around θ/Ω=0.6,1,2,…. Closer to the parametric resonance, the amplitude will show an exponential rise. Moreover, the greater the ratio, the wider the range of θ will be. All these are in accordance with Bolotin’s study on the dynamic unstable region. From Fig.5, it is apparent that when Δ=0.05, the M of the second and the third are far less than the M without damping. Hereby, damping is effective for preventing instability.
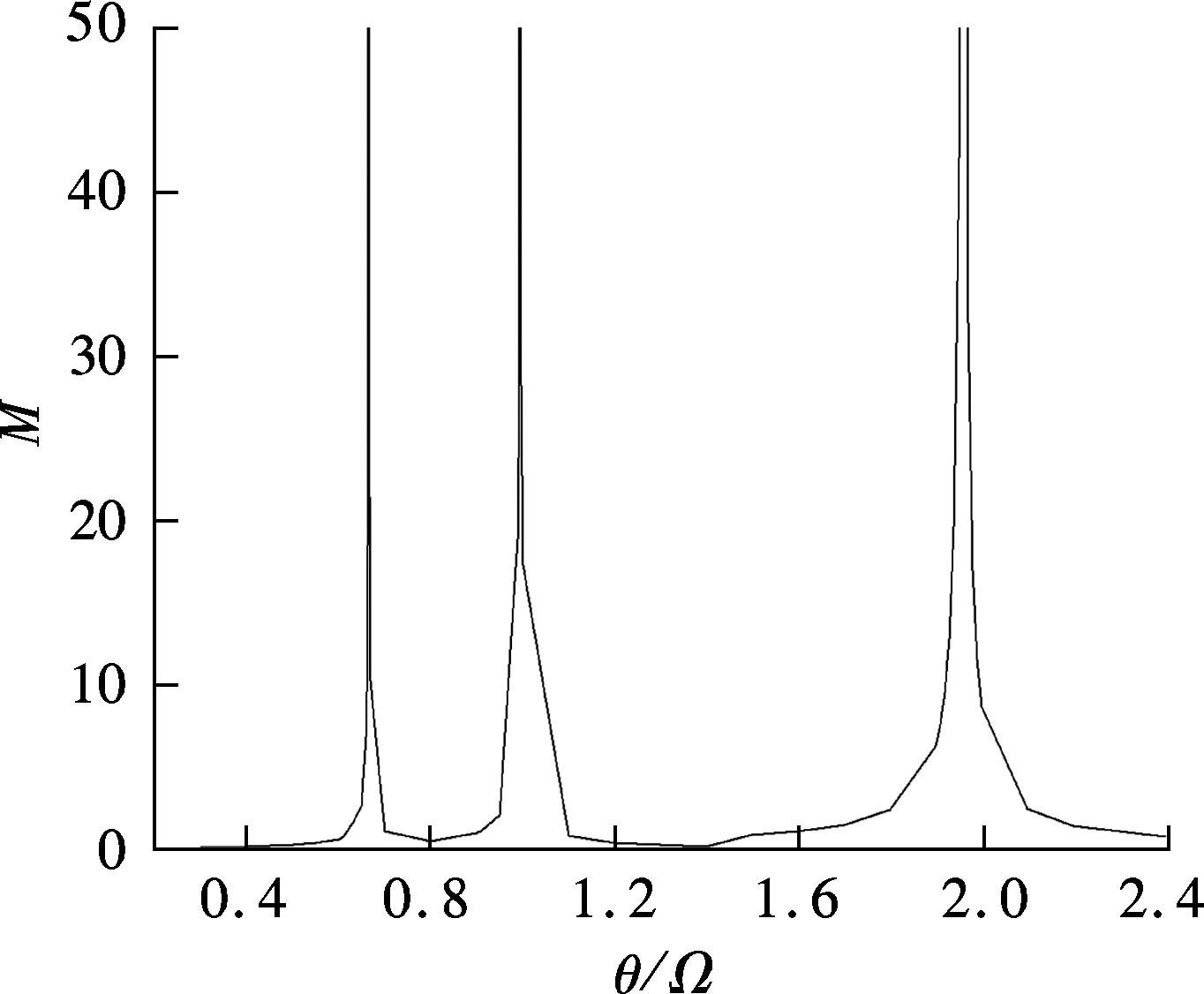
Fig.4 Midspan column deflection (P0/Pcr=0.2,Δ=0)
Fig.5 Midspan column deflection (P0/Pcr=0.2,Δ=0.05)
The analysis above shows that the major unstable region is the most dangerous. When t=1, the range of θ/Ω in which the column produces high amplitude is extremely wide; when t=2 or t=3, the range of θ/Ω in which the column can produce high amplitude is extremely narrow. Damping, particularly relatively large damping, has a great influence on the columns when t=2 or t=3. Therefore, with certain damping, it will need an extremely large excitation coefficient to trigger the parametric resonance of the subordinate regions.
From the analysis above, it can be concluded that the original defects have a great impact on the dynamic unstable region of the column. The assumption is described as below: When the largest amplitude surpasses a fixed value, the ratio of perturbed frequency and natural frequency will belong to the unstable region. When the largest amplitude is equal to the fixed value, the two ends of the dynamic unstable region can be defined and the fixed value should be the largest deflection that causes the initial instability of the compression column. There are numerous studies on critical deflection domestically[15-16]. The research theory of Dong et al.[16] is adopted in this paper. For slender columns,
(36)
where l is the length of the column.
The width of the current dynamic unstable region is mainly determined by the ratio of initial deflection and the largest deflection causing the initial instability. In other words, the range of its dynamic unstable region mainly depends on the size of the original defects.
The similarities are obvious when the dynamic unstable regions of Fig.6 and Fig.7 are compared with that of Bolotin. Thus, the theory that there is a consecutive dynamic unstable region is proved. Generally speaking, the cyclic force will cause transverse vibration under any frequency. On most occasions, generally-used vibration isolation and damping are of no use for parametrically excited vibration. As for the safety and reliability of the column, the first unstable region is the most dangerous. When the damping is large enough, the column needs a sufficiently large excitation coefficient to produce the second and the third unstable region. From the analysis above, it can be concluded that the larger the original defects, the higher the amplitude and the wider the unstable region will be, which means that most of the frequency ratios of the parametric resonance may be located at the unstable region.
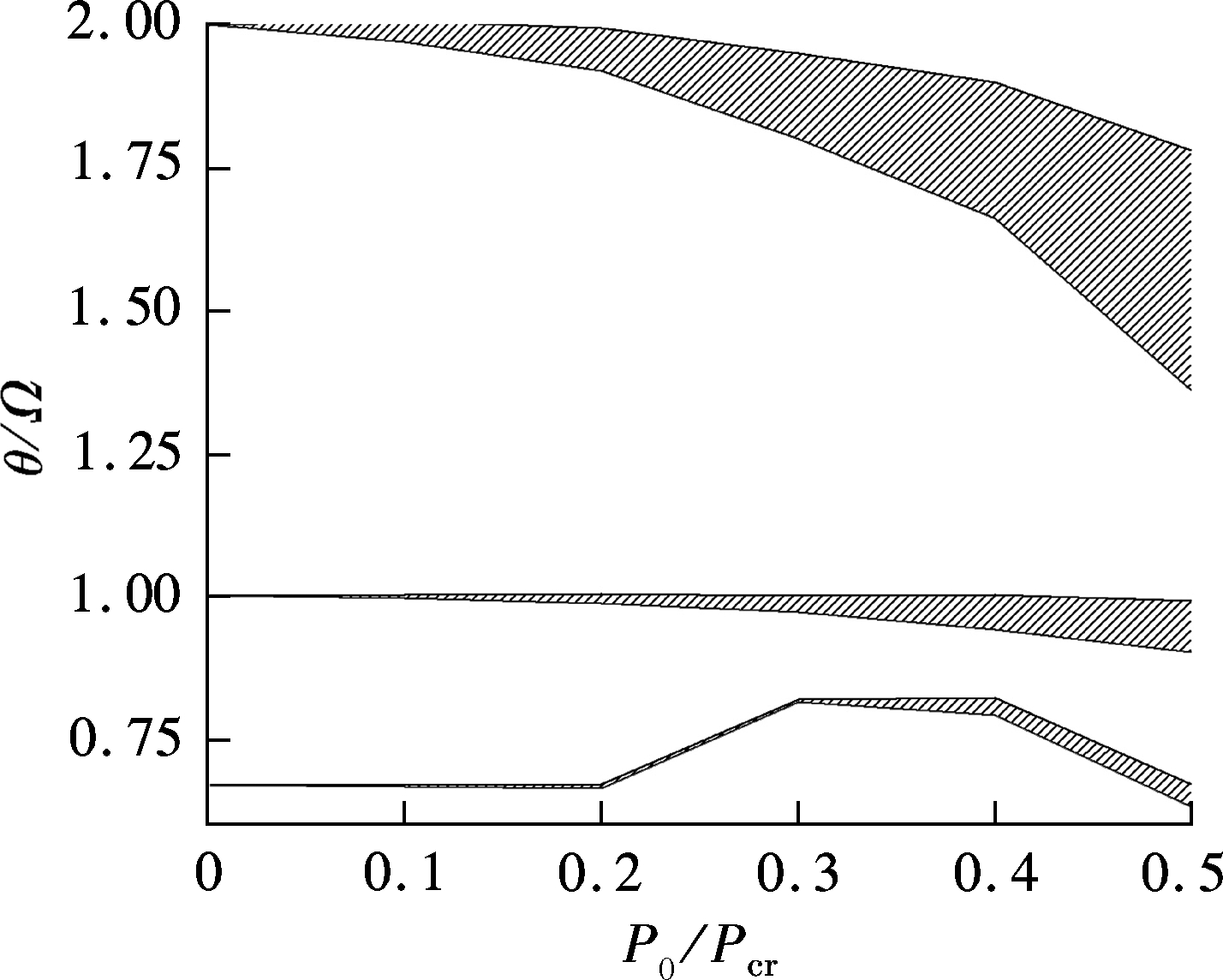
Fig.6 Dynamic unstable region (fmax/f0=10,Δ=0)
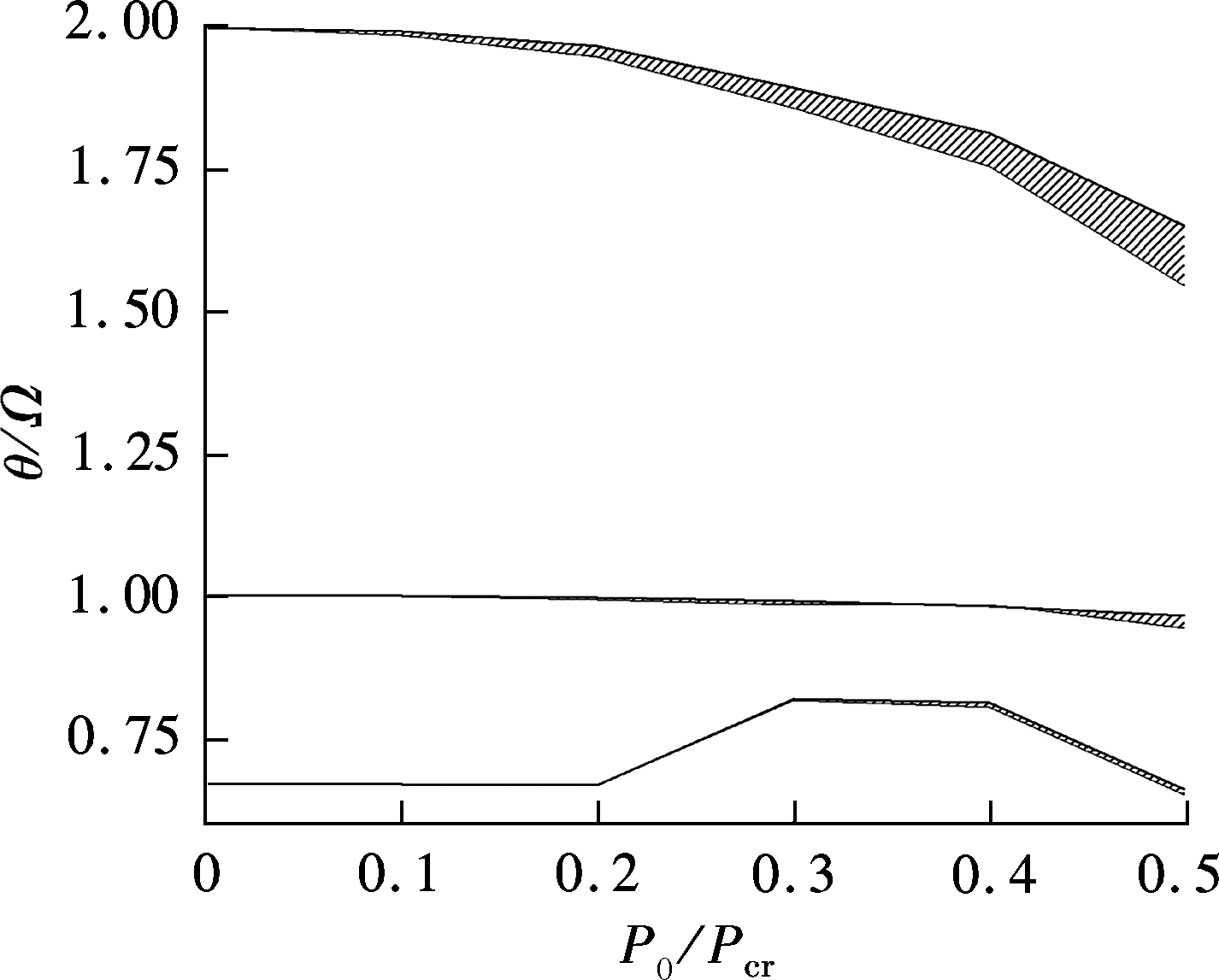
Fig.7 Dynamic unstable region (fmax/f0=40,Δ=0)
1) The existence of original defects does not change the fact that there is parametric resonance when the columns are stressed. However, for the dynamic unstable region, the larger the original defects, the wider the unstable region will be. Thus, the possibility of instability caused by parametric resonance will also increase.
2) Original defects are proportional to the amplitude of columns. The existence of damping baffles vibration, and thus prevents the amplitude rising to infinity.
3) The unstable region is related to its corresponding simple harmonic wave. The occurrence of k parametric resonance is only related to the k simple harmonic wave of the longitudinal force.
[1]Movchan A A. The direct method of Liapunov in stability problems of elastic systems[J]. Journal of Applied Mathematics and Mechanics, 1959, 23(3): 686-700. DOI:10.1016/0021-8928(59)90161-3.
[2]Tong Y H, Zhang L X, Shi P, et al. A common linear copositive Lyapunov function for switched positive linear systems with commutable subsystems[J]. International Journal of Systems Science, 2013, 44(11): 1994-2003. DOI:10.1080/00207721.2012.683830.
[3]Bolotin V V. The dynamic stability of elastic systems[M].San Francisco, CA,USA: Pergamon Press,1964:12-132.
[4]Wu B, Diebold G J. Mathieu function solutions for the photoacoustic effect in two- and three-dimensional structures and optical traps[J]. International Journal of Thermophysics, 2012, 33(10): 2185-2193. DOI:10.1007/s10765-012-1266-1.
[5]Raftoyiannis I G. Parametric resonance of steel bridges pylons due to periodic traffic loads[J]. Archive of Applied Mechanics, 2012, 82(10): 1601-1611. DOI:10.1007/s00419-012-0666-9.
[6]Wang J F, An W G, Song X H. Method for improving dynamic unstable boundary of Mathieu equation[J].Journal of Vibration and Shock, 2015,34(12):182-188.(in Chinese)
[7]Wang L H, Yi Z P, Zhang H. Dynamic stability of arch with the geometrical imperfection subject to the periodic load[J]. Journal of Hunan University, 2007, 34(11):16-20.(in Chinese)
[8]Wang X J, Wang L, Qiu Z P. Failure analysis of dynamic buckling of initial geometric imperfections[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(12):1484-1489.(in Chinese)
[9]Holzer S M. Stability of columns with transient loads[J].Journal of the Engineering Mechanics Division, 1970, 96(6):913-930.
[10]Xie W-C. Dynamic stability of structures[M].New York: Cambridge University Press,2006:45-63.
[11]Holzer S M. Response bounds for columns with transient loads[J].Journal of Applied Mathematics,1971,38(1):157-161. DOI:10.1115/1.3408736.
[12]Chopra A K. Dynamics of structures[M].New Jersey， USA: Prentice Hall,2011:114-119.
[13]Anderson T L, Moody M L. Parametric vibrations of columns[J].Journal of Engineering Mechanics, 1969, 95(3):665-677.
[14]Liu Y Z, Chen L Q. Nonlinear vibrations[M]. Beijing: Higher Education Press, 2001:152-168. (in Chinese)
[15]Wu X G, Zheng B L, He P F, et al. Deflection governing equation of constrained buckling on column[J].Journal of Tongji University, 2011,39(6):798-801. (in Chinese)
[16]Dong G W, Li Z Y, Zhao J Y. Determination of the maximum deflection of long slender compression rod[J].Mechanical Research and Application, 2014,27(1):15-18.(in Chinese)
References：
摘要：为了研究初始缺陷在周期性瞬时荷载作用下对杆件动力稳定性的影响,采用近似求解方法和傅里叶周期稳定解的方法,考虑初始缺陷对杆件的影响,对在周期性瞬时荷载作用下杆件的动力稳定性进行理论分析．同时通过对杆件不同挠度的研究,采用Maple软件得到了杆件的动力不稳定性．理论分析结果表明:初始缺陷越大,杆件的稳定解的振幅越大,不稳定区域越宽,发生参数共振导致失稳的可能性越大．在相同初始缺陷条件下,杆件的阻尼是有效降低杆件发生动力失稳的重要因素．在马奇耶方程基础上,推导了杆件初始缺陷与挠度的具体关系式,得到了在不同初始缺陷下杆件的动力不稳定区域．分析表明,实际工程中减少杆件的初始缺陷能够加强杆件的动力稳定性．
关键词：周期性瞬时荷载;参数振动;初始缺陷;动力稳定性
中图分类号：TU311.3
Foundation item：The National Natural Science Foundation of China (No.51078354).
Citation：：Cai Yong, Xie Jiawei. Stability of columns with original defects under periodic transient loadings[J]．Journal of Southeast University (English Edition),2017,33(1):64-69．
DOI：10.3969/j.issn.1003-7985.2017.01.011.
DOI：10.3969/j.issn.1003-7985.2017.01.011
Received 2016-06-26.
Biography：Cai Yong(1968—),male, doctor, associate professor, caiyong@csu.edu.cn.