Abstract：LetR be an associative ring with unity 1. The existence of the Moore-Penrose inverses of block matrices over R is investigated and the sufficient and necessary conditions for such existence are obtained. Furthermore, the representation of the Moore-Penrose inverse of 
is given under the condition of EBF=0, where E=I-CC† and F=I-A†A. This result generalizes the representation of the Moore-Penrose inverse of the companion matrix 
due to Pedro Patrício. As for applications, some examples are given to illustrate the obtained results.
Key words：companion matrix; Moore-Penrose inverse; ring
Let R be an associative ring with unity 1 and involution *, which is an anti-automorphism of degree 2 in R: (x*)*=x, (x+y)*=x*+y* and (xy)*=y*x*for all x,y∈R.
An element a∈R is said to be regular if there is an element a- of R such that aa-a=a, or equivalently axa=a is a ring consistent equation. In this case, a- is called a {1}-inverse of a. Let Mm×n(R) denote the ring of all m×n matrices over R. We denote Mn×n(R), Mn×1(R) and M1×n(R) by Mn(R), Rn and R(n), respectively. A matrix A is said to be Moore-Penrose invertible with respect to *, if there is A† such that
AA†A=A, A†AA†=A†,(AA†)*=AA†,(A†A)*=A†A
It is well known that the Moore-Penrose inverse is unique if it exists.
The existence and representations of the Moore-Penrose inverse (MP-inverse) of matrices over various settings have been considered by several scholars[1-4]. Recently, Hartwig and Patrício[5] obtained new expressions for the MP-inverse of the matrix 
over a *-regular ring. Zhu et al.[6] investigated the MP-inverse of 
over a *-regular ring satisfying SC2. It is well-known that R is a *-regular ring if and only if all the elements in R are MP-invertible, and that M2(R) is a *-regular ring if and only if R is a regular*-ring satisfying SC2[5]. That is to say, in this case, there is always the MP-inverse of A∈M2(R) over a *-regular ring. In Ref.[7], the conditions for the existence of the MP-inverse of the (n+1)×(n+1) companion matrix in the form 
over an arbitrary ring are considered and the formulae of M† is established. This paper is to present some equivalent conditions concerning the existence of MP-inverse of block matrices over an arbitrary ring. In what follows, we use the symbols R(A)={
x∈Rn} and Rr(A)={
x∈R(n)} to denote the range of A and the row range of A, respectively.
Lemma 1[7] Let a∈R be a regular element, and a- be a regular inverse of a. The following conditions are equivalent:
1) a is Moore-Penrose invertible;
2) u=aa*+1-aa- is a unit. Moreover, (a†)*=u-1a.
Lemma 2 Suppose that A∈Mn(R) and A is regular, then the following are equivalent:
1) A is Moore-Penrose invertible;
2) R(A)=R(AA*) and Rr(A)=Rr(A*A);
3) Matrix equations A=AA*X and YA*A=A have solutions over Mn(R).
Furthermore, if A is Moore-Penrose invertible, then A†=A*XY*(AA-)*, where X, Y are the corresponding solution sets of the matrix equations in 3).
Proof 2)⟺3) It is clear. Thus we only need to prove 1)⟺2).
2)⟹1). By hypothesis, there exist X, Y such that A=AA*X and YA*A=A. Then A=A(A*AY*)X and A=Y(X*AA*)A. This implies that R(A)=R(AA*A) and Rr(A)=Rr(AA*A). Thus, A is Moore-Penrose invertible (see Ref.[8]).
1)⟹2). It is well known that A† exists if and only if R(A)=R(AA*A) and Rr(A)=Rr(AA*A). So we obtain R(A)=R(AA*) and Rr(A)=Rr(A*A).
By Ref.[8], we have that v=AA*+I-AA- is a unit of Mn(R). Also, v-1=AA-(YX*)AA-+I-AA-(YX*)AA*. It is simple to check that A†=A*XY*(AA-)*.
Proposition 1 Suppose that 
such that A,B are regular. Then M is Moore-Penrose invertible if and only if A and B are both Moore-Penrose invertible.
Proof We give the decomposition of M as follows:
(1)
and
(2)
By Ref.[9], it is simple to determine that M is regular. According to Eqs.(1) and (2), it follows that
and
By Lemma 2, M is Moore-Penrose invertible if and only if MM*X=M and YM*M=M are consistent.
.
AA*x2=A
(3)
BB*x4=B
(4)
.
y2A*A=A
(5)
y3B*B=B
(6)
In view of Eqs.(3) to (6), one can see that A,B are MP-invertible if and only if MM*X=M and YM*M=M are consistent, as desired.
In the following, we will characterize the MP-invertibility of 
under the condition of EBF=0, where E=I-CC† and F=I-A†A.
e. If M is Moore-Penrose invertible, then
M†
where
M1=-u-1C†BA†v-1
M2=u-1C†[I-BA†v-1(BA†)*E]
M3=TA†v-1
M4=TA†v-1(BA†)*E+F(C†B)*u-1C†
T=I-F(C†B)*u-1C†B
Proof Note that EBF=0 and M is regular according to Ref.[9]. We give the decomposition of M as follows:
.
From YM*M=M, we have
(7)
So, we obtain
y1C*C=0
(8)
y2[A*A+(BA†A)*EBA†A]=A
(9)
y3C*C=C
(10)
y4[A*A+(BA†A)*EBA†A]=0
(11)
It is clear that Eqs.(8), (10) and (11) are always consistent. Also, y2[A*A+(BA†A)*EBA†A]=A is equivalent to y2A*[I+(BA†)*EBA†]=AA†. Set v=I+(BA†)*EBA†. It is simple to check that vAA†=AA†v. If v is invertible, then Eq.(9) is consistent, and y2=v-1(A†)* is a solution.
Conversely, suppose that Eq.(9) is consistent. From y2A*AA†vAA†=AA† and v*=v, we obtain that R(AA†)=R(AA†vAA†) and Rr(AA†)=Rr(AA†vAA†). By Ref.[8], we find that AA†v+I-AA† is invertible. Note that AA†v+I-AA†=v. Thus, v is invertible.
Similarly, we give the decomposition of M as follows:
(12)
which leads to
(13)
.
From MM*X=M, it follows
(14)
Therefore,
AA*x1=0
(15)
AA*x2=A
(16)
(CC*+BFB*)x3=C
(17)
(CC*+BFB*)x4=0
(18)
It is simple to determine that Eqs.(15), (16) and (18) are consistent by Lemma 1. That implies that M† exists if and only if Eqs.(9) and (17) are both consistent. By EBF=0, we can find that Eq.(17) is equivalent to
[I+C†BF(C†B)*]C*x3=C†C
(19)
Set u=I+C†BF(C†B)*. Thus, C†Cu=uC†C.
If u is invertible, then Eq.(19) is consistent, and x3=(C†)*u-1 is a solution.
Conversely, assume that Eq.(19) is consistent.
From C†CuC†CC*x3=C†C and u*=u, we obtain R(C†C)=R(C†CuC†C) and Rr(C†C)=Rr(C†CuC†C). By Ref.[8], we find that C†Cu+I-C†C is invertible. Note that C†Cu+I-C†C=u. Hence, it follows that u is invertible.
By direct computation, it is simple to find that
and
are the solutions of MM*X=M and YM*M=M. Using Lemma 2, M†=M*XY*(MM-)*. A direct computation yields M†
M1=-u-1C†BA†v-1
M2=u-1C†[I-BA†v-1(BA†)*E]
M3=TA†v-1
M4=TA†v-1(BA†)*E+F(C†B)*u-1C†
T=I-F(C†B)*u-1C†B
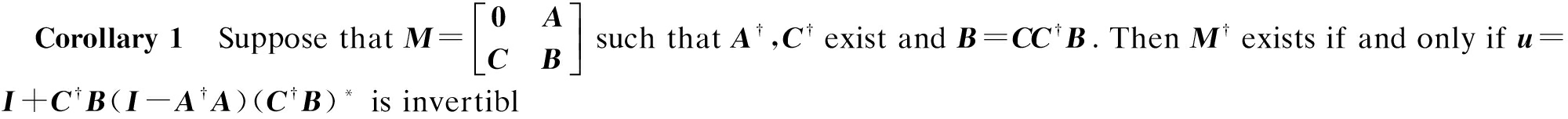e.
If M is Moore-Penrose invertible, then M†, where
M1=-u-1C†BA†, M2=u-1C†, M3=TA†
M4=(I-A†A)(C†B)*u-1C†
T=I-(I-A†A)(C†B)*u-1C†B
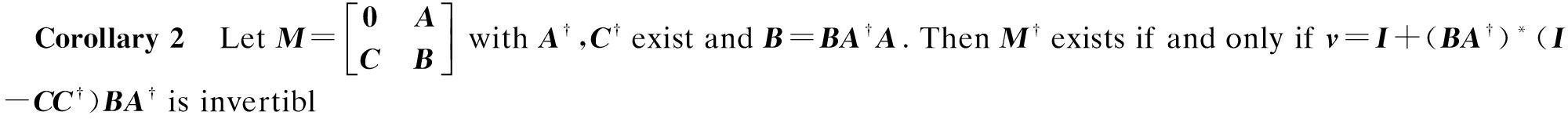e.
If M is Moore-Penrose invertible, then M†
.
Note that I+B*(I-A†A)B is invertible if and only if I+BB*(I-A†A) is also invertible. Then we have the following result which generalizes the relative results of Ref.[7].
Corollary 3 Given a∈R such that a† exists and 
T, then the following are equivalent:
1) The companion matrix is Moore-Penrose invertible.
2) 1+(1-a†a)b*b(1-a†a) is a unit of R.
3) 1+b*b(1-a†a) is a unit of R.
4) 1+(1-a†a)b*b is a unit of R.
Example 1 Suppose that S=Z12 and R is the matrix ring over S with transposition as the involution, and set 
, 
, 
and . By a direct computation, we have C†
.
Example 2 Consider the complex matrix ring R with transposition as the involution, and set , where 
, 
and 
.
r. Then by Lemma 2, C†=C*XY*(CC-)*, then we have C†
s. Using Theorem 1, we can obtain
M†
[1]Cline R E. Representations for the generalized inverse of a partitioned matrix [J]. Journal of the Society for Industrial and Applied Mathematics, 1964, 12(3): 588-600. DOI:10.1137/0112050.
[2]Cline R E. Representations for the generalized inverse of sums of matrices [J]. Journal of the Society for Industrial and Applied Mathematics Series B Numerical Analysis, 1965, 2(1): 99-114. DOI:10.1137/0702008.
[3]Hung C H, Markham T L. The Moore-Penrose inverse of a partitioned matrix 
[J]. Czechoslovak Mathematical Journal, 1975, 25(3):354-361.
[4]Hung C H, Markham T L. The Moore-Penrose inverse of a partitioned matrix 
[J]. Linear Algebra and Its Applications, 1975, 11(1):73-86. DOI:10.1016/0024-3795(75)90118-4.
[5]Hartwig R E,Patrício P. When does the Moore-Penrose inverse flip [J]. Operators and Matrices, 2012, 6(1): 181-192. DOI:10.7153/oam-06-13.
[6]Zhu H H, Chen J L, Zhang X X, et al. The Moore-Penrose inverse of 2×2 matrices over a certain *-regular ring [J]. Applied Mathematics and Computation, 2014, 246: 263-267. DOI:10.1016/j.amc.2014.08.026.
[7]Patrício P. The Moore-Penrose inverse of a companion matrix [J]. Linear Algebra and Its Applications, 2012, 437(3): 870-877. DOI:10.1016/j.laa.2012.03.019.
[8]Patrício P. The regular sum [J]. Linear and Multilinear Algebra, 2014, 63(1): 185-200. DOI:10.1080/03081087.2013.860592.
[9]Patrício P, Puystjens R. About the von Neumann regularity of triangular block matrices [J]. Linear Algebra and Its Applications, 2001, 332-334: 485-502. DOI:10.1016/s0024-3795(01)00295-6.
References：
摘要：假设R是一个有单位元1的结合环．探讨了R上分块矩阵Moore-Penrose逆的存在性,得到了环上分块矩阵的Moore-Penrose逆存在性的充要条件．进而,在EBF=0条件下,其中E=I-CC†和F=I-A†A,给出了Moore-Penrose逆的表达式
此结果推广了Pedro Patrício 关于友矩阵
的Moore-Penrose逆表达式．作为应用,给出一些例子验证了所得到的结果．
关键词：友矩阵;Moore-Penrose 逆; 环
中图分类号：O151.2
Foundation items：The National Natural Science Foundation of China (No.11371089), the Natural Science Foundation of Jiangsu Province (No.BK20141327), Specialized Research Fund for the Doctoral Program of Higher Education (No.20120092110020), the Natural Science Foundation of Jiangsu Higher Education Institutions of China (No.15KJB110021).
Citation：：Wang Long, Chen Jianlong. A note on the Moore-Penrose inverse of a companion matrix[J]．Journal of Southeast University (English Edition),2017,33(1):123-126．
DOI：10.3969/j.issn.1003-7985.2017.01.020.
DOI：10.3969/j.issn.1003-7985.2017.01.020
Received 2014-11-01．
Biographies：Wang Long (1988—), male, graduate; Chen Jianlong (corresponding author), male, doctor, professor, jlchen @seu.edu.cn.