Abstract：Two complementary firms’ information sharing and security investment are investigated. When two complementary firms with heterogeneous assets are both breached, it is assumed that they suffer different losses which are associated with their information assets. Some insights about optimal strategies for the firms and the attacker are obtained by the game theory, which forms a comparison with those derived from substitutable firms, and those derived from complementary firms with homogenous loss. In addition, both the unit transform cost of investment and the extent of firms’ loss affect the optimal strategies. Assuming that firms can control information sharing, security investments and both of them, respectively, the effect of the social planner is further analyzed on the information sharing, firms’ aggregate defence, the aggregate attack and social total cost. Finally, some policy advice is provided through numerical simulation. Results show that firms are willing to choose security investment centrally rather than individually, but an intervention in information sharing by the social planner may not necessarily be preferable.
Key words：complementary firm; contest success function; security investment; information sharing; leakage cost
Facing the increasing incidence of cyber-attacks and security breaches, a considerable number of firms have invested heavily in information security technology and investment strategies to reduce the likelihood of major damages arising from these security events[1-3]. Security investment requires costly funding, planning, sustained effort through time, involving build-up of infrastructure, culture, and competence; while information sharing, such as firm collaboration and sharing security knowledge with other firms[4-5], may be more or less free aside from leakage costs as a consequence of sharing[6]. Therefore, it has been a trend that government and public organizations foster a movement toward sharing information about security events among different organizations and sectors[7-9].
Two firms may operate independently in different markets, or they may be so strongly interconnected. The interdependence between firms has been widely stressed[10-12]. Liu et al.[4] considered information assets to be complementary or substitutable. Information assets are complementary if the combined information assets of two firms are of significant value while the information asset of a single firm is not valued by a hacker. Hence, successful hacking attempts in the first firm leads to penetrated cross traffic toward the other firm. Information assets belonging to two firms are substitutable if the incremental benefit of attacking the second firm (after successfully penetrating the first one) is lower than the effort for a hacker. Hence, a hacker will stop if he has penetrated one of the firms and gained access to the assets.
Liu et al.[4] discussed security decisions about knowledge sharing and security investment for two complementary firms or two substitutable firms. Nevertheless, they did not consider attacker behaviour and the leakage cost of information sharing. Gao et al.[7] made further discussion about security investments and information sharing for complementary firms in consideration of attacker behaviour and leakage cost. Gao et al.[7,13] assumed two complementary firms incurred equal monetary loss when an information breach occurs, and they obtained some results which formed sharp comparisons with those of common (substitutive) firms derived by Hausken[6]. However, two firms with different assets can have heterogeneous monetary loss when an information breach occurs, even though they are complementary. For instance, in a major commercial airplane company, the tail-section design of a new airplane model is outsourced to a vendor firm. A hacker who is interested in obtaining business intelligence about the whole design of the new airplane will have to obtain design information from both the firms. The principal firm with higher assets than vendor in this model will have more monetary loss if the information system of business intelligence is breached successfully[4]. Another example, before the information sharing between Walmart and Proctor & Gamble, they can reach an agreement that the firm leaking the information will be held liable[4]. Therefore, when an information breach occurs, only the breached firm suffers the loss and the other firm is covered by the agreement.
In the paper written by Hausken[14-15], the attacker’s attack depends on the resource constraint and attack efficiency when a substitutable firm’s assets is attacked. Hausken[6] considered that one of two firms retains a fraction of its own assets when he analyzed different firms’ profit. Therefore, we assume that a firm’s loss is equal to its assets when an information system is breached successfully, in order to simplify the expressions of notations and facilitate calculation.
Firm i and firm j invest ti and tj in information security technology to defend their assets, respectively. The security investment expenditure of firm i and firm j are citi and cjtj, respectively, where ci and cj are the inefficiency of security investment for firm i and firm j, or an unit transformation cost of firm i’s and firm j’s security investment, respectively[6]. Firm j shares an amount of sj with firm i means that firm j delivers si to firm i. Hence, the actual security investment that contributes to firm i is ti+γsj, where γ∈(0,1) measures the efficiency of information sharing. Parameter γ describes the similarity and the compatibility between two firms’ information technology environments[4]. For example, γ should be relatively large if both firms use the same kinds of security products, but relatively small if one firm switches to other kinds of security products.
An attacker launches a cyber-security attack of magnitude Ti against firm i and Tj against firm j to appropriate as much as possible of the assets. The cyber-attack expenditure against firm i or firm j is C, and C is the inefficiency of cyber-attacks or an unit transformation cost of cyber-attacks[6]. If two complementary firms have heterogeneous monetary loss ri and rj, when their information systems are both breached successfully, the attacker obtains a benefit of ri+rj. Parameter α (α<1[6]) was introduced to describe the two firms’ relationship in resisting cyber-attacks, because firms are always interdependent. When α is positive, two firms are cooperative in defending themselves. Positive interdependence between firms also means that the attacker’s attack against one firm becomes channeled further to a degree of α to the other firm. When α=0, the firms are 100% independent. This means that one firm’s security investment exclusively defends itself. When α is negative, each firm’s security investment is detrimental to the other firm, and merely strengthens one’s own firm. Therefore, firm i’s aggregate defence and attack’s aggregate attack against firm i are finally given by
(1)
where α is restricted to ensure that both 
, 
are positive and are further restricted when necessary[7].
According to widely used security breach probability function depending on aggregate defence and aggregate attack [7,16-17], the probability that firm i’s information system is breached is as follows:
(2)
Since information sharing is risky for both firms, leakage cost might be inflicted on firm i as a result of such sharing. Therefore, the leakage cost of firm i is[6-7]
(3)
where φ1 is the inefficiency (unit cost) of own leakage;φ2 is the efficiency (unit benefit) of the other firm’s leakage (since one firm benefits from the other firm); φ3 is the efficiency (unit benefit) of joint leakage. Therefore, when the information systems of both firm i and firm j are breached successfully, the expected cost of firm i and firm j, and the attack’s expected benefit is given by
(4)
(5)
(6)
where ti and si are firm i’s decision variables;tj and sj are firm j’s decision variables; and Ti and Tj are the attacker’s decision variables.
Similar to Hausken[6] and Gao et al.[7], firm i’s and firm j’s information sharing in equilibrium strategies are given by the first-order conditions as follows (The equilibrium strategies for firm j can be obtained only by replacing symbol i and j with each other, which are omitted in our subsequent discussion for simplification):
(7)
Proposition 1 One firm’s information sharing decreases/increases with its monetary loss caused by a security breach, when the other firm’s rate of return on security investment is/is not high enough. In order to facilitate analysis, ri/ci and 
/ci (i=1,2) are both defined as the rate of return on security investment. One firm’s information sharing increases/decreases with the other firm’s monetary loss caused by a security investment, when the other firm’s rate of return on security investment is/is not high enough.
).
Proof It follows from φ1≥φ2+φ3, and 2φ1>φ3. The first-order conditions of two firms’ security investment and the attacker’s security investment are given by
(8)
(9)
(10)
q.(8) into Eq.(9) yields
(11)
Solving Eq.(8) gives
(12)
Solving function (10) gives
(13)
Combining Eqs.(12) and (13), we can obtain
(14)
which, together with Eq.(13), yields
(15)
and furthermore,
(16)
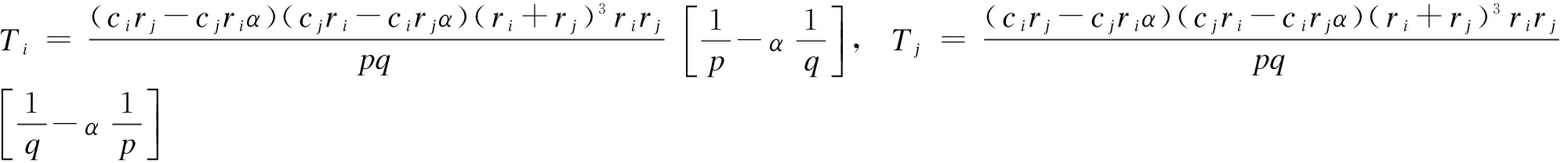
where p=Crirj(1-α)+(cirj-cjriα)(ri+rj), q=Crirj(1-α)+(cjri-cirjα)(ri+rj).
With the increase of firm i’s monetary loss ri, firm i needs to decrease the joint probability of a security breach to maintain its expected cost. Firms’ aggregate defence consists of security investment and information sharing. The joint probability of a security breach decreases regardless of whose (firm i’s or firm j’s) aggregate defence increases.
When firm j’s rate of return on security investment is not high enough, with the increase of firm i’s monetary loss ri, firm i has two kinds of strategies to decrease the joint probability of a security breach. First, firm i can increase its security investment and further increase its aggregate defence. Secondly, firm i can share information with the other firm (firm j) and further increase the other firm’s aggregate defence. That is ∂si/∂ri>0. When firm j’s rate of return on security investment is high enough, compared with firm j, firm i’s information sharing only has less effect on the other firm (firm j). This makes firm i change its information sharing to security investment and further increases its aggregate defence. Thus, firm i’s information sharing decreases with its monetary loss when firm j’s rate of return on security investment is high enough.
Similarly, with the increase of firm j’s monetary loss rj, firm j needs to decrease the joint probability of a security breach to maintain its expected cost. When firm j’s rate of return on security investment is not high enough, firm i prefers to increase its own security investment and further increases its own aggregate defence to decrease the joint probability of a security breach. Nevertheless, when firm j’s rate of return on security investment is high enough, firm i prefers to share information with firm j to help firm j increase firm j’s aggregate defence. However, both Hausken[6] and Gao et al.[7] showed that firms’ information sharing is independent of the monetary loss caused by a security breach. Gao et al.[13] showed that information sharing never depends on each firm’s inherent vulnerability.
Next, we study the impact of the firm’s monetary loss on the firm’s aggregate defence and attacker’s aggregate attack. When α→0, there are
(17)
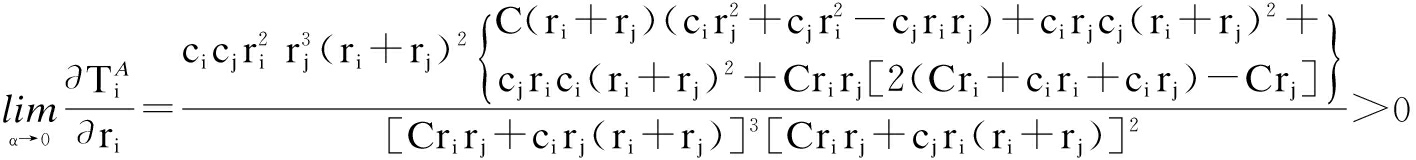
(18)
(19)
(20)
where p=Crirj(1-α)+(cirj-cjriα)(ri+rj), q=Crirj(1-α)+(cjri-cirjα)(ri+rj).
/∂rj is influenced by the firms’ monetary loss and their unit transform cost, so it is unfixed. Particularly, 
/∂rj>0 when two firms have the same monetary loss and unit transform cost.
Proposition 2 1) One firm’s aggregate defence and attacker’s aggregate attack against this firm both increase with the increase of the firm’s monetary loss. That is 
/∂ri>0, /∂ri>0. 2) Firm i’s aggregate defence decreases with firm j’s monetary loss. The attacker’s aggregate attack against firm i increases with firm j’s monetary loss when two firms have the same monetary loss and unit transform cost. That is 
/∂rj<0, and 
/∂rj>0 when cj=ci and ri=rj.
It is straightforward to understand that the attacker will increase its aggregate attack against firm i with the increase of firm i’s monetary loss. This is because, with the increase of firm i’s monetary loss, the attacker can obtain more benefits after a successful breach. Firm i will increase its aggregate defence, and further decreases the joint security breach probability. Hausken[6] obtained a similar result for one firm in the case of substitutive firms. However, Gao et al.[7] showed that one firm’s aggregate defence and the attack’s aggregate attack against this firm both increase with the sum of both firms’ monetary loss. Gao et al.[13] showed that one firm’s aggregate defence increases with the firm’s monetary loss, but the attacker’s aggregate attack decreases with it.
According to the above analysis, firm j needs to increase its aggregate defence with the increase of its monetary loss. For two complementary firms, each firm’s expected cost is closely related to the joint security breach probability. Therefore, in order to help firm j increase its aggregate defence, firm i will increase its information sharing by decreasing its aggregate defence. According to the above analysis, the attacker increases its aggregate attack against firm j with the increase of firm j’s monetary loss. In addition, the attacker can obtain benefit if and only if two complementary firms are breached successfully. Thus, the attacker needs to increase its aggregate attack against firm i at the same time. However, Gao et al.[7] showed that firm i’s aggregate defence and the attacker’s aggregate attack against firm i only increase with the sum of both firms’ monetary loss. Hausken[6] showed that firm i’s aggregate defence and the attacker’s aggregate attack against firm i are both independent of the monetary loss caused by a security breach against firm j.
Similar to Ref.[6], welfare analysis is needed to show whether a social planner should be allowed to control information sharing and security investment, and how regulation at the level of sharing and investment affects social welfare. Naturally, a social planner minimizes the following social total cost：
(21)
Assume that a social planner can specify two firm’s security investment, information sharing and both of them, respectively. There are four cases regarding firm i’s information sharing, aggregate defence and aggregate attack at equilibrium.
Case 1 Neither information sharing nor security investment is controlled centrally.
Case 2 Only information sharing is controlled centrally.
Case 3 Only security investment is controlled centrally.
Case 4 Both information sharing and security investment are controlled centrally.
Therefore,
and
The difference between this paper and Gao et al.’s[7] is only the firm’s monetary loss is caused by a security breach, so, we assume ci=cj=f to facilitate our calculation. In the above four equilibrium security decisions, the social total cost is calculated separately.
When firms make decisions individually, the social total cost is
When social planners only choose information sharing centrally, the social total cost is
·
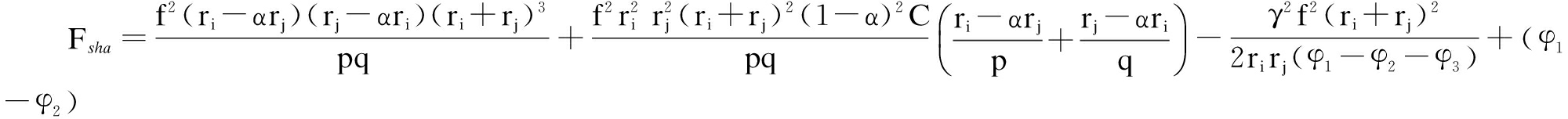where p=Crirj(1-α)+f(rj-αri)(ri+rj), q=Crirj(1-α)+f(ri-αrj)(ri+rj).
·
).
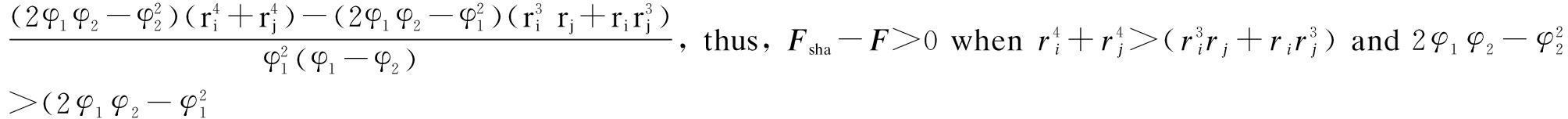Similar to the above, when φ1-φ2≥φ3, there is
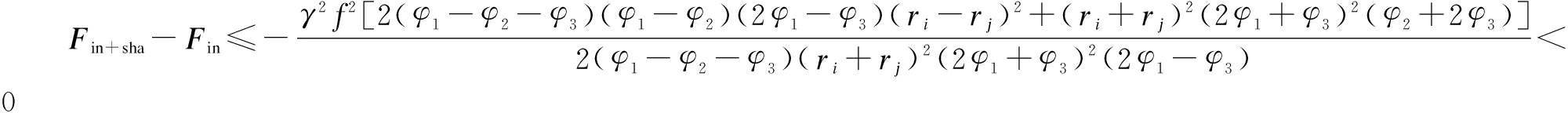
Proposition 3 1) Compared to the case when information sharing is controlled individually, the firm’s information sharing is higher when information sharing is controlled centrally by social planners, but a firm’s aggregate defence and its aggregate attack are equal. That is sish>si,sish+in>siin; 
, 
; 
, 
. 2) Compared to the case when firms control security investment individually, a firm’s information sharing is lower when information sharing is controlled centrally by social planners. That is si>siin, sish>sish+in. 3) Given that both firms control security investment individually, when social planners control information sharing centrally, the social total cost is higher than that when both firms choose their information sharing individually. Given that social planners control security investment centrally, when social planners control information sharing centrally, the social total cost is lower than that when both firms choose information individually. That is Fsha>F, Fin+sha<Fin.
Given that both firms choose security investment individually, each firm’s strategies to make the optimal investment is based on its own condition. Thus, in this condition, when the social planner controls information sharing centrally, the social total cost is higher than that when firms control information sharing individually, which is caused by the information asymmetry and the incoordination of strategies between the firms and social planners. However, when the social planner controls both security investment and information sharing centrally, security investment and information sharing can complement each other because there is neither incoordination nor information asymmetry. Therefore, when the social planner control both security investment and information sharing centrally, the total social cost is lower than that when only the social planner controls security investment centrally.
Let α=0.2. ci=cj=C=0.3, γ=0.8, φ1=1.5, φ2=0.8, φ3=0.1, rj=2, and ri increases (0.5 once) from 2 to 5. The effect of the firm’s monetary loss on firms’ optimal strategies is analyzed by calculating the social total cost in all above four cases. Then, the social total cost changes with the increase of firm i’s monetary loss in four equilibrium strategies, respectively, as shown in Fig.1.
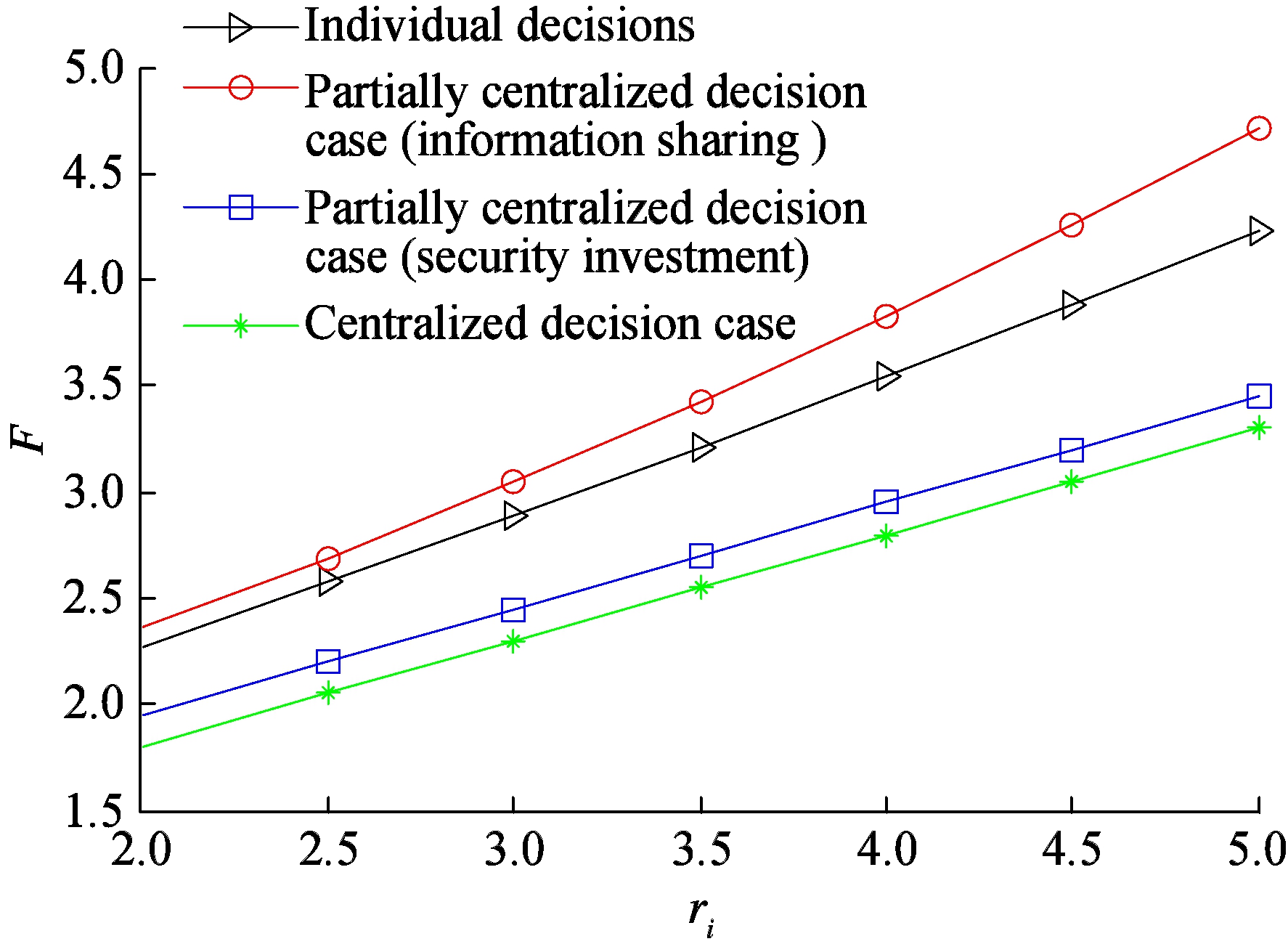
Fig.1 Social total cost in four equilibrium strategies respectively (rj=2)
The social total cost in Proposition 3 is shown in Fig.1, which is consistent with those for substitutive firms[6,13] and those for complementary firms with equal monetary loss[7]. Besides, when firms choose security investment individually, with the increase of the difference between two firms’ monetary loss, the decision that firms control information sharing centrally will have more impact on the social total cost, and the impact remains unchanged when firms control security investment centrally. In addition, according to Fig.1, when social planners control security investment centrally, the social total cost which is negatively related with social welfare is lower than that when both firms make security investment individually, no matter whether information sharing is controlled individually or centrally. According to the above analysis, some policy advice is given as follows:
1) Firms are willing to choose security investment centrally rather than individually, whether information sharing is controlled centrally or not.
2) When the social planner does not control firms’ security investment, the firms are willing to choose information sharing individually rather than centrally. Nevertheless, when social planners control the security investment centrally, the firms will like to choose information sharing centrally rather than individually.
3) The social planner has two choices in making their decision to increase social welfare. The first choice is to control both firms’ security investment and firms’ information sharing centrally, and the second choice is to control neither firms’ security investment nor firms’ information sharing centrally.
The security investments, information sharing and cyber-attacks are discussed using complementary firms with heterogeneous monetary loss caused by a successful breach. Many propositions obtained by Hausken et al.[6-7] has changed, when complementary firms suffer heterogeneous monetary loss. Besides, the influence of the gap between two firms’ monetary loss is analyzed by using social total cost and firms’ decisions, and then some policy advice is given. Some interesting research directions are worth further investigating. First, one can validate the results of this paper by allowing the value of an information asset to be different for the hacker and for the two firms. Secondly, it may be interesting to extend our results when considering a hacker’s information sharing. Thirdly, one can consider security problems that introduce some evolutionary learning dynamics for information sharing and security investment.
[1]Cavusoglu H, Raghunathan S, Cavusoglu H. Configuration of and interaction between information security technologies: The case of firewalls and intrusion detection systems [J]. Information Systems Research, 2009, 20(2): 198-217. DOI:10.1287/isre.1080.0180.
[2]Gao X, Zhong W J, Mei S E. A game-theory approach to configuration of detection software with decision errors [J]. Reliability Engineering & System Safety, 2013, 119: 35-43. DOI:10.1016/j.ress.2013.05.004.
[3]Gao X, Zhong W J. Information security investment for competitive firms with hacker behaviour and security requirements [J]. Annals of Operations Research, 2015, 235(1):277-300. DOI:10.1007/s10479-015-1925-2.
[4]Liu D, Ji Y, Mookerjee V. Knowledge sharing and investment decisions in information security [J]. Decision Support Systems, 2011, 52(1): 95-107. DOI:10.1016/j.dss.2011.05.007.
[5]Liu Z, Tian X, Shi Q. Governance mechanisms of knowledge sharing in network virtual community [J]. Chinese Journal of Management, 2015, 12(9): 1394-1401. (in Chinese)
[6]Hausken K. Information sharing among firms and cyber attacks [J]. Journal of Accounting and Public Policy, 2007, 26(6): 639-688. DOI:10.1016/j.jaccpubpol.2007.10.001.
[7]Gao X, Zhong W J, Mei S E. A game-theoretic analysis of information sharing and security investment for complementary firms [J]. Journal of the Operational Research Society, 2013, 65(11):1682-1691. DOI:10.1057/jors.2013.133.
[8]Gordon L A, Loeb M P, Lucyshyn W, et al. The impact of information sharing on cyber security under investment: A real options perspective [J]. Journal of Accounting and Public Policy, 2015, 34(5):509-519. DOI:10.1016/j.jaccpubpol.2015.05.001.
[9]Gao X, Zhong W. A differential game approach to security investment and information sharing in a competitive environment [J]. IIE Transactions, 2016, 48(6): 511-526. DOI:10.1080/0740817x.2015.1125044.
[10]Büyükkarabacak B, Valev N. Credit information sharing and banking crises:An empirical investigation [J]. Journal of Macroeconomics, 2012, 34(3):788-800. DOI:10.1016/j.jmacro.2012.03.002.
[11]Sayogo D S, Pardo T A, Bloniarz P. Information flows and smart disclosure of financial data: A framework for identifying challenges of cross boundary information sharing [J]. Government Information Quarterly, 2014, 31: S72-S83. DOI:10.1016/j.giq.2013.12.004.
[12]Gao P, Nie J, Xie Z. Strategies of information sharing in supply chain with remanufacturing considering the existence of green consumers [J]. Journal of Industrial Engineering/Engineering Management. 2014, 28(4):193-200. (in Chinese)
[13]Gao X, Zhong W, Mei S. Security investment and information sharing under an alternative security breach probability function [J]. Information Systems Frontiers, 2015, 17(2):423-438. DOI:10.1007/s10796-013-9411-3.
[14]Hausken K. Strategic defense and attack of complex networks [J]. International Journal of Performability Engineering, 2009, 5(1): 13-30.
[15]Hausken K. Income, interdependence, and substitution effects affecting incentives for security investment [J]. Journal of Accounting and Public Policy, 2006, 25(6): 629-665. DOI:10.1016/j.jaccpubpol.2006.09.001.
[16]Hausken K.Whether to attack a terrorist’s resource stock today or tomorrow [J]. Games and Economic Behavior, 2008, 64(2): 548-564. DOI:10.1016/j.geb.2008.02.001.
[17]Hausken K, Zhuang J. Defending against a stockpiling terrorist [J]. The Engineering Economist, 2011, 56(4): 321-353. DOI:10.5711/1082598316121.
References：
摘要：调查了互补型企业的信息分享和安全投资问题.当具有资产差异性的2个互补型企业都被攻击时，假设这2个企业都产生不同的损失，且损失程度与企业信息资产相关联.通过博弈分析获得具有资产差异性的互补型企业和攻击者的最优决策.该最优决策与替代型企业和损失无差异的互补型企业情况下的最优决策形成鲜明对比.此外，投资的单位转换成本和企业损失程度都影响其最优决策.假设企业能分别控制信息分享、安全投资和同时控制两者，进一步分析了社会工作者在信息分享、企业总防御、黑客总攻击和社会总成本中的作用.最后，通过数值仿真给出了相关的策略建议.结果显示：虽然企业更倾向于社会工作者集中进行安全投资，但是社会工作者对信息分享的干预并不一定有利.
关键词：互补型企业;成功函数;安全投资;信息分享;泄露成本
中图分类号：C931
Received：2016-12-19．
Foundation item：The National Natural Science Foundation of China (No.71371050).
Citation：：Cai Chuanxi, Mei Shu’e, Zhong Weijun．Security investment and information sharing for complementary firms with heterogeneous monetary loss[J]．Journal of Southeast University (English Edition),2017,33(2):241-248．
DOI：10.3969/j.issn.1003-7985.2017.02.019.
DOI：10.3969/j.issn.1003-7985.2017.02.019
Biographies：Cai Chuanxi (1985—), male, graduate; Mei Shu’e (corresponding author), female, doctor, professor, meishue@seu.edu.cn.