Some additive results for the generalized Drazin inverse in a Banach algebra
Guo Li1,2 Chen Jianlong1 Zou Honglin1
(1School of Mathematics, Southeast University, Nanjing 211189, China)(2School of Mathematics and Statistics, Beihua University, Jilin 132013, China)
Abstract:Leta,bbe two generalized Drazin invertible elements in a Banach algebra. An explicit expression for the generalized Drazin inverse of the suma+bin terms ofa,b,ad,bdis given. The generalized Drazin inverse for the sum of two elements in a Banach algebra is studied by means of the system of idempotents. It is first proved thata+b∈Aqnilunder the condition thata,b∈Aqnil,aba=0 andab2=0 and then the explicit expressions for the generalized Drazin inverse of the suma+bunder some new conditions are given. Also, some known results are extended.
Keywords:generalized Drazin inverse; Banach algebra; nilpotent element; quasi-nilpotent element
Biography:Guo Li (1980—), female, doctor, associate professor, guomingli95@163.com.
Throughout this paper,Adenotes a unital Banach algebra with 1. Fora∈A, we useσ(a) to denote the spectrum ofa. An elementa∈Ais called quasi-nilpotent if the spectrumσ(a)={0}. LetA-1,AnilandAqnildenote the sets of all invertible, nilpotent and quasi-nilpotent elements inA, respectively. The Drazin inverse[1]of an elementa∈Ais the elementx∈A, which satisfies the following three equations:
ax=xa,xax=x,a-a2x∈Anil
The Drazin inverse ofa∈Ais denoted byaDif it exists and it is unique. The concept of the generalized Drazin inverse in a Banach algebra was introduced by Koliha[2]. An idempotent elementp∈Ais a spectral idempotent ofa∈Aifap=pa∈Aqnilanda+p∈A-1. The elementpabove is unique if it exists and it is denoted asaπ. Ifaπexists, the generalized Drazin inverse of an elementa∈Ais defined asad=(a+aπ)-1(1-aπ)=(1-aπ)(a+aπ)-1. LetAddenote the set of all generalized Drazin inverse elements inA. It is obvious thataπ=1-aad. From the definition, the generalized Drazin inverse ofa∈Ais also characterized as the unique elementx∈Asatisfying
ax=xa,xax=x,a-a2x∈Aqnil
The Drazin inverse is first studied by Drazin[1]in associative rings and semigroups. The generalized Drazin inverse is investigated for rings by Hartwig[3]and for Banach algebras by Koliha[2]. The Drazin inverse and the generalized Drazin inverses and their applications are very important in various applied mathematical fields such as singular differential equations, singular difference equations, Markov chains, iterative methods and so on[4-6].
In 1958, Drazin[1]first studied the representation for the Drazin inverse of the sum of two Drazin invertible elements in a ring and proved that (a+b)D=aD+bDunder the conditionab=ba=0. Later, Koliha[2]gave the representations of (a+b)dunder the same condition in a Banach algebra. In 2001, Hartwig et al.[7]gave the formula (P+Q)Dunder the conditionPQ=0. Cvetkovi -Ili
-Ili et al.[8]generalized the result of Ref.[7] to bounded linear operators in an arbitrary complex Banach space. In 2004, Gonz
et al.[8]generalized the result of Ref.[7] to bounded linear operators in an arbitrary complex Banach space. In 2004, Gonz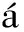 lez and Koliha[9]gave the formula for (a+b)dunder the conditionsabπ=a,aπb=bandbπabaπ=0 which are weaker thanab=0 in Banach algebras. In 2010, Deng and Wei[10]derived a result under the conditionPQ=QP, whereP,Qare bounded linear operators. In 2011, Cvetkovi
lez and Koliha[9]gave the formula for (a+b)dunder the conditionsabπ=a,aπb=bandbπabaπ=0 which are weaker thanab=0 in Banach algebras. In 2010, Deng and Wei[10]derived a result under the conditionPQ=QP, whereP,Qare bounded linear operators. In 2011, Cvetkovi -Ili
-Ili et al.[11]extended the result of Ref.[10] to Banach algebras. Liu et al.[12]deduced the explicit expressions for (a+b)Dunder the conditionsa2b=abaandb2a=bab, whereaandbare complex matrices. Recently, Zou et al.[13]studied the corresponding results for the generalized Drazin inverse in Banach algebra. More results on the generalized Drazin inverse can be found in Refs.[14-15]. In this paper, we first prove thata+b∈Aqnilunder the condition thata,b∈Aqnil,aba=0 andab2=0. Then, we introduce some new conditions and give the explicit expressions for the generalized Drazin inverse of the suma+b, wherea,bare generalized Drazin invertibles inA. As corollaries, many results in Refs.[7-9,14] are generalized.
et al.[11]extended the result of Ref.[10] to Banach algebras. Liu et al.[12]deduced the explicit expressions for (a+b)Dunder the conditionsa2b=abaandb2a=bab, whereaandbare complex matrices. Recently, Zou et al.[13]studied the corresponding results for the generalized Drazin inverse in Banach algebra. More results on the generalized Drazin inverse can be found in Refs.[14-15]. In this paper, we first prove thata+b∈Aqnilunder the condition thata,b∈Aqnil,aba=0 andab2=0. Then, we introduce some new conditions and give the explicit expressions for the generalized Drazin inverse of the suma+b, wherea,bare generalized Drazin invertibles inA. As corollaries, many results in Refs.[7-9,14] are generalized.
LetP=(p1,p2,…,pn) be a total system of idempotents inAifpipj=δi,jpifori,j=1,2,…,nand pi=1. Given a total systemPof idempotents inA, we consider the setMn(A,P)⊂Mn(A) consisting of all matricesM=[
pi=1. Given a total systemPof idempotents inA, we consider the setMn(A,P)⊂Mn(A) consisting of all matricesM=[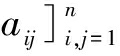 with elements inAsuch thataij∈piApjfor alli,j∈{1,2,…,n}. Following Ref.[9], we know thatMn(A,P) is a unital Banach algebra with unit. Also, it is proved thatφ:A→Mn(A,P) given by
with elements inAsuch thataij∈piApjfor alli,j∈{1,2,…,n}. Following Ref.[9], we know thatMn(A,P) is a unital Banach algebra with unit. Also, it is proved thatφ:A→Mn(A,P) given by
φ
is an isometric Banach algebra isomorphism.
Ifa∈Ais a generalized Drazin invertible, letp=aadand the total system isP=(p, 1-p). Then, we have the following matrix representations:
wherea11∈(pAp)-1anda22∈((1-p)A(1-p))qnil.
1 Preliminary
Lemma1[9] Letp2=p,x,y∈Aand letx=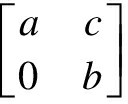 ,y=
,y=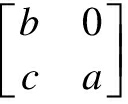 relative to a total system of idempotents (p, 1-p) forxand (1-p,p) fory.
relative to a total system of idempotents (p, 1-p) forxand (1-p,p) fory.
1) Ifa∈(pAp)dandb∈((1-p)A(1-p))d, thenx,y∈Adand
(1)
whereu=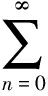 (ad)n+2cbnbπ+
(ad)n+2cbnbπ+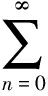 aπanc(bd)n+2-adcbd.
aπanc(bd)n+2-adcbd.
2) Ifx∈Ad[resp.y∈Ad] anda∈(pAp)d, thenb∈((1-p)A(1-p))d,xd[resp.yd] is given by Eq.(1).
Lemma2[9] Leta,b∈Aqnil. Ifab=0, thena+b∈Aqnil.
Lemma3[9] Leta,b∈Adandab=0, thena+b∈Adand
Lemma4[13] Leta,b∈Adsuch thata2b=abaandb2a=bab, then the following conditions are equivalent:
a+b∈Ad, 1+adb∈Ad,c=aad(a+b)bbd∈Ad
In this case, we have
(a+b)d=ad(1+adb)+aπb(ad)2((1+adb)d)2+
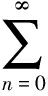 (bd)n+1(-a)naπ+
(bd)n+1(-a)naπ+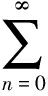 (n+1)bπa(bd)n+2(-a)naπ
(n+1)bπa(bd)n+2(-a)naπ
2 Main Results
In this section, fora,b∈Ad, we will investigate some formulae of (a+b)din terms ofa,b,adandbd. Before proving our main results, we need to prove the following result.
Lemma5 Leta,b∈Aqnil. Ifaba=0,ab2=0, thena+b∈Aqnil.
Proof Froma,b∈Aqnil, it follows thata2,b2∈Aqnil. The conditionaba=0 implies thatab,ba∈Anil⊂Aqnil. Sinceba∈Aqnil,b2∈Aqnilandbab2=0, we haveba+b2∈Aqnilby Lemma 2. Similarly, we can obtaina2+ab∈Aqnil. Also, note that (a+b)2=a2+ab+ba+b2=(a2+ab)+(ba+b2) and (a2+ab)(ba+b2)=a2ba+a2b2+ab2a+ab3=0, we deduce that (a+b)2=(a2+ab)+(ba+b2)∈Aqnilby Lemma 2 again, which yieldsa+b∈Aqnil.
Next we start with an important special case for our main theorem.
Theorem1 Leta∈Aqnil,b∈Ad. Ifabπ=a,bπaba=0 andbπab2=0, thena+b∈Adand
(2)
Proof First, assume thatb∈Aqnil, thenbπ=1,aba=0 andab2=0. By Lemma 5,a+b∈Aqnil. Eq.(2) holds as (a+b)d=0. Ifb∉Aqnil, thenp:=bbd≠0. We use a matrix representation relative to the total systemP=(p, 1-p)=(bbd,bπ) of idempotents, wherep≠0. We haveb=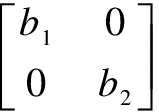 anda=
anda= , whereb1∈(pAp)-1,b2∈((1-p)A(1-p))qnil. Expressing the conditionabπ=ain a matrix form, we prove thata11=0 anda21=0. For the sake of simplicity, we writea1:=a12anda2:=a22. Then we havea+b=
, whereb1∈(pAp)-1,b2∈((1-p)A(1-p))qnil. Expressing the conditionabπ=ain a matrix form, we prove thata11=0 anda21=0. For the sake of simplicity, we writea1:=a12anda2:=a22. Then we havea+b=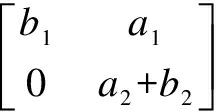 . Similarly, if we express the conditionbπaba=0 andbπab2=0 in a matrix form, we can prove thata2b2a2=0 anda2
. Similarly, if we express the conditionbπaba=0 andbπab2=0 in a matrix form, we can prove thata2b2a2=0 anda2 =0. Sincea∈Aqnil, thena2∈((1-p)A(1-p))qnil. By Lemma 5,a2+b2∈((1-p)A(1-p))qnil. Using Lemma 1, we can obtain thata+b∈Adand
=0. Sincea∈Aqnil, thena2∈((1-p)A(1-p))qnil. By Lemma 5,a2+b2∈((1-p)A(1-p))qnil. Using Lemma 1, we can obtain thata+b∈Adand
whereu=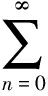 (
(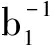 )n+2a1(a2+b2)n. Computing the right side of Eq.(2) in the matrix form, we can prove that Eq.(2) holds.
)n+2a1(a2+b2)n. Computing the right side of Eq.(2) in the matrix form, we can prove that Eq.(2) holds.
Corollary1[9] Leta∈Aqnil,b∈Ad. Ifabπ=aandbπab=0, thena+b∈Adand
Example1 LetAbe the algebra of all complex 3×3 matrices, and leta=b= . Then we can check thataandbsatisfya∈Aqnil,abπ=a,bπaba=0 andbπab2=0, butbπab≠0.
. Then we can check thataandbsatisfya∈Aqnil,abπ=a,bπaba=0 andbπab2=0, butbπab≠0.
Next, we present our main theorem, which is a generalization of Theorem 3.5 in Ref.[9].
Theorem2 Leta,b∈Ad. Ifabπ=a,aπb=b,bπabaaπ=0 andbπab2aπ=0, thena+b∈Adand
(a+b)d=bdaπ+bπad+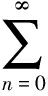 (bd)n+2a(a+b)naπ+
(bd)n+2a(a+b)naπ+
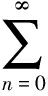 bπ(a+b)nb(ad)n+2-
bπ(a+b)nb(ad)n+2-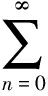 (bd)n+2a(a+b)nbad-
(bd)n+2a(a+b)nbad-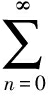 bda(a+b)nb(ad)n+2-
bda(a+b)nb(ad)n+2-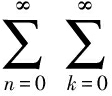 (bd)k+2a(a+b)n+k+1b(ad)n+2
(bd)k+2a(a+b)n+k+1b(ad)n+2
(3)
Proof Ifa∈Aqnil, then the conditions satisfy Theorem 1. By Theorem 1, Eq.(3) holds. Ifa∈A-1, thenb=aπb=0=bd, andbπ=1. Obviously, Eq.(3) holds. Thus, we assume thatais neither quasinilpotent nor invertible, and use the matrix representation of elements relative to the total systemP=(p, 1-p)=(aad,aπ) of idempotents, wherep≠0. We havea= andb=
andb=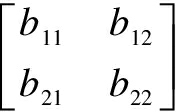 , wherea1∈(pAp)-1,a2∈((1-p)A(1-p))qnil. Sinceaπb=b, we obtain thatb11=0,b12=0. Writeb1:=b21,b2:=b22. Using Lemma 1, we have
, wherea1∈(pAp)-1,a2∈((1-p)A(1-p))qnil. Sinceaπb=b, we obtain thatb11=0,b12=0. Writeb1:=b21,b2:=b22. Using Lemma 1, we have
Sinceabπ=a, we havea2 b1=0 anda2
b1=0 anda2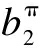 =a2. The conditionsbπabaaπ=0 andbπab2aπ=0 give that
=a2. The conditionsbπabaaπ=0 andbπab2aπ=0 give that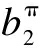 a2b2a2=0 and
a2b2a2=0 and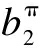 a2
a2 =0. Sincea2∈((1-p)A(1-p))qnil,a2
=0. Sincea2∈((1-p)A(1-p))qnil,a2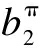 =a2,
=a2,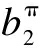 a2b2a2=0 and
a2b2a2=0 and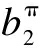 a2
a2 =0, applying Theorem 1 to the elementsa2,b2, we conclude thata2+b2∈((1-p)A(1-p))dand
=0, applying Theorem 1 to the elementsa2,b2, we conclude thata2+b2∈((1-p)A(1-p))dand
By Lemma 1, we have
wherew=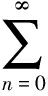 (a2+b2)π(a2+b2)nb1(
(a2+b2)π(a2+b2)nb1(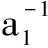 )n+2-(a2+b2)db1
)n+2-(a2+b2)db1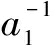 . Sincea2
. Sincea2 =0, we have
=0, we have
(a2+b2)π=1-(a2+b2)(a2+b2)d=1-(a2+b2)·
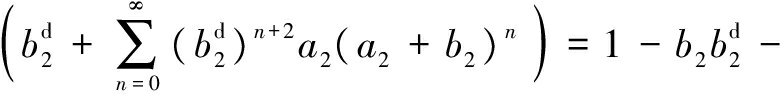
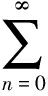 (
( )n+1a2(a2+b2)n=
)n+1a2(a2+b2)n= -
-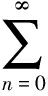 (
( )n+1a2(a2+b2)n
)n+1a2(a2+b2)n
And then
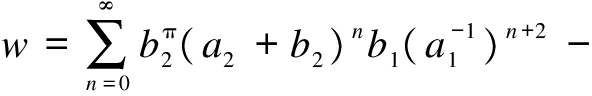
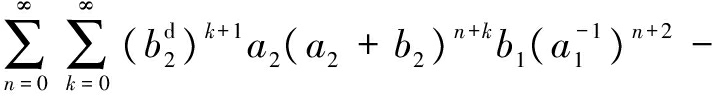

Computing the right side of Eq.(3) in the matrix form, we can prove that Eq.(3) holds.
Corollary2[9] Leta,b∈Ad. Ifabπ=a,aπb=b,bπabaπ=0, thena+b∈Adand
(a+b)d=bdaπ+bπad+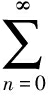 (bd)n+2a(a+b)naπ+
(bd)n+2a(a+b)naπ+
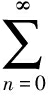 bπ(a+b)nb(ad)n+2-
bπ(a+b)nb(ad)n+2-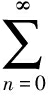 (bd)n+2a(a+b)nbad-
(bd)n+2a(a+b)nbad-
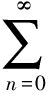 bda(a+b)nb(ad)n+2-
bda(a+b)nb(ad)n+2- (bd)k+2a(a+b)n+k+1b(ad)n+2
(bd)k+2a(a+b)n+k+1b(ad)n+2
Proof It is clear thatbπabaaπ=0 andbπab2=0 byaπb=bandbπabaπ=0. Then, we can complete the proof by Theorem 2.
Now, we will give another main result which generalizes Theorem 2.1 in Ref.[14].
Theorem3 Leta,b∈Ad. Ifbaπ=b,aπbπaba=0,aπbπab2=0 andaπbbdabbd=0, thena+b∈Adand
(a+b)d=ad+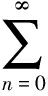 (ad)n+2b(a+b)n(a+b)π+
(ad)n+2b(a+b)n(a+b)π+
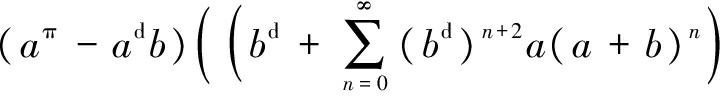
(4)
Proof First, assume thata∈Aqnil, thenaπ=1, and the condition givesbπaba=0,bπab2=0 andbbdabbd=0. Sincebπab2=0, thenab2=bbdab2. So, we haveabbd=bbdabbd. Then,abπ=a. By Theorem 1, (a+b)d=bd+ (bd)n+2a(a+b)n. Then, Eq.(4) holds. Ifa∈A-1, thenaπ=0 andb=baπ=0. Clearly, Eq.(4) holds. Thus, we assume thatais neither quasinilpotent nor invertible. We use a matrix representation relative to the total systemP=(p, 1-p)=(aad,aπ) of idempotents, wherep≠0. We have
(bd)n+2a(a+b)n. Then, Eq.(4) holds. Ifa∈A-1, thenaπ=0 andb=baπ=0. Clearly, Eq.(4) holds. Thus, we assume thatais neither quasinilpotent nor invertible. We use a matrix representation relative to the total systemP=(p, 1-p)=(aad,aπ) of idempotents, wherep≠0. We have
wherea1∈(pAp)-1,a2∈((1-p)A(1-p))qnil. Expressing the conditionbaπ=bin a matrix form, we prove thatb11=0 andb21=0. For the sake of simplicity, we writeb1:=b12andb2:=b22. Then, we have
By Lemma 1,bd= andbπ=
andbπ=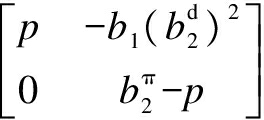 . The conditionsaπbπaba=0 andaπbπab2=0 give that
. The conditionsaπbπaba=0 andaπbπab2=0 give that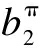 a2b2a2=0 and
a2b2a2=0 and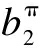 a2
a2 =0. Expressing the conditionaπbbdabbd=0 in a matrix form, we obtain thatb2
=0. Expressing the conditionaπbbdabbd=0 in a matrix form, we obtain thatb2 a2b2
a2b2 =0. Since
=0. Since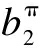 a2
a2 =0, then
=0, then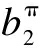 a2
a2 =0. So we havea2
=0. So we havea2 =b2
=b2 a2
a2 . So,b2
. So,b2 a2b2
a2b2 =0 implies thata2
=0 implies thata2 =0. Thus, the following conditionsb2∈Ad,a2∈Aqnil,a2
=0. Thus, the following conditionsb2∈Ad,a2∈Aqnil,a2 =0,
=0,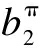 a2b2a2=0,
a2b2a2=0,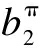 a2
a2 =0 are satisfied. Hence, we can apply Theorem 1 to obtain an expression of (a2+b2)d.
=0 are satisfied. Hence, we can apply Theorem 1 to obtain an expression of (a2+b2)d.
By Lemma 1, we prove that
wherev=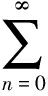 (
(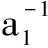 )n+2b1(a2+b2)n(a2+b2)π-
)n+2b1(a2+b2)n(a2+b2)π- (a2+b2)d.
(a2+b2)d.
Computing the right side of Eq.(4) in the matrix form, we can prove that Eq.(4) holds.
Example2 LetAbe the algebra of all complex 3×3 matrices, and takea=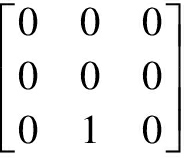 andb=
andb=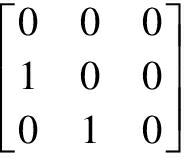 . Clearly,baπ=b,aπbπaba=0,aπbπab2=0 andaπbbdabbd=0, butaπbπab≠0.
. Clearly,baπ=b,aπbπaba=0,aπbπab2=0 andaπbbdabbd=0, butaπbπab≠0.
Remark1 We define sumSn(a,b)=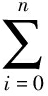 bian-i+
bian-i+ bn-i-1aibforn≥0. If the lower limit of a sum is greater than its upper limit, we always set the sum to be 0. Whenaba=0 andab2=0, we can prove thatSn(a,b)=(a+b)n. It can be proved that the (a+b)nin Theorem 1 to Theorem 3 can be replaced bySn(a,b).
bn-i-1aibforn≥0. If the lower limit of a sum is greater than its upper limit, we always set the sum to be 0. Whenaba=0 andab2=0, we can prove thatSn(a,b)=(a+b)n. It can be proved that the (a+b)nin Theorem 1 to Theorem 3 can be replaced bySn(a,b).
Finally, we will give another main result.
Theorem4 Leta,b∈Ad. Ifabπ=a,bπa2b=bπabaandbπb2a=bπbab, thena+b∈Adand

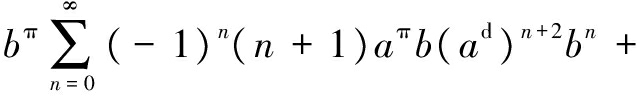

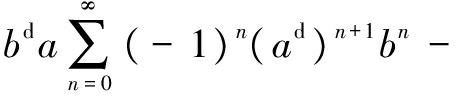
(5)
Proof First, assume thatb∈Aqnil, thenbπ=1, and the conditionsbπa2b=bπabaandbπb2a=bπbabgive thata2b=abaandb2a=bab. By Lemma 4, (a+b)d=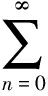 (-1)n(ad)n+1bn+
(-1)n(ad)n+1bn+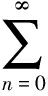 (-1)n(n+1)aπb(ad)n+2bn. Eq.(5) holds. Ifb∉Aqnil, we use a matrix representation relative to the total systemP=(p, 1-p)=(bbd,bπ) of idempotents, wherep≠0. We have
(-1)n(n+1)aπb(ad)n+2bn. Eq.(5) holds. Ifb∉Aqnil, we use a matrix representation relative to the total systemP=(p, 1-p)=(bbd,bπ) of idempotents, wherep≠0. We have
whereb1∈(pAp)-1,b2∈((1-p)A(1-p))qnil. Similar to the proof of Theorem 1, byabπ=a, we have
Sincebπa2b=bπabaandbπb2a=bπbab, we prove a2=b2a2b2and
a2=b2a2b2and b2=a2b2a2. By Lemma 4, we havea2+b2∈Adif and only if 1+
b2=a2b2a2. By Lemma 4, we havea2+b2∈Adif and only if 1+ a2∈Ad. Noting thatb2∈((1-p)A(1-p))qnil, we have
a2∈Ad. Noting thatb2∈((1-p)A(1-p))qnil, we have =0. Then
=0. Then

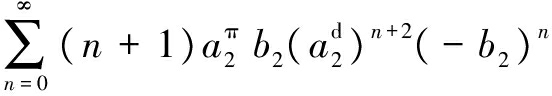
Using Lemma 1, we can prove thata+b∈Adand
whereu=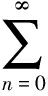 (
(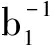 )n+2a1(a2+b2)n(a2+b2)π-
)n+2a1(a2+b2)n(a2+b2)π-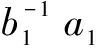 (a2+b2)d.
(a2+b2)d.
Computing the right side of Eq.(5) in the matrix form, we can prove that Eq.(5) holds.
Example3 LetAbe the algebra of all complex 2×2 matrices, and takea=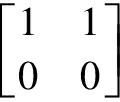 andb=
andb= . Clearly,bd=
. Clearly,bd= andbπ=
andbπ= . Then, we can check thata,bsatisfyabπ=a,bπa2b=bπabaandbπb2a=bπbab, butb2a≠bab.
. Then, we can check thata,bsatisfyabπ=a,bπa2b=bπabaandbπb2a=bπbab, butb2a≠bab.
[1]Drazin M P. Pseudo-inverses in associative rings and semigroups [J].TheAmericanMathematicalMonthly, 1958,65(7): 506-514. DOI:10.2307/2308576.
[2]Koliha J J. A generalized Drazin inverse [J].GlasgowMathematicalJournal, 1996,38(3): 367-381. DOI:10.1017/s0017089500031803.
[3]Hartwig R E. On quasinilpotents in rings [J].PanamericanMathematicalJournal, 1991,1(1): 10-16.
[4]Ben-Israel A, Greville T N E.Generalizedinverses:Theoryandapplications[M]. 2nd ed. New York: Springer-Verlag, 2003.
[5]Castro-Gonz lez N, Dopazo E, Martínez-Serrano M F. On the Drazin inverse of sum of two operators and its application to operator matrices [J].JournalofMathematicalAnalysisandApplications, 2009,350(1): 207-215. DOI:10.1016/j.jmaa.2008.09.035.
lez N, Dopazo E, Martínez-Serrano M F. On the Drazin inverse of sum of two operators and its application to operator matrices [J].JournalofMathematicalAnalysisandApplications, 2009,350(1): 207-215. DOI:10.1016/j.jmaa.2008.09.035.
[6]Ljubisavljevi J, Cvetkovi
J, Cvetkovi -Ili
-Ili D S. Additive results for the Drazin inverse of block matrices and applications [J].JournalofComputationalandAppliedMathematics, 2011,235(12): 3683-3690.
D S. Additive results for the Drazin inverse of block matrices and applications [J].JournalofComputationalandAppliedMathematics, 2011,235(12): 3683-3690.
[7]Hartwig R E, Wang G R, Wei Y M. Some additive results on Drazin inverse [J].LinearAlgebraandItsApplications, 2001,322(1): 207-217. DOI:10.1016/s0024-3795(00)00257-3.
[8]Cvetkovi -Ili
-Ili D S, Djordjevi
D S, Djordjevi D S, Wei Y. Additive results for the generalized Drazin inverse in a Banach algebra [J].LinearAlgebraandItsApplications, 2006,418(1): 53-61. DOI:10.1016/j.laa.2006.01.015.
D S, Wei Y. Additive results for the generalized Drazin inverse in a Banach algebra [J].LinearAlgebraandItsApplications, 2006,418(1): 53-61. DOI:10.1016/j.laa.2006.01.015.
[9]Gonz lez N C, Koliha J J. New additive results for the g-Drazin inverse [J].ProceedingsoftheRoyalSocietyofEdinburghSectionA:Mathematics, 2004,134(6): 1085-1097. DOI:10.1017/s0308210500003632.
lez N C, Koliha J J. New additive results for the g-Drazin inverse [J].ProceedingsoftheRoyalSocietyofEdinburghSectionA:Mathematics, 2004,134(6): 1085-1097. DOI:10.1017/s0308210500003632.
[10]Deng C Y, Wei Y M. New additive results for the generalized Drazin inverse [J].JournalofMathematicalAnalysisandApplications, 2010,370(2): 313-321. DOI:10.1016/j.jmaa.2010.05.010.
[11]Cvetkovi -Ili
-Ili D S, Liu X J, Wei Y M. Some additive results for the generalized Drazin inverse in a Banach algebra [J].ElectronicJournalofLinearAlgebra, 2011,22(1): 1049-1058. DOI:10.13001/1081-3810.1490.
D S, Liu X J, Wei Y M. Some additive results for the generalized Drazin inverse in a Banach algebra [J].ElectronicJournalofLinearAlgebra, 2011,22(1): 1049-1058. DOI:10.13001/1081-3810.1490.
[12]Liu X J, Wu S X, Yu Y M. On the Drazin inverse of the sum of two matrices [J].JournalofAppliedMathematics, 2011,2011:831892. Doi:10.1155/2011/831892.
[13]Zou H L, Mosi D, Chen J L. Generalized Drazin invertibility of product and sum of two elements in a Banach algebra and its applications [J].TurkishJournalofMathematics, 2017,41:548-563. Doi:10.3906/mat-1605-8.
D, Chen J L. Generalized Drazin invertibility of product and sum of two elements in a Banach algebra and its applications [J].TurkishJournalofMathematics, 2017,41:548-563. Doi:10.3906/mat-1605-8.
[14]Benítez J, Liu X J, Qin Y H. Representations for the generalized Drazin inverse in a Banach algebra [J].BulletinofMathematicalAnalysisandApplications, 2013,5(1): 53-64.
[15]Mosi D. More results on generalized Drazin inverse of block matrices in Banach algebras [J].LinearAlgebraandItsApplications, 2013,439(8): 2468-2478. DOI:10.1016/j.laa.2013.07.006.
D. More results on generalized Drazin inverse of block matrices in Banach algebras [J].LinearAlgebraandItsApplications, 2013,439(8): 2468-2478. DOI:10.1016/j.laa.2013.07.006.
References
Banach代数中元素之和的广义Drazin逆的一些结果
郭 丽1,2 陈建龙1 邹红林1
(1东南大学数学学院, 南京 211189)(2北华大学数学与统计学院, 吉林 132013)
摘要:令a,b为Banach代数中的2个广义Drazin可逆的元素.用a,b,ad,bd给出元素a+b和的广义Drazin逆的明确表达式.利用Banach代数中的幂等系统研究了2个元素之和的广义Drazin逆. 对于Banach代数中元素a,b,首先证明了如果a,b∈Aqnil,aba=0且ab2=0, 则a+b∈Aqnil. 并在一些新的条件下给出了a+b和的广义Drazin逆的表达式, 推广了近期的一些结果.
关键词:广义Drazin逆; Banach代数; 幂零元; 拟幂零元
中图分类号:O151.21
DOI:10.3969/j.issn.1003-7985.2017.03.020
Received2016-12-16.
Foundationitems:The National Natural Science Foundation of China (No.11371089, 11371165), the Natural Science Foundation of Jilin Province (No.20160101264JC), the Specialized Research Fund for the Doctoral Program of Higher Education (No.20120092110020), the Natural Science Foundation of Jiangsu Province (No.BK20141327), the Fundamental Research Funds for the Central Universities, the Foundation of Graduate Innovation Program of Jiangsu Province (No.KYZZ15-0049).
Citation:Guo Li, Chen Jianlong, Zou Honglin.Some additive results for the generalized Drazin inverse in a Banach algebra[J].Journal of Southeast University (English Edition),2017,33(3):382-386.
DOI:10.3969/j.issn.1003-7985.2017.03.020.
 lez and Koliha[9]gave the formula for (a+b)dunder the conditionsabπ=a,aπb=bandbπabaπ=0 which are weaker thanab=0 in Banach algebras. In 2010, Deng and Wei[10]derived a result under the conditionPQ=QP, whereP,Qare bounded linear operators. In 2011, Cvetkovi
lez and Koliha[9]gave the formula for (a+b)dunder the conditionsabπ=a,aπb=bandbπabaπ=0 which are weaker thanab=0 in Banach algebras. In 2010, Deng and Wei[10]derived a result under the conditionPQ=QP, whereP,Qare bounded linear operators. In 2011, Cvetkovi
 . Then we can check that
. Then we can check that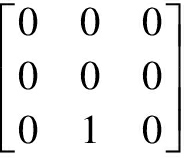 and
and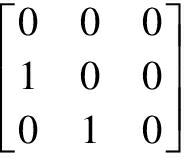 . Clearly,
. Clearly, lez N, Dopazo E, Martínez-Serrano M F. On the Drazin inverse of sum of two operators and its application to operator matrices [J].
lez N, Dopazo E, Martínez-Serrano M F. On the Drazin inverse of sum of two operators and its application to operator matrices [J].