Tab.1 Material parameters of carcass ply and belt ply

StructurelayerDensity/(kg·m-3)E11/MPaE22/MPaE33/MPaG13/MPaG23/MPaG31/MPaμ1μ2μ3Carcassply10359322.762.763114.144.140.470.470.005Beltply12001.03×1044.134.133584.824.820.470.474×10-4
Abstract:To investigate the fatigue damage of epoxy asphalt pavement (EAP) under a heavy load and and temperature load, the load-figure of the heavy load on the steel bridge deck pavement (SBDP) was simulated first, and the temperature distribution of SBDP during the temperature-fall period in winter was also calculated. Secondly, the moving heavy load coupled with the most unfavorable temperature load was applied to the SBDP, and the tensile stress on the top of SBDP was calculated. Finally, the fatigue damage of EAP was evaluated considering the extreme situation of heavily overloaded and severe environments. The results show that both the heavy load and the temperature load during the temperature-fall period can increase the tensile stress on the top of SBDP significantly. In the extreme situation of heavily overloaded and severe environments, a fatigue crack is easily generated, and thus the SBDP should avoid the coupling effects of the heavy load and the temperature load in winter.
Key words:epoxy asphalt concrete; steel bridge deck pavement; fatigue crack; heavy load; temperature load
Epoxy asphalt concrete (EAC) has been proved to be an excellent material and widely used in steel bridge deck pavement (SBDP)[1]. However, investigations show that cracking is a major issue in the epoxy asphalt pavement (EAP) and seriously affects the serviceability of SBDP[2].
The SBDP usually carries the heavy traffic volume due to its unique position in the road network. The research team of Southeast University[3] investigated the traffic flow of SBDP in the Yangtze River Basin. The result shows that the axle loads of running trucks on the SBDP mainly range from 80 to 350 kN, and the volume of overloaded trucks (The axle load exceeds the standard axle load of 100 kN) is about 80% of the whole traffic volume. In addition, the SBDP is climatically sensitive due to the high thermal conductivity of the steel bridge deck, and considerable temperature loads are induced during the temperature-fall period. The heavy load coupled with the temperature load can accelerate crack development, especially in cold conditions when the cracking resistance of EAC is weak. The previous research focused on the crack initiation and propagation laws of EAC[4-5], and heavy load was also included in some research[2], but the impact of temperature variations on the crack behavior is seldom investigated. Based on the in-service condition of SBDP in the Yangtze River Basin, this research calculated the mechanical response of SBDP under the coupling of heavy load and the most unfavorable temperature load during the temperature-fall period in winter. The fatigue damage of EAP was evaluated, considering the extreme situation of heavily overloaded and severe environments.
1.1.1 Tire model
As the radial tire 11.00R20-18PR is the typical tire used for the freight trucks[6-7], this research developed an radial tire 11.00R20-18PR model by the finite element (FE) software ABAQUS.
In general, the radial tire is made of rubber and rubber-cord composites, composed of crown ply, sidewall, carcass ply, rubber liner, bead, and belt ply. The rubber is usually regarded as a hyperelastic material, and its mechanical behavior can be represented as
U=C10(I1-3)+C20(I1-3)2+C30(I1-3)3
(1)
where U is the strain energy; I1 is the strain invariant; Ci0 (i=1,2,3) are the material parameters.
Li et al.[6-7] gave the material parameters of rubber and rubber-cord composites for the radial tire, which are used in this research, as shown in Tab.1 and Tab.2. In the tire model, the rubber part was simulated by solid and hyperelastic elements, and the cord part was simulated by membrane elements. The FE model of the radial tire 11.00R20-18PR is shown in Fig.1.
To validate the effectiveness of the tire model, the tire inflating process was simulated with the standard inner tire pressure of 0.85 MPa, as shown in Fig.2. The simulated results are compared with the measured results conducted by Li et al.[6], as listed in Tab.3. As can be seen, the simulated results agree well with the measured results, and thus the tire model in Fig.1 is reliable.
Tab.1 Material parameters of carcass ply and belt ply

StructurelayerDensity/(kg·m-3)E11/MPaE22/MPaE33/MPaG13/MPaG23/MPaG31/MPaμ1μ2μ3Carcassply10359322.762.763114.144.140.470.470.005Beltply12001.03×1044.134.133584.824.820.470.474×10-4
Tab.2 Material parameters of other components

StructurelayerDensity/(kg·m-3)μC10/MPaC20/MPaC30/MPaCrownply10250.50.77-0.070.10Sidewall11250.50.94-0.200.20Bead11250.50.33-0.020.01

Fig.1 FE model of radial tire 11.00R20-18PR

Fig.2 Deformation of tire after inflating
Tab.3 Comparison of simulated and measured results

ParameterMeasuredresults/mmSimulatedresults/mmRelativedeviation/%Diameter105310600.66Width2692793.72Height2702731.11
1.1.2 Tire-SBDP interaction model
The 9.6-m-long SDBP model with a 14-mm-thick steel bridge deck and 55-mm-thick EAC pavement was established. The static modulus and Poisson ratio of steel were 2.1 GPa and 0.3 in the model, and those of the EAC were 950 MPa and 0.2[8]. The boundary condition was set as a fixed constraint at the bottom of model, and the steel bridge deck was merged with the pavement, assuming that only vertical displacement occurs.
The extended Lagrange multiplier method was used to define the contact condition between the tire and SBDP, and the tire-SBDP model is given in Fig.3.

Fig.3 Tire-SBDP interaction model
1.2.1 Tire-SBDP contact area
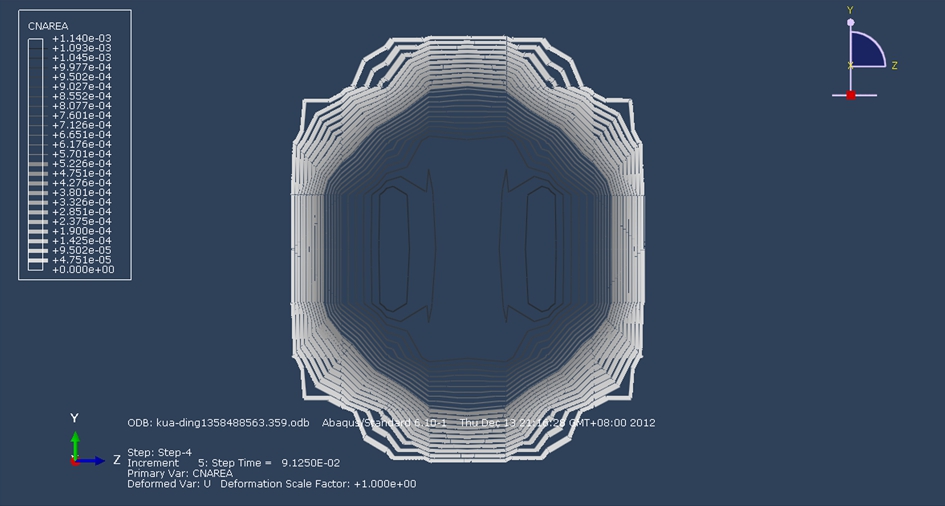
The tire-SBDP contact area under different axle loads is given in Fig.4. As can be seen, the contact area changes from oval to rectangle with the increase in the axle load, and the contact area of heavy load is an approximate rectangle. As shown in Fig.5, the width of the contact area changes little with the axle load, and the length linearly increases with the increase in axle load.
Referring to the load-figure of the roadway pavement, the dual wheel load of overloaded truck on the SBDP can be simplified as a double-rectangle load-figure, as shown in Fig.6, and the parameters of double-rectangle load-figure are listed in Tab.4.

(a) (b)


(c) (d)


(e) (f)
Fig.4 Tire-SBDP contact area under different axle loads. (a) 100 kN; (b) 150 kN; (c) 200 kN; (d) 250 kN; (e) 300 kN; (f) 350 kN

Fig.5 Width and length of tire-SBDP contact area
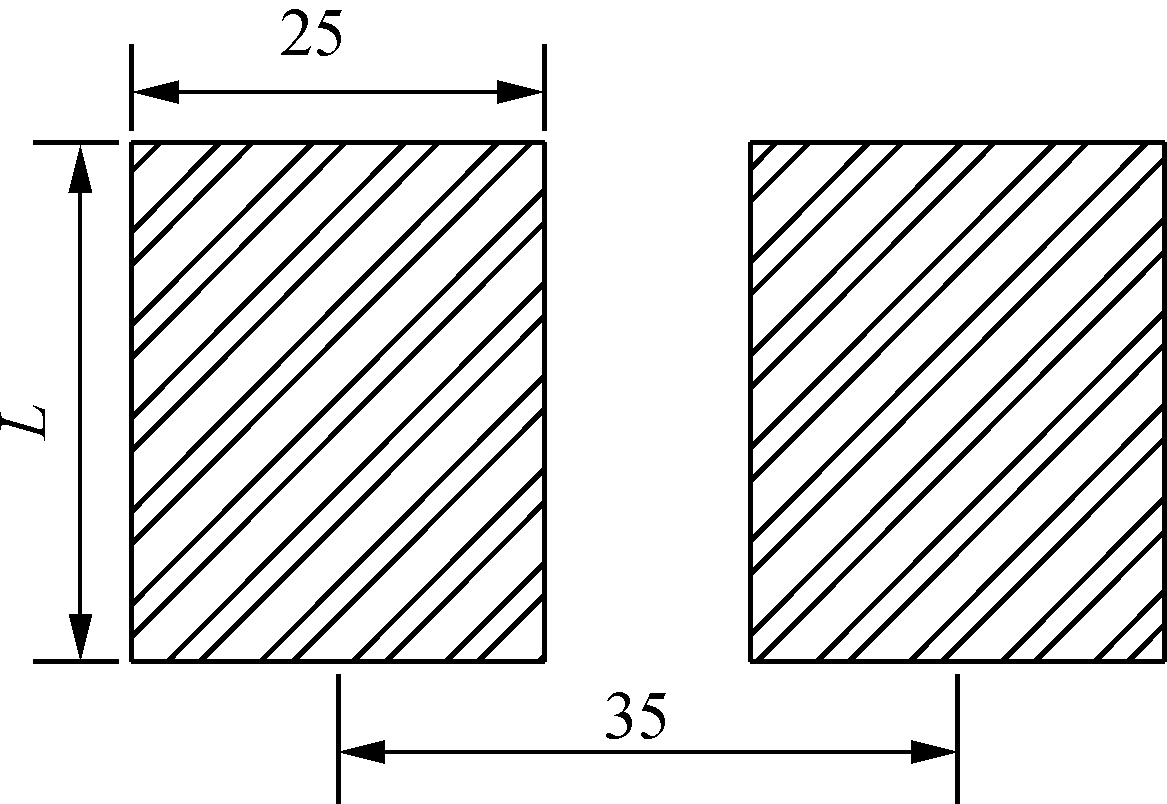
Fig.6 Double-rectangle load-figure (unit:mm)
Tab.4 Parameters of double-rectangle load-figure

Axleloads/kNLength/mAveragepressure/MPa1500.170.892000.210.962500.251.013000.291.043500.331.08
1.2.2 Pressure distribution
The pressure distribution under different axle loads is calculated, and some results are given in Fig.7.

(a)
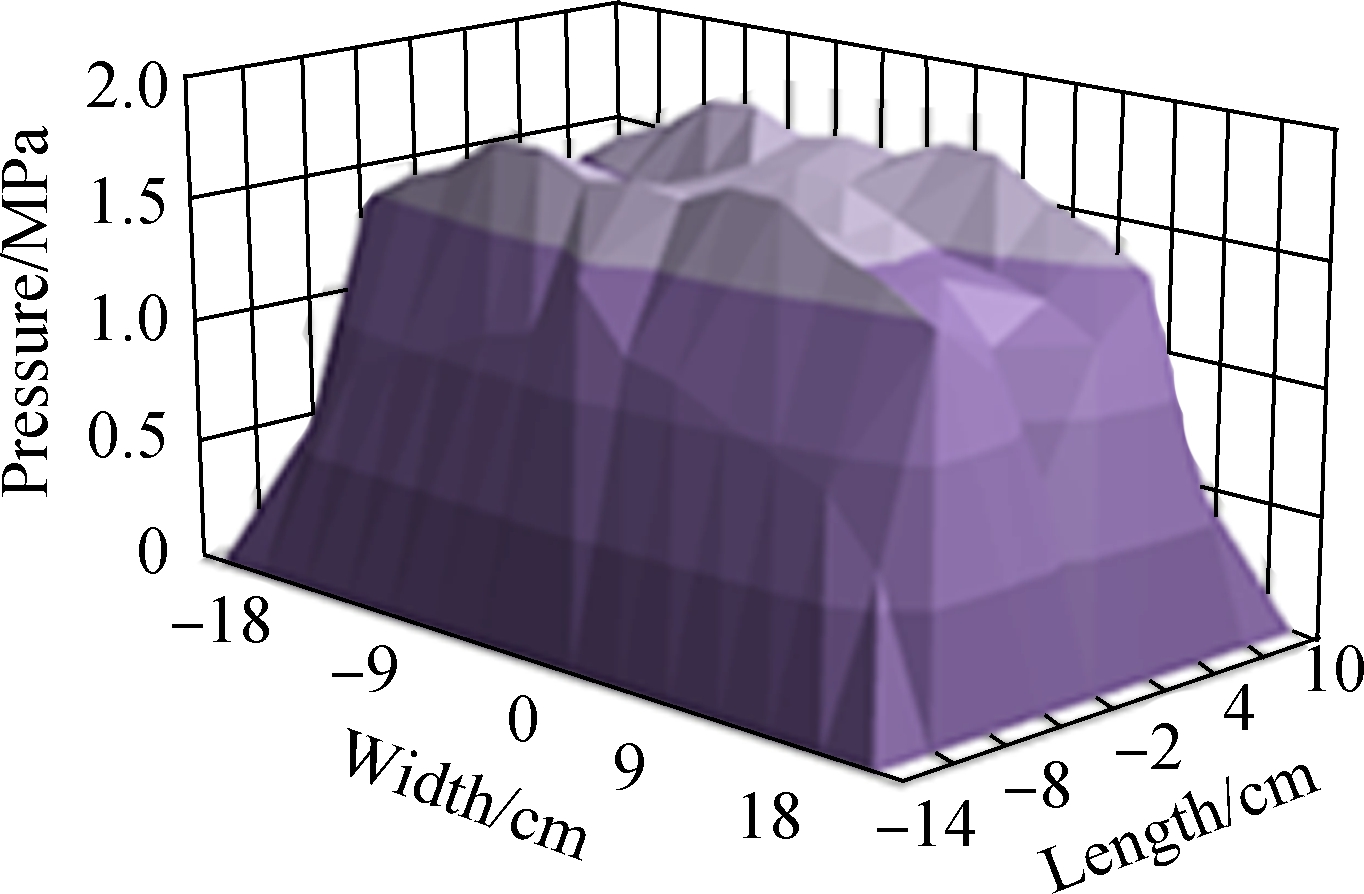
(b)
Fig.7 Pressure distribution under different axle loads.
(a) 150 kN; (b) 350 kN
As shown in Fig.7, the non-uniformity of the pressure distribution characteristics are complex and irregular. To facilitate the mechanical analysis of SBDP, the double-rectangle uniform load is used to simulate the dual wheel load on the SBDP, and the average pressures under different axle loads are given in Tab.5. However, the simulated results show that the mechanical response under the double-rectangle uniform load is smaller than the response under the loading of the tire model. Therefore, the non-uniformity coefficient k is designed to reflect the non-uniformity effect of pressure distribution on the mechanical response, and the value of k is equal to the ratio of the responses under the two loading types. Tab.5 lists the value of k considering different mechanical responses.
Tab.5 Value of k under different axle loads

MechanicalresponsesAxleloads/kN150200250300350Maximumverticaldisplacement1.3491.5511.7151.7531.822Maximumtensilestressonpavement1.3891.6961.7651.8041.876Maximuminterlaminarshearstress1.6531.9002.1012.1462.232
The temperature drop is liable to induce a temperature contraction crack in the SBDP, and the crack will further deteriorate coupled with the heavy load. In this section, the temperature distribution of SBDP during the temperature-fall period in winter is simulated.
Qian et al.[9] developed an thermal field model of the steel bridge and simulated the temperature distribution of EAP in summer. The same thermal field model is used in this research. The simulation results are given in Fig.8.

Fig.8 Temperature distribution of SBDP in winter
According to the simulation results, the temperature gradient of the temperature-fall period in winter (12:00—24:00) can be fitted by[10]
ΔT=T0exp(-ay)+b
(2)
where ΔT is the temperature difference; y is the vertical axle, with the origin of the coordinates lying on the steel bridge deck and the positive direction running downward; and T0, a and b are the parameters to be determined.
As shown in Fig.8, the temperature difference along the pavement depth at 18:00, 20:00, 22:00, and 24:00 is insignificant and can be regarded as the constant value; that is 6, 3, -1, and -5 ℃, respectively. The temperature gradient at 12:00, 14:00, and 16:00 can be fitted as
ΔT=23.186exp(-14.17y)-1.80
(3)
ΔT=18.549exp(-3.05y)-0.62
(4)
ΔT=12.763exp(-22.25y)-4.16
(5)
The temperature load of the established SBDP model during the temperature-fall period in winter was calculated, and the temperature contraction coefficients of steel and EAC are 1.2×10-5 and 1.58×10-5 ℃, respectively. The modulus of EAC at different temperatures are given in Tab.6[8,11]. The maximum temperature load during the temperature-fall period and the moving heavy load with the speed of 80 km/h are applied to the model, and the loading position of heavy load is set according to Ref.[2]. As I-type crack caused by the tensile stress on the pavement is the major early distress in SBDP, this research mainly focuses on the tensile stress on the top of SBDP, as shown in Fig.9.
Tab.6 Modulus of EAC MPa
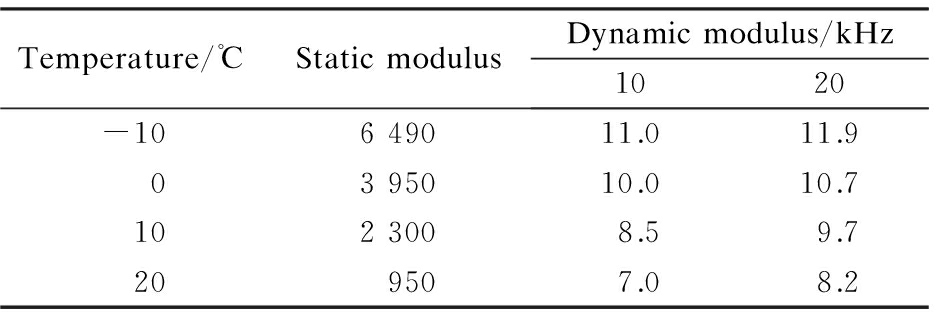
Temperature/℃StaticmodulusDynamicmodulus/kHz1020-10649011.011.90395010.010.71023008.59.7209507.08.2
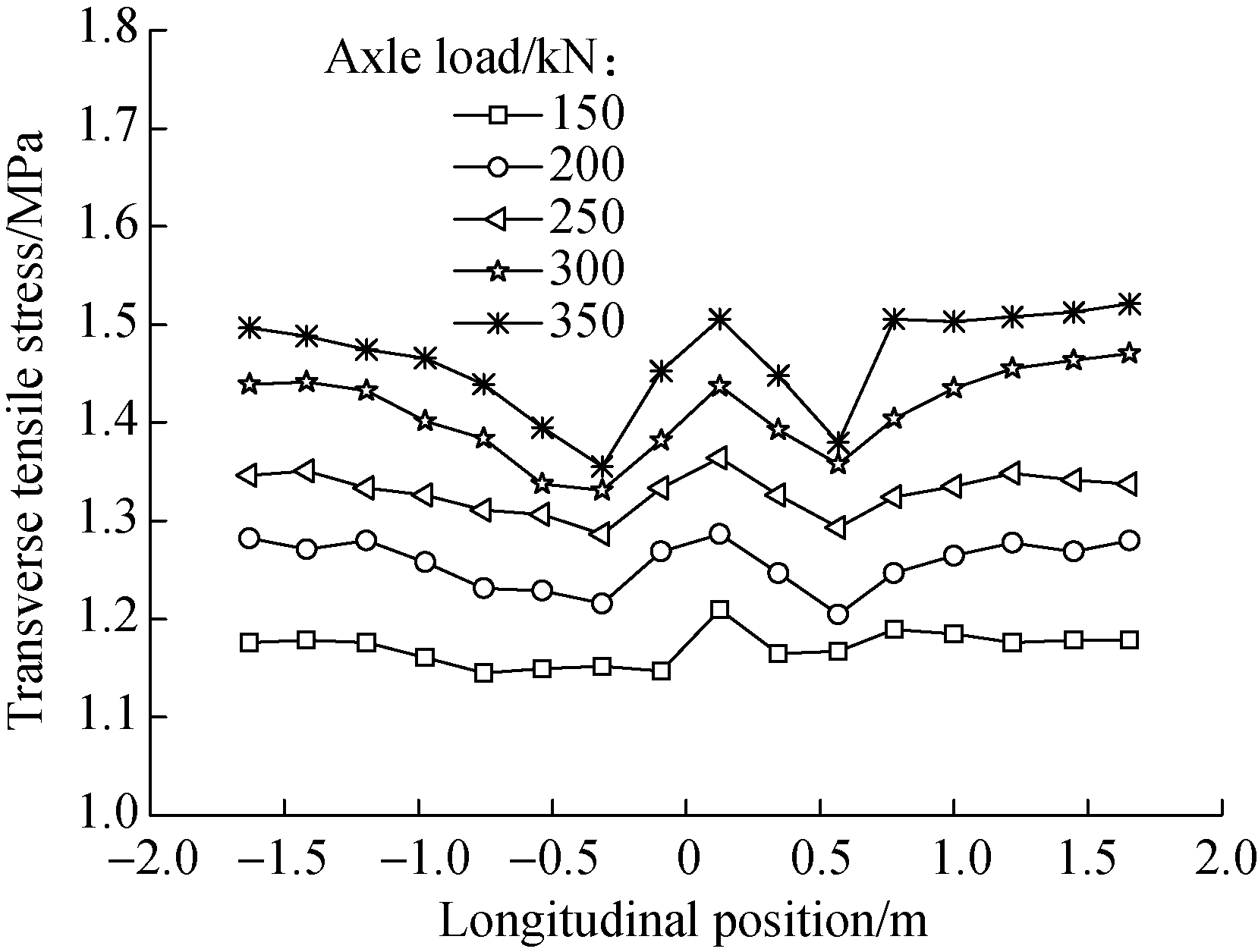 (a)
(a)

(b)
Fig.9 Tensile stress on the top of SBDP. (a) Transverse tensile stress; (b) Longitudinal tensile stress
It can be seen from Fig.9 that the longitudinal tensile stress on the top of SBDP is greater than the transverse tensile stress, and the peak values of both the transverse and longitudinal tensile stress locate near the diaphragm plate. The maximum transverse tensile stress under the axle-load of 150, 200, 250, 300 and 350 kN are, respectively, 1.21, 1.28, 1.36, 1.45 and 1.52 MPa, and the maximum longitudinal tensile stress are, respectively, 2.01, 2.29, 2.68, 3.06 and 3.41 MPa. Chen et al.[2] calculated the tensile stress on the top of SBDP under 30% overload and a constant low temperature, and the maximum transverse and longitudinal tensile stresses are, respectively, 0.8 and 1.377 MPa. Therefore, it can be concluded that both the heavy load and temperature load during the temperature-fall period can increase the tensile stress upon SBDP significantly.
Fatigue crack is one of the major failure types in the EAP, and Luo et al.[5] developed a fatigue simulation model to predict the service life of EAP as
(6)
where N is the load repetitions; ω is the damage variable, and the value of ω ranges from 0 to 1; when ω=0, it means that the material is not damaged; when ω=1, it means that the material is completely damaged; ε is the non-local equivalent strain. This model can be used in this research.
According to the simulation results, the tensile strain on the top of EAP is given in Tab.7, and the equivalent strain for fatigue test of EAC is set to be 342×10-6, which is the maximum tensile strain with the axle load of 350 kN. In addition, the equivalent strain is enlarged appropriately considering the extreme situation of a heavy overload and severe environment. Therefore, 400 and 600 με are also selected as the equivalent strain. The service life of EAP is calculated and the results are listed in Tab.8.
Tab.7 Equivalent strain for the fatigue test

Axleload/kNMaximumtensilestrain/10-6150200.2200229.5250274.5300309.5350342.0
Tab.8 Service life of EAP times

ωEquivalentstrain/10-63424006000.01104.19103.64102.240.05106.87105.97103.680.201010.72109.32105.740.401013.781011.98107.370.601016.451014.29108.800.801019.511016.961010.440.991026.841023.321014.36
As shown in Tab.8, the damage rate is accelerated with the increase in strain, and when the strain is 342×10-6, damage appears in the EAP after 104load repetitions, and after 1027 load repetitions, the EAP will be completely damaged. When the strain is 6×10-4, the EAP is initially damaged and completely damaged after 102 load repetitions and 1014 load repetitions, respectively. Actually, pavements usually lose service capability before the asphalt concrete is completely damaged, and the service life of SBDP should be determined by the service capability. Therefore, the four-point bending fatigue test of EAC is conducted to investigate the service capability of EAP at different damage variables. The test temperature and load frequency are set to be -10 ℃ and 10 Hz, and the result is given in Fig.10.

Fig.10 Modulus of EAC changes with load repetitions
The modulus ratio of EAC, which is the ratio of modulus after cycling load and initial modulus, can reveal the modulus loss of EAC during the fatigue test[5]. When the strain is 400 με, crack initiation occurs in the EAC after approximately 4×105 load repetitions, and the ratio of modulus is 0.94 after 5×106 load repetitions, but no apparent damage appears in the EAC specimen, and fatigue failure eventually occurs in the EAC specimen after 7×1011 load repetitions. When the strain is 6×10-4, crack initiation occurs rapidly, and the modulus of the EAC specimen declines sharply after 9×105 load repetitions. After 107 load repetitions, the ratio of modulus is 0.22, and fatigue failure occurs in the EAC specimen. Compared the fatigue test results with the estimated results in Tab.8, fatigue failure occurs when the damage variable of EAP reaches about 0.4. In addition, the crack initiation occurs when the damage variable of EAP ranges from 0.01 to 0.05. As shown in Tab.8, when the strain is low, the EAP can withstand the great traffic flow at low temperatures, but in the extreme situation of heavy overloads and severe environments, excessive vehicle load repetitions can cause the modulus of EAC to decline sharply, and a fatigue crack is easily generated. Therefore, to improve the serviceability, the SBDP should avoid the coupling effect of heavy load and temperature load in winter.
1) The load-figure of a heavy load on the SBDP can be simplified as a double-rectangle uniform load, and a non-uniformity coefficient is designed to reflect the non-uniformity effect of pressure distribution on the mechanical response.
2) Both the heavy load and temperature load during the temperature-fall period can increase the tensile stress on the top of SBDP significantly.
3) In the extreme situation of a heavy overload and a severe environment, the modulus of the EAC declines sharply, and a fatigue crack is easily generated.
References
[1]Huang W. Integrated design procedure for epoxy asphalt concrete-based wearing surface on long-span orthotropic steel deck bridges [J]. Journal of Materials in Civil Engineering, 2016, 28(5): 04015189. DOI:10.1061/(asce)mt.1943-5533.0001470.
[2]Chen L L, Qian Z D, Wang J Y. Multiscale numerical modeling of steel bridge deck pavements considering vehicle-pavement interaction [J]. International Journal of Geomechanics, 2016, 16(1): B4015002. DOI:10.1061/(asce)gm.1943-5622.0000461.
[3]Zhang C C, Shi C H, Zhou X Y, et al. Research on behavior characteristic and key pavement technology of continuous bridge deck system with super length and high flexibility [R]. Nanjing: Southeast University, 2013.
[4]Qian Z D, Wang J Y, Chen L L, et al. Three-dimensional discrete element modeling of crack development in epoxy asphalt concrete [J]. Journal of Testing and Evaluation, 2015, 43(2): 1-13. DOI:10.1520/jte20140086.
[5]Luo S, Qian Z D, Harvey J. Experiment on fatigue damage characteristics of epoxy asphalt mixture [J]. China Journal of Highway and Transport, 2013, 26(2): 20-25. (in Chinese)
[6]Li W, Xia Y, Xia Y M. Finite element analysis for cord force of truck radial tire [J]. Chinese Quarterly of Mechanics, 2002, 23(3): 323-330. (in Chinese)
[7]Chen T J, Huang W, Qian Z D. Research on the loading pattern of asphalt pavement on orthotropic steel deck [J]. Shanghai Highways, 2007, 3: 35-40. (in Chinese)
[8]Chen L L. Research on dynamic parameters of epoxy asphalt mixture [D]. Nanjing: School of Transportation, Southeast University, 2009.
[9]Qian Z D, Liu Y. Mechanical analysis of waterproof bonding layer on steel bridge deck under bridge-temperature-load coupling effect [J]. Journal of Southeast University (Natural Science Edition), 2012, 42(4): 729-733. (in Chinese)
[10]Liu Y, Qian Z D, Hu H Z. Thermal field characteristic analysis of steel bridge deck during high-temperature asphalt pavement paving [J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2811-2821. DOI:10.1007/s12205-016-0027-2.
[11]Chen L L, Qian Z D, Luo S. Experimental study on dynamic modulus of thermosetting epoxy asphalt mixture for steel deck pavement [J]. Journal of Southeast University (English Edition), 2010, 26(1): 112-116.
摘要:为研究重载和温度荷载耦合作用对环氧沥青铺装结构疲劳损伤的影响,首先模拟了钢桥面铺装重载的荷载图示,同时计算了冬季降温过程中钢桥面铺装结构的温度分布.然后,将移动重载和最不利温度荷载施加到钢桥面铺装结构,计算铺装表面拉应力.最后,考虑严重超载和恶劣低温等不利条件,进行环氧沥青铺装结构疲劳损伤分析.结果表明:重载和降温过程产生的温度荷载都可显著增加铺装表面拉应力,严重超载和恶劣低温等不利条件下,钢桥面铺装容易产生疲劳裂缝,因此,应该尽量避免冬季重载和温度荷载的耦合作用.
关键词:环氧沥青混凝土;钢桥面铺装;疲劳裂缝;重载;温度荷载
中图分类号:U443.33
DOI:10.3969/j.issn.1003-7985.2017.04.014
Received 2017-04-06,
Revised 2017-08-22.
Biographies:Liu Yang (1989—), male, graduate; Qian Zhendong (corresponding author), female, professor, qianzd@seu.edu.cn.
Foundation items:The National Natural Science Foundation of China (Nos.51378122, 51678146), the Scientific Research Foundation of Graduate School of Southeast University (No.YBJJ1680).
Citation:Liu Yang, Qian Zhendong, Zhang Meng. Fatigue damage analysis of epoxy asphalt pavement for steel bridges considering coupled effects of heavy load and temperature variations[J].Journal of Southeast University (English Edition),2017,33(4):478-483.
DOI:10.3969/j.issn.1003-7985.2017.04.014.