In recent years, there has been a significant amount of progress in developing intelligent transportation system (ITS)applications such as vehicle navigation systems, intelligent cruise control systems and advanced driver assistance systems[1-3].These applications require detailed road environment information to handle the challenges of the complex traffic scenarios.A digital map can provide detailed information of the road environment for these applications.Therefore, efficient and reliable digital maps are crucial to further the development of ITS applications[4-6].Road modeling is the vital part of generating digital maps.From a technical point of view, a satisfactory road model for digital maps should realize an optimal balance between the following two requirements: efficiency and reliability.First, the efficiency requirement is relevant to the data storage of the road model.A road model should have an efficient and compact data structure to reduce the data storage such that the road model can effectively transfer road information via wireless networks.Secondly, the reliability requirement is relevant to the quality of the road model.A road model should contain the road geometry information with the desired accuracy and integrity[1,3,5].
It is a consensus that the efficiency requirement and the reliability requirement are contradictory during the process of road modeling.The tradeoff for the increased accuracy of a road model is the cost of increased data storage.Therefore, it is difficult for a road model to satisfy the aforementioned two requirements simultaneously[1,5-7].The previous studies considered the reliability requirement excessively while ignoring the efficiency requirement during the process of road modeling.In order to balance these two requirements well, it is better to select an appropriate spline curve to build a road model.Currently, various spline curves were widely selected to build road models in previous literature[1,3,7-11].For example, the Hermite spline curve is a representative interpolating spline curve and the Hermite spline-based road model can be locally adjusted.However, the Hermite spline curve has a disadvantage that large amounts of data points need to be stored and processed.Therefore, it is difficult for the Hermite spline model to comply with the efficiency requirement.Moreover, the B-spline curve is a representative approximating a spline curve and the B-spline-based road model has an advantage that the change of local control points do not affect the entire shape of the road model, which makes local modification of a road model possible.However, it is difficult to extract road geometry information and the calculation of the first and second derivatives of the function is complicated.Therefore, the availability of the B-spline-based road model is poor.
In this paper,a probe vehicle equipped with a single-enclosure GPS+INS positioning system measures the raw roadway geometry data and acquired data will be processed manually to remove the outliers.Then, the cardinal spline is selected to build an initial road model.The initial road model is specified by a series of control points and tension parameters.In view of the initial road model, a gradual optimization algorithm is proposed to determine reasonable control points and optimal tension parameters according to the degree of the change of road curvature.Selection of reasonable control points can improve data storage efficiency and optimal tension parameters can satisfy a desired accuracy.Consequently, the road modeling method proposed in this paper realizes a near-optimal balance between the efficiency and the reliability requirements.
1 Road Modeling
Currently, a spline curve can generally be divided into two categories: the approximating spline and interpolating spline.The cardinal spline is a family of interpolating spline.To the best of the authors’ knowledge, the cardinal spline has been researched for a long time in the field of the CAD/CAM industry and the cardinal spline representation of the road geometry is rarely applied in the field of road modeling in the previous literature[12-13].In order to realize a near-optimal balance between the efficiency and reliability requirements, the cardinal spline is selected to build the initial road model and a gradual optimization algorithm is developed to determine reasonable control points and optimal tension parameters of this road model.
1.1 Cardinal spline road model
The processed data points of the roadway geometry from a probe vehicle equipped with a single-enclosure GPS+INS positioning system are used to build the cardinal spline road model.The cardinal spline road model is a sequence of individual piecewise cubic curves joined to form a larger curve, and each cardinal spline segment is defined by four control points Pi-1,Pi,Pi+1,Pi+2, with the curve drawn only from Pi to Pi+1.The tangent at each control point Pi is calculated using the previous and next control points on the spline, without being given by humans.A single cardinal spline segment can be completely determined by four consecutive control points, in which the middle two control points are the endpoints of the cardinal spline segment and the other two control points are used to calculate the tangents at the endpoints of this cardinal spline segment.Let us suppose that Pi-1,Pi,Pi+1,Pi+2 are four given consecutive control points (each of them has x and y values)and P(u)is a parametric cubic polynomial between the control points Pi and Pi+1 (u is the parameter).Hence, the boundary condition for establishing a single cardinal spline segment using four points Pi-1 to Pi+2 is
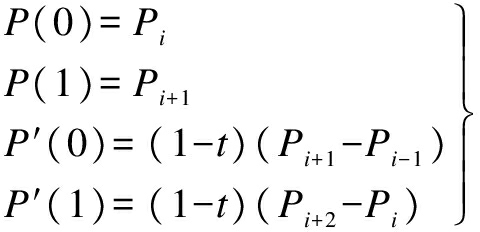
(1)
where P(0)and P(1)are the position vectors of P(u)at the two endpoints of the spline segment between Pi and Pi+1, respectively; P′(0)and P′(1)are the tangent vectors of P(u)at the two endpoints of the spline segment between Pi and Pi+1, respectively; and t is a tension parameter which affects the tightness of the cardinal spline road model.
Additionally, u is the parameter of the spline segment and ranges from 0 to 1 between Pi and Pi+1 (see Fig.1).
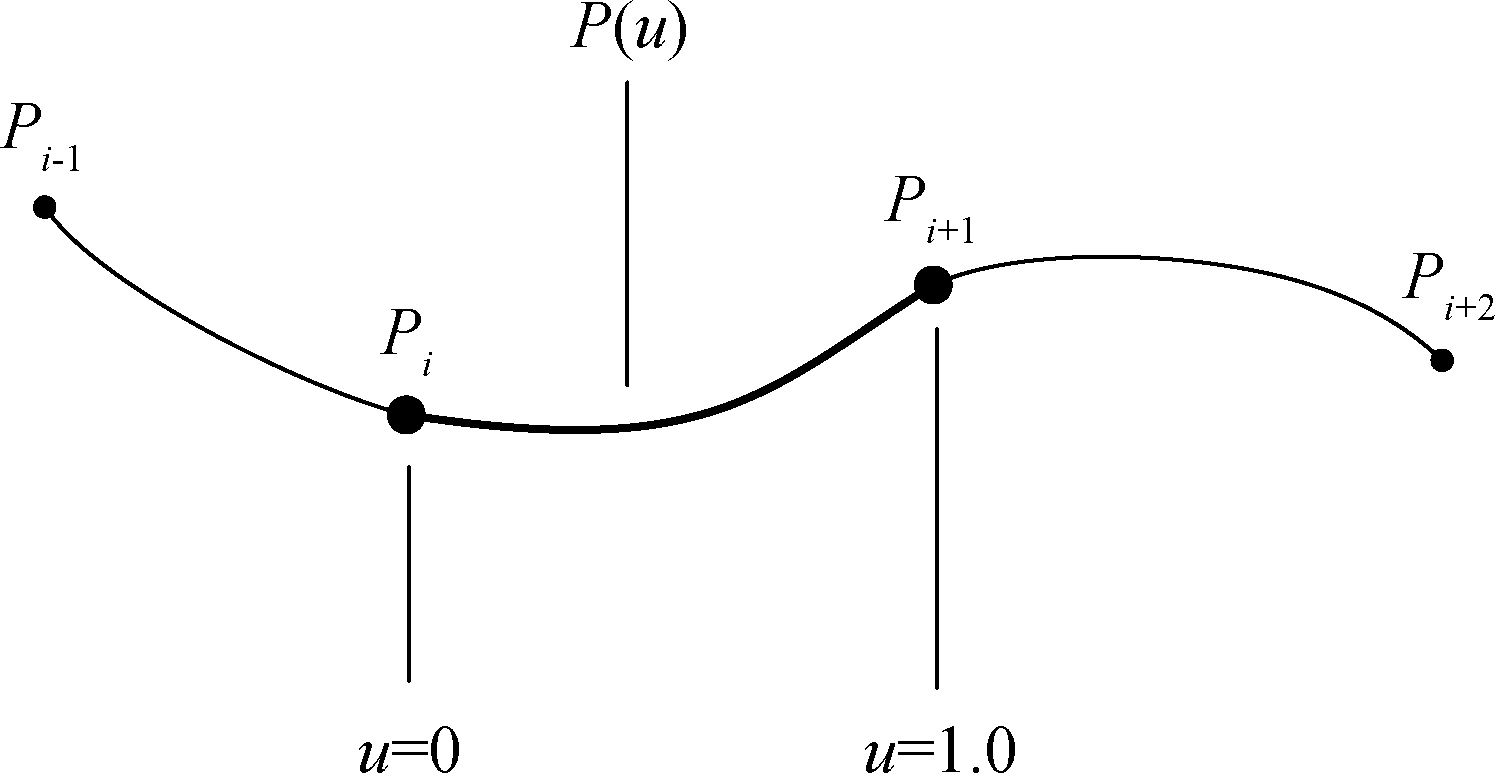
Fig.1 The spline segment when u ranges from 0 to 1 between Pi and Pi+1
Eq.(1)is converted into a matrix form, as follows:
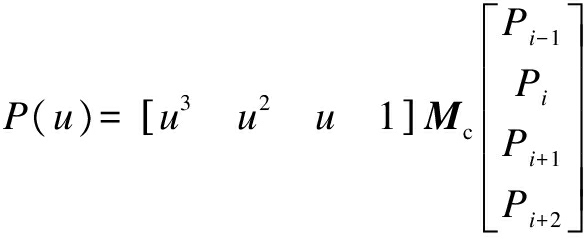
(2)
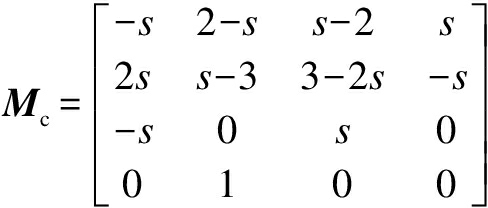
(3)
where s=1-t/2.
Eq.(2)is expanded into a polynomial form:
P(u)= Pi-1(-su3+2su2-su)+
Pi[(2-s)u3+(s-3)u2+1]+
Pi+1[(s-2)u3+(3-2s)u2+su]+
Pi+2(su3-su2)
(4)
Now, we can decompose Eq.(4)into the components of the x and y directions in the two-dimensional plane, and obtain the following expression of the cubic polynomial of the spline segment between the control points Pi and Pi+1 in the x and y directions:
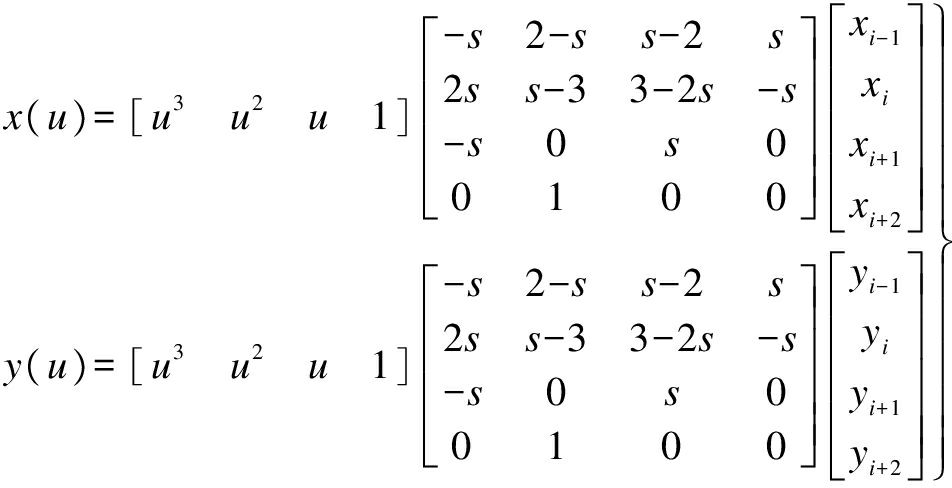
(5)
where 0≤u≤1.
Then, after the expansion of Eq.(5), the cardinal spline segment between the control points Pi and Pi+1 is given as
(6)
where
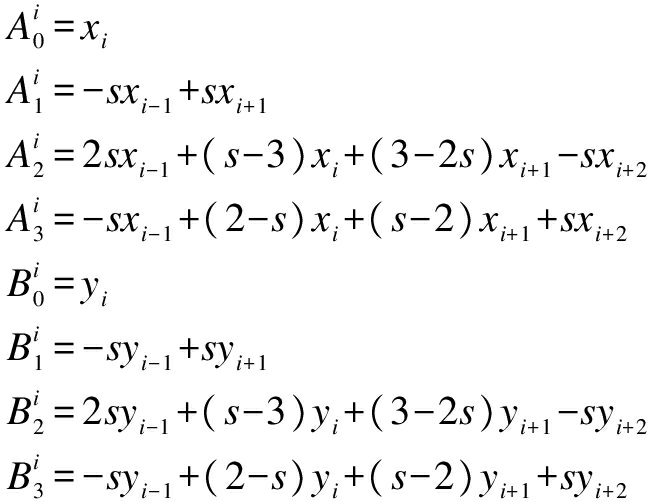
Thus, it can be seen that each cardinal spline segment is specified by four given consecutive control points and a tension parameter which is determined according to the control requirements and accuracy requirements of the actual application scenarios.The cardinal spline road model with different values for the tension parameter will produce different curves through a given series of control points.The cardinal spline road model with four different values for the tension parameter passes through the same series of control points, as shown in Fig.2.
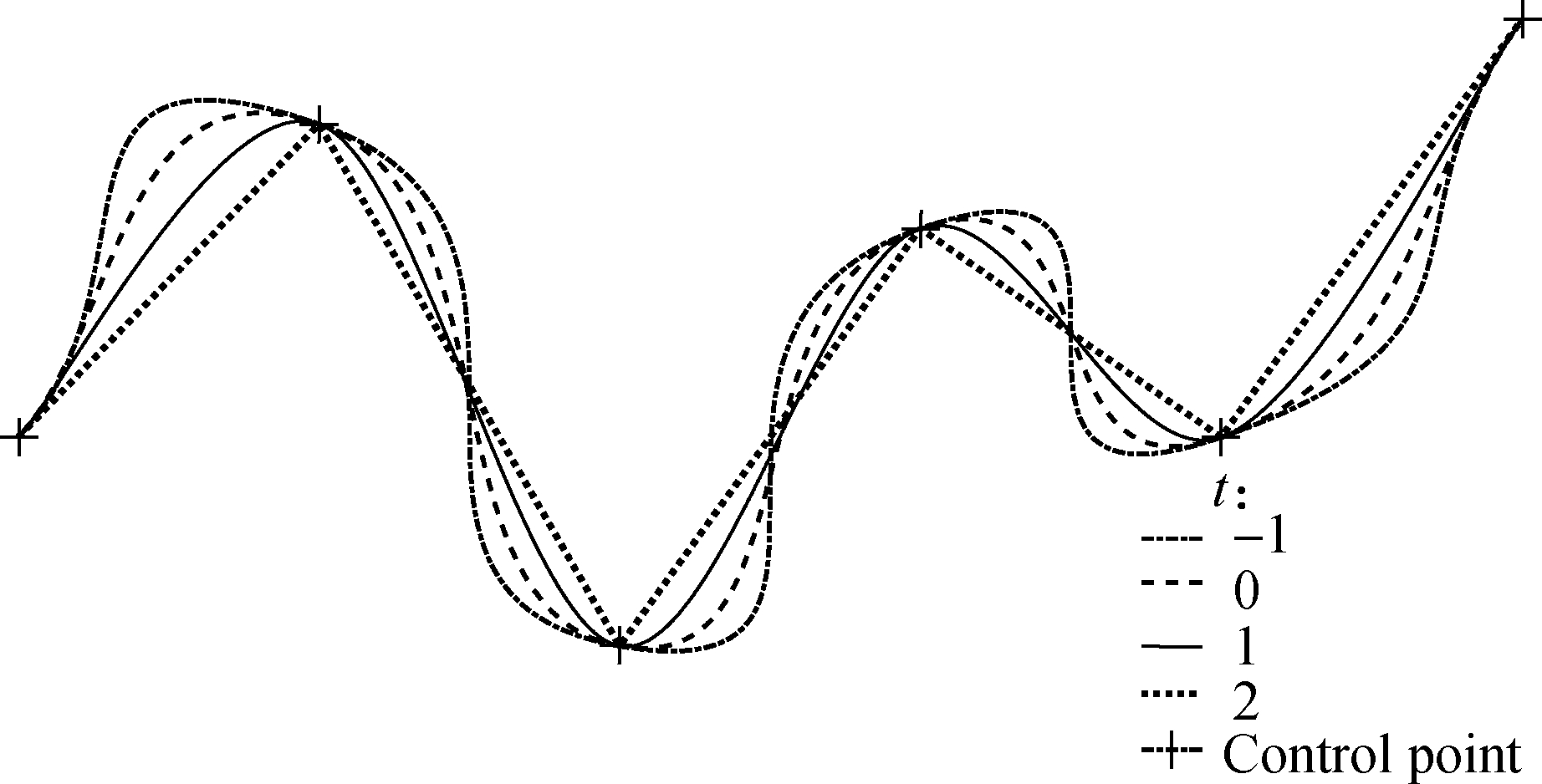
Fig.2 The cardinal spline road model with four different values for the tension parameter
Note that the cardinal spline road models in Fig.2 share the same tangent line at the starting point, which is the line drawn from the starting point to the next point along the curve.Likewise, the shared tangent at the ending point is the line drawn from the ending point to the previous point on the curve.The tangent line at other points is parallel to the line drawn from the previous point to the next point along the curve.
1.2 Gradual optimization algorithm for road modeling
The input of this algorithm is the set of the processed trajectory data points of the probe vehicle, and the output is the near-optimal cardinal spline road model, which can realize a near-optimal balance between the two requirements of efficiency and reliability.A gradual optimization algorithm for road modeling consists of two main steps: The selection of control points and the adjustment of tension parameters.
In the first step, due to the fact that the curvature of urban roads varies greatly, we need to select appropriate points from a series of data points as the control points of the cardinal spline road model according to the degree of the change of road curvature.Due to the useful features of the cardinal spline such as flexibility and local modification, the distribution of control points should be dense in the road section with the large curvature change and the distribution of control points can be properly sparse in the road section with the small curvature change, which can give consideration to the reliability and efficiency requirements.The curvature is calculated as
(7)
where C is the curvature value; y′ is the first derivative of the fitted curve; y″ is the second derivative of the fitted curve.
It is shown from Eq.(7)that the focus of the curvature is to obtain the first and second derivatives of the fitted curve.Based on this, we first perform natural cubic spline interpolation of sequential data points in order to obtain the first and second derivatives of the interpolation at each data point.Furthermore, the curvature value of each data point is calculated by Eq.(7).During this step, we select control points for the cardinal spline road model by comparing the curvature values of two adjacent data points.The threshold of curvature change is artificially preset according to the actual application.If the threshold value is too small, the data volume of the cardinal spline road model will not decrease obviously, and too large a value will lead to an incomplete road shape and loss of precision.In this paper, the threshold value is set to be 0.01.
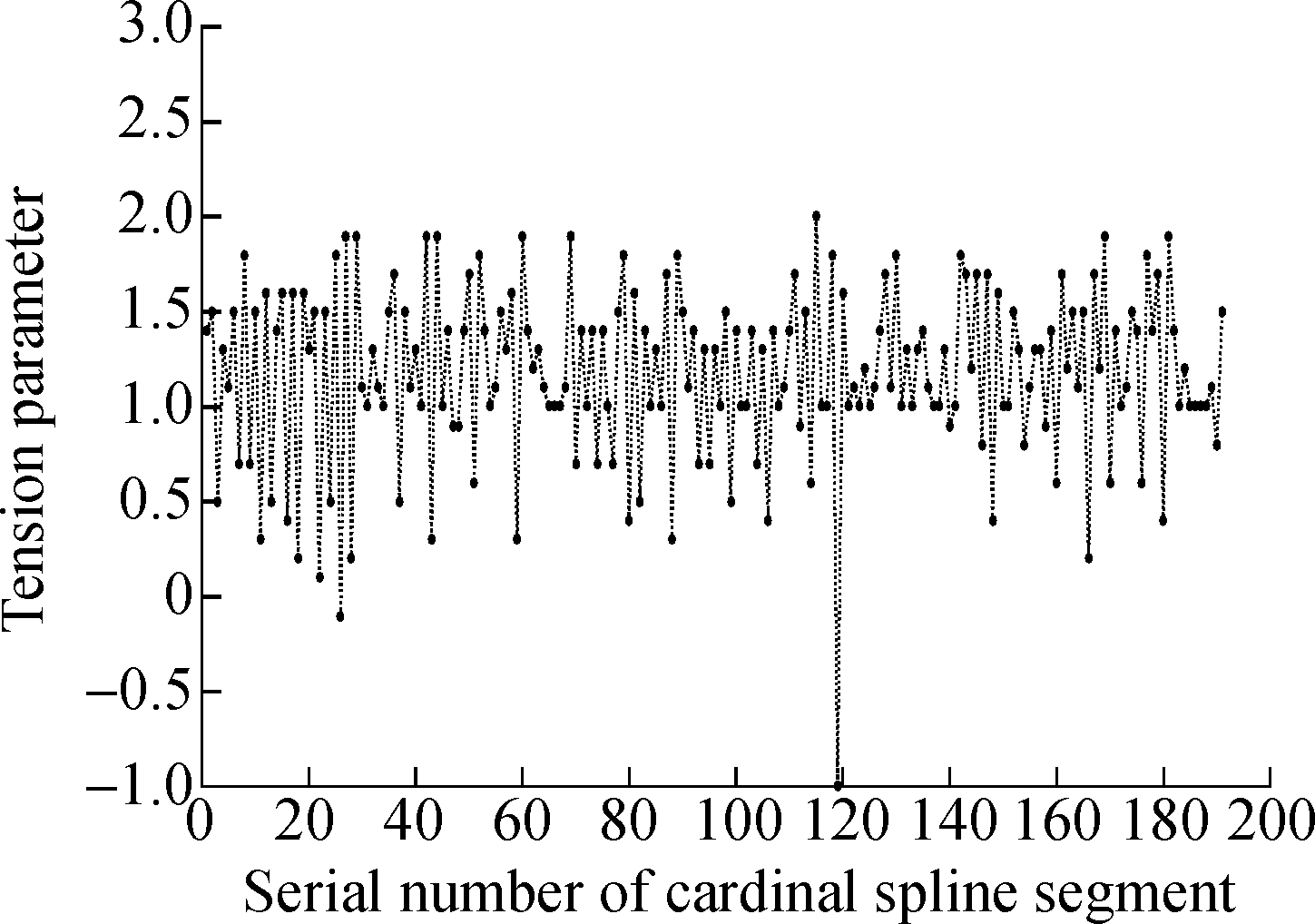
In the second step, the value of the tension parameter for each cardinal spline segment which is specified by a set of control points from the previous step are initially set to be -1.Then, the tension parameter of each cardinal spline segment is gradually adjusted independently by minimizing the error between the given data points and the cardinal spline segment.Generally, the adjustment range of tension parameters is between -1 and 2 in this paper.The least-square method is applied to find optimal tension parameters.
2 Experimental Results
2.1 Experiment setup
To evaluate the performance of the proposed road modeling method, experiments are carried out on a Chery TIGGO5 SUV vehicle.The Olympic Sports Center of Nanjing City is selected as the experimental site.The raw road geometry data was collected using the probe vehicle equipped with a GPS+INS vehicle positioning system (NovAtel SPAN-CPT system).NovAtel SPAN-CPT system is an accurate and reliable GPS+INS vehicle positioning system, which can provide accurate positioning information via post-processing even under adverse environments[14].In this paper, the probe vehicle was driven at a stationary driving speed of 40 to 60 km/h along the centerline of the lane.
2.2 Road modeling
We select appropriate control points for the cardinal spline road model from sequential obtained raw data points according to the change of curvature value.First, we perform natural cubic spline interpolation of sequential data points acquired from the trajectory of the probe vehicle in order to obtain the first and second derivatives of the interpolation at each data point.Then, the curvature value of each data point is calculated by Eq.(7).The threshold value of curvature change in the gradual optimization algorithm is set to be 0.01 with an overall consideration of the efficiency and reliability requirements in this paper.Then, we set the initial value of the tension parameter for each cardinal spline segment to be -1.The tension parameter for each cardinal spline segment is adjusted independently by minimizing the error between the given data points and the cardinal spline segment.The adjustment range of tension parameters is between -1 and 2 in this paper.Fig.3 shows the process of road modeling.
2.3 Performance evaluation of road modeling
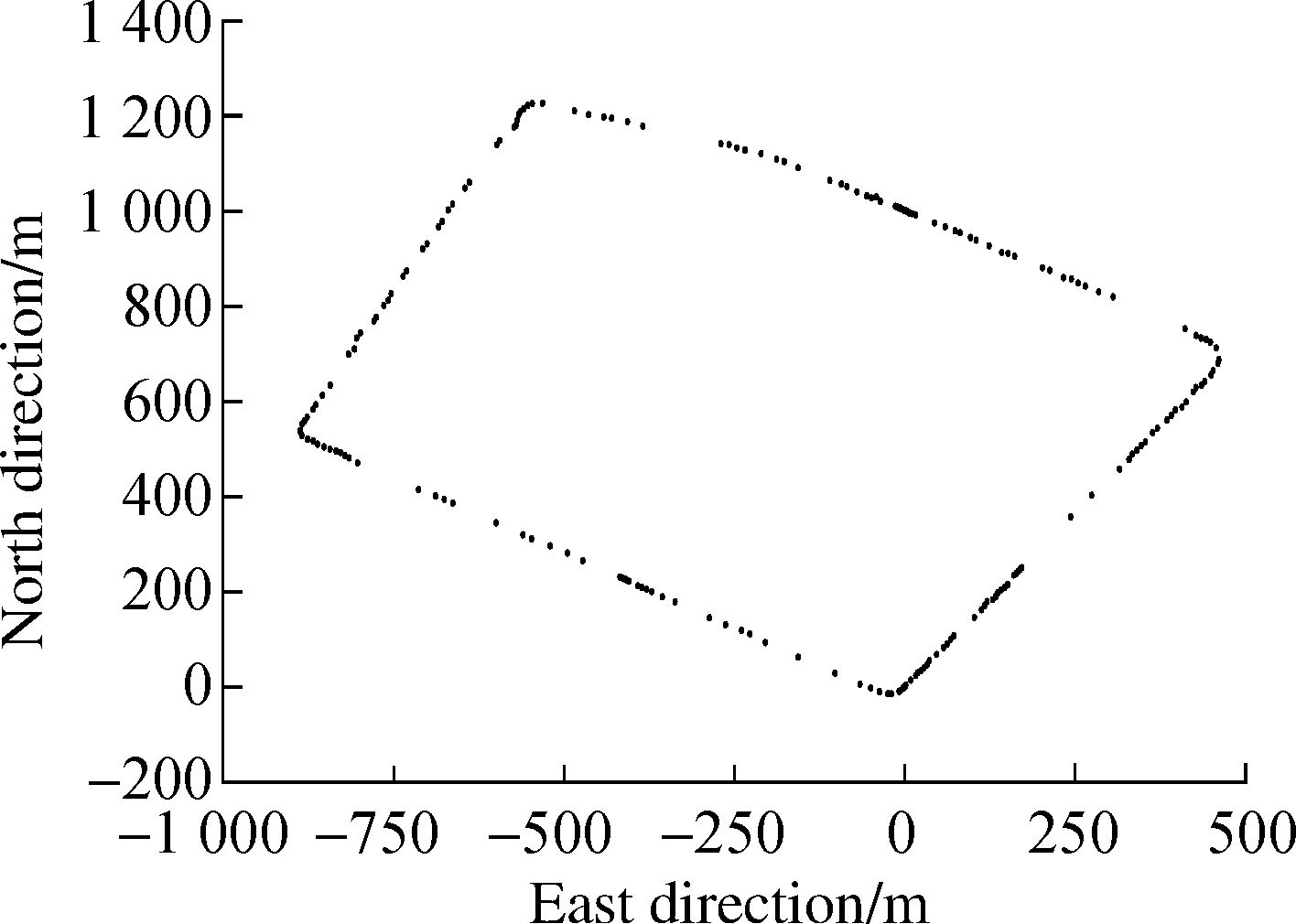
The 378 raw position data points are used for the inputs of the cardinal spline road model based on the gradual optimization algorithm.After the selection of control points and the adjustment of the tension parameter, the near-optimal cardinal spline road model is achieved, which contains 193 control points.There are 192 individual cardinal spline segments in this experiment.To evaluate the performance of the proposed road modeling method, we conduct a comparison with a B-spline road model proposed in Ref.[1].The B-spline road model has been proven to outperform various previous road modeling methods, including methods using polygons, clothoids and partial types of spline curves.The specific comparison results are presented in Tab.1 and Tab.2.
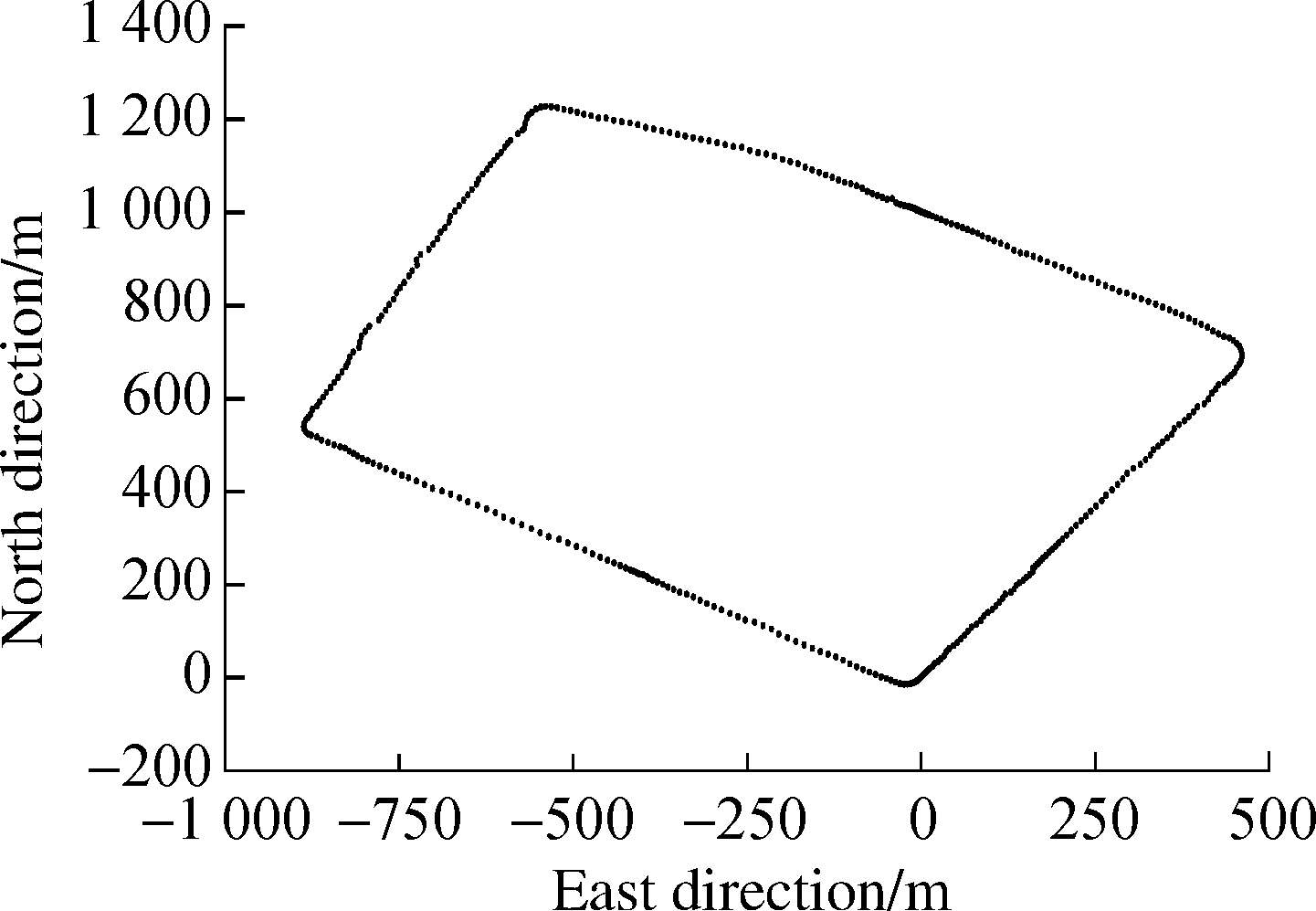
(a)
(b)
(c)

(d)
Fig.3 The process of road modeling.(a)Raw data points from the trajectory of the probe vehicle; (b)Selection result of control points; (c)Adjustment result of tension parameters; (d)Result of road modeling
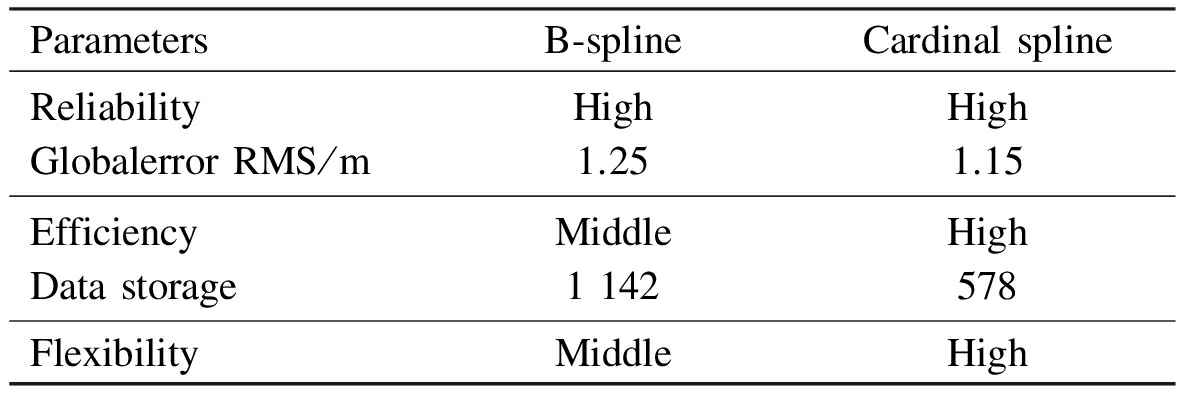
Tab.1 Efficiency comparison of two methods
ParametersB⁃splineCardinalsplineReliabilityGlobalerrorRMS/mHigh1.25High1.15EfficiencyDatastorageMiddle1142High578FlexibilityMiddleHigh
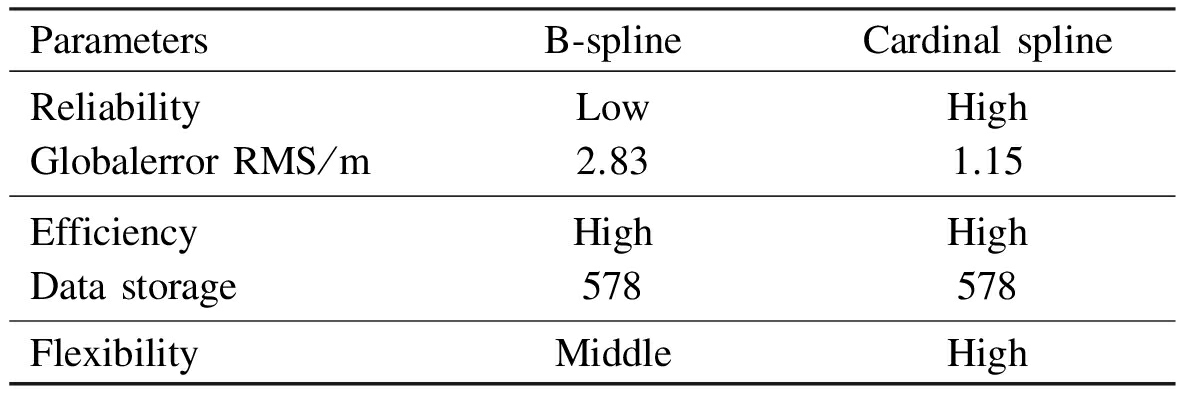
Tab.2 Reliability comparison of two methods
ParametersB⁃splineCardinalsplineReliabilityGlobalerrorRMS/mLow2.83High1.15EfficiencyDatastorageHigh578High578FlexibilityMiddleHigh
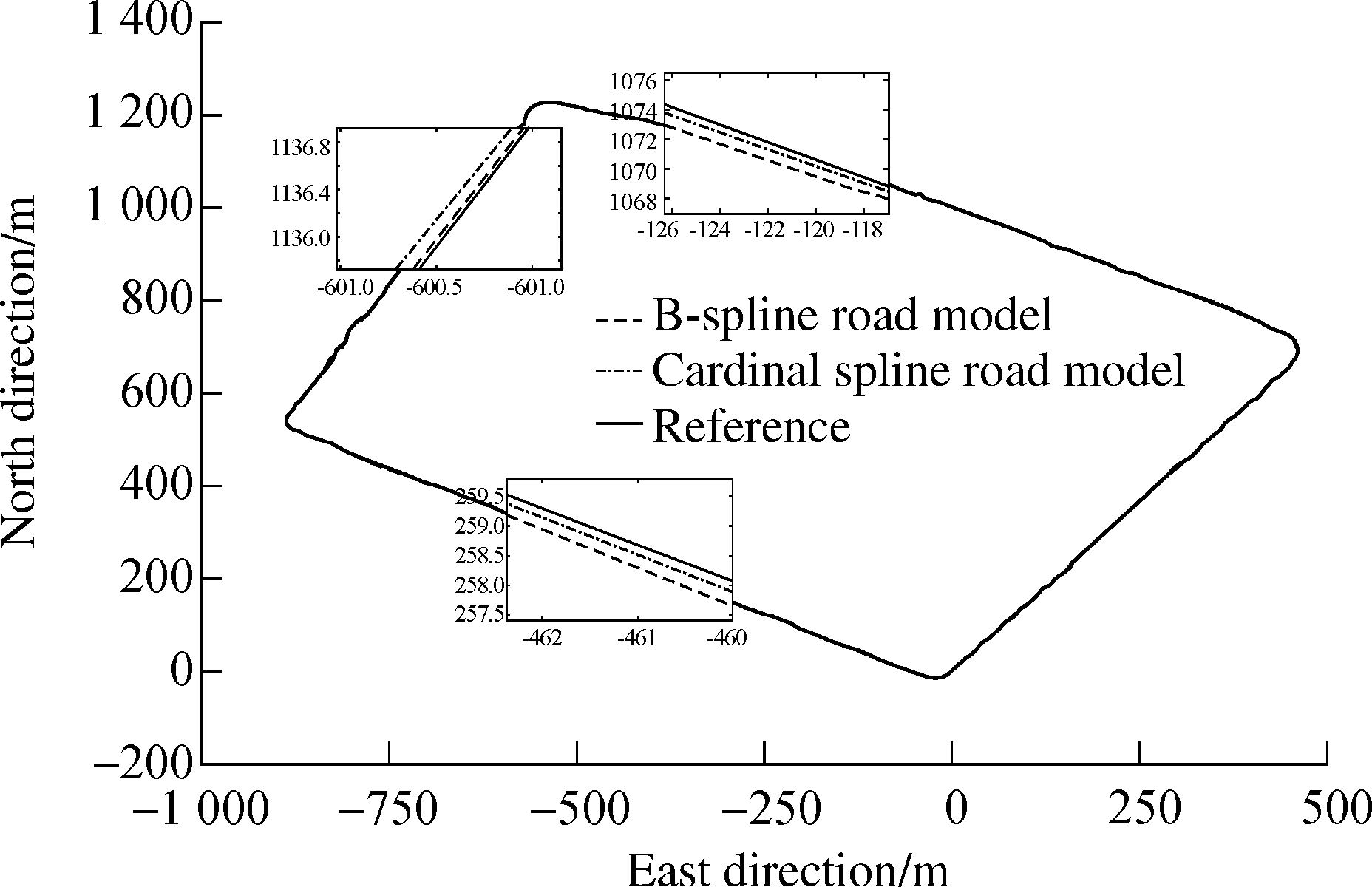
Fig.4 Efficiency comparison of two methods
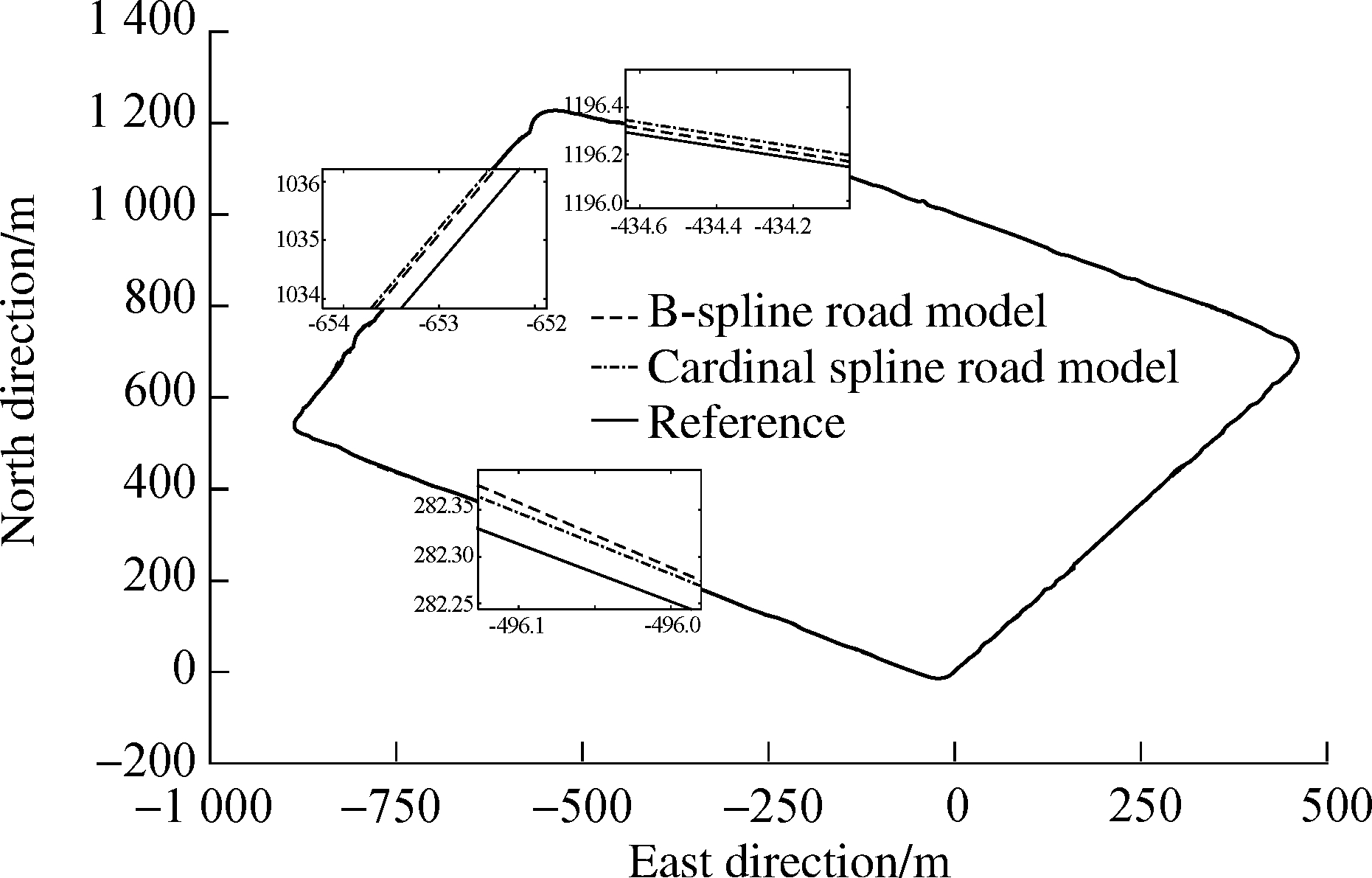
Fig.5 Reliability comparison of two methods
From the comparison results above, the B-spline road modeling method achieves the global accuracy of 1.25 m by using 1 142 floating-point numbers and achieves the global accuracy of 2.83 m by using 578 floating-point numbers.Meanwhile, the cardinal spline road modeling method proposed in this paper achieves the global accuracy of 1.25 m by using 578 floating-point numbers.Fig.4 shows the efficiency comparison of two methods.Results show that the cardinal spline road modeling method uses fewer data points to meet a desired global accuracy than the B-spline road modeling method does.Fig.5 shows the reliability comparison of two methods.Results show that the cardinal spline road modeling method achieves a better global accuracy than the B-spline road modeling method does in the case of using the same number of data points.It is obvious that the cardinal spline road modeling method outperforms the B-spline road modeling method.In general, this method commendably realizes a near-optimal balance between the efficiency and reliability requirements.
3 Conclusion
In this paper, we have studied a road modeling method for digital maps based on the cardinal spline that can balance the efficiency and reliability requirements.A probe vehicle equipped with a single-enclosure GPS+INS positioning system measured the raw roadway geometry data.Also, a gradual optimization algorithm is presented to determine reasonable control points from the raw data points according to the degree of the change of road curvature.The gradual optimization algorithm can ensure that the near-minimum number of the control points and optimal tension parameters for the cardinal spline road model are selected to achieve desired accuracy.The experiments demonstrate that compared with the conventional method based on B-spline,the proposed road modeling method occupies less data storage and achieves higher accuracy.
References
[1]Jo K, Sunwoo M.Generation of a precise roadway map for autonomous cars[J].IEEE Transactions on Intelligent Transportation Systems, 2014, 15(3): 925-937.DOI:10.1109/tits.2013.2291395.
[2]Kim S W, Liu W, Ang M H, et al.The impact of cooperative perception on decision making and planning of autonomous vehicles [J].IEEE Intelligent Transportation Systems Magazine, 2015, 7(3): 39-50.DOI:10.1109/mits.2015.2409883.
[3]Gwon G P, Hur W S, Kim S W, et al.Generation of a precise and efficient lane-level road map for intelligent vehicle systems [J].IEEE Transactions on Vehicular Technology, 2017, 66(6): 4517-4533.DOI:10.1109/tvt.2016.2535210.
[4]Guo C, Kidono K, Meguro J, et al.A low-cost solution for automatic lane-level map generation using conventional in-car sensors [J].IEEE Transactions on Intelligent Transportation Systems, 2016, 17(8): 2355-2366.DOI:10.1109/tits.2016.2521819.
[5]Du J, Barth M J.Next-generation automated vehicle location systems: Positioning at the lane level [J].IEEE Transactions on Intelligent Transportation Systems, 2008, 9(1): 48-57.
[6]Ziegler J, Bender P, Schreiber M, et al.Making Bertha drive—An autonomous journey on a historic route [J].IEEE Intelligent Transportation Systems Magazine, 2014, 6(2): 8-20.
[7]Jiménez F, Naranjo J E, García F, et al.Limitations of positioning systems for developing digital maps and locating vehicles according to the specifications of future driver assistance systems [J].IET Intelligent Transport Systems, 2011, 5(1): 60-69.DOI:10.1049/iet-its.2010.0042.
[8]Okaniwa S, Nasri A, Lin H, et al.Uniform B-spline curve interpolation with prescribed tangent and curvature vectors [J].IEEE Transactions on Visualization and Computer Graphics, 2012, 18(9): 1474-1487.
[9]Ben-Arieh D, Chang S, Rys M, et al.Geometric modeling of highways using global positioning system data and B-spline approximation [J].Journal of Transportation Engineering, 2004, 130(5): 632-636.DOI:10.1061/(asce)0733-947x(2004)130:5(632).
[10]Wedel A, Badino H, Rabe C, et al.B-spline modeling of road surfaces with an application to free-space estimation [J].IEEE Transactions on Intelligent Transportation Systems, 2009, 10(4): 572-583.DOI:10.1109/tits.2009.2027223.
[11]Zhang T, Arrigoni S, Garozzo M, et al.A lane-level road network model with global continuity [J].Transportation Research Part C: Emerging Technologies, 2016, 71(1): 32-50.DOI:10.1016/j.trc.2016.07.003.
[12]Bhandari A, Marziliano P.Fractional delay filters based on generalized cardinal exponential splines [J].IEEE Signal Processing Letters, 2010, 17(3): 225-228.DOI:10.1109/lsp.2009.2036386.
[13]Wang S, Qin S, Guan C.Feature-based human model for digital apparel design [J].IEEE Transactions on Automation Science and Engineering, 2014, 11(2): 620-626.DOI:10.1109/tase.2014.2300876.
[14]NovAtel Inc.SPAN-CPT single enclosure GNSS/INS receiver[EB/OL].(2017-01-05)[2017-08-31].http://www.novatel.com/support/info/documents/564.