Welding assembly is a main joining method in actual industry products and it is widely applied to various kinds of metal structure assembly and fabrication, such as aerospace and aircraft, radar antennas, automobile, marine vessel structures, etc[1-2].Particularly, the assembly precision for the thin-wall welding assembly structure plays an important role in product functionality and overall performance. In the welding assembly process for thin-wall parts, different variations and welding temperatures will affect assembly structure deformation. The effect of the welding temperature on welding deformation and welding stress is significant in the welding process for thin-wall parts, while the welding deformation and welding stress have an influence on welding precision. Therefore, the research on welding temperature field distribution is essential for the actual welding assembly process for thin-wall parts.
The thin-wall welding assembly, including aeronautical thin-wall structures assembly, aircraft panel assembly and so on, has been studied and analyzed by many researchers. Murakawa et al.[3-5]proposed a prediction method for the welding distortion of thin plate structures in the welding assembly process based on the inherent stress theory and interface element formulation. Moreover,thermal elastic plastic FE analysis, eigenvalue analysis, the elastic FE analysis method and the three-dimension thermal elastic-plastic FE model are adopted to predict and calculate the welding deformation for thin plate structures. Moein et al.[6]predicted the residual stress states for the butt-welded aluminum alloy plates through FE welding simulation. Ikushima et al.[7-8] proposed an idealized explicit FE method based on the iterative substructure method to analyze welding deformation and residual stress for the large scale problem of the welding process. Chen et al.[9] proposed the thermal elastic-plastic FE model to deal with the welding simulation for a plate structure considering heat input and welding speed, which aims to analyze welding distortion. Choi et al.[10] proposed a variable simulation model to analyze welding joining process distortion for the ship structure. Joo et al.[11] analyzed the effect of heat sinks on the welding deformation and stress through FE simulation. Zeng et al.[12] developed a local equivalent welding element type to carry out welding simulation. Huang et al.[13] employed a local solid model and global shell model based on the inherent stress theory to predict laser welded deformation for thin sheets. C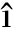
ndea et al.[14] analyzed the effect of thermal field on steel components under the CO2 environment in welding process. Das et al.[15] studied the friction stir lap welding of aluminum alloy to coated steel sheets under different tool rotational speeds and welding speeds to analyze the welding strength. Okano et al.[16] considered the convective heat transfer in the welded pool to analyze the relationship between welding heat input and angular distortion and the effect of welded thickness on the angular distortion. However, fewer researchers pay attention to the influence of various comprehensive factors on the welding assembly temperature distribution for thin-wall parts, including welding direction, different welding thicknesses, welding parameters and welding heat source parameters, etc.
In this paper, the welding thermal characteristics of T-shape thin-wall assembly parts of different thicknesses are emphatically analyzed by finite element simulation and the multiscale modeling method. Simultaneously, the heat source model is established, and different welding technology parameters, heat source parameters and welding directions are taken into account to analyze temperature field distribution under the conditions of 6, 12 and 18 mm away from the bottom of welding joining thin-wall part. Furthermore, the fillet weld with different parameters is employed to analyze the temperature distribution for thin-wall parts of three kinds of thicknesses.
1 Welding Structure Finite Element Model for Thin-Wall Parts Assembly
There is a large number of parts in the antenna thin-wall parts assembly process including riveting assembly and welding assembly, and the assembly relationship between those parts is very complicated. The tooling layout, the locating way of location elements, the clamping method of clamping the elements, the position or location relationship of the thin-wall parts are also taken into consideration. The local assembly structure model for an antenna thin-wall part is shown in Fig.1.
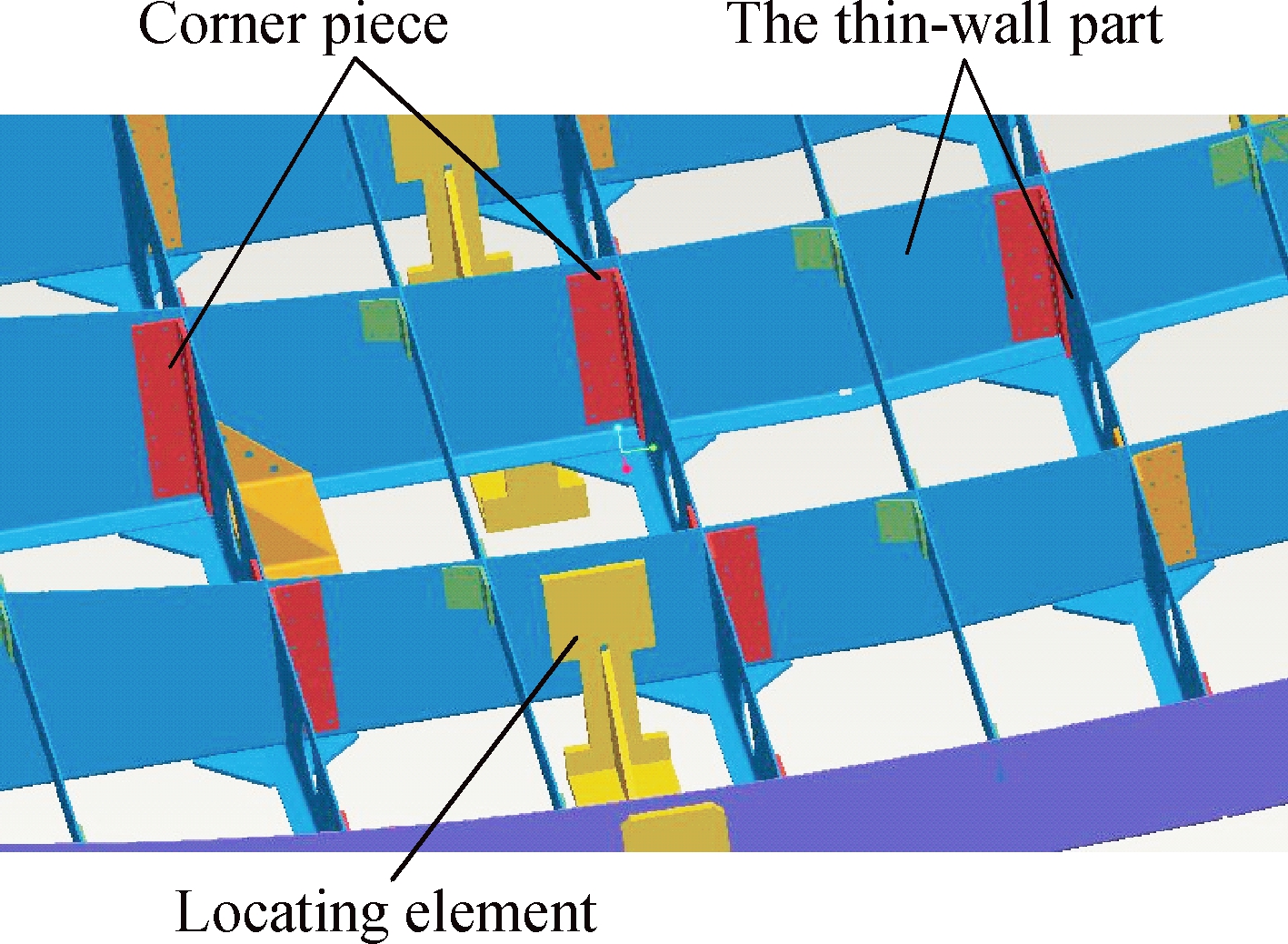
Fig.1 Assembly structure model for an antenna thin-wall part
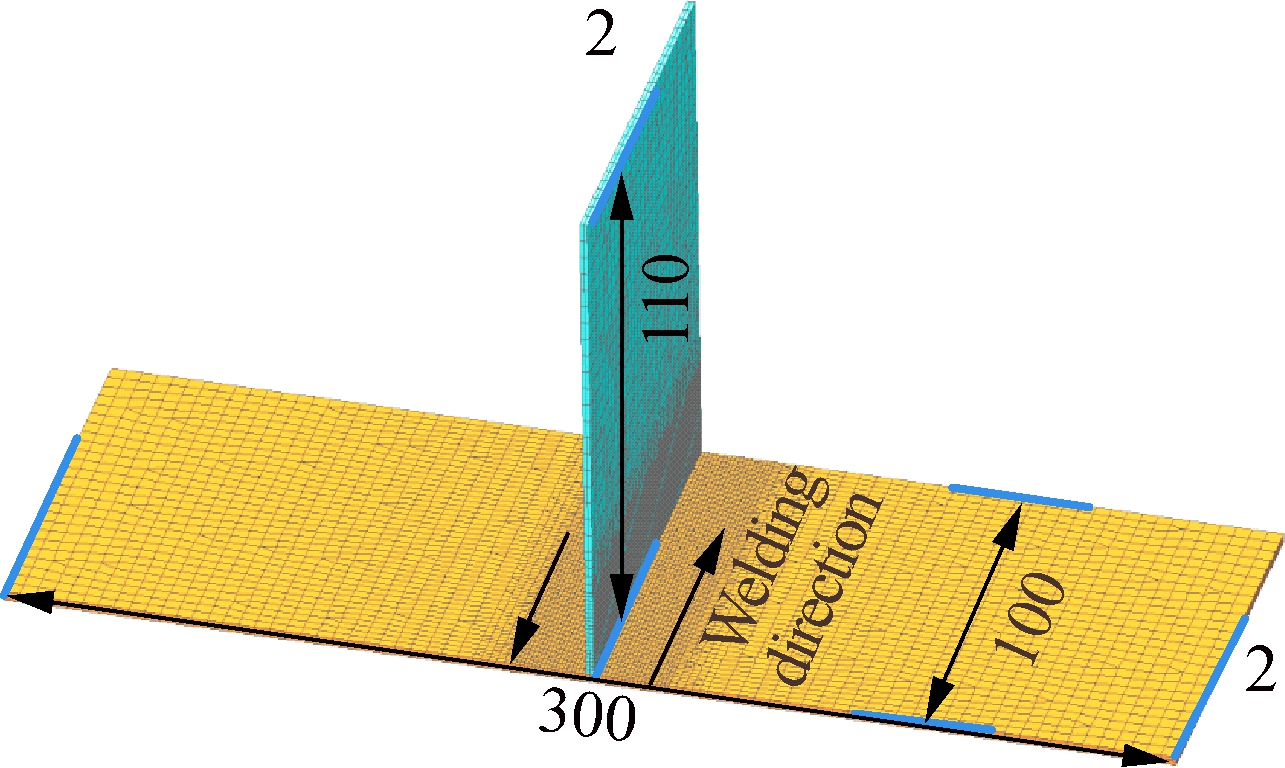
In addition, in order to meet the requirement of assembly accuracy for thin-wall parts, the position of every component in the previous actual assembly process needs to be constantly adjusted. Due to the riveting or welding assembly for the thin-wall parts and other components assembly, assembly deformation and errors will be generated, especially in the welding assembly process. The welding temperature can greatly affect the thin-wall parts deformation and assembly deformation. Therefore, in this paper, the welding thermal characteristics for thin-wall part assembly are mainly studied and analyzed, the T-shape thin-wall part assembly structure model especially is taken as a welding assembly research object, which is a local structure from the overall assembly structure model. What is more, the effect of welding direction on the welding thermal characteristic is taken into consideration. Therefore, the welding direction is represented by the black arrow and its size is shown in Fig.2, including the thickness of 2, 4 and 6 mm. Simultaneously, when the influence of the other welding direction on the welding characteristic is analyzed, their welding directions are shown in Fig.2(d), and their thicknesses correspond to the thickness of thin-wall parts in Figs.2(a),(b) and (c). For the FE model of T-shape assembly structure,since the mesh element far away from the contact zone has less impact on the welding temperature, in order to save calculation time, the mesh element is very dense near the contact zone between two thin-wall parts. Also, the mesh element is relatively sparse away from the contact zone, which is beneficial for the accuracy of finite element simulation by multiscale modeling.
(a)
(b)
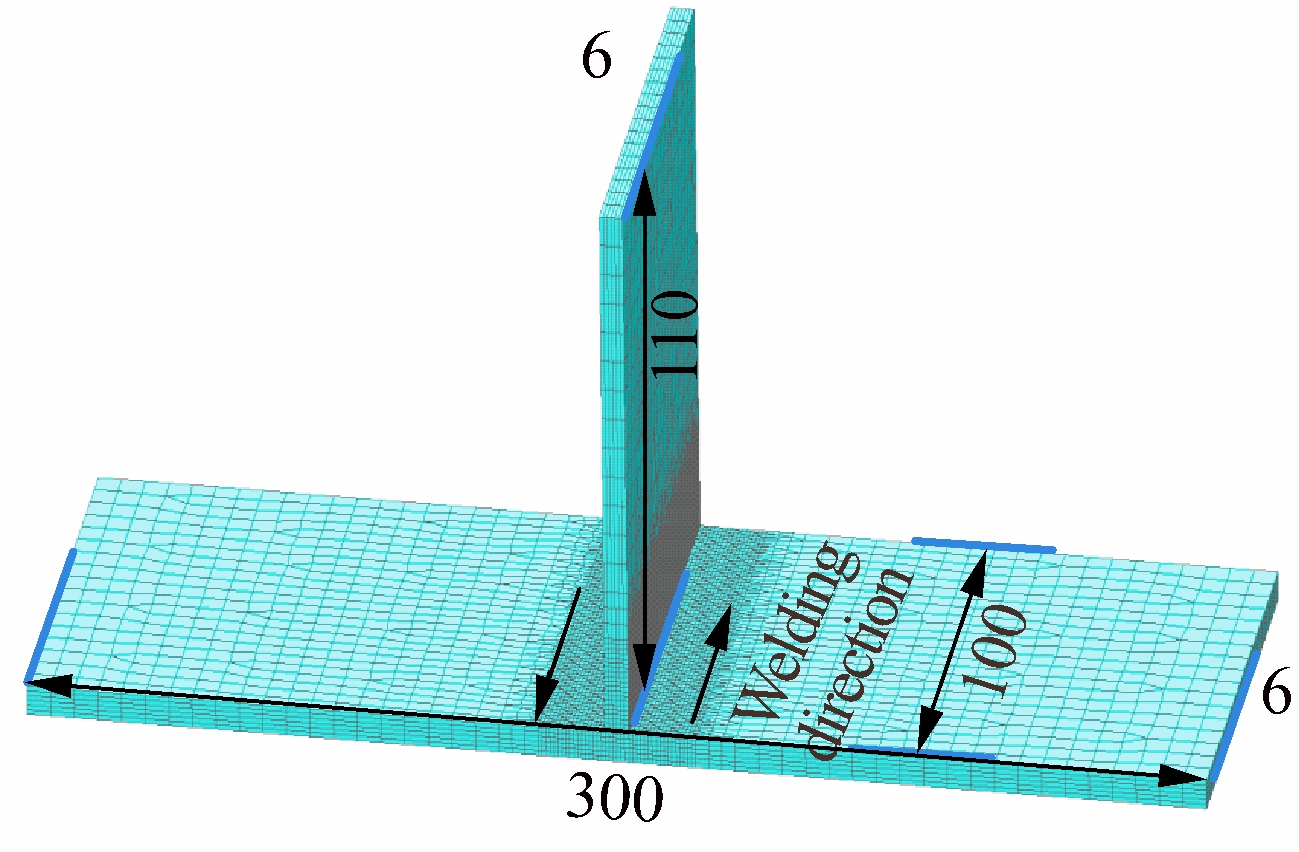
(c)
(d)
Fig.2 Finite element model of T-shape thin-wall assembly structure for different thicknesses and different welding directions. (a) With the thickness of the thin-wall part of 2 mm; (b) With the thickness of the thin-wall part of 4 mm; (c) With the thickness of the thin-wall part of 6 mm; (d) For thin-wall assembly structure
2 Establishment of Heat Source Model
In the welding process, in order to control and reduce welding deformation, the welding heat source for higher energy density is generally adopted. The whole welding process is a complicated heat reaction process by moving the welding arc. The heat of welding heat source is partially transferred to the thin-wall parts of the aluminum alloy material, which has a certain influence on the heating area. In order to effectively analyze the welding deformation and temperature field distribution of thin-wall parts, it is necessary to determine the type of welding heat source in the welding assembly process. In this paper, the double ellipsoid heat source type is adopted. The heat source model is shown in Fig.3.
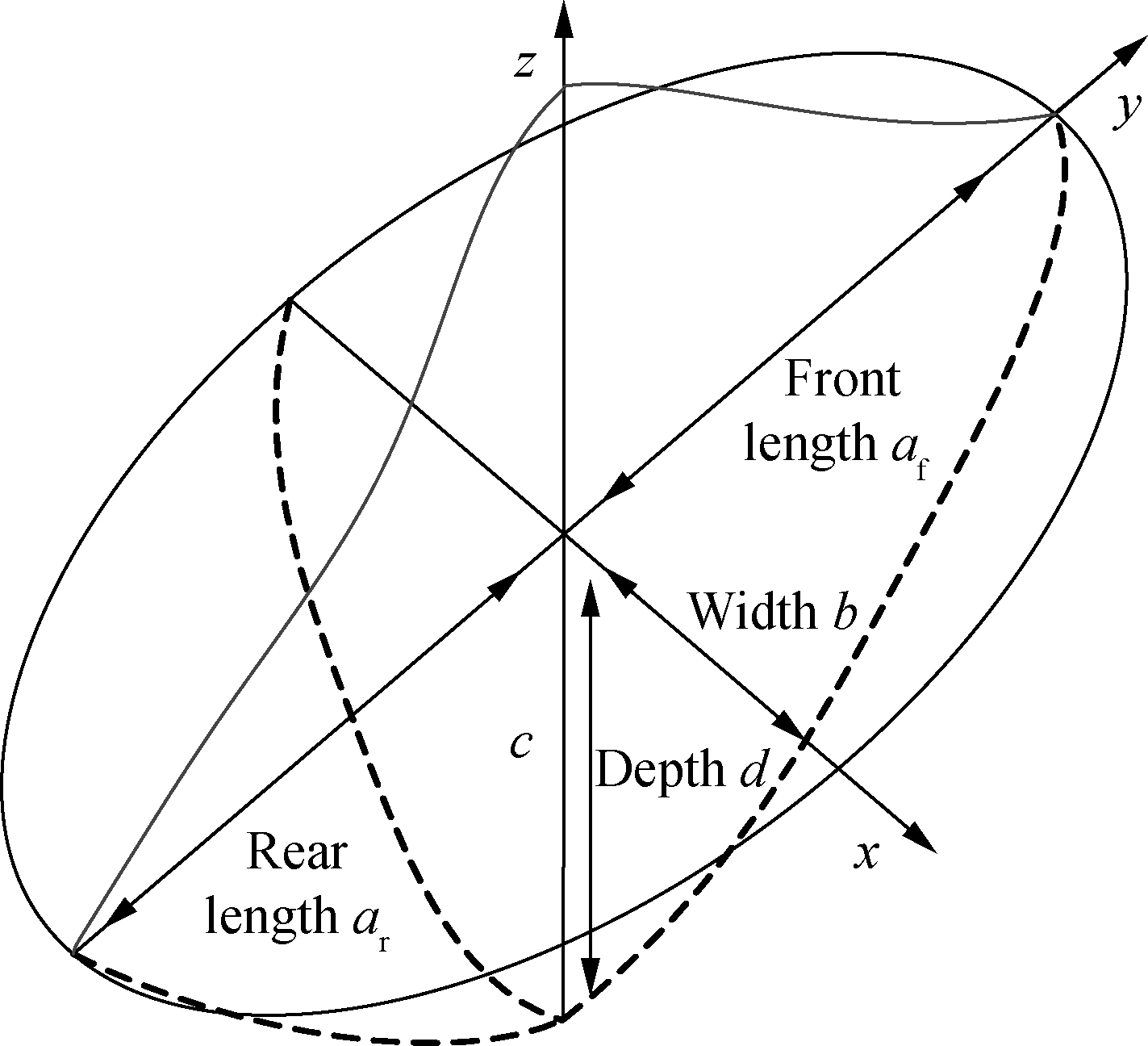
Fig.3 Double-ellipsoid heat source model
In the calculation process of ellipsoid heat source density function, it is found that the first half ellipsoid does not abruptly change like the actual temperature gradient, while the temperature gradient distribution of the second half ellipsoid is slower. In order to overcome this shortcoming, the double ellipsoid heat source distribution function is proposed, where the first half part is the quarter ellipsoid and the second half part is the other quarter ellipsoid. It is assumed that the energy fraction of the first half ellipsoid is ff, and the energy fraction of the second half ellipsoid is fr, where ff+fr=2, and then the heat source distribution function of the first half ellipsoid is expressed as[17]
(1)
Similarly,the heat source distribution function of the latter half ellipsoid is
(2)
where Qf and Qr represent the thermal input of front and rear parts of the ellipsoid; af and ar denote the length of front and rear parts of the ellipsoid; b and c are the width and penetration depth, respectively, and they are independent from each other. While welding different materials, parameters af, ar, b and c have different values, and the parameters are shown in Fig.3.
Simultaneously,in the welding process, the welding heat source is applied to the welds by the internal generated heat of weld unit, and the effective heat input will be converted into the heat generation intensity, which is[18]
(3)
where U and I represent the welding voltage and welding current, respectively; η denotes the thermal efficiency; V is the weld element volume, m3; λ is the volumetric coefficient which can fine-tune the heat flux to achieve temperature distributions, λ=1.
According to the above formulas, the relative parameters can be obtained to carry out FE simulation analysis. In this paper, the heat source parameters in Tab.1 are adopted to calculate thermal input and heat source distribution. When carrying out the FE simulation, those parameters are input, synthesizing with the parameters of other factors to analyze and compare the obtained simulation results, which will provide a comparable foundation for thermal characteristics analysis for thin-wall welding assembly structures.
Tab.1 Heat source parameters of the thin-wall assembly part with different thicknesses
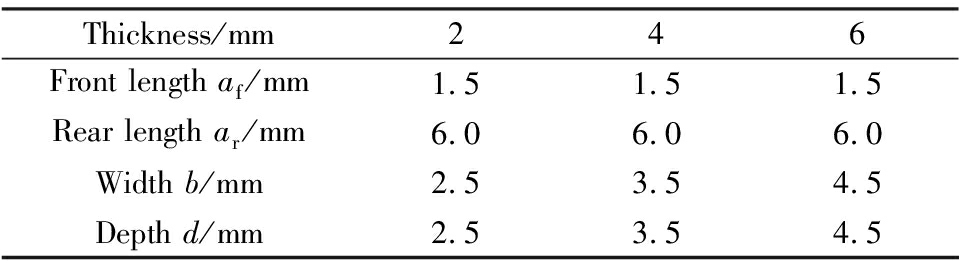
Thickness/mm2 4 6 Front length af/mm1.51.51.5Rear length ar/mm6.06.06.0Width b/mm2.53.54.5Depth d/mm2.53.54.5
3 Thermal Characteristics Analysis for Welding Assembly
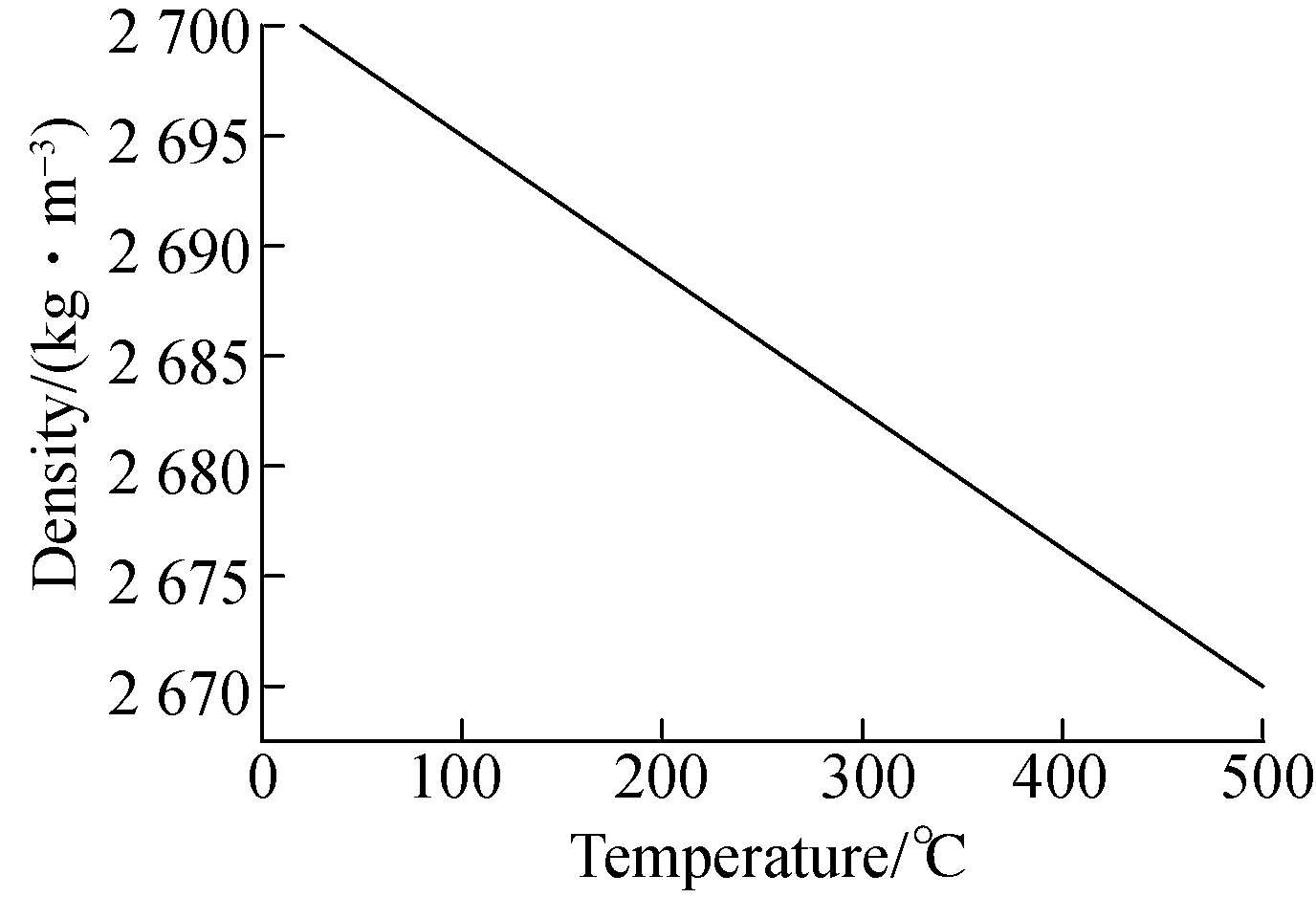
In this paper, the material of the thin-wall welding assembly structure for T-shape is 6082 aluminum alloy. The material properties are constantly changing with variable temperatures to some extent. The Poisson’s ratio is adopted to be 0.32 in finite element simulation analysis. Other mechanical property parameters and thermal property parameters, such as Young’s modulus, density, thermal conductivity, specific heat capacity, and thermal expansion coefficient, are also continually changing. Their changing curves with variable temperatures are shown in Fig.4. Simultaneously, the thermal characteristics of the thin-wall welding assembly structure are analyzed by finite element simulation under the constraint conditions of the bottom four corners of T-shape thin-wall assembly part being fixed and the middle top zone of the vertical thin-wall part being clamped. Also, the material property parameters are inputted to obtain the temperature distribution results of T-shape thin-wall assembly structures.
(a)
(b)
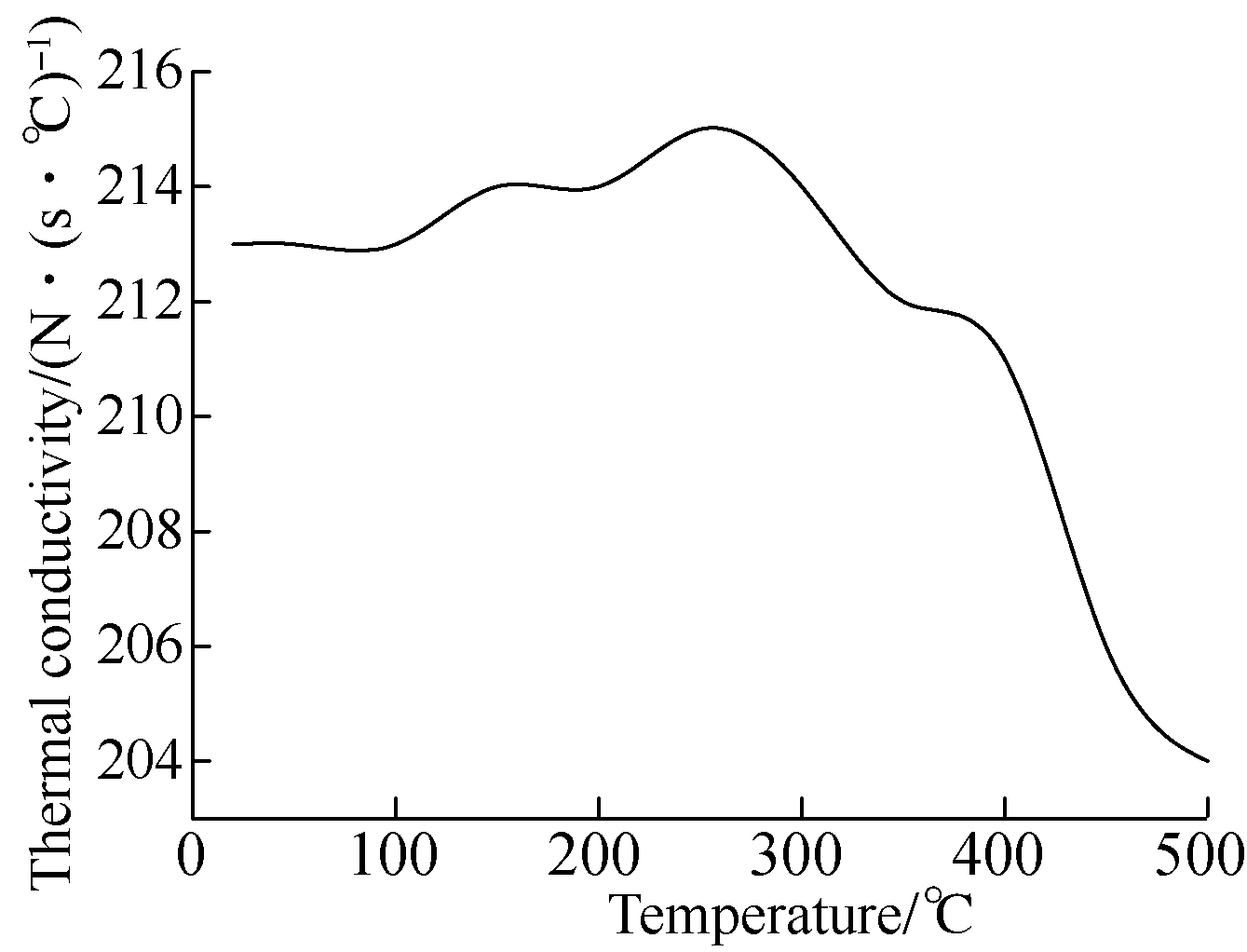
(c)
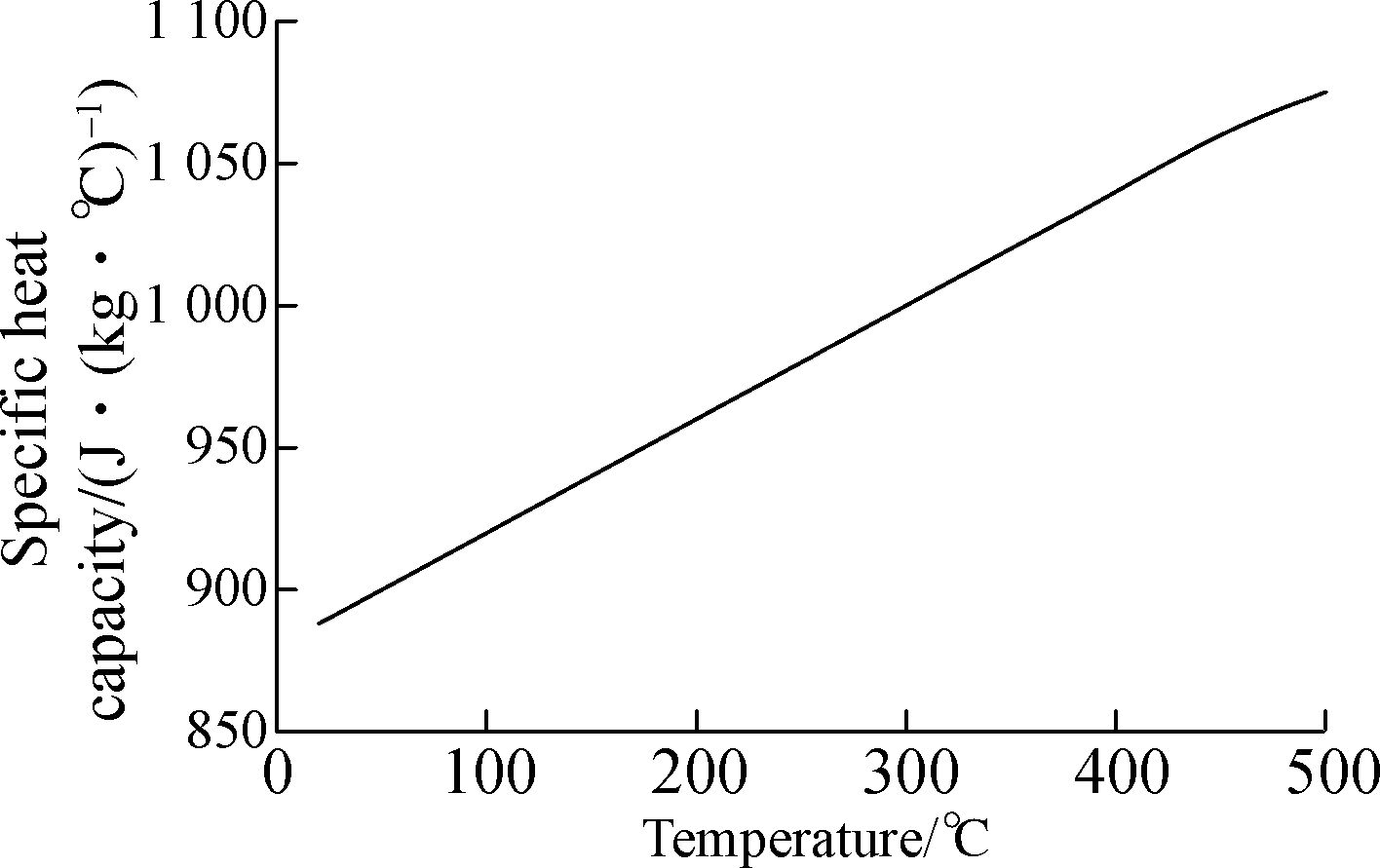
(d)
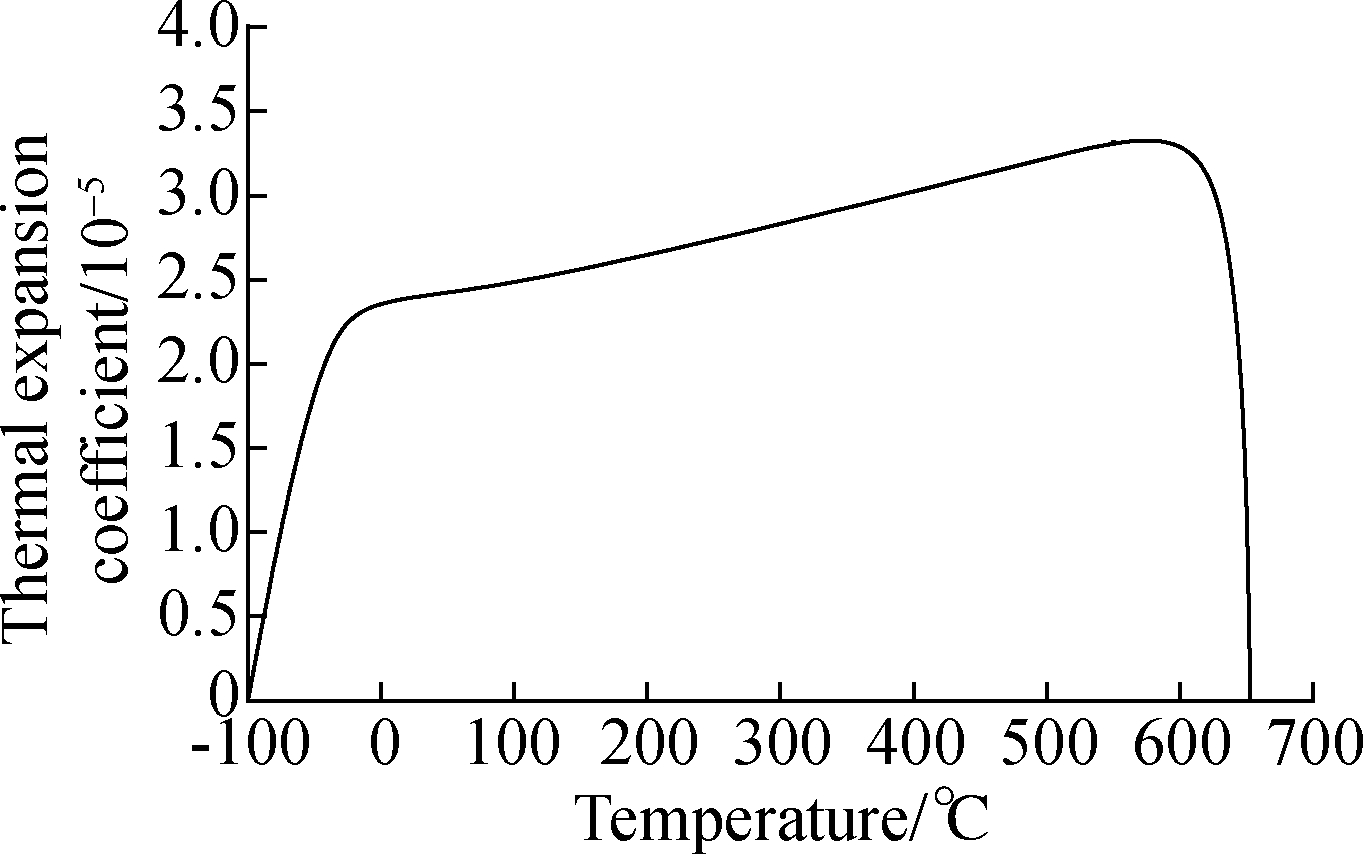
(e)
Fig.4 The material property parameter curves with variable temperatures. (a) Young’s modulus; (b) Density; (c) Thermal conductivity;(d) Specific heat capacity; (e) Thermal expansion coefficient
In addition, the weld line parameters of three different thicknesses of the T-shape thin-wall welding parts are set, namely the weld widths of the thin-wall welding assembly structures are 4, 6 and 8 mm, respectively. In this paper, its weld type is the fillet weld, and the weld line finite element model is shown in Fig.5.
Fig.5 The weld line finite element model
Due to the effect of many factors on temperature field distribution for welding assembly, in this paper, the welding direction, the thin-wall parts thickness and the welding process are taken into account to analyze the thermal characteristics of welding assembly for thin-wall parts. For the thin-wall welding assembly structure with the thickness of 2, 4 and 6 mm, in order to better analyze the welding temperature distribution, the welding parameters with the welding voltage of 20 V, the welding current of 180 A, the welding velocity of 12 mm/s and the welding efficiency of 0.8 are given. Under the above constraint conditions, their temperature distribution nephogram for different times are shown in Fig.6.
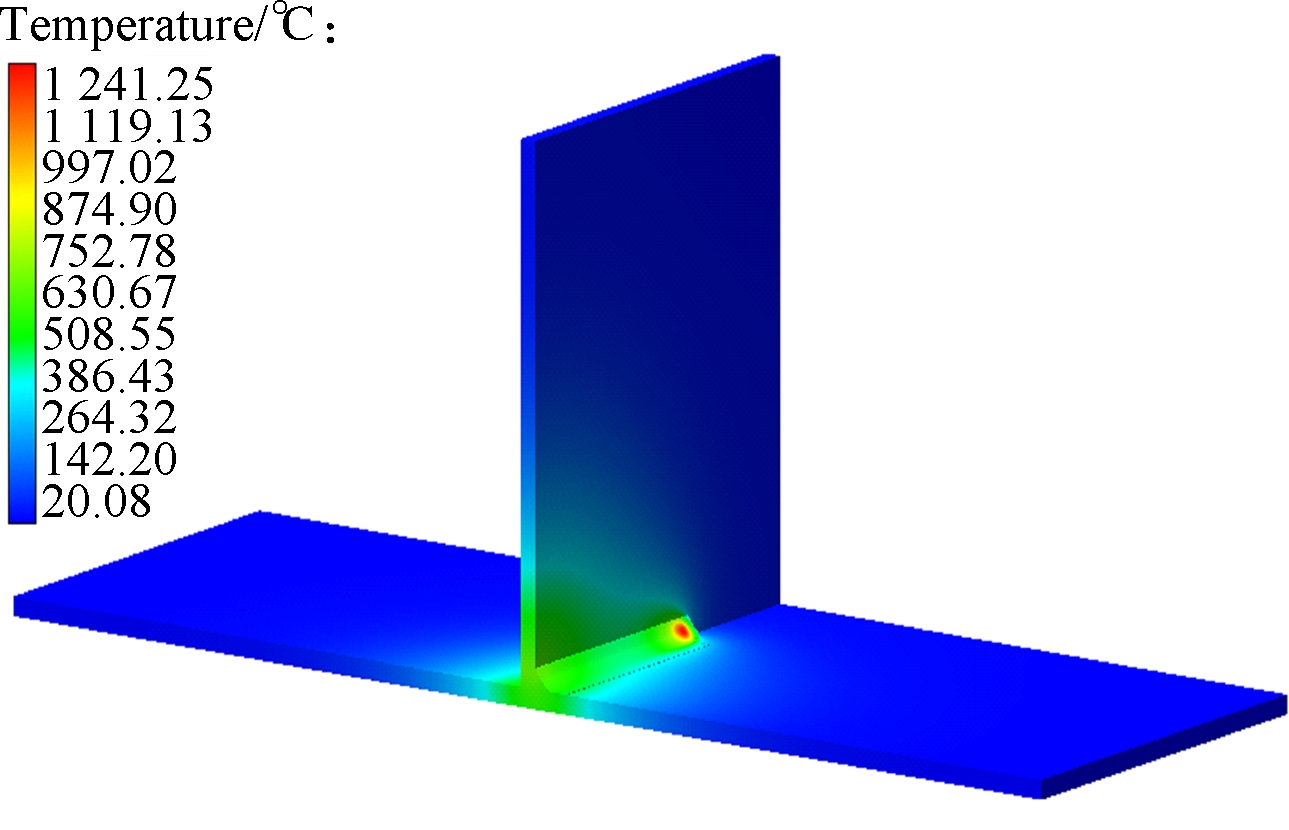
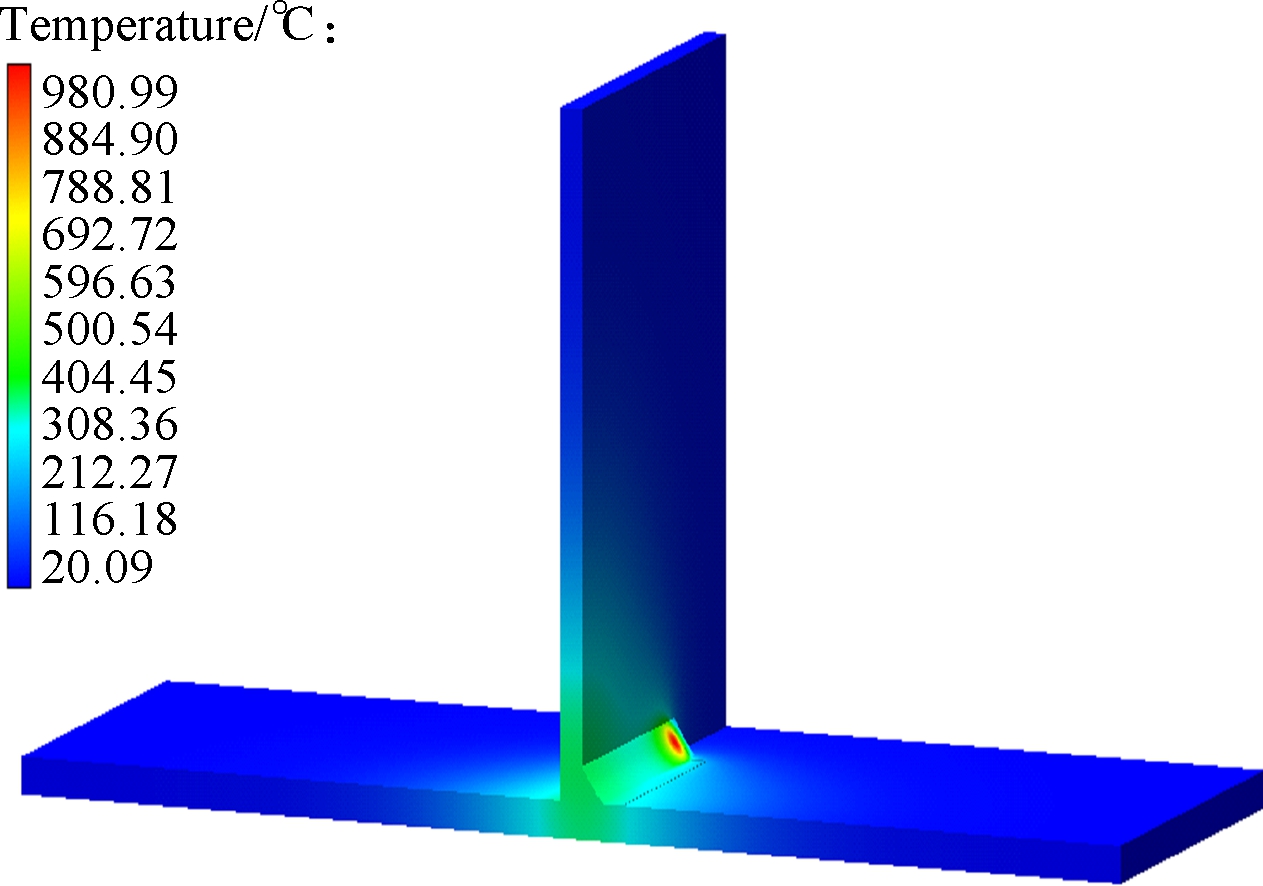
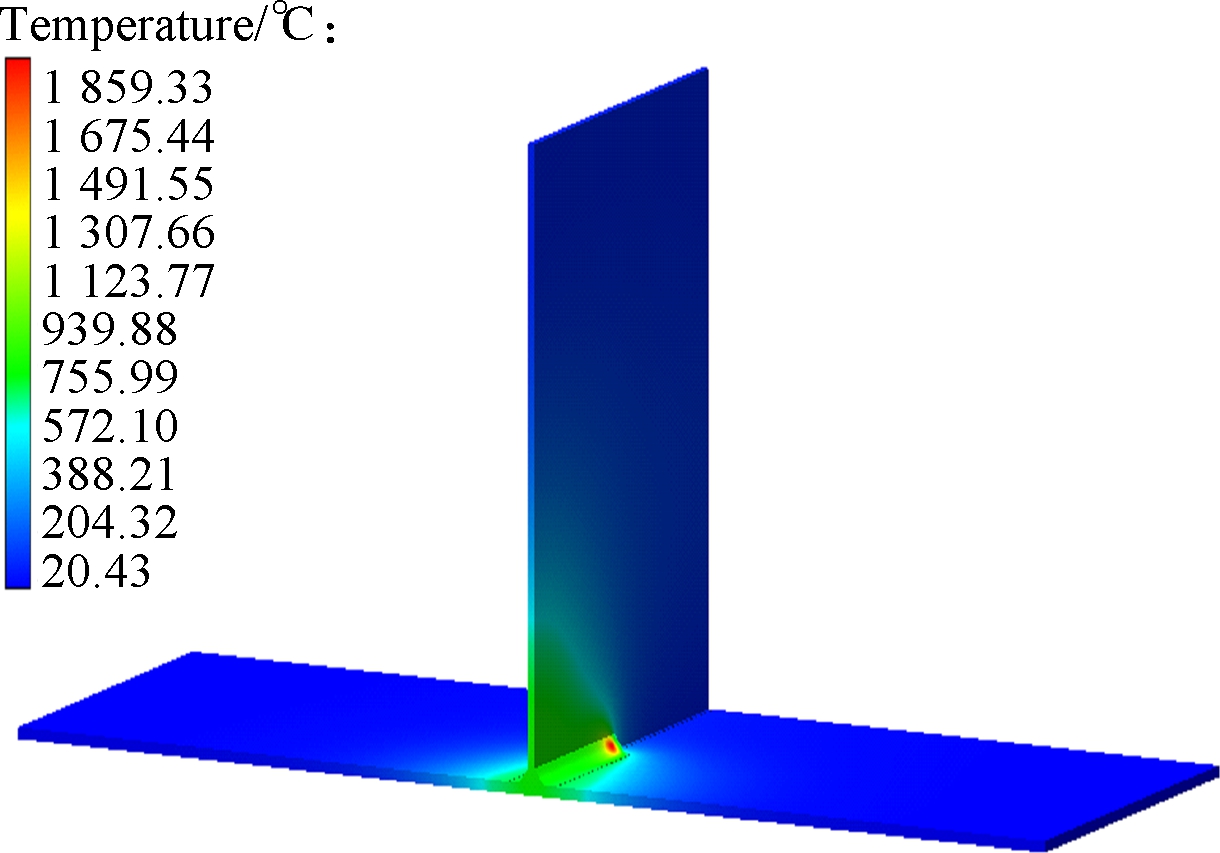
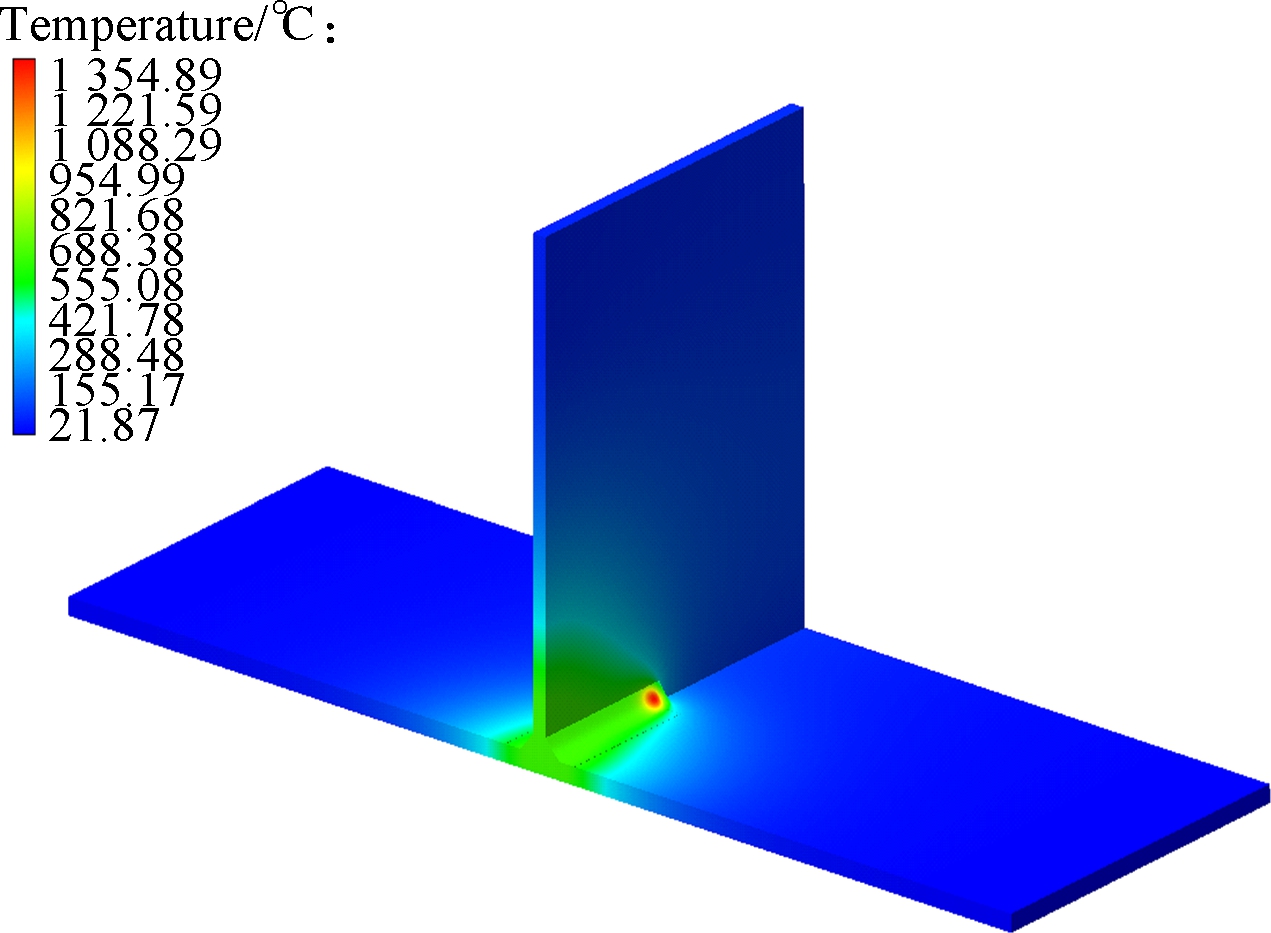
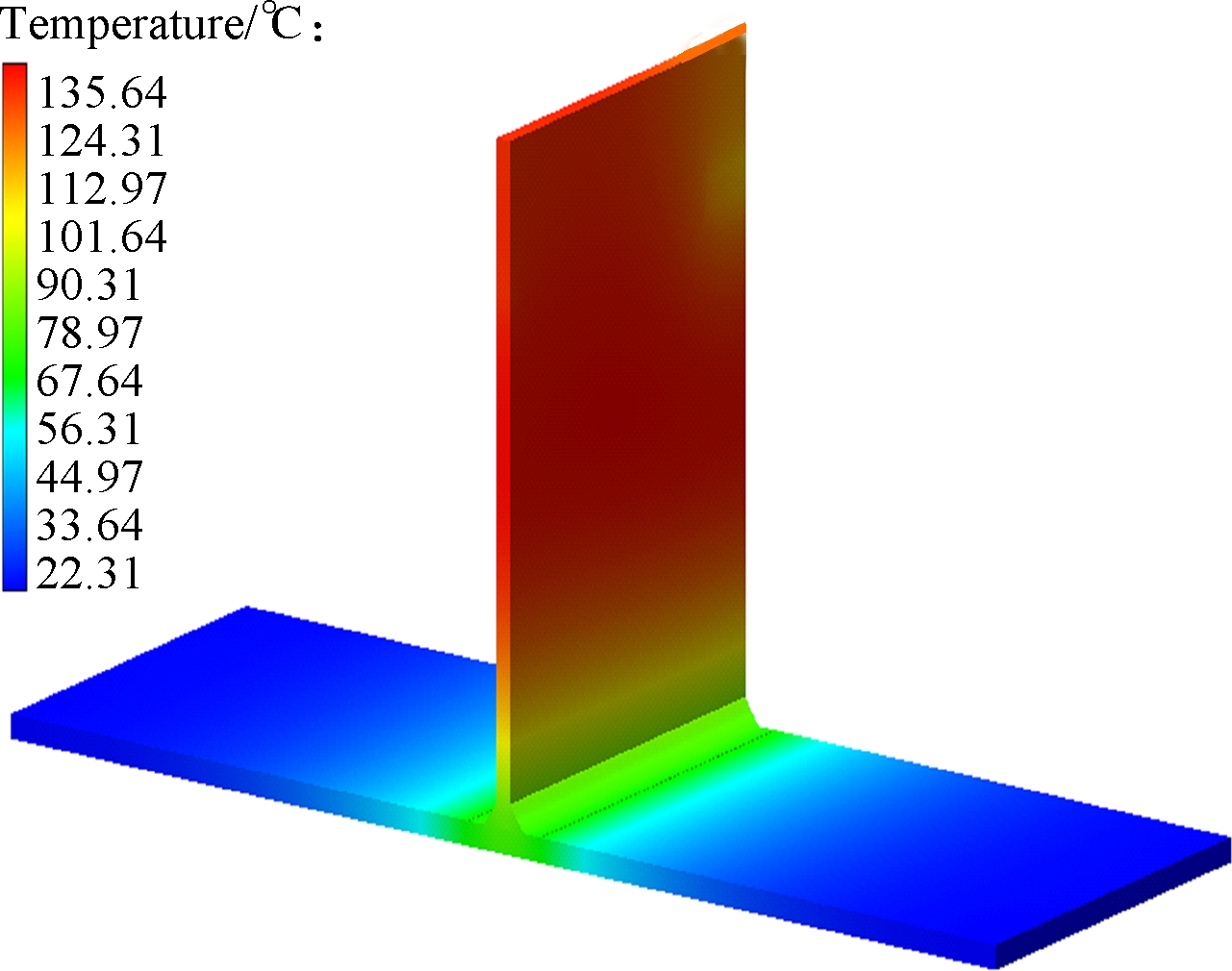
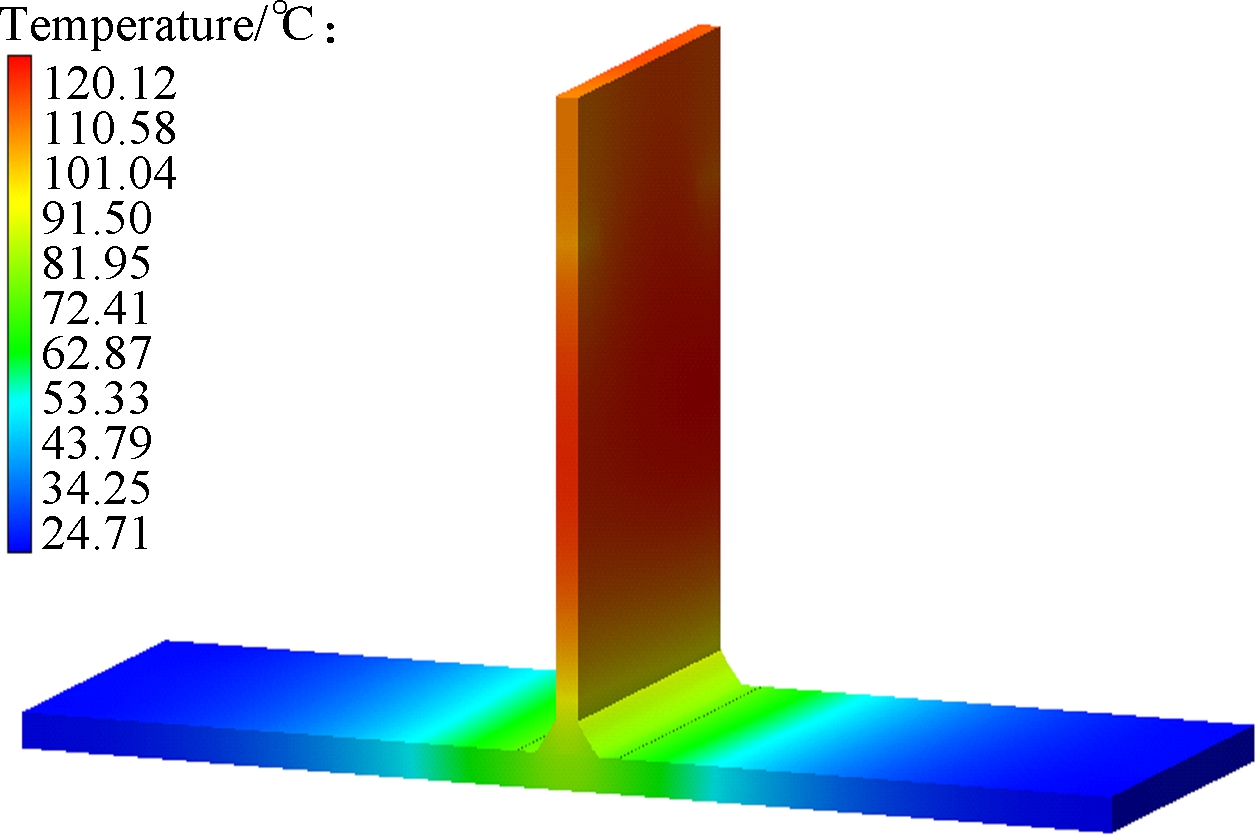
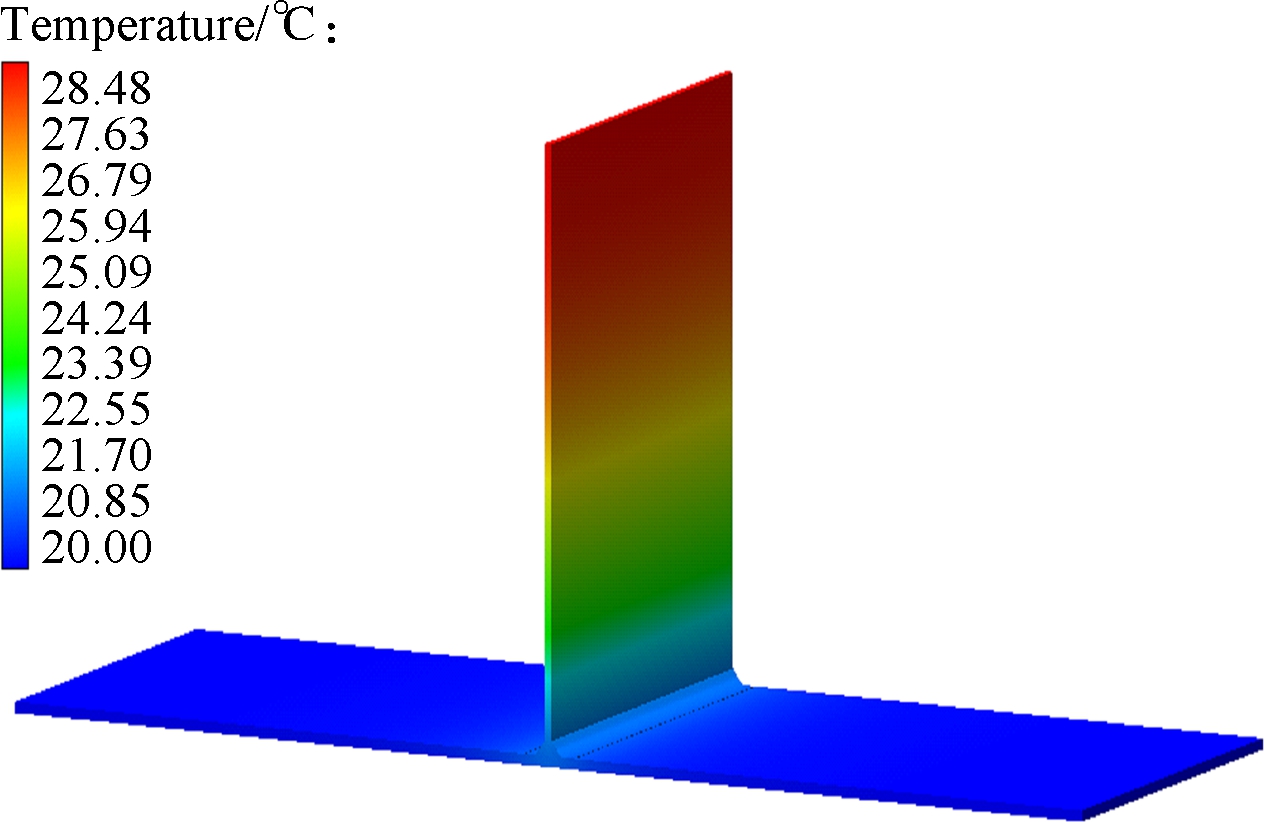
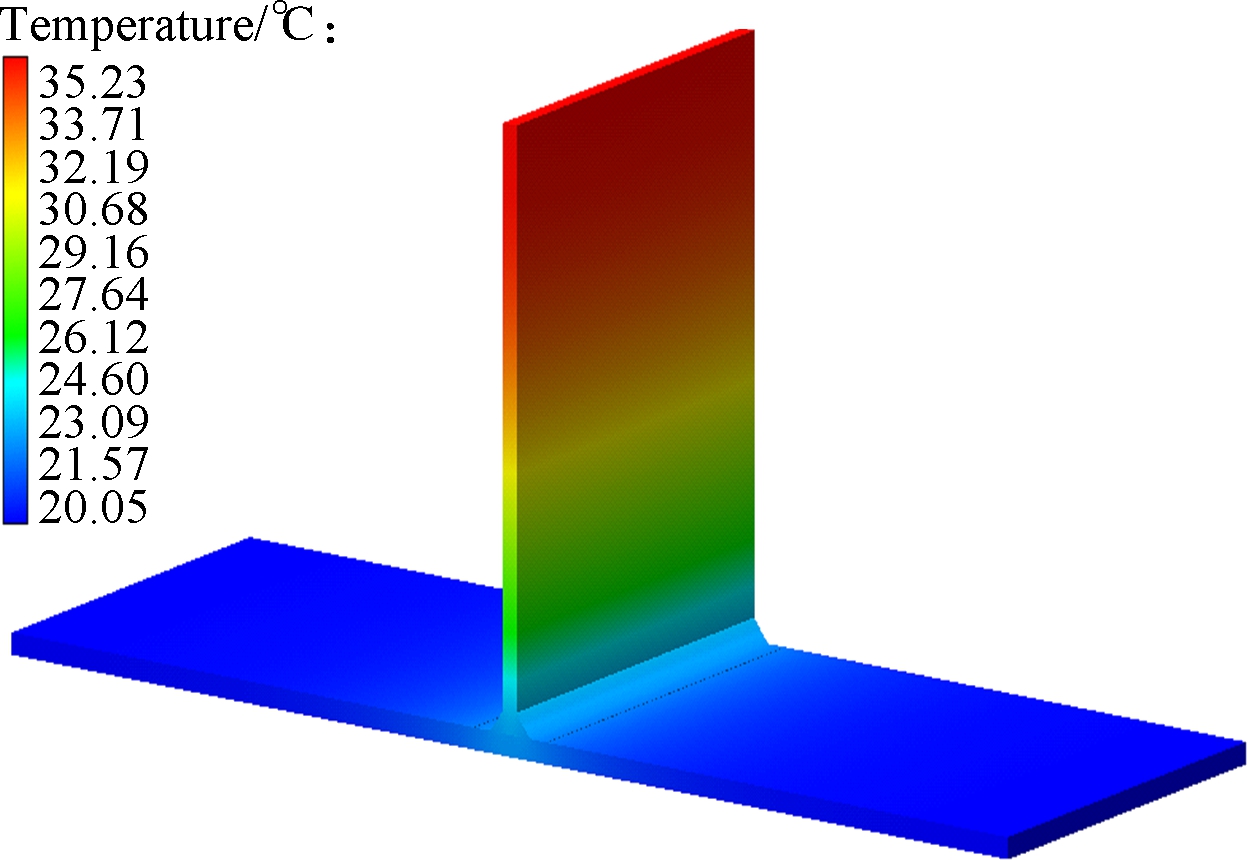
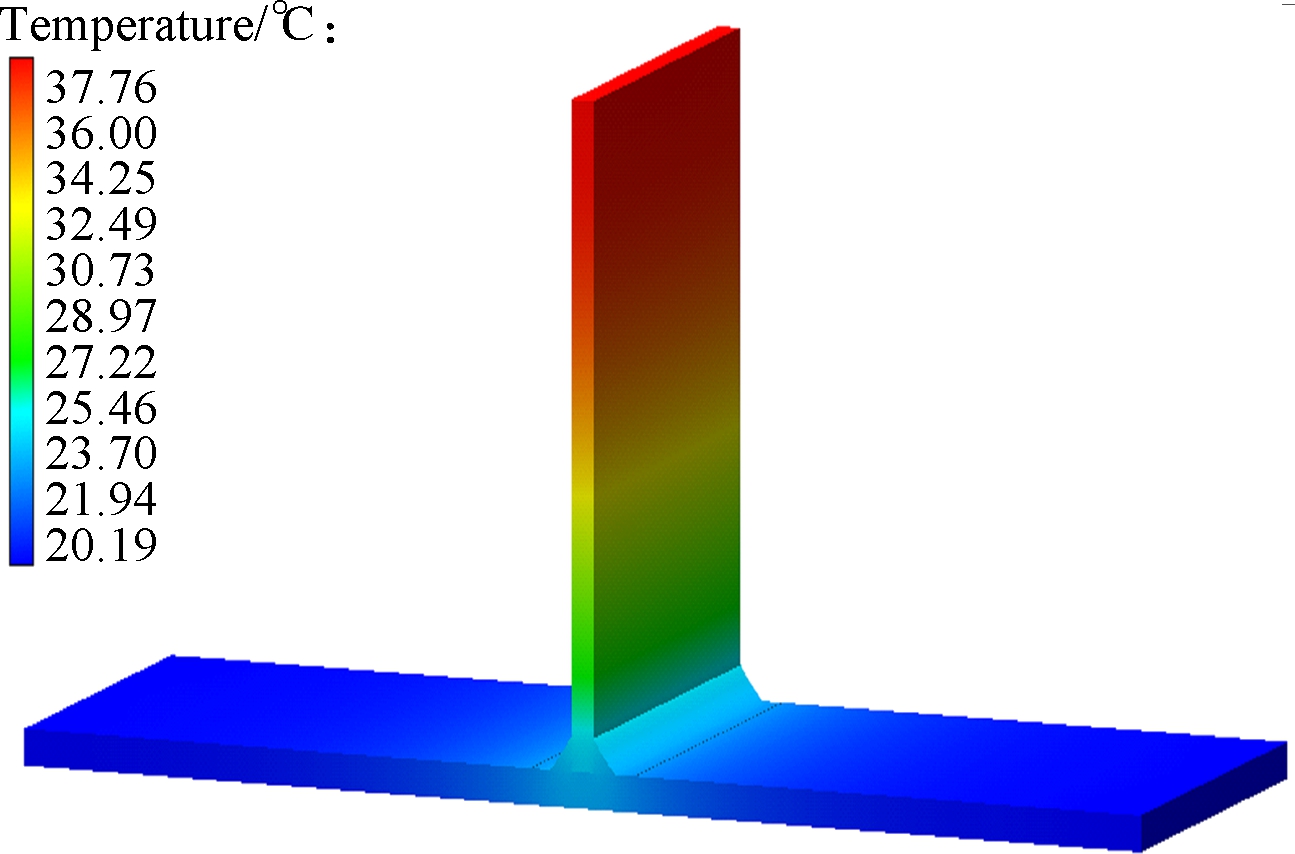
Figs.6(a) to (c) are the group with temperature distribution nephogram at 15 s, Figs.6(d) to (f) are the group with temperature distribution nephogram at 32 s, Figs.6(g) to (i) are the group with temperature distribution nephogram at 60 s, Figs.6(j) to (l) are the group with temperature distribution nephogram at 180 s, and their welding direction for different thicknesses of thin-wall parts are, respectively, shown in Figs.2(a),(b) and (c). T2-15s denotes that the thickness of the thin-wall assembly structure is 2 mm, the temperature distribution is at 15 s, and the welding direction is shown in Fig.2(a). In Figs.6(a) to (c),for the thin-wall assembly structure of three different thicknesses, their maximum temperatures are 1 816.46, 1 241.25 and 980.99 ℃, respectively, when it is at 15 s. In Figs.6(d) to (f), the maximum temperatures are 18 59.33, 1 354.89 and 1 096.71 ℃, respectively. Furthermore, in Figs.6(g) to (i), for the thin-wall assembly structure of three different thicknesses, their maximum temperatures are 150.34, 135.64 and 120.12 ℃, respectively. At this moment, the welding joining process has been completed, and the welding process is in the cooling process, in which the temperature will be decreased to the ambient temperature of 20 ℃. In Figs.6(j) to (l), for the thin-wall assembly structure of three different thicknesses, their maximum temperatures are 28.48, 35.23 and 37.76 ℃,respectively. Fig.7 shows the temperature distribution nephogram of the thin-wall assembly structure with the thickness of 2 mm at the time of 32 and 60 s, and the welding direction of which is shown in Fig.2(d). Their maximum temperatures are 1 859.73 and 149.93 ℃,respectively. According to the above descriptions and explanations, it can be seen that the temperature continuously decreases with the increase of the thickness of the thin-wall assembly structure to some extent from the point view of the maximum temperature. Compared with the maximum temperatures of Fig.6(d) and Fig.7(a), their temperatures have a little difference under different welding directions and the same thickness of the thin-wall assembly structure, which means that the welding direction has a certain effect on the welding temperature value or less influence on it under the constraint conditions in this work.
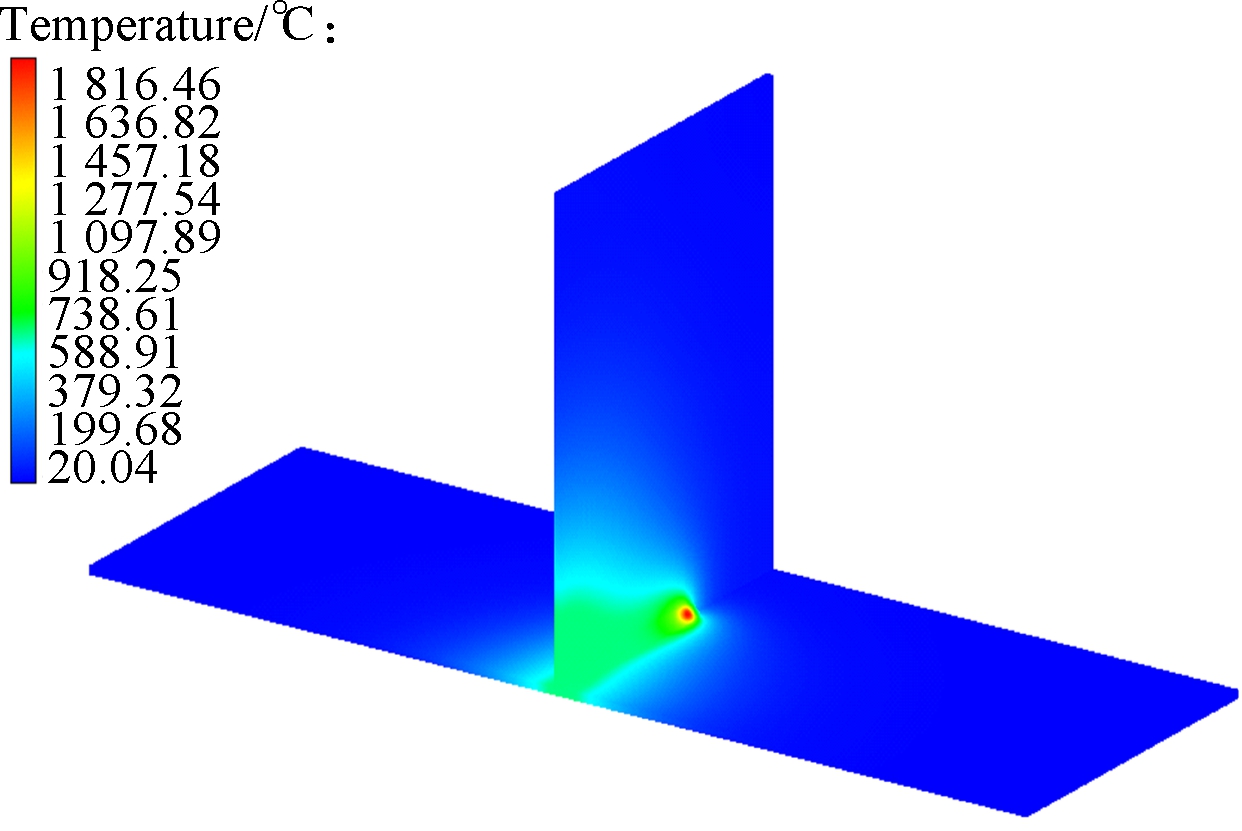
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
(k)
(l)
Fig.6 Temperature distribution nephogram for different times. (a) T2-15s; (b) T4-15s; (c) T6-15s; (d) T2-32s; (e) T4-32s; (f) T6-32s; (g) T2-60s; (h) T4-60s; (i) T6-60s; (j) T2-180s; (k) T4-180s; (l) T6-180s
(a)
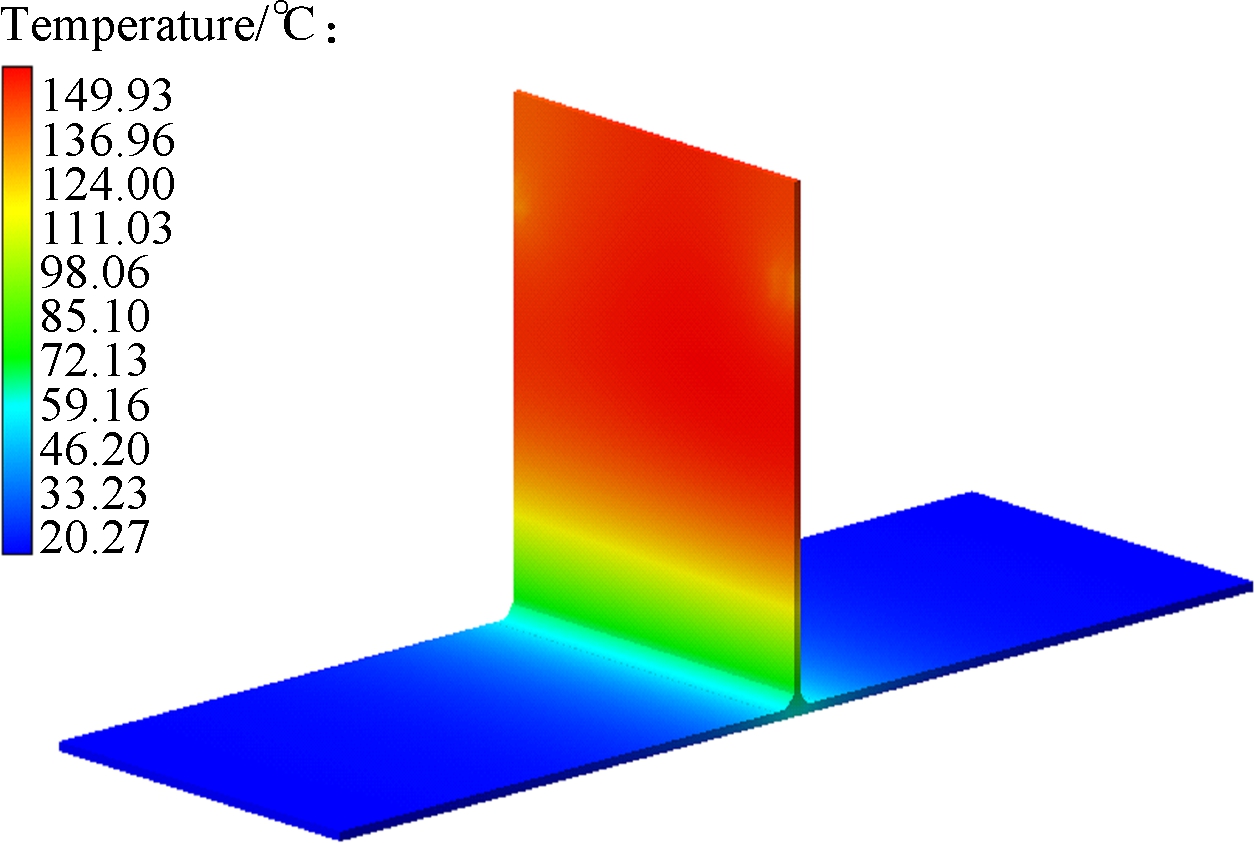
(b)Fig.7 Temperature distribution nephogram. (a) T2R-32s;(b) T2R-60s
In order to study the detailed states of temperature field distribution for the thin-wall assembly structure, in this paper, some points on the thin-wall part are chosen to obtain their temperature curves so as to provide an analysis foundation for studying the welding deformation of temperature-dependence for the complex thin-wall assembly structure. The layout of some chosen points on the thin-wall part is shown in Fig.8. When the thickness of the thin-wall part is 2 mm, according to the welding direction in Fig.2(a), the distance from the bottom of the vertical thin-wall part is 6, 12 and 18 mm, respectively. The point temperature curves based on finite element simulation are shown in Fig.9.
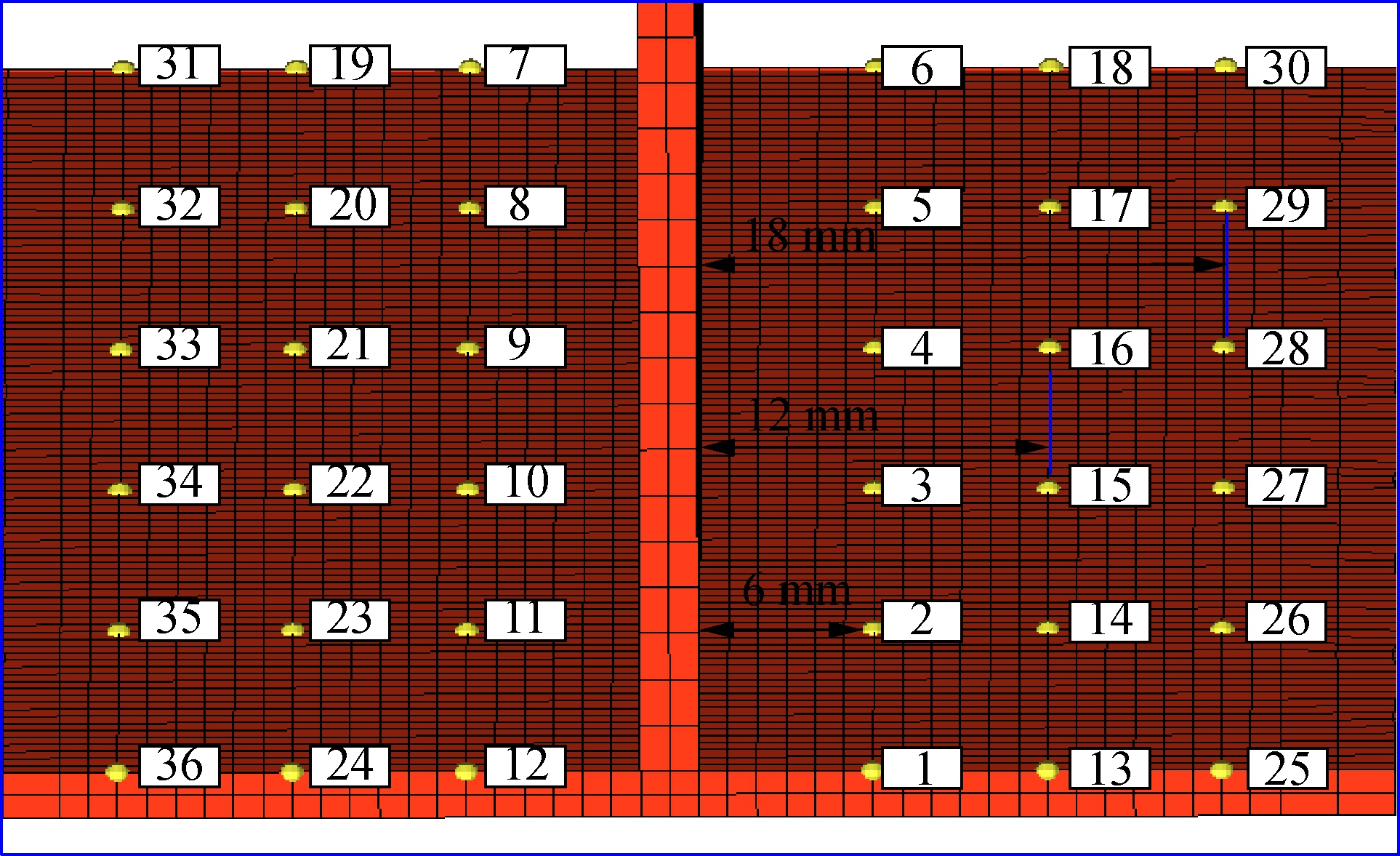
Fig.8 The point’s layout diagram on the thin-wall part
In Fig.9, from the point view of the overall tempera-ture curve, it can be seen that when the distance from the bottom of the vertical thin-wall part is the same, their temperature curves of the chosen points on the thin-wall part are basically similar at the beginning from the weld-ing direction. For example, in Figs.9(a),(b) and (c), the highest temperatures of points 1 and 7, points 13 and 19, points 25 and 31 are similar. The only difference is the time for reaching the highest temperature. It is the same for other points. In addition, it can be also seen from Fig.9 that when the distances of both sides of the vertical thin-wall part become farther apart, their highest temperatures decrease. According to the variable temperature curves, at the beginning, the temperature increases with increase in time, and then it decreases with increasing time. The temperatures of some points show no change. Finally, the temperatures are balanced when reaching the ambient temperature. For such a result, the reason is that when the first weld line is carried out, the temperature constantly increases, and then it moves into the cooling process. After that, it comes the welding process to complete the second weld line with the departure of the welding heat source. Finally, it gradually reaches the ambient temperature, which agrees well with above analysis results.
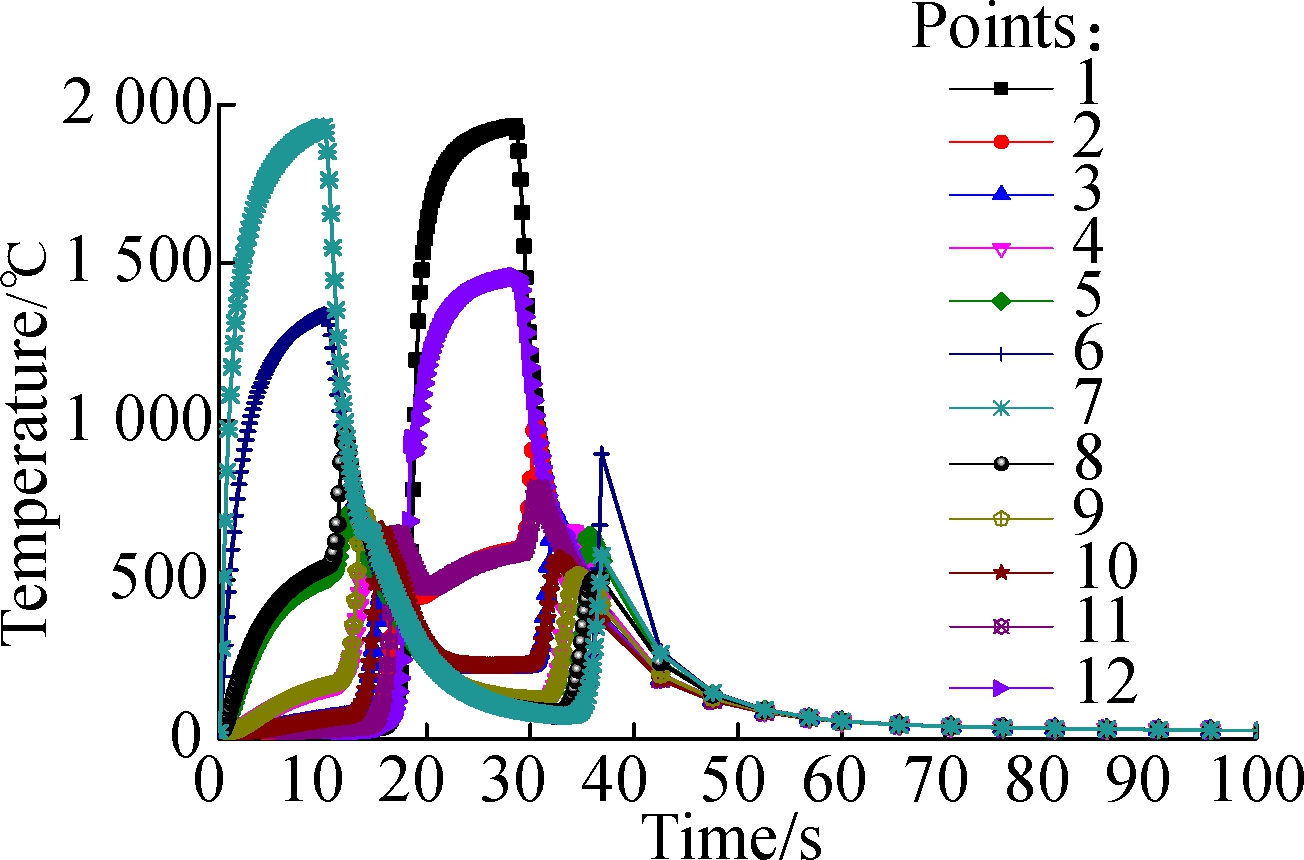
(a)
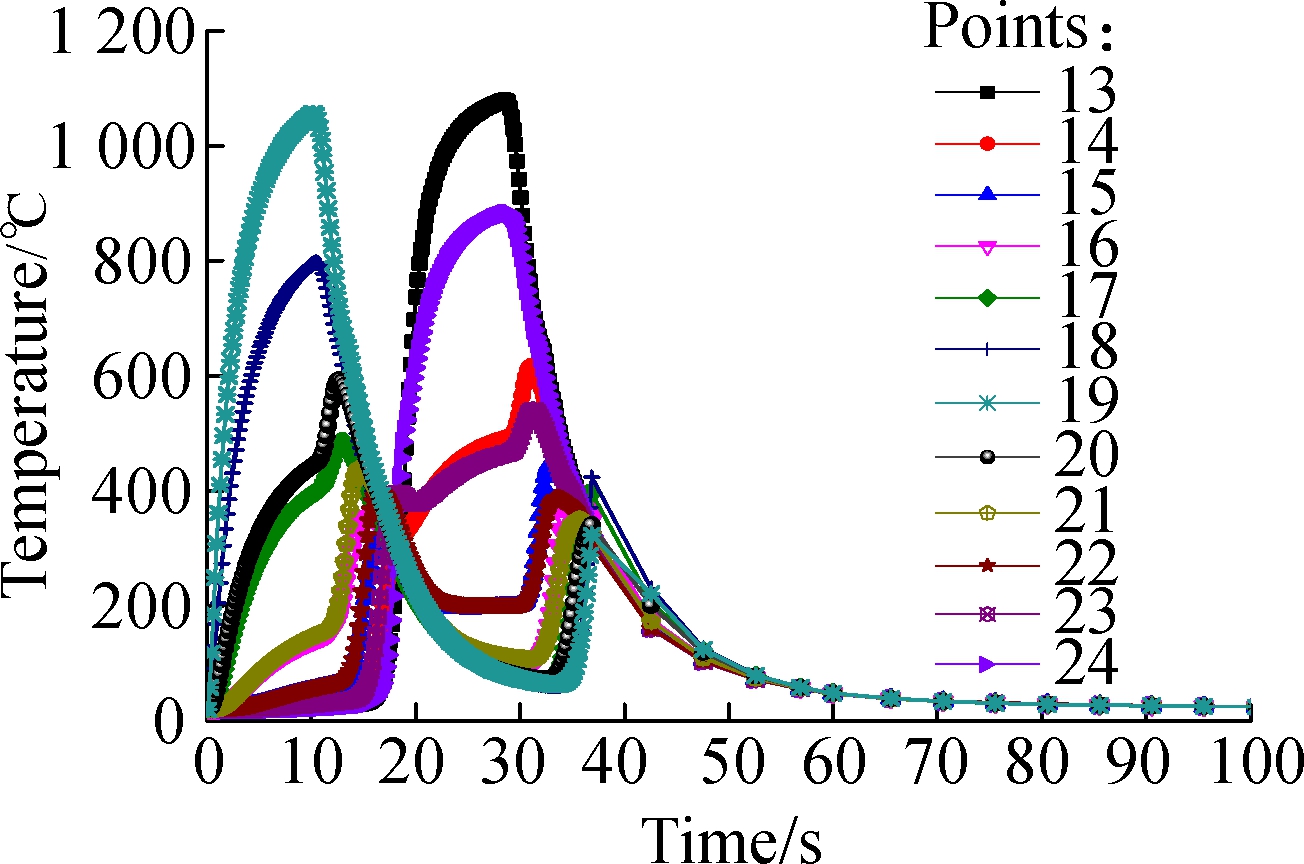
(b)
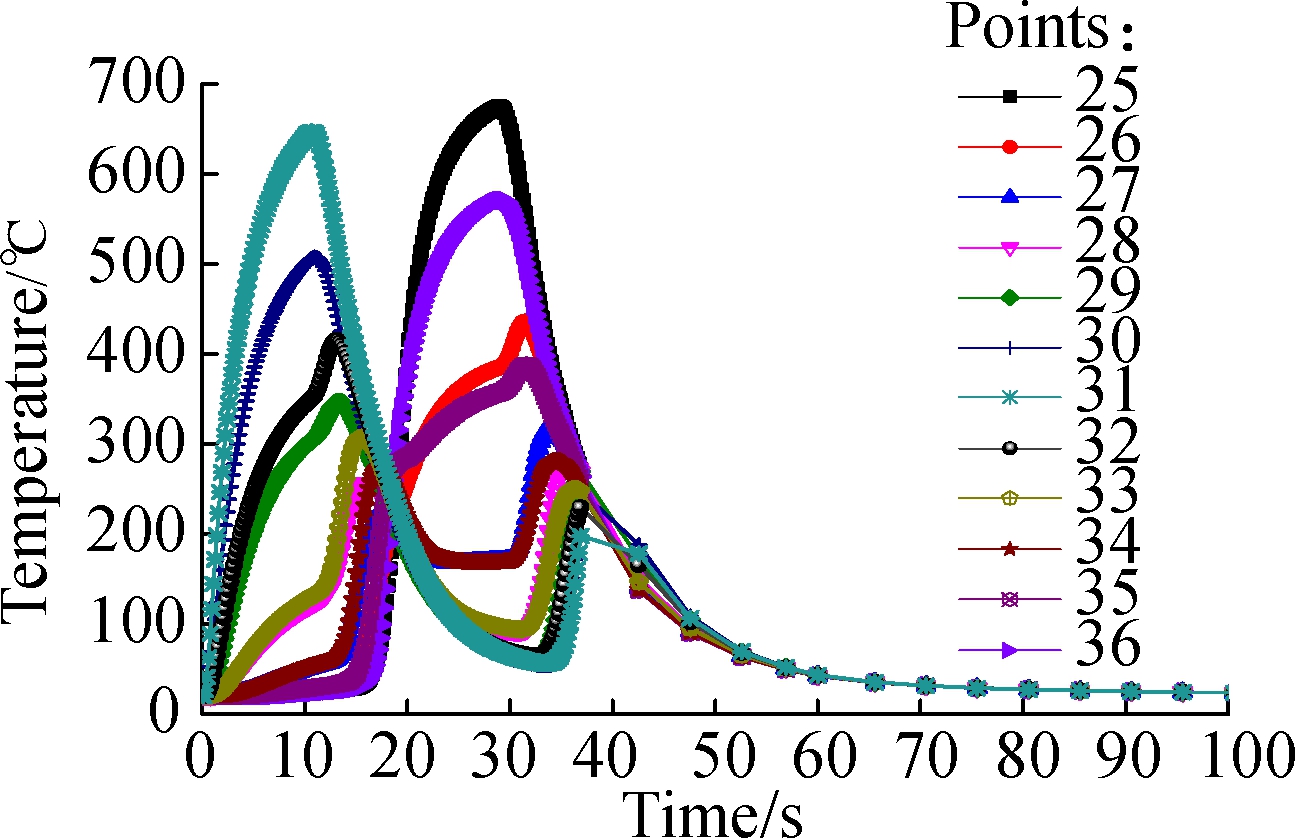
(c)
Fig.9 Point temperature curves with different distances from the bottom of vertical thin-wall part. (a) 6 mm; (b)12 mm; (c)18 mm
3.1 Effect of different welding directions on temperature distribution
When the thicknesses of thin-wall parts are 2, 4 and 6 mm, respectively, the effect of the welding direction on temperature distribution is analyzed and compared with the variable temperatures of some selected points on the two welding directions for each thin-wall part. The welding direction on the thin-wall part is shown in Fig.2. The node temperature curves for points 3, 15 and 27 are shown in Fig.10.
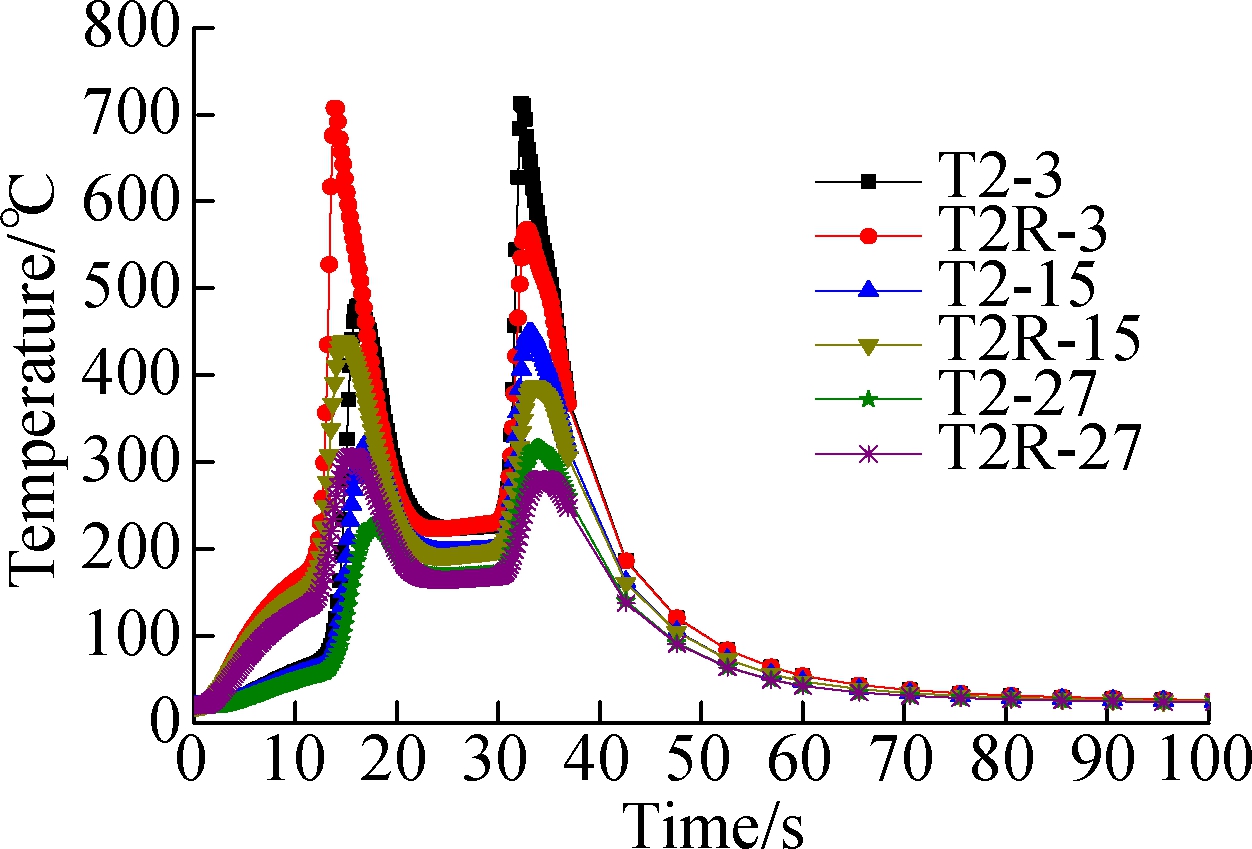
(a)
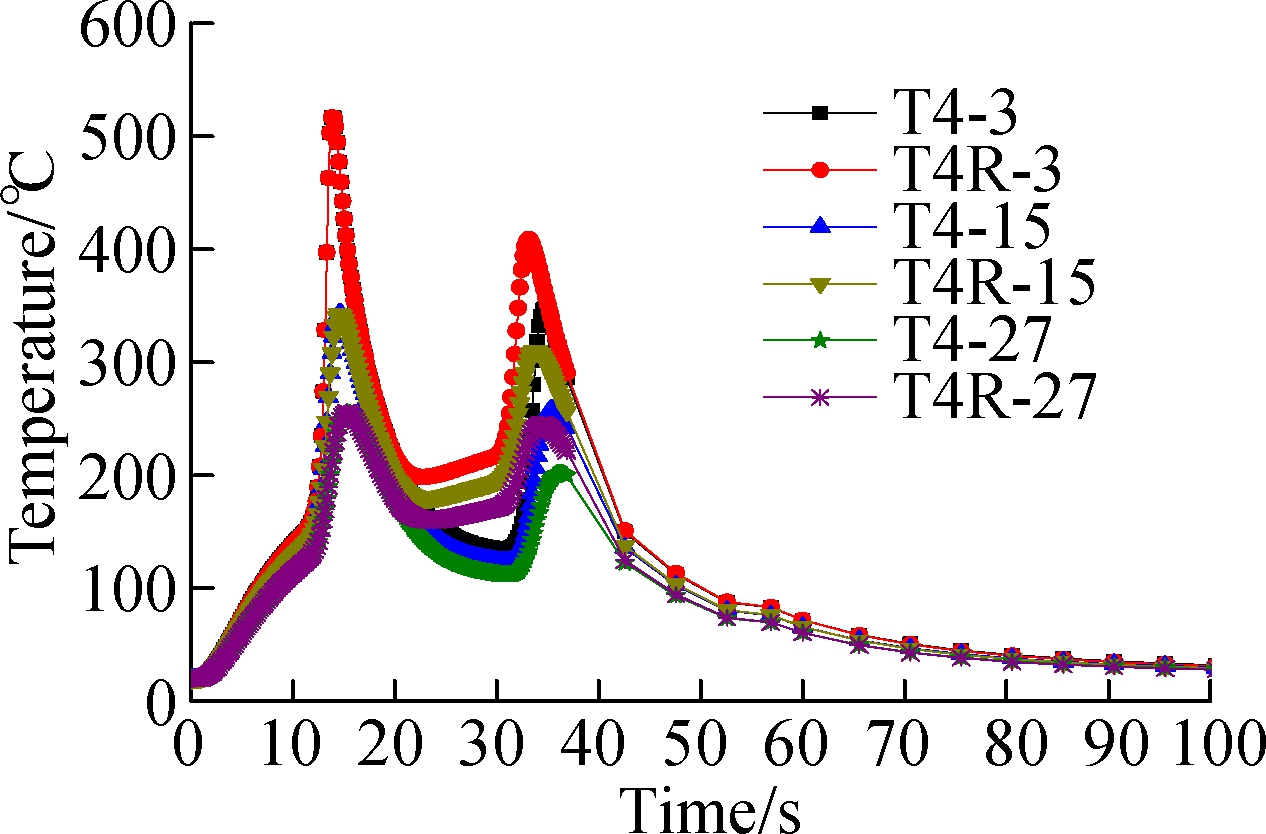
(b)
(c)
Fig.10 Point temperature curves under different welding directions for points 3,15 and 27. (a) With the thickness of thin-wall part of 2 mm; (b)With the thickness of thin-wall part of 4 mm;(c)With the thickness of thin-wall part of 6 mm
In Fig.10(a), T2-3 represents point 3 on the thin-wall part with the thickness of 2 mm and its welding direction is shown in Fig.2(a); T2R-3 represents point 3 on the thin-wall part with the thickness of 2 mm and its welding direction is shown in Fig.2(d). Their welding directions are opposite. For the temperature curves of T2-3 and T2R-3, at the beginning, the temperature increases with the increase in time to a certain degree. When it is around 15 s, it decreases with the increasing time; when it is around from 20 to 30 s, the temperatures of these points show no change. After that, it increases or decreases, and finally the temperatures of these points are balanced when reaching the ambient temperature, which also further proves that the previous descriptions are correct. Simultaneously, it can be seen from the temperature curves that, at the early stage, the temperature of T2-3 is lower than that of T2R-3; at the middle stage, their temperatures are almost the same no matter whether they are T2-3 and T2R-3, T2-15 and T2R-15, or T2-27 and T2R-27, etc. However, in Fig.10(b) and (c), at the early stage, the temperature of T4-3 is very close to that of T4R-3, so is that of T6-3 and T6R-3. At the middle stage, the temperature value of T4R-3 is greater than that of T4-3, and so are those of T6-3 and T6R-3. At the final stage, the temperature increases with the increase in time, after that, their temperature decreases, and finally, the temperature curves are gradually balanced. The results show that the welding direction has a certain impact on temperature change, and it can be seen from Fig.10 that the effect of different welding thicknesses on the temperature distribution of the same point is also significant, which will provide an analysis basis for optimizing the welding assembly structure and improving welding assembly precision in future.
3.2 Effect of different welding parameters on welding temperature
When the distances from the bottom of the vertical thin-wall part are 6 and 12 mm, respectively, the thin-wall part with the thickness of 2 mm is used as a research example. Under different welding parameters, the effects of different welding parameters on the welding temperature are analyzed, and the welding parameters are shown in Tab.2.
According to Tab.2, three group parameters are set for analyzing the thin-wall part with the thickness of 2 mm. The temperature curves of points 3 and 16 under different welding parameters are shown in Fig.11.
Tab.2 Welding parameters of thin-wall assembly parts
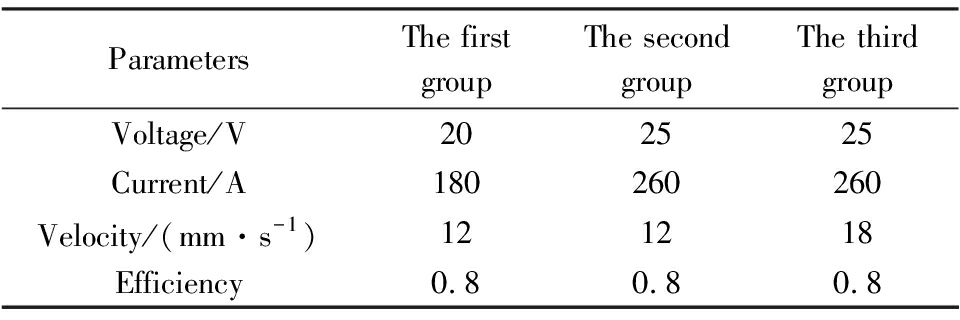
ParametersThe first groupThe second groupThe third groupVoltage/V202525Current/A180260260Velocity/(mm·s-1)121218Efficiency0.80.80.8
(a)
(b)
Fig.11 Node temperature curve diagram under different welding parameters. (a) For point 3; (b) For point 16
In Fig.11(a), T2-18012-3, T2-26012-3 and T2-26018-3 represent point 3 on the thin-wall part with the thickness of 2 mm and their welding directions are shown in Fig.2(a), their welding currents are 180 and 260 A, and their welding velocities are 12 and 18 mm/s, respectively. The welding parameters correspond to the first, second and third groups in Tab.2. For the temperature curves of T2-18012-3 and T2-26012-3, with the increase of the welding current and welding voltage, when the welding velocity remains unchanged, the maximum temperature of T2-18012-3 is lower than that of T2-26012-3.When the welding velocity increases and other parameters show no change, compared with the temperature curve of T2-26012-3, the temperature of T2-26012-3 is higher than that of T2-26018-3. The results of T2-26012-16 and T2-26018-16 are also accurate in Fig.11(b). For the thin-wall assembly structure of the same thickness, it can be seen that when the heat source is moving, the greater the moving speed, the smaller the heating area, and the highest temperature will be decreased. Therefore, the welding temperature field distribution can be altered by adjusting the welding velocity and other welding parameters.
3.3 Effect of different thicknesses and heat source parameters on welding temperature
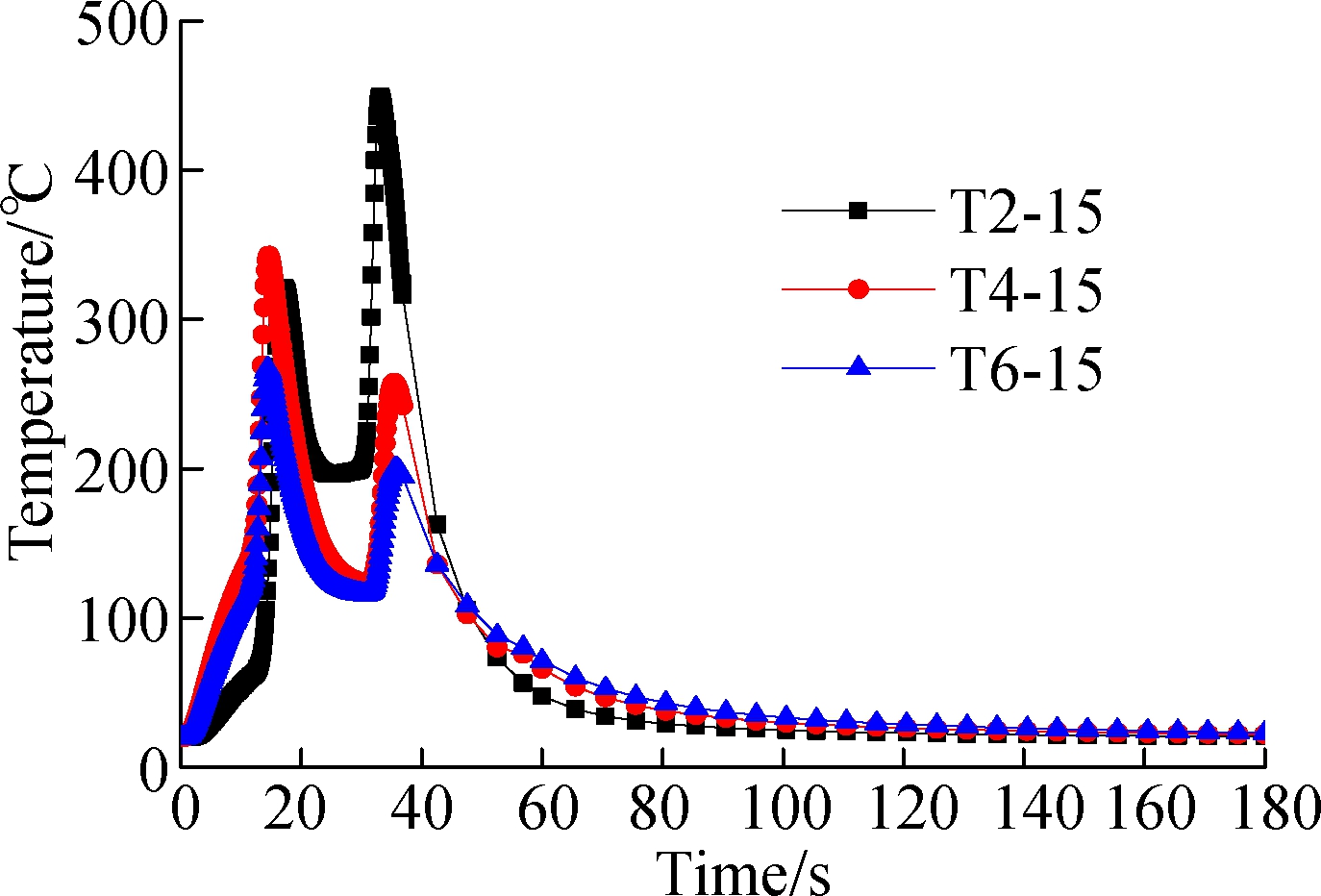
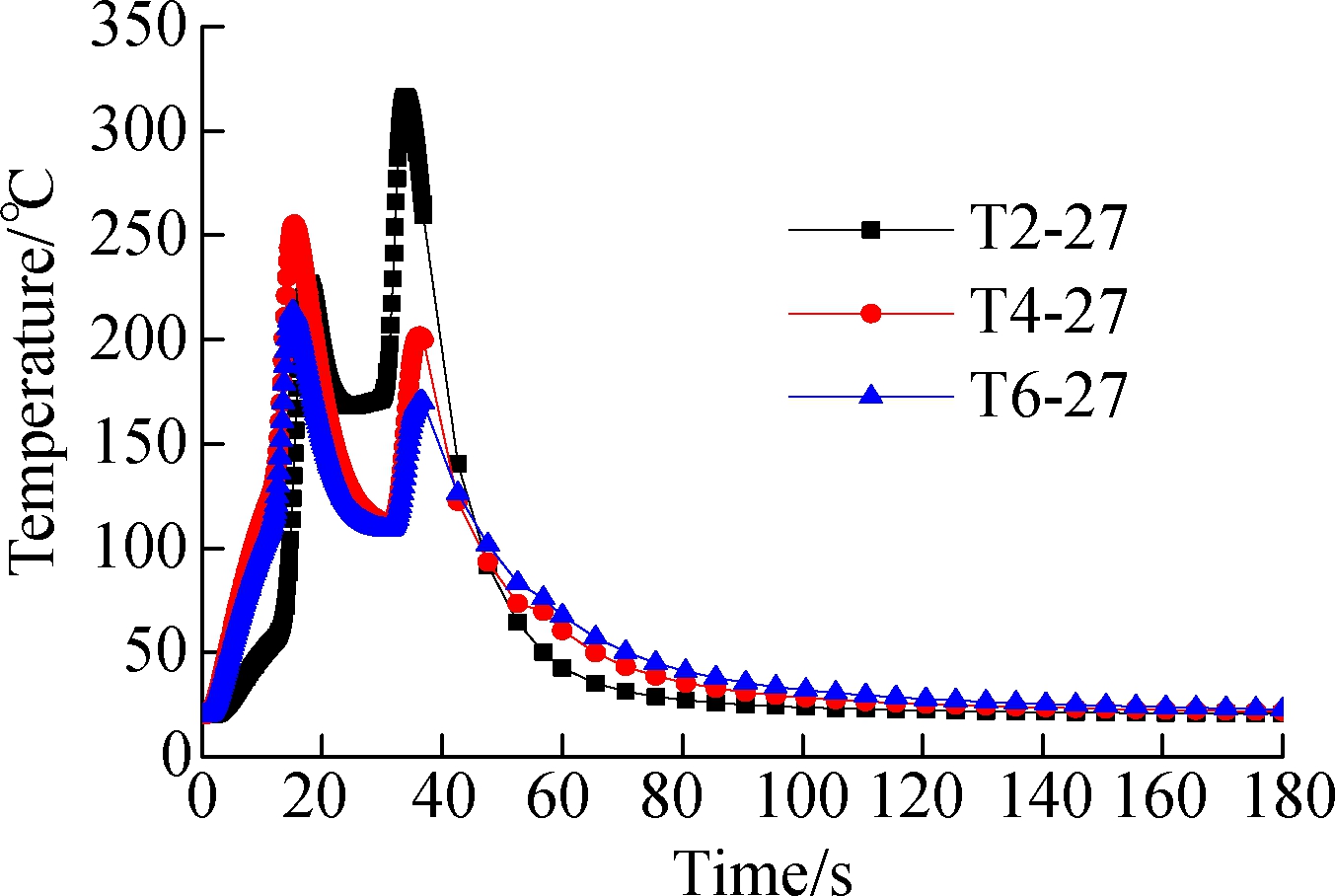
According to the temperature curves of some certain points on the thin-wall part, when the welding parameters are set to be the first group in Tab.2, the effect of the welding thicknesses including 2, 4 and 6 mm, and heat source parameters on the welding temperature field are clearly expounded and analyzed. In this paper, points 3, 15 and 27 are chosen for the T-shape parts under different thin-wall thicknesses and heat source parameters for the same welding parameters. The point temperature curves considering the above two comprehensive factors are shown in Fig.12.
In Fig.12, at the beginning, the temperature increases with the increase in time to some degree; when it is around 17 s, it decreases with the increasing time; when it is around from 20 to 35 s, the point temperatures almost show no change. After that, it increases and then decreases, and finally, the point temperature is balanced when reaching the ambient temperature, which also agrees well with the above analysis results. In Fig.12(a), for the temperature curves of T2-3, T4-3 and T6-3, at the beginning, the highest temperature of T4-3 is a little higher than that of T2-3 and T6-3. But from the point view of the overall temperature curve, the temperature of T2-3 is higher than that of T4-3, and the temperature of T4-3 is higher than that of T6-3. In Figs.12(b) and (c), so are the temperature curves of T2-15, T4-15 and T6-15, and T2-27, T4-27 and T6-27. The results show that with the increase of thickness of the thin-wall part, the welding temperature will decrease in most cases under the conditions of the same welding parameters and the increasing width and depth in Tab.1. Therefore, the welding temperature field distribution can be altered by changing the welding thickness and adjusting the welding heat source parameters. Meanwhile, in the assembly process of the large-size welding structure, an appropriate thickness of the thin-wall part and some optimal heat source parameters can be obtained based on the above analysis results for improving the welding assembly precision of thin-wall structures.
(a)
(b)
(c)
Fig.12 Point temperature curves under two comprehensive factors. (a) Temperature curve diagram for point 3; (b) Temperature curve diagram for point 15; (c) Temperature curve diagram for point 27
4 Conclusions
1) For the thin-wall assembly structure of the same thickness, when the heat source is moving, the greater the moving speed, the smaller the heating area, the highest temperature will be decreased. Therefore, the welding temperature field distribution can be altered by adjusting the welding velocity.
2) Under the conditions of the same welding parameters and the increasing welding width and depth, with the increase of the thickness of thin-wall parts, the welding temperature will be decreased in most cases. Therefore, the welding temperature field distribution can be adjusted by changing welding thickness and heat source parameters.
3) In the welding process, the effect of welding direction, different welding thicknesses, welding heat source parameters and welding parameters on the welding temperature distribution is different to certain degree, which will provide the analysis basis for further research of welding parameter optimization in future.
[1]Deng D,Murakawa H, Liang W. Numerical simulation of welding distortion in large structures[J]. Computer Methods in Applied Mechanics & Engineering, 2007, 196(45/46/47/48):4613-4627.DOI:10.1016/j.cma.2007.05.023.
[2]Ma N, Wang J,Okumoto Y. Out-of-plane welding distortion prediction and mitigation in stiffened welded structures[J]. International Journal of Advanced Manufacturing Technology, 2016, 80(5):1371-1389.DOI:10.1007/s00170-015-7810-y.
[3]Murakawa H, Deng D, Ma N, et al. Applications of inherent strain and interface element to simulation of welding deformation in thin plate structures[J]. Computational Materials Science, 2012, 51(1):43-52.DOI:10.1016/j.commatsci.2011.06.040.
[4]Murakawa H, Okumoto Y, Rashed S, et al. A practical method for prediction of distortion produced on large thin plate structures during welding assembly[J]. Welding in the World, 2013, 57(6):793-802.DOI:10.1007/s40194-013-0071-1.
[5]Wang R, Zhang J, Serizawa H, et al. Study of welding inherent deformations in thin plates based on finite element analysis using interactive substructure method[J]. Materials & Design, 2009, 30(9):3474-3481.DOI:10.1016/j.matdes.2009.03.015.
[6]Moein H, Sattari-Far I. Different finite element techniques to predict welding residual stresses in aluminum alloy plates[J]. Journal of Mechanical Science and Technology, 2014, 28(2):679-689.DOI:10.1007/s12206-013-1131-6.
[7]Ikushima K, Itoh S, Takakura D, et al. Large-scale analysis of welding deformation and residual stress problem by idealized explicit FEM using iterative substructure method[J]. Quarterly Journal of the Japan Welding Society, 2014, 32(4):223-234.DOI:10.2207/qjjws.32.223.
[8]Ikushima K, Shibahara M. Large-scale non-linear analysis of residual stresses in multi-pass pipe welds by idealized explicit FEM[J]. Welding in the World, 2015, 59(6):839-850.DOI:10.1007/s40194-015-0263-y.
[9]Chen Z, Chen Z, Shenoi R A. Influence of welding sequence on welding deformation and residual stress of a stiffened plate structure[J]. Ocean Engineering, 2015, 106:271-280.DOI:10.1016/j.oceaneng.2015.07.013.
[10]Choi W, Chung H. Variation simulation of compliant metal plate assemblies considering welding distortion[J]. Journal of Manufacturing Science and Engineering, 2015, 137(3):031008. DOI:10.1115/1.4029755.
[11]Joo S M, Bang H S, Bang H S, et al. Numerical investigation on welding residual stress and out-of-plane displacement during the heat sink welding process of thin stainless steel sheets[J]. International Journal of Precision Engineering and Manufacturing, 2016, 17(1):65-72.DOI:10.1007/s12541-016-0009-9.
[12]Zeng P, Gao Y, Lei L P. Local equivalent welding element to predict the welding deformations of plate-type structures[J]. Science in China Series E: Technological Sciences, 2008, 51(9): 1502-1506.DOI:10.1007/s11431-008-0114-9.
[13]Huang H, Wang J, Li L, et al. Prediction of laser welding induced deformation in thin sheets by efficient numerical modeling[J]. Journal of Materials Processing Technology, 2016, 227:117-128.DOI:10.1016/j.jmatprotec.2015.08.002.
[14]C
ndea L, Haiegan C, Pop N, et al. The influence of thermal field in the electric arc welding of X60 carbon steel components in the CO2 environment[J].Applied Thermal Engineering, 2016, 103: 1164-1175.DOI:10.1016/j.applthermaleng.2016.05.004.
[15]Das H, Jana S S, Pal T K, et al. Numerical and experimental investigation on friction stir lap welding of aluminium to steel[J]. Science and Technology of Welding and Joining, 2014, 19(1):69-75.DOI:10.1179/1362171813y.0000000166.
[16]Okano S, Tsuji H, Mochizuki M. Temperature distribution effect on relation between welding heat input and angular distortion[J]. Science and Technology of Welding and Joining, 2016, 22(1):59-65.DOI:10.1080/13621718.2016.1185313.
[17]Goldak J, Chakravarti A, Bibby M. A new finite element model for welding heat sources[J]. Metallurgical Transactions B, 1984, 15(2):299-305.
[18]Bhatti A A, Barsoum Z, Murakawa H, et al. Influence of thermo-mechanical material properties of different steel grades on welding residual stresses and angular distortion[J]. Materials and Design, 2015, 65:878-889.DOI:10.1016/j.matdes.2014.10.019.