Deployable space structures for future communication and observation have gained more and more attention over the past few decades[1]. The AstroMesh is a mesh reflector for large aperture space antenna systems[2]. Compared to other mesh reflectors, the AstroMesh achieves uncharacteristically low levels of total mass, stowed volume, surface distortion, cost, and program schedule duration[3]. The AstroMesh also has inherent advantages in structural efficiency, thermal dimensional stability, and relatively high stiffness-to-weight ratios[4-5]. With those distinct features, it is an ideal form of deployable mesh reflector antennas and well worth being studied.
The Astro technology developed by Astro Aerospace Corporation[1] is mature, with models of approximately 6 and 12 m offset circular apertures fully developed and validated. Ref.[6] described the results of a critical design for the 13-m antenna reflectors and their validation plans and then two large deployable antenna reflectors on board ETS-VIII were successfully deployed in orbit[7]. The emergence of electrostatic forming technology also provides an approach to improve surface accuracy[8]. Recently, Fan et al.[9] investigated an analytical algorithm to design the pretensions of asymmetrical ring truss cable-net space-borne antennas for engineering convenience. Li et al.[10] investigated a way to simulate the deployment dynamics of a large-scale mesh reflector of the satellite antenna.
To achieve a light weight and high packaging efficiency, materials such as cables and membranes are selected to form a space structure. However, those flexible structures cannot usually be described by simple mathematical functions, so designers proposed a process known as force-finding to achieve an ideal shape[11]. This paper focuses on the force-finding process of antenna cable nets. Force-finding methods for cable net structures have been developed by many researchers. Flexible cables have to be tensioned to obtain the initial shape and stiffness of a structure. The initial tension forces in the self-equilibrium state are also called prestresses. Flexible tension structures such as cable nets do not have a definite shape, so the design process of those structures is divided into force design and shape design. Linkwitz et al.[12-13] developed the force density method, which utilizes a system of linear equations to denote the equilibrium condition of nonlinear systems. The method of dynamic relaxation was first applied to tension structures by Day et al[14-15]. As for force design, with the determined configuration, the only chance to influence its inner properties is to specify or optimize the distribution of prestresses in it to achieve the equilibrium configuration[16]. The shape of AstroMesh’s cable nets should satisfy the required accuracy of the reflecting surface to ensure the optimum working performance[17]. With a given shape, the force-finding process investigates the distribution of initial forces (prestresses). A novel method based on the singular value decomposition of the equilibrium matrix of cable nets by optimization methods with shape constraints was proposed by Li et al[18]. Niu et al.[19] applied a genetic algorithm to achieve multi-objective optimization. Two different formulations of the objective function were used to obtain equilibrium pretension forces, one of which was the unbalanced force and the other was the root mean square (RMS)[20]. The methods took the deformation of trusses into consideration but the unknown variables were member forces rather than coefficients, which may cause difficulties in satisfying the equilibrium equations. The optimization of the electrostatic forming membrane reflector antenna (EFMRA) was presented by Liu et al[5].
The main purpose of this paper is to propose a force-finding method to obtain the optimized forces of an antenna cable net according to a specific shape and fixed boundary condition. The method can find the optimized prestresses to satisfy the surface accuracy, corresponding to the constrained initial shape. Then, a discrete algorithm (genetic algorithm) and a continuous algorithm (gradient-based algorithm) are discussed and compared in numerical examples.
1 Force-Find Method
AstroMesh embodies a new concept for deployable space structures: A pair of ring-stiffened geodesic cable domes, in which the ring is a truss deployed by a single cable (see Fig.1). The reflector of AstroMesh consists of two parabolic curved nets placed back-to-back in tension across the rims of a deployable graphite-epoxy ring truss.
As shown in Fig.2, the AstroMesh reflector is divided into two parts, the supporting truss and the cable-net structure. The cable-net structure is composed of a front cable net, a back cable net and some vertical tension cables. Connected by vertical tension cables to maintain the profile, the two nets are placed back-to-back. The supporting truss is connected to the cable-net structure to provide sufficient stiffness and make sure that the whole structure can be folded and deployed precisely and smoothly in space. In this paper, to simplify the problem, we assume that the truss is rigid enough without any elastic deformation. In this way, nodes in cable nets are divided into free nodes and fixed nodes. Free nodes are in the middle of a net and surrounded by a circle of fixed nodes connected to the rigid truss.
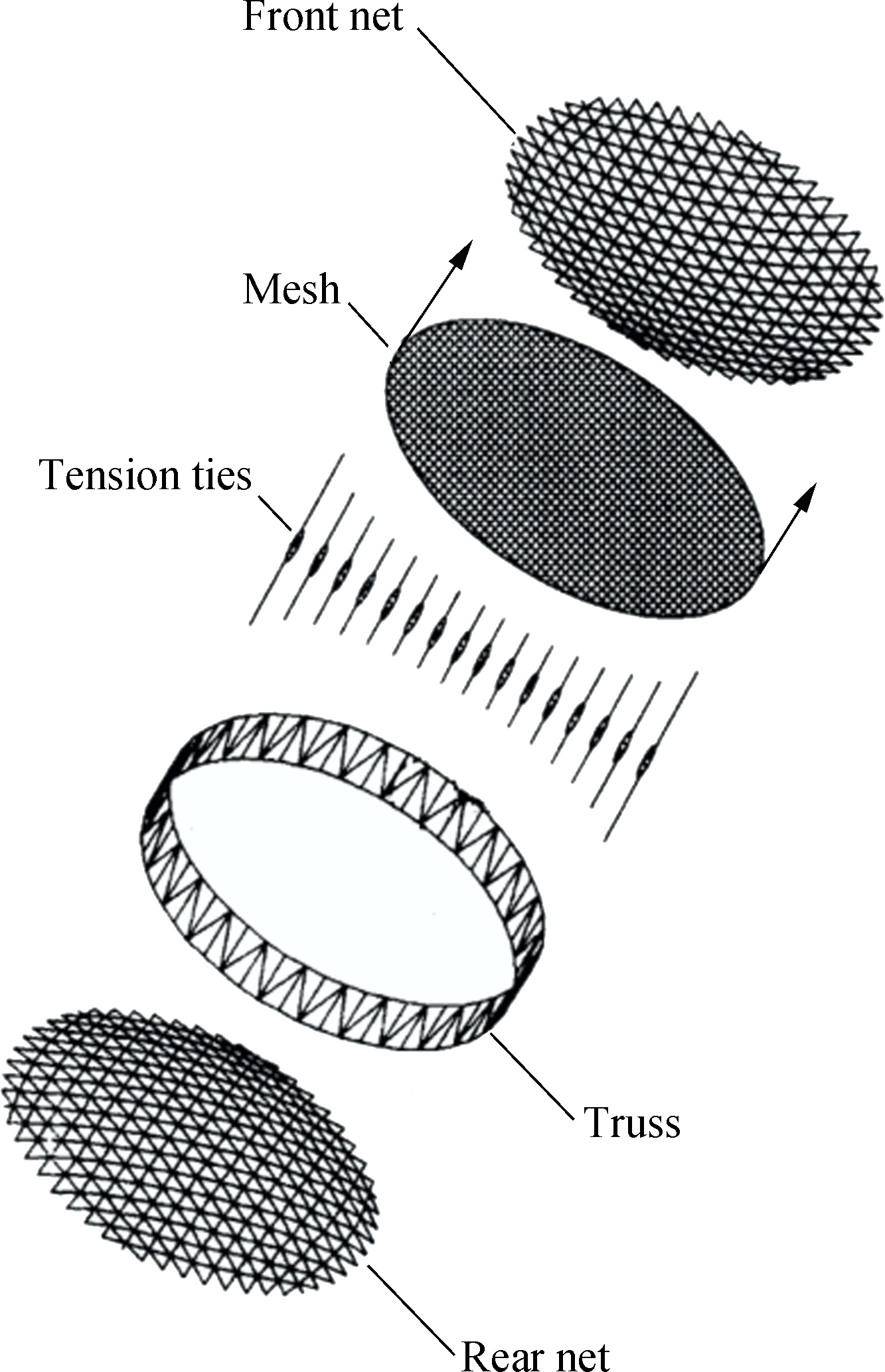
Fig.1 Components of AstroMesh reflectors[2]

Fig.2 The composition of AstroMesh
The geometry of AstroMesh is known as a prior condition. Node i in the net is shown in Fig.3, which connects cables 1,2,…,j. The free node in AstroMesh connects to a vertical cable to maintain the shape. The equilibrium equations of node i can be calculated as follows[21-22]:
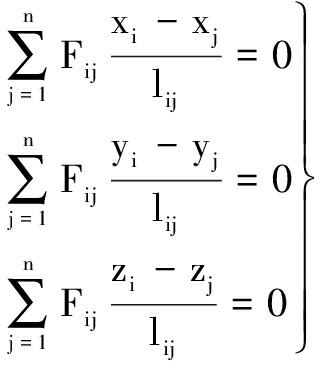
(1)
where fij and lij are the tension force and the length of cable ij, respectively; n is the summation of cables connected to node i; and xi,yi,zi are the coordinates of all free nodes.
With the given geometry, the topology and coordinates of cable nets can be determined. Therefore, the equilibrium condition of all the free nodes can be written in terms of the unknown cable forces as follows:
M3k×r fr×1=0
(2)
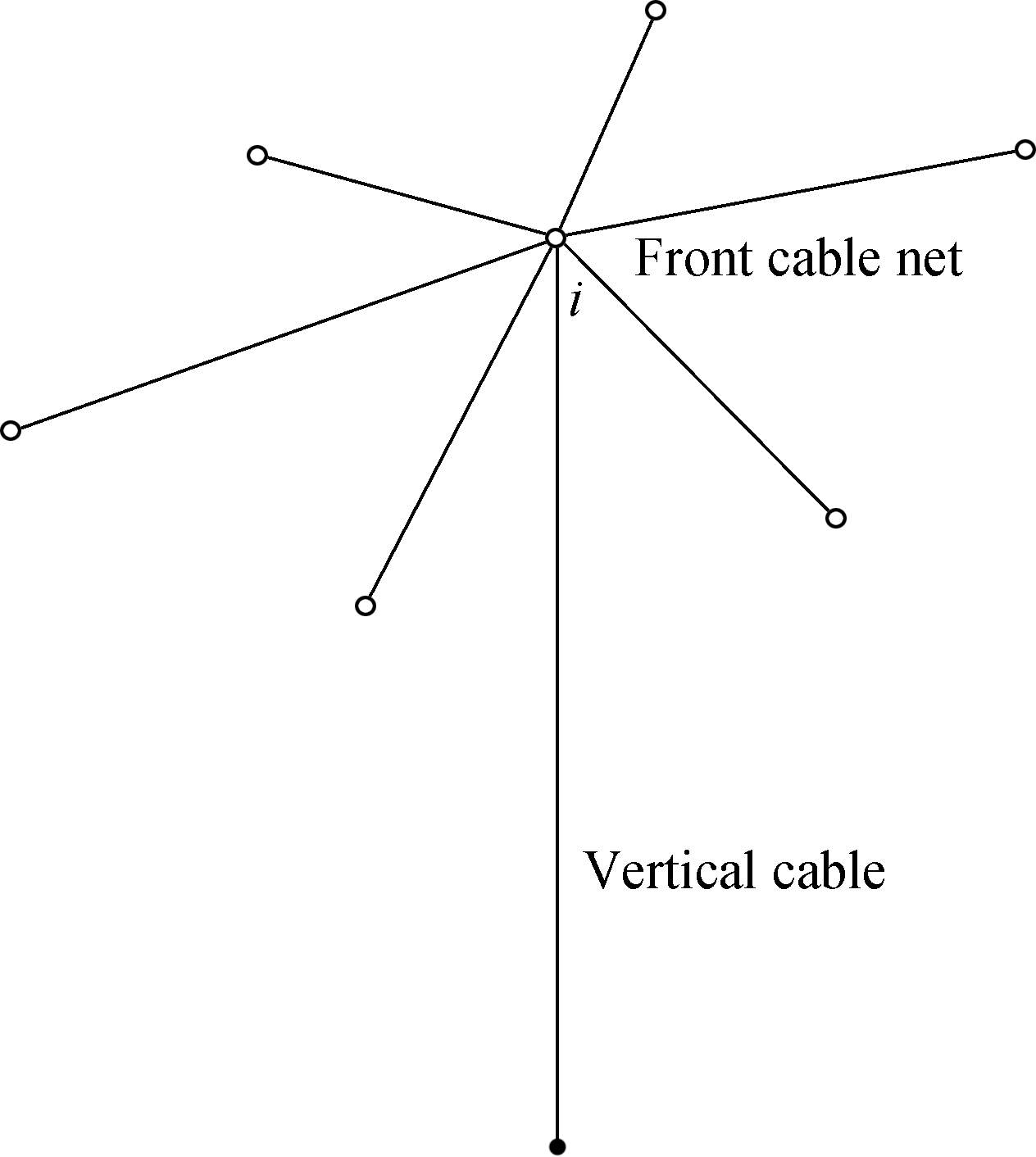
Fig.3 Connecting condition of node i in the cable-net
where M is the equilibrium matrix; k is the total number of all free nodes; r is the number of cables; f is the column vector of unknown cable forces. The structure is prestressed without any external forces so the right side of Eq.(2) is 0.
The force-finding process is to find a vector f, which satisfies the equilibrium condition. In most cases, cable-net structures are not statically determinated since 3k<r and there are a plenty of force modes. Therefore, singular value deposition is conducted to decompose the equilibrium matrix M to obtain its rank as well as force modes as follows:
(3)
where Σ is the block diagonal matrix whose elements are the singular values of M.
Then, the number of force modes is defined as
s=r-R
(4)
where s is the number of force modes; and R is the rank. The matrix Vr×r can be expressed as {v1,v2,v3,…,vr}, of which the last s columns contribute to structural force modes. The force modes can be deduced as
Vr×s={vr-s+1,vr-s+2,…,vr}
(5)
The equilibrium equation can be written as
MVr×s=0
(6)
It should be noted that the cable force vector f can be written as a linear combination of the force modes by coefficients α:
f=α1vr-s+1+α2vr-s+2+…+αsvr
(7)
Eq.(7) can be expressed as
f=Vr×sα
(8)
Since the solution of Eq.(2) is not unique, more constraints should be added to obtain an optimal solution of the force-finding problem. The distribution of structural members is chosen as the objective function[17-20]:
(9)
Meanwhile, cables cannot bear compression so the values of forces should be greater than 0. Then, the force-finding method of a cable net structure in AstroMesh is formulated as follows:
(10)
s.t. fi>0, Mf=0
Substituting Eq.(8) into Eq.(10), the optimization problem in Eq.(10) is transformed to a problem as
![]()
s.t. Vα>0
(11)
It should be noticed that Eq.(11) implies that the cable forces satisfy Eq.(2) naturally. Besides, it is also an effective access to reduce the member of variables and improve calculation efficiency, especially when there are many unknown variables. Then, an optimal algorithm should be carefully selected to solve the problem.
2 Numerical Examples
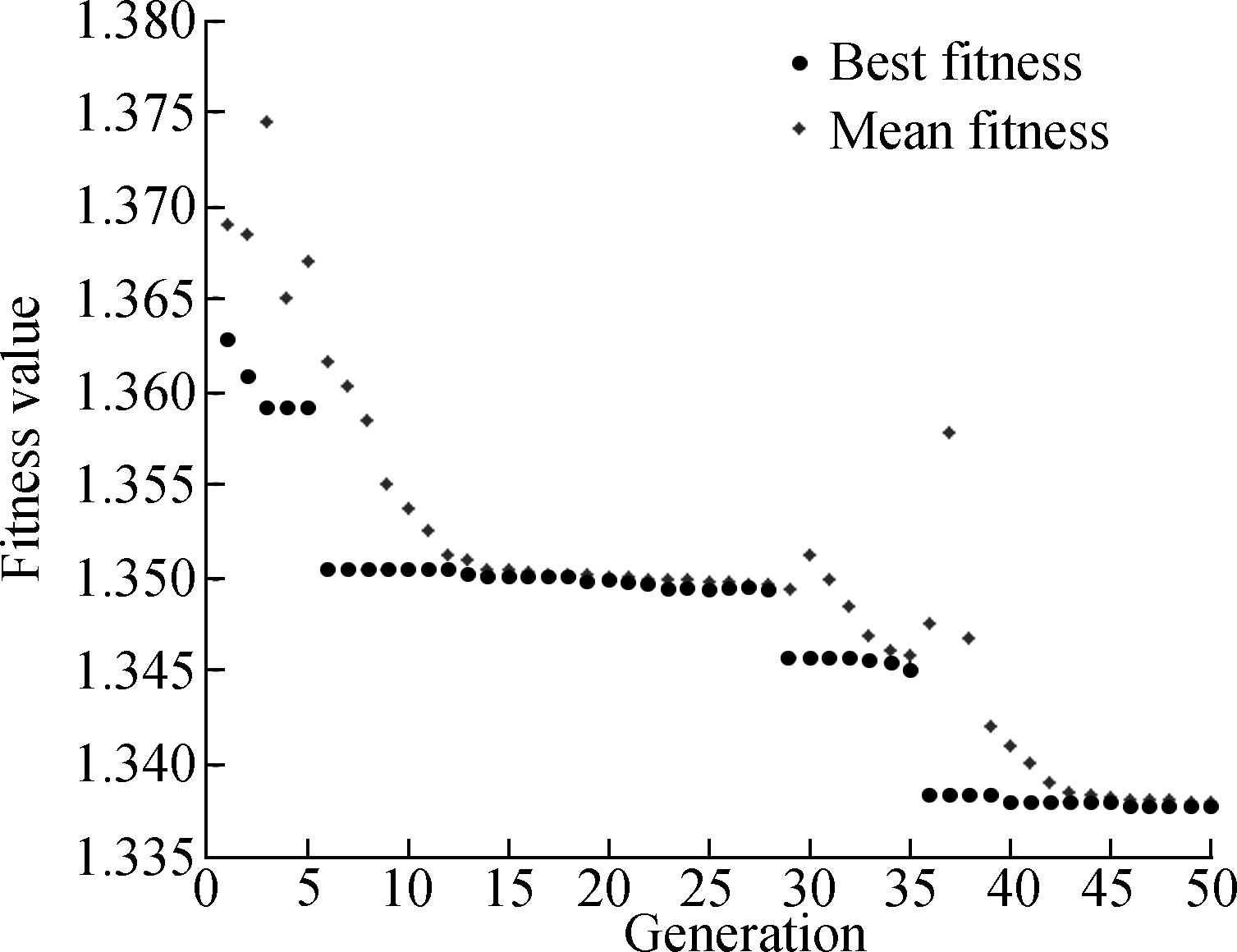
Numerical examples are analyzed in this section to validate the efficiency of the proposed method. Two optimization algorithms are used to find the optimal solutions of Eq.(2).Method Ⅰ is sequential quadratic programming (SQP), a kind of nonlinear optimal algorithm, and Method Ⅱ is the genetic algorithm (GA). It should be notable that the starting point of the SQP algorithm should be given in advance while that of the genetic algorithm is generated randomly. When we solve an optimal problem by Method Ⅰ, it is likely that the solution will trap into a local optimum so the starting point of iterations should be selected carefully to avoid immature convergence. Also, when compared to other nonlinear optimal algorithms, the SQP method can obtain the smallest value of the objective function in this case. Moreover, the SQP method converges quickly and saves computing time. The genetic algorithm is a powerful optimal strategy but it may not be the best choice for a persistent problem as it uses a randomly scattered starting point. Also, there is a small difference between each obtained solution by the genetic algorithm due to the random initial population.
2.1 A planar cable net
A planar cable net composed of 4 free points, 6 fixed points and 12 cable members is analyzed in this subsection. The numbering condition is shown in Fig.4 with solid circles denoting fixed points. The prescribed coordinates are x=[0.5; 0.5; 0.7; 0.7; 0; 0; 0.4; 0.8; 1.2; 1.2; 0.8; 0.4] and y=[0.5; 0.5; 0.7; 0.7; 0; 0; 0.4; 0.8; 1.2; 1.2; 0.8; 0.4]. Set the starting point of SQP to be f1=[ 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1] and f2=[0.375; 0.227; 0.271; 0.580; 0.834; 0.466; 0.347; 0.742; 0.523; 0.477; 0.487; 0.199], respectively.
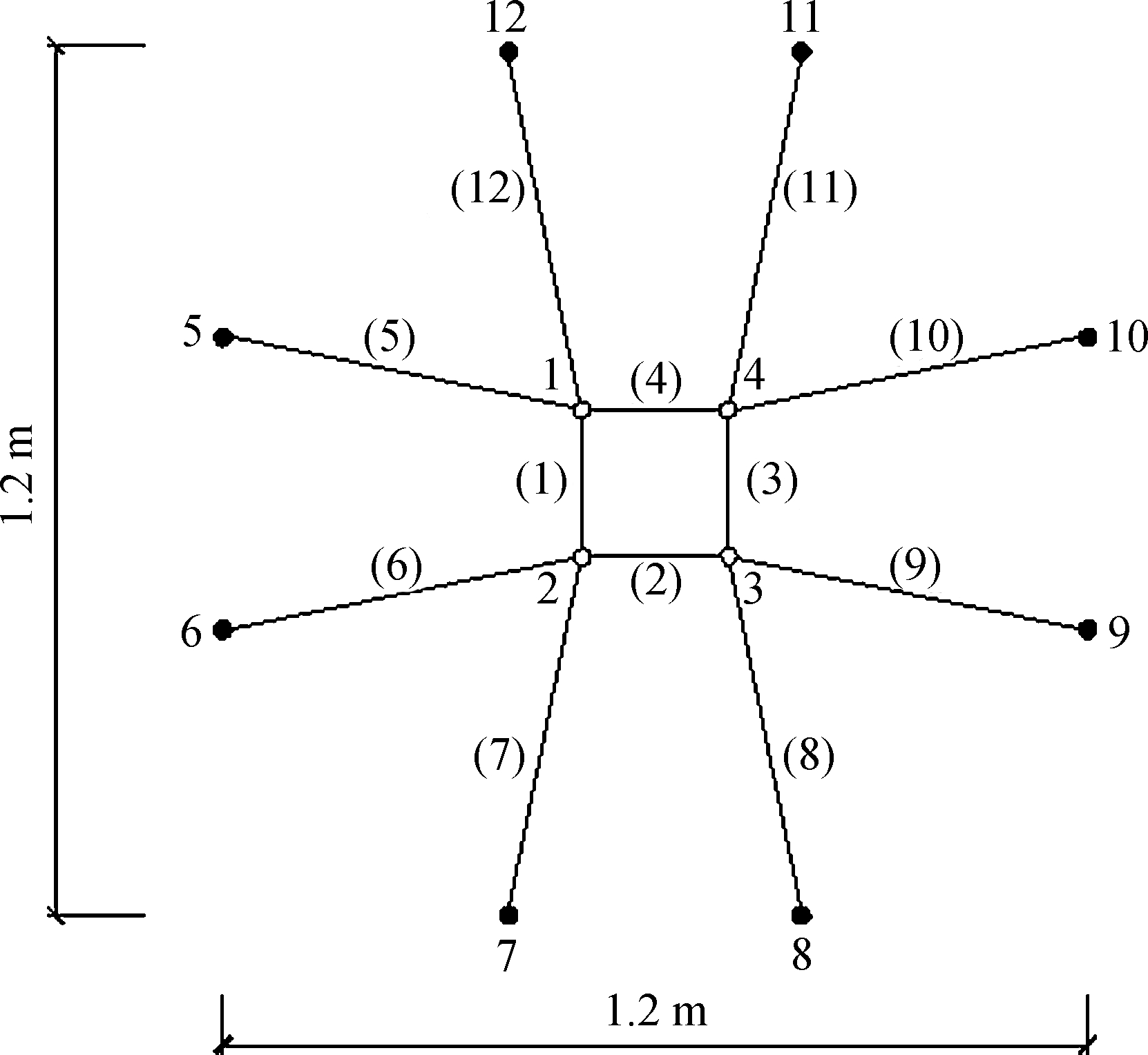
Fig.4 The numbering condition of a planar cable net
Two algorithms are used to find the optimal solution to Eq.(2). The numbering condition of each structural member is shown in Fig.4 and the optimized forces are shown in Tab.1 and Tab.2, respectively. The iterative processes are plotted in Fig.5 and Fig.6, respectively. It is notable that the elementary unit of force in Tab.1 and Tab.2 is N.
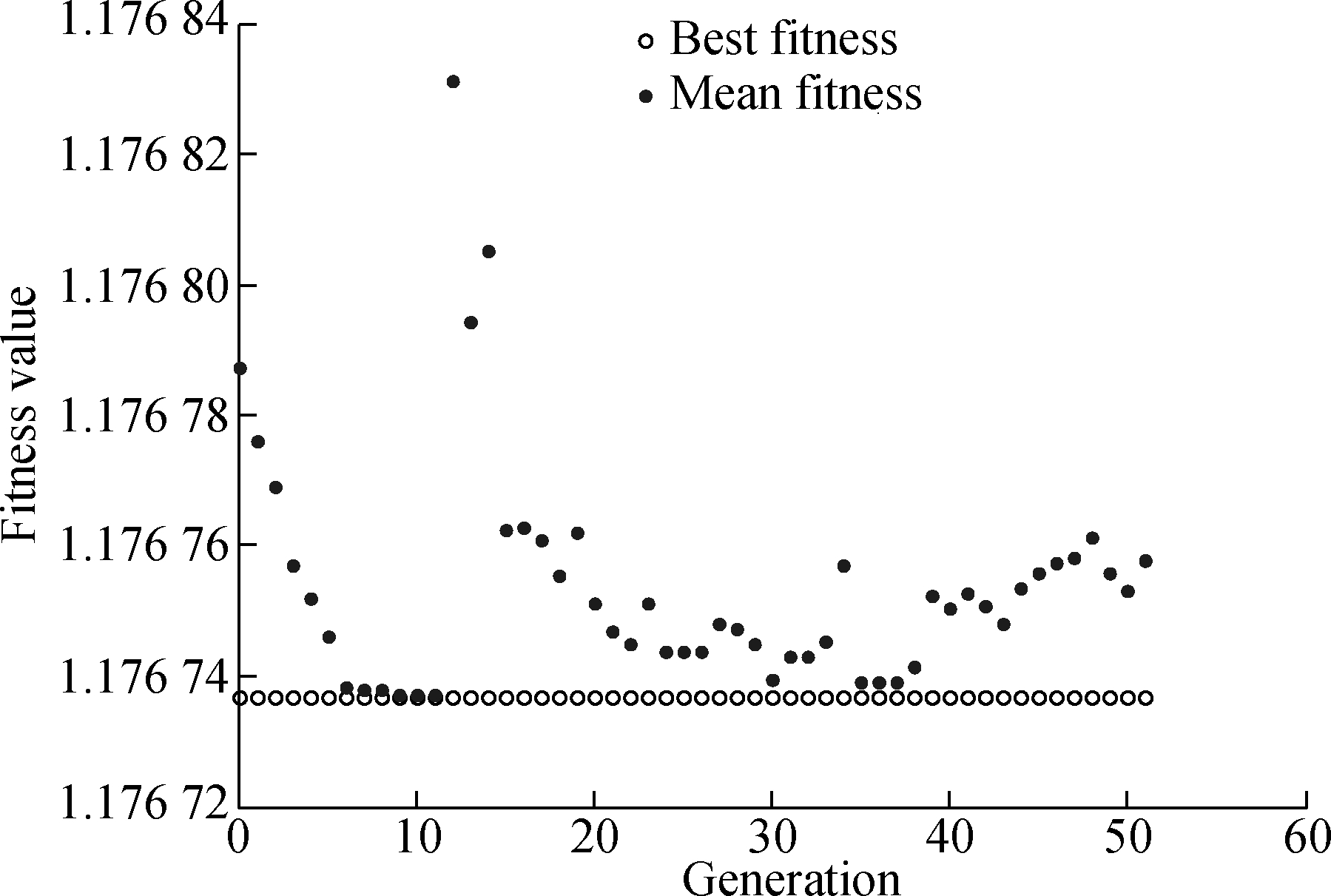
Fig.5 Iterative process to achieve the optimal force distribution by genetic algorithm
Tab.1 Optimized results by the genetic algorithm
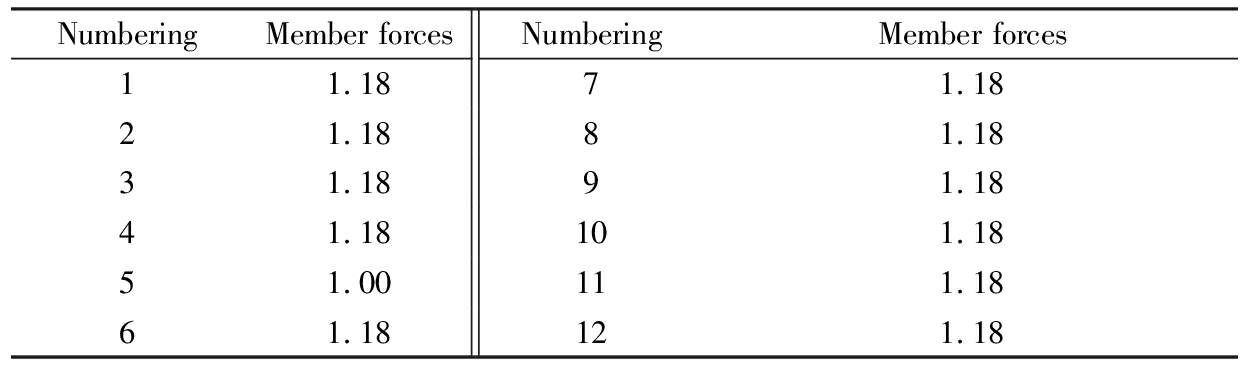
NumberingMember forcesNumberingMember forces11.1871.1821.1881.1831.1891.1841.18101.1851.00111.1861.18121.18
2.2 AstroMesh cable nets
2.2.1 Symmetric cable net
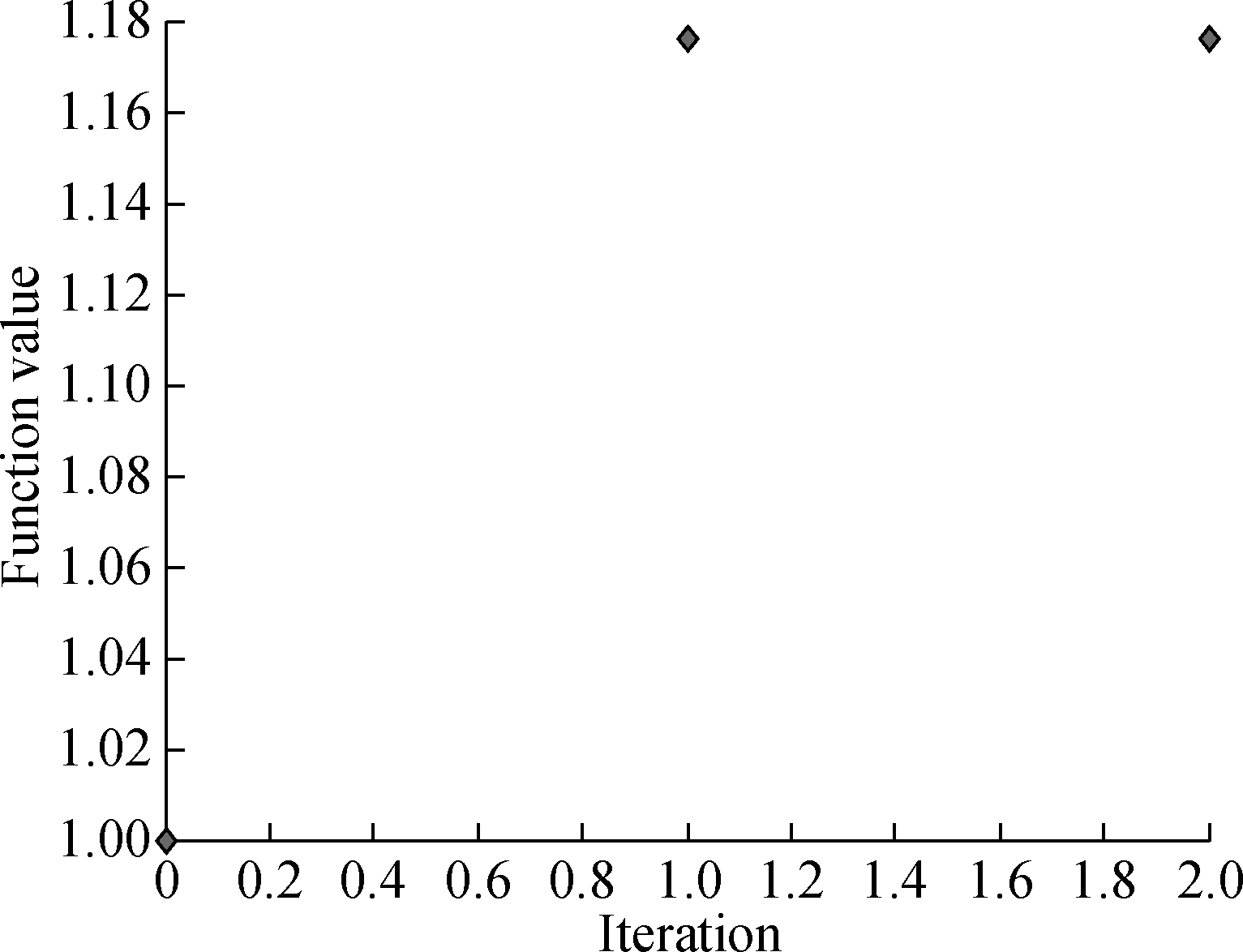
Tab.2 Optimized results of different initial values by SQP
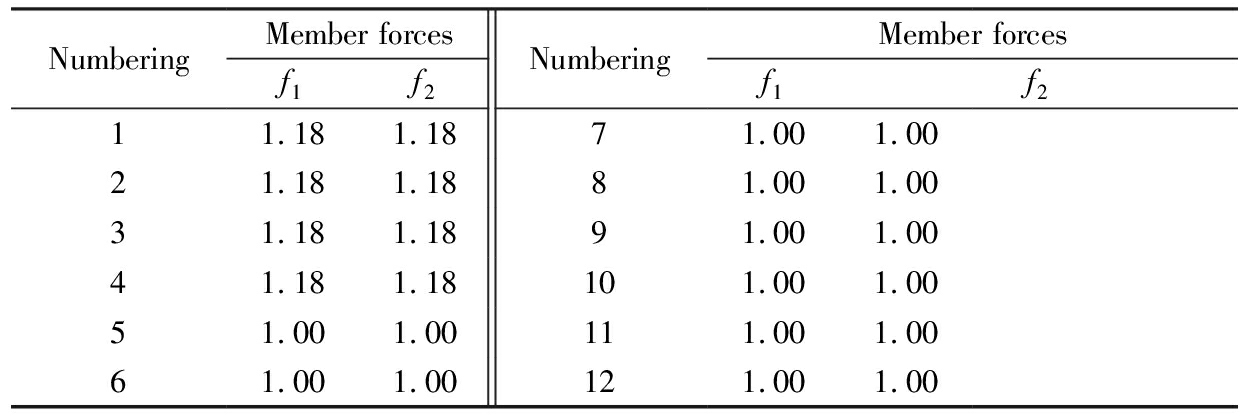
NumberingMember forcesf1f2NumberingMember forcesf1f211.181.1871.001.0021.181.1881.001.0031.181.1891.001.0041.181.18101.001.0051.001.00111.001.0061.001.00121.001.00

(a)
(b)
Fig.6 Iterative process to achieve the optimal force distribution by SQP.(a) f1; (b) f2
The cable net in symmetric AstroMesh is shown in Fig.7. The inscribed regular hexagon is subdivided into the same equilateral triangles with the side of 0.1 m, of which the vertices are mapped on the parabolic surface. The diameter of the aperture is 10 m and the focal length is 6 m for both nets. The minimum distance between the nets is 0.2 m. Due to the symmetrical property, we only study the front cable net for simplicity. The values of the forces in all vertical members are set to be 5 N.
The iterative process of the GA and SQP are shown in Fig.8 with the best function value (best fitness in GA) of 1.194 9 and 1.379 4, respectively. Therefore, it is concluded that the nonlinear optimal algorithm is more suitable for this problem. Due to the symmetric property of the cable net, a group of representative cables numbered 1 to 48 are shown in Fig.9. The optimized vector f, solved by the SQP method, is shown in Fig.10. The vertical coordinate is the ratio of forces in each member to the largest cable force.
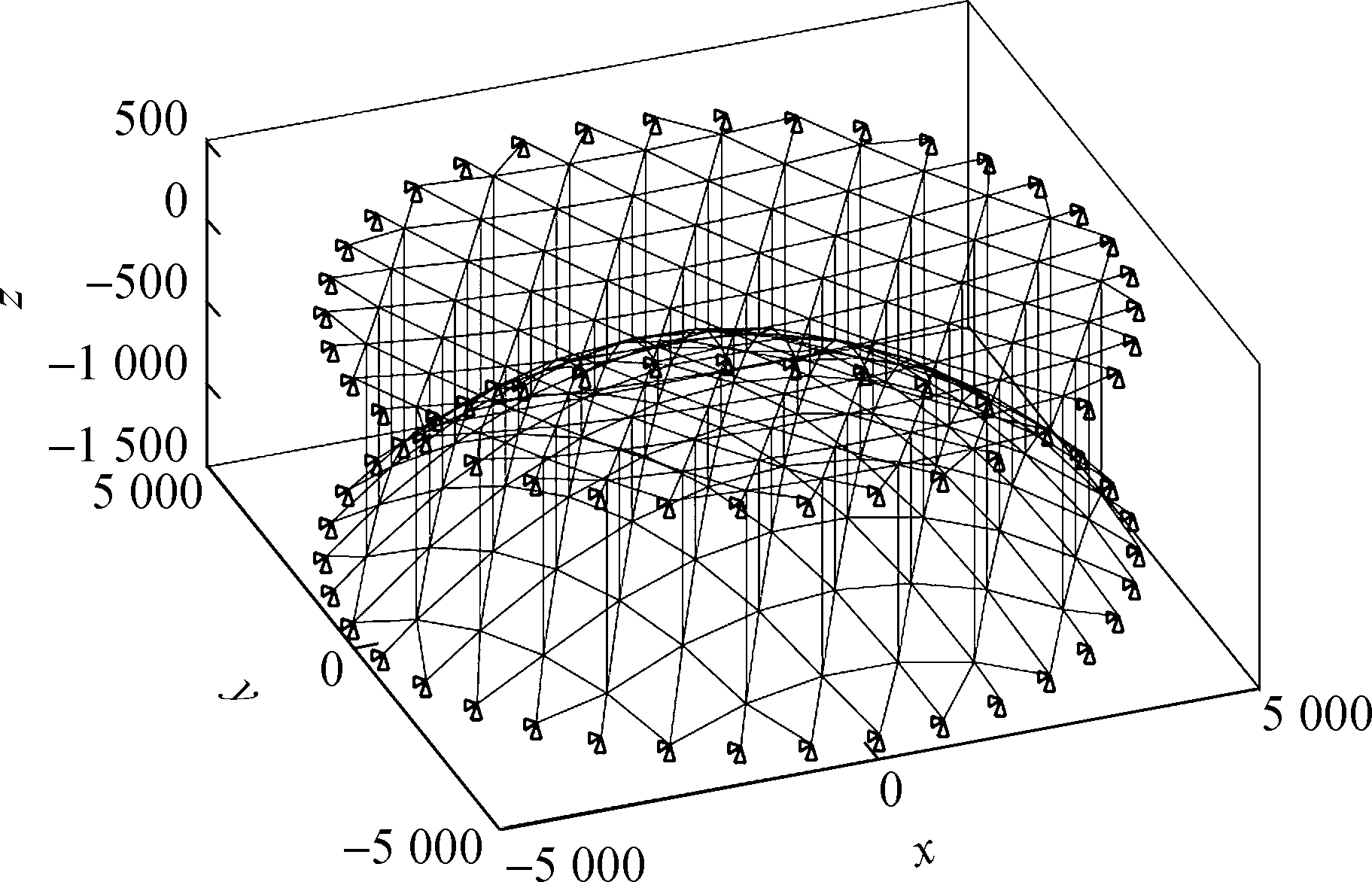
Fig.7 Cable nets in symmetric AstroMesh

(a)
(b)
Fig.8 Iterative process of a symmetric cable net.(a) SQP; (b) GA
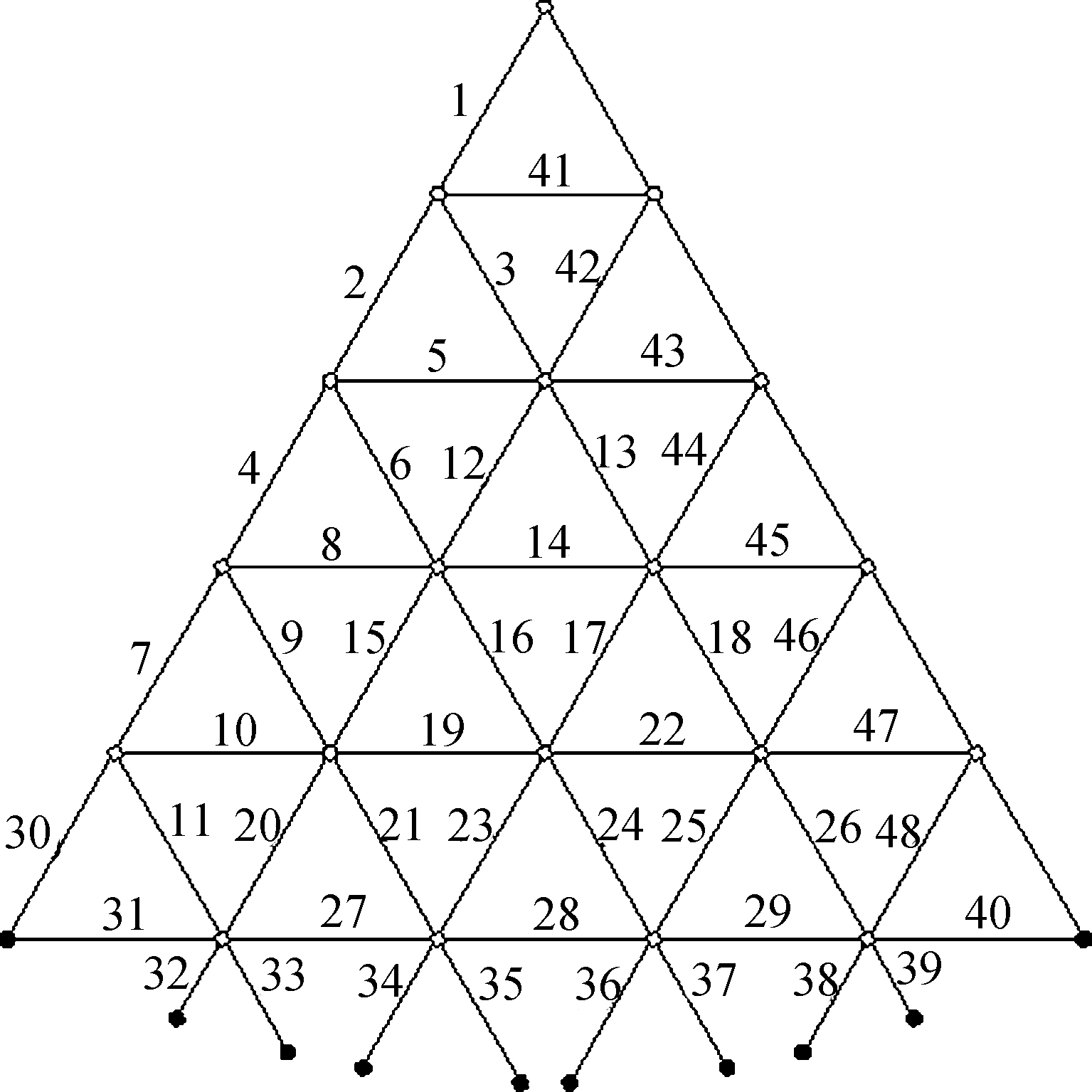
Fig.9 Numbering of a group of cables
2.2.2 Asymmetric cable net
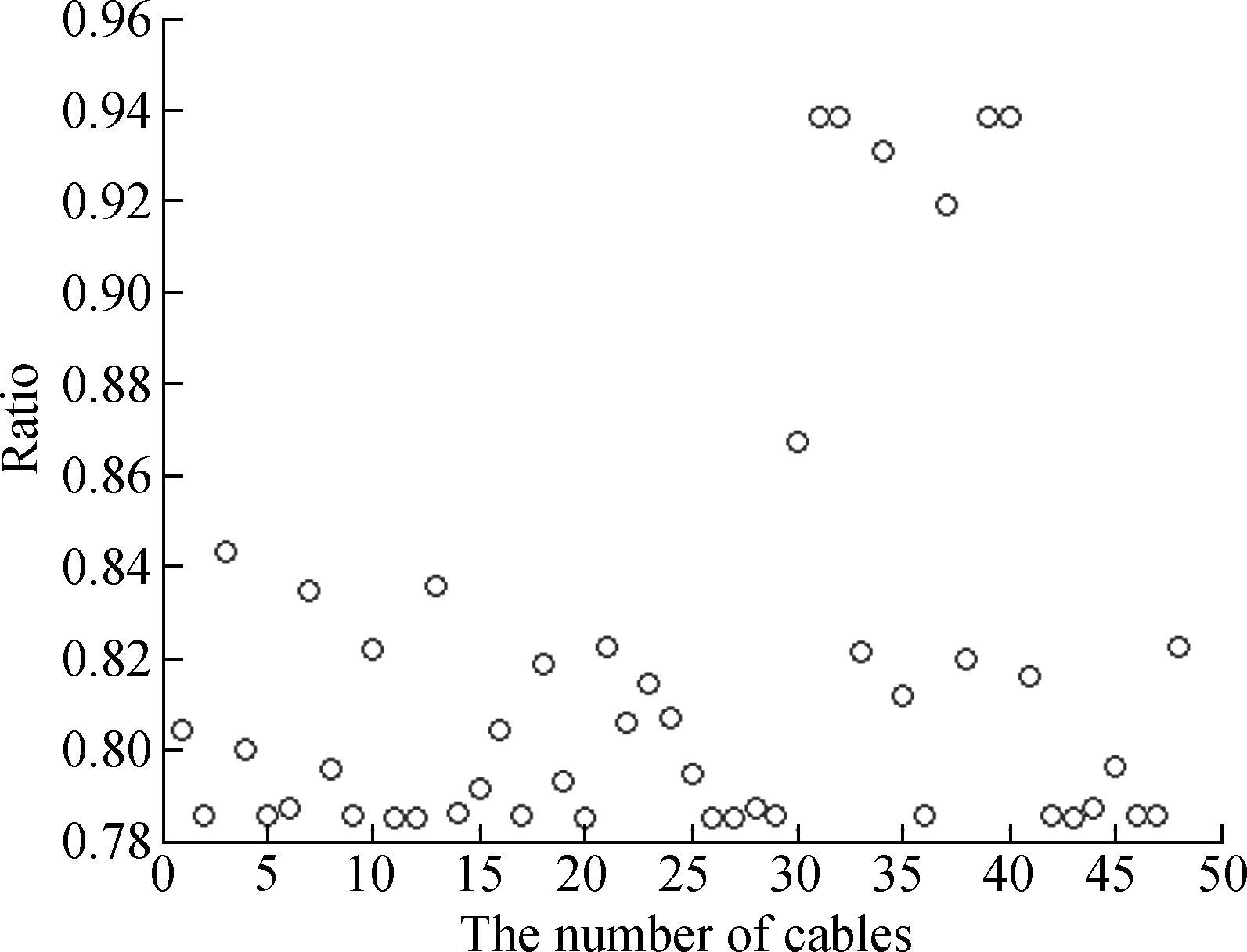
Fig.10 Force distribution in symmetric cable net of the group in Fig.9
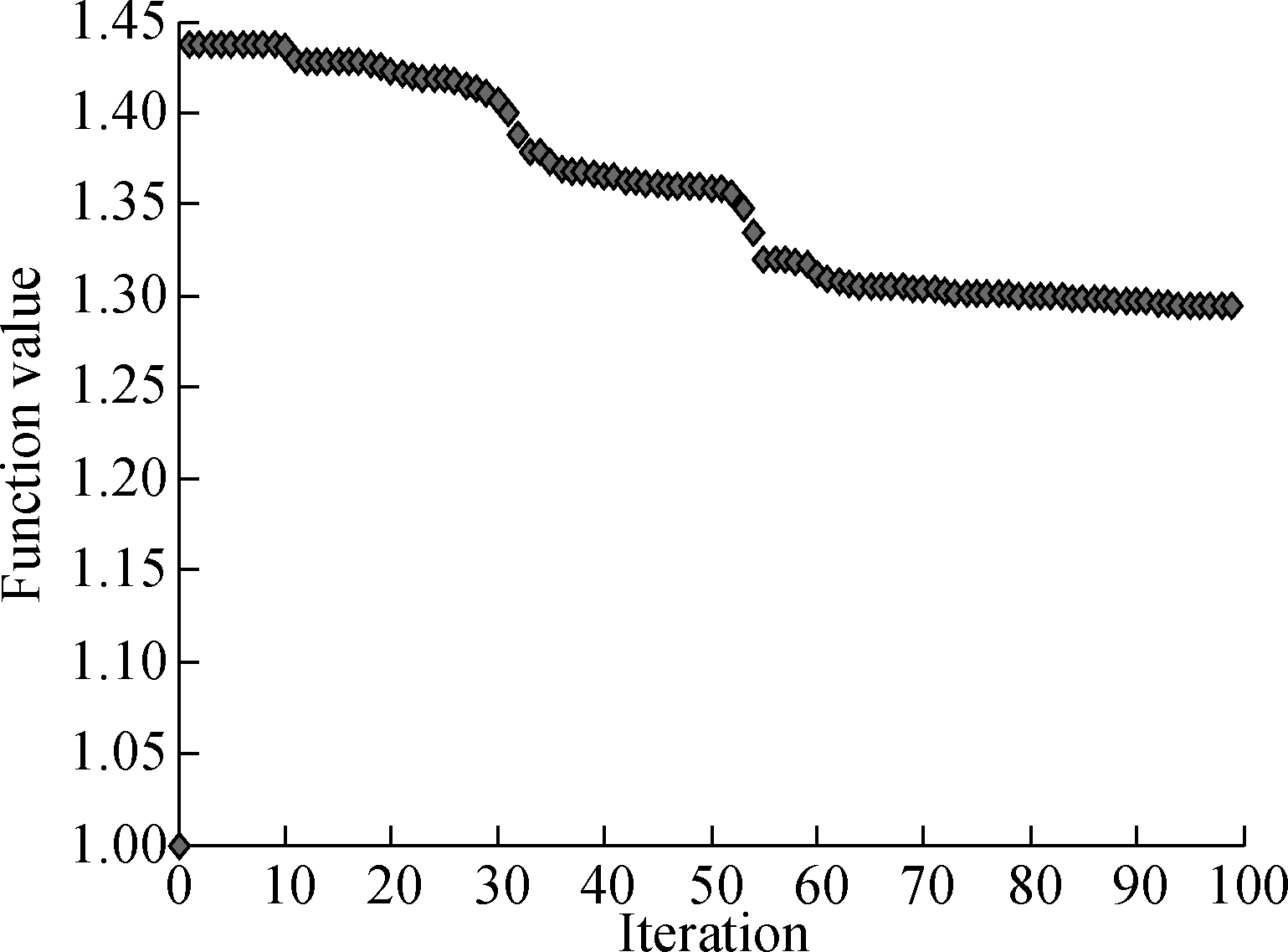
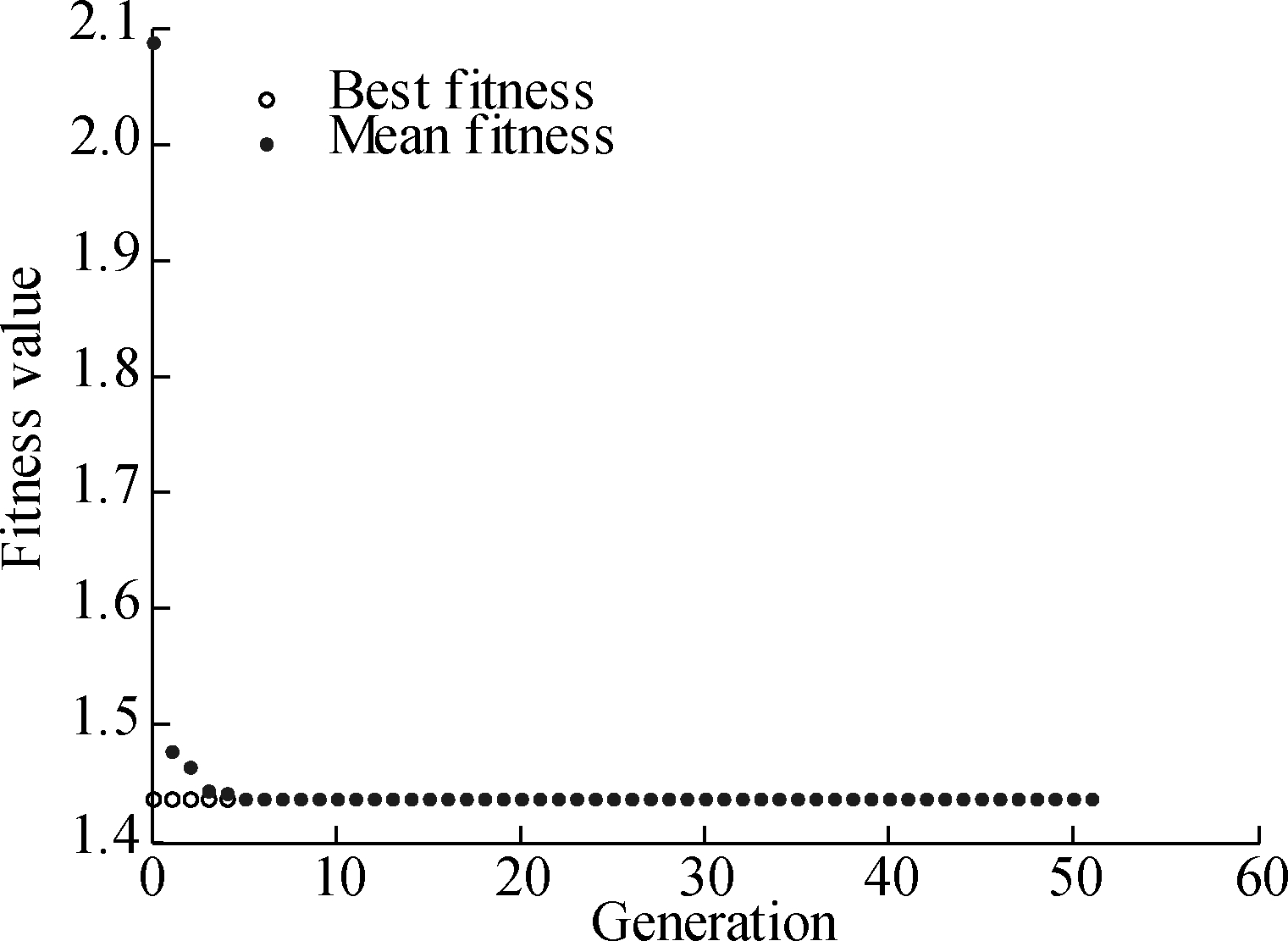
The cable net in asymmetric AstroMesh is shown in Fig.11. The inscribed regular hexagon is subdivided into the same equilateral triangles with the side of 0.1 m, of which the vertices are mapped on the parabolic surface. The diameter of the aperture is 10 m and the focal lengths are 40 and 6 m for the front net and back net, respectively. The minimum distance between the nets is 0.4 m. Different from the structure in subsection 3.2.1, both nets are taken into consideration. The SQP method and the GA are used to obtain the optimal distribution of prestress and the iterative processes are shown in Fig.12.
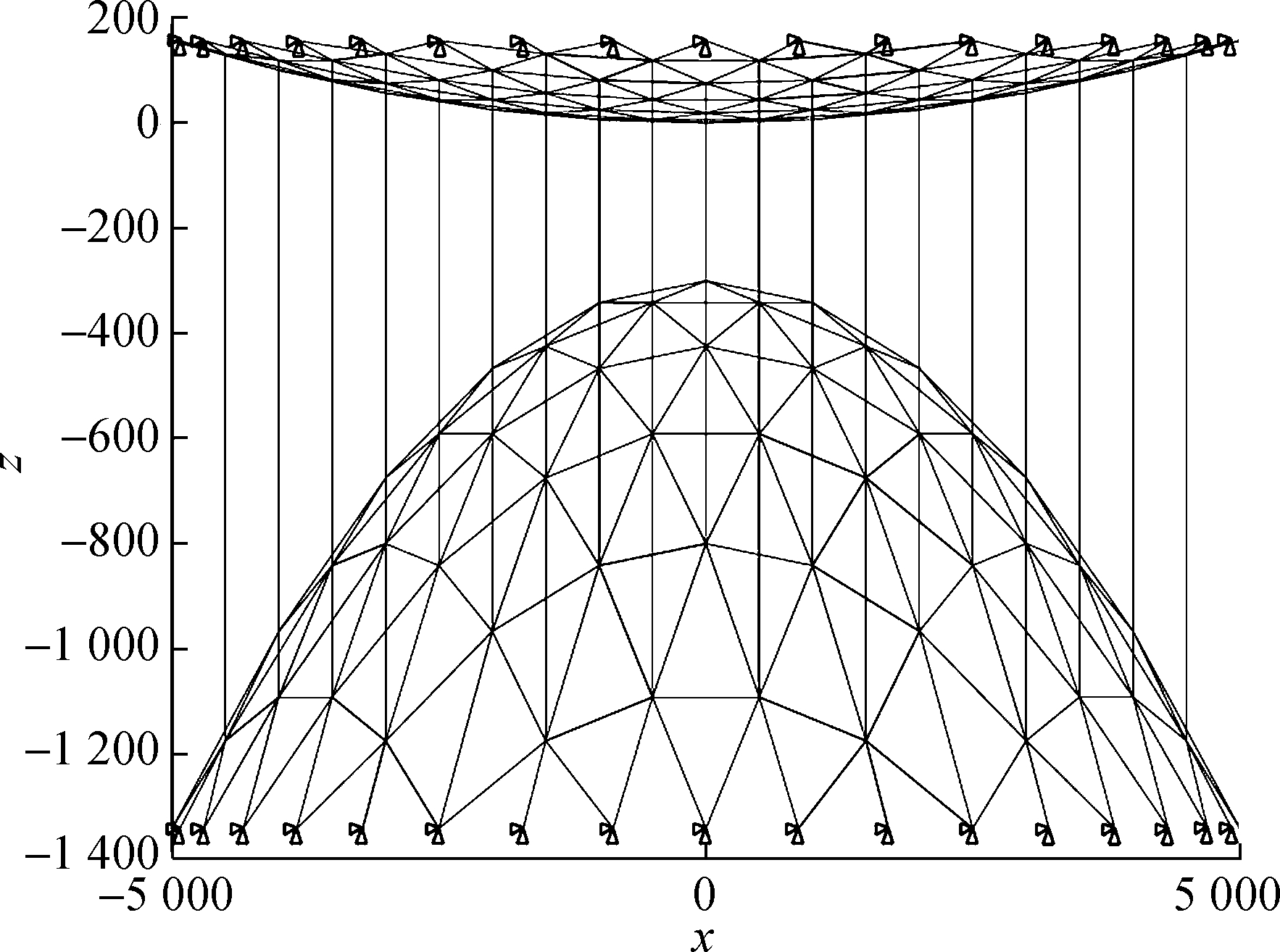
Fig.11 Cable nets in asymmetry AstroMesh
Due to the symmetrical property of each cable net,the cables numbered 1 to 48 (see Fig.6) from the optimized vector f (solved by the SQP method) are taken as an example and the result of the front net is shown in Fig.13. The vertical coordinate is the ratio of each member force to the largest cable force.
3 Conclusion
A force-finding method for the antenna cable net is proposed in this paper. Since the uniformity of cable forces has a great impact on the profile accuracy, with the given shape and boundary conditions, the proposed method is an optimal method to obtain a uniform distribution of cable forces, which can be categorized as force design. After the singular value deposition is performed on the equilibrium matrix, the distribution of prestress can be expressed in terms of force modes. Moreover, the equilibrium condition can always be satisfied exactly in the process. Numerical examples are carried out and the results demonstrate that the proposed force-finding method is effective for mesh reflector antenna.
(a)
(b)
Fig.12 Iterative process of an asymmetric cable net.(a) SQP; (b) GA

Fig.13 Force distribution in asymmetric cable net of the group in Fig.9
Both the genetic algorithm and successive quadratic programming are used to obtain the optimal result. The genetic algorithm proves to be better at converging when there are more structural members. It should also be noticed that the initial points of successive quadratic programming exert an effect influence on the computational time and the number of iterations. When there are fewer members in a structure, it is very likely that two methods achieve the same value of the objective function. Turning to more complicated structures, using the successive quadratic programming can obtain a better result though the nonlinear optimal method may trap into a local optimum. In this research, the boundary rings are supposed to be fixed, which is not in compliance with the fact. Therefore, the force-finding process including the rings will be studied in the future.
[1]Tibert A G, Pellegrino S. Deployable tensegrity reflectors for small satellites [J]. Journal of Spacecraft and Rockets, 2002, 39(5): 701-709. DOI:10.2514/2.3867.
[2]Thomson M W. The AstroMesh deployable reflector[C]//Fifth International Mobile Satellite Conference (IMSC’97). Orlando, FL, USA, 1997: 393-398.
[3]Thomson M W. AstroMeshTM deployable reflectors for Ku and Ka band commercial satellites [C]//20th AIAA International Communication Satellite Systems Conference and Exhibit. Montreal, Quebec, Canada,2002. DOI:10.2514/6.2002-2032.
[4]Liu W, Li D X, Yu X Z, et al. Exact mesh shape design of large cable-network antenna reflectors with flexible ring truss supports [J]. Acta Mechanica Sinica, 2014, 30(2): 198-205. DOI:10.1007/s10409-014-0029-6.
[5]Liu C, Shi Y. Comprehensive structural analysis and optimization of the electrostatic forming membrane reflector deployable antenna [J]. Aerospace Science and Technology, 2016, 53: 267-279. DOI:10.1016/j.ast.2016.03.026.
[6]Meguro A,Tsujihata A, Hamamoto N, et al. Technology status of the 13 m aperture deployment antenna reflectors for Engineering Test Satellite Ⅷ[J]. Acta Astronautica, 2000, 47(2): 147-152. DOI:10.1016/s0094-5765(00)00054-0.
[7]Meguro A,Shintate K, Usui M, et al. In-orbit deployment characteristics of large deployable antenna reflector on board Engineering Test Satellite Ⅷ[J]. Acta Astronautica, 2009, 65(9): 1306-1316. DOI:10.1016/j.actaastro.2009.03.052.
[8]Eastwood I, Thomson M, Fang H F.Prospects of large deployable reflector antennas for a new generation of geostationary Doppler radar satellites[C]//Proceedings of AIAA Space 2007 Conference and Exposition. Long Beach, CA, USA, 2007: 1-11. DOI:10.2514/6.2007-9917.
[9]Fan Y, Li T, Ma X.An analytic algorithm for pretension design of asymmetrical ring truss cable-net antennas [J]. Journal of Harbin Institute of Technology, 2015, 47(1): 124-128.
[10]Li P, Liu C, Tian Q,et al. Dynamics of a deployable mesh reflector of satellite antenna: Parallel computation and deployment simulation [J]. Journal of Computational and Nonlinear Dynamics, 2016, 11(6):061005. DOI:10.1115/1.4033657.
[11]Lewis W J.Tension structures: Form and behaviour [M]. Thomas Telford, 2003.
[12]Linkwitz K, Schek H J. Einige bemerkungen zur berechnung von vorgespannten seilnetzkonstruktionen [J]. Archive of Applied Mechanics, 1971, 40(3): 145-158. DOI:10.1007/bf00532146.
[13]Schek H J. The force density method for form finding and computation of general networks[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3(1): 115-134. DOI:10.1016/0045-7825(74)90045-0.
[14]Day A S, Bunce J. The analysis of hanging roofs [J]. Arup Journal, 1969, 9: 30-31.
[15]Barnes M R. Form-finding and analysis of prestressed nets and membranes [J]. Computers and Structures, 1988, 30(3): 685-695. DOI:10.1016/0045-7949(88)90304-5.
[16]Zhang J Y.Structural morphology and stability of tensegrity structures [D].Kyoto: Department of Architecture, Kyoto University, 2007.
[17]Yang B, Shi H, Thomson M,et al. Optimal design of initial surface profile of deployable mesh reflectors via static modeling and quadratic programming[C]//The 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Palm Springs, CA, USA, 2009. DOI:10.2514/6.2009-2173.
[18]Li G, Guan F. Optimization of pretension in net of AstroMesh deployable reflector and engineering application [J]. Acta Mechanica Solida Sinica, 2006, 27(12): 174-179.
[19]Niu Z, Wang S, Wang L. Multiobjective optimization of the pretensioning force in the tri-directional cable net of an AstroMesh deployable reflector [J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 39(3): 2541-2569.
[20]Li T J, Jiang J, Deng H Q. Form-finding methods for deployable mesh reflector antennas[J]. Chinese Journal of Aeronautics, 2013, 26(5): 1276-1282.
[21]Tanaka H, Natori M C. Shape control of space antennas consisting of cable network [J]. Acta Mechanica Sinica, 2004, 55(3): 519-527.
[22]Zhang J Y, Ohsaki M. Tensegrity structures: Form, Stability and System [M]. Springer, 2015.