Due to the great security demands, since the end ofWorld War Ⅱ, a growing need has arisen to investigate the behavior of thin-walled steel members under intentional or accidental impulsive loads (e.g. explosions). In the 1950s, a series of experiments were implemented by Symonds et al.[1-3] to investigate the dynamic plastic behavior of steel solid beams sustaining impulsive loads. They studied the impacts of rate effect, strain hardening and axial restraints on dynamic plastic behavior of beams, and a rigid-plastic analytic model was proposed to predict the member permanent deformations. Humphreys[4] conducted blast tests on flat steel beams, and the test results were compared with theoretical predictions given by a rigid-plastic analysis. Based on a series of impact tests on clamped aluminum beams, Menkes and Opat[5] established the three failure modes of metal solid beams under impulse (i.e., large inelastic deformations, tensile tearing and transverse shear failures at the supports). In general, thin-walled members exhibit more complex behavior under impulsive loading due to the local wall deformations followed by member global responses. Wegener and Martin[6] studied the dynamic performance of simply supported hollow steel beams of the square tube section, and a plastic analysis based model was proposed to predict the beams’ global and local permanent deformations. Bambach et al.[7] performed a series of transverse impact tests on steel square hollow sections, and severe local plastic deformations beneath the impactor were observed for the non-compact hollow sections. Jama et al.[8] investigated the blast responses of square hollow sections. The test results show that plastic deflections, tensile tearing at the supports and local collapse of upper flange are three fundamental deformation modes for the sections under blast. Nassr et al.[9-10] performed a series of full-scale blast tests on W-sections. Most of the post-blast beams and columns in their tests exhibited only global deflections, and none of them exhibited local buckling or fracture at any cross-section. Remennikov and Uy[11] studied the near-field blast responses of tubular steel columns infilled with or without concrete, and the measurements with respect to the hollow sections showed that each of them sustained large plastic flexural deformation and localized tearing failure of the upper and bottom flanges at the mid-span.
Test results have revealed that thin-walled members undergo localized deformation (e.g., cross-section distortion) followed by global response generally as they are subjected to impulsive loading. Although the traditional rigid-plastic analysis and yield line mechanisms of the cross-sections can be used to predict the impact response, they are only suitable for some simple problems. The shell finite element analysis (SFEA) is suitable for problems covering complex material and geometrical nonlinearities; however, it is difficult for us to extract the key factors which affect the impact behavior of members based only on SFEA in general. The generalized beam theory, an alternative to SFEA, can provide an insight into the behavior of thin-walled prismatic members under impact due to its intrinsic structural clarity.
GBT is generally used to perform elastic vibration and buckling analyses of thin-walled prismatic members[12-13]. Recently, it has been extended to simulate the linear and nonlinear static behavior of thin-walled members and frames with arbitrary cross-sections and is made of different materials[14-19]. Rui et al.[20] proposed a doubly modal GBT formulation for dynamic analysis of thin-walled members; however, it is just a first-order model and only suitable for linear elastic members. This research aims at presenting a new nonlinear explicit dynamic model based on the GBT for numerical simulations of the transient dynamic responses of thin-walled steel members under impact. The numerical discretization scheme adopted herein is similar to that in Ref.[21], which concerns the application of GBT to fire simulations of restrained steel beams.
1 Constitutive Material Model
1.1 Thermo-visco-plastic constitutive relationship for steel
The dynamic plastic behavior of steel at ambient and elevated temperatures exhibits the coupling of rate hardening and thermal softening effects. Several efficient constitutive material models have been developed to describe it, such as the Johnson-Cook model[22], the Cowper-Symonds model[1] and the RK model[23]. In this paper, the rate hardening model proposed by Perzyna[24] is utilized as follows:
(1)
where σ0 denotes the flow stress concerning the material quasi-static tensile loading; Cowper and Symonds[1] suggested that D=40.4 s-1 and q=5 for mild steel; ![]() denotes the equivalent plastic strain rate. As
denotes the equivalent plastic strain rate. As ![]() exceeds 0.1 s-1, the adiabatic temperature rising induced by the conversion of material plastic work into heat must be taken into account in analysis. This is also supported by the numerical modeling of steel tubular beams under blast [25]. Jama et al.[25] showed that the thermal softening induced by the adiabatic temperature rising has small but no negligible effect on beam blast behavior. To take the thermal softening effect into account, we modify σ0 as a function with respect to the material temperature T, and the formulation recommended by the Australian code AS4100—1998[26] is used, i.e.,
exceeds 0.1 s-1, the adiabatic temperature rising induced by the conversion of material plastic work into heat must be taken into account in analysis. This is also supported by the numerical modeling of steel tubular beams under blast [25]. Jama et al.[25] showed that the thermal softening induced by the adiabatic temperature rising has small but no negligible effect on beam blast behavior. To take the thermal softening effect into account, we modify σ0 as a function with respect to the material temperature T, and the formulation recommended by the Australian code AS4100—1998[26] is used, i.e.,

(2)
where σy0 denotes the steel yield stress at the ambient temperature, and the steel temperature-dependent Young’s modulus reads[26]
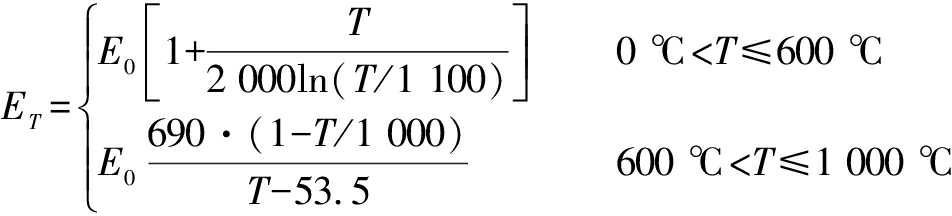
(3)
where E0=ET as T=0 ℃. Moreover, the steel thermal elongation recommended by EC3[27] is adopted in this work. It is noteworthy that the strain hardening effect is not taken into account herein. To accomplish a geometrical nonlinear analysis, the stress-strain relationship should be transformed into the true stress-logarithmic strain law, i.e.,
εt=ln(1+ε), σt=σ(1+ε)
(4)
1.2 Integration scheme for the constitutive model
Constitutive modeling for steel are based on: 1) The isotropic elastic behavior defined by generalized Hooke’s law; 2) J2-plasticity with isotropic hardening and associated flow rule; 3) Additive decomposition of the strain increments; and 4) Isotropic thermal deformations. In general, to solve the set of nonlinear constitutive equations, an incremental integration procedure should be performed. For a given strain increment, we need to update the stress, the plastic strain, the plastic strain rate and the temperature, so that the consistency condition can be complied with (i.e., the stress remains on the yield surface) on each quadrature point. Two kinds of integration schemes (i.e., explicit and implicit schemes corresponding to the forward Euler and backward Euler methods, respectively) can be utilized to implement the updating procedure. Due to the deficiency of the explicit scheme in preserving the consistency condition, an implicit scheme proposed by Zaera and Fernandez-Saez[28] is used to solve the set of incremental equations in this work.
The implicit integration scheme consists of two steps. For a given plastic loading, an elastic predictor for the new stress-state is given first, and then, an iterative procedure, so called plastic return, is performed to project the elastic predictor onto the revised yield surface. The elastic predictor is
![]() ·Δε
·Δε
(5)
where De denotes the stiffness matrix; σold is the previous stresses; and Δε is the strain increments. The revised yield surface can be given by
(6)
where Φold represents the previous yield function; Φnew is the updated yield function; σnew is the updated stress vector which lies on the revised yield surface;Δλ is the plastic ![]() is the equivalent plastic strain rate. Based on the additive decomposition of strain increments, σnew is written as
is the equivalent plastic strain rate. Based on the additive decomposition of strain increments, σnew is written as
![]() ·
·![]() ·αTΔT
·αTΔT
(7)
where αT denotes the thermal expansion coefficients, and the adiabatic temperature increment is
(8)
where η is the Taylor-Quinney ![]() is the equivalent stress with respect to σnew; Cp is the specific heat; ρ is the density. To solve Eqs.(5) to (8), the Newton-Raphson iterative procedure is used. Taking linearization on Eqs.(6) to (8) yields the next iterative value of Φnew as
is the equivalent stress with respect to σnew; Cp is the specific heat; ρ is the density. To solve Eqs.(5) to (8), the Newton-Raphson iterative procedure is used. Taking linearization on Eqs.(6) to (8) yields the next iterative value of Φnew as
(9)
The next iterative value of σnew and T is
(10)
(11)
where ![]() I is the unit matrix; Δt is the time step. Although the explicit expressions of δλ and δT can be obtained by the solution of Eqs.(9) to (11), more convenient expressions can be given by[28]
I is the unit matrix; Δt is the time step. Although the explicit expressions of δλ and δT can be obtained by the solution of Eqs.(9) to (11), more convenient expressions can be given by[28]
![]() ·
·![]()
(12)
(13)
where ![]() denotes the equivalent stress of the elastic predictor; and G is the shear modulus. Substituting Eqs.(12) and (13) into Eq.(10), we can obtain the new iterative stresses
denotes the equivalent stress of the elastic predictor; and G is the shear modulus. Substituting Eqs.(12) and (13) into Eq.(10), we can obtain the new iterative stresses ![]()
1.3 Illustration of the constitutive model
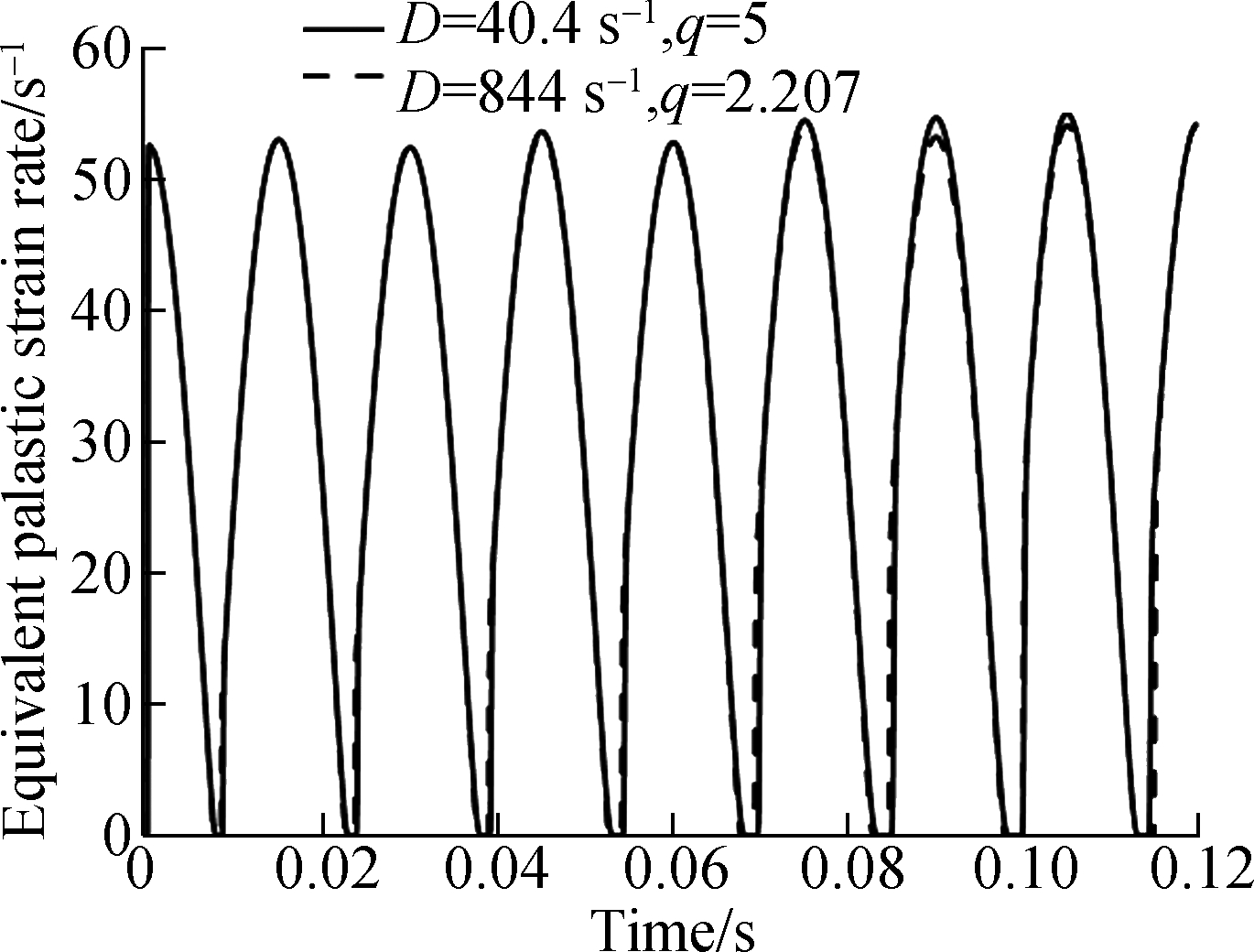
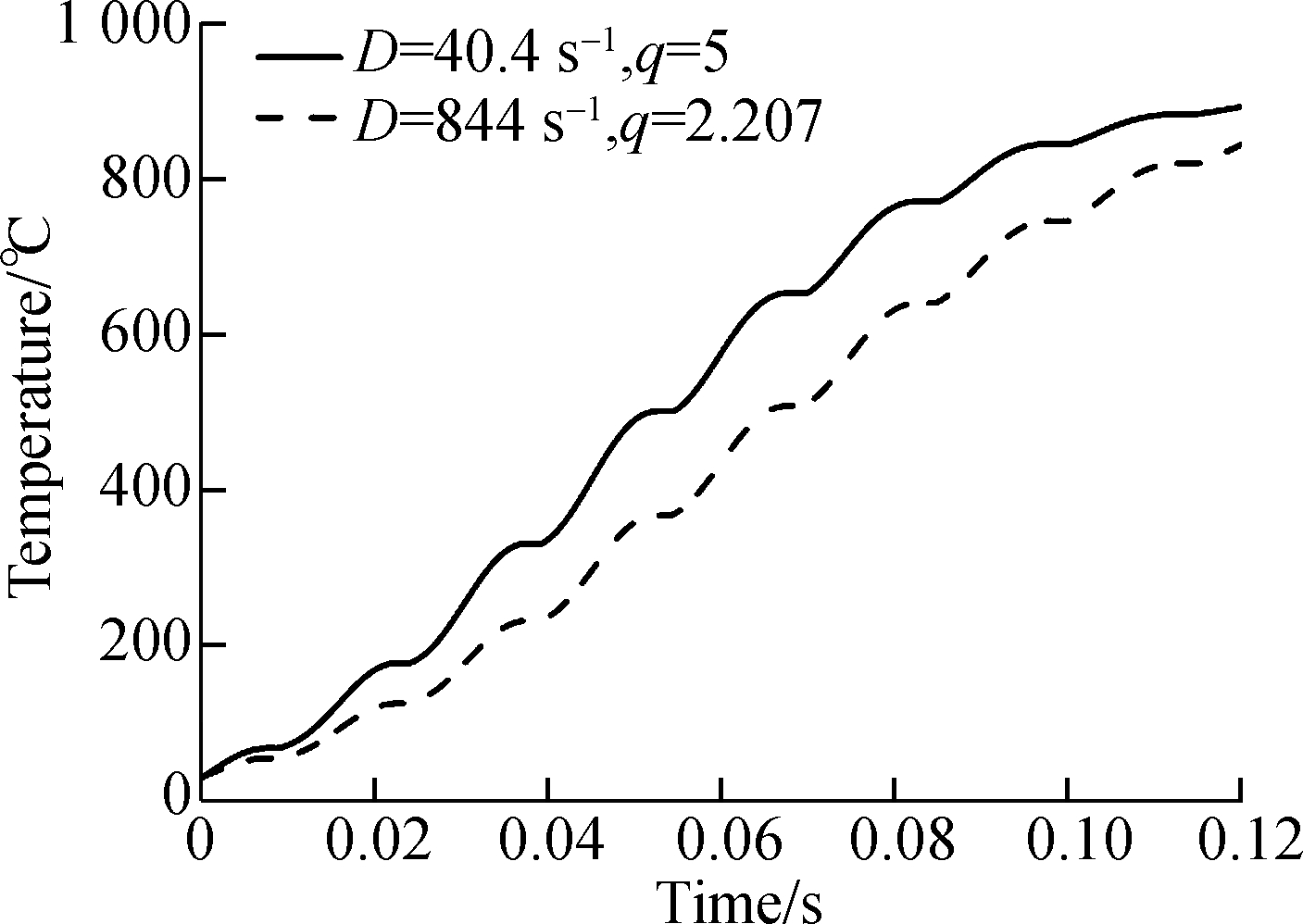
To illustrate the implicit integration scheme, a dynamic plastic loading for steel under plane stress is investigated in this section. All the related material constants are listed in Tab.1. As mentioned before, for the mild steel, D=40.4 s-1 and q=5 are recommended in general. However, based on a series of Kolsky bar tests on mild steel, Marais et al.[29] suggested that D=844 s-1 and q=2.207 recently, so two results are calculated herein. We assume that the strain components varying with time are
(14)
where εx0,εy0 and γxy0 denote the strain amplitudes corresponding to the plane stress state. For a given strain amplitude vector {0.15, 0.1, 0.05} and a tc value of 0.03, the variations of stresses, equivalent plastic strain rate and temperature are plotted in Fig.1. Clearly, the case with D=40.4 s-1 and q=5 exhibits a much stronger rate strengthening effect. Due to the lack of further experimental investigations on the dynamic plastic behavior of constructional steel, the widely accepted values of 40.4 s-1 and 5 are employed in the forthcoming analysis.
Tab.1 Material constants of the steel
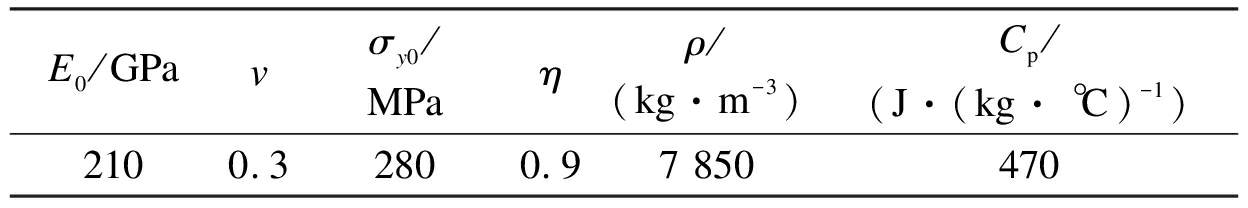
E0 /GPavσy0 /MPaηρ/(kg·m-3)Cp/(J·(kg· ℃)-1)2100.32800.97 850470

(a)
(b)
(c)
Fig.1 Results for the given harmonic loading. (a) Stress; (b) Equivalent plastic strain rate; (c) Adiabatic temperature rising
2 Theoretical Model
2.1 Kinematic relationship and strains
The cross-section displacement field is built upon the linear superposition of the GBT cross-section deformation modes. The amplitude of each GBT mode varies along the member length, and they are also the unknowns for GBT analysis. The displacement formula is

(15)
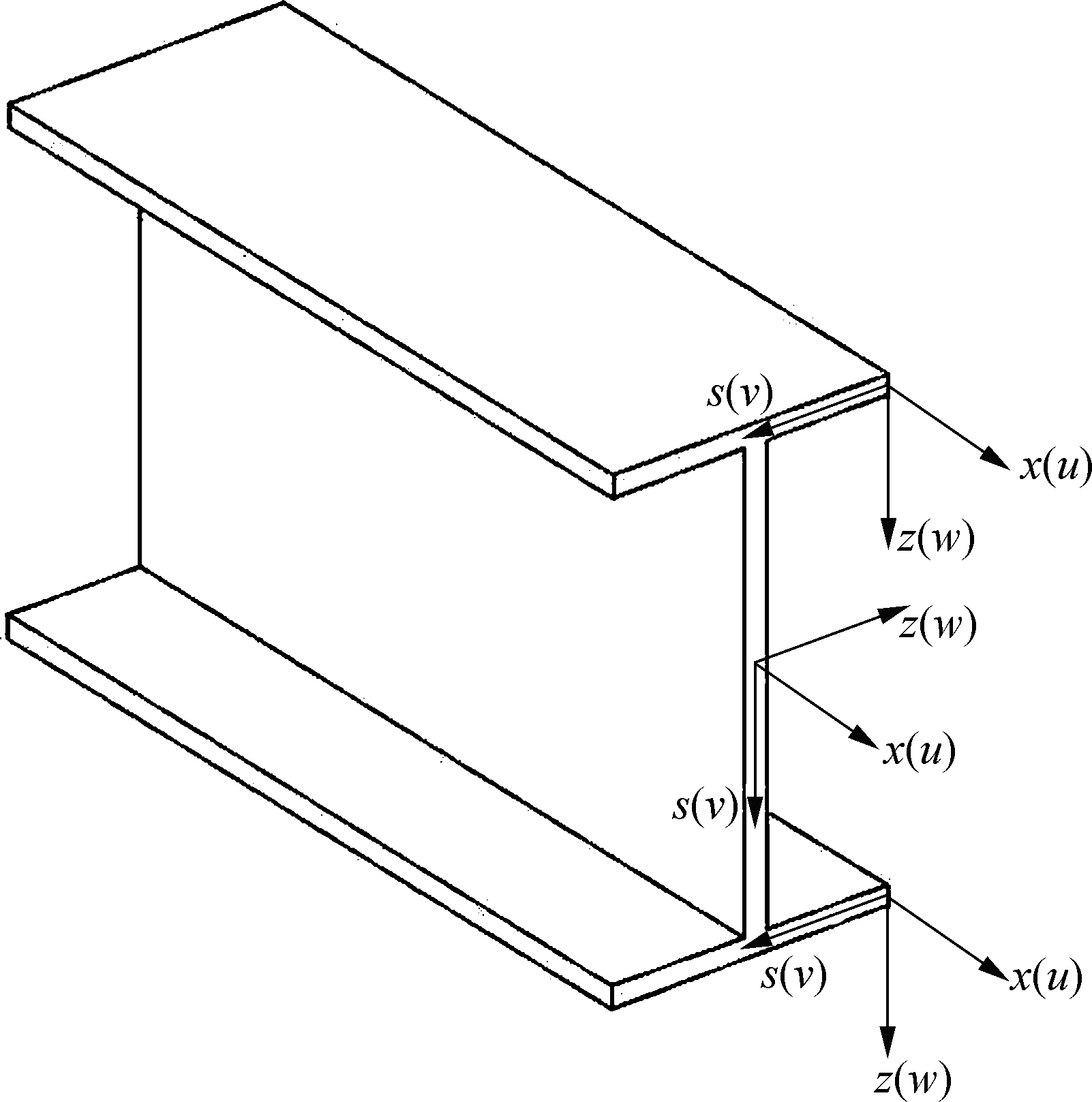
Fig.2 Definition of the GBT coordinates
where u, v and w denote the membrane displacements along the member longitudinal axis, arc-length coordinate of the wall and normal direction of the wall, respectively (see Fig.2). Moreover, the Kirchhoff’s thin plate assumption is employed. The wall mid-surface displacement is
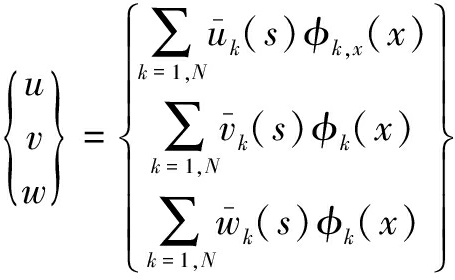
(16)
where N denotes the number of GBT modes involved; ![]() and
and ![]() are the cross-section displacement profiles of the k-th GBT mode; φk represents the amplitude function of the k-th GBT mode. Just as in the classic GBT, the out-of-plane warping displacement u depends on φk,x, which is due to the fact that no membrane shear strain is assumed for the open cross-sections.
are the cross-section displacement profiles of the k-th GBT mode; φk represents the amplitude function of the k-th GBT mode. Just as in the classic GBT, the out-of-plane warping displacement u depends on φk,x, which is due to the fact that no membrane shear strain is assumed for the open cross-sections.
The Green-Lagrange strain tensor is employed to measure the deformation at any material point. First, we derive the displacement gradients as

(17)
and then based on the relationship between the Green-Lagrange strain tensor E and H, we obtain
![]() ·H)
·H)
(18)
For plane stress problems,only three components related to wall in-plane deformations are required, i.e.,
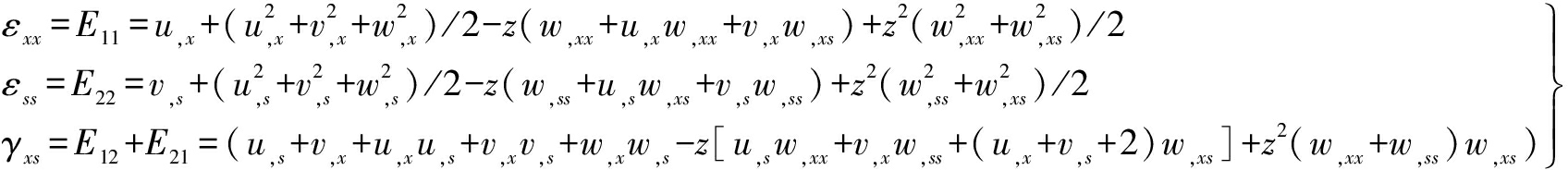
(19)
where εxx,εss,γxs are the longitudinal extension strain, the transverse extension strain and the in-plane shear strain, respectively. Clearly, two parts, i.e., membrane deformation and bending related terms, compose the strain measures. In general, z2 related to the terms in Eq.(19) is ignored, which has no effect on the model accuracy[16,19].
GBT cross-section analysis[30], the first step for a GBT analysis, yields the cross-section deformation modes. The retrieved GBT modes depend on the cross-section discretization scheme. As shown in Fig.2, three translational displacements (u, v, w) combined with a rotational displacement along the x axis are assigned to each node on cross-section, and then the interpolation of the node displacements approximates the cross-section displacement field. A set of unconstraint or admissible cross-section deformation modes should be calculated first[30-31], and then a generalized orthogonalization procedure is performed to obtain the GBT modes.
2.2 Cubic B-splines
Since the out-of-plane warping displacement depends on the derivative of the amplitude function (see Eq.(16)), the interpolation function of φk must possess the first-order continuity at the nodes between two adjacent elements. The Hermite polynomial interpolations are used in general[15-19], but we prefer to use the cubic B-splines, which is favorable for enforcing even the second-order continuity, to approximate φk. Based on the Cox-de Boor recursion formulation[32-33], for the B-splines, a knot vector should be defined first and it is expressed as
ψ={α1,α2,...,αm+7}=
{x1,x1,x1,x1,x2,...,xm,xm+1,xm+1,xm+1,xm+1}
(20)
where both the components x1 and xm+1 are repeated four times, so we call Ψ as an open knot vector, which implies that the cubic B-splines built upon Ψ are interpolatory at the two boundary knots. Starting with piecewise constants, the basis functions are obtained by
(21)
(22)
where superscript p represents the polynomial order, and subscript k denotes the knot index. Clearly, m+3 cubic B-spline basis functions can be computed by the recursive procedure. Moreover, the r-th order derivative of the basis function is
(23)
Any cubic spline function f defined on the interval [x1, xm+1] can be expressed as
(24)
where β represents the undetermined coefficient, and subscript j implies that point x lies in the j-th coordinate interval.
2.3 Weak-form of the dynamic equations
Provided that a prismatic member is subdivided into n elements along its length, the wall mid-surface displacements (see Eq.(16)) for the r-th element can be approximated by
{u,v,w}T=Nr(x,s)·![]()
(25)
where the element generalized displacement vector is
(26)
where index N denotes the total number of cross-section deformation modes involved, and ![]() represents the weight of
represents the weight of ![]() with respect to the j-th cross-section deformation modes (i=r, r+1, r+2, r+3; j=1,2,…,N). The shape function can be expressed as
with respect to the j-th cross-section deformation modes (i=r, r+1, r+2, r+3; j=1,2,…,N). The shape function can be expressed as
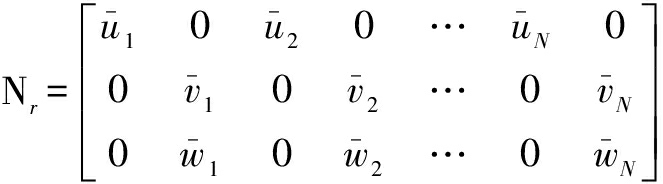 ·
·
[Wr Wr+1 Wr+2 Wr+3]
(27)
where the first matrix refers to displacement profiles of GBT cross-section deformation modes, and the sub-matrix Wj (j=r, r+1, r+2, r+3) concerning the amplitude of the j-th GBT mode is written as

(28)
Then the kinematic relationship (see Eq.(15)) can be rewritten as
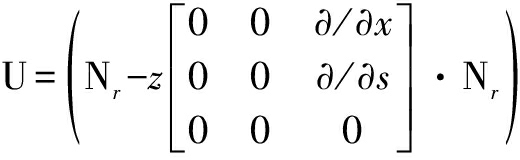 ·
·![]()
(29)
Therefore, we have
ε={εxx,εss,γxs}T=(BL+BNL)·![]()
(30)
where the linear strain matrix reads

(31)
and the nonlinear one is
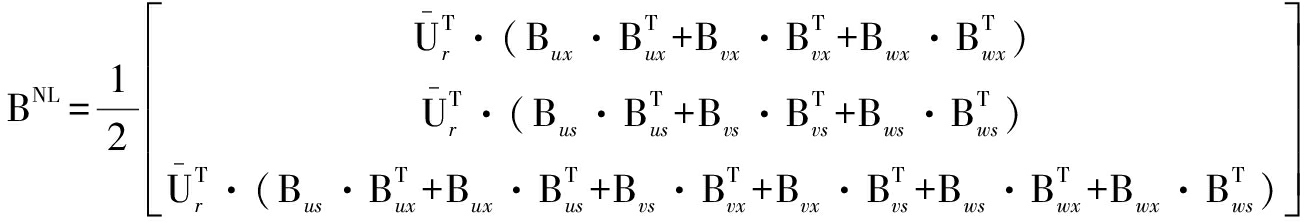
(32)
where ![]() obtained from the previous iteration is substituted into Eq.(32) for the calculation of BNL at each time step, and the gradient vectors in Eqs.(30) to (32) are
obtained from the previous iteration is substituted into Eq.(32) for the calculation of BNL at each time step, and the gradient vectors in Eqs.(30) to (32) are
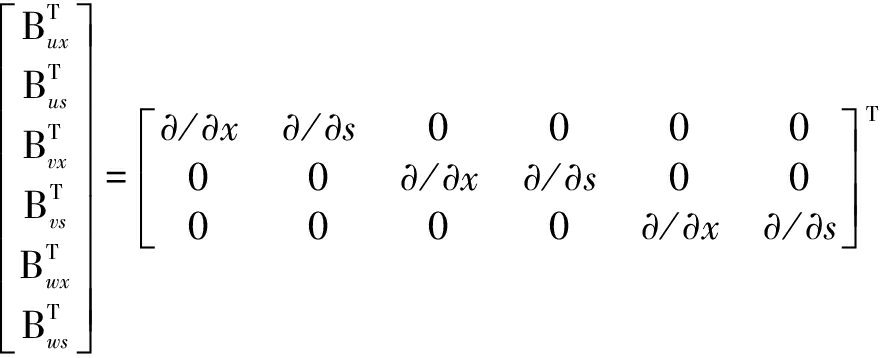 ·
·
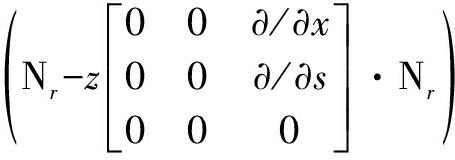
(33)
Based on Eq.(30), we can derive the variation of strain components with respect to ![]() as
as
δε=(BL+2BNL)·![]()
(34)
The equation of motion for an explicit transient dynamic analysis can be given by
Μ·![]() ·
·![]()
(35)
where M is the member mass matrix; C is the damping matrix; Fint is the equivalent member internal force vector; Fext is the equivalent external force vector. For an impulsive response analysis, the damping effect can be ignored in general since the energy dissipation caused by the plastic deformation is significantly greater than that dissipated by damping.
The mass matrix for the r-th element is
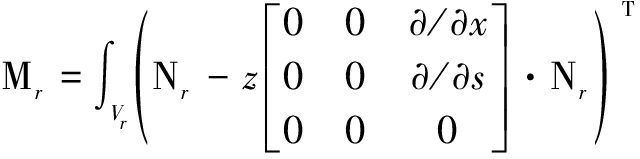 ·
·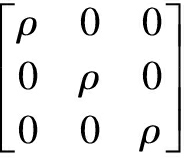 ·
·
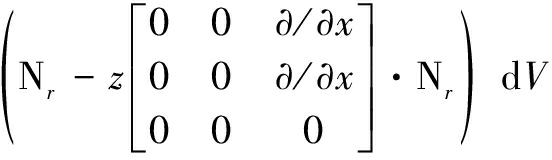
(36)
where the domain of integration Vr denotes the overall volume of the r-th element.
Based on the principle of virtual work, the equivalent internal force vector for the r-th element can be given by
![]() ·{σxx,σss,τxs}TdV
·{σxx,σss,τxs}TdV
(37)
and the element equivalent external force vector can be given by
![]() ·qdA
·qdA
(38)
where the external excitation q acts on the wall mid-surface of the domain Ωr.
Assembling the derived element equivalent internal force vector, the external force vector and the mass matrix of each element, we can obtain their global counterparts (Fint, Fext and M) for the overall member. Please note that the plane stress state is assumed herein (i.e., σzz=0, τzx=0, τzs=0).
The classic central differencing scheme is utilized to perform the explicit time integration procedure. Assuming that one has obtained the acceleration ![]() velocity
velocity ![]() and displacement
and displacement ![]() at the moment tk, the velocity
at the moment tk, the velocity ![]() at time station k+1/2 is
at time station k+1/2 is
![]() ·
·![]()
(39)
The displacement ![]() next time station is
next time station is
![]() ·
·![]()
(40)
After this, we need to update the member geometric and the stress state on each quadrature point. Additionally, the acceleration at time station k+1 can be solved by Eq.(35). And then the next incremental step can continue on. Due to the conditional stability of the explicit integration scheme, the time step size should be selected small enough to capture the response frequencies and other nonlinear effects. The time incremental size enforcing the convergence for an explicit dynamic integration scheme depends on the largest eigenvalue of the dynamic equilibrium eigen-system, which can be calculated by the GBT elastic vibration analysis. However, the Courant-Friedrichs-Lewy condition, a more convenient guideline, is sufficient for estimating it.
To alleviate the shear locking which leads to over-stiff results for member deformations, a selective reduced integration scheme[34] is employed, i.e., the stretching and bending related terms are calculated by the full integration scheme, but the shear deformation related terms are computed by the reduced integration method.
3 Illustrative Examples
This section aims to show the potential and validation of the proposed GBT formulation as it is used to simulate the impulsive response of thin-walled steel members. The developed GBT code was implemented through FORTRAN programming and run on a desktop PC with a 3.2 GHz Xeon CPU and 2GB RAM. Three test cases are given, and they concern three thin-walled steel members with different cross-sections and boundary constraints subjected to transverse triangle impulses. The member displacement and stress solutions obtained from the GBT analyses are compared with their SFEA counterparts. Due to the modal nature of GBT, the solution concerning the contribution of GBT modes to deformed member configuration is involved.
3.1 Example Ⅰ
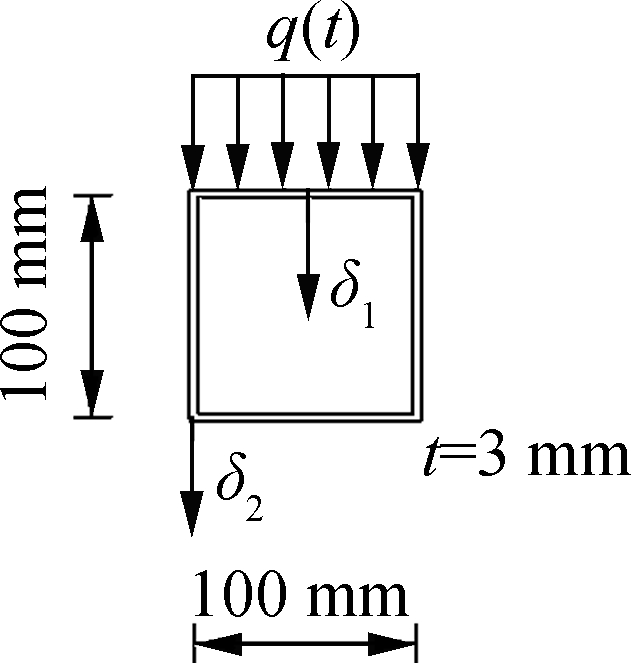
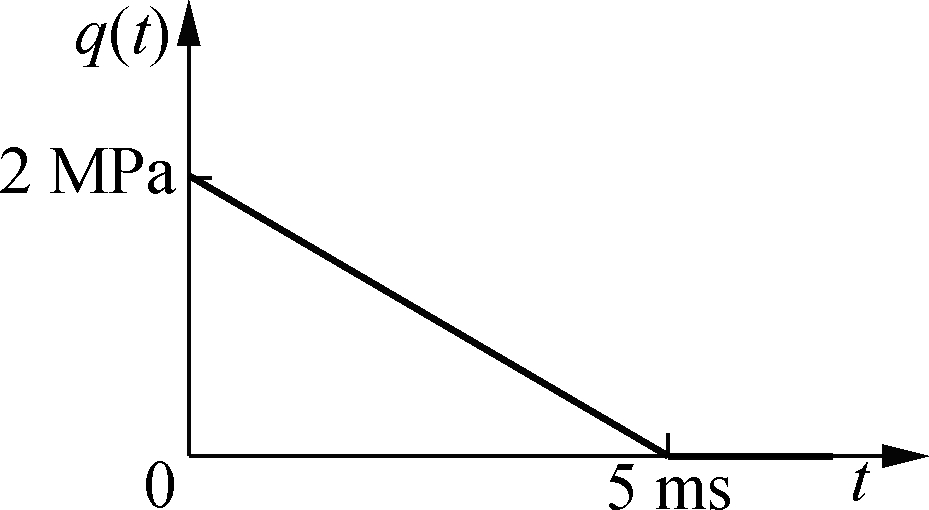
Fig.3 plots a fixed steel tubular beam subjected to a distributed triangle impulse on its top flange. The mass density, elastic modulus, Poisson’s ratio and yield stress at ambient temperature of the beam are 7 850 kg/m3, 210 GPa, 0.3 and 350 MPa, respectively, and the other material constants concerning the strain rate effect and the adiabatic temperature rising are identical to those used in Section 2. For the proposed GBT model, the cross-section discretization involves ten uniform sub-walls per flange and ten uniform sub-walls per web, which leads to 120 deformation modes. Concerning the longitudinal discretization, 46 non-uniform beam elements are used, specifically, eight uniform elements for x≤160 mm, thirty uniform elements for 160<x≤2840 mm, and eight uniform elements for 2840<x≤3000 mm. Therefore, the discretization leads to a total of 17 640 degrees of freedom (DOFs), only 12.21% of the number required by its counterpart, a finite element model built upon the 4-node shell elements of the Belytchko-Tsay formulation type with roughly uniform mesh size (144 480 DOFs).
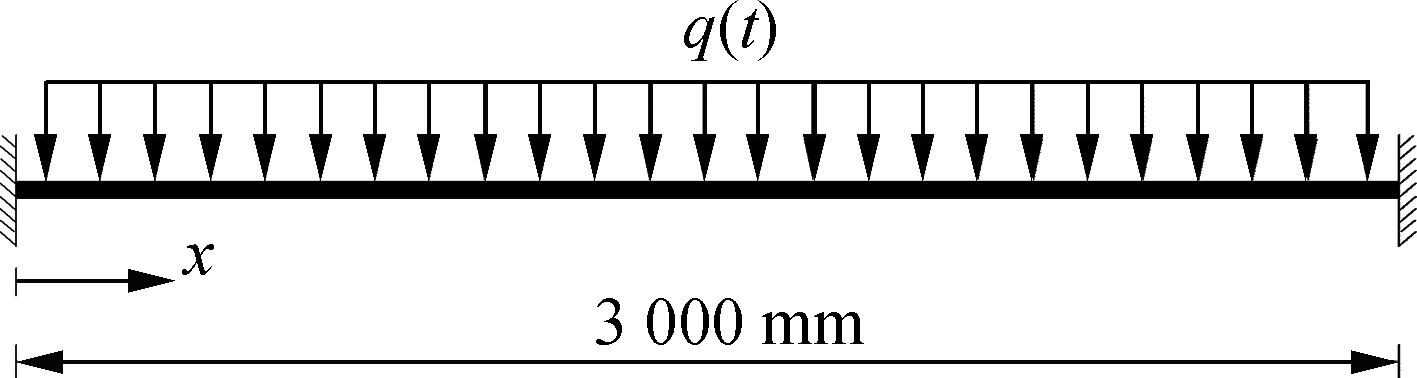
(a)
(b)
(c)
Fig.3 Fixed steel SHS beam subjected to an impulsive load. (a) Overall view of the beam; (b) Cross-section dimensions; (c) Pressure vs. time curve
Although all of the 120 GBT cross-section deformation modes are included into the GBT analysis, only a few of them, which are depicted in Fig.4, play significant roles in the simulation of beam response. The contribution of each GBT mode to the deformed configuration of the beam is quantified by modal participation factor Pk as[35]
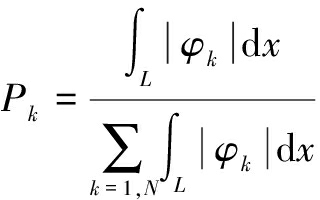
(41)
where the beam length L is the domain of the integration.
Fig.5 plots the modal participation diagram of the beam deformation under impact, where the width of each color filled strip represents the corresponding participation of the indicated mode. It shows that the four local plate modes 6-9 contribute mostly to the beam configuration at the initial loading, and then their contributions are gradually surpassed by that of the major-axis bending (mode 2). After a large increase of the beam global deflection, the contribution of the longitudinal cross-section extension (mode 1) begins to rise up due to the so-called catenary action. Generally, the impact behavior of a SHS beam exhibits the cross-section distortion or buckling followed by the global deformation (e.g., bending), and the two kinds of deformations can be considered to be uncoupled and sequential[25,36]. Clearly, those are also confirmed by present GBT analysis. Due to the increasing participation of major-axis bending, the associated global shear mode 42 prevails in all the shear modes. Moreover, to account for the effects of shear lag, the flange warping shear modes 45 and 47 are also important participators. Concerning the transverse extension modes, they account for the Poisson’s effects and cannot be excluded in analysis though their participation is relatively small (see Fig.5). For example, mode 81 describes the transverse deformations of top- and lower-flanges during the major-axis bending, and its contribution grows up along with the increase of beam deflection.
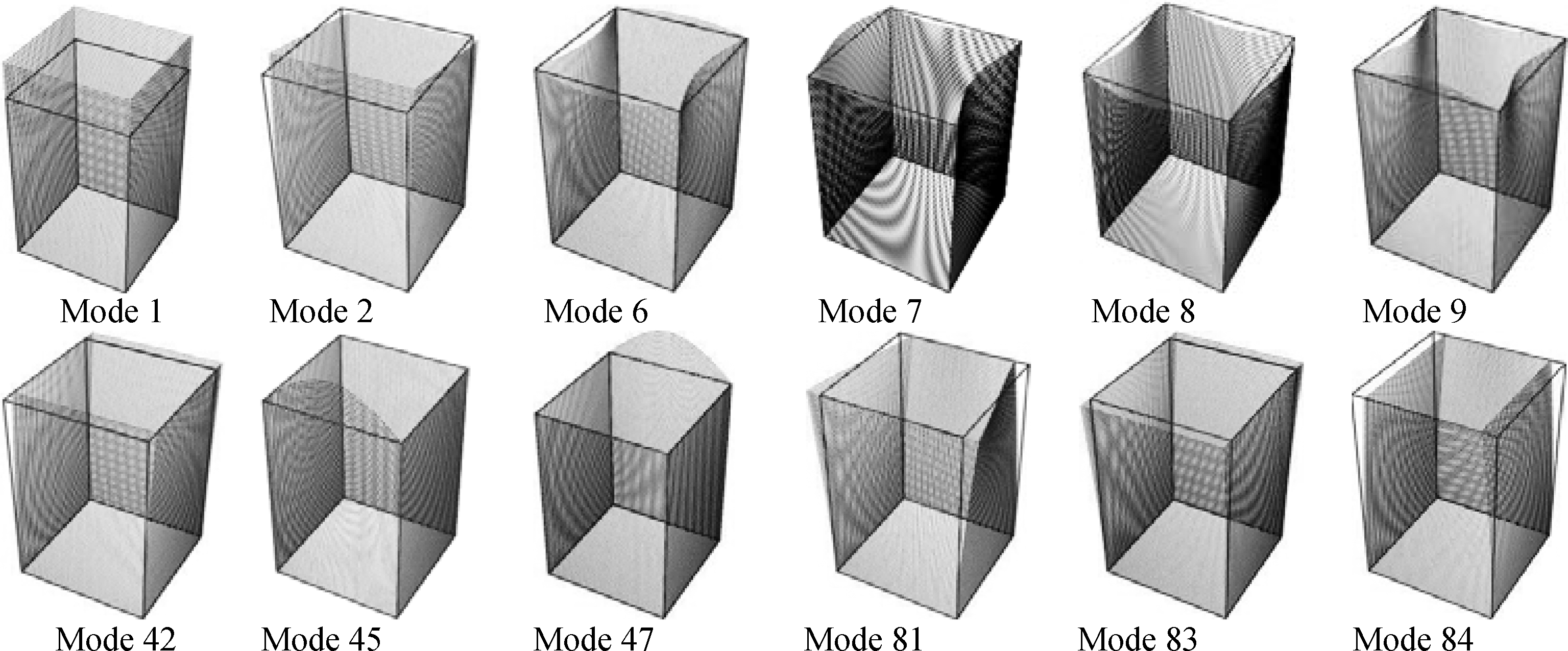
Fig.4 Most relevant cross-section deformation modes participating in the impulsive response of the SHS beam
Fig.6 shows the displacement results obtained from the proposed model and the corresponding SFEA, where the mid-span vertical displacements of the top flange δ1 and the bottom flange δ2, as shown in Fig.3, are selected to accomplish the comparison. It is clear that the two displacement-time curves referring to δ1 are virtually coincident (see Fig.6(a)). Although the curves with respect to (δ1-δ2) exhibit some discrepancies (see Fig.6(b)), especially when time exceeds 3 ms, the mean absolute error is only 0.68 mm. Moreover, Fig.6(b) shows the local deformation response completes at about 0.8 ms, and the global deformation response prevails after 0.8 ms, which is also supported by the modal result. Fig.5 shows that the participation factor of mode 2 exceeds 50% at 0.8 ms.
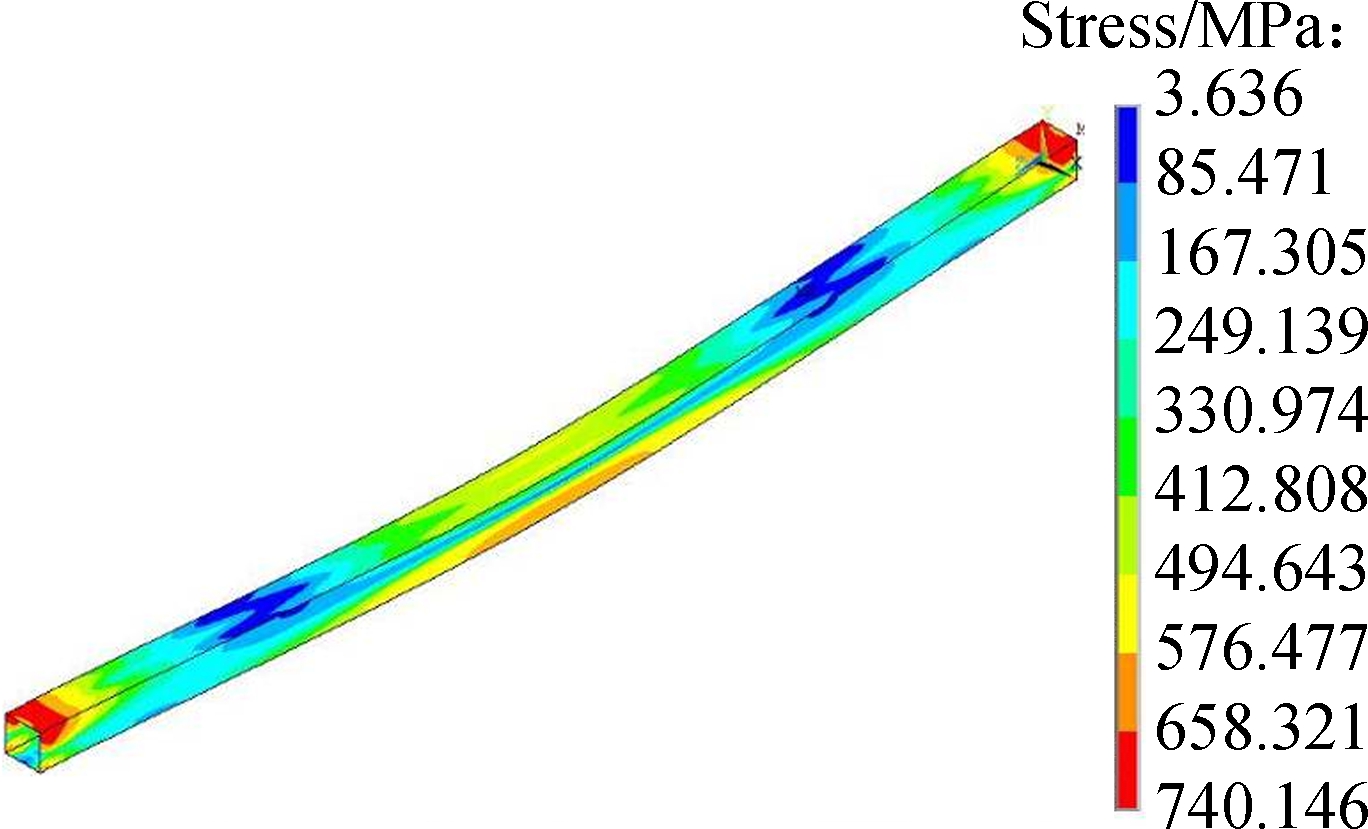
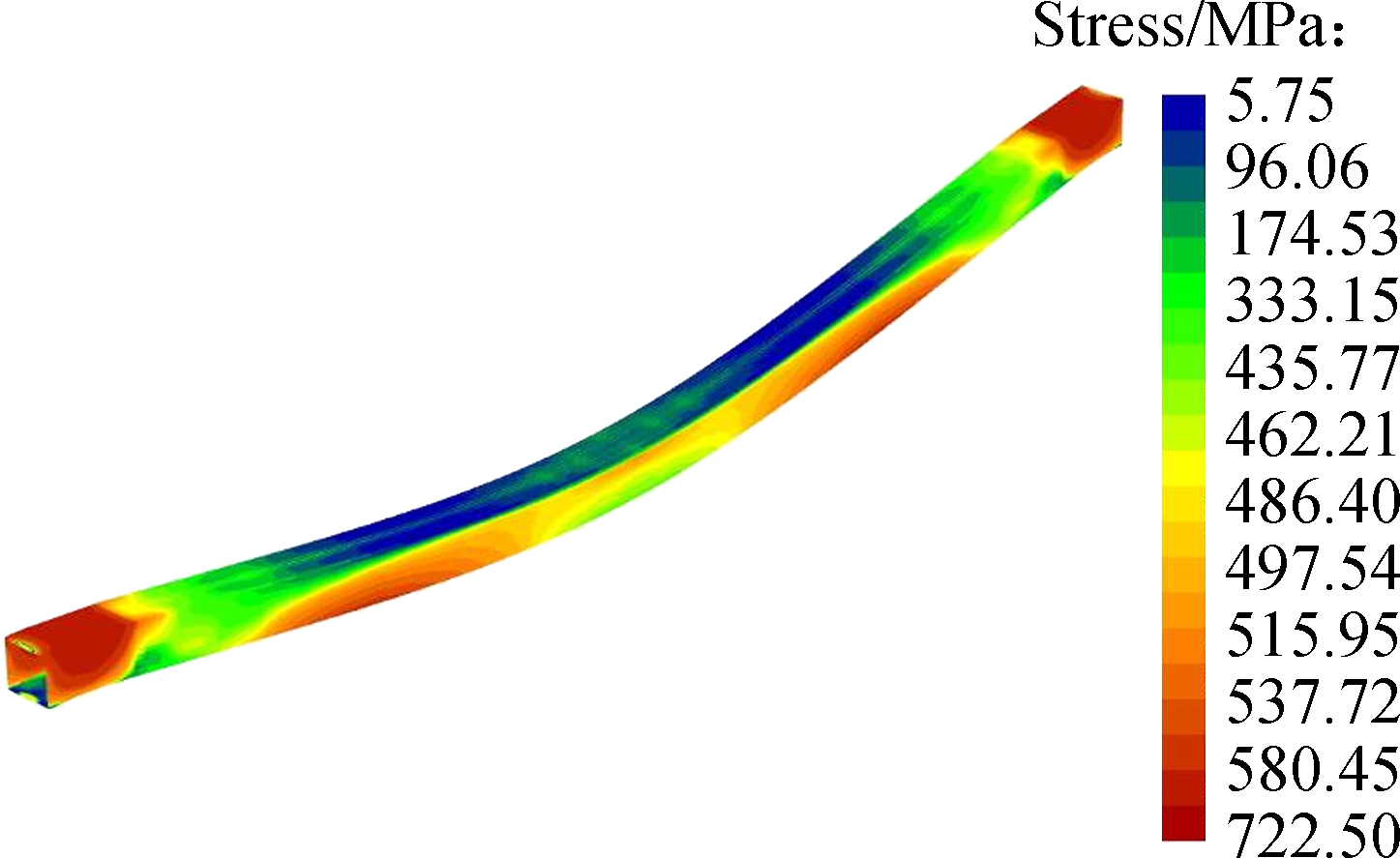
Fig.7 concerns the comparison of three-dimensional contours of the wall mid-surface Mises stresses and the deformed beam configurations at 3 and 7 ms after the impact loading. Once again, a good resemblance between the the GBT result and the SFEA result can be observed. The Mises stress distributions show that the plastic hinges emerge at the two supports where the mixed loading of the global axial extension, the major-axis bending and the shear deformation occurs.
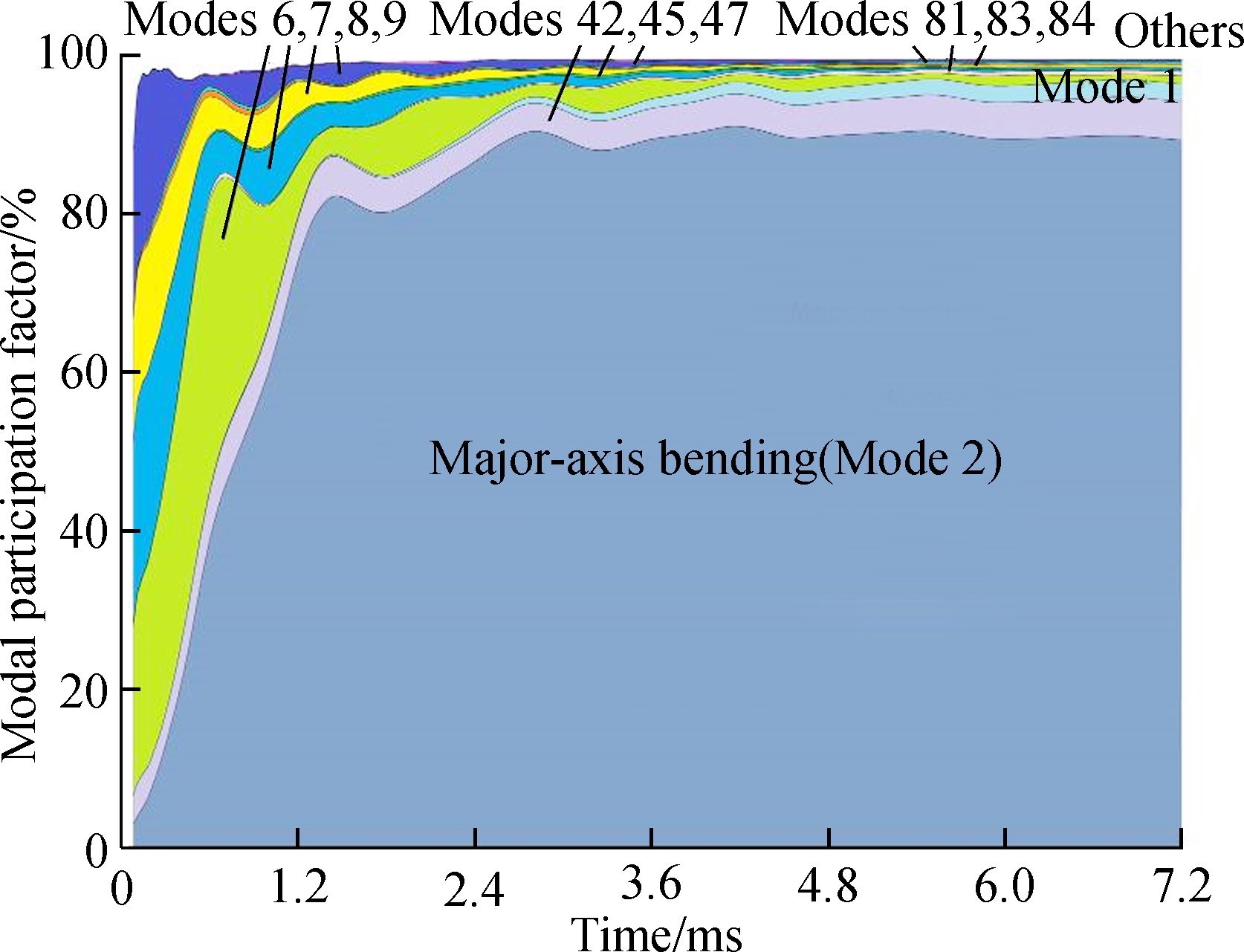
Fig.5 GBT modal participation diagram regarding the impact response of the SHS beam

(a)

(b)
Fig.6 Displacement responses predicted by present GBT analysis and SFEA.(a) Change of δ1 over the time; (b) Difference between the top and bottom flange deflections over the time
3.2 Example Ⅱ
(a)

(b)

(c)
(d)
Fig.7 Deformed configurations and 3D distributions of the mid-surface Von-Mises stress of the fixed SHS beam predicted by SFEA and present GBT analysis. (a) SFEA result when t=3 ms; (b) GBT result when t=3 ms; (c) SFEA result when t=7 ms; (d) GBT result when t=7 ms
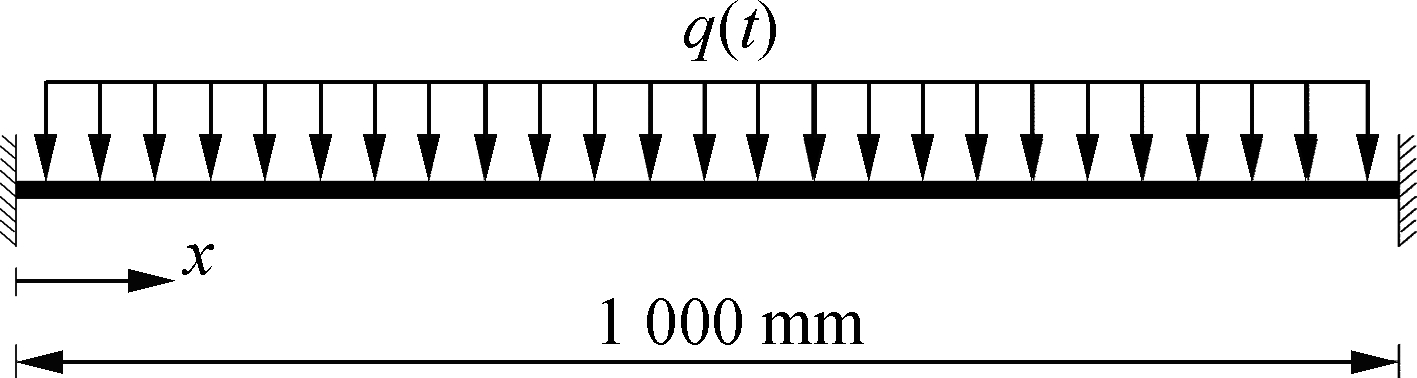
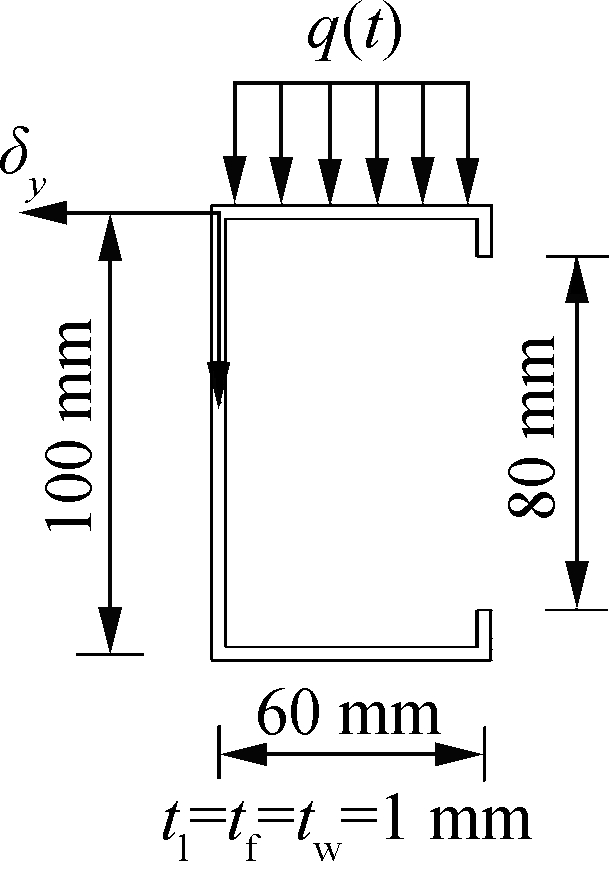
Fig.8 plots a cantilever lipped-C beam subjected to a distributed triangle impulse on its top flange. All the material constants adopted are the same as those used in the previous section. For present GBT analysis, the cross-section discretization involves ten uniform sub-walls per flange, twenty uniform sub-walls per web and two uniform sub-walls per lip, which leads to 135 deformation modes. Moreover, the beam length is discretized by thirty non-uniform elements, where twenty of them with the equal length of 20 mm are used for the beam segment nearby the fixed end (x≤400 mm), and the other ten are used for the left beam segment (x>400 mm), which leads to a total of 13 365 DOFs. The corresponding finite element model based on 4-node shell-163 elements has roughly uniform mesh discretization, and the DOFs amount to 118 188. Note that the DOF number of the proposed GBT model is only 11.31% of that required by the SFEA counterpart.
(a)
(b)
(c)
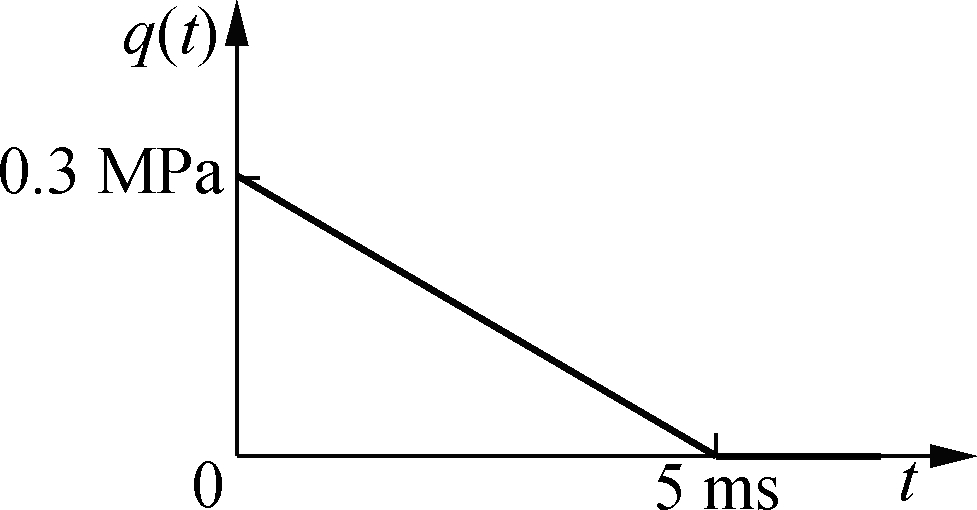
Fig.8 Lipped-C cantilever beam subjected to an impulsive load. (a) Overall view of the beam; (b) Cross-section dimensions; (c) Pressure vs. time curve
Fig.9 plots the cross-section deformation modes which contribute to the beam impulsive response mostly, and Fig.10 plots the participation diagram of the most relevant GBT modes for the beam under impact. As the loading progresses, the beam undergoes a severe local deflection of top flange initially, which is described by the local plate modes 7-10, and then the cross-section distortion prevails, where we can find that the joint participation of the two distortional modes 5 and 6 experiences a rapid increase and reaches its maximum value of 66.14% at 0.815 ms. Concerning the global response, it is clear that the off-shear-center external loading can induce the flexural-torsional deformation of the beam (modes 2 and 4), but we find the minor-axis bending (mode 3) is also one of the important participators (see Fig.10). This is mainly due to the cross-section distortion which leads to the change of flexural behavior of the beam. Due to the growing contributions of the three rigid-body global modes 2-4, it is visible that the contributions of their associated warping shear modes 52-54 increase as well. Concerning the contributions of transverse extension modes, modes 100-102 play significant roles throughout the loading. The large local deflections of the top flange and web lead to the significant increase of membrane strains in top flange and web, and modes 100-102 mainly account for the Von K rm
rm n nonlinearity.
n nonlinearity.
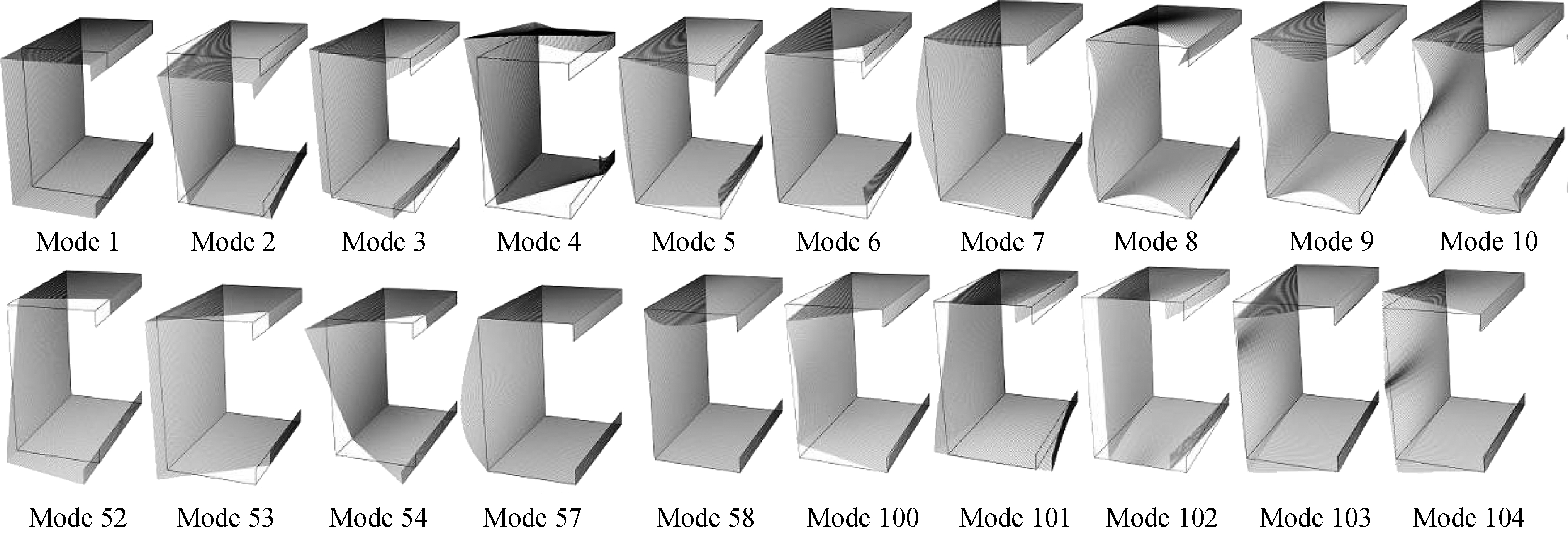
Fig.9 Most relevant cross-section deformation modes taking part in the impulsive response of the lipped C-beam
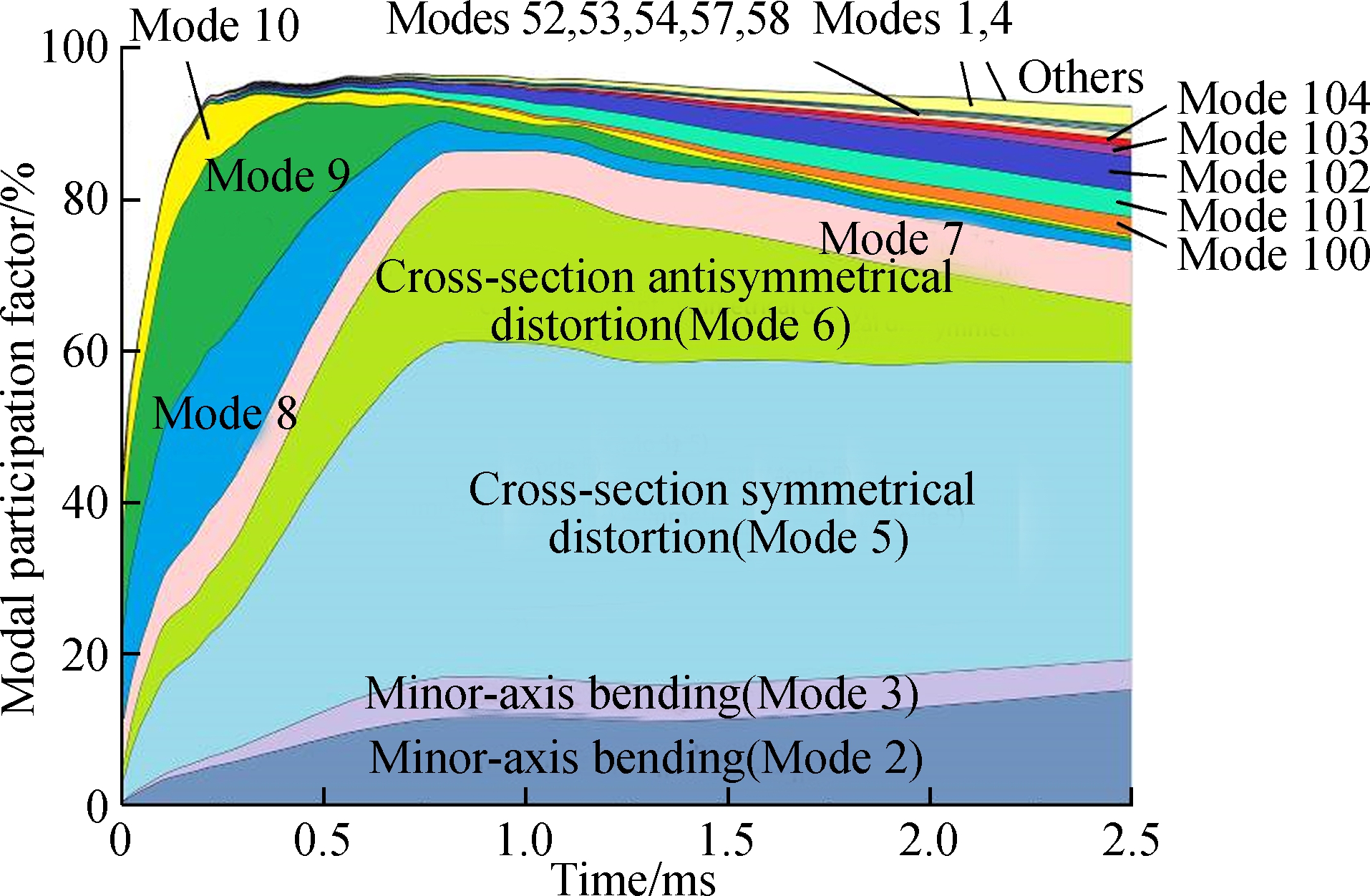
Fig.10 GBT modal participation diagram for lipped C-beam
Fig.11 shows the comparison of the horizontal and vertical displacements of the top flange-web corner at the cantilever tip between the proposed GBT and the SFEA. Although the the displacement predictions by GBT and SFEA follow the same general trend, and also agree well each other at the beginning, there are considerable discrepancies after a large deformation, which stem from membrane locking occurring in the web. As shown in Fig.12, the mid-surface Mises stress distributions predicted by proposed GBT analysis display that the bending deformations are accompanied by slight parasitic membrane deformations in the web. The membrane locking stems from the kinematic inadequacy in present GBT formulation which adopts a linear ![]() function and a cubic
function and a cubic ![]() function, so that the two transverse membrane stretching related terms
function, so that the two transverse membrane stretching related terms ![]() and
and ![]() have different degrees of polynomial variation. This induces the over-stiff element equivalent internal forces. In general, to remove the membrane locking requires using a higher-order interpolation of
have different degrees of polynomial variation. This induces the over-stiff element equivalent internal forces. In general, to remove the membrane locking requires using a higher-order interpolation of ![]() Nevertheless, the overall impulsive behavior of the lipped-C beam can be captured by the proposed GBT formulation. A remarkable resemblance on beam deformed configurations between the two kinds of predictions can be observed (see Fig.12). Concerning the distribution of Mises stress, an overall similarity between the two results are clearly visible.
Nevertheless, the overall impulsive behavior of the lipped-C beam can be captured by the proposed GBT formulation. A remarkable resemblance on beam deformed configurations between the two kinds of predictions can be observed (see Fig.12). Concerning the distribution of Mises stress, an overall similarity between the two results are clearly visible.
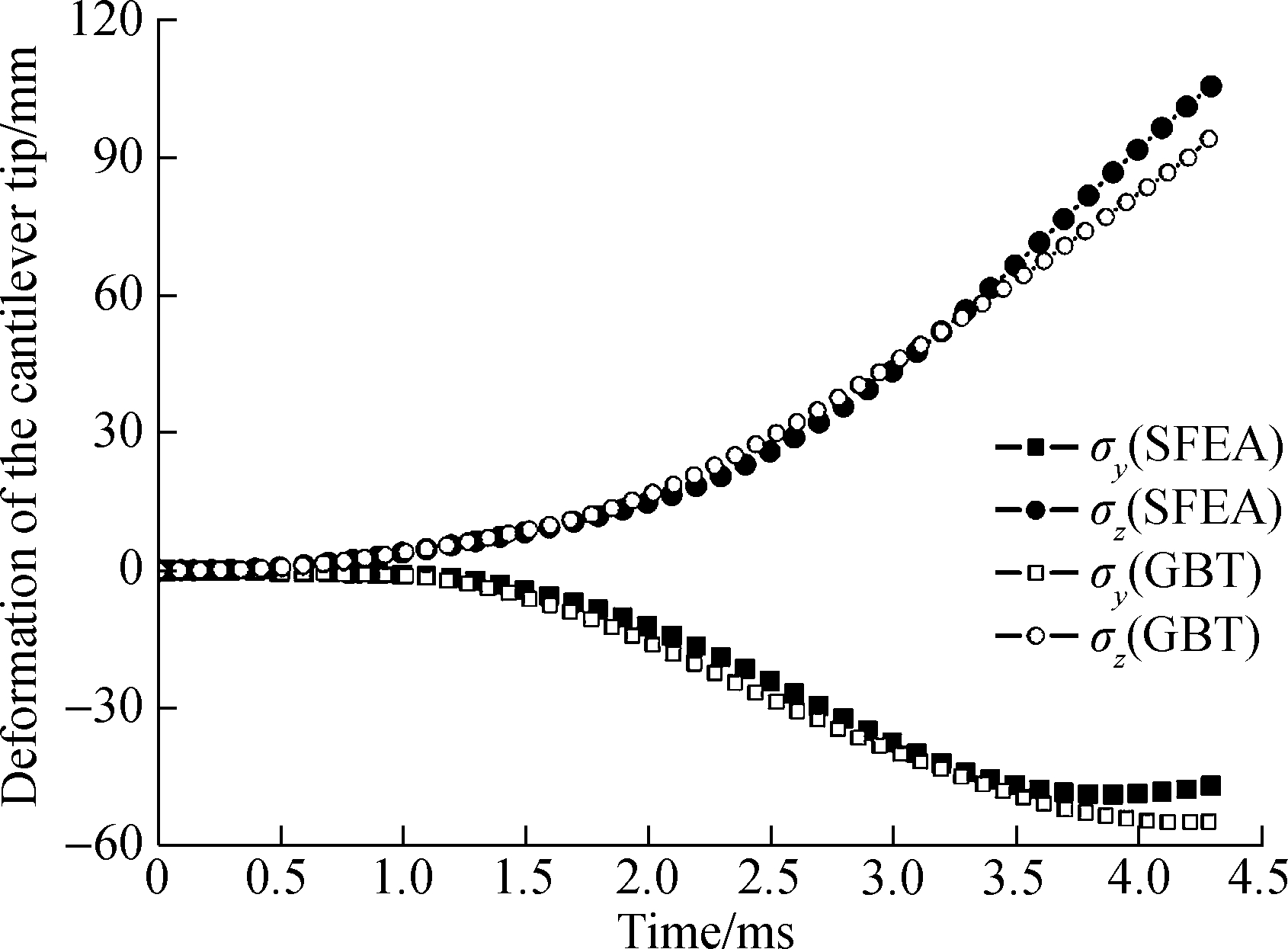
Fig.11 Displacement responses predicted by SFEA and present GBT analysis
3.3 Example Ⅲ
Fig.13 shows a steel square plate with a thickness of 2 mm subjected to a distributed triangle impulse on its top surface, where its two adjacent edges are fixed, and the other two edges are free and stiffened by a 5 mm thick flange, respectively. Except for the two values of 200 GPa and 280 MPa are assigned to the Young’s modulus and uniaxial yield stress herein, the other material constants adopted are the same as those used in the previous two examples. The GBT cross-section discretization adopted involves 100 uniform sub-walls in the web and six uniform sub-walls in the flange (seen as a T-shaped cross-section), which leads to 318 GBT modes. Regarding the longitudinal discretization (seen as a cantilever T-section beam with a length-distributed constraint), thirty non-uniform elements are used, specifically, four uniform elements for the beam segment nearby the fixed end (x<40 mm), four uniform elements for 40≤x<100 mm, four uniform elements for 100≤x<180 mm and eighteen uniform elements for the left portion (x>180 mm), leading to a total of 31 482 DOFs, only 23.4% of the number required by the corresponding finite element model built upon 11 000 roughly uniform shell-163 elements (134 532 DOFs).

(a)
(b)

(c)
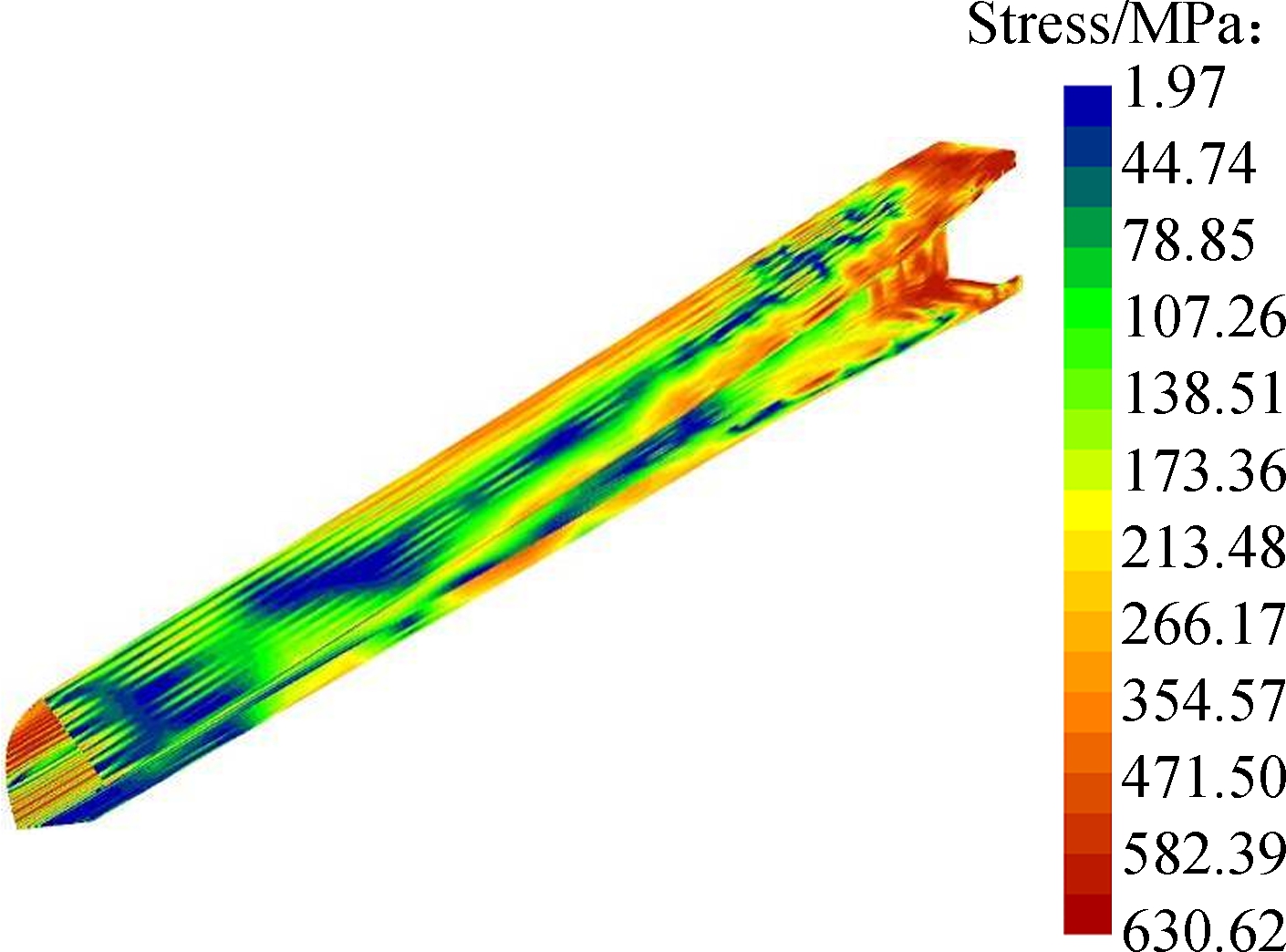
(d)
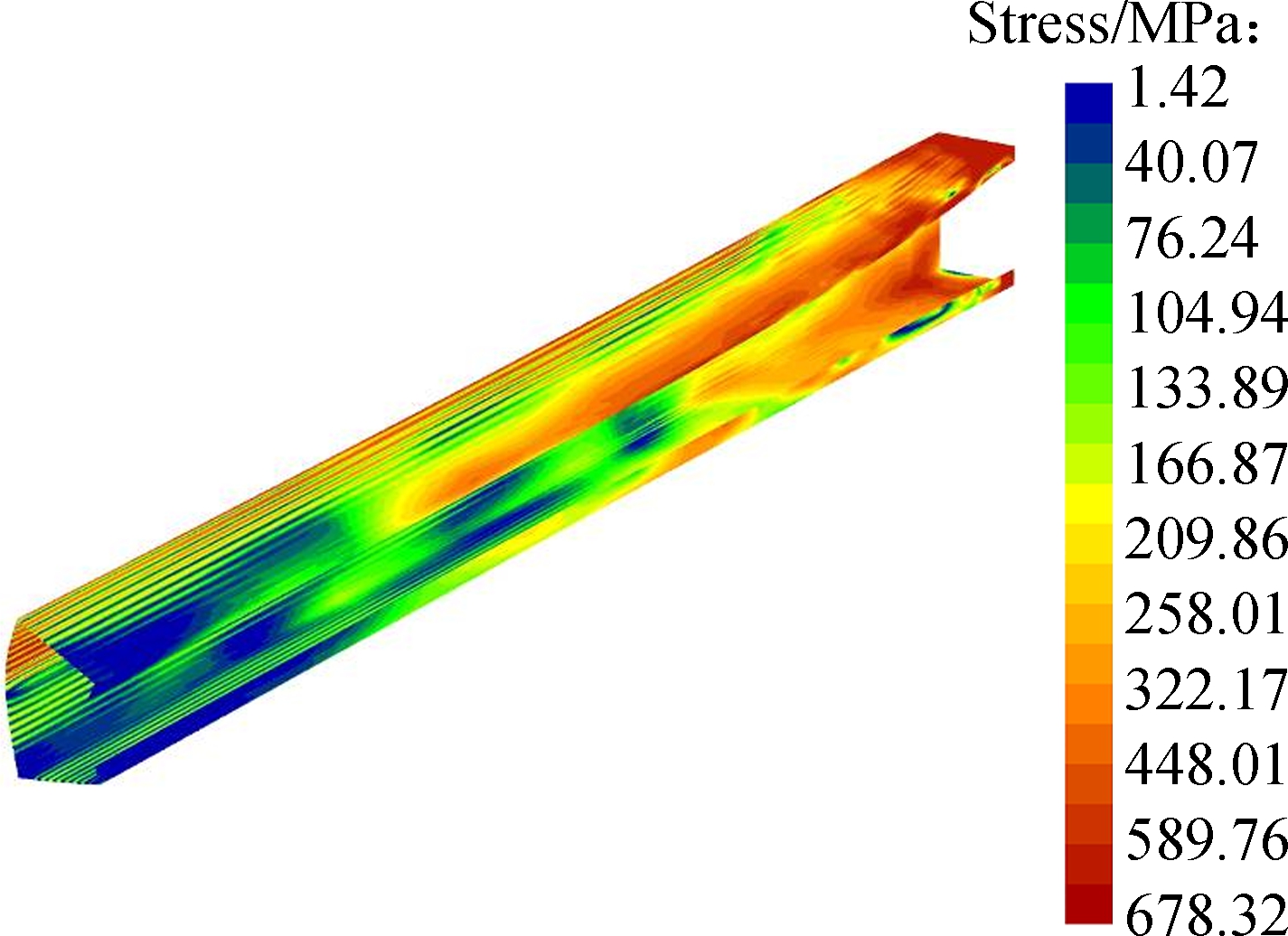
Fig.12 Deformed configurations and 3D distributions of the mid-surface Von-Mises stress of the lipped-C beam predicted by SFEA and proposed GBT. (a) SFEA result when t=1.62 ms; (b) GBT result when t=1.62 ms; (c) SFEA result when t=2.52 ms; (d) GBT result when t=2.52 ms

(a)

(b)
Fig.13 Stiffened square plate subjected to an impulsive load. (a) Geometric dimensions; (b) Pressure vs. time curve
Fig.14 plots the most relevant cross-section deformation modes which contribute to the member response, and the modal analysis concerning the evolutions along the loading is depicted in Fig.15. Initially, the local deformation (i.e., the deflection of web) prevails, so that the modal participation diagram is almost comprised of the local plate modes 2-22 before 0.34 ms (see Fig.15). As the loading progresses, it is expected that the high freq-uency related deformations show a trend of attenuation. We find that the participation of high-order local plate modes starts to decrease at a much earlier moment. The distortional mode 1 reflects the y-direction (in-plane) flexure of the flange, and its participation exhibits a constant increase all along. Concerning the warping shear modes, mode 108 characterizes the constant membrane shear deformation in the flange, whose participation grows along with the rising participation of mode 1. The web warping shear mode 110 shows dominant participation among all the shear modes, which implies that a reference point in the web closer to the two longitudinal edges possesses a larger membrane shear strain. Due to the fact that the web is a two-way slab, the transverse extension modes play significant roles as well. The web transverse uniform extension (mode 213) prevails, whose participation increases along with the progress of transverse bending of the web due to the Von K rm
rm n nonlinearity.
n nonlinearity.
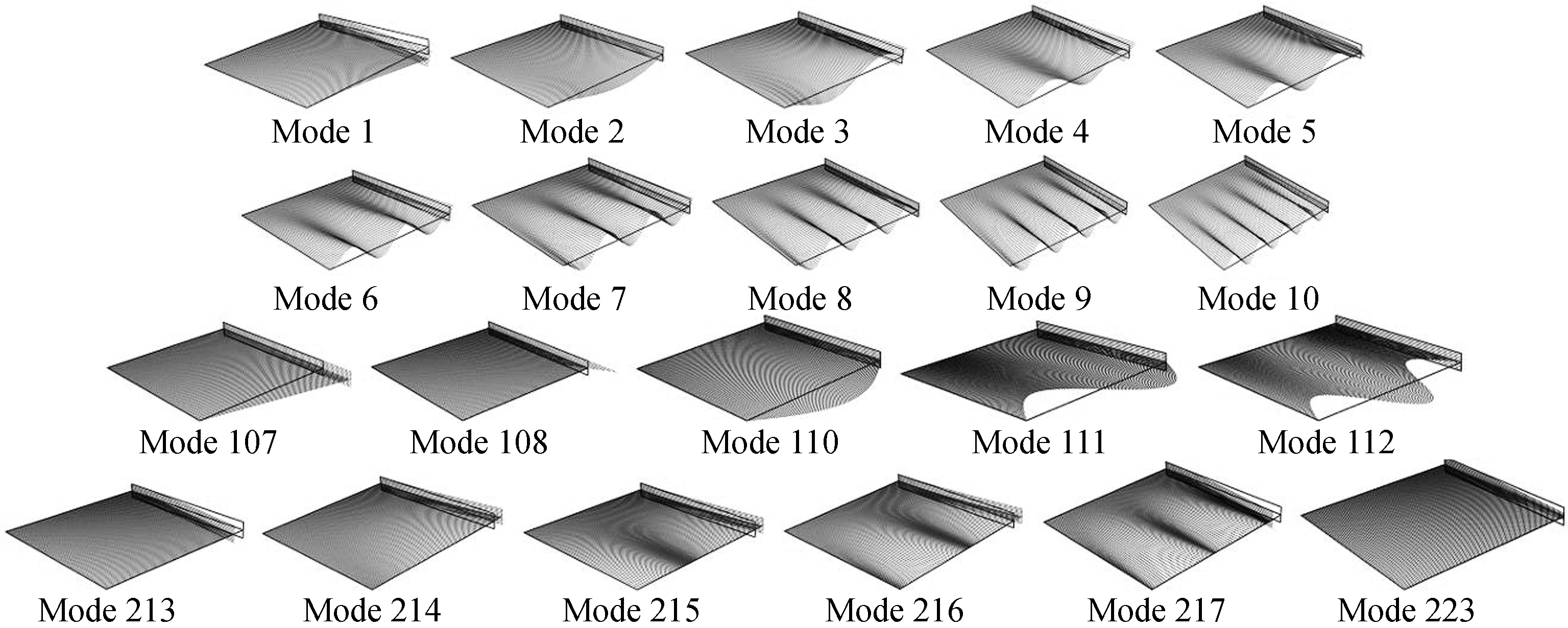
Fig.14 Most relevant cross-section deformation modes which participate in the member response
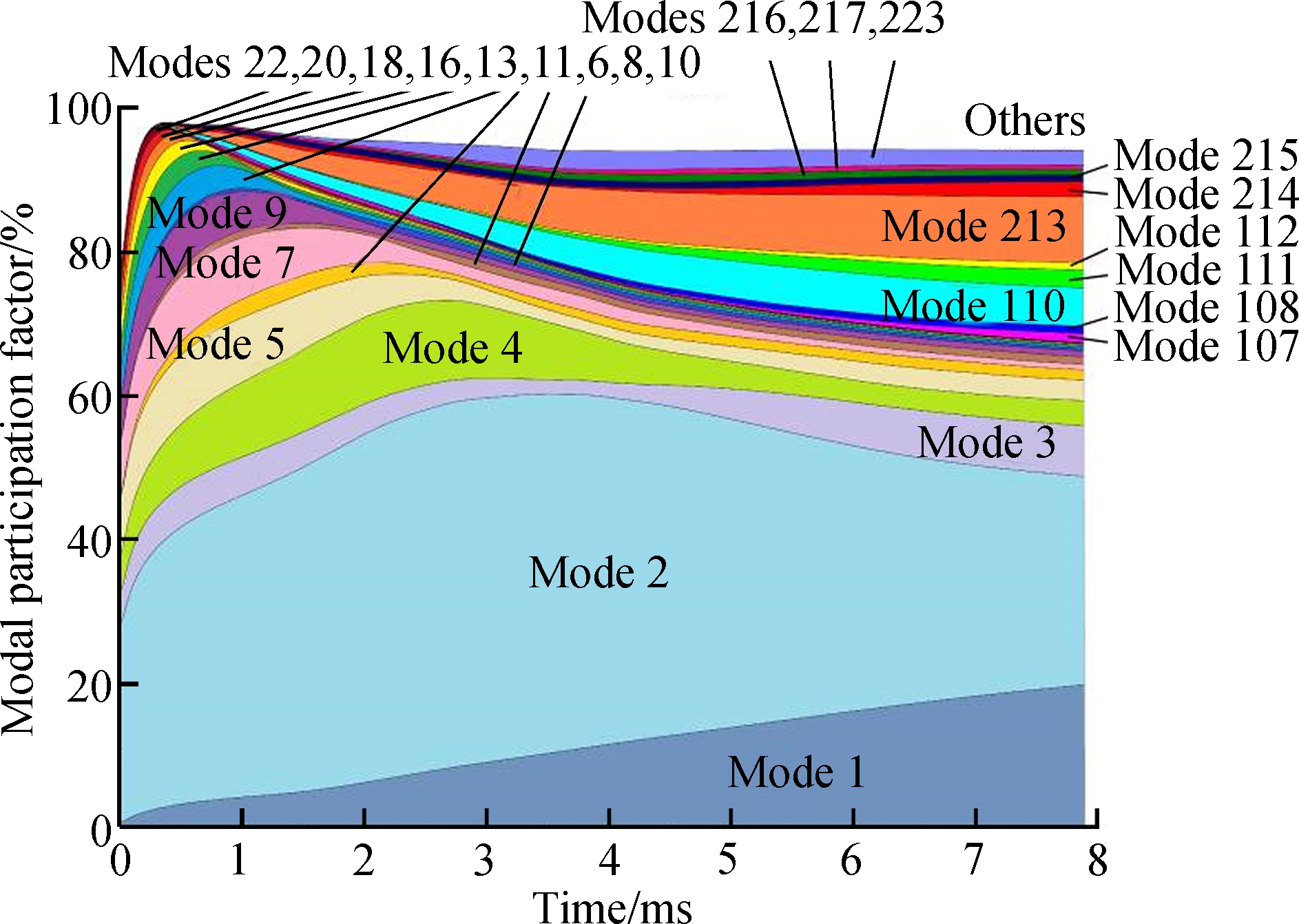
Fig.15 GBT modal participation diagram regarding the impact response of the stiffened plate
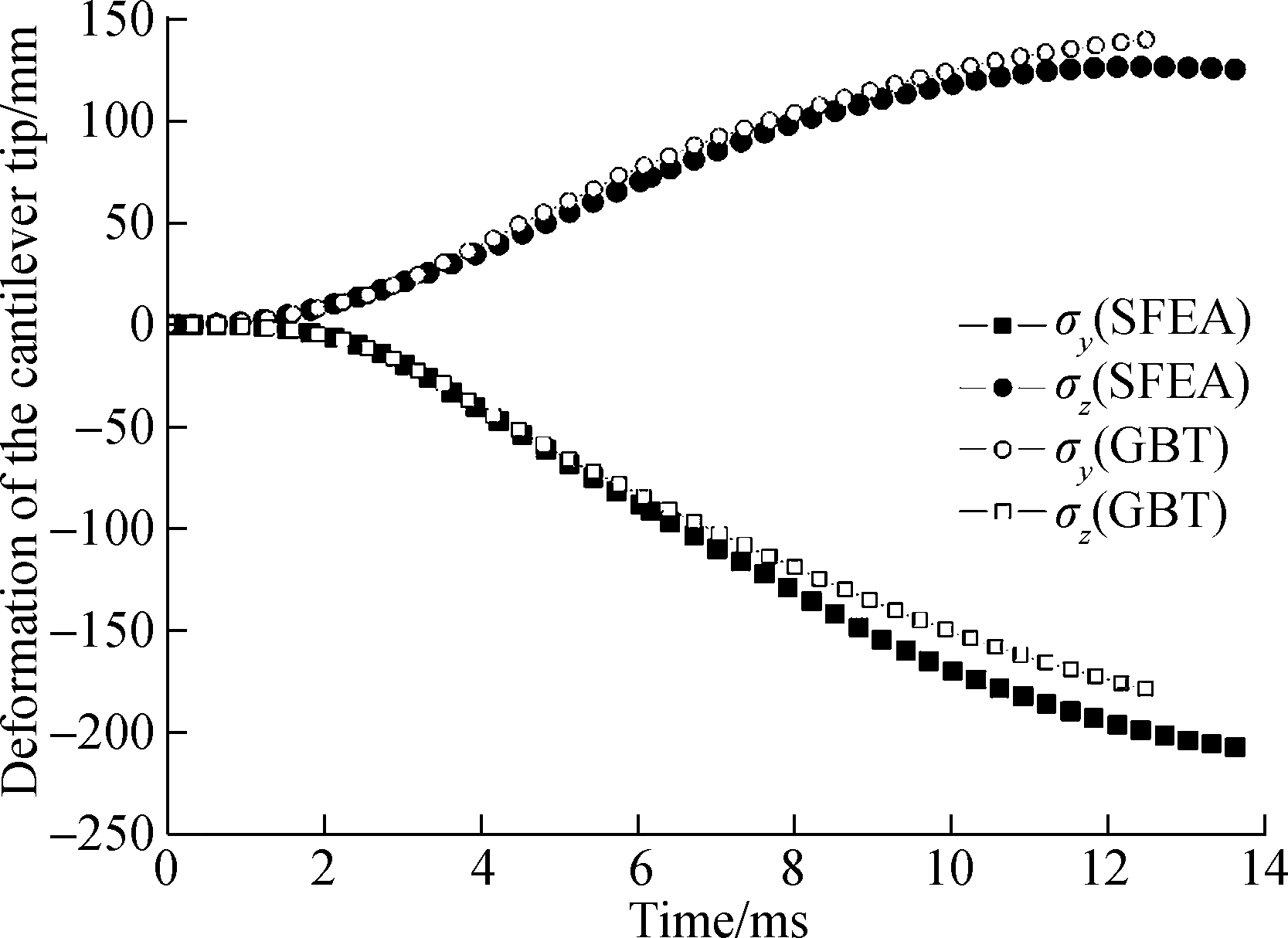
Fig.16 Comparison of the flange-web-node displacements at the cantilever tip between the proposed GBT model and the shell-element-based model
Fig.16 concerns the comparison of displacements at the cantilever tip between the proposed GBT and the shell finite element predictions. It is clear that the GBT results agree well with the SFEA results before 4 ms, and from then the discrepancies start to increase, especially for δz. The over-stiff GBT result, as mentioned before, is mainly due to the membrane locking in the web. In addition, the kinematic inadequacy stemming from the linear interpolation of ![]() makes the GBT lack accounting for the Poisson’s effect in each wall segment, which can also produce over-stiff solutions.
makes the GBT lack accounting for the Poisson’s effect in each wall segment, which can also produce over-stiff solutions.
(a)
(b)
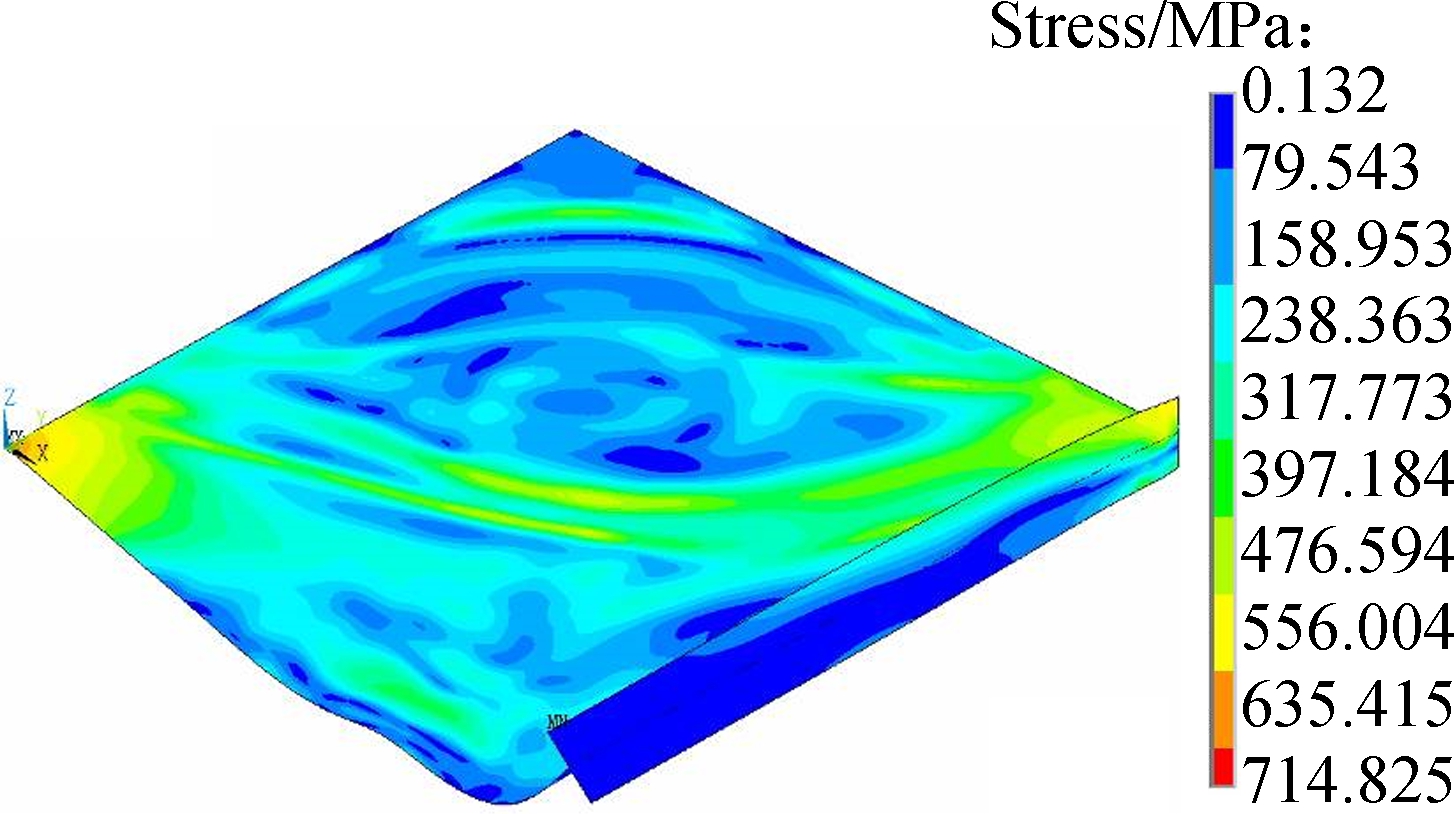
(c)
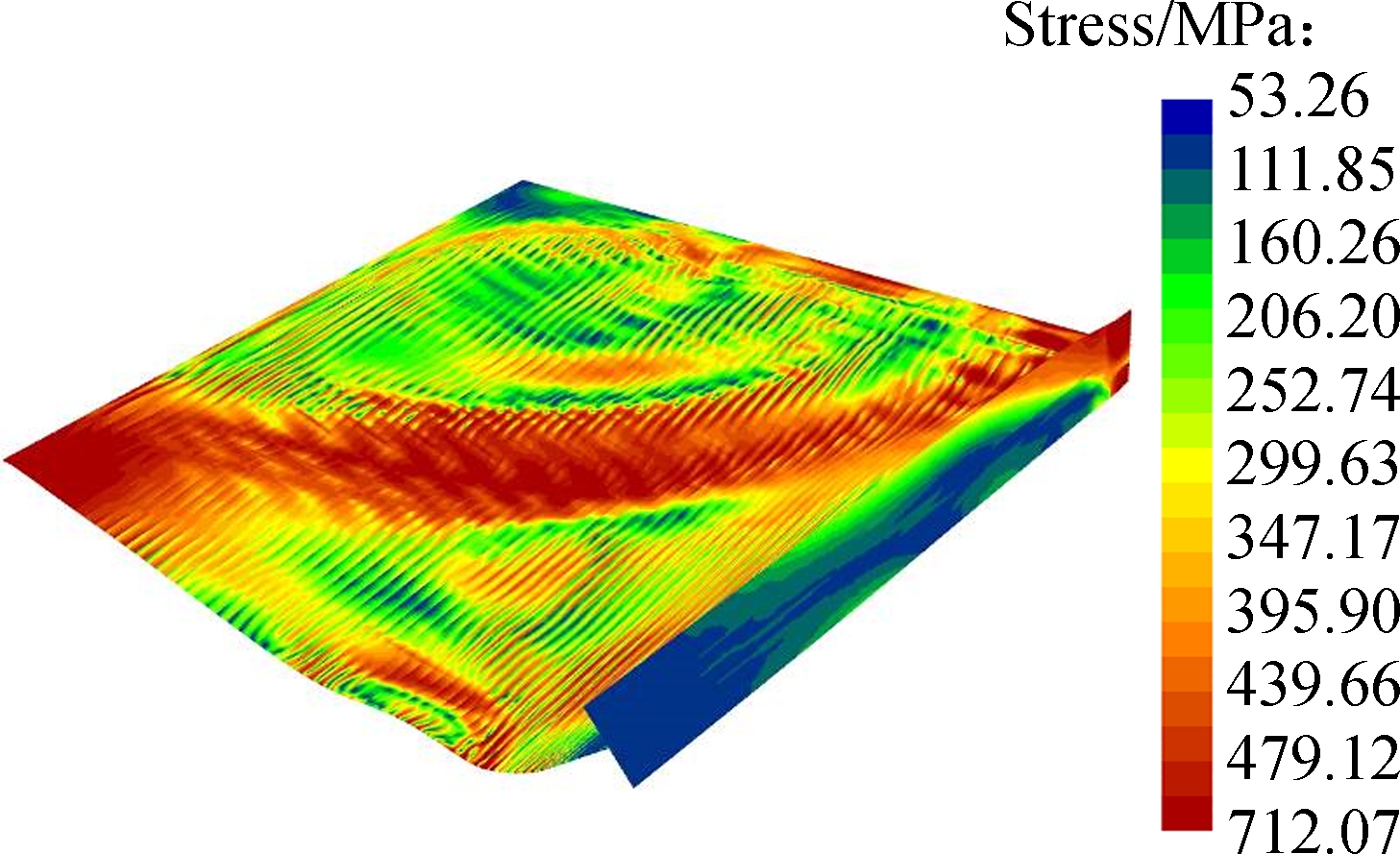
(d)
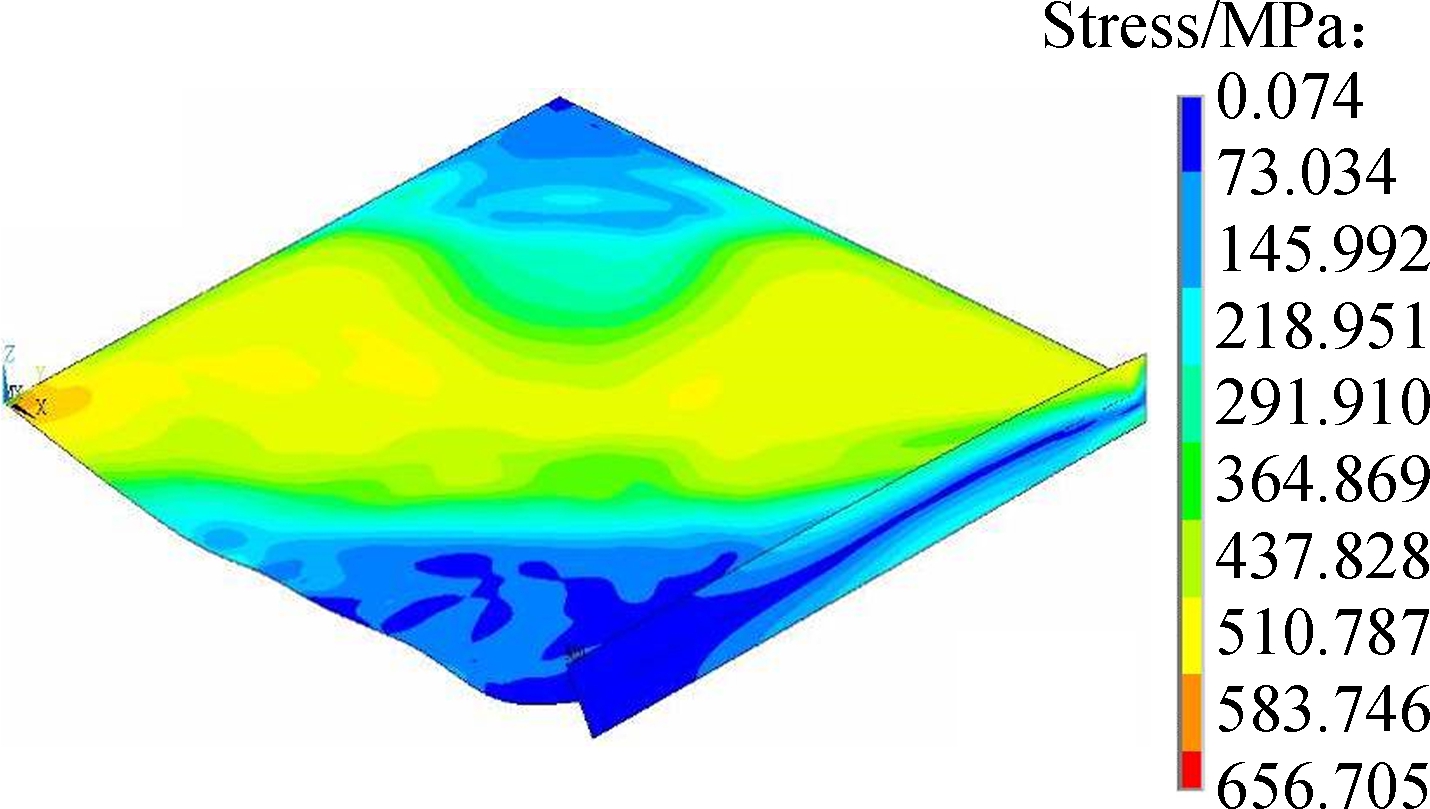
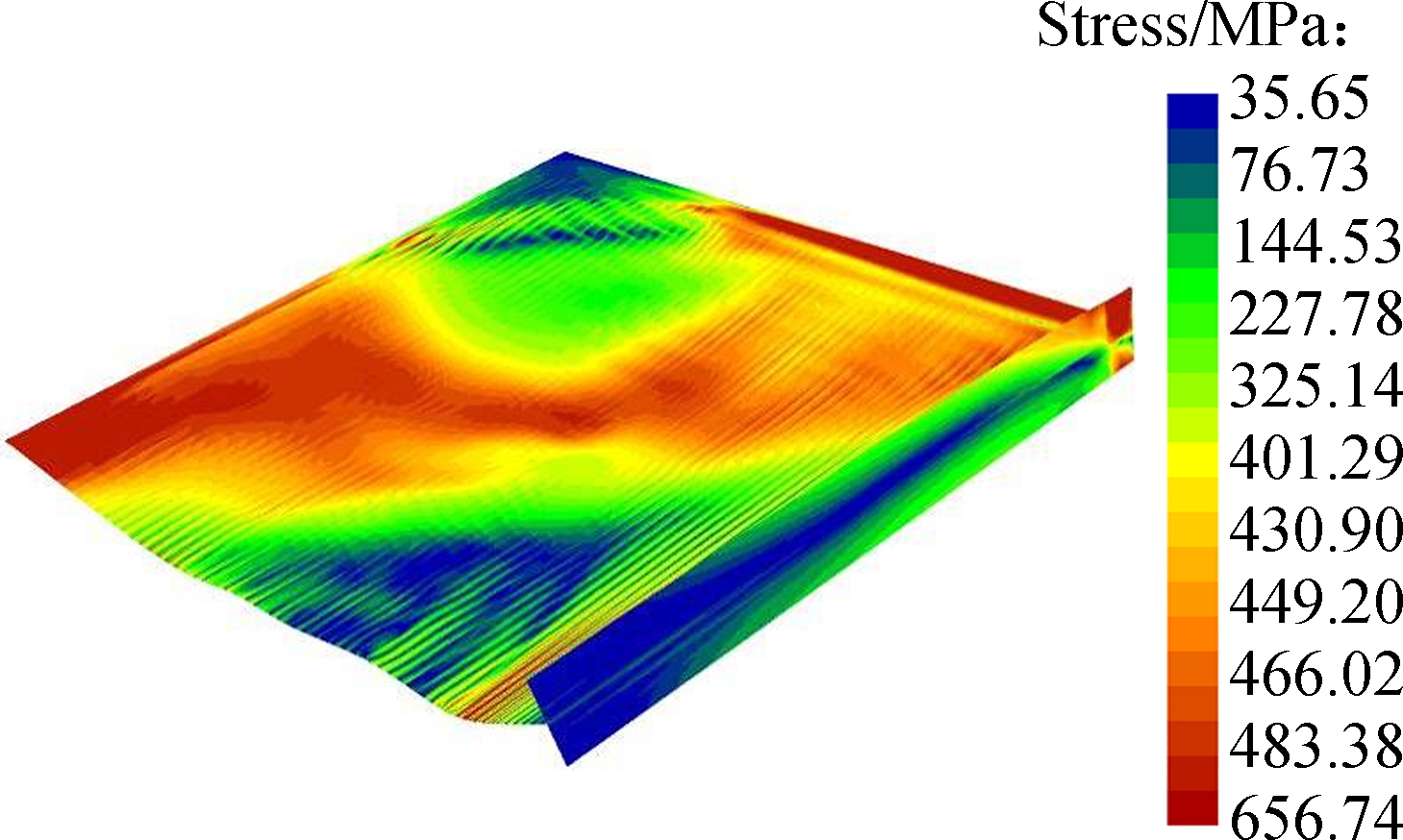
Fig.17 Deformed configurations and 3D distributions of the mid-surface Von-Mises stress of the stiffened plate predicted respectively by SFEA and proposed GBT. (a) SFEA result when t=3 ms; (b) GBT result when t=3 ms; (c) SFEA result when t=5 ms; (d) GBT result when t=5 ms
Fig.17 plots the three-dimensional diagrams of mid-surface Mises stress and the deformed beam configurations predicted by GBT analysis and SFEA. They are in good agreement despite the existence of small differences. From the present GBT predictions we can observe that an overestimation of the mid-surface Mises stress occurs in the vicinity of the flange-web edge where the web sustains severe transverse bending, which is due to membrane locking. Generally, the clamped boundary requires a simultaneous satisfactory of the null warping displacements and non-null shear stresses along the x=0 edge, which can lead to another kinematic inadequacy. Since both the two requirements actually depend on the amplitude function derivatives, where the null warping displacements needs φk,x=0 (see Eq.(16)), but non-null shear stress needs φk,x≠0 (see Eq.(19)), a contradiction appears and makes dealing with the boundary condition more problematic. To apply the clamped boundary, we let the amplitude function and their derivatives for all the deformation modes vanish at x=0, which induces an over-estimation of Mises stress at the fixed edge, as shown in Figs.17(b) and (d).
4 Discussion
It has been proved that the developed GBT formulation is a highly efficient numerical tool for the simulation of impact behavior of thin-walled steel members. It is as efficient as the traditional beam finite elements, but leads to rigorous results, which is the same as that of the shell finite elements. Abambres et al.[37] verified that for an equivalently accurate analysis, the number of DOFs required by a GBT model is only about 25% of that required by the corresponding SFEA. In this paper, we reach the same conclusion. The maximum GBT-to-SFEA DOF ratio is only 23.4% in the above case studies.
For the analyses of large and complex steel frames, it is important to keep the balance between the computational efficiency and accuracy. The multi-scale techniques[38] may be another alternative, but they still depend on the shell finite elements. The proposed GBT formulation can be a breakthrough for the problem. To simulate steel frames, though the current research needs further extension, it can be a preliminary exploration. For simulating steel frames with GBT, the main difficulty lies in the modeling of different kinds of steel joints. Fortunately, recent advances[17] in modeling different kinds of steel joints in the framework of GBT might help with this issue.
Although only three test cases were used to verify the proposed model, it is enough to conclude that it is a computationally efficient and structurally clarifying alternative to SFEA for the analyses of the impact behavior of thin-walled members. A more comprehensive verification of the proposed GBT model can be retrieved from Ref.[39].
5 Conclusion
1) The kinematic inadequacies stemming from the linear interpolation of ![]() and the method of applying the clamped boundary condition make the proposed GBT formulation exhibit some element locking, which leads to the differences between the GBT and SFEA results. Nevertheless, proper assessments of the impact behavior of thin-walled steel members can be achieved from the revised GBT code.
and the method of applying the clamped boundary condition make the proposed GBT formulation exhibit some element locking, which leads to the differences between the GBT and SFEA results. Nevertheless, proper assessments of the impact behavior of thin-walled steel members can be achieved from the revised GBT code.
2) The developed GBT formulation is much more computationally efficient than the SFEA. The GBT meshes involved in three illustrative examples are much coarser than their SFEA counterparts, and also the number of DOFs involved in each GBT analysis is far less than that involved in the corresponding SFEA.
3) For some materially and geometrically nonlinear problems, it was verified[14,18-19] that the GBT with linear ![]() functions can find accurate solutions, but we highly suggest that the current approach for the calculation of cross-section deformation modes should be improved, because the adoption of higher-order interpolation of
functions can find accurate solutions, but we highly suggest that the current approach for the calculation of cross-section deformation modes should be improved, because the adoption of higher-order interpolation of ![]() may offer significant advantage on alleviating the element locking.
may offer significant advantage on alleviating the element locking.
[1]Cowper G R, Symonds P S. Strain hardening and strain rate effects in the impact loading of cantilever beams [R]. Providence, USA: Brown University, 1958.
[2]Symonds P S, Mentel T J. Impulsive loading of plastic beams with axial constraints [J]. Journal of the Mechanics and Physics of Solids, 1958, 6(3):186-202. DOI:10.1016/0022-5096(58)90025-5.
[3]Bodner S R, Symonds P S. Experimental and theoretical investigation of the plastic deformation of cantilever beams subjected to impulsive loading [J]. Journal of Applied Mechanics, 1962, 29(4):719-728. DOI:10.1115/1.3640660.
[4]Humphreys J S. Plastic deformation of impulsively loaded straight clamped beams [J]. Journal of Applied Mechanics, 1965, 32(1):7-10. DOI:10.1115/1.3625788.
[5]Menkes S B, Opat H J. Broken beams—Tearing and shear failures in explosively loaded clamped beams [J]. Experimental Mechanics, 1973, 13(11):480-486. DOI:10.1007/bf02322734.
[6]Wegener R B, Martin J B. Predictions of permanent deformation of impulsively loaded simply supported square tubes steel beams [J]. International Journal of Mechanical Sciences, 1985, 27(1/2):55-69. DOI:10.1016/0020-7403(85)90066-9.
[7]Bambach M R, Jama H, Zhao X L, et al. Hollow and concrete filled steel hollow sections under transverse impact loads [J]. Engineering Structures, 2008, 30(10): 2859-2870. DOI:10.1016/j.engstruct.2008.04.003.
[8]Jama H H, Nurick G N, Bambach M R, et al. Steel square hollow sections subjected to transverse blast loads [J]. Thin-Walled Structures, 2012, 53:109-122. DOI:10.1016/j.tws.2012.01.007.
[9]Nassr A A, Razaqpur A G, Tait M J, et al. Experimental performance of steel beams under blast loading [J]. Journal of Performance of Constructed Facilities, 2011, 26(5):600-619. DOI:10.1061/(asce)cf.1943-5509.0000289.
[10]Nassr A A, Razaqpur A G, Tait M J, et al. Dynamic response of steel columns subjected to blast loading [J]. Journal of Structural Engineering, 2014, 140(7): 04014036-1-04014036-15. DOI:10.1061/(asce)st.1943-541x.0000920.
[11]Remennikov A M, Uy B. Explosive testing and modelling of square tubular steel columns for near-field detonations [J]. Journal of Constructional Steel Research, 2014, 101:290-303. DOI:10.1016/j.jcsr.2014.05.027.
[12]Davies J M, Leach P. First-order generalized beam theory [J]. Journal of Constructional Steel Research, 1994, 31(2/3):187-220. DOI:10.1016/0143-974x(94)90010-8.
[13]Davies J M, Leach P, Heinz D. Second-order generalized beam theory [J]. Journal of Constructional Steel Research, 1994, 31(2/3):221-241. DOI:10.1016/0143-974x(94)90011-6.
[14]Silvestre N, Camotim D. Nonlinear generalized beam theory for cold-formed steel members [J]. International Journal of Structural Stability and Dynamics, 2003, 3(4):461-490. DOI:10.1142/s0219455403001002.
[15]Gonçalves R, Camotim D. Generalised beam theory-based finite elements for elastoplastic thin-walled metal members [J]. Thin-Walled Structures, 2011, 49(10):1237-1245. DOI:10.1016/j.tws.2011.05.011.
[16]Gonçalves R, Camotim D. Geometrically non-linear generalized beam theory for elastoplastic thin-walled metal members [J]. Thin-Walled Structures, 2012, 51(2):121-129. DOI:10.1016/j.tws.2011.10.006.
[17]Basaglia C, Camotim D, Silvestre N. Post-buckling analysis of thin-walled steel frames using generalized beam theory (GBT) [J]. Thin-Walled Structures, 2013, 62:229-242. DOI:10.1016/j.tws.2012.07.003.
[18]Abambres M, Camotim D, Silvestre N. Physically non-linear GBT analysis of thin-walled members [J]. Computers and Structures, 2013, 129:148-165. DOI:10.1016/j.compstruc.2013.04.022.
[19]Abambres M, Camotim D, Silvestre N. GBT-based elastic-plastic post-buckling analysis of stainless steel thin-walled members [J]. Thin-Walled Structures, 2014, 83:85-102. DOI:10.1016/j.tws.2014.01.004.
[20]Rui B, Camotim D, Silvestre N. Dynamic analysis of thin-walled members using generalised beam theory (GBT) [J]. Thin-Walled Structures, 2013, 72:188-205. DOI:10.1016/j.tws.2013.07.004.
[21]Duan L P, Zhao J C, Liu S, et al. A B-splines-based GBT formulation for modeling fire behavior of restrained steel beams [J]. Journal of Constructional Steel Research, 2016, 116:65-78. DOI:10.1016/j.jcsr.2015.09.001.
[22]Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1):31-48. DOI:10.1016/0013-7944(85)90052-9.
[23]Rusinek A, Zaera R, Klepaczko J R. Constitutive relations in 3-D for a wide range of strain rates and temperatures—Application to mild steel [J]. International Journal of Solids and Structures, 2007, 44(17):5611-5634. DOI:10.1016/j.ijsolstr.2007.01.015.
[24]Perzyna P. Fundamental problems in viscoplasticity [J]. Advances in Applied Mechanics, 1966, 9:244-368. DOI:10.1016/s0065-2156(08)70009-7.
[25]Jama H H, Bambach M R, Nurick G N, et al. Numerical modelling of square tubular steel beams subjected to transverse blast loads [J]. Thin-Walled Structures, 2009, 47(12):1523-1534. DOI:10.1016/j.tws.2009.06.004.
[26]Standards Association of Australia. AS4100—1998 Steel structures: Section 12. Fire[S]. Sydney: Standards Australia, 1998.
[27]British Standards Institution. Eurocode 3: Design of steel structures: Part 1.2 General rules-structural fire design[S]. London: British Standards Institution, 2005.
[28]Zaera R, Fernandez-Saez J. An implicit consistent algorithm for the integration of thermoviscoplastic constitutive equations in adiabatic conditions and finite deformations [J]. International Journal of Solids and Structures, 2006, 43(6):1594-1612. DOI:10.1016/j.ijsolstr.2005.03.070.
[29]Marais S T, Tait R B, Cloete T J, et al. Material testing at high strain rate using the split-Hopkinson pressure bar [J]. Latin American Journal of Solids and Structures, 2004, 1:319-339.
[30]Gonçalves R, Ritto-Correa M, Camotim D. A new approach to the calculation of cross-section deformation modes in the framework of generalized beam theory [J]. Computational Mechanics, 2010, 46(5):759-781. DOI:10.1007/s00466-010-0512-2.
[31]Silvestre N, Camotim D, Silva N F. Generalized beam theory revisited: From the kinematical assumption to the deformation mode determination [J]. International Journal of Structural Stability and Dynamics, 2011, 11(5):969-997. DOI:10.1142/S0219455411004427.
[32]Cox M G. The numerical evaluation of B-splines [J]. IMA Journal of applied Mathematics, 1972, 10(2):134-149. DOI:10.1093/imamat/10.2.134.
[33]de Boor C. On calculating with B-splines [J]. Journal of Approximation Theory, 1972, 6(1):50-62. DOI:10.1016/0021-9045(72)90080-9.
[34]Hughes T J R, Cohen M, Haroun M. Reduced and selective integration techniques in the finite element analysis of plates [J]. Nuclear Engineering and Design, 1978, 46(1):203-222. DOI:10.1016/0029-5493(78)90184-X.
[35]Silvestre N, Camotim D. Local-plate and distortional post-buckling behavior of cold-formed steel lipped channel columns with intermediate stiffeners [J]. Journal of Structural Engineering, 2006, 132(4):529-540. DOI:10.1061/(ASCE)0733-9445(2006)132:4(529).
[36]Wegener R B, Martin J B. Predictions of permanent deformation of impulsively loaded simply supported square tubes steel beams [J]. International Journal of Mechanical Sciences, 1985, 27(1/2):55-69. DOI:10.1016/0020-7403(85)90066-9.
[37]Abambres M, Camotim D, Silvestre N, et al. GBT-based structural analysis of elastic-plastic thin-walled members [J]. Computers and Structures, 2014, 136:1-23. DOI:10.1016/j.compstruc.2014.01.001.
[38]Dujc J, Brank B, Ibrahimbegovic A. Multi-scale computational model for failure analysis of metal frames that includes softening and local buckling [J]. Computer Method in Applied Mechanics and Engineering, 2010, 199(21/22):1371-1385. DOI:10.1016/j.cma.2009.09.003.
[39]Duan L P. A generalized beam theory (GBT) based beam finite element model and its application to fire-resistance and blast-resistance analyses of steel structures [D]. Shanghai: School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, 2016. (in Chinese)