There have been several severe earthquakes that caused damage to underground structures in recent years. For example, in Kobe, Japan, an earthquake[1] led to the collapse of Daikai subway station. The earthquake of 1999[2] in Duzce, Turkey, destroyed several highway tunnels. These earthquakes have drawn considerable attention to earthquake-induced damage on underground structures, among which liquefaction is one destructive phenomenon. When the excess pore pressure increases and reaches initial effective stress caused by overburdened soil, the soil tends to liquefy, which means that it is likely to lose its bearing capacity. Afterwards, several effects follow, including floatation, lateral ground spreading and large settlement, exerting detrimental impact on underground structures[3-6].
With the rapid urbanization in China, traffic congestion has become increasingly serious, thus leading to the hasty construction of rail transit to relieve the traffic burden. However, many underground structures, like subway stations and tunnels, are located in liquefiable soil. Taiyuan Metro Line 2 in Shanxi Province, China is an example, where large deformation caused by liquefaction has a significant influence on underground structures, calling for special attention in construction.
An underground structure will inevitably cut through liquefied soil in the course of large-scale construction of a transit rail, thus requiring a higher anti-seismic specification. The distribution of the liquefied soil layers has a significant influence on the seismic response of underground structures. Seismic performance of underground structures on liquefied soil has been extensively studied, involving analytical and numerical analysis[7-14], as well as experimental investigations[15-21]. Previous research has explored structures with various cross sections in a liquefiable soil under different conditions. It is found that earthquake-induced liquefaction might cause damage to underground structures due to the floatation or the loss of bearing capacity resulting from the change of excess pore water pressure.
All the research mentioned above concerned structures which were surrounded by liquefiable soil. Once a site is detected with a large range of liquefiable soil, it is necessary either to take measures reducing the liquefiable range, or to switch to another location which is more suitable for the placement of underground structures. However, it is rare that a structure is located in such a large range of liquefied soil. More common in practice, liquefied soil is likely distributed anywhere in the underground structure and covers a relatively small area. Both the structure and the soil may react differently when liquefied soil is situated in different places, but research in this field is rare.
In Ref.[22], we designed six conditions when liquefied soil is located at different parts of the structure, to identify the response of underground structures, the distribution of liquefied area, the change law of pore pressure and so on. However, we did not take time change and seismic peak values into account. In Ref.[23], different moments from the time when the soil is primarily liquefied to the moment that large deformation occurs are considered. However, we only compared the response characteristics of the underground structure when it is surrounded by liquefiable soil or no liquefiable soil.
Based on previous studies, the idealized rectangular tunnel cross-section, with a monolayer and two crosses, was used as the underground structure. Four idealized cases that are more common and representative[22] are considered in this paper. They are when liquefaction occurs all around the structure (Situation 1), below the structure (Situation 2), on the two sides of structure (Situation 3), and a contrast condition when no liquefaction occurs (Situation 4). FLAC3D software was employed to carry out numerical analysis.
1 Finite Difference Element Model
Coupled dynamic-groundwater flow calculations can be performed with FLAC3D. By default, the pore fluid simply responds to changes in the pore volume caused by mechanical dynamic loading; the average pore pressure remains essentially constant in the analysis [24].
1.1 Constitutive model for soil
During cyclic loading, the pore pressures may build up considerably in some sands, which will lead to liquefaction when the effective stress approaches zero. The Finn model was chosen as a built-in constitutive model contained in FLAC3D to account for the basic physical process. Based on the standard Mohr-Coulomb plasticity model, the Finn model and mechanism are described as[25]
(1)
where Δεvd is the increment of plastic volume strain; γ is the engineering shear strain; and εvd is the accumulated irrecoverable volume strain.
In addition to the usual parameters, such as the friction, moduli, cohesion and so on, the four constants of C1,C2,C3 and C4 in Eq.(1) are difficult to obtain. Therefore, an alternative and simpler formula proposed by Byren[26]is used.
(2)
where C1 and C2 are the constants with the relationship as follows:
(3)
C1=7 600(Dr)-2.5
(4)
(5)
where Dr is the relative densities and (N1)60 is the normalized standard penetration test values. We can obtain that
(6)
As a consequence, in engineering if we can attain the normalized standard penetration test values of (N1)60, it is easier to achieve the parameters of the Finn model.
Based on the Finn model, Chen[27] added the step of post-liquefaction, considering the state of zero effective and non-zero effective after initial liquefaction, which is termed post liquefaction Finn (PL-Finn). He also compared the PL-Finn model with the Finn model, and came to the conclusion that when the two models adopt Rayleigh damping, the time it takes to liquefy is shorter when using the PL-Finn model than using the Finn model; however, the results after liquefaction are almost the same. As we use the same criteria to compare different situations, the difference when using Rayleigh damping in the PL-Finn model, compared to the Finn model, can be ignored.
1.2 Physical model
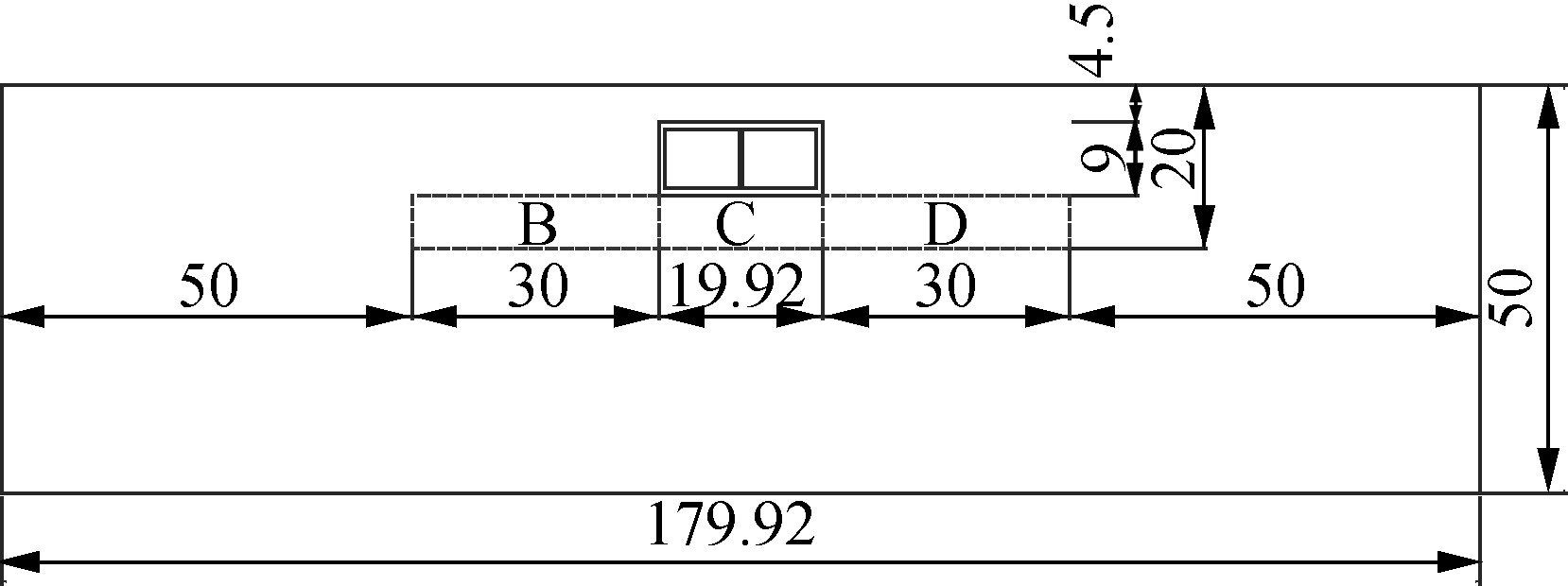
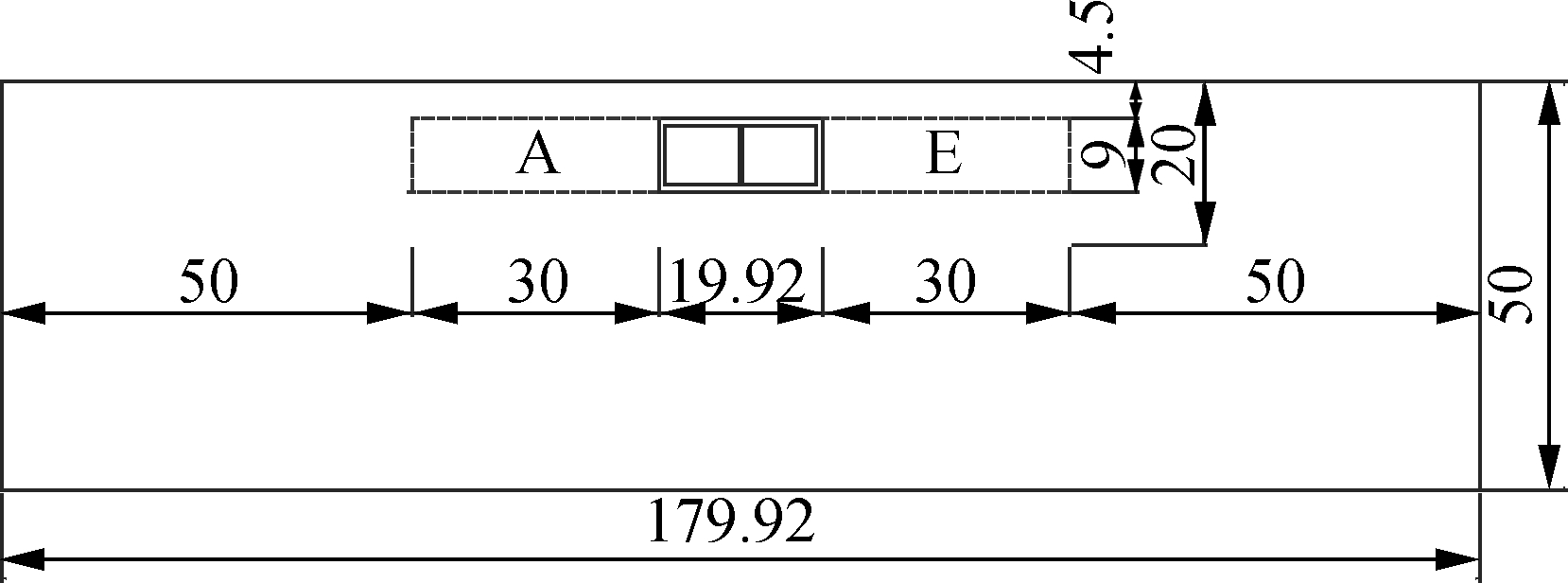
The seismic behavior related to liquefaction of a rectangular tunnel in a ground model was investigated. The overall dimensions and the location of the tunnel are shown in Fig.1. The defined liquidized strata is located at 20 m in depth and 79.92 m in width in a horizontal direction beneath the surface of soil, according to Refs.[28-29] (areas A to E). It is necessary to estimate the liquefaction of 20 m beneath the ground. Four typical situations are designed in this paper: liquefied soil around the structure (areas A to E), under the structure (areas B, C and D), at two flanks of the structure (areas A and E), and the contrast condition of the structure on non-liquefied soil. The soil deposits of liquefiable soil of sand and non-liquefiable soil of clay are assumed to be homogeneous. The thickness of soil is 50 m over the bedrock. The underground structure is actually a one-story and two-span subway tunnel, of which the cross section is shown in Fig.2. It was slightly modified in dimension in order to fix the finite difference element mesh. The portrait length of the models is 1 m, which is assumed to be a plane-strain condition.
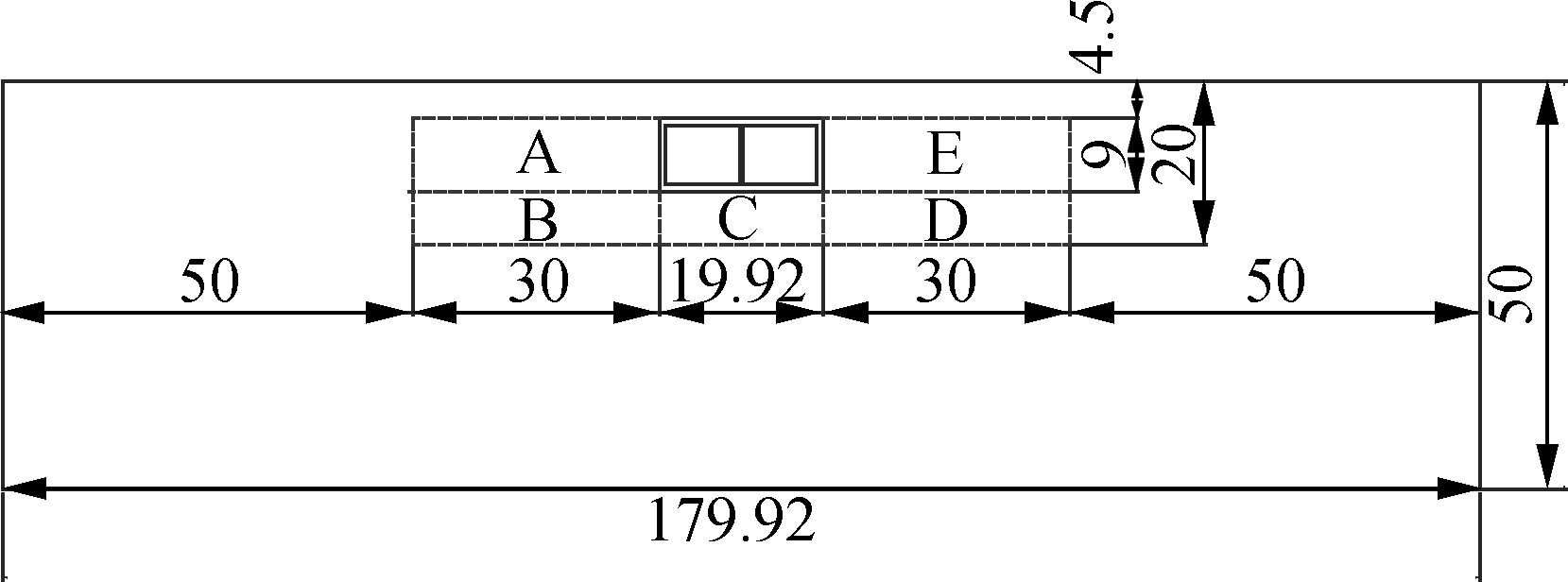
Fig.1 Cabinet experimental samples(unit: m)
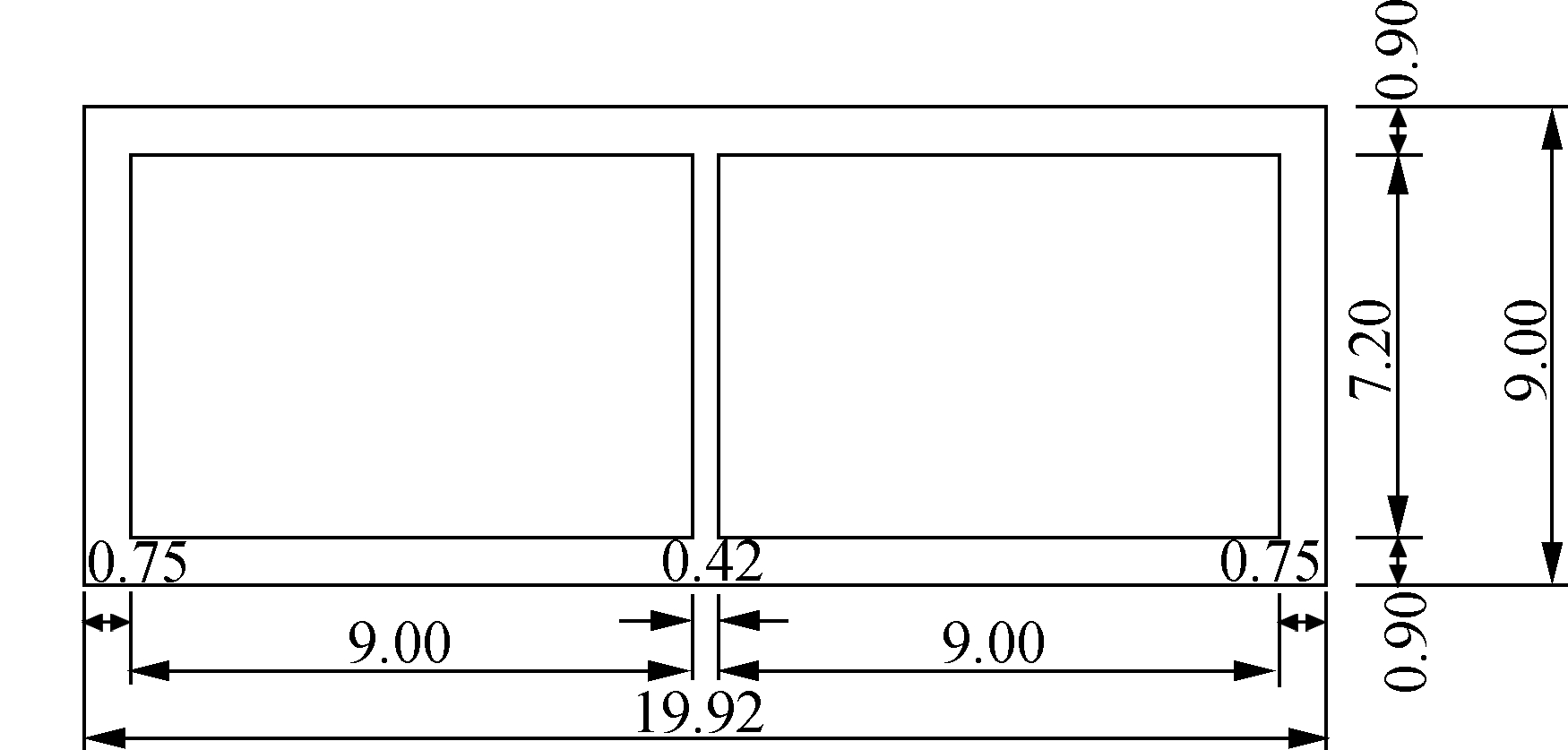
Fig.2 Transverse section of the underground structure(unit: m)
1.3 Finite element mesh
The depth of the analyzed domain was 50 m and the thickness was set to be an assumed soil deposit. According to Ref.[29], the distance between the free-field zone determines the width. The distance from the underground structure must be large enough, so that the dynamic behavior of the underground structure and the area close to it are not affected by the reflected vibration. With the structure at the center, a domain of 179.92 m was used in the analysis. According to the test of the thickness of the plane-strain elements, in order to ensure that the seismic events from the base can be adequately transmitted[29], it is found that a thickness of about 1.5 m is enough for the earthquake motion employed. Thus, the solid elements with a thickness smaller than or equal to 1.5 m is suitable. A thickness of 1 m is chosen in this paper.
The buried depth of the underground structure is 4.5 m. Altogether, there are 4 329 elements and 8 968 nodes. They are all Brick-type mesh in FLAC3D. The element mesh is shown in Fig.3.

Fig.3 Numerical computation grid
A larger mesh with an additional 60 m on each side of the original one is also analyzed. The elements inside the range of the original domain are exactly the same as those of the smaller one. The lateral displacement, at the top middle of the subway tunnel, is compared in Fig.4, where very small differences are found. Other variables, including the acceleration and vertical displacement, are also considered, and the differences are all ignored. Therefore, in this regard, the accuracy of the smaller mesh is thought to be sufficient.
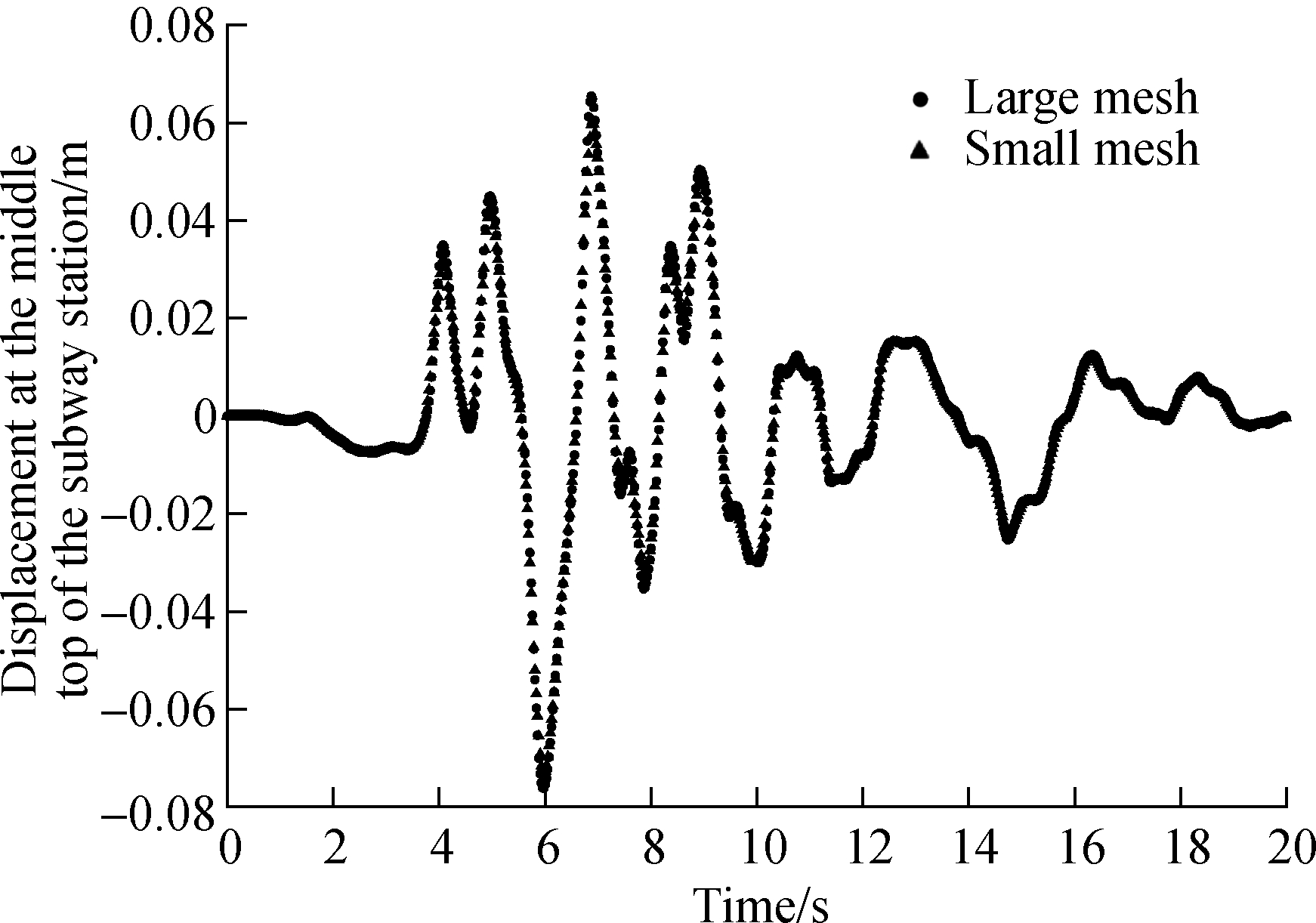
Fig.4 Comparison between the lateral displacement responses of the subway tunnel for the two meshes
1.4 Material properties
The sandy ground was simulated by means of the aforementioned generalized plasticity PL-Finn model during the analysis. The non-liquefiable soil of clay was modeled through the standard Mohr-Coulomb plasticity model. Liquefiable sand with the (N1)60 value of 7 and the clay of Taiyuan Metro Line 2 were chosen here. All the parameters were obtained from the geological prospecting report of Metro Line 2 in Taiyuan City in China. It has been verified that there are large scales of liquefiable soil, and the metro line runs through it. The cyclic and undrained triaxial tests were carried out by the design institute[30]. It is noteworthy that the parameters are suitable to reflect the standard liquefied soil of Taiyuan.
The underground structure was simulated by the linear elastic model. Both the soil and the structure were modeled by utilizing solid elements. In addition, the interface of the glued model between the soil and the underground structure was also modeled here with no slip or separation occurring between the soil and structure. The parameters of the structure are taken as the typical elastic properties of concrete, as shown in Tab.1.
Tab.1 Material parameters
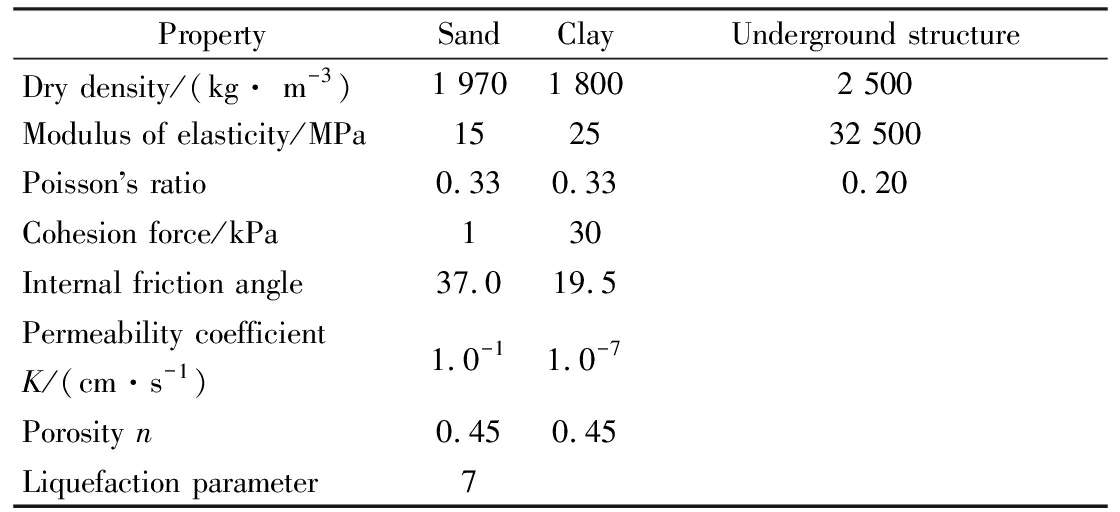
PropertySandClayUnderground structureDry density/(kg· m-3)1 9701 8002 500Modulus of elasticity/MPa 152532 500Poisson s ratio0.330.330.20Cohesion force/kPa130Internal friction angle37.019.5Permeability coefficient K/(cm·s-1)1.0-11.0-7Porosity n0.450.45Liquefaction parameter7
1.5 Material damping
In time-domain programs, Rayleigh damping is commonly adopted to provide damping that is approximately frequency-independent over a restricted range of frequencies. It might only require a minimal percentage of damping for many dynamic analyses that involve large strains[31]. The critical damping ratio of 5% is chosen in this paper, which is also employed for the underground structure.
1.6 Boundary conditions
The free-field boundary is applied in analysis. The underground water level is assumed to be located at the top of the underground structure, which is a common situation.
1.7 Input earthquake motion
The site of the seismic wave of Taiyuan City was adopted as the horizontal excitation in the analysis. The 0.1g acceleration (ACC) is shown in Fig.5(a), the Fourier spectrum of which is manifested in Fig.5(b). To study different cases, the earthquake motion is scaled to 0.1g, 0.15g, 0.2g, 0.3g and 0.4g, respectively. The motion of earthquakes is inputted from the fixed boundary at the base. The length of the excitation is truncated to 20 s to improve the efficiency of analysis since the major motion of the excitation has already stopped.
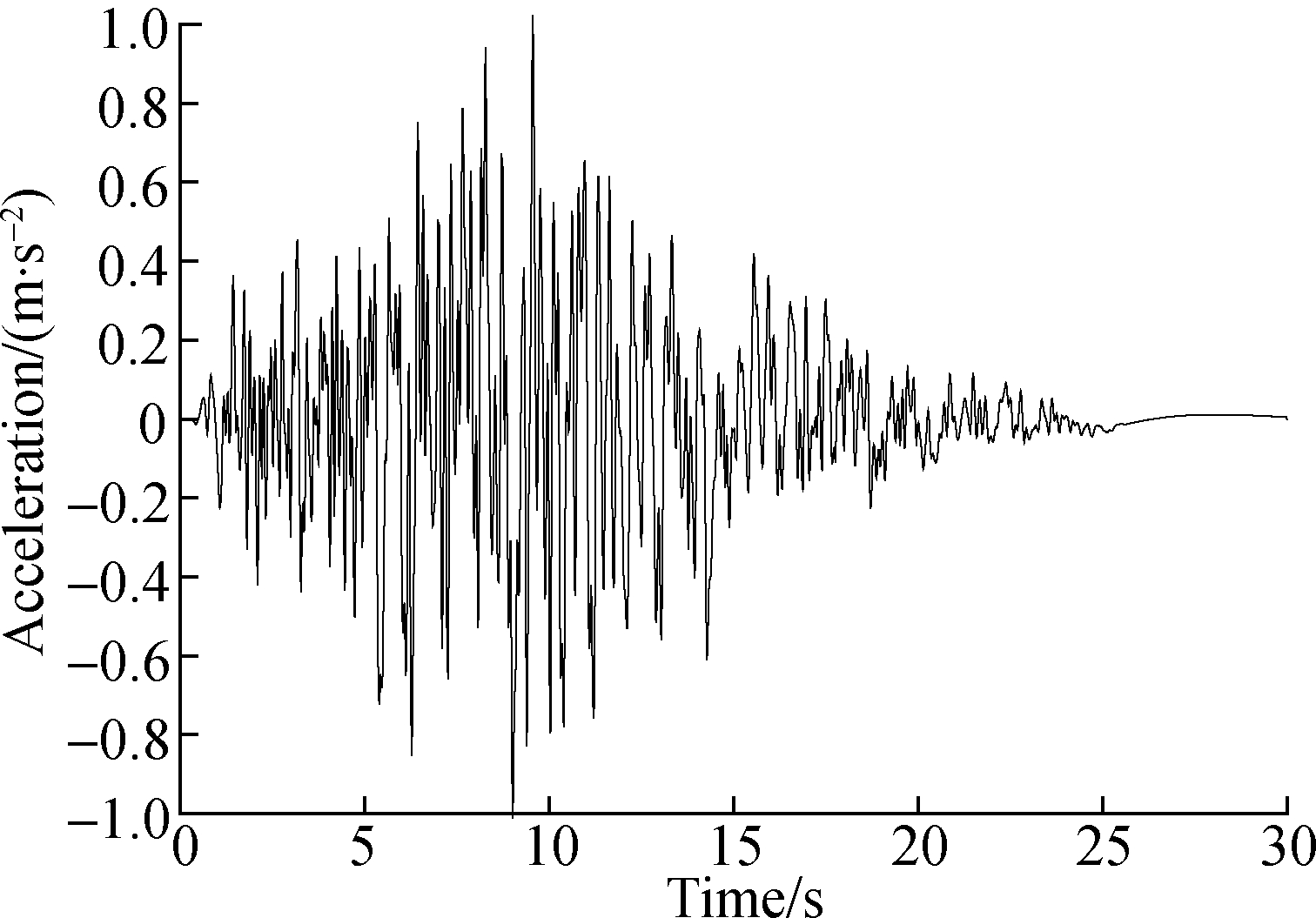
(a)
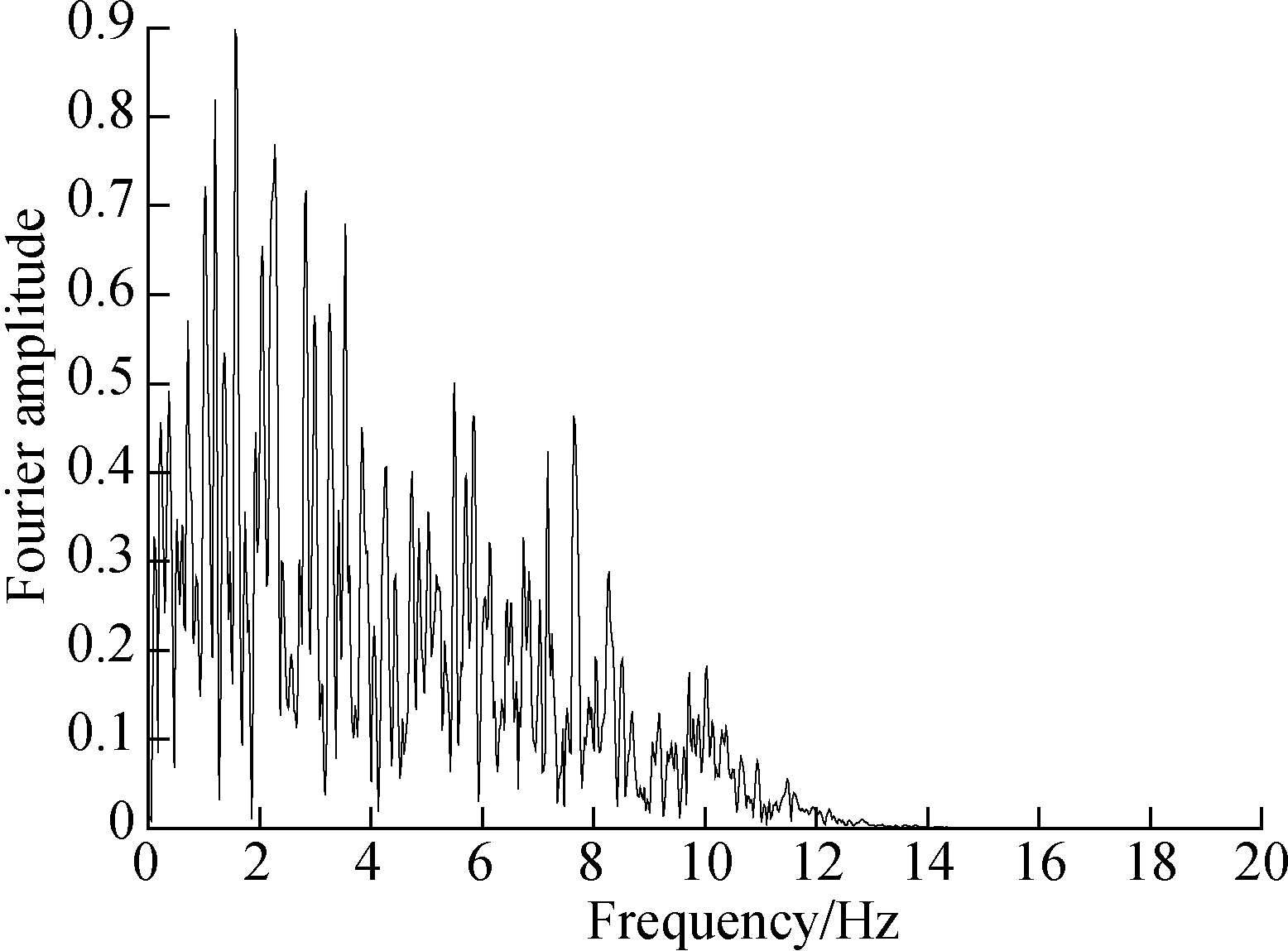
(b)
Fig.5 Seismic acceleration-time history curve and Fourier spectrum.(a) Seismic acceleration-time history curve;(b) Fourier spectra of acceleration
1.8 Analysis procedure
First, an initial stress field in equilibrium was obtained beforehand, and the construction history of the structure was taken into account. The material model for the soil, used in the initial static run, was the standard Mohr-Coulomb plasticity model. Then, the static pore pressure and the effective stress were utilized as the initial conditions for the subsequent dynamic run with the input excitation. The location of liquefied soil is shown in Fig.6, and the initial pore pressure distribution is shown in Fig.7. The displacement and velocity were set to be zero before dynamic analysis. Therefore, the displacements analyzed here were all dynamic-related responses.

(a)
(b)
(c)
Fig.6 Location of liquefied soil (unit:m). (a) Situation 1; (b) Situation 2; (c) Situation 3

(a)

(b)

(c)
Fig.7 Pore water pressure distribution. (a) Situation 1;(b) Situation 2; (c) Situation 3
Since it was expected that considerable deformation of the soil and underground structure will occur, a large deformation formulation of the FLAC3D program was adopted in the seismic analyses. In the large-strain mode, grid-point coordinates were updated at each step according to computed displacements, and non-linearity was possible[32]. If a very large mesh deformation occurred, the calculation might stop, informing the researchers of the specific position where it went wrong. This situation only occurs in a liquefied condition to help the researchers decide where the large deformation occurs. However, in the non-liquefied condition, this will not occur, signifying that there will be no large deformation.
1.9 Analysis cases
There are 20 different cases altogether with the liquefiable soil at different positions of the structure (see Fig.6), accompanied by different acceleration input excitations. The case described in Situation 4, namely the structure is on non-liquefiable soil, is considered.
2 Numerical Results of Soil in Different Cases
When there was a large deformation, the location where the soil encountered the deformation, the distribution of liquefied area, the change of the excess pore-water pressure ratio, as well as the distribution of pore water pressure, were investigated and compared in different situations. This step was for a comprehensive insight into the seismic behavior of the liquefiable soil when it was located in different positions around the structure.
2.1 The time of the occurrence of large deformation
The time of the occurrence of large deformation under different peak seismic wave inputs in three situations is shown in Tab.2. Under the same input of seismic wave, large deformation caused by liquefaction takes place earliest when liquefied soil is around the structure. The higher the peak value is, the more prone to liquefaction that leads to a large deformation. This is reasonable since there is the largest amount of liquefiable soil in Situation 1. However, in Situation 4 when there is no liquefiable soil, no large deformation occurs. This verifies that it is the liquefiable soil that causes large deformation. In addition, from the beginning of the deformation, we can see that a large deformation occurs after the peak seismic wave at 8 s. and the large deformation takes place earlier in Situation 2 than in Situation 3. Thus, it is indicated that the large deformation occurs faster when the liquefaction occurs at the bottom than on two sides.
Tab.2 The time when large deformation of soil occurring under different accelerations
s

Situation0.1g0.15g0.2g0.3g0.4gSituation 111111198Situation 21511131010Situation 31414131211Situation 4No large deformation occurring
2.2 Location of the occurrence of large deformation
Mesh deforming occurs when a large deformation of soil occurs at 0.1g, as shown in Fig.8. It is clear that when the liquefied soil is around a structure, the large deformation mostly occurs at the arch angle of station floor where the shear force is sufficient to create a large shear deformation. The position just under the floor proves to be the most difficult to deform or destroy where the soil, just under the structure, is not easy to liquefy, which is consistent with the specification[28]. This is due to a higher overburden of the soil under the structure than in other parts. Large deformation on two sides of the structure cannot be observed.
(a)
(b)
![]() (c)
(c)
(d)
Fig.8 Mesh deforming figures when large deformation of the soil is occurring.(a) Situation 1;(b) Situation 2; (c) Situation 3; (d) Situation 4
The soil on the two sides of the structure is not likely to liquefy, which is believed to result from smaller overburden stress. When liquefied soil is under a structure, a large deformation area is mostly at the arch angle of the station floor but not under the structure, which affects the soil below. Thus, the primary concern is supposed to be the liquefied soil found under the structure, especially in a large range when extending to two sides of the bottom. The code for seismic design of urban rail transit structures[28] illustrates that the hazard of liquefaction is mainly from the outside of the base. Soil just below the liquefaction bearing layer is the hardest part to liquefy. The area which liquefies first will affect the soil under the structure that has not liquefied, thus leading to the loss of side soil pressure in the lateral support.
2.3 Distribution of liquefied area
The distribution of liquefied area with the acceleration of 0.1g and 0.3g is shown in Fig.9, where the color white represents the state of liquefied now and post liquefied, the color gray represents post liquefied state, the color black represents non-liquefied state. This indicates that when liquefied soil is around a structure, soil on the left and right of the structure does not easily liquefy, even when a large deformation has occurred in another place. This occurs since the pore pressure in the soil, which is close to the sidewall of a structure, easily dissipates. The presence and floatation of the underground structure brings about a large shear deformation of the two sides, which contributes to the lowering of excess pore pressure. This is reasonable for most medium-loose and medium-dense sand. When there is a large shear deformation, the sand tends to dilate, which will lead to the lowering of excess pore pressure if the sand is saturated[29].
(a)
(b)
(c)
(d)
(e)
(f)
Fig.9 Distribution of the liquefied area. (a) Situation 1 with the acceleration of 0.1g;(b) Situation 1 with the acceleration of 0.3g;(c) Situation 2 with the acceleration of 0.1g; (d) Situation 2 with the acceleration of 0.3g;(e) Situation 3 with the acceleration of 0.1g;(f) Situation 3 with the acceleration of 0.3g
Soil beneath the two sides of the structure is the first to liquefy, and then with the increase of the seismic peak value, the soil far away also liquefies. It is the same in both Situation 1 and Situation 2.
When the liquefied soil is located around the two sides of the structure, the condition is more likely to be well-distributed with a slighter liquefaction, compared with the other two situations.
It can be seen that the distribution of the liquefied area is in accord with the above-mentioned mesh deforming figures.
2.4 Change of excess pore water pressure ratio ru
Generally, the concept of the pore water pressure ratio (PPR) ru is often applied to describe liquefaction[24]. In three-dimensional numerical calculation, the definition of ru is
(7)
where ![]() is the average effective stress of the element before dynamic calculation and
is the average effective stress of the element before dynamic calculation and ![]() is the average effective stress of the element during the process of dynamic calculation.
is the average effective stress of the element during the process of dynamic calculation.
(8)
(9)
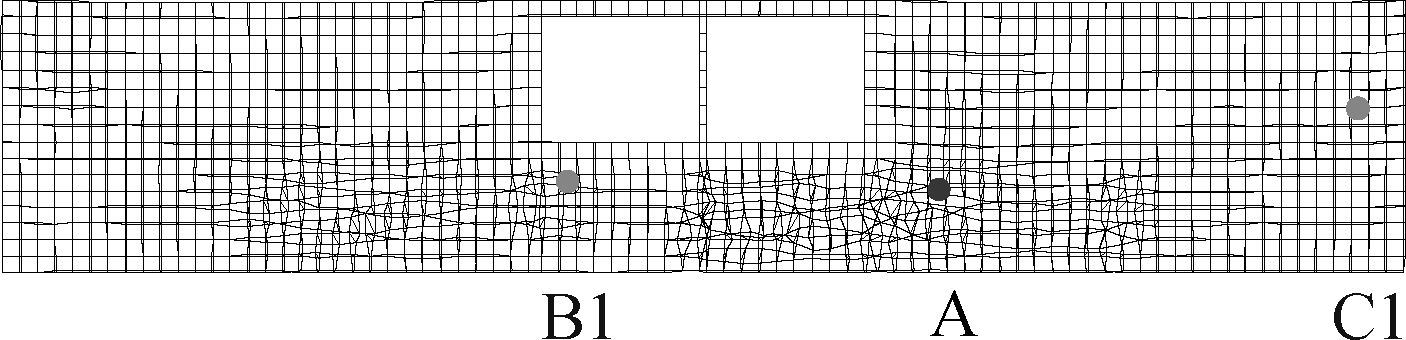
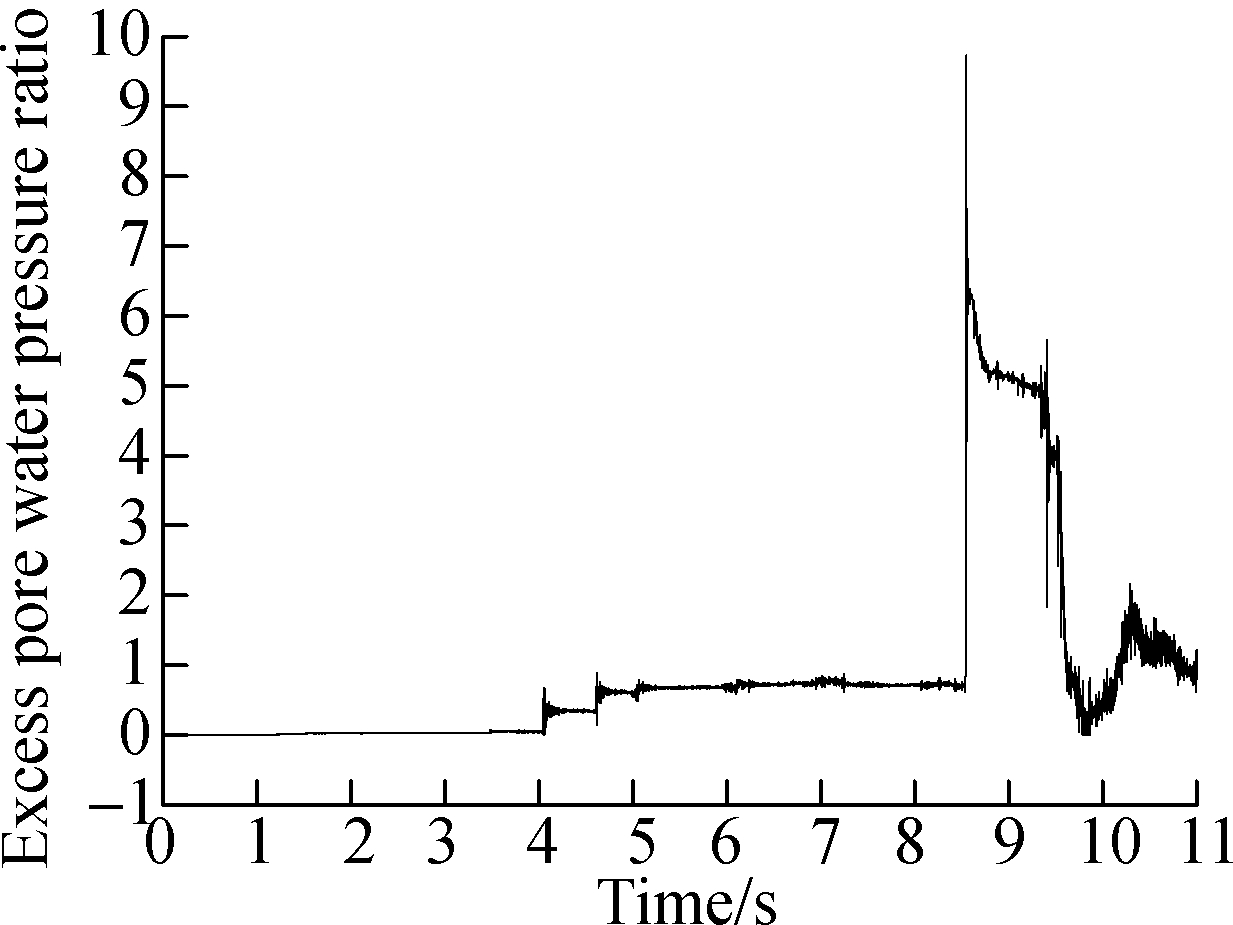
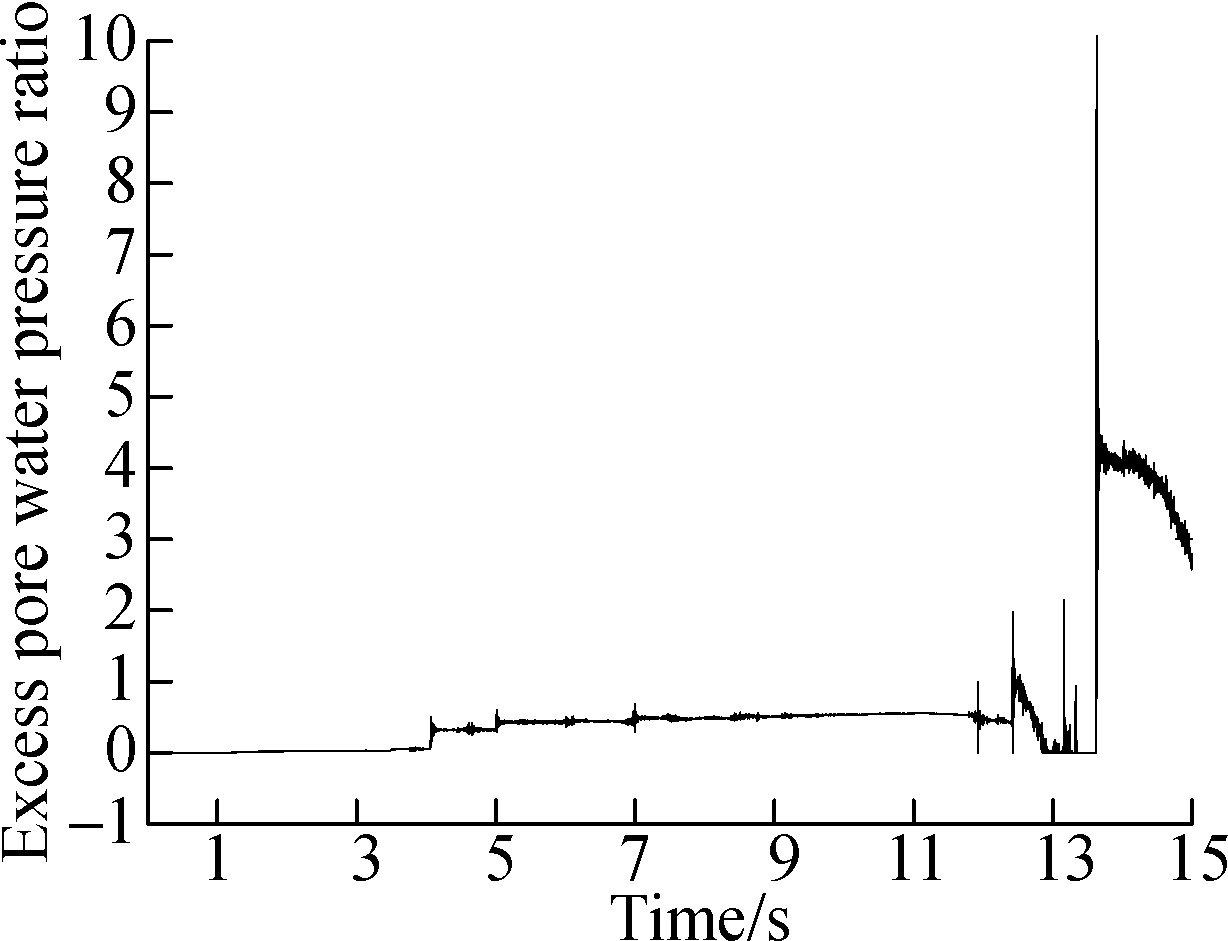
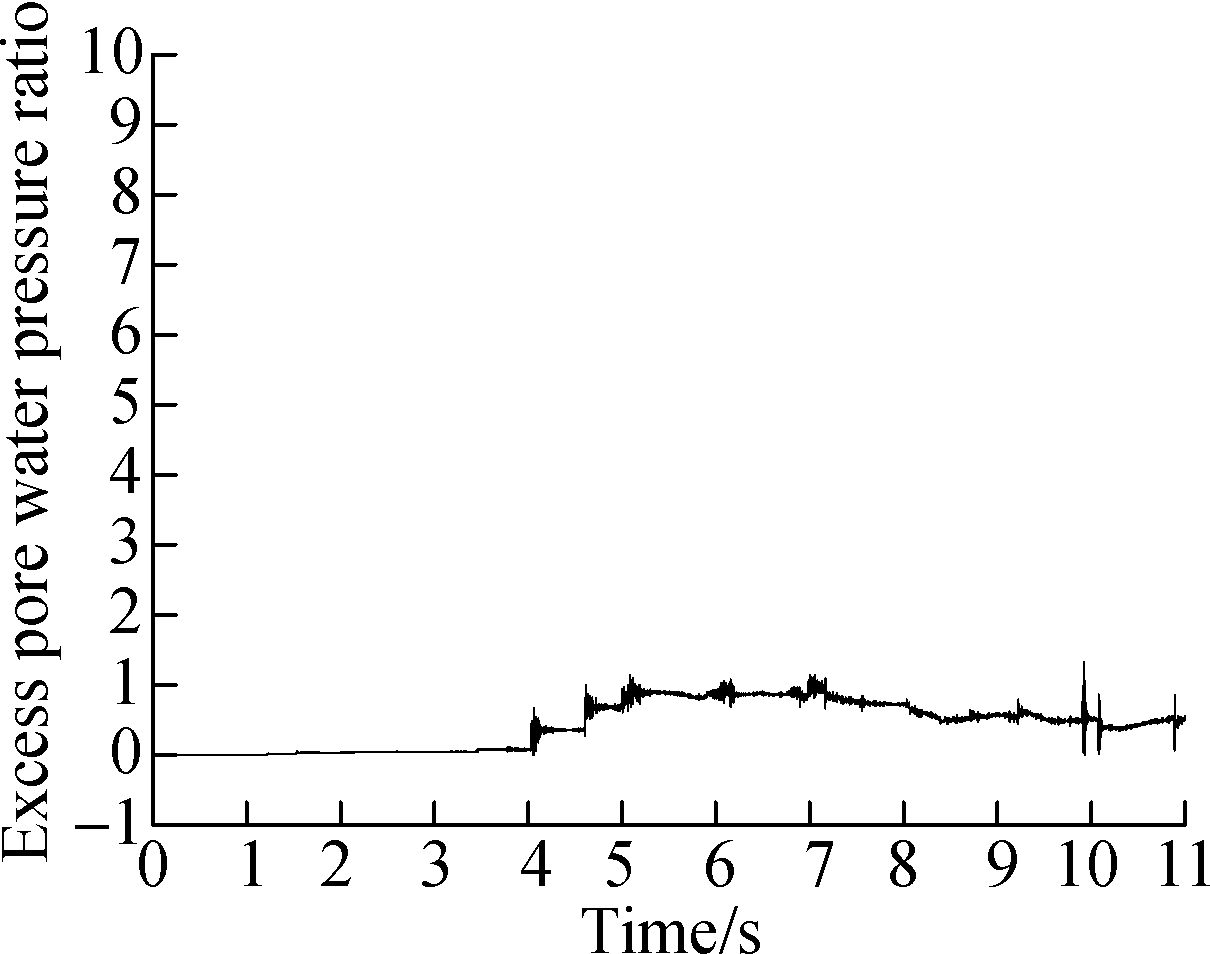
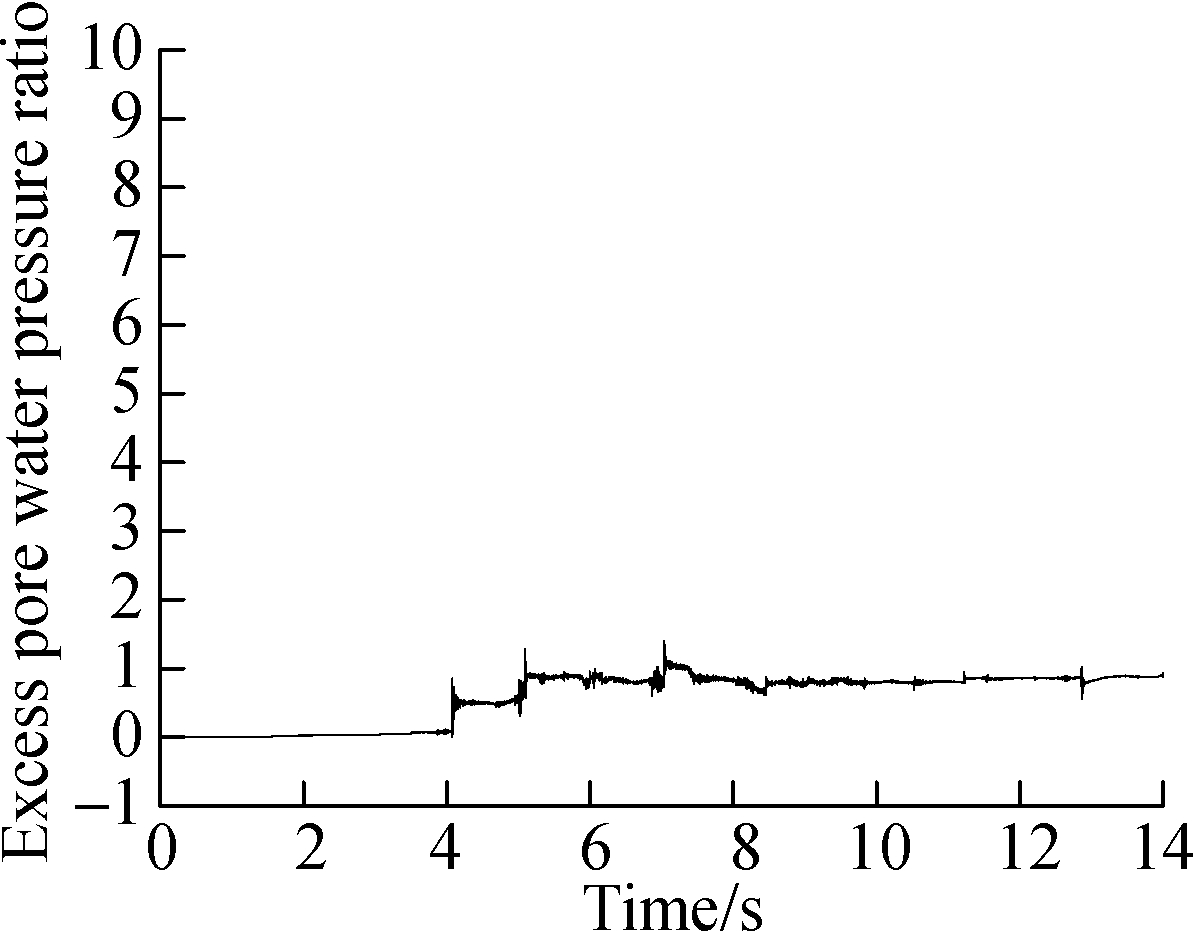
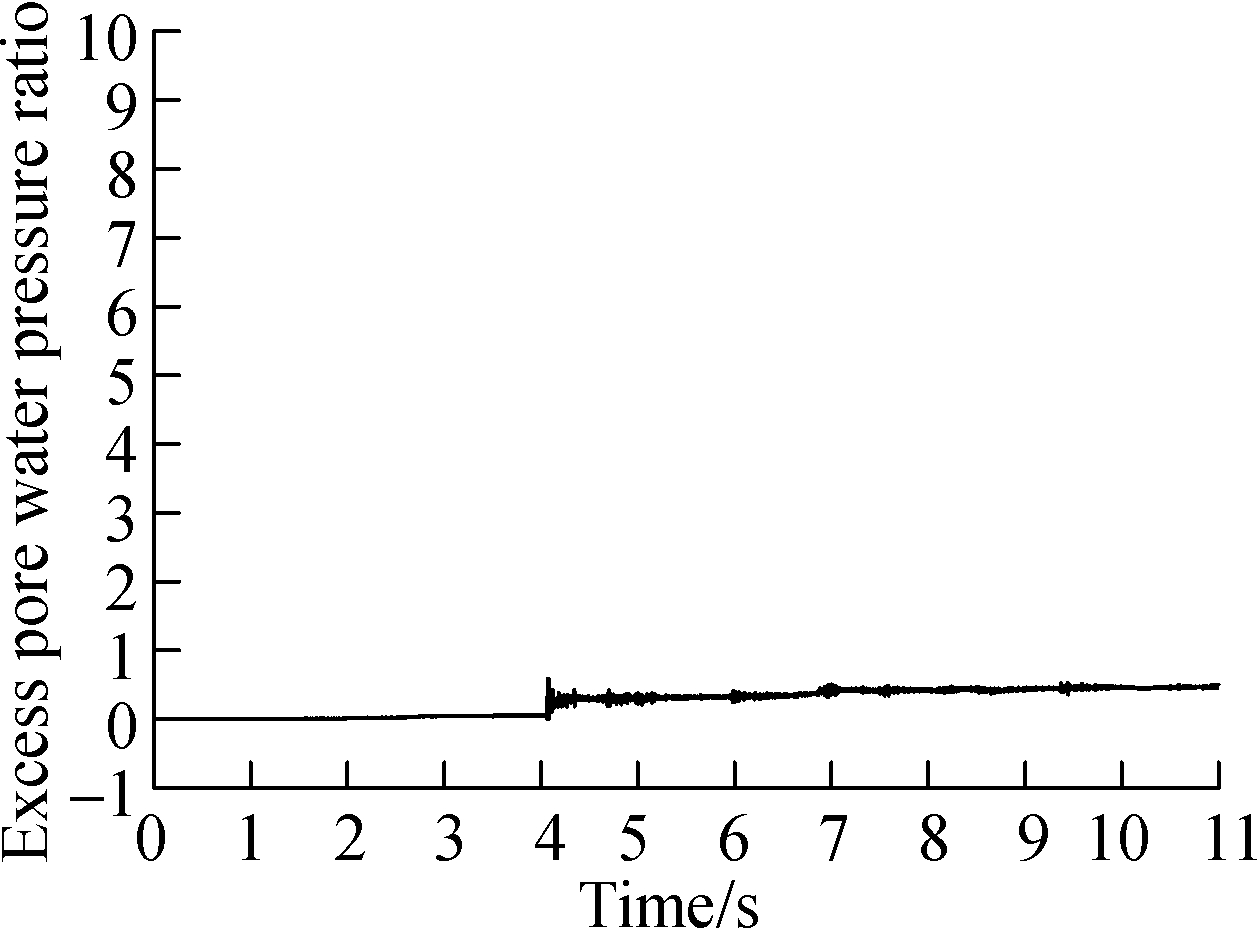
During calculation, when ru=1, it signifies that the average effective stress of the element is zero, meaning that the saturated sand is liquefied. This paper is based on this assumption. The locations of large deformation are chosen as monitoring points in three situations respectively, as denoted by the dot points of A, B and C in Fig.7. We also added two green monitoring points of B1 and C1 in Situation 1, which are in the same positions of points B and C, to compare the difference. The PPR time-history curve shown in Fig.9 aims to depict the law of changes from the time when the liquefaction occurs to the time when the large deformation appears.
From Figs.10(a),(b) and (d), it can be seen that the primary liquefaction occurs between the time of 5 and 7 s, which is 1 to 2 s before the large deformation occurs, and afterwards, the peak seismic value is evident, and the PPR shows a sharp increase. It conforms to the studies that a large deformation occurs several times after liquefaction, and damage to the structure is observed [4]. The ultimate PPR of point A is the largest, while the value of point C is the smallest.
Compared with points B and C, although B1 and C1 are located in the same position, they do not have a large deformation. The values of PPR are less than those of point B and point C. Judging from the value, we can see that the soil around point C1 is not liquefied, while the soil around point B1 has been liquefied for some time. It has been verified previously that point B1, situated near the arch angle of the structure, is easy to liquefy, while point C1, located on the two sides of the structure with less burden, since the pore pressure easily dissipates, is not likely to liquefy.
3 Analysis of Structure Response
3.1 Displacement vector of the structure
(a)
(b)
(c)
(d)
(e)
Fig.10 Excess pore water pressure ratio distribution of monitoring points. (a) Point A in Situation 1; (b) Point B in Situation 2; (c) Point B1 in Situation 1;(d) Point C in Situation 3;(e) Point C1 in Situation 1
The floatation and the subsidence of underground struc-tures induced by soil liquefaction have become relatively serious problems, especially floatation. Damage to underground pipelines due to floatation, has been reported[33-34] .Through numerical analysis, Liu et al.[29] revealed the uplift of a subway station caused by liquefaction under strong earthquake excitation.
Fig.11 shows the maximum displacement vector (MDV) of a structure under different conditions when a large deformation occurs. Situation 4 at the time of 20 s is chosen as a contrast condition. From the values, we can see that as the input seismic peak value increases, the total motion amplitude increases according to different situations. When the structure is situated on non-liquefiable soil, as indicated in Situation 4, the value is always the smallest, showing that a large deformation is caused by liquefaction. On the condition of 0.1g with a slight liquefaction, as in Situation 2, the movement is small. However, when the acceleration increases, the total displacement changes with a surge, and it becomes the largest of the four situations at the acceleration of 0.2g and 0.3g. It can be concluded that although the soil on the two sides of the structure does not easily liquefy compared with other situations, it can still bring about a large displacement of the structue. Less overburden of the soil on the two sides can cause a faster dissipation of pore-water pressure, leading to a less lateral bracing force and a larger inertia force. This makes the structure affected by the excitation of the earthquake more horizontal and serious. When soil liquefies, the lateral bracing force decreases more severely in contrast with non-liquefied soil.
In Situation 1, when the liquefiable soil is around the structure, we can see that the movement of the structure is upward. Compared to Situation 4 when the structure is on non-liquefiable soil, the structure mainly moves horizontally, which confirms the previous studies. While liquefied soil is on the two sides in Situation 3, the structure floats slightly. However, in Situation 2, when liquefiable soil is under the structure, the movement is not only upward but also declines. It is then inferred that it is the soil on the bottom of the structure that causes the vertical movement of the structure. The change of the vertical supporting force induced by liquefaction may account for this phenomenon.
3.2 Lateral deformation of the underground structure
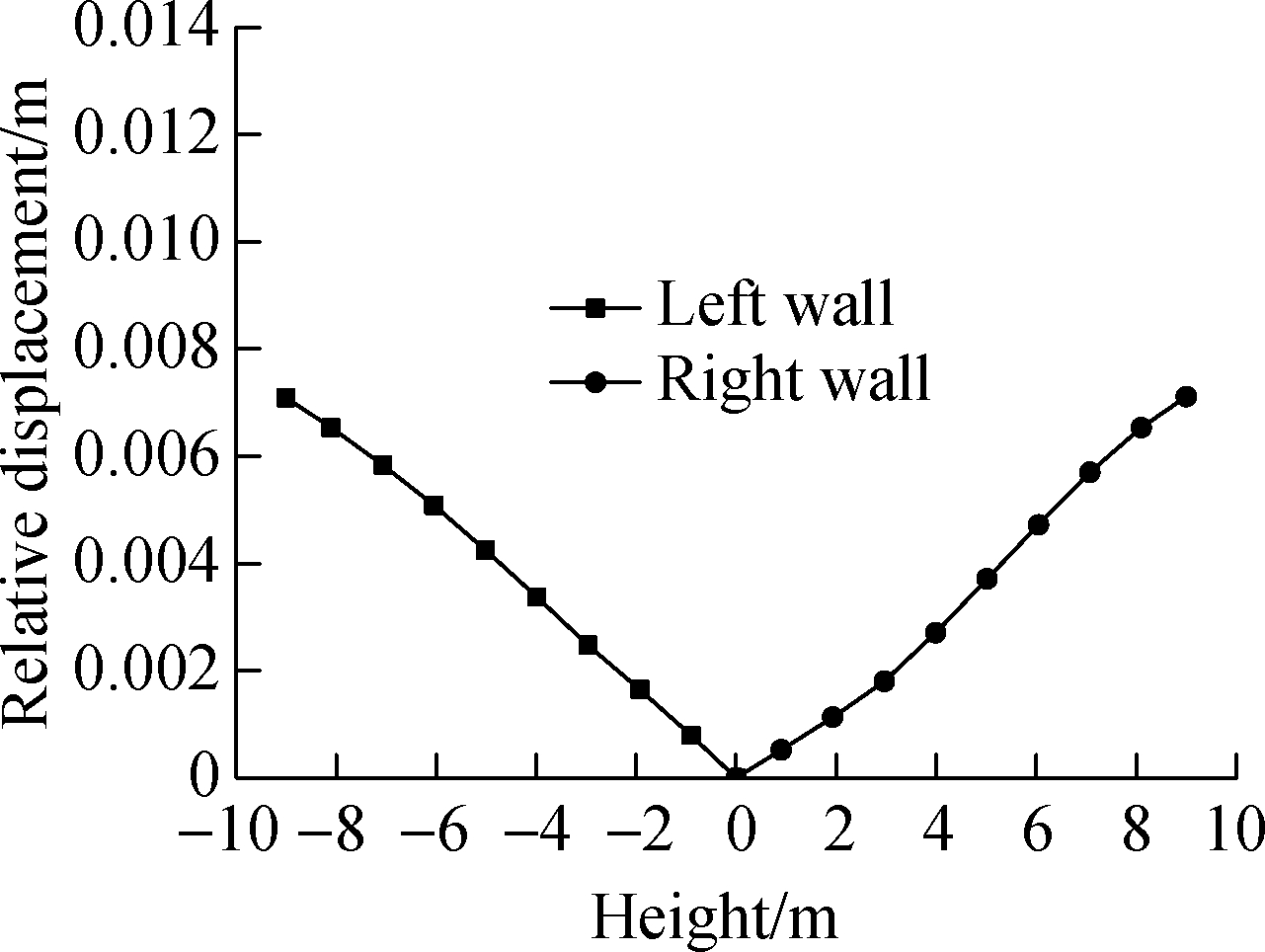
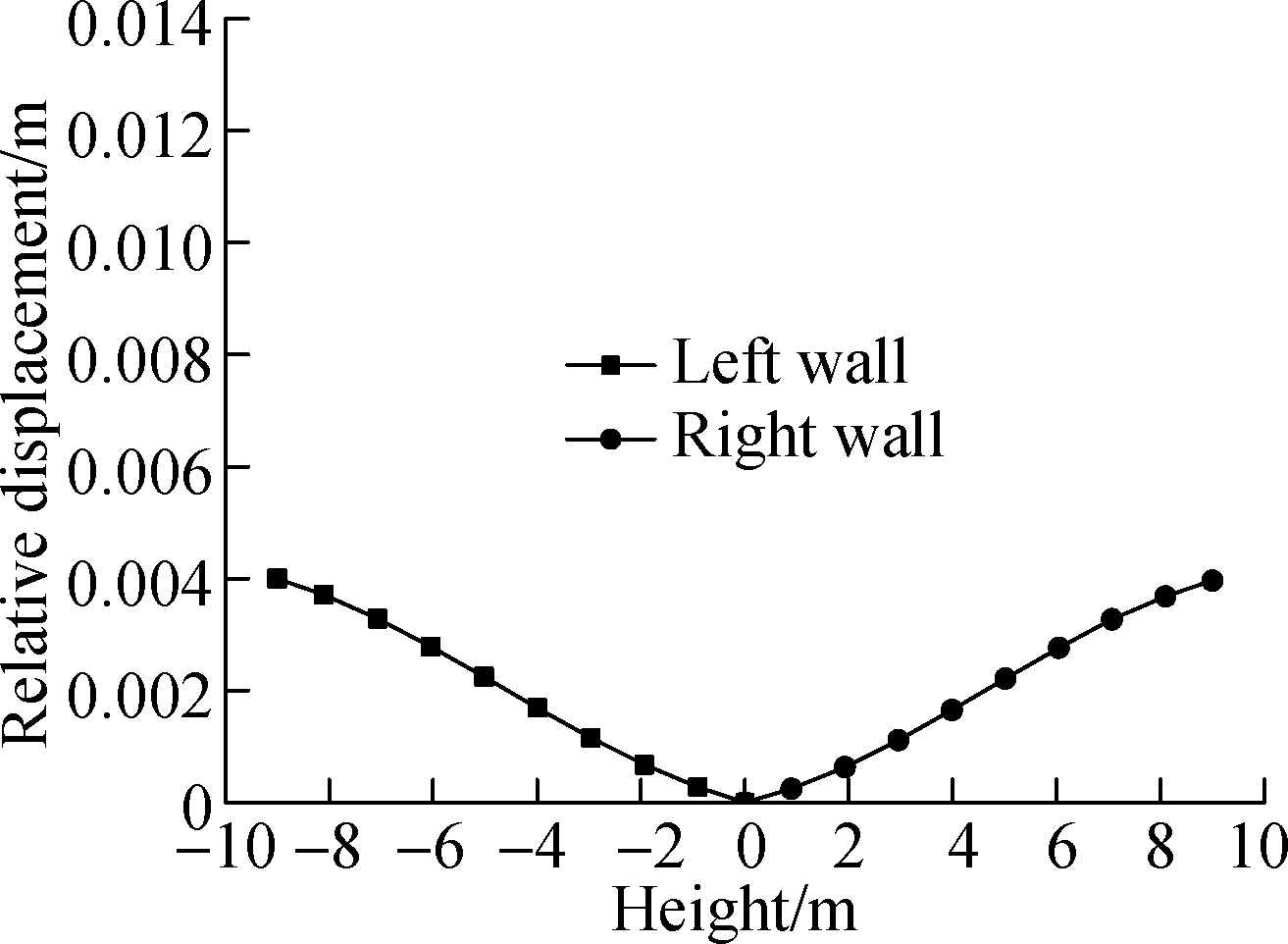
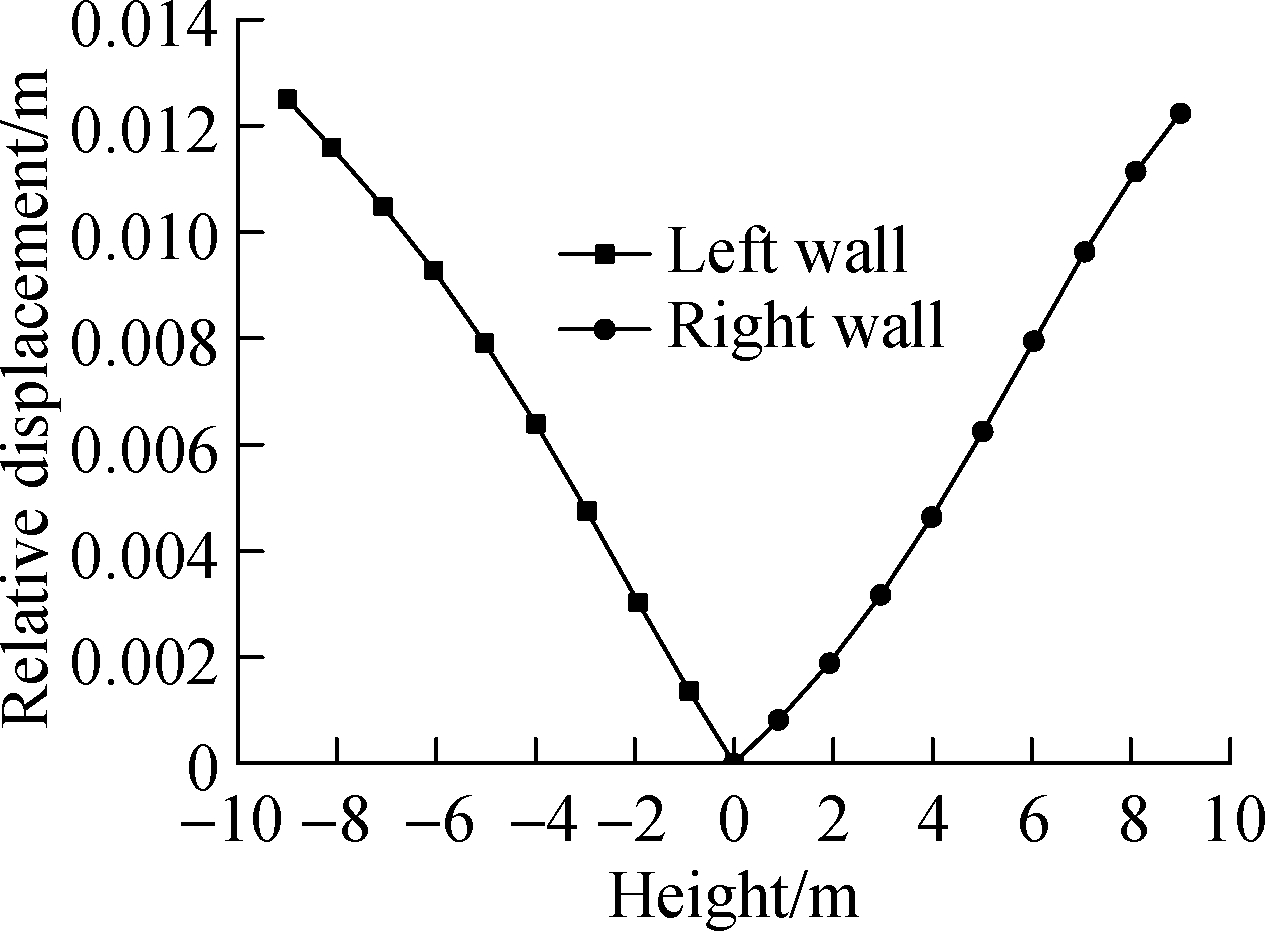
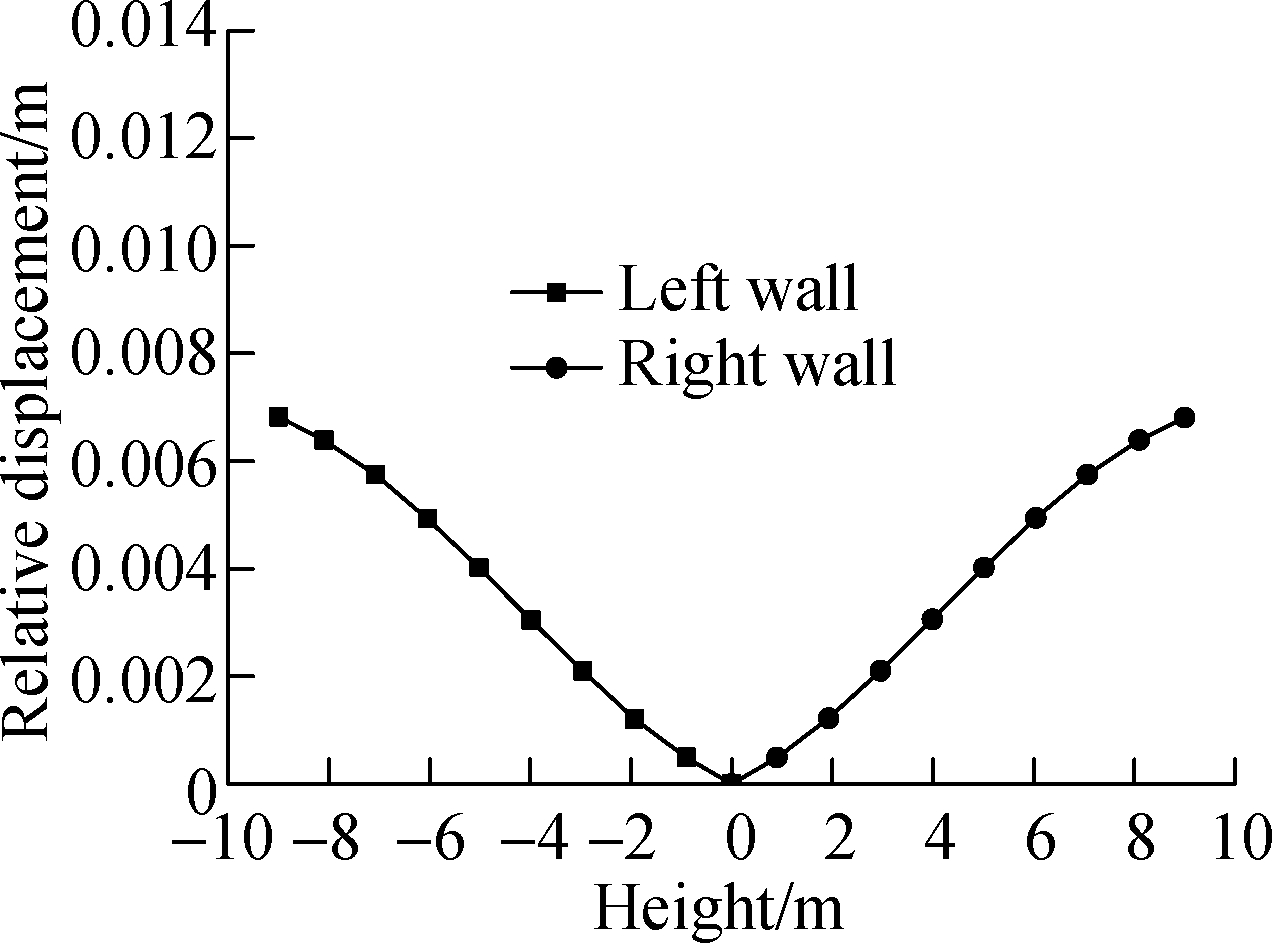
Under earthquake loading, the deformations of the left wall and the right wall were roughly the same with an ACC of 0.1g as shown in Fig.12. The maximum lateral deformation occurred during the strong earthquake motion between 5 and 15 s. However, the peak values are different, with the value of 7.1, 4.0, 12.5 and 6.8 mm in the four situations respectively. It is thus deduced that the differential displacement of the side wall is the smallest when the liquefied soil is under the structure with the condition of the same value of seismic wave input. When the liquefied soil is distributed on the two sides of the structure, the value is the largest. It is more likely to result in differential displacement when liquefied soil is on the two sides.
(a)

(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)

(k)
(l)
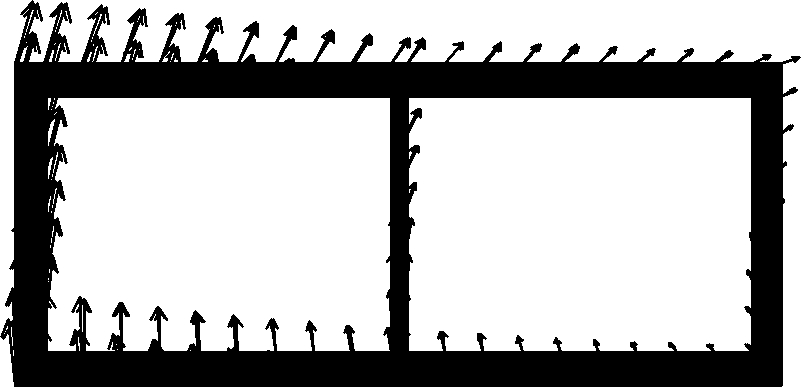
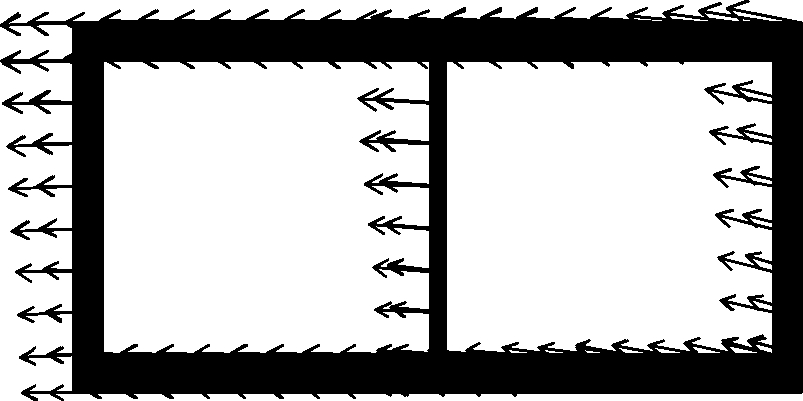
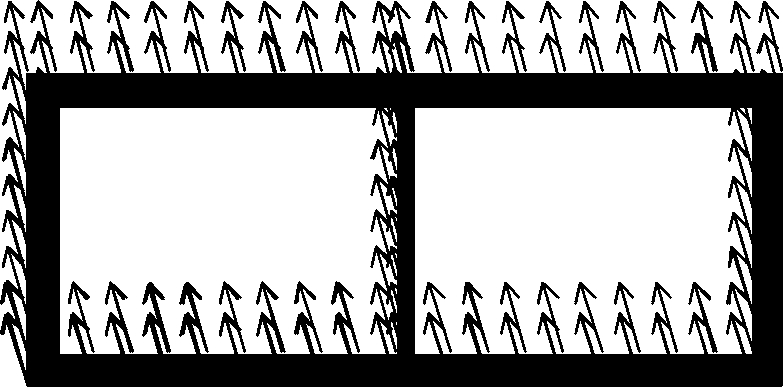
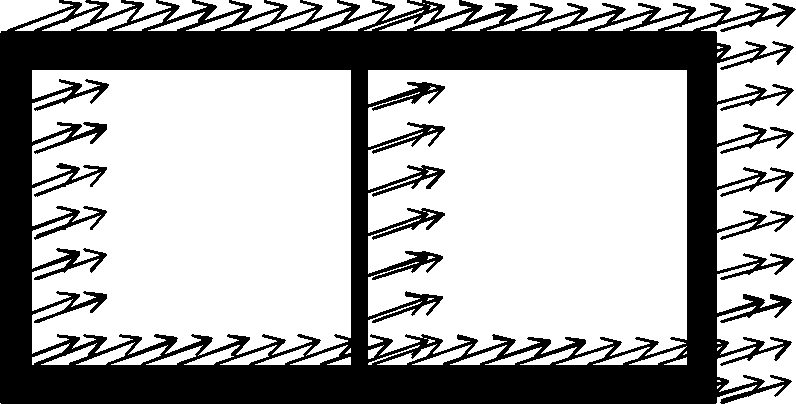
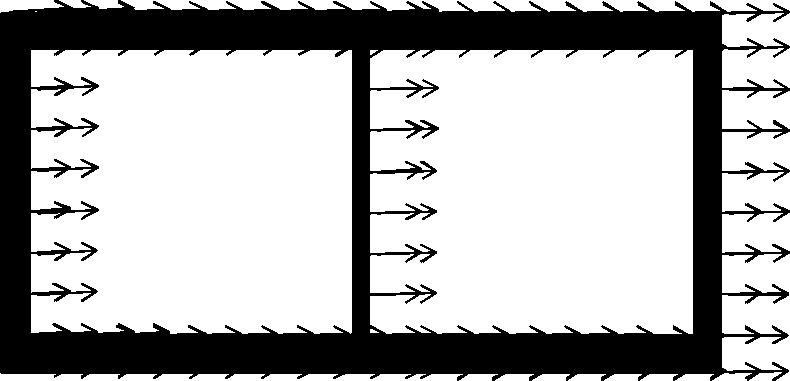
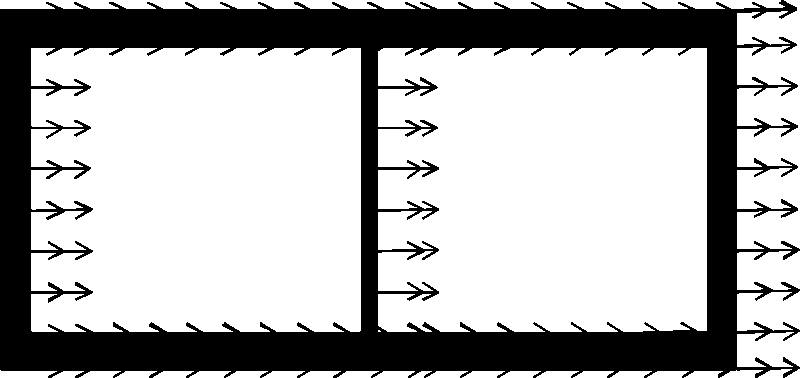
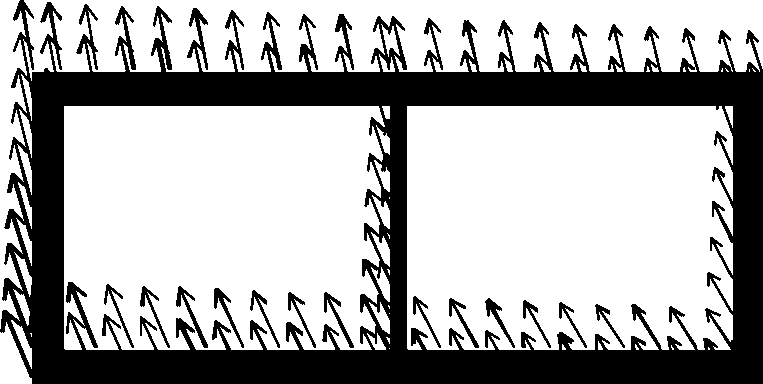
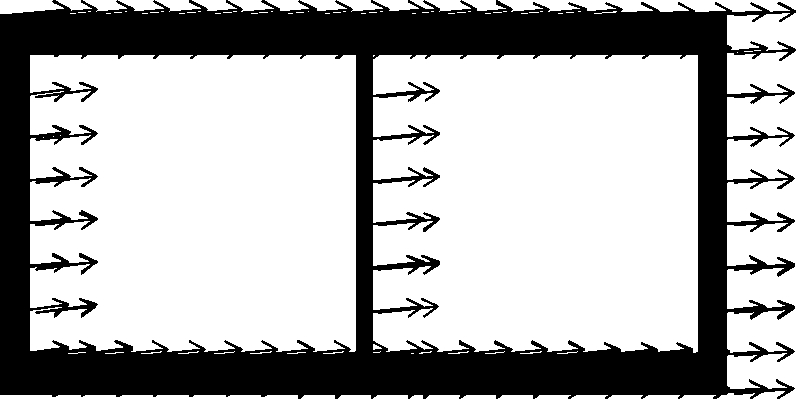
Fig.11 Maximum displacement vector of the structure. (a) Situation 1 with the ACC of 0.1g and the MDV of 26.06 mm; (b) Situation 2 with the ACC of 0.1g and the MDV of 29.84 mm;(c) Situation 3 with the ACC of 0.1g and the MDV of 8.33 mm; (d) Situation 4 with the ACC of 0.1g and the MDV of 0.33 mm; (e) Situation 1 with the ACC of 0.2g and the MDV of 111.7 mm; (f) Situation 2 with the ACC of 0.2g and the MDV of 187.1 mm; (g) Situation 3 with the ACC of 0.2g and the MDV of 261.5 mm;(h) Situation 4 with the ACC of 0.2g and the MDV of 40.31 mm; (i) Situation 1 with the ACC of 0.3g and the MDV of 158.7 mm; (j) Situation 2 with the ACC of 0.3g and the MDV of 222.9 mm; (k) Situation 3 with the ACC of 0.3g and the MDV of 451.3 mm; (l) Situation 4 with the ACC of 0.3g and the MDV of 88.51 mm
(a)
(b)
(c)
(d)
Fig.12 Lateral deformation of the underground structure in different situations. (a) Situation 1; (b)Situation 2; (c)Situation 3; (d) Situation 4
4 Conclusion
1) The soil on the two sides of the bottom is easily liquefied with a large deformation, whereas soil close to the structure and on the two sides has less possibility of being liquefied.
2) The primary liquefaction occurs at the time between 5 and 7 s. The PPR has a sharp increase of 1 or 2 s before the large post-liquefaction deformation occurs.
3) Under the horizontal seismic wave input, the structure manifests a vertical displacement, which is different from the non-liquefied soil that moves mainly horizontally. When liquefied soil is distributed on the two sides of the structure, the movement is the largest under a relatively large earthquake excitation. Vertical movement of the structure is mainly caused by the liquefied soil under the structure.
4) Under the same value of seismic wave input, the differential displacement of the sidewall is the smallest when the liquefied soil is under the structure, while when liquefied soil is on two sides of the structure, the value is the largest. It is, therefore, easier to create differential displacement when liquefied soil is on the two flanks.
[1]Tajiri M. Damage done by the great earthquake disaster of the Hanshin-Awaji district to the Kobe municipal subway system and restoration works of the damage [J].Japanese Railway Engineering, 1997, 36(2): 19-23.
[2]Menkiti C O, Mair R J, Miles R. Highway tunnel performance during the 1999 Duzce earthquake [C]//Proceedings of the 15th International Conference on Soil Mechanics and Geotechnical Engineering. Istanbul, Turkey, 2001: 1365-1368.
[3]Chen Y M, Liu H H, Zhou Y D. Analysis on flow characteristics of liquefied and post-liquefied sand [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1139-1143. (in Chinese)
[4]Holzer T L, Youd T L. Liquefaction, ground oscillation, and soil deformation at the Wildlife Array, California [J]. Bulletin of the Seismological Society of America, 2007, 97(3): 961-976. DOI:10.1785/0120060156.
[5]Chou H S, Yang C Y, Hsieh B J, et al. A study of liquefaction related damages on shield tunnels[J]. Tunnelling and Underground Space Technology, 2001, 16(3):185-193. DOI:10.1016/s0886-7798(01)00057-8.
[6]Berrill J B. A study of high-frequency strong ground motion from the San Fernando earthquake[D]. California: Soil Mechanics Laboratory, California Institute of Technology, 1975.
[7]Liu H B, Song E X. Earthquake induced liquefaction response of subway structure in liquefiable soil [J].Rock and Soil Mechanics, 2005,26: 381-386.DOI:10.3969/j.issn.1000-7598.2005.03.009. (in Chinese)
[8]Liu G L, Song E X, Liu H B. Numerical modeling of subway tunnels in liquefiable soil under earthquakes and verification by centrifuge tests [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(12):1815-1822. (in Chinese)
[9]Liu H B, Song E X. Effects of burial depth on the liquefaction response of underground structures during an earthquake excitation [J]. Journal of Tsinghua University (Science and Technology), 2005, 45(3): 301-305. DOI:10.3321/j.issn:1000-0054.2005.03.008. (in Chinese)
[10]Wang G, Zhang J M, Wei X. Seismic response analysis of a subway station in liquefiable soil [J]. Chinese Journal of Geotechnical Engineering, 2011,33(10): 1623-1627. (in Chinese)
[11]Zhuang H Y, Long H, Chen G X, et al. Seismic responses of surrounding site of subway station in liquefiable foundation [J]. Chinese Journal of Geotechnical Engineering, 2012,34(1):81-88. (in Chinese)
[12]He J P, Chen W Z. The numerical analysis of dynamic characteristics for shallow underground structures in LP field [J]. Chinese Journal of Underground Space and Engineering, 2013, 9(1): 66-72. (in Chinese)
[13]He J P. Study of seismic response of structure on liquefied soil [D].Shandong:School of Civil Engineering, Shandong University, 2012. (in Chinese)
[14]Huo H, Bobet A, Fern ndez G, et al. Analytical solution for deep rectangular structures subjected to far-field shear stresses [J]. Tunnelling and Underground Space Technology, 2006, 21(6): 613-625. DOI:10.1016/j.tust.2005.12.135.
ndez G, et al. Analytical solution for deep rectangular structures subjected to far-field shear stresses [J]. Tunnelling and Underground Space Technology, 2006, 21(6): 613-625. DOI:10.1016/j.tust.2005.12.135.
[15]Comes R C. Numerical simulation of the seismic response of tunnels in sand with an elastoplastic model [J]. Acta Geotech, 2014, 9(4):613-629. DOI:10.1007/s11440-013-0287-7.
[16]He J P, Chen W Z. Numerical experiment of anti-liquefaction measure with gravel stone drainage layer ground underground structure [J]. Rock and Soil Mechanics, 2011,32(10): 3177-3184. (in Chinese)
[17]He J P, Chen W Z. Numerical experiment and analysis for liquefaction in a non-free-field with gravel stone drainage layer around underground structures [J]. Journal of Shandong University (Engineering Science), 2011,41(3): 93-100. (in Chinese)
[18]Chen G X, Zuo X, Wang Z H, et al. Shaking table model test of subway station structure under far field and near field ground motion [J]. Journal of Zhejiang University (Engineering Science), 2010, 44(10): 1955-1961. (in Chinese)
[19]Zuo X, Chen G X, Wang Z H, et al. Shaking table test on ground liquefaction effect of soil-metro station structure under near-and-far field ground motions [J]. Rock and Soil Mechanics, 2010, 31(12): 3733-3740. DOI:10.16285/j.rsm.2010.12.021. (in Chinese)
[20]Popescu R, Prevost J H, Deodatis G, et al. Dynamics of nonlinear porous media with applications to soil liquefaction [J]. Soil Dynamics and Earthquake Engineering, 2006, 26(6):648-665. DOI:10.1016/j.soildyn.2006.01.015.
[21]Madabhushi S P G, Schofield A N. Centrifuge modelling of tower structures on saturated sands subjected to earthquake perturbations [J]. Géotechnique, 1993, 43(4): 555-565. DOI:10.1680/geot.1993.43.4.555.
[22]Liu C X, Tao L J, Bian J, et al. Research on seismic response of the soil and underground structure caused by liquefiable soil in different positions [J]. Journal of Hunan University (Natural Sciences), 2017, 44(5):143-156. DOI:10.16339/j.cnki.hdxbzkb.2017.05.017. (in Chinese)
[23]Liu C X, Tao L J, Bian J, et al. Research on seismic response of underground structure on liquefiable soil[J]. Railway Standard Design, 2017,11(17):133-139. (in Chinese)
[24]Itasca Consulting Group Inc. Fluid-mechanical interaction, fast Lagrangian analysis of continua in 3D dimensions, Version 3.0, user’s manual [M]. Minnesota: Ttasca Consulting Group Inc, 2005:1-180.
[25]Martin G R, Finn W D L, Seed H B. Fundamentals of liquefaction under cyclic loading [J]. Journal of the Geotechnical Engineering Division, 1975, 101(5):423-438.
[26]Byrne P. A cyclic shear-volume coupling and pore-pressure model for sand[C]//Proceedings of the Second International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics. St. Louis, MO,USA, 1991:47-55.
[27]Chen Y M. Study on large deformation test and calculation method of sand liquefaction [D].Nanjing:Institute of Geotechnical Engineering, Hohai University, 2007. (in Chinese)
[28]Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of P.R.C. GB 50909—2014 Code for seismic design of urban rail transit structures[S]. Beijing: China Planning Press,2014:121-122. (in Chinese)
[29]Liu H B, Song E X. Seismic response of large underground structures in liquefiable soils subjected to horizontal and vertical earthquake excitations[J]. Computers and Geotechnics, 2005, 32(4): 223-244. DOI:10.1016/j.compgeo.2005.02.002. (in Chinese)
[30]China Railway Fifth Survey And Design Institute Group Co., Ltd. Geological prospecting report of Metro Line 2 in Taiyuan [R].China: CRCC, 2015. (in Chinese)
[31]Chen Y M, Xu D P. The foundation and engineering examples of FLAC/FLAC3D [M]. Beijing: China Water Power Press,2013:303-305. (in Chinese)
[32]Itasca Consulting Group Inc. Dynamic analysis, fast lagrangian analysis of continua in 3D dimensions, Version 3.0, user’s manual [M]. Minnesota: Ttasca Consulting Group Inc,2005: 1-140.
[33]Koseki J, Matsuo O, Ninomiya Y, et al. Uplift of sewer manholes during the 1993 Kushiro-Oki earthquake[J]. Soils and Foundations, 1997, 37(1): 109-121. DOI:10.3208/sandf.37.109.
[34]Hamada M, Isoyama R, Wakamatsu K. Liquefaction-induced ground displacement and its related damage to lifeline facilities [J]. Soils and Foundations, 1996,36(Special):81-97. DOI:10.3208/sandf.36.special_81.