Let 
be an (n+1)-dimensional pseudo-Riemannian manifold of index 1, i.e. Lorentz space. When the Lorentz space has constant curvature c, we call it a Lorentz space form, denoted by 
with de Sitter space 
and anti-de Sitter space 
Suppose that Mn is a spacelike hypersurface immersed in 
where Mn is said to be spacelike if the metric on Mn induced from that on is positive definite. The spacelike hypersurface with constant scalar curvature or constant mean curvature has been extensively studied in de Sitter space 
anti-de Sitter space 
and the general Lorentz space[3]. It is worth noting that all the above results were obtained for the case where the ambient manifolds possess very good symmetric properties. Furthermore, when is locally symmetric but does not have symmetry in general, many results can be found. For example, Liu et al.[4-5] obtained some rigidity theorems independently for complete noncompact Mn with a constant scalar curvature, where satisfies the following two conditions: Condition 1) For any spacelike vector μ and any time-like vector ν, 
Condition 2) For any space-like vectors μ and ν, 
where c1,c2 are real constants; and 
is the sectional curvature of 
On the other hand, as a natural generalization of hypersurface with constant scalar curvature or with constant mean curvature, the linear Weingarten hypersurface has been extensively studied during the past decades[6-10]. A hypersurface is said to be linear Weingarten if its (normalized) scalar curvature R and its mean curvature H satisfy R=aH+b, where a and b are real constants. Motivated by this observation, Yang[10] extended the theorems in Refs.[4-5] to the linear Weingarten case.
Recently, Wang and Liu[11] investigated the rigidity problems for compact Mn with constant scalar curvature in which satisfies Condition 1) and Condition 3): For any spacelike vectors μ and ν, 
Inspired by the above observations, we continue to study the rigidity for linear Weingarten spacelike hypersurface Mn in where is locally symmetric and satisfies Condition 1) and Condition 3).
1 Preliminaries
Let be a locally symmetric space and Mn be an n-dimensional spacelike hypersurface immersed in For any p∈Mn, we choose a local orthonormal frame e1,e2,…,en+1 in Mn around p such that e1,e2,…,en are tangent to Mn. Let ω1,ω2,…,ωn+1 be the corresponding dual co-frame. We shall use the following standard convention for indices:
1≤A,B,C,…≤n+1, 1≤i,j,k,…≤n
The structure equations of 
are given by
where 
are the components of the curvature tensor of 
Restricting these forms to Mn, we have ωn+1=0. Since 
by using Cartan’s lemma, we have
Let 
be the second fundamental form, the mean curvature vector and the mean curvature of Mn, respectively.
The structure equations of Mn are
The Gauss equations are
(1)
where R is the normalized scalar curvature and 
The Codazzi and Ricci equations are
where the covariant derivative of hij is defined as
Similarly, the components hijkl of the second derivative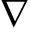 
2h are given as
The Laplacian Δhij of hij is defined as 
By direct calculation, we obtain
=
We then choose a local frame of orthonormal vector fields {ei} such that at p∈Mn,
hij=λiδij
Then it follows, at p, that
(2)
Set φij=hij-Hδij, and it is easy to confirm that φ is traceless and
where φ=(φij) is a real matrix. Moreover, 
=S-nH2≥0 with equality holds if and only if Mn is totally umbilical.
Following Cheng and Yau[12], we introduce the operator W associated with φ acting on any smooth function f by
(3)
Then, setting f=nH in Eq.(3), we obtain
(4)
Lemma 1[13] Let β1,β2,…,βn be real numbers such that 
Then
Moreover,the equality holds if and only if at least (n-1) of βi′s are equal.
Lemma 2[11] Let Mn(n>2) be a spacelike hypersurface immersed in locally symmetric Lorentz space If hijk≥0, then 
Lemma 3[6] Let X be a smooth vector field on the complete non-compact Riemannian manifold Mn, such that divMX does not change sign on Mn, where div represents the divergence operator. If |X|∈L1(M), then divMX=0.
Lemma 4 Let Mn(n>2) be a spacelike hypersurface immersed in locally symmetric Lorentz space which satisfies Condition 1) and Condition 3). Then
where c=2c2+c1/n.
Proof First, we observe that the local symmetry of implies that 
thus
(5)
Since satisfies Condition 1) and Condition 3),
(6)
2nc2(S-nH2)
(7)
Then the lemma can be proven easily by substituting Eqs.(5) to (7) into Eq.(2).
Lemma 5[14] Let Mn be a linear Weingarten spacelike hypersurface immersed in locally symmetric Lorentz space with 
Then L=W+((n-1)aΔ/2) is elliptic.
Lemma 6 Let Mn(n>2) be a spacelike hypersurface immersed in locally symmetric Lorentz space which satisfies Condition 1) and Condition 3) with hijk≥0 and R=aH+b. Then
(8)
where c=2c2+c1/n.
Proof First, we obtain from Eq.(1) that
(9)
Since is locally symmetric, 
is a constant[10]. Substituting Eq.(9) into (4), we have
(10)
Applying Lemmas 2 and 4 to Eq.(10), we obtain
(11)
Let μi=λi-H, we can obtain
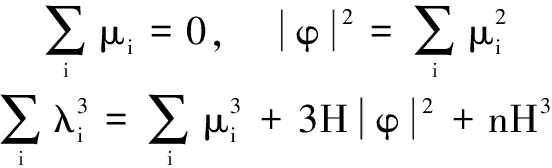
Using Lemma 1, we obtain that
(12)
Substituting (12) into (11), we have
L(nH)≤ nc+(+nH2)2-n2H4-
2 Main Results
Theorem 1 Let be a locally symmetric Lorentz space which satisfies Condition 1) and Condition 3). Suppose that Mn(n>2) is a compact linear Weingarten spacelike hypersurface immersed in with hijk≥0. If 
then either S=nH2 or 
When S=nH2, Mn is totally umbilical. When 
Mn has two distinct principle curvatures, one of which is simple.
Proof First, we consider the quadratic form
By using the orthogonal transformation
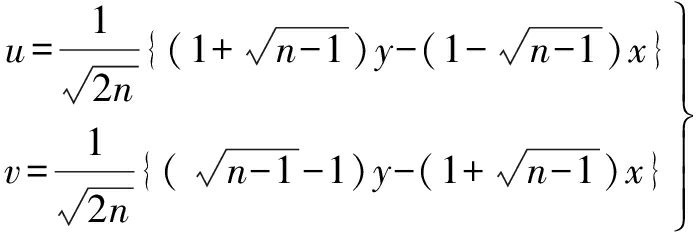
We obtain that
Set 
It is not difficult to verify that u2+v2=x2+y2=+nH2=S. Then
(13)
Substituting(13) into (8), we obtain
(14)
On the other hand, since L is self-adjoint and Mn is compact,
(15)
Then, from (14), (15) and we obtain that
If 
then ≡0 and Mn is totally umbilical. If 
then all the above inequalities become equalities. Especially, when equality in Lemma 1 holds, we then obtain that Mn has two distinct principle curvatures, one of which is simple.
Furthermore, when Mn is complete noncompact, we have the following extension of Theorem 1.
Theorem 2 Let be a locally symmetric Lorentz space which satisfies Condition 1) and Condition 3). Suppose that Mn(n>2) is a complete noncompact linear Weingarten spacelike hypersurface immersed in with hijk≥0. If H can attain the maximum on Mn and 
then either S=nH2 or 
When S=nH2, Mn is totally umbilical. When 
Mn has two distinct principle curvatures, one of which is simple.
Proof According to the proof in Theorem 1, we obtain
Due to the fact that 
we can immediately conclude that
(16)
Noting that L is elliptic and H attains its maximum on Mn, by using the maximum principle, we can obtain that H is a constant. Consequently,
Hence,λi is constant for each i=1,2,…,n. Furthermore, L(nH)=0 and we obtain from (16) that
(17)
By using the same argument as in Theorem 1, the proof can be completed easily.
Remark 1 Since S is bounded, H is bounded as well. Then H can attain its maximum on Mn since hijk≥0. Hence, the assumption that H can attain the maximum on Mn in Theorem 2 can be removed. So, the main difference between Theorem 2 and Theorem 1.6 in Ref.[10] lies in the assumption that sup H is attained at some points or not.
If the metric and Ricci tensors of a Lorentz space are homotetic[15], we call it Einstein spacetime. For the spacelike hypersurface in Einstein spacetime, we have the following result.
Theorem 3 Let be a locally symmetric Einstein spacetime which satisfies Condition 1) and Condition 3). Suppose that Mn(n>2) is a complete non-compact linear Weingarten spacelike hypersurface immersed in with |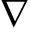H|∈L1(M), where L1(M) represents the space of Lebesgue integrable functions on Mn. If 
then either S=nH2 or When S=nH2, Mn is totally umbilical. When Mn has two distinct principle curvatures, one of which is simple.
Proof According to Ref.[15], we have
L(nH)=divM(P(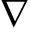H))
where 
and I denotes the identity operator. Furthermore, since 
and nH2≤S, both H and A are bounded on Mn. Hence, the operator P is bounded. Then, from |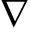H|∈L1(M), we obtain that
|P(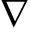H)|∈L1(M)
(18)
Thus, from (16), (18) and Lemma 3, we obtain that L(nH)=0. By using the same argument as in Theorem 2, the proof is completed easily.
Remark 2 The Lorentz space form satisfies both Condition 2) and Condition 3), where-c1/n=c2=c.
References
[1]Zhang S. Stability of spacelike hypersurfaces in de Sitter space [J]. Proceedings of the American Mathematical Society, 2015, 143(2): 851-857.
[2]Chu Y W, Zhai S J.On spacelike hypersurfaces with constant scalar curvature in the anti-de Sitter space[J].Differential Geometry and Its Applications,2011,29(6):737-746. DOI:10.1016/j.difgeo.2011.08.002.
[3]Zhang S C. Rigidity theorem for complete spacelike hypersurfaces with constant scalar curvature in Lorentz spaces[J].Israel Journal of Mathematics,2011,189(1):177-188. DOI:10.1007/s11856-011-0155-9.
[4]Liu J, Wei L. A gap theorem for complete space-like hypersurface with constant scalar curvature in locally symmetric Lorentz spaces [J]. Turkish J Math, 2010, 34(1): 105-114.
[5]Zhang S C, Wu B Q. Rigidity theorems for complete spacelike hypersurfaces with constant scalar curvature in locally symmetric Lorentz spaces[J].Journal of Geometry and Physics,2010,60(2):333-340. DOI:10.1016/j.geomphys.2009.10.005.
[6]Aquino C P, de Lima H F. On the geometry of linear Weingarten hypersurfaces in the hyperbolic space[J].Monatshefte für Mathematik,2013,171(3/4):259-268. DOI:10.1007/s00605-013-0476-3.
[7]Chao X L,Wang P J.Linear weingarten hypersurfaces in riemannian space forms[J].Bulletin of the Korean Mathematical Society,2014,51(2):567-577. DOI:10.4134/bkms.2014.51.2.567.
[8]Wang P J, Chao X L. Linear Weingarten submanifolds in unit sphere[J].Archiv der Mathematik,2016,106(6):581-590. DOI:10.1007/s00013-016-0881-7.
[9]Chao X L, Wang P J. Linear Weingarten hypersurfaces in locally symmetric manifolds[J].Hokkaido Mathematical Journal,2017,46(1):29-40. DOI:10.14492/hokmj/1498788095.
[10]Yang D. Linear Weingarten spacelike hypersurfaces in locally symmetric Lorentz space [J].Bulletin of the Korean Mathematical Society,2012,49(2):271-284. DOI:10.4134/bkms.2012.49.2.271.
[11]Wang Y N, Liu X M. Compact space-like hypersurfaces with constant scalar curvature in locally symmetric Lorentz spaces[J].Archivum Mathematicum,2012(3):163-172. DOI:10.5817/am2012-3-163.
[12]Cheng S Y,Yau S T.Hypersurfaces with constant scalar curvature[J].Mathematische Annalen,1977,225(3):195-204. DOI:10.1007/bf01425237.
[13]Okumura M.Hypersurfaces and a pinching problem on the second fundamental tensor[J].American Journal of Mathematics,1974,96(1):207. DOI:10.2307/2373587.
[14]de Lima H F, de Lima J R. Complete linear Weingarten spacelike hypersurfaces immersed in a locally symmetric Lorentz space[J].Results in Mathematics,2012,63(3/4):865-876. DOI:10.1007/s00025-012-0237-y.
[15]de Lima H F,de Lima J R.Characterizations of linear weingarten spacelike hypersurfaces in einstein spacetimes[J].Glasgow Mathematical Journal,2013,55(3):567-579. DOI:10.1017/s0017089512000754.
is investigated, where the (normalized) scalar curvature R and mean curvature H of Mn satisfy R=aH+b, and a,b are real constants. First, an estimate of the upper bound of the function L(nH) is given, where L is a second-order differential operator. Then, under the assumption that the square norm of the second fundamental form is bounded by a given positive constant, it is proved that Mn must be either totally umbilical or contain two distinct principle curvatures, one of which is simple. Moreover, a similar result is obtained for complete noncompact spacelike hypersurfaces in locally symmetric Einstein spacetime. Hence, some known rigidity results for hypersurface with constant scalar curvature are extended for the linear Weingarten case.
中类空超曲面