Recently, mobile cloud computing (MCC) has been a great paradigm that combines wireless network service and cloud computing to enable mobile terminals (MTs) to take advantage of the abundant wireless resource and vast computation power ubiquitously[1-2]. With the emergence of more sophisticated applications, MTs expect to offload partial computing modules to be dealt with by the cloud service due to the limited battery power and smaller computing capabilities, which may impede the performance of service quality extremely[3]. However, the MCC introduces high latency since application data is sent to powerful servers which are distant from the MTs. Mobile edge computing (MEC) is widely regarded as a promising solution to address the problem. In terms of network topology, the computing or storage resources of the MEC are supposed to be in proximity of the MTs[4]. The MEC server is typically collocated with a base station in a network cell, and it is accessible to nearby MTs via a one-hop wireless connection[5]. In spite of its physical closeness to the MTs, the MEC server faces the drawback of limited computation resources.
The wireless networks are confronted with many challenges due to their limited radio and backhaul communications capabilities. The previous signal processing and transmission techniques applied in the conventional cellular networks may not be efficient enough to meet the above requirements[6]. The deployment of low-cost small cells is a very promising approach for efficient frequency reuse and spectrum sharing[7]. Small cells with a small coverage area and low transmission power usually include microcells, picocells, femtocells and relays. Heterogeneous networks (HetNets), which consist of numerous small cells and the traditional macro cells, meet MTs’ high-rate requirements. Therefore, in the scenario of offloading tasks to the MEC server, there is competition among numerous MTs over both constrained communication resources in HetNets and limited computation resources in the MEC[8].
In this paper, a joint cloud and wireless resource allocation scheme based on the evolutionary game (JRA-EG)is proposed for overlapping HetNets in mobile edge computing environments to satisfy MTs’ offloading requirements and reduce MTs’ cost. The main contributions of this paper are listed as follows. First, in the scenario of MEC, overlapping HetNets are considered. One base station and one MEC server configured on it constitute a service provider. Due to the differences in the capacity of wireless and cloud resources for different SPs, dynamic SP selection is included in this paper. Secondly, to measure the MTs’ cost for task offloading in MEC environments, the cost function is established, which consists of not only the energy consumption and time delay, but also the monetary cost. MTs with tasks offloading requirements in one service area form a population. In addition, different populations form a non-cooperative game. Thirdly, an evolutionary game is built to model the service provider selection and resource allocation of MTs. Centralized and distributed algorithms are used to obtain the EE of the JRA-EG game model, respectively. Simulation results indicate that both the centralized algorithm and distributed algorithm can reach the EE rapidly. The differences between them are the convergence speed and trajectory stability. Compared with the existing schemes, the JRA-EG scheme can save more energy and has less time delay when the data size becomes larger.
1 System Model
1.1 Network model
In the mobile edge computing scenario, the HetNets are composed of one macro base station (MBS) and K small base stations (SBS). Each base station (BS) connects to a data center named cloudlets, which provide computation resources. The MBS and the corresponding cloudlets constitute the macro service provider (MSP). A SBS and the corresponding cloudlets form a small service provider (SSP). As shown in Fig.1, K SSPs are overlaid with one MSP, providing communication and computation services to Ⅰ MTs in a particular area of a two-tier cellular network. The set of MSP and SSPs is denoted as K={0,1,2,...,K}, in which 0 represents the MSP and {1,2,...,K} denotes the SSPs. Orthogonal wireless sub-channels which have no interference with each other are allocated to the macro cell and small cells. Moreover, there are J service areas denoted as J={1,2,...,J}. Area 1 is only covered by the macro cell network. Area j∈{2,3,...,J} is covered by a macro cell and several small cells. The number of MTs in area j is denoted as Nj, 
In the model, a MT with multiple radio transceivers is capable of connecting to different service providers (SP). However, this model assumes that the user can only select one SP for wireless transmission, resource scheduling and task offloading on a mission. In addition, the mobility of MTs is not considered.
For each MT, the tasks are characterized as (di,bi). di is the number of instructions to be executed and bi is the input data size required to be transferred. Tasks of MT i must be completed within 
which is the maximum time delay that does not impact MTs’ experience.
For base stations, the available spectrum bandwidth of BS k is Wk. The bandwidth of each BS is averaged and allotted to all MTs connected to it. Considering the difference of BSs, the MTs are capable of acquiring different bandwidth by choosing different BSs. Moreover, the number of MTs connecting to BS k is denoted as nk.
Cloudlets can deal with tasks from all MTs connecting to them concurrently due to their multi-tasking capability. In order to get the utmost use of computation resources, cloudlets allocate all resources they have to the MTs according to a fair formula. Cloudlets of BS k are capable of handling Fk instructions per unit time and tasks of MT are allocated to Fk/nk instructions.
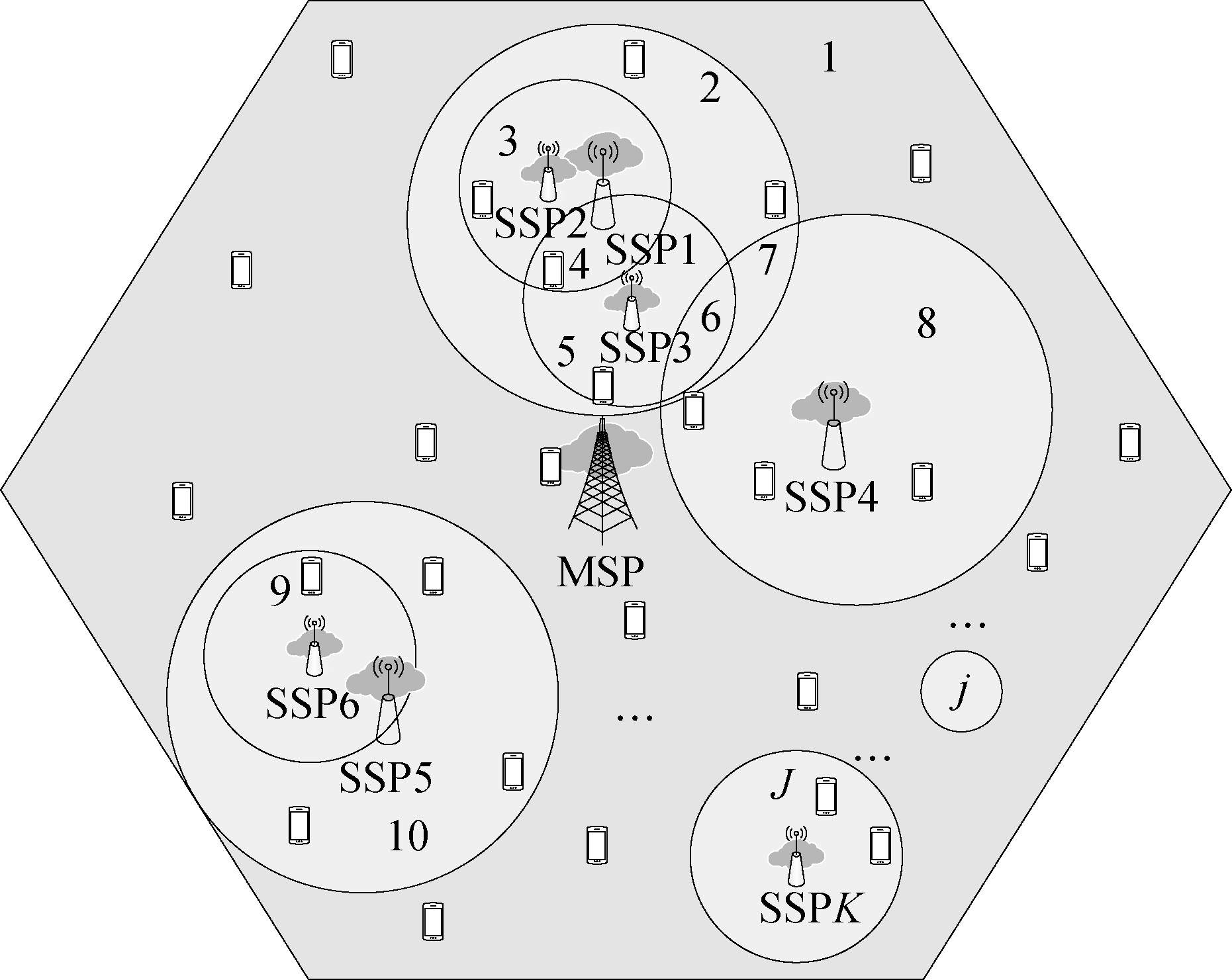
Fig.1 Overlapping HetNets in mobile edge computing environment
1.2 Communication model
Orthogonal sub-channels are allocated to the MTs of macro and small cells. Therefore, there is no interference with each other. Specifically, the channel between each base station (BS) and its associated MTs experiences a fixed distance path-loss, a slow lognormal shadowing and Rayleigh fast fading. It is assumed that there is no power control and an adaptive multilevel quadrature amplitude modulation (M-QAM) is applied. Each BS assigns rate dynamically according to the received signal to noise ratio (SNR) per MT. Assuming the identical statistics over all frequency sub-channels and using adaptive modulation with L discrete rates, the long-term expected throughput (in bit/(s·Hz)) is expressed as[9]
(1)
where l∈{1,2,...,L} and [Γl,Γl+1) denotes the interval of SNR.
It is assumed that both SBSs and MBS schedule their MTs in a round robin (RR)[10]. In this situation, all the MTs subscribed to the same SP share the long-term expected throughput equally which is straightforward for the RR scheduling algorithm. ηk denotes the throughput for BS k. Hence, the expected throughput Rk for the MT subscribing to BS k can be calculated as Rk=(Wkηk)/nk.
1.3 Computation model
The task offloading time delay 
consists of four parts[11]： the uplink communication delay 
downlink delay 
backhaul link delay 
and cloud task processing delay 
The backhaul link rate between BS and Cloudlets is so high and the distance between them is so short that is too small to be considered. Compared with input data size bi, the output data size from cloudlets is small, so the downlink delay 
is regarded as constant ξ.
In addition, 
is given as 
and 
is defined as 
where ri=Rk=wiηk and fi=Fk/nk if MT i selects SP k. wi is defined as Wk/nk since MT i selects SP k. Hence, the time delay can be also written as
(2)
The energy consumption 
of MT i including uplink and downlink energy consumption is
(3)
where pi represents the transmission power of MT i. Note that there is no power control so that pi is fixed. 
denotes the received power of MT i when it receives the output data.
The monetary cost of MT i consists of two parts. The first part is the communication cost and the second part is the computation cost. qk and gk are the price per unit transmission rate and the charge per unit computation resources of SP k, respectively.
Ci(fi,wi)=qkwiηk+gk fi
(4)
According to Eqs.(2) to (4), the overhead of the mobile edge computing approach in terms of time delay, energy consumption and monetary cost can be computed as
(5)
where 
is the impact factor of overtime cost and 
represents the impact factor of energy consumption on the strategy of MT. In addition, the impact factor of monetary cost is denoted as 
The MTs in the same service area cooperate with each other and different service areas compete for the cloud and wireless resources of SPs. The object function of joint cloud and wireless resource allocation is
∀i∈I
(6)
The objective of Eq.(6) is to minimize all MTs’ overhead in the HetNets under the latency constraints.
2 Evolutionary Game Formulation
The joint cloud and wireless resource allocation problem is modeled by taking advantage of a dynamic evolutionary game. Solution refinement and bounded rationality as well as dynamics are the remarkable characteristics of the evolutionary game[12]. Solution refinement ensures the existence and uniqueness of EE. Bounded rationality refers to the fact that players can slowly change their strategies to achieve the EE solution, which is specifically adjusted to the time-varying performance satisfaction. Due to the fact that the communication and computation capacity of each SP is limited, MTs at the different service areas, which are geographically separated, compete to share the available bandwidth and CPU cycles. Here, an evolutionary game is used since it can capture the dynamics of SP selection (i.e., strategy adaptation) based on the available information of the MTs.
An evolutionary joint cloud and wireless resource allocation game (JRA-EG) 
is formulated. I={1,2,...,I} represents the game players. ai is the SP selection strategy of player i. 
is defined as the cost function of MT i that selects SP k in population j.
● Players For a particular service area as shown in Fig.1, each MT in each service area which can choose multiple SPs including MSP and SSPs, is a player of the game. Note that the MTs which can connect only to one SP are not involved in the game.
●Population The population in this evolutionary game refers to the set of MTs in the same service area. The number of populations is J.
●Strategy The strategy of each MT refers to the selection of SP. Accordingly, the SP selection strategy set can be denoted as K={0,1,2,...,K} which refers to the selection of the MSP and K SSPs. sj, which denotes the SP selection strategy set of population j, is the subset of K. The MT i in population j selects SP strategy ai from sj. S is a J×(K+1) SP selection state matrix of all populations. Matrix S is composed of elements 0 and 1, where S[j,k]=0 shows that SP k cannot be connected and S[j,k]=1 shows that SP k is accessible.
●Population 
denotes the number of MTs selecting strategy SP k in population j. Then, 
is the population share of SP k in population j, where 
●Population state The population state is denoted as a vector 
where X is the population state space which contains all J populations. Here 
●Cost function The cost is the expected consumption of a player choosing a certain SP selection strategy. The cost of a player is determined by energy consumption, delay cost and monetary cost.
To obtain the cost, the cost function is used to quantify MTs’ consumption on tasks offloading. For a particular population j, the cost of a MT choosing SP k can be expressed as
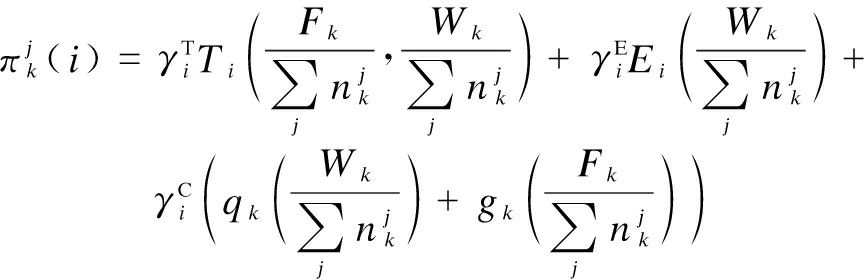
(7)
where 
and 
If MT i connects to SP k, fi=fk and wi=wk.
It is assumed that MTs in population j are requested to offload the identical task load and have the same requirement for impact factor in a task offloading. Therefore, the MTs in a population have an identical task offloading characteristic. Therefore, 
can be simplified as
(8)
The cost, communication resource allocation and computation resource allocation depend on all MTs’ SP selection strategies in terms of the population state as well as the strategies of the SPs.
The definition of EE is as follows.
Definition 1 EE of the game G is a strategy profile 
such that for each player i in I, 
ai∈sj if MT i is in population j. 
is the optimal strategy set except MT i.
The population state space X* can be derived by a*. Therefore, the population state space X* is regarded as EE.
3 Centralized Algorithm for JRA-EG
In this section, the centralized algorithm based on replicator dynamics is introduced.
3.1 Centralized algorithm formulation
In the dynamic evolutionary game, an individual from a population, who is able to replicate itself by the process of mutation and selection, is called a replicator[12]. In this case, a replicator with a lower cost can reproduce itself faster. The replicator process can be modeled by using a series of ordinary differential equations, which is called replicator dynamics. The proposed centralized algorithm based on replicator dynamics provides a method to acquire the population information of others and converges towards an equilibrium selection. The centralized algorithm is also efficient to investigate the speed of convergence of strategy adaptation required to reach a stable solution in the game[10].
We consider an evolutionary game of SP selection in a heterogeneous wireless network where the population of MTs in area j can choose the available MSP and SSPs. The speed of the MT in observing and adapting the SP selection is controlled by gain parameter σ,σ>0. In the game model, the aim of each MT is to minimize its cost. Hence, we can formalize the replicator dynamics as
(9)
where 
is the current cost of the individuals choosing strategy k in population j; 
is the average cost of population j, and σ is the gain parameter for the rate of strategy adaptation. The growth rate 
is relevant to the difference between the cost and the population’s average cost 
as well as the current size of population share 
The average cost of the population can be derived as
(10)
Based on this replicator dynamics of the MTs in population j, the number of MTs choosing SP k increases if the cost is below the average cost. It is impossible for a MT to choose SP k, which provides a higher cost than the current cost. This replicator dynamics satisfies the condition of 
Therefore, if 
then 
3.2 Centralized algorithm design
In the initial phase, all MTs randomly choose one SP from the SP selection strategy sets and the centralized controller computes the initialized population state matrix. Then, each SP allocates communication and computation resources on average according to the number of MTs connected to it. Next, MTs compute individual offloading cost and send it to the centralized controller. The centralized controller computes the average offloading cost of every population. There is a double circulation in the cycle phrase. The algorithm is executed iteratively and each episode consists of population state matrix updating, resource assignment updating, offloading cost updating and information exchanging. Finally, EE is derived when the MTs in each population have the identical offloading cost.
Algorithm 1 Centralized algorithm
Input: I, K, J, Nj, cycle index l and error factor ζ.
Output: The population state space of EE X*.
for all i=1 to I do
MT i in population j randomly choose SP k from sj.
end for
The controller computes the population state vector xj.
Each SP acquires nk and allocates wk and fk on average.
Computes 
by Eq.(8) and 
by Eq.(10).
<ζ,∀j)
for all j=1 to J do
Computes 
by Eq.(9) and update 
for all populations.
Each SP acquires nk and allocates wk and fk on average
Computes by Eq.(8) and by Eq.(10)
end for
end while
Evolutionary equilibrium X* is derived.
4 Distributed Algorithm for JRA-EG
When a centralized controller is unavailable, each MT has to evolve its SP selection decision gradually and independently. The reinforcement learning approach can reach the target by analyzing the surrounding environment. In this case, a Q-learning algorithm[13-14], which is a type of reinforcement learning, is applied to the solve the JRA-EG problem.
4.1 Distributed algorithm formulation
In this section, a distributed algorithm for JRA-EG based on Q-learning is formulated. In the distributed algorithm, complete cost information of other MTs in the same or different populations is no longer required for SP selection due to the learning ability. The distributed algorithm acquires the EE of the evolutionary game by Q-value.
For the distributed algorithm, ai∈sj is the current selection strategy state of MT i in population j. ui is the control state for MT i in population j which is the subsequent selection strategy of MT i.
The subsequent state of ai is denoted as
(11)
where l denotes the evolutionary times, and l=0 denotes the initial state. For all MTs in all populations, the current selection strategy state vector al can be denoted as 
The control vector can be denoted as 
For MT i, the selection strategy 
at time l is chosen from sj if MT i belongs to population j. 
is the subsequent selection state of MT i from sj.
The distributed algorithm acquires the EE of the evolutionary game by the Q-value. The Q-value is used to maintain the knowledge of MTs about each SP, and the decision can be made by MT i based on the Q-value. In Section 2, we have assumed that the MTs in population j are requested to offload the identical task load and have the same requirement for the impact factor in a task offloading. Therefore, the Q-value of MTs in the same population j selecting the same SP k is identical. The MTs in population j share the Q-value vector Q[j,k], k∈K. Therefore, the dimension of Q-value is J×(K+1) since there are J populations and K+1 SPs. If population j cannot connect to SP k, Q[j,k] is identically equal to zero. The distributed algorithm starts with Q0=[0]J×(K+1).
For iteration times t=0,1,2,,..., the distributed algorithm updates the iterative Q-value using the learning rate λt by
(12)
where t is the iteration times of the Q-value; λ is the learning rate, 0≤λt<1; and θ is the discount factor, 0<θ≤1; Qj is the 1×(K+1) row vector; and πj(al,ul) denotes the cost vector of population j. πj(al,ul) can be derived by
(13)
can be computed by 
according to Eq.(7) and Eq.(8). Here, 
means that MT i selects SP k. wk and fk can be computed as wk=Wk/nk and fk=Fk/nk, where 
denotes the number of all MTs who select SP k.
Let 
be the initial state. Assume that there is a feedback control 
on compact set 
is computed by
(14)
Then, the subsequent SP selection strategy 
is obtained.
All populations update the iterative Q-value by
Qt+1(al,ul)= (1-λt)Qt(al,ul)+
(15)
where Q and π(al, ul) are J×(K+1) matrices.
Finally, the optimal SP selection strategy 
and optimal control vector 
are obtained and then the optimal resource allocation is obtained when the Q-value converges. The Q-value converges to
(16)
The convergence property of the distributed algorithm is associated with learning rate λt. Once Q* converges, the EE of JAR-EG is obtained. Theorem 1 describes the convergence condition.
Theorem 1 For t=1,2,..., let Qt(al,ul) be updated by Eq.(15). If λt,t=1,2,..., satisfies
(17)
and θ satisfies 0<θ≤1, then the iterative Q-value Qt(al,ul) converges to its optimal value as t→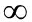
, that is 
Proof The proof is similar to that in Ref.[13].
After the Q-value converges, the evolutionary game reaches the evolutionary equilibrium 
and X*.
4.2 Distributed algorithm design
In the distributed algorithm, all MTs need to compare the current Q-value with other strategies’ Q-values and adjust their selection strategy by themselves.
The initialization is similar to the centralized algorithm.Different from the centralized algorithm, the algorithm imports Q-learning rate, discount factor, learning possibility and Q-value. In the cycle phrase, there are three circulations. In each episode, the resource allocation, SP selection strategy, offloading cost and Q-value are updated. Unlike the centralized algorithm, every individual needs to utilize the Q-value to learn the change of the entire network. The algorithm does not stop until the Q-value matrix of each MT is identical.
Algorithm 2 Distributed algorithm
Input: I,λ,θ, error factor ζ.
Output: Population state space of EE X*.
for all i=1 to I do
MT i in population j randomly chooses SP k from sj.
end for
Each SP acquires nk and allocates wk and fk on average.
Computes π(al,ul) by Eq.(13) and Q by Eq.(15).
<ζ,∀j)
for all j=1 to J do
for all i=1 to Nj do
rand=rand() is a random number between 0 and 1.
if (rand≤ρ)
MT i randomly chooses SP k from sj.
else
MT i chooses SP by Eq.(11) and Eq.(14).
end if
Each SP acquires nk and allocates wk and fk averagely for MTs.
Computes π(al,ul) by Eq.(13) and Q by Eq.(15).
end for
end for
end while
Evolutionary equilibrium X* is derived.
5 Performance Analysis and Evaluation
5.1 Parameter settings
The simulation scenario is described in Fig.1. We regard HetNets with one MSP and four SSPs, K=4. So, the SP strategy set is K={0,1,2,3,4}. We set the number of population J=2K and the number of MTs in population j is randomly distributed between 0 and 100. The bandwidth and processing ability of SPs are respectively set to be W=[200,80,80,80,80] Hz and F=[80, 40, 40,40, 40] 109 cycles. The throughput of BSs is set to be η=[1.5,2,2,2,2] bit/(s·Hz) and the transmission power of MTs is p=[10,5,5,5,5] mW. The price for communication resources is [0.5, 0.1, 0.1, 0.1, 0.1] dollar/MHz. The charge for computation resource is 0.1 dollar/(106cycles). For the distributed algorithm, the discount factor is set to be θ=0.98[13] and the learning possibility ρ=0.1[12].
5.2 Performance evaluation of JRA-EG scheme
The impact of gain parameter σ on the convergence speed of the centralized algorithm is shown in Fig.2. The curves for different numbers of MTs in the whole service areas describe the changing trends of running time with increasing σ. We observe that the time to reach equilibrium becomes shorter with the increase in σ when σ<0.01, which implies that the convergence speed keeps increasing. The changing trends of convergence speed flatten out when σ>0.01. However, the running time to reach the EE becomes unstable when the gain parameter σ>0.035. This is because the growth rate 
of population share is too fast to find the EE. Throughout the analysis above, we can use the gain parameter σ∈[0.01,0.035] in the simulation.
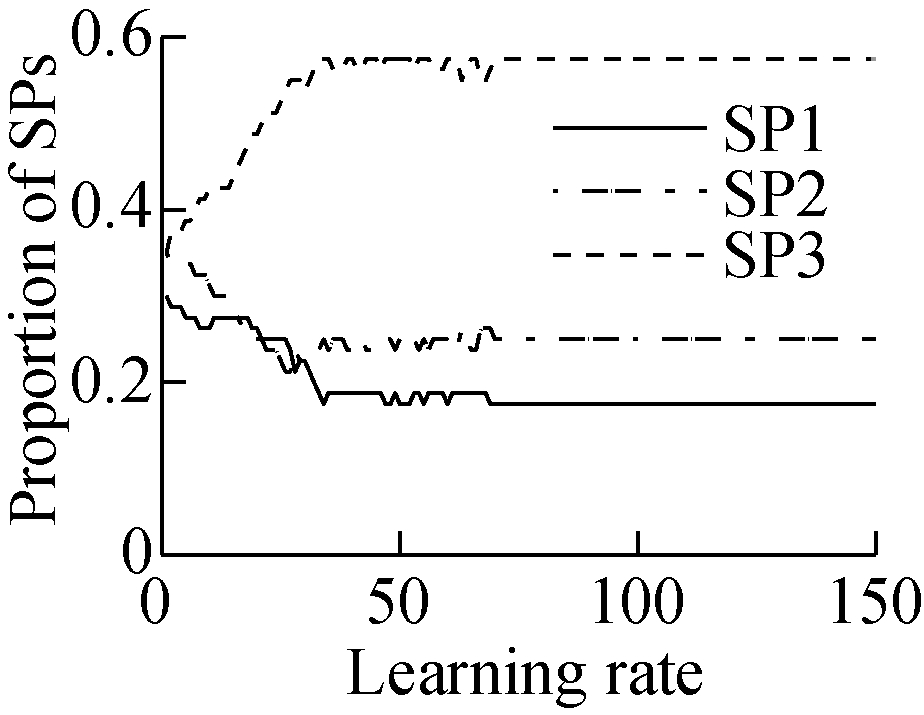
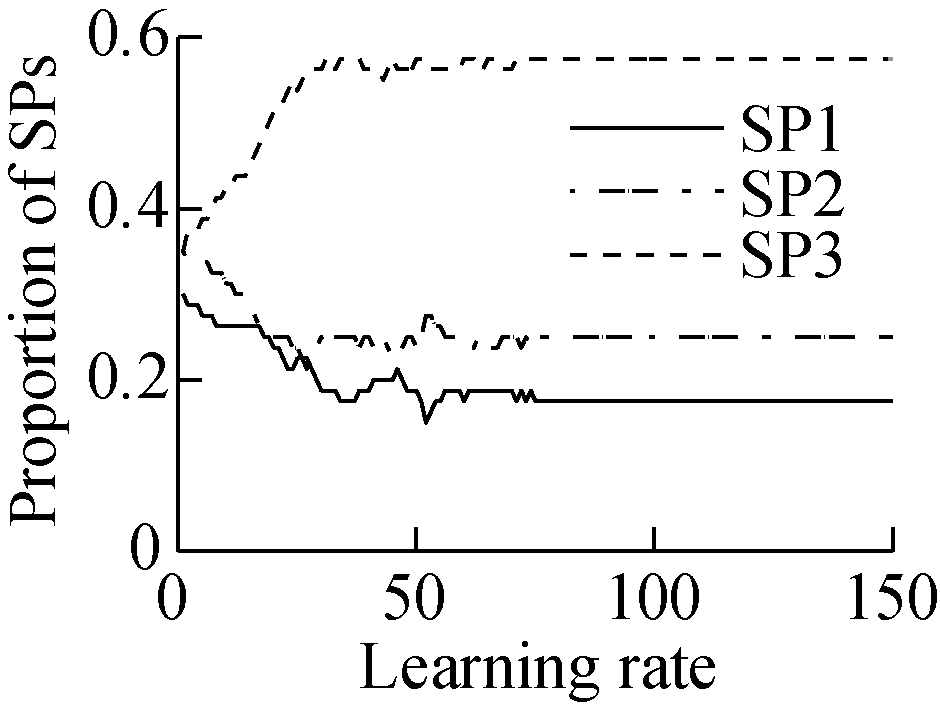
In order to study the impact of the learning rate in the distributed algorithm, we set the learning rate 
to be four different functions, 
and 
respectively. The four learning rate functions all satisfy the convergence criterion Eq.(17). From Fig.3 we can see that with four different learning rates 
the iterative population shares are all convergent to the optimal value. In comparison with Fig.3, we can see that the fluctuation of the convergence curves of 
and 
are slightly smaller than that of 
However, the convergence curve shows a wide fluctuation for 
when finding the equilibrium point. The reason is that the value of the learning rate is very small at the beginning, resulting in the MTs choosing SP randomly(see Fig.3(d)).
In Fig.4, the population evolution algorithm, centralized algorithm and distributed algorithm are compared. In Refs.[12,15-16], a population evolution algorithm is used to achieve the EE. The population evolution algorithm not only relies on the centralized controller to collect population cost information, but also depends on each MT when comparing individual cost with the average cost of the population it belongs to. From Fig.4, we can conclude that the convergence speed of the centralized algorithm is the fastest and that of the distributed algorithm is the slowest. Besides, the curve of the centralized algorithm approach is smooth and steady while the other two algorithms fluctuate with the increase in iteration times until reaching equilibrium. The population evolution algorithm and the distributed algorithm change the population state individually so that the changing speed is inconsistent among the loop episodes. Compared with the population evolution algorithm, the centralized algorithm has a faster equilibrium speed while the distributed algorithm has no requirement for population information exchange. To sum up, both the centralized and distributed algorithms can reach EE rapidly and have their respective advantages.
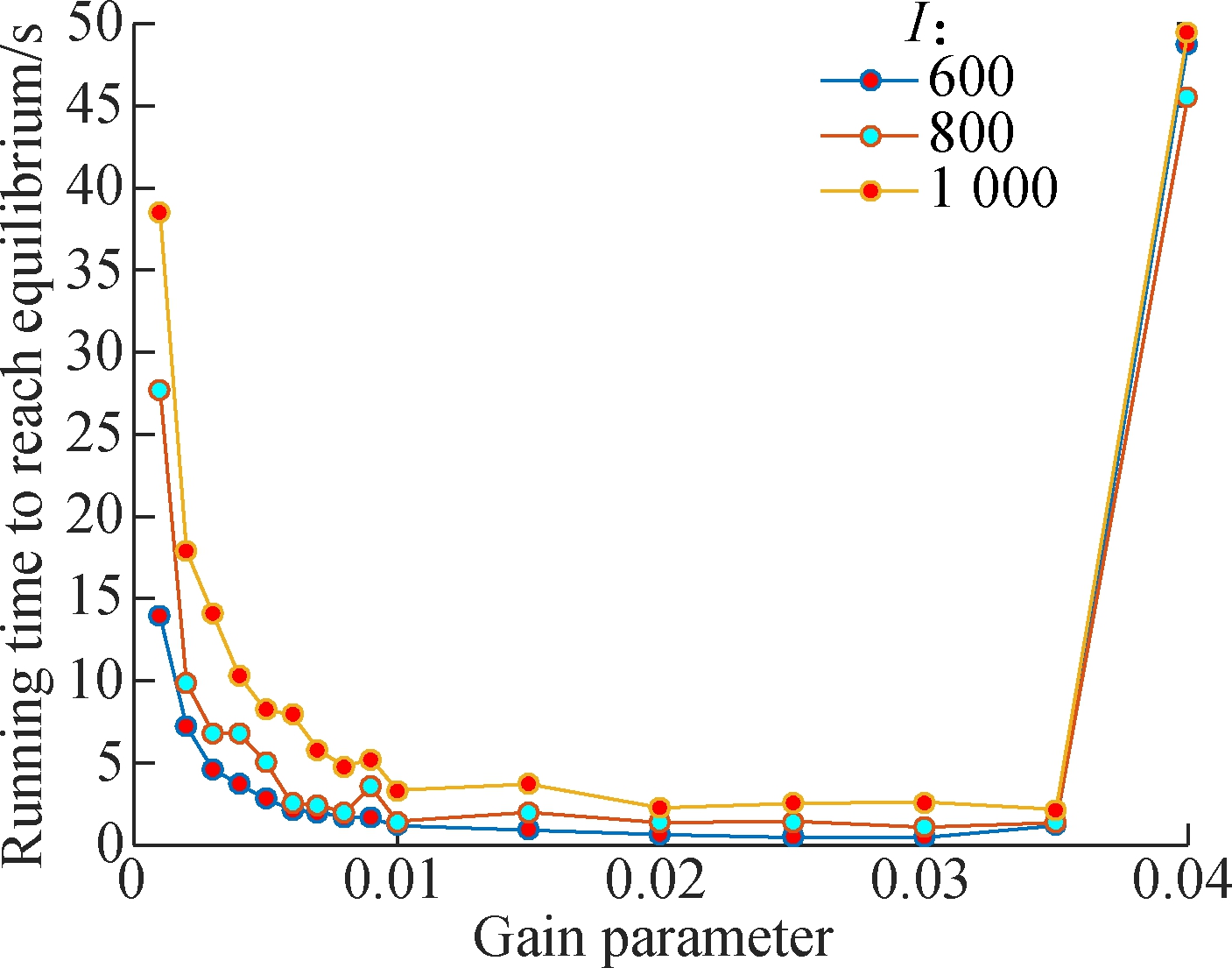
Fig.2 Equilibrium time with different gain parameters in the centralized algorithm
(a)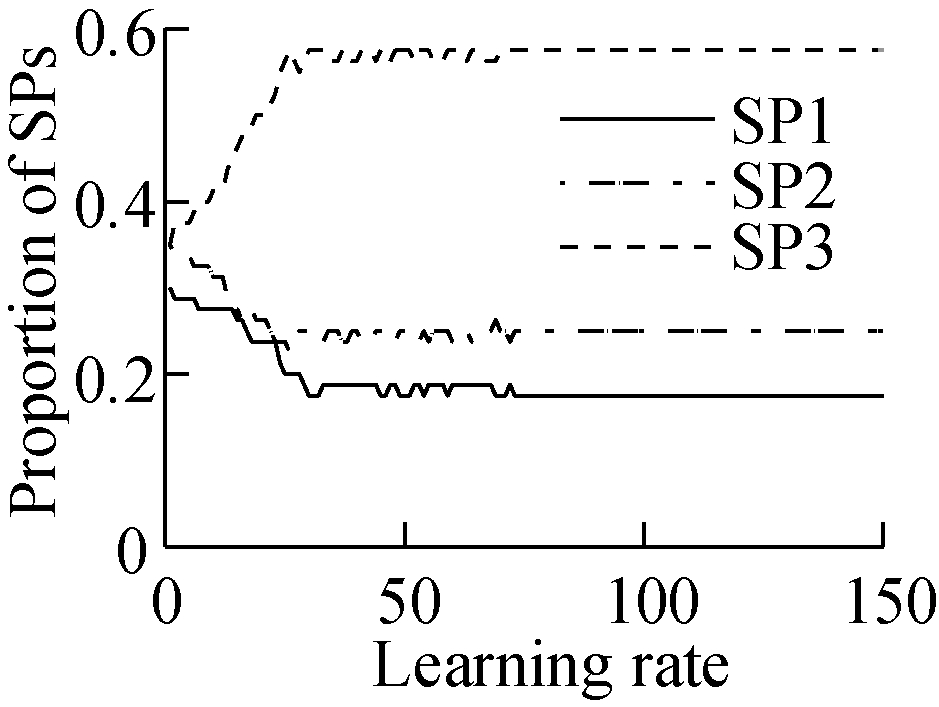
(b)
(c)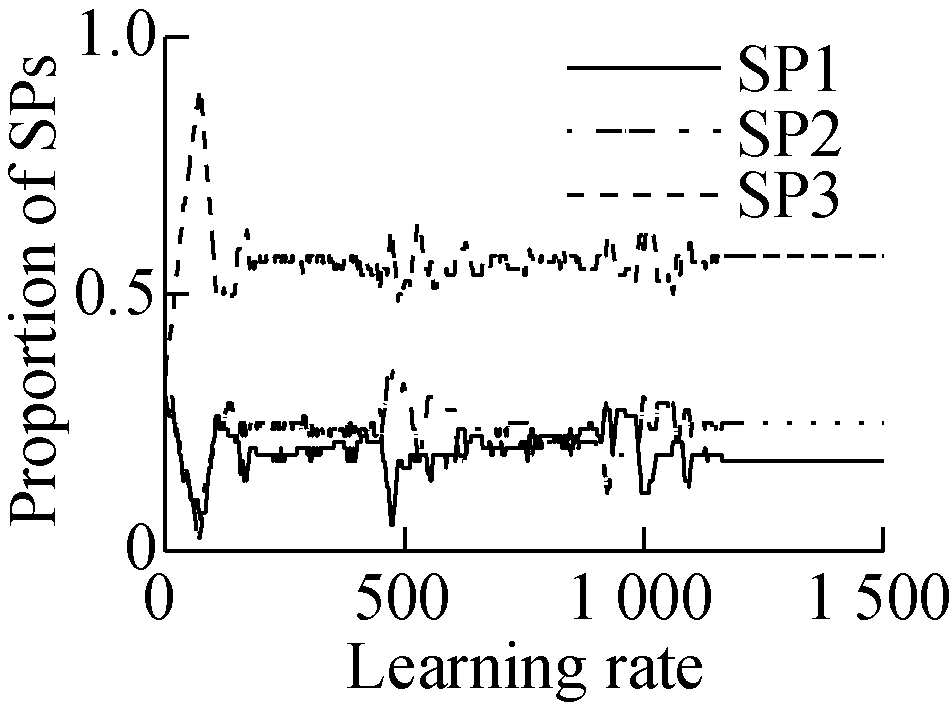
(d)
Fig.3 The effect of the learning rate in the distributed algorithm.
(a) λ=0.7; (b) λ=1-1/(t+1); (c) λ=0.5(sin(t+1)+1); (d) λ=0.5(cos(t+1)+1)
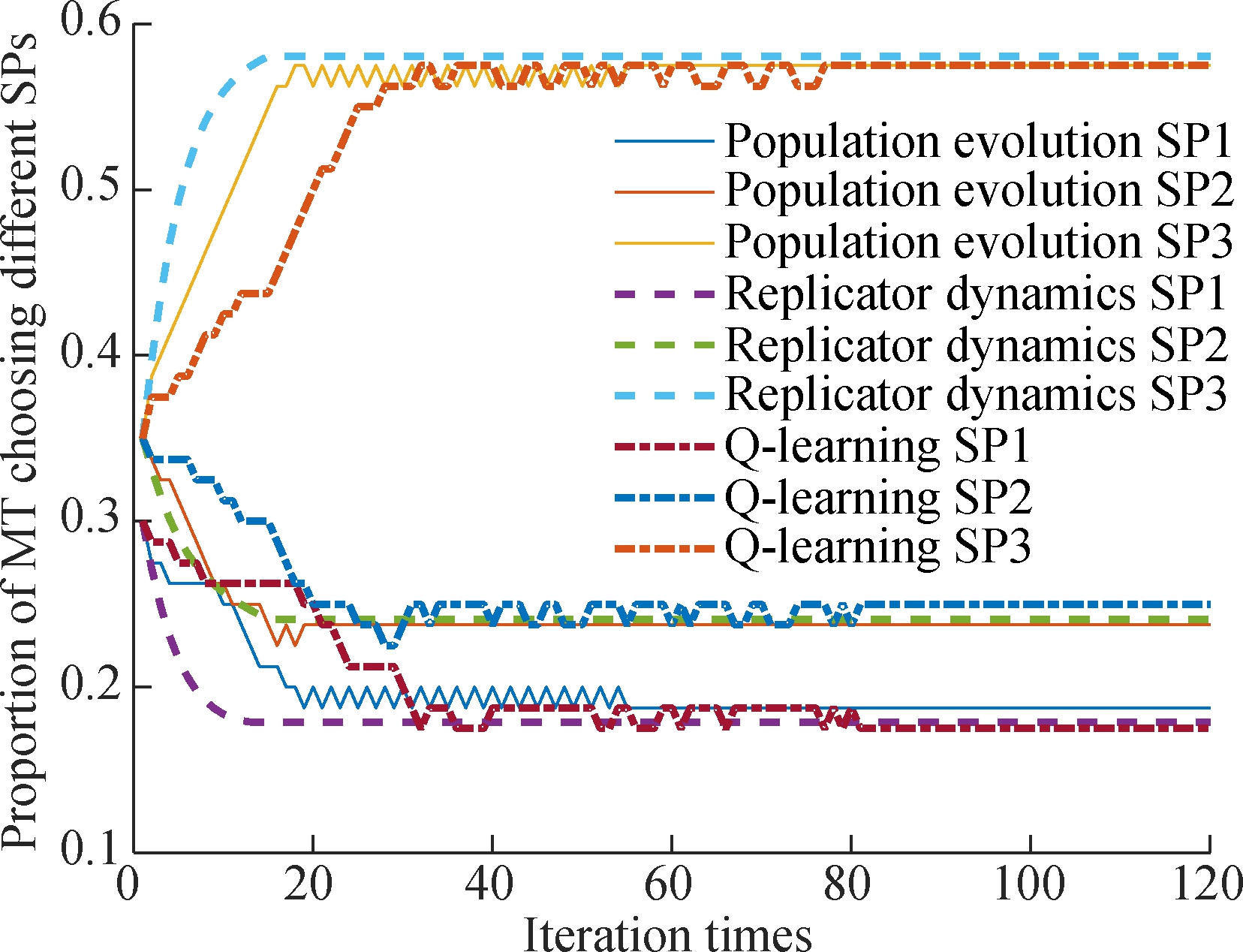
Fig.4 Algorithm comparison among population evolution, centralized algorithm and distributed algorithm
From Fig.5, we can observe that the increasing tendency of EE, ES and proposed JAR-EG schemes of energy consumption differ from each other. The increasing speed of the EE scheme is the fastest while that of the proposed scheme is the slowest. At the beginning, the ES scheme consumes the least energy and the proposed scheme consumes the most energy. However, the energy consumption of the proposed scheme becomes less with the input data size increasing. When the input data size is larger than 8 Mbit, the energy consumption of the proposed scheme is the lowest. The delay consumption comparison among the EE, ES and proposed JAR-EG schemes is described in Fig.6. We can clearly observe that the proposed scheme has the least time delay compared with the other schemes. By analyzing the energy consumption and time delay of the EE, ES and proposed JAR-EG schemes, we can conclude that the proposed JRA-EG scheme has better performance and effectiveness when input data size becomes larger.
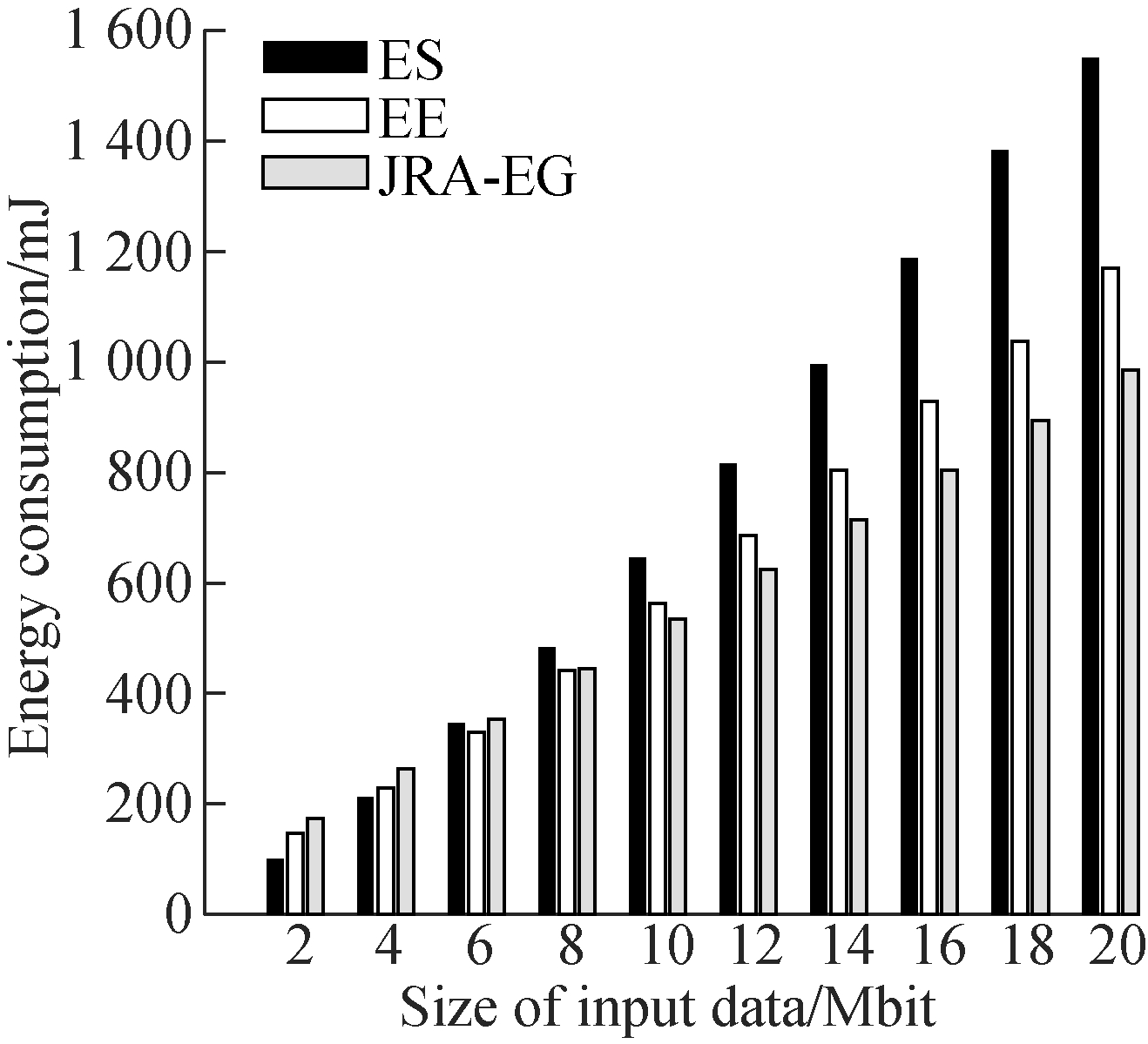
Fig.5 Energy consumption comparison
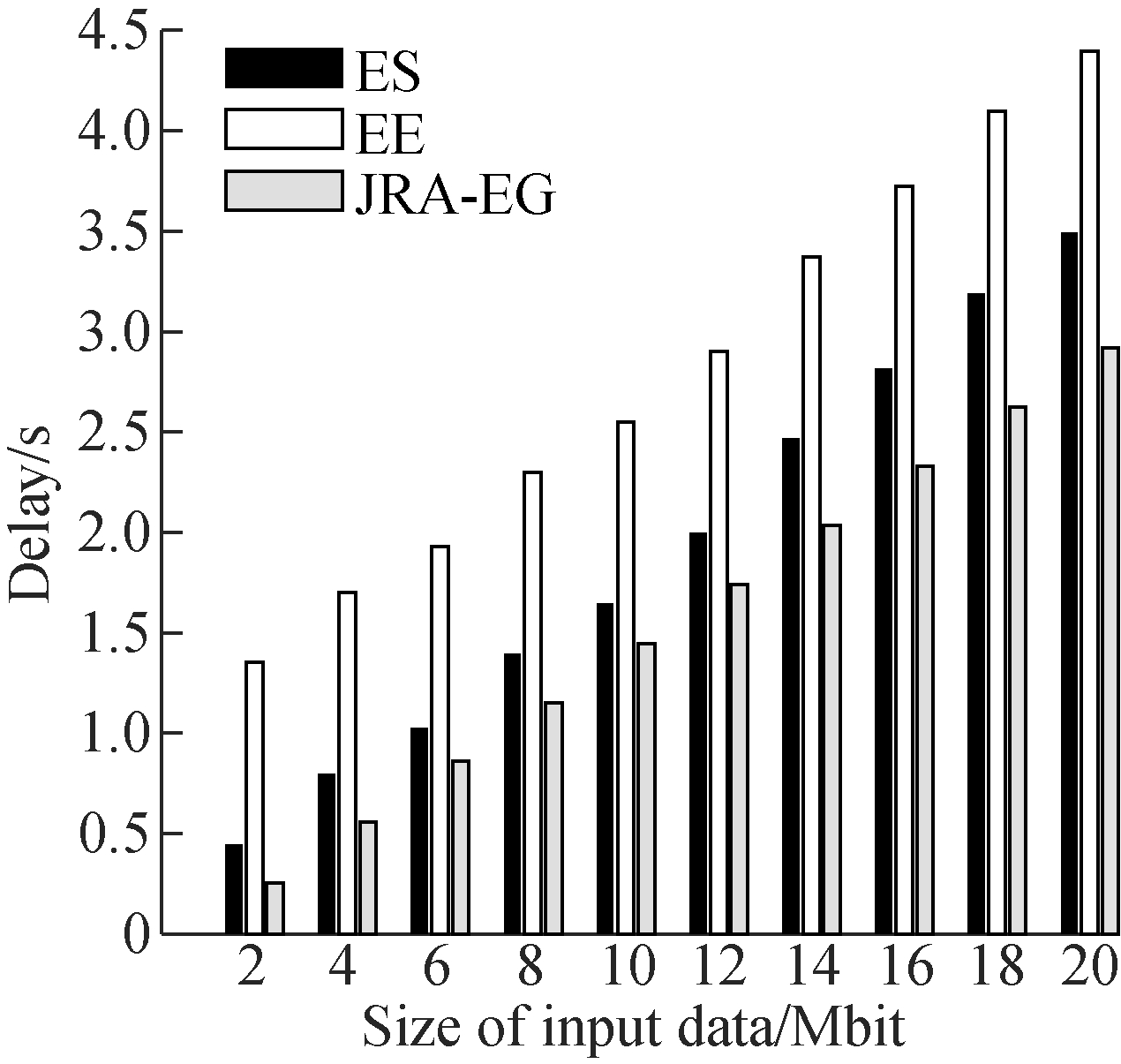
Fig.6 Time delay comparison
6 Conclusion
In this paper, we solve the problem of joint communication and computation resource allocation based on the evolutionary game (JRA-EG) in mobile edge computing environments. To the best of our knowledge, the work is the first one of integrating the SP selection with resource allocation so as to achieve the minimum joint mobile terminals’ energy consumption, time delay and monetary cost. An evolutionary game is established to select SPs and allocate cloud and wireless resources dynamically. We take advantage of the centralized algorithm based on replicator dynamics and the distributed algorithm based on Q-learning to obtain the EE of the JRA-EG game model, respectively. Simulation results verified the effectiveness of the centralized algorithm and distributed algorithm.
[1] Khan A U R, Othman M,Madani S A, et al. A survey of mobile cloud computing application models[J]. IEEE Communications Surveys & Tutorials, 2014, 16(1): 393-413.DOI:10.1109/surv.2013.062613.00160.
[2] Barbarossa S,Sardellitti S, Di Lorenzo P. Communicating while computing: Distributed mobile cloud computing over 5G heterogeneous networks[J]. IEEE Signal Processing Magazine, 2014, 31(6):45-55.DOI:10.1109/msp.2014.2334709.
[3] Niyato D, Wang P, Hossain E, et al. Game theoretic modeling of cooperation among service providers in mobile cloud computing environments [C]// 2012 IEEE Wireless Communications and Networking Conference. Shanghai, China, 2012:3128-3133. DOI: 10.1109/WCNC.2012.6214343.
[4] Wang C M, Liang C C, Yu F R, et al. computation offloading and resource allocation in wireless cellular networks with mobile edge computing [J]. IEEE Transactions on Wireless Communications, 2017, 16(8):4924-4938. DOI: 10.1109/TWC.2017.2703901.
[5] Rimal B P, Van D P, Maier M. Mobile-edge computing vs. centralized cloud computing in fiber-wireless access networks [C]//2016 IEEE Conference on Computer Communications Workshops. San Francisco, CA, USA, 2016:16285777. DOI: 10.1109/INFCOMW.2016.7562226.
[6] Mao Y Y, Zhang J, Letaief K B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12):3590-3605. DOI:10.1109/jsac.2016.2611964.
[7] Xu J, Chen L X, Ren S L. Online learning for offloading andautoscaling in energy harvesting mobile edge computing[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(3): 361-373. DOI:10.1109/tccn.2017.2725277.
[8] Wang C M, Yu F R, Liang C C, et al. Joint computation offloading and interference management in wireless cellular networks with mobile edge computing[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7432-7445. DOI:10.1109/tvt.2017.2672701.
[9] de la Roche G,Valcarce A, Lopez-Perez D, et al. Access control mechanisms for femtocells[J]. IEEE Communications Magazine, 2010, 48(1): 33-39. DOI:10.1109/mcom.2010.5394027.
[10] Zhu K, Hossain E,Niyato D. Pricing, spectrum sharing, and service selection in two-tier small cell networks: A hierarchical dynamic game approach[J]. IEEE Transactions on Mobile Computing, 2014, 13(8): 1843-1856. DOI:10.1109/tmc.2013.96.
[11] Mach P,Becvar Z. Mobile edge computing: A survey on architecture and computation offloading[J]. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1628-1656. DOI:10.1109/comst.2017.2682318.
[12] Niyato D, Hossain E. Dynamics of network selection in heterogeneous wireless networks: An evolutionary game approach[J]. IEEE Transactions on Vehicular Technology, 2009, 58(4):2008-2017. DOI:10.1109/tvt.2008.2004588.
[13] Wei Q L, Lewis F L, Sun Q Y, et al. Discrete-time deterministic Q-learning: A novel convergence analysis[J]. IEEE Transactions on Cybernetics, 2017, 47(5): 1224-1237. DOI:10.1109/tcyb.2016.2542923.
[14] Mwanje S S, Schmelz L C, Mitschele-Thiel A. Cognitive cellular networks: A Q-learning framework for self-organizing networks[J]. IEEE Transactions on Network and Service Management, 2016, 13(1): 85-98. DOI:10.1109/tnsm.2016.2522080.
[15] Do C T, Tran N H, Tran D H, et al. Toward service selection game in a heterogeneous market cloud computing [C]//2015 IFIP/IEEE International Symposium on Integrated Network Management(IM). Ottawa, ON, Canada, 2015:44-52. DOI: 10.1109/INM.2015.7140275.
[16] Yan S, Peng M G,Abana M A, et al. An evolutionary game for user access mode selection in fog radio access networks[J]. IEEE Access, 2017, 5: 2200-2210. DOI:10.1109/access.2017.2654266.