Recently, cognitive radio (CR) has been proposed to overcome the problem of limited available spectrum[1]. CR enables secondary users (SUs) to randomly access the spectrum. Due to the time-varying of the wireless channel, the signal-to-noise ratio (SNR) may become too low to obtain a reliable spectrum sensing. Hence, cooperative spectrum sensing (CSS) is proposed to deal with this issue[2]. In existing CSS, SUs need to send their local sensing information to the fusion center (FC), and then the FC makes a global decision[3]. However, this fusion scheme provides more opportunities for malicious secondary users (MSUs) to launch Byzantine attacks[4].
Nowadays, a series of solutions have been made to recognize MSUs. A reliable reference algorithm was proposed to reduce the influence of MSUs on spectrum sensing[5]. A trust node-assisted reference algorithm was put forward, in which the trust node was applied to screen out MSUs[6].
The traditional MSU detection scheme usually achieves a poor detection performance in a massive MSU and the low-SNR region. To enhance the performance in a relatively hash environment, a bilateral threshold detection scheme is put forward to resist Byzantine attacks.
1 System Model
1.1 Cooperative spectrum sensing
In this paper, an IEEE 802.22 wireless access network is considered, as shown in Fig.1. It consists of a CRN with one PU, one FC, and N SUs. Each SU performs the estimation of the energy value from the PU and sends it to the FC. Then, the FC decides the availability/unavailability of the PU. Therefore, each SU performs the energy detection for a time duration τ0. If we denote the sampling rate by fs, the energy value of SUi is given by
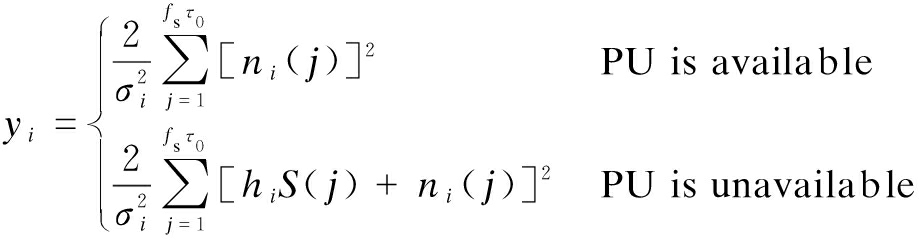
(1)
where hi denotes the channel gain from PU to SUi; S(j) and ni(j) represent the signal of PU and background noise around SUi, respectively. The noise power 
For a large fsτ0, the energy value that SUi received approximates the Gaussian distribution,
Fig.1 Wireless access network
(2)
where γi=E[|hiS(j)|2] represents the SNR from PU to SUi. We assume that the FC has acquired the detection SNR γi and this can be realized by contacting the SUs[7].
1.2 Attack model
In order to efficiently carry out attacks,MSUs need to predict their own local decisions. By comparing the energy value ym with a local threshold φm, the local decision of MSUm can be reached. A PU is considered available if ym>φm; otherwise, PU is considered unavailable.
After spectrum sensing, the individual sensing report dm of each MSU is generated as
(3)
In this paper, the following Byzantine attack model is employed. Here, MSUs use their local decisions to perform attacks. It first makes a local decision. Then, it generates an abnormal Gaussian distribution value with the attack probability βm.
When the MSUm does not launch an attack, the energy value he/she submits is Ym=ym. That is, he/she submits the energy value received in the energy detection phase. However, when the MSUm launches the attack, the Byzantine attack model is denoted as follows:
(4)
where Λ is a deviation resulting in a falsification of data.
2 Bilateral Threshold Selection Scheme
2.1 Data collection
The FC first picks up the energy values submitted by SUs in the history rounds. Hence, the FC can obtain the actual availability states of PU during the end of these history rounds[8](e.g. by interacting with the PU station). The energy values submitted by SUs and PU states are listed in Tab.1. After the pretreatment of energy values, the normalized energy values are shown in Tab.2.
Tab．1 Collected energy values and PU states
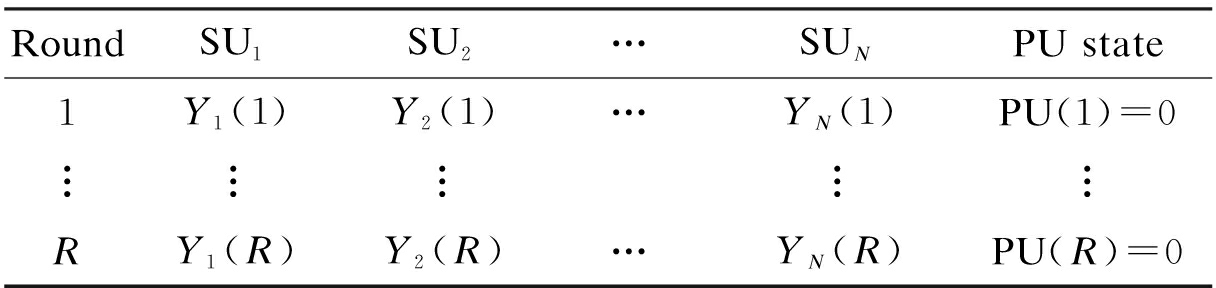
RoundSU1SU2…SUNPU state1Y1(1)Y2(1)…YN(1)PU(1)=0︙︙︙︙︙RY1(R)Y2(R)…YN(R)PU(R)=0
Tab．2 Normalized energy values
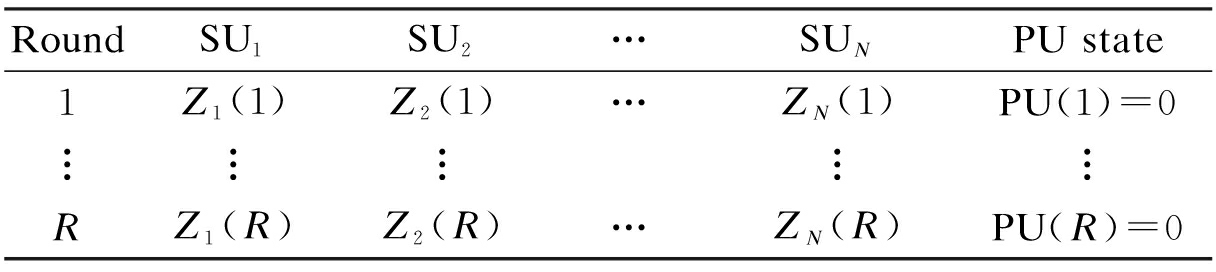
RoundSU1SU2…SUNPU state1Z1(1)Z2(1)…ZN(1)PU(1)=0︙︙︙︙︙RZ1(R)Z2(R)…ZN(R)PU(R)=0
2.2 Pretreatment of energy values
The distributions of energy values submitted by SUi may change with the rounds. Therefore, formula (2) is revised as follows:
(5)
Drawing on the reference of standard normal distribution, the energy values are pretreated as
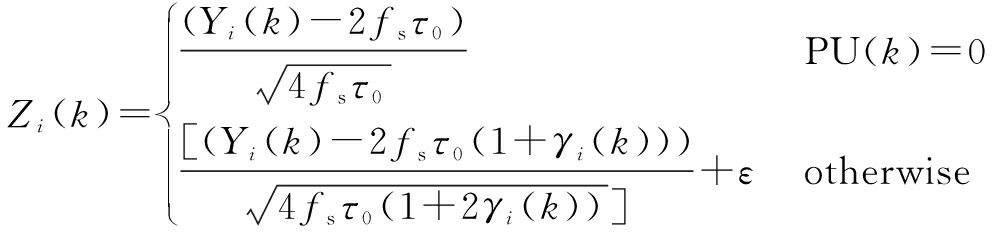
(6)
where ε is a positive data bias. Therefore, for NSUn
(7)
Formula (7) describes the distributions of the normalized energy values of NSUs. However, due to the existence of the attack rounds, the normalized distributions of MSUs under two hypotheses will generate additional changes. The variations of the normalized distributions between NSUs and MSUs will be identified by our bilateral threshold selection scheme.
2.3 Classification accuracy for normalized energy values
After treatment, Tab.2 can be obtained, and then the FC needs to analyze the normalized energy values in R rounds. The FC uses a rated value evaluation method to obtain the decision results of SUi in R rounds:
(8)
where 
represents a decision result of SUi in the k-th round. 
denotes the rated value of SUi in R rounds. U(·) is the step function. For SUi, the selection of the rated value is shown in Definition 1.
Definition 1 The selection of the rated value 
should minimize the deviation between the result vector 
and PU state vector {PU(k)}k=1,2,…,R in R rounds.
⊕Hi(k,s)]
(9)
where ⊕ denotes exclusive-or logic. Therefore, the classification accuracy of SUi is
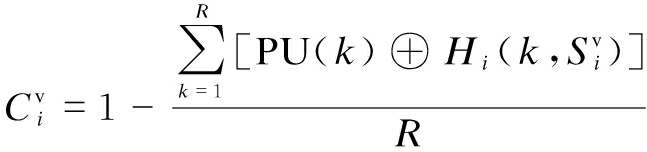
(10)
Owing to the fact that there are only R rounds used in Eqs.(8) and (9), a traversal algorithm is presented to find the rated value and classification accuracy 
which is described as follows:
Step 1 Conduct an ascending sort to the normalized energy values. That is, {Zi(1),Zi(2),…,
…,Zi(lR)}, where Zi(l1)≤Zi(l2)≤…≤Zi(lR).
Step 2 Construct a candidate set of the rated value 
where 
Step 3 Traverse all the values of the candidate set, and select a value 
which minimizes Eq.(9). Therefore, the rated value 
and the classification accuracy 
of SUi can be calculated by Eq.(10).
2.4 Bilateral threshold for normalized energy values
Here, two probabilities are introduced: recognition probability and misclassification probability. Recognition probability is the probability that MSUs are correctly recognized, while misclassification probability is the probability that a NSU is mistaken for a MSU.
For SUi, the distributions of the normalized energy values obtained by the FC satisfy (7). According to the law of large numbers, the theoretical rated value 
of SUi is calculated as
(11)
where Pi(z|H0) and Pi(z|H1;ε) are the distributions under H0 and H1 in (7). P1 and P0 denote the probabilities that PU is present and absent, respectively. Solving the above gives
(12)
Hence, the theoretical classification probability p(ε) of SUi is
(13)
Then, a random variable is introduced:
(14)
It is clear that 
Therefore, the theoretical classification accuracy 
of SUi is
(15)
Given the misclassification probability τ, the fluctuating range Δ can be calculated as
(16)
According to the central limit theorem, we can derive from the above expression that
(17)
Clearly, the recognition probability is a monotone decreasing function of Δ. To maximize the recognition probability, we write formula (17) as an equation. Therefore,
uiL=p(ε)-Δ=p(ε)-
(18)
uiH=p(ε)+Δ=p(ε)+
(19)
Eqs.(18) and (19) describe the relationship between the misclassification probability and the bilateral threshold of classification accuracy 
As can be seen from the above expressions and (15), with the increase of R, the bilateral threshold {uiL,uiH} and the theoretical classification accuracy both converge to p(ε) and the convergence rate of {uiL,uiH} is geometric. In addition, owing to the pretreatment of the energy values, each SU has the same bilateral threshold in the FC. With the increase of R, for NSUn, its classification accuracy 
is coincident with 
Therefore, it will fall into the [unL,unH]. However, for MSUm, owing to the attack rounds, its classification accuracy 
is not consistent with 
Therefore, it will fall outside [umL,umH] as the number of samples R increases.
3 Description of the Bilateral Threshold Selection Scheme
In this part, the steps of the selection algorithm are introduced.
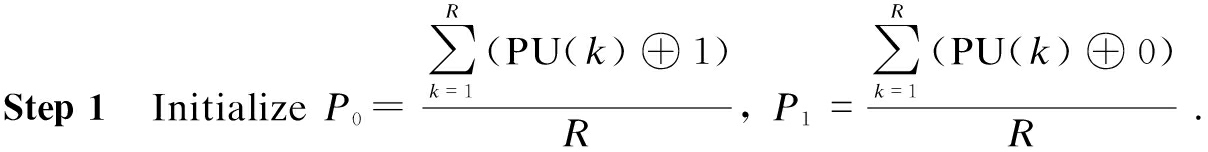
Step 2 For each SUi, the FC converts the energy values Yi(k) into Zi(k) via (6).
Step 3 FC calculates p(ε) and {uiL,uiH} by (17), (22) and (23).
Step 4 Calculate through the traversal algorithm
Step 5 If ∉[uiL,uiH], then add SUi to the blacklist.
In order to demonstrate the effectiveness of the selection scheme, a simple likelihood ratio scheme is adopted to achieve the PU state as follows:
Step 1 Pick out the energy values YUj(k) of the SUs not included in the blacklist.
Step 2 Calculate likelihood ratio
Step 3 If Lr>1, then PU is available. Otherwise PU is unavailable.
As is shown from the scheme, P1 and P0 are counted by the actual state of the PU from Tab.2. PUj(y|Hv)(v=0,1) are the original distributions of the energy values in (5). {Uj}j=1,2,…,M are the SU indices not belonging to the blacklist in the selection algorithm.
4 Simulation Results
If the parameters are not listed explicitly in the figures, parameters are set by default as follows. The number of SUs is 50. The number of samples R is 100. The sampling frequency fs is 10 kHz. The sensing duration τ0 is 5 ms, the noise power 
The misclassification probability τ is 0.05, and the signal to noise ratio γi(k) fluctuates between -10 and -5 dB. The data bias ε is 1, and the deviation Λ is 2fsτ0γm.
Fig.2 shows the MSUs screened out by our selection algorithm. Owing to the normalization of the energy values, SUs with different SNRs have the same bilateral thresholds. In Fig.2, a NSU is misclassified as a MSU
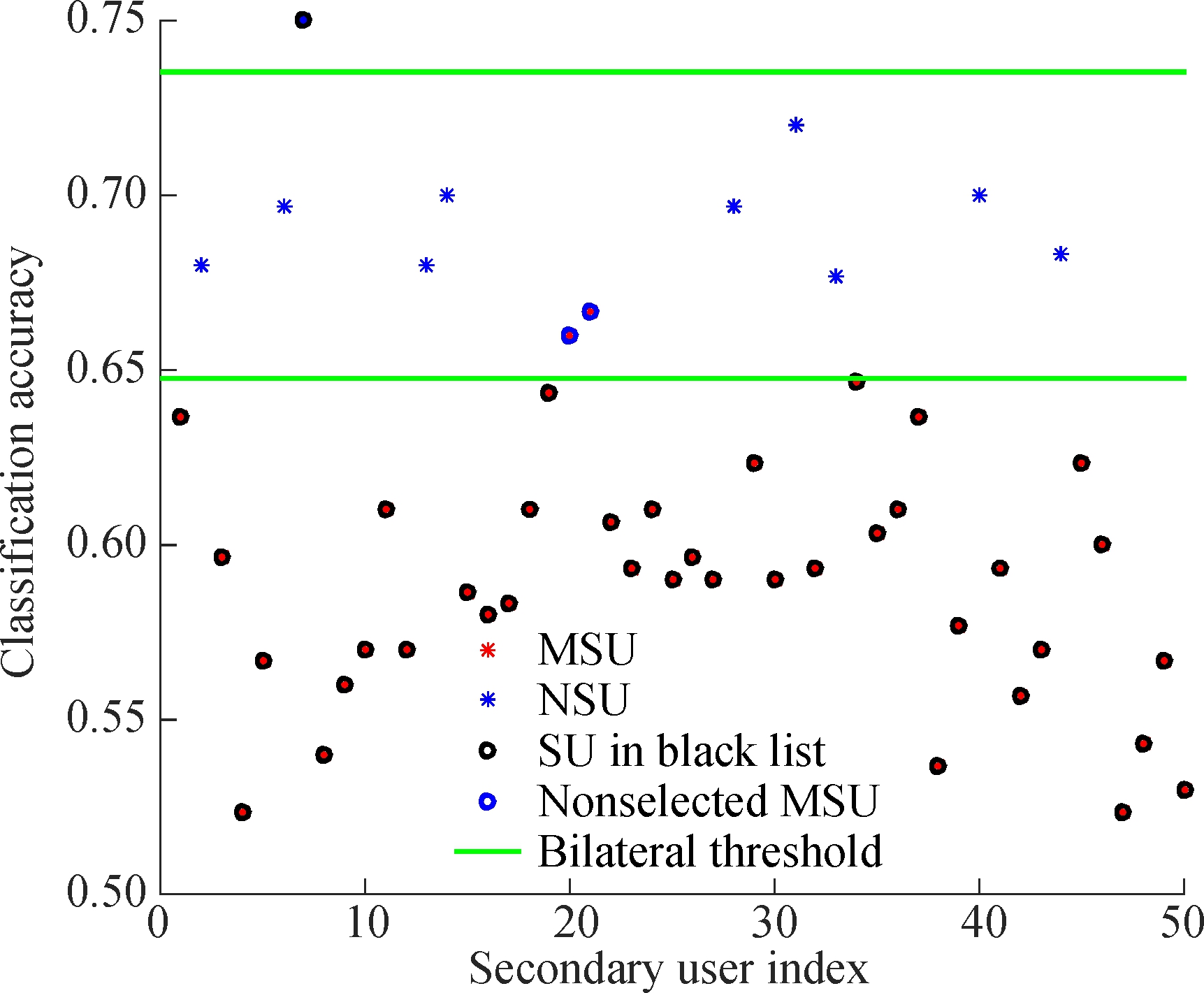
Fig.2 The filter result of MSUs in selection algorithm(βm∈[0.2，0.4])
(Its index is 7), and two MSUs are not screened out (Their indices are 20 and 21).
Fig.3 describes the correct sensing probabilities of our selection algorithm and the SVDD algorithm[9] with the rounds increasing. Due to the users’ mobility, the proportion of MSUs will change. The variations of the percentage of MSUs are marked with red circles. From Fig.3, our scheme achieves better performance than the SVDD algorithm. Besides, a large R has a positive impact on sensing performance, which is coincident with Eqs.(18) and (19).
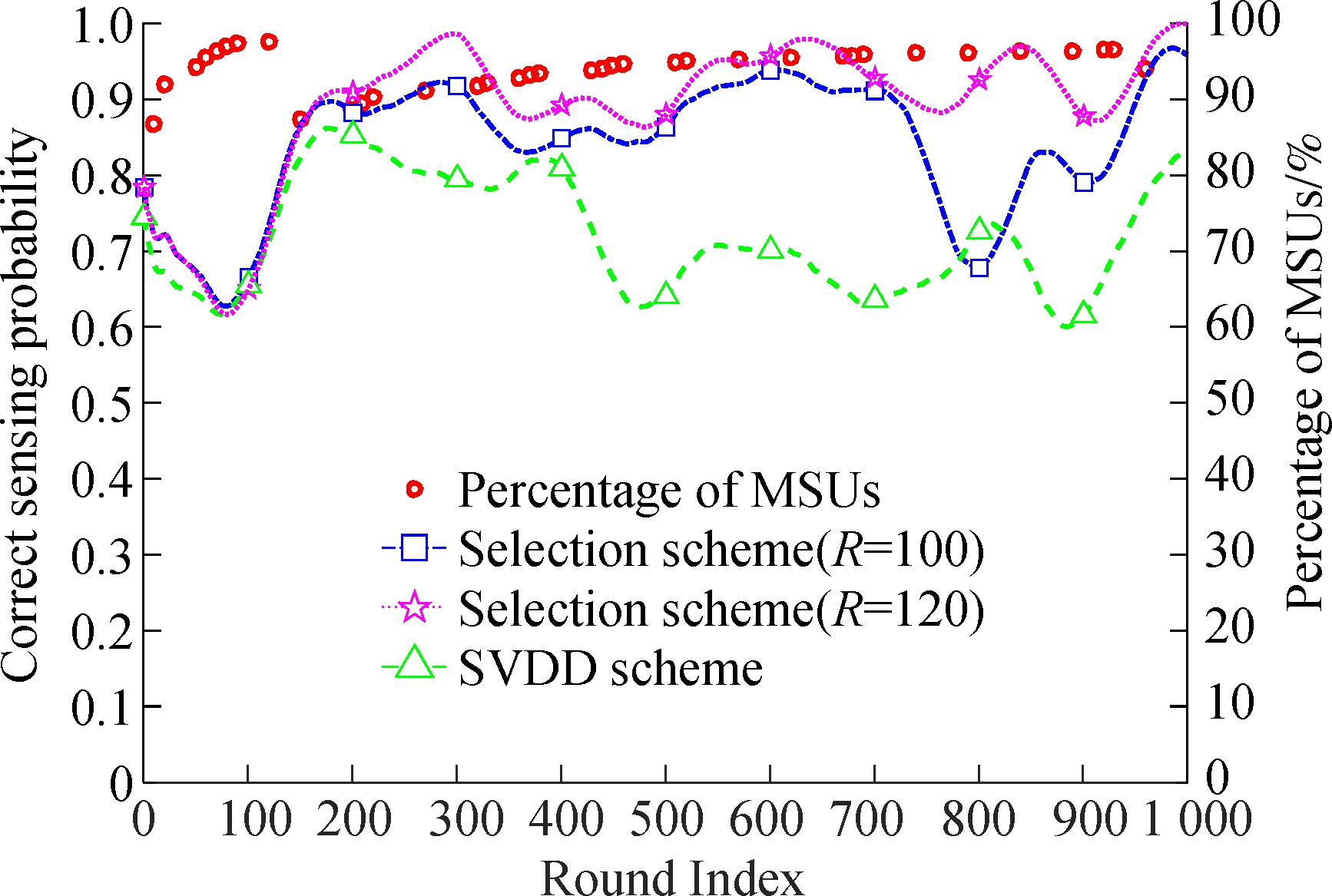
Fig.3 The variation of correct sensing probability with rounds(βm∈[0.1，0.3])
Fig.4 shows the detection probability with the increase in the percentage of MSUs. In this figure, the traditional trust scheme[10] and the critical learning scheme[11] are the worst, while the sensing guard scheme[12] is better than them. This is due to the fact that the sensing guard scheme will impose severe punishments on the SUs who submit false sensing energy values frequently. However, our proposed scheme screens out most MSUs, which ensures excellent detection probability in scenarios with massive MSUs.
Fig.4 The variation of detection probability with percentage of MSUs(βm∈[0.2，0.4])
Fig.5 describes the impact of the percentage of MSUs on false alarm probability. We compare our selection scheme with the above algorithms. From Fig.5, we can see that the data bias ε has a modest impact on the sensing performance of the selection algorithm. Hence, the appropriate value of all data bias is allowed in our scheme.
Fig.5 The variation of false alarm probability with percentage of MSUs(βm∈[0.2，0.4])
5 Conclusion
In this paper, we design a bilateral threshold selection scheme for MSU detection. Besides, we analyze the relationship between misclassification probability and the bilateral threshold. In simulation, we verify the performance of the algorithm in terms of a series of parameters. Hence, the proposed scheme can deal with the byzantine attacks in CSS to improve the robustness of the system.
[1] Haykin S. Cognitive radio:Brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220. DOI:10.1109/jsac.2004.839380.
[2] Guo H Y, Reisi N, Jiang W, et al. Soft combination for cooperative spectrum sensing in fading channels[J]. IEEE Access, 2017, 5: 975-986. DOI:10.1109/access.2016.2628860.
[3] Peng T, Chen B, Xiao J, et al. Improved soft fusion-based cooperative spectrum sensing defense against SSDF attacks [C]//2016 International Conference on Computer, Information and Telecommunication Systems. Kunming, China, 2016: 1-5.
[4] Shen J, Liu S, Zeng L, et al. Optimization of cooperative spectrum sensing in cognitive radio network[J]. IET Communications, 2009, 3(7): 1170. DOI:10.1049/iet-com.2008.0177.
[5] Zhang L, Ding G, Song F, et al. Defending against byzantine attack in cooperative spectrum sensing relying on a reliable reference [C]//2016 International Conference on Communications in China. Chengdu, China, 2016: 1-6.
[6] He X F, Dai H Y, Ning P. A Byzantine attack defender in cognitive radio networks: The conditional frequency check[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 2512-2523. DOI:10.1109/twc.2013.031313.121551.
[7] Zeng F, Li J, Xu J, et al. A trust-based cooperative spectrum sensing scheme against SSDF attack in CRNs [C]//2016 IEEE Trustcom/BigDataSE/ISPA. Tianjin, China, 2016: 1167-1173.
[8] Hyder C S, Grebur B, Xiao L, et al. ARC: Adaptive reputation based clustering against spectrum sensing data falsification attacks[J]. IEEE Transactions on Mobile Computing, 2014, 13(8): 1707-1719. DOI:10.1109/tmc.2013.26.
[9] Farmani F, Abbasi-Jannatabad M,Berangi R. Detection of SSDF attack using SVDD algorithm in cognitive radio networks [C]//2011Third International Conference on Computational Intelligence, Communication Systems and Networks. Bali, Indonesia, 2011: 201-204.
[10] Pei Q Q,Yuan B B, Li L,et al.A sensing and etiquette reputation-based trust management for centralized cognitive radio networks[J].Neurocomputing, 2013, 101: 129-138. DOI:10.1016/j.neucom.2012.08.005.
[11] Chen H F, Zhou M, Xie L, et al. Joint spectrum sensing and resource allocation scheme in cognitive radio networks with spectrum sensing data falsification attack[J]. IEEE Transactions on Vehicular Technology, 2016, 65(11): 9181-9191. DOI:10.1109/tvt.2016.2520983.
[12] Jing Y F, Yu Q Z, Guang Y L. Securing cooperative spectrum sensing against rational SSDF attack in cognitive radio networks[J]. KSII Transactions on Internet and Information Systems, 2014, 8(1): 1-17. DOI:10.3837/tiis.2014.01.001.