Fatigue failure due to repeated traffic load is a significant distress found in asphalt pavements[1-2]. The fatigue resistance is regarded as a main factor influencing the pavements’ service life. Thus, establishing a suitable fatigue model for asphalt mixtures has been paid much attention to for many years.
It is shown that the existing research on fatigue of asphalt mixtures can be classified into three main types: the phenomenon models based on fatigue tests[3-4], the dissipated energy method which ignores the influence of path[5], the mechanical approach including the fatigue crack propagation models based on fracture mechanics and the fatigue damage evolution models based on damage mechanics[6]. Among the three categories, damage mechanics based on thermodynamics is given increasing attention due to its sufficient theoretical basis.
Whichever method is employed, it is acknowledged that the fatigue damage evolutions of asphalt mixtures are influenced by different control modes used during fatigue experiments. Stress control and strain control are two common control modes in laboratory fatigue tests. However, most of the present research emphasized the fatigue damage evolution law under only one of the two control modes, by employing a dynamic modulus, complex modulus or dissipated energy as the evaluation indices[7-9]. The definition of these damage evaluation indices was always artificial. In addition, only a few researchers have studied the mechanism of two control modes simultaneously. Castelo Branco et al.[10-11] demonstrated that no matter when derived from the controlled strain or the controlled-stress mode of loading, the values of the dissipated energy index of asphalt mixtures are similar. In the area of asphalt, Shan et al.[12] proposed a converting method for the interconversions of the fatigue damage evolution rule under different control modes. Nevertheless, the two investigations are both conducted on the theory of dissipated energy and fracture mechanics. A unified fatigue model was established and the difference of damage evolution under the two control modes was ignored[13]. Furthermore, the effect of multilevel loading on the fatigue damage under two different control modes is a subject of on-going research since whether asphalt has coaxing effects is still unclear.
The objective of this study is to compare the fatigue damage evolution mechanism of asphalt mixtures under two different control modes. A fatigue damage model for asphalt mixtures under controlled-stress and controlled-strain modes was established based on thermodynamics. A suitable dissipative potential function was chosen according to the fatigue characteristic of the asphalt mixtures. Specifically, the damage variable used here was deduced instead of being artificially defined. The difference in damage evolution under different control modes was compared after the model verification. Finally, the influence of multilevel loading on the fatigue damage under two different control modes was preliminarily interpreted using the model.
1 Theory of Damage Mechanics
The essence of damage is the flaw in micro-structures. The nucleation and development of micro-flaws are defined as the evolution of damage. Based on continuum mechanics, in damage mechanics, a field variable is introduced to describe a damage status. Damage constitutive equations and damage evolution laws are deduced from the laws of thermodynamics.
A damage variable can be directly defined as the volume percentage of microcracks and microvoids occupying the whole bulk[14]. Practically, researchers prefer employing the ratio of timely mechanical parameters, such as modulus and residual strength, to the original ones as a damage variable[8]. However, few of these damage variables are directly deduced from thermodynamics.
Under the condition of a constant temperature, the Helmholtz free energy of elastic materials with brittle failure can be expressed as
φ=φ(ε,D)
(1)
where φ is the Helmholtz free energy; ε is the present strain; and D is the damage variable.
Employing the strain equivalence hypothesis, the expression of Helmholtz free energy for damaged materials is
(2)
where ρ is the density of the material; E0 and φ0 are the initial elastic modulus and initial Helmholtz free energy, respectively.
Helmholtz free energy is taken into the Clausius-Duhem inequation:
(3)
where σ is the present stress; 
are the gradients of the corresponding parameters.
The damage constitutive model can be acquired from the first thermodynamical law：
(4)
The releasing rate of the damage energy is
For the restriction 
the consistency condition is introduced: FD(Y,D)=0.
The Lagrange multiplier method is employed to solve the consistency condition: 
Thus,
(5)
where λ is the Lagrange multiplier, and 
is the gradient of λ.
2 Fatigue Damage Model for Asphalt Mixtures
In this section, a damage variable related to dynamic modulus was deduced from thermo-dynamic laws and a uniform fatigue model for damage under both controlled-stress and controlled-strain modes was established.
2.1 The dissipation potential
As Lema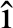
tre[17] promoted, ignoring visco-plasticity of asphalt mixtures, the dissipation potential of damage can be expressed as
(6)
where w is the dissipation potential; m and A are the nonnegative material parameters that characterize damage evolution, which can be determined by experimental data. A similar format was also used by Onifade et al[15].
An associated micro-crack formation and propagation criterion is introduced and expressed as
FD=w(Y)-R(r)=0
(7)
where R(r) is the isotropic damage hardening function.
The resulting damage evolution law is given as a power-law type:
(8)
The damage hardening variable r can be obtained as a function of the Lagrange multiplier λ and expressed as[16]
(9)
In the previous research, the hardening variable r always had no practical senses[15-17]. Zhu et al.[18] proposed the cohesive force as the hardening variable of asphalt mixtures in the viscoelastic-viscoplastic damage constitutive model. In this damage model, the modulus of resilience μ was employed as the hardening variable to characterize the development of micro-plasticity, which is affected only by damage during a loading cycle. Since the dynamic modulus μ is negatively correlated with D, the damage evolution can be expressed as
(10)
2.2 Damage variable
To simplify the derivation of damage variable, it is assumed that Y and μ are irrelevant. Thus,
(11)
where μ and μ0 are the present and the original dynamic modulus, respectively. Then,
D=AYm(μ0-μ)+c
(12)
The boundary conditions 
are taken into Eq.(12). So,
(13)
where μmin is the dynamic modulus at failure.
Substituting Eq.(13) into Eq. (12), the damage variable definition is obtained:
(14)
The related dynamic modulus in Eq.(14) can be measured by experiments.
2.3 Fatigue damage evolution
During the process of cyclic loading, the damage variable increases with the increase in the number of loadings. The kinetic law of D under the two control modes can be inferred from Eq.(10).
2.3.1 Fatigue damage evolution under a controlled-stress mode
During each cycle, the irreversible reduction of modulus only occurs during loading process. It is supposed that the gradient of the hardening variable and the gradient of stress is directly proportional[19-20]:
〈
(15)
where K is a material parameter related to D; σ is the timely stress during a loading cycle; and 
Thus, according to Eq.(10), the damage rate is
(16)
where E(n) is the dynamic modulus during the n-th cycle.
During each stress cycle, the dynamic modulus E(n) is regarded as a constant and the decreasing E(n) after the n-th stress cycle can be expressed as E0(1-D). The integral of one stress cycle is
(17)
where σmax is the peak stress and it is a constant.
Furthermore, D can also be regarded as a constant during a stress cycle. Thus,
(18)
Then,
(19)
The boundary conditions 
are taken into Eq.(19), and
(20)
where N is the fatigue life of the asphalt mixture under the stress loading level σmax.
Thus,
(21)
2.3.2 Fatigue damage evolution under a controlled-strain mode
During each controlled-strain fatigue cycle, the irreversible reduction of the dynamic modulus only occurs during loading. According to Eq.(15), due to the simplification that the dynamic modulus during each loading cycle is constant, the gradient of the hardening variable can be expressed as
(22)
where ε is the timely strain during a loading cycle, and 
Thus, according to Eq.(10), the damage rate is
〈
(23)
And the integral of a loading cycle is
(24)
where εmax is the peak strain and it is a constant.
The hypothesis here is that if D keeps constant during each strain cycle, the integral is
(25)
Then,
(26)
The boundary conditions are considered, and
(27)
Thus,
(28)
From Eqs.(21) and (28), the fatigue damage evolutions under two different control modes can be generalized with the restriction m≥0.
(29)
3 Model Calibration and Parameter Identification
To ensure that the fatigue failure mode of asphalt mixtures can be classified into quasi-brittle damage, the experimental data used in this paper are from the following situations: 1) Under the controlled-stress mode at a moderate temperature of 20 ℃, visco-plastic deformation is insignificant and resilient strain occupies the most during the process of fatigue[8]; 2) Under the controlled-strain mode at a moderate temperature of 15 ℃, the mode belongs to high-cycle fatigue, which means that the fatigue life of asphalt mixtures is greater than 10 000 cycles[9]. For both experiments, the loading rate was set to be 10 Hz and the load form is half-sinusoidal wave. The properties of the asphalt mixtures used in the experiments can be found in the original dissertation.
3.1 Fatigue damage model under a controlled-stress mode
The fatigue damage model for asphalt mixtures under a controlled-stress mode was calibrated using the experimental data from Liu[8]. The direct tension test was employed for controlled-stress fatigue experiment under five different stress levels. The specimens were cut from rutting plates to the following dimensions: 250 mm×50 mm
×50 mm. The fatigue test equipment was MTS-810. No fewer than three specimens were tested under each stress level. The average dynamic modulus during the cyclic loading process was recorded as shown in Fig.1. As shown in Tab.1, when the fatigue life ratio is 0.1, the dynamic modulus was chosen as the initial modulus. The average dynamic modulus of the last 5 cycles was chosen as the critical modulus of rupture.
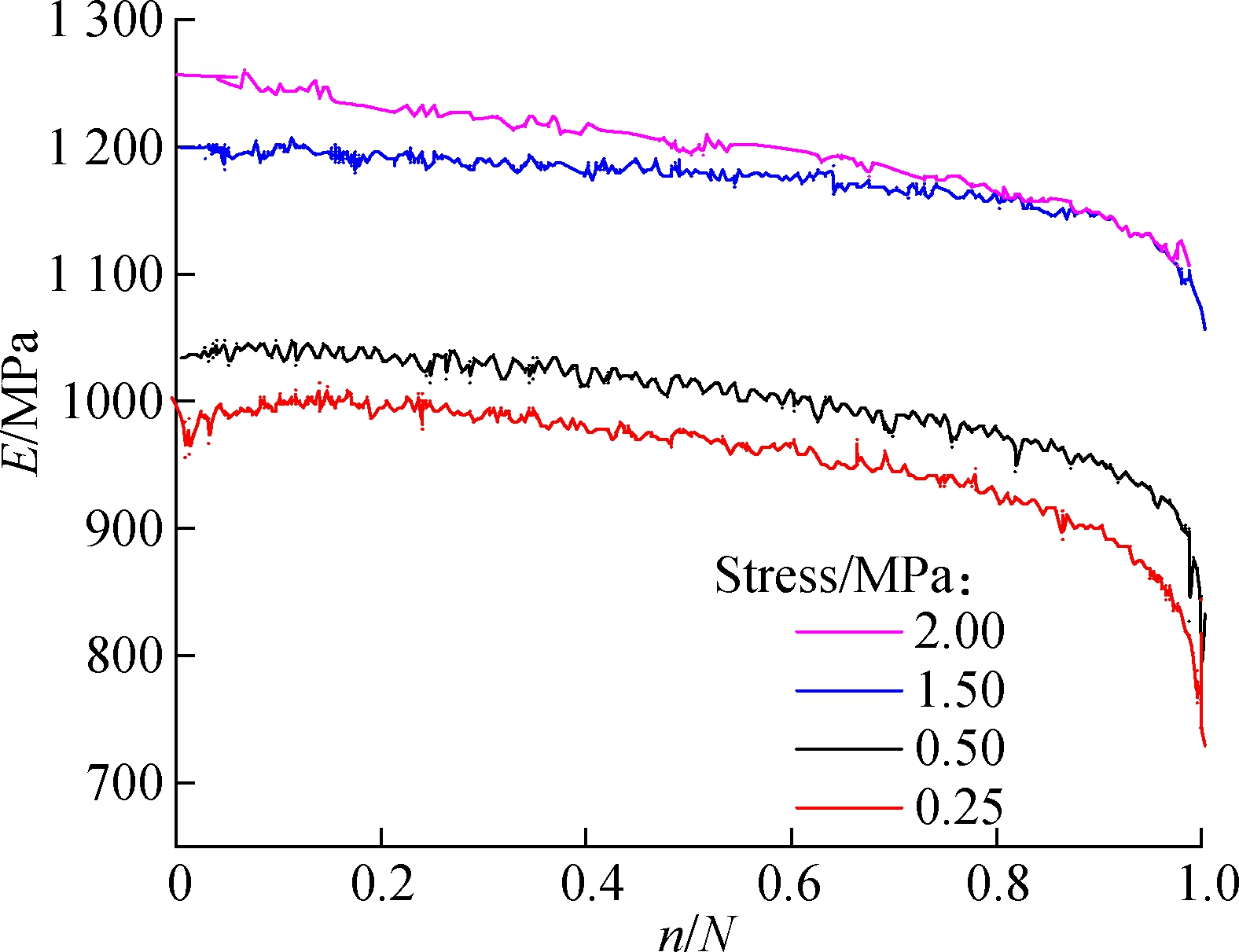
Fig.1 The dynamic modulus attenuation rule under controlled-stress mode
The static loading strength f is 1.228 MPa. The dynamic resilient modulus is used to calculate the damage variable as Eq.(14). The results are shown in Fig.2. The damage variables are calculated and the damage evolution laws are predicted under different stress levels.
To determine m, it is supposed that 
is a power function of the stress level. The stress level is described as 
The fitting result is shown in Fig.3.
Thus, the fatigue damage evolution law of the asphalt mixtures under a controlled-stress mode can be expressed as follows:
Tab.1 Initial and critical moduli under controlled-stress mode
Stress level σ/MPaNumber of failure cycle NfInitial modulusμ0/MPa Mean value of μ0/MPaCvCritical modulusμmin/MPaMean value of μmin/MPaCv0.25154 4491 056200 3371 07361 7051 07872 0321 1141 0800.025974916705845860.130.56 8741 1635 4471 02122 4541 0851 0920.096236316636390.031.55521 1774061 2004691 2211 1990.021 0451 0511 0331 0430.012.02231 2102271 2081801 2531 2240.021 0531 0741 1051 0770.02Note:Cv is the coefficient of variance.
(a)
(b)
(c)
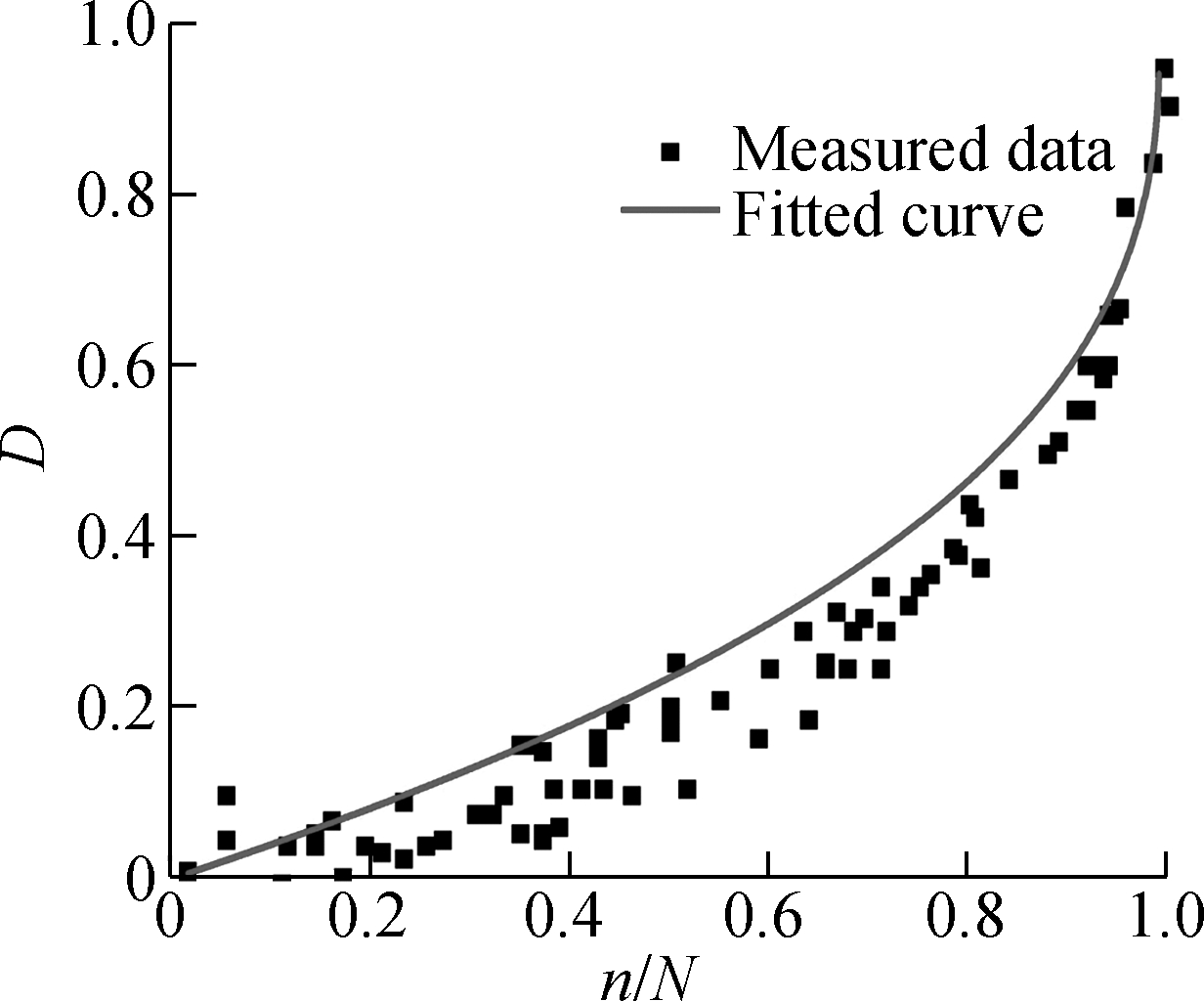
(d)
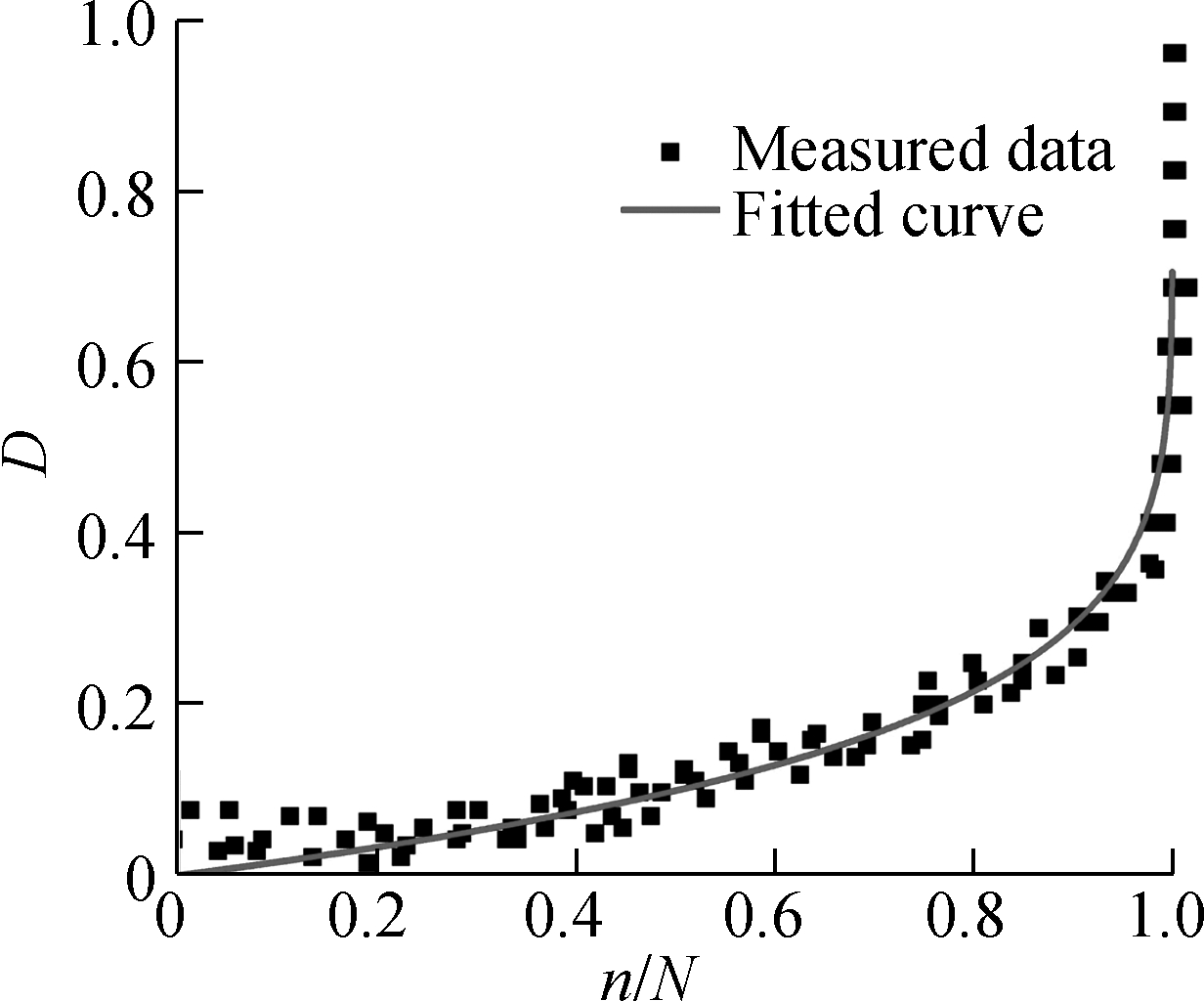
Fig.2 The damage evolution laws under different stress levels. (a) δ=0.25 MPa, m=5.620, R2=0.807 8;(b) δ=1.00 MPa, m=4.812, R2=0.986;(c) δ=1.50 MPa, m=3.525, R2=0.985;(d) δ=2.00 MPa, m=1.600, R2=0.800
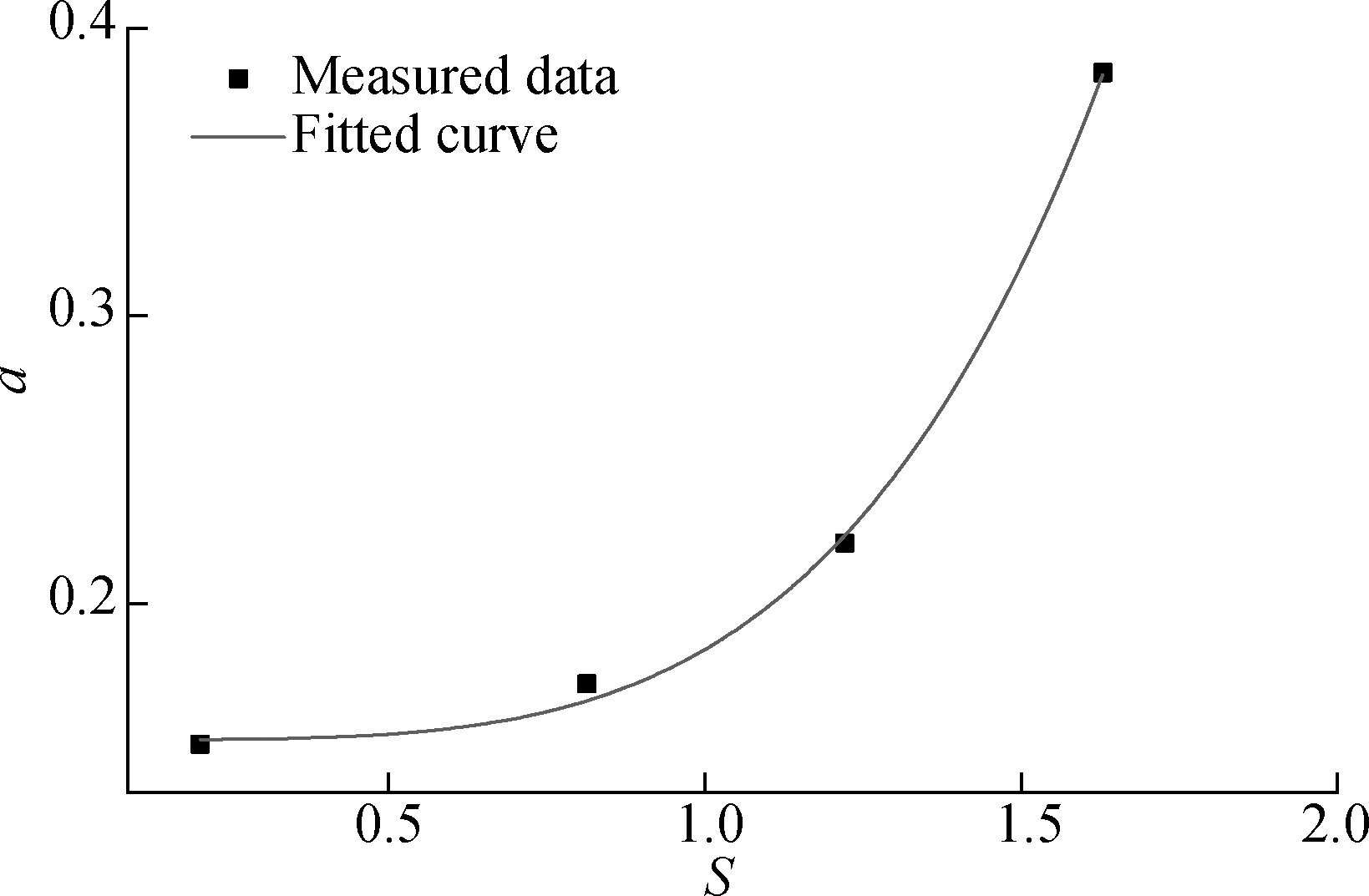
Fig.3 The relationship between a and S under a=0.152 7+0.31 23S4.105 0, R2=0.999
(30)
where S=σmax/1.228.
3.2 Fatigue Damage Model under a Controlled-Strain Mode
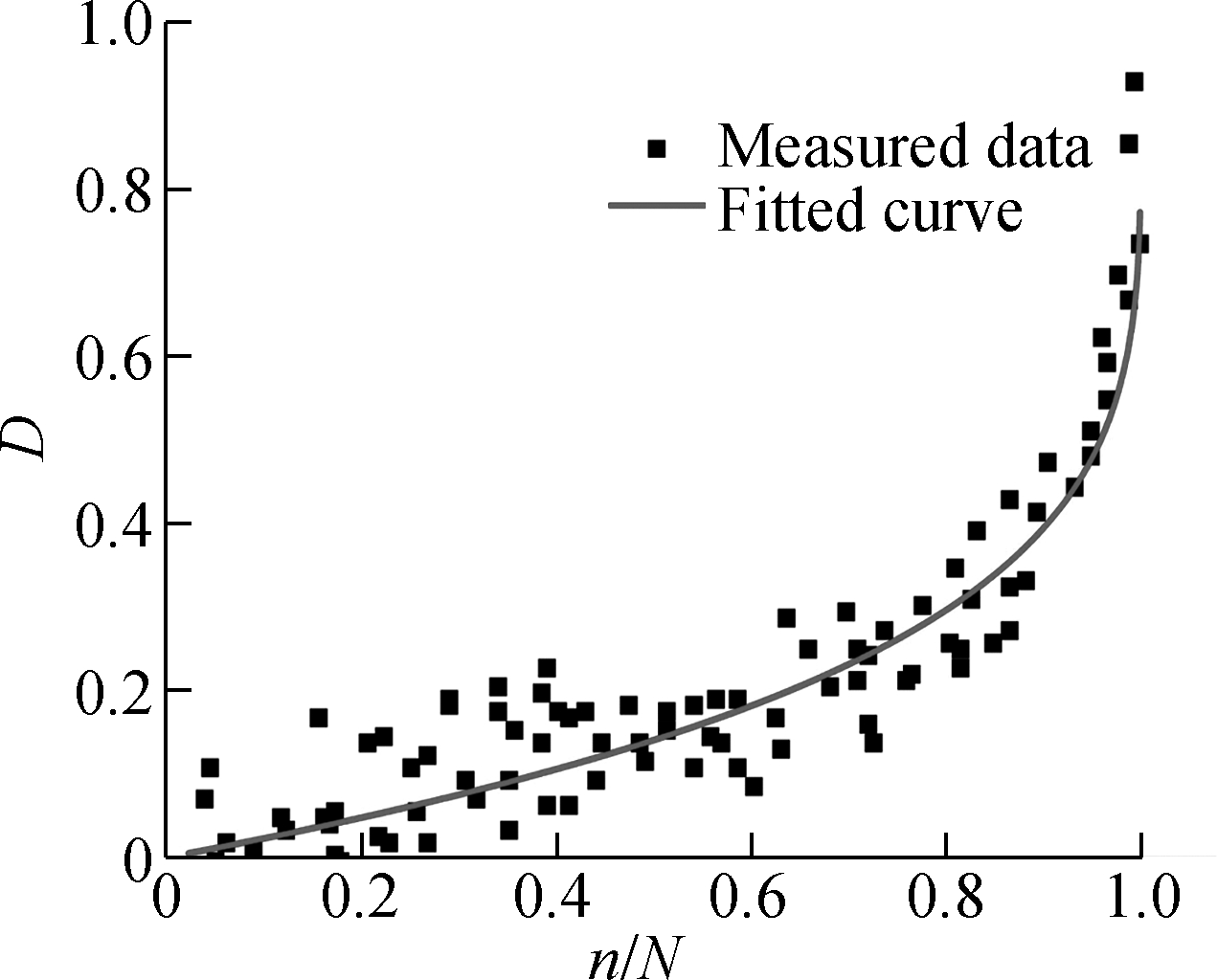
The experimental data under four different strain levels were used to calibrate the fatigue damage model under a controlled-strain mode[9]. The four-point bending test method was adopted. The dimension of the specimen is 380 mm × 50 mm × 65 mm. The fatigue test equipment is Cooper NU-14. The average dynamic modulus during the cyclic loading process is recorded as shown in Fig.4. Tab.2 is the mean value of the critical modulus. The dynamic modulus at the 100th cyclic loading is chosen as the initial modulus. The inflection point on the curve of dynamic modulus is set as the critical modulus of rupture. The damage variables calculated and the damage evolution laws predicted are shown in Fig.5. It can be seen that the fitting effect is not in competition with that under the stress-controlled mode.
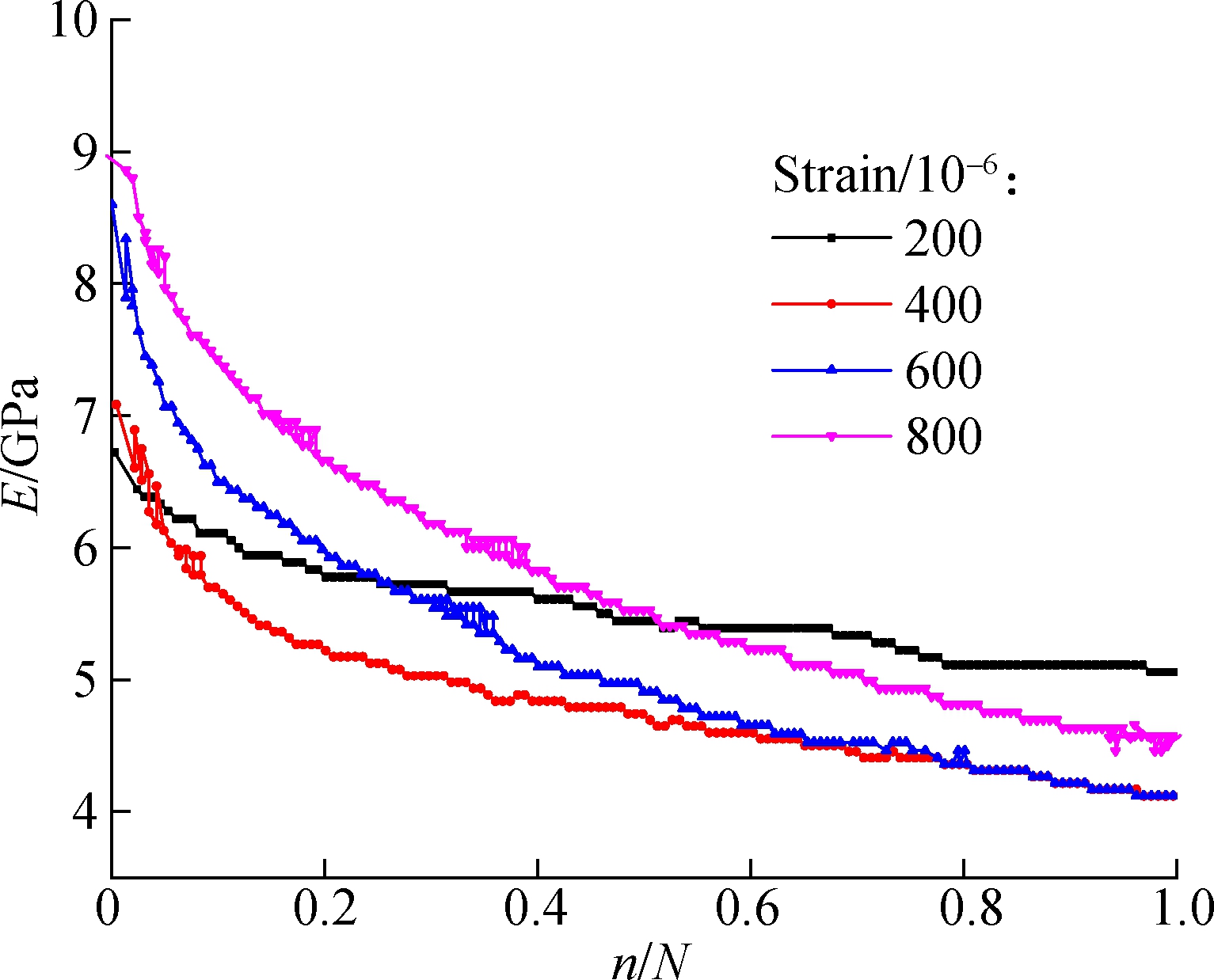
Fig.4 The dynamic modulus during the loading process under controlled-strain mode
Tab.2 Mean value of initial and critical moduli under controlled-strain mode
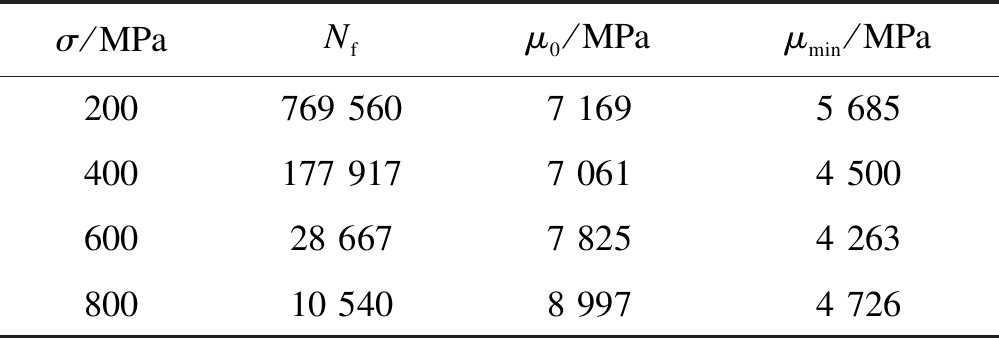
σ/MPaNfμ0/MPaμmin/MPa200769 5607 1695 685400177 9177 0614 50060028 6677 8254 26380010 5408 9974 726
(a)
(b)
(c)
(d)
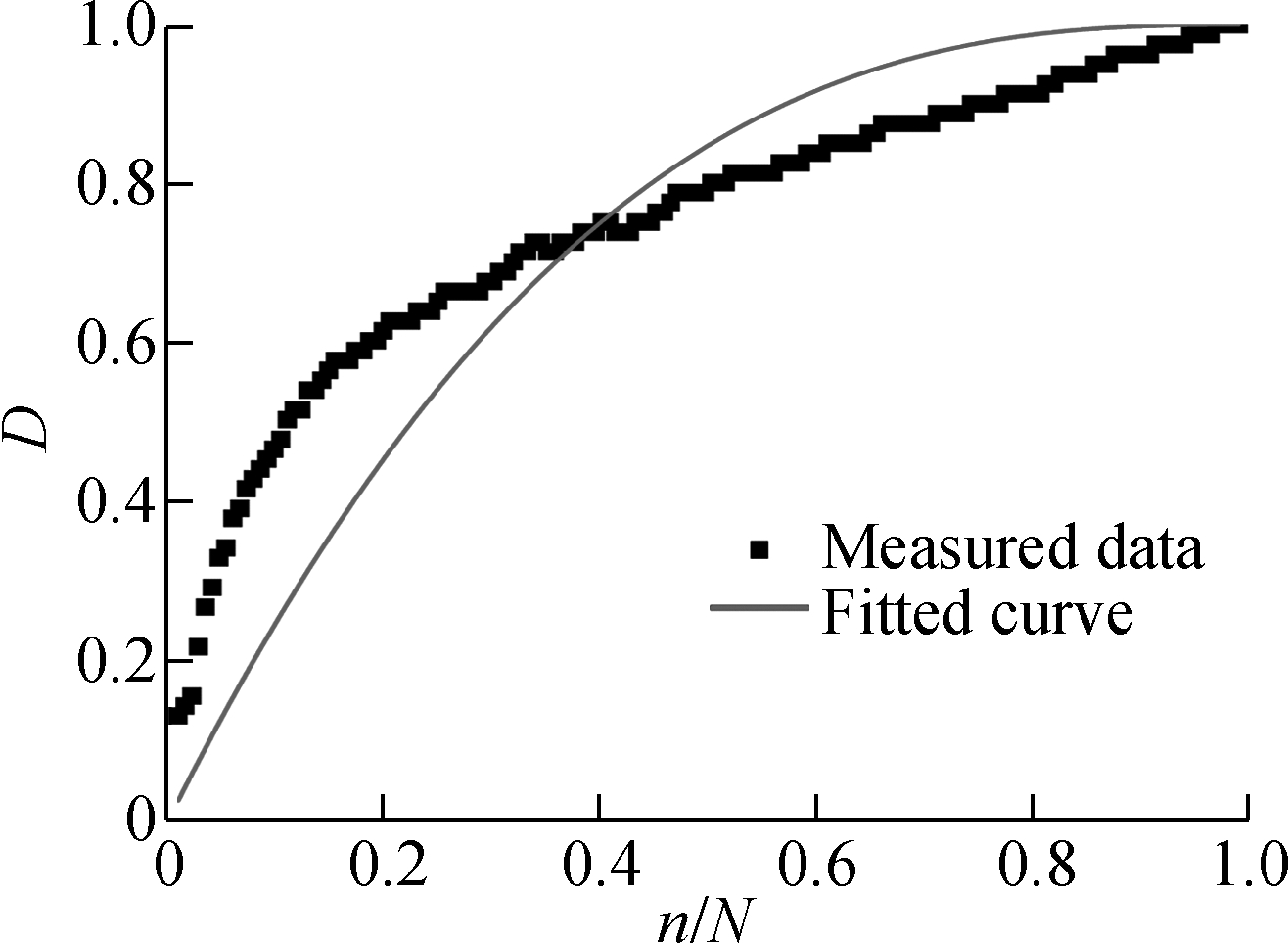
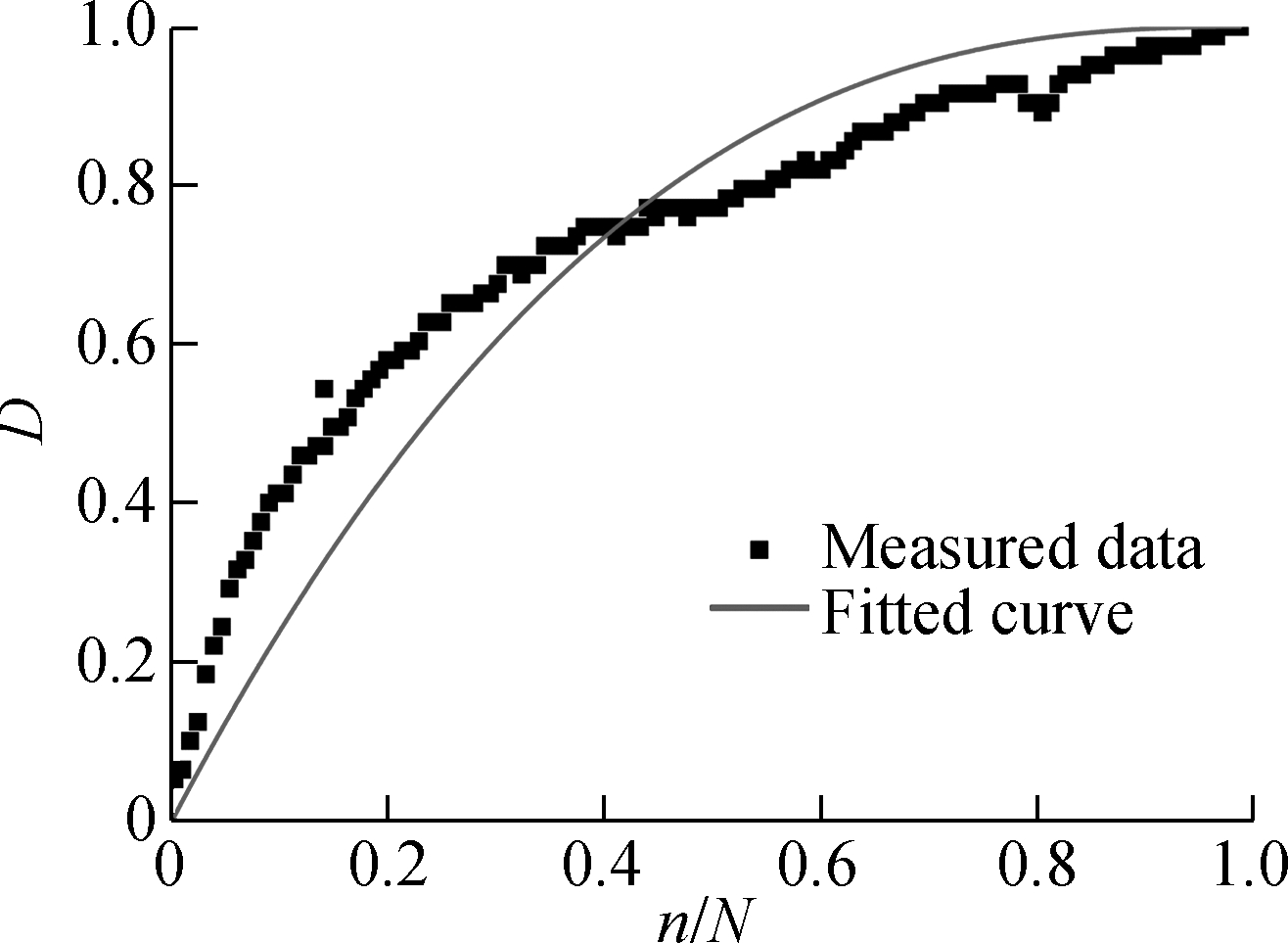
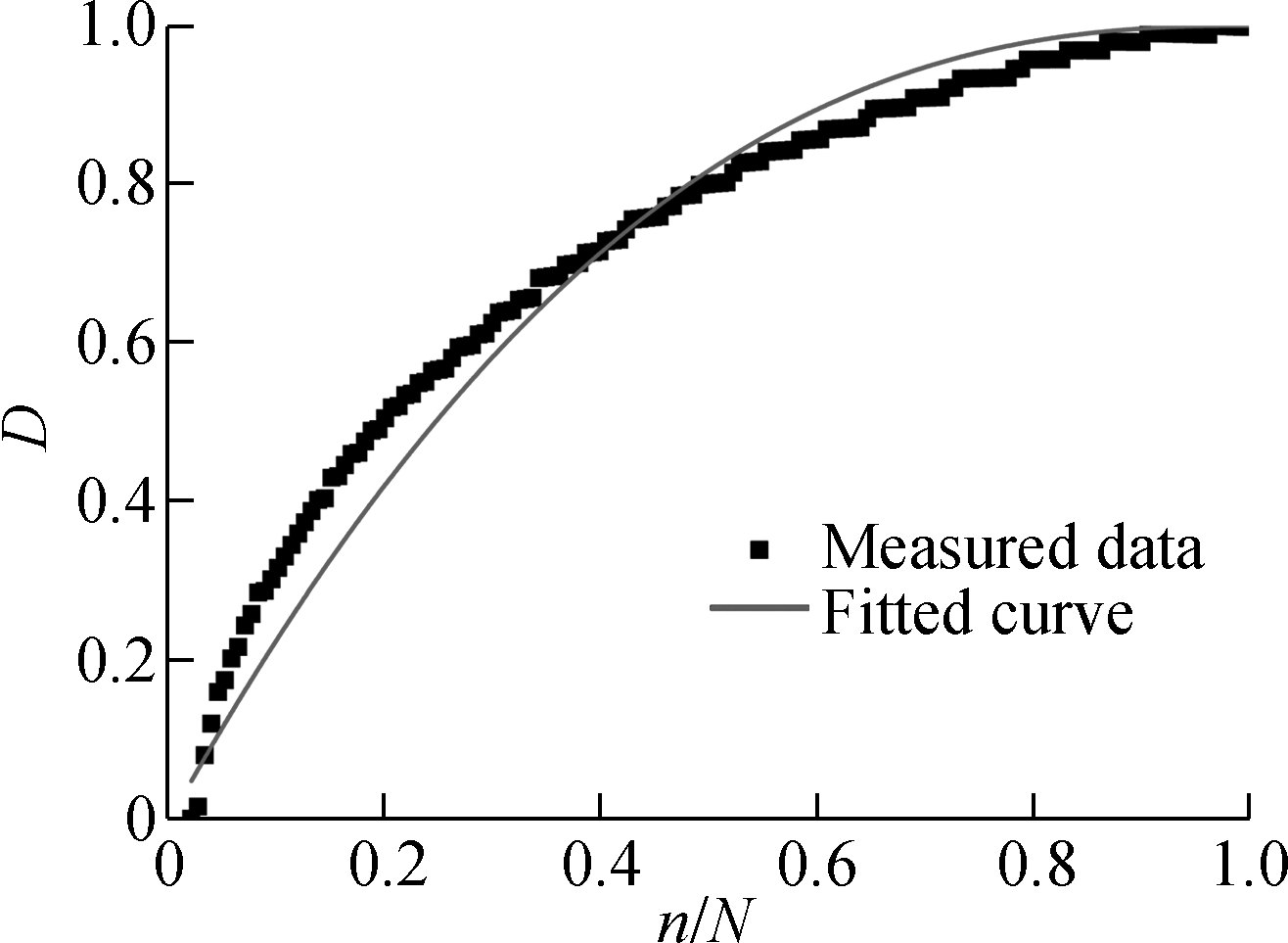
Fig.5 The damage evolution laws under different strain levels. (a) ε=2×10-4, m=0.706 4, R2=0.996;(b) ε=4×10-4, m=0.662 7, R2=0.975;(c) ε=6×10-4, m=0.614 7, R2=0.983;(d) ε=8×10-4, m=0.593 4, R2=0.958
As shown in Fig.5, the measured damage evolution is faster than that of the predicted result in the initial. The gap between them becomes smaller when the cycle number increases. It is because only the flexural modulus is used in representation of damage. The flexural modulus is calculated by the maximum tensile stress and the maximum strain of the beam during the bending test. However, the stress state is more compressive than that in the direct tensile test. According to Ref.[21], the attenuation laws of tensile modulus and compressive modulus are different. Thus, a more accurate damage model considering complex stress state should be established for the bending test in the future. Employing the deduced model, the correlation between m and strain level is shown in Fig.6.
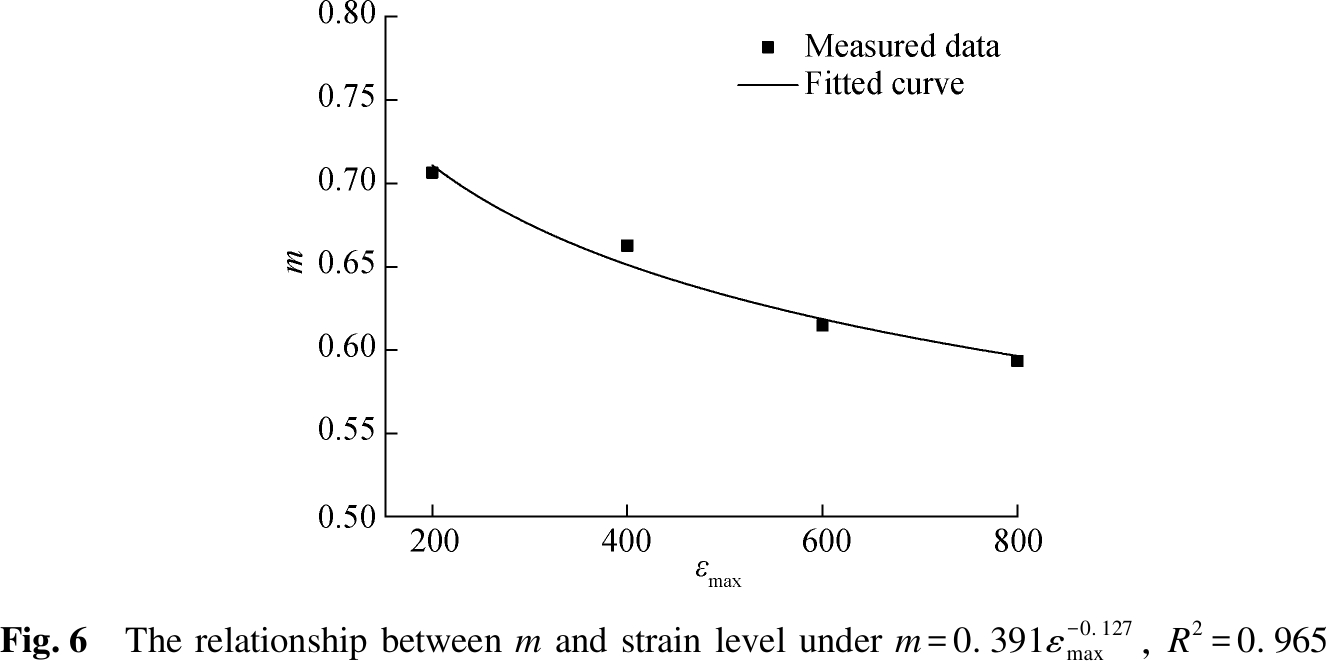
Thus, the fatigue damage evolution law of the asphalt mixture under a controlled-strain mode can be expressed as
(31)
3.3 Discussion
Considering the condition that m≥0, D≥0 
the characteristic curves of damage evolution with the increasing number of loading cycles are shown in Fig.7.
Fig.7 The damage evolution laws under two control modes
As shown in Fig.7 , the fatigue damage model interprets the kinematic laws of damage under two different control modes. During the processes of stress-controlled loading, damage evolves slowly in the initial stage while it increases abruptly before fracture. Inversely, under a strain-controlled mode, the damage evolution rate is high at first. A relatively stable platform appears in the latter part of the evolution curve.
When m=0, the fatigue damage model is the same as the Miner fatigue theory. It corresponds to the situation when a loading level is a specific value or large enough to destroy the specimen at once.
4 Interpretation in Multilevel Loading
The fatigue damage model can also interpret the effect of different loading sequences on the fatigue life of asphalt mixtures under two different control modes. The damage equivalence principle is used here to calculate the equivalent cycle numbers.
As shown in Fig.8, suppose that stress σ1 has been cyclically loaded for n1 times, the fatigue life of the second stress level σ2 needs to be predicted. To reach the same damage level under σ2, the equivalent cycle numbers of n1 is
(32)
(33)
Fig.8 Prediction of fatigue life under multilevel loading
The number of residual cycle is n2=N2-ne. The calculation process is the same as that under a controlled-strain mode.
The results 
predicted under two control modes is shown in Tab.3.
Tab.3 Normalized fatigue life under two control modes
Loading sequenceControlled-stress modeControlled-strain modeLow→High level>1<1High→Low level<1>1
The model interprets the fact that under a controlled-stress mode, a sequence from a low loading level to a high level can prolong fatigue life, which is similar to the training effect of metal. While under a controlled-strain mode, a sequence from a low level to a high loading level accelerates the damage evolution[9]. Further experimental validation will be conducted in the future.
5 Conclusions
1) A uniform fatigue damage model under two control modes is established based on thermodynamic laws. The damage variable related with dynamic modulus is deduced: 
2) The damage evolution law of asphalt mixtures under controlled-stress and controlled-strain modes can be interpreted by the model 
As the loading level decreases, the value of m increases.
3) The sequence of multilevel loading has inverse effects on the fatigue damage evolution under two control modes. A sequence from a low loading level to a high level can prolong fatigue life under a controlled-stress mode while it can accelerate the damage evolution under a controlled-strain mode.
4) The fatigue damage model for asphalt mixtures is simple enough for engineering use. However, in future research, the viscous dissipated energy and heat dissipation should be considered in the whole free energy.
[1]Kim J,Koh C. Development of a predictive system for estimating fatigue life of asphalt mixtures using the indirect tensile test[J]. Journal of Transportation Engineering, 2012, 138(12): 1530-1540. DOI:10.1061/(asce)te.1943-5436.0000452.
[2]Yang J, Wang H P, Liao H. Key influential factors of fatigue and self-healing properties of asphalt mixture[J].Journal of Southeast University (Natural Science Edition), 2016, 46(1): 196-201.(in Chinese)
[3]Yu J M, Tsai B W, Zhang X N, et al. Development of asphalt pavement fatigue cracking prediction model based on loading mode transfer function[J].Road Materials and Pavement Design, 2012, 13(3): 501-517. DOI:10.1080/14680629.2012.695240.
[4]Botella R, Pérez-Jiménez F E, Miro R, et al. New methodology to estimate the fatigue behavior of bituminous mixtures using a strain sweep test[J]. Construction and Building Materials, 2017, 135: 233-240. DOI:10.1016/j.conbuildmat.2016.12.190.
[5]Shen S H, Carpenter S. Development of an asphalt fatigue model based on energy principles[J]. Asphalt Paving Technology:Association of Asphalt Paving Technologists—Proceedings of the Technical Sessions, 2007, 76:525-573.
[6]Karki P, Li R, Bhasin A. Quantifying overall damage and healing behaviour of asphalt materials using continuum damage approach[J]. International Journal of Pavement Engineering, 2015, 16(4): 350-362. DOI:10.1080/10298436.2014.942993.
[7]Ni F J, Yu B,Gu X Y, et al. Characterization of fatigue damage of hot mix asphalt based on residual strength[J]. Journal of Materials in Civil Engineering, 2017, 29(8): 04017075. DOI:10.1061/(asce)mt.1943-5533.0001908.
[8]Liu H F. Research on nonlinear fatigue damage properties of asphalt mixture based on the decay of strength and stiffness [D]. Changsha: Changsha University of Science and Technology, 2012: 29-74. (in Chinese)
[9]Wu Z Y. Research on cumulative fatigue damage of asphalt mixture and asphalt layer based on multi-level amplitude loading [D]. Guangzhou: South China University of Technology, 2014: 24-62 (in Chinese)
[10]Castelo Branco V T F, Masad E, Bhasin A, et al. Fatigue analysis of asphalt mixtures independent of mode of loading[J]. Transportation Research Record: Journal of the Transportation Research Board, 2008, 2057: 149-156. DOI:10.3141/2057-18.
[11]Zheng J L. Application of burgers model to the analysis of fatigue characteristic of bitumous mixtures [J]. Journal of Changsha Communications Institute, 1995, 11(3)：32-42. (in Chinese)
[12]Shan L Y, Tan Y Q, Xu Y N, et al. Fatigue damage evolution rules of asphalt under controlled-stress and controlled-strain modes[J]. China Journal of Highway and Transport, 2016, 29(1): 16-21,74. DOI:10.19721/j.cnki.1001-7372.2016.01.002.(in Chinese)
[13]Masad E, Castelo Branco V T F, Little D N, et al. A unified method for the analysis of controlled-strain and controlled-stress fatigue testing[J]. International Journal of Pavement Engineering, 2008, 9(4): 233-246. DOI:10.1080/10298430701551219.
[14]Sun B, Li Z X. A multi-scale damage model for fatigue accumulation due to short cracks nucleation and growth[J].Engineering Fracture Mechanics, 2014, 127: 280-295. DOI:10.1016/j.engfracmech.2014.06.014.
[15]Onifade I, Birgisson B, Balieu R. Energy-based damage and fracture framework for viscoelastic asphalt concrete[J]. Engineering Fracture Mechanics, 2015, 145: 67-85. DOI:10.1016/j.engfracmech.2015.07.003.
[16]Onifade I, Balieu R, Birgisson B. Interpretation of the Superpave IDT strength test using a viscoelastic-damage constitutive model[J]. Mechanics of Time-Dependent Materials, 2016, 20(3): 421-439. DOI:10.1007/s11043-016-9297-9.
[17]Lematre J. A course on damage mechanics [M]. New York: Springer-Verlag, 1996: 96-97.
[18]Zhu H R, Sun L.A viscoelastic-viscoplastic damage constitutive model for asphalt mixtures based on thermodynamics[J]. International Journal of Plasticity, 2013, 40: 81-100. DOI:10.1016/j.ijplas.2012.07.005.
[19]Li Z X, Chan T H T,Ko J M. Fatigue damage model for bridge under traffic loading: Application made to Tsing Ma Bridge[J]. Theoretical and Applied Fracture Mechanics, 2001, 35(1): 81-91. DOI:10.1016/S0167-8442(00)00051-3.
[20]Chan T H T, Li Z X,Ko J M. Fatigue analysis and life prediction of bridges with structural health monitoring data: Part Ⅱ: application[J]. International Journal of Fatigue, 2001, 23(1): 55-64. DOI:10.1016/S0142-1123(00)00069-4.
[21]Lü S, Wang X Y, Liu C C, et al. Fatigue damage characteristics considering the difference of tensile-compression modulus for asphalt mixture[J]. Journal of Testing and Evaluation, 2018, 46(6): 20170114. DOI:10.1520/jte20170114.