As more vehicles are driven on the road, traffic conflicts and vehicle collisions take place much more frequently than before. Especially around urban intersections and highway on-ramps, merging vehicles have to adjust their speeds based on the observed state of vehicles on their target lane. The interactions between vehicles are partly responsible for capacity drops and even traffic congestion[1-2]. Comparatively, the situation is worse on highways. Different vehicles generally have different driving properties. It is difficult for merging drivers to judge whether other drivers will yield during their merging maneuvers. Apart from that, special topographical conditions such as circular ramps or upslopes tend to cause blind zones. As a result, merging drivers are likely to make wrong decisions. For example, they may operate merging maneuvers without noticing approaching vehicles. In such a case, it is possible that serious traffic accidents arise.
Several studies have focused on mitigating merging conflicts around certain bottlenecks. To reduce traffic jams around on-ramps, ramp metering and variable speed limits are developed and widespread[3-4]. Ramp metering is utilized to adjust the traffic flow merging from on-ramps. Common strategies of ramp metering include local ramp metering and coordinated ramp metering[5-6]. Variable speed limit is mainly used for traffic safety. It not only warns drivers of downstream congestion and potential collisions, but also provides a real-time speed limit to upstream traffic flow in some urgent situations[7]. Although both ramp metering and variable speed limit can effectively decrease traffic accidents and improve traffic efficiency, their deployment highly depends on fixed detectors. Traffic state information received by traditional sensors only involves traffic flow characteristics at certain points. Therefore, the methods of ramp metering and variable speed limit take little account of individual vehicles’ dynamic properties.
With advanced sensing and communication technologies, a connected vehicle environment has been regarded as the future trend of the transportation system. This new technology is applied in various aspects to improve traffic performance, including traffic safety[8], intersection signal control[9-10], performance assessment of traffic flow[11-12] and dynamic control of intelligent vehicles[13-14]. With regard to interactions between mainline and on-ramp vehicles, connected vehicle technology can enhance traffic safety and significantly increase traffic efficiency. Accordingly, the control framework and control programs are implemented[15]. In the merging control method developed in this paper, the state information of connected and automated vehicles is sent to the roadside control unit, and then the control command is transmitted back to the individual vehicle[16]. It is assumed that vehicles within the control range are completely subject to control instructions.
This paper proposes a cooperative merging control strategy where merging trajectory planning is turned into an optimal control problem. To achieve the minimization of vehicle acceleration as the optimization objective, the classical variational method and the quadratic programming method are sequentially discussed. Also, an ACC model is introduced for avoiding omissions. Based on the characteristics of control and state variables under various control methods, the arrival time and possible optimal time of a single vehicle are determined and used for control instructions. The arrival time here means the time vehicle spends driving from the current position to the merging point, while the optimal time represents the time covered by either optimization method. In this way, merging orders are formed accordingly, in which vehicles from both the main road and on-ramp pass the merging point.
1 Related Work
Most earlier studies on merging control focused on the automated highway system (AHS)[17]. Kachroo and Li[18] discussed the characteristics (acceptability, availability and pursuability) of merging gaps. Given acceptable gaps, three different control laws—linear, optimal and parabolic control laws were introduced. Antoniotti et al.[19] proposed a merging control algorithm to improve the merging operation on highways with several junctions. The control of on-ramp and mainline vehicles involved merging and yielding maneuvers, respectively. In 1999, Ran et al.[16] put forward a control model. It was made up of infrastructure support, vehicle to vehicle (V2V) cooperation, and dynamic control of individual vehicles. The V2V cooperation was expected to create acceptable gaps. Afterwards, a real-time merging algorithm for AHS was proposed by Lu et al[8]. Based on the speed of main lane vehicles, it was intended to provide merging trajectory planning for on-ramp vehicles.
Under the connected vehicle environment, vehicle to infrastructure (V2I) communications enable real-time information exchange between vehicles and roadside control units. Under such circumstances, automated control strategies are implemented for cooperative merging operations[20-22]. A merging control system in a connected vehicle environment is generally divided into two parts. The higher-level controller determines the merging sequence and the lower focuses on merging trajectories.
Regarding the lower-level controller, merging control of individual vehicles is usually considered to be an optimization problem. Assuming that all the vehicles were connected and automated, Xie et al.[15] proposed a merging control strategy. A nonlinear optimization problem is formulated, taking second-by-second vehicle accelerations as decision variables. Rios-Torres et al.[23] optimized vehicle acceleration with a closed-form solution. This method was verified by simulation, with fuel consumption and travel time of connected vehicles considerably reduced. Roncoli et al.[24] put forward a lane-changing control strategy for vehicles at motorway bottlenecks. It was an extended version of an optimal control strategy and was intended for the maximization of traffic throughput. In 2016, Ntousakis et al.[25] proposed a merging control algorithm for longitudinal trajectory planning of merging vehicles. The control problem minimized vehicle acceleration, its first derivative and second derivative, respectively. Later, Ntousakis et al.[26] extended the finite-horizon optimal control problem. A time-varying linear quadratic regulator method was taken and model predictive control (MPC) was applied.
It should be noted that most studies on the lower-level controller make the assumption that the merging sequence of vehicles has been determined by a higher-level controller. However, there is actually very little research considering merging sequence. Athans[27] discussed several existing merging sequences and chose the optimal one to perform the merging operation. On the basis of the selected merging sequence, the linear time-invariant optimal regulator was utilized to make control planning. Li et al.[28] proposed a solution tree generation algorithm to implement cooperative driving at lane closures. With appropriate driving schedules provided by this algorithm, vehicles can pass the closing point safely. Nevertheless, the determination of the merging sequence in the above two studies takes much time, which is unsuitable for real-time application. Ntousakis et al.[29] discussed two merging sequence algorithms to determine the vehicle order passing the merging point. The first algorithm was based on the first-in-first-out (FIFO) rule, which defines the vehicle order as the sequence of entering the control zone. The merging sequence in the second algorithm is dependent on the time that vehicles spent going to the merging point at a certain constant speed. Both algorithms are easy to operate but barely correspond to the real driving characteristics of the vehicles.
2 Method
2.1 Cooperative control area
As shown in Fig.1, the cooperation section consists of a highway segment, an on-ramp and an acceleration lane. A roadside control unit is assumed to be located at the junction of the main road and the on-ramp. The communication range of this control unit is regarded to be a constant. Here, the dedicated short-range communication (DSRC) is the wireless communication technology applied to the connected vehicle environment. For the sake of simplicity, lane-changing behavior is not allowed within this region. So, only the rightmost lane of the main road and the one-lane on-ramp are considered. Besides, the position of a certain on-ramp vehicle is approximated as its position in the main lane (the shaded block in Fig.1), where it is mapped with the base point of the control unit.
All the vehicles involved are assumed to be wirelessly connected and automatically controlled. When a vehicle enters the control zone, it sends state information to the roadside control unit via V2I communication in real time. The information includes the instantaneous speed, acceleration and position. In view of the characteristics of the merging trajectory, the control unit determines arrival time as well as optimal time included. Corresponding control instructions are then transmitted to the individual vehicle. In Fig.1, a merging point is fixed for all vehicles to reduce complexity. Also, it is at the edge of the control zone so that vehicles have enough time to adjust their speeds before merging maneuvers. The following subsections describe the optimal control methods in detail and the cooperative merging control strategy.
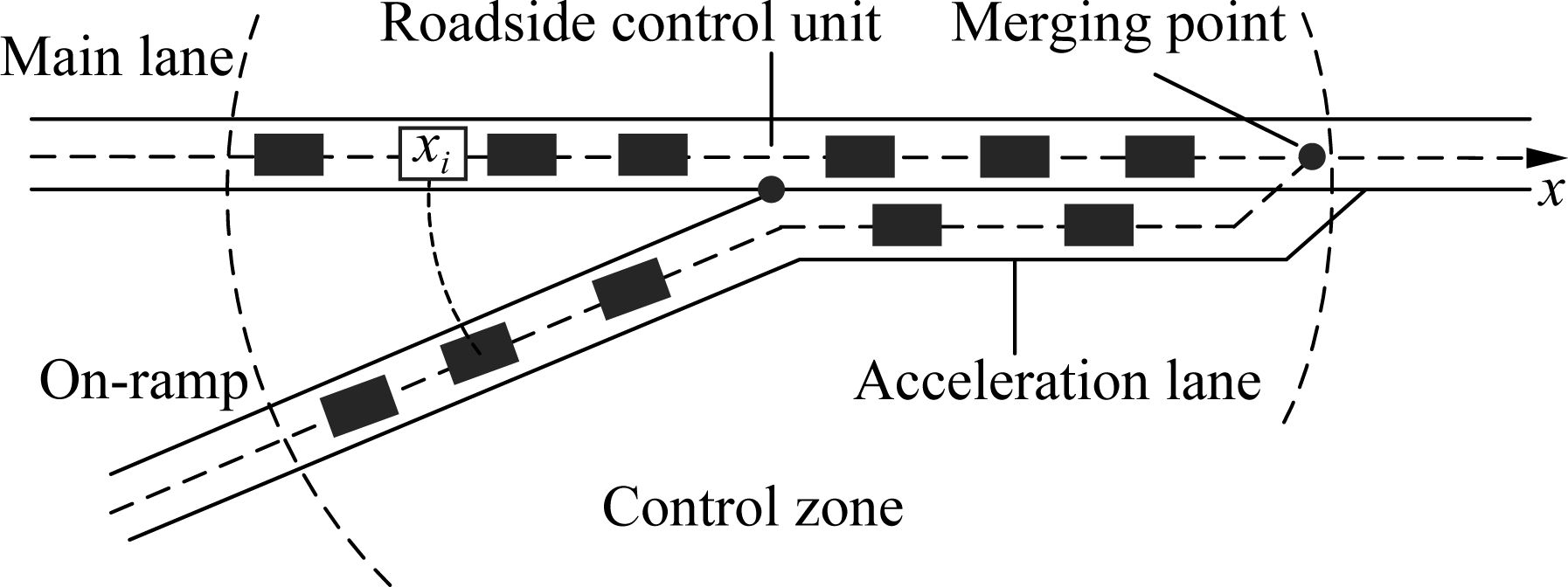
Fig.1 Cooperation area of mainstream lane and on-ramp
2.2 Optimal control model
The control of each vehicle is regarded as a discrete process which is composed of several time intervals. Vehicle state (position and velocity) at a certain time is largely influenced by the state at the end of the last time interval and the control variable (acceleration) during the current time interval:
where k is the index of time interval; v(k) and x(k) are the vehicle speed and position at the end of time interval k, respectively; and u(k) is the vehicle acceleration during this interval, which is assumed to be a constant. The length of each interval is set to be τ.
As fuel consumption monotonically increases with vehicle acceleration, minimizing vehicle acceleration can indirectly minimize fuel consumption[23]. Furthermore, the minimization of acceleration can improve passenger comfort to some extent[25]. Therefore, the optimal control problem for a single vehicle is expressed to minimize the sum of squares of acceleration:
where ψ is the total number of time intervals involved in the vehicle’s control process.
The whole control process is divided into two parts, ψ=m+mcs, where m and mcs are the number of time intervals in the optimal control process and the constant speed process, respectively. In the first part, vehicle accelerations are determined by an optimization method which is either the variational method or the quadratic programming method. Then, vehicle speed remains constant. The above optimization function is accordingly transformed into min ![]()
In the optimal control process, the initial state (v(0) and x(0)) and the final state (v(m) and x(m)) are known. In addition, the optimal control problem needs to satisfy the following constraints:
![]() ∀k∈[0,ψ]
∀k∈[0,ψ]
where umin, umax are the minimum deceleration and the maximum acceleration; i, i+1 are the indices of two contiguous vehicles in the same lane; and xsafe is the safe space for avoiding collisions.
2.2.1 Classical variational method
The variational method has been widely used for analytical solutions in optimal control problems. Considering the necessary conditions in Ref.[30] and vehicle dynamics mentioned above, variations of acceleration, speed and position are expressed as
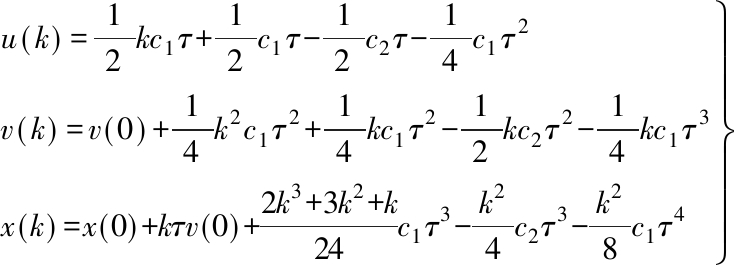
where c1 and c2 are the constants. Given the optimal time and the initial and final conditions, it is easy to judge whether the results obtained by this method are under constraints or not.
2.2.2 Quadratic programming method
In theory, using the variational method to search for completely constrained variables severely restricts the selection of arrival time and optimal time. On some occasions, no combination of these two parameters can be found to make control results satisfy all the constraints. Comparatively, the quadratic programming method is more flexible as it always takes constraints into account during the optimization. In this method, the constraints are the same as those listed in the preceding section.
2.2.3 Adaptive cruise control model
It is likely that no feasible solution is obtained by either of the above two methods. In such a case, the ACC control law is utilized as compensation. Unlike the variational method or the quadratic programming, it covers the whole control process. The ACC model applied is formulated as[25]
ades=K1(vf-vl)+K2(xl-xf-hdvf)
where ades is the desired acceleration; vf, xf are the speed and position of the following vehicle; vl, xl are the speed and position of the leading vehicle; hd is the desired time headway; and K1, K2 are the constants which are set to be 1.19 and 1.72, respectively.ades is limited to the range of the minimum deceleration and the maximum acceleration. This model aims at the same speed as the leading vehicle with a constant headway. The calculation of the desired acceleration is implemented repeatedly for each control variable in each time interval.
2.3 Cooperative merging control strategy
The cooperative merging control strategy determines the control variables of the whole control process when a new vehicle reaches the control area. When the variational method or the quadratic programming method works, vehicle accelerations in the optimal control process are produced. Vehicle acceleration after this process is expected to be zero. If neither of them is workable, the ACC model is employed. The actual arrival time of the new vehicle depends on the results of the ACC model. As shown in Fig.2, the priority of the variational method, the quadratic programming method and the ACC model are in descending order.
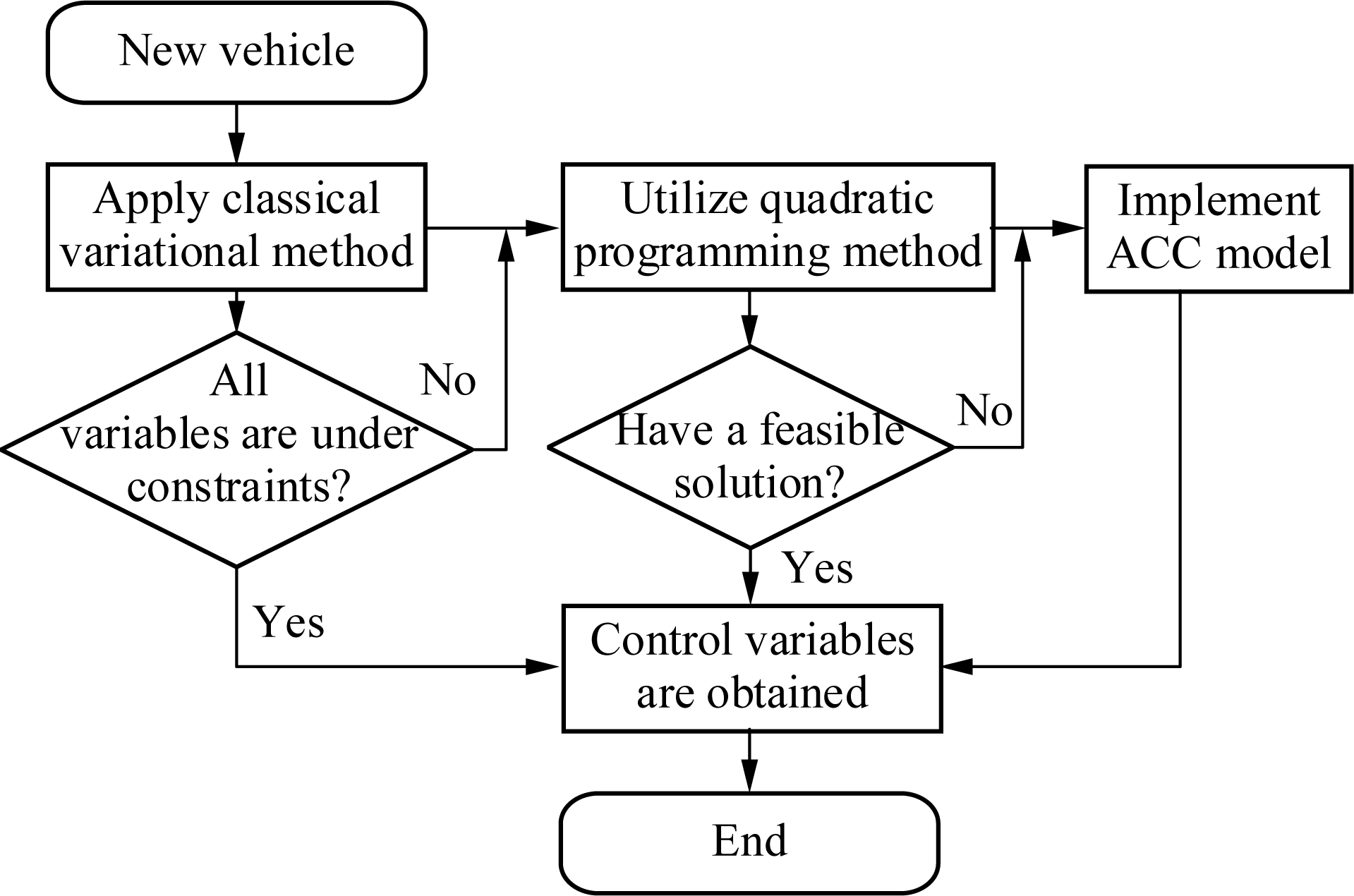
Fig.2 Flowchart of cooperative merging control strategy
When a vehicle enters the cooperation zone, the variational method is tried first. The specific process is presented in Fig.3 and has the following steps:
Step 1 Collect information about the remaining arrival time of vehicles in the cooperation area and trajectory of the actual leader. If this vehicle is an on-ramp vehicle, go to Step 2.1, otherwise Step 2.2.
Step 2.1 Initialize the arrival time by adding a desired time headway on the maximum arrival time collected in Step 1.
Step 2.1.1 Increase the optimal time from zero to arrival time with a one-second increment each time. If control and state variables under current arrival time and optimal time satisfy constraints, select this combination and go to Step 3. Otherwise, the next optimal time is tried similarly. If no optimal time meets requirements, go to Step 2.1.2.
Step 2.1.2 If no combination of arrival time and optimal time meets requirements, drop the current method and try the quadratic programming method. Otherwise, increase the current arrival time with a one-second increment and repeat the process in Step 2.1.1.

Fig.3 Application of variational method/quadratic programming method
Step 2.2 Initialize the arrival time by adding a desired time headway to the remaining arrival time of the actual leader.
Step 2.2.1 If the value of arrival time conflicts with any on-ramp vehicle’s (the gap between two arrival times is less than hd), increase it with a one-second increment until no conflict arises. After that, the selection of the optimal time is similar to that in Step 2.1.1. If no one meets the requirements, go to Step 2.2.2, otherwise go to Step 3.
Step 2.2.2 If all combinations have been tried but none of them meets requirements, drop the current method and try the quadratic programming method. Otherwise, increase the current arrival time with a one-second increment and repeat the process in Step 2.2.1.
Step 3 Generate vehicle merging trajectory with control variables derived from a given arrival time and optimal time. All information is temporarily stored in the control unit, which may be used for the next new vehicle.
When the variational method is not applicable, the quadratic programming method is tried. The specific process is very similar to the operation under the variational method. It is also divided into three steps, of which descriptions are omitted due to limited space. The key difference between the two methods lies in the judgement basis for the selection of the arrival time and optimal time. As shown in Fig.3, a feasible solution can be obtained by the quadratic programming method.
If neither the variational method nor the quadratic programming method is in operation, the ACC model is implemented. The optimal process is no longer involved and vehicle trajectory during the whole process is totally determined by the ACC model. Based on trajectory information of the actual leader stored in the roadside control unit, the model calculates accelerations of the new vehicle step by step.
3 Results
3.1 Simulation set-up
To verify the proposed strategy, a highway on-ramp merge area with the layout in Fig.1 is simulated in Matlab. The range of the control area is set to be 200 m, which is within the communication range of DSRC. The direction of the x-coordinate is consistent with the driving direction. Then, the position of the control unit is 0, the start position of the cooperation area is -200 m, and the merge point position is 200 m. The minimum deceleration and the maximum acceleration are -3 and 3 m/s2, respectively. Vehicles involved are assumed to have the same properties and their lengths are set to be 5 m. The simulation time for each scenario is 30 min and time interval τ is set to be 0.1 s. It is assumed that traffic inflow from the on-ramp to the cooperation zone is controlled by a fixed-time traffic signal. The green time ratio is 0.5.
3.2 Traffic performance with variations of simulation parameters
In simulation scenarios, green time, safe spacing and desired time headway seem to be the most important parameters. Their impacts on traffic performance are evaluated by three traffic demand levels—low, medium and high levels. Some parameters in above cases are listed in Tab.1.
Tab.1 Simulation parameters in various traffic demand scenarios

Traffic demandTraffic volume/(vehicle·h-1)Main laneOn-rampDesired speed/ (m·s-1)Low50030025Medium1 00050022High1 50080019
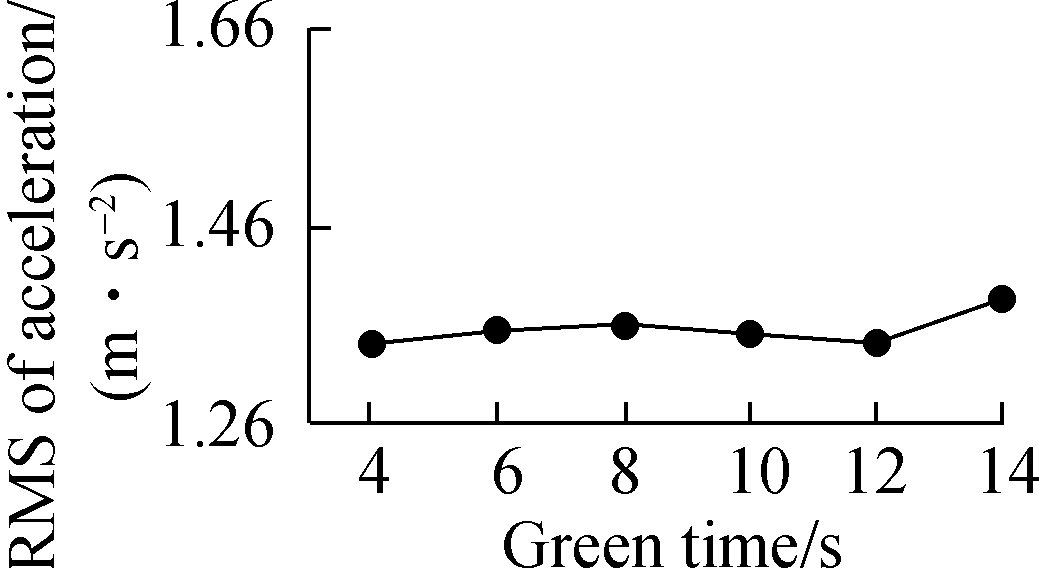
Due to limited space, only results in the medium scenario are presented. Figs.4 to 7 illustrate the RMS of acceleration, average speed, RMSE of time headway and collision rate under various simulation parameters. Note that the collision rate is the ratio of the collision number of adjacent vehicles to the combined number of adjacent vehicles. It can be found that the desired time headway has greater impact compared to green time and safe spacing.
(a) 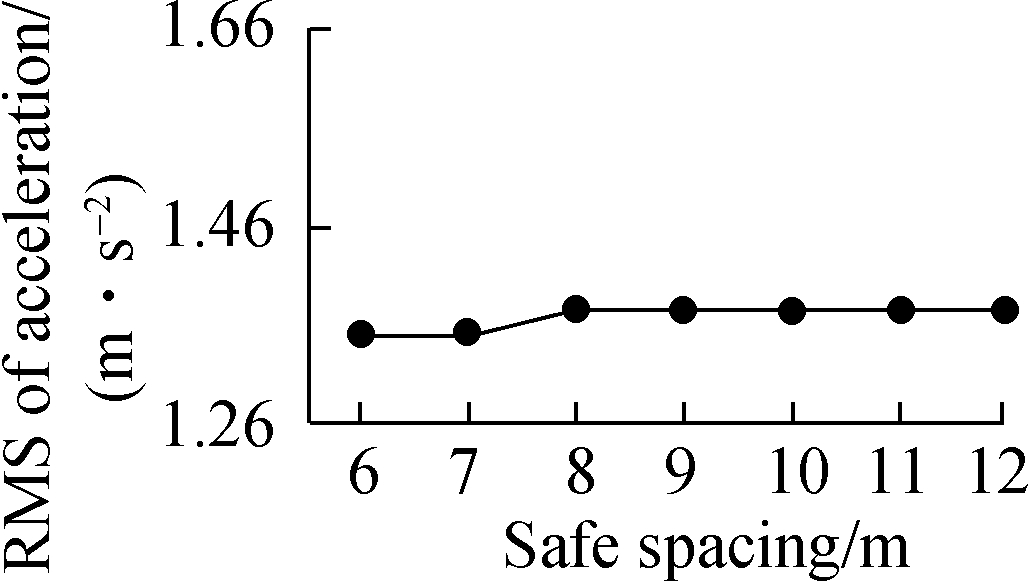
(b) 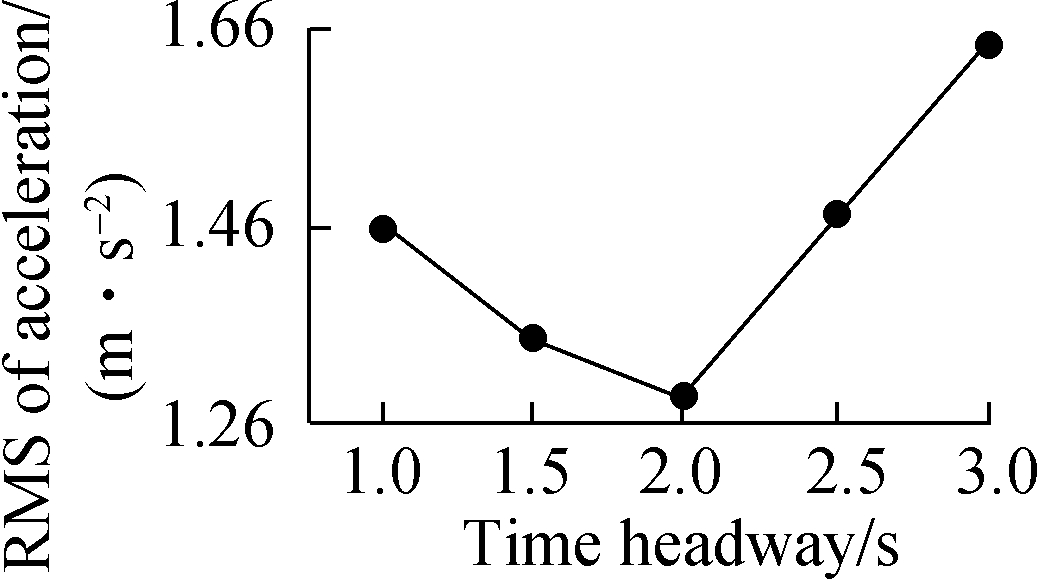
(c)
Fig.4 RMS of acceleration with various parameters. (a) Green time; (b) Safe spacing; (c) Time headway
(a) 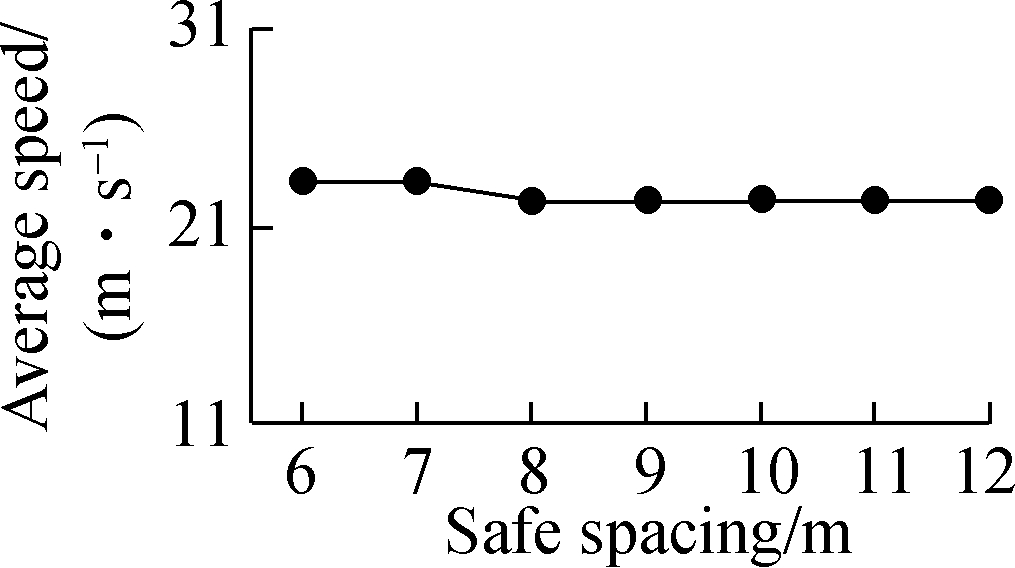
(b) 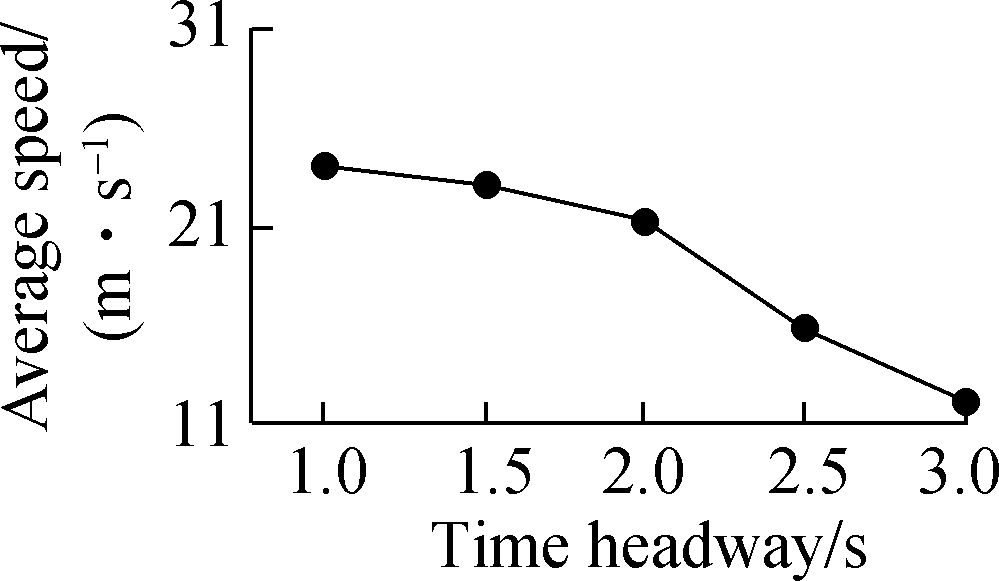
(c)
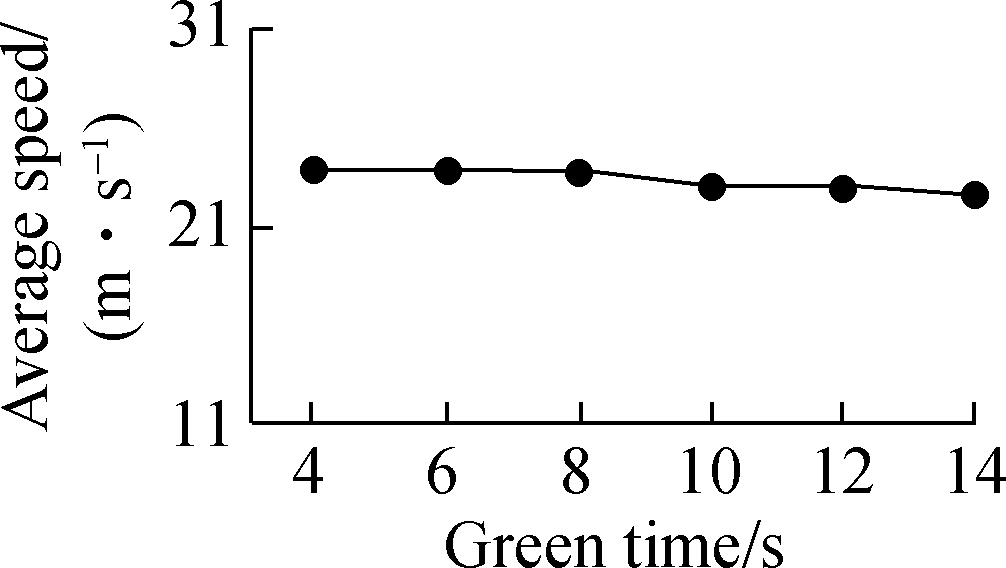
Fig.5 Average speed with various parameters. (a) Green time; (b) Safe spacing; (c) Time headway
(a) 
(b) 
(c)
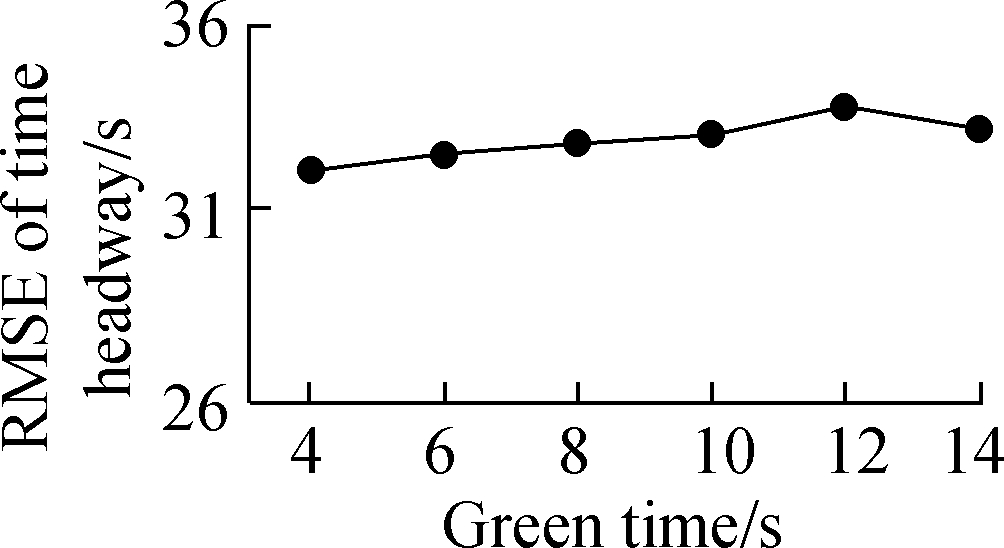
Fig.6 RMSE of time headway with various parameters. (a) Green time; (b) Safe spacing; (c) Time headway
(a) 
(b) 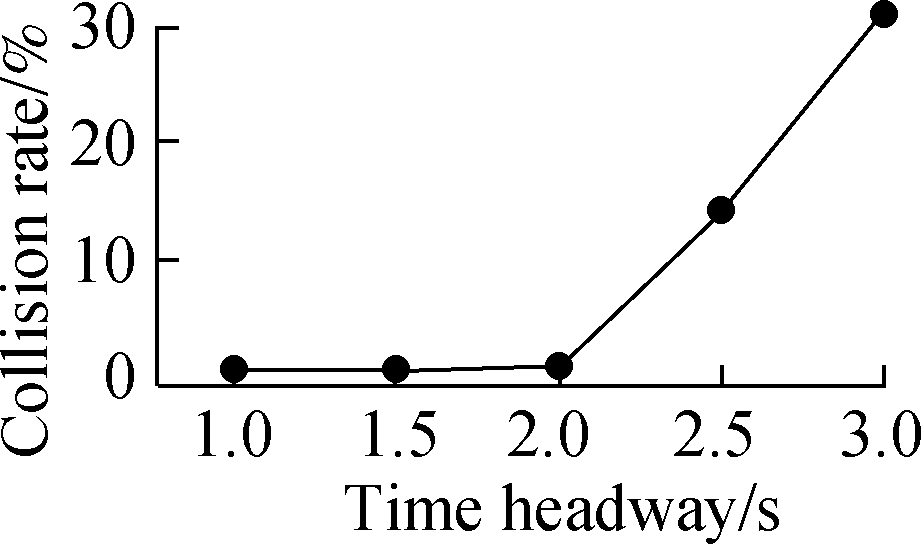
(c)
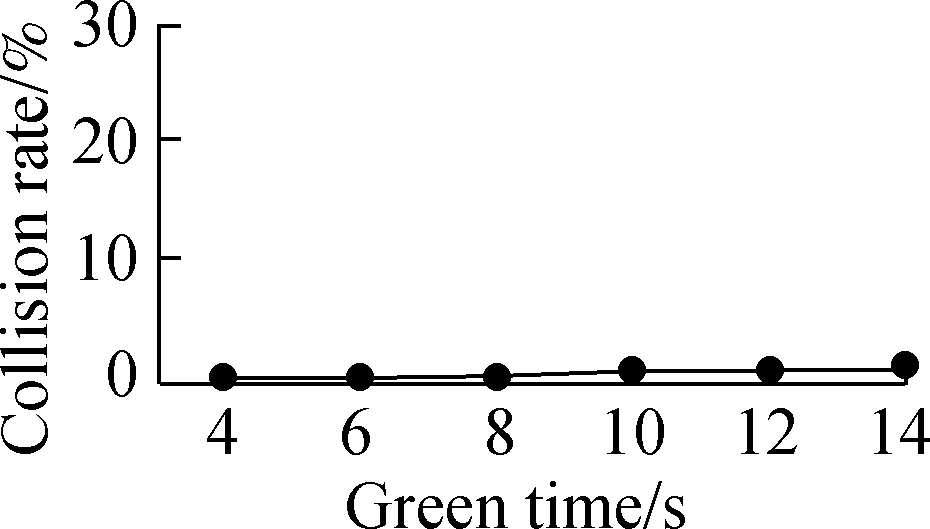
Fig.7 Collision rate with various parameters. (a) Green time; (b) Safe spacing; (c) Time headway
The RMS of acceleration in Fig.4(c) drops from 1.46 to 1.28 m/s2 when the desired time headway increases from 1 to 2 s. After that, it has a sharp increase to 1.66 m/s2, where the desired time headway is 3 s. When the desired time headway is smaller than 2 s, the following vehicles constantly adjust their accelerations to be close to the actual leaders and meet safety requirements at the same time. The variation of vehicle acceleration is frequent, which is responsible for a higher RMS of acceleration. Similarly, when a high desired time headway is set, vehicles continually change their accelerations to follow leading vehicles with enough spacing. In Fig.5(c), the average speed shows a reduction trend as the desired time headway increases. This may be due to the fact that the following vehicles are induced to move at a relatively low speed to create a higher time headway with their leaders. The RMSE of time headway in Fig.6(c) is dramatically decreased when the desired time headway is less than 2.5 s. This value then slightly goes up with the increase in the desired time headway. In such a traffic demand case, it is more likely to form vehicle platoons with a 2.5 s time headway than other setting values. The collision rate (see Fig.7(c)) has a slow rise as the desired time headway changes from 1 to 2 s and then it grows noticeably. As the desired time headway increases, especially more than 2 s, more extreme decelerations are produced and lead to a growing collision rate. In contrast, more than four performance indicators maintain the same level with the variation of green time or safe spacing. In particular, the collision rate is approximately zero during the variations of green time (see Fig.7(a)) and safe spacing. In a low or high demand case, the impacts of the three parameters on traffic performance are extremely close to those in the above analysis. Accordingly, in the following test scenarios, green time and safe spacing are set to be constant (10 s and 6 m, respectively). The desired time headways with low, medium and high demand is 2, 2 and 1.5 s, respectively.
3.3 Traffic performance with various traffic demand levels
With above simulation parameters, the proposed strategy is tested and compared with the optimal control-based strategy in Ref.[25]. In the reference strategy, vehicle accelerations solved by the optimal control method and the ACC model are compared in each time interval. The most restrictive one is selected. Whenever a new vehicle enters the control zone, the second algorithm in Ref.[29] is employed to provide the merging sequence. With an Intel Core i5-3230M CPU (2.60 GHz) and 4.00 GB RAM, the average processing time for the proposed strategy is about 0.08 s. It is short enough and is negligible in this paper.
Simulation results at low, medium and high demand levels are shown in Tab.2. It is clear that the cooperative merging control strategy consistently outperforms the optimal control-based strategy in all demand scenarios. These results are graphically shown in Fig.8.
Tab.2 Traffic performance with various traffic demand levels

Traffic indicatorLowOptimal controlCooperative controlMediumOptimal controlCooperative controlHighOptimal controlCooperative controlRMS of acceleration/(m·s-2)6.991.3513.641.359.731.27Average speed/(m·s-1)32.4724.8735.6922.8830.7219.27RMSE of time headway/s73.8857.5844.0932.9827.0220.72Collision rate/%0.310 4.670 11.563.16
(a)
(b)
(c)
(d)
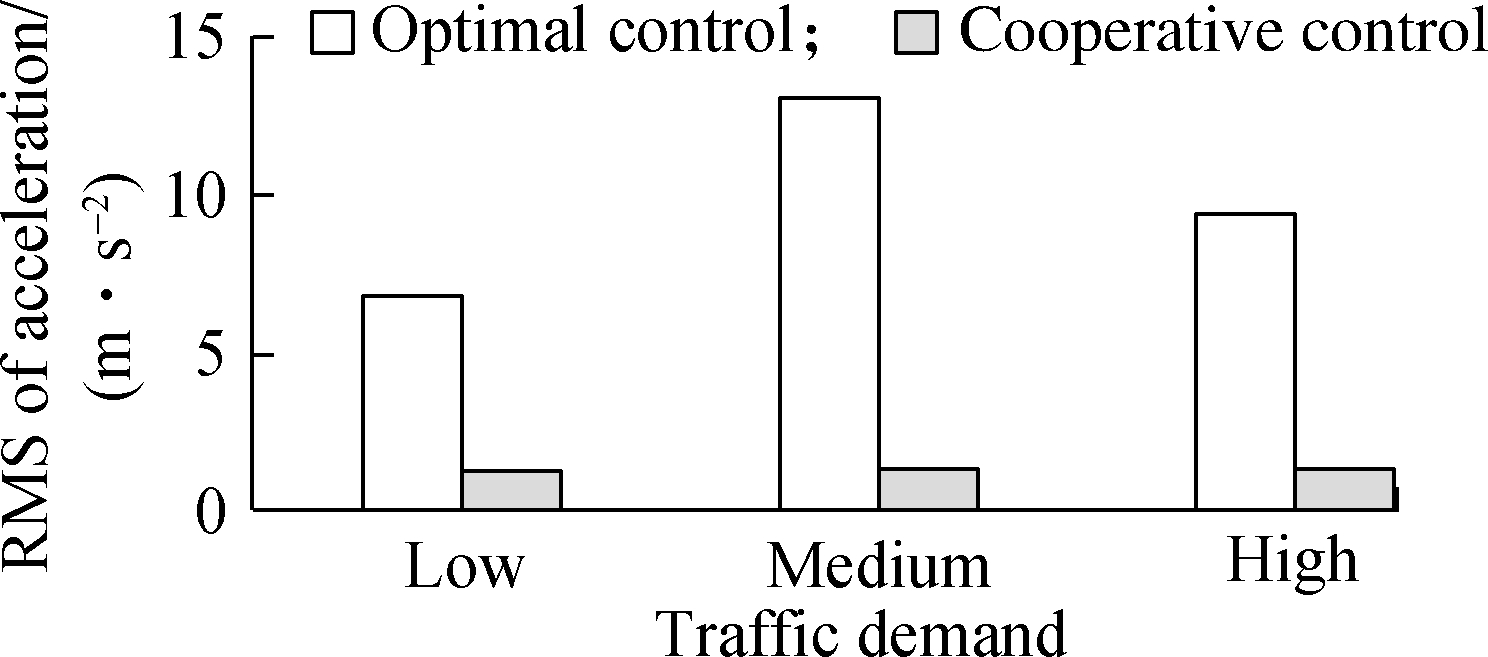
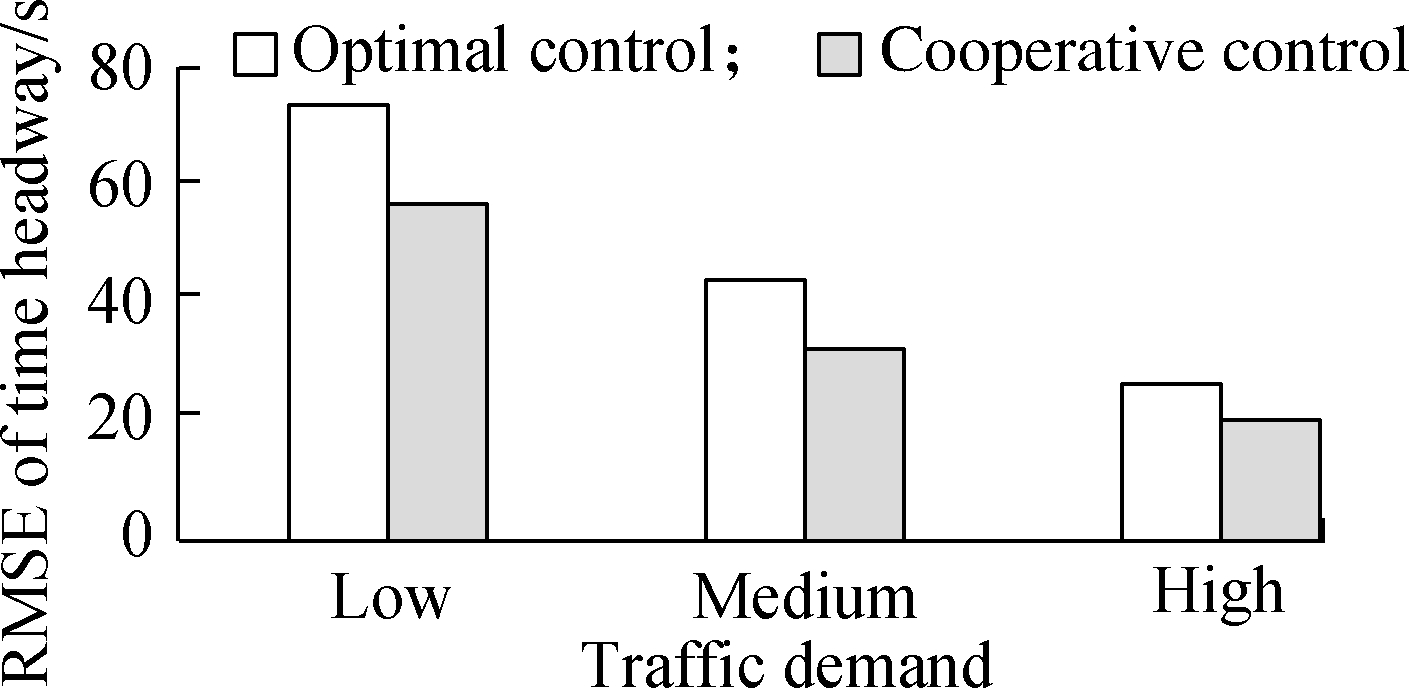
Fig.8 Traffic performance under various traffic demand levels. (a) RMS of acceleration; (b) Average speed; (c) RMSE of time headway; (d) Collision rate
In Fig.8(a),the RMS of acceleration in the optimal control strategy shows significant changes in the variation of traffic demand. The largest value (13.64 m/s2) is medium demand, which indicates low passenger comfort. It remains stable (around 1.3 m/s2) in the cooperative control strategy and is considerably lower than the reference strategy at each demand level. With regard to traffic efficiency (see Fig.8(b)), despite the higher average speeds in the optimal strategy than in the proposed strategy, they remain far from the desired values. Especially in the medium demand case, the relative error between the average speed and desired speed reaches up to 62.23%, which is much higher than that in the proposed strategy. The RMSE of time headway in Fig.8(c) decreases with the increase in traffic demand, both in the optimal control strategy and the cooperative control strategy. At the same time, the gap between these two strategies drops from 16.3 s in a low demand level to 7.7 s in a high demand case. Therefore, when the traffic volume increases, the improvement of the new control scheme in traffic flow stability decreases. Moreover, the proposed strategy improves traffic safety, as shown in Fig.8(d). In medium and high demand conditions, collision rates (0 and 3.16%) are much lower compared with the optimal control strategy (4.67% and 11.56%, respectively).
The results of the simulation tests in Matlab show that the most important simulation parameter in the new control scheme is the desired time headway. Before this strategy is implemented, an appropriate value of the desired time headway needs to be set. In comparison, traffic performance indicators are little influenced by green time and safe spacing. In strategy implementation, the values of the above two parameters can be selected from common values without particular consideration. In addition, it is demonstrated that the proposed cooperative merging control strategy can provide safe and efficient control instructions for vehicles around a highway on-ramp. Compared with the optimal control-based strategy, the cooperative merging control strategy performs better in various traffic demand conditions, in terms of RMS of acceleration, average speed, RMSE of time headway and collision rate.
4 Conclusions
1) The collaborative merging control strategy provides control instructions for merging trajectory planning of individual vehicles. To solve the optimal control problem of vehicle acceleration, the classical variational method or the quadratic programming method is used. An ACC control law is additionally presented for compensation.
2) Simulation tests in Matlab illustrate that the desired time headway has significant impacts on traffic performance while green time and preset safe spacing have little impact. Additionally, the effectiveness of the proposed strategy is verified in terms of passenger comfort, traffic efficiency, traffic stability and safety.
3)The cooperative merging strategy compares three different control methods without consideration of the time delay caused by computational delay and communication latency. This issue needs to be dealt with in the following study of real-time applications.
[1]Wan X, Jin P J,Yang F, et al. Modeling vehicle interactions during merge in congested weaving section of freeway ramp[J]. Transportation Research Record: Journal of the Transportation Research Board,2014,2421:82-92.DOI:10.3141/2421-10.
[2]Leclercq L, Marczak F, Knoop V L, et al. Capacity drops at merges: Analytical expressions for multilane freeways[J].Transportation Research Record: Journal of the Transportation Research Board, 2016,2560:1-9.DOI:10.3141/2560-01.
[3]Papamichail I, Kampitaki K, Papageorgiou M, et al. Integrated ramp metering and variable speed limit control of motorway traffic flow[J].IFAC Proceedings Volumes, 2008,41(2):14084-14089.DOI:10.3182/20080706-5-kr-1001.02384.
[4]Hassan H M, Abdel-Aty M A, Choi K, et al. Driver behavior and preferences for changeable message signs and variable speed limits in reduced visibility conditions[J].Journal of Intelligent Transportation Systems, 2012,16(3):132-146.DOI:10.1080/15472450.2012.691842.
[5]Zhang G H, Wang Y H. Optimizing coordinated ramp metering: A preemptive hierarchical control approach[J]. Computer-Aided Civil and Infrastructure Engineering,2013,28(1):22-37.DOI:10.1111/j.1467-8667.2012.00764.x.
[6]Kan Y H, Wang Y B, Papageorgiou M, et al. Local ramp metering with distant downstream bottlenecks: A comparative study[J]. Transportation Research Part C: Emerging Technologies,2016,62:149-170.DOI:10.1016/j.trc.2015.08.016.
[7]Coleman J A, Paniati J F, Cotton R D, et al. FHWA study tour for speed management and enforcement technology [R]. US Department of Transportation,1995.
[8]Lu X Y, Tan H S, Shladover S E, et al. Automated vehicle merging maneuver implementation for AHS[J]. Vehicle System Dynamics,2004,41(2):85-107.DOI:10.1076/vesd.41.2.85.26497.
[9]Guler S I, Menendez M, Meier L. Using connected vehicle technology to improve the efficiency of intersections[J]. Transportation Research Part C: Emerging Technologies,2014,46:121-131.DOI:10.1016/j.trc.2014.05.008.
[10]Feng Y H, Head K L, Khoshmagham S, et al. A real-time adaptive signal control in a connected vehicle environment[J]. Transportation Research Part C: Emerging Technologies,2015,55:460-473.DOI:10.1016/j.trc.2015.01.007.
[11]Smith S, Razo M. Using traffic microsimulation to assess deployment strategies for the connected vehicle safety pilot[J].Journal of Intelligent Transportation Systems,2016,20(1):66-74.DOI:10.1080/15472450.2014.889941.
[12]Zhao Y J, Wagh A, Hou Y F, et al. Integrated traffic-driving-networking simulator for the design of connected vehicle applications: Eco-signal case study[J]. Journal of Intelligent Transportation Systems,2016,20(1):75-87.DOI:10.1080/15472450.2014.889920.
[13]Ge J I, Orosz G. Dynamics of connected vehicle systems with delayed acceleration feedback[J].Transportation Research Part C: Emerging Technologies,2014,46:46-64.DOI:10.1016/j.trc.2014.04.014.
[14]Learn S, Ma J Q, Raboy K, et al. Freeway speed harmonisation experiment using connected and automated vehicles[J]. IET Intelligent Transport Systems,2018,12(5):319-326.DOI:10.1049/iet-its.2017.0149.
[15]Xie Y C, Zhang H X, Gartner N, et al. Collaborative merging behaviors and their impacts on freeway ramp operations under connected vehicle [C]// Transportation Research Board (TRB) Committee on Traffic Flow Theory and Characteristics Symposium Celebrating 50 Years of Traffic Flow Theory and Midyear Meeting. Portland, OR, USA,2015:392.
[16]Ran B, Leight S, Chang B. A microscopic simulation model for merging control on a dedicated-lane automated highway system[J].Transportation Research Part C: Emerging Technologies,1999,7(6):369-388.DOI:10.1016/s0968-090x(99)00028-5.
[17]Cheon S. An overview of automated highway systems (AHS) and the social and institutional challenges they face [R]. Berkeley, CA, USA: University of California Transportation Center,2003.
[18]Kachroo P, Li Z.Vehicle merging control design for an automated highway system [C]//IEEE Conference on Intelligent Transportation System. Boston, MA, USA,1997:224-229.
[19]Antoniotti M, Desphande A, Girault A.Microsimulation analysis of multiple merge junctions under autonomous AHS operation [C]// IEEE Conference on Intelligent Transportation System. Boston, MA, USA,1997:147-152.
[20]Rios-Torres J, Malikopoulos A A. A survey on the coordination of connected and automated vehicles at intersections and merging at highway on-ramps[J].IEEE Transactions on Intelligent Transportation Systems,2017,18(5):1066-1077.DOI:10.1109/tits.2016.2600504.
[21]Rios-Torres J, Malikopoulos A A. Automated and cooperative vehicle merging at highway on-ramps[J].IEEE Transactions on Intelligent Transportation Systems,2017,18(4):780-789.DOI:10.1109/tits.2016.2587582.
[22]Xie Y C, Zhang H X, Gartner N H, et al. Collaborative merging strategy for freeway ramp operations in a connected and autonomous vehicles environment[J]. Journal of Intelligent Transportation Systems,2017,21(2):136-147.DOI:10.1080/15472450.2016.1248288.
[23]Rios-Torres J, Malikopoulos A, Pisu P.Online optimal control of connected vehicles for efficient traffic flow at merging roads [C]//2015 IEEE 18th International Conference on Intelligent Transportation Systems. Las Palmas, Spain,2015:2432-2437.
[24]Roncoli C,Bekiaris-Liberis N, Papageorgiou M. Lane-changing feedback control for efficient lane assignment at motorway bottlenecks[J]. Transportation Research Record: Journal of the Transportation Research Board,2017,2625:20-31.DOI:10.3141/2625-03.
[25]Ntousakis I A, Nikolos I K, Papageorgiou M. Optimal vehicle trajectory planning in the context of cooperative merging on highways[J].Transportation Research Part C: Emerging Technologies,2016,71:464-488.DOI:10.1016/j.trc.2016.08.007.
[26]Ntousakis I A, Nikolos I K, Papageorgiou M.Cooperative vehicle merging on highways-model predictive control [C]//Transportation Research Board 96th Annual Meeting. Washington, DC, USA,2017.
[27]Athans M. A unified approach to the vehicle-merging problem[J]. Transportation Research,1969,3(1):123-133.DOI:10.1016/0041-1647(69)90109-9.
[28]Li L, Wang F Y, Zhang Y.Cooperative driving at lane closures [C]// Procedings of the 2007 IEEE Intelligent Vehicles Symposium. Istanbul, Turkey, 2007:1156-1161.
[29]Ntousakis I A, Porfyri K, Nikolos I K, et al. Assessing the impact of a cooperative merging system on highway traffic using a microscopic flow simulator[C]//ASME 2014 International Mechanical Engineering Congress and Exposition. Montreal, Quebec, Canada,2014:V012T15A 024. DOI:10.1115/IMECE2014-39850.
[30]Struwe M.Variational methods [M]. Berlin: Springer,2006.