The soil compactor often works in the field of the construction site, factories, etc. Its operating principle is a combination of the static force of the vehicle and the dynamic force of the drum to compact the soil ground, asphalt and other materials. The vibration excitations from the deformable terrain and drum are thus transmitted to the driver through the isolation systems of the cab and the vehicle. Consequently, the cab’s isolation system is one of the most important factors to improve the vehicle ride quality.
The basic research of the tire-deformable terrain contact[1-4] and interaction between the rigid drum and elastic-plastic soil[5] indicated that the vibration response of the vehicle was greatly influenced by off-road terrains. Almost all the cab’s isolation system of soil compactors was equipped by the rubber mounts with high stiffness characteristic and low damping of rubber material[6-9]. Therefore, the stiff rubber property helped suppress only high-frequency vibrations and noise, contrariwise, the low damping of the natural rubber generated the high magnitude vibrations which can reduce the vehicle’s ride quality[6]. The effects of design parameters of the cab’s rubber mounts on the ride quality was evaluated[7]. An optimal design for the cab’s new rubber mounts of soil compactors was built via the finite element model, and the new rubber mount was then produced and tested for the vehicle’s cab[8]. The parameters of the cab’s rubber mounts were also optimized to increase the ride quality[9]. The results showed that the vehicle’s ride quality was significantly improved. However, the research results also showed that the large-amplitude shock of the cab existed in the low-frequency region at the direction of forwarding motion. This is one of the reasons that causes the tiredness of the driver while working, cracking surfaces of the cab and other problems. Thus, to solve this problem, the low damping coefficients of the cab’s rubber mounts need to be improved.
In this study, a 3-D dynamic model of the soil compactor was established based on the deformable terrain models[1,4-5]. The vibration excitations consist of the drum/tires-deformable terrain contact under the condition of the vehicle traveling and an excitation (28 Hz) of the drum under the condition of the vehicle working on elastic-plastic soil. Experimental investigation was used to validate the model and verify its accuracy. The cab’s rubber mounts were supplemented by auxiliary hydraulic mounts (AHM) to evaluate the ride quality, and the damping coefficients of the AHM were then optimized by the genetic algorithm to enhance the vehicle’s ride quality. The performance of AHM was evaluated through the weighted RMS and the PSD of acceleration responses of the vertical driver’s seat, the cab’s pitch and roll angle in the low-frequency region. The aim of this study is to improve the ride quality and control the cab shaking.
1 Soil Compactor Model
1.1 Vehicle dynamic model
A 3-D nonlinear dynamic model of the vehicle with 9 degrees of freedom (DOF) considering the interaction between wheels and off-road terrains is established to evaluate the cab’s ride quality (see Fig.1).
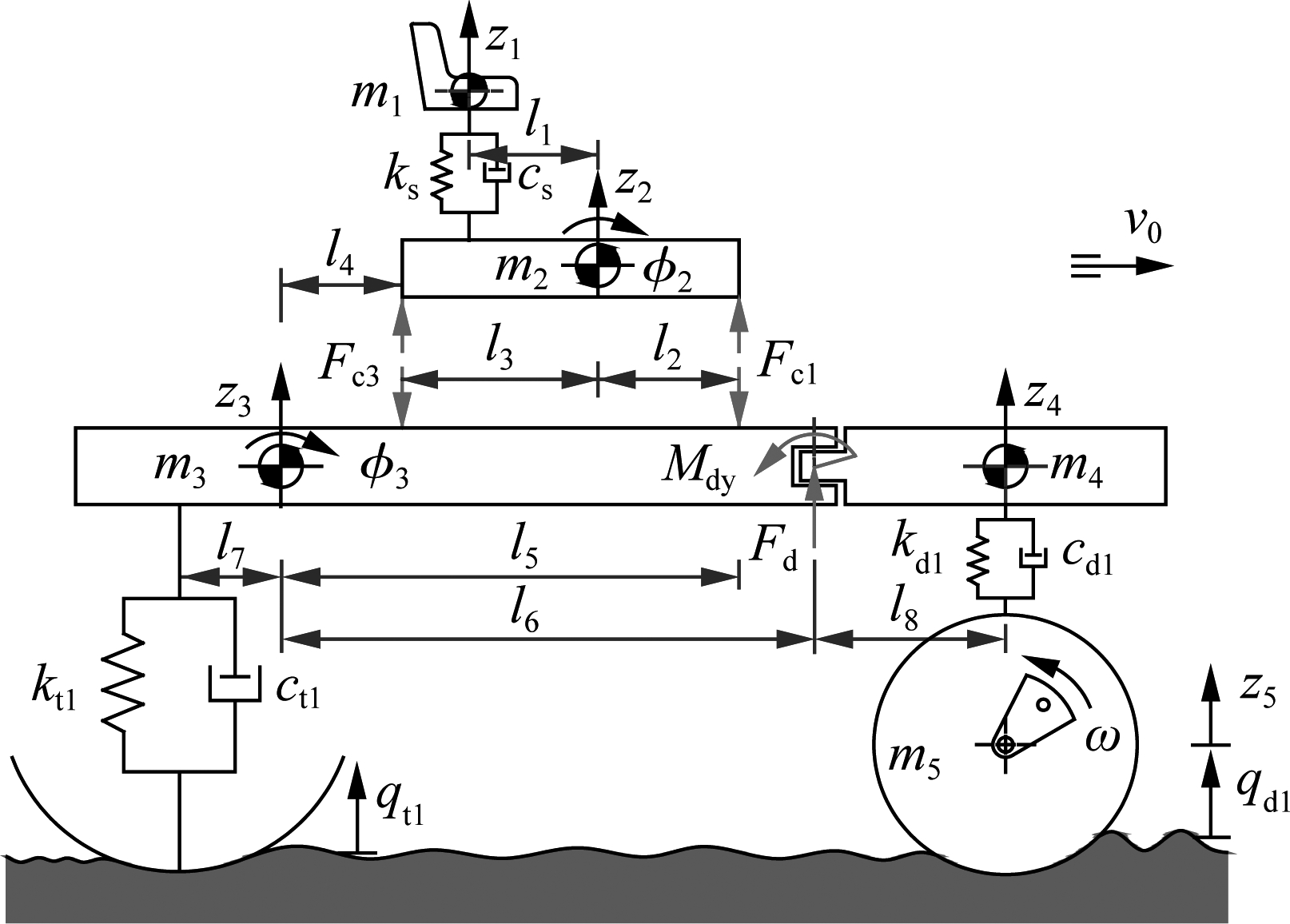
(a)
(b)
Fig.1 3-D dynamic model of a vibratory soil compactor. (a) Side view; (b) Front view
As shown in Fig.1, zv and mv are the vertical displacement and mass at the centre of gravity of the driver’s seat, the cab, the rear/front vehicle frame and the drum; φ2 and φ3 are the pitch angles at the centre of gravity of the cab and the rear frame; θj is the roll angle at the centre of gravity of the cab, the rear/front frame and the drum; ks, kd1,2, kt1,2 and cs, cd1,2, ct1,2 are the stiffness and damping coefficients of the driver’s seat suspension, the drum’s rubber mounts and tires, respectively ; Fci are the dynamic reaction forces of the cab’s isolation mounts; qd1,2 and qt1,2 are the excitations of the off-road terrains; lu and bv are the distances of the vehicle (i=1, 2,3,4; j=2,3,4,5; u=1,2,…, 8; v=1,2,…,5).
Based on the vehicle dynamic model in Fig.1, and by applying Newton’s second law of motion, the motion equations of the soil compactor can be represented in the matrix form as
(1)
where M, C and K are the mass, damping and stiffness matrices, respectively; Z is the displacement vector; and F(t) is the exciting force vector.
1.2 Cab’s isolation system model
The cab’s isolation system of the soil compactor was equipped by four rubber mounts to isolate the transmittal vibration sources from the rear vehicle frame to the cab floor. Due to the low performance of the old rubber mount in improving the ride quality, especially the high pitch angle of the cab, a new optimal design of the cab’s rubber mounts was then carried out to improve the cab’s ride quality[8]. However, its vibration isolation performance is still small in the low-frequency region.
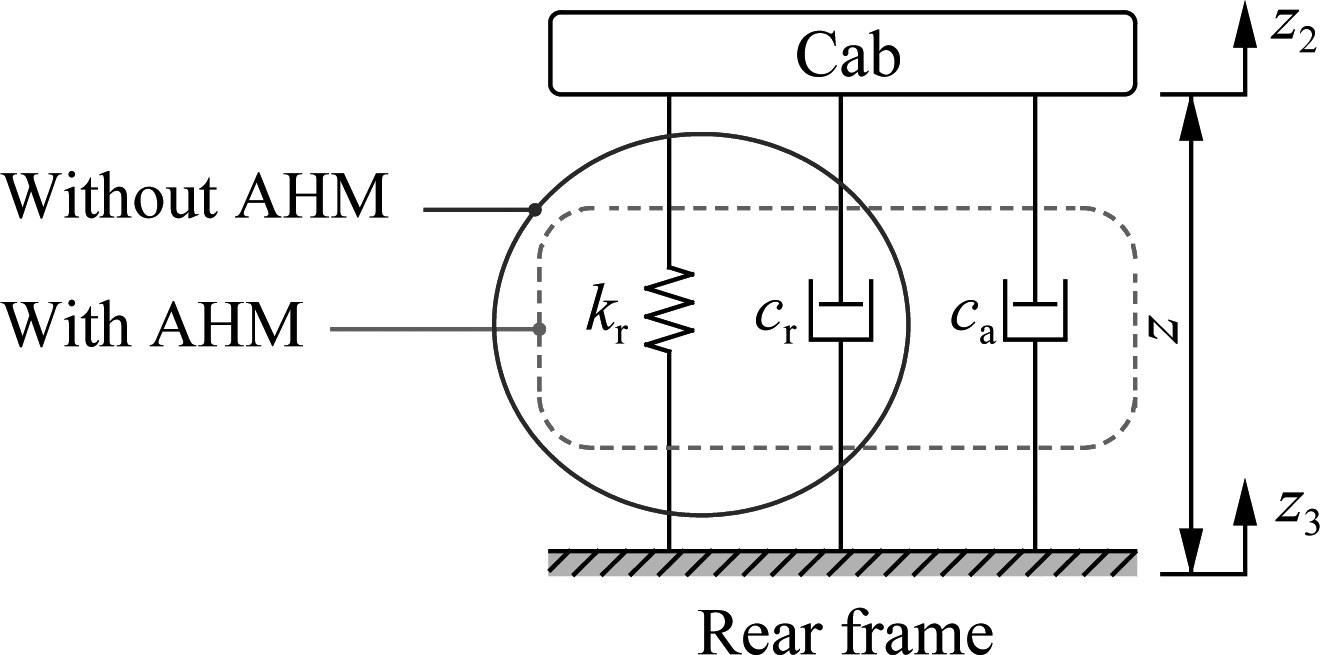
Fig.2 Cab’s isolation system model
In this study, a new rubber mount supplemented by the AHM is proposed to further improve the cab’s ride quality. The lumped parameter model is shown in Fig.2, where kr and cr are the stiffness and damping coefficient of the new rubber mount, respectively; ca is the damping coefficient of the AHM added in the cab’s rubber mounts.
The corresponding dynamic force of mount i of the cab’s isolation system is given as
(2)
where zi=z2i-z3i and 
are the displacements and the relative velocities of the cab floor and the rear vehicle frame at mount i, and they are given by
(3)
(4)
where i=1, 2, then α= 1, v=5 and δ=i+1; and i=3, 4, then 
=2, v=4 and δ=i-1.
1.3 Vehicle and terrain interaction models
1.3.1 Wheels-deformable soil contact
Under the condition of the vehicle travelling, the drum/tires are assumed to move on a deformable terrain with the terrain surface roughness. Based on the model of Bakker and Wong[1-2], when a wheel moves on a random terrain surface q(t) of the deformable terrain, under the effect of the static and dynamic loads of the wheel, the terrain is then sunk by zoa, as shown in Fig.3. The pressure pg and the shear stress τg arising from the soil compression in the deformable region (arc of oa) thus impact on the wheel. Thus, the reaction force Fg of the terrain under the wheel is given as
Fg=
Bpgrcosθdθ+Bτgrsinθdθ
(5)
pg and τg are given by Bakker[1] as follows:
(6)
where kc and kφ are the soil stiffness coefficients for sinkage and internal friction, respectively; n is the sinkage exponent; b is the smaller dimension of the contact patches and the widths of the drum/tire B; r is the radius of the drum/tire; c is the soil cohesion coefficient; φ is the angle of the internal friction; K is the shear deformation modulus; and j=rs[θa(t)-θ] in which s is the slip ratio of the drum/tire.
Fig.3 Wheel-deformable terrain contact model
Assume that lar is the average roughness line of the terrain surface, and thus, the sinking of the terrain zx can be determined by zx=q(t)+zoa-
, herein, q(t) is the random excitation of the off-road terrain surface and it is described as follows.
According to the ISO proposal[10], the spectral density of the off-road terrain surface is written as
(7)
The value S(Ω0) provides a measure for the random terrain with the reference spatial frequency Ω0 = 1/(2π) cycle/m. More specifically, assuming that the vehicle moves with a constant speed v0, the off-road terrain irregularities can then be simulated by
(8)
where N is the number of intervals; φi is a random phase uniformly distributed between 0 and 2π; and ω=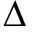nv0 is the fundamental temporal frequency.
The desired terrain roughness can be yielded by choosing a value in the spectral density ranges.
According to the vehicle dynamic model in Fig.1 and the wheels-deformable soil contact model in Fig.3, the excitation forces Ft and Fd of the drum and tires are described by
(9)
j=1,2
(10)
1.3.2 Drum and elastic-plastic soil interaction
The soil compactor uses the most of its time to work on the elastic-plastic soil. Therefore,according to Adam and Kop[5], a model of the rigid drum and elastic-plastic soil interaction is established in Fig.4. The elastic-plastic property of soil can be expressed via a plasticity factor ε and a damping ratio of plastic soil γ as
(11)
where ε is the compression ratio; kse is the elastic stiffness; ksp is the compression stiffness; cse is the compression damper.
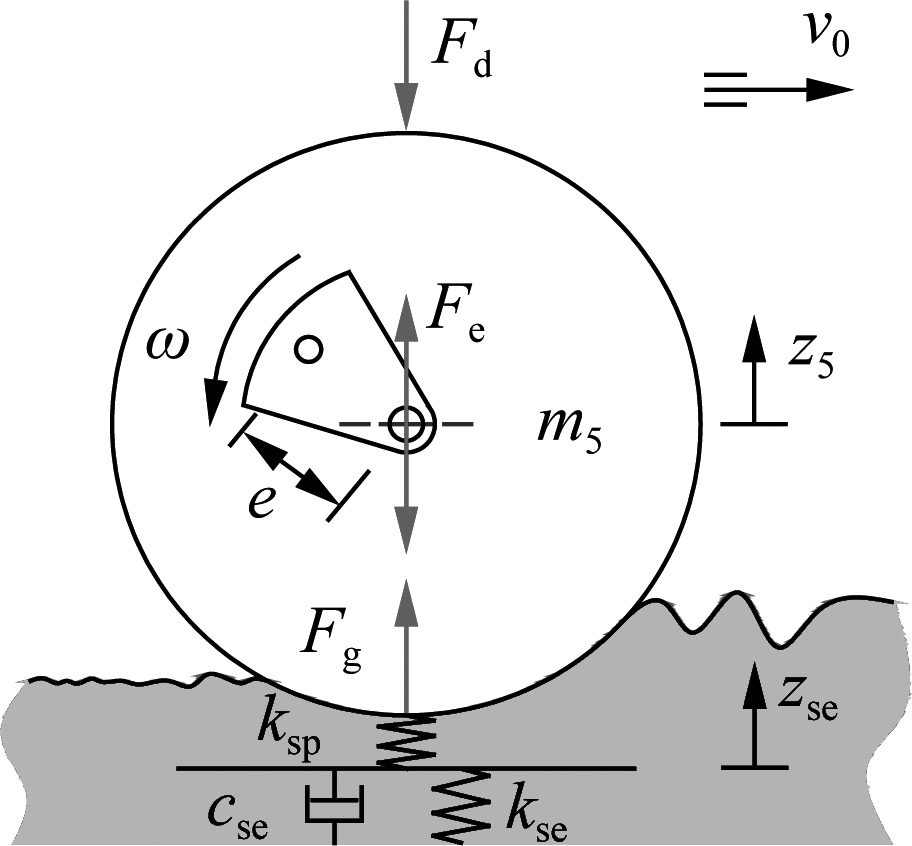
Fig.4 Rigid drum and elastic-plastic soil interaction model
In a vibration cycle of the drum-soil interaction,there are two or three distinct phases that occur in the motion of the drum and they are described as follows:
1) Loading phase: The gravel-soil ground is compressed by the drum, thus, the density is increased and it has become elastic. The elastic stiffness and compression stiffness of the gravel-soil ground are increased while the compression damper is decreased. In order to describe the relation of z5, ε and γ, the vibration equation of the drum is given as[7]
(12)
2) Unloading phase: The drum moves upward, and the gravel-soil ground is restored. The vibration equation of the drum is written as
(13)
3) Drum-Hope phase: The gravel-soil ground has become elastic, the drum is easy to separate from the soil ground surface, and the vibration equation is written as
(14)
From Eqs.(12) to (14), the motion of drum z5 and excitation force Fd is then determined.
2 Experimental Model
2.1 Evaluating criteria
The ride quality is mainly evaluated via the weighted RMS acceleration response. In addition, according to ISO 2631-1[11], the PSD acceleration response are also applied to estimate the effect of vibration on the endurance limit of the human body. It is suggested that a low-frequency range below 10 Hz seriously affected the driver’s health and safety. In this study, the ride quality of the cab’s isolation system is evaluated via the PSD and the weighted RMS of acceleration responses of the vertical driver’s seat, cab’s pitch and roll angle in the frequency and time domains. Thus, the smaller PSD and weighted RMS values mean that the system has the better ability compared to the corresponding isolation mounts. The expression of the weighted RMS value is given as
(15)
where awt is the acceleration (translational and rotational) depending on the duration of the simulation T.
2.2 Experiment model
In order to confirm the model’s accuracy, an experimental condition of the soil compactor using the cab’s new rubber mounts was made under the same simulated condition when the vehicle worked on an elastic-plastic soil ground. Three test steps are described as follows:
Sept 1 Preparation step: Instruments for the experiment include a soil compactor, the Belgium LMS dynamic test and the analysis system; and ICP© three-direction acceleration sensors are used to measure the vibration accelerations. The sensors are installed on the driver’s seat and the cab floor at the four locations of the isolation mounts, as shown in Fig.5.
Sept 2 Measurement step: The multi-point measurement method is applied, and the process of measurement is performed under an excitation frequency 28 Hz of the drum when the vehicle compacted at a very slow speed v0 = 0.83 m/s.
Sept 3 Data extraction step: The data measurements are carried out including the vertical accelerations at the driver’s seat and at four measurement points on the cab floor.
The acceleration responses of cab’s pitch and roll angle
Fig.5 Diagrammatic sketch of the experimental set-up
are calculated as
(16)
where 
are the vertical accelerations, respectively; lc and bc are the distance between measurement points.
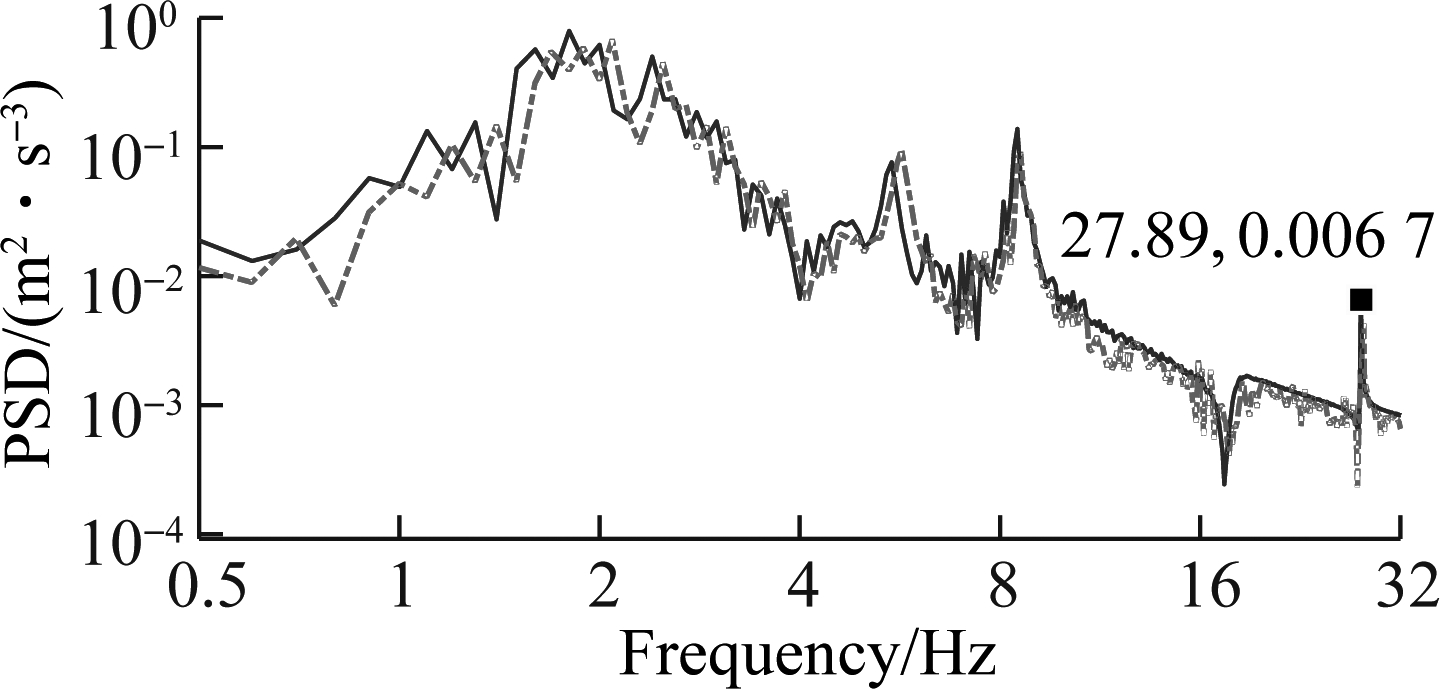
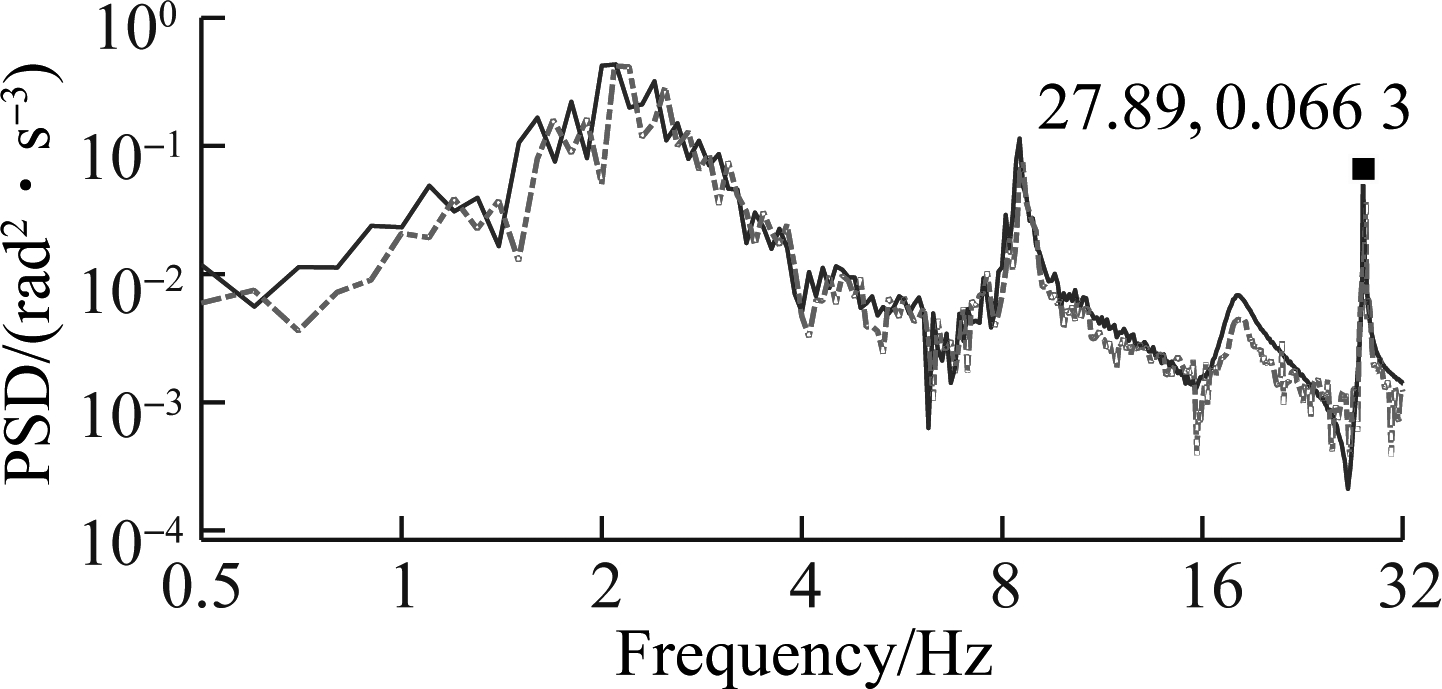
Experimental and simulation results of the PSD and weighted RMS of acceleration responses are plotted in Fig.6 and listed in Tab.1. The comparison results indicate that the simulation results almost agree with the tests regarding the frequency of the various peaks in the responses and the trend. In addition, the weighted RMS values of the vertical driver’s seat, cab’s pitch and roll angles also have a small deviation of 10.1%, 11.3% and 12.6% in comparison with the measured values. It implies that the mathematical model of the vibratory roller is an accurate and feasible model.
(a)
(b)
(c)
Fig.6 Acceleration PSD responses of the driver and cab. (a) Driver’s seat heave; (b) Cab pitch angle; (c) Cab roll angle
Tab.1 Comparison results of experiment and simulation
Parameterawzs/(m·s-2 awϕc rad·s-2 awθc rad·s-2 Experimental0 790 440 150Simulation0 710 390 131Deviation %10 111 312 6
3 Results and Discussion
3.1 Influence of auxiliary hydraulic mounts
3.1.1 Under the condition of the vehicle travelling
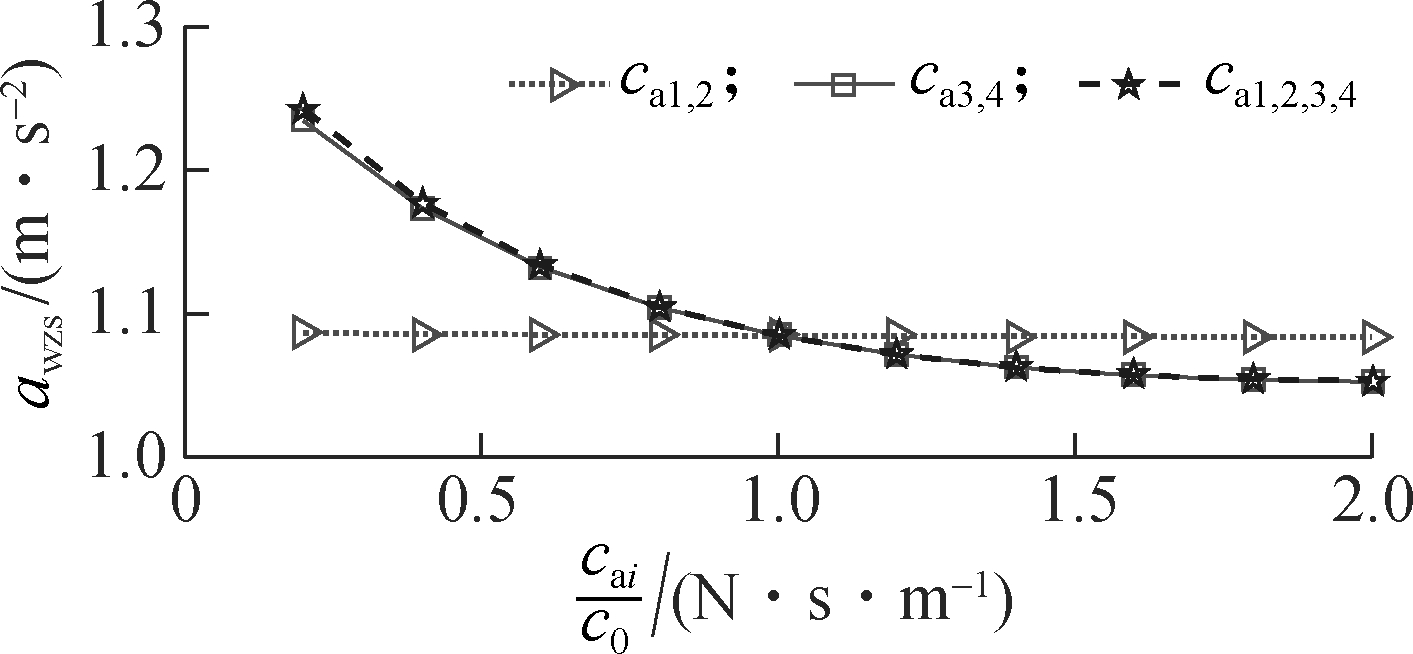
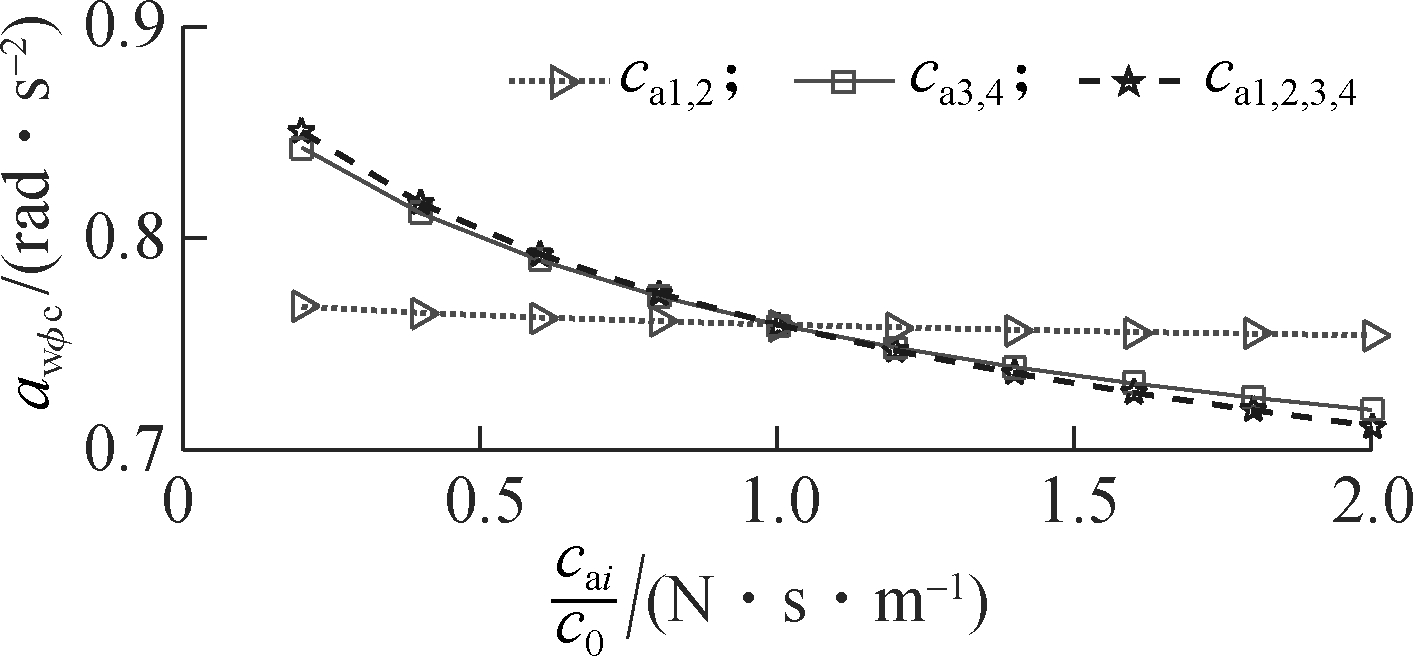
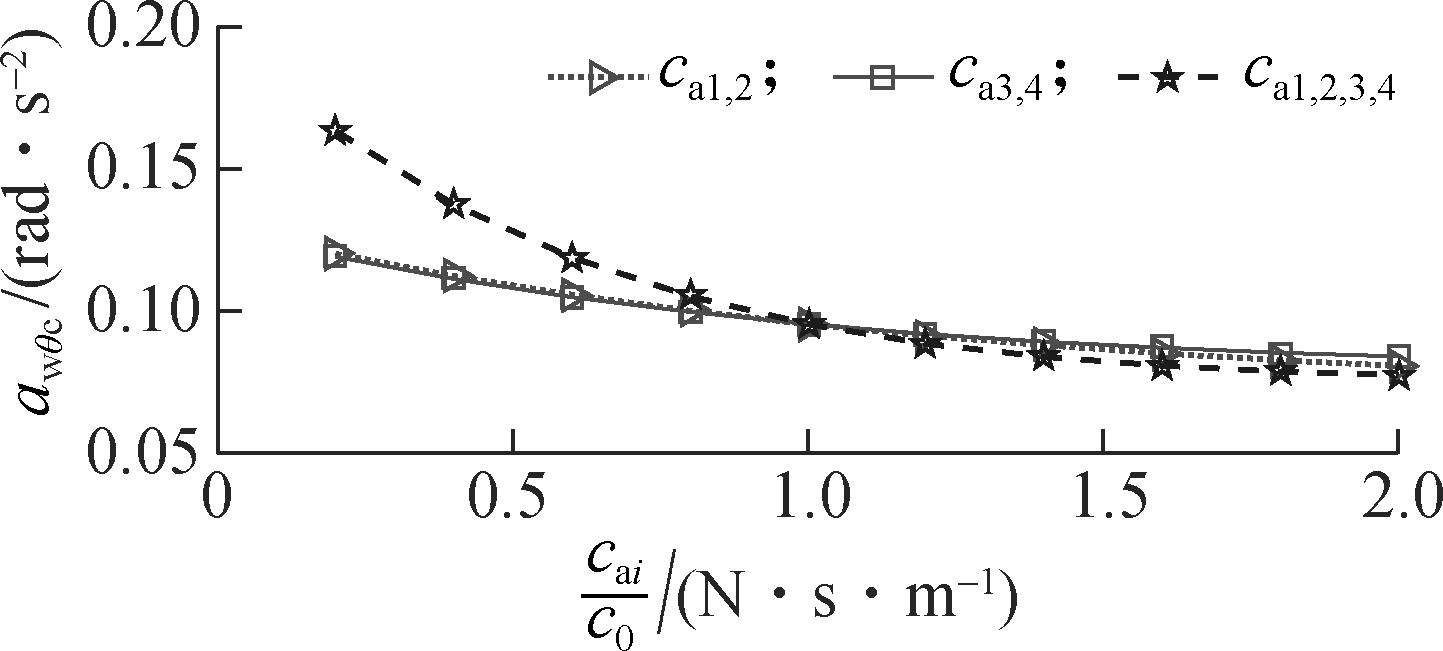
In order to evaluate the influence of the damping coefficients of the AHM on the cab’s ride quality under the condition of the vehicle traveling, the parameters of the vehicle[6] and a Grenville soil deformation with its poor terrain classification q(t)[3-4] are chosen to simulate at a low vehicle velocity v0=1.67 m/s. Assume that the initial damping coefficients of the AHM are c0=1.5
103 N·s/m. The damping coefficients of AHM cai=0.2c0, 0.4c0,…, 2.0c0 in three different cases of the front-end mounts ca1,2, the rear-end mounts ca3,4 and all mounts ca1,2,3,4 are respectively simulated. The results are shown in Fig.7.
(a)
(b)
(c)
Fig.7 Effect of the damper coefficients on a soft soil ground. (a) Driver’s seat heave; (b) Cab pitch angle; (c) Cab roll angle
Fig.7 shows that the weighted RMS acceleration responses of the driver’s seat heave awzs, the cab’s pitch and roll angle (awφc and awθc) are slightly affected by the damping coefficients of the front-end mounts ca1,2, whereas these values are strongly affected by the damping coefficients of the rear-end mounts ca3,4 and of all mounts ca1,2,3,4. However, the influence of ca1,2,3,4 on the ride quality is insignificant in comparison with ca3,4, thus, ca3,4 are chosen to analyze the results. When 0.2c0 ≤ca3,4 ≤1.6c0, the results show that all values of awzs, awφc and awθc are strongly reduced; when 1.6c0≤ca3,4 <2.0c0, all values of awzs, awφc and awθc are lightly reduced, especially the value of awzs is tendentiously enhanced by 1.8c0 ≤ca3,4 ≤2.0c0, as shown in Fig.7(a). Thus, the cab’s ride quality can be greatly improved when ca1,2=1.0c0 and 1.2c0≤ca3,4 ≤1.6c0.
3.1.2 Under the condition of the vehicle working
Under the condition of the soil compactor working on the workshop,an elastic-plastic soil ground with a high density soil[5] and a very slow-speed vehicle (v0=0.68 m/s) are chosen to simulate under an excitation (28 Hz) of the drum. Also, assume that the initial damping coefficients of AHM are c0=1.5
103 N·s/m. The damping coefficients cai=0.2c0, 0.4c0,…, 2.0c0 with three different cases of ca1,2, ca3,4, and ca1,2,3,4, are also evaluated, respectively.
The simulation results in Fig.8 show that the impact of the damping coefficients ca1,2, ca3,4, and ca1,2,3,4 is similar under the condition of the vehicle traveling. Consequently, the damping coefficients of the rear-end mounts, ca3,4, are also chosen to analyze the results. Figs.8(a),
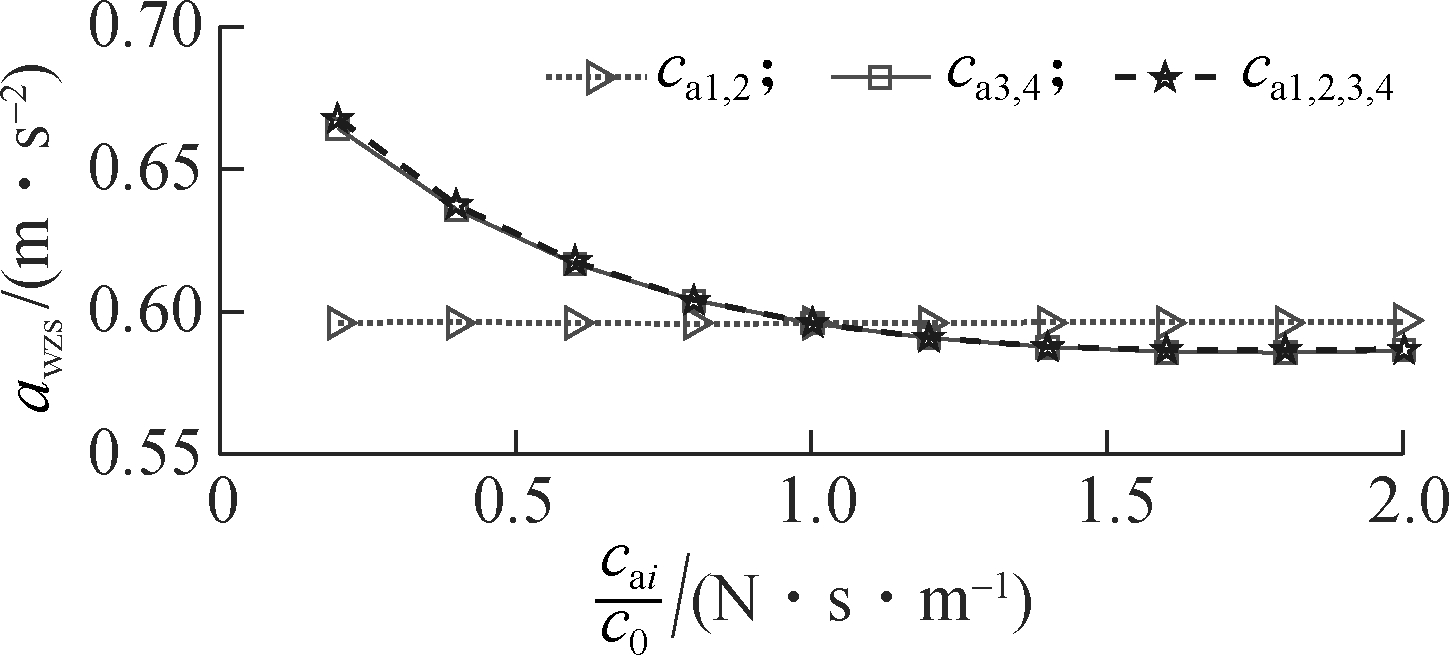
(a)
(b)
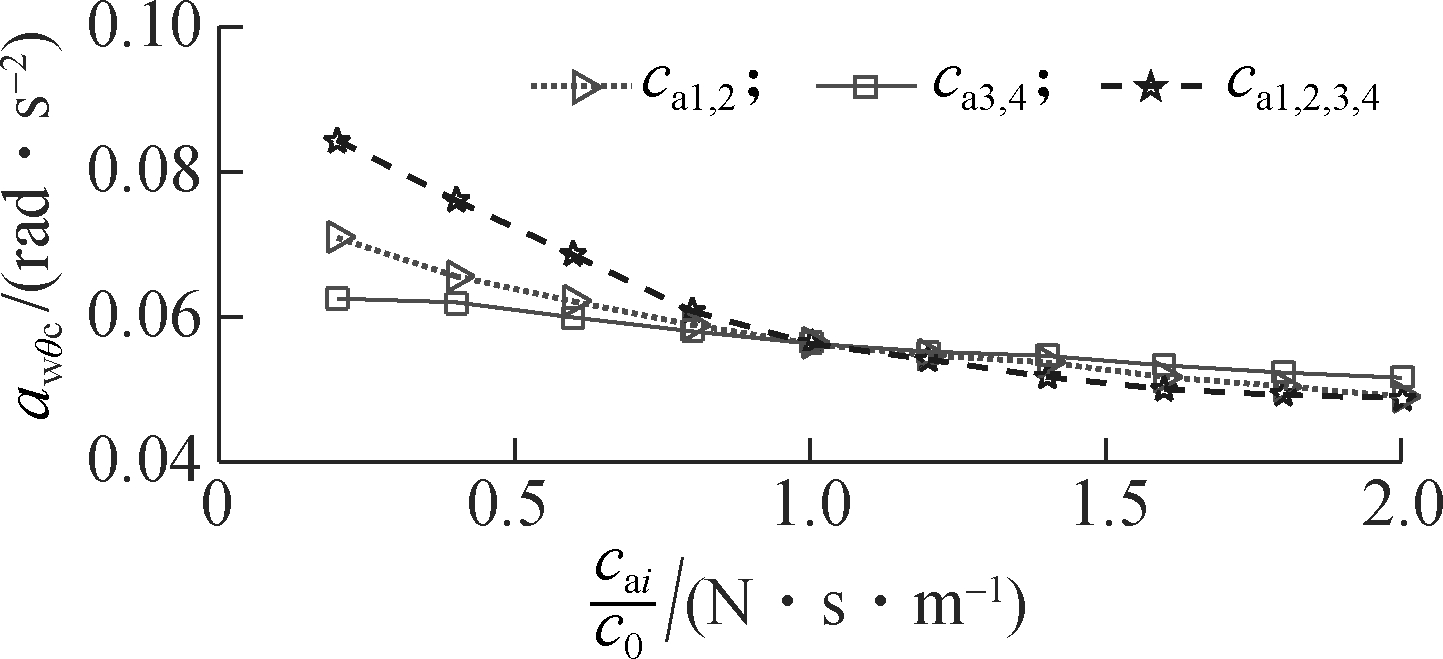
(c)
Fig.8 Effect of the damper coefficients on elastic-plastic soil. (a) Driver’s seat heave; (b) Cab pitch angle; (c) Cab roll angle
(b) and (c) show that when 0.2c0≤ca3,4 <1.4c0, all the values of awzs, awφc and awθc are clearly reduced; however, when 1.4c0≤ca3,4 ≤2.0c0, the value awφc is significantly enhanced (see Fig.8(b)). Therefore, the cab’s ride quality can be clearly improved when ca1,2=1.0c0 and 1.0c0≤ca3,4 ≤1.4c0.
3.2 Performance of the AHM
The analysis results show that the ride quality is insignificantly affected by ca1,2, whereas it is strongly affected by ca3,4. The results also show that the ride quality is greatly improved when 1.2c0≤ca3,4 ≤1.6c0 under the condition of the vehicle traveling and 1.0c0≤ca3,4 ≤1.4c0 under the condition of the vehicle working. In order to choose the optimal values of the damping coefficients, a genetic algorithm program is used to optimize the objective functions.
3.2.1 Genetic algorithm program
The GA is defined as finding a vector variable through constraint conditions to reach the objective function[12-13], and it is written as
Finding a vector x=[x1, x2,…, xn]T to optimize
F(x)=[f1(x),f2(x),…,fn(x)]T
(17)
s.t. gi(x) ≤0 i=1, 2,…, p
hj(x) = 0 j=1, 2,…, q
where F(x) is the objective function which must be either maximized or minimized; p and q are the numbers of inequality constraints and equality constraints.
The structure of GA includes encoding, population initialization, fitness evaluation, parent selection, genetic operations and termination criterion.
The goal of the GA is to seek the optimal damping coefficients ca3,4 to obtain the minimum awz values in Eq.(15) via the subsystem model in two cases of the vehicle traveling and working. In order to find the minimum awz values, the fitness value J is applied to calculate objective functions as[13-14]
(18)
s.t.
(19)
where αz is the weight coefficient of awz values; ca3,4 are the damping coefficients of the AHM at the rear-end mounts, and the initial value of ca3,4 for GA under the condition of the vehicle traveling is 1.8×103≤ca3,4≤2.4×103 N·s/m and under the condition of the vehicle working is 1.5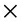103≤ca3,4 ≤2.1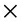103 N·s/m.
The individuals with the higher fitness value J which is obtained via the simulation model show that the obtained damping coefficients ca3,4 are good. Therefore, the resultant individuals are updated before the evolution process ends, and the optimal individuals can be obtained.
In order to seek the optimal values of ca3,4 in the cases of the vehicle traveling and working, the weight coefficient αz respectively are αzs=0.548, αφc=0.366 and αθc=0.086, which are determined by the percent of awzs (54.8%), awφc (36.6%) and awθc (8.6%) with the cab’s rubber mounts without AHM in Tab.2. The maximum generation is 600.
Tab.2 Weighted RMS values on a soft soil ground
Parameterawzs m·s-2 awϕc rad·s-2 awθc rad·s-2 Without AHM1 350 900 211With AHM1 050 730 087Reduction %22 2%18 8%58 7%
The optimal result in Fig.9 shows all the fitness values J obtained in the case of the vehicle traveling. The maximum values J are not increased from the evolutionary generation of 462 to the end. Therefore, the optimal individuals can be obtained at the generation of 462, and the optimal value sought via GA is ca3,4 = 2 335 N·s/m. Similarly, the optimal value under the condition of the vehicle working is ca3,4 = 1 882 N·s/m.
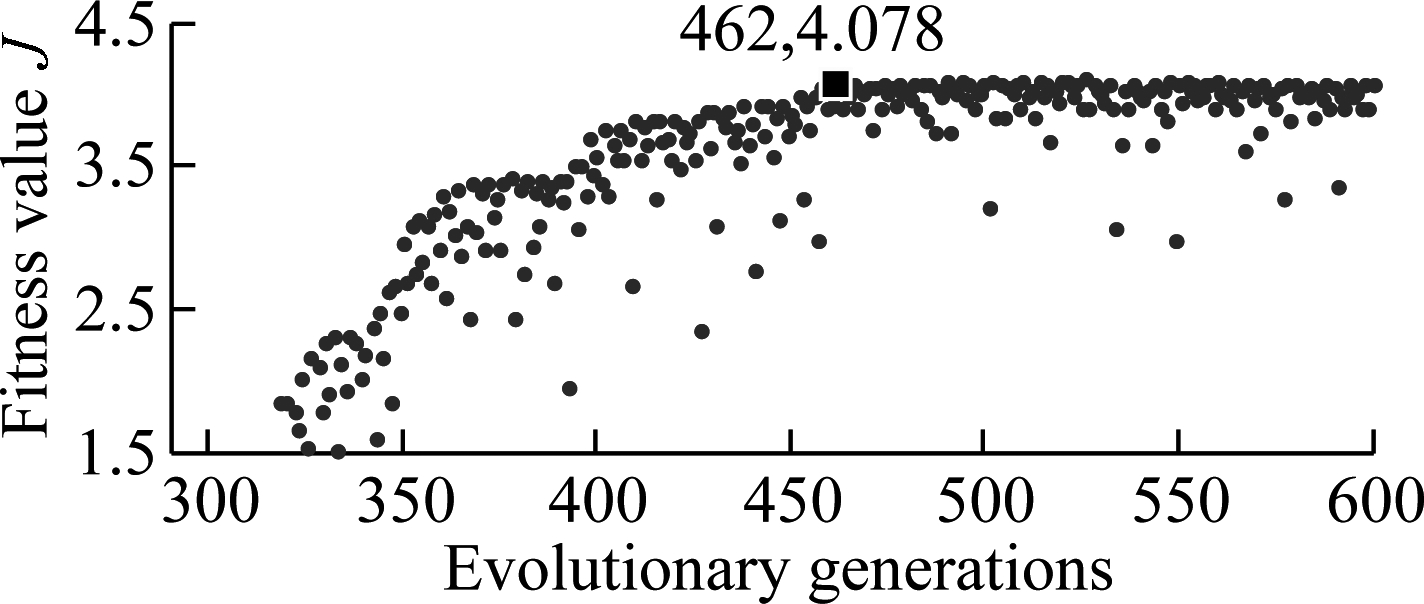
Fig.9 Fitness results of the optimal running process
3.2.2 Performance on the deformable terrain
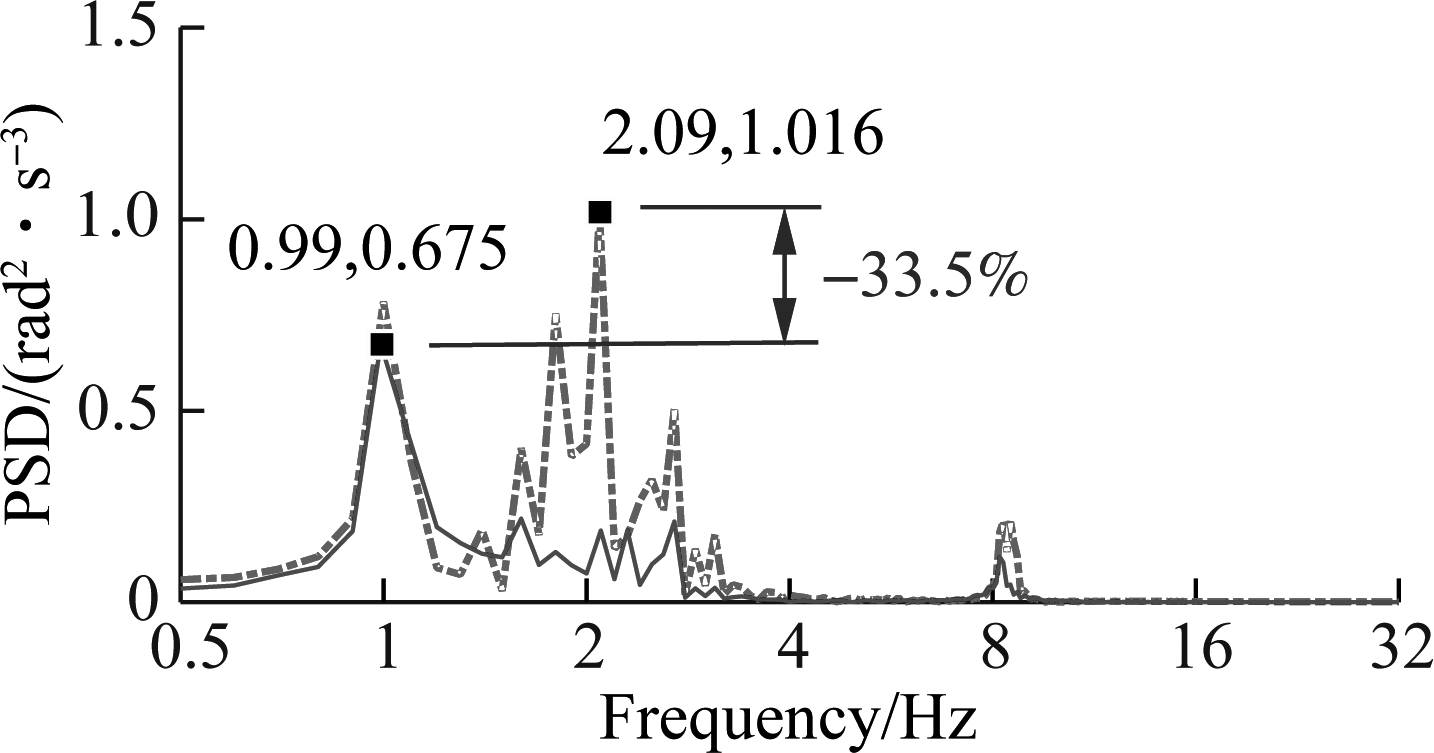
With the optimal damping coefficients of ca1,2=1 500 and ca3,4 =2 335 N·s/m, the weighted RMS and PSD of acceleration responses under the condition of the vehicle travelling are listed in Tab.2 and shown in Fig.10. The results in Tab.2 show that the values of awzs, awφc and awθc are clearly decreased by 22.2%, 18.8% and 58.7% in comparison with the cab’s rubber mounts without AHM.
In addition, the results in Figs.10(a), (b) and (c) also show that the AHM added in the cab’s isolation system have almost no effect on the resonance frequencies of the rubber mounts. In addition, the maximum PSD values of the driver’s seat heave, cab’s pitch and roll angles are strongly reduced by 35.4%, 33.5 6% and 48.3% in the low-frequency region (below 10 Hz). Thus, the driver’s ride comfort and health are clearly improved by the AHM.
3.2.3 Performance on the elastic-plastic soil
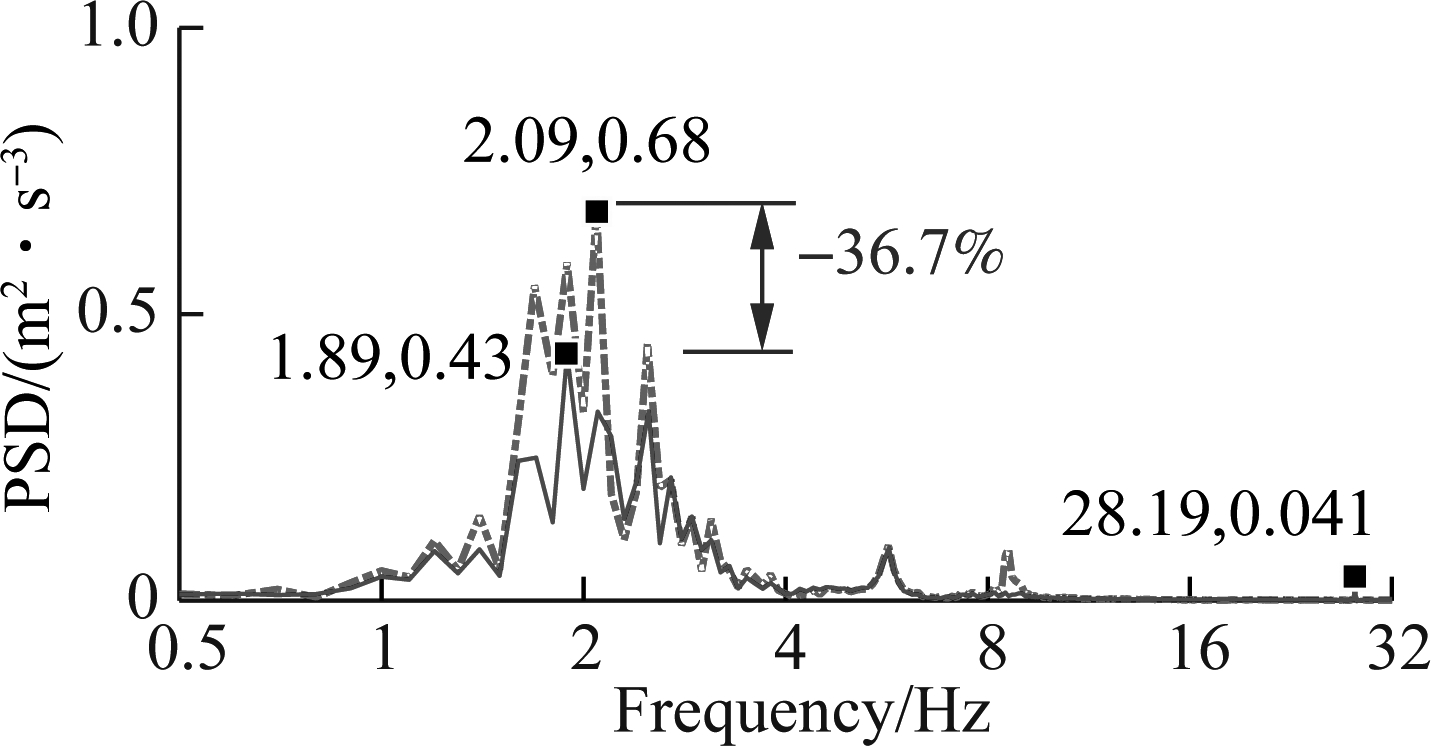
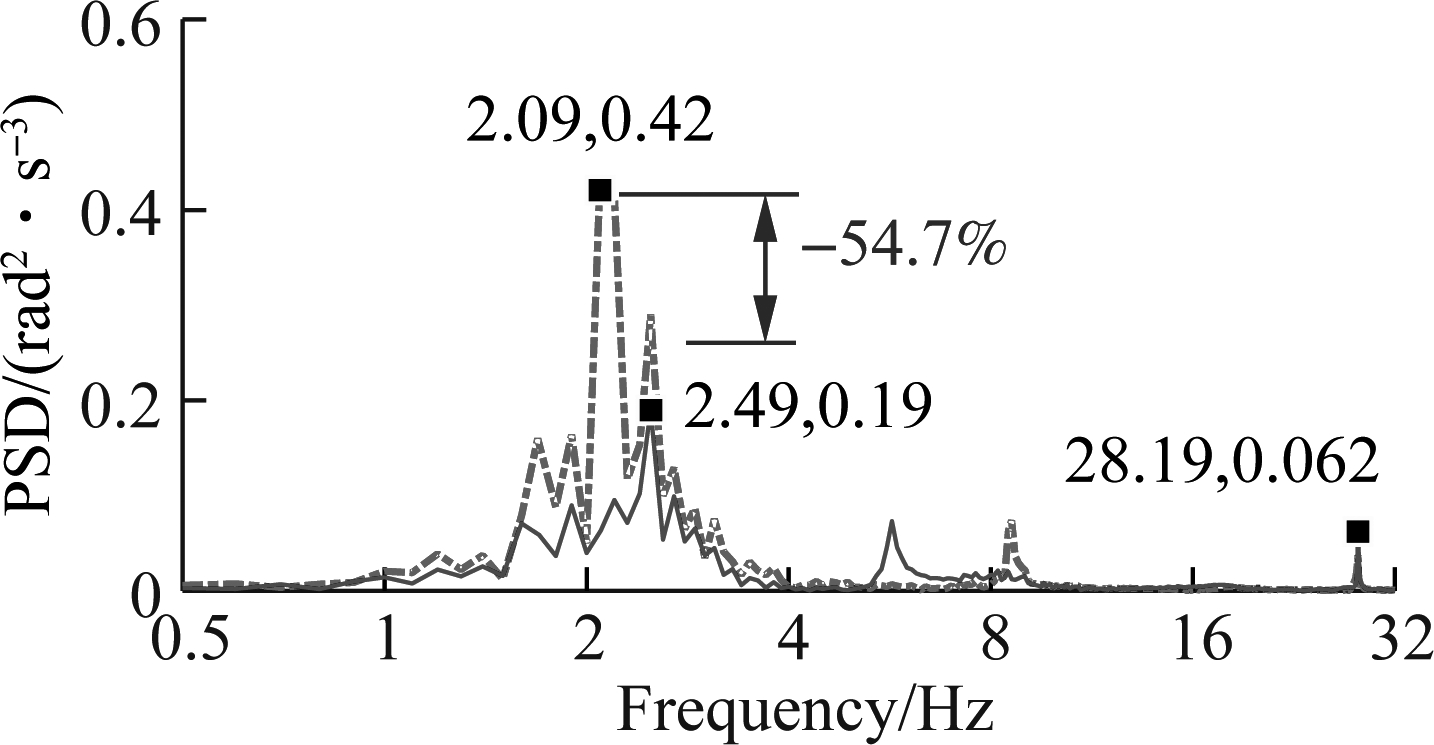
With the optimal damping coefficients of ca1,2=1 500 and ca3,4 =1 882 N·s/m, the weighted RMS and PSD of acceleration responses under the condition of the vehicle working are also given in Tab.3 and Fig.11. The results in Tab.3 also show that the values of awzs, awφc and awθc are reduced by 18.3%, 46.1% and 58.8% in comparison with the cab’s rubber mounts without AHM.
(a)
(b)
(c)
Fig.10 The acceleration PSD responses on a soft soil ground. (a) Driver’s seat heave; (b) Cab pitch angle; (c) Cab roll angle
(a)
(b)
(c)
Fig.11 The acceleration PSD responses on elastic-plastic soil. (a) Driver’s seat heave; (b) Cab pitch angle; (c) Cab roll angle
Besides, the results in Figs.11(a), (b) and (c) also show that the AHM have no effect on the resonance frequencies of the rubber mounts, and the maximum PSD values of the driver’s seat heave, cab’s pitch and roll angles are clearly decreased by 36.7%, 54.7% and 50.6% in the low-frequency region (below 10 Hz). Consequently, the driver’s ride comfort and health are also enhanced by the AHM under the condition of the vehicle working.
Tab.3 Weighted RMS values on an elastic-plastic soil ground
Parameterawzs m·s-2 awϕc rad·s-2 awθc rad·s-2 Without AHM0 710 390 131With AHM0 580 210 054Reduction %18 346 158 8
4 Conclusions
1) The driver’s ride comfort is strongly affected by the damping coefficients ca3,4 of the AHM under the operation conditions of the vehicle.
2) With optimal damping coefficients ca1,2=1 500 and ca3,4 =2 335 N·s/m, the weighted RMS acceleration responses of the driver’s seat, the cab’s pitch and roll angle are clearly reduced by 22.2%, 18.8%, 58.7% under the condition of the vehicle travelling.
3) With optimal damping coefficients ca1,2=1 500 and ca3,4 =1 882 N·s/m, the maximum PSD acceleration responses of the driver’s seat, the cab’s pitch and roll angle are greatly decreased by 36.7%, 54.7% and 50.6% under the condition of the vehicle working. Therefore, the vehicle’s ride quality is significantly improved by auxiliary hydraulic mounts.
[1] Bekker M. Introduction to terrain-vehicle systems[M]. Ann Arbor, USA: University of Michigan Press, 1969.
[2] Wong J. Theory of ground vehicles[M]. New York, NY, USA: John Wiley & Sons, 2001.
[3]Mitschke M. Dynamik der Kraftfahrzeuge[M]. Berlin: Springer-Verlag, 1972. DOI:10.1007/978-3-662-11585-5.
[4] Nguyen V L, Zhang J R, Jiao R Q et al. Effect of the off-road terrains on the ride comfort of construction vehicles[J]. Journal of Southeast University (English Edition), 2019, 35(2): 191-197. DOI:10.3969/j.issn.1003-7985.2019.02.008.
[5] Adam D, Kopf F. Theoretical analysis of dynamically loaded soils[C]//Proceedings of European Workshop Compaction of Soils and Granular Materials. Paris, France, 2000: 207-220.
[6] Nguyen V L, Zhang J R, Le V Q, et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts [J]. Shock and Vibration, 2018, 2018:8527574-1-8527574-17. DOI: 10.1155/2018/8527574.
[7] Kordestani A, Rakheja S, Marcotte P, et al. Analysis of ride vibration environment of soil compactors[J]. SAE International Journal of Commercial Vehicles, 2010, 3(1): 259-272. DOI:10.4271/2010-01-2022.
[8] Li J Q, Zhang Z F, Xu H G, et al. Dynamic characteristics of the vibratory roller test-bed vibration isolation system: Simulation and experiment[J]. Journal of Terramechanics, 2014, 56: 139-156. DOI:10.1016/j.jterra.2014.10.002.
[9] Le V Q, Nguyen K T. Optimal design parameters of cab’s isolation system for vibratory roller using a multi-objective genetic algorithm[J]. Applied Mechanics and Materials, 2018, 875: 105-112. DOI:10.4028/www.scientific.net/amm.875.105.
[10] International Organization for Standardization. ISO/TC108/SC2/WG4 N57 Reporting vehicle road surface irregularities [S]. Stuttgart, Germany: Thieme Medical Publishers, 1982.
[11] International Organization for Standardization. ISO 2631-1 Mechanical vibration and shock—Evaluation of human exposure to whole body vibration—Part 2: General requirement [S]. Geneva, Switzerland: International Organization for Standardization, 1997.
[12] Nariman-Zadeh N, Salehpour M, Jamali A, et al. Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm (MUGA)[J]. Engineering Applications of Artificial Intelligence, 2010, 23(4): 543-551. DOI:10.1016/j.engappai.2009.08.008.
[13] Crews J H, Mattson M G, Buckner G D. Multi-objective control optimization for semi-active vehicle suspensions[J]. Journal of Sound and Vibration, 2011, 330(23): 5502-5516. DOI:10.1016/j.jsv.2011.05.036.
[14] Wang W, Song Y L, Xue Y B, et al. An optimal vibration control strategy for a vehicle’s active suspension based on improved cultural algorithm[J]. Applied Soft Computing, 2015, 28: 167-174. DOI:10.1016/j.asoc.2014.11.047.