Soft active materials are utilized to manufacture soft machines, and they emerge as an exciting engineering field. Dielectric elastomer actuators (DEAs) are a kind of soft active materials which can deform in response to voltage[1-2], and they are used in a variety of innovative applications, such as medical devices[3], and unmanned flight systems[4], etc. Suitably designed DEAs usually cause giant voltage-induced deformation and beauty phase transitions prior to electric breakdown[5]. Yu et al.[6] studied the propagation of wrinkles in dielectric elastomers after observing the skin and feet of animals. Huang and Suo[7] theoretically analyzed the transition in DE membranes under uniaxial loads. Lu and Suo[8] studied the electromechanical phase transition between bulged and unbulged states in a dielectric tube. Recently, Godaba et al.[9] observed wrinkle patterns in DE membranes, and the flat and wrinkled regions coexisted.
Recently, DEAs coupled with electrodes and lighter gas have been developed as soft pumps and robots. Zhu et al.[10] studied a thin-walled DE balloon and analyzed its nonlinear oscillation. Chen et al.[11] analyzed the dynamic performance of DE balloon actuators driven by a pressure and a voltage. Zhang et al.[12] presented balloon actuators based on DEs, and the initial volume was important for large deformation.
This paper investigates analytical models for circular DE membranes, and studies dynamic patterns on their surfaces. The performance of DE balloon actuators coupled with helium gas is also proposed, and the mass change can be controlled for application in soft-actuated air vehicles. The purpose of this research is to optimize the parameters and theoretical models of DEs, and to give some guidelines for intelligent soft robots and devices.
1 Equations for Deformation
Fig.1 illustrates the experimental setup for observing the phase transitions on a circular DE film. Voltage is programmed with the software of Labview and amplified by a high voltage amplifier (10/40 A). Cameras are employed to capture the side view of DE actuators. A circular membrane is axisymmetric in its configuration, as shown in Fig.1, consisting of an active region with electrodes and a passive part. The voltage is then applied to the active region which expands into a new state of equilibrium. In the case of the pre-stretch λpre=1, the volt-age will induce compressive stresses in the passive region, and the thin membrane can experience out-of-plane bulging due to the loss of tension (LT).

1— Circular DE actuator; 2— Camera to take pictures and videos of the side view; 3—Computer; 4—BNC 2120 junction box; 5—High voltage amplifier
Fig.1 Experimental setup for a circular DE membrane
In the actuated state, the circular active part undergoes homogeneous, equal-biaxial deformation, which is different from the passive region. λr and λθ are the stretches in the radial and hoop directions, respectively. Using geometry, ∂λθ/∂R=λr/R-λθ/R. R is the reference radius of an arbitrary point in the active region, and r is the deformed radius of the same particle during the actuated state.
The element in a circular DE membrane undergoes tri-axial stresses σr, σφ and σθ which correspond to nominal stresses Sr, Sφ and Sθ, respectively. Mechanical equilibrium requires that ∂σr/∂r=(σθ-σr)/r. Therefore, the state equation can be written as a sum of two parts  can be calculated. Then, we obtain σθ=λθSθ. When Sθ=0, the loss of tension that induces phase transitions is apparent.
can be calculated. Then, we obtain σθ=λθSθ. When Sθ=0, the loss of tension that induces phase transitions is apparent.
The state of the active part is governed by 
The stretch ratio of the radius is λi, namely λi=ri+1/ri. The function related to λi and λpre is expressed by
(1)
The relationship between the voltage and the stretch is given. Furthermore, the dielectric breakdown voltage is calculated by ![]()
(2)
Fig.2(a) presents a spherical DE membrane with the original radius R and thickness H. It consists of monolayer elastomer (VHB or natural rubber), and carbon grease is smeared on the exterior and interior surfaces of the spherical membrane to serve as electrodes. Inner initial pressure p0 is equal to the atmospheric pressure. The gas is pumped into the balloon, and then the actuator is sealed. Consequently, the actuator is subject to pressurep1, and the radius and thickness become r1 and h1, respectively, as shown in Fig.2(b). Fig.2(c) shows that the balloon deforms to an equilibrium state with radius r2 and thickness h2 corresponding to current pressure p2 and voltage Φ. In Fig.2(d), we define ![]()

Fig.2 Schematic of a DE spherical shell. (a) Original state; (b) Pre-stretched state; (c) Actuation state; (d) Deformed state of the element in a DE film subjected to tri-axial stresses
In Fig.2, from states (a) to (c),thermodynamics dictates that the arbitrary variation of free energy in a DE membrane should equal the work done by the voltage, pressure and inertia, so that 
From Figs.2(a) and (b), the stretch ratio in the gas pumping process is prescribed as ![]() and V1 is the volume. The pressure in the balloon is
and V1 is the volume. The pressure in the balloon is
(3)
The fixed amount of gas is enclosed. Combining the ideal gas law, the internal pressure of a DE balloon actuator is
(4)
Then, the pressure decreases with the increase in the volume caused by the voltage, and it is described as
(5)
The condition of dielectric breakdown is expressed[13] as EDB=30.6λ1.13×106. The voltage corresponding to EDB is ΦDB=EDBHλ-2.
Fig.3 shows that DE balloon actuators are characterized by the desired nonlinear pressure-prestretch relationship λ1=r1/R. The curves follow the trends predicted by analytical models. The original radius R is 3.50, 7.25 and 12.75 cm, respectively. In Fig.3(a), the stretch limit Jlim=175 and shear modulus μ=35 kPa are used. Electric breakdown always occurs at about Ф = 6 kV. From Fig.3(b), the parameters μ=350 kPa, and Jlim=35. Electric breakdown commonly occurs at about Ф=3 kV. The original thicknesses of the rubbers are chosen to be 0.25, 0.4 and 0.47 mm, respectively. It is found that the peak pressure in a rubber balloon is greater than that of a VHB spherical shell. The limit stretch of natural rubber is much smaller than that of the VHB material.

(a)
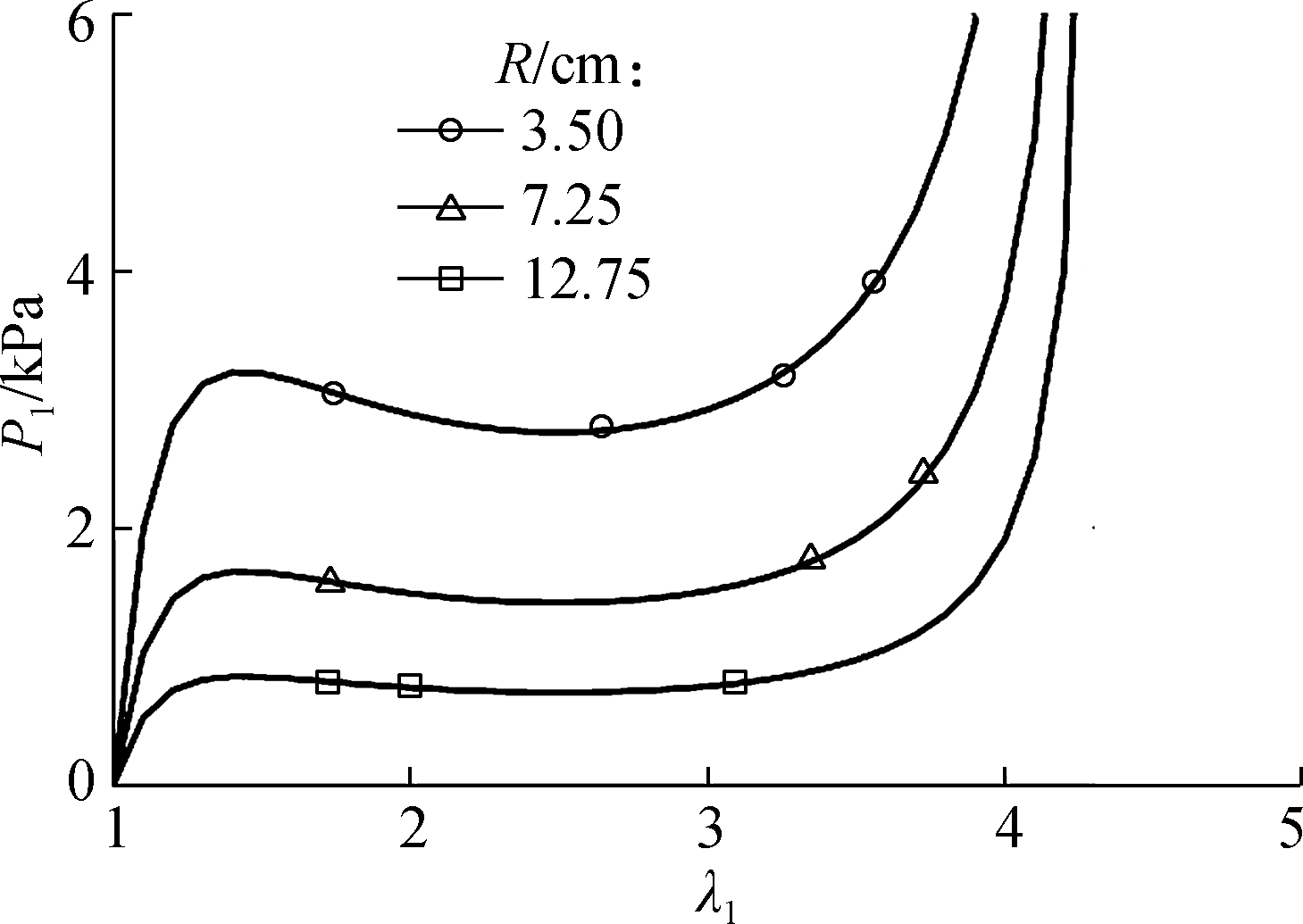
(b)
Fig.3 Pressure p1 in gas pumping process as a function of pre-stretch λ1. (a) Pressure change in VHB 4910 balloon shells; (b) Pressure change in natural rubber balloons
Fig.4 plots the gas law for numbers of molecules within a rubber balloon and a VHB balloon, respectively. The rhombus curve represents the number of gas moles in a rubber balloon, and the dotted line shows that in a VHB 4910 spherical shell. With the same original diameter (7 cm) and pre-stretch, the initial thickness of VHB membrane is 1 mm, for rubber it is 0.25 mm. As a result, the gas amount in the rubber balloon is more than that in the VHB balloon, because VHB is a softer material.

Fig.4 Relationship between the number of gas moles and pre-stretch
2 Discussion
Phase transitions are observed on circular DE membranes (the original thickness H=1 mm) with different pre-stretch λpre. In the pre-stressed state, thin membranes are flat, as shown in Fig.5(a) and Fig.6(a). When the voltage is relatively small, the membrane keeps flat and elongates around the frame. As the voltage further increases, the tensile stress in the passive region decreases gradually. At a critical voltage, bulging (see Fig.5(c), λpre=1) or wrinkles (see Fig.6(c), λpre=4) appears. Wrinkled regions can spread over the entire membrane within a short time.

(a) (b) (c)
Fig.5 The phase transition from the flat state to bulging state under different voltages. (a) 0 kV; (b) 7 kV; (c) 9.5 kV

(a) (b) (c)
Fig.6 The phase transition from the flat state to wrinkle state under different voltages. (a) 0 kV; (b) 5.5 kV; (c) 6.6 kV
For DE balloons, when the voltage is applied to double-layer spherical membranes, the volume change is larger than that of monolayer DE balloons. A new method is also used to obtain a large deformation of a DE balloon. After dielectric breakdown of the inner rubber, we continue to apply the voltage to the double-layer spherical VHB membranes and the balloon further expands its volume without gas leakage. This process can increase the mass change and it is controlled in the flight robot system[14].
3 Conclusions
1) This paper investigates the calculation models for the analysis of circular and spherical DE membranes. Phase transitions among flat, bulging and wrinkles can be theoretically predicted and experimentally observed in a narrow voltage range prior to electrical failure.
2) The analytic models of soft balloon actuators combining free energy and the ideal gas law can provide guidance for experiments. Larger deformations of multi-layer DE balloons are also explored. The spherical DE membranes can be utilized in a giant deformation to produce the controlling force, and they have potential application for soft flight robots.
3) It is hoped that the proposed theory and results will help the design of DEAs and maximize their actuation performance.
[1] Zhang H, Zhang Z S. Phase transitions of dielectric elastomers in a circular frame [J]. Journal of Southeast University (English Edition), 2017, 33(4): 387-390. DOI: 10.3969/ j.issn.1003-7985.2017.04.001.
[2] Wu J F, Li J Q, Song A G, et al. Electrostrictive properties on polyurethane elastomers [J]. Journal of Southeast University(Natural Science Edition), 2008, 38(3):439-443. DOI:10.3321/j.issn:1001-0505.2008.03. 015.(in Chinese)
[3] Roche E T,Wohlfarth R, Overvelde J T B, et al. A bioinspired soft actuated material [J]. Advanced Materials, 2014, 26(8): 1200-1206. DOI:10.1002/adma.201304018.
[4] Zhang H, Zhou Y F, Dai M, et al. A novel flying robot system driven by dielectric elastomer balloon actuators [J]. Journal of Intelligent Material Systems and Structures, 2018,29(11):2522-2527.DOI:10.1177/1045389x18770879.
[5] Mao G Y, Huang X Q, Diab M, et al. Controlling wrinkles on the surface of a dielectric elastomer balloon [J]. Extreme Mechanics Letters, 2016, 9: 139-146. DOI:10.1016/j.eml.2016.06.001.
[6] Yu J, Chary S, Das S, et al. Gecko-inspired dry adhesive for robotic applications [J]. Advanced Functional Materials, 2011, 21(16): 3010-3018. DOI:10.1002/adfm. 201100493.
[7] Huang R, Suo Z G. Electromechanical phase transition in dielectric elastomers [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2012, 468(2140):1014-1040. DOI:10.1098/rspa.2011.0452.
[8] Lu T Q,Suo Z G. Large conversion of energy in dielectric elastomers by electromechanical phase transition [J]. Acta Mechanica Sinica, 2012, 28(4): 1106-1114. DOI:10.1007/s10409-012-0091-x.
[9] Godaba H, Zhang Z Q, Gupta U, et al. Dynamic pattern of wrinkles in a dielectric elastomer [J]. Soft Matter, 2017, 13(16): 2942-2951. DOI:10.1039/c7sm00198c.
[10] Zhu J,Cai S Q, Suo Z G. Nonlinear oscillation of a dielectric elastomer balloon [J]. Polymer International, 2010, 59(3): 378-383. DOI:10.1002/pi.2767.
[11] Chen F F, Wang M Y. Dynamic performance of a dielectric elastomer balloon actuator [J]. Meccanica, 2015, 50(11):2731-2739.DOI:10.1007/s11012-015-0206-0.
[12] Zhang H, Wang Y X, Zhu J, et al. Balloon actuators based on the dielectric elastomer [C]//IEEE International Conference on Industrial Technology. Toronto, Canada, 2017: 654-658. DOI:10.1109/icit. 2017.7915436.
[13] Koh S J A, Keplinger C, Li T F, et al. Dielectric elastomer generators: How much energy can be converted? [J]. ASME Transactions on Mechatronics, 2011, 16(1): 33-41. DOI:10.1109/tmech.2010.2089635.
[14] Zhang H, Wang Y X,Godaba H, et al. Harnessing dielectric breakdown of dielectric elastomer to achieve large actuation [J]. Journal of Applied Mechanics, 2017, 84(12): 121011. DOI:10.1115/1.4038174.