In the classical continuum mechanics, every material point only interacts with its closest material points, and it is assumed that the force and displacement of every material point are continuous when it deforms, which causes an inherent limitation when formulating the crack initiation and propagation because damage causes discontinuities. Without some special treatments, even some modified methods based on the classical continuum mechanics cannot break through this limitation. In 2000, Professor Silling of Sandia National Laboratories put forward a novel non-local mechanics theory named peridynamics, it is particularly suitable for dealing with discontinuous mechanical problems[1]. The theory uses spatial force integral equations instead of partial differential equations to model the mechanical behavior of material when it deforms even if it is damaged[2]. It can simulate the crack initiation and propagation spontaneously. With the development of peridynamics, the theory has experienced three phases, which are bond-based, ordinary state-based, and non-ordinary state-based peridynamics[3-4]. In the bond-based peridynamic theory, the pairwise force constitutive function was established according to the energy balance function as in the classical continuum mechanics, and the pairwise interaction force between material points includes the relative mechanical information of material[5]. In recent years, the bond-based peridynamic model has been widely used in the simulation of large deformation, complex crack propagation, damage and progressive failure process of the concrete structure, laminated composite materials and so on[6]. It has shown advantages in dealing with the discontinuous mechanical problems, while its limitation of fixed Poisson’s ratio affects its simulating effect and application range.
Due to the oversimplified assumption that any pair of the interaction force is independent of other bonds’ interaction forces, and some PD material parameters are assumed as the bond-constant, Poisson’s ratios of the bond-based peridynamics are constant values. The two-dimensional bond-based peridynamics can only model materials with Poisson’s ratio of 1/3, while the three-dimensional bond-based peridynamics model of 1/4[7]. In order to overcome this limitation, a modified mechanical method based on the bond-based peridynamics was proposed by Gerstle et al.[8], and the new model was called the micropolar peridynamic model. Compared with the bond-based peridynamic model, the pairwise peridynamic moment as well as pairwise peridynamic force is added to the pairwise constitutive equations in the micropolar peridynamic model. The micropolar peridynamic model was effectively used in the quasistatic simulation of crack initiation and propagation, especially in the research field of concrete materials, and the fracture mechanism of the concrete was observed reliably[9-10]. Aziz[11] developed a constitutive damage model based on micropolar peridynamics to simulate the damage process of concrete beams. In the simulation, the crack mouth opening displacement and load of notched beams were researched, and simulation results matched very well with laboratory experimental ones, which showed that this method was effective. Yaghoobi et al.[12] used the micropolar peridynamic approach for fracture analysis in a fiber reinforced concrete structure, and the interacting force was applied to material particles indirectly. The results showed that this approach can improve the computational effectiveness. Since the micropolar peridynamic method is intuitionistic and suitable for the meshfree computational method, the micropolar peridynamic method can be implemented combined with some developed computational methods[13-14]. Roy et al.[15] combined the micropolar peridynamics and lattice model to establish a practical method called the micropolar peridynamics lattice model (MPLM). This theory viewed the structure as a combination of interacting point mass, and the constitutive behavior of material can be captured by calculating inter-particle forces and moments, so it is easy to implement this method in practical application. Combined with the finite element method, Yu et al.[16] used the micropolar peridynamic model to solve static mechanical problems by deducing the function of the micropolar model for static mechanical problems, and in this method the fictitious damping term was no longer needed to be considered, thus the computational accuracy and efficiency were improved. In terms of the elastic-plasticity mechanics, Madenci et al.[17] constructed the yield surface based on the relationship between the equivalent plastic stretch and effective stress, and the plastic deformation with isotropic hardening was researched. Although the aforementioned literature laid a foundation for the study of the micropolar peridynamics, some details about the constitutive models of micropolar peridynamic forces, moments and transformation of different configurations remain to be discussed, and there is little literature about the simulation of plastic deformation behavior based on the peridynamic approach.
In this study, the theoretical basis of the bond-based peridynamics is illustrated, and the improved micropolar peridynamic model is established on this basis. By transforming the peridynamic bond from the truss element to the beam element, the force and moment equation of the micro-beam is deduced, so that the micropolar peridynamic model allows not only pairwise forces but also pairwise moments to act on every bond. Taking account of interacting forces and moments between related material points, the motion equation of material points can be obtained in a local configuration. By setting the local configuration of every material point, and calculating the relative transforming matrix, the constitutive equation in forms of matrices can be established in the global configuration. Finally, the numerical simulation and experiment of a metal plate with a hole were implemented, respectively, and the validity of this method was identified and the damage evolution of the metal plate was studied.
1 Bond-Based Peridynamics
Compared with the classical continuum mechanics, the peridynamics is a novel mathematical model to deal with mechanical problems based on the non-local theory. In peridynamics, the material is divided into infinitesimal material points, the force of the material can be obtained by the peridynamic force analysis of every material point. As shown in Fig.1, a material point x in spatial region B has an internal subregion R, which is defined as
R={x∈B:x′-x≤δ⟹x′∈B}
(1)
Fig.1 The schematic of the peridynamic model
The parameter δ is defined as the peridynamic horizon, in which only material points x′ whose relative positions to x are less than the peridynamics horizon can interact with the material point x. In reference configuration, the material points located in the peridynamic horizon are the family members of material point x labeled as the material point x′ in Fig.1. In the deformed configuration, the new coordinates of the material points x and x′ are y and y′, respectively. Then, the relative position vector and the relative displacement vector in the reference configuration are
ξ=x′-x, η=u′-u
(2)
where x and x′ are the coordinate vectors of the material points; u and u′ are the displacement vectors.
Therefore, the relative position in the deformed configuration is
η+ξ=(u′+x′)-(u+x)
(3)
According to the peridynamics theory, the force between material points x and x′ is called the peridynamic pairwise force f. In the internal subregion of material point x, the internal force density Lu(x) at time t is defined as
(4)
The peridynamic pairwise force f is exerted on material point x by other material points in the internal subregion R. Then, based on Newton’s Second Law, the motion equation of the material point x is obtained as
(5)
where ρ is the density of material; b is the external loading force density.
According to the law of energy conservation, the strain energy density ω can be calculated as
(6)
where ω is a scalar-valued function; σ and ε are the stress and strain vectors, respectively.
The peridynamic pairwise force f is defined by Professor Silling as
(7)
where c is a bond-constant parameter obtained by linearizing the pairwise force function f; s is the stretch of bond defined as in the classical continuum mechanics as follows:
(8)
In order to describe the history-dependent effect of the damage, a scalar function μ(t,ξ) is added to the following peridynamic pairwise force function:
(9)
where sc is the critical stretch, which can be calculated from the function of the critical energy release rate as in the bond-based peridynamic model.
The damage degree of the material point can be defined as a weighted ratio φ(x,t), which is the weighted ratio of the number of broken bonds to the total number of initial family bonds.
(10)
2 Improved Micropolar Peridynamic Constitutive Equation
As known in the bond-based peridynamics, there are pairwise forces between two interactional material points, and they are equal in amount while being in opposite directions. Compared to the bond-based peridynamics, the micropolar peridynamics views a bond as a beam, and it can bear not only stretching but also bending moment. Different from the central-force bond-based peridynamics, the pairwise moment and pairwise force are added into its constitutive model in the micropolar peridynamics together. As shown in Fig.2, the bond L between the material points i and j is viewed as a micro-beam. Due to being subjected to moment loads, the material points were rotated.
Fig.2 The micropolar peridynamic model
2.1 Micropolar peridynamic model
According to the micropolar peridynamics theory, the sum of all pairwise forces and moments that act on material point i can be expressed as
(11)
where Fi and bi are the vector-valued pairwise force and the external force per unit volume acting on material point i; ΔVi is the volume of material point i; Mi and mi are vector-valued pairwise moments and the external moment per unit volume acting on material point i. In these vectors, bi and mi are the externally applied force and moment per unit volume acting on the material point i; Ii is the mass moment of inertia; 
are the acceleration and angular acceleration of material point i, respectively.
In the coordinate X′O′Y′, when the volume ΔVi becomes infinitesimally small, the value of (Ii/Vi) tends to zero, so the equation of motion of material point i can be expressed in the form of the bond-based peridynamics as
(12)
where fij and mij are the pairwise force and the moment of the material points i with their family members.
As mentioned above, it is assumed that the bond of the micropolar peridynamic model is viewed as a beam, so Eq.(12) of the two-dimensional model can be transformed in the form of matrix as F′=K′U′. Here, F′ is the pairwise force and moment function, and U′ is the displacement and rotation. They can be expressed as
(13)
where 
are the displacements of material points in x and y directions;
,
are the rotating angles of the material points.
According to the equation of the deflection curve, the stiffness matrix K(ε)′ of the bond (viewed as a micro-beam) in the micropolar peridynamic model can be expressed as
(14)
where ε is the strain value of the material point; K(ε)′ is a function that depends on ε; l is the length of the undeformed bond; c, d are the parameters of the micropolar peridynamic model, which can be used to evaluate the internal energy of all bonds within their family in the micropolar peridynamic model. Unlike traditional micropolar peridynamics, the values of c, d change according to the strain value ε. When material points are in the plastic deformation phase, the constitutive equation of the micropolar peridynamic model needs to be re-established. For a given material, its energy in the micropolar peridynamic model is equal to the strain energy in the classical continuum mechanics, then c, d can be obtained. According to Gerstle et al.[8], c and d for a plane stress micropolar peridynamic model are given as
(15)
where E(ε) is a function of elastic modulus ε; v is Poisson’s ratio. Poisson’s ratio of the micropolar peridynamic model is no longer a constant. Considering the non-negative of the parameters c and d, Poisson’s ratio v can be changed from 0 to 1/3 in the two-dimensional peridynamic model.
2.2 Relationship between peridynamic pairwise force and elastic-plastic behavior
As shown in Eq.(13), the peridynamic pairwise forces of material point i in x-axis and y-axis are
,
,
and the displacement of a material point can be calculated as
(16)
where 
are the displacements of the material point i in adjacent time steps. Under the condition of small deformation, the strain values of material points can be calculated by the difference algorithm as follows[18]:
(17)
where ui-2, ui-1, ui, ui+1, ui+2 are the displacements of the adjacent material points in the order from top to bottom or from left to right. Eq.(17) are the difference equations of midpoint, left point and right point, respectively. The strain value εx and εy are calculated in different directions. Through calculating the strain value of every material point in every time step, the strain values can be obtained.
According to Generalized Hook’s Law, the stress of material point i can be obtained.
(18)
When the stress of the material point exceeds its elastic limit, the metal will undergo plastic deformation. In the stage of plastic deformation, its volume change is elastic while its shape change is caused by the stress deviatoric tensor. Considering the convenience of calculation, the Von Mises yield criterion is adopted. It can be expressed as
(19)
where σs is the yield stress; 
exceeds the yield stress σs, the material point will undergo plastic deformation. The material of Q235c is taken as an example, and the stress of uniaxial tensile in plastic deformation can be obtained according to the test data[19].
(20)
where n is the enhancement coefficient, 0≤n≤1. The power-enhanced elastic-plastic model is adopted. Then, the function of elastic modulus E(ε) can be defined.
(21)
The value of E(ε) is similar to the tangent modulus. However, compared with the fixed tangent modulus, the value of the elastic modulus is more effective to establish the constitutive equation of the improved micropolar peridynamic model.
2.3 Numerical calculation method of the micropolar peridynamic model
The pairwise force and moment equations of the micro-beam in the micropolar peridynamics are calculated as Eq.(11) in each own local configuration. Due to discretization, it is necessary to transform the pairwise force and moment functions from the local configuration to the global configuration. As shown in Fig.3, the local configuration of material points i and j is X′O′Y′, the global configuration of all material points is coordinate XOY. In local coordinate, bond L is viewed as the X′-axis, and there is angle θ between bond L and the X-axis of the global configuration. The positions of material points i and j are (xi,yi), (xj,yj).
According to the relationship between the local configuration and global configuration, the following transformation of pairwise force and displacement can be obtained.
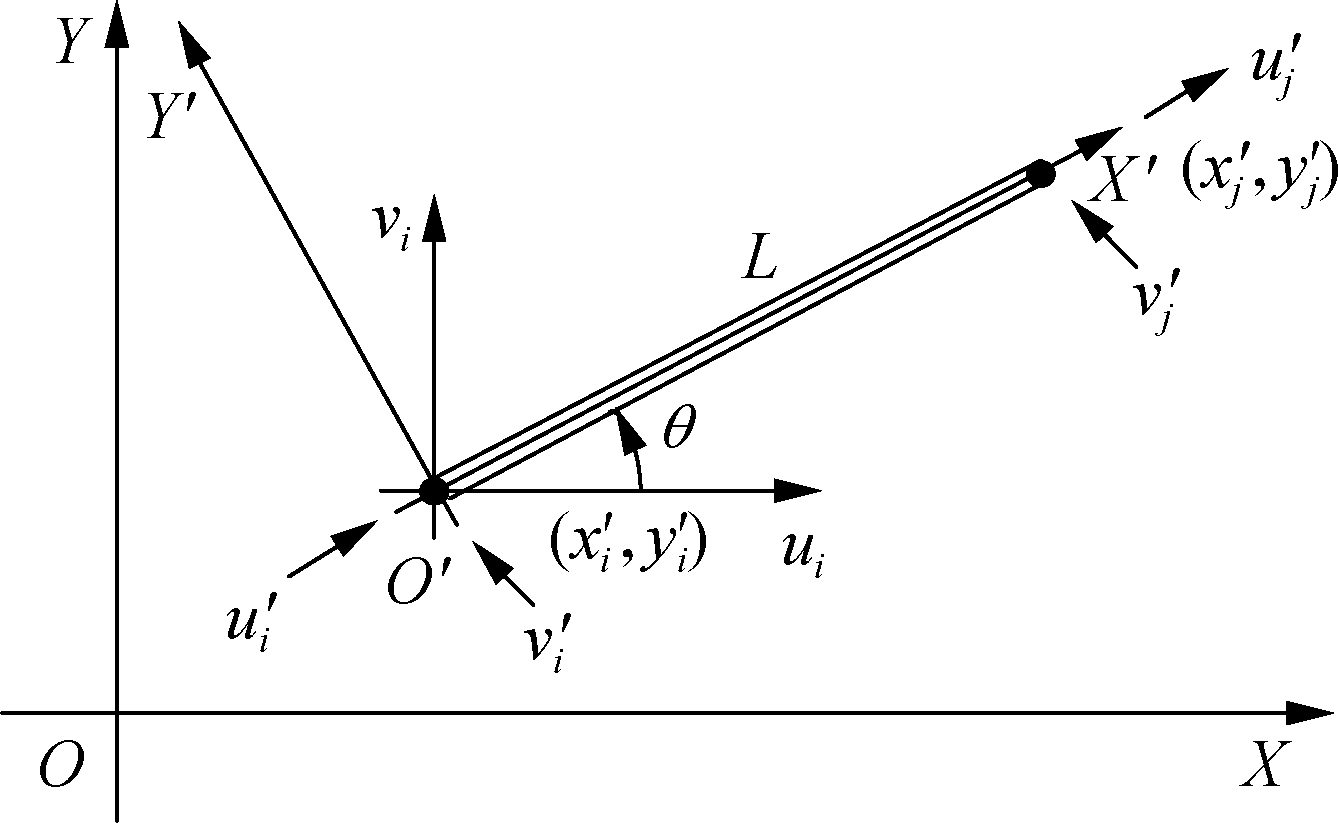
Fig.3 Local configuration and global configuration
(22)
By submitting Eq.(22) into equation F′=K′U′, the constitutive equation of the micropolar peridynamic model in the global configuration can be obtained.
(23)
where
The numerical solution of the micropolar peridynamic model is an explicit method for calculation. The material points are generated by discretizing, and some relative parameters of modeling are obtained according to the numerical solution method of the bond-based peridynamics. The most important step is to calculate the total peridynamic force and moment of each material point. In a balance state of the internal peridynamic force, the equation of motion as equation F=KU can be expressed as
(24)
where j is the number of the material points which belong to the family members of material point i; n is the number of time steps.
3 Numerical Implementation and Experiments
The aforementioned improved micropolar peridynamic model is validated by simulating the damage evolution of the metal plate which has a hole in the center. This model is compared with the physical tensile experiment of metal plates analyzed by the digital image correlation method (DIC). The metal plates of Q235c are used in this experiment, and they are subjected to different velocity boundary conditions. By analyzing the digital images of the metal plates during the process of deformation, the displacement values of the scattered spots in the metal plates can be obtained, and then the strain distribution of the metal plates can be obtained to research the damage mechanism of the metal plate.
3.1 Numerical implementation on metal plates
As discussed above, it is more practical for simulating material mechanical behaviors with appropriate Poisson’s ratios by the improved micropolar peridynamic model. As Fig.4 shows, a metal plate with a central hole is modeled by the improved micropolar peridynamics. The length and width of the plate are 60 and 25 mm, respectively, and the thickness is 5 mm which is much smaller than other sizes, so it can be regarded as a two-dimensional structure. There is a central hole of which the radius is 2.5 mm in the plate. The material of this plate is Q235c, and its mechanical parameters are as follows: Young’s modulus is E=235 GPa, Poisson’s ratio is v=0.3, the yield stress is σs=243.38 MPa, and the density is ρ=7 850 kg/m3. In the stage of plastic deformation, the function of stress and strain can be expressed as σ=950ε0.31, and the enhancement coefficient n=0.31. Since the adaptive dynamic relaxation (ADR) is adopted in the numerical solution method, the time step is Δt=1.0 s. These metal plates are subjected to different velocity boundary conditions including 27.5, 30.0, 32.5, 37.5, 42.5 μm/s.
Fig.4 The metal plate with a central hole
According to the principle of the modeling of peridynamics, the spacing between material points in this model is Δx=0.1 mm, so the number of discretized material points is 151 500, including material points in the fictitious material layer along the boundary areas of the plate. The peridynamic horizon δ=3.015Δx, and the velocity of boundary condition is v (unit: m/s) as mentioned above. According to the critical energy release rate of Q235c, the critical stretch sc is defined as 0.17.
3.2 Comparison analysis
In order to verify the effectiveness of the improved micropolar peridynamic model, some physical tensile tests of the metal plate were implemented, and the DIC method was used to analyze the displacement and strain distribution during the process of stretching. DIC is a type of non-contact measurement method, which can acquire the displacement and strain data by comparing the displacements of scattered spots in the material before and after deformation. In this experiment, the DIC system was used to take photos during the stretching process of the metal plate, and the strain distribution of the process can be acquired from the displacements of material points. By comparing the results of the numerical implementations with the results analyzed by DIC, the effectiveness of the proposed model can be verified.
As shown in Fig.5, a metal plate with a central hole was installed on the mechanical testing machine (Model CMT5105). According to the simulation above, five metal plates were tested with the different velocity boundary conditions as mentioned above. These velocity boundary conditions acted upon the edges in the vertical direction.
(a)
(b)
Fig.5 Tensile experiment of the metal plates. (a) Mechanical testing machine;(b) The metal plate
Since the traditional peridynamics is suitable for simulating the mechanical behaviors of the micro-elastic materials, it cannot simulate the plastic deformation effectively for metal materials. With the different constitutive equations, the improved micropolar peridynamic model can simulate the plastic deformation as well as the elastic deformation. By analyzing the results of the improved micropolar peridynamic model, the plastic deformation occurs at the time step of 81, and these material points are located in the areas close to the horizontal diameter of the central hole. The results of three methods are shown in Fig.6. Fig.6(a) is the digital image of the DIC method, and its boundary condition is 50 μm. Figs.6(b) and (c) are the simulation results of the improved micropolar peridynamic model and bond-based peridynamic model, respectively. Their boundary condition is 44.55 μm. Since the improved micropolar peridynamic model takes the constitutive equation of the plastic deformation into consideration, Fig.6(b) is closer to the result of DIC, in which the central hole has deformed into an ellipse, and the simulation result has more practical local deformation characteristics than that of the bond-based peridynamic model.
Through the quantitative analyses of the strain distribution during the damage process, the validities of these two methods were verified. When the boundary condition is 3.0 mm in the vertical direction, the strain distribution εx of the DIC in the horizontal direction is shown in Fig.7(a), and the calculation results of the bond-based peridynamics
(a)
(b)
(c)
Fig.6 Deformations of the metal plate. (a) Deformation of DIC; (b) Deformation of the improved micropolar peridynamics; (c) Deformation of the bond-based peridynamics
and improved micropolar peridynamics are obtained as shown in Fig.7(b) and Fig.7(c), respectively. The maximum strain is located in the horizontal diameter of the central hole where it is more likely to be damaged under the boundary condition in the vertical direction. The strain distributions of the bond-based peridynamic and improved micropolar peridynamic models are almost identical to the analysis results of the DIC. However, the maximum value of the strain εx of the improved micropolar peridynamic model is 8.36×10-2, which is closer to the experimental result of DIC than the result of the bond-based peridynamic model by a factor of 7.2%. Due to variable Poisson’s ratio of the improved micropolar peridynamics, it is more accurate to simulate the damage evolution of the metal materials.
3.3 Damage evolution of the metal plate
As shown in Fig.8, the metal plate was damaged gradually under the undergoing boundary condition. With the help of the proposed improved micropolar peridynamic model, the damage degree was quantitatively calculated as Eq.(10). When the boundary condition was 4.15 mm as shown in Fig.8(a), the metal plate was damaged and
(a)
(b)
(c)
Fig.7 Strain analysis of tensile experiments. (a) Result of DIC; (b) Numerical result of the bond-based peridynamics; (c) Numerical result of the improved micropolar peridynamics
the crack initiated. The length of the crack was 0.2 mm, and the material points located in the area of the horizontal diameter of the central hole were damaged sharply with higher strain values than other material points. As shown in Fig.8(b), the damage factor of these material points was higher than that of other material points dramatically. When the boundary condition increased to 5.1 mm, the metal plate was in the phase of crack propagation with the crack length increasing to 3.0 mm, and the maximum of the damage factors was 0.66 as shown in Figs.8(c) and (d). Meanwhile, the changes of damage factors directly reflected the crack initiation and propagation. When the boundary condition was 6.84 mm, the metal plate was almost broken and the crack length L was 9.5 mm on one side of the metal plate, as shown in Figs.8(e) and (f), and the maximum of damage factors was 0.82.
(a)
(b)
(c)
(d)
(e)
(f)
Fig.8 Damage evolution of the metal plate. (a) Initial stage (DY=4.15 mm); (b) Damage factor of initial stage (L=0.2 mm); (c) Crack propagate (DY=5.10 mm); (d) Damage factor of crack propagate (L=3.0 mm); (e) Almost broken (DY=6.84 mm); (f) Damage factor of almost broken (L=9.5 mm)
The relationship between the boundary condition at different velocities and the crack length was studied. In Fig.9, due to its symmetrical structure, the crack located in only one side of the metal plate was studied. The speed of the velocity boundary condition was 27.5 μm/s. When the boundary condition was 4.15 mm, the crack initiated. The crack length increased with the ever-increasing boundary condition. When the boundary condition was 6.84 mm, the crack length no longer increased, reaching the maximum value of the crack length of 9.5 mm, and the metal plate was broken completely. Meanwhile, the relationship between different boundary conditions at different velocities was studied. The crack initiated at a fixed boundary condition of 4.15 mm, and all the final crack lengths were 9.5 mm under different velocity boundary conditions, while the speeds of crack propagation were different under different velocity boundary conditions. When the velocity of the boundary condition increased, the crack length decreased at the same boundary load, and it seemed that the speed of crack propagation lagged behind the boundary conditions.
Fig.9 Crack lengths under different velocity boundary conditions
Through the improved micropolar peridynamic model, the displacement and strain values of material points were calculated, and the damage degree can be quantitatively calculated. Thus, the relationship between structural shape, material physical parameters and external loads can be obtained, and the damage mechanism of the metal plate can be obtained.
4 Conclusions
1) An improved micropolar peridynamic model is developed, and the constitutive equations of the model in the stages of elastic and plastic deformations are put forward. Considering the elasticity-plasticity of metal, the deformation stage is estimated based on the Von Mises yield criterion, and the constitutive equation of plastic deformation is studied.
2) The proposed improved micropolar peridynamic model is implemented to simulate the damage evolution of the metal plates with a central hole. In order to verify the validity of the improved model, the numerical results of the model are compared with those of the bond-based peridynamic model and physical experiments analyzed by DIC. Compared with the bond-based peridynamic model, the maximum strain in the deformation stage is enhanced by 7.2%, and the damage evolution is quantitatively studied by calculating the damage factor in the improved model.
3) The damage evolution of the metal plate is analyzed, the relationship between crack lengths and velocity boundary conditions is studied. As the velocity of the boundary condition increases, the crack propagation speed is also increased, and the crack length is decreased at the same boundary load.
[1] Silling S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209. DOI:10.1016/s0022-5096(99)00029-0.
[2] Madenci E, Oterkus E. Peridynamic theory and its applications[M]. New York: Springer, 2014: 54-89.
[3] Silling S A, Askari E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & Structures, 2005, 83(17/18): 1526-1535. DOI:10.1016/j.compstruc.2004.11.026.
[4] Roy Chowdhury S, Masiur Rahaman M, Roy D, et al. A micropolar peridynamic theory in linear elasticity[J]. International Journal of Solids and Structures, 2015, 59: 171-182. DOI:10.1016/j.ijsolstr.2015.01.018.
[5] Qiao P Z, Zhang Y, Zhang H, et al. A review on advances in peridynamics[J]. Chinese Quarterly of Mechanics, 2017(1): 5-17. (in Chinese)
[6] Oterkus E, Madenci E. Peridynamics for failure prediction in composites[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Honolulu, Hawaii, USA, 2012: 157-169. DOI:10.2514/6.2012-1692.
[7] Warren T L, Silling S A, Askari A, et al. A non-ordinary state-based peridynamic method to model solid material deformation and fracture[J]. International Journal of Solids and Structures, 2009, 46(5): 1186-1195. DOI:10.1016/j.ijsolstr.2008.10.029.
[8] Gerstle W, Sau N, Silling S. Peridynamic modeling of concrete structures[J]. Nuclear Engineering and Design, 2007, 237(12/13): 1250-1258. DOI:10.1016/j.nucengdes.2006.10.002.
[9] Yaghoobi A, Chorzepa M G. Fracture analysis of fiber reinforced concrete structures in the micropolar peridynamic analysis framework[J]. Engineering Fracture Mechanics, 2017, 169: 238-250. DOI:10.1016/j.engfracmech.2016.11.004.
[10] Gerstle W, Sau N, Aguilera E. Micropolar peridynamic constitutive model for concrete[C]//19th International Conference on Structural Mechanics in Reactor Technology (SmiRT 19). Toronto, Canada, 2007: 1-8.
[11] Aziz A. Simulation of fracture of concrete using micropolar peridynamics[D]. Albuquerque, NM, USA: The University of New Mexico, 2014.
[12] Yaghoobi A, Chorzepa M G. Fracture analysis of fiber reinforced concrete structures in the micropolar peridynamic analysis framework[J]. Engineering Fracture Mechanics, 2017, 169: 238-250. DOI:10.1016/j.engfracmech.2016.11.004.
[13] Yu K, Xin X J, Lease K B. A new method of adaptive integration with error control for bond-based peridynamics[C]//Proceeding of the World Congress on Engineering and Computer Science. San Francisco, CA, USA, 2010: 1-7.
[14] Liu R W, Xue Y Z, Lu X K, et al. Simulation of ship navigation in ice rubble based on peridynamics[J]. Ocean Engineering, 2018, 148: 286-298. DOI:10.1016/j.oceaneng.2017.11.034.
[15] Roy Chowdhury S, Masiur Rahaman M, Roy D, et al. A micropolar peridynamic theory in linear elasticity[J]. International Journal of Solids and Structures, 2015, 59: 171-182. DOI:10.1016/j.ijsolstr.2015.01.018.
[16] Yu Y T, Zhang Q, Gu X. Application of micropolar peridynamic model in solving static problems[J]. Chinese Quarterly of Mechanics, 2017(1): 50-57. DOI:10.15959/j.cnki.0254-0053.2017.01.005.(in Chinese)
[17] Madenci E, Oterkus S. Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening[J]. Journal of the Mechanics and Physics of Solids, 2016, 86: 192-219. DOI:10.1016/j.jmps.2015.09.016.
[18] Xu Z L. Elastic mechanism[M]. Beijing: Higher Education Press, 2016:192-219. ( in Chinese)
[19] Zhang Q L, Jin M, Zhang H S, et al. Experiment research on material characteristics of Q235 under small deformation cyclic loading[J]. Journal of Mechanical Engineering, 2017, 53(20): 69-76. (in Chinese)