The launch safety of the propellant charge severely restricts the development of modern high-performance weapons all over the world. Under low temperatures, the propellant grain has an enhanced brittleness, and the root cause of bore burst is the fractures of propellant grains during the collision and press processes in the propellant bed[1]. According to the relevant domestic and international studies, no matter how complex the mechanics environment inside the gun bore is, bore burst will not occur if there is no fracture of the propellant grains[2]. At present, the relevant studies have mainly focused on the whole propellant bed, and only a few studies have investigated individual propellant grains. The press and fracture study of individual propellant grain plays a significant role in the launch safety evaluation of the propellant charge.
Due to the complex mechanics environment of the propellant charge, most studies on individual propellant grain are still based on physical experiments.Chen et al.[3] studied the damage mechanisms and its evolution of explosive materials using a long-pulse, low-velocity gas gun, and then studied the damage properties of polymer bonded explosives under dynamic loading by drop weight tests. Zhang et al.[4] applied static compression load to the lateral surface of the propellant granule to study the mechanical properties of the propellant granule. The press and fracture processes of the propellant grain are essentially a transformation process from a continuous medium to discontinuous medium of particle material[5]. The fracture study of propellant grain based on a physical experiment is limited by the current experimental techniques and safety factors, whereas the numerical simulation methods can provide the important means of conducting fracture study. The fracture of a single particle can be modeled based on the extended finite element method (XFEM), but the initial cracks need to be preset[6]. The discrete element method (DEM) provides an efficient way to model the fracture process and investigate its effect on the behavior of particles[7-10]. Particle fracture has been recently modeled using DEM based on the bonded-particle model, where a particle is modeled using an agglomerate composed of a large number of smaller particles bonded together[11]. Robertson et al.[12] established a DEM model of crushable grain by bonding elementary spheres in “crystallographic” arrays. A discrete element method model has been developed, in which grains are characterized by aggregations of a maximum of 14 elementary spherical particles[13]. Cil et al.[14] modeled the fracture of individual silica sand particles by adopting the bonded-particle model. Wang et al.[15] studied the effects of particle fracture on the shear failure behavior based on the bonded-particle model. Wang et al.[16] simulated the direct shear tests of irregular ballast stones by constructing clump particles. For DEM studies of propellant grain, Hong et al.[17-18] established the fracture model of the propellant grain and analyzed its mechanical property under impact load. Jiang et al.[19-20] simulated the fragmentation process of the propellant grain impact rigid wall with different initial azimuth angles, and then studied the fracture mechanisms of the propellant grain during the propellant charge. However, the initial defects of the propellant grain have not been considered in current studies, as well as the effect of the initial defects on the mechanical property and the fracture mechanism of the propellant grain.
As an explosive, the initial defects of the propellant grain cannot be preset due to the material processing and safety issue. The physical test has no way to be carried out, so the numerical study is unique. The objective of this paper is to model the press and fracture process of propellant grain, and investigate the effects of initial defects on its mechanical properties. The DEM model of propellant grain is established and then the initial defects are introduced to it using PFC3D. Through a series of numerical unconfined uniaxial compression tests, the press and fracture mechanism of the propellant grain with initial defects are simulated and compared to the propellant grain without the initial defects.
1 DEM Model
The discrete element method (DEM) was introduced by Cundall et al.[21] for the analysis of discontinuous granular material. In the DEM, the granule is discreted into an assembly of rigid elements, and the dynamic behavior is represented numerically by a timestepping algorithm. The calculations are performed alternately between the application of Newton’s second law to the particles and a force-displacement law at the contacts, so that the overall movements of the granular system are obtained. The DEM allows relative motions between distinct particles, and there is essentially no limit to the magnitude of displacement that can be modeled, making it a suitable technique for solving large-displacement discontinuous medium problems.
The PFC3D is a procedure that simulates the movements and interactions of spherical discrete particles based on the DEM. The computation of the PFC3D is potentially more efficient, because contact detection between spherical objects is much simpler than that between angular objects. PFC3D is able to model brittle material by allowing spherical particles to be bonded together as an assembly, and the resulting synthetic material is capable of fracturing by utilizing the breakage of bonds to represent the damage. As it uses the spherical particles to discrete the propellant grain, the constitutive model must be chosen appropriately, and the bonded-particle model after the model parameters calibration process is used to establish the DEM model of the propellant grain.
1.1 Constitutive model
In DEM, the mechanical response of a material is governed by interactions at its contacts between the constituent particles and between particles and boundaries[22]. In the PFC3D, the mechanical properties of the macroscale material are reproduced through the constitutive characteristics of the microscale particles. The constitutive behavior of a material is described by the constitutive model, which consists of three parts: a contact-stiffness model, a slip and separation model, and a bonding model.
The contact model describes the physical behavior occurring at a contact. This paper uses the default stiffness model and the linear-spring model, in which the contact stiffness provides an elastic relationship between the contact force and the relative displacement. The slip behavior is defined by the friction coefficient, which forces a relationship between shear and normal forces, such that the two contacting entities may slip relative to one another. As for the bonding model, the parallel-bond model that can transmit both force and moment between particles is chosen to set up the bonded-particle model.
1.2 Bonded-particle model
The unconfined uniaxial compression physical test of the propellant grain is shown in Fig.1. As can be seen, the geometric shape of the propellant grain is a regular hexagonal prism with seven small holes, and the side surfaces of the propellant grain have a plum pattern caused by the material processing. In this paper, the bonded-particle model represents the propellant grain by a bonded regular hexagonal assembly, which is generated by a random distribution of the bonded particles with a given porosity. In the resulting assembly, the holes between particles and the irregularity of the side surfaces can partially cancel the difference between the simplified model and actual specimen. To balance the calculation accuracy and efficiency, a suitable discrete number of 10 887 spherical particles were selected to establish the assembly. The relevant parameters are shown in Tab.1.

Fig.1 Unconfined uniaxial compression physical test
Tab.1 Bonded-particle model parameters

ParameterValueDensity of propellant grain/(kg·m-3)2 000Height of propellant grain/mm11.40Length of hexagon side/mm5.70Porosity of particle model/%25.95Particle minimum radius Rmin/mm0.20Particle ball-size ratio Rmax/Rmin1.50Friction coefficient0.50
The bonded-particle model (BPM) is classically built considering initially intact media[23]. The propellant grain material is simulated as an assembly of the bonded spherical particles. To establish a compacted assembly with a small porosity, the most robust modeling approach is the radius-expansion scheme. As shown in Fig.2, a population of particles with artificially small radii was initially created within a specified container by confining walls. Then, the radii of all the particles were expanded until the desired porosity was obtained and they were allowed to move freely until they reached the initial equilibrium state, and finally parallel bonds were installed throughout the assembly. With this method, the condition throughout the synthetic assembly was isotropic and can be subjected to material testing. The bonded-particle model of the propellant grain is shown in Fig.3.


(a) (b)
Fig.2 Radius-expansion scheme. (a) Initial diagram;(b) Final diagram

Fig.3 Bonded-particle model
In this paper,the unconfined uniaxial compression test was used to simulate the press and fracture processes of the propellant grain. After the bonded-particle assembly was generated and compacted within a set of confining walls, the confining walls were removed, while the top and bottom walls continued to act as loading plates. The unconfined compression test model is shown in Fig.4, in which all walls are frictionless. The loading process was applied by moving the top and bottom walls toward one another at the velocity of 5.7 × 10-3 m/s, which was slow enough to ensure a quasi-static response. The force on the plate was the external load on the propellant grain, and the loading phase continued until the specified test-termination criterion was reached.

Fig.4 Unconfined uniaxial compression test model
1.3 Calibration of the model parameters
The model parameters cannot be related directly to a set of relevant material properties in the PFC3D. The correspondence between the synthetic material and a particular physical material must be established by simulated material testing, which means that the relationship between the model micro-parameters and the material macro-properties must be determined first by means of a calibration process. In a calibration process, the responses of the PFC synthetic material were compared directly with the relevant measured responses of the intended physical material, and then the appropriate model parameters were chosen to reproduce the relevant material properties as measured in laboratory tests.
The material properties of propellant grain are shown in Tab.2. Through the calibration process, the complete set of micro-parameters of unconfined uniaxial compression test is listed in Tab.3. In addition, the simulated results are as follows: Young’s modulus E=586.90 MPa, Poisson’s ratio ν=0.182, the peak strength σf=15.21 MPa. By comparing the stress-strain curves of the numerical test and the physical test shown in Fig.5, it can be seen that the simulated results basically correspond with the laboratory results.
Tab.2 Material properties of the propellant grain

ParameterValueEnvironment temperature/℃-40Youngs modulus E/MPa585.09Poissons ratio ν0.181Peak strength σf/MPa15.10
Tab.3 Micro-parameters of DEM model

ParameterValueContact modulus/MPa424.00Stiffness ratio1.175Parallel-bond radius multiplier1.0Parallel-bond modulus/MPa424.00Parallel-bond stiffness ratio1.175Parallel-bond normal strength/MPa11.20Parallel-bond shear strength/MPa11.20

Fig.5 Stress-strain curves of the unconfined compression test
To reproduce the macroscale material behavior of the propellant grain, a calibration process to determine the microscopic parameters of the bonded-particle model was carried out by a set of numerical experiments of unconfined uniaxial compression tests. The calibration conclusions are summarized as follows.
1) The modulus and peak strength measured during the numerical test are only slightly affected by packing variations in an arbitrary assembly composed of arbitrarily packed particles joined by parallel bonds.
2) The initial Young’s modulus of the material is linearly related to the value of the contact stiffnesses. Parallel bonds increase the contact stiffness, and its increase rate is approximately 50%, whereas the bond strength has little effect on Young’s modulus.
3) For a certain assembly geometry, the Poisson’s ratio of the material depends on the ratio of the shear contact stiffness to the normal contact stiffness.
4) The peak strength of the material depends both on the friction coefficient and the bond strength. For a fixed friction, as bond strength is increased, the material exhibits greater peak strength, but much smaller axial strain.
2 Press and Fracture Processes
2.1 Fracture mechanism
Micro-cracks in a synthetic material may only form between the bonded particles. The formation mechanism of the micro-crack is determined by the bond failure type, which indicates whether the bond failed as the result of its normal or shear strength being exceeded. During a compression test, the parallel bonds break in a progressive manner, which means that the compression-induced micro-cracks gradually coalesce into macro-cracks or fractures as the axial load increases. After the unconfined compression test was completed, the micro-cracks of the propellant grain were monitored and visualized. As shown in Fig.6, the fracture is represented directly by the formation and tracking of a large number of micro-cracks, in which the red indicates normal bond failure and the blue indicates shear bond failure.


(a) (b)
Fig.6 Bond failure distribution without initial defect. (a) Front view;(b) Top view
The fracture mechanism of the propellant grain under compression is governed by the formation, growth, and eventual interaction of the micro-cracks. From the crack monitoring in Fig.6, it can be seen that micro-cracks first initiate on the top and bottom surfaces of the propellant grain, and the bond failure is mainly normal failure. The macroscopic failure mechanism of the compression-induced micro-cracks forms a single fracture surface at a 45-degree angle throughout the propellant grain, and the bond failure near the fracture surface is mainly shear failure. According to the propagation direction of the fracture surface, the fracture mechanism of the propellant grain under the unconfined uniaxial compression is the global shear failure.
During the compression test, the parallel bonds break in a progressive manner. The appearance of the narrow region of the intense micro-cracking ahead of macro-cracks, which means that the compression-induced micro-cracks gradually coalesce into macro-cracks or fractures with the increase in axial load. The micro-cracks generally form in locations where the minimum principal stress exceeds the local tensile strength of the material, and thus preferentially propagate along the maximum principal stress direction. The fracture mechanism of the propellant grain under compression is governed by the formation, growth and eventual interaction of the micro-cracks.
2.2 Fracture process analysis
According to the stress-strain curves and the corresponding bond failure number in Fig.7, the process can be divided into four ordinal phases: the elastic deformation phase, crack initiation phase, crack stable propagation phase, and crack unstable propagation phase.
1) Elastic deformation phase: During the early loading stages of the compression test, the axial stress increases linearly with the axial strain, and the elastic constants are determined from the linear portion of the stress-strain curves. During this phase, there is no compression-induced crack form, indicating that the material is undamaged during the elastic deformation phase.

Fig.7 Stress-strain curves and bond failure number
2) Crack initiation phase: When the axial stress reaches about 65% of the peak strength, micro-cracks begin to initiate at the top and bottom surfaces of the propellant grains. The initiation of the micro-crack indicates that the mechanical properties of the propellant grain begin to transform from the linear elasticity to nonlinear elastoplasticity. During this phase, the increase in the number of compression-induced cracks is very slow.
3) Crack stable propagation phase: When the axial stress reaches about 80% of the peak strength, the growth rate of the compression-induced crack is relatively faster, and the bond failure is mainly shear failure during this stage. As the damage develops gradually, the micro-cracks begin to steadily expand from the top and bottom surfaces to the interior of the propellant grain.
4) Crack unstable propagation phase: After the axial stress reaches peak strength, the axial stress exhibits a drop rapidly, whereas the total number of cracks increases suddenly. Until the axial stress drops to 80% of the peak strength, the crack propagates throughout the propellant grain with a shear fracture surface. At this point, the propellant grain loses compressive capacity and begins to show fracture.
From the above analysis, it can be concluded that the press and fracture processes of the propellant grain essentially are the processes of crack initiation and propagation.
3 Effects of the Initial Defects
3.1 Introduction of the initial defects
The material heterogeneity should be taken into account when realistically modelling the material behavior[24]. To pursue a more realistic model, the joint plane assigned to the smooth-joint contact model can be used to model the initial defects of the synthetic material in the PFC3D. The contacts between balls across the joint plane are changed to non-bonded smooth-joint contacts, in which the friction coefficients are smaller than those in the default contact model. Thus, the joint plane can represent the weakness plane of the physical material, and these introduced initial defects resemble the pre-cracks in the microstructure.
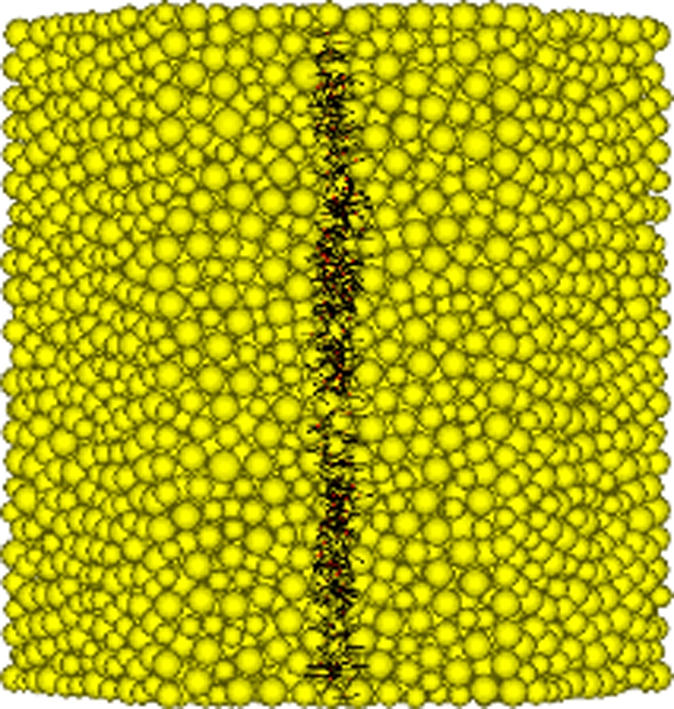
A joint plane can be defined with a prescribed position and orientation, and the number of initial defects can be controlled by specifying the activated ratio of the smooth-joint contact model on the joint plane. In this paper, two types of initial defects, initial surface defects and initial internal defects, are introduced into the DEM model. The pre-crack distribution of the initial surface defects is located in the two joint planes near the top and bottom surfaces, as shown in Fig.8. The initial internal defects are distributed in the joint plane arranged along the axial direction of the propellant grain, as shown in Fig.9. The black part denotes the location of the joint plane, and the initial defects are randomly distributed in the joint plane within a prescribed percentage.


(a) (b)
Fig.8 Diagram of the initial surface defects. (a) Front view;(b) Top view

(a) (b)
Fig.9 Diagram of the initial internal defects. (a) Front view;(b) Top view
3.2 Effects on the fracture mechanism
For the two types of initial defect models,a range of 0% to 25% initial defects were selected for the unconfined uniaxial compression test. According to the press and fracture processes discussed above, the crack initiation and propagation are the key to determining the fracture mechanism of the propellant grain. Thus, the number and location of the potential micro-cracks are limited by the number and location of the initial pre-cracks in the initial specimen.
Fig.10 shows the change trend of the total number of bond failures versus the percentage of initial defects, when the axial stress of the propellant particles drops to 80% of the peak strength under the unconfined compression test. As the total number of initial defects increases, the bond failure number of the propellant grain with initial surface defects decreases gradually. As for the initial internal defects, the bond failure number slightly fluctuates near the bond failure number without initial defects.

Fig.10 Bond failure number vs. initial defect percentage
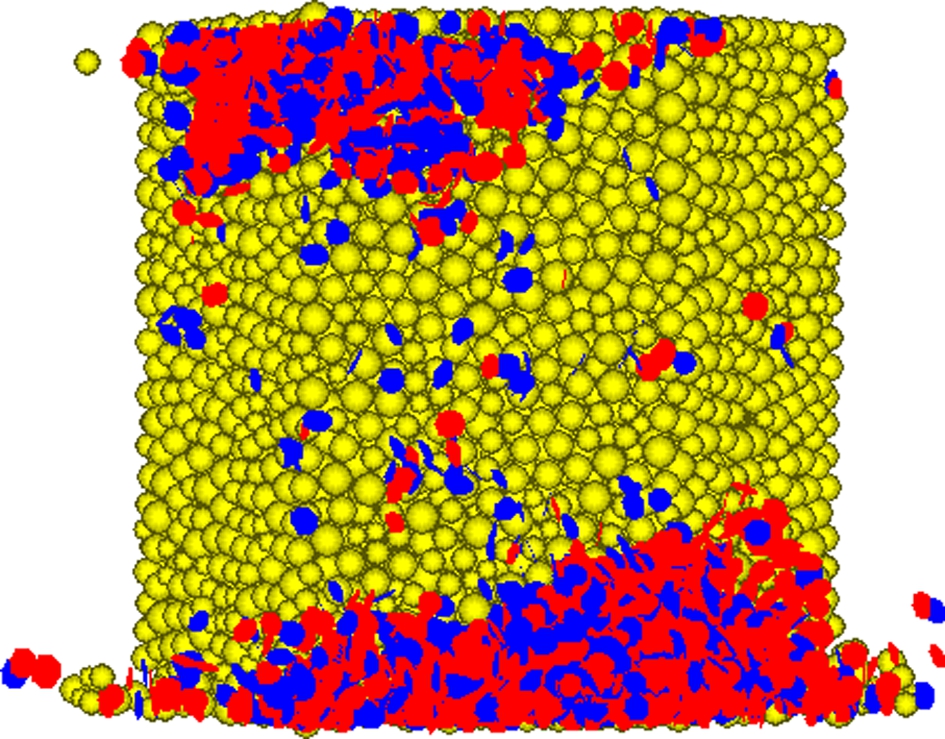
Due to space limitations, Figs.11 and 12 only show the bond failure distribution of the propellant grain with 17.5% initial surface and internal defects, respectively.

(a) (b)
Fig.11 Bond failure distribution with initial surface defect. (a) Front view;(b) Top view


(a) (b)
Fig.12 Bond failure distribution with initial internal defect. (a) Front view;(b) Top view
By analyzing the bond failure distributions of 0% to 25% initial surface defects, it can be concluded that the fracture mechanism of the propellant grain with initial surface defects is local shear failure. Specific details are as follows: 1) As initial surface defects increase, the propellant grain is highly likely to show local failure; 2) The crack propagation of local failure is on a relatively small scale, and as a result, the total number of compression-induced cracks is gradually reduced, as shown in Fig.10; and 3) The bond failure distribution mainly exists near the top and bottom of the propellant grain, finally forming two fracture surfaces at each joint plane.
According to the bond failure distributions of 0% to 25% initial internal defects, the fracture mechanism of the propellant grain with initial internal defects is global tensile failure. Specific details are as follows: 1) As the initial internal defects increases, the fracture surface of the propellant grain is approaching closer to the joint plane; 2) The total number of compression-induced cracks remains basically unchanged, indicating that the fracture mechanism of the propellant grain is global failure; and 3) The bond failure mechanism corresponding to initial internal defects is mainly normal bond failure.
In the DEM model of the propellant grain, most of the compression-induced cracks nucleate at the initial defects, which can reproduce many of the essential features of the brittle fracture phenomenon. Under external force, the initial defects interact with each other, which may promote the earlier onset of distributed damage formation. Then, the localized damage induces global stress redistribution and the crack propagation direction, thereby changing the fracture mechanism of the propellant grain.
Indeed,the growth and propagation of the tension and shear fractures in the brittle material result from the nucleation and coalescence of micro-cracks within the fracture process zone[25]. During the fracture process of propellant grain, most of the compression-induced cracks nucleate at the initial defects, which can reproduce many of the essential features of the brittle fracture phenomenon. Under the external force, the interaction and coalescence of micro-cracks may promote the earlier onset of distributed damage formation, and then the localized damage induces global stress redistribution. Fracture propagation is most likely influenced by the amount and orientation of pre-micro-cracks. The pre-micro-cracks may affect the propagation of fractures and might thus have non-negligible impacts on the mechanism fracture mechanism of propellant grain.
3.3 Effects on peak strength
The peak strength is one of the significant factors representing the mechanical properties of propellant grain. The line chart of peak strength under unconfined compression test is shown in Fig.13.
As shown in Fig.13, no matter whether the initial surface defects or the initial internal defects, the peak strength of the unconfined compression test both exhibit a nearly linear decline trend. The existence of two types of initial defects both weakens the material strength. At 25% initial defects, the peak strength corresponding to the initial surface defects is reduced to 10.82 MPa (which is about 71.1% of the peak strength without initial defects), whereas the peak strength corresponding to the initial internal defects is reduced to 13.34 MPa (which is about 87.7% of the peak strength without initial defects). By comparing the rates of the two decline lines, it can be concluded that the initial surface defects contribute more strongly to weakening the peak strength of the propellant grain than the initial internal defects. Furthermore, the propellant grain with initial surface defects may be weaker due to its local fracture mode, in which the overall compressive capacity of the propellant grain cannot be fully utilized. At a large scale, the fractures control the strength and deformation properties of the propellant grain. At a smaller scale, micro-cracks affect both the mechanical properties of the propellant grain, and thus have direct consequences on the stability of fractures.

Fig.13 Peak strength vs. initial defect percentage
4 Conclusions
1) The DEM model of propellant grain is capable of satisfactorily reproducing the fracture process and typical characteristics of propellant grain including, linear elastic behavior at small deformations, nucleation of stress induced micro-cracks before failure, and the development of macroscopic failure surfaces through the coalescence of these micro-cracks.
2) The fracture mechanism of the propellant grain depends on the propagation direction of the fracture surface, and the fracture mechanism under the unconfined uniaxial compression is the global shear failure.
3) The presence of initial defects may change the fracture mechanism of the propellant grain. The fracture mechanism of the initial surface defects is the local shear failure on the top and bottom of the propellant grain, whereas the fracture mechanism of the initial internal defects is the global tensile failure along the weakness plane.
4) The initial defects weaken the peak strength of the propellant grain, and the initial surface defects have a stronger weakening effect than initial internal defects. Thus, the carrying and filling process of the propellant grain needs to minimize the initial defects as far as possible.
[1] Rui X T, Yun L F, Wang G P, et al. Direction to launch safety of ammunition [M]. Beijing: National Defense Industry Press, 2009. (in Chinese)
[2] Rui X T, Feng B B, Wang Y, et al. Research on evaluation method for launch safety of propellant charge [J]. Acta Armamentarii, 2015, 36(1): 1-11. (in Chinese)
[3] Chen P W, Dai K D, Huang F L, et al. Ultrasonic evaluation of the impact damage of polymer bonded explosives [J]. Journal of Beijing Institute of Technology(English Edition), 2004, 13(3): 242-246.
[4] Zhang Y L, Luo X B, Gou Y Q, et al. Study on the mechanical properties of propellant granule[J]. Equipment Environmental Engineering, 2010, 7(3): 27-30. (in Chinese)
[5] Jiang S P, Rui X T, Hong J, et al. Numerical simulation of impact breakage of gun propellant charge[J]. Granular Matter, 2011, 13(5): 611-622. DOI:10.1007/s10035-011-0276-1.
[6] Druckrey A M, Alshibli K A. 3D finite element modeling of sand particle fracture based on in situ X-Ray synchrotron imaging[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(1): 105-116. DOI:10.1002/nag.2396.
[7] Hong J, Li J X, Shen Y, et al. Particle fracture model based on the discrete element method[J]. Journal of Tianjin University (Science and Technology), 2018, 51(12): 1253-1259. (in Chinese)
[8] Zhang Z C, Zhao C F, Zhang X. Simulation study on influence of load position on static crushing form of ballasts[J]. Railway Engineering, 2014(11): 152-156.(in Chinese)
[9] Cil M B, Alshibli K A. 3D evolution of sand fracture under 1D compression[J]. Géotechnique, 2014, 64(5): 351-364. DOI:10.1680/geot.13.p.119.
[10] Zhou W, Yang L F, Ma G, et al. DEM analysis of the size effects on the behavior of crushable granular materials[J].Granular Matter, 2016, 18(3): 64. DOI:10.1007/s10035-016-0656-7.
[11] Xu K, Zhou W, Ma G, et al. Review of particle breakage simulation based on DEM [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 880-889. (in Chinese)
[12] Robertson D, Bolton M D. Dem simulations of crushable grains and soils [C]//4th International Conference on Micromechanics of Granular Media Powders and Grains. Sendai, Japan, 2001: 623-626.
[13] Alonso EE, Tapias M, Gili J. Scale effects in rockfill behaviour[J]. Géotechnique Letters, 2012, 2(3): 155-160. DOI:10.1680/geolett.12.00025.
[14] Cil M B, Alshibli K A. 3D assessment of fracture of sand particles using discrete element method[J]. Géotechnique Letters, 2012, 2(3): 161-166. DOI:10.1680/geolett.12.00024.
[15] Wang J F, Yan H B. On the role of particle breakage in the shear failure behavior of granular soils by DEM[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(8): 832-854. DOI:10.1002/nag.1124.
[16] Wang Z J, Jing G Q, Yu Q F, et al. Analysis of ballast direct shear tests by discrete element method under different normal stress[J].Measurement, 2015, 63: 17-24. DOI:10.1016/j.measurement.2014.11.012.
[17] Hong J. Study on granular system dynamics of propellant bed with press and fracture [D]. Nanjing: Nanjing University of Science and Technology, 2007. (in Chinese)
[18] Hong J, Rui X T. Dynamic simulation for impact and fracture of propellant grain[J]. Journal of Ballistics, 2010, 22(1): 61-64. (in Chinese)
[19] Jiang S P, Rui X T, Li C. Simulation of impact fragmentation of propellant grains [J]. Chinese Journal of Applied Mechanics, 2013, 30(5): 741-747. (in Chinese)
[20] Jiang S P, Rui X T, Wang Y, et al. Dynamics simulation of gun propellant charge with compress and fracture based on discrete element method[J]. Scientia Sinica (Physica,Mechanica & Astronomica), 2013(8): 965-970.(in Chinese)
[21] Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47.
[22] Suchorzewski J, Tejchman J, Nitka M. Discrete element method simulations of fracture in concrete under uniaxial compression based on its real internal structure[J]. International Journal of Damage Mechanics, 2018, 27(4): 578-607. DOI:10.1177/1056789517690915.
[23] Jiménez-Herrera N, Barrios G K P, Tavares L M. Comparison of breakage models in DEM in simulating impact on particle beds[J]. Advanced Powder Technology, 2018, 29(3): 692-706. DOI:10.1016/j.apt.2017.12.006.
[24] Varela Valdez A, Morel S, Marache A, et al. Influence of fracture roughness and micro-fracturing on the mechanical response of rock joints: A discrete element approach[J]. International Journal of Fracture, 2018, 213(2): 87-105. DOI:10.1007/s10704-018-0308-5.
[25] Moosavi S, Scholtès L, Giot R. Influence of stress induced micro-cracks on the tensile fracture behavior of rocks[J]. Computers and Geotechnics, 2018, 104: 81-95. DOI:10.1016/j.compgeo.2018.08.009.