Travel time is the most intuitionistic index to reflect the running condition, which is an important foundation for constructing intelligent transportation systems (ITS)[1]. With accurate travel time information, on the one hand, travelers can make better travel choices; on the other hand, traffic managers can improve traffic management decisions[2].
There are many methods for predicting the travel time, such as mathematical statistics methods[3-4] and machine learning methods[5]. Since the travel time prediction has typical nonlinear characteristics, the travel time prediction based on machine learning methods is more accurate than the methods based on mathematical statistics. Therefore, the travel time prediction method has gradually transferred to machine learning methods, such as artificial neural networks[6-7], support vector machines (SVM)[8-10], Kalman filters[11], the kernel-clustering algorithm[12] and the K nearest method[13-14]. A variety of models are proposed based on the methods. However, it is difficult for traffic researchers and managers to explain the relationship between indicators and the predicted travel time through these models. In view of this, the gradient boosting decision tree (GBDT) is used to build the travel time prediction model in this paper. GBDT combines the advantages of data mining to dig deep into the impact of variables on the predicted travel time.
The GBDT model provides a flexible framework to adopt different types of predictors as the input variables (for instance, traffic flow, speed, density, occupancy, number of vehicles, traffic state parameter and data-time variables). Meanwhile, the GBDT model understands the diverse influences of different variables on the predicted travel time, explores the nonlinear relationship between variables and the predicted travel time, and has good interpretability.
1 Travel Time Prediction Model Based on GBDT
GBDT is an iterative decision tree algorithm, which is based on the idea of boosting iteration. The foundation of GBDT is the classification and regression tree (CART) algorithm. Except for the first decision tree generated using the original indicator, the target in each iteration minimizes the loss function value of the current learner, that is, the loss function always falls along its gradient direction. By successive iterations, the final residual approaches zero. The results of all trees are added up as the final prediction result[15-17].
Suppose that ![]() is the K-dimensional variable that affects travel time. yi is the response variable of the travel time, namely the target variable. For N training samples {(X1,y1),(X2,y2),…,(XN,yN)}, the GBDT modeling process is described as follows.
is the K-dimensional variable that affects travel time. yi is the response variable of the travel time, namely the target variable. For N training samples {(X1,y1),(X2,y2),…,(XN,yN)}, the GBDT modeling process is described as follows.
1) Initialize the learner, that is
(1)
where f0(X) is the initial decision tree with only one root node; L(yi,c) is the loss function; yi is the i-th training data; c is a constant value that minimizes the loss function.
Travel time prediction is a regression problem. In GBDT, there are many loss functions for the regression problem, such as the squared loss function, absolute value loss function, and Huber loss function.The squared loss function used in the GBDT model is
(2)
where f(x) is the learner obtained from the current iteration.
2) Let the number of iterations be m=1,2,…,M, and the negative gradient of the i-th training data is
(3)
According to all samples and their negative gradient direction (xi,gmi)(i=1,2,…,N), a decision tree Tm consisting of J leaf nodes is obtained. The j-th leaf node region is Rmj(j=1,2,…,J). The best residual fitting value of each leaf is
(4)
The learner obtained in this iteration is
(5)
where I(xi∈Rmj) is the explanatory function of the i-th training data in the j-th leaf node region, and
3) After the m-th iteration, the final model is expressed as
(6)
Via the times that a variable appears in the decision tree and the performance of the model after each segmentation, the variable importance of the model can be obtained[17].
(7)
(8)
where Tm is the m-th decision tree in GBDT F with J leaf nodes; 1j(Xk) is the indicator function that the variable Xk is chosen as split variable at node j in decision tree Tm; ![]() is the squared error improvement of the corresponding node after selecting variable Xk to split;
is the squared error improvement of the corresponding node after selecting variable Xk to split; ![]() is the importance value of variable Xk in GBDT F;
is the importance value of variable Xk in GBDT F; ![]() is the importance value of variable Xk in the decision tree Tm.
is the importance value of variable Xk in the decision tree Tm.
2 Data
In this paper, the VISSIM simulation software developed by PTV is used to analyze the travel time in the freeway. The length of 1 048.28 m between the airport interchange and Lukou interchange is selected as the research area.Time detectors are set at both ends of the selected freeway section. The route diagram is presented in Fig.1.

Fig.1 The study area
VISSIM simulation software is calibrated according to actual hourly traffic flow on the Nanjing Airport freeway from Nanjing to the Airport investigated at a airport toll station from 9:00 to 15:00 on August 22, 2017. Since the actual traffic flow does not include congestion, in order to cover the states of free-flow, transition and congestion in the freeway, the traffic flow is increased by 600 veh/h from the actual measured value of the previous period during 15:00—17:00, which reflects the congestion state. Only increasing the number of vehicles cannot lead to congestion. However, based on the state of transition, the authors guarantee that all variables are constant, and continue to increase the traffic flow to characterize the state of congestion.
Through investigation, the vehicle proportion of car, truck, bus and taxi on the freeway is 0.42∶0.12∶0.26∶0.2.
In the freeway, the expected speed distributions of car, truck, and bus is 120, 100, and 100 km/h. The speed distributions of cars, trucks, buses, and taxis are shown in Fig.2.
Using different random seed numbers, the experiment is simulated 133 times and the simulation time is 28 800 s. Finally, 133 sets of data are obtained, which represent 133 days’ data of 9:00—17:00. Data of 133 d are divided into two data sets, in which 27 to 133 d of data are used as training data sets and 1 to 26 d of data are used as test data sets.
The travel time is obtained at the sampling interval of 300 s. Ti is used to represent the travel time at time step i (i is the current period), where i=1,2,…,93, represents 93 time periods from 9:15 to 17:00 (The first three periods 9:00 to 9:15 are taken as the pretreatment time of VISSIM). Considering the short-term prediction of travel time,the prediction period is set to be 10 min ahead.

(a)

(b)

(c)

(d)
Fig.2 Speed distribution. (a) Cars; (b) Trucks; (c) Buses; (d) Taxis
3 Establishment and Verification of the Model
3.1 Variables of the model
3.1.1 Traffic state parameter
In the Highway Capacity Manual[18], the freeway traffic state is divided into six grades (namely A to F) by means of average speed and density. As we all know, speed, density, and traffic flow are three basic parameters, which are interrelated. If the values of two parameters are known, the third one can be calculated. The standard of traffic state classification of a freeway is shown in Tab.1.
Tab.1 The standard of traffic state classification of a freeway[18]

Traffic stateDensity range/(vehicle·(km·lane)-1)Design speed/(km·h-1)120100Speed/(km·h-1)Traffic flow/(vehicle·(h·lane)-1)Speed/(km·h-1)Traffic flow/(vehicle·(h·lane)-1)A17.7120.7820104.6710B29.0120.31 350104.61 170C41.8113.61 830103.91 680D56.3100.12 17096.12 090E72.485.82 40083.92 350F>72.4<85.8>2 400<83.9>2 350
In this study, traffic state parameters refer to the standard of traffic state classification of the freeway, let x=1,2,…,6 represent traffic states A to F, respectively. This paper combines existing traffic state levels and describes the freeway at a low level. Therefore, the traffic state of the freeway is divided into three categories.The free-flow state includes traffic states A and B, namely, xf=1,2. The transition state includes traffic states C and D, namely xt=3,4. The congestion state includes traffic states E and F, namely xc=5,6. The traffic state parameter is X={xf,xt,xc}.
The travel time is affected by traffic states. In order to clarify the impact of traffic states on travel time prediction, the traffic state parameter in current period Xi is introduced into the GBDT model.
3.1.2 Variables of the model
Traffic flow, speed, and density are three basic parameters that characterize traffic flow characteristics and affect the travel time of the vehicle. In addition, occupancy and the number of vehicles also have a certain impact on travel time. Therefore, traffic flow in current period Qi, speed in current period Vi, density in current period Ki, occupancy in current period Ri and the number of vehicles in current period Ni are introduced as input variables.
Other factors that have been discussed in previous studies[19] are also considered, that is, Ti is the travel time in current period; Ti-1 is the travel time at time step i-1; Ti-2 is the travel time at time step i-2; ΔTi is the change of travel time over two adjacent time steps, ΔTi=Ti-Ti-1; ΔTi-1 is the changes of travel time over two adjacent time steps, ΔTi-1=Ti-1-Ti-2.
The target variable of the model, namely the predicted travel time, is the travel time at time step i+1, which is denoted as Ti+1.
3.2 Results and verification of the model
In GBDT, there are five parameters that need to be determined, namely, the number of leaf nodes in a single regression tree J, learn rate η, the amount of attribute sampling Sa, subsample fraction f, and the number of regression trees M. The paper uses data mining software Salford systems developed by the Salford Company of the United States to establish the GBDT model. After repeated experiments, all the parameters of the GBDT model are obtained, that is {J,η,Sa,f}={9,0.01,9,0.6}. The optimal number of regression trees based on the minimum value of the objective function is automatically determined. The number of regression trees is 923.
The training data sets are used to train the model, and the test data sets are used for testing. The results show that the error of the model in the training data sets is 3.59%, and that in the test data sets is 3.94%.
To test the effectiveness of the GBDT model, the back propagation (BP) neural network model with three-layer feedforward perceptron algorithm and the SVM model with radial basis function (RBF) as the kernel function are also established by using the same training data sets. Then, the same test data sets are used for testing.Tab.2 is the error of different models.
Tab.2 MAPE of different models %

Data setGBDTBP neural networkSVMTraining data3.594.496.47Test data3.944.706.54
3.3 Analysis of variables
The importance values of variables are determined in the GBDT model by the times of variables appearing in the decision tree. The relative importance value of the GBDT model is indicated in Fig.3. It can be seen from Fig.3 that the most important influence variable is the travel time in current period Ti. The travel time of the current period has the greatest influence on the travel time of the next period. As expected, the immediate previous traffic state will influence traffic in the near future. The influences of Ri, ΔTi, Ni, and ΔTi-1 on the model are relatively small, indicating that the occupancy and the number of vehicles cannot directly affect the predicted travel time. The influence of the time difference on the model is less than that of the travel time of the two

Fig.3 The relative importance value
periods close to the predicted travel time.
In the GBDT model, the partial dependency value (PDV) of the prediction model and each variable on the prediction results are shown in Fig.4. From Fig.4, each variable has a highly nonlinear relationship with the predicted travel time. Taking Ti as an example, when Ti<60 s, the PDV for the predicted travel time is the smallest fixed value, and the change of Ti has little effect on the predicted travel time. When 60 s<Ti<65 s, the PDV for the predicted travel time increases sharply. However, when 65 s<Ti<180 s, the PDV for the predicted travel time increases slowly. When Ti>180 s, the PDV for the predicted travel time becomes a fixed value again. The analysis results of the GBDT model show that the influences of the variable Ti and the predicted travel time have a typical nonlinear relationship. Only when 60 s<Ti<180 s, the change of Ti has a greater impact on the predicted travel time.
3.4 Accuracy of the model
Fig.5 is a comparison between the travel time of the 5th day in the test data sets and the travel time obtained with different models. As indicated in Fig.5, the GBDT model can accurately predict the change of travel time.
4 Conclusions
1) The comparison of model prediction results shows that the error of the GBDT model is smaller than those of the BP neural network model and the SVM model.
2) In the GBDT model, travel time in current period Ti has the highest importance value. The travel time of the current period has the greatest influence on the travel time of the next period. As expected, the immediate previous traffic state will influence the traffic in the near future. The traffic state parameter in current period Xi has a greater influence on the predicted travel time, which is similar to the driving characteristics on the road. The number of vehicles in current period Ni and the time difference ΔTi-1 have a small influence on the predicted travel time, indicating that the number of vehicles and the time difference cannot directly affect the travel time.

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

(j)

(k)
Fig.4 The partial dependency value of each variable on the prediction result. (a) Ti; (b) Xi; (c) Ti-2; (d) Vi; (e) Ti-1; (f) Ki; (g) Qi; (h) Ri; (i) ΔTi; (j) Ni; (k) ΔTi-1
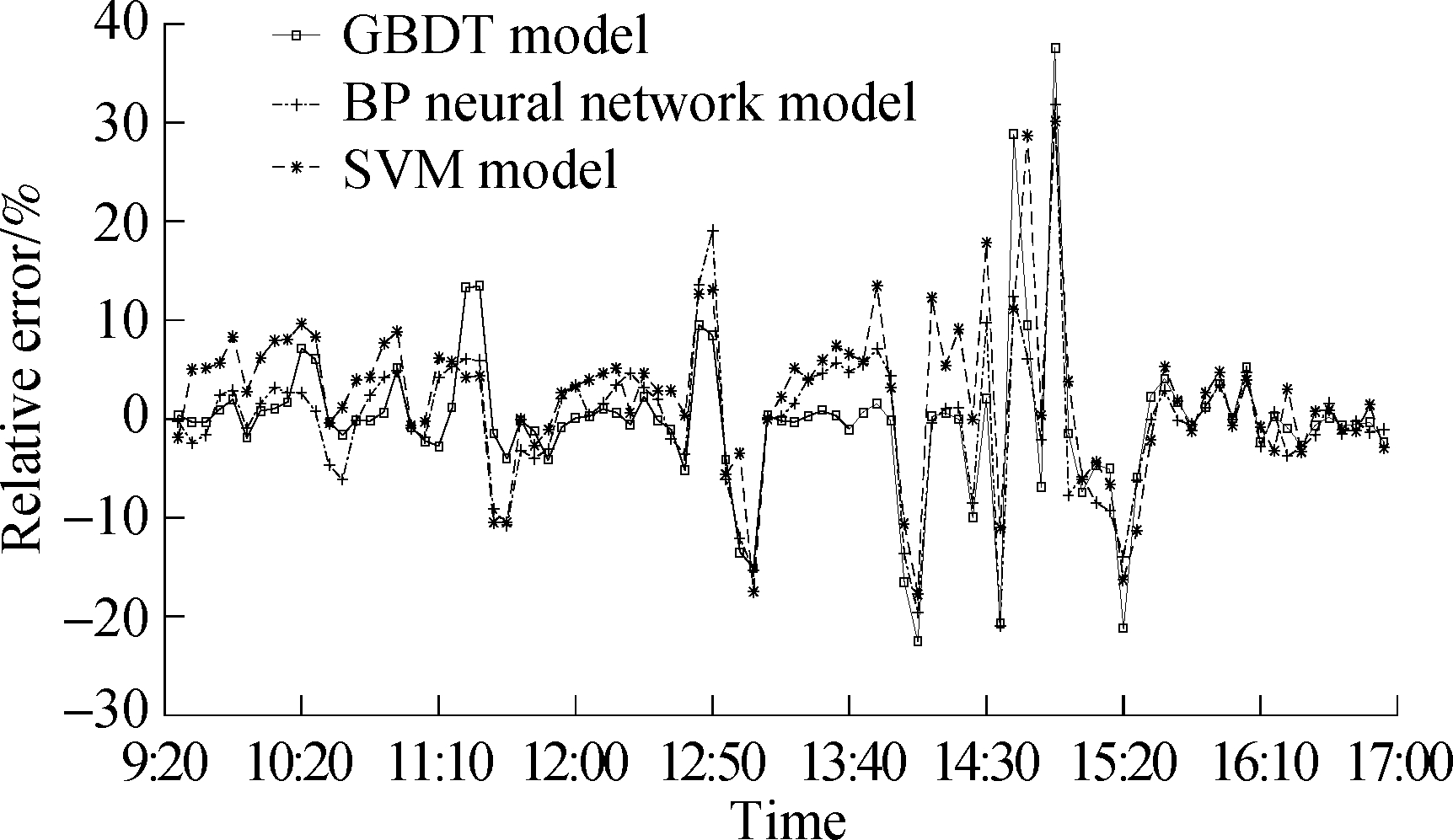
Fig.5 Error comparison of three models
3) The partial dependency value of the variable on the prediction results indicates that the GBDT model can accurately capture the nonlinear relationship between the variables and the predicted travel time.
4) The GBDT model will be applied to other research sections for verification in the subsequent study. However, data obtained by VISSIM limits diversity. In future research, the variables of weather, characters of drivers, and other variables (holidays, working days, non-working days, morning peak, evening peak and so on) affecting travel time will be considered in the GBDT model.
[1] Lee W H, Tseng S S, Tsai S H. A knowledge based real-time travel time prediction system for urban network[J]. Expert Systems with Applications, 2009, 36(3): 4239-4247. DOI:10.1016/j.eswa.2008.03.018.
[2] Miranda D M, Conceição S V. The vehicle routing problem with hard time windows and stochastic travel and service time[J]. Expert Systems with Applications, 2016, 64: 104-116. DOI:10.1016/j.eswa.2016.07.022.
[3] Oh S, Byon Y J, Jang K, et al. Short-term travel-time prediction on highway: A review on model-based approach[J]. KSCE Journal of Civil Engineering, 2018, 22(1): 298-310. DOI:10.1007/s12205-017-0535-8.
[4] Farokhi Sadabadi K, Hamedi M, Haghani A. Evaluating moving average techniques in short-term travel time prediction using an AVI data set[C]//Transportation Research Board 89th Annual Meeting. Washington, DC, USA, 2010.
[5] Julio N, Giesen R, Lizana P. Real-time prediction of bus travel speeds using traffic shockwaves and machine learning algorithms[J]. Research in Transportation Economics, 2016, 59: 250-257. DOI:10.1016/j.retrec.2016.07.019.
[6] Liu W M, Li S S. Freeway travel time prediction simulation research based on big data[J]. Computer Simulation, 2017, 34(3): 395-399. (in Chinese)
[7] Cai H R, He L L. A combined offline travel time prediction model based on speed matrix and artificial neural network[J]. Journal of Zhejiang Sci-Tech University (Natural Sciences Edition), 2017(6): 851-858. (in Chinese)
[8] Yu B, Yang Z Z, Yao B Z. Bus arrival time prediction using support vector machines[J]. Journal of Intelligent Transportation Systems, 2006, 10(4): 151-158. DOI:10.1080/15472450600981009.
[9] Reddy K K, Anil Kumar B, Vanajakshi L. Bus travel time prediction under high variability conditions[J]. Current Science, 2016, 111(4): 700. DOI:10.18520/cs/v111/i4/700-711.
[10] Sun X Y, Zhang H, Tian F L, et al. The use of a machine learning method to predict the real-time link travel time of open-pit trucks[J]. Mathematical Problems in Engineering, 2018, 2018: 1-14. DOI:10.1155/2018/4368045.
[11] Kumar B A, Vanajakshi L, Subramanian S C. Bus travel time prediction using a time-space discretization approach[J]. Transportation Research Part C: Emerging Technologies, 2017, 79: 308-332. DOI:10.1016/j.trc.2017.04.002.
[12] Zhao J D, Guo Y J, Duan X H. Dynamic path planning of emergency vehicles based on travel time prediction[J]. Journal of Advanced Transportation, 2017, 2017: 1-14. DOI:10.1155/2017/9184891.
[13] Gal A, Mandelbaum A, Schnitzler F, et al. Traveling time prediction in scheduled transportation with journey segments[J]. Information Systems, 2017, 64: 266-280. DOI:10.1016/j.is.2015.12.001.
[14] Zhao J D, Gao Y, Tang J J, et al. Highway travel time prediction using sparse tensor completion tactics and K-nearest neighbor pattern matching method[J]. Journal of Advanced Transportation, 2018, 2018: 1-16. DOI:10.1155/2018/5721058.
[15] Ahmed M M, Abdel-Aty M. Application of stochastic gradient boosting technique to enhance reliability of real-time risk assessment[J]. Transportation Research Record: Journal of the Transportation Research Board, 2013, 2386: 26-34. DOI:10.3141/2386-04.
[16] Friedman J H. Stochastic gradient boosting[J]. Computational Statistics & Data Analysis, 2002, 38(4): 367-378. DOI:10.1016/s0167-9473(01)00065-2.
[17] Friedman J H, Meulman J J. Multiple additive regression trees with application in epidemiology[J]. Statistics in Medicine, 2003, 22(9): 1365-1381. DOI:10.1002/sim.1501.
[18] National Research Council. HCM2010: Highway capacity manual [M]. 5th ed. Washington, DC, USA: Transportation Research Board, 2010.
[19] Zhang Y R, Haghani A. A gradient boosting method to improve travel time prediction[J]. Transportation Research Part C: Emerging Technologies, 2015, 58: 308-324. DOI:10.1016/j.trc.2015.02.019.