The vibratory roller is a type of soil compactor which is mainly used in the field of the construction project on roads, railways, airports, and so on. Its operating principle is a combination of the static force of the vehicle and the dynamic force of the drum to compact soil, asphalt and other materials[1-3]. Thus, designers always want the vertical excitation force of the drum on the terrain ground to achieve the maximum value whereas these excitation vibrations are transmitted to the cab via isolation mounts to achieve the minimum value.
The basic research on interaction models of the tyre-soft soil and the drum-elastoplastic soil indicated that the vibration responses were greatly influenced by off-road terrains[4-7]. The excitations from off-road terrains and the vibratory drum were almost transmitted to the driver via the cab’s isolation system and the seat suspension. Thus, the cab’s isolation system was one of the most important factors to improve the vehicle’s ride comfort.
The cab’s isolation system of the soil compactor was mainly equipped with the rubber mounts[2,8]. The effect of design parameters of cab’s rubber mounts on the ride dynamics was analyzed via experiment and simulation[2]. The cab’s rubber mounts were then supplemented by auxiliary hydraulic mounts to optimize the ride comfort[3]. Three cab’s isolation mounts of the vibratory roller including rubber mounts, hydraulic mounts and pneumatic mounts were also given to analyze the performance of cab’s isolation systems based on the simulation and experiment[8]. The results show that the ride comfort was greatly improved by hydraulic mounts. However, the results also show that vibrations of the driver’s seat heave and the cab shaking were still significant under various operating conditions. Therefore, in order to enhance the vehicle’s ride comfort and control the cab shaking, it is necessary to control hydraulic mounts.
The combined control methods were developed for semi-active suspension systems using the magneto-rheological fluid to improve the driver’s ride comfort as well as the safety of passengers, such as the PID-neural control, fuzzy-PID control[9-11]. In order to enhance the control performance, the optimal control methods were then applied, such as neuro-fuzzy control with the fuzzy rules optimized by the genetic algorithm[11], fuzzy-PID control with the control rules optimized by a cultural algorithm[12], and fuzzy-skyhook control using the multi-objective microgenetic algorithm[13]. The results show that optimal controls were better than traditional controls. However, all above research mainly investigated the performance of control methods; thus, the simple quarter car models were mostly used by researchers.
In this study, based on the interaction models of the vibratory roller and deformable terrains[3,8], a nonlinear dynamic model of a single drum vibratory roller is established via Matlab/Simulink software. The vibration excitations consist of the drum/tyre-deformable terrain interaction when the vehicle travels and an excitation frequency, 28 Hz, of drum when the vehicle compacts on elastoplastic soils. A semi-active cab’s hydraulic mounts (SHM) used the magneto-rheological fluid is studied via the optimal fuzzy-PID control. Especially, a new optimal method of the fuzzy control rules based on the genetic algorithm is successfully developed for the optimal fuzzy-PID control. The performance of the SHM is then evaluated via the weighted RMS acceleration responses of the driver’s seat heave and the cab’s pitch angle under different operation conditions. The aim of this study is to improve the ride comfort and control the cab shaking of the vibratory roller.
1 Off-Road Vibratory Roller Models
1.1 Vibratory roller dynamic model
A single drum vibratory roller considering the interaction of wheels and off-road terrains is selected. A 7 DOF nonlinear dynamic model of the vehicle is established to analyze the performance of SHM with optimal fuzzy-PID control, as plotted in Fig.1, where Zi and mi are the vertical displacements and masses at centre of gravity of the driver’s seat, the cab, the rear/front vehicle frame, and the drum; φ2 and φ3 are the angular displacements at centre of gravity of the cab and the rear vehicle frame; Fc1 and Fc2 are the dynamic reaction forces of cab’s hydraulic mounts; qd and qt are the excitations of the terrains; lj is the distances of the vehicle (i=1,2,…,5; j=1,2,…,8).

Fig.1 Lumped parameter model of the vibratory roller
Based on the dynamic model in Fig.1 and application of Newton’s second law, the general dynamic differential equation for the vehicle is given by the following matrix form:
(1)
where M, C, and K are the mass, damping, and stiffness matrices, respectively; Z is the displacement vector; F(t) is the exciting force vector.
1.2 Semi-active cab’s hydraulic mount model
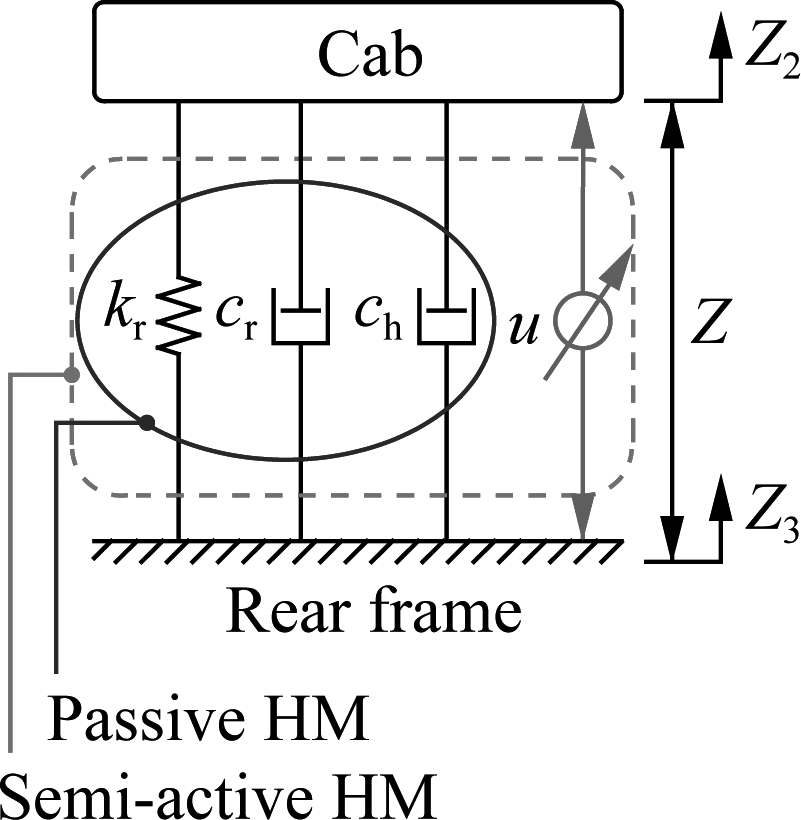
A passive cab’s hydraulic mount (PHM) includes a main rubber, a damping plate driven by the bolt, and a closed chamber filled with the fluid. The fluid flowing in the upper-lower chamber is derived by the transfer of a damping plate via the annular orifice and the orifice[9]. The basic structure of an SHM is also similar to that of a PHM. However, the fluid in the closed chamber is used by a magneto-rheological (MR) fluid with adjustable damping. In addition, the damping plate is equipped with an electro-magnet coil and a flux guide. When the coil current changes, a magnetic field in the flux guide also changes; thus, the viscosity of MR fluid in the annular orifice simultaneously changes. Consequently, the vibration damping can be adjusted according to the road surfaces. MR fluid flows in the upper-lower chamber are also derived by the transfer of the damping plate through the annular orifice and orifices (see Fig.2(a)).

(a)
(b)
Fig.2 Semi-active cab’s isolation system. (a) Simple SHM; (b) Lumped parameter model
The lumped parameter model is described in Fig.2(b). Herein, kr and cr are the stiffness and damping coefficient of the rubber mount. The liquid damping force of the SHM is carried out by ![]() in which ch is the damping constant and u is an active damping force which is optimized by the optimal fuzzy-PID control.
in which ch is the damping constant and u is an active damping force which is optimized by the optimal fuzzy-PID control.
The corresponding dynamic force of mount i of the cab’s isolation mounts is given by
(2)
where ![]() and Z2i, Z3i are the relative velocities and the displacements of the cab floor and the rear vehicle frame at mount i (i=1,2).
and Z2i, Z3i are the relative velocities and the displacements of the cab floor and the rear vehicle frame at mount i (i=1,2).
1.3 Wheels-deformable soil interaction model
Under actual operation conditions, the drum and tyres often interact with deformable terrains. Thus, a drum/ elastic tyre-deformable terrain contact of the vehicle traveling and a drum-elasoplastic soil interaction of the vehicle working are assumed to establish the model.
1.3.1 Wheels-deformable soil contact model
The drum-soft terrain contact model was investigated based on the model of Bakker and Wong[4-5]. When the vehicle is traveling, under the effect of the static and dynamic loads of the drum, the terrain Zoa is sunk, as shown in Fig.3(a).

(a)

(b)
Fig.3 Drum/tyres-soft soil contact model. (a) Rigid drum; (b) Elastic tyre
The pressure pg and the shear stress τg are generated from the soil compression in the deformable area region (arc of oa) thus impact contrarily on the drum. Consequently, the reaction force Fg of the soil under the drum is given as[3]
Fg=![]() Bdpgrdcosθdθ+
Bdpgrdcosθdθ+![]() Bdτgrdsinθdθ
Bdτgrdsinθdθ
(4)
pg and τg are given by Bakker[4] as follows:
(5)
where kc and kφ are the soil stiffness coefficients for sinkage and internal friction; n is the sinkage exponent; b is the dimension of the contact patches; B and r are the width and the radius of the drum; c is the soil cohesion coefficient; φ is the angle of the internal friction; K is the shear deformation modulus, and j=rs[θa(t)-θ], in which s is the slip ratio of the drum.
Assuming that lar is the average roughness line of the terrain surface, thus, the sinking of the soil Zx in Eq.(5) can be determined by
Zx=q(t)+Zoa-Zox=q(t)+Z5-Z0-Zox
(6)
where Z0 is the static sinkage; Zox is the sinking of the soil in the arc region of ox; q(t) is the random excitation of the terrain surface and it is described as follows:
According to the ISO proposal[7,14], the spectral density of the off-road terrain surface is written as
![]() (7)
(7)
where the value of S(Ω0) provides a measure for the random terrain with the reference frequency Ω0=1/2π cycle/m.
More specifically, assuming that the vehicle moves at a constant speed v0, and the random terrain surfaces can be simulated by the series
(8)
where N is the number of intervals; φi is a random phase uniformly distributed between 0 and 2π, and  ω=
ω= nv0 is the fundamental temporal frequency. Mitschke[6] gave the spectral density ranges for the unpaved off-road classifications including classification ranges from good to very poor. The roughness terrain surface can be yielded by choosing a value in the spectral density ranges.
nv0 is the fundamental temporal frequency. Mitschke[6] gave the spectral density ranges for the unpaved off-road classifications including classification ranges from good to very poor. The roughness terrain surface can be yielded by choosing a value in the spectral density ranges.
The motion equations of the drum-soft terrain contact can bewritten as
(9)
When the elastic tire traverses on a soft terrain, under the effect of the static and dynamic loads of the tyre, the terrain also sinks. Two deformable characteristics are presented in the tyre-terrain contact region. One of the deformations is the tyre and the terrain (the region of bob′) and the other one is the unique terrain (the region of b′a)[7], as shown in Fig.3(b).
pg and τg are generated from the deformable regions of bob′ and b′a are described by the total reaction forces of terrain under the tyre as follows:
Fg=![]() Btpgrtcosθdθ+
Btpgrtcosθdθ+![]() Btτgrtsinθdθ
Btτgrtsinθdθ
(10)
where pg and τg are determined in Eq.(5).
The vertical excitation forces Ft into the rear vehicle frame are described as
1.3.2 Drum-elastoplastic soil interaction model
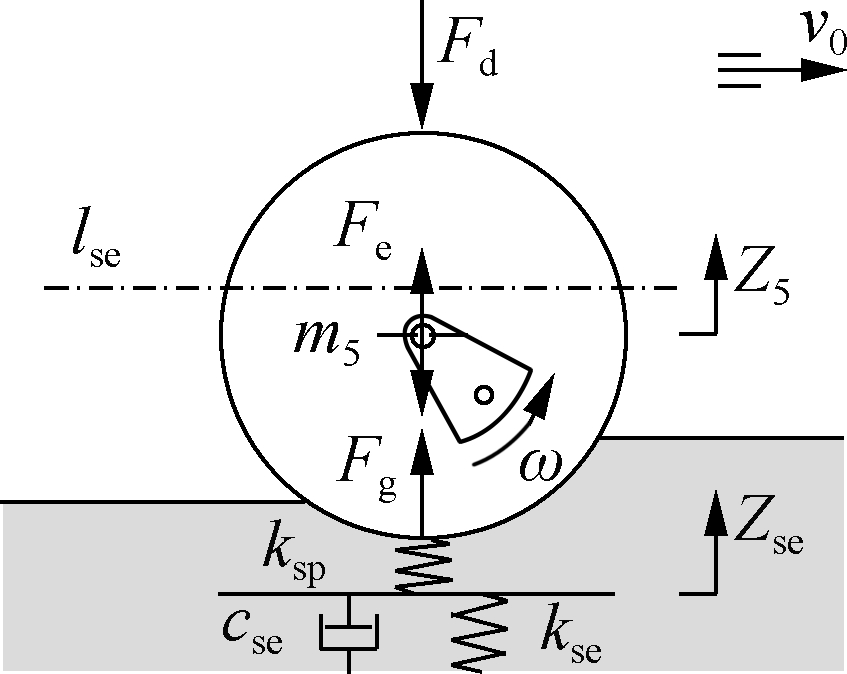
In this study,based on the elastoplastic properties of soil[3,8], a parameter model of the drum-elastoplastic soil interaction is built in Fig.4, where Zse is the vertical motion of the elastic terrain deformation; e and g are the eccentricity of the rotating mass and the gravitational acceleration; m is the total mass of the front frame and drum; me is the rotating eccentric mass; ksp and kse are the plastic and elastic stiffness constants; cse is the elastic damping constant; lse is the abbreviation of the static equilibrium; Fe is the vertical projection of the rotating eccentric mass; Fg is the dynamic force yielded by the plastic deformation of the soil surface layer.
(a)

(b)
Fig.4 Drum-elastoplastic soil interaction model. (a) Loading phase; (b) Drum-hop phase
In an exciting vibration cycle of the drum, the motion of the drum on a soil patch may result in two or more often three distinct phases including the loading phase, unloading phase, and drum-hope phase. In order to determine the relation of Z5 and the excitation forces Fd, the vibration equations of the drum-elastoplastic soil interaction are given via three distinct phases as[2,9]
+εγmeeω3cosωt+meeω2sinωt
(12)
(13)
(14)
Substituting Eqs.(12), (13) and (14) into Eq.(9), both the values of Z5 and Fd are then determined.
2 Optimal Fuzzy-PID Control
2.1 SHM model with fuzzy-PID control
The performance of fuzzy-PID control depends on the suitable selection of the fuzzy inference system (FIS). In order to further enhance the control performance, an optimal fuzzy-PID control in which the FIS optimized by the genetic algorithm (GA) is studied and applied to the SHM, and the model is described in Fig.5.
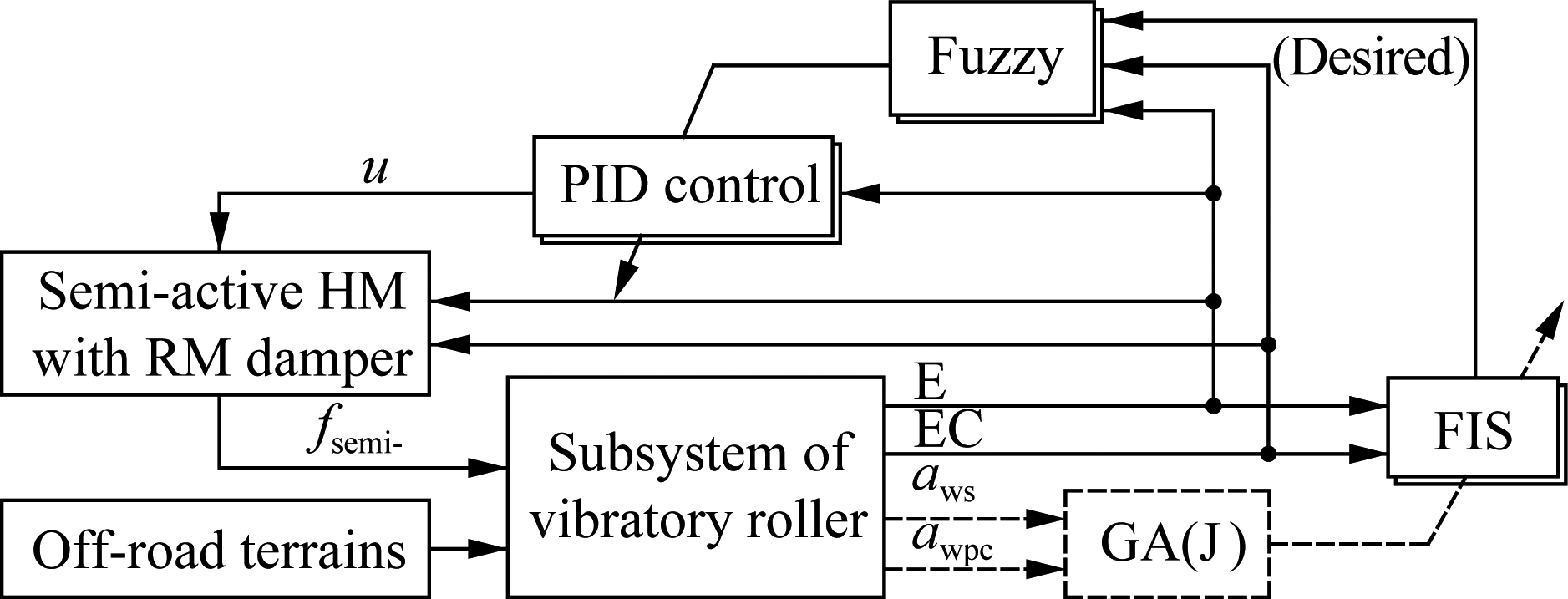
Fig.5 Optimal fuzzy-PID control model
As shown in Fig.5, the fuzzy control includes two inputs and three outputs in which 2-inputs denoted by E and EC are the vertical displacement error (E) and the vertical velocity error (EC) of the cab frame, and 3-outputs denoted as ![]() are the proportionality factors, respectively. The proportional, integral, and derivative parameters in PID control are defined as Kp, Ki, and Kd which can be automatically tuned. u is the actual control force of MR fluid, and fsemi- is the semi-active control force of HM. The force output of the PID control is given as
are the proportionality factors, respectively. The proportional, integral, and derivative parameters in PID control are defined as Kp, Ki, and Kd which can be automatically tuned. u is the actual control force of MR fluid, and fsemi- is the semi-active control force of HM. The force output of the PID control is given as
(15)
In order to find the optimal values for Kl (l=p,i,d), assuming their variable ranges are ![]() Kl is then decided by the fuzzy control as
Kl is then decided by the fuzzy control as
(16)
Hence,we can rewrite Eq.(16) as
(17)
The basic fuzzy control consists of fuzzification interface, FIS, and defuzzification interface. First, the crisp values in fuzzification are transformed into linguistic variables, FIS is then used by control rules in accordance with inference rules, and finally, the linguistic variables are transformed back to crisp values via defuzzification into the physical plant. The fuzzy control can be designed in the following three steps.
1) Choosing fuzzy control in-outputs. The linguistic variables of two inputs are defined by the positive big (PB), positive small (PS), zero (ZO), negative small (NS), and negative big (NB); and of these three outputs are also defined by small (S), medium small (MS), medium (M), medium big (MB), and big (B). Two input variables E and EC belong to [-0.25, 0.25]; and three output variables ![]() are calibrated over the interval [0, 1].
are calibrated over the interval [0, 1].
2) Membership function. The shape of membership functions of in-output variables is used by the triangular function, and the degree of memberships is from 0 to 1[15].
3) The control rules. The initial control rules are established as follows:
If E is A and EC is B then ![]() is Q.
is Q.
where A and B are the linguistic variables of two inputs; G, H, and Q are the linguistic variables of three outputs, respectively.
The fuzzy control rules are selected by the minimum function and the centroid method of Mamdani[15-16], and the above control rules are then optimized by the GA.
2.2 Optimization of control rules
2.2.1 Genetic algorithm program
The goal of GA is to seek the maximum or the minimum values of one or more objective functions using computational techniques, and it is defined as[3,17-18]
Find the vector x={x1,x2,…,xn}T to optimize
F(x)={f1(x),f2(x),…,fn(x)}T
(18)
s.t. gi(x)≤0 i=1,2,…,p
hj(x)=0 j=1,2,…,q
where F(x) is the vector of objective functions, which must be either maximized or minimized; p and q are the numbers of inequality constraints and equality constraints.
2.2.2 Application GA program to optimize FIS
The GA is used to seek the optimal control rules to obtain the minimum values of the weighted RMS acceleration responses of the driver’s seat heave and the cab’s pitch angle via the subsystem model. The optimal process of the GA is described via three steps as follows:
Step 1 Encoding mechanism and initial population. In the FIS, there are 25 control rules that contain a total of 75 elements. The 75 elements are then connected into a string of a chromosome which is regarded as a vector. The linguistic variables of two inputs, E and EC, are encoded by the numbers as {NB, NS, ZO, PS, PB}={0, 1, 2, 3, 4} = [aj]1×5, and of three outputs, ![]() are also encoded by the numbers as {S, MS, M, MB, B}={5, 6, 7, 8, 9}= [bj]1×5. Moreover, the individuals in the initial population are randomly generated. For each gene, the value of the gene is also selected as a random positive integer in the range of 0≤aj≤4 and 5≤bj≤9. The size of the initial population is 100, j=1,2,…,5.
are also encoded by the numbers as {S, MS, M, MB, B}={5, 6, 7, 8, 9}= [bj]1×5. Moreover, the individuals in the initial population are randomly generated. For each gene, the value of the gene is also selected as a random positive integer in the range of 0≤aj≤4 and 5≤bj≤9. The size of the initial population is 100, j=1,2,…,5.
Step 2 Objective function and fitness value. The minimum values of the weighted RMS values of the driver’s seat heave aws and the cab’s pitch angle awpc in Eq.(20) are selected as objective functions. In order to find the minimum values of aws and awpc, the fitness value J is simplified to calculate objective functions as[3,18]
(19)
where φws and φwpc are the weight coefficients of aws and awpc values.
The individuals with the higher fitness value J demonstrate that the obtained control rules are better. Therefore, resultant individuals are updated before the evolution process ends, and the optimal individuals can be obtained.
Step 3 Genetic operations. After establishing the initial population and selecting the parents, genetic operations are then performed. Herein, the crossover probability of 0.95 and mutation probability of 0.05 are used in 200 generations. Therefore, the arithmetic crossover is performed on 95% of the selected parents, whereby two children are created from the weighted sum of two parents, and children of the remaining 5% of selected parents are exact copies of them. Crossover operation is performed until the population number is doubled. Then, each individual undergoes the mutation operation, which is the process of randomly changing the values of genes in a chromosome with a probability of 0.05. The mutation can create new genetic material in an existing individual and add diversity to the genetic characteristics of the population. Finally, through the fitness value J, only the optimal individuals are selected for the population of the next generation. The GA’s flowchart is plotted in Fig.6.
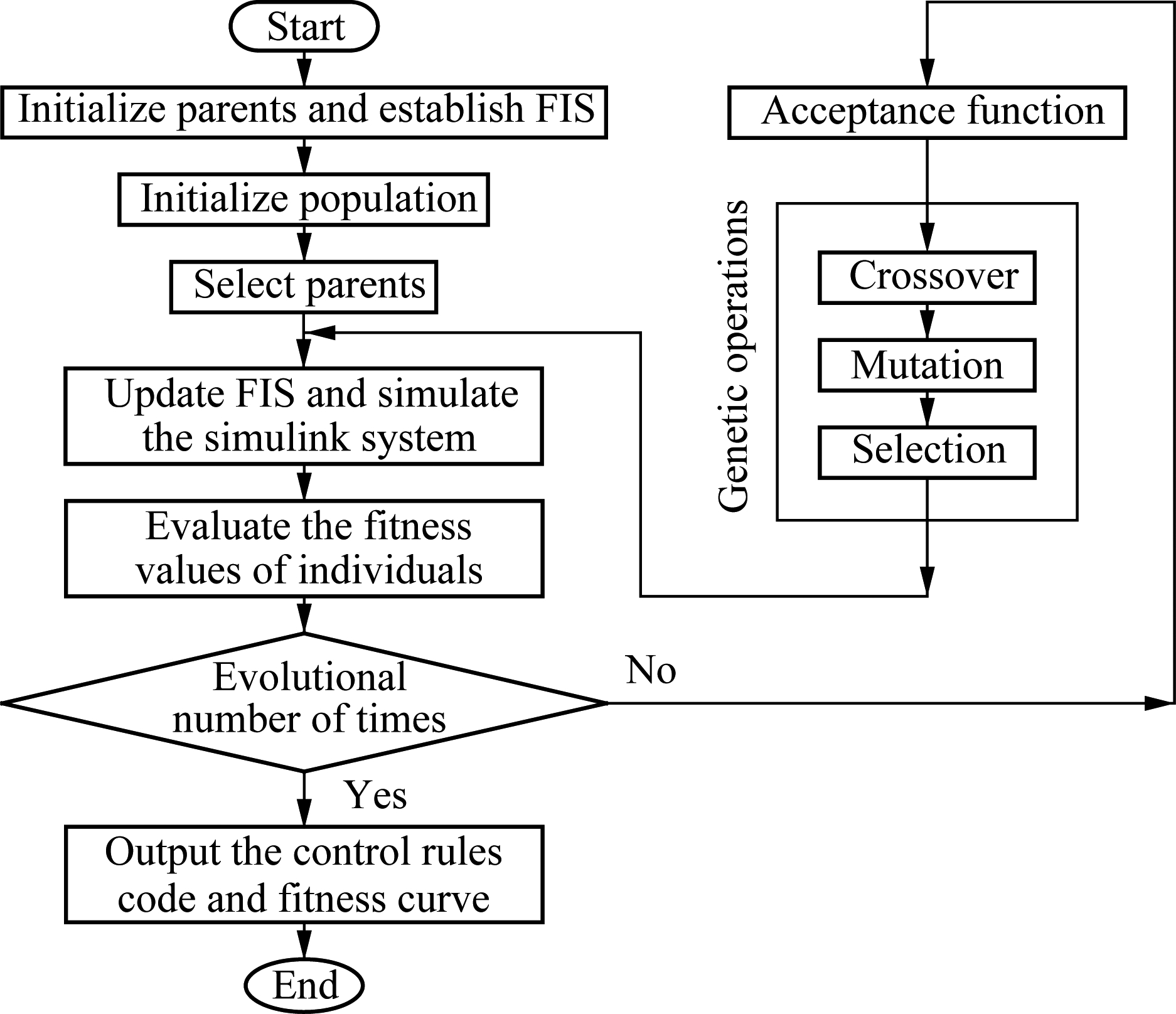
Fig.6 Flow chart of GA program for the FIS
2.2.3 Optimal result of fuzzy control rules
In order to seek optimal control rules, the vehicle is assumed to move on a poor terrain surface of Grenville soil[5] at a constant speed v0=6 km/h. The values of φws=0.522 and φwpc=0.478 are determined by the percent of weighted RMS values aws (52.2%) and awpc(47.8%) with the PHM. The maximum generation is 200.
The result in Fig.7 shows that the maximum fitness value J is obtained from the evolutionary generation of 143 to the end. Therefore, the optimal individuals can be obtained at the generation of 143. By decoding, the optimal control rules are listed in Tab.1. The optimal control rules are then used for the optimal fuzzy-PID controller to simulate and analyze the results.
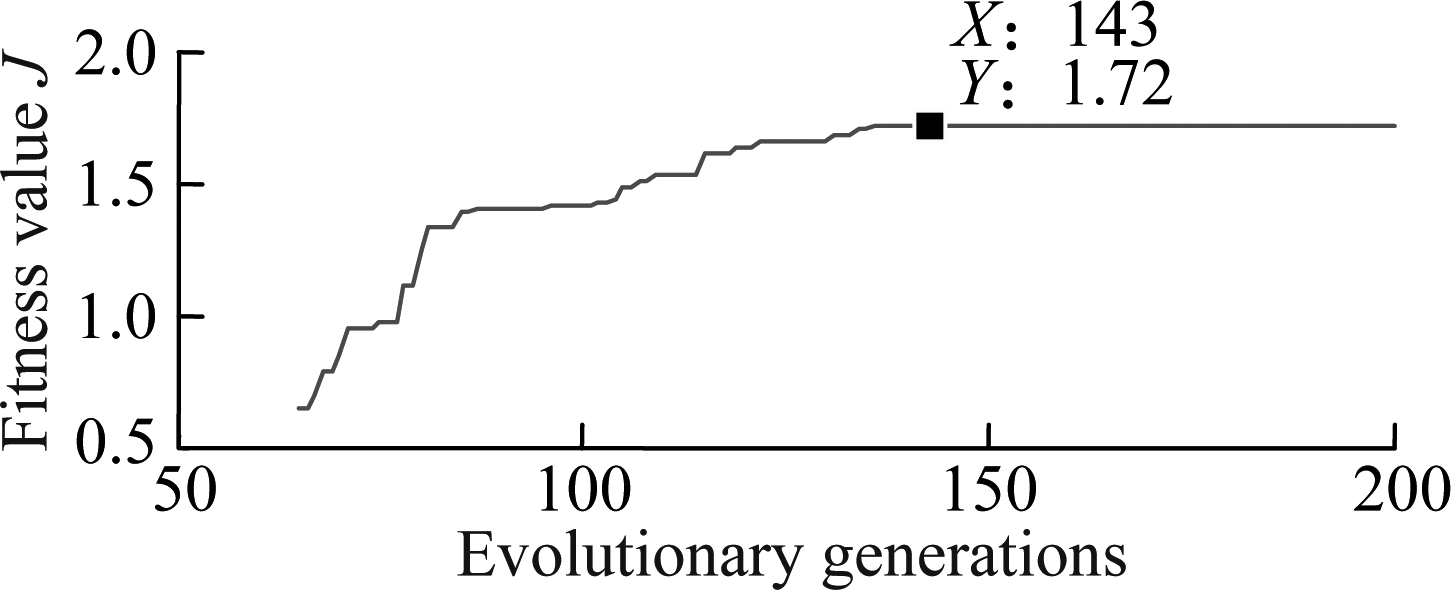
Fig.7 The curve of fitness value
Tab.1 Optimal control rules of the fuzzy-PID control

ECK′pK′iK′dNBNSZOPSPBNBNSZOPSPBNBNSZOPSPBNBBMBMSSSSSMSMSPSMSSSMSNSMMMMMSSMSMSMMNBMMSSSZOMSSMMMSMSMMMBNBBMBSMSPSSSBBMBMSMMMBMBNBMSMSMSMSPBSSMMBBMMMBBBPSSMSMB
3 Results and Control Performance Analysis
3.1 Evaluate criteria
According to the standard ISO 2631-1[19], the effect of vibration on the ride comfort is evaluated by the weighted RMS acceleration value as follows:
(20)
where awt is the acceleration (translational and rotational) that depends on the time of measurement T.
The weighted RMS acceleration responses of the driver’s seat heave aws and the cab’s pitch angle awpc are then used to evaluate the performance of the SHM.
3.2 Control performance on deformable terrains
Under the condition of the vibratory roller traveling on the soft terrain, the reference parameters of the vehicle[8], four types of unpaved off-road classifications of Mitschke[6] and two typical soft terrains of LETE sand and Grenville soil[5] are chosen to evaluate the control performance at a vehicle velocity of v0 = 6 km/h.
The simulation results of the acceleration responses on Grenville soil with the poor terrain surface are shown in Fig.8. The acceleration responses of the SHM with optimization are clearly decreased in comparison with both the PHM and the SHM without optimization. Concurrently, the results in Tab.2 also show that the weighted RMS values of the driver’s seat heave and the cab’s pitch angle are strongly reduced by 39.0% and 35.9% in comparison with PHM.
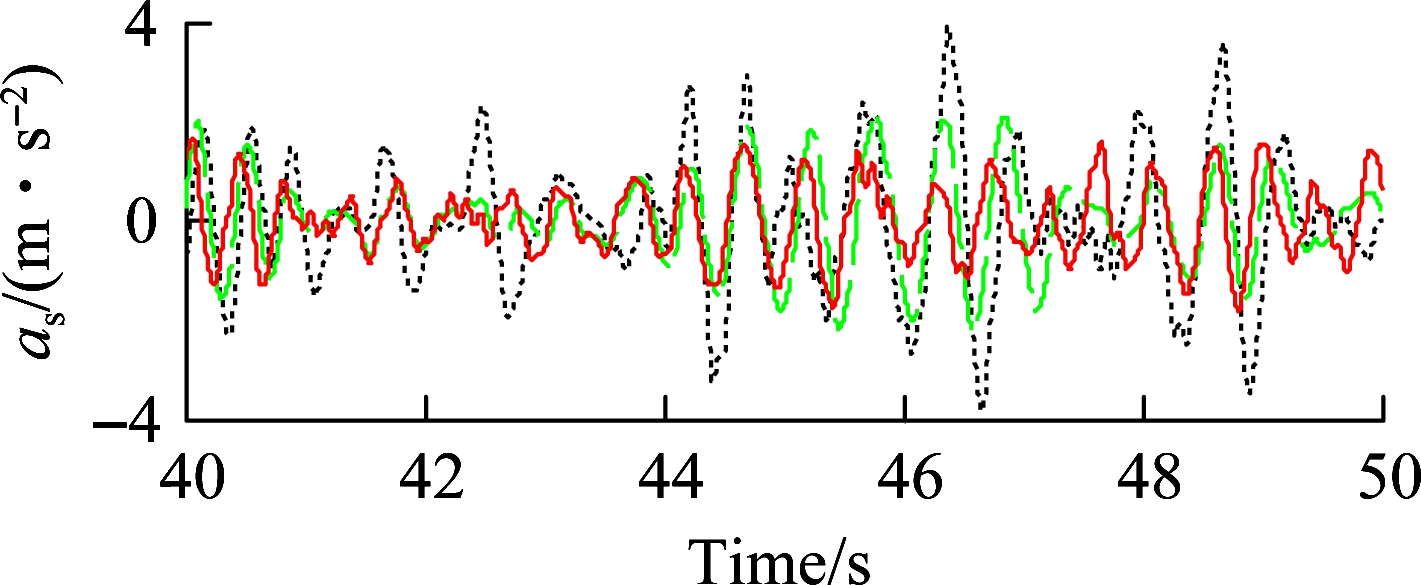
(a)

(b)
Fig.8 The acceleration responses on a soft terrain of Grenville soil. (a) Driver’s seat heave; (b) Cab’s pitch angle
Tab.2 Control performance on a soft terrain

Parameteraws/(m·s-2)awpc/(rad·s-2)PHM1.281.17SHM without optimization0.880.84SHM with optimization0.780.75
The comparison results of the weighted RMS acceleration responses on two typical terrains of LETE sand and Grenville soil with four types of terrain surface roughness are shown in Fig.9. The results show that the weighted RMS values are clearly affected by the terrain surfaces roughness. The weighted RMS values are low on a good terrain and high on a very poor terrain. In addition, the soft terrains also impact clearly on the driver’s ride comfort. The compared results in Figs.9(a) and (b) show that the weighted RMS value of the driver’s seat heave on Grenville soil is higher than that on the LETE sand; On the contrary, that of the cab’s pitch angle on Grenville soil is lower than that on the LETE sand. It implies that when the vehicle travels on the LETE sand, the vertical driver’s ride comfort is enhanced while the comfortable shake of the driver is decreased; whereas, when the vehicle travels on Grenville soil, the vertical driver’s ride comfort is reduced while the comfortable shake of the driver is significantly improved.
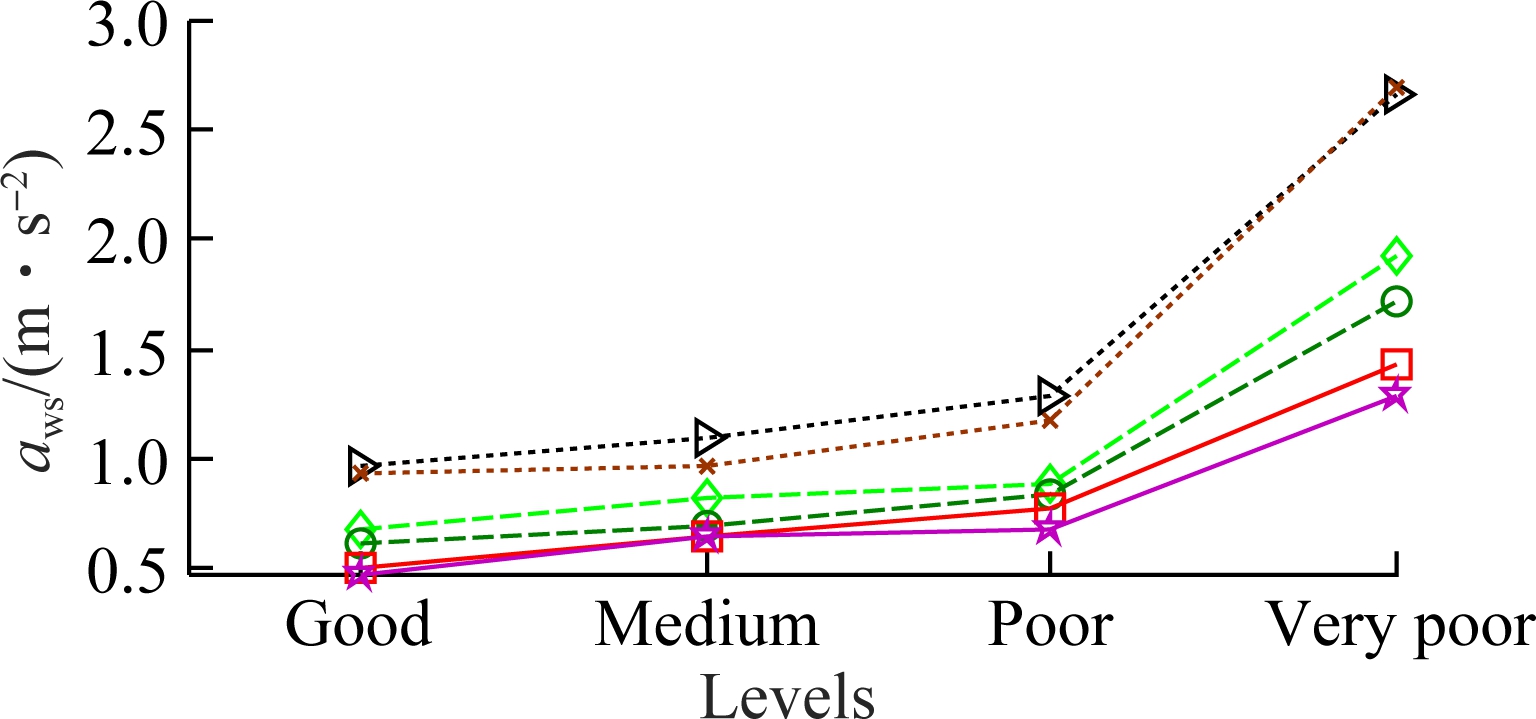
(a)
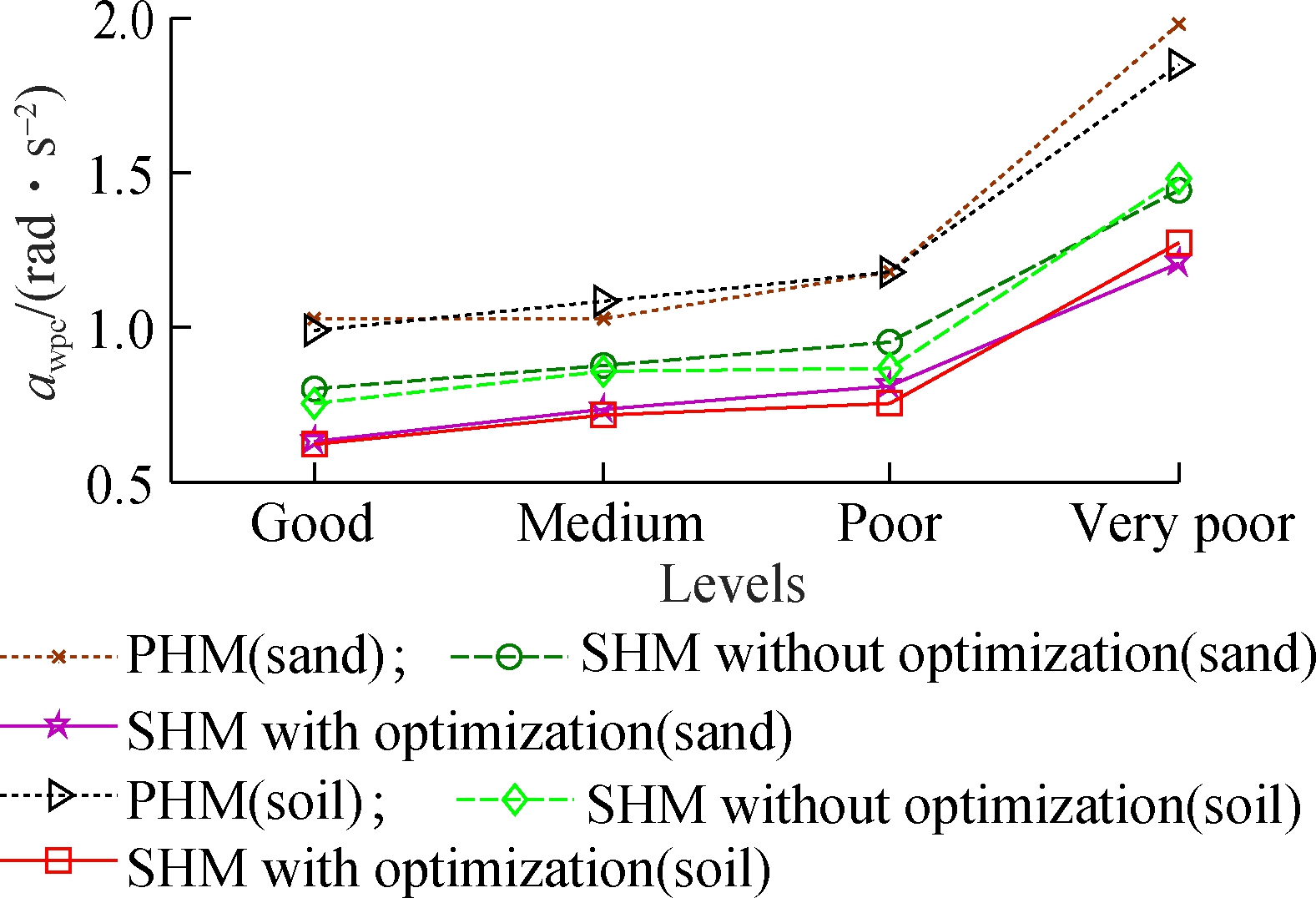
(b)
Fig.9 Weighted RMS acceleration responses on various terrains. (a) Driver’s seat heave; (b) Cab’s pitch angle
Using the SHM with optimization, the weighted RMS values are lower than that of both PHM and SHM without optimization under various terrain surfaces of both LETE sand and Grenville soil. Thus, the SHM with optimization can remarkably improve the driver’s ride comfort and cab shaking on deformable terrain surfaces.
3.3 Control performance on the speed region
A range of vehicle velocities from 1 to 12 km/h and a poor terrain surface of the Grenville soil are chosen to analyze the control performance in the condition of the vehicle traveling.
The results in Fig.10 show that the vehicle velocities greatly affect on the driver’s ride comfort and the cab shaking. When the vehicle velocity ranges from 8 to 12 km/h, the weighted RMS values of the driver’s seat heave with SHM is significantly increased, whereas, that of the cab’s pitch angle is slightly enhanced. It implies that the vertical driver’s ride comfort is reduced and the comfortable shake of the driver is insignificantly affected with the increasing vehicle velocity.
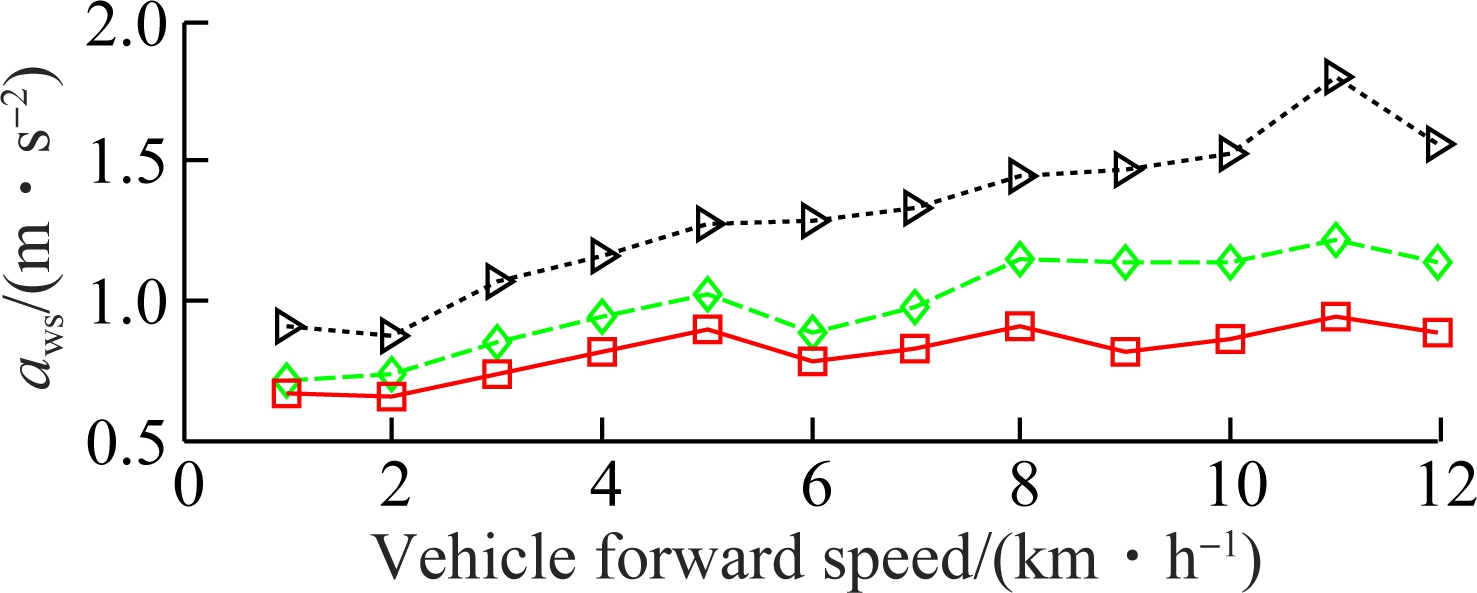
(a)

(b)
Fig.10 Weighted RMS acceleration responses in the vehicle speed region. (a) Driver’s seat heave; (b) Cab’s pitch angle
When the vehicle velocity ranges from 1 to 5 km/h, the weighted RMS values of the driver’s seat heave and the cab’s pitch angle are remarkably increased with all the cab’s isolation mounts. Therefore, the driver’s ride comfort is greatly influenced in this vehicle velocity. However, the weighted RMS values of the SHM with optimization are lower than those of both PHM and SHM without optimization in all vehicle velocity ranges, especially the vehicle velocity ranging from 6 to 7 km/h. This result is very important since the vehicle forward speed ranges usually from 5 to 8 km/h when the vehicle travels on soft terrain. Consequently, the driver’s ride comfort and the cab shaking are significantly improved by SHM with optimization.
3.4 Control performance on elastoplastic soils
In order to evaluate the performance of SHM with optimizationon elastoplastic soil grounds, three typical elastoplastic soils including a low-density soil, a medium-density soil, and a high-density soil[2] are simulated at a vehicle velocity of v0=3 km/h under an exciting frequency 28 Hz of the vibratory drum.
The acceleration responses of the driver’s seat heave and the cab’s pitch angle when the vehicle drives on a high-density soil are shown in Fig.11. Using the SHM with optimization, the acceleration responses are clearly decreased in comparison with those of both the PHM and the SHM without optimization. The results in Tab.3 also show that the weighted RMS values of the driver’s seat heave and the cab’s pitch angle are significantly, reduced by 34.6% and 47.3% in comparison with the PHM.
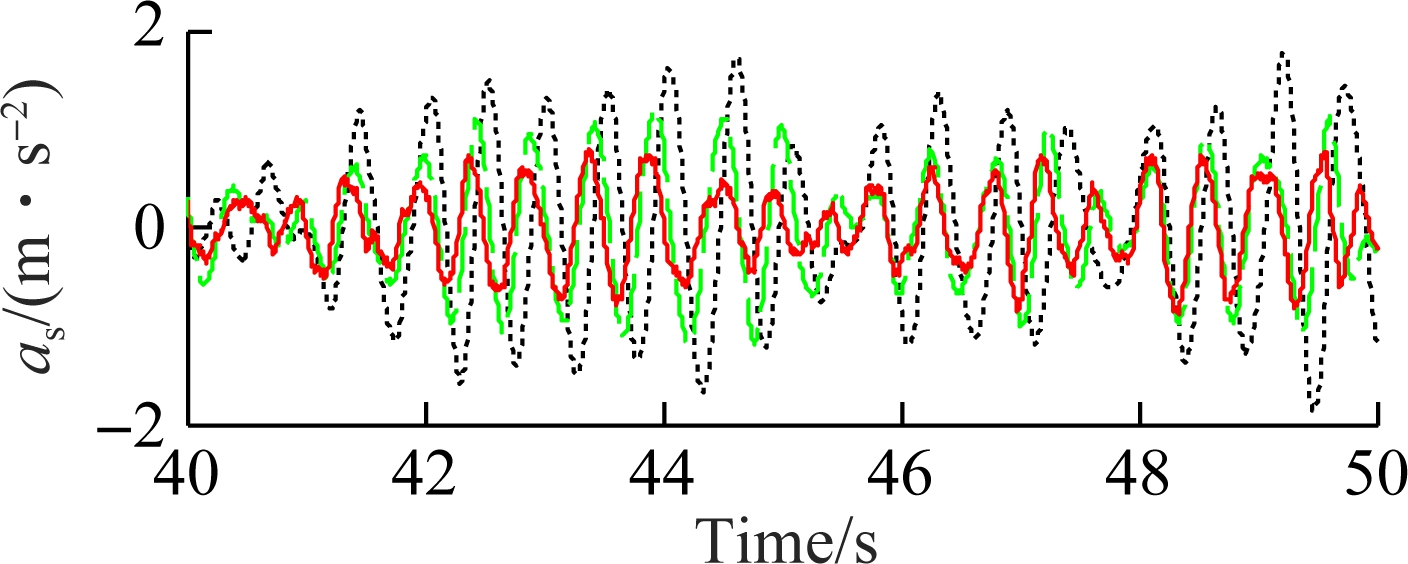
(a)
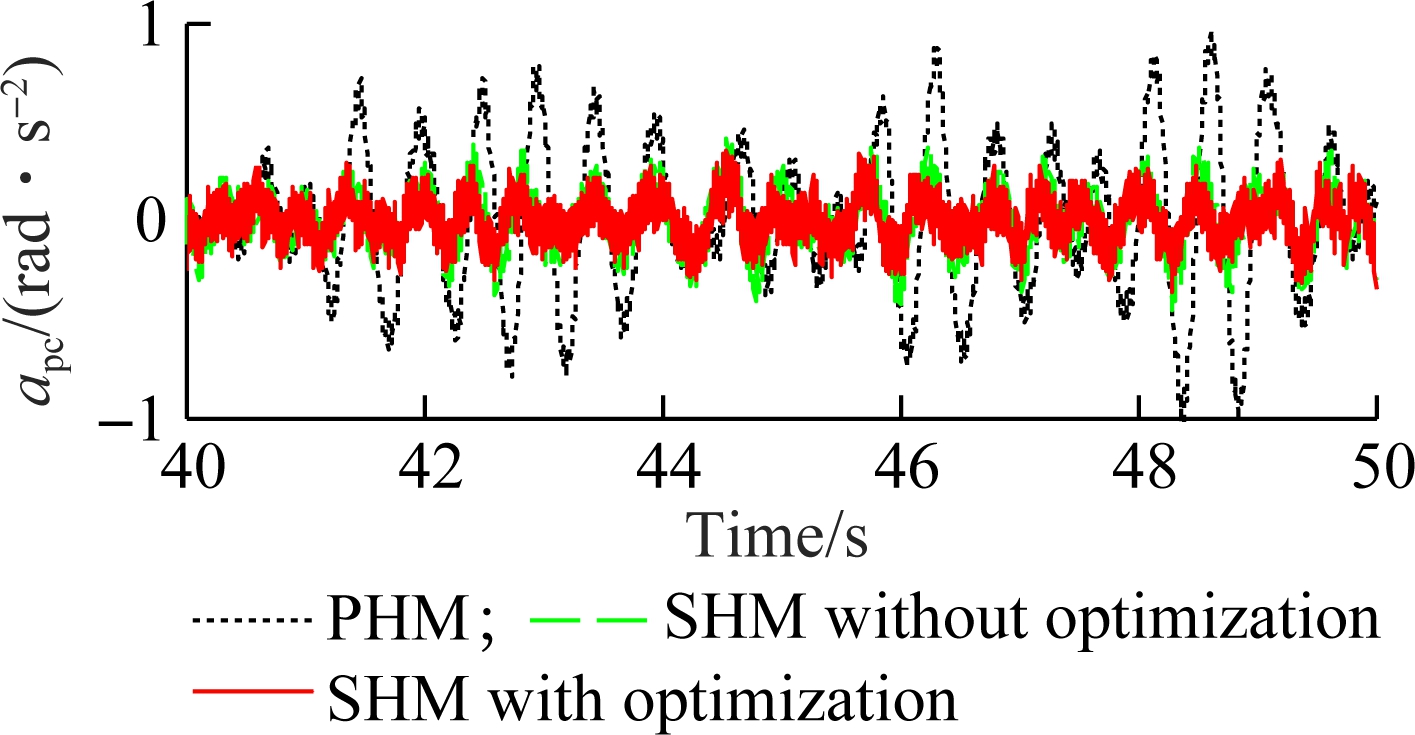
(b)
Fig.11 The acceleration responses on a high-density soil ground. (a) Driver’s seat heave; (b) Cab’s pitch angle
Tab.3 Control performance on a high-density soil

Parameteraws/(m·s-2)awpc/(rad·s-2)PHM0.780.38SHM without optimization0.590.23SHM with optimization0.510.20
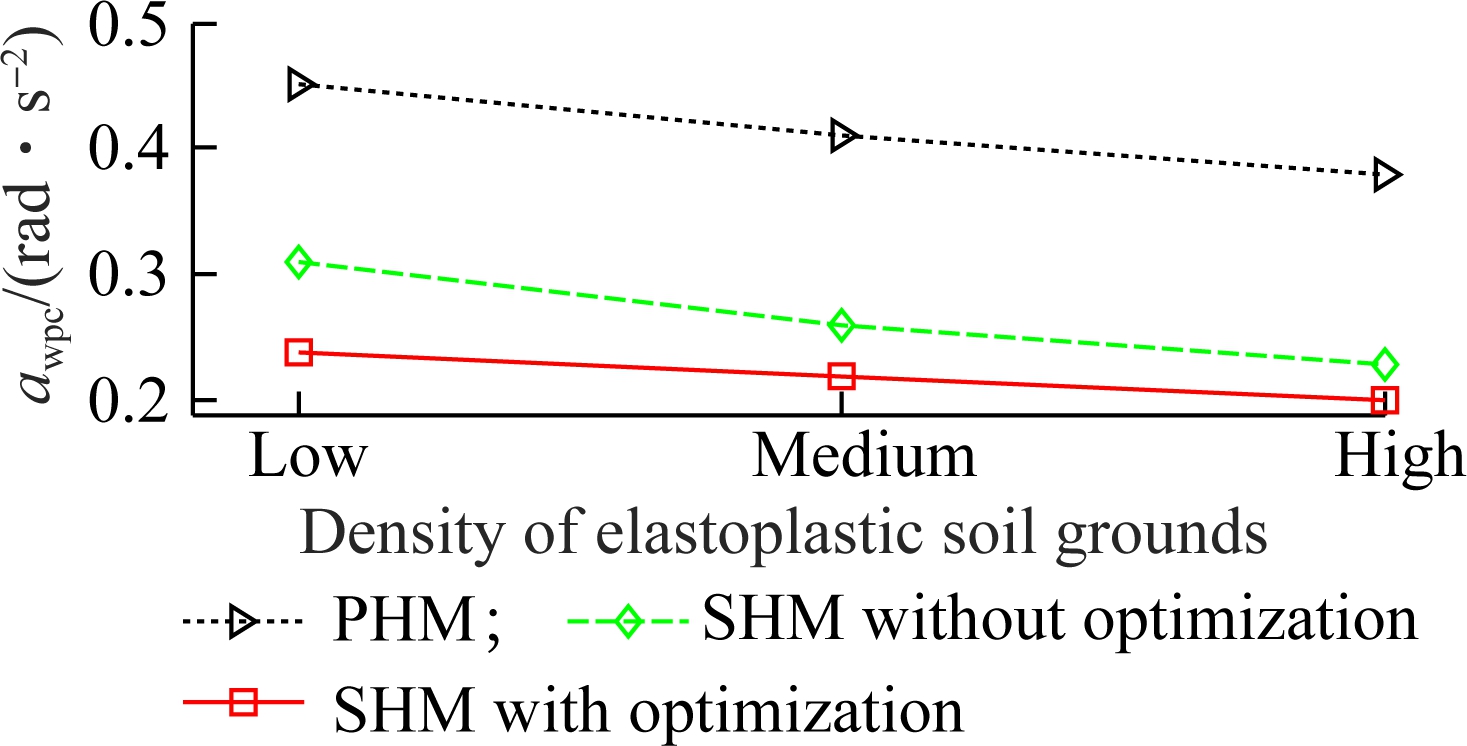
Furthermore, the simulation results of the weighted RMS values on three types of elastoplastic soil grounds are also shown in Fig.12. The comparison results show that the weighted RMS values are significantly affected by elastoplastic soil grounds. The weighted RMS value of the driver’s seat heave is low while that of the cab’s pitch angle is high on a low-density soil. In contrast, the weighted RMS value of the driver’s seat heave is progressively increased, while of that cab’s pitch angle is gradually reduced on both medium-high-density soils. Therefore, the comfortable shake of the driver is significantly affected by a low-density soil and the vertical driver’s ride comfort is strongly influenced by a high-density soil. In addition, the weighted RMS acceleration responses of SHM with optimization are reduced in comparison with PHM and SHM without optimization under all elastoplastic soils. Consequently, the driver’s ride comfort and the cab shaking also are significantly improved by using SHM with optimization.
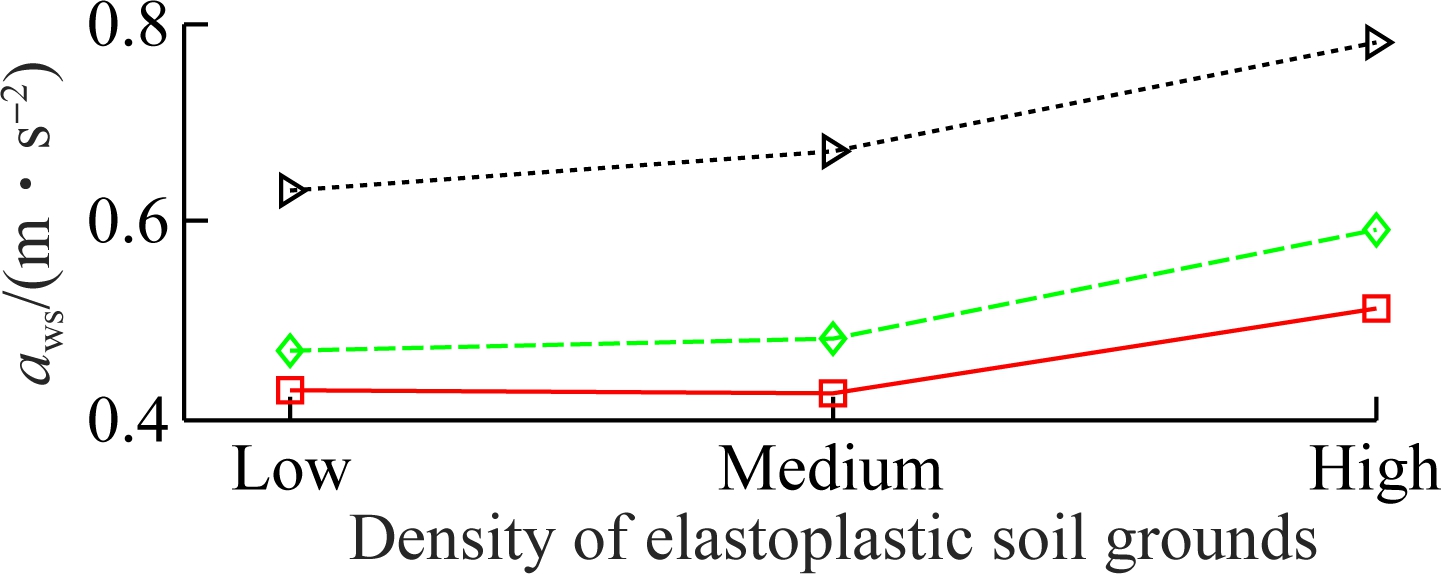
(a)
(b)
Fig.12 Weighted RMS values on elastoplastic soil grounds. (a) Driver’s seat heave; (b) Cab’s pitch angle
4 Conclusions
1) The driver’s ride comfort and the cab shaking are strongly affected by the off-road terrains under various operation conditions, especially at the vehicle velocity ranging from 8 to 12 km/h and on very poor terrain surfaces of Grenville soil under the condition of the vehicle travelling, and on a high-density soil of the elastoplastic soil ground under the condition of the vehicle working.
2) A new optimal method of the FLC rules based on the GA program is successfully developed and applied for the optimal fuzzy-PID control. The control result of the SHM with optimization is better than both the PHM and SHM without optimization under different operation conditions.
3) In particular, using the SHM with optimization, the driver’s ride comfort and the cab shaking are greatly improved at the vehicle velocity ranging from 6 to 7 km/h under the condition of the vehicle traveling and on the elastoplastic soils under the condition of the vehicle working.
[1]Adam D, Kopf F. Theoretical analysis of dynamically loaded soils[C]//Proceedings of European Workshop Compaction of Soils and Granular Materials. Paris, France, 2000: 207-220.
[2]Kordestani A, Rakheja S, Marcotte PhD P, et al. Analysis of ride vibration environment of soil compactors[J]. SAE International Journal of Commercial Vehicles, 2010, 3(1): 259-272. DOI:10.4271/2010-01-2022.
[3]Nguyen V L, Zhang J R, Hua W L, et al. Ride quality evaluation of the soil compactor cab supplemented by auxiliary hydraulic mounts via simulation and experiment [J]. Journal of Southeast University (English Edition), 2019, 35(3): 273-280. DOI:10.3969/j.issn.1003-7985.2019.03.001.
[4]Bekker M. Introduction to terrain-vehicle systems[M]. Ann Arbor, USA: University of Michigan Press, 1969.
[5]Wong J Y. Data processing methodology in the characterization of the mechanical properties of terrain[J]. Journal of Terramechanics, 1980, 17(1): 13-41. DOI:10.1016/0022-4898(80)90014-2.
[6]Mitschke M. Dynamik der kraftfahrzeuge[M]. Berlin, Germany: Springer-Verlag, 1972. DOI:10.1007/978-3-662-11585-5.
[7]Nguyen V L, Zhang J R, Jiao R Q, et al. Effect of the road-off terrains on the ride comfort of construction vehicles [J]. Journal of Southeast University (English Edition), 2019, 35(2): 191-197. DOI:10.3969/j.issn.1003-7985.2019.02.008.
[8]Nguyen V L, Zhang J R, Le V Q, et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts [J]. Shock and Vibration, 2018, 2018: 1-17. DOI:10.1155/2018/8527574.
[9]Yildirim  . Vibration control of suspension systems using a proposed neural network [J]. Journal of Sound and Vibration, 2004, 277(4/5): 1059-1069. DOI:10.1016/j.jsv.2003.09.057.
. Vibration control of suspension systems using a proposed neural network [J]. Journal of Sound and Vibration, 2004, 277(4/5): 1059-1069. DOI:10.1016/j.jsv.2003.09.057.
[10]Kasemi B, Muthalif A G A, Rashid M M, et al. Fuzzy-PID controller for semi-active vibration control using magnetorheological fluid damper[J]. Procedia Engineering, 2012, 41: 1221-1227. DOI:10.1016/j.proeng.2012.07.304.
[11]Nguyen S D, Nguyen Q H, Choi S B. A hybrid clustering based fuzzy structure for vibration control—Part 2: An application to semi-active vehicle seat-suspension system[J]. Mechanical Systems and Signal Processing, 2015, 56/57: 288-301. DOI:10.1016/j.ymssp.2014.10.019.
[12]Wang W, Song Y L, Xue Y B, et al. An optimal vibration control strategy for a vehicle’s active suspension based on improved cultural algorithm[J]. Applied Soft Computing, 2015, 28: 167-174. DOI:10.1016/j.asoc.2014.11.047.
[13]Chen Y, Wang Z L, Qiu J, et al. Hybrid fuzzy skyhook surface control using multi-objective microgenetic algorithm for semi-active vehicle suspension system ride comfort stability analysis [J]. Journal of Dynamic Systems, Measurement, and Control, 2012, 134(4): 1-14. DOI: 10. 1115/1.4006220.
[14]International Organization for Standardization. ISO/TC108/SC2/WG4 N57 Reporting vehicle road surface irregularities [S]. Stuttgart, Germany: Thieme Medical Publishers, 1982.
[15]Mamdani E H. Advances in the linguistic synthesis of fuzzy controllers[J]. International Journal of Man-Machine Studies, 1976, 8(6): 669-678. DOI:10.1016/s0020-7373(76)80028-4.
[16]Nguyen V L, Zhang J R, Le V Q, et al. Performance analysis of air suspension system of heavy truck with semi-active fuzzy control [J]. Journal of Southeast University (English Edition), 2017, 33(2): 159-165. DOI:10.3969/j.issn.1003-7985.2017.02.006.
[17]Nariman-Zadeh N, Salehpour M, Jamali A, et al. Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm (MUGA)[J]. Engineering Applications of Artificial Intelligence, 2010, 23(4): 543-551. DOI:10.1016/j.engappai.2009.08.008.
[18]Crews J H, Mattson M G, Buckner G D. Multi-objective control optimization for semi-active vehicle suspensions[J]. Journal of Sound and Vibration, 2011, 330(23): 5502-5516. DOI:10.1016/j.jsv.2011.05.036.
[19]International Organization for Standardization. ISO 2631-1 Mechanical vibration and shock-evaluation of human exposure to whole body vibration—Part 1: General requirements [S]. Geneve, Switzerland: International Organization for Standardization, 1997.