Rolling bearings are the core components of rotating machinery. According to statistics, 30% of rotating machinery faults are related to rolling bearings[1]. Therefore, the evaluation of rolling bearing performance degradation is of great significance. Performance degradation evaluation attempts to extract features from acquired data information to identify and quantify history and ongoing degradation processes[2]. Since the degradation process of a rolling bearing is relatively slow, detecting the incipient fault effectively and describing the health status accurately are the core concerns of rolling bearing intelligent maintenance.
In recent years,much research has focused on the evaluation of rolling bearing performance degradation. Boškoski et al. [3] extracted the Jensen-Renyi entropy based on the wavelet packet transform coefficients to characterize the degradation performance of the bearing. Rai et al.[4] used the ensemble empirical mode decomposition(EEMD) to extract the singular values and energy instantaneous entropy of each intrinsic mode function (IMF) as the fault characteristics. Jia et al.[5] used the diffusion map (DM) to reduce the original features dimension nonlinearly and used it for the fault detection and performance degradation evaluation of the device. Wang et al.[6] used locally linear embedding (LLE) dimension reduction and fuzzy C-means(FCM) to complete the degradation assessment, and the results show that LLE has strong nonlinear dimensionality reduction capability. However, the DM and LLE do not provide an explicit mapping matrix from high-dimensional space to low-dimensional embedded space, and dimension reduction needs to recalculate the training samples when the new samples are processed, thus they are not suitable for online evaluation. Widodo et al.[7] used the PCA method to reduce the original bearing characteristics. Lu et al.[8] used EMD decomposition to extract IMFs energy as the feature vector, and reduced the dimension using PCA. Liao et al. [9] extracted the wavelet packet decomposition(WPD) node energy and performed the PCA transformation to extract the principal component fault characteristics. However, the PCA method only captures the global structure of the dataset and selects the first few principal components with larger variance as the fault features, and local structure information are ignored.
Although effective signal processing techniques like EMD, EEMD etc., are commonly used to denoise and retain impulsive features from the bearing signals, they suffer from the issues of false IMFs, mode-mixing occurrence and end effects, etc. VMD is a signal decomposition method that decomposes the signal into different IMFs in the variational framework[10], which can suppress mode-mixing and end effects more effectively compared to traditional EMD and EEMD methods. As an effective signal decomposition tool, VMD has been successfully used in fault diagnosis in recent years[11-12]. Therefore, in this paper, VMD has been utilized for fault feature extraction from the raw bearing signal for performance degradation evaluation.
Neighborhood preserving embedding (NPE) is a linear approximation of the LLE nonlinear dimension reduction algorithm[13]. NPE reveals the local structure information of the observed dataset and finds more meaningful information than PCA. Compared to nonlinear dimension reduction methods, such as DM, LLE and Isomap, NPE provides a specific embedding matrix for new sample dimension reduction, and thus it is more suitable for online process monitoring[14-15]. However, the problem of NPE that useful embedding information is easily suppressed by irrelevant embedding information still persists, which will lead to the loss of fault sensitive information in the bearing performance degradation evaluation process.
To overcome the problems mentioned above in this paper, VMD is used to decompose the vibration signal, and the features such as singular values and relative energies of the IMFs are extracted to form the feature set. Then, a novel embedding selection-based NPE (ESNPE) method is proposed to extract useful embedding features for the bearing degradation index performance improvement. Firstly, the NPE method is used to extract the embedding matrix of the observed normal dataset. Secondly, given that fault has no definite projection for a certain embedding, the Spearman correlation coefficient is employed in the ESNPE method to calculate the trend value and evaluate the effectiveness of each embedding. Then, useful embeddings are preserved and irrelevant embeddings are abandoned through the first-order difference method in the early degradation stage of bearing degradation. Finally, the SVDD model is used to construct the degradation index of the rolling bearing performance. The analysis of the rolling bearing experimental data verifies that the proposed method has superiority in improving the incipient fault sensitivity and stability of the degradation index.
1 Feature Extraction
1.1 VMD theory
In contrast to the traditional recursive decomposition method, VMD decomposes the signal in the variational framework. Through constructing the constrained variational problem, the center frequency and bandwidth of each IMF are continuously updated during the search for the optimal solution. The corresponding constrained variational model is[11]
(1)
where f is the time domain signal; uk and wk are the model function and the center frequency of the k-th IMF, respectively; K represents the number of IMFs; ∂t represents the partial derivative of time t; σt is a unit pulse function;* denotes a convolution calculation.
To solve the constraint variation problem, the Lagrangian multiplier λ(t) and the penalty term α are introduced, and the augmented Lagrangian function is obtained as
(2)
The Lagrangian function is solved by the variable alternating iterative optimization method[11], and finally the mode functions uk and frequency band center wk of the corresponding IMF are obtained.
1.2 Feature extraction
In this section, VMD is used for fault feature extraction due to its special advantages. Suppose that a signal f with N points is decomposed by VMD and modal functions uk(k=1,2,…,K) are obtained, the relative energy of each IMF can be expressed as
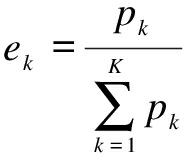
(3)
where ![]() denotes the energy of uk,uk=[xk1,xk2,…,xkN].
denotes the energy of uk,uk=[xk1,xk2,…,xkN].
According to the matrix theory, the singular value is an intrinsic feature of a matrix and is unique[16]. Each modal function uk performs a Hilbert envelope analysis, and matrix SK×N is constructed with each envelope signal arranged in a row-wise manner. Matrix SK×N performs singular value decomposition to obtain K singular values as
S=UQVT
(4)
where UTU=I; VTV=I; Q is a K×N diagonal matrix, Q=diag(s1,s2,…,sK), and sk(k=1,2,…,K) are the singular values of matrix SK×N. Then the singular values can be used as fault features.
In the VMD decomposition process, the existence of the penalty term α can effectively reduce the Gaussian noise, which makes the IMFs sparse. Therefore, the reconstructed signal f′ has a higher signal to noise ratio compared to original signal f.
(5)
The indicators in the time domain of the reconstructed signal f′=[y1,y2,…,yl,…,yN] are extracted as fault features as well. Finally, the fault features of signal f are obtained as shown in Tab.1.
Tab.1 Fault features based on VMD

FeatureExpressionAbsolute meanXam=1N∑Nl=1ylPeak to peakXpp=max(yl)-min(yl)Root mean square(RMS)Xrms=1N∑Nl=1y2lKurtosisXkur=1X4rms∑Nl=1(yl-y)4Shape factorXsf=XrmsXamCrest factorXcf=max(yl)XrmsKurtosis coefficientXkc=1N∑Nl=1y4l(std(yl))4Impulse factorXif=max(yl)XamRelative energies[e1,e2,…,eK]Singular values[s1,s2,…,sK]
![]() is the mean value of the reconstructed signal.
is the mean value of the reconstructed signal.
2 Proposed ESNPE Method
2.1 NPE theory
The original feature space is high-dimensional, and usually contains redundant information that is unrelated to the bearing fault, which affects the performance degradation assessment results. NPE aims to optimally reduce the high dimension by preserving the local manifold structure of the given dataset[13]. Given dataset X={x1,x2,…,xn}∈Rm with n samples and m dimension, the weight matrix W is computed by minimizing the following error function:
(6)
where coefficient wij in W represents the linear combination coefficient to reconstruct xi by its k nearest neighbors, which follows that ![]() and wij=0 if xj is not a neighbor of xi. The objective of NPE is to find an embedding transformation matrix P=[p1,p2,…,pd]∈Rm that maps high-dimensional data X into d dimensional feature space Y=[y1,y2,…,yn]∈Rd,d≤m,yi=xiP. The minimizing objective function is as follows:
and wij=0 if xj is not a neighbor of xi. The objective of NPE is to find an embedding transformation matrix P=[p1,p2,…,pd]∈Rm that maps high-dimensional data X into d dimensional feature space Y=[y1,y2,…,yn]∈Rd,d≤m,yi=xiP. The minimizing objective function is as follows:
(7)
Then, the calculation of the transformation matrix P is converted into solving the eigenvalue problem:
XMXTP=λXXTP
(8)
where M=(I-W)T(I-W); λ is the eigenvalue. Eigenvectors with corresponding d smallest eigenvalues form the embedding transformation matrix P=[p1,p2,…,pd]∈Rm.
2.2 Spearman correlation coefficient
During the gradual degradation process of the rolling bearing performance, the trend of useful features changes over time as degradation develops. The Spearman correlation coefficient[17], which is one of the three correlation coefficients, is commonly used to quantify the correlation between two variables. The greater the absolute value of the coefficient, the stronger the correlation. In this study, the size of the coefficient is used to describe the trend value of the feature sequence, and the formula is as
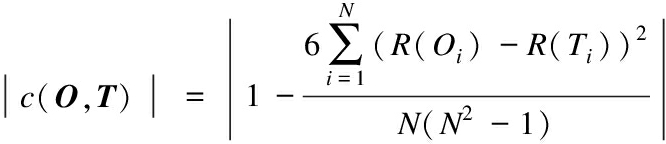
(9)
where R(Oi) and R(Ti) are the ranks of feature sequence O and time sequence T,O=[O1,O2,…,ON],T=[T1,T2,…,TN]; N denotes the length of time series;|c(O,T)| is the trend value.
2.3 Simulation analysis
To analyze the fault reflection capability of embedding information acquired by NPE in the performance degradation evaluation process, a simple simulation process is designed as
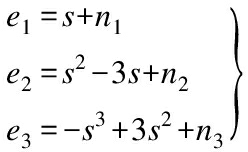
(10)
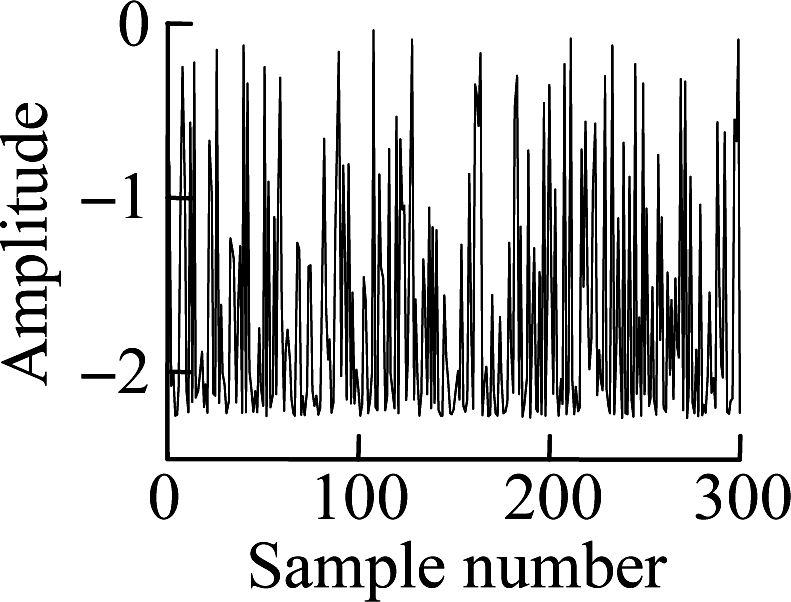
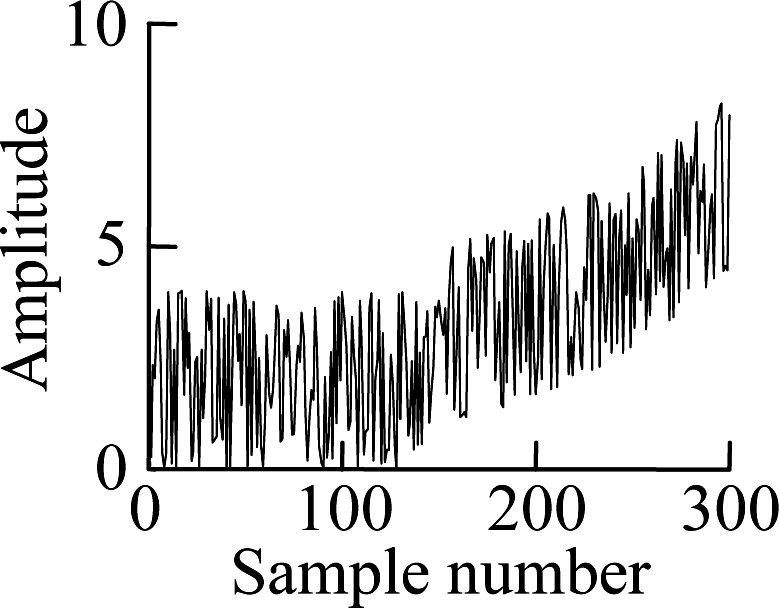
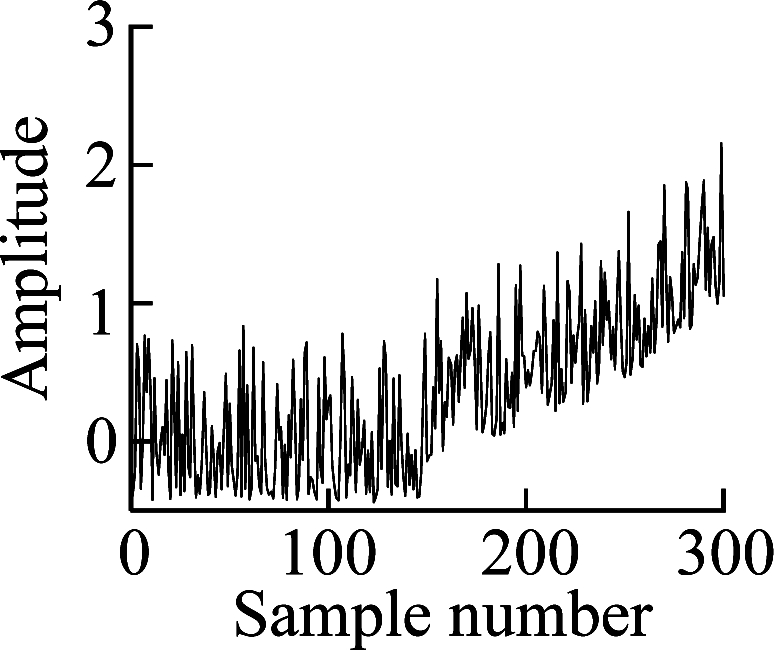
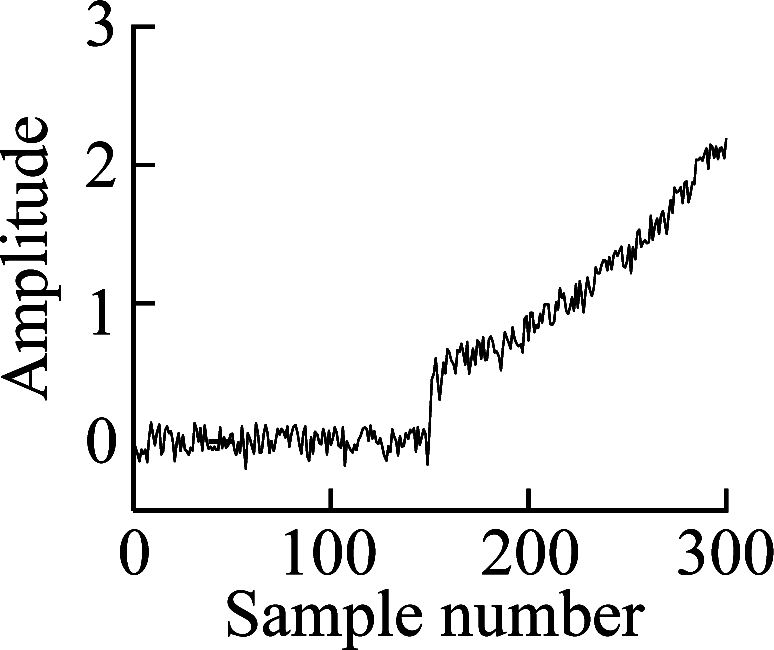
where ei denotes independent features, i=1,2,3; ni is the individual Gaussian noise, ni~N(0,0.01); s∈[0.01,2]. A feature dataset X with 300 samples is generated by Eq.(10). Feature e3 is nonlinearly increased from sample point 151 to sample point 300 by adding e0.01×(j-150), where j is the sample number. The first 150 samples in X are denoted as normal samples and the NPE algorithm is performed to obtain the transformation matrix P. Then dataset X is embedded into P to obtain each embedding.
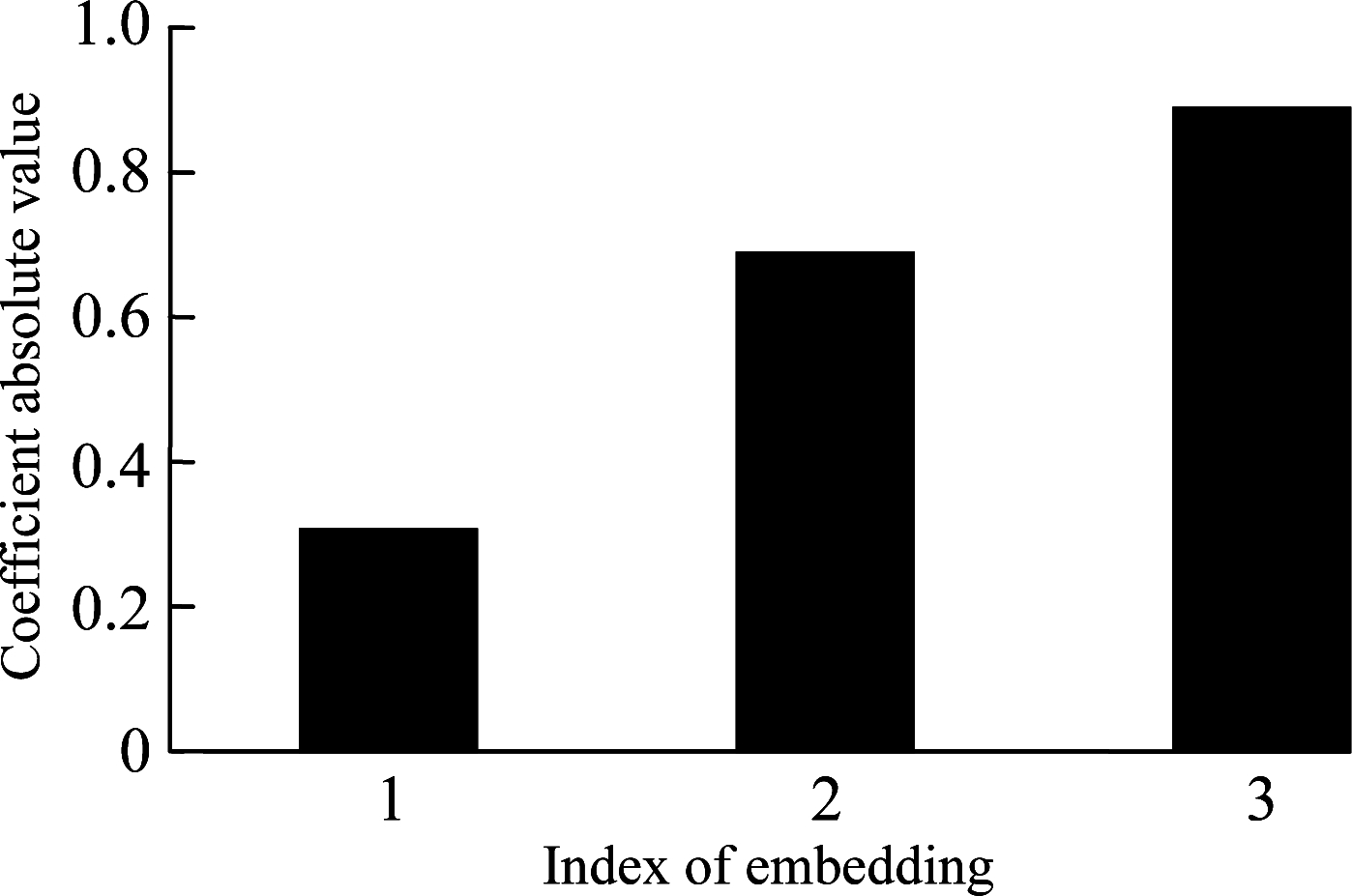
The embedding results are shown in Fig.1. The second and the third embeddings increase obviously when fault occurs, which can be regarded as useful embeddings. Yet, the first embedding fluctuates with a large variance and cannot reflect the fault situation effectively, which can be regarded as irrelevant information. Therefore, the useful information of the second and the third embeddings will be suppressed by the useless first embedding if the first embedding is retained in the evaluation process. At the same time, the Spearman correlation coefficient is calculated for each embedding feature, and it can be seen that the coefficient can effectively quantify the trend of feature sequence, and useful embedding features have corresponding higher trend values. Thus, it is possible to find useful embeddings and abandon irrelevant embeddings using the Spearman correlation coefficient when employing NPE for the monitoring process.
(a)
(b)
(c)

(d)
(e)
(f)
(g)
Fig.1 Simulation analysis results of NPE. (a) Simulation feature e1; (b) Simulation feature e2; (c) Simulation feature e3; (d) First embedding feature; (e) Second embedding feature; (f) Third embedding feature; (g) Spearman correlation coefficient of each embedding
2.4 ESNPE method
Although NPE has the advantage in preserving dataset local structure, the problem that the fault has no definite projection to a certain embedding still exists and useful embeddings are easily suppressed by irrelevant embeddings. In this section, the ESNPE method based on the Spearman correlation coefficient is proposed. Fault sensitive embedding features are extracted by preserving useful embedding information and abandoning irrelevant embedding information, which aims to improve the performance of the degradation index in the evaluation process of rolling bearings.
The performance degradation of rolling bearings is a relatively slow process and most of the time is taken up during the material damage accumulation. The RMS indicator is commonly used for indicating the bearing degradation process for its stability, but it is insensitive to incipient faults. Thus, we can find effective embeddings extracted by NPE through the trend analysis in the early degradation stage before the RMS indicator reaches the 3σ threshold. The larger the trend value, the more important the embedding. Therefore, we use the trend value as the index to select useful embeddings. In this paper, we use the Spearman correlation coefficient to select the useful embeddings of NPE. The ESNPE process for the bearing performance degradation evaluation is as follows.
1) Set fi(i=1,2,…) as the vibration signal of the i-th continuous sampling of the vibration sensor. The RMS value of fi is calculated, and when the RMS of fn+j (j=1,2,…,m,m<n) does not satisfy the 3σ principle as shown in formula (11), determine Y=[f1,f2,…,fn] as an early embedding selection signal set. Y is extracted features in Tab.1 and an m-dimensional feature dataset E=[x1,x2,…,xn]∈Rm is obtained.
|RMSn+j-μ|>3σ
(11)
where μ and σ are the mean value and standard deviation of the RMS of Y.
2) A normal dataset A is divided from E and normalized, A=[x1,x2,…,xt]∈Rm, with t samples and m dimension. The NPE algorithm is performed to obtain the embedding transformation matrix P=[p1,p2,…,pd]∈Rm, where d is the dimension of the embedding space.
3) E is normalized and embedded into matrix P . Then the embedding feature matrix F is obtained as
F=[F1,F2,…,Fd]n×d=ETP
(12)
4) F is normalized and the trend value of Fi is calculated as Eq.(9),1≤i≤d. Then the trend values are arranged in a descending order as C={|c1|,|c2|,…,|cd|}, where|ci|≥|cj|, i<j.
5) The first-order difference method is performed in C as
di=|ci|-|ci+1| i=1,2,…,d-1
(13)
and D={d1,d2,…,dd-1} is obtained.
6) Find the maximum extreme point dl in D, 1<l<d, and preserve the l embedding eigenvectors Pb in matrix P corresponding to the previous|ci|in C, 1≤i≤l, where ![]() Pb⊆P. Then Pb is considered to be the useful embedding transformation matrix.
Pb⊆P. Then Pb is considered to be the useful embedding transformation matrix.
7) As for the new sample x, embed x into Pb to obtain the l-dimensional embedding feature y as
y=xTPb
(14)
Furthermore, y needs to be standardized to obtain the l-dimensional feature y′.
(15)
where μ and σ are the mean value and standard deviation of each embedding feature in Fnor, Fnor=ATPb corresponding to the normalized normal dataset A. Then, y′ is the embedding feature obtained by the ESNPE method from high dimension to low dimension.
3 Rolling Bearing Performance Degradation Ev-aluation Process
In this section,the SVDD model is used to obtain the performance degradation index and complete rolling bearing performance degradation evaluation. SVDD is commonly used in the health monitoring of equipment, which constructs a minimum hypersphere that contains most target samples in the high-dimensional feature space. The distance between the monitor sample and center a is considered as the degradation index used to describe the status deviation from the normal state. When the distance is smaller than radius R of the hypersphere, it represents the normal state of the equipment. As the distance exceeds radius R, it indicates the early degradation of the equipment performance. Large distance means the severe degradation of the performance. Therefore, the distance is used to monitor the health status of the rolling bearing, and for more details about SVDD, please refer to Ref.[18].
This paper presents a performance degradation evaluation method based on VMD and ESNPE for rolling bearing. The specific process is as follows.
3.1 Offline modeling
Offline modeling involves the implementation of the ESNPE method and the construction of the SVDD model for bearing performance degradation evaluation.
1) The RMS value of each vibration signal is calculated, and the embedding selection signal set Y is determined according to the 3σ principle. The vibration signal is decomposed by VMD and the features in Tab.1 are extracted, and a m-dimensional feature dataset E=[x1,x2,…,xn]∈Rm is obtained.
2) A normal feature dataset A=[x1,x2,…,xt]∈Rm is divided from E and normalized, t<n. The NPE algorithm is performed in A to extract the embedding transformation matrix P.
3) The embedding feature matrix F=[F1,F2,…,Fd] is obtained as Eq.(12), and the trend value of each Fi is calculated using the Spearman correlation coefficient, 1<i<d. The useful embedding space Pb is selected according to the first-order difference method.
4) A is embedded into Pb to obtain the training feature dataset A′, and A′ is normalized. The SVDD model is constructed to obtain the center a and radius R of the hypersphere model. Then, radius R is set as the health threshold to monitor bearing early degradation.
(16)
3.2 Online monitoring
In the online monitoring process, the monitoring signal is input into the built model and converted into the degradation index to indicate the performance state of bearing.
1) Each monitoring signal f is decomposed by the VMD method. The features in Tab.1 are extracted and m-dimensional sample x is obtained.
2) The embedding feature y′ of sample x is obtained by embedding x into space Pb as Eqs.(14) and (15).
3) The distance between the monitor sample y′ and the center a of the SVDD is obtained.
4) The distance index is used as the degradation index of the rolling bearing performance evaluation process and the performance degradation curve is plotted.
4 Experimental Verification and Analysis
4.1 Experimental data description
In this paper, the experimental data of the bearing accelerated degradation test published by IEEE PHM2012 Challenge is used for analysis and verification. The experimental data comes from the PRONOSTIA test bench[19]. The structure distribution and sensor arrangement of the test bench are shown in Fig.2. The PRONOTSTIA test bench is designed to perform related tests such as abnormality detection, fault diagnosis and prediction of bearings. The main purpose of the test is to collect the experimental data of the bearing from the normal state to failure state.

Fig.2 PRONOSTIA test bench
The experimental system is driven by a motor, and the torque is transmitted to the rotating shaft through the reducer at a speed of 1 800 r/min. The experimental bearing is mounted on the rotating shaft, and the thermocouple is mounted on the outer ring of the bearing to monitor the bearing temperature in real time. The test bench applies 4 000 N radial load to the bearing through the hydraulic device. The vibration acceleration sensor is installed in the horizontal and vertical directions of the bearing. The sensor type is DYTRAN 3035B, and the vibration signal is collected by the NI acquisition card. The sampling frequency is 25.6 kHz. The sampling time lasts for 0.1 s and is repeated every 10 s.
4.2 Performance degradation evaluation
This section analyzes the full-life vibration data of a bearing numbered 1-3, and the parameters of this bearing is shown in Tab.2. The number of sampling points of the sensor is 2 560. A small number of samples during the initial running—in the period that the equipment is ignored, and 1 752 samples of bearing 1-3 are analyzed.
Tab.2 Parameters of bearing 1-3
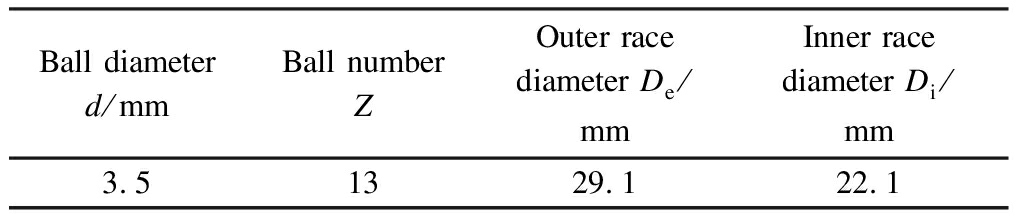
Ball diameter d/mmBall numberZOuter race diameter De/mmInner race diameter Di/mm3.51329.122.1
The RMS trend in the whole life of the bearing vibration signal is shown in Fig.3. The RMS is stable at the beginning and then increases with the degradation of the bearing performance. According to the 3σ principle, 1 220 samples were chosen for the embedding selection for the ESNPE method from bearing 1-3, in which the first 500 samples were divided into a normal sample set for this bearing.
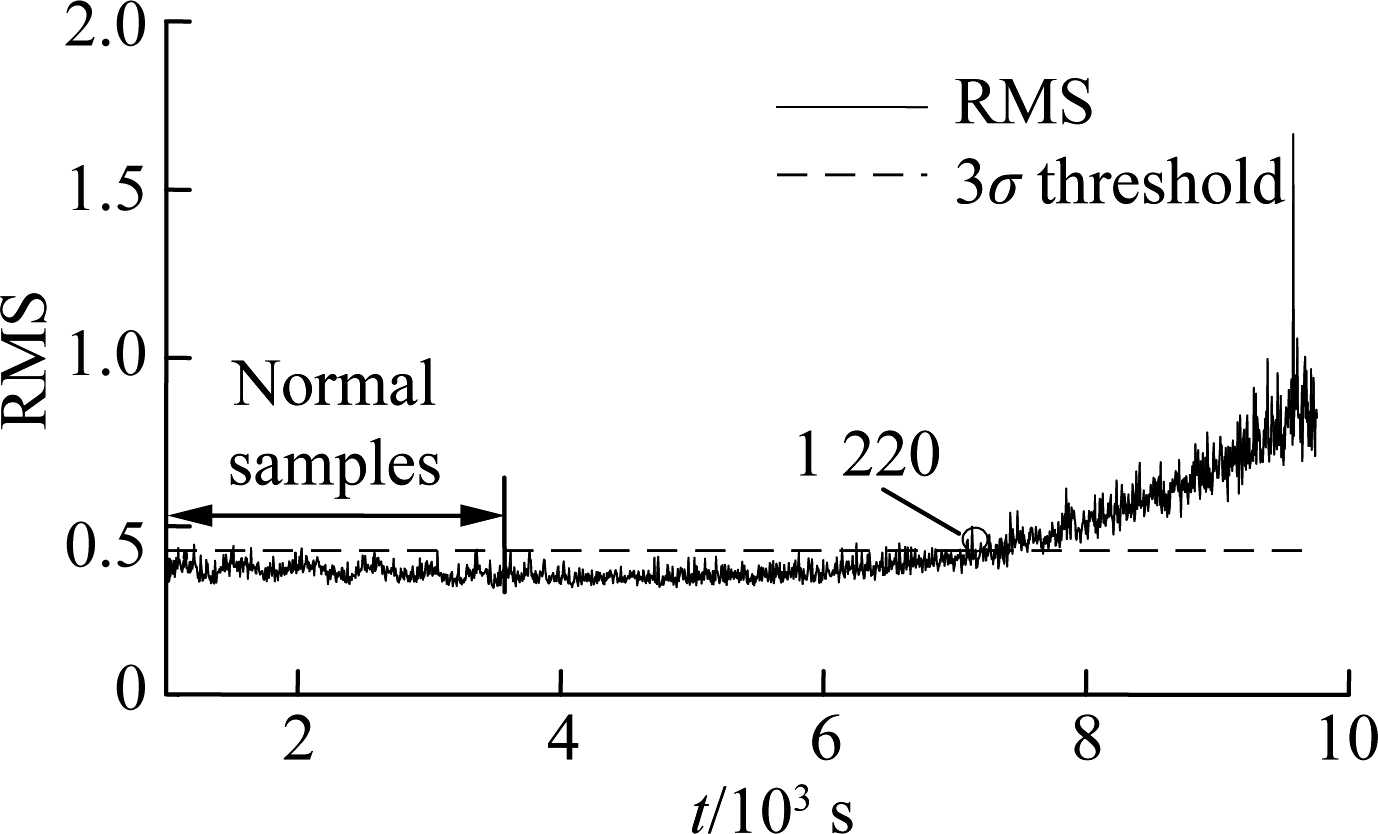
Fig.3 The whole life RMS trend of bearing 1-3
To determine the number of IMFs K for VMD decomposition, the maximum kurtosis method[20] is adopted in this paper. The signal at 15 000 s was selected and decomposed into different number of IMFs, and the result of the maximum kurtosis of each IMF is shown in Fig.4. It can be seen that the maximum kurtosis curve has reached its peak when K is set to be 5, and a similar conclusion could be drawn at other sample time. Thus, K=5 for VMD decomposition is appropriate for this bearing.
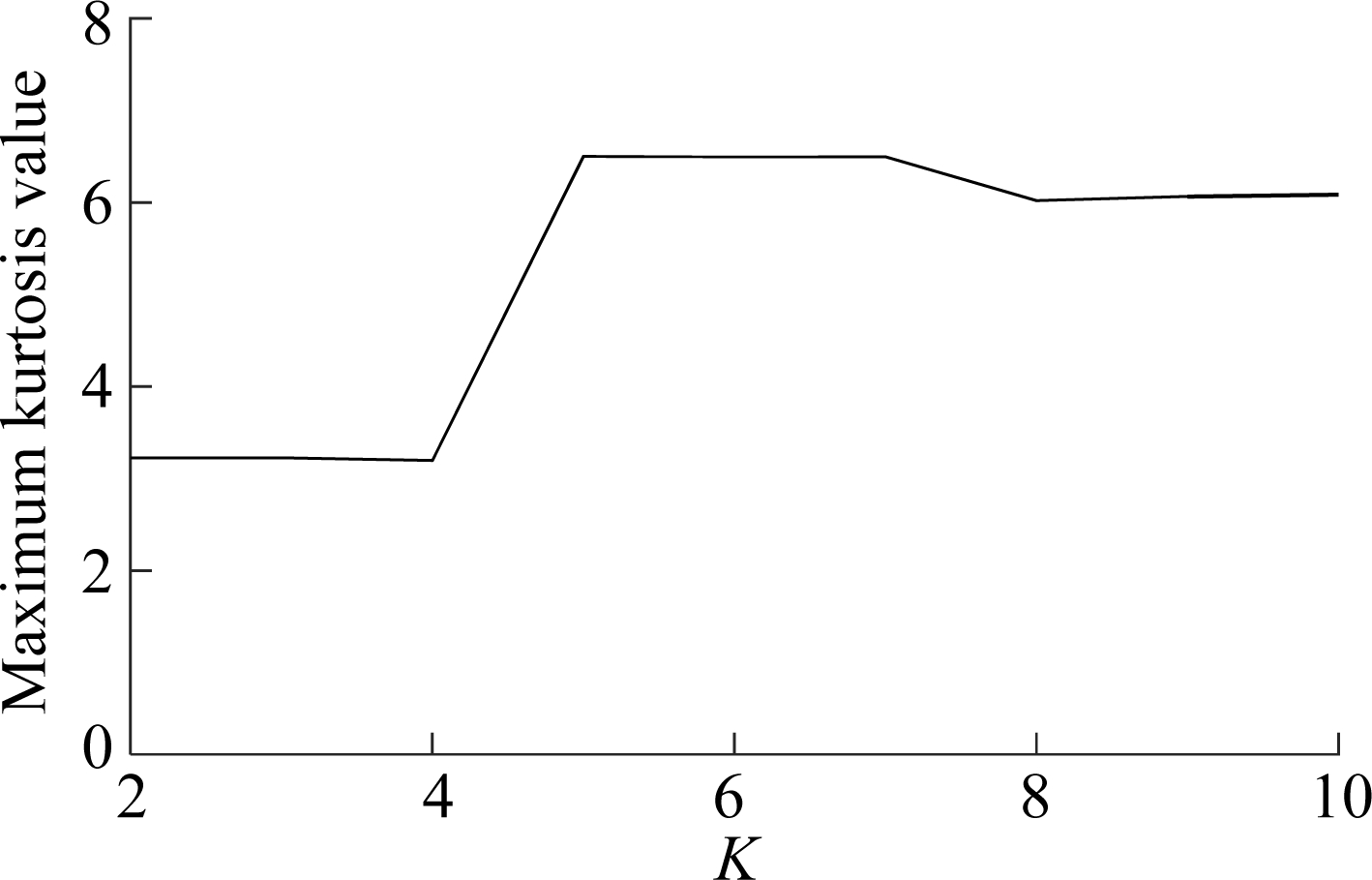
Fig.4 The relationship between the number of IMFs and the maximum kurtosis
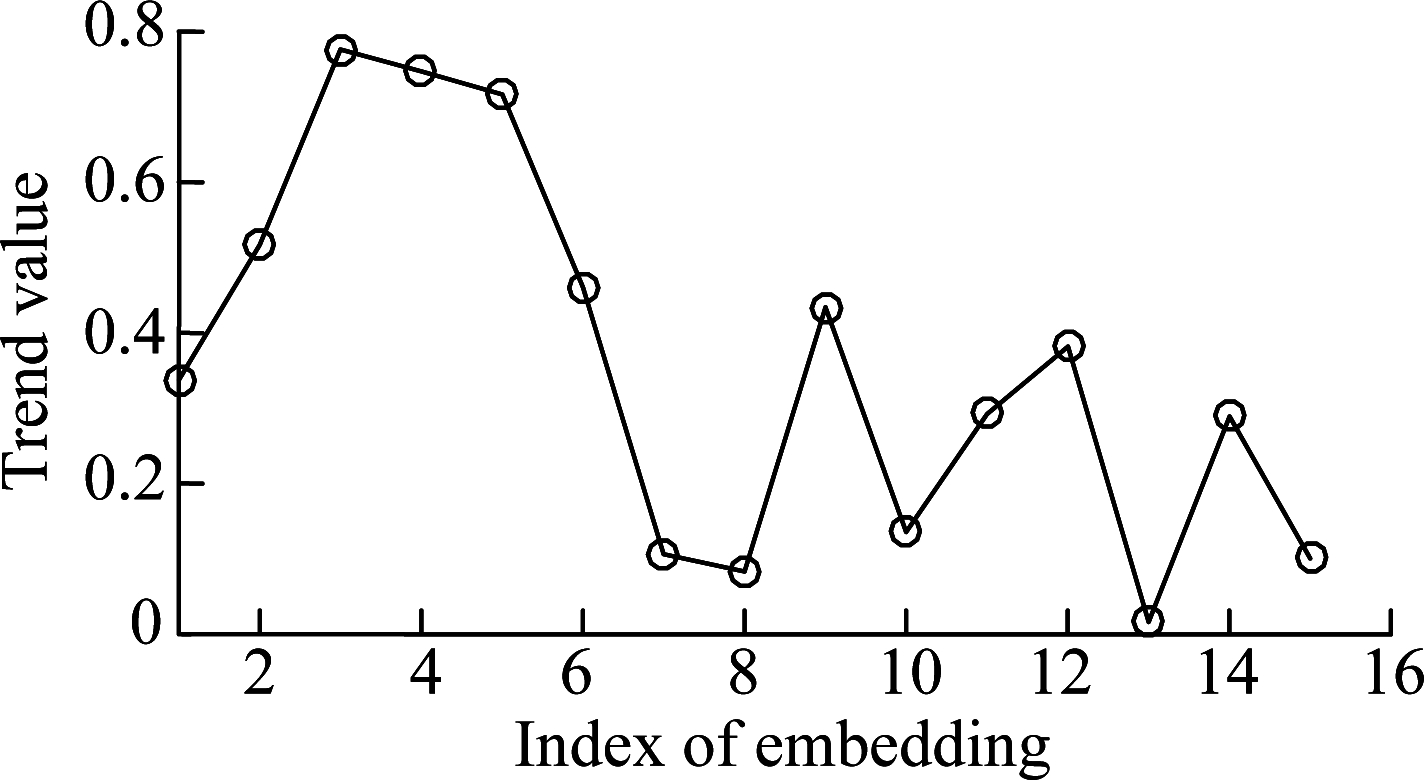
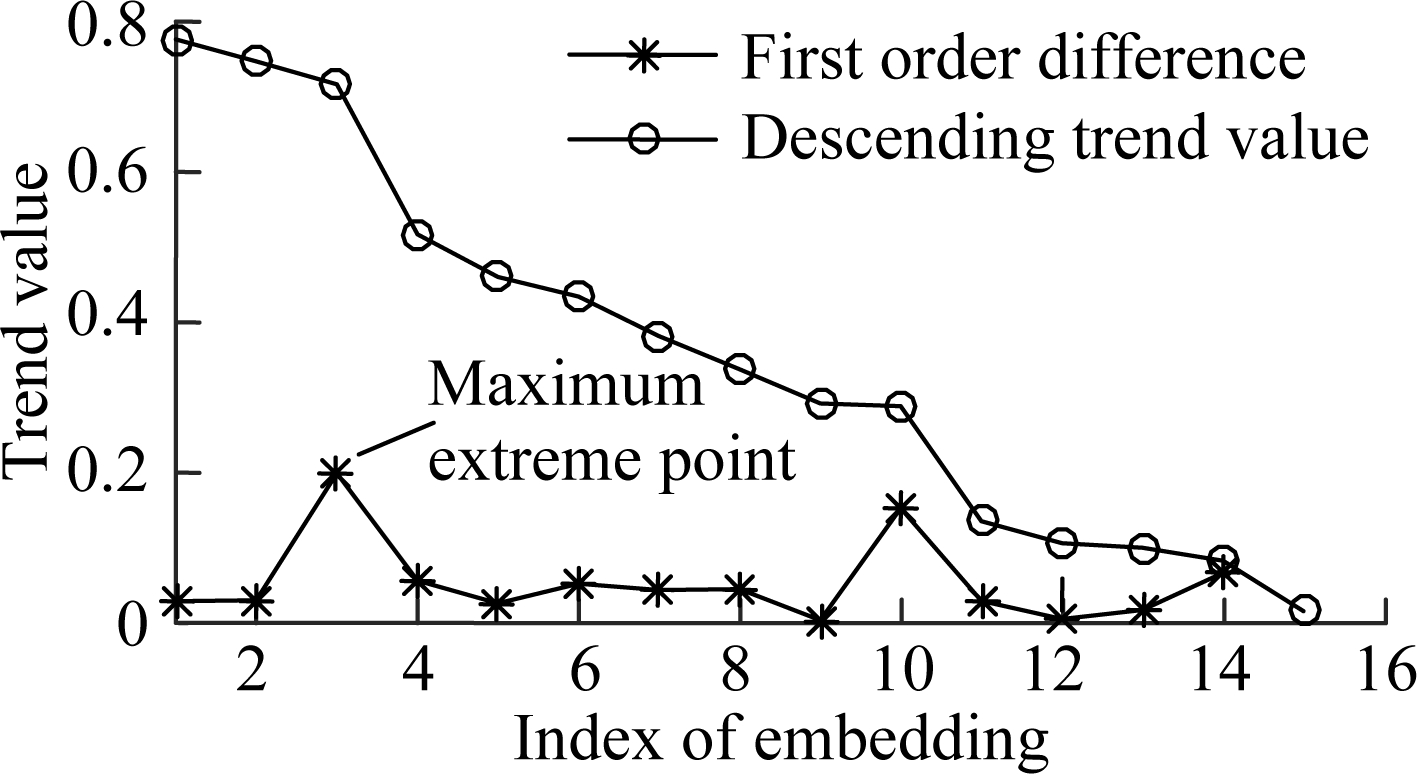
Therefore, 18 original features were extracted in Tab.1. The NPE algorithm was performed in normal dataset and the embedding feature matrix of 1 220 embedding selection samples was calculated. The trend value based on the Spearman correlation coefficient of each embedding feature is shown in Fig.5. It can be seen that the trend of each embedding feature in the early stage of the bearing is different. The maximum extreme point was selected in the first-order difference plot and the corresponding embedding space was preserved, where the useful embedding space of bearing 1-3 was Pb=[p3,p4,p5].
(a)
(b)
Fig.5 Trend values of embeddings and first-order difference plot. (a) Trend value for each embedding; (b)Descending trend value and first-order difference
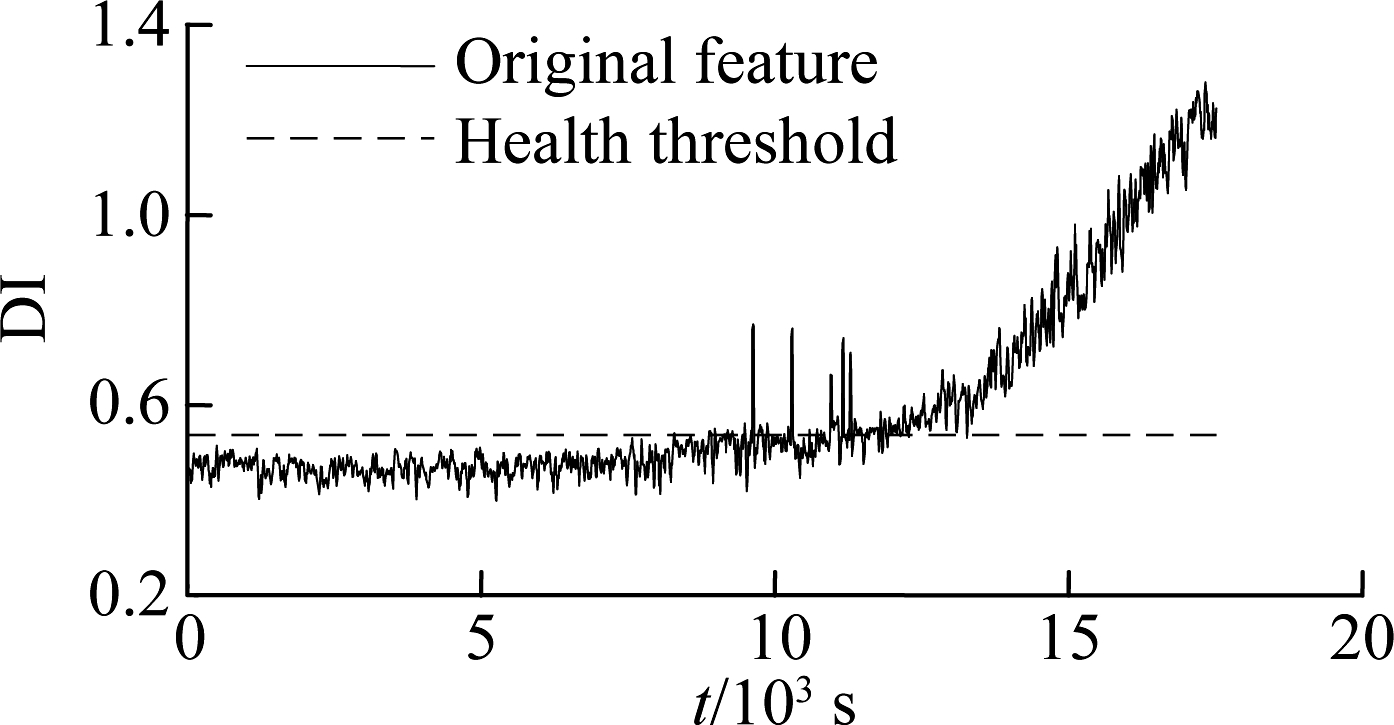
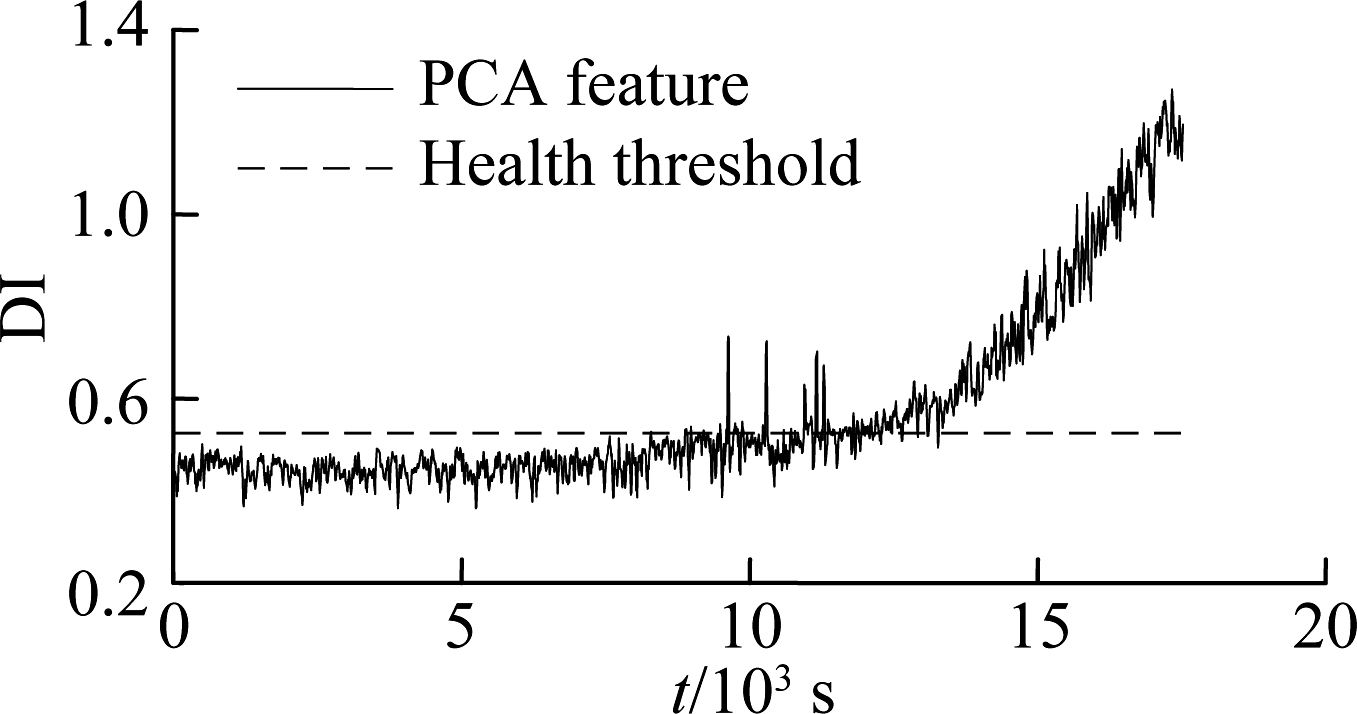
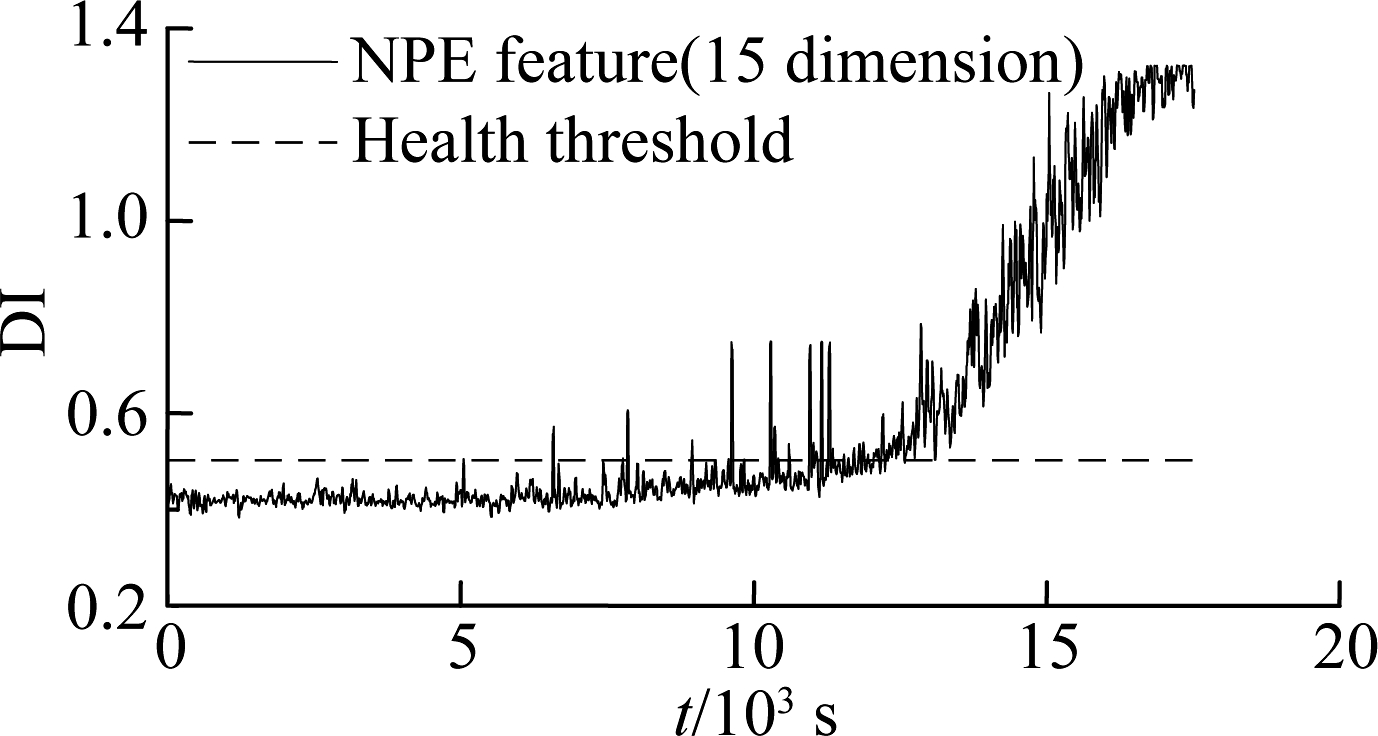
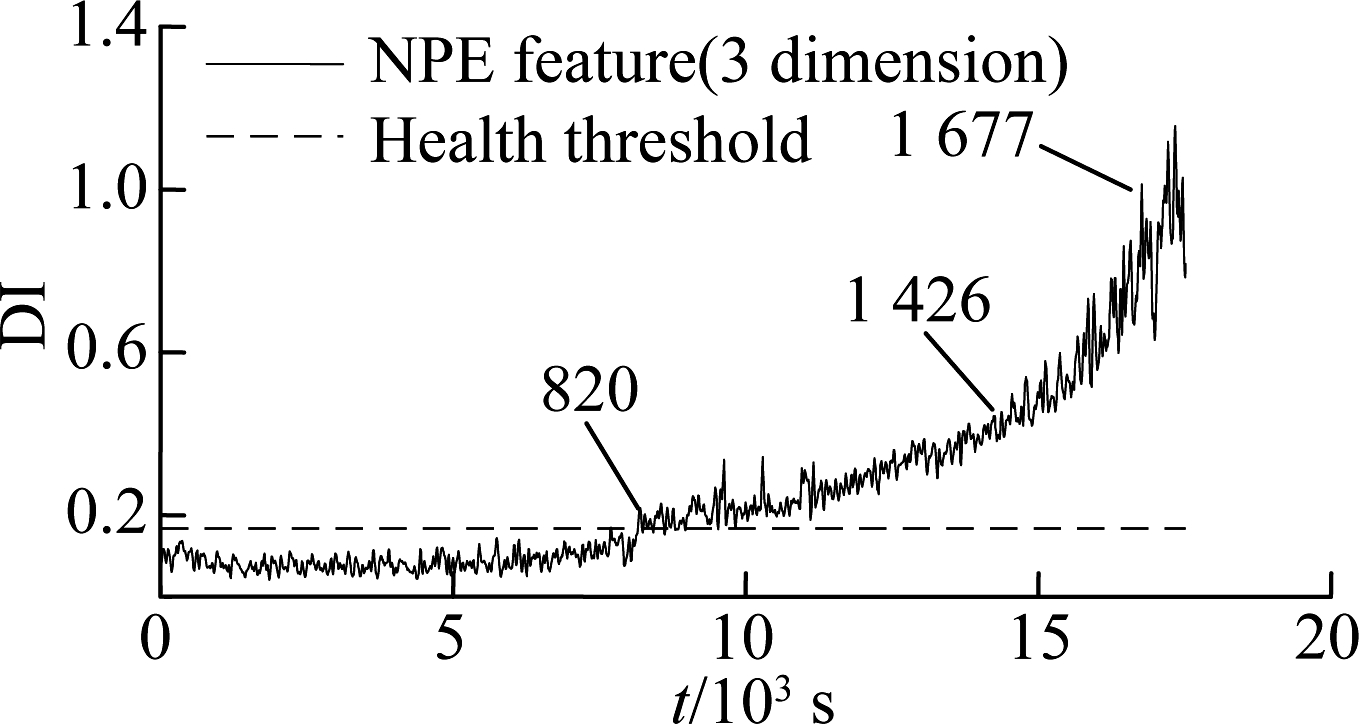
After the useful embedding space was specified, the embedding features of the normal sample set were used to construct the SVDD model after normalization. The distance between whole life samples and center a was calculated. The results are shown in Fig.6. For comparison, the distance index based on original features, the features obtained by the traditional PCA method and NPE features were also calculated, where the PCA method preserved a 85% contribution rate and the NPE method preserved 15 embeddings. The health threshold is the radius R of each constructed SVDD model.
(a)
(b)
(c)
(d)
Fig.6 Degradation index obtained by different methods. (a) Original feature; (b) PCA feature; (c) NPE feature; (d) ESNPE feature
Several conclusions can be drawn from the comparison of Fig.3 and Fig.6: 1) The distance index obtained by ESNPE features has the greatest incipient fault sensitivity and stability compared to the NPE method, PCA method and original features. There is an obvious rise at 8 200 s in Fig.6(d), which is much earlier than the RMS indicator in Fig.3. This demonstrates that the strategy preserving the useful manifold embedding information in ESNPE is effective. 2) The distance index obtained by original features has a more obvious trend than the RMS indicator, especially in the late stage of bearing degradation. This indicates that the VMD-based original features contain valid fault information, and can reflect bearing degradation to more extent.
In Fig.6(d), the distance index based on ESNPE features is stable and below the health threshold in the early stage before 8 200 s, which means a normal state of rolling bearing. It begins to show an obvious increase in 8 200 s corresponding to the initial material damage of the bearing, and monotonically increases nonlinearly with the crack propagation in the following running process. The index reaches the maximum in the final, which means the severe degradation.Therefore, the distance index based on the VMD and the ESNPE method proposed in this paper can describe the process of bearing performance degradation effectively.
4.3 Evaluation results verification
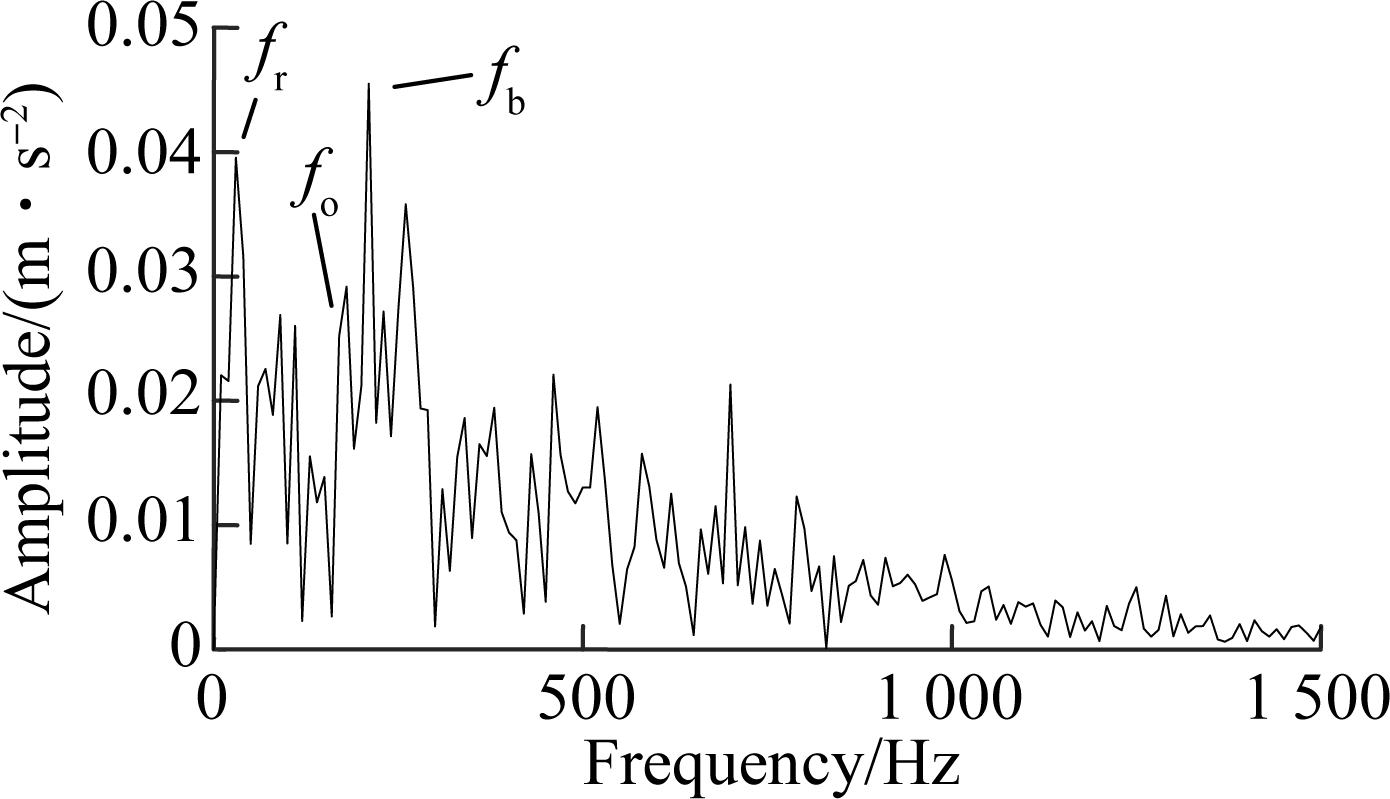
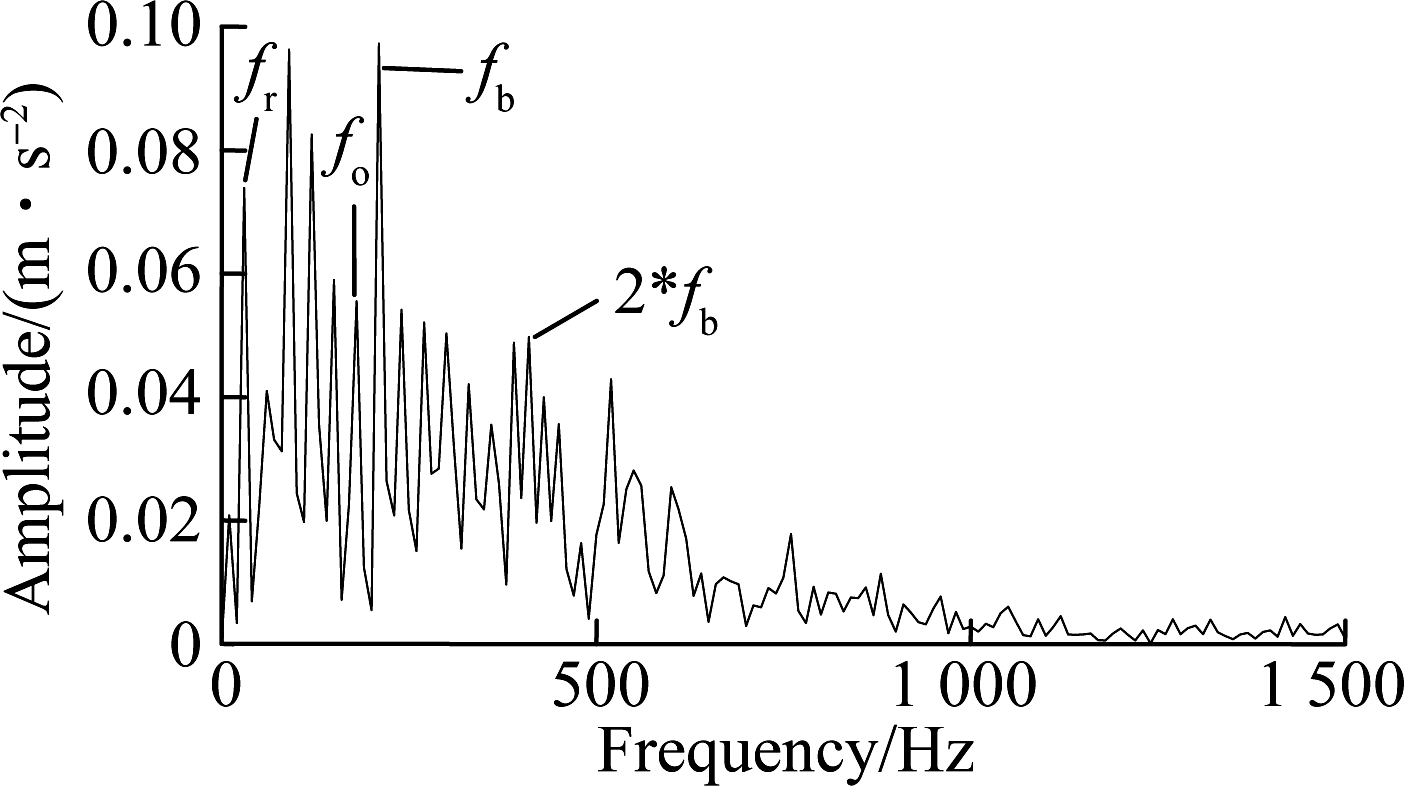
In order to prove the fault sensitivity capability of the proposed ESNPE method, the 8 200 s,14 260 s and 16 770 s samples of bearing 1-3 in Fig.6 are analyzed, as these samples are corresponding to the incipient fault,medium fault and severe fault of the bearing. The characteristic frequencies of bearing 1-3 are shown in Tab.3.
Tab.3 Characteristic frequencies of bearing 1-3 Hz
frfcfbfifo3013215222168
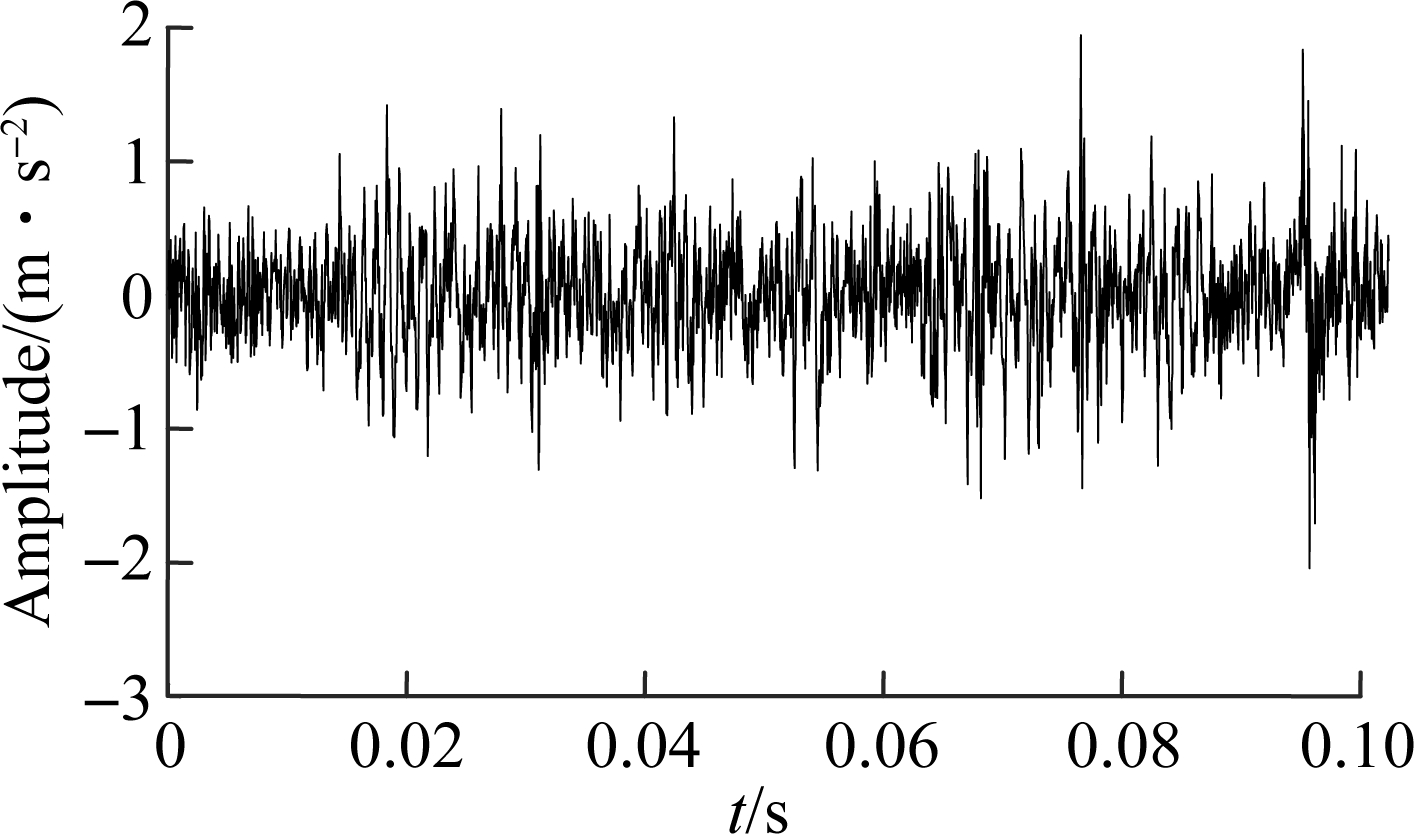
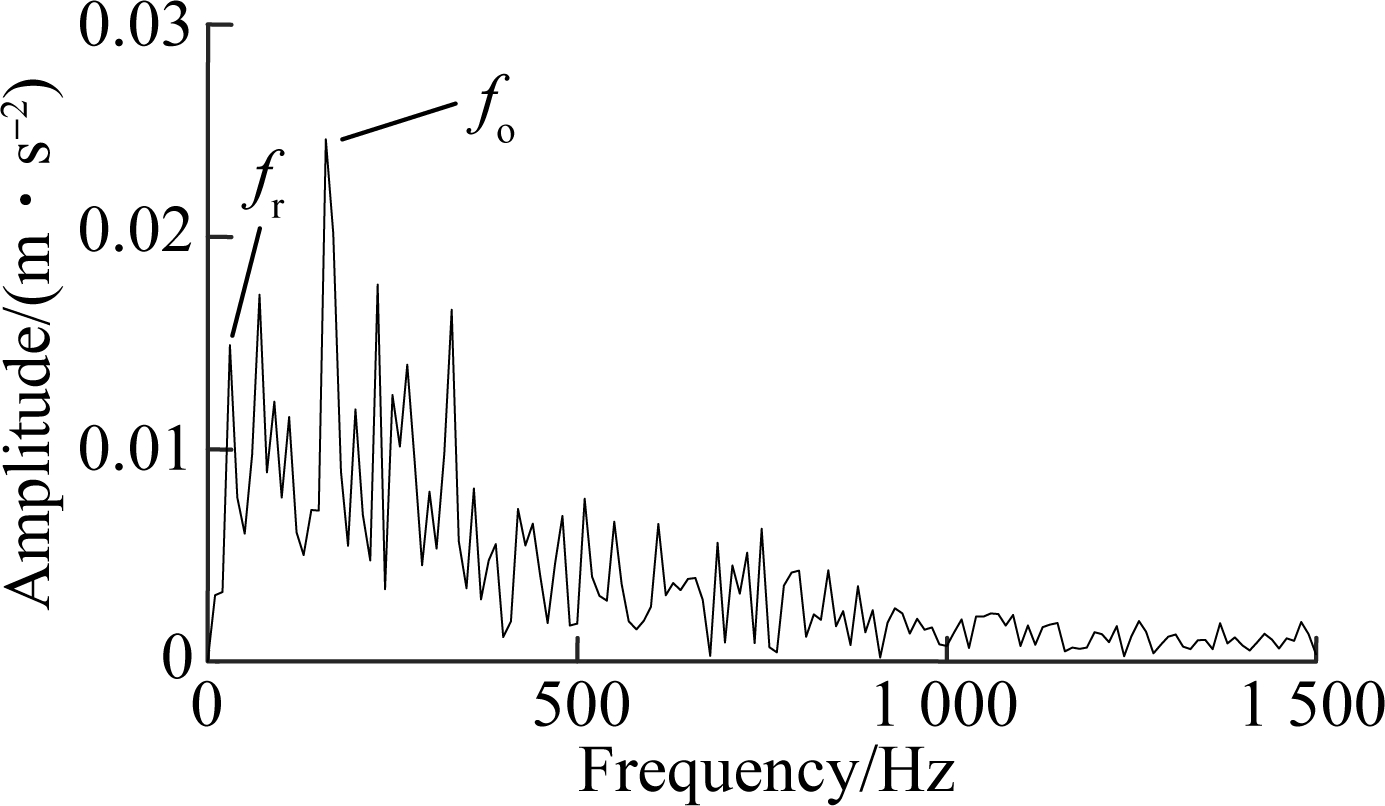
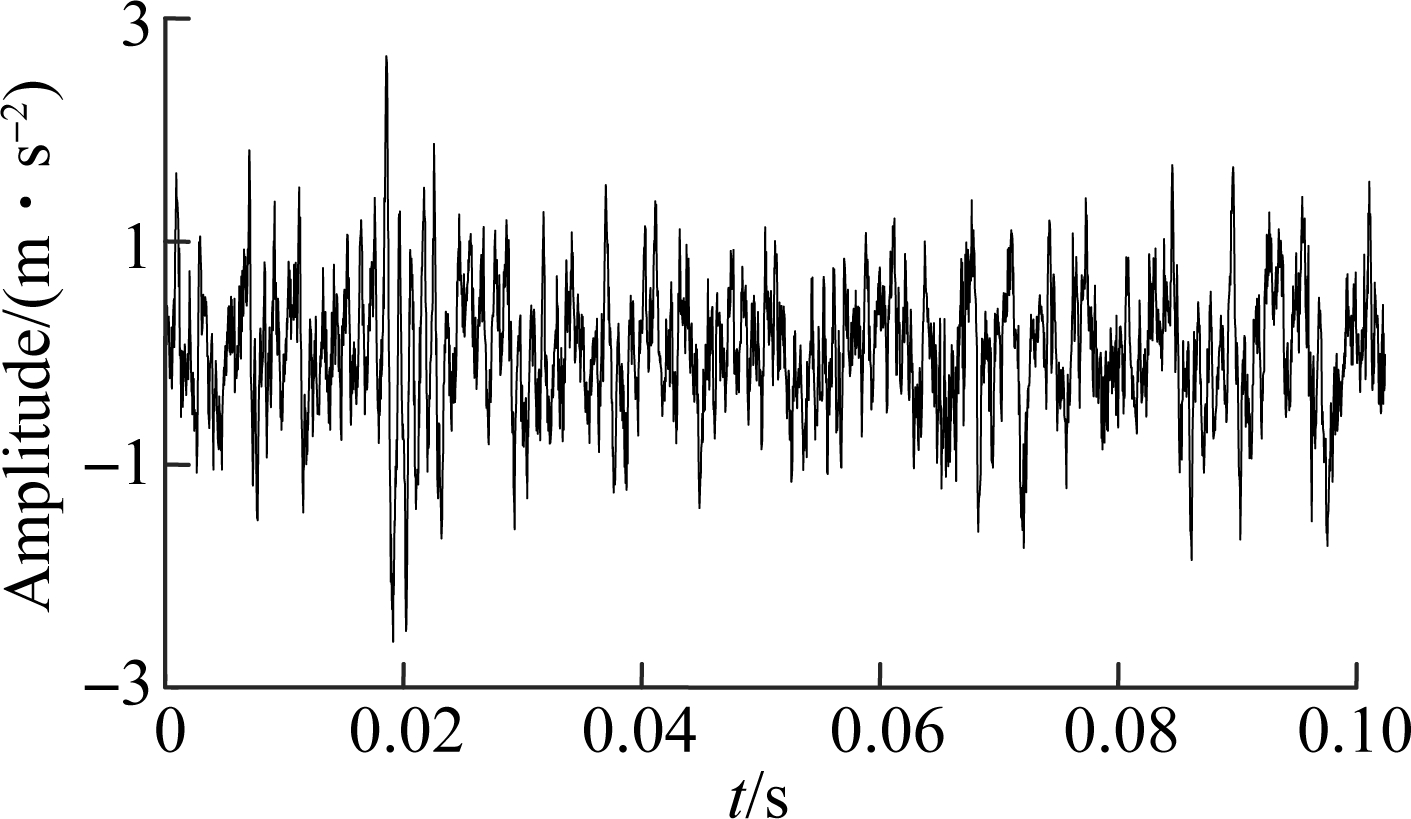
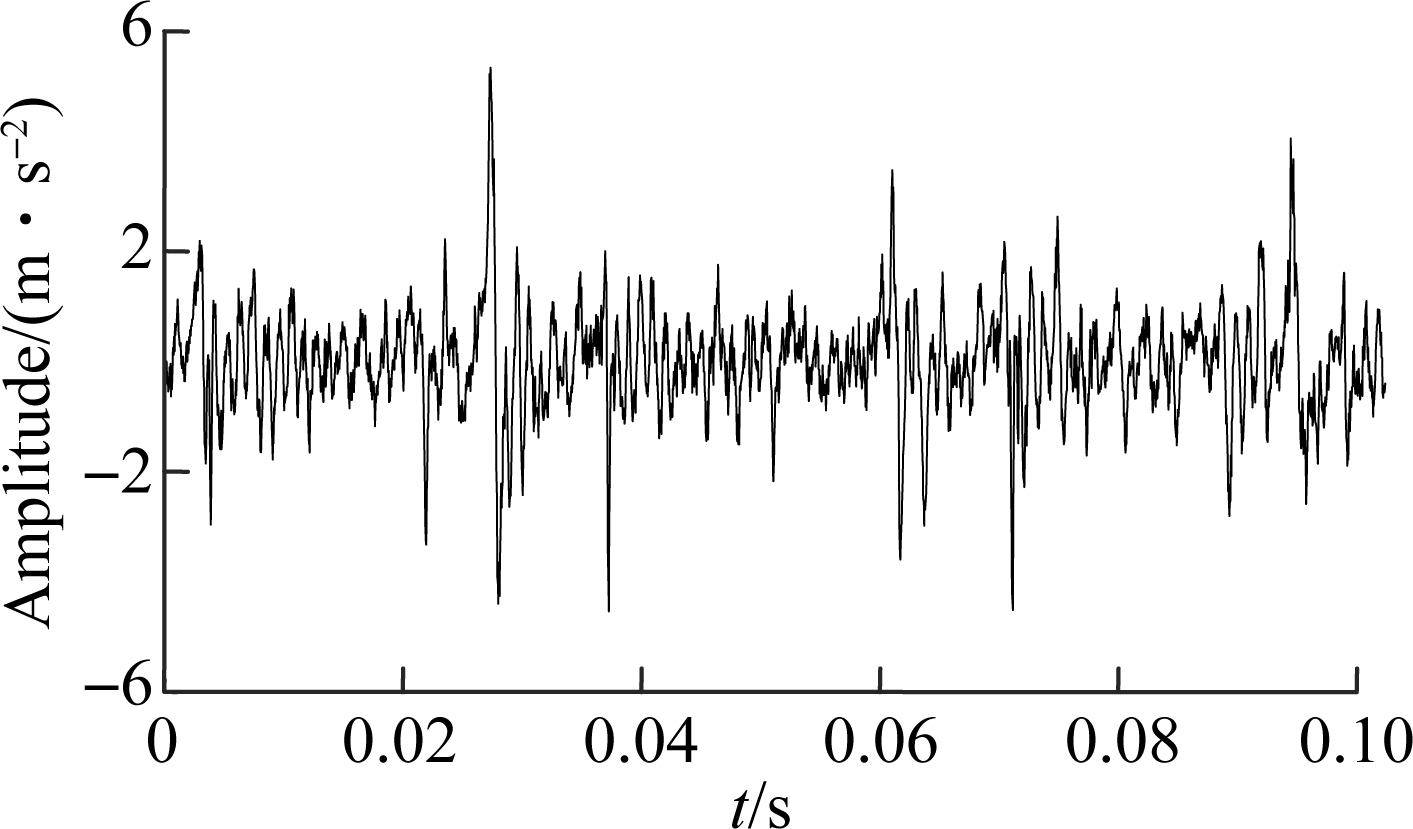
The three signals are decomposed by VMD. The fault sensitive IMF which has the maximum kurtosis is chosen and the IMF envelop spectra are presented in Figs.7 to 9. It can be found from Fig.7 that there is an obvious shock in 170 Hz, which is supposed that the early degradation has occured at 8 200 s. In Fig.8, there is a higher impactamplitude in 215 Hz which can be judged to be the medium degradation. The degradation becomes severe in Fig.9 since the characteristic frequency is more obvious. Therefore, the degradation process evaluation effectiveness of the proposed method is verified.
(a)
(b)
Fig.7 Analysis of 82 00 s vibration data. (a) Time domain;(b) Envelop spectrum
(a)
(b)
Fig.8 Analysis of 14 260 s vibration data. (a) Time domain;(b) Envelop spectrum
(a)
(b)
Fig.9 Analysis of 16 770 s vibration data. (a) Time domain;(b) Envelop spectrum
5 Conclusions
1) Features such as singular values and relative energies extracted by VMD contain the valid fault information of the rolling bearing. The distance index fused by the features performs better than traditional RMS indicator for rolling bearing performance evaluating process.
2) The ESNPE method proposed in this paper overcomes the useful embeddings suppression issue of NPE. The degradation index based on the ESNPE features shows better incipient fault sensitivity and stability than the NPE method, PCA method and original features. This indicates that using the Spearman correlation coefficient to select the useful embeddings of NPE in the early degradation stage is effective. The embedding selection strategy can also be introduced to some other manifold learning algorithms, such as GLSA and LPP to further improve monitoring performance.
3) The distance index fused by SVDD based on VMD and the ESNPE method can effectively describe the performance degradation process of the rolling bearing. Simultaneously, the evaluation result was verified by the VMD and envelop spectrum analysis, which is of positive significance for the intelligent maintenance of rolling bearing.
[1]Yang Z B, Jia M P. GA-1DLCNN method and its application in bearing fault diagnosis[J]. Journal of Southeast University(English Edition), 2019, 35(1): 36-42.
[2]She D M, Jia M P, Zhang W. Deep auto-encoder network method for health assessment of rolling bearings[J]. Journal of Southeast University(Natural Science Edition), 2018, 48(5): 801-806.(in Chinese)
[3]Boškoski P, Gašperin M, Petelin D, et al. Bearing fault prognostics using Rényi entropy based features and Gaussian process models[J].Mechanical Systems and Signal Processing, 2015, 52—53: 327-337. DOI:10.1016/j.ymssp.2014.07.011.
[4]Rai A, Upadhyay S H. An integrated approach to bearing prognostics based on EEMD-multi feature extraction, Gaussian mixture models and Jensen-Rényi divergence[J].Applied Soft Computing, 2018, 71: 36-50. DOI:10.1016/j.asoc.2018.06.038.
[5]Jia X D, Jin C, Buzza M, et al. A deviation based assessment methodology for multiple machine health patterns classification and fault detection[J].Mechanical Systems and Signal Processing, 2018, 99: 244-261. DOI:10.1016/j.ymssp.2017.06.015.
[6]Wang F T, Chen X T, Yan D W, et al. Fuzzy C-means using manifold learning and its application to rolling bearing performance degradation assessment[J]. Journal of Mechanical Engineering, 2016, 52(15): 59-64. DOI:10.3901/JME.2016.15.059.(in Chinese)
[7]Widodo A, Yang B S. Application of relevance vector machine and survival probability to machine degradation assessment[J].Expert Systems With Applications, 2011, 38(3): 2592-2599. DOI:10.1016/j.eswa.2010.08.049.
[8]Lu C, Yuan T, Tang Y N. Bearing performance degradation assessment and prediction based on EMD and PCA-SOM [J]. Journal of Vibroengineering, 2014, 16(3) : 1387-1396.
[9]Liao L X, Lee J. A novel method for machine performance degradation assessment based on fixed cycle features test[J].Journal of Sound and Vibration, 2009, 326(3/4/5): 894-908. DOI:10.1016/j.jsv.2009.05.005.
[10]Dragomiretskiy K, Zosso D. Variational mode decomposition[J].IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/tsp.2013.2288675.
[11]Li Z P, Chen J L, Zi Y Y, et al. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive[J].Mechanical Systems and Signal Processing, 2017, 85: 512-529. DOI:10.1016/j.ymssp.2016.08.042.
[12]Zhang M, Jiang Z N, Feng K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump[J].Mechanical Systems and Signal Processing, 2017, 93: 460-493. DOI:10.1016/j.ymssp.2017.02.013.
[13]He X, Cai D, Yan S, et al. Neighborhood preserving embedding[C]//Tenth IEEE International Conference on Computer Vision (ICCV′05). Beijing, China, 2005:1-6. DOI:10.1109/iccv.2005.167.
[14]Miao A M, Ge Z Q, Song Z H, et al. Time neighborhood preserving embedding model and its application for fault detection[J].Industrial & Engineering Chemistry Research, 2013, 52(38): 13717-13729. DOI:10.1021/ie400854f.
[15]Miao A M, Song Z H, Wen Q J, et al. Process monitoring based on generalized orthogonal neighborhood preserving embedding[J].IFAC Proceedings Volumes, 2012, 45(15): 148-153. DOI:10.3182/20120710-4-sg-2026.00097.
[16]Golafshan R, Yuce Sanliturk K. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults[J].Mechanical Systems and Signal Processing, 2016, 70-71: 36-50. DOI:10.1016/j.ymssp.2015.08.012.
[17]Su L M, He H S. Multi-attribute decision making method based on interval number of Spearman rank correlation coefficient [J]. Statistics and Decision, 2019, 6: 51-53. (in Chinese)
[18]Liu Y, Chen J, Pan Y N, Equipment performance degradation assessment based on SVDD and information fusion technology [J]. Vibration and Shock, 2009,28: 21-24.(in Chinese)
[19]Nectoux P, Gouriveau R, Medjaher K, et al. PRONOSTIA: An experimental platform for bearings accelerated life test [C]// IEEE International Conference on Prognostics and Health Management. Colorado, USA, 2012: 1-8.
[20]Li H, Wu X, Liu T, et al. Variational modal decomposition and improved adaptive resonance techniques in application of bearing fault feature extraction [J]. Vibration and Shock, 2018,31(4):719-725.(in Chinese)