Over the past years, digital images have played a major role in communication through the internet and other broadcast media. Moreover, digital images are one of the most important evidences for criminal investigations in courts. Unfortunately, with the rapid development of sophisticated multimedia processing technology, digital images can be tampered easily with invisible traces. Due to this fact, many researchers have begun to deal with the problem of digital image forgery. Copy-move forgery constitutes one of the most preliminary types of digital image forgeries, where regions of an image are cut and pasted onto some other locations within the same image[1].
In recent years,passive forensics approaches have been extensively and successfully used in copy-move forgery detection[2]. They detect traces of tampering without using prior information, while active approaches need to embed information into a source image. Passive approaches usually consist of four main steps[3]: 1) Pre-processing. Some pre-processing operations, such as low pass filtering, color conversion, image resizing, subdivision, and key-points extraction, etc., are very necessary; 2) Feature extraction. The suitable features are extracted from the overlapping or non-overlapping blocks for block-based approach, and obtained from the neighborhood of each key-point for key-points-based approach; 3) Feature matching. The potential copy-move pairs are detected by searching image pixels or patches with similar features; 4)Post-processing. False alarms are removed and the missing regions are restored. Moreover, the copy-move regions are highlighted.
Feature extraction is one of the most important steps in copy-move forgery detection. So, many works have been proposed for extracting suitable features. These features can be grouped in two categories: spatial-based features and transform-based ones. The spatial-based features include the red, green and blue components[4], histogram of orientated gradients[5], and the multi-level dense descriptor[6]. The transform domain-based features can be categorized as frequency-based, moment-based, and dimensionality reduction-based. Frequency-based features include discrete Cosine transform[1], discrete wavelet transform[7], Fourier-Mellin transform[8], and polar Cosine transform[9]. Moment-based features include the Zernike moment[10-11], Tchebichef moment[12], and polar complex exponential moment[13]. Dimensionality reduction-based features include singular value composition[14] and principal component analysis[15]. The spatial-based features usually have less computational complexity and perform better in a plain case than the transform-based features, while the transform-based features are usually more robust to some additional operations than the spatial-based features. So, in order to take the advantage of both the spatial-based features and the transform-based ones, some researchers use fractional transforms to extract the features of the region of interest[16-19]. Mathematically, fractional transforms can be regarded as a rotation of signals in the time (or space)-frequency plane, and, therefore, have attracted much attention[16]. Moreover, all the spatial-based features and transform-based features mentioned before are extracted from the graying versions of color forged images or from three color channels independently. As a result, they ignore the importance of color information or the correlation between color channels and the entirety of the three channels[18-20]. So, the quaternion-based method[18-20], where the three channels of color image are encoded into the imaginary parts of the quaternion representation (QR), is also used to process color forged images efficiently. Finally, the fractional quaternion-based feature, i.e., fractional quaternion Zernike moments (FrQZMs), is considered in this paper.
Besides feature extraction, feature matching also plays an important role. Exhaustive search is the simplest and most straightforward algorithm to find the best matching feature, but it has extremely high complexity. Therefore, some researchers have paid much more attention to finding an effective feature matching algorithm. Approximate nearest-neighbor search strategy[3-4,8,10-11] becomes a good solution to this problem. In Ref.[8], simple lexicographic sorting is used to speed-up feature matching, but it is very sensitive to noise. In addition, some sophisticated fast search algorithms, such as kd-tree search[3] and locality sensitive hashing (LSH)[11], are considered to improve the robustness. However, these algorithms are still too slow when computing the nearest-neighbor field for the large images generated by today’s cameras. A much better result can be achieved by the PatchMatch algorithm in Ref.[10]. Bi et al.[4] improved the PatchMatch algorithm by considering the priority-based matching based on the reflective offset priority and the position priority. Nonetheless, the PatchMatch algorithm[4,10] is still affected significantly by its random initialization. When random initialization is not well, many iterations are needed and some mismatching arises. So, the approximate nearest neighbor field obtained by the reliable order-statistics-based approximate nearest neighbor search algorithm (ROSANNA) is used to improve the random initialization in the PatchMatch algorithm.
1 Some Preliminaries
In this section, we recall some quaternion color representation, FrQZMs and ROSANNA.
1.1 Quaternion number and quaternion color representation
Quaternions are the generalizations of complex numbers. A quaternion has one real part and three imaginary parts given as
q=a+bi+cj+dk
(1)
where a, b, c, d R, and i, j, k are three imaginary units obeying the following rules
R, and i, j, k are three imaginary units obeying the following rules
i2=j2=k2=-1, ij=-ji=k
jk=-kj=i, ki=-ik=j
(2)
If the real part a= 0, q is called a pure quaternion.
Let f(r, θ) be an RGB image defined in polar coordinates, and each pixel can be represented as a pure quaternion by the quaternion representation
f(r,θ)=fR(r,θ)i+fG(r,θ)j+fB(r,θ)k
(3)
where fR(r, θ), fG(r, θ) and fB(r, θ) are respectively the red, green and blue components of the pixel (x, y).
1.2 Fractional quaternion Zernike moments
Let f(r, θ) be an RGB image represented by Eq.(3), and the right-side FrQZMs is introduced as
(4)
where α is the fractional parameter, α  R+; n and m are the order and the repetition, respectively, satisfying the condition that |m|≤n and n-|m| are even; μ is a unit pure quaternion such as μ =ai+bj+ck, a, b, c
R+; n and m are the order and the repetition, respectively, satisfying the condition that |m|≤n and n-|m| are even; μ is a unit pure quaternion such as μ =ai+bj+ck, a, b, c R,
R, ![]() Rαn,m(r) is the real-valued radial polynomial given as
Rαn,m(r) is the real-valued radial polynomial given as
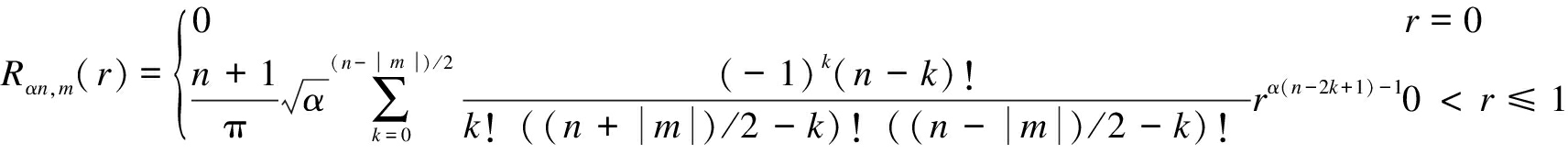
(5)
For a digital RGB image f(x,y) of size N×N, the right-side discrete DFrQZMs can be written as
(6)
where rx,y and θx,y are given as
(7)
1.3 ROSANNA
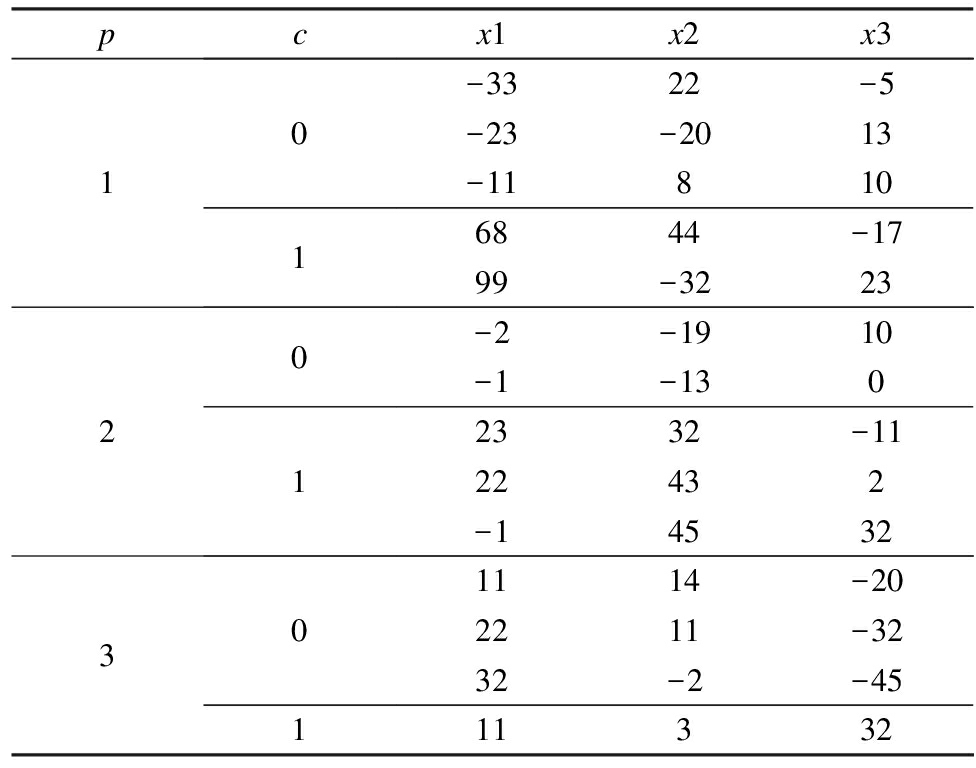
The ROSANNA algorithm first proposed by Verdoliva et al.[21] is a fast approximate nearest neighbor search algorithm based on the properties of ordered vectors. It is used to search the approximate nearest neighbor field for some applications, such as image retrieval, and feature matching. In order to speed up the search, ROSANNA first divides the search space into some small subspaces and then processes the search in subspaces. Moreover, Verdoliva et al.[21] present a new method to ensure that the space partitions effectively. This new method is based on the index and the sign of the largest components. Tab.1 shows an example of space partition for fourteen 3D data (x1, x2, x3).
Tab.1 An example of space partition for fourteen 3D data
pcx1x2x3101-3322-5-23-2013-118106844-1799-3223201-2-1910-1-1302332-1122432-145323011114-202211-3232-2-4511332
In Tab.1, the fourteen 3D data are first classified into three classes (p=1, 2, 3) according to the position of the largest components. Then, each class is further divided into two subclasses; i.e., c=1 for the positive values, and c=0 for the negative values. Finally, the fourteen data are divided into six subspaces according to p and c. Experimental results in Ref.[21] show that ROSANNA works very well for both unstructured data and real-world structured data.
2 Proposed Copy-Move Forgery Detection Algorithm
This section describes the proposed algorithm in detail. Fig.1 shows the framework of the proposed algorithm.
The proposed algorithm also includes four stages: the pre-processing stage, feature extraction stage, feature matching, and post-processing. In the feature extraction stage, FrQZMs features are extracted from the overlapping blocks. The reason of using FrQZMs feature is that FrQZMs has the following advantages:1) FrQZMs uses the QR to process color images and the main advantage of the QR lies in that a color image can be treated holistically as a vector field; 2) FrQZMs can utilize the advantages of both the transform-based features and spatial-based features; 3) FrQZMs uses all the four components of each FrQZM coefficient to consider the magnitude information as well as the phase information. In the feature matching stage, the potential copy-move block pairs with the same or similar features are identified by the matching algorithm. In this paper, the improved PatchMatch algorithm and the ROSANNA algorithm are combined for effective feature matching. The improved PatchMatch algorithm used in Refs.[4,19] considers the priority-based matching based on the reflective offset priority and the position priority. The improved PatchMatch has demonstrated better performance than most of the current matching algorithms, such as the kd-tree algorithm[3], the locality sensitive hashing algorithm[11] and the original PatchMatch algorithm[22]. However, as described in subsection 1.3, the random initialization in the improved PatchMatch algorithm affects the performance of PatchMatch significantly; moreover, the ROSANNA algorithm is used to search the approximate nearest neighbor field for feature pre-matching, thus the probability of obtaining the optimal matching patch from the ROSANNA algorithm is usually higher than that from the random algorithm. So, in this paper, the approximate nearest neighbor field obtained by ROSANNA is used to improve the random initialization in the PatchMatch algorithm.
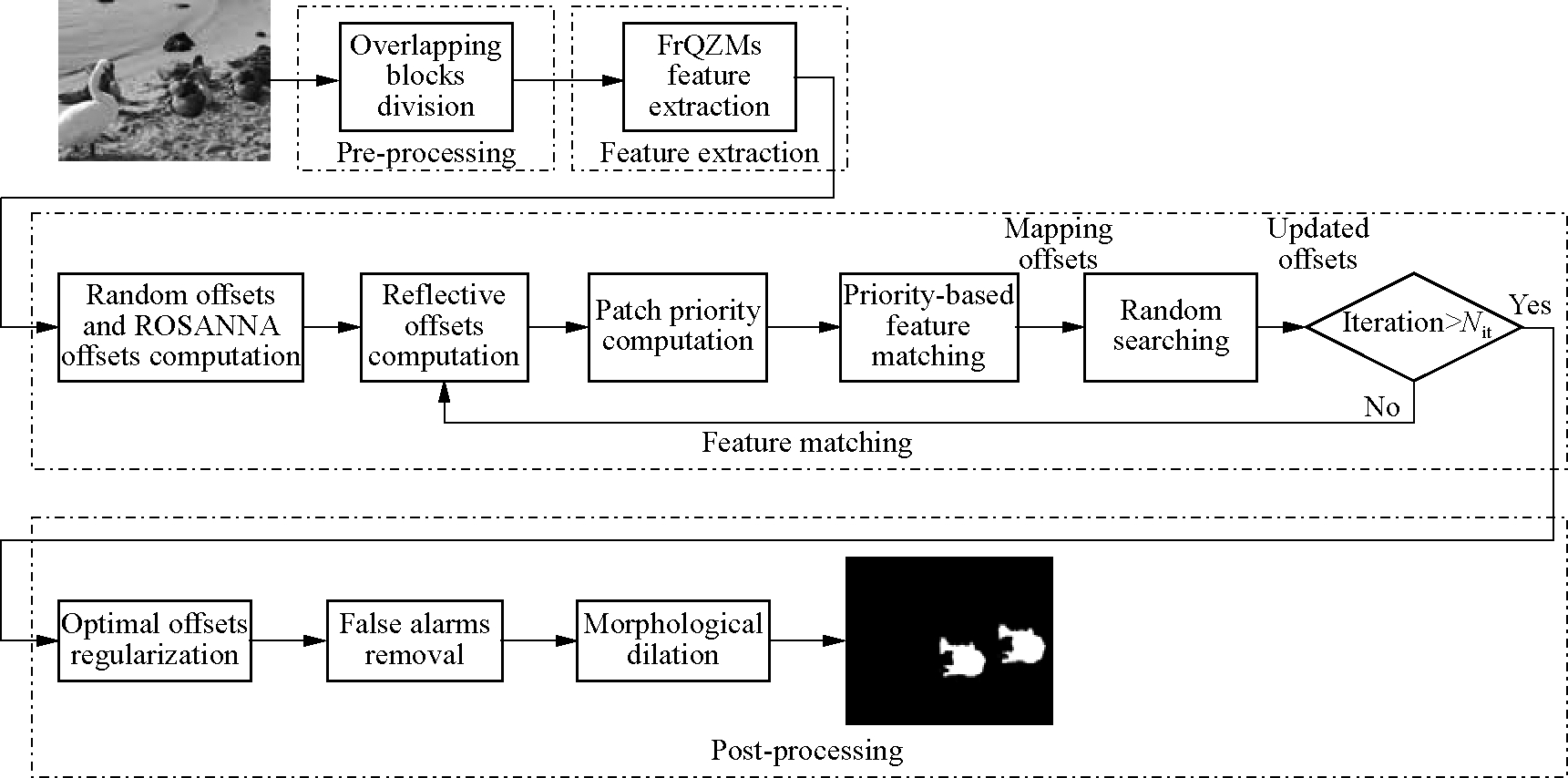
Fig.1 The framework of the proposed copy-move forgery detection algorithm
The detailed steps are summarized as follows.
1) Overlapping patches division. In order to achieve pixel-level accuracy, the forged image is divided into numbers of overlapping patches with a step of 1 pixel, and each block is then represented by a pure quaternion matrix using the QR shown in Eq.(3). Moreover, in order to make the proposed algorithm robust to scaling and rotation distortion, a multi-scale strategy is considered here by dividing the forged image into two overlapping circular patches with the size of radius 4 and 8 pixels for each position.
2) FrQZMs feature extraction. The FrQZMs feature up to the 5th order is computed for each circle patch.
3) Random offsets and ROSANNA offsets computation: Each patch is assigned by random mapping offsets and ROSANNA offsets. The random mapping offsets are obtained from independent uniform samples across the full image, while the ROANAAN offsets are derived from the approximate nearest neighbor field by the ROSANNA algorithm.
4) Reflective offsets computation. For each patch, two types of reflective offsets are calculated from random offsets and ROSANNA offsets: random reflective offset RORandom and ROSANNA reflective offset ROROSANNA. Taking ROROSANNA as an example, suppose that Pj(xj, yj) and Pk(xk, yk) are the corresponding patches for Pi(xi, yi) and Pj(xj, yj), respectively, according to their corresponding ROSANNA offset MO(Pi)=(xj, yj)-(xi, yi) and MO(Pj)=(xk, yk)-(xj, yj). The reflective offset of a target patch Pi according to the ROSANNA offset can be achieved by the following equation:
ROROSANNA(Pi) = MO(Pi)+ MO(Pj)
(8)
The reflective offset RORandom(Pi) according to random offset for the patch Pi can be obtained using a similar way.
5) Patch priority computation: For each target patch Pi, two types of candidate patches to be matched for Pi are found and their priorities are then calculated. As for the two types of candidate patches, the first type Candsi,I are obtained by the random offsets of the patches in the neighborhood of Pi, while the second type Candsi,II is obtained by the ROSANNA offset of Pi itself.
The priorities of Candsi,I are determined by the patches Neighi,I in the neighborhood of Pi, which is used to find Candsi,I. In detail, they are determined by the random reflective offsets and the positions of the corresponding patches Neighi,I according to the following equation:
Pr(Candsi,I)=Pr(RORandom(Neighi,I))+Pr(Position(Neighi,I))
(9)
where
(10)

(11)
where dist(Pi, Neighi,I) represents the physical Euclidean distance between the target patch Pi and each patch Neighi,I in the neighborhood of Pi.
The priorities of Candsi,II are decided by the random ROSANNA offset and the position of Pi according to the following equation:
Pr(Candsi,II)=Pr(ROROSANNA(Pi))+Pr(Position(Pi))
(12)
where Pr(Position(Pi)) = 1.
(13)
where the objective of setting Pr(Position(Pi)) to 1 is that, the candidate patches Candsi,II can have higher priorities than the candidate patches Candsi,I when they have the same random offset priorities, i.e., Pr(ROROSANNA(Pi))=Pr(RORandom(Neighi,I)).
6) Priority-based feature matching: The patches are matched in order of priorities according to their corresponding FrQZMs features. If the feature distance between a candidate patch and the target patch Pi is smaller than that between the current optimal matched patch and Pi, this candidate patch is used to update the current optimal matched patch and then the feature matching ends. Finally, the offset of each patch is updated according to the optimal matched patch of each patch.
7) Random searching: In order to minimize the risk of local minima, random searching is carried out around the target patch Pi to check whether there is a better matched patch or not. If there is a better matched patch, the offset of Pi is further updated.
8) Propagation: If the number of iterations from Steps 4) to 7) is greater than threshold Nit, the updated offsets obtained in the previous step are regarded as the final optimal offsets and the iteration ends; otherwise, the updated offsets are used to replace the random offsets and the ROSANNA offsets of Step 4) and then the steps from Steps 4) to Step 7) repeat. Note that, only one type of offsets, i.e., the updated offsets, are considered in a new iteration. The random offsets and the ROSANNA offsets are not used in the new iteration. In addition, the priority computation refers to the method of the first type given in Eq.(9).
9) Post-processing of optimal offsets: Since the optimal offsets may be affected significantly under an attack with noise, compression, geometric deformations, illumination changes and look-alike regions, dense linear fitting used in Ref.[10] is used to regularize the offsets. The dense linear fitting of the obtained optimal offsets is implemented by a mean-squares linear model over a circular neighborhood of radius 6. If the mean-square error of a circular neighborhood for a pixel is smaller than 300, this pixel is regarded as being tampered. The reason is that the copied part should match the pasted part in copy-move forgery. So, the pixels in the copied part should have very similar offsets, thus all of them are mapped to the pixels in the pasted part. So are the pixels in the pasted part.
10) Post-processing of detected regions: Two operations are employed to remove false alarms. The first one is used to remove the very small detected regions (the size is smaller than 1 200 pixels) because these regions usually correspond to noise. The second one is to remove the matched regions very close to each other (the distance between them is smaller than 50 pixels) because the very close regions usually correspond to a uniform background. In addition, a morphological dilation with a circular structuring element of a radius of 10 is used to smooth the detected regions and restore the missing regions.
3 Experimental Results and Analysis
In this section, we evaluate the performance of the proposed algorithm through various experiments. The experimental results are presented as quantitative and visual data. The quantitative results adopt the following pixel-level F-measure:
F=2×![]()
(14)
where Recall represents the probability that a forgery is detected, while Precision shows the probability that a detected forgery is truly forged. They are defined as
![]()
(15)
where TP is the number of correctly detected pixels; FN is the falsely missed forged pixels; and FP is the number of pixels erroneously detected as having been forged. These experiments were implemented in Matlab2010 on a ThinkStation P500 with 2.40 GHz CPU and 16 GB RAM.
3.1 Experimental datasets
The experiments are carried out on two publicly available datasets. The first dataset FAU[3] has 48 original images and 43 of them are with a 3 000×2 000 resolution. The second dataset GRIP[10] is composed of 80 original images with a 768×1 024 or 1 024×768 resolution. Typically, the forged images in the two datasets are generated by extracting many snippets from the original images and then coping and pasting these snippets into their corresponding source images. In order to evaluate the robustness of the copy-move forgery detection algorithm, the forged images in both the datasets undergo some additional operations and attacks. The additional operations and their parameter are listed in Tab.2. Some representative tampering images and their corresponding ground truth images are shown in Fig.2.
Tab.2 Additional operations and attacks in two datasets
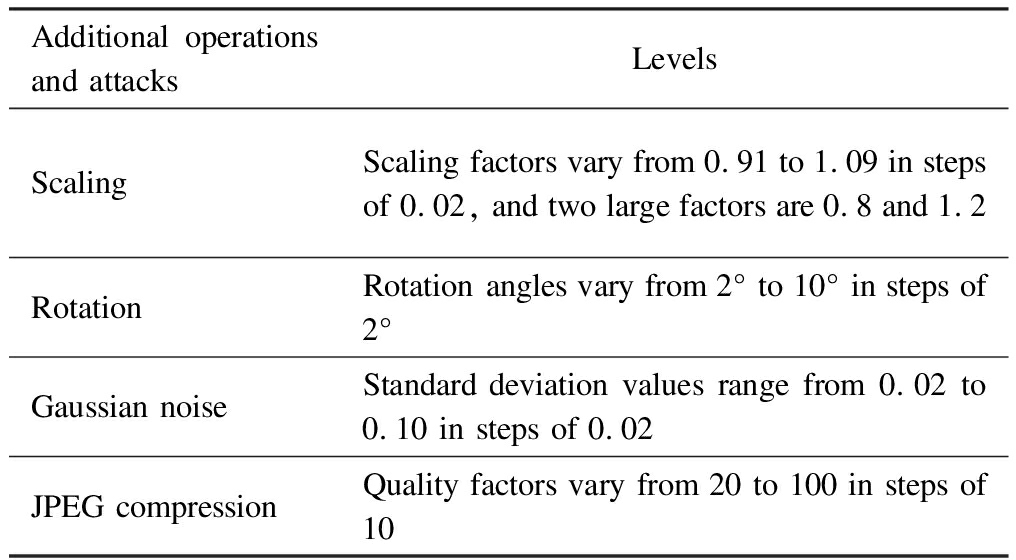
Additional operations and attacksLevelsScalingScaling factors vary from 0.91 to 1.09 in steps of 0.02, and two large factors are 0.8 and 1.2RotationRotation angles vary from 2° to 10° in steps of 2°Gaussian noiseStandard deviation values range from 0.02 to 0.10 in steps of 0.02JPEG compressionQuality factors vary from 20 to 100 in steps of 10

(a)

(b)

(c)

(d)

(e)
Fig.2 Some representative copy-move forged images from two datasets under different additional operations and their corresponding ground truth images. (a) Plain; (b) Gaussian noise (standard deviation 0.04); (c) JPEG compression (quality factor 40); (d) Rotation (angle 4°); (e) Scaling (factor 1.2)
3.2 Test of the proposed color image forgery detection algorithm
The proposed algorithm uses some parameters that are the same as those in Refs.[19, 21] for the feature matching step, and the same as Ref.[10] for the post-processing step. The rest parameters are set according to the experiments. For the FrQZMs feature extraction, the unit pure quaternion μ is the commonly used one ![]() and the fractional parameter α will be discussed in the following test. For the feature matching by the improved PatchMatch algorithm, the number of PatchMatch iterations Nit is 5.
and the fractional parameter α will be discussed in the following test. For the feature matching by the improved PatchMatch algorithm, the number of PatchMatch iterations Nit is 5.
The fractional orders are different, and the FrQZMs features are also different. As a result, the performance of forgery detection is also different. Therefore, the effect of the fractional order is evaluated for the proposed algorithm. For the 80 plain copy-move forged images in the GRIP dataset, the fractional orders vary from 1 to 19 with a step size of 1. The F-measure values of different fractional orders are given in Fig.3. It can be observed from this figure that the F-measure values are fluctuating slightly and falling overall with the increase in fractional orders and the optimal fractional order is 2. Therefore, the fractional order 2 is considered in the following experiments for the proposed algorithm.
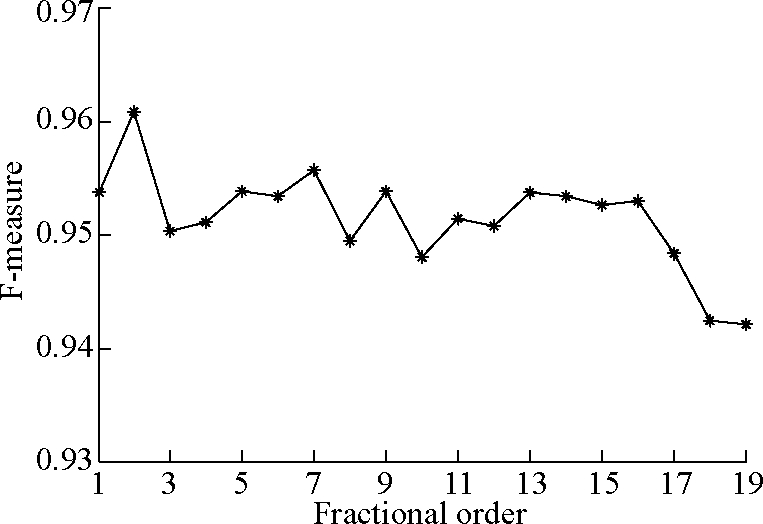
Fig.3 Pixel-level F-measure values of the proposed algorithm with different fractional orders
In order to evaluate the performance of the proposed copy-move forgery detection algorithm, the proposed algorithm is compared with some current algorithms, such as Bi2017[4], Bi2016[6], Zandi2016[9], Cozzolino2015[10], Chen2018[19], and Li2016[23]. Bi et al.[4] utilized a novel and fast reflective offset-guided searching algorithm. Bi et al.[6] used an adaptive polar based filtering in the last step of the CMFD to improve matching results. Zandi et al.[9] proposed a new interest point detector by utilizing the advantages of both keypoint-based and block-based algorithms. Cozzolino et al.[10] proposed an algorithm based on polar Zernike moments and the PatchMatch algorithm. Their algorithm overall outperforms some previous algorithms proposed by Christlein et al.[3,24-25]. Chen et al.[19] proposed an algorithm based on FrQZMs and the PatchMatch algorithm. Li et al.[23] used quaternion discrete cosine transform (QDCT) coefficients as the feature. The comparison results are presented in Tab.3 for the plain copy-move forgery. Since some of the state-of-the-art algorithms report result only in one of two datasets, the symbols “—” in Tab.2 represent that there are no results for Zandi2016 and Bi2016 on the GRIP dataset. The results in this table indicate that the proposed algorithm is better than other algorithms except for Bi2017 for the GRIP dataset.
Tab.3 Pixel-level F-Measure values for the plain copy-move forged images

DatasetBi2016Zandi2016Li2016Cozzolino2015Bi2017Chen2018ProposedGRIP——0.923 50.940 60.969 80.953 30.960 9FAU0.887 20.923 00.936 20.937 20.938 70.935 50.944 9
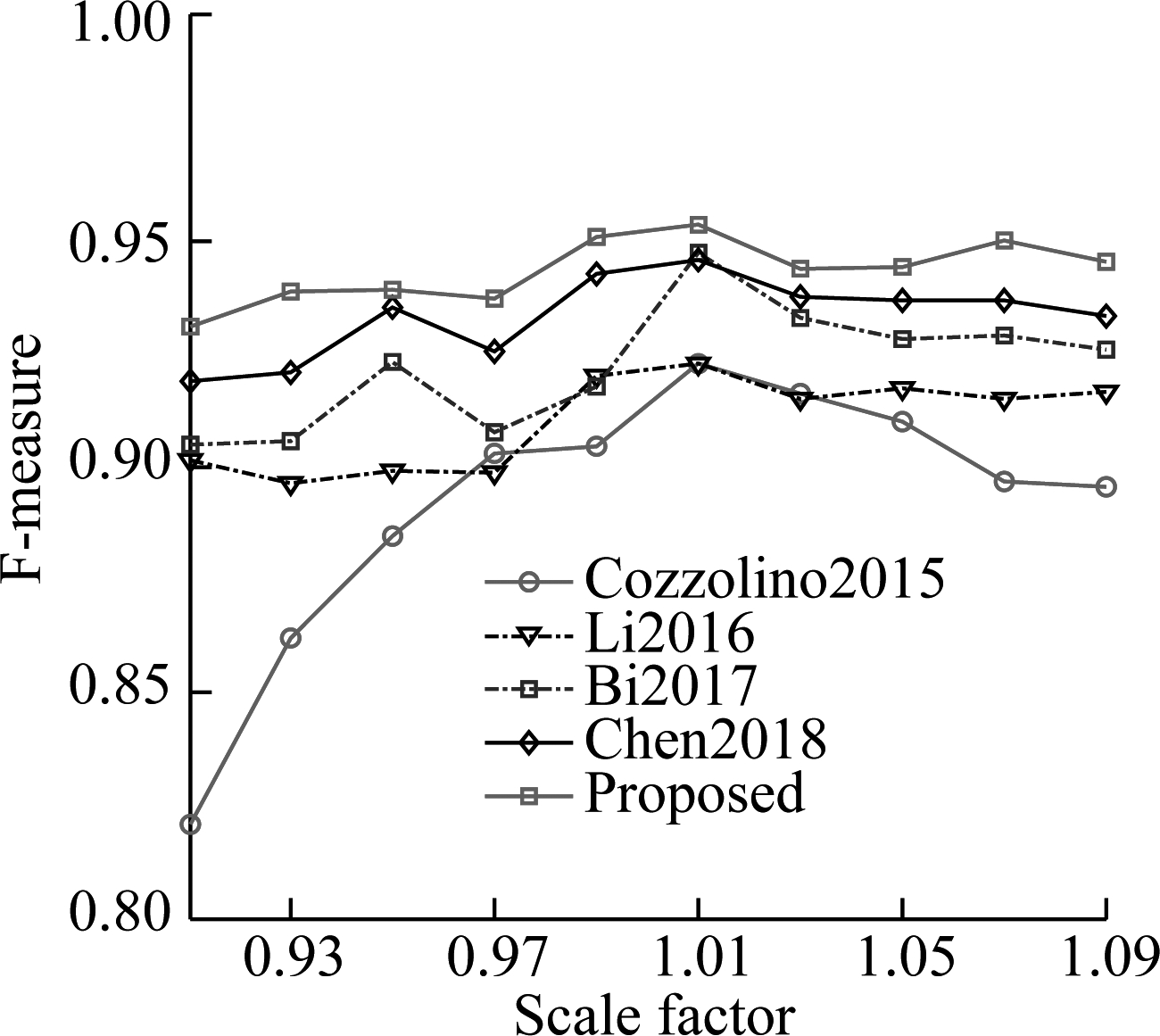
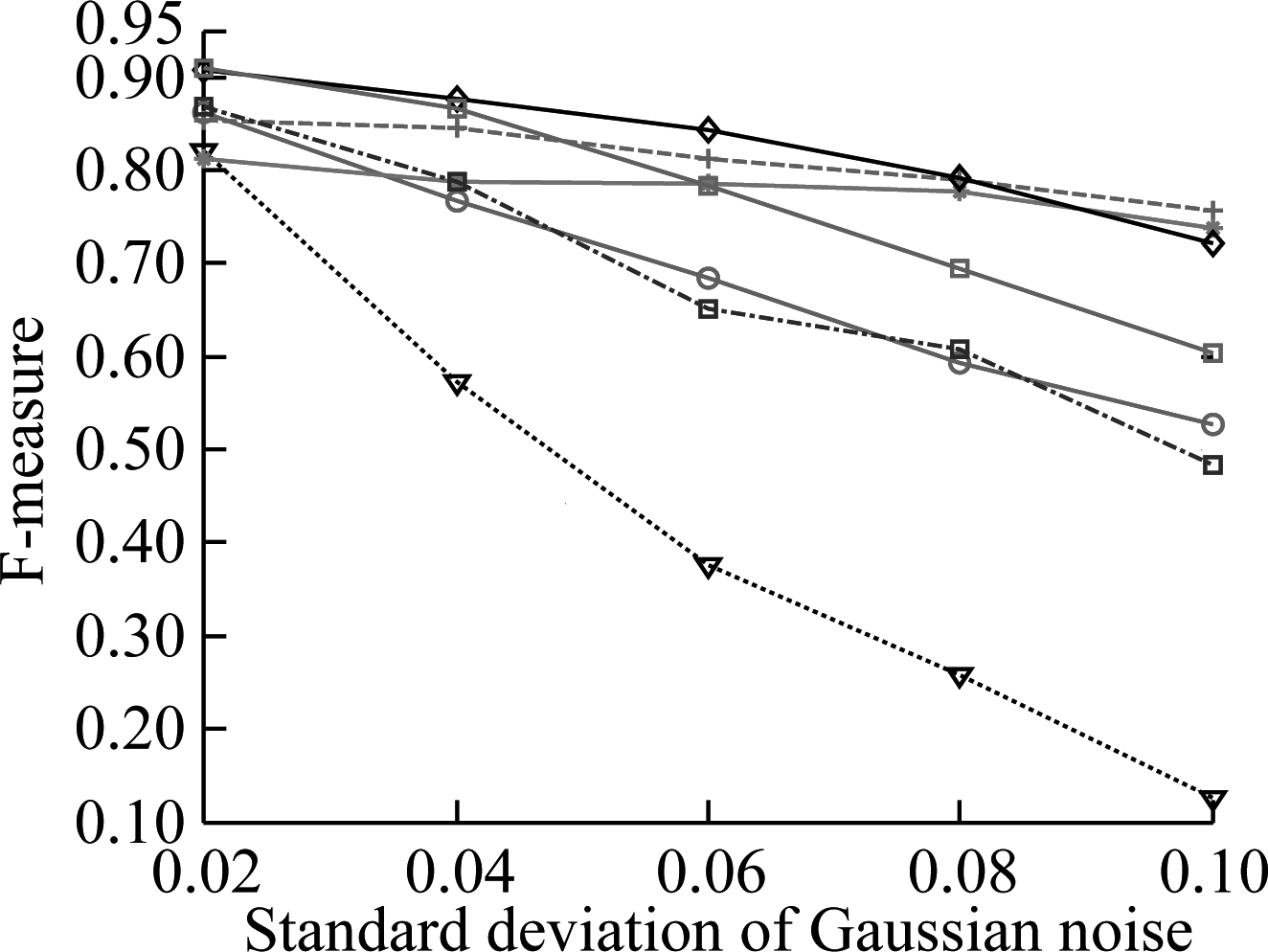
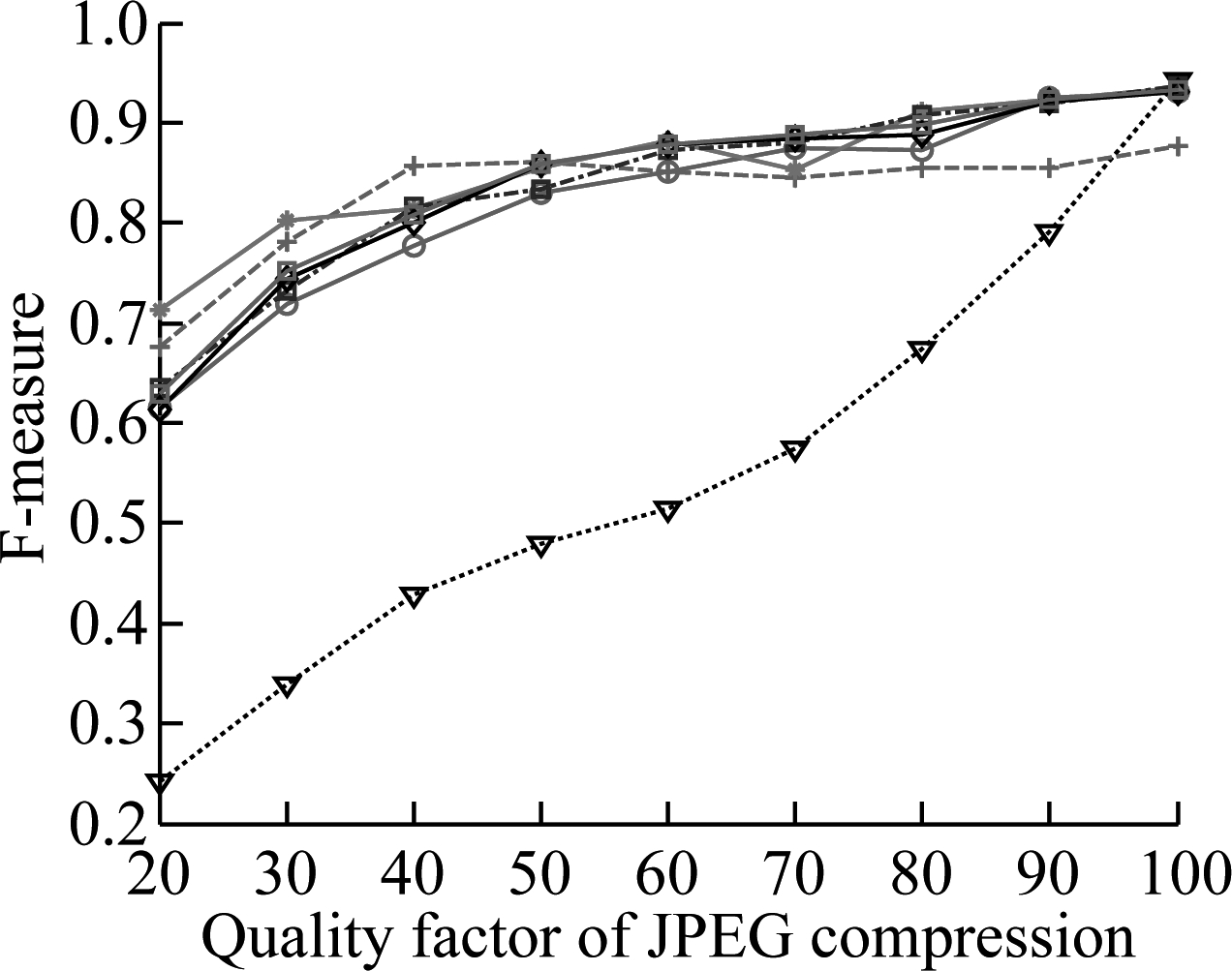
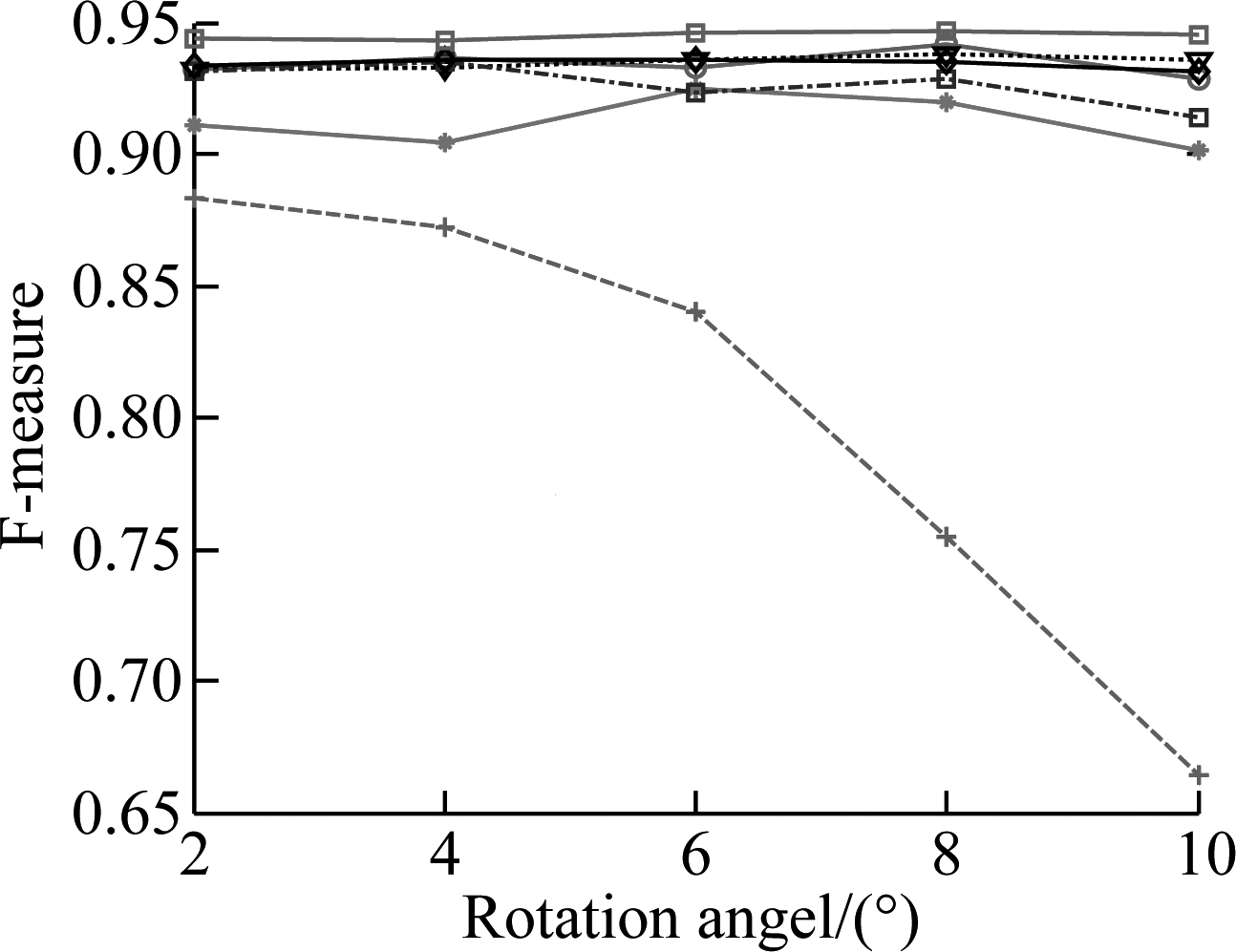
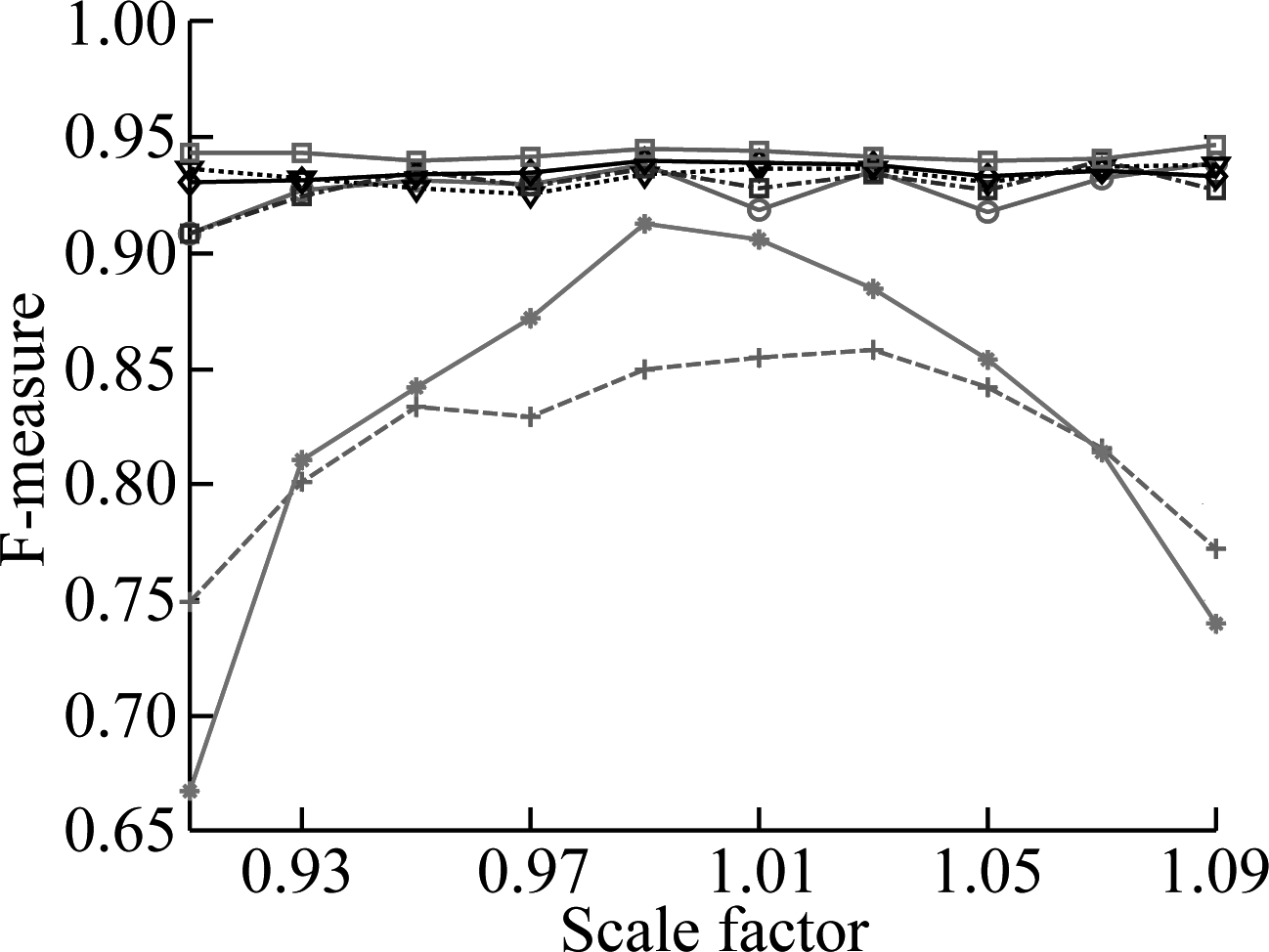
However, the real challenge is to detect the forged images under different kinds of additional operations and attacks. In order to evaluate the robustness of the proposed algorithm, four different additional operations and attacks listed in Tab.2 are considered. The results of F-measure values for two datasets are shown in Fig.4 and Fig.5,respectively. In addition, in order to demonstrate the performance of using a multi-scale, Tab.4 presents the results for the scaling additional operation with the large factors (scaling factors 0.8 and 1.2). It can be observed from these results that: 1) F-measure values usually decrease with the increase in the additional operation levels and attack levels; 2) The proposed algorithm achieves an overall better performance than other compared algorithms, especially for the GRIP dataset. In order to better comprehend these results, the visual results are provided in Fig.6, where red indicates correct detection, and the false alarms are in green. The columns of each subfigure, from left to right are blank, with Gaussian noise with standard deviation 0.04, JPEG compression with quality factor 40, rotation with an angle of 4°, scaling with factor 1.2. The results in Fig.6 show that the proposed algorithm performs well in false detection and detecting details.
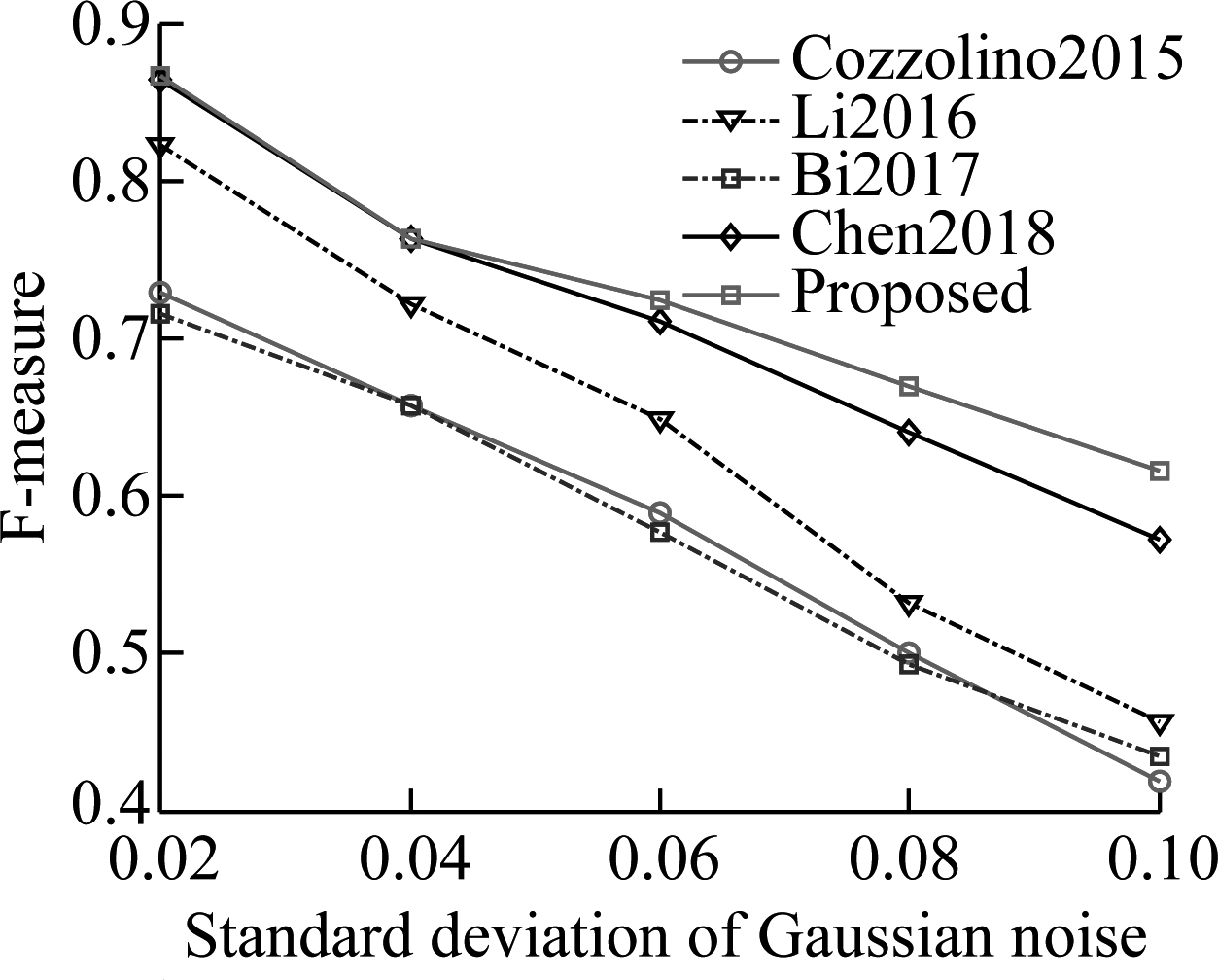
(a)
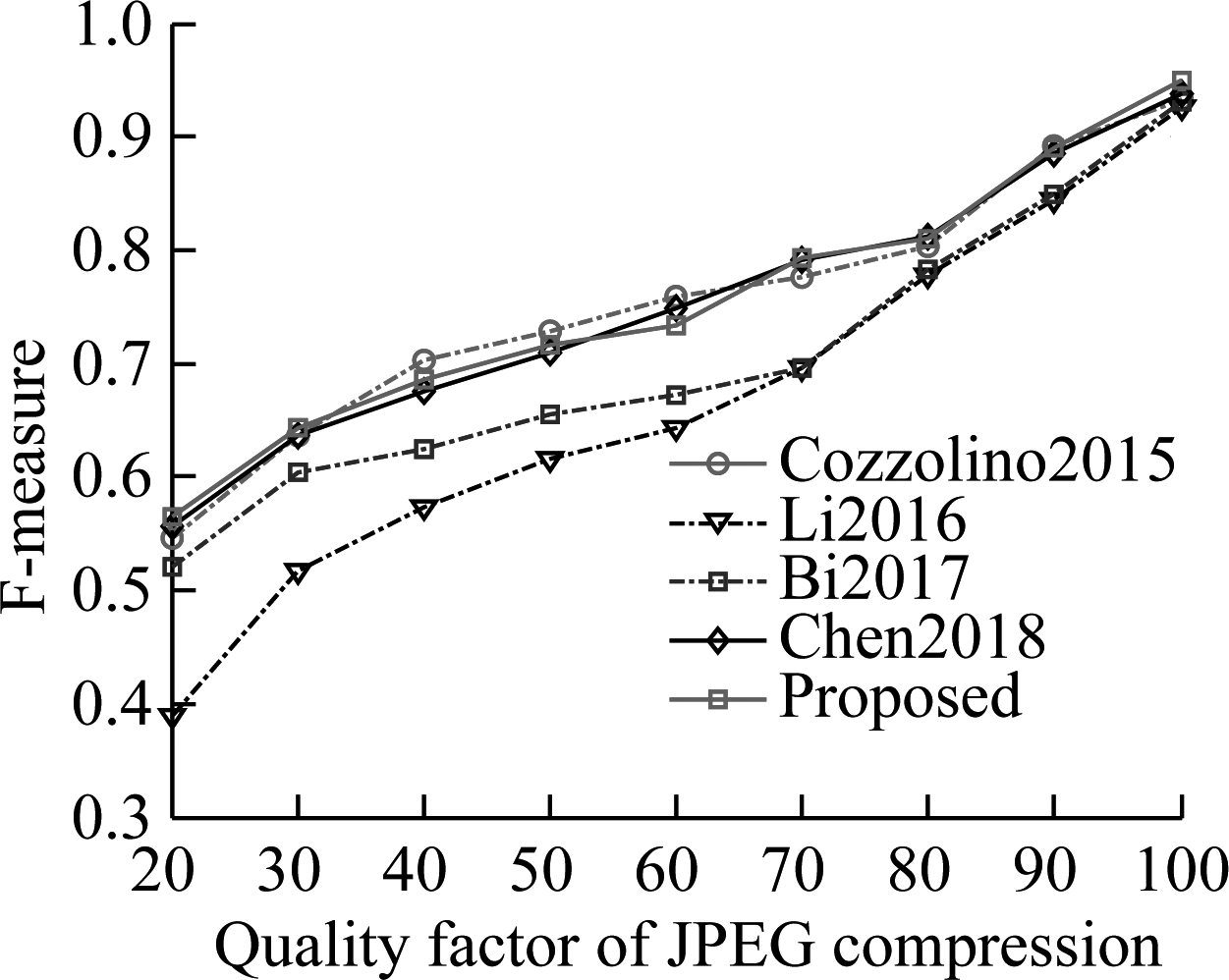
(b)
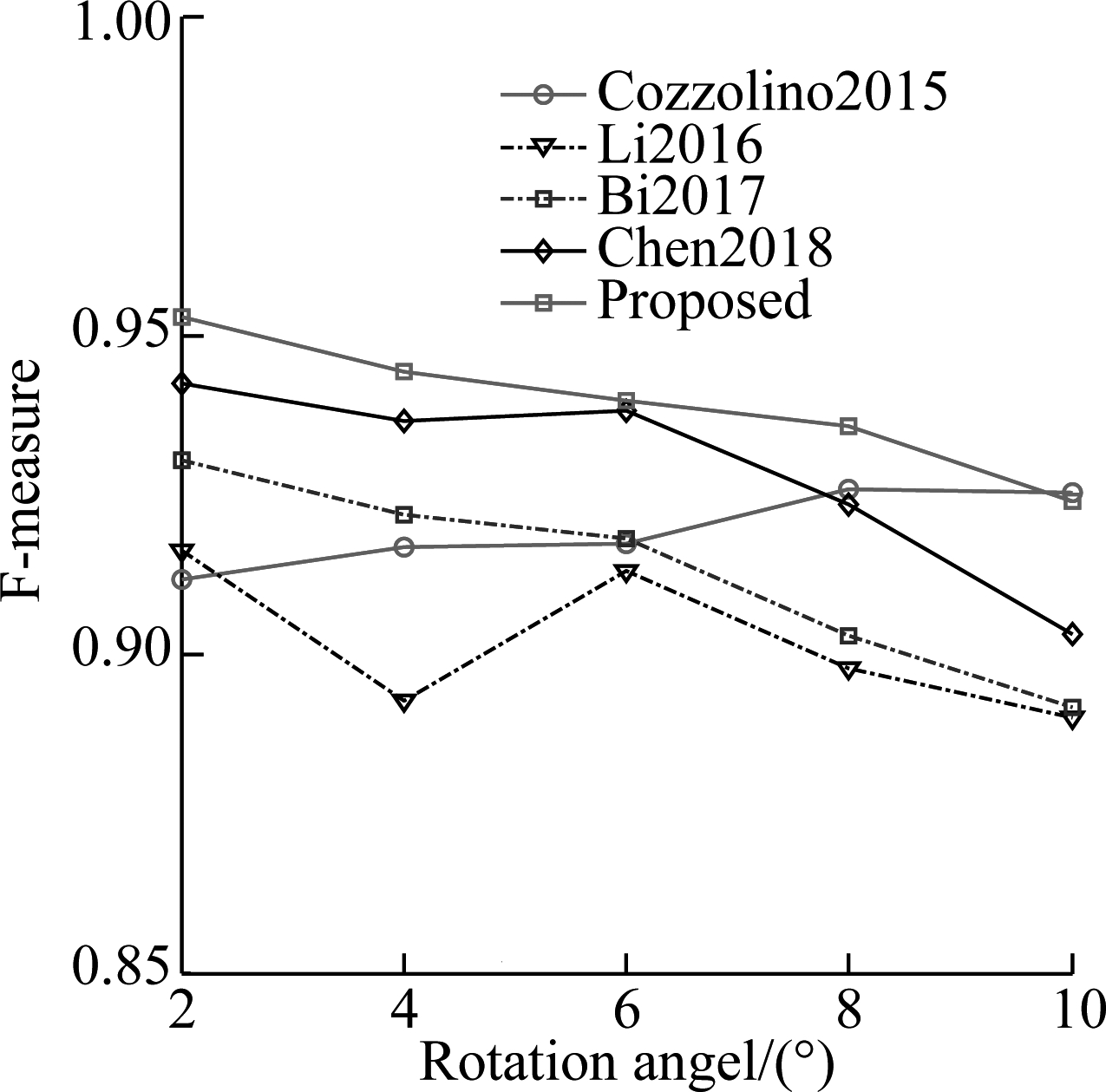
(c)
(d)
Fig.4 Pixel-level F-measure values for four types of additional operations and attacks on GRIP dataset. (a) Gaussian noise operation; (b) JPEG compression operation; (c) Rotation operation; (d) Scaling operation
(a)
(b)
(c)
(d)
![]()
Fig.5 Pixel-level F-measure values for four types of additional operations and attacks on FAU dataset. (a) Gaussian noise operation; (b) JPEG compression operation; (c) Rotation operation; (d) Scaling operation
Tab.4 Pixel-level F-measure values for the scaling additional operations with large factors on GRIP dataset
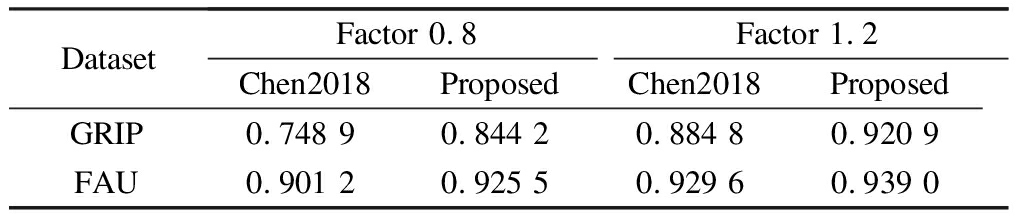
DatasetFactor 0.8Factor 1.2Chen2018ProposedChen2018ProposedGRIP0.748 90.844 20.884 80.920 9FAU0.901 20.925 50.929 60.939 0
Therefore, the proposed algorithm performs better than other compared algorithms not only in F-measure values but also in visual data. The main reasons are as follows: 1) The FrQZMs feature in the proposed algorithm not only considers color information but also uses the quaternion-based method to utilize both the magnitude and phase information, while four compared algorithms (Cozzolino 2015, Bi2016, Zandi2016 and Bi2017) extract features from the gray image; 2) The proposed algorithm adopts the fractional feature FrQZMs using the advantages of both the spatial-based feature and the transform-based feature and uses a more effective matching algorithm—the improved PatchMatch algorithm, while the compared quaternion-based algorithm Li2016 is based on the QDCT feature and classical lexicographical matching; 3) Compared to the FrQZMs-based algorithm Chen2018, the proposed algorithm introduces ROSANNA to improve the propagation process of the PatchMatch algorithm.

(a)

(b)

(c)

(d)

(d)
Fig.6 Visual results correspond to the copy-moved forged images shown in Fig.2 under different additional operations for the proposed algorithm. (a) Localization results for Fig.2(a); (b) Localization results for Fig.2(b); (c) Localization results for Fig.2(c); (d) Localization results for Fig.2(d); (e) Localization results for Fig.2(e)
4 Conclusion
In this paper, we proposed a robust copy-move forgery detection algorithm based on FrQZMs and the improved PatchMatch algorithm. FrQZMs have been considered for extracting features from color forged images. The FrQZMs feature not only uses the quaternion-based method to utilize color information effectively, but also makes use of both the advantages of the spatial-based features and the transform-based ones. The PatchMatch algorithm has been improved by using ROSANNA offsets during the first propagation stage. The experimental results show that the proposed algorithm outperforms some current algorithms not only in F-measure value but also in visual data.
[1]Fridrich A J, Soukal B D, Lukáš J. Detection of copy-move forgery in digital images[C]// Proceedings of Digital Forensic Research Workshop. Cleveland, OH, USA, 2003:1-10.
[2]Sitara K, Mehtre B M. Digital video tampering detection: An overview of passive techniques[J]. Digital Investigation, 2016, 18: 8-22. DOI:10.1016/j.diin.2016.06.003.
[3]Christlein V, Riess C, Jordan J, et al. An evaluation of popular copy-move forgery detection approaches[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(6): 1841-1854. DOI:10.1109/tifs.2012.2218597.
[4]Bi X L, Pun C M. Fast reflective offset-guided searching method for copy-move forgery detection[J]. Information Sciences, 2017, 418/419: 531-545. DOI:10.1016/j.ins.2017.08.044.
[5]Lee J C, Chang C P, Chen W K. Detection of copy-move image forgery using histogram of orientated gradients[J]. Information Sciences, 2015, 321: 250-262. DOI:10.1016/j.ins.2015.03.009.
[6]Bi X L, Pun C M, Yuan X C. Multi-level dense descriptor and hierarchical feature matching for copy-move forgery detection[J]. Information Sciences, 2016, 345: 226-242. DOI:10.1016/j.ins.2016.01.061.
[7]Bashar M, Noda K, Ohnishi N,et al. Exploring duplicated regions in natural images[J]. IEEE Transactions on Image Processing, 2010. DOI:10.1109/tip.2010.2046599.
[8]Bayram S, Sencar H, Memon N. An efficient and robust method for detecting copy-move forgery[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Taipei, China, 2009: 1053-1056. DOI:10.1109/icassp.2009.4959768.
[9]Zandi M, Mahmoudi-Aznaveh A, Talebpour A. Iterative copy-move forgery detection based on a new interest point detector[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(11): 2499-2512. DOI:10.1109/tifs.2016.2585118.
[10]Cozzolino D, Poggi G, Verdoliva L. Efficient dense-field copy-move forgery detection[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(11): 2284-2297. DOI:10.1109/tifs.2015.2455334.
[11]Ryu S J, Kirchner M, Lee M J, et al. Rotation invariant localization of duplicated image regions based on Zernike moments[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(8): 1355-1370. DOI:10.1109/tifs.2013.2272377.
[12]Chen B J,Coatrieux G, Wu J S, et al. Fast computation of sliding discrete Tchebichef moments and its application in duplicated regions detection[J]. IEEE Transactions on Signal Processing, 2015, 63(20): 5424-5436. DOI:10.1109/tsp.2015.2451107.
[13]Hosny K M, Hamza H M, Lashin N A. Copy-move forgery detection of duplicated objects using accurate PCET moments and morphological operators[J]. The Imaging Science Journal, 2018, 66(6): 330-345. DOI:10.1080/13682199.2018.1461345.
[14]Kang X B, Wei S M. Identifying tampered regions using singular value decomposition in digital image forensics[C]//2008 International Conference on Computer Science and Software Engineering. Wuhan, China, 2008:926-930. DOI:10.1109/csse.2008.876.
[15]Zhan L F, Zhu Y S. Passive forensics for image splicing based on PCA noise estimation[C]//2015 10th International Conference for Internet Technology and Secured Transactions (ICITST). London, UK, 2015:78-83. DOI:10.1109/icitst.2015.7412062.
[16]Namias V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(3): 241-265. DOI:10.1093/imamat/25.3.241.
[17]Xiao B, Li L P, Li Y, et al. Image analysis by fractional-order orthogonal moments[J]. Information Sciences, 2017, 382/383: 135-149. DOI:10.1016/j.ins.2016.12.011.
[18]Chen B J, Yu M, Su Q T, et al. Fractional quaternion cosine transform and its application in color image copy-move forgery detection[J].Multimedia Tools and Applications, 2019, 78(7): 8057-8073. DOI:10.1007/s11042-018-6595-z.
[19]Chen B J, Yu M, Su Q T, et al. Fractional quaternionzernike moments for robust color image copy-move forgery detection[J]. IEEE Access, 2018, 6: 56637-56646. DOI:10.1109/access.2018.2871952.
[20]Subakan Ö N, Vemuri B C. A quaternion framework for color image smoothing and segmentation[J]. International Journal of Computer Vision, 2011, 91(3): 233-250. DOI:10.1007/s11263-010-0388-9.
[21]Verdoliva L, Cozzolino D, Poggi G. A reliable order-statistics-based approximate nearest neighbor search algorithm[J]. IEEE Transactions on Image Processing, 2017, 26(1): 237-250. DOI:10.1109/tip.2016.2624141.
[22]Cozzolino D, Poggi G, Verdoliva L. Copy-move forgery detection based on PatchMatch[C]// IEEE International Conference on Image Processing. New York, USA, 2014: 5312-5316.DOI:10.1109/icip.2014.7026075.
[23]Li C, Ma Q, Xiao L M, et al. An image copy move forgery detection method using QDCT[C]//Proceedings of the International Conference on Internet Multimedia Computing and Service—ICIMCS’16. Xi’an, China, 2016:5-8. DOI:10.1145/3007669.3007689.
[24]Bravo-Solorio S, Nandi A K. Exposing duplicated regions affected by reflection, rotation and scaling[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Prague, Czech Republic, 2011: 1880-1883. DOI:10.1109/icassp.2011.5946873.
[25]Amerini I, Ballan L, Caldelli R, et al. Copy-move forgery detection and localization by means of robust clustering with J-linkage[J]. Signal Processing: Image Communication, 2013, 28(6): 659-669. DOI:10.1016/j.image.2013.03.006.