Cellular users tend to run computation-intensive applications, which require many computing resources.To meet this requirement, the idea of cellular edge computing is introduced, in which computing servers are located in the base stations (BSs) and users’ applications are offloaded to BSs to execute[1-2]. There are two types of resources to be scheduled: the communication resource used during the offloading and the computing resource used during the execution. Hence, there are two types of delay, that is, communication delay and computing delay, in cellular edge computing systems. This paper studies the resource scheduling problem for cellular edge computing systems which minimizes the communication delay and computing delay.
There are many related studies in the literature. According to the assumptions of delay, they can be classified into three categories. For the first category[3-7], only the transmission delay or execution delay is considered. However, queueing related delay is not considered. The second category of the scheduling algorithm is based on the queuing theory model. For this category[8-12], in addition to transmission delay and execution delay, the queueing related delay is also considered. However, this category assumes that the queue can be modelled as the traditional queue (e.g., the M/M/1 queue) so that the delay formulas of the queueing theory can be readily applied. The third category of the scheduling algorithm is based on the backpressure (BP) scheduling framework. For this category, the queueing related delay is also considered. Furthermore, this category does not make any assumption of the model of the queue and uses the framework of BP scheduling which was established in Refs.[13-14] to design scheduling algorithms. A typical resource scheduling algorithm of this category is derived as follows[13-19]: Firstly, consider that the average delay and average queue length are interchangeable by Little’s Law; secondly, define the queue length-based Lyapunov function; finally, design the backpressure scheduling algorithm which minimizes the conditional drift of the Lyapunov function by the method in Refs.[13-14].
In this work, we focus on the backpressure-based scheduling algorithms. Existing backpressure-based scheduling algorithms have two limitations. Firstly, existing BP scheduling algorithms were all based on the queue length which did not control the delay directly. Actually, due to the lack of delay formulas, the existing backpressure-based scheduling algorithms cannot solve the delay control problem directly but have to solve the queue length control problem instead. Secondly, most existing backpressure-based scheduling algorithms only considered the single-cell scenario. For this scenario, the scheduler only needs to decide how to allocate communication resources between users. However, the multi-cell scenario.is more practical than the single-cell scenario. In fact, for the multi-cell scenario, in addition to deciding how to allocate communication resources between users, the scheduler still needs to decide how to assign BSs to users. Therefore, this work will extend the traditional backpressure-based scheduling algorithms by studying the scheduling algorithm which solves the delay control problem directly for multi-cell cellular edge computing systems.
1 System Models
Consider a multi-cell cellular edge computing system, in which time is slotted and the duration of each slot is T(unit: s). Let I denote the total number of users.
For the communication resource, assume that there are a total of R subcarriers and J BSs in the system. At the beginning of each slot, the communication scheduler allocates subcarriers and BS for the applications of users. For each subcarrier allocation, let si,e and di,e denote the number of subcarriers and the index of BS allocated to the e-th application of user i, respectively. Let mi,j(·) denote the subcarrier-slot mapping function which maps the number of allocated subcarriers to the number of slots needed to offload an application from user i to BS j. Assume that the subcarrier-slot mapping function mi,j(·) is a monotonic decreasing function of the variable. For BS allocation, let Ψi denote the set of BSs accessible by user i(i.e., BS j can receive the signal from user i with a signal-to-interference-plus-noise-ratio exceeding a threshold), then we have di,e
Ψi.
For the computing resource, assume that there are a total of Fj virtual machines (VMs) in BS j. At the beginning of each slot, the computing scheduler of each BS j allocates VMs for the applications offloaded to itself. Let gj,i,e denote the number of VMs allocated to the e-th application of user i by BS j where di,e=j. Assuming that at most gmax VMs can be allocated to an application, then we have gj,i,e≤gmax. Let ui(·) denote the VM-slot mapping function which maps the number of allocated VMs to the number of slots needed to execute an application of user i, which is a monotonic decreasing function of the variable.
1.1 Communication delay model
There are I communication queues, one for each user. For the i-th communication queue, let Ui(n-1) denote the number of applications in the queue at the beginning of slot n, Xi,j(n) denote the number of applications offloaded to BS j(i.e., leaving the queue) during slot n, and Ai(n) denote the number of applications arriving to the queue at the end of slot n. The value of Xi,j(n) can be written as
(1)
where 1{·} equals one if the condition is true and zero otherwise and ni,e represents the index of slot at the beginning of which the values of si,e and di,e are given. Hence, the evolution of the i-th communication queue is described as
(2)
where (·)+=max(·, 0).
The constraints on the scheduling variables (ni,e, si,e, di,e) are stated as follows. Let ri,e(n) denote the number of subcarriers allocated to the e-th application of user i during slot n, that is
(3)
Then, let Ri,j(n) denote the total number of subcarriers allocated to the link from user i to BS j during slot n, that is
(4)
For any two users i and k, if there is a BS which is accessible to both i and k, we say that user k is a competitor user of user i. Let Ωi denote the set of the competitor users of user i. Then for each user i and BS jΨi, we have the following constraint:
(5)
Finally, the formula of communication delay is derived as follows. Let Γi,tot(n) denote the total delay experienced by all applications in the i-th communication queue until slot n+1. Then, we have
(6)
Let Γi(n) denote the time-average of Γi,tot(n), that is, Γi(n)=Γi,tot(n)/n, as the measure of the communication delay experienced by the applications of user i. Then, we can express Γi(n) as a virtual queue:
Γi(n)=Γi(n-1)-εΓi(n-1)+εUi(n)T
(7)
where ε is the smoothing coefficient and takes the value of 1/n. Since 1/n approaches zero with the increase in n, we can alternatively set ε to be a positive constant. Finally, let Wi(n) denote the normalized version of Γi(n), that is, Wi(n)=Γi(n)/T. Then, we have
Wi(n)=Wi(n-1)-εWi(n-1)+εUi(n)
(8)
1.2 Computing delay model
For each BS j, there are I computing queues, one for each user. For the i-th computing queue in BS j, let Qj,i(n) denote the number of applications in the queue at the end of slot n+1, and Yj,i(n) denote the number of applications finishing the execution (i.e., leaving the queue) during slot n+1. The value of Yj,i(n) can be written as
(9)
Recall that a total of Xi,j(n) applications leave the i-th communication queue at the end of slot n, as described in Eq.(1). We assume that these applications enter the i-th computing queue in BS j at the end of slot n+1. Hence, the evolution of the i-th computing queue in BS j is described as
Qj,i(n)=(Qj,i(n-1)-Yj,i(n))++Xi,j(n)
(10)
The constraints on the scheduling variables (vj,i,e, gj,i,e) are stated as follows. Let fj,i,e(n) denote the number of VMs allocated to the e-th application of user i in BS j during slot n+1, that is
(11)
Then, let Fj,i(n) denote the total number of VMs allocated to user i in BS j during slot n+1, that is
(12)
Then for each BS j and user i, we have the constraint:
(13)
Finally, the formula of computing delay is derived as follows. Let Ξj,i,tot(n) denote the total delay experienced by all applications in the i-th computing queue in BS j until slot n+1. Then, we have
(14)
Let Ξj,i(n) denote the time-average of Ξj,i,tot(n), that is, Ξj,i(n)=Ξj,i,tot(n)/n, as the measure of the computing delay experienced by the applications of user i in BS j. Then, we can express Ξj,i(n) as a virtual queue:
Ξj,i(n)=Ξj,i(n-1)-εΞj,i(n-1)+εQj,i(n)T
(15)
Let Zj,i(n) denote the normalized version of Ξj,i(n), that is, Zj,i(n)= Ξj,i(n)/T. Then, we have
Zj,i(n)=Zj,i(n-1)-εZj,i(n-1)+εQj,i(n)
(16)
2 Virtual Delay Queue-Based Backpressure Scheduling
2.1 The proposed scheduling algorithm
Define the Lyapunov function as
(17)
According to the Lyapunov optimization technique, the conditional Lyapunov drift can be calculated as Δ(n)=E{L(n)-L(n-1)|W(n-1), Z(n-1)}, where E{·} is the expectation operation, W(n-1)=[W1(n-1),…, WI(n-1)], and Z(n-1)=[Z1,1(n-1),…, ZJ,I(n-1)]. Substituting Eq.(17) into the above equation, we have
where the first six terms can be upper bounded by a constant under the expectation operation. Using the concept of opportunistically maximizing an expectation, the above expression is minimized by the algorithm that obtains the values of W(n-1) and Z(n-1) and minimize 
Furthermore, substituting Eqs.(2) and (10) into the above equation, the objective can be upper bounded as
where the first three terms can also be upper bounded by a constant.Therefore, the final form of the optimization problem for each n is
(18)
where Xi,j(n) and Yj,i(n) are determined by scheduling variables (ni,e, si,e, di,e) and (vj,i,e, gj,i,e) which must satisfy the constraints in Eqs.(3) to (5) and (11) to (13). Note that Xi,j(n) and Yj,i(n) are decoupled in both the objective and constraints in (18), and therefore can be optimized separately as follows.
The subproblem of optimizing communication resource scheduling variables can be written as
(19)
where Xi,j(n) is determined by scheduling variables (ni,e, si,e, di,e) which must satisfy the constraints in Eqs.(3) to (5). This is a typical backpressure scheduling problem[13-14]. The proposed communication resource scheduling algorithm is presented as follows. We initially set tmpWi=(1-ε)Wi(n-1)+ εUi(n-1) and tmpZj,i=(1-ε)Zj,i(n-1)+εQj,i(n-1) for each i and j. For each application e of user i satisfying di,e=j and ni,e≤n≤ni,e+mi,j(si,e)-1, update Ri←Ri-si,e and Rk←Rk-si,e for each kΩi. Let Li contain the index of applications of user i which has not been allocated any subcarrier yet. For each n, the algorithm performs the following steps.
1) Determine the pair (i*, j*)=arg min (tmpZj,i-tmpWi) over all feasible user i’s (i.e., Ri>0 and Li is not empty) and BS jΨi. If there is no feasible user, the algorithm stops.
2) If there is an e*Li*(n) with di*,e*=j* and si*,e*>0, then update si*,e*←si*,e*+1; otherwise, pick the application which arrives the earliest and denoted as e*, then set ni*,e*=n, si*,e*=1, and di*,e*=j*. Update Ri*←Ri*-1 and Rk←Rk-1 for each kΩi*. If mi*,j*(si*,e*)=1, remove this e* from Li*(n).
3) For each j and i, update 
and tmpZj,i= 
where if ni,e=0, γi,e=1 and δi,e=0; if ni,e=n, γi,e=1-1/mi,j(si,e) and δi,e=1. Go back to step 1).
The subproblem of optimizing computing resource scheduling variables can be written as
(20)
where Yj,i(n) is determined by scheduling variables (vj,i,e, gj,i,e) which must satisfy the constraints in Eqs.(11) to (13). This is a typical max-weight scheduling problem. The proposed computing resource scheduling algorithm is presented as follows. We initially set tmpZj,i=(1-ε)Zj,i(n-1)+εQj,i(n-1) for each j and i. For each application e of user i satisfying di,e=j and vj,i,e≤n+1≤vj,i,e+ui(gj,i,e)-1, update Fj,i←Fj,i-gj,i,e and Fj,k←Fj,k-gj,i,e for each k≠i. Let Pj,i contain the index of applications of user i in BS j which have not been allocated any VM yet. For each BS j on each n, the algorithm performs the following steps.
1) Determine user i*=arg max tmpZj,i over all feasible user i’s(i.e., Fj,i>0 and Pj,i is not empty). If there is no feasible user, the algorithm stops.
2) If there is an e*Pj,i* with gj,i*,e*>0, then update gj,i*,e*←gj,i*,e*+1; otherwise, pick the application arriving earliest as e*, then set vj,i*,e*=n+1 and gj,i*,e*=1. Update Fj,i*←Fj,i*-1 and Fj,k←Fj,k-1 for each k≠i*. If gj,i*,e*=gmax, remove this e* from Pj,i*.
3) Update 
for each i, where λi,e=1 if vj,i,e=0, or λi,e=1-1/ui(gj,i,e) if vj,i,e=n+1. Go back to Step 1.
The computation complexity of the proposed algorithm is analyzed as follows. The proposed scheduling algorithm consists of two parts. For the first part, the value of (tmpZj,i-tmpWi) is calculated for each user i and each BS j. Thus, the computational complexity of this calculation is O(IJ). Furthermore, according to the algorithm, such calculation is executed until there is no feasible user. Since the number of subcarriers is limited, the number of times of calculating the value of (tmpZj,i-tmpWi) will be no more than a constant. Therefore, the computational complexity of the first part of the proposed algorithm is O(IJ). For the second part, for each BS j, the value of tmpZj,i is calculated for each user i. Thus, the computational complexity of this calculation is O(I). Furthermore, according to the algorithm, such calculation is executed until there is no feasible user. Since the number of VMs in each BS is limited, the number of times of calculating the value of tmpZj,i will be no more than a constant. Therefore, the computational complexity of the second part of the proposed algorithm is O(I). The overall computational complexity of the proposed algorithm is O(IJ).
2.2 Traditional queue length-based backpressure scheduling
To benchmark the performance of the proposed scheduling algorithm, the traditional queue length-based scheduling algorithm is introduced as follows.According to Refs.[13-19], a typical traditional queue length-based backpressure scheduling is derived as follows: Firstly, define the queue length-based Lyapunov function; then, design the backpressure scheduling algorithm which minimizes the conditional drift of the Lyapunov function.
Therefore,for the considered multi-cell cellular edge computing system, we firstly define the Lyapunov function as
(21)
Then we design the backpressure scheduling algorithm which minimizes the conditional drift of the Lyapunov function as follows. The conditional Lyapunov drift is Δ(n)=E{L(n)-L(n-1)|U(n-1), Q(n-1)}, where U(n-1)=[U1(n-1),…, UI(n-1)], and Q(n-1)=[Q1,1(n-1),…, QJ,I(n-1)]. After similar derivations[14], the following optimization problem should be solved for each n:
(22)
where Xi,j(n) and Yj,i(n) are determined by scheduling variables (ni,e, si,e, di,e) and (vj,i,e, gj,i,e) which must satisfy the constraints in Eqs.(3) to (5) and (11) to (13). Note that Xi,j(n) and Yj,i(n) are also decoupled in (22). Therefore, the optimization problem in (22) can also be decomposed into two subproblems, where the communication resource scheduling subproblem is
(23)
and the computing resource scheduling subproblem is
(24)
These optimization subproblems and those in (19) and (20) are very similar. Therefore, according to Refs.[13-19], we use the same procedure to solve these optimization subproblems except that the value of delay is replaced by the value of queue length. Finally, the computational complexity of the traditional algorithm is analyzed as follows. The traditional scheduling algorithm also consists of two parts. For the first part, the core step is to calculate the value of queue length difference for each user i and each BS j. Thus, the computational complexity of the first part of the traditional algorithm is O(IJ). For the second part, for each BS j, the core step is to calculate the value of queue length for each user i. Thus, the computational complexity of the second part of the traditional algorithm is O(I). The overall computational complexity of the traditional queue length-based backpressure scheduling algorithm is also O(IJ). Therefore, the proposed delay-based scheduling algorithm and the traditional queue length-based scheduling algorithm have the same computational complexity.
3 Performance Evaluation
Consider a time-slotted multi-cell cellular edge computing system. Assume that there are J=3 BSs. As illustrated in Fig.1, the geographical positions of these BSs are: (0, 1), (0.866, -0.5), and (-0.866, -0.5) in kilometer. A total of I=20 users are uniformly distributed over the area covered by BSs. For each run, we generate a snapshot of the distribution of the users. For each user i, assume that his/her applications arrive according to a Poisson process with the average inter-arrival time of Ti(unit:s). Unless otherwise stated, the value of Ti is set to be 5 slots. Let dij represent the distance between user i and BS j. If dij<1.5B, user i is considered to be a neighbor of BS j. Then sets Ψi and Ωi can be determined for each user i. For any user i and BS j, the function mi,j(·) is set as follows. If dij≤0.2 km, then set the function as mi,j(1)=2 and mi,j(2)=1, as shown in Fig. 2(a); if 0.2 km<dij<0.6 km, then set the function as mi,j(1)=3, mi,j(2)=2 and mi,j(3)=1, as shown in Fig. 2(b); if dij≥0.6 km, then set the function as mi,j(1)=4, mi,j(2)=3, mi,j(3)=2 and mi,j(4)=1, as shown in Fig. 2(c). The value of gmax is set to be 3, and the function ui(g) is set as ui(1)=6, ui(2)=2, and ui(3)=1. The value of R will be changed for different simulations. The value of Fj is set as follows. For odd-numbered j, we set Fj=10; for even-numbered j, we set Fj=ρj×10 where the value of ρj will be changed for different simulations.
The main performance metric considered in this paper is delay, which consists of two parts: the communication delay and the computing delay. For each parameter setting, we firstly collect the communication delay and computing delay experienced by each application of each user, then average these values over all applications and all users, and finally calculate the average total delay as the summation of the average communication delay and average computing delay. For each parameter setting, we run the simulation experiment independently one hundred times and average the results. Additionally, we consider a total of four different scheduling algorithms: The first is the proposed delay-based scheduling algorithm (i.e., (19) and (20)), abbreviated as the Dly algorithm; the second is the joint delay-based communication resource scheduling (i.e., (19)) and the queue length-based computing resource scheduling (i.e., (24)), abbreviated as the DlyQue algorithm; the third is the joint queue length-based communication resource scheduling (i.e., (23)) and the delay-based computing resource scheduling (i.e., (20)), abbreviated as the QueDly algorithm; and the final is the traditional queue length-based scheduling (i.e., (23) and (24)), abbreviated as the Que algorithm.
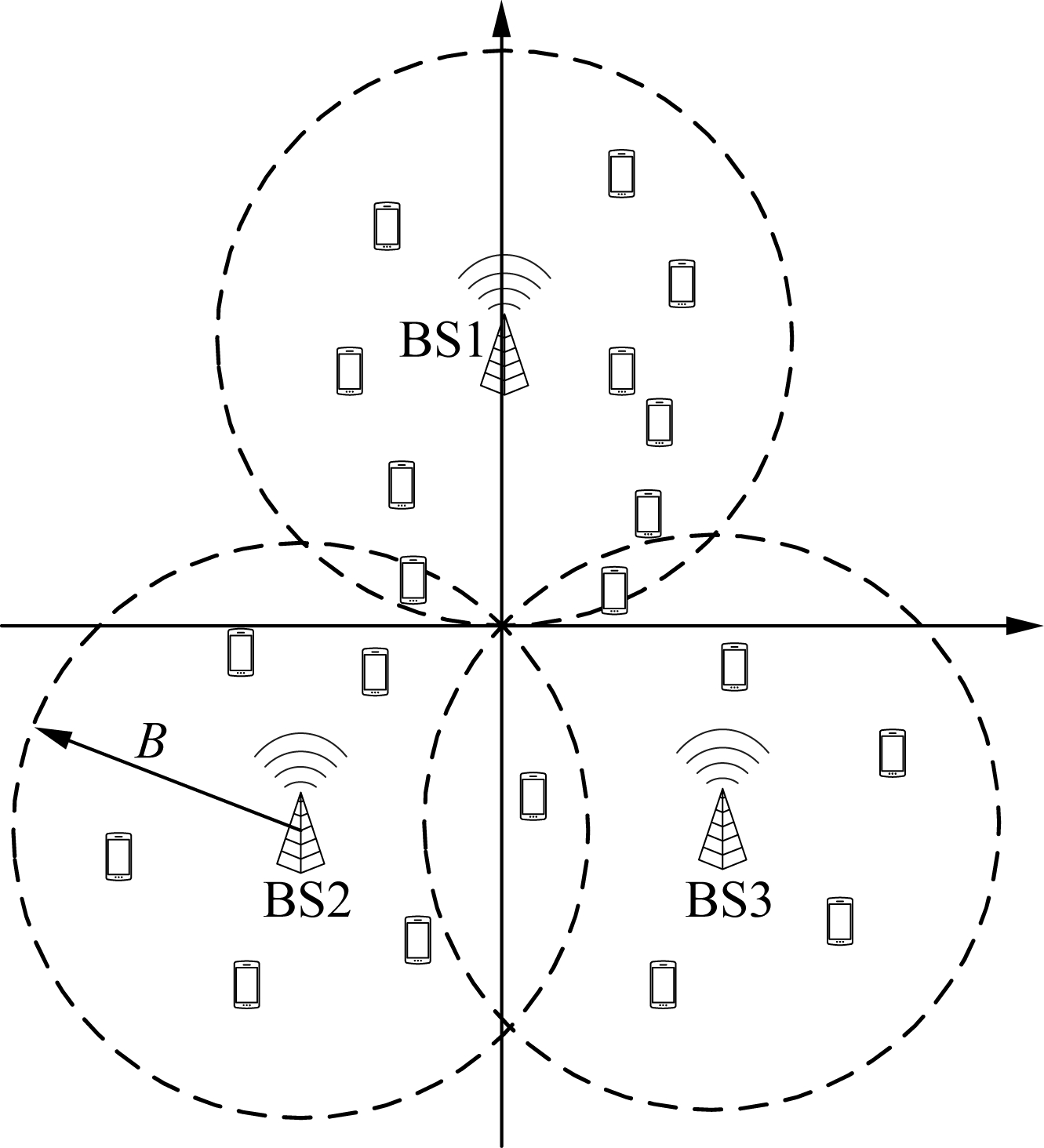
Fig.1 The simulated multi-cell cellular edge computing system
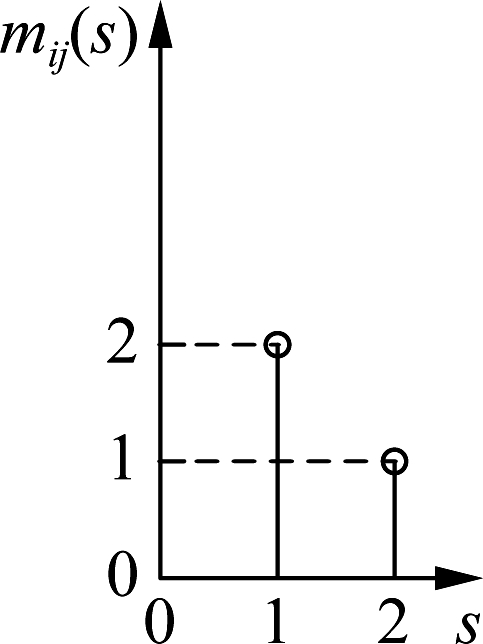
(a)
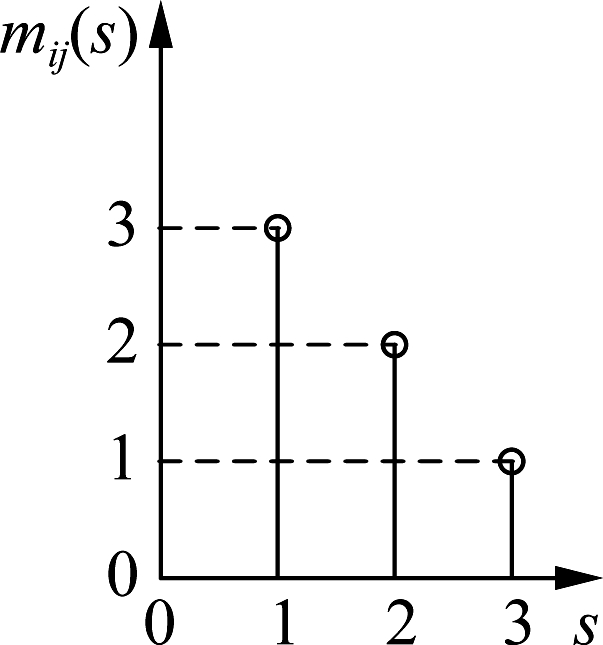
(b)
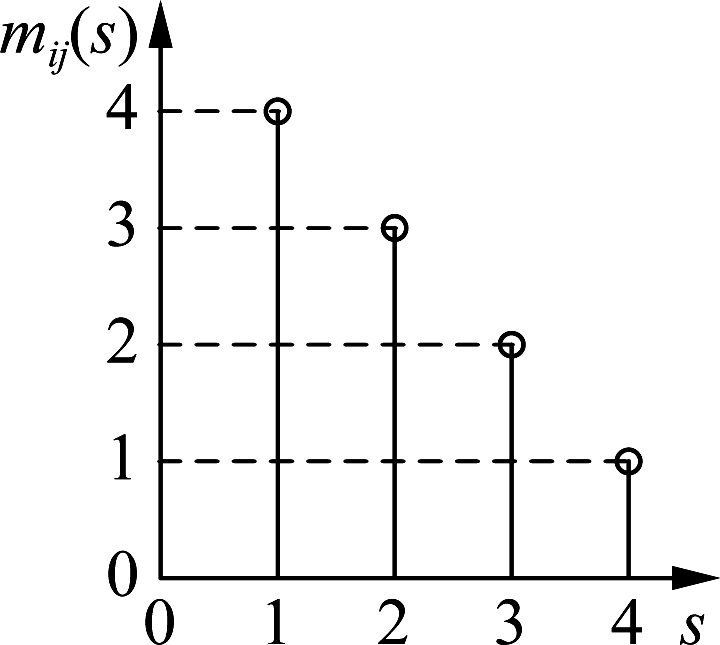
(c)
Fig.2 The function mi,j(s) used in the simulation. (a) The distance is less than or equal to 0.2 km; (b) The distance is between 0.2 and 0.6 km; (c) The distance is greater than or equal to 0.6 km
Fig. 3 shows the simulation results of the normalized value of the total delay (i.e., measured in slot) with different R (i.e., the total number of subcarriers in the system) for different resource scheduling algorithms. In this experiment, we set Fj=5 for even-numbered j and change R from 10 to 20. According to the results in the figure, we can observe that the delay of the proposed algorithm (i.e., the Dly algorithm) is always better than that of the other three queue length-based algorithms. For example, when R=16, the delay of the Que, DlyQue, and QueDly algorithm is 3.5, 3.0, and 2.7 slots, respectively, while the delay of the proposed Dly algorithm is 2.5 slots, with a 28%, 17%, and 7% off, respectively. This is due to the fact that the proposed Dly algorithm controls delay directly, while the other queue length-based algorithms do not. Therefore, we can conclude that the delay performance of the proposed delay-based algorithm is better than that of the queue length-based algorithm.
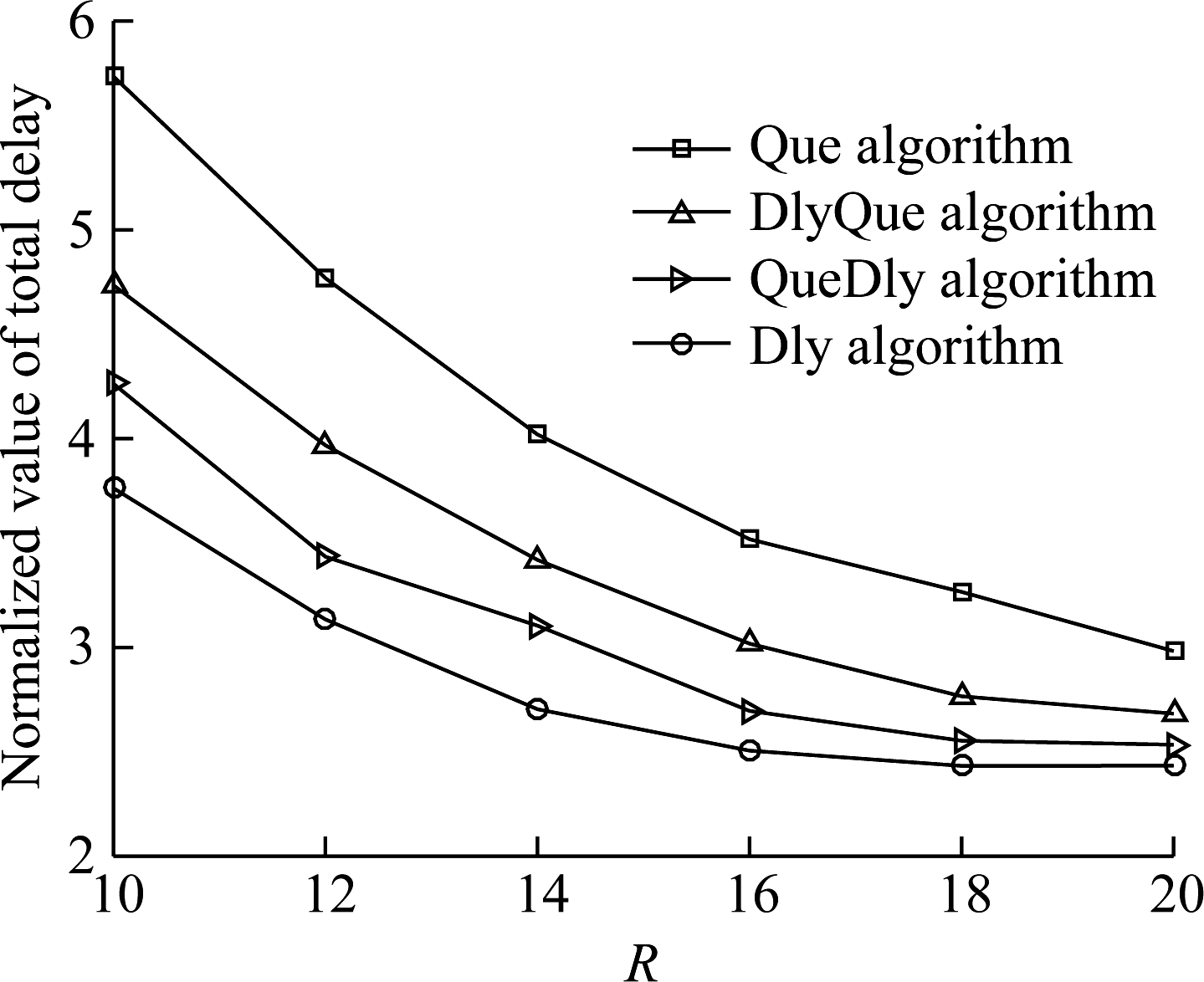
Fig.3 Impact of the total number of subcarriers on the delay performance
Fig. 4 shows the simulation results of the normalized value of the total delay for different values of the total number of VMs in even-numbered BSs. In this experiment, we set R=16 and decrease the value of Fj from 10 to 5 for even-numbered j. According to the curves in the figure, we can observe that, with the decrease of Fj for even-numbered j, the heterogeneity of BSs increases, then the difference between the proposed Dly algorithm and the other three queue length-based algorithm increases. For example, when Fj for even-numbered j is 4 (i. e., the computing resource configuration is very heterogeneous), the delay of the Que, DlyQue, and QueDly algorithms is 5.8, 5.0, and 3.2 slots, respectively, while the delay of the proposed Dly algorithm is 2.6 slots, with a 55%, 48%, and 18% improvement, respectively. Therefore, we can conclude that the proposed Dly algorithm is more capable of evenly distributing traffic load across BSs with different computing capabilities than the queue length-based algorithm.
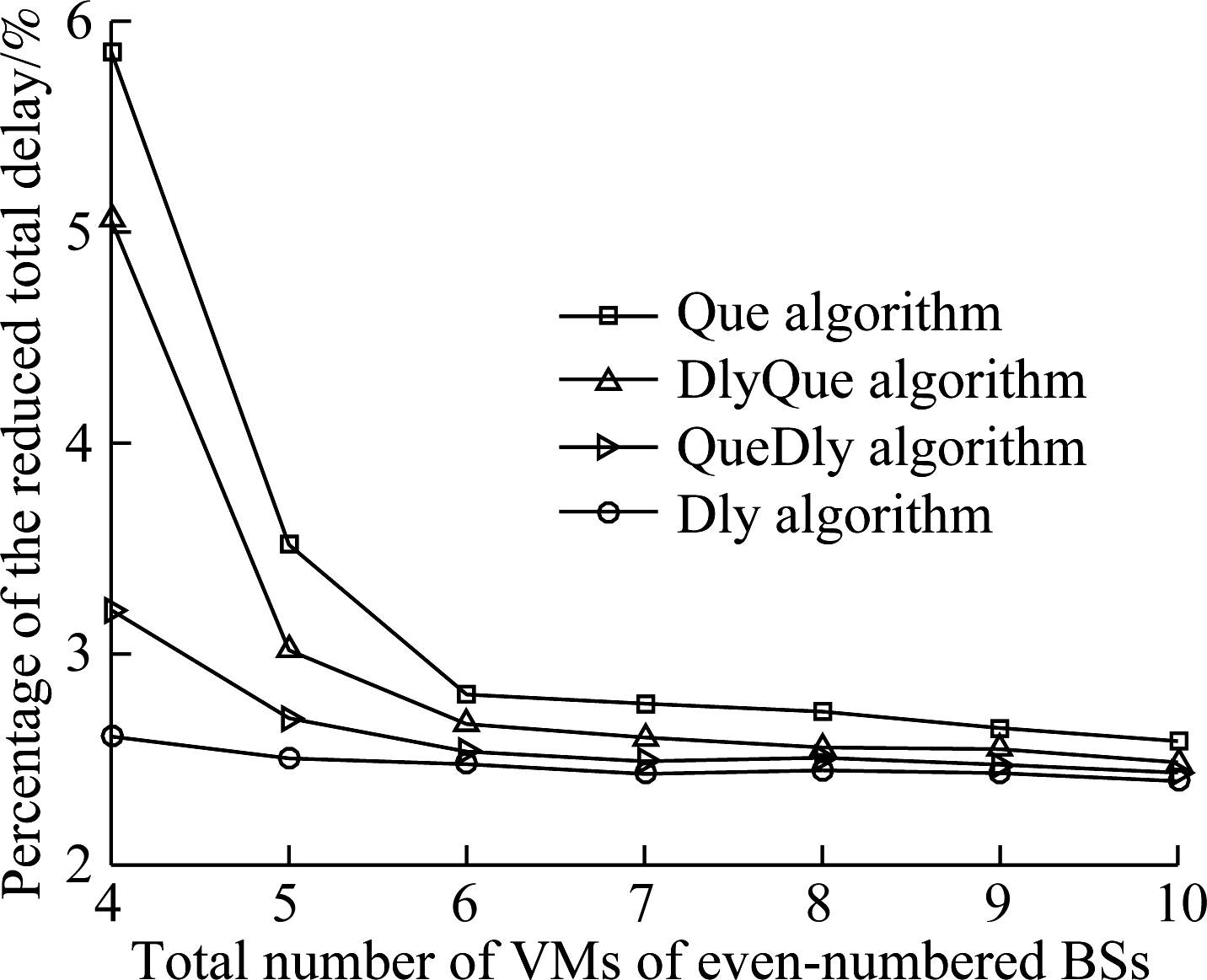
Fig.4 Impact of the heterogeneity of BSs on the delay performance
Fig.5 shows the simulation results of the percentage of the reduced total delay (i.e., (1-dDly/dQue)×100%, where dDly and dQue represent the total delay of the proposed Dly algorithm and traditional Que algorithm, respectively.) for different values of the smoothing coefficient ε. In this experiment, we set R=16 and Fj=5 for even-number j and change ε from 10-3 to 1. According to the curves in the figure, we can observe that, with the increase in ε, the difference between the proposed Dly algorithm and the traditional Que algorithm decreases. For example, when ε=10-3, the percentage of the reduced total delay is 27%; when ε=1, the percentage of the reduced total delay is 2%. Therefore, we can conclude that the traditional Que algorithm can be considered to be a special case of the proposed Dly algorithm when the smoothing coefficient ε=1.
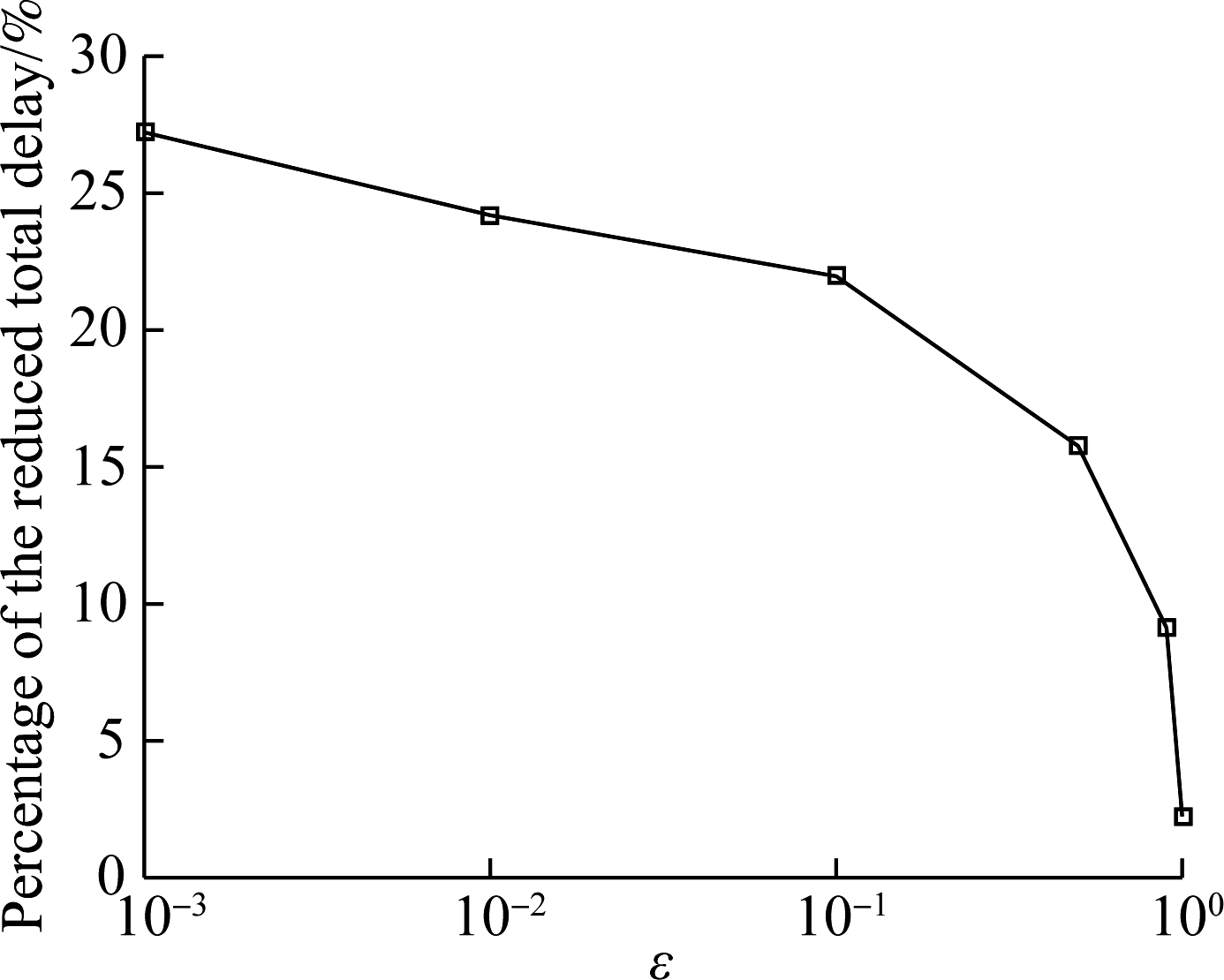
Fig.5 Impact of the smoothing coefficient on the delay performance
4 Conclusions
1) The analytical formulas of the communication delay and computing delay in multi-cell cellular edge computing systems were derived and expressed as virtual queues.
2) A novel backpressure resource scheduling algorithm was proposed to stabilize the virtual delay queues.
3) Simulation results show that the delay performance of the proposed algorithm is better than that of the queue length-based traditional algorithm, and the proposed algorithm is more capable of evenly distributing traffic load across BSs than the traditional one.
[1]Tran T X, Hajisami A, Pandey P, et al. Collaborative mobile edge computing in 5G networks: New paradigms, scenarios, and challenges[J].IEEE Communications Magazine, 2017, 55(4): 54-61. DOI:10.1109/mcom.2017.1600863.
[2]Guo H Z, Liu J J, Zhang J. Computation offloading for multi-access mobile edge computing in ultra-dense networks[J].IEEE Communications Magazine, 2018, 56(8): 14-19. DOI:10.1109/mcom.2018.1701069.
[3]Dinh T Q, La Q D, Quek T Q S, et al. Learning for computation offloading in mobile edge computing[J].IEEE Transactions on Communications, 2018, 66(12): 6353-6367. DOI:10.1109/tcomm.2018.2866572.
[4]Wang F, Xu J, Wang X, et al. Joint offloading and computing optimization in wireless powered mobile-edge computing systems [J]. IEEE Transactions on Wireless Communications, 2018, 17(3): 1784-1797.DOI: 10.1109/TWC.2017.2785305.
[5]Wu Y, Ni K J, Zhang C, et al. NOMA-assisted multi-access mobile edge computing: A joint optimization of computation offloading and time allocation[J].IEEE Transactions on Vehicular Technology, 2018, 67(12): 12244-12258. DOI:10.1109/tvt.2018.2875337.
[6]Zhou J Z, Zhang X, Wang W B. Joint resource allocation and user association for heterogeneous services in multi-access edge computing networks[J].IEEE Access, 2019, 7: 12272-12282. DOI:10.1109/access.2019.2892466.
[7]Du J B, Zhao L Q, Chu X L, et al. Enabling low-latency applications in LTE-A based mixed fog/cloud computing systems[J].IEEE Transactions on Vehicular Technology, 2019, 68(2): 1757-1771. DOI:10.1109/tvt.2018.2882991.
[8]Guo S S, Wu D L, Zhang H X, et al. Resource modeling and scheduling for mobile edge computing: A service provider’s perspective[J].IEEE Access, 2018, 6: 35611-35623. DOI:10.1109/access.2018.2851392.
[9]Chen L X, Zhou S, Xu J. Computation peer offloading for energy-constrained mobile edge computing in small-cell networks[J].ACM Transactions on Networking, 2018, 26(4): 1619-1632.
[10]Ko S W, Han K F, Huang K B. Wireless networks for mobile edge computing: Spatial modeling and latency analysis[J].IEEE Transactions on Wireless Communications, 2018, 17(8): 5225-5240. DOI:10.1109/twc.2018.2840120.
[11]Fan Q, Ansari N. Application aware workload allocation for edge computing-based IoT[J].IEEE Internet of Things Journal, 2018, 5(3): 2146-2153. DOI:10.1109/jiot.2018.2826006.
[12]Yang L C, Zhang H L, Li M, et al. Mobile edge computing empowered energy efficient task offloading in 5G[J].IEEE Transactions on Vehicular Technology, 2018, 67(7): 6398-6409. DOI:10.1109/tvt.2018.2799620.
[13]Tassiulas L, Ephremides A. Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks[J].IEEE Transactions on Automatic Control, 1992, 37(12): 1936-1948. DOI:10.1109/9.182479.
[14]Neely M J. Stochastic network optimization with application to communication and queueing systems[J].Synthesis Lectures on Communication Networks, 2010, 3(1): 1-211. DOI:10.2200/s00271ed1v01y201006cnt007.
[15]Lü X, Ni W, Tian H, et al. Optimal schedule of mobile edge computing for Internet of Things using partial information [J]. IEEE Journal on Selected Areas in Communications, 2017, 35(11): 2606-2615. DOI: 10.1109/JSAC.2017.2760186.
[16]Kim Y, Kwak J, Chong S. Dual-side optimization for cost-delay tradeoff in mobile edge computing[J].IEEE Transactions on Vehicular Technology, 2018, 67(2): 1765-1781. DOI:10.1109/tvt.2017.2762423.
[17]Feng H, Llorca J, Tulino A M, et al. Optimal control of wireless computing networks[J].IEEE Transactions on Wireless Communications, 2018, 17(12): 8283-8298. DOI:10.1109/twc.2018.2875740.
[18]Du J B, Yu F R, Chu X L, et al. Computation offloading and resource allocation in vehicular networks based on dual-side cost minimization[J].IEEE Transactions on Vehicular Technology, 2019, 68(2): 1079-1092. DOI:10.1109/tvt.2018.2883156.
[19]Kim Y, Lee H W, Chong S. Mobile computation offloading for application throughput fairness and energy efficiency[J].IEEE Transactions on Wireless Communications, 2019, 18(1): 3-19. DOI:10.1109/twc.2018.2868679.