In recent years, optical secure communication based on chaotic synchronization has become an active area of research in the cross-convergence of international nonlinear science and information science [1-3]. Scientists proposed a variety of chaotic synchronization methods and applied them to secure communications. Kocamaz et al. [4] studied the passive control-based chaos synchronization with circuit design for secure communication and found that a single state passivity-based synchronization signal can be effectively used for secure data communication applications in the real environment. Mata-Machuca and Aguilar-Lopez[5] studied the adaptative synchronization of complex dynamical networks with fractional-order nodes and its application in secure communications employing chaotic parameter modulation. Durdu and 
studied the exponential stability for encrypts of signals in the synchronization of chaotic systems. Smaoui et al.[7]proposed a novel secure communication scheme based on the Karhunen Loéve decomposition and the synchronization of a master and a slave hyperchaotic Lü system. However, the low-dimensional chaotic system is easily deciphered, and hyperchaotic systems are not suitable for practical applications due to their complex structure [8].
With the discovery of delayed chaotic systems, new ideas are proposed for secure communication. Since the time-delayed chaotic system can generate multiple positive Lyapunov exponents and is not limited by the system dimension, a large number of studies on time-delayed chaotic systems have been carried out. Oden et al. [9] proposed a chaos communication scheme based on a chaotic optical phase carrier generated with an optoelectronic oscillator with nonlinear time-delay feedback. Maheri and Arifin[10] put forward the synchronization of chaotic systems which is defined based on the exponential stability for the encrypts of signals. Abd et al.[11] developed a new cascade-coupled chaotic synchronization model based on the first-order nonlinear time-delayed chaotic system. However, as one of the best communication models, the delayed nonlinear Schrödinger equation is rarely used for secure communication. In fact, the propagation model of optical fibers is described by the nonlinear Schrödinger equation, so the optical fiber transmission system cannot be separated from the nonlinear Schrödinger equation. Yin et al.[12] proposed an optical secure communication scheme based on chaos synchronization,which provides a theoretical basis for studying the delayed nonlinear Schrodinger equation. Therefore, this paper will study exponential synchronization for the delayed nonlinear Schrödinger equation.
1 Chaos Generation
This paper devises optical secure communication based on the perturbed nonlinear Schrödinger equation[13-15] by chaos synchronization. The nonlinear Schrodinger equation is
iut+uxx+α|u|2u+i[γ1uxxx+γ2|u|2ux+
γ3(|u|2)xu]=μucosω(x-ct)
(1)
where γi(i=1,2,3)are real parameters;α is a positive constant;μ,ω≥0 denote the amplitude and the frequency of the parametric excitation, respectively.More details for the model can be seen in Refs.[13,15].
Suppose that Eq.(1) has traveling wave solutions in the form
μ(x,t)=a(ξ)exp(-iΩt) ξ=x-ct c>0
(2)
where c represents the transmission speed of wave.
By the method of Ref.[13], we have
γ1φ″-cφ+λφ3=μφcos(ωξ)
(3)
where 
refers to the parameter of linear and nonlinear terms. Eq.(3) is a fiber-optic signal transmission system in an ideal environment.
By setting γ1=1 and using transformation 
Eq.(3) can be rewritten as a set of two autonomous differential equations as below:
(4)
Next, we consider the delayed system (4) which can be written as
(5)
If u=0，Eq.(5) is changed into
(6)
1.1 Analysis of homoclinic orbits
It is known from the calculation that Eq.(6) has three equilibrium points, 
and E3(0,0). Let JEi be the Jacobian matrix for these equilibrium points, then we obtain
It is easy to find that its eigenvalues are 
Therefore, we conclude that E1and E2are the center equilibriums and E3is a saddle point for any c>0.Furthermore, Eq.(6) has the following Hamiltonian function:
(7)
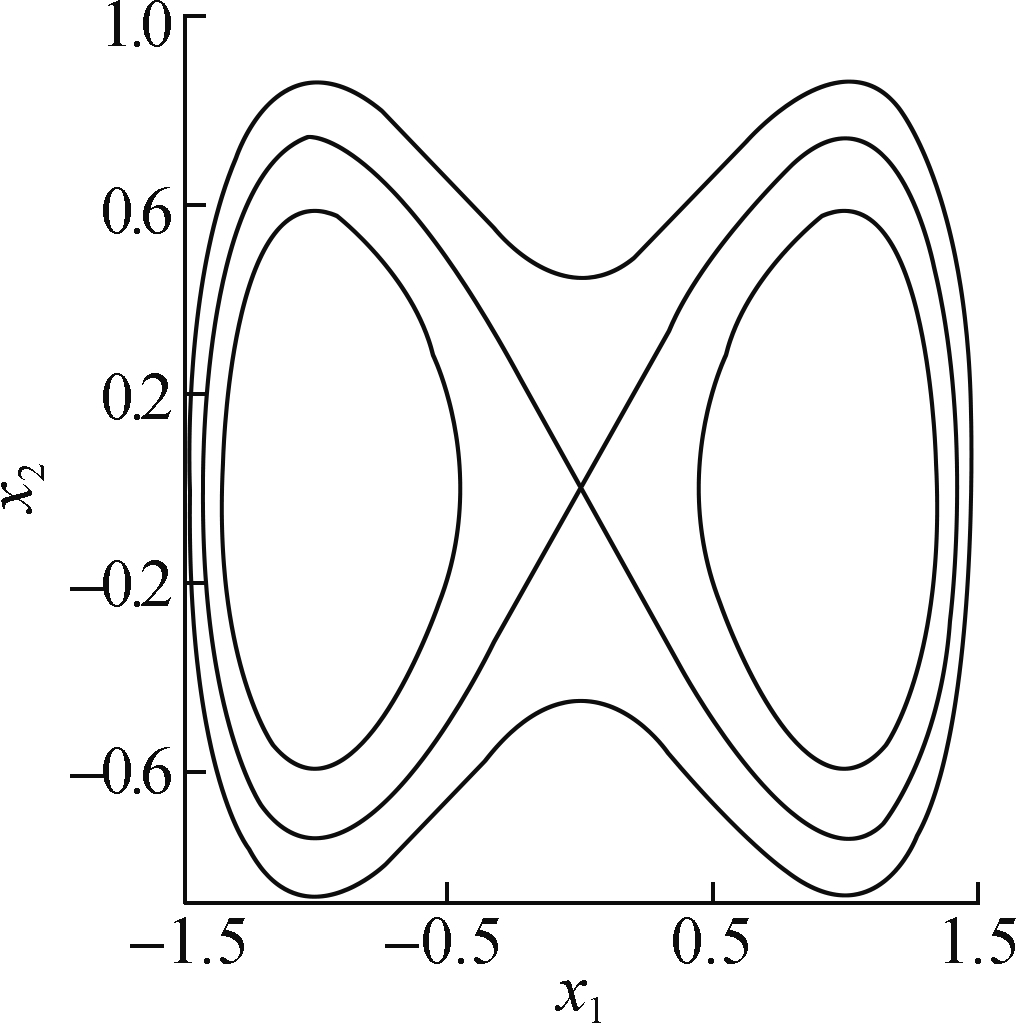
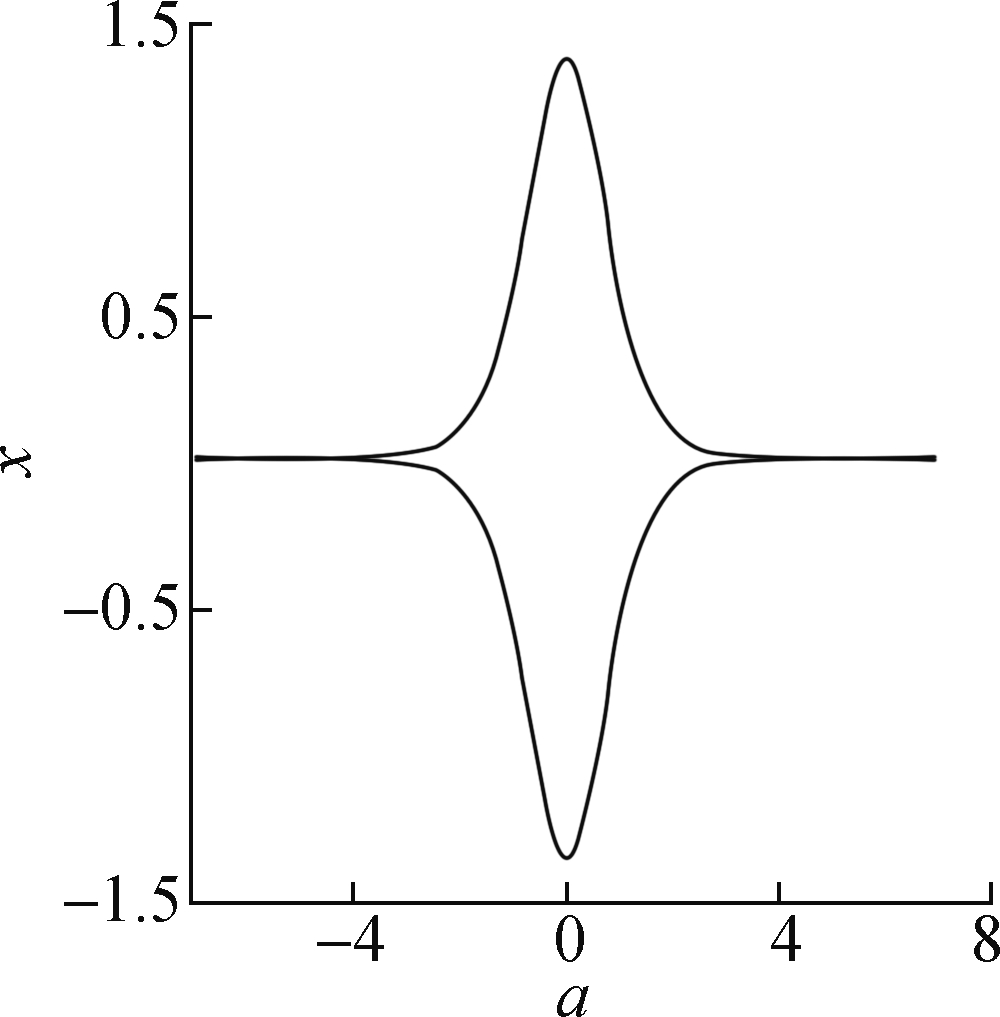
where h is a constant. It is noted that the Hamiltonian function is composed of two homoclinic orbits at point E3. According to the bifurcation theory[13], Eq.(6) has two optical solitons followed by two homoclinic orbits: the positive one achieves its crest at 
(see Fig.1 as λ=2.2,c=2.2).
(a)
(b)
Fig.1 The profile of soliton in the unperturbed system. (a) Phase portrait of Eq.(6); (b) The profile of solitary
1.2 Analysis of chaos
The optical soliton always turns into chaos under the perturbation formed as Eq.(1). We cannot ignore such a fact that the solitary wave solution of the nonlinear evolution equation is equivalent to the homoclinic orbit of the corresponding dynamic system. In this section, we will prove that homoclinic orbit evolves into chaos under external disturbance by using the Melnikov method.
Unperturbed homoclinic orbits can be written as (a,b)=(a0(t),b0(t)). According to the Melnikov method, the Melnikov function for Eq.(3) is defined as
(8)
where 
is a function of ω.
According to the Melnikov method, chaos occur if M(t0)=0 and M′(t0)≠0 for some t0. We observe that M(0)=0 and M′(0)≠0. Hence, the optical soliton can turn into chaos under the perturbation.
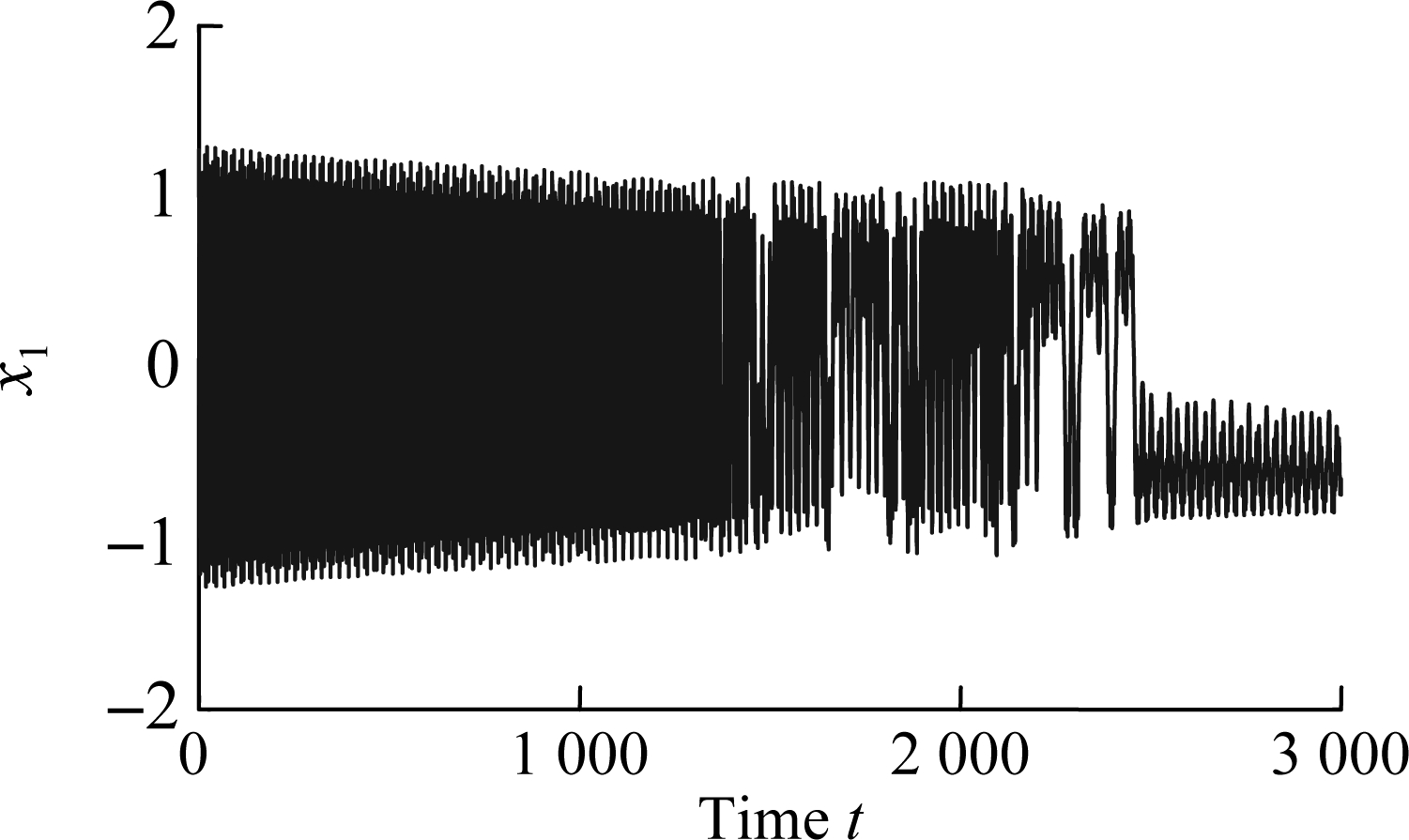
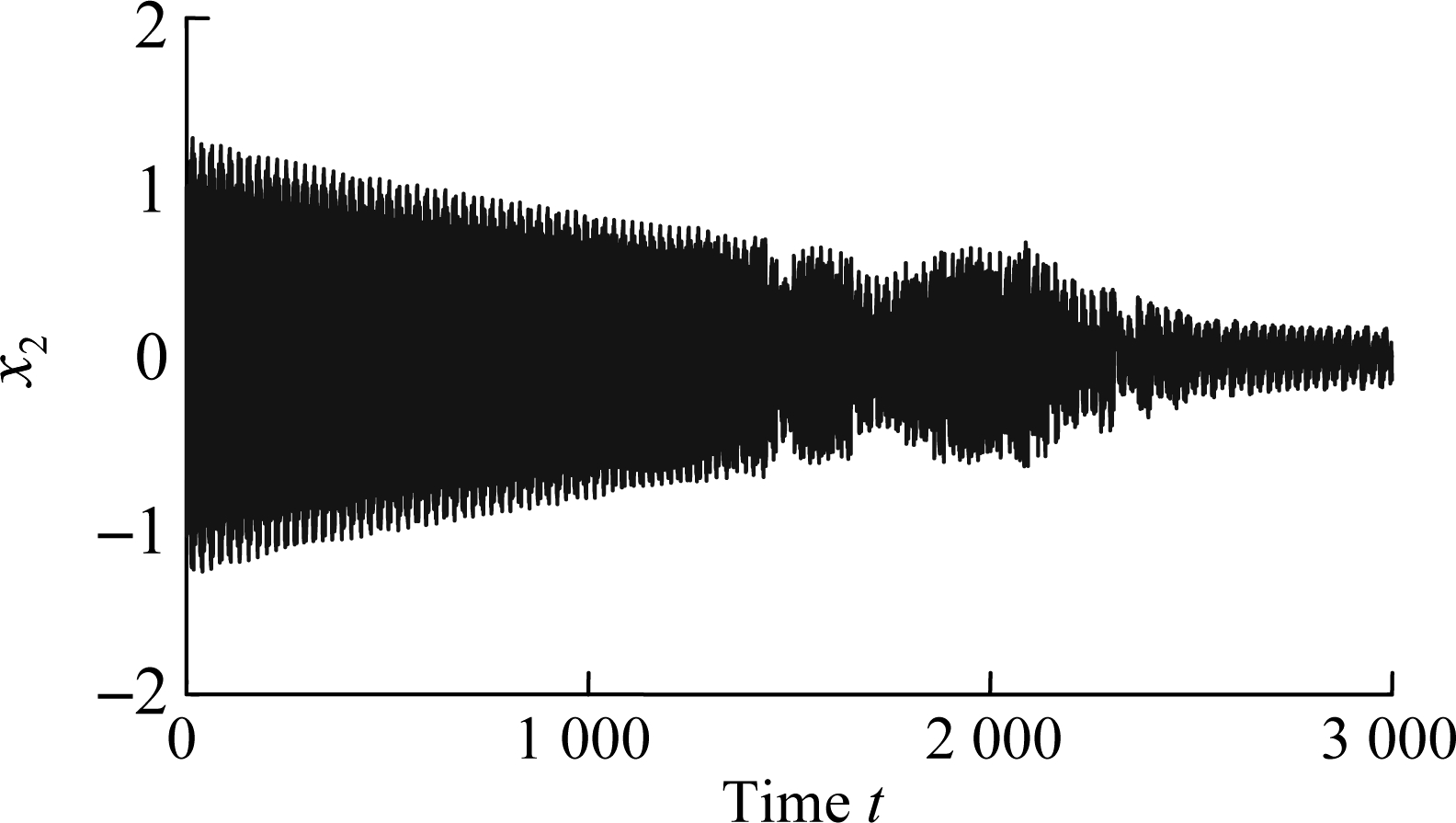
To verify the above fact, we will investigate the Lyapunov exponents, phase portraits and time series of Eq.(6).The parameters of Eq.(6) used for simulations are listed as follows: ω=0.27,τ=0.1,c=0.8,λ=2.2, μ=0.47. Then the Lyapunov exponents are shown in Fig.2, the phase portrait is shown in Fig.3, and the time series are shown in Fig.4. As can be seen in Fig.2, the Lyapunov exponents are positive so that the motion of Eq.(3) is chaotic. The phase portrait and corresponding time series also show the existence of chaos.
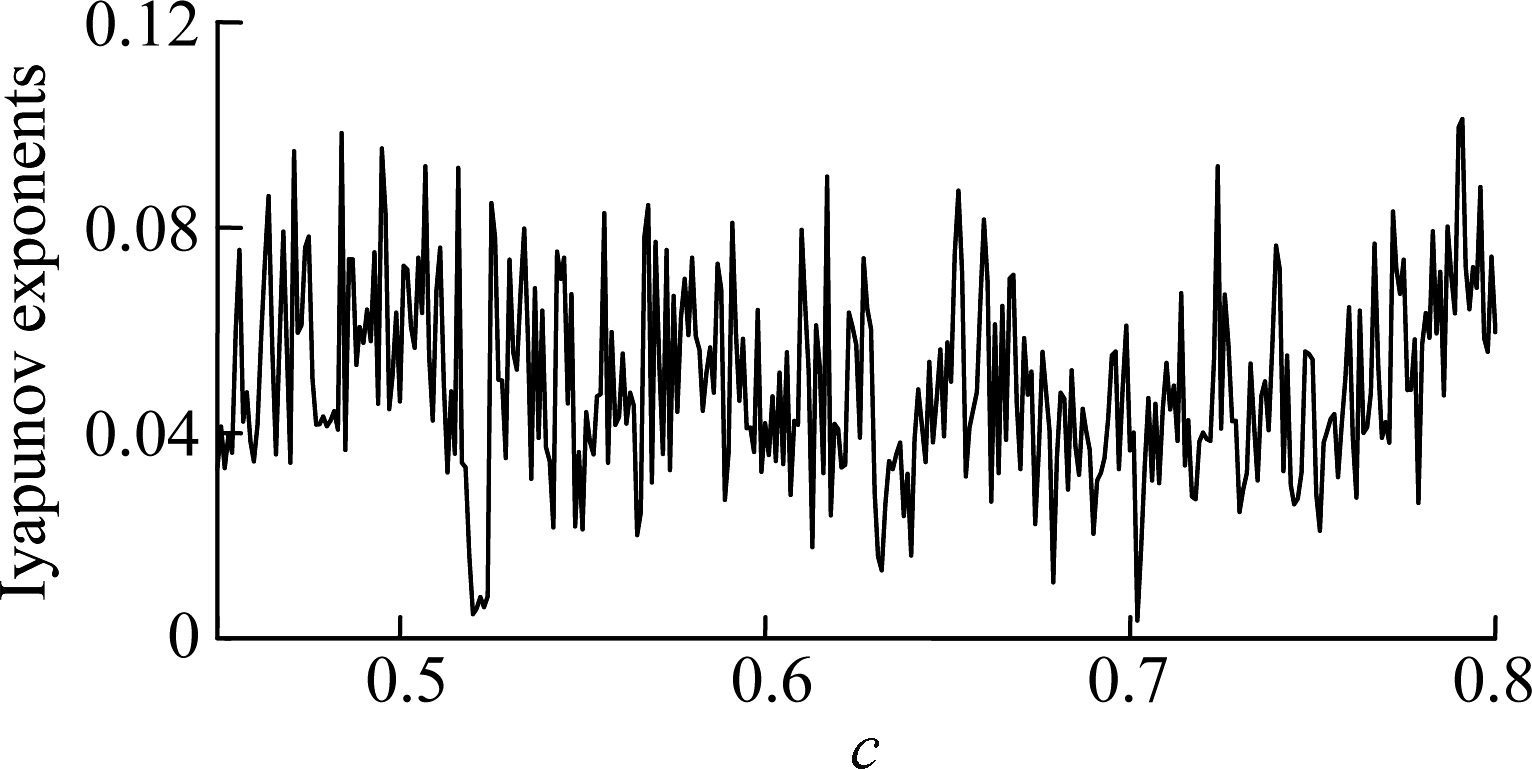
Fig.2 Lyapunov exponents versus c of system (5)
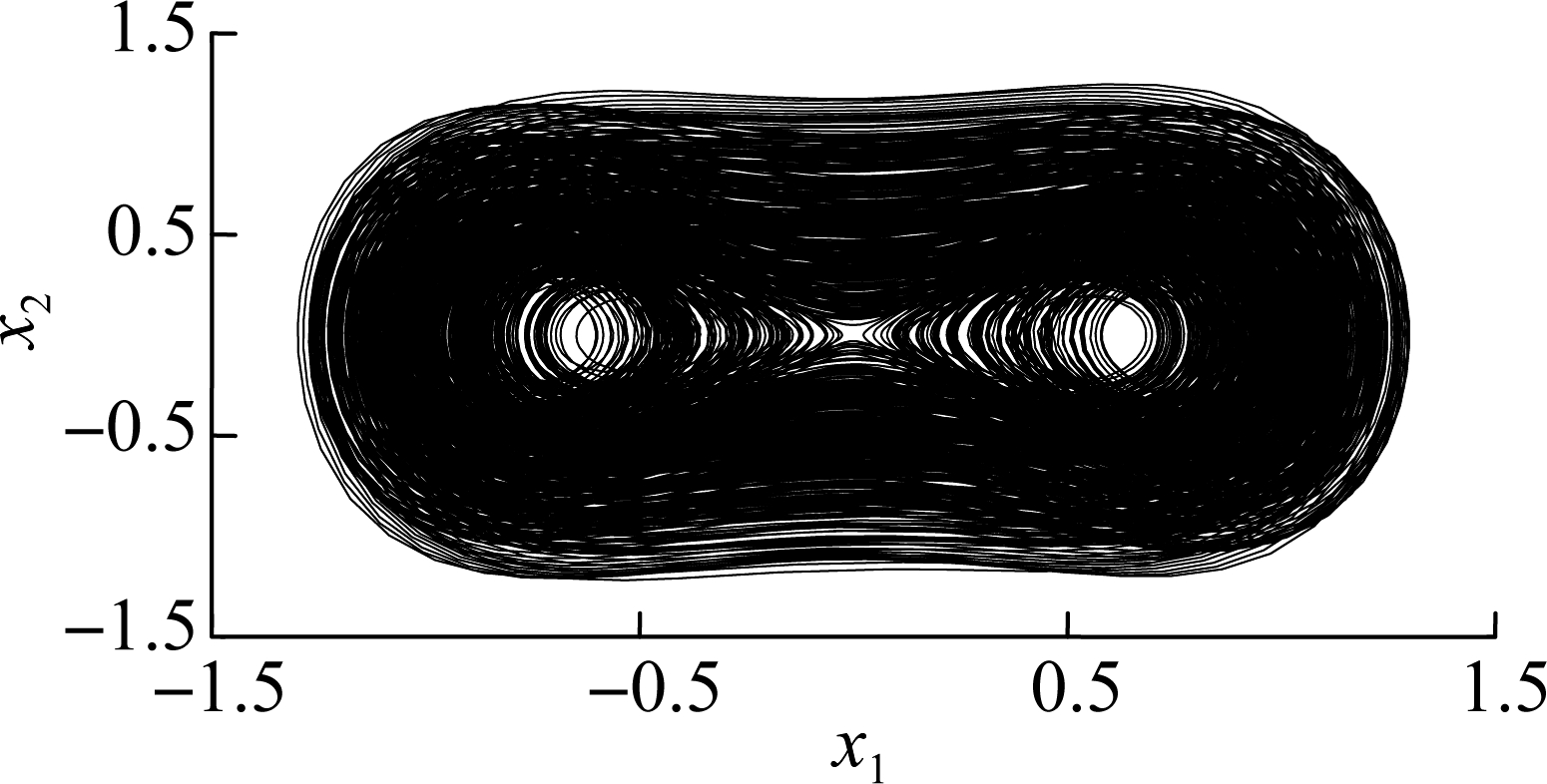
Fig.3 Phase portrait x1-x2
(a)
(b)
Fig.4 The time series of x1 and x2. (a) x1; (b) x2
2 Problem Description
2.1 Exponential stability
In this section, we consider the delayed system (4).For ease of description, the delayed system can be written as
(9)
Let Eq.(9) for the drive system and the correspond-ing response system be as below:
(10)
where 
are parameters to be estimated; μ1 and μ2 are the controllers to be designed to achieve exponential synchronization between the drive system and the response system.
The error signal is selected as e(t)=y(t)-x(t), and the controller is the error feedback control as below:
(11)
where K is the control gain matrix which makes the trajectory between the driving chaotic system (9) and the response chaotic system (10) achieve exponential synchronization.
Definition 1 The system is exponentially stable if θ>0,ρ>0 and for each e(t) solution of the system, the following inequality holds:
(12)
where θ is the exponential convergence rate; ‖·‖ denotes the Euclidean norm of a vector.
The controller is selected as the form of (11) and the error variables between systems (9) and (10) are
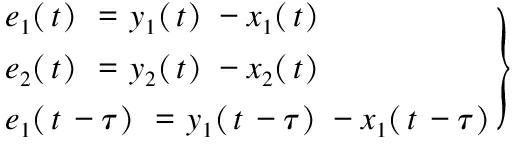
(13)
Then, we obtain the error system:
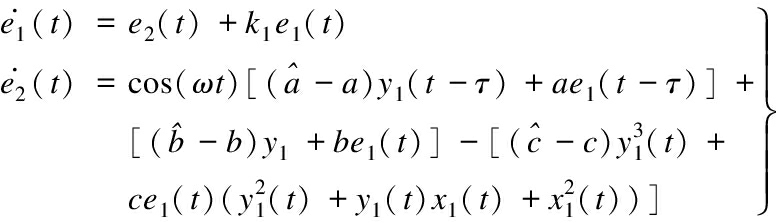
(14)
Furthermore, let e(λ)={e1(λ),e2(λ)}T=φ(λ),λ∈[-τ,0].
2.2 Synchronization based on exponential stability
Theorem 1 The response system(10) will synchro-nize exponentially with the driving system (9) for any initial values. If φ(λ)≠0, the exponential synchron-ization controls are chosen as control laws and the following matrix inequalities hold:
The undetermined parameters of response system (10) are as below:
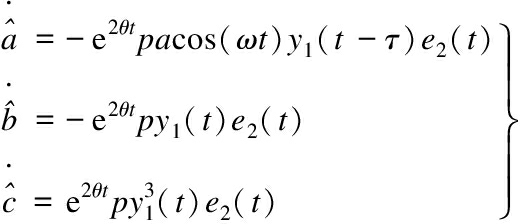
(15)
where p,q,θ>0.
Proof Let
(16)
where 
respectively. The time derivatives of function (16) for the error system (14) and control laws (11) are
(17)
Substituting Eq.(14) into Eq.(17) yields
eTAe
(18)
where
From Theorem 1, A<0,and we obtain 
V(e(0))=
(19)
For η>0,
(20)
For
V(e(t))≥e2θp‖e(λ)‖2
(21)
Therefore,
‖2
(22)
That is
(23)
where ρ=ηp-1. Therefore, in this case, the synchronization of driving system (9) and response system (10) are sufficiently achieved.
3 Results and Discussion
3.1 Simulation
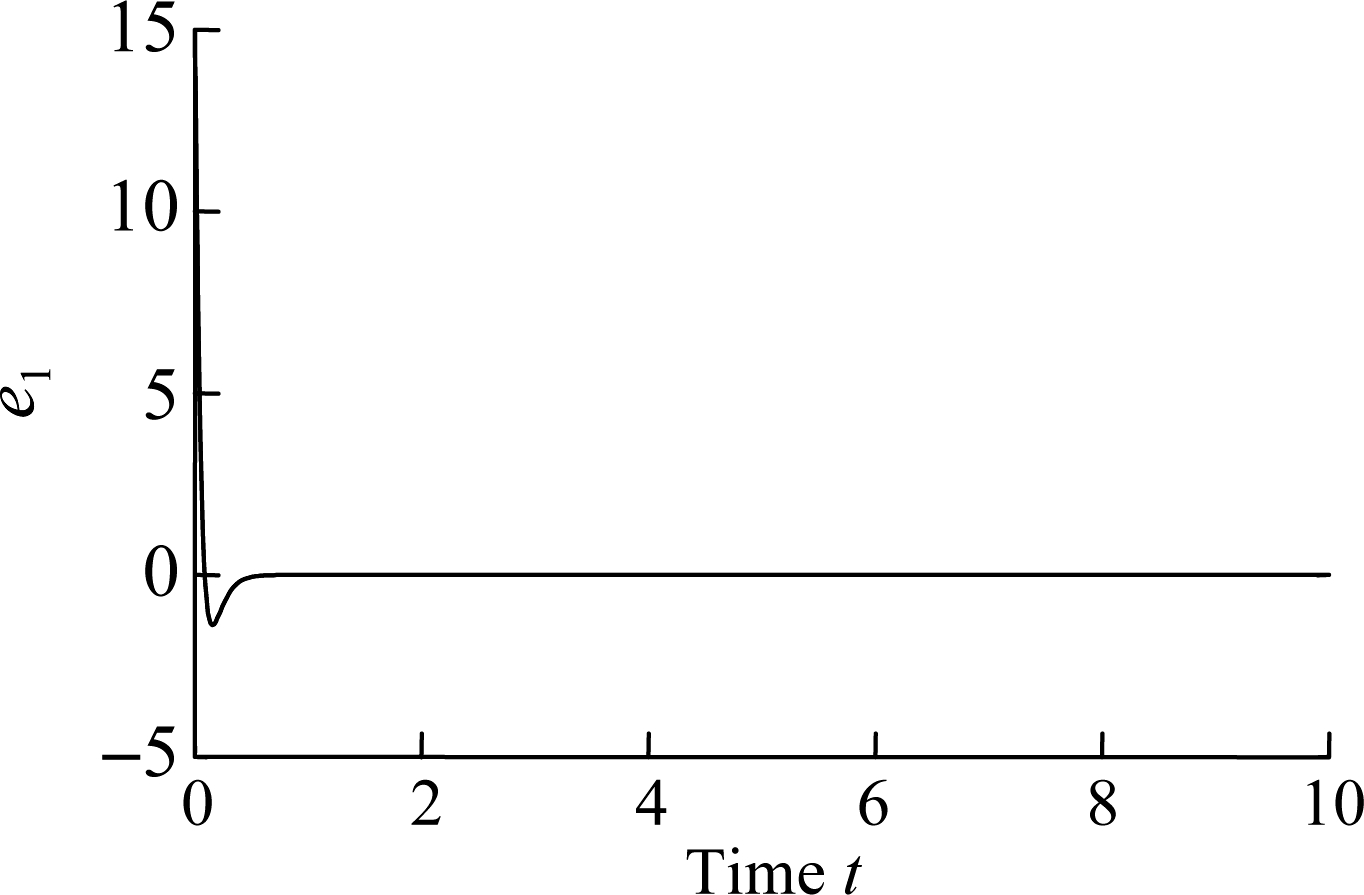
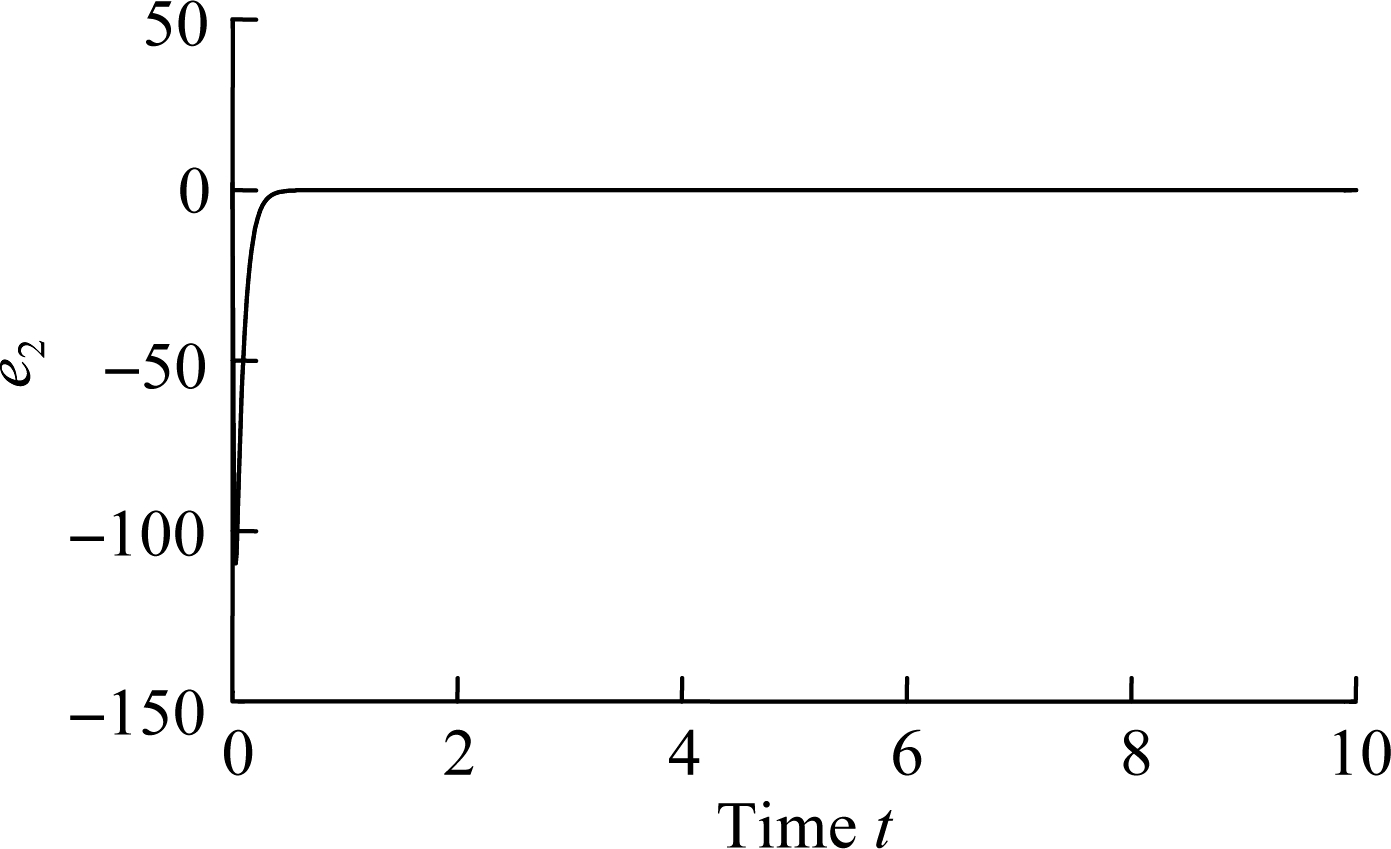
In this section, we will analyze the performance of the delay chaotic secure communication system. System (12) was simulated in Matlab-Simulink and the results are shown in Fig.5. The initial conditions of the response system and driving system are x0=[0.03 0.01]T, y0=[15 2]T, respectively. The initial value of the parameters is chosen as 
When the exponential convergence rate θ=0.2, we obtain p=2.6, q=0.52, k1=-15.5, k2=-13.8.
(a)
(b)
Fig.5 The error curves. (a) Error e1;(b) Error e2
Fig.5 shows the synchronization difference (error) between systems (9) and (10). It is obvious that the error system tends to zero very fast(within 1s), indicating that the signal is sent and received faster with a better accuracy.
3.2 Discussion
Undoubtedly, there are abundant research results regarding chaotic secure communication, especially for the increasing number of alternative communication models. Considering that the propagation model of optical fibers is described by the nonlinear Schrchrödinger equation as we mentioned in section 1, the nonlinear Schrchrödinger equation with time delay is studied and applied to secure communication in this paper. Firstly, the optical fiber communication model studied in this paper is different from that in Refs.[9,11-12]. This paper studied the delay nonlinear Schrchrödinger equation while Ref.[9]studied the chaos communication scheme based on a chaotic optical phase carrier generated with an optoelectronic oscillator. Ref.[11] studied the chaotic synchronization model based on the first-order nonlinear time-delayed Lü system. Secondly, the chaotic phenomena in this paper (see Fig.3) are different from those in the famous Lorenz system, Chen system and Lü system. Thirdly, the exponential synchronization controller designed in this paper is similar to that in Ref.[16]. Finally, the numerical simulation results show that systems (9) and (10) achieve synchronization in a very short time. By comparing with Refs.[10,12], the synchronization speed in this paper is the fastest.
4 Conclusions
1) In this paper, the optical secure communication based on the delayed nonlinear Schrödinger equation was studied. Chaotic signals are obtained with periodic perturbation. Lyapunov exponential spectra, phase portrait and time series are used to prove the existence of chaotic signals.
2) The sufficient criteria for the exponential synchronization of time-delay chaotic systems were obtained by employing the Lyapunov stability theory and linear matrix inequality technology.
3) Despite the differences between the driving system and the response system, the exponential synchronization can still be achieved by the driving-responding synchronization method. Numerical simulation shows that the error tends to zero in a very short time (within 1 s).
[1]Vaseghi B, Pourmina M A , Mobayen S. Secure communication in wireless sensor networks based on chaos synchronization using adaptive sliding mode control [J].Nonlinear Dynamics, 2017,89(3): 1689-1704. DOI: 10.1007/s11071-017-3543-9.
[2]Xiong L, Liu Z L, Zhang X G. Dynamical analysis, synchronization, circuit design, and secure communication of a novel hyperchaotic system[J]. Complexity, 2017, 2017: 1-23. DOI:10.1155/2017/4962739.
[3]Acho L. A chaotic secure communication system design based on iterative learning control theory[J].Applied Sciences, 2016, 6(10): 311. DOI:10.3390/app6100311.
[4]Kocamaz U E, Cicek S, Uyaroglu Y. Secure communication with chaos and electronic circuit design using passivity-based synchronization [J]. Journal of Circuits systems and Computers, 2018,27(4)：1850057. DOI: 10.1142/S0218126618500573.
[5]Mata-Machuca J L, Aguilar-Lopez R. Adaptative synchronization in multi-output fractional-order complex dynamical networks and secure communications [J]. European Physical Journal Plus, 2018,133：14. DOI: 10.1140/epjp/i2018-11840-4.
[6]Durdu A, 
Y. The shortest synchronization time with optimal fractional order value using a novel chaotic attractor based on secure communication[J]. Chaos, Solitons & Fractals, 2017, 104: 98-106. DOI:10.1016/j.chaos.2017.08.008.
[7]Smaoui N, Zribi M, Elmokadem T. A novel secure communication scheme based on the Karhunen-Loéve decomposition and the synchronization of hyperchaotic Lü systems[J]. Nonlinear Dynamics, 2017, 90(1): 271-285. DOI:10.1007/s11071-017-3660-5.
[8]Ding M Z, Ding E J, Ditto W L, et al. Control and synchronization of chaos in high dimensional systems: Review of some recent results[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 1997, 7(4): 644-652. DOI:10.1063/1.166284.
[9]Oden J, Lavrov R, Chembo Y K, et al. Multi-Gbit/s optical phase chaos communications using a time-delayed optoelectronic oscillator with a three-wave interferometer nonlinearity[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2017, 27(11): 114311. DOI:10.1063/1.5007867.
[10]Maheri M, Md Arifin N. Application adaptive exponential synchronization of chaotic dynamical systems in secure communications[J]. Advances in Difference Equations, 2017, 2017: 96. DOI:10.1186/s13662-017-1158-6.
[11]Abd M H, Tahir F R, Al-Suhail G A, et al. An adaptive observer synchronization using chaotic time-delay system for secure communication [J].Nonlinear Dynamics, 2017, 90(4): 2583-2598.
[12]Yin J L, Duan X C, Tian L X. Optical secure communication modeled by the perturbed nonlinear Schrödinger equation[J]. Optical and Quantum Electronics, 2017, 49(10): 317. DOI:10.1007/s11082-017-1111-7.
[13]Yin J L, Zhao L W, Tian L X. Melnikov’s criteria and chaos analysis in the nonlinear Schrödinger equation with Kerr law nonlinearity[J]. Abstract and Applied Analysis, 2014, 2014: 1-12. DOI:10.1155/2014/650781.
[14]Taghizadeh N, Mirzazadeh M, Mahmoodirad A. Application of Kudryashov method for high-order nonlinear Schrödinger equation[J]. Indian Journal of Physics, 2013, 87(8): 781-785. DOI:10.1007/s12648-013-0296-2.
[15]Gao H, Xu T Z, Wang G W. Optical solitons for the perturbed nonlinear Schrodinger equation with Kerr law and non-Kerr law nonlinearity[J]. Zeitschrift Fur Naturforschung Section A—A Journal of Physical Sciences, 2018,73(4): 315-321.DOI: 10.1515/zna-2017-0400.
[16]Wan P, Sun D H, Chen D, et al. Exponential synchronization of inertial reaction-diffusion coupled neural networks with proportional delay via periodically intermittent control[J].Neurocomputing, 2019, 356: 195-205. DOI:10.1016/j.neucom.2019.05.028.