As a new group of non-homogeneous materials, functionally graded (FG) materials have some desirable performances to meet special needs in engineering design[1-2]. Recently, with the rapid development of micro-technologies, FG materials have been widely applied in the micro-electro-mechanical system (MEMS) and nano-electro-mechanical system (NEMS). Many micro-scale experiments[3-4] observed the significant size-dependent effects on the mechanical and physical properties of micro sized systems. Due to the classical continuum theory failing to capture the size effects of microstructures, Lim et al.[5] extended Eringen’s nonlocal elasticity theory[6] to include the nonlocality of higher-order strain gradients, and firstly proposed the nonlocal strain gradient theory (NSGT) within the thermodynamic framework. Afterwards, the NSGT was extensively used to study the size-dependent behaviors of small scaled uniform and homogeneous structures[7-13].
The nonlocal strain gradient models have been developed to study the size-dependent behaviors of FG microstructures[14-17]. For instance, Ebrahimi et al.[18] derived the buckling equations of a transverse FG higher-order curved nanobeam by using Hamilton’s principle. Then, the closed form solutions are obtained by employing the Fourier series method. Sahmani et al.[19] explored the nonlinear vibration characteristics of multilayer FG grapheme platelet reinforced composite nanobeams subjected to axial loads based on the NSGT and third-order shear deformable beam theory. In this work, the governing equation and associated boundary conditions are developed and solved with the aid of Hamilton’s principle and Galerkin method. Lü et al.[20-21] investigated the influence of material uncertainties caused by defects on the nonlinear bending and free vibration behaviors of transverse FG nanobeams. Al-Shujairi et al.[22-23] studied the dynamic stability, buckling and free vibration behaviors of transverse FG sandwich microbeams according to the NSGT, established the governing equations by using Hamilton’s principle and solved them via the differential quadrature method.
In addition to these transverse FG microstructures aforementioned, some works focused on the mechanical behaviors of axially functionally graded (AFG) microstructures, whose material properties or geometrical size vary along the length direction. For example, Ghayesh et al.[24] examined the size effects of the nonlinear bending and forced vibrations of an AFG Bernoulli-Euler tapered microbeam by using the modified couple stress theory, Hamilton’s principle, Galerkin method and Newton-Raphson technique. With the help of NSGT and Hamilton’s principle, Rajasekaran et al.[25] and Khaniki et al.[26] investigated the mechanical behaviors of non-uniform nanobeams with a variable cross section along their length. In their works, the governing equations were solved, respectively, by employing the finite element method and the generalized differential quadrature method. Li et al.[27] used the NSGT to examine the bending, buckling and free vibrations of AFG microbeams with the aid of Hamilton’s principle and the generalized differential quadrature method. Based on the NSGT, Karami et al.[28] studied the free vibration behaviors of AFG porous nanotubes by using Hamilton’s principle and the generalized differential quadrature method.
It can be seen from the previous published literature that the studies of static bending of the AFG microbeams are more limited than those about the bending of regular and transverse FG microbeams. To the best of authors’ knowledge, there is no reported work related to the comprehensive analysis on the bending behavior of AFG microbeams bearing concentrated and various distributed loads. This paper will fill this gap in the literature. The size effect is taken into account with the NSGT. The material properties of the AFG microbeam are assumed to vary as a sinusoidal form. The equations of motion and the related boundary conditions are derived via the minimum potential energy principle. The numerical solutions of the governing differential equations are reduced to ordinary equations by means of the Galerkin method. The effects of the ratio of the material length scale parameter to the beam height, the material nonlocal parameter and the FG parameter on the bending deformation of a simply supported microbeam are examined in detail. Some of the results in the present study are compared with existing results in the literature and a good agreement has been observed.
1 Nonlocal Strain Gradient Theory
According to the NSGT[5], the nonlocal strain field of every particle in an elastic continuum contains a high-order strain tensor, and the nonlocal stress at a reference point depends on both the nonlocal strain filed within the region near the reference point. The total stress tensor can be written as
(1)
where the classical nonlocal stress tensor ![]() are, respectively, defined as
are, respectively, defined as
(2)
(3)
where ξ is the material nonlocal parameter; εxx and εxx,x , respectively, denote the strain and strain gradient components; l is the material length scale parameter; E denotes the elastic modulus.
Substituting Eqs.(2) and (3) into Eq.(1), one can obtain the unified form of the constitutive relation based on the NSGT as
(4)
It is of interest that the constitutive equation based on the nonlocal elasticity theory (NET) or pure strain gradient theory (SGT) can be recovered by setting l = 0 or ξ = 0 in Eq.(4), and the constitutive equation based on the classical elasticity theory (CET) is recovered by setting l = 0 and ξ = 0 simultaneously in Eq.(4).
2 Governing Equations
Consider an AFG simply supported microbeam that has length L, thickness h and width b, as illustrated in Fig.1. The elastic modulus E varying continuously and smoothly along the x direction can be expressed as
(5)
where E0 denotes Young’s modulus when x = 0; η is the FG parameter and it dictates the material variation profile through the length of the size-dependent AFG beam.
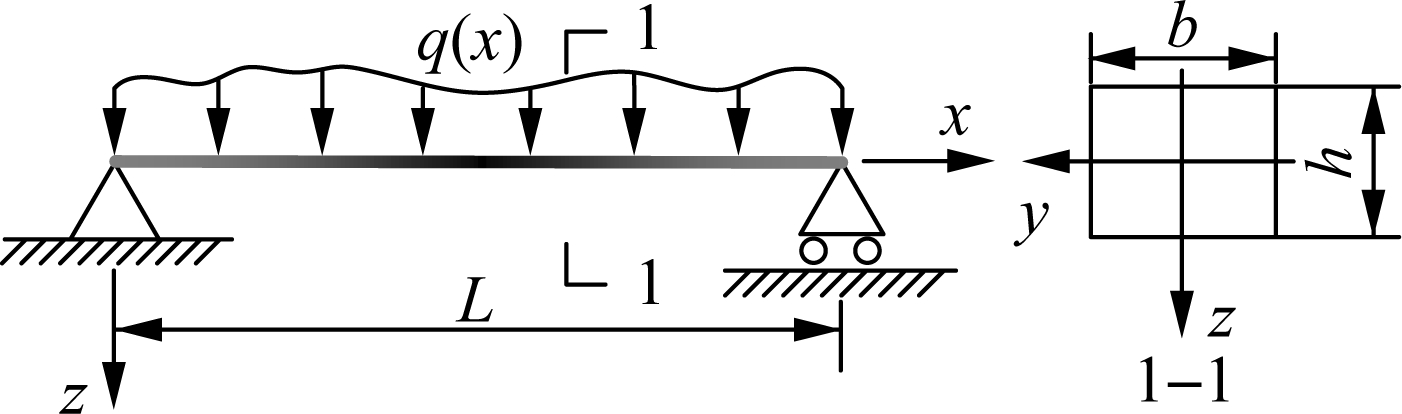
Fig.1 Simply supported AFG micro-beam subjected to an arbitrarily distributed load
The displacement field of a Bernoulli-Euler beam takes the form
(6)
where u, v and w denote the displacements along the length (x), width (y) and thickness (z) directions, respectively. Thus, the non-zero strain and strain gradient components can be given by
(7)
Based on the NSGT, the virtual strain energy given by Li et al.[7] is
(8)
where V is the volume that the elastomer occupies. By substituting Eqs.(2), (3), (4) and (7) into Eq.(8) and using integration by parts, the virtual strain energy can be obtained as
(9)
Here, we consider the moment resultants as
(10)
By substituting Eq.(4) into Eq.(10), it gives
(11)
The virtual potential energy of the external load can be expressed as
δW=-![]() qδwdx
qδwdx
(12)
where q is the distributed transverse load.
According to the principle of minimum potential energy, in all possible displacement fields of a conservative system, the true displacement field minimizes the total potential energy of the system, so the first variation of the total potential energy is zero, namely
δΠ=δU+δW=0
(13)
Substituting Eqs.(9) and (12) into Eq.(13) and using integration by parts, it yields
(14)
Then, one can obtain the size-dependent governing differential equation in the framework of the Bernoulli-Euler beam theory and the NSGT as
![]() +q=0
+q=0
(15)
with classical boundary conditions
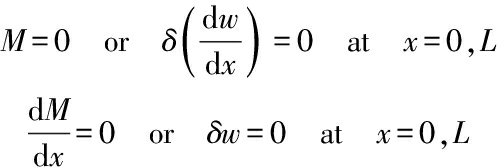
(16a)
and non-classical boundary conditions
(16b)
In view of the moment Eq.(11), the governing differential Eq.(15) based on the NSGT can be explicitly written as the following displacement form:
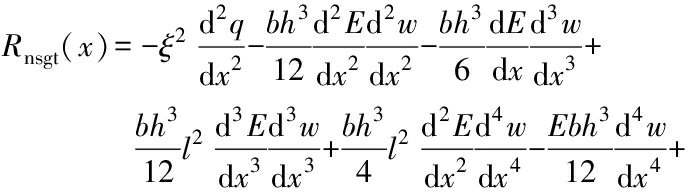
(17)
Based on the NET (l=0), SGT (ξ=0) and CET (l=0 and ξ=0), Eq.(17) can be simplified as
(18a)
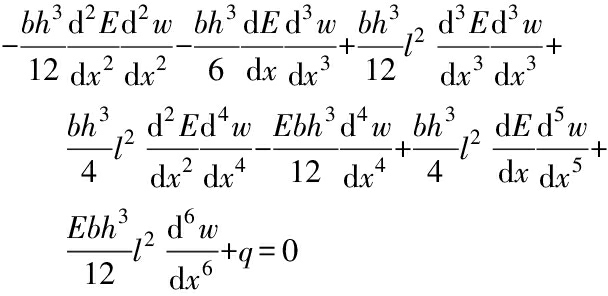
(18b)
(18c)
where Eqs.(18a), (18b) and (18c) are governing differential equations based on the NET, SGT and CET, respectively.
3 Analytical Solutions
The numerical solution method of simply supported AFG microbeams exposed to various distributed loads for the static bending problem is presented in this section. It first reduces the governing differential equations to ordinary equations by using the Galerkin method for AFG microbeams based on the NSGT.
The boundary conditions for simply supported AFG microbeams can be written as
(19)
Considering boundary conditions Eq.(19), the deflection equation can be defined as
(20)
where n denotes the number of shape functions; Wn denotes the unknown coefficients. For bending, we take the Fourier series expansion of the distributed transverse load as the form
(21a)
where
(21b)
denotes the Fourier coefficient.
According to the Galerkin method, substituting Eq.(20) into the governing differential Eq.(17), multiplying it by the n-th mode shape and integrating over the length of the beam, the equivalent integral form of the governing Eq.(17) is obtained as
(22a)
where Rnsgt(x) denotes the residual; the n-th shape function is given as
(22b)
For the sake of generality, the dimensionless material length scale parameter Dl, dimensionless material nonlocal parameter Dξ and dimensionless ordinate Dx are, respectively, defined as
(23)
By substituting Eqs.(20) and (21) into the governing Eq.(17), the residual Rnsgt(x) can be obtained as
![]() ·
·
Wncos(Dxπ)cos(nDxπ)-r(η-1)·![]() ·
·![]() ·
·![]()
(24a)
where
(24b)
3.1 Concentrated load
For the type of concentrated load, the transverse load q can be expressed as
(25a)
where P is the magnitude of the concentrated load acting on the middle point of the beam; δ() is the Dirac delta function. The coefficient Qn is given as
(25b)
By inserting Eq.(24) into Eq.(22) and setting n = 3, it obtains
(26)
Substituting Eq.(25) into Eq.(26), one can obtain the non-zero coefficients as

(27)
where
![]()
![]()
![]()
![]()
![]()
![]()
(28)
Then, the nonlocal strain gradient solution for the deflection of the AFG Bernoulli-Euler microbeam with simply supported ends subjected to a concentrated load can be calculated approximately as
(α1α5+α3)sin(3Dxπ)]
(29a)
For the sake of generality, the dimensionless deflection can be written as

(α1α5+α3)sin(3Dxπ)]
(29b)
3.2 Uniform load
For the type of uniform distributed load, the transverse load q can be expressed as
q(x)=q0
(30)
where q0 is a constant. Then, the nonlocal strain gradient solution for the deflection of the AFG Bernoulli-Euler microbeam with simply supported ends subjected to a uniform distributed load can be approximately calculated via the Galerkin method as
![]()
(α1α6-α3)sin(3Dxπ)]
(31a)
For the sake of generality, the dimensionless deflection can be written as
![]()
![]()
(α1α6-α3)sin(3Dxπ)]
(31b)
where
(31c)
3.3 Linear load
For the type of linearly distributed load, the transverse load q is assumed as
q(x)=q0Dx
(32)
The corresponding nonlocal strain gradient solution for the deflection can be approximately calculated via the Galerkin method as
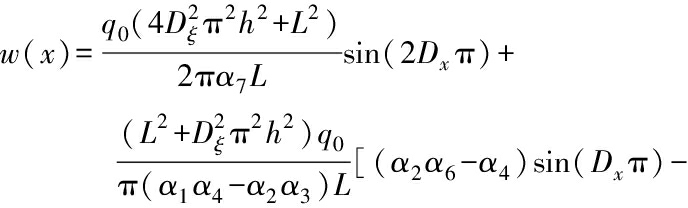
(α1α6-α3)sin(3Dxπ)]
(33a)
For the sake of generality, the dimensionless deflection can be written as
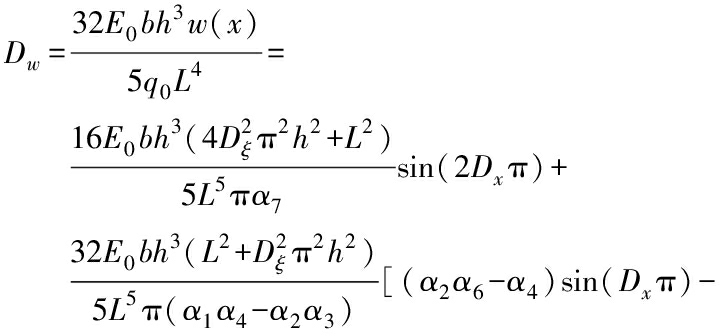
(α1α6-α3)sin(3Dxπ)]
(33b)
where
(33c)
3.4 Sinusoidal load
In this subsection, the numerical solution of a simply supported AFG microbeam for the static bending problem based on various types of theories, such as NSGT, NET, SGT and CET, are compared. The sine distributed load applying on the microbeam is assumed to be
q(x)=q0sin(Dxπ)
(34)
3.4.1 Nonlocal strain gradient solution
Based on the NSGT, the numerical solution of deflection can be obtained via the Galerkin method as
![]()
(α1+5α3)sin(3Dxπ)]
(35a)
For the sake of generality, the dimensionless deflection can be written as
![]()
![]()
(α1+5α3)sin(3Dxπ)]
(35b)
where
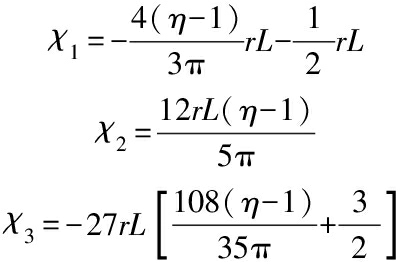
(35c)
3.4.2 Nonlocal elastic solution
Considering the sine distributed load Eq.(34), the nonlocal elasticity solution for the deflection of a simply supported AFG microbeam can be numerically calculated by substituting Eqs.(20) and (21) into governing Eqs.(18a) and (22) with setting n=3.
(χ1+5χ2)sin(3Dxπ)]
(36a)
For the sake of generality, the dimensionless deflection can be written as

(χ1+5χ2)sin(3Dxπ)]
(36b)
3.4.3 Strain gradient solution
Considering the sine distributed load Eq.(34), the strain gradient solution for the deflection of a simply supported AFG microbeam can be numerically calculated by substituting Eqs.(20) and (21) into governing Eqs.(18b) and (22) with setting n=3.
(α1+5α3)sin(3Dxπ)]
(37a)
For the sake of generality, the dimensionless deflection can be written as
![]()
![]()
(α1+5α3)sin(3Dxπ)]
(37b)
3.4.4 Classical elastic solution
Considering the sine distributed load Eq.(34), the classical elasticity solution for the deflection of a simply supported AFG microbeam can be numerically calculated by substituting Eqs.(20) and (21) into governing Eqs.(18c) and (22) with setting n=3.
(χ1+5χ2)sin(3Dxπ)]
(38a)
For the sake of generality, the dimensionless deflection can be written as
![]() ·
·![]() ·
·
[(χ2+5χ3)sin(Dxπ)-(χ1+5χ2)sin(3Dxπ)]
(38b)
4 Numerical Results and Discussion
The beam is made of silicon with material parameters E0=201.92 GPa and l=0.053 5 nm[17]. The geometrical parameters are as b=2h, L=20h. Numerical results are presented to evaluate the effects of the material nonlocal parameter ξ, the ratio of the material length scale parameter to the beam height Dl and the FG parameter η on the static bending behavior of AFG microbeams.
4.1 AFG microbeam subjected to a concentrated force
Fig.2(a) shows the normalized bending deflection Dw of a simply supported AFG microbeam with a concentrated force applied at the middle point as a function of the ratio of the material length scale parameter to the beam height Dl (while Dξ=10 and η=5). As can be observed in the figure, each curve forms a different sinusoidal hump whose peak rises with the decreasing value of Dl. It illustrates that the bending flexibility of the microbeam decreases with the decrease of the geometrical size of microbeams, which agrees with the numerical results in Ref.[27] very well. The double dot dash curve (Dl = 0, Dξ = 0 and η = 1) in the figure indicates the normalized bending deflection of the simply supported AFG microbeam with the geometrical size L being infinite and the material nonlocal parameter ξ being zero while the FG parameter η being 1. It is found that the maximum dimensionless deflection is approximately equal to 1, which verifies the accuracy of the numerical results in this paper.
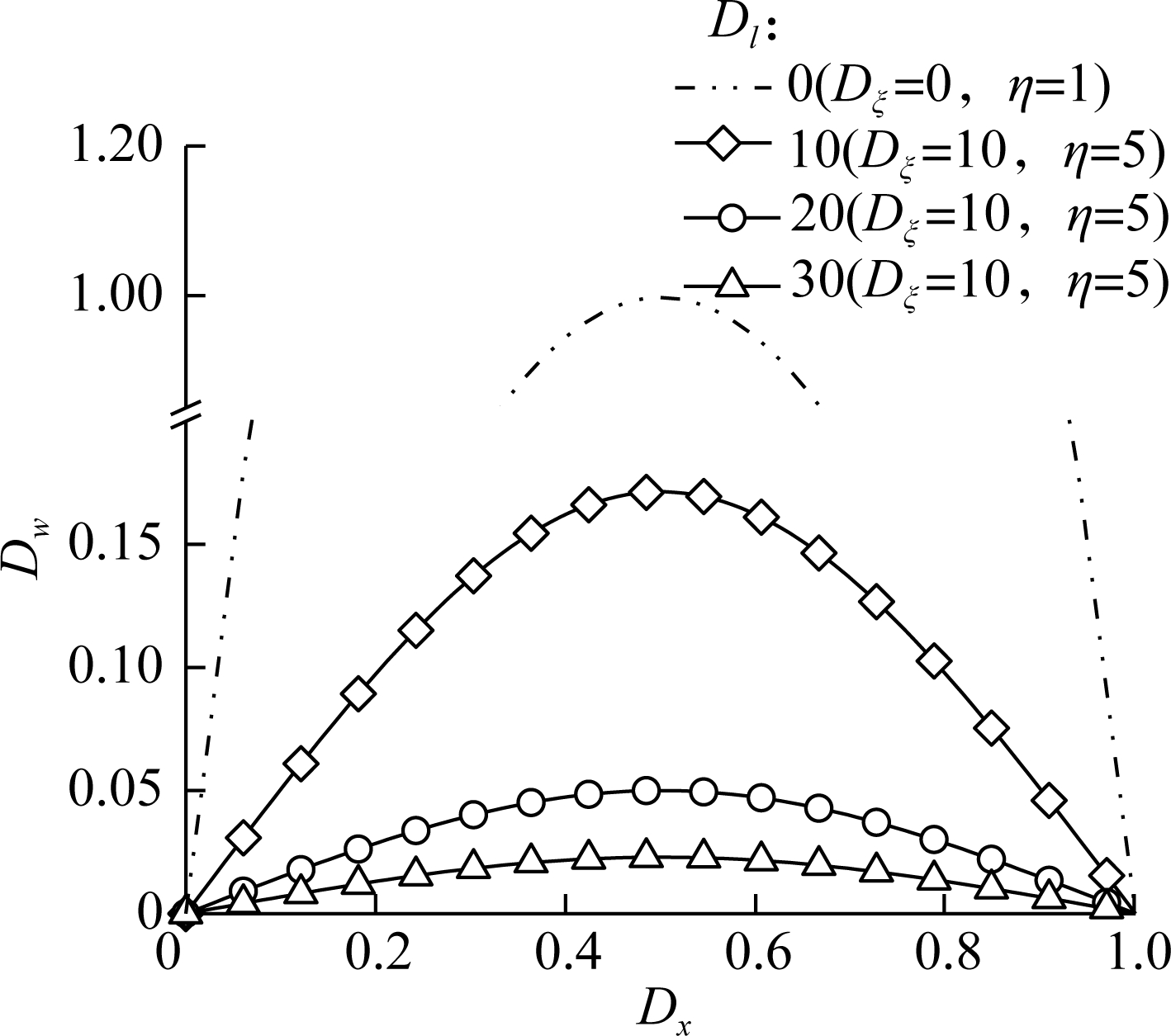
(a)

(b)
(c)
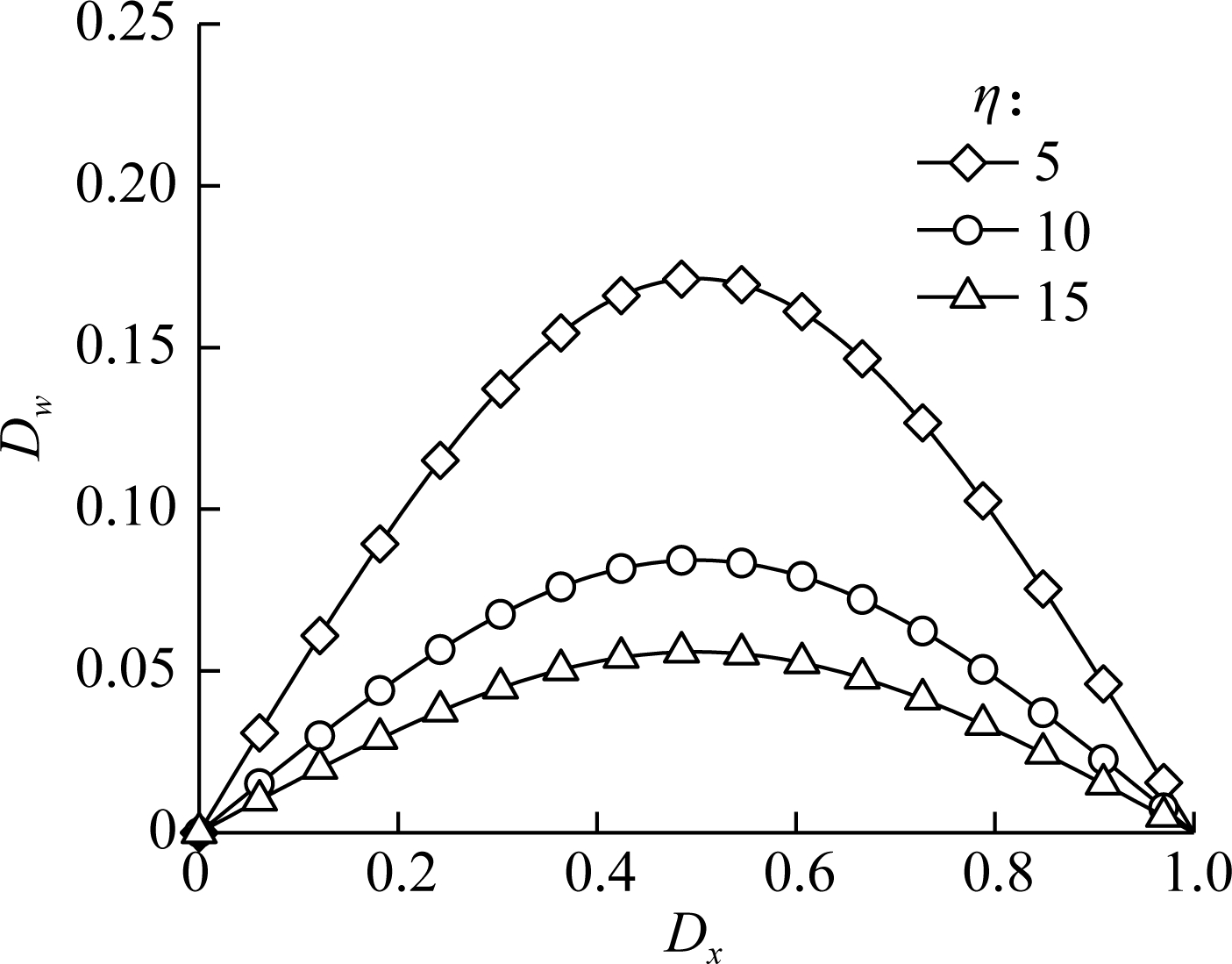
Fig.2 Normalized deflection versus normalized coordinate of the microbeam bearing the concentrated load at the middle point with various parameters. (a) Geometrical size; (b) Material nonlocal parameter; (c) FG parameter
To numerically investigate the effect of the material nonlocal parameter on the bending deformation of the AFG microbeam, a series of specified dimensionless material nonlocal parameters are considered. Fig.2(b) presents the normalized deflection Dw of a simply supported AFG microbeam with a concentrated force applied at the middle point with different values of the dimensionless material nonlocal parameter Dξ (while Dl=10 and η = 5). It is clear that the deformations increase with increasing Dξ, and the deformations increase more obviously when the value of Dξ is larger. This explains that the bending flexibility increases with the increase in the material nonlocal parameter.
Fig.2(c) plots the normalized deflection Dw of a simply supported AFG microbeam with a concentrated force applied at the middle point as a function of the FG parameter η (while Dξ=10 and Dl=10). It is found that the FG parameter plays an important role in controlling the transverse deflection of the AFG microbeam, and the deformation decreases with the increase in the FG parameter η. It is because the effective elastic modulus increases with the increase in η. However, this example can only show the trend of the variation of the transverse deformation of AFG microbeams subjected to a concentrated force affected by the ratio of the material length scale parameter to the beam height Dl, the material nonlocal parameter Dξ and the FG parameter η. To illustrate this more deeply, some more complicated problems, such as an AFG simply supported microbeam subjected to various transverse distributed loads, are investigated as follows.
4.2 AFG microbeam subjected to distributed loads
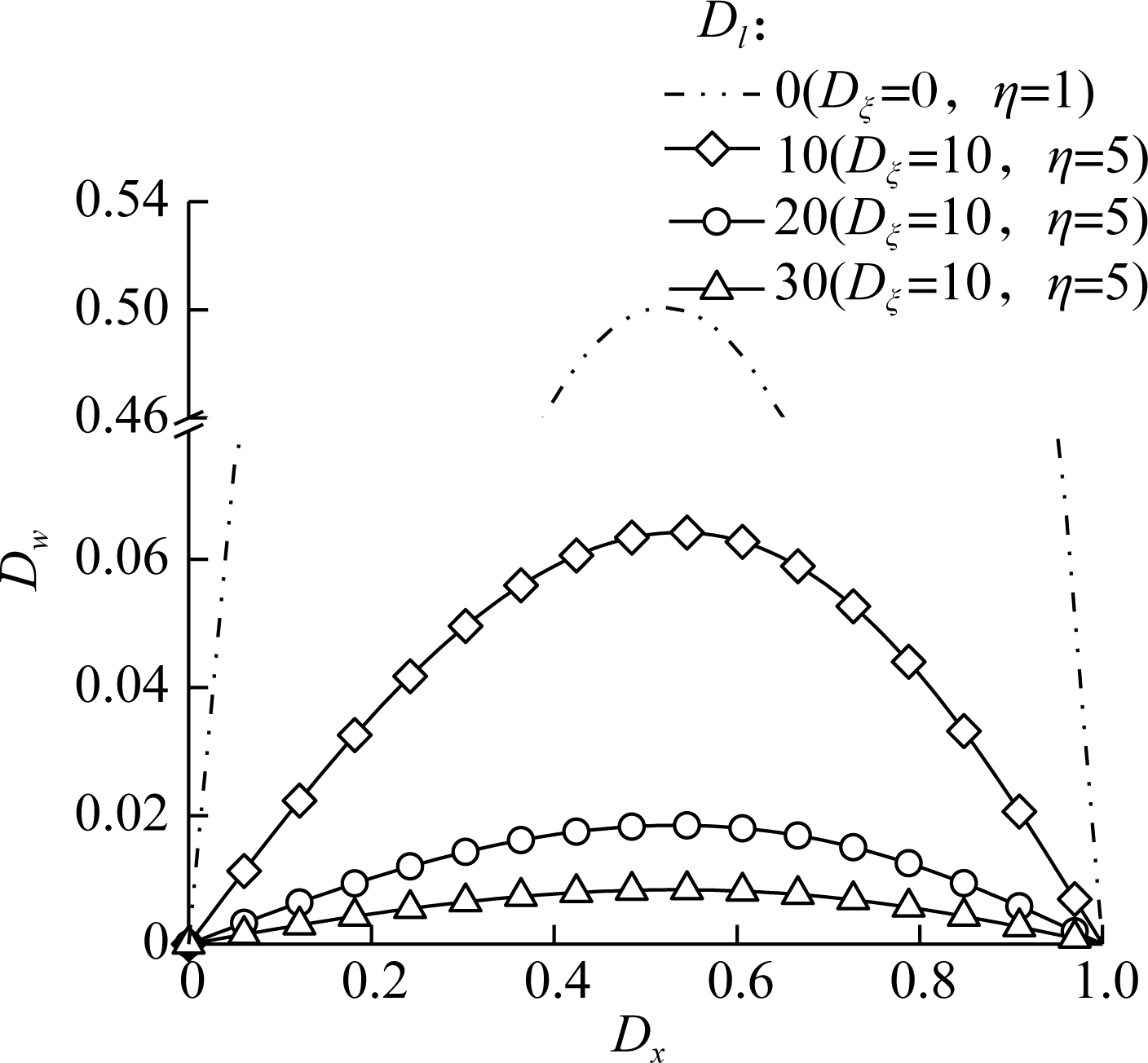
Fig.3(a) shows the normalized deflection Dw of a simply supported AFG microbeam suffering a linearly distributed load (q(x)=q0Dx) with different ratios of the material length scale parameter to the beam height Dl (while Dξ=10 and η = 5). It is clear that each curve forms a hump whose peak rises with the decrease of Dl. It illustrates that the bending flexibility decreases with the decrease of the geometrical size of microbeam structures. However, the maximum deflection occurs on the right side of the middle point, which is attributed to the asymmetrical distribution of loads. The double dot dash curve in the figure indicates the normalized deflection of the corresponding microbeam without considering the FG effect while the geometrical size L is infinite (Dl=0) and the material nonlocal parameter ξ is zero (Dξ=0). It is clear that the maximum dimensionless deflection also occurs on the right side of the middle point of the microbeam.
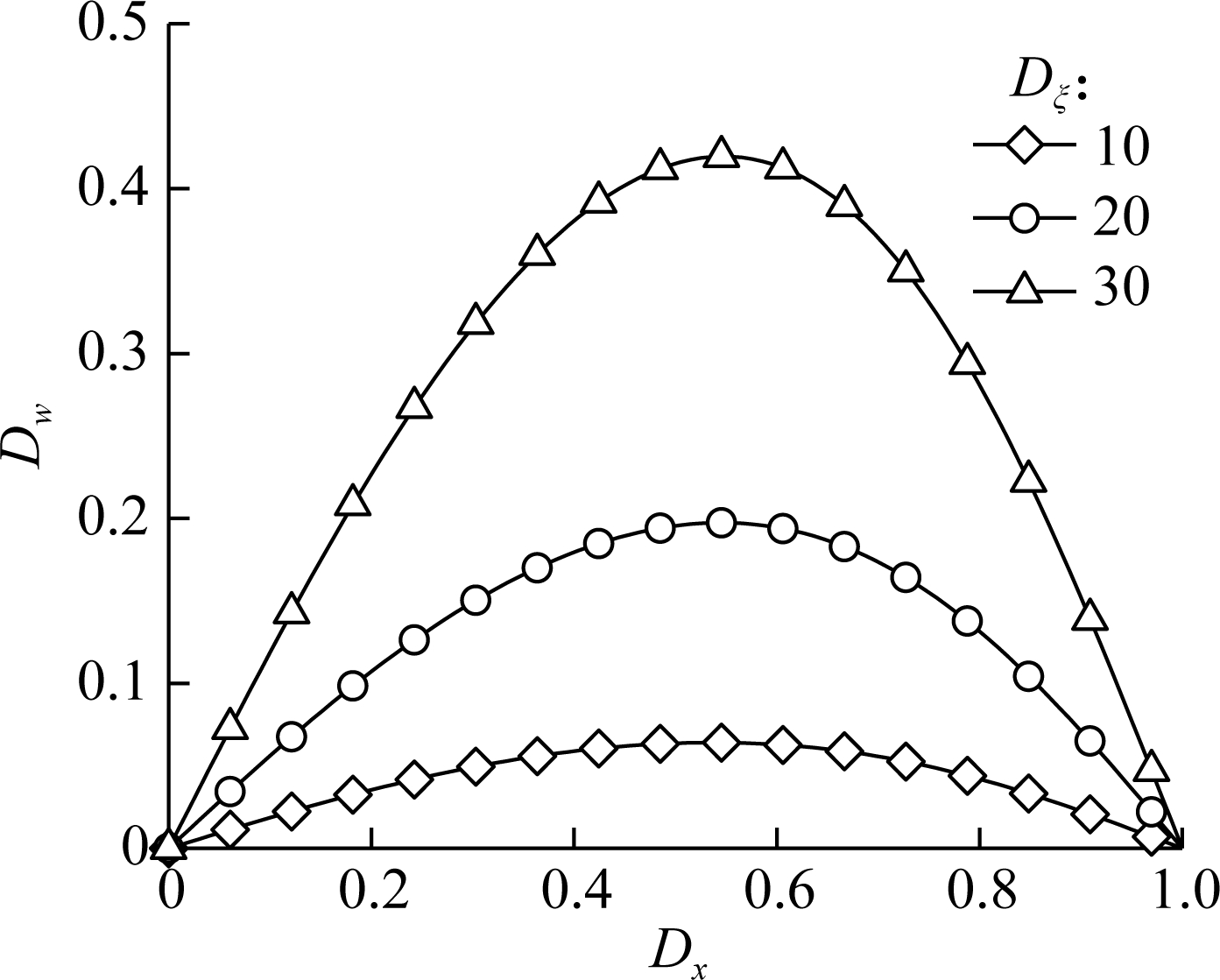
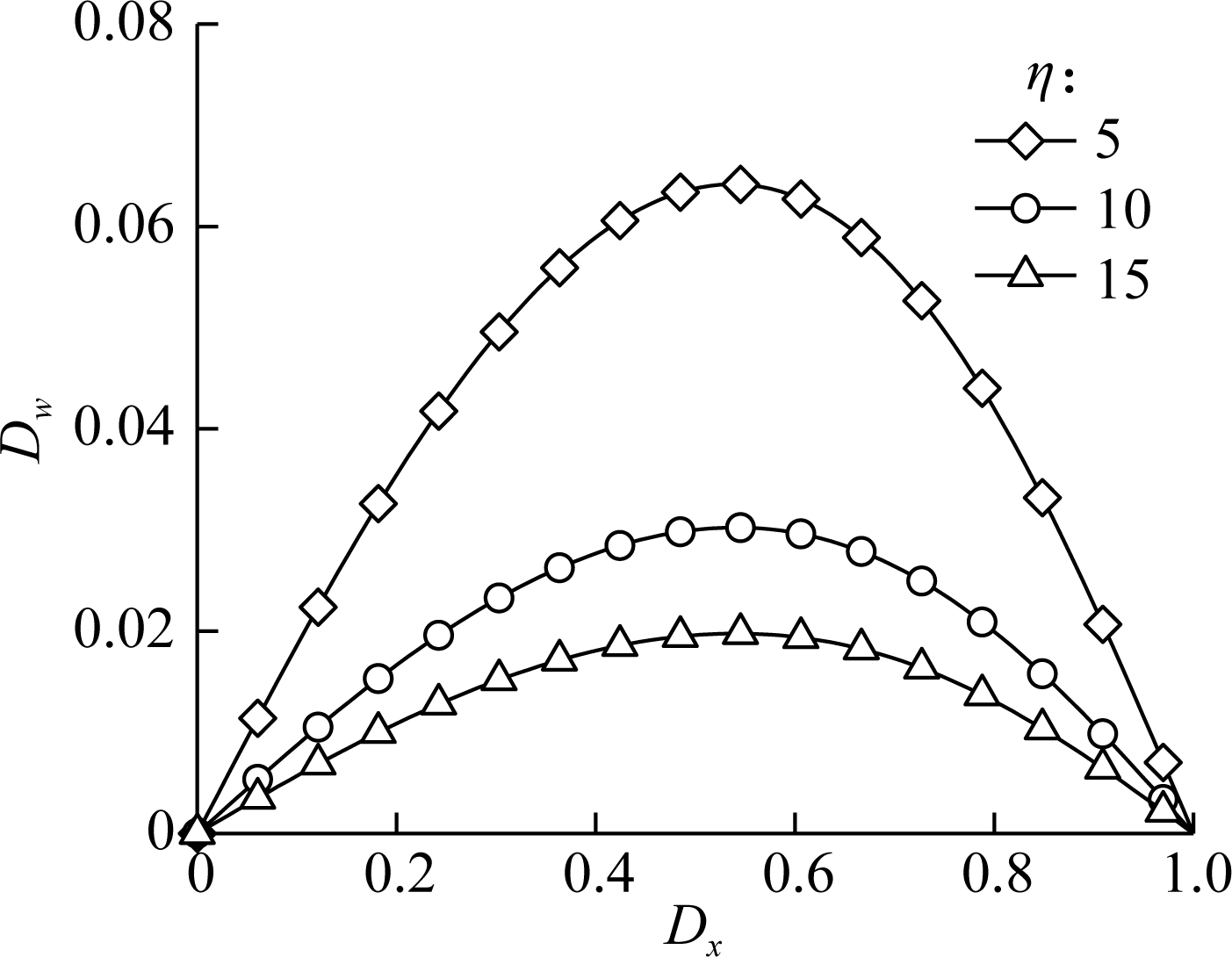
Fig.3(b) and Fig.3(c) present the normalized deflection Dw of a simply supported AFG microbeam suffering a linearly distributed load (q(x) =q0Dx), a series of specified dimensionless material nonlocal parameters Dξ (while Dl=10 and η=5) and FG parameter η (while Dξ=10 and Dl=10) are considered, respectively. It can be seen that both increasing the material nonlocal parameter ξ and decreasing the FG parameter η will lead to an increase in the bending flexibility.
(a)
(b)
(c)
Fig.3 Normalized deflection versus the normalized coordinate of the microbeam suffering the transverse linear load with various parameters. (a) Geometrical size; (b) Material nonlocal parameter; (c) FG parameter
Fig.4(a) and Fig.4(b) show the normalized deflection Dw of a simply supported AFG microbeam suffering a transverse uniform load (q(x)=q0) and a transverse sinusoidal load (q(x)=q0sin(Dxπ)) with different ratios of the material length scale parameter to the beam height Dl (while Dξ=10 and η=5), respectively. As can be seen in the figures, each curve forms a different sinusoidal hump whose peak rises with the decrease of Dl. It illustrates that the bending flexibility of the microbeam decreases with the decrease of the geometrical size of the microbeams. The double dot dash curve in the figure indicates the normalized deflection of the microbeam without considering the FG effect while the geometrical size L is infinite (Dl=0) and the material nonlocal parameter ξ is zero (Dξ=0). It is clear that the maximum dimensionless deflection is approximately equal to 1, which verifies the accuracy of the numerical results in this paper.
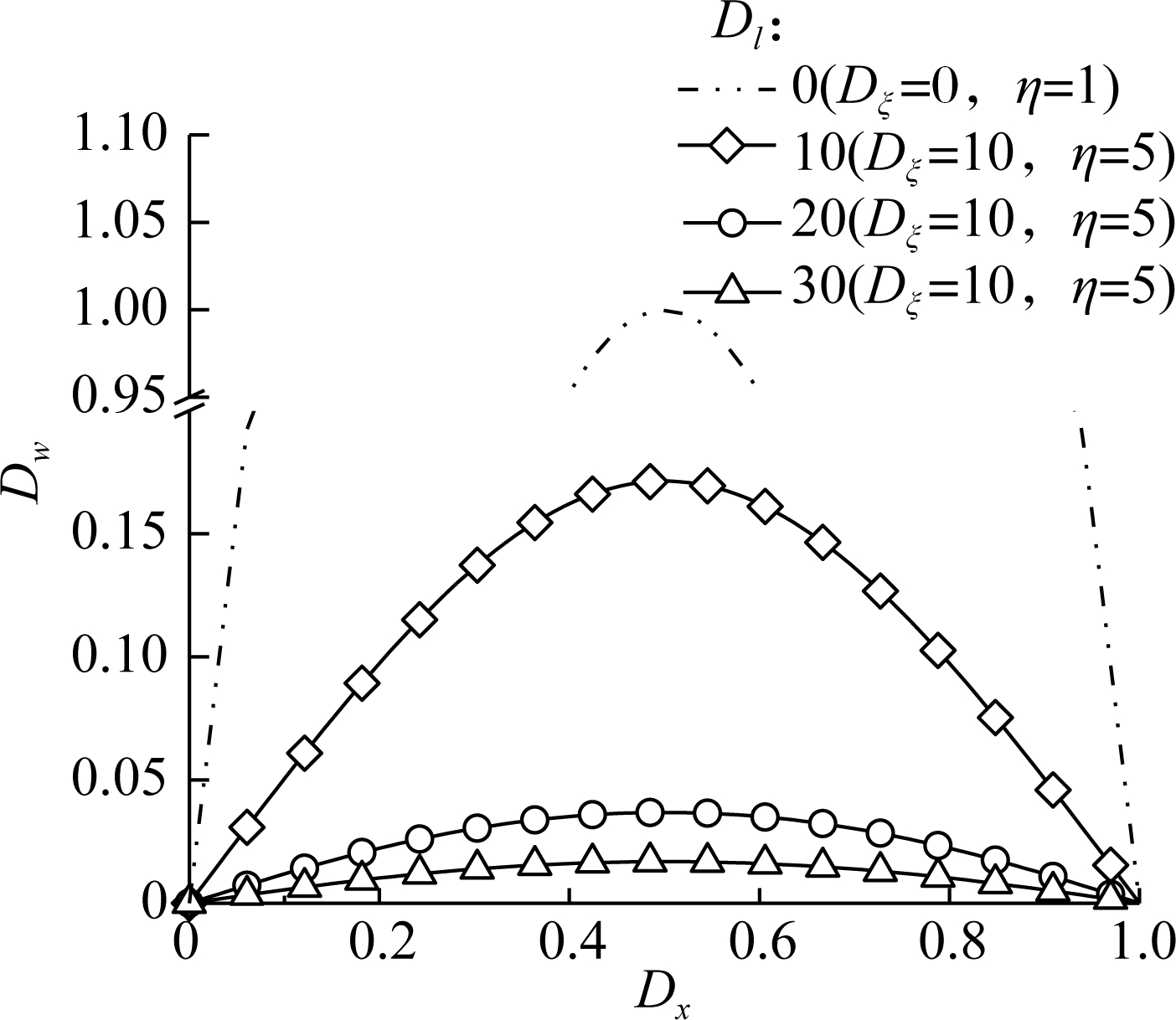
(a)
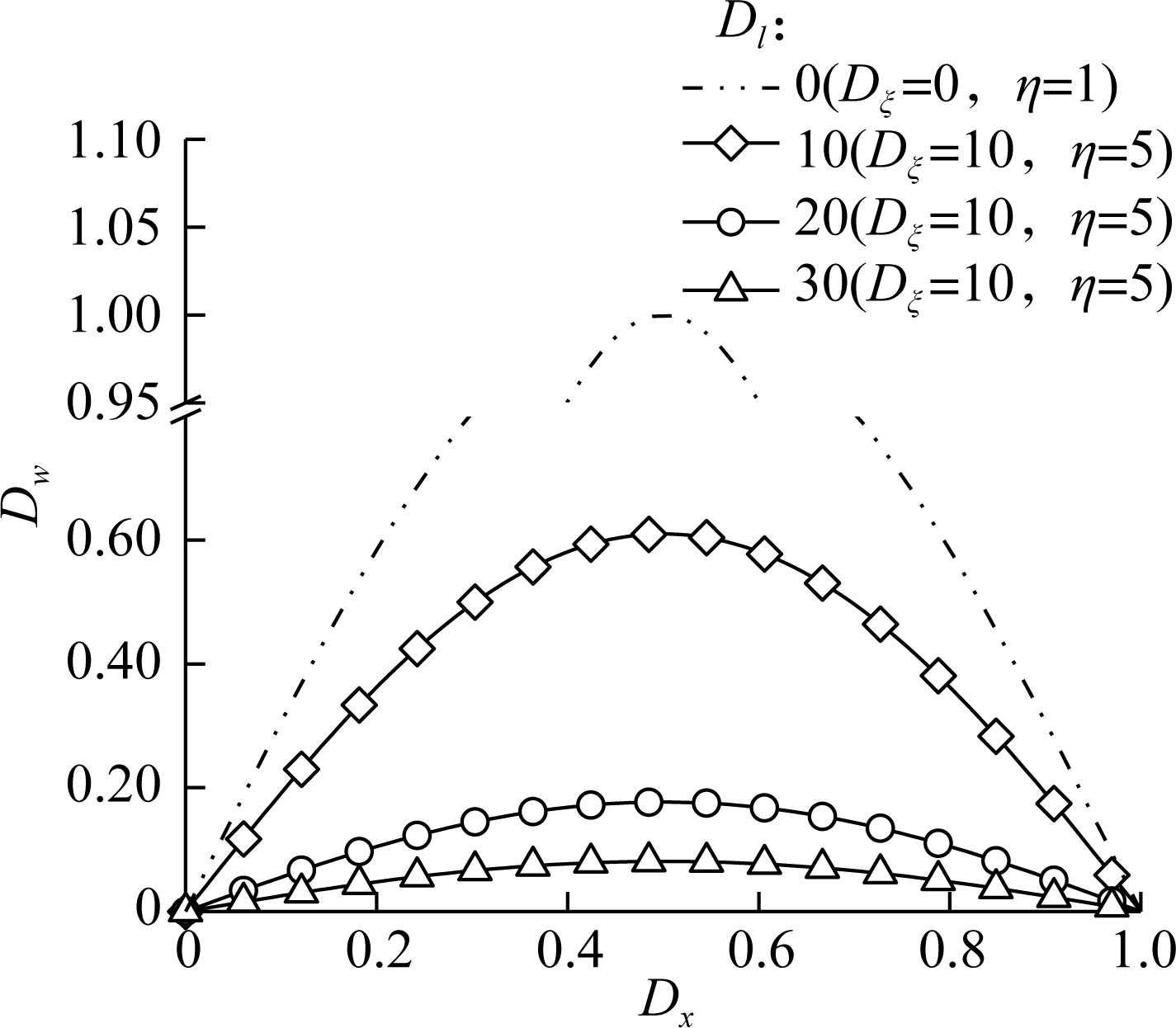
(b)
Fig.4 Normalized deflection versus the normalized coordinate of the microbeam bearing the transverse load with various geometrical sizes. (a) Uniform load; (b) Sinusoidal load
Fig.5(a) and Fig.5(b), respectively, plot the normalized deflection Dw of a simply supported AFG microbeam bearing a transverse uniform load (q(x)=q0) and a transverse sinusoidal load (q(x)=q0sin(Dxπ)), and a series of specified dimensionless material nonlocal parameters Dξ (while Dl=10 and η=5) are considered. It is clear that the deformation increases with increasing Dξ, and the deformation increases more obviously when the value of Dξ is larger. This explains that the bending flexibility increases with the increase in the material nonlocal parameter.
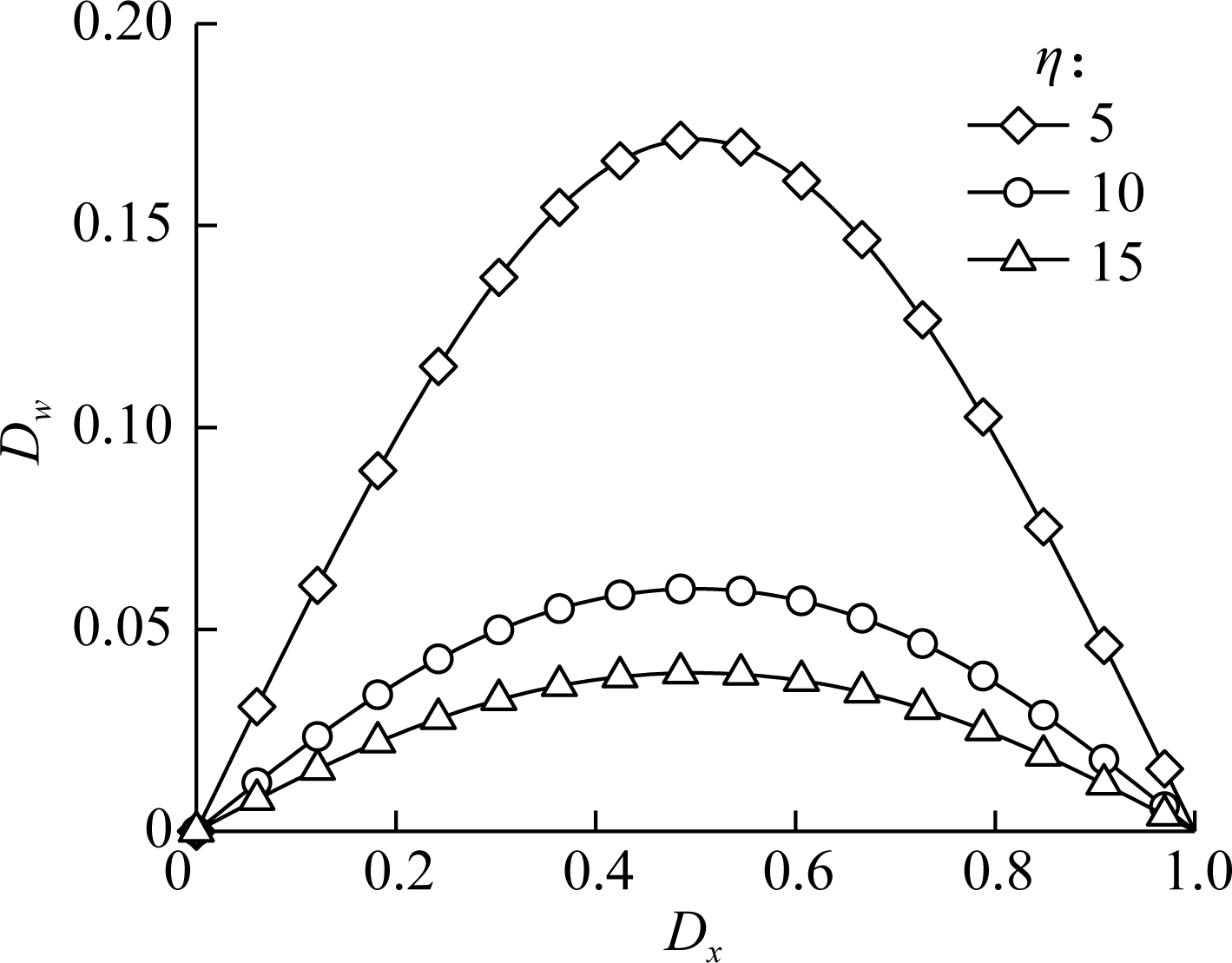
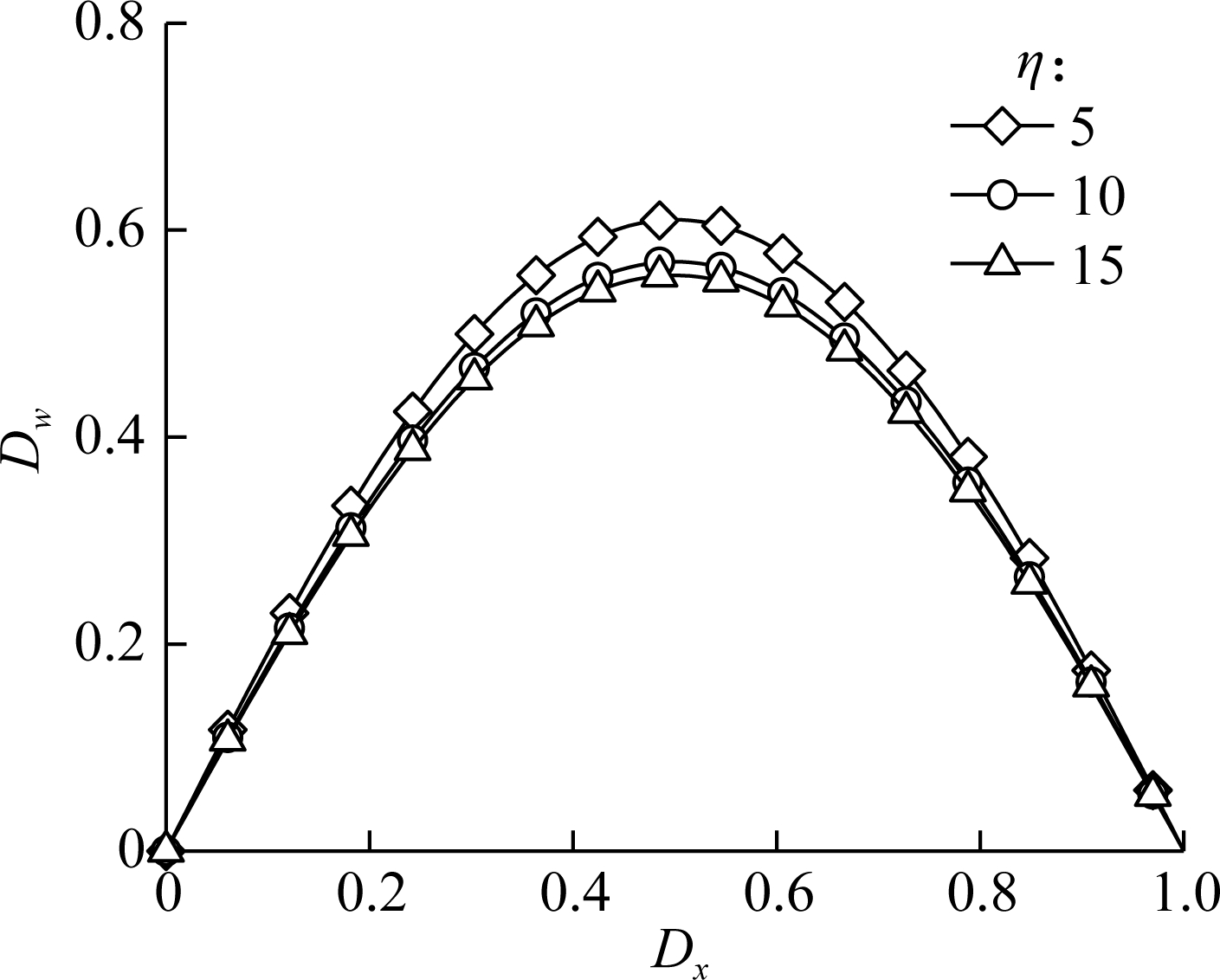
Fig.6(a) and Fig.6(b), respectively, present the normalized deflection Dw of a simply supported AFG microbeam bearing a transverse uniform load (q(x)=q0) and a transverse sinusoidal load (q(x)=q0sin(Dxπ)), and a series of specified FG parameters η (while Dξ=10 and Dl=10) are considered. It is found that the FG parameter has a significant effect on the bending deflection of the AFG microbeam, and the deformation decreases with the increase in the FG parameter η.
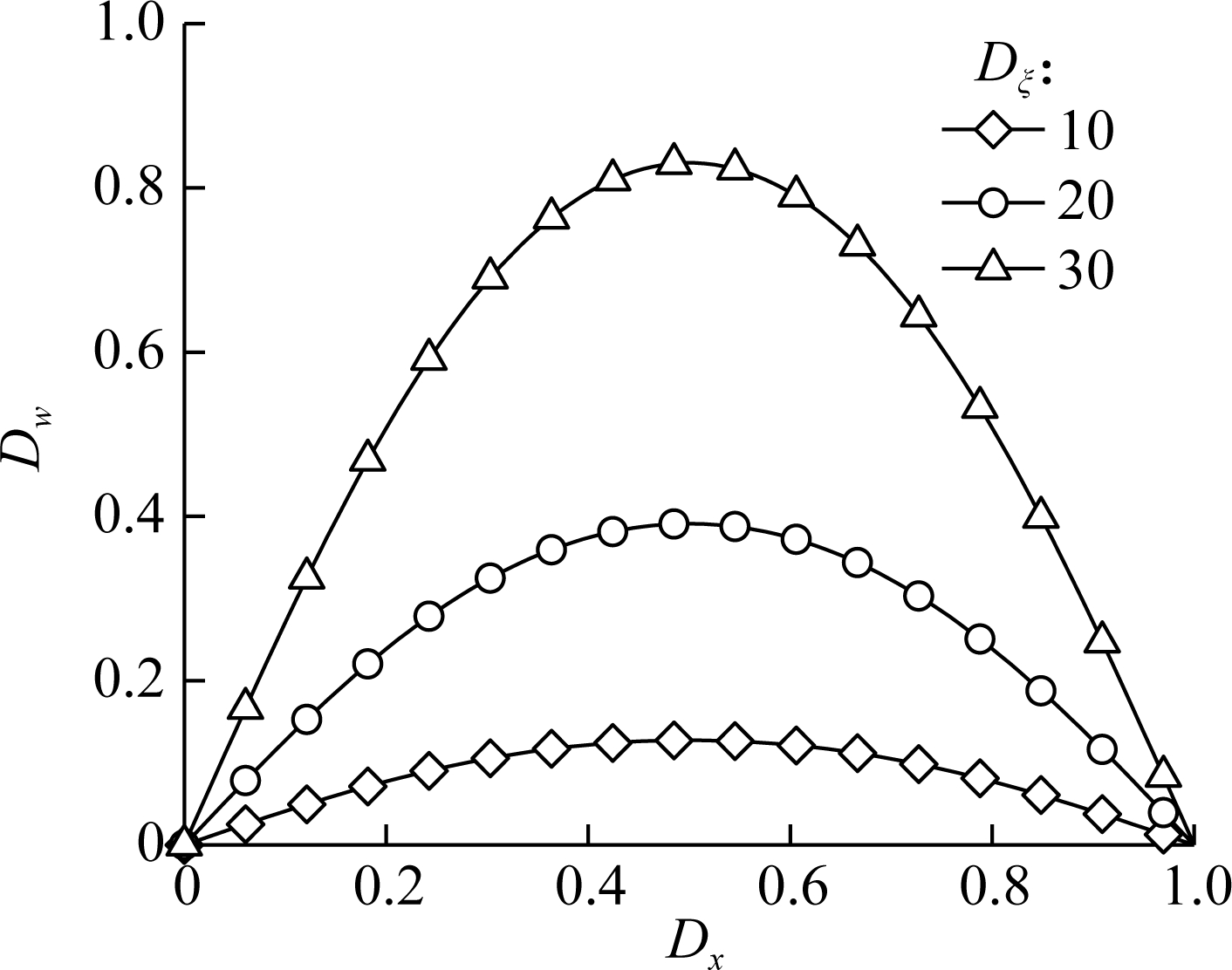
(a)
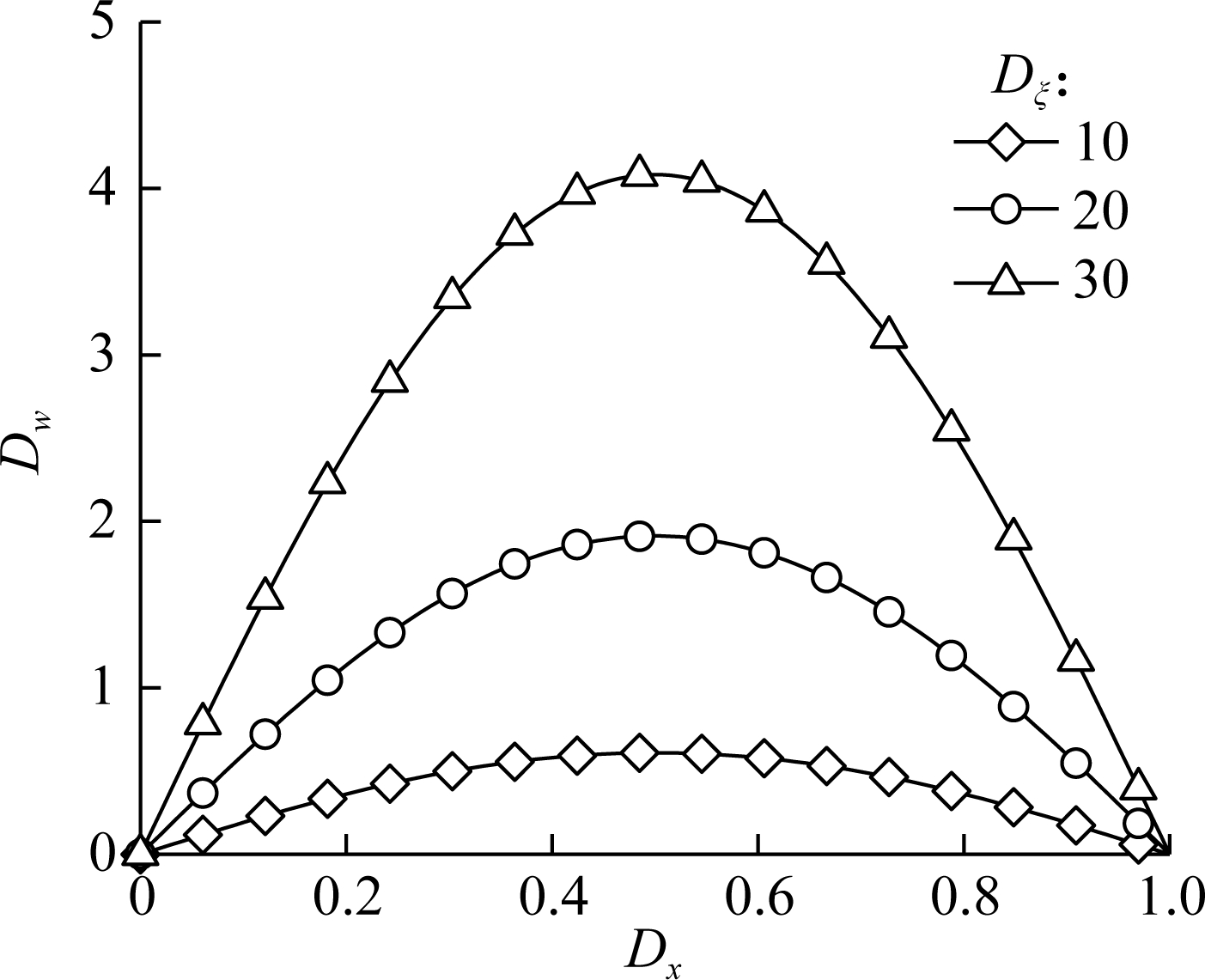
(b)
Fig.5 Normalized deflection versus the normalized coordinate of the microbeam bearing transverse loads with various material nonlocal parameters. (a) Uniform load; (b) Sinusoidal load
(a)
(b)
Fig.6 Normalized deflection versus the normalized coordinate of the microbeam bearing transverse loads with various FG parameters. (a) Uniform load; (b) Sinusoidal load
4.3 Discussions on results via different theories
These aforementioned examples can only show the variation trend of the bending deformation of AFG microbeams subjected to a transverse load based on the NSGT. As an example, the transverse deformation of an AFG simply supported microbeam subjected to a sinusoidal load within the frameworks of NSGT, NET, SGT and CET are compared according to Eqs. (35), (36), (37) and (38).
As shown in Fig.7, the normalized deflection Dw of a simply supported AFG microbeam subjected to the same sinusoidal load (q(x)=q0sin(Dxπ)) with Dξ=10, Dl=10 and η = 5 based on different elasticity theories are compared. As can be seen, the bending deflection of the AFG microbeam based on the CET is larger than that considering the SGT but smaller than that considering the NET, and the bending deflection based on the NSGT is in between. It means that the stiffness of the AFG microbeam calculated within the framework of SGT shows a “hardening” effect and the stiffness calculated within the framework of NET shows a “softening” effect, which is consistent with the numerical results described in Ref.[10]. This physical phenomenon has been revealed reasonably by Lü et al.[20] as the former accounts for the higher-order deformation mechanism and the latter takes the inter-atomic long-range force into consideration.
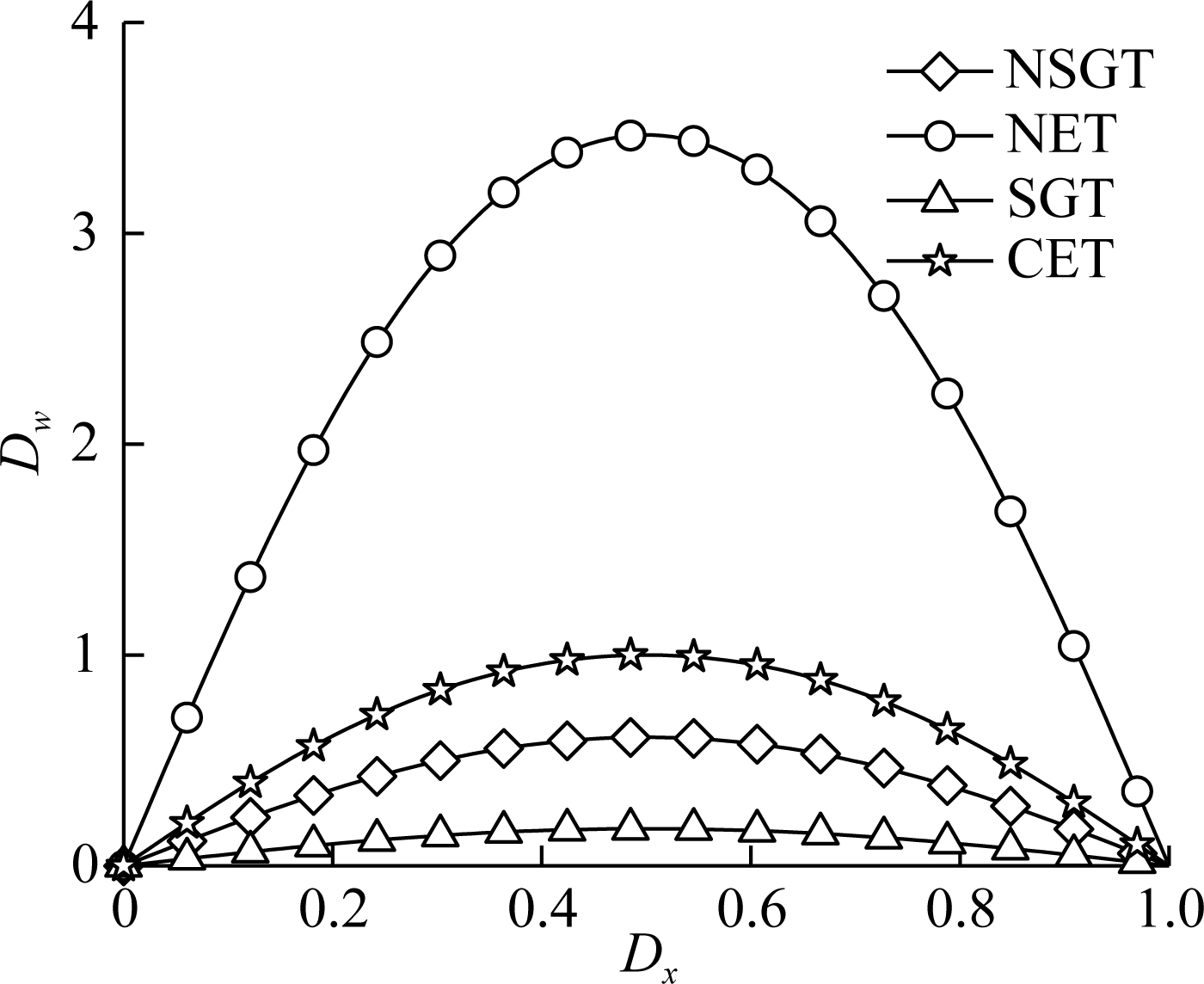
Fig.7 Normalized deflection versus the normalized coordinate of the microbeam bearing the transverse sinusoidal load within different frameworks of elasticity theories
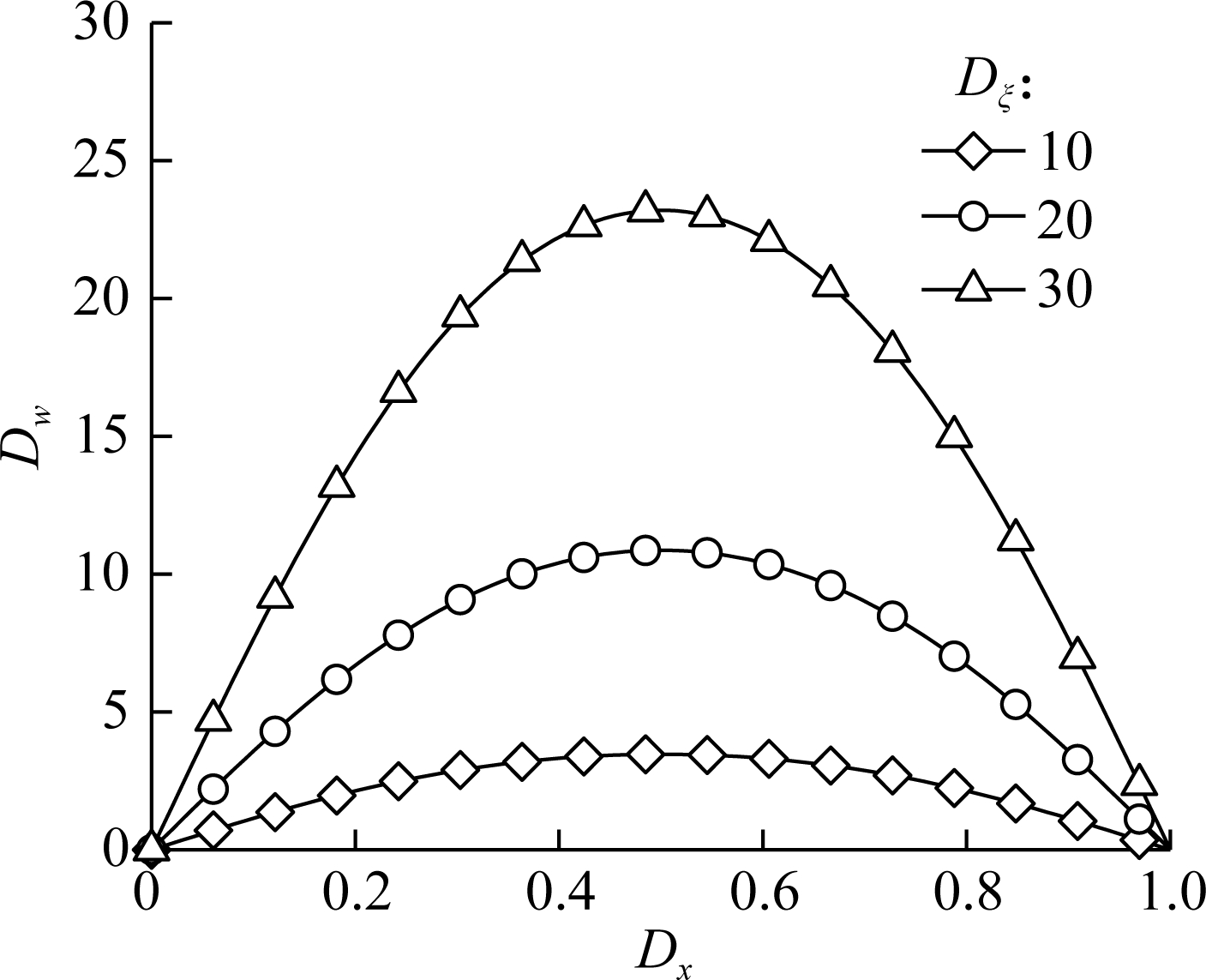
Fig.8(a) and Fig.8(b) show the normalized deflection Dw of a simply supported AFG microbeam suffering a transverse sinusoidal load (q(x)=q0sin(Dxπ)) based on the NET and SGT, respectively. A series of specified dimensionless material nonlocal parameters Dξ (while η = 5) are considered in Fig.8(a), and a series of specified ratios of the material length scale parameter to beam height Dl (while η = 5) are considered in Fig.8(b). As can be seen, the bending flexibility increases with increasing Dξ within the framework of NET, and the bending flexibility decreases with increasing Dl within the framework of SGT.
(a)
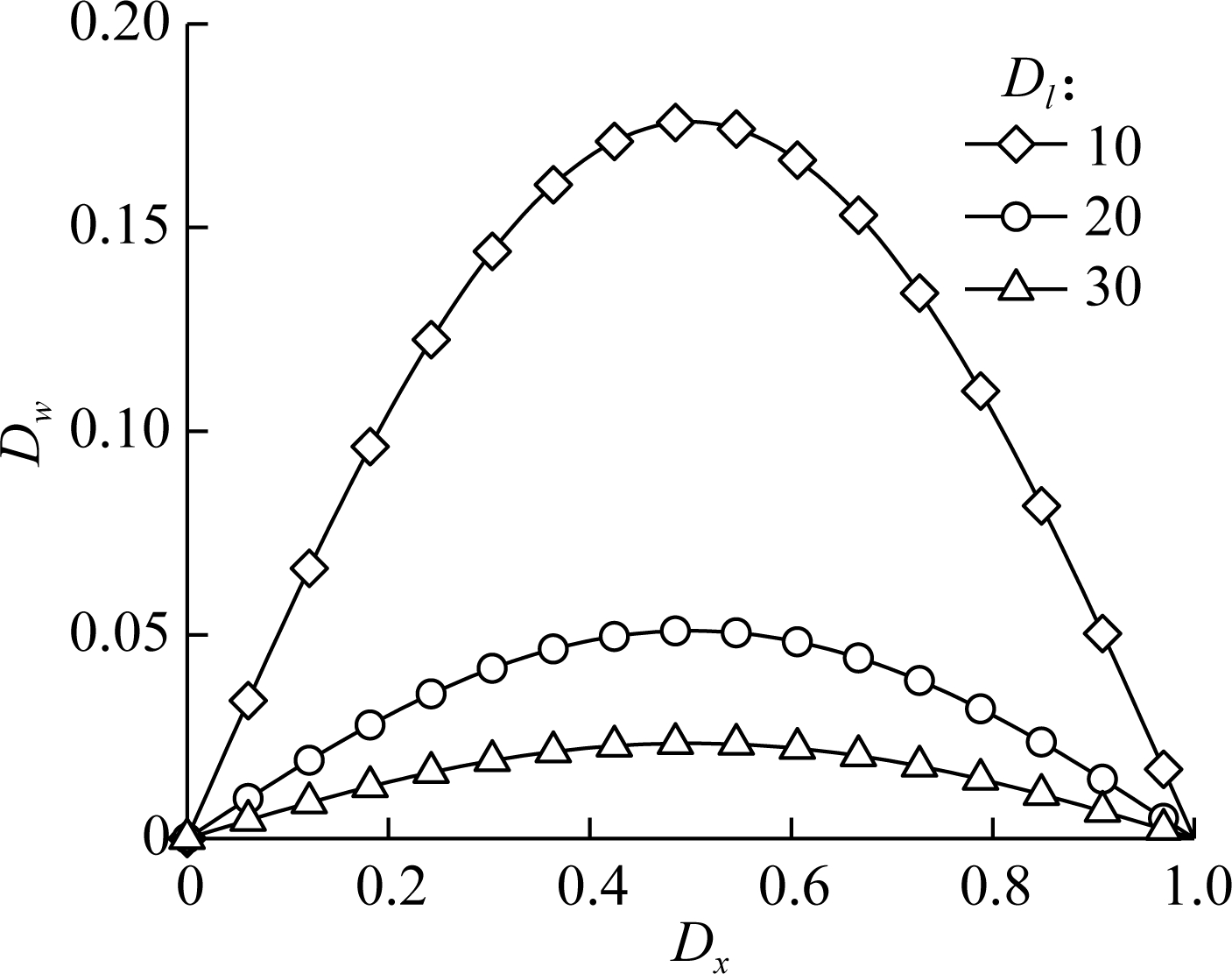
(b)
Fig.8 Normalized deflection versus the normalized coordinate of the microbeam bearing the transverse sinusoidal load. (a) With various material nonlocal parameters within the framework of NET; (b) With various geometrical sizes within the framework of SGT
5 Conclusions
1) A size-dependent Bernoulli-Euler beam model, which accounts for the longitudinal sinusoidal law variation of FG material, is derived based on the NSGT and minimum potential energy principle. Considering various transverse loads, the governing differential equations are solved by employing the Galerkin method.
2) When considering the concentrated and distributed loads, the bending flexibility decreases with the increase in the ratio of the material length scale parameter to the height of the microbeams.
3) The material nonlocal parameter plays an important role in controlling the bending flexibility of AFG microbeams. When considering the concentrated and distributed loads, the bending flexibility increases with the increase in the material nonlocal parameter.
4) The AFG parameter has a significant effect on the transverse deflection of the AFG microbeam, and the deformation decreases with the increase in the FG parameter when considering the concentrated and distributed loads.
5) The transverse deformation of AFG microbeams presents a stiffness “softening” effect within the framework of NET and a stiffness “hardening” effect within the framework of SGT, and the stiffness based on the NSGT is in between.
[1]Zhao L, Chen W Q, Lü C F. Symplectic elasticity for bi-directional functionally graded materials[J].Mechanics of Materials, 2012, 54: 32-42. DOI:10.1016/j.mechmat.2012.06.001.
[2]Naebe M, Shirvanimoghaddam K. Functionally graded materials: A review of fabrication and properties[J].Applied Materials Today, 2016, 5: 223-245. DOI:10.1016/j.apmt.2016.10.001.
[3]Kouzeli M, Mortensen A. Size dependent strengthening in particle reinforced aluminium[J].Acta Materialia, 2002, 50(1): 39-51. DOI:10.1016/s1359-6454(01)00327-5.
[4]Lam D C C, Yang F, Chong A C M, et al. Experiments and theory in strain gradient elasticity[J].Journal of the Mechanics and Physics of Solids, 2003, 51(8): 1477-1508. DOI:10.1016/s0022-5096(03)00053-x.
[5]Lim C W, Zhang G, Reddy J N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation[J].Journal of the Mechanics and Physics of Solids, 2015, 78: 298-313. DOI:10.1016/j.jmps.2015.02.001.
[6]Eringen A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J].Journal of Applied Physics, 1983, 54(9): 4703-4710. DOI:10.1063/1.332803.
[7]Li L, Hu Y J, Li X B. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory[J].International Journal of Mechanical Sciences, 2016, 115/116: 135-144. DOI:10.1016/j.ijmecsci.2016.06.011.
[8]Xu X J, Wang X C, Zheng M L, et al. Bending and buckling of nonlocal strain gradient elastic beams[J].Composite Structures, 2017, 160: 366-377. DOI:10.1016/j.compstruct.2016.10.038.
[9]Lu L, Guo X M, Zhao J Z. Size-dependent vibration analysis of nanobeams based on the nonlocal strain gradient theory[J].International Journal of Engineering Science, 2017, 116: 12-24. DOI:10.1016/j.ijengsci.2017.03.006.
[10]Zhang B, Shen H M, Liu J, et al. Deep postbuckling and nonlinear bending behaviors of nanobeams with nonlocal and strain gradient effects[J].Applied Mathematics and Mechanics, 2019, 40(4): 515-548. DOI:10.1007/s10483-019-2482-9.
[11]Ouakad H M, El-Borgi S, Mousavi S M, et al. Static and dynamic response of CNT nanobeam using nonlocal strain and velocity gradient theory[J].Applied Mathematical Modelling, 2018, 62: 207-222. DOI:10.1016/j.apm.2018.05.034.
[12]Farajpour A, Ghayesh M H, Farokhi H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes[J].International Journal of Mechanical Sciences, 2019, 150: 510-525. DOI:10.1016/j.ijmecsci.2018.09.043.
[13]Lu L, Guo X M, Zhao J Z. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects[J].Applied Mathematical Modelling, 2019, 68: 583-602. DOI:10.1016/j.apm.2018.11.023.
[14]Li L, Li X B, Hu Y J. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material[J].International Journal of Engineering Science, 2016, 102: 77-92. DOI:10.1016/j.ijengsci.2016.02.010.
[15]Li L, Hu Y J. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material[J].International Journal of Engineering Science, 2016, 107: 77-97. DOI:10.1016/j.ijengsci.2016.07.011.
[16]Li L, Hu Y J. Post-buckling analysis of functionally graded nanobeams incorporating nonlocal stress and microstructure-dependent strain gradient effects[J].International Journal of Mechanical Sciences, 2017, 120: 159-170. DOI:10.1016/j.ijmecsci.2016.11.025.
[17]Tang H S, Li L, Hu Y J. Coupling effect of thickness and shear deformation on size-dependent bending of micro/nano-scale porous beams[J].Applied Mathematical Modelling, 2019, 66: 527-547. DOI:10.1016/j.apm.2018.09.027.
[18]Ebrahimi F, Barati M R. A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams[J].Composite Structures, 2017, 159: 174-182. DOI:10.1016/j.compstruct.2016.09.058.
[19]Sahmani S, Aghdam M M. Nonlocal strain gradient beam model for nonlinear vibration of prebuckled and postbuckled multilayer functionally graded GPLRC nanobeams[J].Composite Structures, 2017, 179: 77-88. DOI:10.1016/j.compstruct.2017.07.064.
[20]Lü Z, Liu H. Nonlinear bending response of functionally graded nanobeams with material uncertainties[J].International Journal of Mechanical Sciences, 2017, 134: 123-135. DOI:10.1016/j.ijmecsci.2017.10.008.
[21]Lü Z, Qiu Z P, Zhu J J, et al. Nonlinear free vibration analysis of defective FG nanobeams embedded in elastic medium[J].Composite Structures, 2018, 202: 675-685. DOI:10.1016/j.compstruct.2018.03.068.
[22]Al-Shujairi M, ![]() Ç. Dynamic stability of sandwich functionally graded micro-beam based on the nonlocal strain gradient theory with thermal effect[J].Composite Structures, 2018, 201: 1018-1030. DOI:10.1016/j.compstruct.2018.06.035.
Ç. Dynamic stability of sandwich functionally graded micro-beam based on the nonlocal strain gradient theory with thermal effect[J].Composite Structures, 2018, 201: 1018-1030. DOI:10.1016/j.compstruct.2018.06.035.
[23]Al-Shujairi M, ![]() Ç. Buckling and free vibration analysis of functionally graded sandwich micro-beams resting on elastic foundation by using nonlocal strain gradient theory in conjunction with higher order shear theories under thermal effect[J].Composites Part B: Engineering, 2018, 154: 292-312. DOI:10.1016/j.compositesb.2018.08.103.
Ç. Buckling and free vibration analysis of functionally graded sandwich micro-beams resting on elastic foundation by using nonlocal strain gradient theory in conjunction with higher order shear theories under thermal effect[J].Composites Part B: Engineering, 2018, 154: 292-312. DOI:10.1016/j.compositesb.2018.08.103.
[24]Ghayesh M H, Farokhi H, Gholipour A, et al. Nonlinear bending and forced vibrations of axially functionally graded tapered microbeams[J].International Journal of Engineering Science, 2017, 120: 51-62. DOI:10.1016/j.ijengsci.2017.03.010.
[25]Rajasekaran S, Khaniki H B. Bending, buckling and vibration of small-scale tapered beams[J].International Journal of Engineering Science, 2017, 120: 172-188. DOI:10.1016/j.ijengsci.2017.08.005.
[26]Khaniki H B, Hosseini-Hashemi S, Nezamabadi A. Buckling analysis of nonuniform nonlocal strain gradient beams using generalized differential quadrature method[J].Alexandria Engineering Journal, 2018, 57(3): 1361-1368. DOI:10.1016/j.aej.2017.06.001.
[27]Li X B, Li L, Hu Y J, et al. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory[J].Composite Structures, 2017, 165: 250-265. DOI:10.1016/j.compstruct.2017.01.032.
[28]Karami B, Janghorban M. On the dynamics of porous nanotubes with variable material properties and variable thickness[J].International Journal of Engineering Science, 2019, 136: 53-66. DOI:10.1016/j.ijengsci.2019.01.002.