Evaluation of seismic risk to highway bridges is the crucial mission in the pre-earthquake design and post-earthquake response of transportation network, which particularly focused on direct and indirect economic losses caused by lifeline bridges. Fragility functions have played a favorable role in the recovery efforts and loss estimation of highway bridges, which calculate the component-level and system-level damage probability by defining the damage indices of components and employing the related assumptions. The seismic fragility analyses have focused on the establishment methods of fragility models and different application objects during recent decades[1-6]. The small-to-medium-span highway bridges became the most concerning type of bridge structures[1-2], and the fragility was used to compare and select isolation strategies[3] and retrofit measures[4] for those types of bridges. For long-span cable supported bridges, Zhong et al.[5] systematically completed the seismic fragility evaluation of cable-stayed bridges. Furthermore, in the past studies on the seismic evaluation of suspension bridges, the effects of the spatial variations of earthquake motions were concerned in the seismic evaluation of long-span suspension bridges[6]. Nie et al.[7] selected the rational constraint systems of Xihoumen suspension bridge to optimize the seismic performance through the deterministic analysis. The seismic performance of new Tacoma Narrows Bridge and Vincent Thomas suspension bridge was studied using the fragility technique, but the emphasis was on the component-level fragility and damaging potential of towers[8-9].
The performance objective is an acceptable risk probability of different levels of damage and loss under a given level seismic hazard. Guidelines for Seismic Design of Highway Bridges (JTG/T B02-1—2008)[10] stipulated the two-level fortification named E1 and E2 and defined the two stage seismic performance targets. Therefore, the key to evaluating the two-level seismic performance of bridges from the view of damage probability should apply the fragility functions to guide engineering practice. In addition, it should be noted that the adjacent spans of San Francisco-Oakland Bay Bridge, a simply supported steel truss bridge, fell off during the 1989 Loma Prieta earthquake event and caused the closure of the transportation link[11]. Since the suspension bridges have a longer vibration period, lower damping and more complex vibration modes than the conventional highway bridges, both the mutual influence and relative importance between adjacent structures are the keys to obtaining a comprehensive evaluation of the overall bridge structure. A comprehensive indicator to achieve the overall seismic performance of long-span suspension bridges under two-level seismic hazard will be appealing, but it is still in its infancy.
In this study, the seismic performance corresponding to seismic objectives of the overall system for suspension bridges under two-level earthquake hazard was evaluated under the fragility function framework. A typical long-span suspension bridge in China was selected. A set of finite element models were built using OpenSEES[12] to perform nonlinear time-history analyses, which incorporated the uncertainties of ground motions and structural properties. Firstly, the PSDMs and capacity models were established and defined based on multiple bridge components, respectively. Secondly, combined with the seismic hazard of the bridge site, the fragility curves of various bridge components were derived to pinpoint the critical components and risk regions under different hazard levels. The repair cost ratios of the overall bridge system were calculated to assess the seismic performance through the derived fragility curves of critical components. In addition, the derived repair cost ratios were used to compare the seismic performance of as-built bridges and retrofitted bridges under two-level seismic hazard, further validating the availability of repair cost ratios and the effectiveness of retrofit measures.
1 Numerical Modeling of the Suspension Bridge
This study selected a common type of suspension bridge constructed in China. As shown in Fig.1, the total 731 m length is made up of a simply supported main-span suspension bridge of 636 m and a steel box-girder approach bridge with three continuous spans of 30, 35 and 30 m.
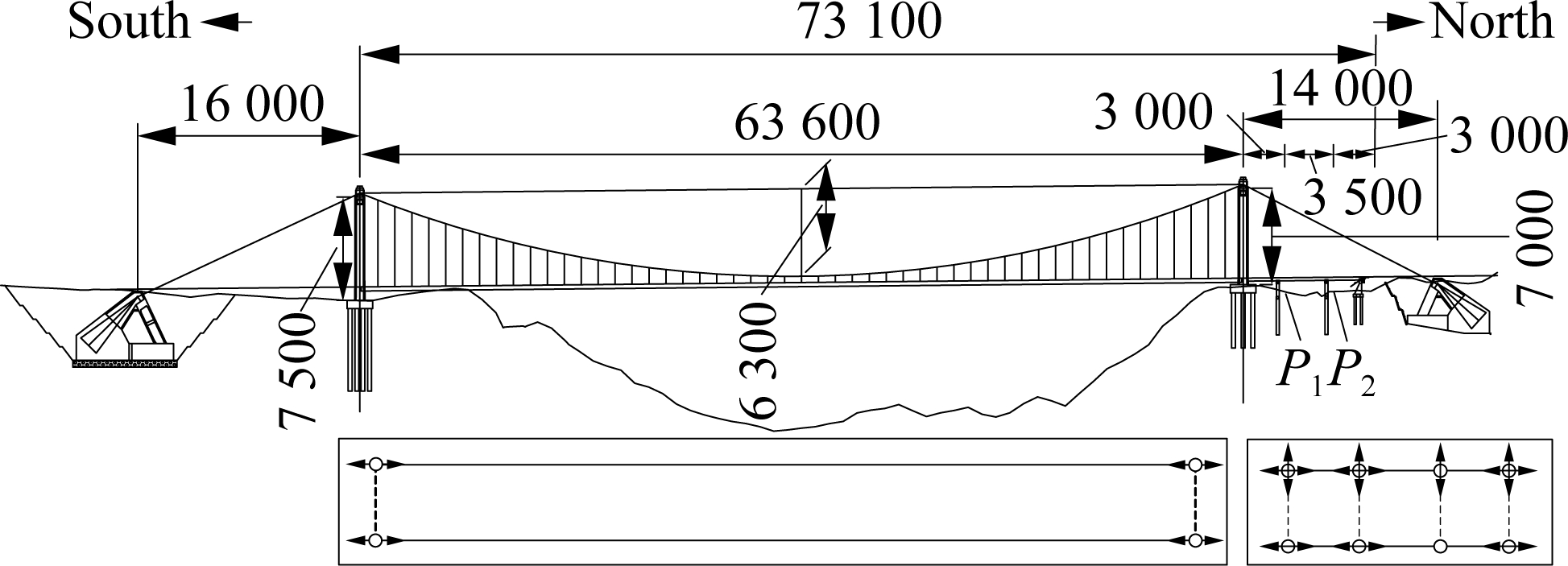
Fig.1 Elevation of the suspension bridge and plane layout of the bearings (unit: cm)
The main bridge has a thin-wall steel girder along the longitudinal direction, with an overall width of 31 m and a height of 3 m. The gate-type tower is designed with two RC box-section legs, of which the bottom section is 5.5 m wide and 7.0 m high at the south side and those of north side are 5.5 and 6.9 m, respectively. One crossbeam is installed at a distance of 10 m from the top of the tower to boost the lateral stiffness. The bored piles with diameters of 2.2 m are adopted to serve as the foundations of towers. The areas of main cables and suspenders are 0.162 6 and 0.001 316 m2, respectively. Gravity anchorage is designed to employ the main cable anchorage on both sides. The approach bridges are two separate bridges on the north side with the same configurations. For each bridge, a three-span continuous steel box-girder bridge is supported by two double-column bents with an integral pile-shaft in middle span. The width and depth of the steel girders are 12.75 and 1.53 m, respectively. The circular section with a diameter of 1.8 m is used in 7-m-high columns. The cast-in-drilled-hole piles serve as the foundation, which are 1.9 m in diameter. The pile-bent is adopted for the seat type abutments, in which the piles are provided by a circular section with a diameter of 1.5 m. The height of the backwall of the abutment is 1.88 m.
A detailed nonlinear 3D model of the selected bridge was built in the software package OpenSEES[14]. A distributed plasticity fiber model was used to represent the sections of towers and columns to account for material nonlinearity. Simultaneously, P-Δ effect was captured in the models of towers. Each fiber was simulated with a stress-strain relationship depending on the represented confined concrete, unconfined concrete and longitudinal reinforcement. Mander model[13] and bilinear relation were adopted to simulate the behaviors of concrete and steel, respectively. The material mechanical indices of the concerning sections, such as the strength, axial compression ratios (ACR), and longitudinal reinforcement ratios ρ are listed in Tab.1, which meet the requirements[10].
The responses of main cables were simulated using the nonlinear tension-only elements, which were modeled as the finite large-displacement truss elements using the Ernst method[14] to account for the sag effect. The response of each suspender was also simulated using a truss element and their initial stress was also considered in their simulations as shown in Fig.3(a). Elastic beam elements were used to simulate the crossbeams of towers and the stiffening girder, as well as the girders and cap beams of the approach bridges. The stiffness of foundations was simulated by using both translational and rotational linear springs at the base of the towers and columns. The elastic and linear components are expected to remain in normal working conditions during a seismic event.
The pot bearings were applied to the initial design (case 1), which became significant factors in the overall responses and functionality of the bridge. The plane layout of bearings is shown in Fig.1, where the arrows represent the sliding direction and the fixed bearings are designed at the second pier (P2) of each approach bridge along the north direction. The response of sliding pot bearings (SPB) was modeled using a bilinear material[10], as detailed in Fig.2(b). Meanwhile, the response of fixed direction was set as constraint.
Tab.1 Materials mechanical indices for concerned sections

SectionLocationConcreteLongitudinal barStirrupStrength/MPaACRStrength/MPaρ/%Strength/MPaρ/%Section ⅠTower bottom550.1595003.7604001.256Section ⅡConnection between tower and crossbeam550.1365002.8054000.797Section ⅢColumn bottom350.0373351.6133350.800
(a)
(b)
(c)
(d)

(e)
Fig.2 Force-displacement relationships of various components. (a) Cable system; (b) Sliding pot bearings; (c) Pounding; (d) Abutment backfill; (e) Abutment pile

(a)
(b)
(c)
Fig.3 Mechanical behaviors of constraint of the retrofitted approach bridges. (a) Laminated elastomeric bearing; (b) Shear key; (c) Cable restrainer
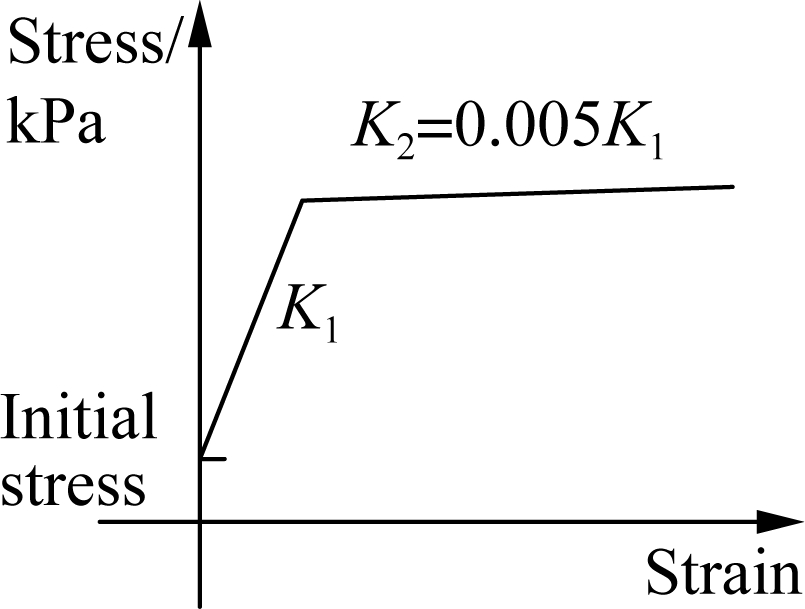
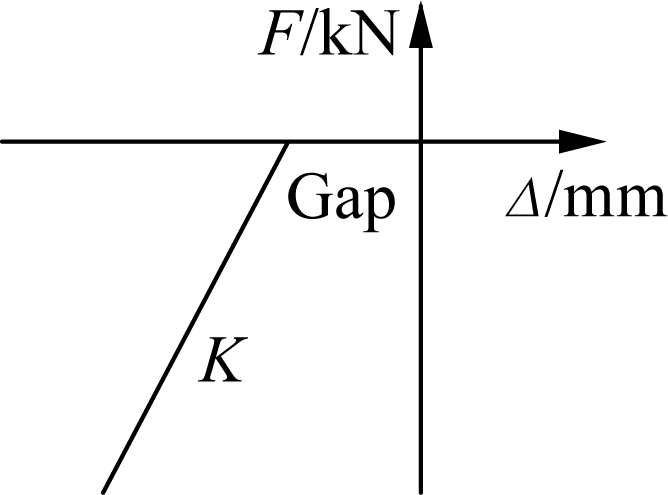
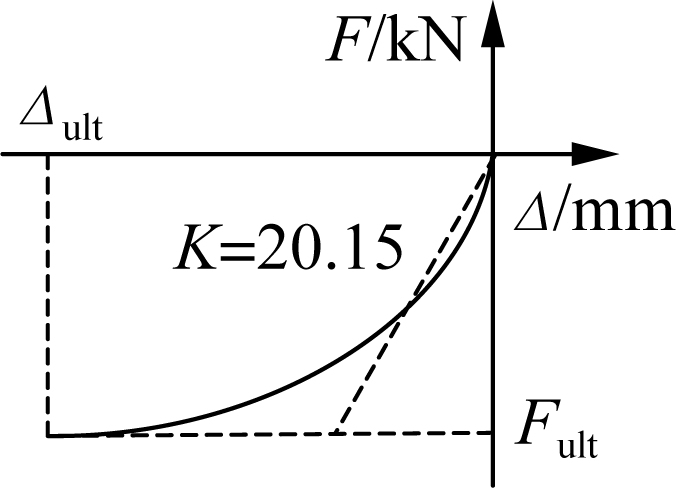
The simulation diagram of seat type abutments can be seen in Ref.[15]. A simple hyperbolic force-displacement relationship is proposed by Shamsabadi et al. [16] that can simulate the back ll soil stiffness per width of the abutments, as shown in Fig.2(d). Pile foundation provides longitudinal and transverse stiffness to the abutments. The trilinear relationship per pile associated with the modeling parameters is presented in Fig.2(e) according to Caltrans[17]. The pounding effects (see Fig.2(c)) were simulated using gap elements with Kelvin materials, but the dissipation of hysteretic energy during pounding was conservatively disregarded[18]. The stiffness of the pounding springs between the girders and abutments was advised to be ten times that of the backfill soil stiffness[19]. However, the sum of axial stiffness of adjacent girders was served as the estimation of the impact stiffness value[20].
ll soil stiffness per width of the abutments, as shown in Fig.2(d). Pile foundation provides longitudinal and transverse stiffness to the abutments. The trilinear relationship per pile associated with the modeling parameters is presented in Fig.2(e) according to Caltrans[17]. The pounding effects (see Fig.2(c)) were simulated using gap elements with Kelvin materials, but the dissipation of hysteretic energy during pounding was conservatively disregarded[18]. The stiffness of the pounding springs between the girders and abutments was advised to be ten times that of the backfill soil stiffness[19]. However, the sum of axial stiffness of adjacent girders was served as the estimation of the impact stiffness value[20].
This study set the contrast case (case 2) to illustrate the shortage of initial design of the overall bridge system. The suspension span used a fluid viscous damper equipped between the deck and each pedestal. Moreover, the restraint systems of the approach bridges were changed, which consisted of laminated elastomeric bearings, transverse concrete shear keys and longitudinal cable restrainers according to earthquake damage experience. The constitutive model of fluid viscous dampers is expressed as
(1)
where α is a positive exponent and the value depends on the piston head orifice, which is 0.3; CD is the viscous damping coefficient, of which the value is 4 000 kN·m-α·sα; ![]() is the velocity of damper; and sgn( ·) is the signum function.
is the velocity of damper; and sgn( ·) is the signum function.
The laminated elastomeric bearings (LEB) have been widely applied to the small-to-medium-span highway bridges in China. It is noted that the bearings are simply placed between the superstructures and substructures without any anchoring measures. The design can protect the substructures during earthquakes, and the piers show relatively low damage ratios[21]. In order to calculate the seismic demands of the retrofitted approach bridges, the corresponding mechanical models of restraint system components were applied to this study after summarizing the related experiment results.
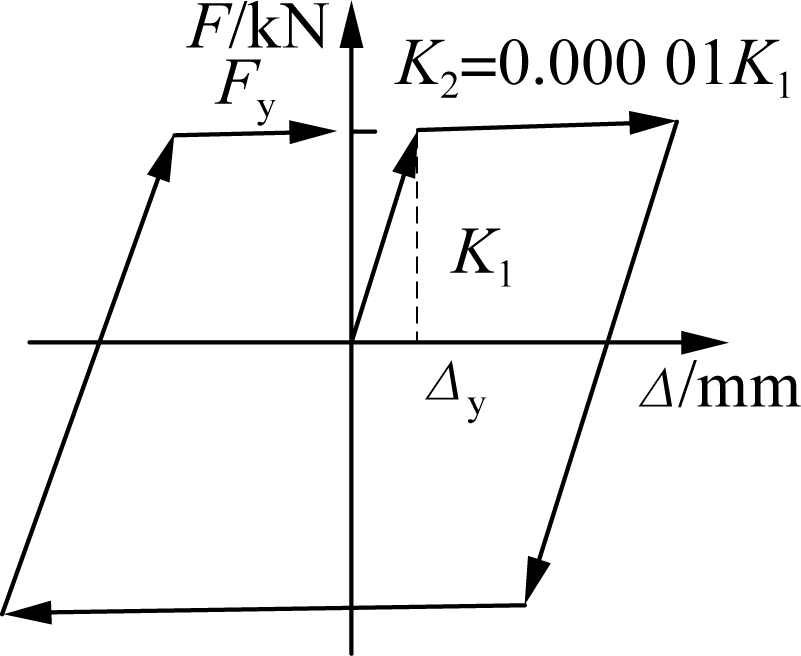
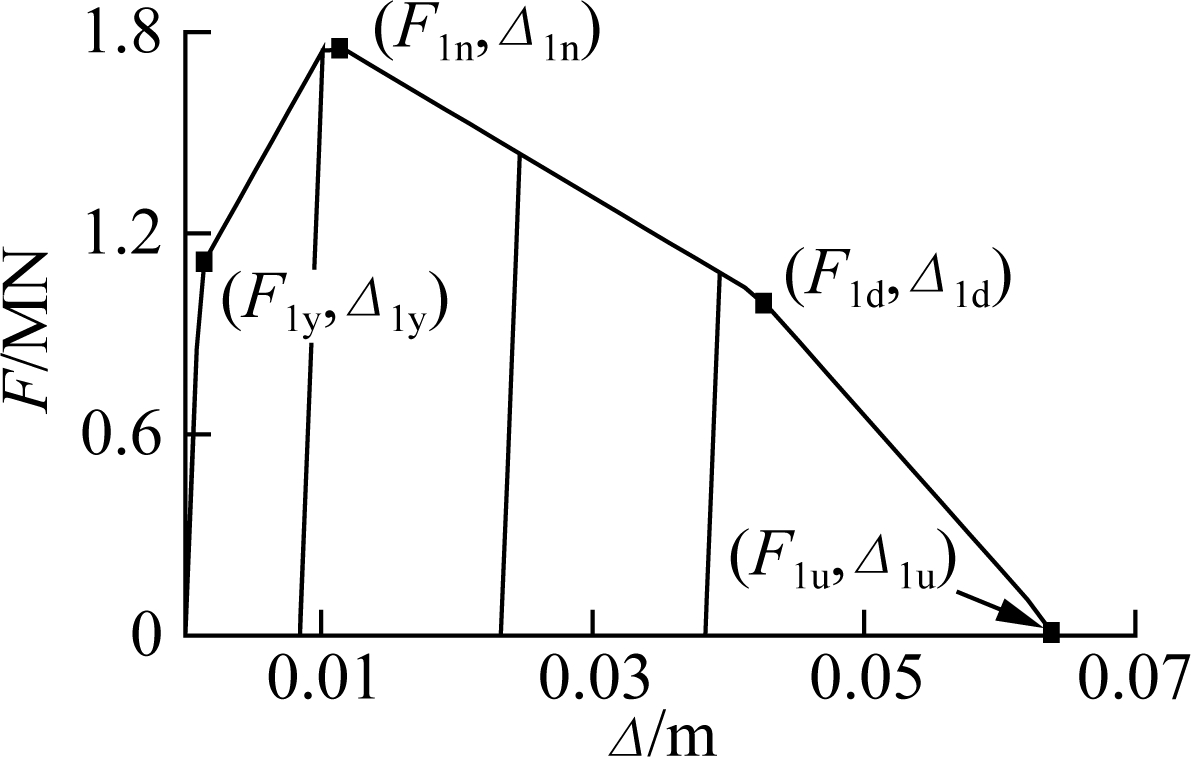
According to the experimental results of laminated elastomeric bearings and shear keys[21-22], their force-displacement relationships can be obtained as shown in Fig.3(a) and (b). The two key points marked rectangles and circles indicate the initial walking and obvious sliding responses of laminated elastomeric bearings. For shear keys, the detailed parameters marked Δ1y, Δ1n, Δ1d and Δ1u represent the yield, nominal, degraded, and ultimate deformations, respectively, which can be obtained from the method proposed by Xu et al.[22] according to the realistic design. The mechanical model of shear keys simultaneously considers the behavior of concrete and steel under earthquakes. As shown in Fig.3(c), the cable restrainers were modeled as nonlinear tension-only elements with an initial slack according to the recommendation of Paddget[4].
2 Demand and Capacity Models
PSDMs employ a large number of nonlinear time-history analyses to account for the uncertainties of ground motions, which need a wide range of intensity of the selected earthquake records. This study, respectively, selected a suite of 80 ground motions and 20 Los Angeles-pertinent ground motions from the PEER strong motion database and the SAC project database to conduct the PSDMs, which can reflect the characteristics of the site condition. The principle of selecting ground motions can consult the studies presented by Refs.[23-24]. Fig.4 shows the distributions of peak ground accelerations (PGA), earthquake magnitudes M, epicentral distances R of the selected records, and the acceleration response spectra of two orthogonal components. The majority of earthquake records with PGA ranging from 0.1g to 0.5g. Statistically significant yet nominally identical 100 three-dimensional numerical models of the bridges were built using the Latin Hypercube Sampling to account for uncertainties, such as material strength, component properties, deck mass, and damping in the simulations (see Tab.2). 100 bridge model-ground motion pairs were created to perform a series of nonlinear time-history analyses, where one of the two components of ground motions was loaded along the longitudinal direction of bridges and the other component was input along the transverse direction. This study selected the geometric mean values of earthquake intensity of two components as the representative values.
PSDMs were built using the cloud approach and the peak seismic demands of critical components were adopted as the engineering demand parameters (EDP) including cross-sections of towers and columns, bearings, cable system, abutments, etc. The detailed EDP can be seen in the vulnerability analysis of components in the following section.
The selection of optimal intensity measure (IM) can be implemented by logarithmic linear regressions of data obtained from the finite element analyses. PGA, PGV, PGD, spectral acceleration at 0.4 s (Sa0.4) and 10 s (Sa10) were chosen as the IM candidates[1-2]. To assess the optimal IM comprehensively, the average values of the IM candidates over the concerned bridge components are presented in Tab.3. βd|IM and R2 can characterize efficiency, while b and ζ can, respectively, measure practicality and proficiency. The last column is the relative closeness ![]() that is intended to provide a multiple performance measurement by the TOPSIS method[25], of which the principle is that the optimal al-ternative should have the shortest distance to the ideal solution and the longest distance to the negative-ideal solution. The method follows the procedure outlined below:
that is intended to provide a multiple performance measurement by the TOPSIS method[25], of which the principle is that the optimal al-ternative should have the shortest distance to the ideal solution and the longest distance to the negative-ideal solution. The method follows the procedure outlined below:

(a)
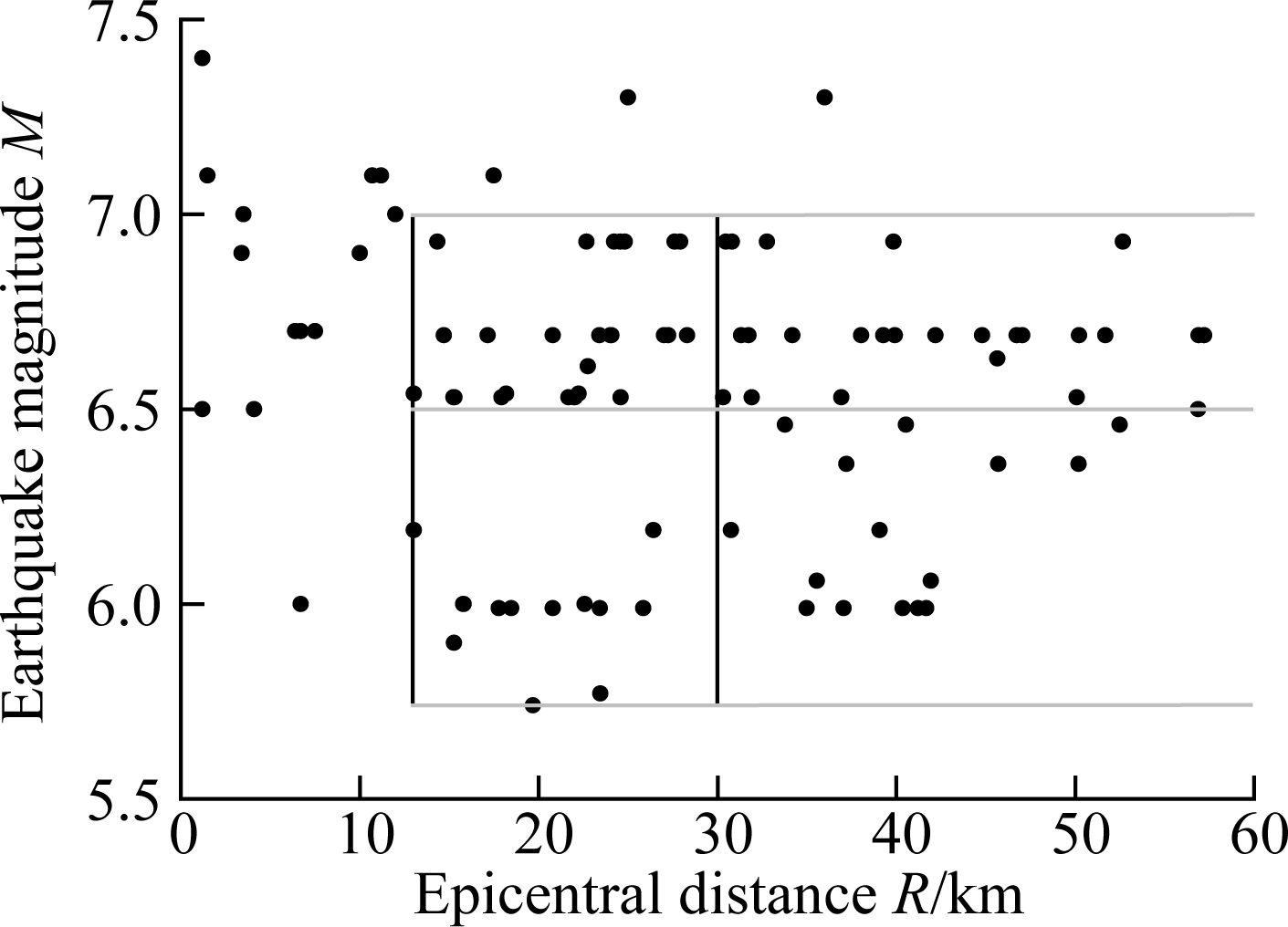
(b)
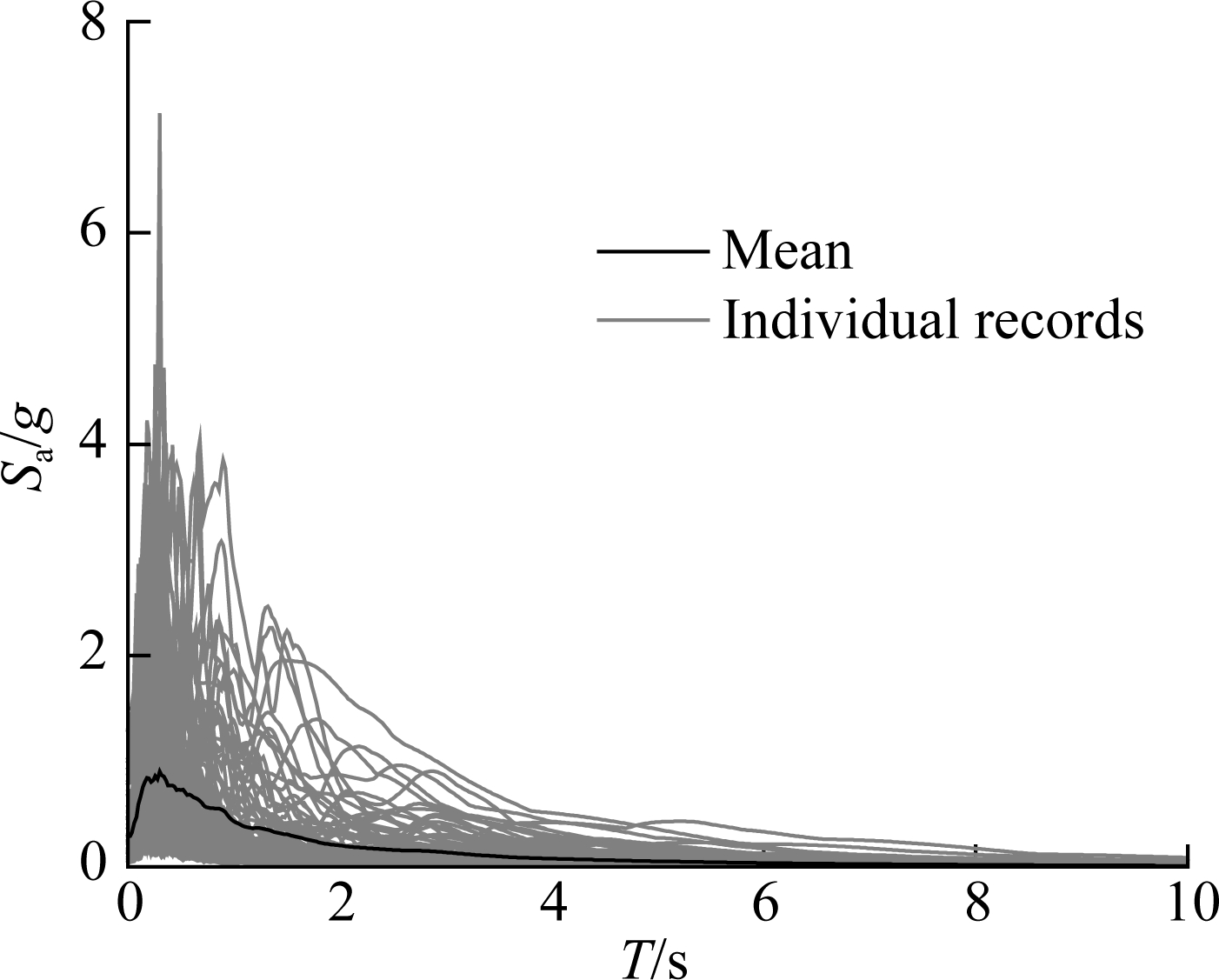
(c)

(d)
Fig.4 Characteristics of the selected ground motions. (a) Distribution of PGA; (b) Distributions of M and R; (c) Acceleration response spectra of the longitudinal direction; (d) Acceleration response spectra of the transverse direction
Tab.2 Uncertainty parameters incorporated into the modeling

Modeling parameterProbability distributionMeanVariation coefficientConcrete compressive strength/MPaNormal46.60.149[10]Steel yield strength/MPaLognormal569.60.0743[10]Friction coefficientUniform0.030.33[5]Backfill soil passive stiffness of abutments/(kN·mm-1·m-1)Uniform20.15 0.25[16]Per pile stiffness of abutments/(kN·mm-1)Uniform70.29[16]Deck-deck gap/mmNormal7600.2[2]Deck massUniform10.1[2]Damping ratioNormal0.020.15[10]
Tab.3 Average measures and reference indices for the IM candidates

IMβd|IMR2bζC∗iCase 1Case 2Case 1Case 2Case 1Case 2Case 1Case 2Case 1Case 2PGA0.5970.5650.7410.6131.2500.8830.4890.6940.9280.683PGV0.5680.4610.7740.7201.0240.7640.5560.6930.8450.881PGD0.7490.5650.5940.5850.7380.5651.0541.1600.3810.439Sa040.6670.5920.6900.5801.1730.8360.5770.7590.7770.593Sa100.8700.6620.4540.4530.6170.4761.4991.6120.0000.000
1) Preprocess data based on index properties including cost and benefit. For each IM candidate, R2 and b were regarded as the benefit indices, while βd|IM and ζ were served as cost indices. The normalized values z of the two types of indices can be computed based on their initial average values y by the following equations:
(2)
(3)
where subscripts i and j indicate the IM candidates and compared indices, respectively. This is intended to provide a performance measure along an increasing direction.
2) Calculate the normalized decision matrix. The normalized decision parameter fij is calculated as

(4)
3) Calculate the weighted normalized decision matrix. The weighted normalized value Zij is calculated as
Zij=wjfij
(5)
where wj is the weight of the j-th attribute, and ∑wj=1.0. The variation coefficient method can be used to calculate wj as
(6)
where ρj is the variation coefficient of the j-th attribute.
4) Determine the ideal solution ![]()
(7)
5) Calculate the distance measures using the m-dimensional Euclidean norm. The distances ![]() between each alternative and the ideal and negative-ideal solution are given, respectively
between each alternative and the ideal and negative-ideal solution are given, respectively
(8)
6) Calculate the relative closeness ![]() to the ideal solution, which is defined as
to the ideal solution, which is defined as
(9)
and then rank the optimal order according to ![]()
After comparing the calculated ![]() based on the aforesaid steps, PGA and PGV emerged as the best for two cases. Meanwhile, PGA was given in the seismic safety assessment report of site soil. In order to assess the performance based on seismic hazard conveniently, PGA can be selected as the optimal IM.
based on the aforesaid steps, PGA and PGV emerged as the best for two cases. Meanwhile, PGA was given in the seismic safety assessment report of site soil. In order to assess the performance based on seismic hazard conveniently, PGA can be selected as the optimal IM.
The definition of capacity models is the last step in deriving component-level fragility curves. Zhong et al.[5] proposed the component classification method for long-span bridges. The components were considered as primary, secondary and accessory ones. The simulations of foundations, decks, and anchorages were regarded as undamaged components. Consistent with the research of Ramanathan[2], component damage states were generally defined as slight, moderate, extensive and collapse states based on the damage progress of a type of component, demarcated by the damage threshold values. The damage threshold values of bearings were determined to rely on the pounding gaps between adjacent components, seat widths and the damages to bearings themselves. The general definition of damage states for SPB and LEB is given in Fig.5, and the corresponding bearing displacement thresholds for two cases are listed in Tab.4. Effective shear strain (ESS) is used to describe the damage states of laminated elastomeric bearings.
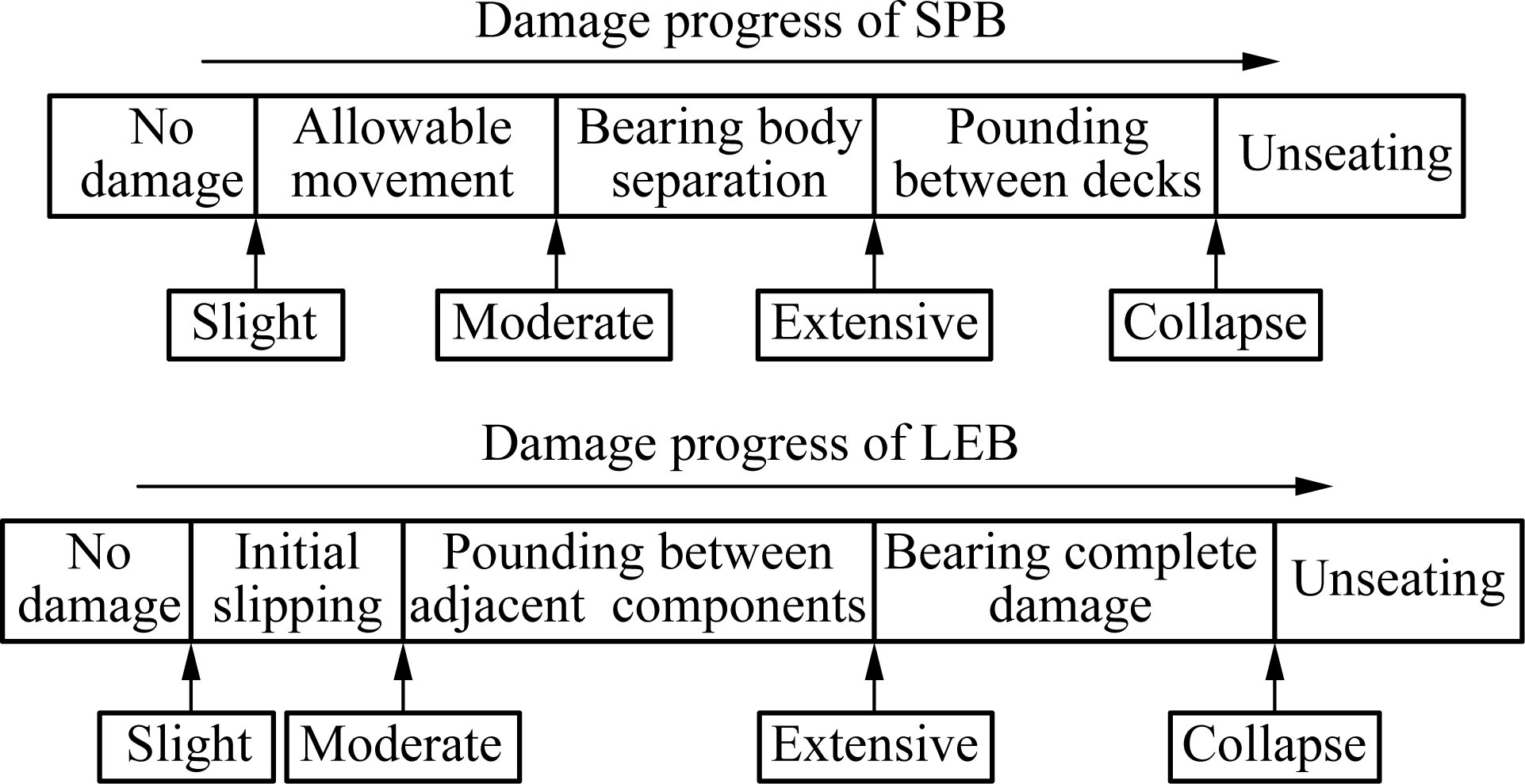
Fig.5 Definition of bearing damage state
Tab.4 Damage threshold values of bearing displacements
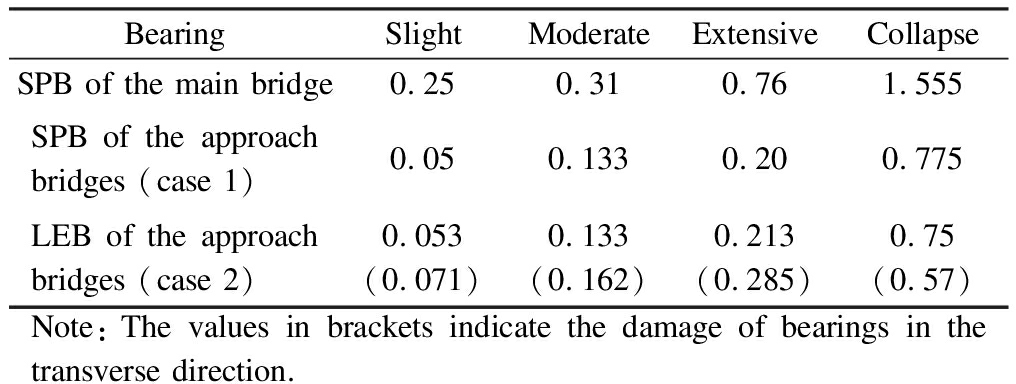
BearingSlightModerateExtensiveCollapseSPB of the main bridge0.250.310.761.555SPB of the approach bridges (case 1)0.050.1330.200.775LEB of the approach bridges (case 2)0.053(0.071)0.133(0.162)0.213(0.285)0.75(0.57)Note: The values in brackets indicate the damage of bearings in the transverse direction.
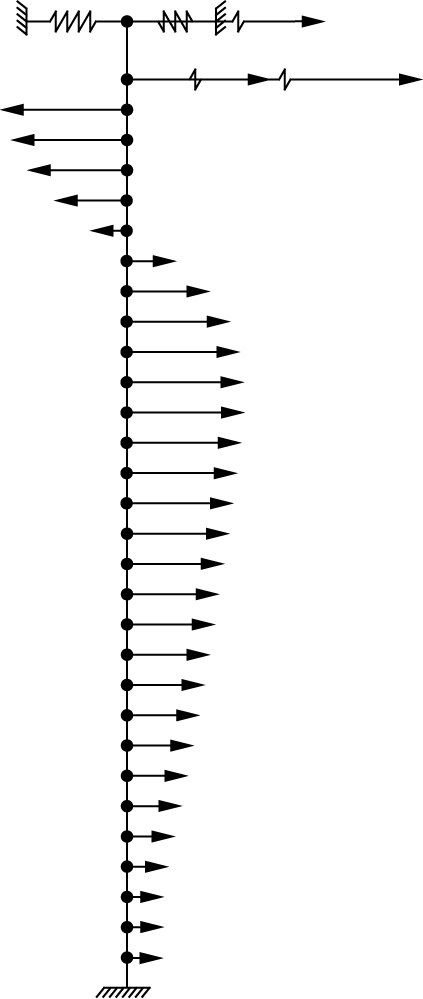
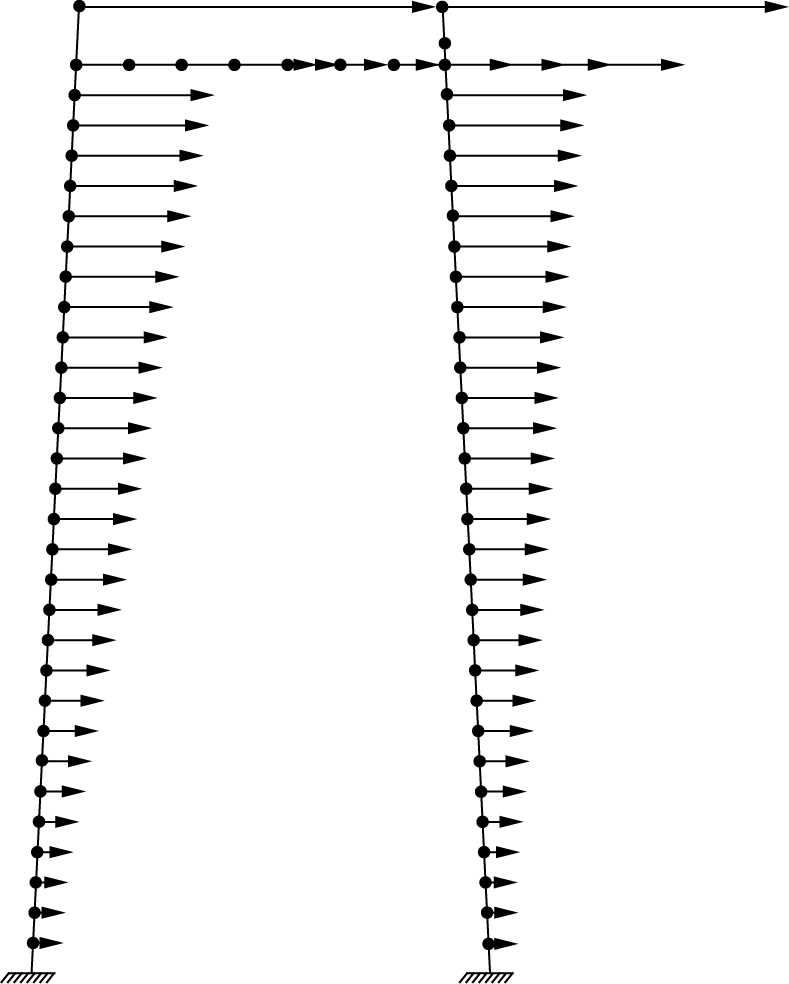
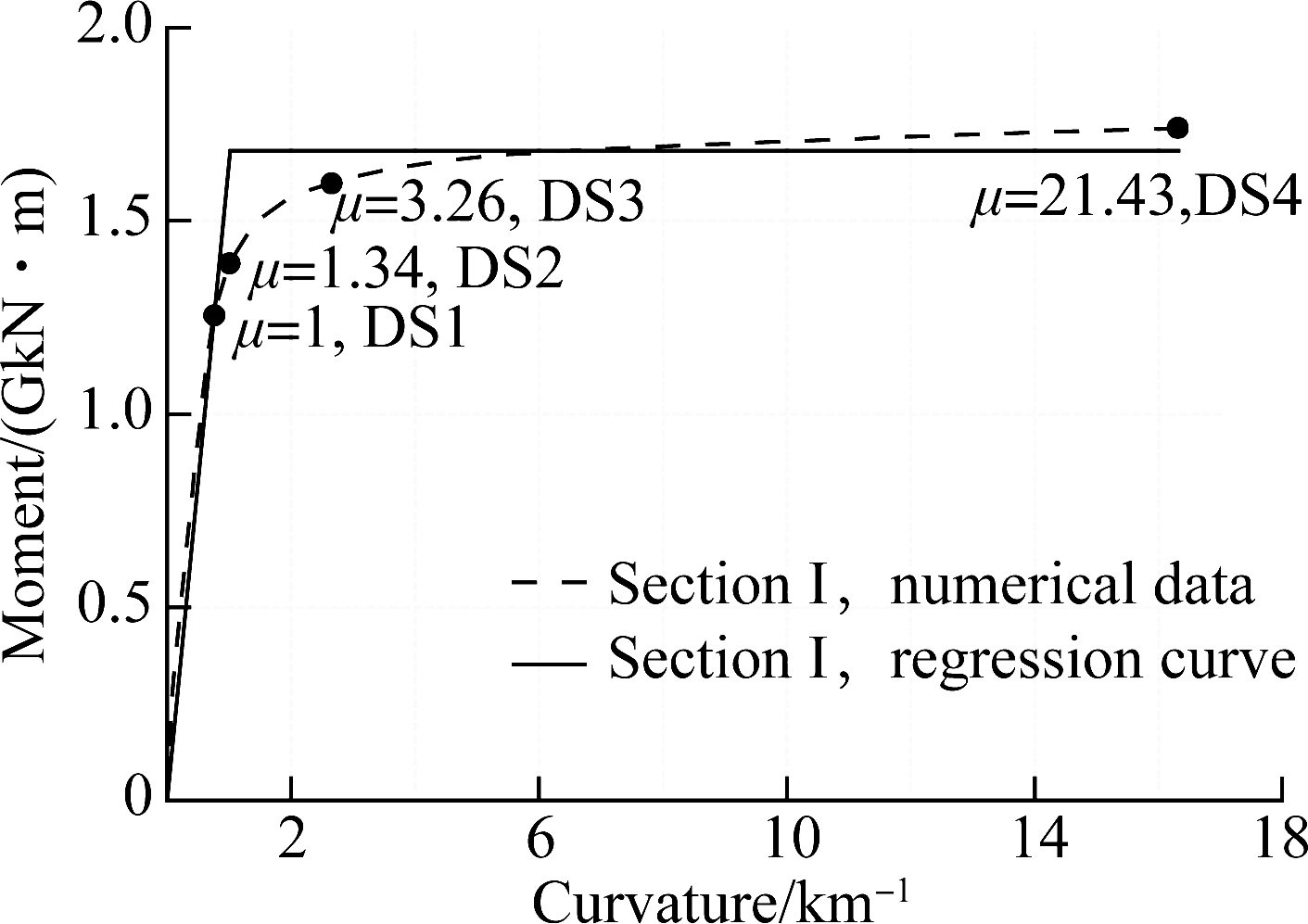
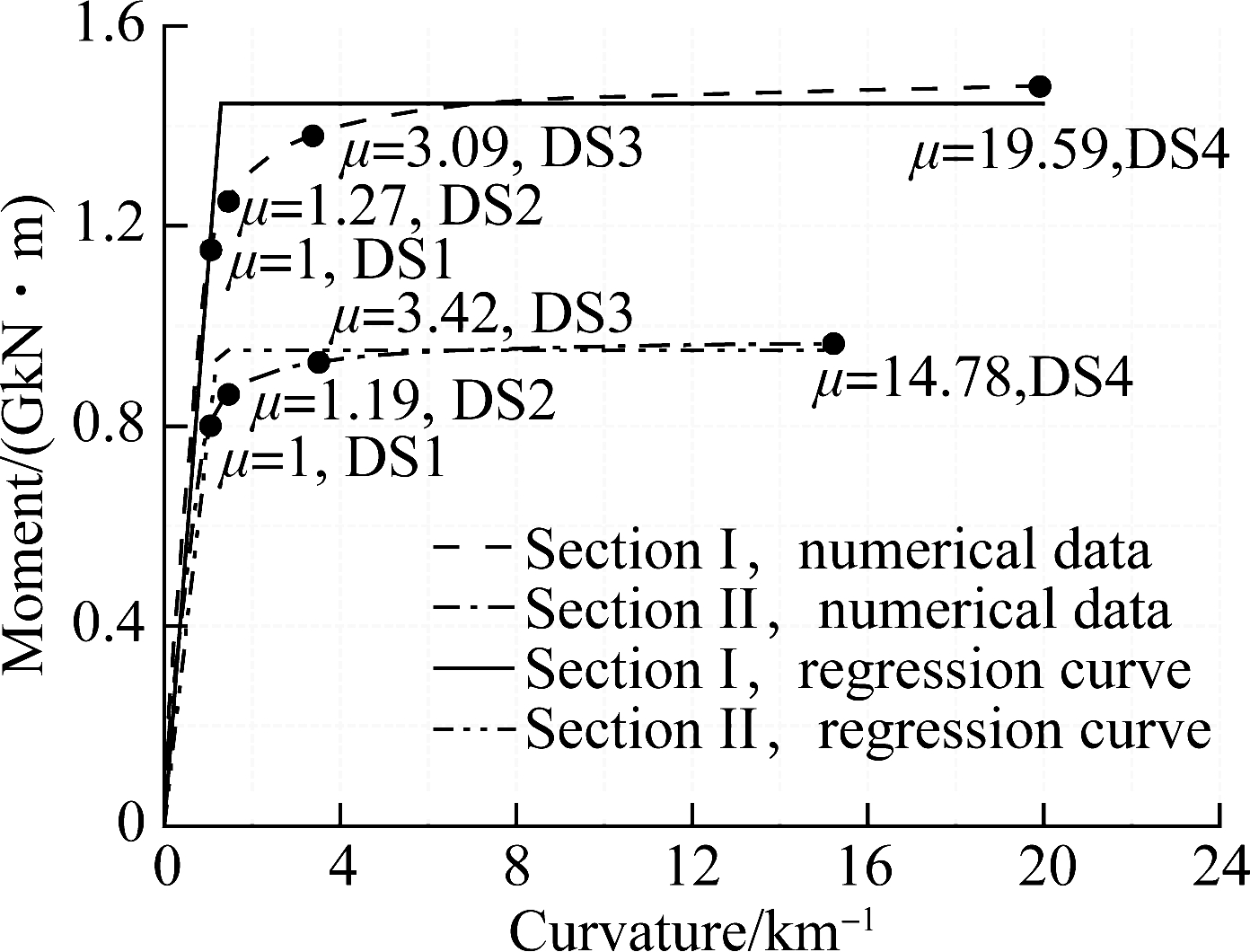
The towers of suspension bridges in the geometric sizes, material strengths, and ACR of the sections are different from the columns of conventional highway bridges. The necessity of the development of modal pushover analysis considering P-Δ effect was noted when defining the damage states of towers. Firstly, the equivalent tower models were required to be developed with fiber beam elements. Secondly, the inertial force distributions were back-calculated from the multi-mode spectral analysis using the 3D bridge model, as shown in Fig.6. Finally, the towers were loaded by the load mode obtained from the last step to carry out the pushover analyses. The plastic regions can be captured with the evolution of curvatures along the height of towers as the loading increases. It is concluded that both Section Ⅰ and Section Ⅱ in Tab.1 are the critical cross-sections in the transverse direction, but the critical cross-section can be selected as Section Ⅰ when loaded along the longitudinal direction. The four different damage states of tower cross-sections in term of curvature ductility were quantified following the physical characteristics, which are in turn the yielding of reinforcing bar, formation of stable plastic hinge, major spalling of the cover concrete and rupture of the reinforcing bar or core concrete crushing. The moment-curvature relationships of critical cross-sections were regressed with bilinear curves based on equal area rule, hence determining their corresponding four limit state thresholds as shown in Fig.7. Similarly, another pushover analysis was applied to the double-column bent of approach bridges (Section Ⅲ) based on Guidelines for Seismic Design of Highway Bridges[10]. Tab.5 lists the limit state thresholds of the bottom section of columns for approach bridges. Results of the pushover analyses indicate that the key cross-sections have a good ductility capacity and the longitudinal ductility capacity of the same sections is better than that of the transverse.
(a)
(b)
Fig.6 Distributions of inertial forces for towers. (a) Longitudinal; (b) Transverse
(a)
(b)
Fig.7 Moment-curvature relationships of critical cross-sections by modal pushover analyses of towers. (a) Longitudinal direction; (b) Transverse direction
Tab.5 Damage threshold values of the bottom sections of columns

Loading directionSlightModerateExtensiveCollapseLongitudinal1.001.446.1625.64Transverse1.001.314.3217.31
The nominal yield strength (i.e. 85% of the ultimate strength) was served as the failure index to define the extensive damage threshold values of the main cables and the collapse damage threshold values for suspenders. The distinguishable elasticity and plasticity deformations of abutments and shear keys can be specified as their slight and moderate damage thresholds[2]. For the expansion joints and seismic measures, only slight damage was defined due to their substitutability[2].
A value of 0.35 was adopted for the dispersions of capacity models in the abutments and RC components including towers and columns[2]. The variation coefficient of cable systems was 0.1, considering the low variability of the steel strands[4]. The descriptive dispersions of the remaining components including bearings, shear keys, expansion joints and seismic measures were employed to be 0.25 and 0.47 for the two lower-level (slight, moderate) and two higher-level (extensive, collapse) damage states, respectively[1].
3 Performance-Based Seismic Assessment of Suspension Bridges
3.1 Component-level fragility based on seismic hazard
Fragility is a conditional probability that gives the potential that seismic demands of a structure reach or exceed a specified damage level under a provided earthquake intensity. When the component-level fragility curves are built with the PSDM generated by the cloud approach, the conditional probability can be written as
![]()
(10)
where Sd and Sc are the mean values of seismic demand and structural capacity, respectively; βd|IM and βc indicate the dispersions of seismic demand conditioned on an IM and structural capacity, respectively; both a and b are log-linear regression coefficients; and Φ( ·) represents the standard normal distribution function. It should be noted that Sc and βc are defined based on the damage state which has been considered.
If the seismic risk analysis is incorporated in the seismic fragility of the structures, the conditional probability for fragility can be defined as
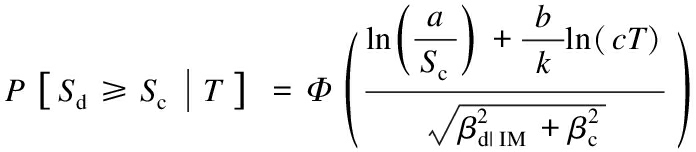
(11)
where the coefficients c and k are related to the seismic activity and attenuation law of the engineering site, which can be fitted with the following equation based on the average annual probability ν and earthquake intensity im of the engineering site[26]:
(12)
and T is the recurrence exceeding im,
(13)
According to the seismic hazard analysis of the engineering site, coefficients c and k in Eq.(11) were determined to be 0.019 26 and -1.881 9, respectively.
Therefore, the component-level fragility curves of suspension bridges based on seismic hazard can be plotted in Fig.8, which can provide a better prediction of the damage potential for bridge components and pinpoint the vulnerable components under earthquakes. In the figure, μ, δb, and δa represent the curvature ductilities of cross-sections, displacements of bearings, and abutments, respectively; subscripts L and T indicate the seismic responses along the longitudinal and transverse directions, respectively; letters after the dashes represent the locations of bridge components; S represents the tower at the south side; M represents the main bridge; A denotes the abutments of the approach bridge; P1 and P2 are the pier orders of the approach bridges as shown in Fig.1; Rm and Rs are the ratios of the maximum forces to yield values of the main cables and suspenders, respectively.
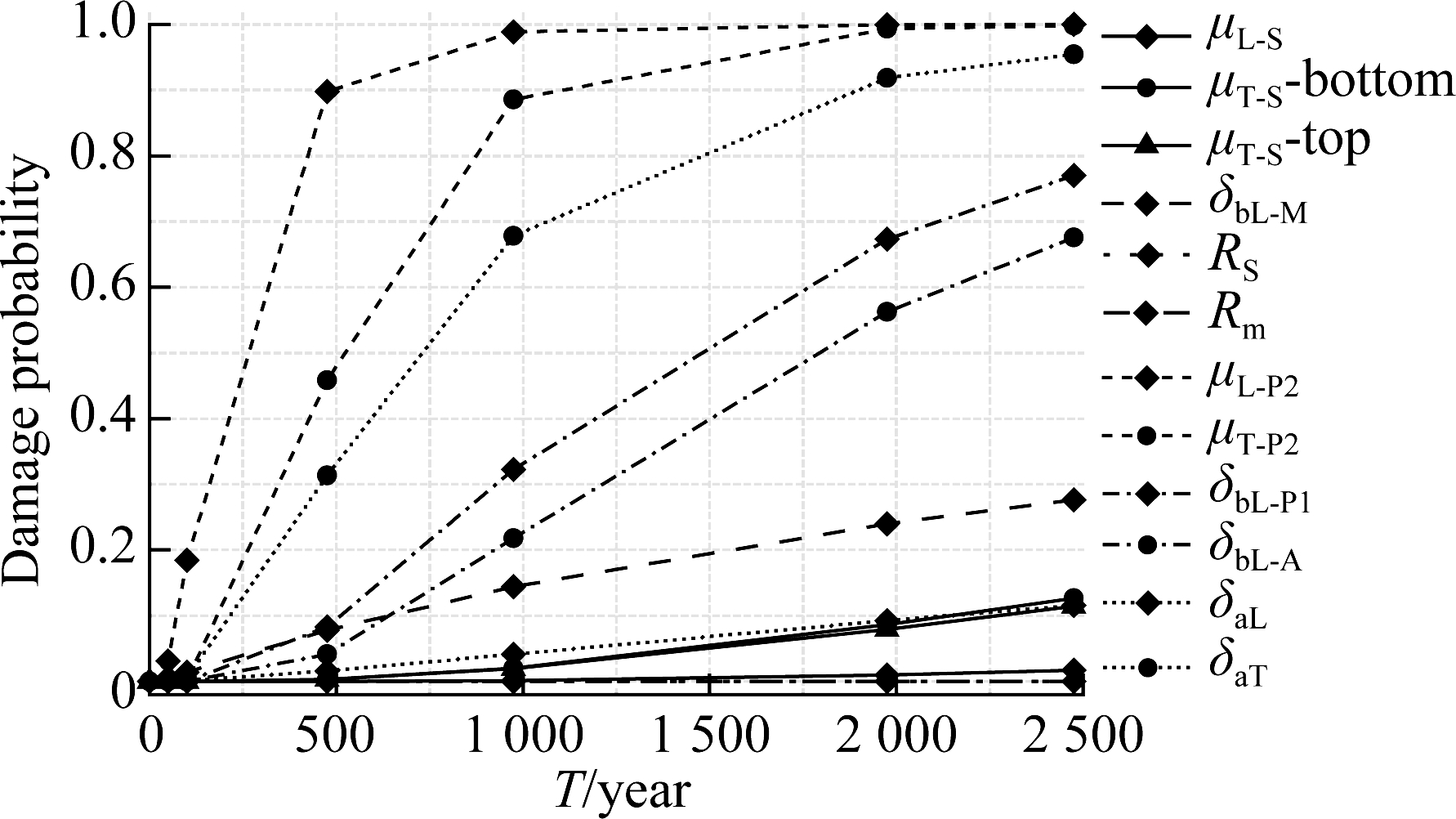
(a)

(b)
Fig.8 Fragility curves of components for the critical damage states. (a) Case 1; (b) Case 2
For case 1, the pot bearings of the main bridge are likely to be the complete damage, and a higher probability of pounding exists between the adjacent decks along the longitudinal direction. Even under the rare earthquake, the damage potential of towers forming a stable plastic hinge is close to 13% in the transverse direction. Under the same circumstances, the extensive damage probability is approximately zero. In addition, the longitudinal seismic demands are much lower than the transverse ones. The cable system is found to be safe in the foreseeable range of earthquake intensity, where the force values are lower than the yield values. It can be viewed from the response data of the fragility analysis that the high stress regions of main cables and suspenders are, respectively, observed to locate at the top of the towers and the side and middle of the suspension span, as shown in Fig. 9. The mean values of their forces under earthquakes are about 15% higher than the forces obtaining from dead loads. The columns of the approach bridges emerge as the most fragile components due to the application of fixed pot bearings, and the large deformations of piers can result in the complete damage of sliding pot bearings, as well as the obvious pounding between decks and abutments. These actions will further lead to the inelastic responses of abutments, which reflect an irrational sequence of damage state occurrences.
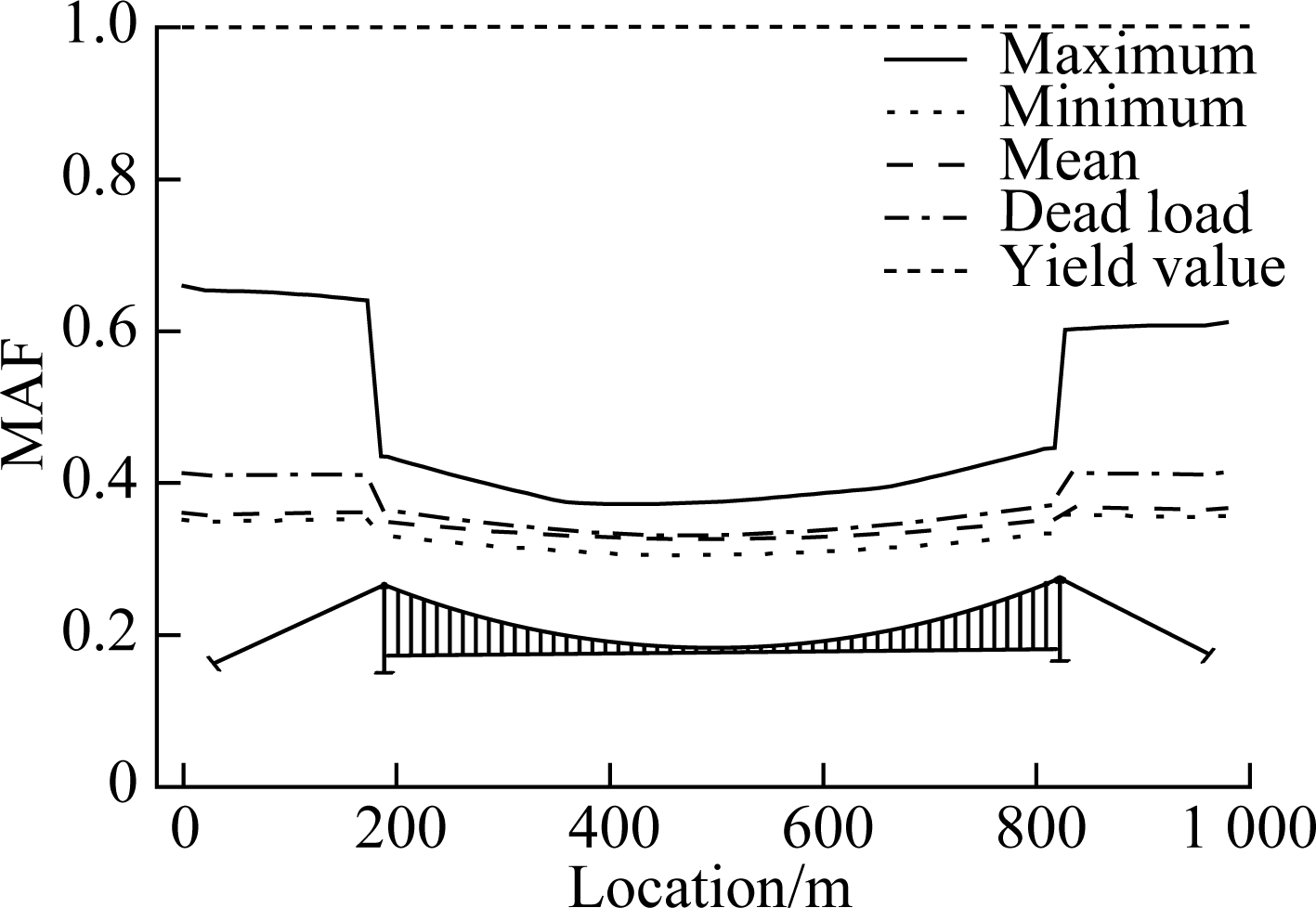
(a)
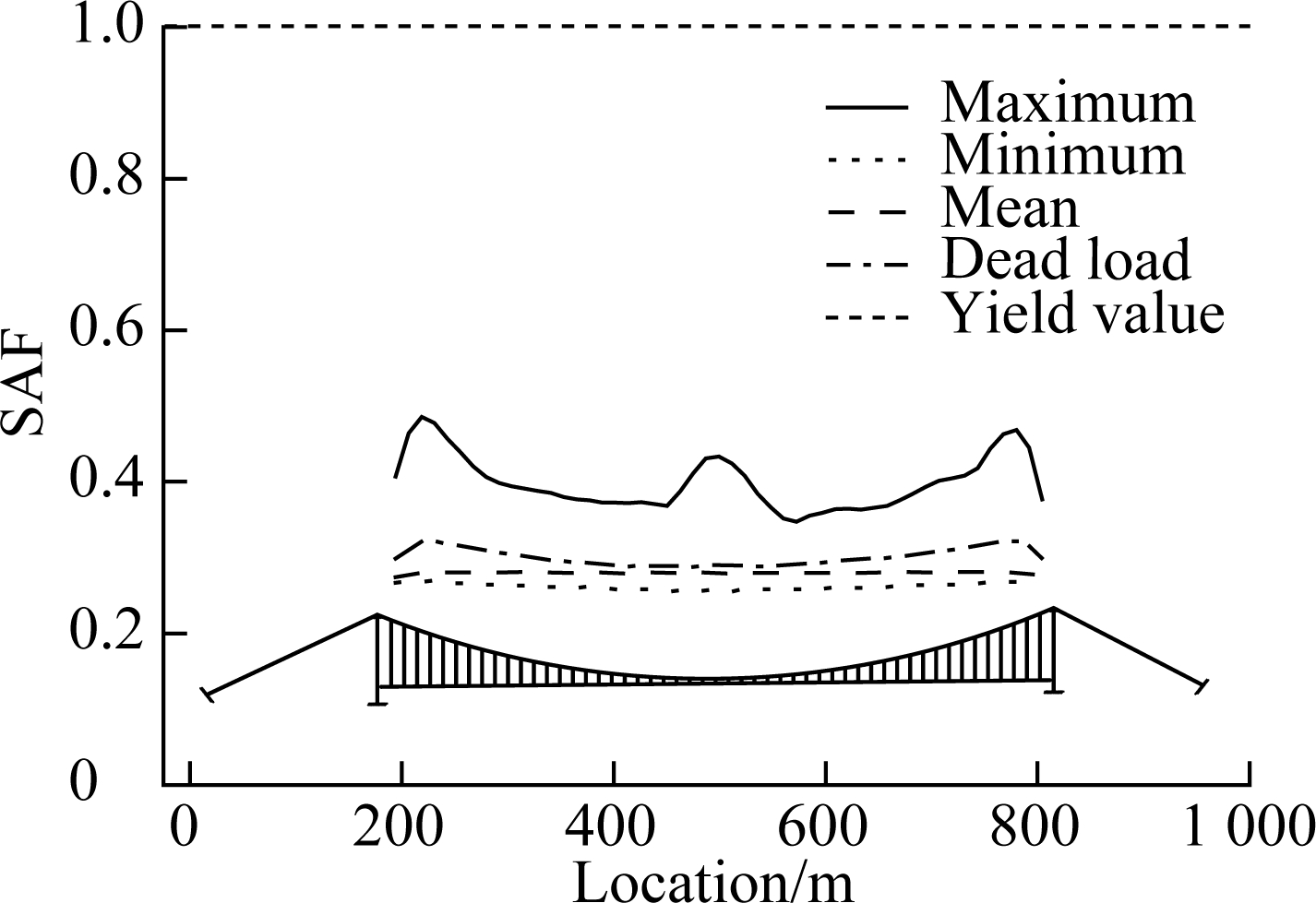
(b)
Fig.9 Force distributions of the cable system. (a) Main cable; (b) Suspender
For case 2 with the retrofit measures, dampers play a limited role in the fragility reduction of the self-damages of bearings in long-span bridges as ground motion intensity increases, but they can effectively reduce the damage potential of pounding between adjacent decks by more than 50% under a rare earthquake with a recurrence of 2 475 years. Also, the effect of dampers on the responses of the towers and cable system can be ignored. The change of the restraint system for approach bridges is beneficial for protecting the piers. Under the rare earthquake, the moderate damage probability of the piers in the longitudinal direction is reduced from 99% to 16%, and that in the transverse direction drops from 99% to 7%. The pounding probability between the decks and abutments of approach bridges is reduced from 67% to 38% by the use of cable restrainers, whereas the obvious sliding of laminated elastomeric bearings greatly increases the damaging potential of the shear keys due to pounding. It can be concluded that the pounding between adjacent decks and the constraint system of approach bridges is the major factor affecting seismic performance.
3.2 System-level performance based on repair cost ratio
Although the damage probability of pinpointed vulnerable bridge components can be calculated by the component-level fragility function, the damage potential of the overall bridge system remains unclear. On the one hand, different components may experience different damage states and their contributions to the system vulnerability are different; on the other hand, a given retrofit measure may have a different effect on the different components. Previous studies[1-3] showed that the bridge system-level fragility values can reflect the overall seismic performance of bridges. Padgett et al.[4] compared the efficiency of different retrofit measures using the overall system-level fragility. However, their system fragility was developed by the serial connection assumptions, while joint probabilistic seismic demand models were used to unite the seismic demands of the components. It is important to note in this study that a key point of the derivation of system-level fragility for the long-span suspension bridge with multiple components depends on the correlations among the critical components and the relative importance between the main bridge and the approach bridges.
As illustrated in Tab.6, the two-level seismic performance objectives of the overall system for suspension bridges are different based on the relative importance of structures and components. The bridge components can be classified as the primary load-carrying components such as towers and columns and secondary replaceable components such as bearings. In addition, it can be seen that the performance objectives of the main bridge is superior to that of the approach bridges, and attention should be paid to the fact that the differences in repair cost and time of the main and approach bridges are significant when the same damage state is achieved. As a result of the findings of component-level fragility analysis and the definition of damage states for bearings, the critical components of the suspension bridge can include towers, columns and bearings in the presented study.
Tab.6 Seismic fortification criteria and performance objectives

Earthquake hazardStructure performance objectiveComponent performanceE1 earthquake(475-year recurrence)No typical emergency repair, open to normal public trafficNo damage to the primary components;possible damage in the serviceable and replaceable componentsE2 earthquake(2 475-year recurrence)Repairable damage for the main bridge, open to normal pub-lic traffic; No collapse of the approach bridge, open to e-mergency vehicles onlyPossible medium damage to the pylons and abutments, etc.; possible extensive damage to the bearings and columns
Since the critical components are neither fully correlated nor totally independent under earthquakes, the repair cost ratios can be used to estimate the repair cost as a ratio of the replacement cost of structures under different levels of seismic hazard, rather than calculating the total cost to replace or repair critical components. Xie et al.[27] derived the repair cost ratio of the conventional highway bridge system by performance-based methodology, which can be given as
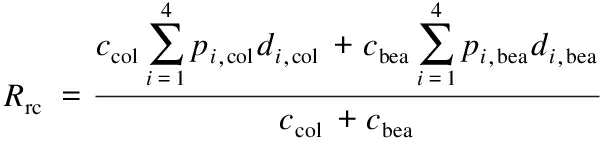
(14)
where Rrc denotes the repair cost ratio; ccol and cbea are the replacement costs for the columns and bearings, respectively; di,col and di,bea are the damage ratios of the columns and bearings at the i-th damage state, respectively; pi,col and pi,bea are the damage probabilities of the columns and bearings at the i-th damage state, respectively. The damage ratio d is the ratio of the repair cost to the replacement cost for evaluating the economic losses. According to the suggestion of HAZUS[28] and the research of Xie et al.[27], the damage ratios of the columns and bearings can be selected from Tab.7. The probability p, a link between the system-level performance based on the repair cost ratios and component fragility functions, is calculated as the difference of the conditional probabilities for the same type of components under different damage states, as shown in Fig.10.
Tab.7 Damage ratios of columns and bearings

ComponentSlightModerateExtensiveCollapseColumns0.030.080.251.00Bearings0.040.100.501.00
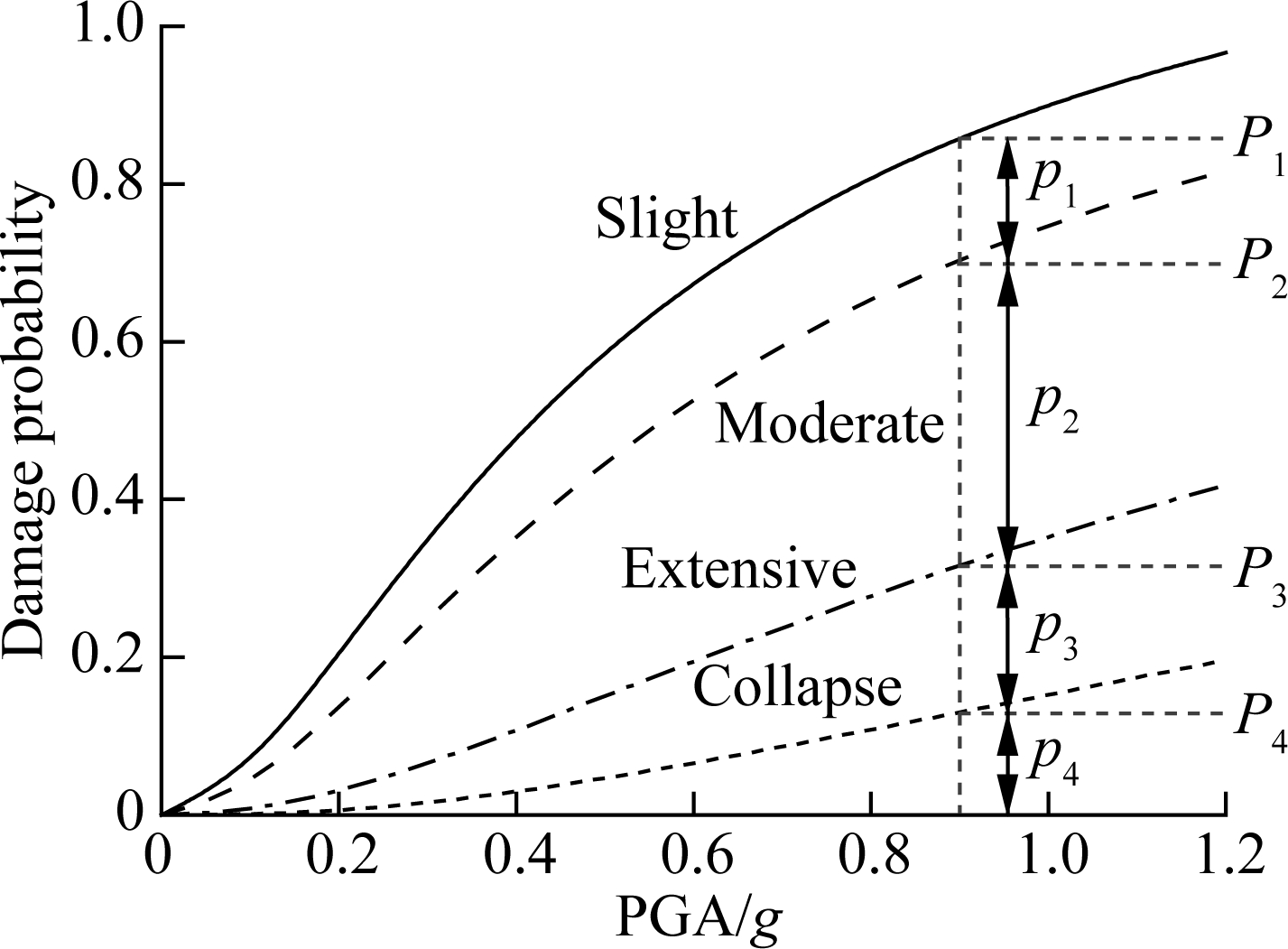
Fig.10 The calculation of the probability p
The replacement costs of columns and bearings primarily depend on the direct and indirect economic losses from changing these damaged components and effect on traffic services. The columns serve as the load-carrying components and their damage will pose a threat to the availability of the overall bridge system, which will result in a long closure of traffic service. Hence, the repair costs of columns should consider the majority of the cost. On the other hand, the replacement costs of bearings are mainly due to their extensive damage, which includes the reinstallation of bearings and resetting of superstructures that may be damaged owing to pounding and unseating. These repairs impact less on traffic services. Zhang et al.[3] pointed out that two sets of weighting ratios can be applied to the replacement costs of columns and bearings, which are 0.85∶0.15 and 0.75∶0.25, respectively. Therefore, this study derived and discussed the closed form expressions of the global repair cost ratios appropriate for the overall system of the suspension bridge based on the foregoing context as follows:

(15)
where subscripts A and M represent the approach bridge and the main bridge, respectively; the subscript tow represents the towers. The other letters and the variables
c, p and d are the same as the aforesaid definitions. If other replacement costs are normalized by the replacement costs of columns ccol,A, Eq. (15) can be given as
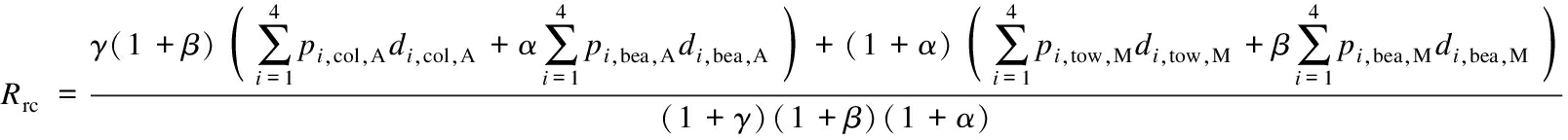
(16)
where α=cbea,A/ccol,A,β=cbea,M/ctow,M, and γ=(cbea,A+ccol,A)/(cbea,M+ctow,M).
This study recommends that β=0.15∶0.85 can be employed for the replacement cost ratio of the towers to the bearings of the main bridge considering that the functionality of towers is consistent with the columns of the approach bridges, while the replacement cost of the columns is 3 times as much as that of bearings for the approach bridges, that is, α=0.25∶0.75. The coefficient γ can be served as an index to reflect the relative importance between the suspension bridge and approach bridges, which is generally less than or equal to 1.0. If γ=0, it implies that the effect of approach bridges is neglected for the seismic evaluation of suspension bridges. It is considered that the seismic performance objectives of approach bridges are as important as the suspension span when γ=1.0. In addition, the installation of supplemental devices such as dampers and cable restrainers will increase the costs of the bridge system in case 2, but their installation costs are lower than those of towers and bearings. Hence, the repair cost ratio of bridges retrofitted with the supplementary devices can be written as
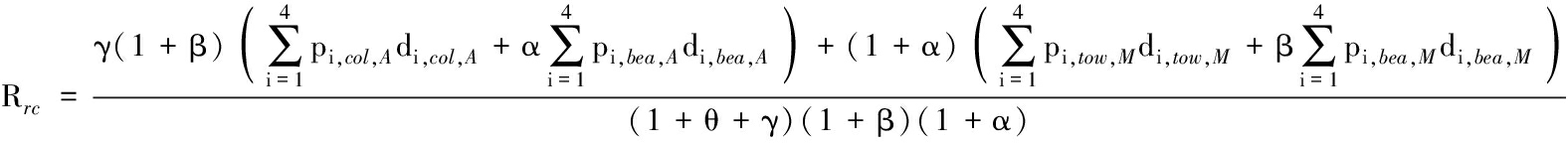
(17)
where θ is the ratio of the cost of supplementary devices to the total cost of towers and bearings. In this study, 5% is assigned to coefficient θ.
The difference in system-level seismic performance based on the repair cost ratio between the main bridge and approach bridges is illustrated in Fig.11. Taking case 1 as an example, the system-level repair cost ratio will be underestimated when disregarding the effect of approach bridges on the overall system performance (γ=0), because the system-level repair cost ratio (black line) is apparently higher than that of main bridge especially in the high earthquake intensity. It can be inferred that the overall seismic performance of the as-built suspension bridge is dominated by the seismic design of the approach bridges. The repair cost ratio of the overall bridge system is increased as the weighting ratio of the approach bridges increases. For example, under the E2 earthquake, the repair cost ratio of the as-built bridge is much higher than that of the main bridge if the importance of approach bridges is equal to the suspension span (γ=1). Therefore, a rational range of weighting ratio γ is supposed to be useful for achieving a balance between the repair costs of the overall bridge system and determining the repair strategies. Taking the interaction between the main bridge and approach bridges and the influence of the seismic performance of approach bridges on traffic services into account, it is pointed out in this study that a weighting ratio range of between 0.6 and 0.8 can be a reasonable choice.
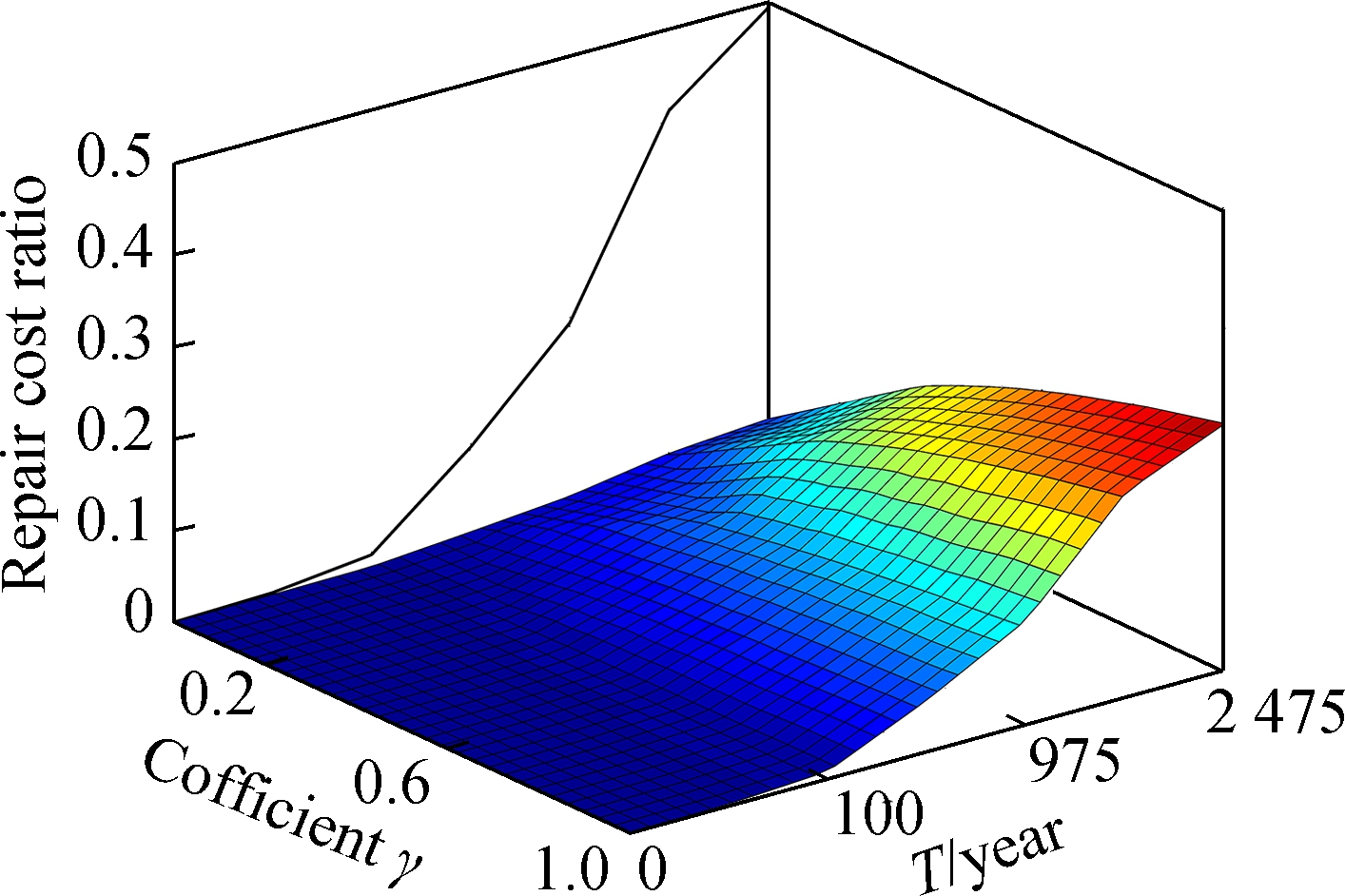
(a)
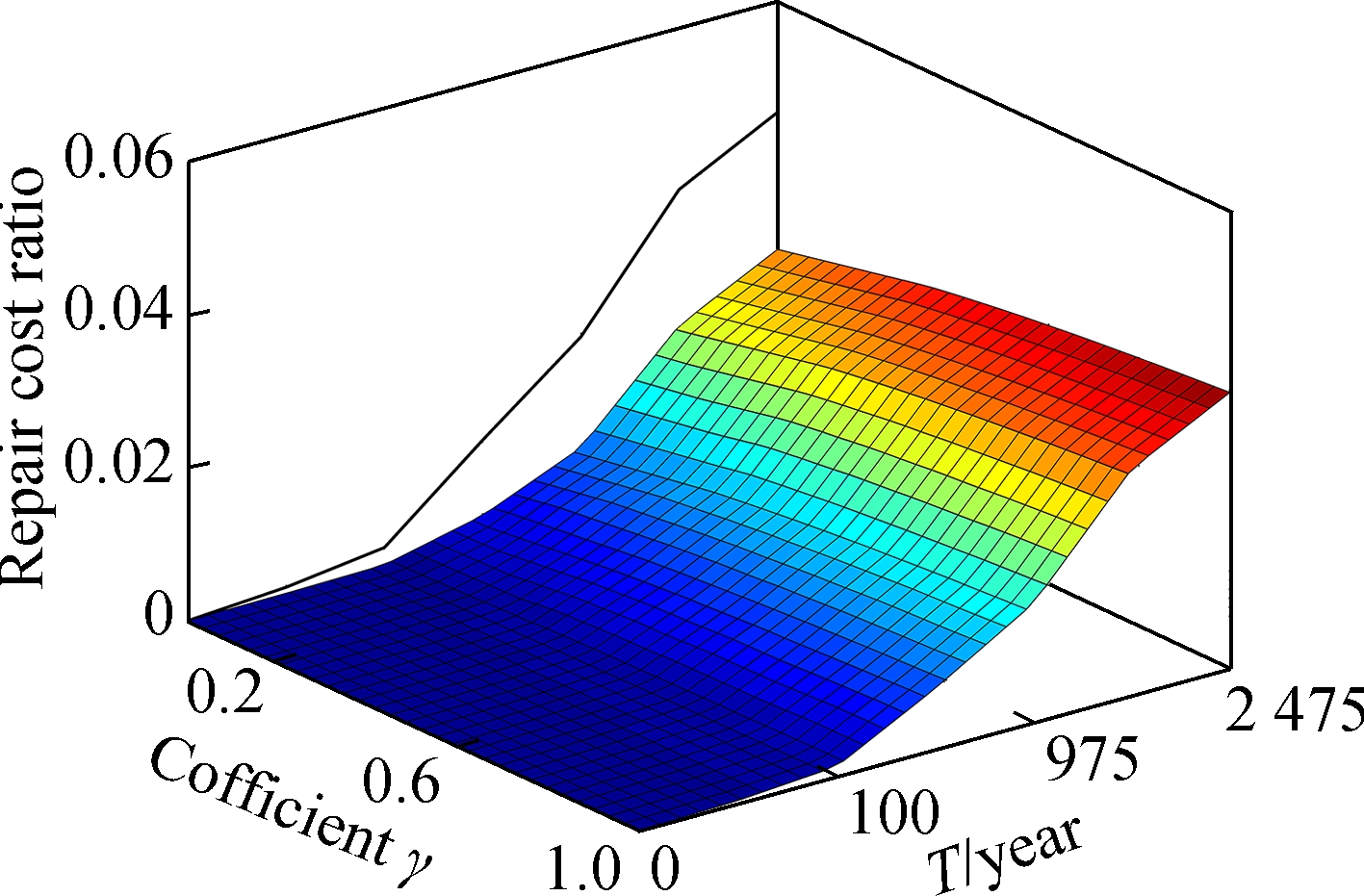
(b)
Fig.11 System-level repair cost ratio surfaces conditioned on coefficient γ and T. (a) Case 1; (b) Case 2
As can be seen from Fig.11, a reduction of RCR can be expected if the main bridge is equipped with fluid dampers, where the value approximates 45% under the E2 earthquake. Dampers play an effective role in the limitation of displacement of the suspension span. Although the approach bridges feature a detailed ductility design of columns intended to resist the rare earthquake hazard, the repair cost ratio of the initial design is reduced from 49% to 5% under the E2 earthquake when the laminated elastomeric bearings and supplemental devices are fully applied to the approach bridges. It is important to mention that although the initial costs of the overall system for the suspension bridge are increased by implementing supplementary devices (e.g., 5% higher cost is considered in this study for the retrofitted bridges equipped with fluid dampers, shear keys and cable restrainers), the post-earthquake expenses to repair the bridge retrofitted with supplementary devices will be decreased substantially. Also, the system-level repair cost ratio is less sensitive to the relative importance of structures in the optimal seismic designs. As shown in Tab. 8, when coefficient γ=0.67, the repair cost ratio of the as-built bridge is 23% under the E2 earthquake, whereas the repair cost ratio for the retrofitted bridge is reduced to 3.5%. Seismic repair of the suspension bridge can be much more cost-effective and more in line with the seismic performance objectives when they are installed with the suitable designed supplementary devices. Therefore, the repair cost ratio considering the relative importance of both components and structures can be a good indicator for evaluating the seismic performance of long-span bridges.
Tab.8 Comparison of the repair cost ratios under two seismic hazard

Seismic hazardRepair cost ratioCase 1Case 2Relative value η/%E1 earthquake0.0480.00785.4E2 earthquake0.2250.03584.4Note:η=Rrc1-Rrc2 Rrc1×100%, where Rrc1 and Rrc2 are the repair cost ratios of case 1 and case 2, respectively.
4 Conclusions
1) Both PGA and PGV emerged as the best IM by the TOPSIS method and the difference was not obvious. The damage state definition of bearings considered the structural design and self-damage. Due to the lack of experimental data, the damage states of towers were defined by developing modal pushover analyses and idealized bilinear fitting methods in the equivalent fiber models.
2) The component-level fragility curves pinpointed the vulnerable bridge components and high stress regions of suspension bridges, where the critical components include the towers, columns and bearings, and the high stress regions are located at the top of towers and at the side and middle of the suspension span. Comparison results of the as-built design and retrofitted design show that the primary factors affecting bridge seismic performance are the pounding between adjacent decks and the constraint system of the approach bridges.
3) The bridge repair cost ratios can serve as good indicators to provide an efficient evaluation of seismic design strategies under two-level seismic hazard, which can take into account the structures with different characteristics and relative importance. However, the repair cost ratios of the bridge system that has the optimum seismic performance are less sensitive to the relative importance of adjacent structures.
[1]Nielson B G, DesRoches R. Seismic fragility methodology for highway bridges using a component level approach[J].Earthquake Engineering & Structural Dynamics, 2007, 36(6): 823-839. DOI:10.1002/eqe.655.
[2]Ramanathan K N. Next generation seismic fragility curves for California bridges incorporating the evolution in seismic design[D]. Atlanta, USA: Georgia Institute of Technology, 2012.
[3]Zhang J, Huo Y L. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method[J].Engineering Structures, 2009, 31(8): 1648-1660. DOI:10.1016/j.engstruct.2009.02.017.
[4]Padgett J E, DesRoches R. Methodology for the development of analytical fragility curves for retrofitted bridges[J].Earthquake Engineering & Structural Dynamics, 2008, 37(8): 1157-1174. DOI:10.1002/eqe.801.
[5]Zhong J, Pang Y T, Jeon J S, et al. Seismic fragility assessment of long-span cable-stayed bridges in China[J].Advances in Structural Engineering, 2016, 19(11): 1797-1812. DOI:10.1177/1369433216649380.
[6]Sgambi L, Garavaglia E, Basso N, et al. Monte Carlo simulation for seismic analysis of a long span suspension bridge[J].Engineering Structures, 2014, 78: 100-111. DOI:10.1016/j.engstruct.2014.08.051.
[7]Nie L Y, Li J Z, Hu S D, et al. Comparison of three kinds of girder end constraint systems for Xihoumen bridge[J]. Bridge Construction, 2006, 36(6): 73-75, 78.(in Chinese)
[8]Arzoumanidis S, Shama A, Ostadan F. Performance-based seismic analysis and design of suspension bridges[J].Earthquake Engineering & Structural Dynamics, 2005, 34(4/5): 349-367. DOI:10.1002/eqe.441.
[9]Karmakar D, Ray-Chaudhuri S, Shinozuka M. Finite element model development, validation and probabilistic seismic performance evaluation of Vincent Thomas suspension bridge[J].Structure and Infrastructure Engineering, 2015, 11(2): 223-237. DOI:10.1080/15732479.2013.863360.
[10]Ministry of Transport of the People’s Republic of China. JTG/T B02-1—2008 Guidelines for seismic design of highway bridges[S]. Beijing: China Communication Publishing, 2008. (in Chinese)
[11]Chen W F, Duan L. Bridge engineering handbook[M]. Boca Raton, USA: CRC Press, 2014: 382-384.
[12]McKenna F, Scott M H, Fenves G L. Nonlinear finite-element analysis software architecture using object composition[J].Journal of Computing in Civil Engineering, 2010, 24(1): 95-107. DOI:10.1061/(asce)cp.1943-5487.0000002.
[13]Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering, 1988, 114(8): 1804-1826. DOI:10.1061/(asce)0733-9445(1988)114:8(1804).
[14]Nazmy A S, Abdel-Ghaffar A M. Non-linear earthquake-response analysis of long-span cable-stayed bridges: Theory[J]. Earthquake Engineering & Structural Dynamics. 1990, 19(1), 45-62. DOI:10.1002/eqe.4290190106.
[15]Wang K H, Lu G Y, Zhang P P. Study on seismic design evaluation methods for highway medium-span and small-span girder bridges based on machine learning [J]. Journal of Highway and Transportation Research and Development, 2019, 36(2): 74-84. (in Chinese)
[16]Shamsabadi A, Rollins K M, Kapuskar M. Nonlinear soil-abutment-bridge structure interaction for seismic performance-based design[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(6): 707-720. DOI:10.1061/(asce)1090-0241(2007)133:6(707).
[17]California Department of Transportation. Caltrans seismic design criteria [S]. Sacramento, CA, USA: California Department of Transportation, 1999.
[18]Muthukumar S, Desroches R. Evaluation of impact models for seismic pounding[C]// 13th World Conference on Earthquake Engineering. Vancouver, BC, Canada, 2004: No. 235.
[19]Li X L, Sun Z G, Wang D S, et al. Longitudinal seismic pounding effect of bridges abutment and backfilling damage[J]. Journal of Chang’an University (Natural Science Edition), 2015, 35(4): 76-82. (in Chinese)
[20]Madani B, Behnamfar F, Tajmir Riahi H. Dynamic response of structures subjected to pounding and structure-soil-structure interaction[J].Soil Dynamics and Earthquake Engineering, 2015, 78: 46-60. DOI:10.1016/j.soildyn.2015.07.002.
[21]Wu G, Wang K H, Lu G Y, et al. An experimental investigation of unbonded laminated elastomeric bearings and the seismic evaluations of highway bridges with tested bearing components[J].Shock and Vibration, 2018, 2018: 1-18. DOI:10.1155/2018/8439321.
[22]Xu L Q, Li J Z. Design and experimental investigation of a new type sliding retainer and its efficacy in seismic fortification[J]. Engineering Mechanics. 2016, 33(2): 111-118. (in Chinese)
[23]Krawinkler H, Medina R, Alavi B. Seismic drift and ductility demands and their dependence on ground motions[J].Engineering Structures, 2003, 25(5): 637-653. DOI:10.1016/s0141-0296(02)00174-8.
[24]Gupta A, Krawinkler H. Behavior of ductile SMRFs at various seismic hazard levels[J].Journal of Structural Engineering, 2000, 126(1): 98-107. DOI:10.1061/(asce)0733-9445(2000)126:1(98).
[25]Opricovic S, Tzeng G H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS[J].European Journal of Operational Research, 2004, 156(2): 445-455. DOI:10.1016/s0377-2217(03)00020-1.
[26]Cornell C A. Calculating building seismic performance reliability: A basis for multi-level design norms[C]// Proceedings of the 11th World Conference on Earthquake Engineering. Acapulco, Mexico, 1996: No. 2122.
[27]Xie Y Z, Zhang J. Optimal design of seismic protective devices for highway bridges using performance-based methodology and multiobjective genetic optimization[J].Journal of Bridge Engineering, 2017, 22(3): 04016129. DOI:10.1061/(asce)be.1943-5592.0001009.
[28]Federal Emergency Management Agency. Multi-hazard loss estimation methodology, earthquake model, HAZUS MH MR4—technical manual [M]. Washington, DC, USA: FEMA Mitigation Div., 2003.