High-ductility cementitious composites (HDCCs) are a kind of high-performance fiber-reinforced cement-based composites exhibiting high ductility under tensile load[1]. Their application prospects are broad, which mainly include concrete structure repair and seismic reinforcement, as well as other projects[2]. As a new type of building material, HDCCs inevitably employ a constitutive relationship to design, calculate, and check its structural bearing and deformation capacities in the application process. In this regard, establishing a scientific and reasonable constitutive relationship is a precursor for the large-scale application of HDCCs. Li et al.[3] investigated the main factors affecting the compressive properties of HDCCs and their uniaxial compressive constitutive equation. Deng et al.[4] established the damage constitutive model of highly ductile concrete based on the double-parameter damage threshold. Maalej et al.[5-6] abstracted and simplified the uniaxial tensile stress-strain curve of HDCCs. Kanda et al.[7] proposed a bilinear uniaxial tensile constitutive model. Such studies included systematic investigations accounting for the constitutive relationship of HDCCs under uniaxial compression, whereas those accounting for the constitutive relationship under uniaxial tension remain relatively rare. The unique multi cracking and strain-hardening characteristics of HDCCs make their constitutive relationship significantly different from that of ordinary concrete or fiber-reinforced concrete, which logically implies that the commonly used tensile constitutive model for concrete is not suitable for HDCCs. In order to make full use of the highly ductile characteristics of HDCCs for their development and feasible applications, their constitutive relationship under uniaxial tension load should be urgently established for structural design and calculation guidance[8-9]. Based on the ideal elastoplastic linear strengthening model and in accordance with the summary of the already existing uniaxial tensile constitutive relationship, this paper highlights the proposal of a constitutive equation for HDCCs that can be used as a guide for the structural bearing capacity design and deformation calculation of HDCCs.
1 Characteristics of the HDCC Uniaxial Tensile Stress-Strain Curve
HDCCs have multiple discernible cracks and strain-hardening characteristics under uniaxial tension. More specifically, their uniaxial tension stress-strain curve displays distinct characteristics from those of ordinary or fiber-reinforced concrete and is typically divided into three stages, as illustrated in Fig.1.

Fig.1 Representative uniaxial tensile stress-strain curve of HDCCs
Initial stage: Elastoplastic phase (OA segment). The specimen exhibits elastic-plastic stress and strain from the loading inset to the occurrence of the first crack (i.e., the OA section). Strain increases gradually with the increase in the load from the origin point O, and the two parameters are observed to exhibit a certain linear relationship with each other. At the end of the OA segment, any further increase in the load results in the gradual transition of deformation from elastic to plastic until preliminary cracking. Deformation of the OA segment is mainly elastic and is supplemented by plastic deformation. In Fig.1, A, σc, and εc correspond to the initial crack point, initial crack stress, and initial crack strain, respectively.
Secondary stage: Steady-state cracking or strain-hardening phase (AB section). At this stage, both load and deformation are continuously increased, and stress is transferred to the matrix from the bridging fibers at the cracks, thereby creating new cracks. Nevertheless, crack propagation is restrained by the fiber bridging stress, thereby maintaining steady-state cracking. With the further increases of load, the number and width of the cracks increase, until the bearing capacity of the HDCC ultimately reaches its maximum. At this phase, point B corresponds to the maximum tensile stress σu and tensile strain εu.
Final stage: Strain-softening stage (BC section). The main crack expands and runs through the entire cross section of the specimen. The bearing capacity then decreases sharply, leading to failure.
2 Simplification of Uniaxial Tensile Stress-Strain Curve of HDCCs
Maalej et al.[5,7] used the above analysis to simplify the tensile relationship curve of HDCCs. In this process, the OA and AB segments are simplified into straight lines, whereas the BC segment can be ignored in practical applications because of the loss of the bearing capacity, as shown in Fig.2(a). The uniaxial tension stress-strain curve of HDCCs is further simplified into an OA-AB bilinear model, as shown in Fig.2(b). According to the characteristics of this simplified stress-strain bilinear model, the ideal elastic-plastic linear hardening model in elastoplastic mechanics can be used to establish the tension constitutive equation.
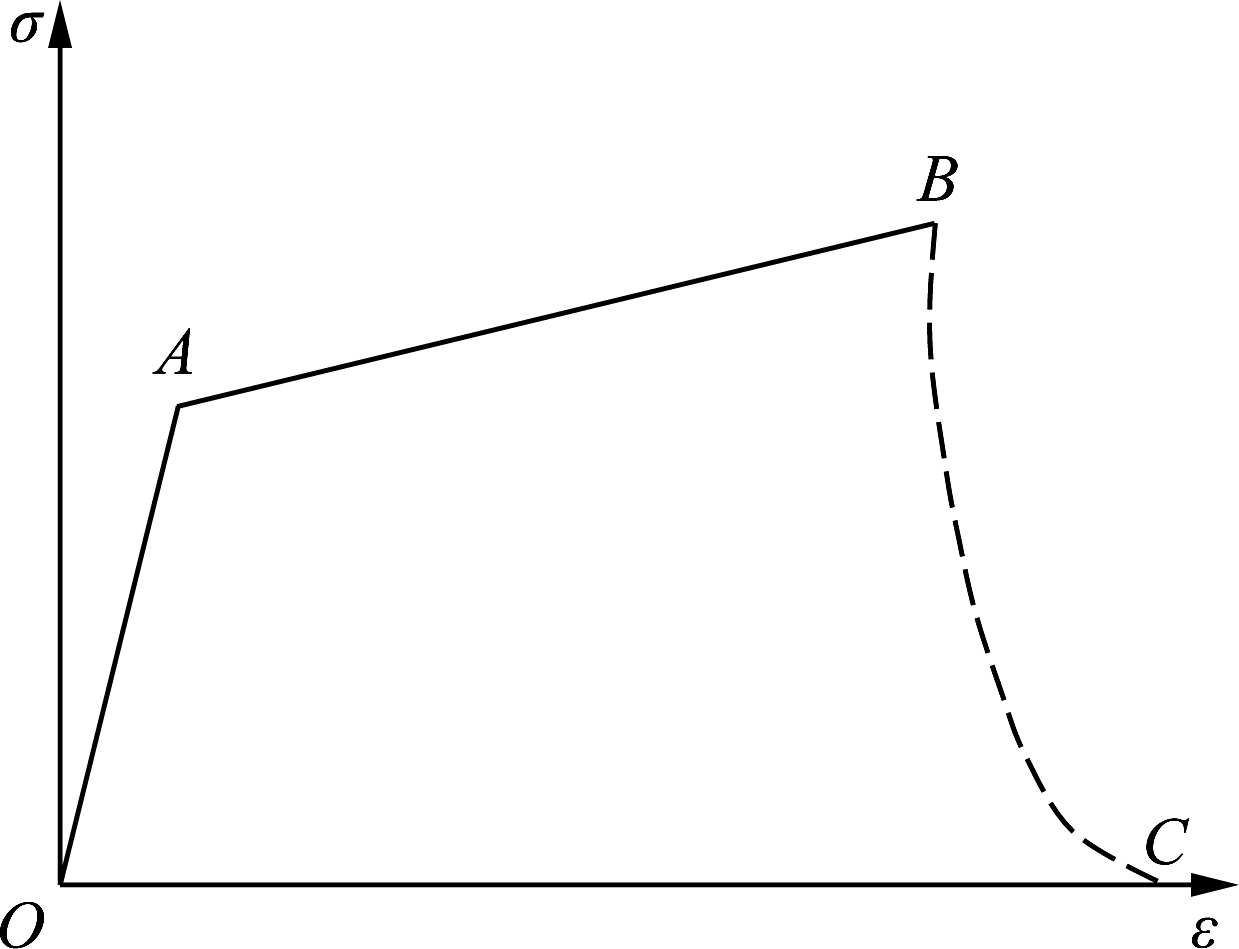
(a)
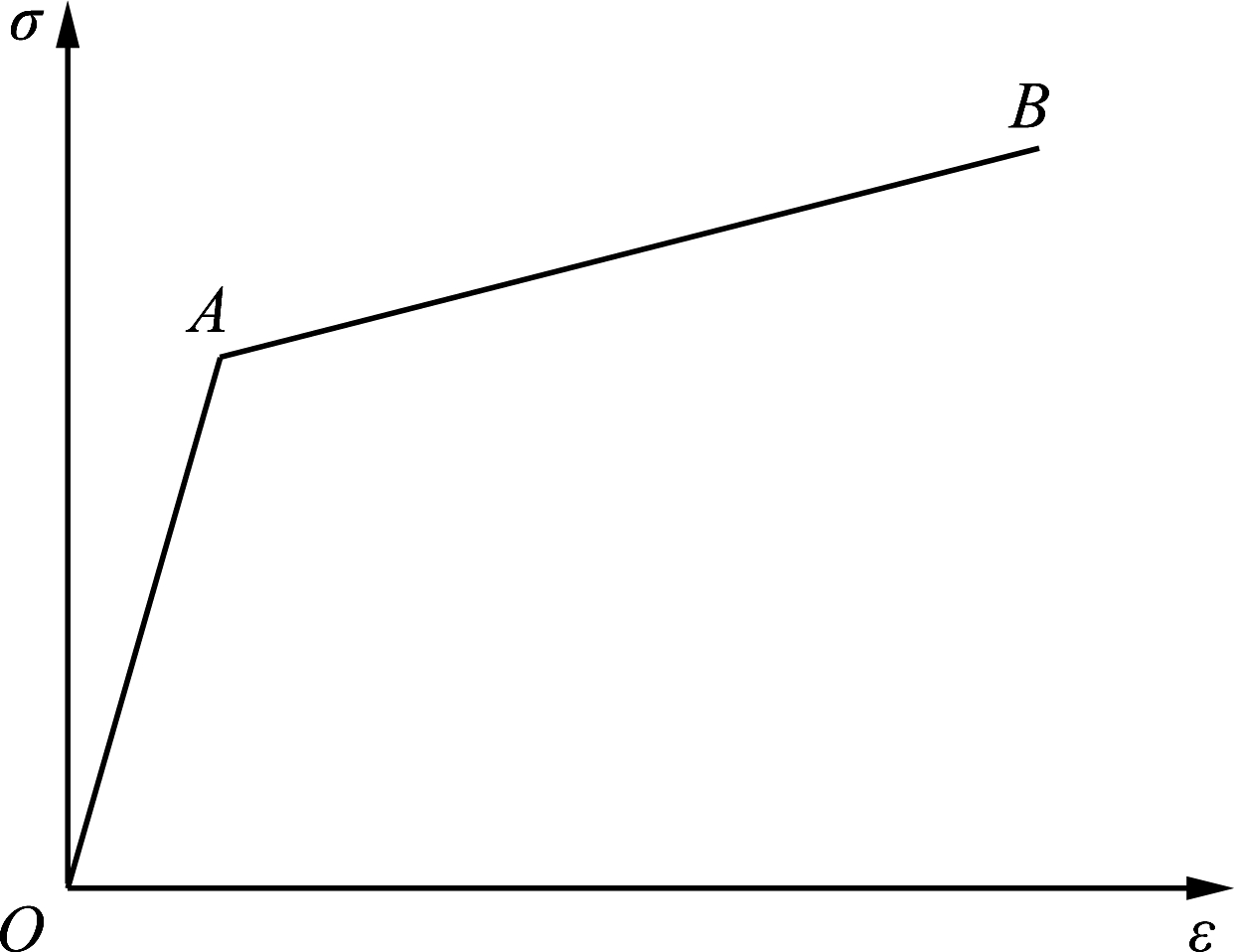
(b)
Fig.2 Simplified uniaxial tensile stress-strain curves for HDCCs[5,7]. (a) Three-segment line;(b) Bilinear
Accordingly, the ideal elastic-plastic linear hardening model of HDCCs can be obtained in two ways.
First, the initial crack point A(εc, σc) and the maximum tensile stress point B(εu, σu) are determined. By connecting the origin, the initial crack point, and the maximum tensile stress point, a two-stage linear equation, as shown in Fig.3(a) ![]() is obtained, where εc, εu, σc, and σu are all measured values.
is obtained, where εc, εu, σc, and σu are all measured values.
Secondly, by fitting the equation of straight line in the elastic stage ![]() the nominal initial crack stress σnc and the nominal initial crack point A(εc, σnc) are determined. Connecting A(εc, σnc) with the actual maximum tensile stress point B(εu, σu) yields the straight line and its equation,
the nominal initial crack stress σnc and the nominal initial crack point A(εc, σnc) are determined. Connecting A(εc, σnc) with the actual maximum tensile stress point B(εu, σu) yields the straight line and its equation, ![]() in the strain-hardening stage, as shown in Fig.3(b), where εc, εu, and σu are measured values, and the nominal initial crack stress σnc is a fitted value.
in the strain-hardening stage, as shown in Fig.3(b), where εc, εu, and σu are measured values, and the nominal initial crack stress σnc is a fitted value.

(a)

(b)
Fig.3 Simplified uniaxial tensile stress-strain curves of HDCCs[5]. (a) Initial crack stress is a measured value; (b) Initial crack stress is a fitted value
The common problems associated with these two methods include the followings:
1) The stress and strain at the initial crack point are difficult to determine. The coordinates of point A depend on the appearance of the initial crack. However, the initial crack normally has a very small width (approximately 100 microns), and the stress drop is not always observable with the initial crack appearance. Thus, there are some subjective factors involved in determining the stress and strain of initial cracks due to the limitation of test accuracy.
2) Taking the measured maximum stress point as the control point of the equation restricts the redundancy of structural design calculation.
3) As in 1), the coordinates of point B are not easily determined under the assumption that the maximum stress point and the softening point do not coincide.
To obtain sufficient design redundancy, the ideal elastic-plastic linear hardening model can be further simplified to an ideal elastic-plastic model, as shown in Fig.4. Here, the initial crack point A(εc, σc) or the nominal initial crack point A(εc, σnc) is first determined. During the elastic stage, ![]() After the initial crack point A, strain increases without any change in stress (i.e., σ(ε)=σc or σ(ε)=σnc). That is, the model only considers the increase of the HDCC’s strain in the strain-hardening stage, but not the increase of the stress caused by the fiber bridging effect, hence making it a conservative model for structural design. The Japan Society of Civil Engineers’ code, “Recommendations for Design and Construction of High Performance Fiber-Reinforced Cement Composites with Multiple Fine Cracks,” adopts this design concept[10].
After the initial crack point A, strain increases without any change in stress (i.e., σ(ε)=σc or σ(ε)=σnc). That is, the model only considers the increase of the HDCC’s strain in the strain-hardening stage, but not the increase of the stress caused by the fiber bridging effect, hence making it a conservative model for structural design. The Japan Society of Civil Engineers’ code, “Recommendations for Design and Construction of High Performance Fiber-Reinforced Cement Composites with Multiple Fine Cracks,” adopts this design concept[10].

Fig.4 Ideal elastic-plastic model for HDCC’s uniaxial tension
3 Establishment of a Simplified Model of Uniaxial Tensile Constitutive Relationship for HDCCs
Accordingly, a new constitutive equation for HDCC tension is proposed on the basis of the ideal elastic-plastic linear hardening model as shown in Fig.5, which is fixated on solving the problems of difficulty in determining the initial crack point and the insufficient or excessive bearing capacity in the already existing bilinear models. The equation constitutes the following characteristics:
1) A valley point of stress is selected during the strain-hardening phase, for straight line fitting.
The valley point of the strain-hardening curve is selected for fitting, not only making full use of the strain-hardening characteristics of HDCCs, but also retaining the appropriate redundancy.
2) The initial crack point is determined from the intersection of two straight lines, and the nominal maximum stress value σnu is determined by the tensile strain value εu corresponding to the measured maximum stress value σu.
The point of intersection of the fitting lines of the elastic segment and the steady cracking stage is the newly defined nominal initial crack point (εnc, σnc). In the steady-state cracking stage, the nominal maximum stress point is (εu, σnu). The uniaxial tension bilinear constitutive equation of HDCCs is more appropriately expressed as follows:
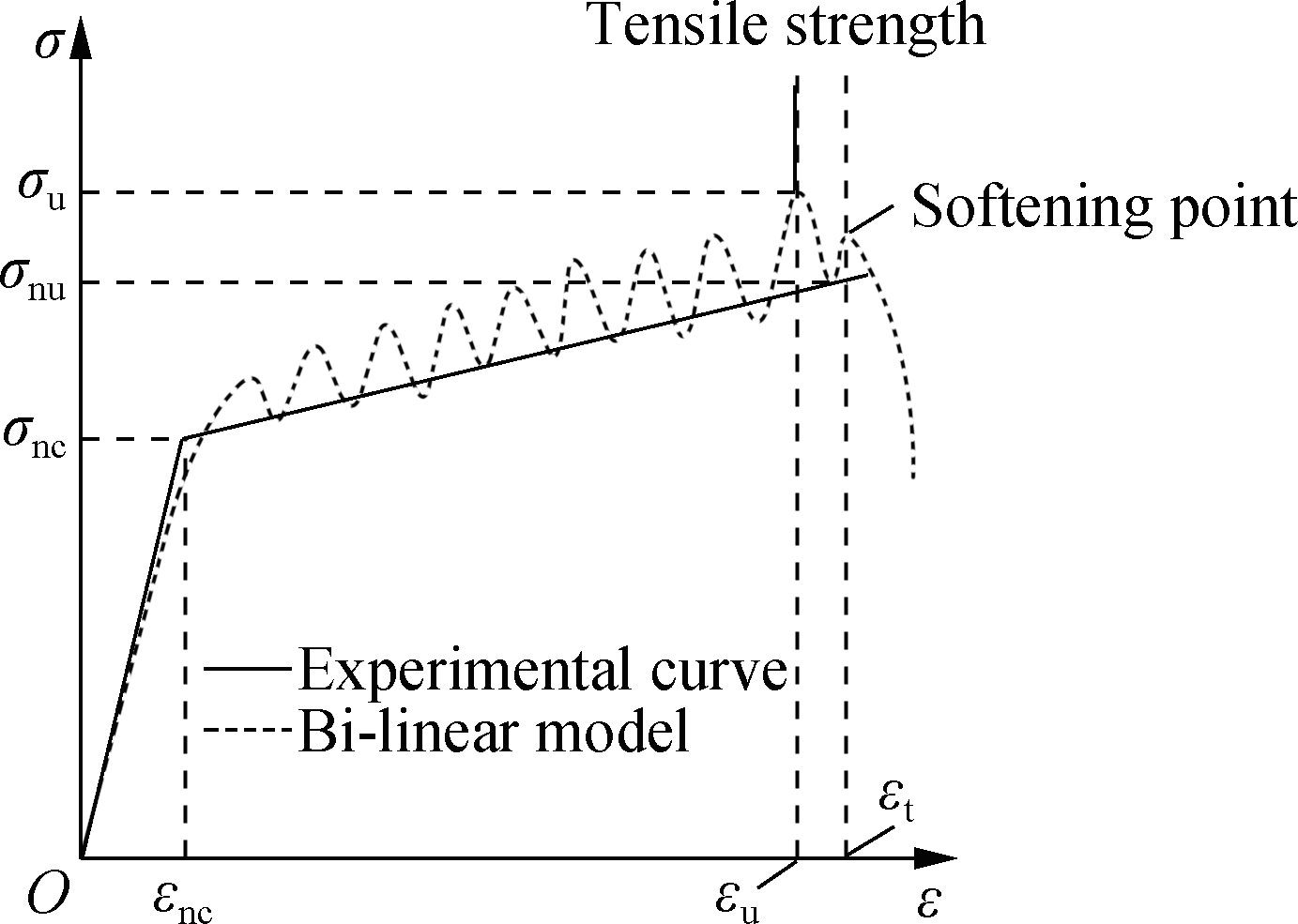
Fig.5 A schematic diagram of the HDCC’s uniaxial tensile constitutive relationship
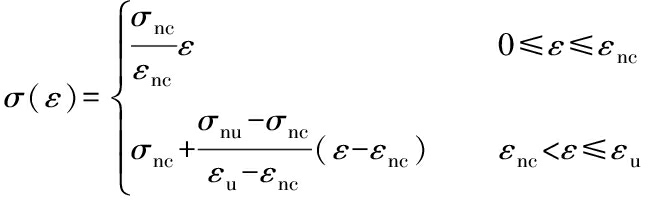
(1)
4 Application Example of HDCC Uniaxial Tensile Bilinear Constitutive Equation
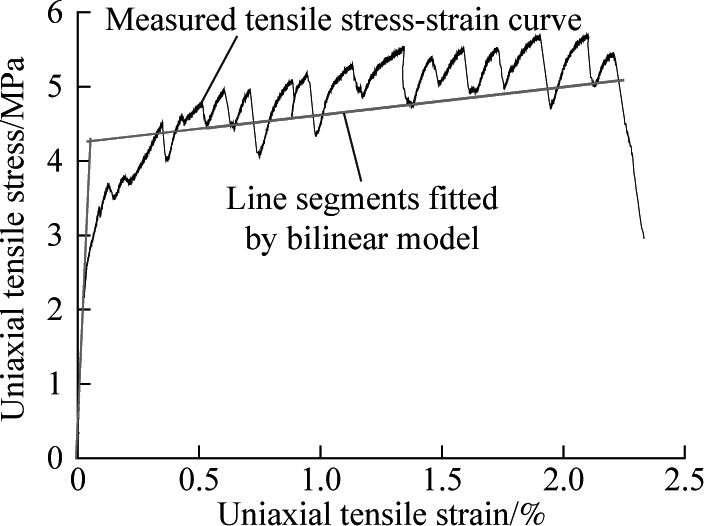
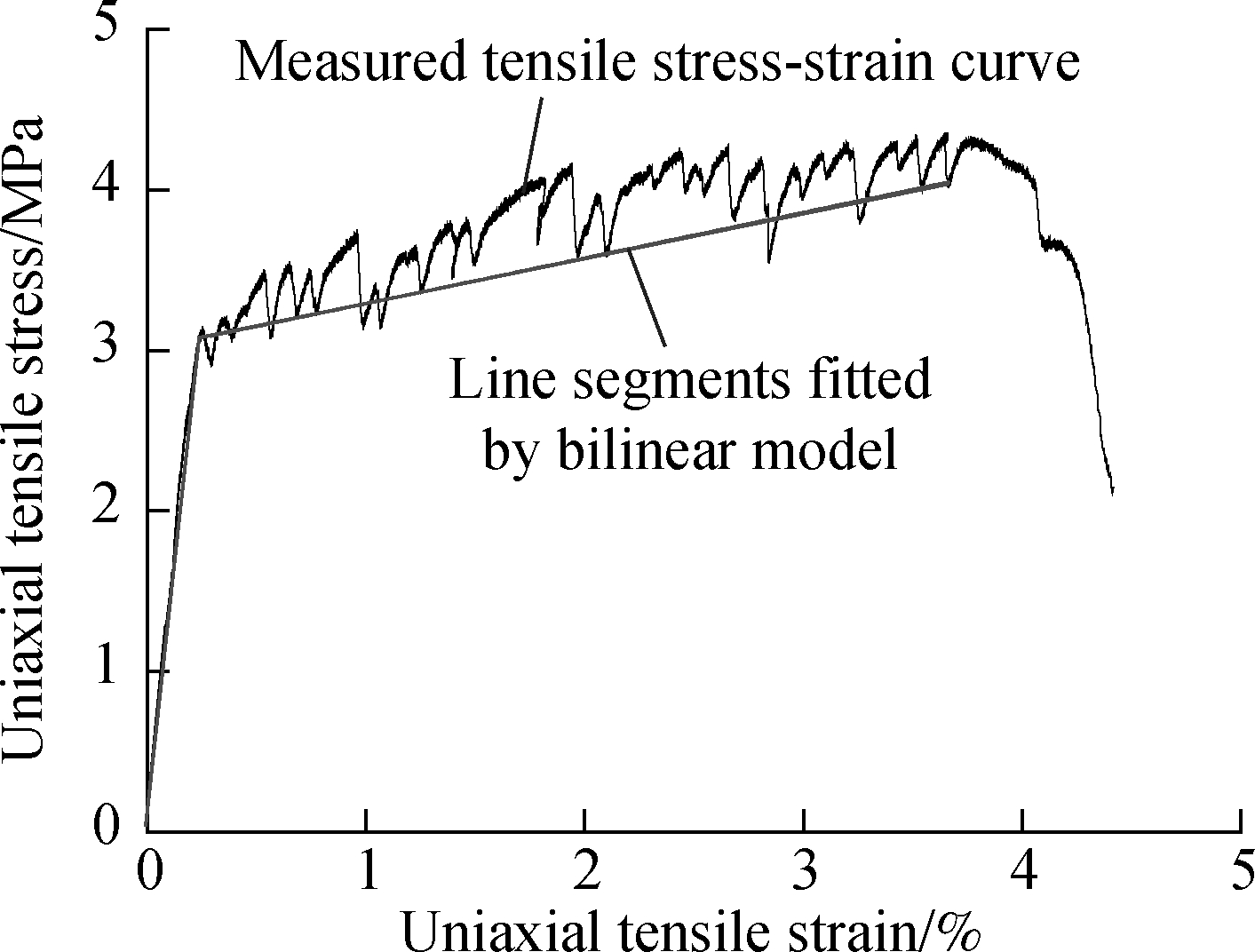
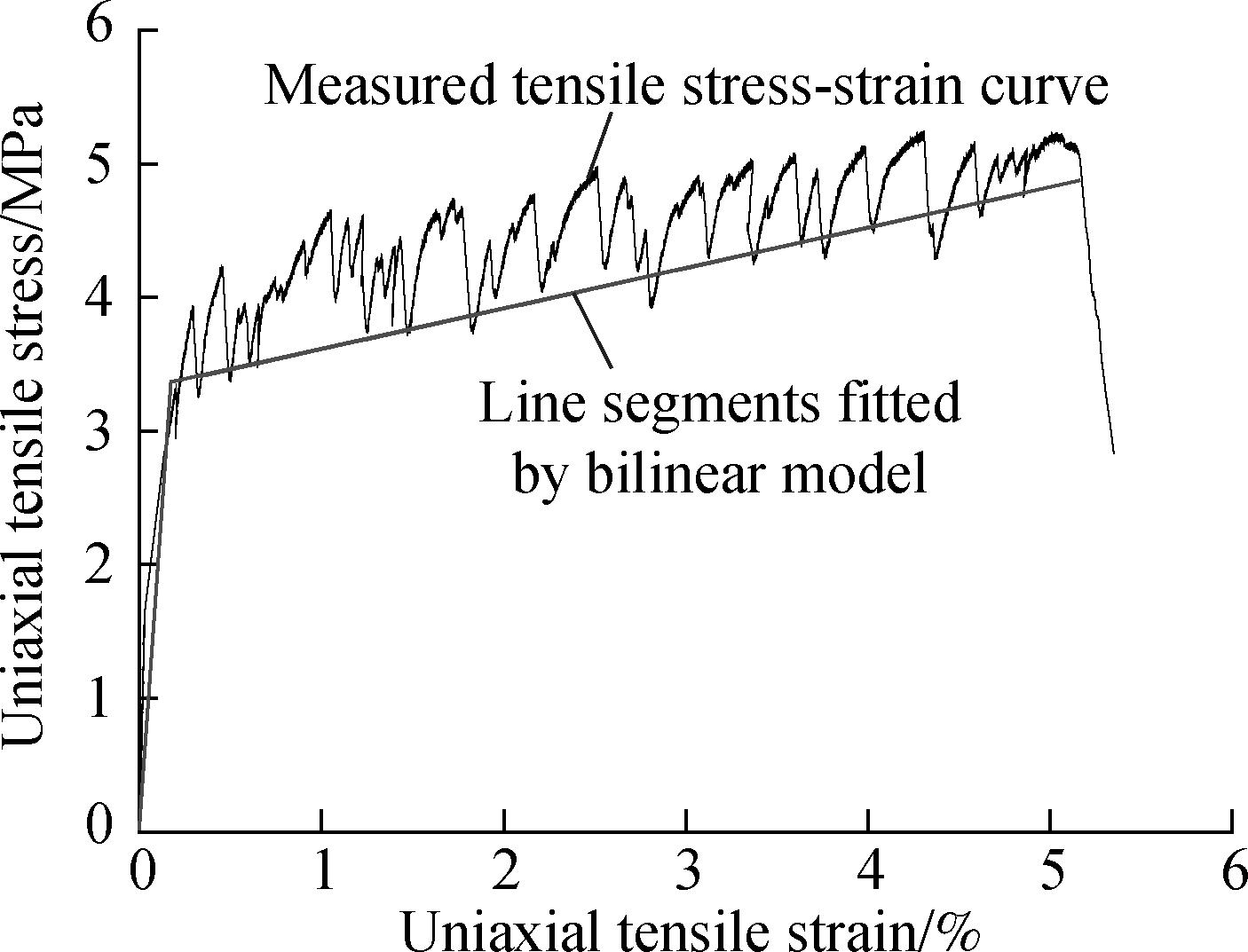
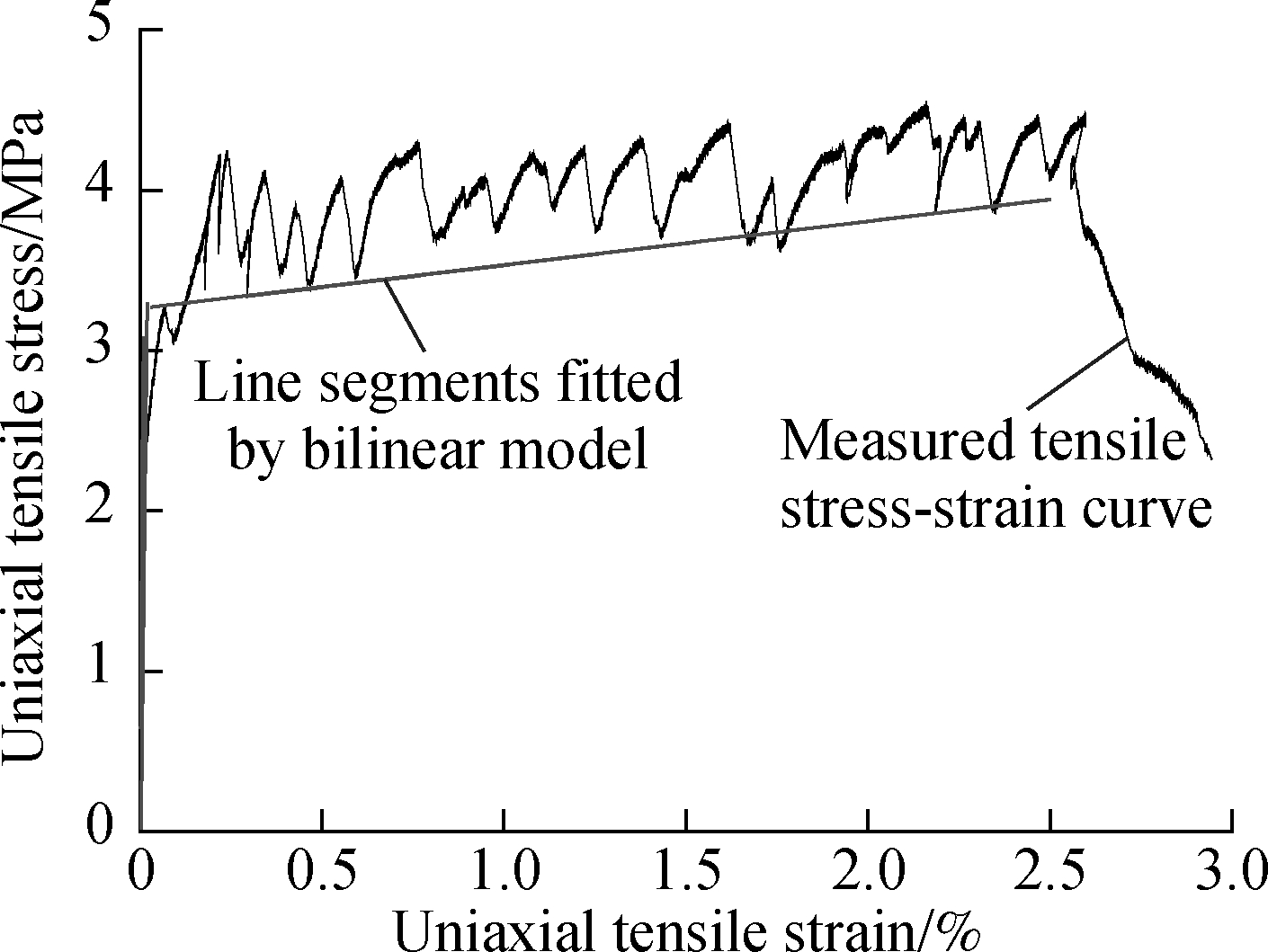
Five groups of HDCC uniaxial tension stress-strain curves[11], numbered H1 to H5, are selected to demonstrate the application of the bilinear model of Eq.(1). The straight lines of the elastic section and the strain-hardening stage are obtained by fitting, as shown in Fig.6. Note that such good consistency displayed by the fitting straight lines with the development trend of the measured curve can be used to characterize the elastic deformation and strain hardening of HDCCs. Moreover, the nominal initial crack strain εnc, nominal initial crack stress σnc, and nominal maximum tensile stress σnu of HDCCs are obtained from the intersection of two straight lines and the maximum stress point on the stress-strain curve, as depicted in Tab.1.
During the HDCC tensile test, the bearing capacity was observed to decrease slightly following the appearance of the first crack, mainly due to cracking of the matrix[12]. Additionally, a peak shape was apparently visible on the stress-strain curve. On this basis, the primary peak point was defined as the initial crack point of the HDCC. For the tension test, the softening point was defined as the point where the bearing capacity decreased significantly with the expansion of the main crack’s width, whereas the strain corresponding to the softening point was defined as the ultimate tensile strain. The initial crack stress, initial crack strain, and ultimate tensile strain of the five groups of HDCCs are summarized in Tab.1 accordingly.
A comparison of the measured values with the nominal values of the bilinear model (see Tab.2) apparently indicated a significant difference in both results for the ratio of the initial cracking stress, whereas the initial cracking strain was higher in the measured values than that in the calculated ones. Moreover, an analysis of the typical uniaxial tension stress-strain curves of HDCCs (see Fig.1) confirmed that the deformation on the front part of segment OA, shown as a straight line, is elastic, whereas its tail end enters a plastic deformation stage, as the straight line assumes a convex curve. Furthermore, as the nominal initial crack point was the bilinear intersections, such point was bound to appear on the left side of the actual initial crack point (see Fig.5), which necessitates the nominal initial crack strain being bound to be smaller than the measured value. Similarly, the nominal initial crack stress was bound to be either larger than the actual value or smaller than the measured value, as it was mainly dependent on the slope of the two straight lines. Namely, a larger linear slope of the elastic section will assume a smaller initial crack stress; otherwise, a larger linear slope of the strain-hardening section will assume a larger initial crack stress.
(a)
(b)
(c)

(d)
(e)
Fig.6 Measured uniaxial tensile stress-strain curve and bilinear model for HDCCs. (a) H1; (b) H2; (c) H3; (d) H4; (e) H5
Tab.1 Measured and fitting values of control points for HDCC uniaxial tensile bilinear constitutive equations
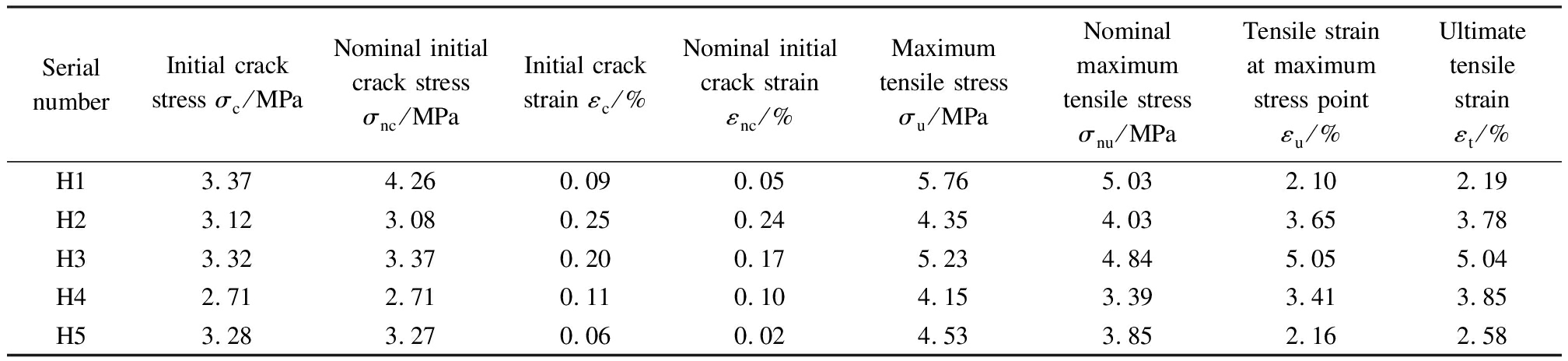
Serial numberInitial crack stress σc/MPaNominal initial crack stress σnc/MPaInitial crack strain εc/%Nominal initial crack strain εnc/%Maximum tensile stress σu/MPaNominal maximum tensile stress σnu /MPaTensile strain at maximum stress point εu/%Ultimate tensile strain εt/%H13.374.260.090.055.765.032.102.19H23.123.080.250.244.354.033.653.78H33.323.370.200.175.234.845.055.04H42.712.710.110.104.153.393.413.85H53.283.270.060.024.533.852.162.58
Tab.2 Ratios of measured to nominal values of HDCCs

Serial numberRatio of measured value to nominal valueInitial crack stressInitial crack strainMaximum stressTensile strain ratio between softening pointand maximum stress pointH10.791.681.151.04H21.021.061.081.04H30.981.141.081.00H41.001.071.221.13H51.003.001.181.19
The ratio of the measured maximum stress to the nominal value of the five groups of HDCCs ranges from 1.08 to 1.22, which is greater than 1, mainly because the straight line in the stress-hardening stage was fitted from the stress valley of the stress-strain curve. As such, the measured value was bound to be larger than the nominal value. Simultaneously, the ultimate tensile strain value of the softening point was bound to be greater than or equal to the tensile strain value of the maximum stress point, according to the position relationship between the maximum stress point and the softening point. Tab.2 indicates that the tensile strain ratio between the softening and maximum stress points of the five HDCC groups varies from 1.00 to 1.19. From these findings, the HDCC’s uniaxial tension bilinear constitutive equation definitely provides a certain bearing capacity and tensile deformation redundancy for engineering structural design applications.
5 Conclusions
1) A simplified bilinear model of the constitutive relationship of HDCCs was established on the basis of the characteristics of the uniaxial tensile stress-strain curve of HDCCs.
2) The ideal elastoplastic linear strengthening model was the basis for the proposed HDCC bilinear tensile constitutive equation, which defines the control points for the nominal initial crack and nominal maximum tensile stress.
3) A comparative evaluation of the test and calculation results of five groups of HDCC experimental data depicted that the measured maximum stress values were larger than the nominal values, typically demonstrating that the ratios ranges from 1.08 to 1.22. Moreover, the ultimate tensile strain at the softening point was greater than or equal to the tensile strain at the maximum stress point, in the ratio range of 1.00 to 1.19.
4) Compared with the common constitutive equation, the application of the proposed uniaxial tension constitutive equation in the HDCC structural design calculations will yield a greater redundancy in the structural bearing capacity and tensile deformation.
[1]Li V C. Progress and application of engineered cementitious composites[J]. Journal of the Chinese Ceramic Society, 2007, 35(4):531-536. (in Chinese)
[2]Guo L P, Chen B, Sun W, et al. Properties of high ductility cementitious composites for repair[J]. Journal of Building Structures, 2018, 39(7): 169-174. (in Chinese)
[3]Li Y, Liu Z J. Study on mechanical performance and constitutive equation of high toughness PVA-FRCC under uniaxial compression[J]. Journal of Building Materials, 2014, 17(4): 606-612. DOI:10.3969/j.issn.1007-9629.2014.04.008.(in Chinese)
[4]Deng M K, Pan J J. Damage constitutive model of high ductile concrete based on the double-parameter damage threshold[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(1): 89-96. DOI:10.13197/j.eeev.2018.01.89.dengmk.010.(in Chinese)
[5]Maalej M, Li V C. Flexural/tensile-strength ratio in engineered cementitious composites[J]. Journal of Materials in Civil Engineering, 1994, 6(4): 513-528. DOI:10.1061/(asce)0899-1561(1994)6:4(513).
[6]Qiao Z,Pan Z F, Leung C K Y, et al. Experimental study and analysis of flexural behavior of ECC/RC composite beams[J].Journal of Southeast University (Natural Science Edition), 2017, 47(4):724-731. (in Chinese)
[7]Kanda T, Lin Z, Li V C. Tensile stress-strain modeling of pseudostrain hardening cementitious composites[J]. Journal of Materials in Civil Engineering, 2000, 12(2): 147-156. DOI:10.1061/(asce)0899-1561(2000)12:2(147).
[8]Vorel J, Boshoff W P. Numerical simulation of ductile fiber-reinforced cement-based composite[J]. Journal of Computational and Applied Mathematics, 2014, 270: 433-442. DOI:10.1016/j.cam.2013.12.021.
[9]Han T S, Feenstra P H, Billington S L. Simulation of highly ductile fiber-reinforced cement based composite components under cyclic loading[J]. ACI Structural Journal, 2003, 100(6):749-757. DOI:10.14359/12841.
[10]Kunieda M, Rokugo K. Recent progress on HPFRCC in Japan required performance and applications[J]. Journal of Advanced Concrete Technology, 2006, 4(1): 19-33. DOI:10.3151/jact.4.19.
[11]Yang Y N. Multi-scale constitutive relation and design theory of ecological high ductility cementitious composites under variable temperature conditions[D].Nanjing: Southeast University, 2017. (in Chinese)
[12]Guo L P, Chen B, Sun W, et al. Effects of aggregate type and fibre on properties of high ductility cementitious composites[J]. Journal of Southeast University (Natural Science Edition), 2017, 47(6):1221-1226. (in Chinese)