As an important part of the railway transportation system, the suitable calculation method for the station carrying capacity of the high-speed railway has been studied in much literature. The method is required to reflect the advantages of the high-speed railway trains such as high speeds, high operation density and advanced train operation control systems.
Huisman et al. [1] calculated the carrying capacity based on the queuing model without the timetable. In Ref.[2], the models for the absolute capacity of the railway networks with different competing objectives including train services, network corridors and train types were proposed. Then, Burdett[3] built a mathematical model for the theoretical capacity of a railway network with more complex train paths. Burdett[4] studied the optimal model for expanding the theoretical capacity of the railway. Lai et al.[5] built an calculation model of the railway capacity based on different signal systems (fixed block system and mobile block system). This study showed that due to the limitations of the structure in the station, signal systems and station structures must be comprehensively considered. Deng et al.[6] built an evaluation model for capacity adaptability and obtained four evaluation indices based on the track utilization. Chen[7] analyzed the factors of the high-speed railway station capacity, and studied the calculation principle and method of high-speed railway station capacity. Hansen[8] also applied different existing railway capacity calculation methods to the Stuttgart project in Germany, such as minimum headway, utilization rate, reliability of timetable, etc., and simulated them for each method.
The European International Railway Union (UIC406) described railway capacity by the blocking time method and timetable compression method[9]. Hansen et al.[10] analyzed signal confirmation time, signal confirmation additional time, train running time, block clearing time and block releasing time based on the blocking time method. On the basis of the blocking time method, the operation time of the trains and the capacity utilization rate were analyzed. Klabes[11] established an optimization model for the capacity calculation method on the basis of the blocking time method and the train operation process. Zhang[12] built the model based on different signal systems and studied the compression method with blocking time. He mainly studied the arrival headway and departure headway of the station. Zhao et al.[13] studied the robust timetabling by identifying the critical block sections. As mentioned above, studies on the blocking time method in the existing literature mainly focused on the railway network and the stations were treated as blocks. However, for large stations with a long throat, it is obviously not suitable that the station is merely treated as one block. Otherwise, it cannot reflect the specific train operation process. Furthermore, there will be a certain operation redundancy time between the trains. Li[14] proposed a division method for the station blocks. Therefore, in this paper, the division method of station blocks is studied. For large stations, the method can speed up the train operation process and refine the train headways at the station more accurately. Liu et al.[15] analyzed the factors for different kinds of the headways of the high-speed railway. Sangphong et al.[16] analyzed the calculation method of the minimum headway of train operation based on the nomogram method. The minimal headway calculated with this method was similar to the result of the existing mathematical formulae, but the method can effectively reduce the complexity of the existing capacity calculation process.
A calculation method of station carrying capacity based on the blocking time method is studied. By dividing the station blocks, a station blocking time method is established to calculate the train operation headway and carrying capacity at the station.
Firstly, based on the station topology, the division method of the station blocks is studied. Then, the routes model is built. The routes are divided into some different types of trains operating at the station. The model can express the relationships between the routes and blocks, and the relationships among the routes are studied by the same blocks and relation time. This method can convert the headway between the trains to the headway between the routes. Therefore, the calculation method of the headway based on the routes model and the CTCS-3 in China is studied. Secondly, considering the speed and number of different kinds of trains at the given stations, the optimal model and algorithm are designed. Finally, a case of Jinan West Station of Beijing—Shanghai high-speed railway is studied. The calculation results show that this calculation method can effectively reduce the station headway, which can effectively improve the utilization of station infrastructure and station carrying capacity.
1 Calculation Method of the Headways at the Station
The headway at the station mainly includes the arrival-arrival headway, the departure-departure headway, the through-through headway, the through-arrival headway, the arrival-through headway, the through-departure headway, and the departure-through headway. According to Refs.[17-18], the arrival headway is the largest. Different kinds of headways need different calculation methods. The method in this paper calculates these headways with a unified approach, including the arrival headway and departure headway based on the station blocks.
The headways in this paper are calculated on the basis of the train routes which the train occupies. The routes are classified into different kinds including departure routes, arrival routes, stopping routes and through routes. The headways are determined by the routes occupied by the adjacent trains. The routes consist of a series of relatively independent station blocks. Therefore, the headway of any two adjacent trains occupying different routes may be different.
In this paper, the train operation process in the station is divided into two main parts. One part is the arrival process, which starts from the train arriving at the station, and ends by stopping at the arrival-departure line. The other part is the departure process, which starts from the train departing from the station, and ends at running in the section. Based on the routes of the two adjacent trains selected, we can judge whether it has a conflict with the train operation or not. If there is a conflict, the station block due to the conflict is marked as the key block, and the interval time of the trains in this block needs more than the minimum interval time. At the same time, for the safety of the whole line, the arrival headway and the departure headway should be considered. Therefore, for any two adjacent trains, the headway needs more than the maximum value among the arrival headway, departure headway and the minimum interval time of the occupation on the station blocks. Therefore, the arrival headway and departure headway are studied in this paper. If the capacity of the arrival-departure line is enough, the key headway is the maximum value between the minimum arrival headway and minimum departure headway, and the occupation time of each station block node can be calculated by the key value.
1.1 Division method of station blocks
Based on the station topology, station blocks are divided into two types: The key station block and the auxiliary station block as shown in Fig.1. The key station block is an important station track that determines the headway between trains directly, and its length cannot be less than 600 m. The auxiliary station blocks are used for the continuity and independence of the blocks, and its length cannot also be less than 600 m. The auxiliary station block cannot determine the headway directly.
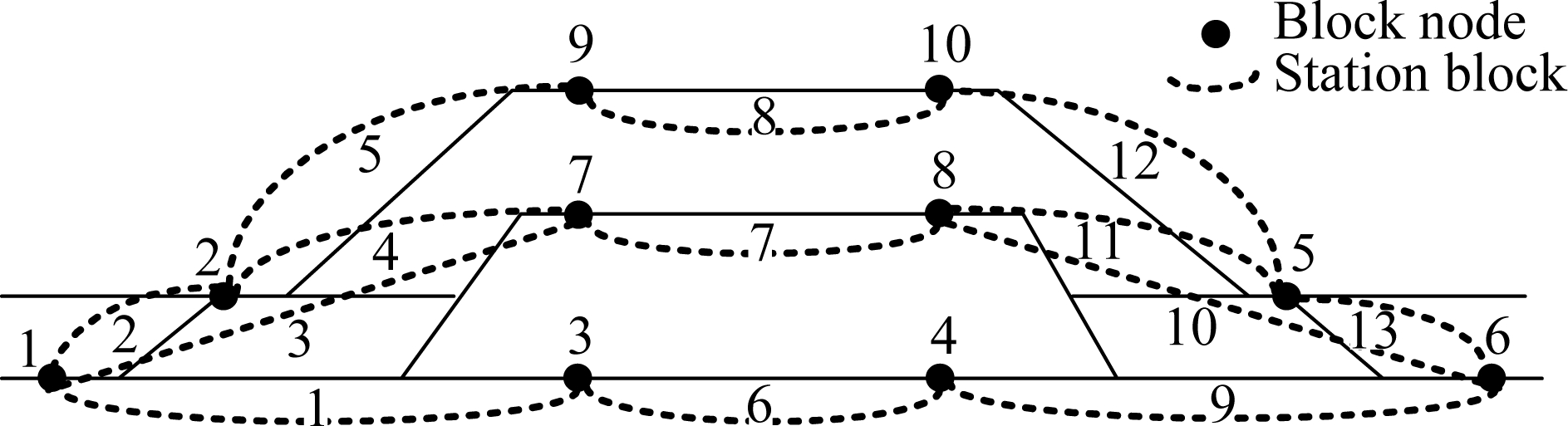
Fig.1 Station blocks and nodes
The presupposed conditions of the station blocks division are as follows:
1) The total length of the station is not less than 2 km.
2) The trains operate in two directions respectively.
3) For the turn-back trains, one arrival train and one departure train can be equal to one turn-back train.
The principle of station blocks division is as follows:
1) Each station block must have one and only one start node. Each station block must have one and only one end node, and there can be no other nodes in this station block.
2) The arrival signals of two throats are key station blocks (e.g. node 1 and node 6), and the station block includes the key station blocks (e.g. blocks 1, 2, 3, 9, 10, and 13).
3) The key switches in the throat are determined as the station block nodes (e.g. node 2 and node 5). The key switch can guide the trains to run onto different arrival-departure tracks.
4) Each arrival-departure track is an independent station block, and there is one station block node on each side of each arrival-departure track (e.g. nodes 3,7,8 and 10).
5) The station blocks are formed by each station block node of an arrival-departure track and adjacent node on the throat. There are no other nodes in this block (e.g. nodes 4, 5, 11, and 12).
6) There are three station blocks for each main line, including two throat blocks and a main line block (e.g. blocks 1, 6, and 9).
The specific algorithm for the station block division is as follows. And, the division result of the station blocks is unique.
Step 1 Determine the block nodes at the arrival signals on each side of the station.
Step 2 Determine the block nodes of each arrival-departure track on the basis of the departure block nodes. The nodes are distributed on the two sides of the arrival-departure tracks.
Step 3 Determine the critical block nodes at the station throats. These nodes can lead to different train routes.
Step 4 The station block can be determined with two adjacent block nodes based on the principles 4) to 6).
Step 5 Due to the block occupation, the blocks with the same start block node or the same end block node can be integrated into one block.
The station block nodes set is defined as P={p∈Z+},and the station blocks set is defined as B={b(p,p′)|p,p′∈P,b∈Z+}, where p,p′ are the start node and end node of block b, respectively. The occupation time mainly includes the train running time and other fixed additional operation times. The train operation time of train l in block b is referred to as 
The sum for other kinds of time including the time for setting up the train route, signal realizing time, approach time, clearing time and releasing time[19] is defined as tf. As shown in Fig.2, the minimal headway among the blocks of train l and train l+1 is the sum of the train operation time of train l and the fixed time tf.
(1)
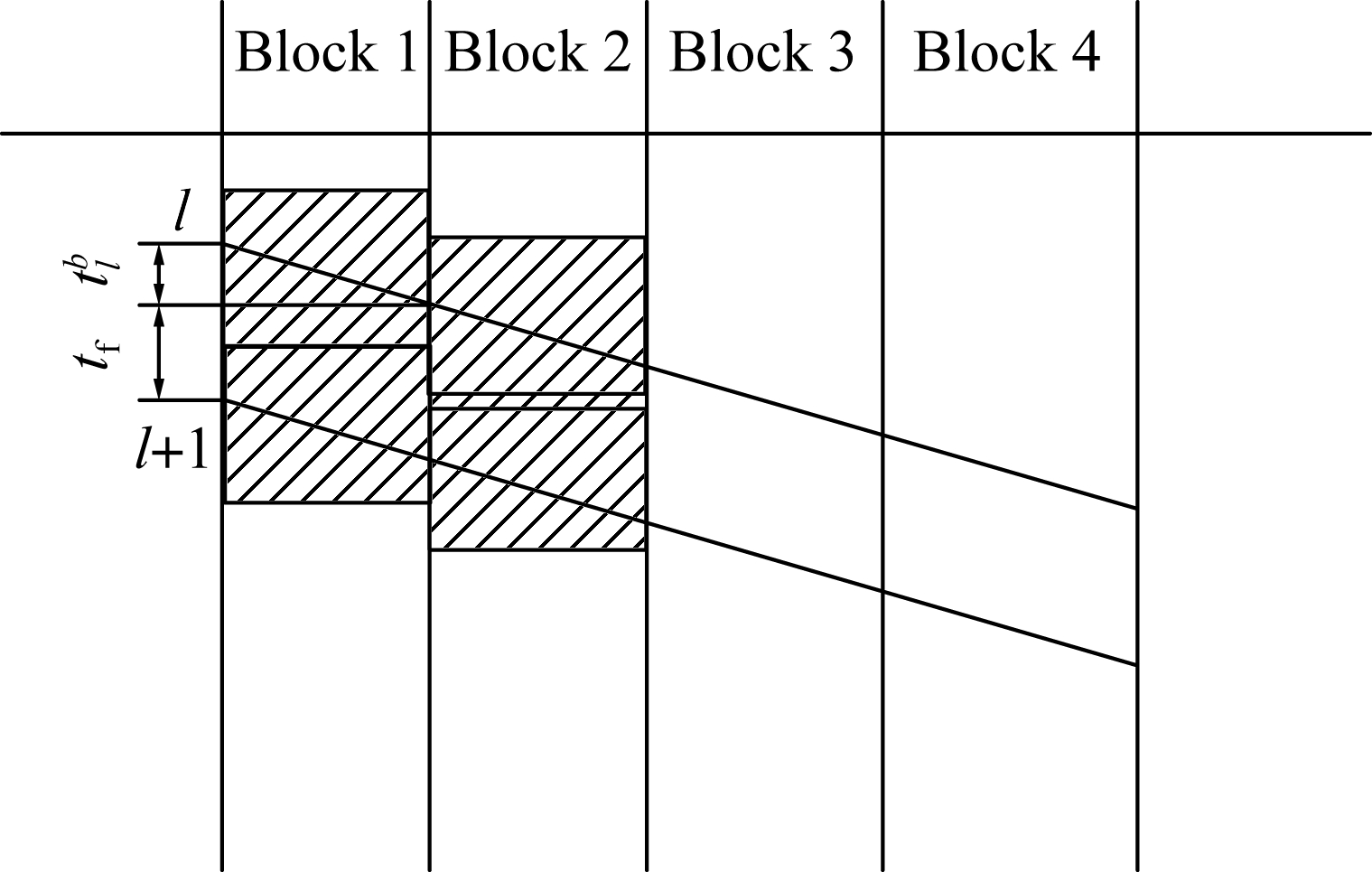
Fig.2 The station blocking time graph
1.2 Routes model
Each route is defined as the set of blocks: 
where rb is the blocks set of route r, k is the type of route r and k=1,2,3,4 expresses the departure, arrival, stop and through. 
indicates the priority of route r and the type of this route is k. The greater the value of the priority, the higher the priority of the route. The relationship of any routes can be determined by the same blocks (physical factor) and the occupied time of these same blocks (time factor).
For the physical factor, when a block is occupied, the corresponding blocks will also be set in the occupied state. These two blocks share the same start block node or the same end block node. Therefore, these two routes are related, otherwise there will be no conflict when any route is occupied. The relationship of the routes resulting from the physical factor can be expressed as
Cnr×nr={cr,r′}
(2)
where cr,r′ is a binary value, if it is 1, the route r and route r′ obtain the same block nodes. Many routes have the same blocks or the same block nodes, but if the same block is released, the related route can be used. Therefore, the time factor can determine the relation time of the routes. The relation time of the routes can be expressed as
Tnr×nr={tr,r′}
(3)
where 
are the end occupied time and start occupied time of block b; tr,r′ is the related time of the route r and route r′, and there may be more than one value with some same blocks included by the two routes.
1.3 Arrival headway
Based on the CTCS-3 train operation control system, the train operates according to the speed-distance braking mode. The throat of some high-speed railway stations is too long, and the limit speed of the switch is low. When the brake deceleration value (absolute value) is not sufficiently small, the train at the station needs to operate at a constant speed for a distance. Therefore, the arrival distance of the train is shown in Fig.3, where Dw, Dbra, Dp, Dthro and Dl indicates the distances of the reaction, braking in the section, safety protection, throat and the train, respectively.
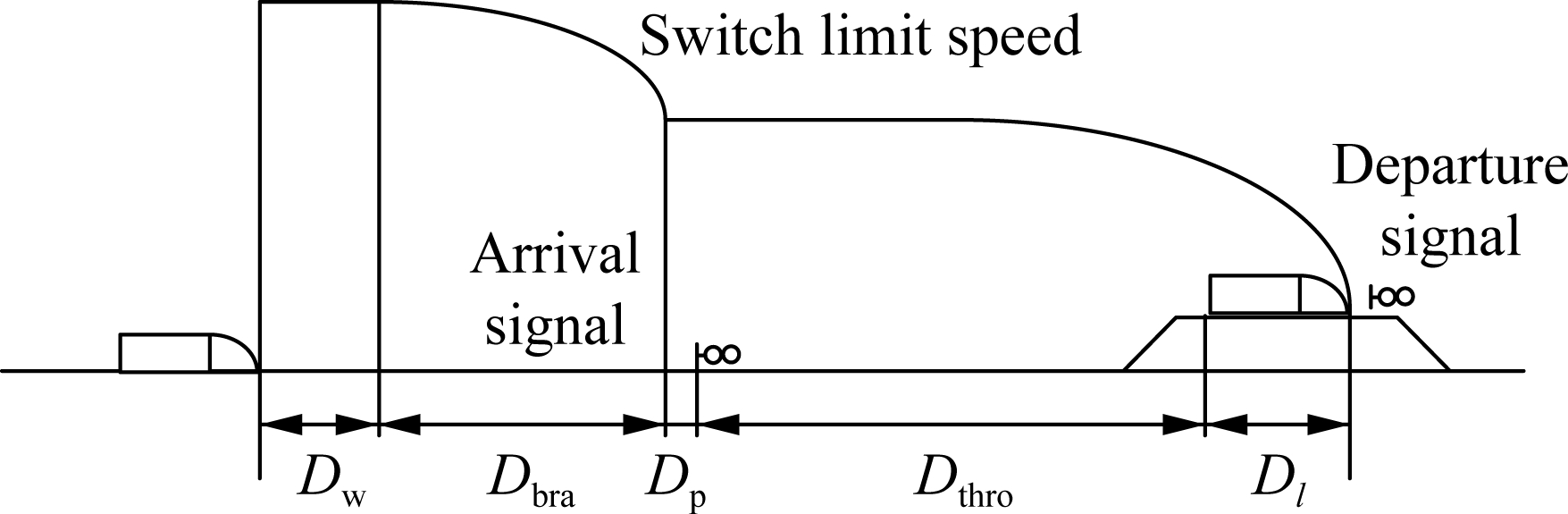
Fig.3 The arrival distance between two arrival trains
The arrival headway ta can be therefore determined as
(4)
where vo is the speed of the train in the section; vc is the speed of the train through the switch; abr1 is the deceleration in the section; abr2 is the deceleration at the station; taa is the additional time of the arrival train, which includes the time of handling the station train route (13 s), driver confirmation time (6 s), CTC confirmation time (3 s), CTC unlocking delay time (3 s), track circuit reaction time (4.3 s), train equipment strain time (3.6 s), and train start delay and empty time (2.5 s), which is 36 s in total[17-18].
When the other conditions are the same, a shorter throat length corresponds to a shorter arrival headway. Therefore, based on the existing signal system in China, the new division method of the station blocks will shorten the arrival headway. As shown in Fig.4, if the blocks at the throat is divided and a signal transmission point is added, the distance of the throat for the arrival headway becomes the distance of the first block. However, the target distance and target speed of the train brake are changed. The target point is set on the end node of the first block. The train operates at the station by gradual deceleration, as shown in Fig.4.
The arrival headway can be expressed as
(5)
where 
is the distance of block b; vx is the target speed of the end node of the first block.
1.4 Departure headway
The departure interval distance is the sum of the dis-
Fig.4 The arrival distance after the throat is divided into several blocks
tance between two section blocks, the train length, safety protection distance and the distance for the additional time of the departure operation. The departure interval distance is shown in Fig.5, where Dd1 and Dd2 are the first and second departure distances of the train in the section, respectively, and Dac is the distance of the acceleration of the train at the station.
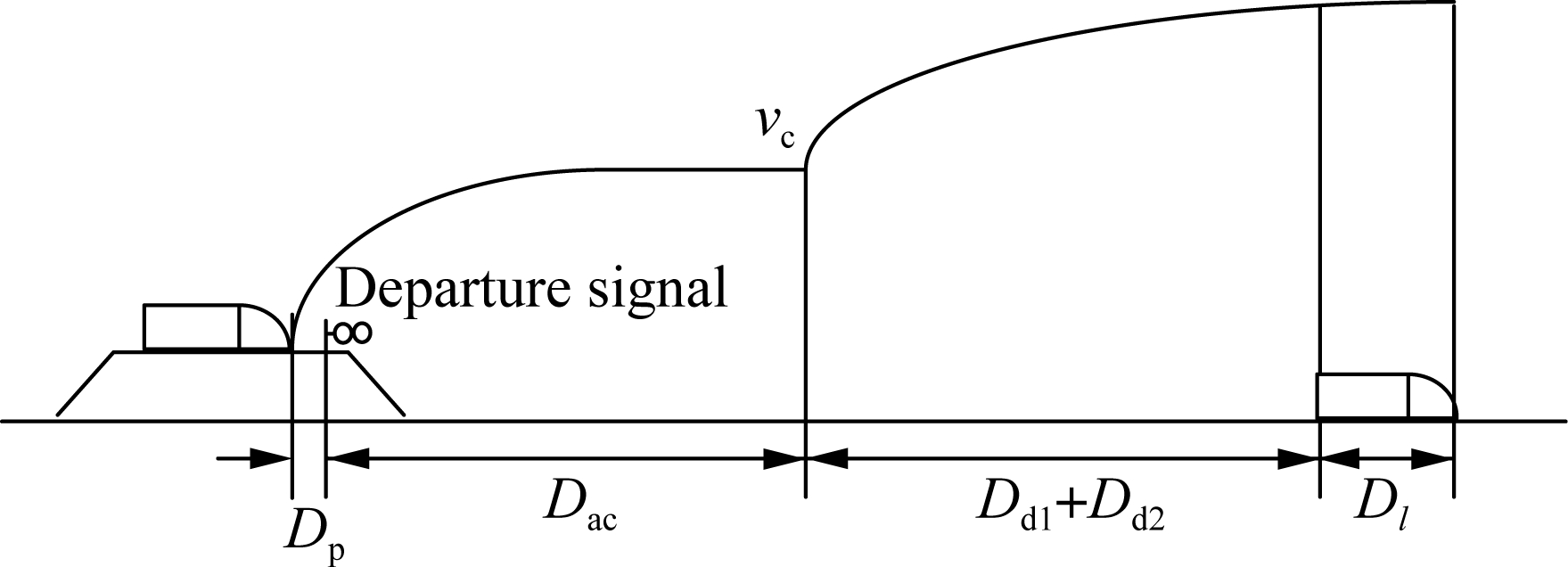
Fig.5 The departure interval distance between two departure trains
The departure headway can be expressed as
(6)
where aac1 is the acceleration of the train operating at the station, and aac2 is the acceleration of the train operating in the section; tad is the additional time of the departure operation of the train. This additional time includes the route open time (13 s), the checking time of the vacant route (4.3 s), the CTC confirmation time (3 s), the CTC unlock delay time (3 s), the vehicle equipment delay time (4.4 s), and the driver’s confirmation time (6 s). Therefore, the additional time is 34 s[17-18].
The departure headway can also be reduced by decreasing the throat length or increasing the switch limit speed. After the station blocks division, the departure headway is shown in Fig.6.
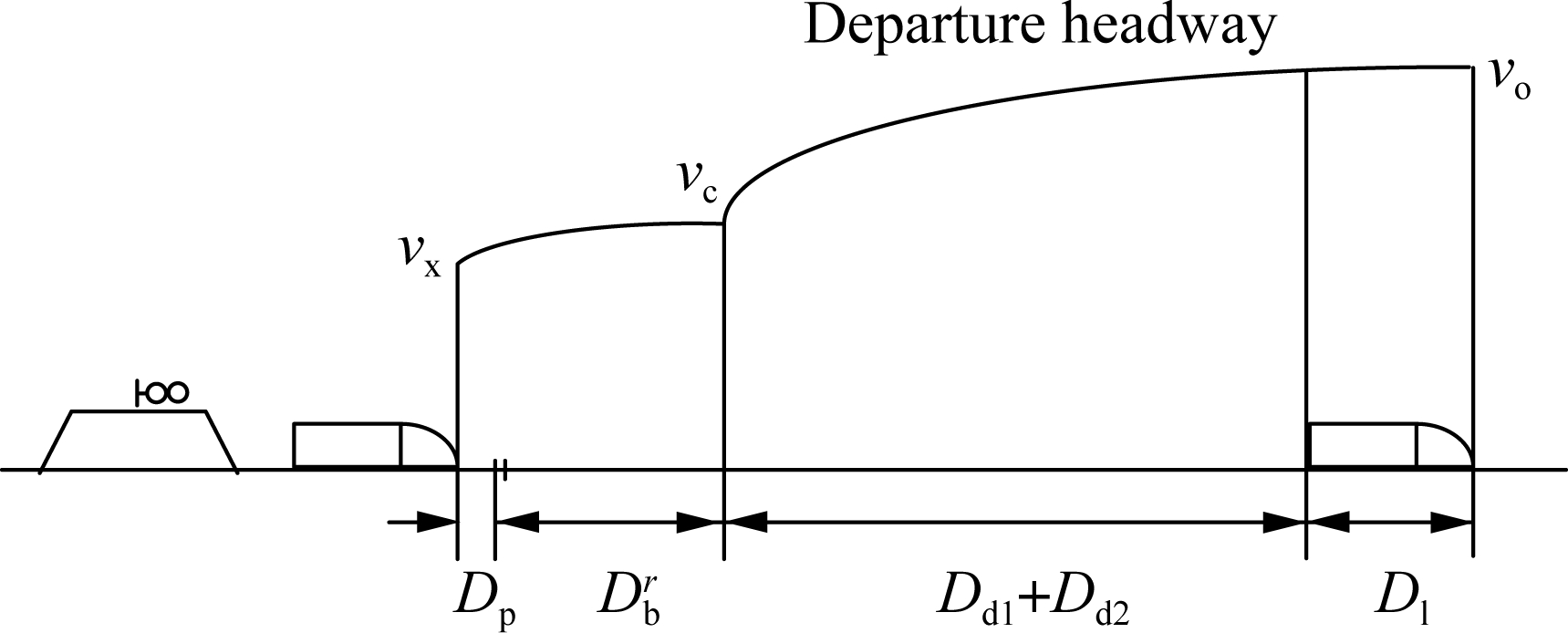
Fig.6 The departure distance after the throat is divided into several blocks
The departure headway can be expressed as
(7)
2 Calculation Method of Station Carrying Cap-acity
2.1 Model
The capacity calculation model of the station is defined as
(8)
s.t.
(9)
(10)
(11)
(12)
(13)
r→l,r′→l+1,∀l∈L
(14)
(15)
(16)
where L={l=1,2,…,nlast} is the train set and nlast is the number of trains; r→l represents that route r is selected by train l; 
is the interval time of block b between train l and train l+1, and block b is both occupied by these two trains at different times, which can be calculated by Eq.(1). tr is the train total operation time through route r. nk is the number of the k type trains. fmin is the minimal train service frequency for all trains at the station. tmin is the minimal effective period time for calculation.
In the model,the objective function is the minimal occupation time of all trains which can be expressed as Eq.(8). Since this method needs the train operation plan in the station as the input data, the minimal occupation time of all trains can express the minimal capacity utilization in a certain time period. On the other hand, the usable capacity is the maximal value under this condition.
The constraints ensure normal occupancy among the train, the route and the blocks. In Eq.(9), a train can only take one route at the same time. In Eq.(10), the same route can be occupied by only one train at the same time. In Eq.(11), the same block can be occupied by only one train at the same time.
In Eq.(12), the final arrival interval time of adjacent trains should not be less than the maximum value among the minimum arrival headway and the maximum block interval time of the same blocks that both routes include. In Eq.(13), the final departure interval time of adjacent trains should not be less than the maximum value among the minimum departure headway and the maximum block interval time of the same blocks that both routes include. Eq.(14) is the calculation method of the arrival time and departure time of the trains.
In Eq.(15), the total number of arrival trains, departure trains and stop trains should not be less than the minimum train service frequency of station.
In Eq.(16), the total arrival interval time and total departure interval time of the trains should not be longer than the effective period of time for calculation.
2.2 Algorithm
Step 1 Parameters setting
Build block set B and route set R on the basis of the topology of the station. Build the relation model among the routes according to Eq.(2). Randomly sort the trains according to the given operation information of the trains at the station, and each sequence scheme is an element of the train sequence set Q={q|q∈Z+}, and nq is the number of the sequence schemes. Initialize q=0. The simulation time set is T[q].
Step 2 Routes updating
Judge if the occupation states need to be changed according to the current time and the occupation states of the routes and the blocks.
Input data: The arrival time of the last train 
Output data: The occupation states of the routes and blocks.
For b=1 to count(B)
zb=0; % zb is 0-1 value, zb=1 means that block b is occupied.
End If
End For
For r=1 to count(R)
For b=1 to count(rb)
If all zb=0
zr=0; %zb is 0-1 value, zr=1 means that route r is occupied.
End If
End For
End For
Step 3 Scheme calculation
Select the current train sequence scheme q for calculation. Initialize train l=0.
For l=1 to nlast
If l=1
For each route
If kr=kl and max(yk) under constraints Eq.(9) and Eq.(10)
r→l; zr=1;
End If
Else
Calculate the arrival headway by Eq.(5) and departure headway by Eq.(7);
Calculate 
based on Eq.(14) under constraints Eq.(12) and Eq.(13);
Step 2();
For each route
If kr=kl and max(yk) and zr==0 under constraints Eq.(9) and Eq.(10)
r→l; zr=1;
End If
End For
End If
For b=1 to count(rb)
zb=1;under constraints Eq.(11)
are the running time and stop time of train l on block b
Calculate the relation time of the routes according to Eq.(1) and Eq.(3);
End For
End For
Step 4 Obtain the optimal scheme and maximal scheme
For q=1 to count(Q)
If constraints Eq.(15) and Eq.(16) are satisfied
Topt=min{T[q]}; qopt=q; % Topt is the occupation time of the optimal scheme and the qopt is the serial number of the optimal scheme.
End If
End For
Cmax=nl; % the maximal capacity
While (Topt+tf<tmin )
Add train l by the method of Step 3;
If constraints Eq.(15) are satisfied
Cmax= Cmax+1;
End If
End While
3 Case Study
3.1 Station blocks
According to the topology of Jinan West Station, the positions of the station blocks and station block nodes are shown in Fig.7. The station has 25 block nodes. Based on the position of each station block node, the station blocks of the station are shown in Tab.1. The station is divided into 33 station blocks, where (1)-(13) are the station blocks of the arrival throat, (14)-(25) are the station blocks of the departure throat, and (26)-(33) are the station blocks of the arrival-departure line or railway line.
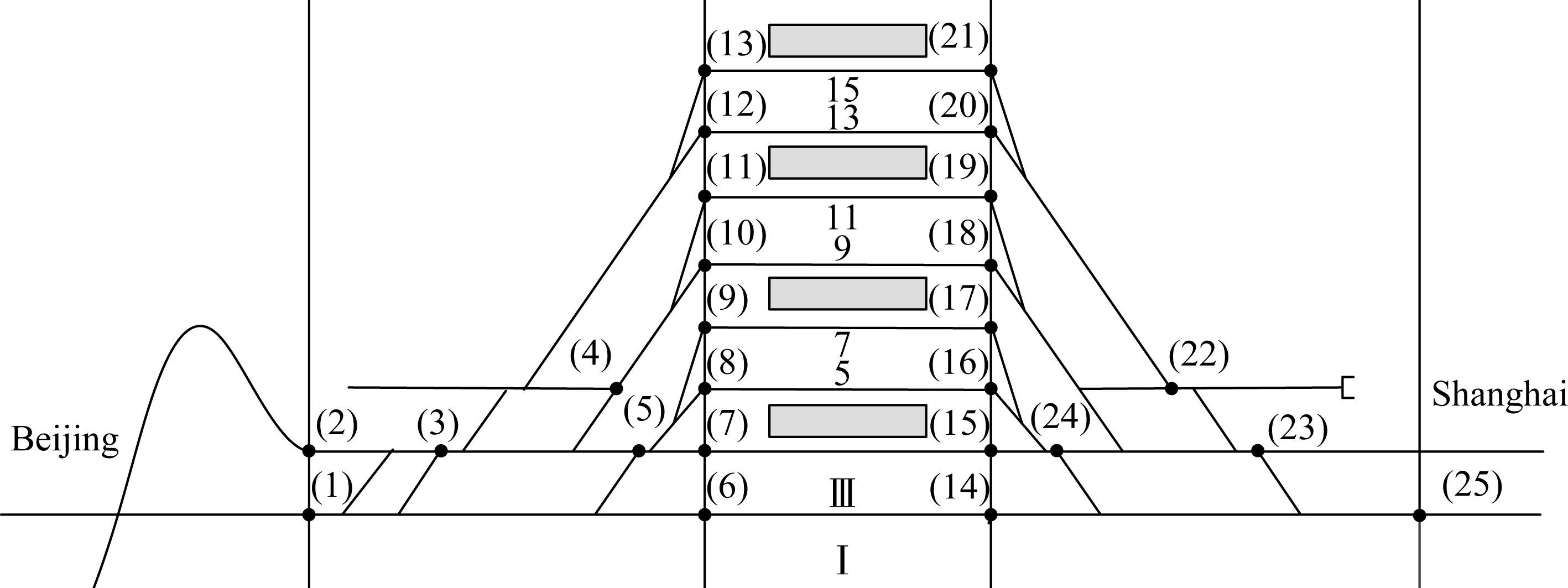
Fig.7 Station block nodes of Jinan West Station
The braking distance at the station is 432.6 m. The braking time is 42 s. The accelerated distance at the station is 721 m. The accelerated time is 70 s. Therefore, based on the length of each block (the data is originally from the topology diagram (CAD) of the station in the project) the average speed at each station block is calculated and shown in Tab.1.
Based on the occupation condition of the block nodes, some blocks need to be integrated. After the integration of the station blocks, there are 18 station blocks, including 10 station blocks of the throat and 8 station blocks of the arrival-departure line/railway line, as shown in Tab.2.
3.2 Train operation routes
According to the information of the station block, the routes can be obtained as shown in Tab.3, which include 5 through routes, 12 stop routes, 8 arrival routes and 8 departure routes. There are two types of priority determination methods. Priority1# is related to the total route length. A shorter route length corresponds to a higher priority. Priority2# is related to the convenience for passengers: a route with a closer platform to the station building has a higher priority, and a smaller value implies a higher priority.
Tab.1 Information of station blocks of Jinan West Station
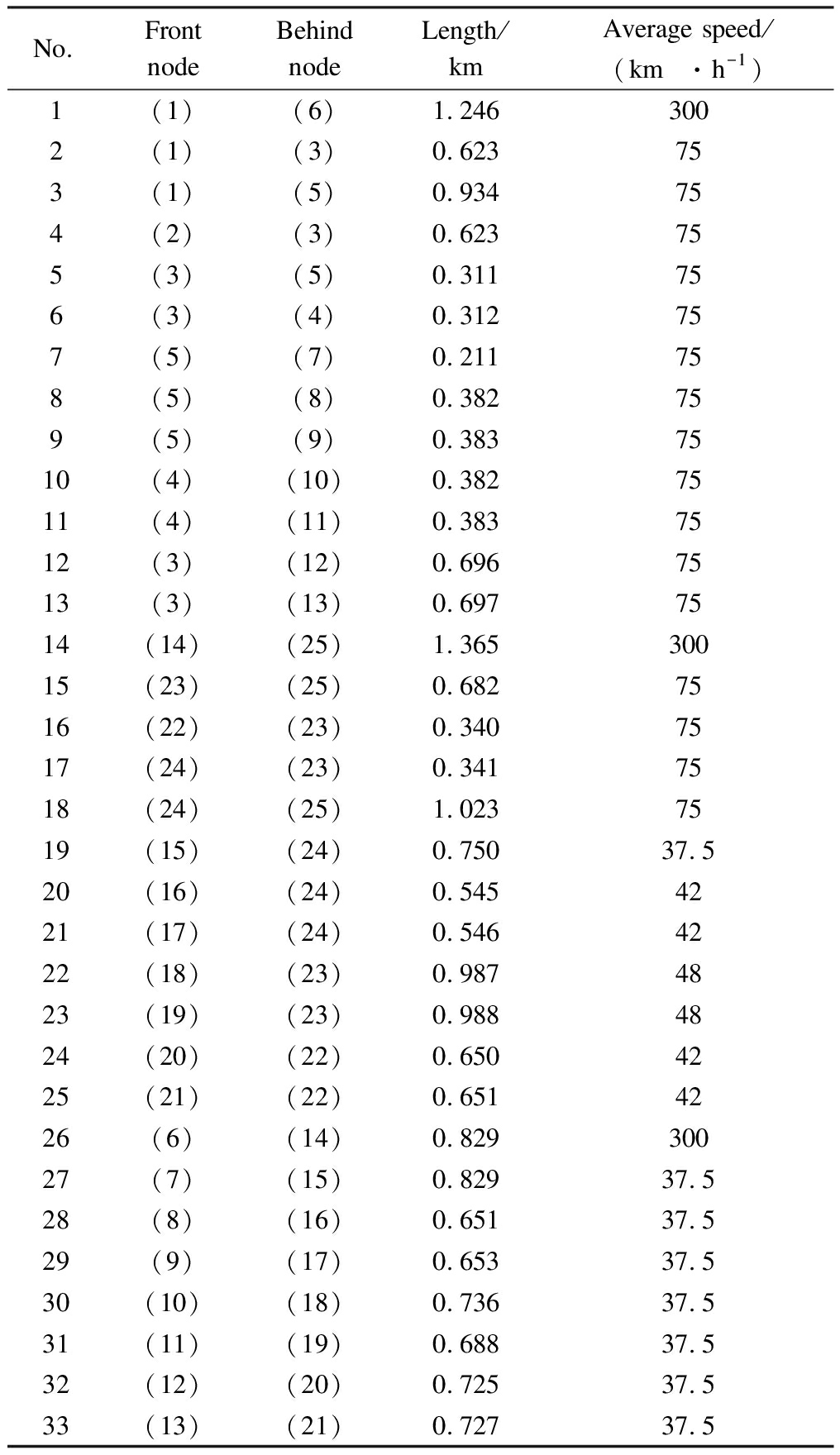
No.Front nodeBehind nodeLength/kmAverage speed/(km·h-1)1(1)(6)1.2463002(1)(3)0.623753(1)(5)0.934754(2)(3)0.623755(3)(5)0.311756(3)(4)0.312757(5)(7)0.211758(5)(8)0.382759(5)(9)0.3837510(4)(10)0.3827511(4)(11)0.3837512(3)(12)0.6967513(3)(13)0.6977514(14)(25)1.36530015(23)(25)0.6827516(22)(23)0.3407517(24)(23)0.3417518(24)(25)1.0237519(15)(24)0.75037.520(16)(24)0.5454221(17)(24)0.5464222(18)(23)0.9874823(19)(23)0.9884824(20)(22)0.6504225(21)(22)0.6514226(6)(14)0.82930027(7)(15)0.82937.528(8)(16)0.65137.529(9)(17)0.65337.530(10)(18)0.73637.531(11)(19)0.68837.532(12)(20)0.72537.533(13)(21)0.72737.5
Tab.2 Information of station blocks after the integration of Jinan West Station
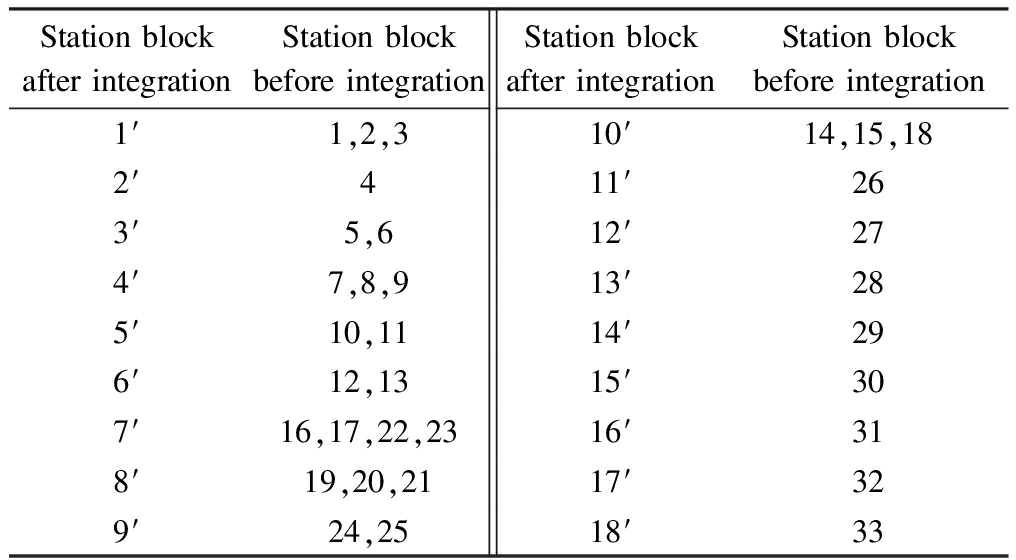
Station block after integrationStation block before integrationStation block after integrationStation block before integration1′1,2,310′14,15,182′411′263′5,612′274′7,8,913′285′10,1114′296′12,1315′30 7′16,17,22,2316′318′19,20,2117′329′24,2518′33
3.3 Headways of Jinan West Station
The speeds of the train are 300 and 250 km/h. The switch limit speed is 80 km/h, and the actual speed of the train when passing through the switch is 75 km/h. The length of the train is 400 m. The safety protection distance is 150 m. For the average value, the distance of arrival-departure line No.9 is the reference value.
The braking distance of the train in the station is 432.6 m,which is much less than the throat length, so the train in the station must run at a constant speed for a distance. The effective length for an arrival-departure line of the high-speed railway in China is 700 m, so this condition is still safe when the train begins to slow down on the arrival-departure line. The brake decelerations of the section and station are -0.7 and -0.5 m/s2. The actual arrival headway before the station blocks are divided is 247 s. Then after the station blocks are divided, the headways are presented in Tab.4.
3.4 Calculation results and discussion
The train operation information, which includes the train’s speed and operation type information, is shown in Tab.5.
For convenient calculation and reasonable capacity utilization, the arrival trains and departure trains can be combined with the through trains and stop trains. As shown in Fig.8, one departure train can be combined with one through train and two stop trains, and one arrival train can be combined with one through train and two stop trains.
After the combinations, the train operation scheme includes one through train, one stop train, one departure train and one arrival train with higher speed, and one through train and one stop train with lower speed.
Based on the six different kinds of trains, 720 kinds of schemes for train operation sequence are calculated and the total occupation time of each scheme can be calculated. The total occupation time is mainly concentrated between 46.4 and 53.2 min. Therefore, the scheme with 46.4 min is the optimal scheme. The sequence of the train operation has a large impact for station capacity.
3.4.1 Calculation result based on priority1#
The train operation sequence of the optimal scheme is 5-2-6-1-3-4. The station blocking time graph of the train operation is shown in Fig.9. By comparing Figs.9 and 10, different train operation sequences will cause different occupation times at the station of the same trains. Therefore, an optimal scheme of the train operation sequence can reduce the total occupation time for the same trains and the usable capacity can be increased.
The routes occupied by each train are as follows: 26, 1, 10, 14, 10, 18, 1, 10, 14, 1, 1, and 6. Since the total occupancy time of all trains is less than 1 h, the current condition does not reach the maximum capacity. Therefore, a number of trains can be increased as shown in Fig.11. The maximum capacity of this solution is 16 train/h. The total train occupancy time is 59.2 min. The minimum arrival interval time between adjacent trains is 2.7 min, the maximum arrival interval is 9.8 min, and the average arrival interval time is 3.7 min. The service frequency of trains at the station is 12 train/h. Under the condition of Fig.10, only two trains can be added to the scheme. The maximum capacity is 14 train/h, which is less than the maximum scheme of Fig.11.
Tab.3 The route information of Jinan West Station
TypeDeparture-arrival line No.Route No.Station block nodesPriority1#Priority2#Through trainⅠⅢ11,6,14,251121,5,7,15,24,252231,3,5,7,15,24,253341,5,7,15,24,23,254451,3,5,7,15,24,23,2555Stop train57911131561,5,8,16,24,2511271,3,5,8,16,24,2521181,5,8,16,24,23,2531091,3,5, 8,16,24,23,2549101,5,9,17,24,2558111,3,5,9,17,24,2567121,5,9,17,24,23,2576131,3,5,9,17,24,23,2585141,3,4,10,18,23,2594151,3,4,11,19,23,25103161,3,12,20,22,23,25112171,3,13,21,22,23,25121Arrival train579111315181,5,8,1618191,3,5,8,1627201,5,9,1736211,3,5,9,1745221,3,4,10,1854231,3,4,11,1963241,3,12,2072251,3,13,2181Departure train579111315262,3,5,8,16,24,2518272,3,5,8,16,24,23,2527282,3,5,9,17,24,2536292,3,5,9,17,24,23,2545302,3,4,10,18,23,2554312,3,4,11,19,23,2563322,3,12,20,22,23,2572332,3,13,21,22,23,2581
Tab.4 The headway information
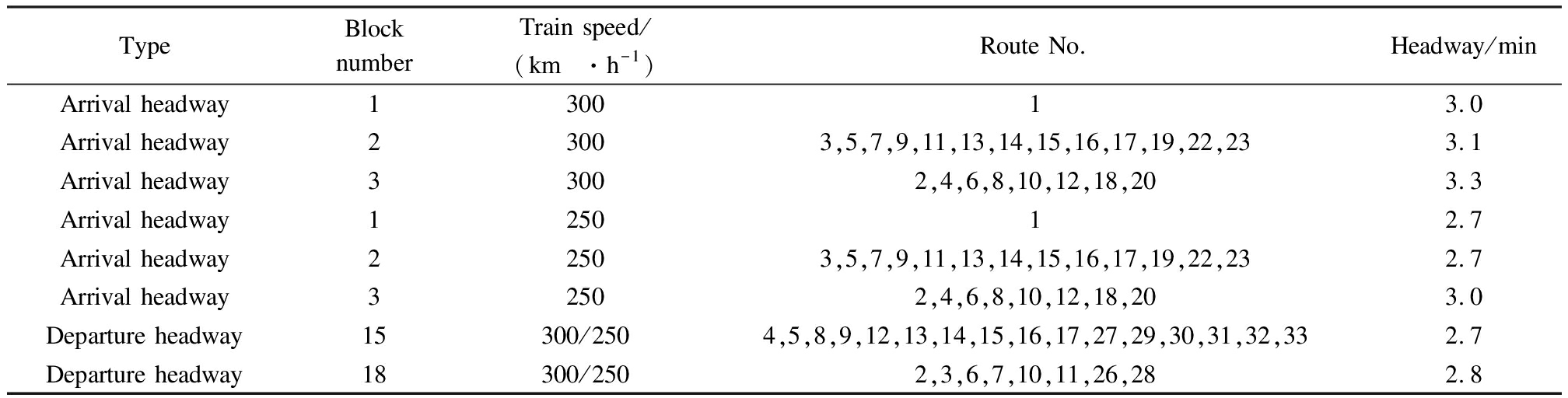
TypeBlocknumberTrain speed/(km·h-1)Route No.Headway/minArrival headway130013.0Arrival headway23003,5,7,9,11,13,14,15,16,17,19,22,233.1Arrival headway33002,4,6,8,10,12,18,203.3Arrival headway125012.7Arrival headway22503,5,7,9,11,13,14,15,16,17,19,22,232.7Arrival headway32502,4,6,8,10,12,18,203.0Departure headway15300/2504,5,8,9,12,13,14,15,16,17,27,29,30,31,32,332.7Departure headway18300/2502,3,6,7,10,11,26,282.8
Tab.5 The train operation information
Train speed/(km·h-1)300300250250300300Operation typeThroughStopThroughStopArrivalDepartureNumber of the trains351111
3.4.2 Calculation result based on priority2#
The train operation sequence of the optimal scheme is 5-2-6-1-3-4. The train-occupied station block diagram is shown in Fig.12.
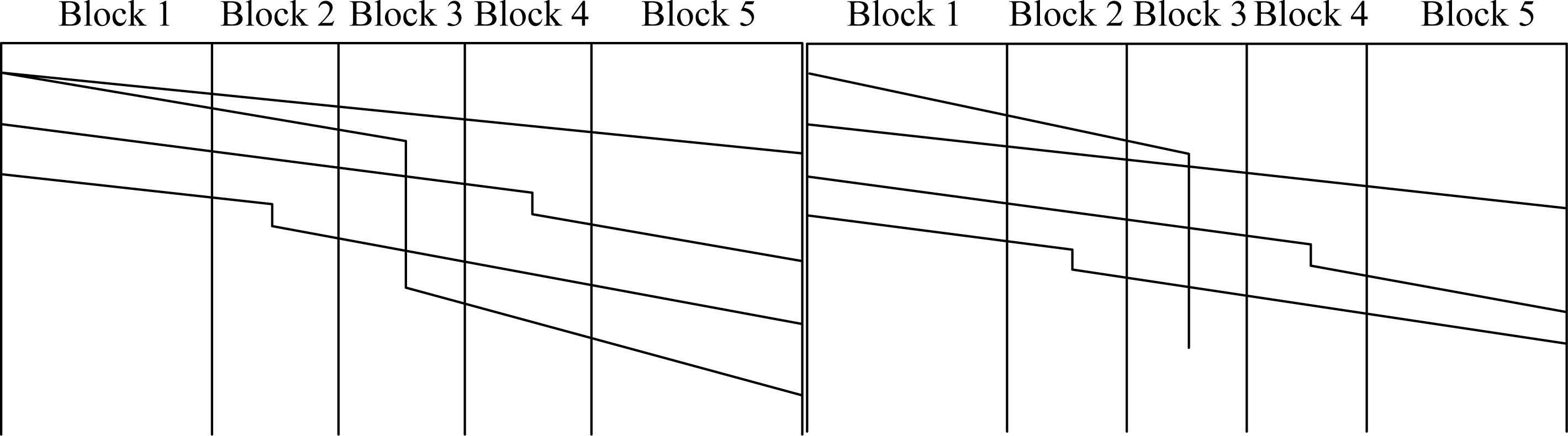
Fig.8 The combination of departure trains or arrival trains with other operation type trains
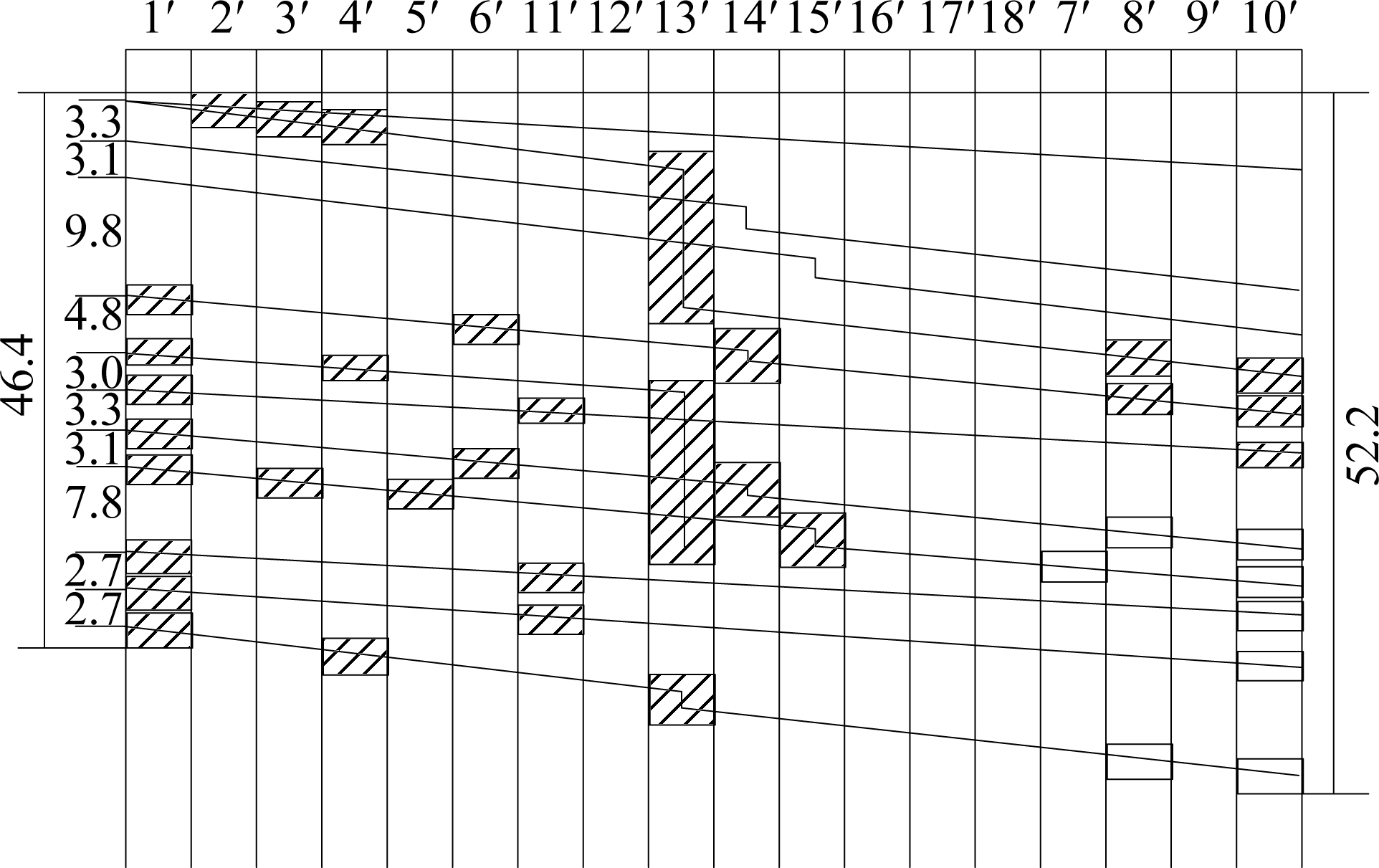
Fig.9 The optimal scheme based on priority1#(unit:min)
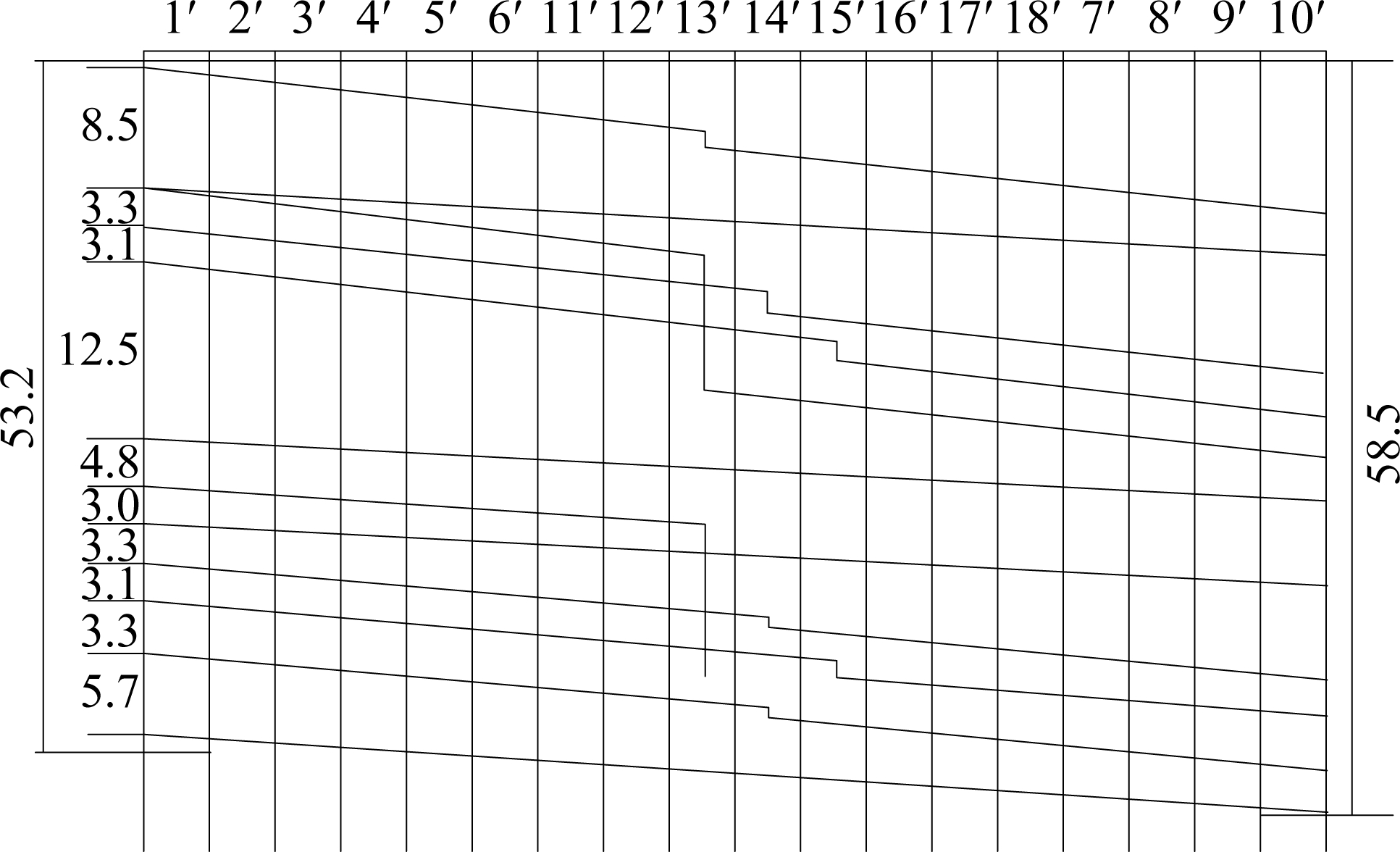
Fig.10 The worst scheme based on priortity1# (unit:min)
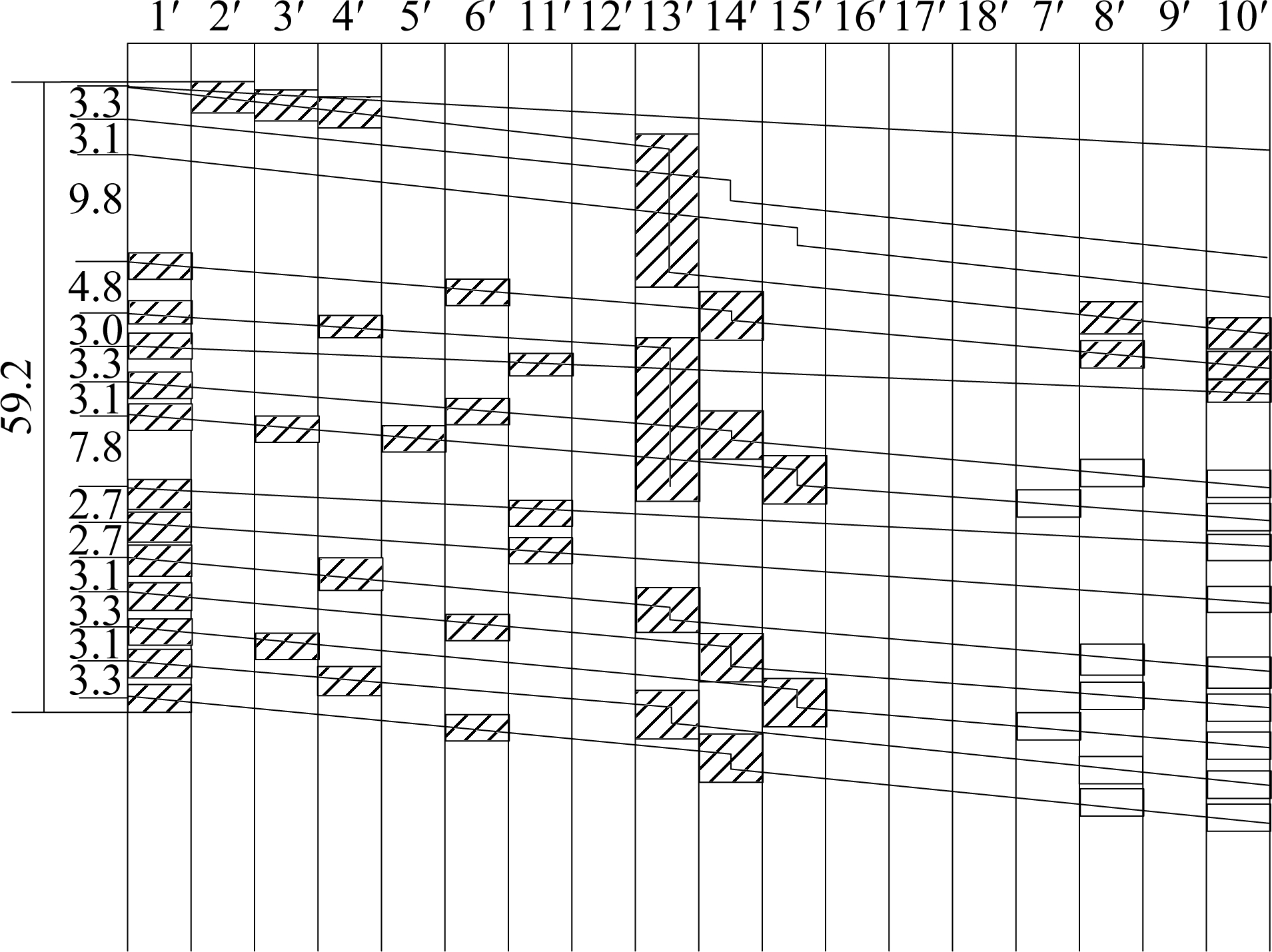
Fig.11 The maximum scheme based on priority1#(unit:min)
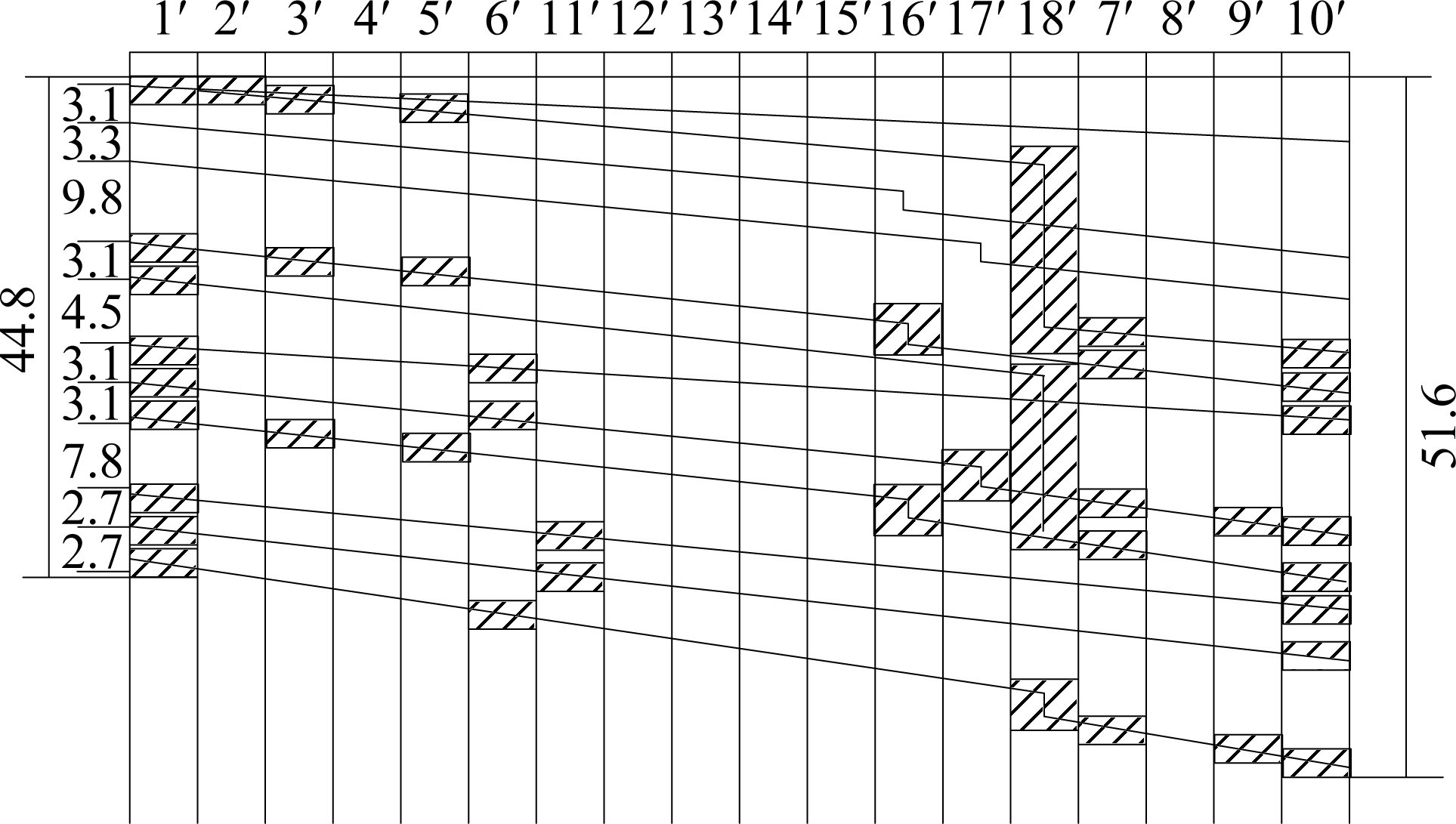
Fig.12 The optimal scheme based on priority2# (unit:min)
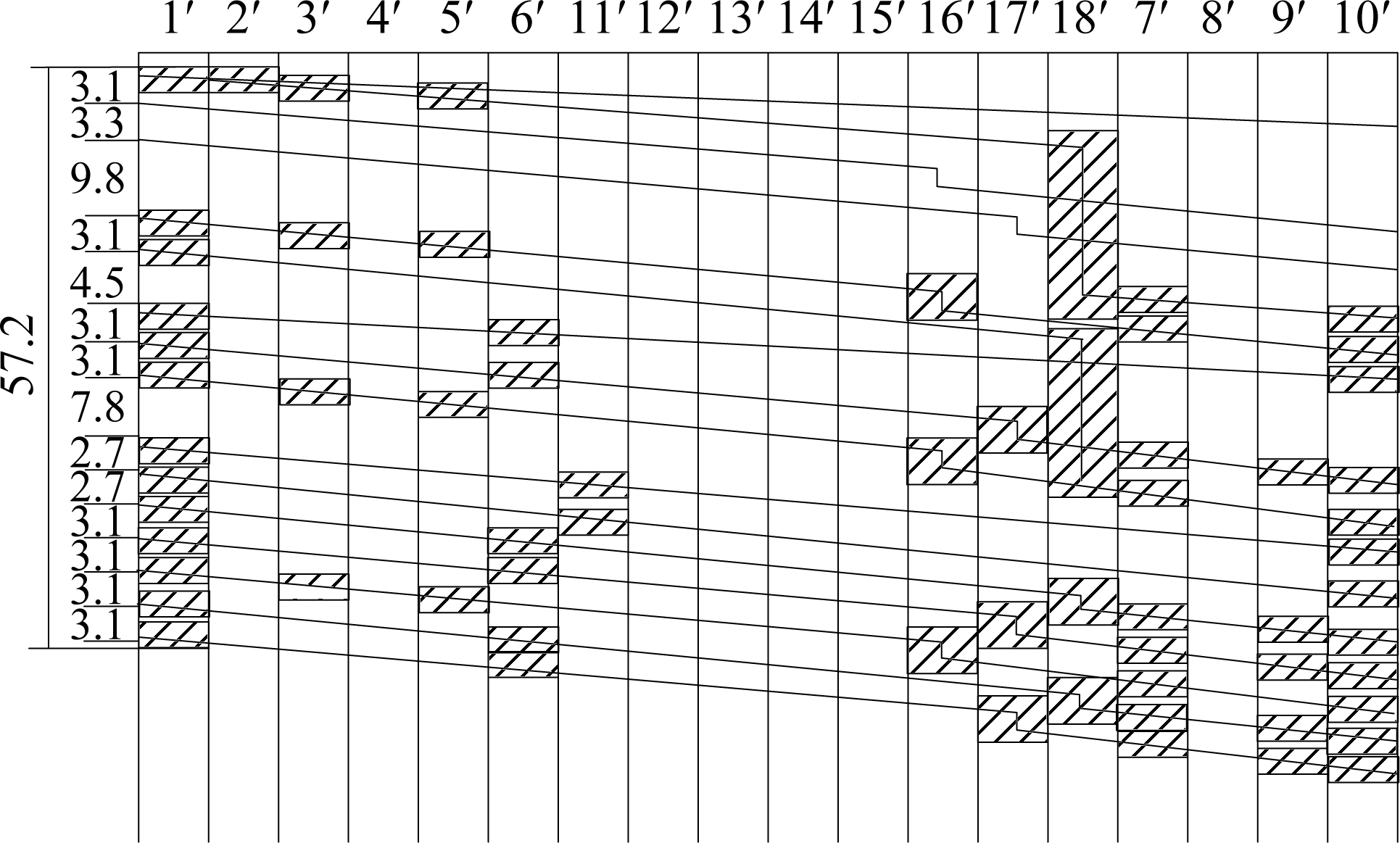
Fig.13 The maximal scheme based on the priority2#(unit:min)
3.4.3 Calculation results analysis
First, the station capacity before dividing the station blocks is calculated. Within 1 h, there are 13 trains at most, as shown in Fig.14.
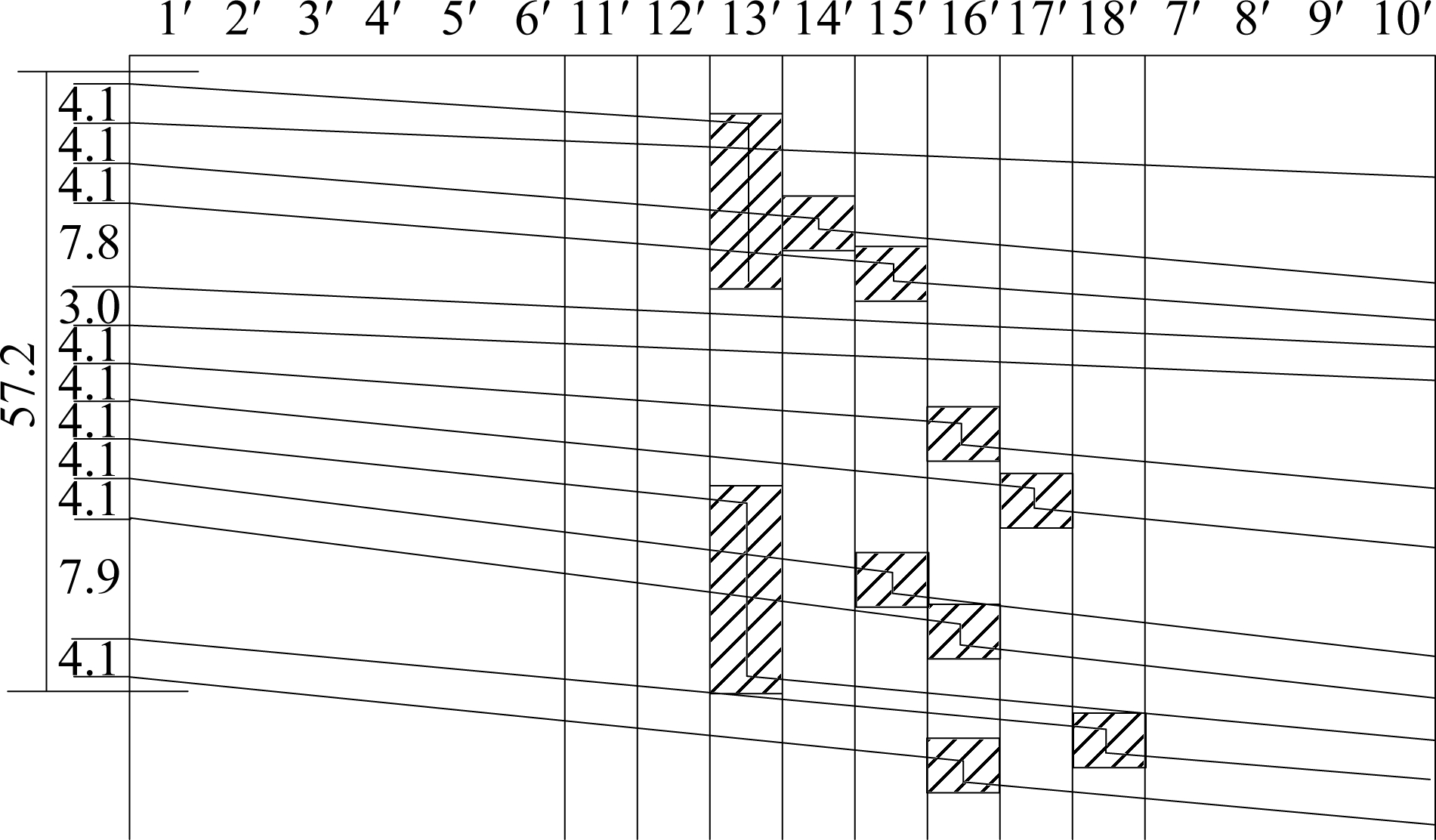
Fig.14 The scheme based on the actual headway(unit:min)
The routes occupied by the trains are as follows: 33, 1, 15, 16, 15, 25, 1, 16, 15, 1, 1, and 17. The total occupation time of all trains is less than 1 h, and the current condition does not reach the maximum capacity. Therefore, more trains can continue to be added as shown in Fig.13. The maximum capacity of this scheme is 16 train/h. The total train occupancy time is 57.2 min. The minimum arrival interval time between adjacent trains is 2.7 min, the maximum arrival interval is 9.8 min, and the average arrival interval time is 3.6 min. The service frequency of trains at the station is 12 train/h.
Then, the calculation results of these schemes are compared in Tab.6.
Tab.6 Comparison and analysis of different schemes
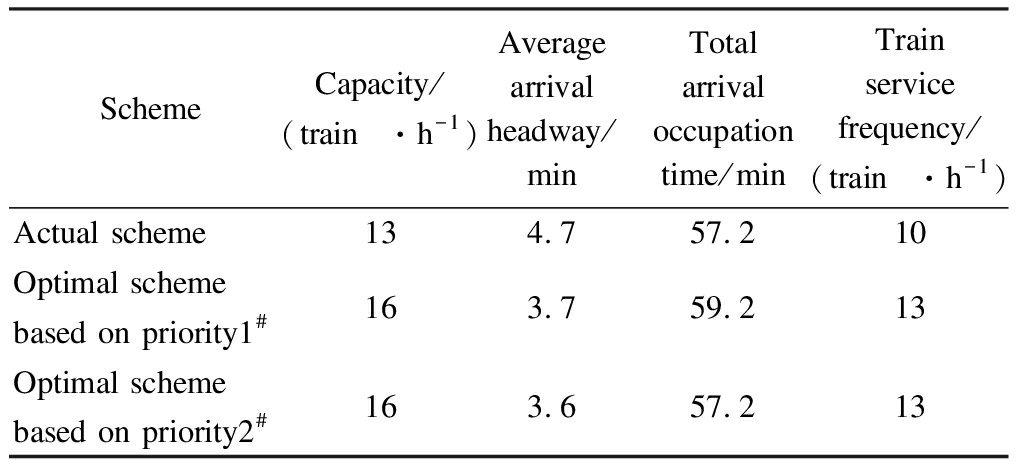
SchemeCapacity/(train·h-1)Average arrival headway/minTotal arrival occupation time/minTrain service frequency/(train·h-1)Actual scheme134.757.210Optimal scheme based on priority1#163.759.213Optimal scheme based on priority2#163.657.213
By dividing the station blocks, the train arrival headway and departure headway can be effectively reduced, which increases the capacity of the station. The station carrying capacity can be increased from 13 to 16 train/h, and the increase ratio is 23%.
In contrast to the scheme based on priority1#, the solutions using priority2# can effectively reduce the total train occupancy time and average train arrival interval time. The number of trains can increase the effective time of the train operation in the next period of time. Therefore, this scheme is more favorable for the calculation of whole-day capacity.
4 Conclusions
1) The headway of the station is mainly affected by the arrival headway and departure headway, and the throat length is one important factor for these headways. Therefore, by dividing the station blocks, the headways can effectively be reduced at the station. Then, the occupation time of all trains can be reduced and the station carrying capacity can be improved by 3 train/h compared with the traditional calculation method.
2) Different train speeds and operation sequences of trains at the station have some influence on the station carrying capacity. Appropriate arrangements for the trains can reduce the total occupation time of all trains. Under certain conditions, the optimal train sequence can increase the station carrying capacity.
3) This paper only studied the carrying capacity for one direction. For the turn-back trains, this method does not consider the whole operation process. In future research, the station block will be divided based on the whole station and the operation conditions of the train in different directions. The carrying capacity of the railway network can be studied based on this method in the future.
4) The calculation method for the station carrying capacity of the high-speed railway in this paper is feasible and can provide effective theoretical support for transport organization.
[1]Huisman T, Boucherie R J, van Dijk N M. A solvable queueing network model for railway networks and its validation and applications for the Netherlands[J].European Journal of Operational Research, 2002, 142(1): 30-51. DOI:10.1016/s0377-2217(01)00269-7.
[2] Burdett R L. Multi-objective models and techniques for analysing the absolute capacity of railway networks[J].European Journal of Operational Research, 2015, 245(2): 489-505. DOI:10.1016/j.ejor.2015.03.020.
[3] Burdett R L. Incorporating complex train paths in an analysis of absolute capacity[J].International Journal of Railway Technology, 2015, 4(4): 73-83. DOI:10.4203/ijrt.4.4.4.
[4] Burdett R L. Optimisation models for expanding a railway’s theoretical capacity[J].European Journal of Operational Research, 2016, 251(3): 783-797. DOI:10.1016/j.ejor.2015.12.033.
[5] Lai Y C, Wang S H. Development of analytical capacity models for conventional railways with advanced signaling systems[J].Journal of Transportation Engineering, 2012, 138(7): 961-974. DOI:10.1061/(asce)te.1943-5436.0000388.
[6] Deng J W, Zhang Y X. Analysis of the influence of arrival and departure of trains on the carrying capacity of express railway station[J]. Journal of Transportation Engineering and Information, 2017, 15(3): 63-70.(in Chinese)
[7] Chen T. The theory and method of capacity calculation on high-speed railway station[D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese)
[8] Hansen I A. Review of planning and capacity analysis for stations with multiple platforms—Case Stuttgart 21[J].Journal of Rail Transport Planning & Management, 2017, 6(4): 313-330. DOI:10.1016/j.jrtpm.2016.12.002.
[9] UIC International Union of Railways. UIC leaflet 406, Capacity[S]. France, UIC International Union of Railways, 2004.
[10] Hansen I A, Pachl J. Railway timetable & traffic[M]. Hamburg, Germany： Eurailpress DVV Rail Media, 2008.
[11] Klabes S G. Algorithmic railway capacity allocation in a competitive European railway market[D]. Germany: Rhine-Westphalia Technical University Aachen, 2010.
[12] Zhang H T. Research on capacity of urban rail transit based on blocking time [D]. Beijing: Beijing Jiaotong University, 2012. (in Chinese)
[13] Zhao W T, Martin U, Cui Y, et al. Operational risk analysis of block sections in the railway network[J].Journal of Rail Transport Planning & Management, 2017, 7(4): 245-262. DOI:10.1016/j.jrtpm.2017.09.003.
[14] Li X J. Reaserch on carrying capacity calculation and reliability assessment method of high-speed railway[D]. Beijing: Beijing Jiaotong University, 2016: 47-64. (in Chinese)
[15] Liu P, Han B M. Optimizing the train timetable with consideration of different kinds of headway time[J]. Journal of Algorithms & Computational Technology, 2017,11(2):148-162. (in Chinese)
[16] Sangphong O, Siridhara S, Ratanavaraha V. Analysis and design of nomographs for minimum headway calculation[J]. Songklanakarin Journal of Science and Technology,2018,40(2):457-466.
[17] Li B, Tian C H. Calculation of headway between tracing trains on PDL [J].Railway Transport and Economy, 2007,29(7):20-22. (in Chinese)
[18] Wei F H, Wu Q, Liu L. The simulating calculation and optimization design of the tracing time interval of trains in aim-interval control mode[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(3): 105-110. DOI:10.16097/j.cnki.1009-6744.2007.03.019.(in Chinese)
[19] Landex A. Methods to estimate railway capacity and passenger delays[D]. Denmark: Technical University of Denmark, 2008.