Nowadays, modern supply chains are complex networks that are spread across the globe. As a consequence, the risk of supply disruption increases as it exists in every link[1]. As pointed out in Ref.[2], 85% of buyers suffered supply disruptions. The occurrence of stock-outs can lead to severe revenue and image losses. A well-known example is the case of Ericsson. A fire at the plant of Ericsson supplier (Philips microchip, at New Mexico) in 2000 led to a loss of about 400 million Euros and Ericsson’s withdrawal from the mobile phone market.
To avoid devastating losses caused by supply disruptions, much research has been done in both academic and practical fields. Fruitful strategies on supply-disruption-management have been developed, such as diversification[3], compensation[4], buffer stock[5], emergency sourcing[6], etc. Emergency sourcing is a commonly utilized strategy. As found in a survey, 63% of enterprises studied in 2008 employed this strategy[7]. Under this strategy, the firm can reroute to a secondary source (e.g., the spot market) in the event of a supply failure. Normally, the emergency procurement requires a high price, nonetheless, the additional cost is only incurred when the shortage occurs. Compensation is another popular strategy for managing supply risks in recent years. For instance, some home appliance stores provide discounted “rain checks” to customers if a product is out of stock[8]. By offering various forms of compensation (e.g., discounts and free service), customers’ reactions to stock-outs can be effectively controlled.
However, a company is not limited to choosing a single pure strategy for managing disruption risk. Under many circumstances, a combination of strategies might be an appropriate choice[9]. In addition to the aforementioned mitigation approaches, a few researchers have started to focus on developing mixed mitigation strategies. Based on inventory buffering and sourcing[10], a mixed mitigation strategy is proposed, consisting of partial sourcing and inventory carrying. Ref.[11] investigated the joint optimization incorporating compensation and redundant capacity sharing. More recently, in view of the dynamic aspects, various types of real-time strategies are developed, such as dynamic sourcing[12], dynamic scheduling or planning[13], and dynamic recovery[14].
To the best of our knowledge, the research of both dynamic and mixed strategy is still in its infancy. Therefore, this paper focuses on designing a dynamic joint compensation and procurement strategy for retailers to manage stock-outs. This study provides the following contributions to the literature of managing disruptions. By taking dynamic aspects into consideration, we propose a new type of dynamic combined strategy for handling supply disruptions. Through this reactive strategy, we present analytical guidance for retailers on how to jointly adjust the compensation level and sourcing quantity over time, depending on disruption length, compensation cost, recovery speed, customer sensitivity, and other contributing factors.
1 Model Formulation
A retailer sourcing from a regular supplier might experience a supply disruption, where no buffer stock is reserved. Market demand is deterministic and normalized to be 1 at time t. Suppose that the supply disruption occurs at time 0 and lasts till time T, that is, a stock-out with the length of T occurs.
Facing a stock-out, impatient customers choose to purchase other alternative goods, causing the retailer losses in terms of lost sales. Patient customers might choose to backorder. To reduce the negative impact caused by the stock-out, the retailer considers the following two countermeasures during the disruption: compensating customers to encourage a higher backorder rate and satisfying customers with emergency sourcing. In the process of jointly using these two strategies, customers exhibit dynamic reactions, and additional cost arises in the period of the stock-out. After the disruption ends, the retailer procures from the regular supplier. The demand 1 is satisfied in real time, while the backlogging demand generated during disruption is successively met at a fixed recovery speed of k, where k is critically linked to the capacity of the regular supplier. Clearly, an additional recovery cost is incurred after the end of the stock-out. In the following, we formulate the demand dynamics and the additional cost caused by the disruption.
Suppose that y(t) customers decide to backorder at time t. In other words, the backorder rate is defined as y(t), which decreases with the waiting time and the customers’ sensitivity α, and increases with the compensation level p(t)[15]. Therefore, we describe the backorder rate y(t) as y(t)=1-α(tmax-t)+p(t). In other words, y(t) customers accept the compensation level p(t) and choose to postpone their purchases. A total compensation cost of 
is required from the retailer, where cp is the unit compensation cost.
The length of the waiting time is characterized by the customers’ arrival time t and the satisfactory time tmax. In practice, the sequence of meeting backlogged demand commonly follows a “first-come first-served” principle. Suppose that there are D(t) backorders accumulated, the marginal increase of D(t) with respect to time is defined as
dD(t)/dt=y(t)
Under this principle, the customer who arrives and decides to backorder at time t will be met at time tmax=T+D(t)/k. Therefore, y(t) can be further identified as
y(t)=1-α[D(t)/k+T-t]+p(t)
where p(t)≥0 and 0≤y(t)≤1. As for the un-backorder demand 1-y(t), the retailer decides to offer x(t) of them with the emergency sourcing policy, and let the rest of them be lost sales, 0≤x(t)≤1-y(t). By procuring sources from a secondary supplier, the retailer achieves replenishments with a zero lead-time and a price ce. Accordingly, an emergency sourcing cost of 
occur.
After the supply of the regular supplier is restored at time T, a total amount of 
backorder demand is generated. To satisfy both the real-time demand and the backlogged demand, the retailer procures from the regular supplier at a price c0. Therefore, it raises an additional recovery cost of 
Summing up, given y(t)=1-α[D(t)/k+T-t]+p(t), the additional cost incurred during the disruption impact period is derived as
In the above expression, these four items respectively represent the compensation cost, the emergency sourcing cost, the lost-sale cost, and the recovery cost.
Given the disruption impact, the retailer makes the decision of how and when to cost-effectively adopt emergency sourcing and compensation, that is, to decide the dynamic quantity x(t) and the compensation level p(t). As indicated in y(t), the compensation level can be identified by y(t). Therefore, let x(t) and y(t) be the decision variables, and D(t) be the state variable. We formulate the above question as the following control model.
(1)
s.t.
=y
(2)
(3)
0≤x≤1-y
(4)
Eq.(2) captures the dynamics of the backlogged demand. In particular, D(0)=0, no demand is backlogged at the initial time of disruption. Eqs.(3) and (4) respectively give the maximum and minimum values of the decision variables y and x. By solving the above model, we achieve the optimal quantity of x and y, denoted as (x*,y*). For notational simplicity, we omit the time index t from this point forward.
2 Optimal Reactive Strategy
To achieve the optimal solution (x*,y*) for the above question via Pontryagin’s minimum principle[16], we first formulate the Hamiltonian function for the above model as follows:
cl(1-y-x)+c0y-λ1y
Accordingly, the derivatives of the Hamiltonian function to the decision variables x and y are given as
and
The Hamiltonian function decreases with x, hence, the optimal x* for minimizing H is achieved as x*=max(x). Let ∂H/∂y=0, combining with the constraints for x and y, i.e., formulae (3) and (4), the optimal (x*,y*) is determined as
x*=1-y*
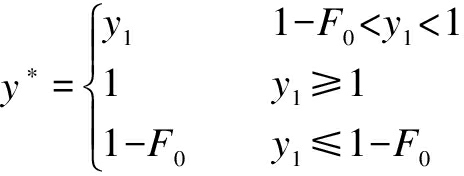
where
(5)
The optimal (x*,y*) can be in three sets of value. Both the value and the corresponding condition rely on the co-state variable λ1, which can be defined as
(6)
Given the above necessary and transversality conditions in Eq.(6), λ1 is described as
(7)
Substituting Eq.(7) into Eq.(5), the optimal solution (x*,y*) can be further identified, as well as the corresponding reactive strategies for mitigating the stock-out, as shown in Proposition 1.
Proposition 1
1) If 
and the strategy is determined as CS.
2) If 
and the strategy is determined as C.
3) If F≤α(t-T), then 
and the strategy is determined as S.
Here, 
and F0 is given in Eq.(5).
As indicated in Proposition 1, the optimal real-time reactive strategy hedging against the stock-out can be in three forms: CS, C, and S. Among them, CS is a combined policy incorporating compensation and emergency sourcing, while C and S are the pure compensation and sourcing strategies, respectively. Under the implementation of CS, the retailer satisfies 
customers by rerouting to an emergency supplier, in the meantime, compensates the rest of them for backordering. If C is utilized, all the customers are backordered because the retailer offers them real-time maximum compensation. By rerouting to a secondary source after the occurrence of a supply shortage, that is, adopting the sourcing strategy S, the retailer meets all the customers’ arriving during the supply disruption.
The time intervals of using the above strategies are essentially linked to the real-time accumulated backorders D and the terminal quantity D(T). If it is optimal to control the terminal quantity under α(t-T), no compensation is provided for gaining more backorders, that is, using the strategy S. Otherwise, compensation is employed. In particular, during the periods in which a small number of backorders are accumulated, i.e., 
The critical time points that switch between these three options are defined by two equations: F=α(t-T) and F=F0+αD/k. In view of the continuity of the state variable D, we find that the direction of the strategy transition is determined. The policy C can switch into CS, and CS can switch into C and CS. Given this property, the optimal strategy for the whole out-of-stock time can be determined by examining the decisions at the initial time 0 and the terminal time T, that is, the initial and the terminal strategies.
In the following, we explore how to construct the optimal dynamic reactive strategy to handle the stock out, starting from time 0 and T. At the beginning of the stock-out, no backorder is accumulated, i.e., D(0)=0. Analyzing the conditions at time 0 and T for the options CS, C, and S, we have Corollary 1.
Corollary 1
1) At the initial time 0, the optimal strategy starts with C if F>αT; with S if F<-αT; and with CS if -αT<F<αT.
2) At the end of the stock-out, the optimal strategy terminates with C if 
3) The optimal strategy is determined to be S for all t∈(0,T), if it is optimal to adopt S at time 0.
Proof of 1) and 2) Let t=0 and t=T, the results can be directly deduced from the conditions stated in Proposition 1. The condition for adopting S at time t is F<α(t-T). Clearly, the inequality holds at any time point t if it holds at time 0.
According to Corollary 1, if it is optimal to adopt sourcing at the beginning of the stock-out, the advantage of S remains thereafter. That is, the retailer contingently procures products from the spot market at a high price, and meets all un-backorder demand during the period of stock-out. Conversely, if the optimal decision of the retailer is determined to be either offering pure compensation or pure sourcing to customers, that is, adopting CS and C, the quantity of sourcing and the level of compensation change over time as the stock-out continues. Consequently, the strategy might switch from CS to C or S at some time points. With regards to the initial strategy C, it can change into CS, then S. As a result, beginning with CS and C at time 0, the optimal strategy can be in six patterns: C, C-CS, C-CS-S, CS, CS-C, and CS-S. The conditions of implementing these strategies are defined by the initial and terminal strategies, as presented in Corollary 1. Among them, the C-CS-S can be first excluded by the initial and terminal conditions.
Given the structures of the optimal strategies, and the conditions for each pattern, combining with the definition of backorders, i.e., dD/dt=y, we next identify the optimal path D* and the transition time points. By doing so, the optimal strategies are determined, as well as the conditions of implementing them, as presented in Proposition 2.
Proposition 2
1) If 
the optimal strategy is S for all t∈(0,T).
2) If 
the optimal strategy is C for all t∈(0,T).
3) If 
the optimal strategy is CS for all t∈(0,T).
4) If 
the optimal strategy is C-CS for all t∈(0,T), where the transition time tp1 between C and CS is given from the equation 
and D(T) is given as tp1+
.
5) If 
the optimal strategy is CS-S for all t∈(0,T), where the transition time tps1 between CS and S is given from F=αt-αT, and D(T) is given as 
6) If 
the optimal strategy is CS-C for all t∈(0,T), where the transition time is tp1, and D(T) is given as 
Proof of 1) In the use of S, we can see that y*=1-α(D/k-t). Substituting it into the state equation dD/dt=y, we have dD/dt=1-α(D/k-t). Solving this differential equation, the optimal path D* for the control model is achieved as D*=kt+k(1-k)(1-e-at/k)/a. Let t=T, the terminal state D*(T) is obtained. Considering that the condition for using S at time 0 is F<0, the result is proved based on Proposition 1. 2) and 3) can be similarly proved. 4) to 6) are directly deduced from Proposition 1 and Corollary 1.
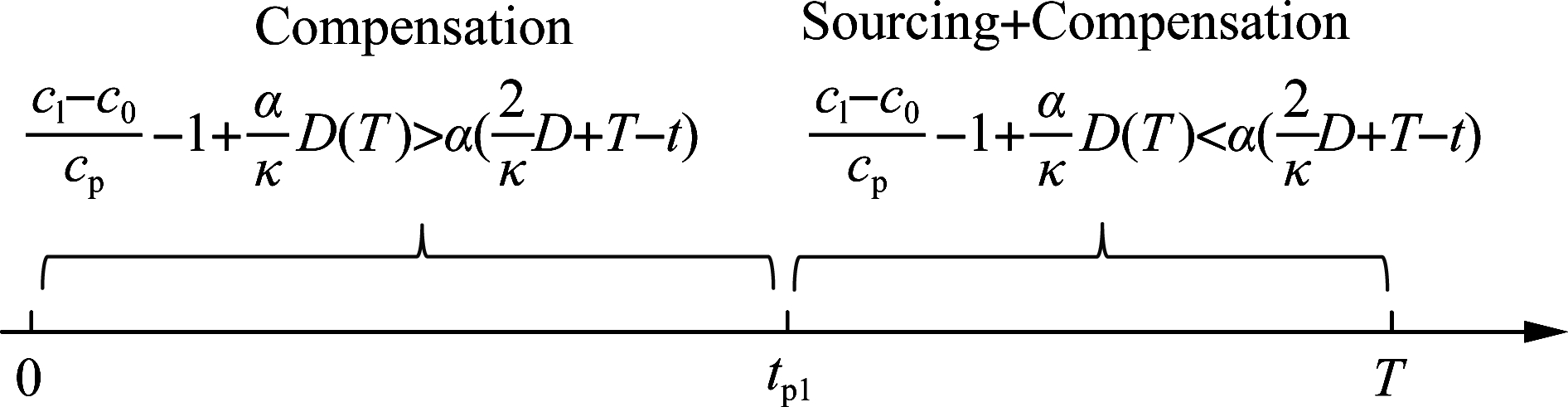
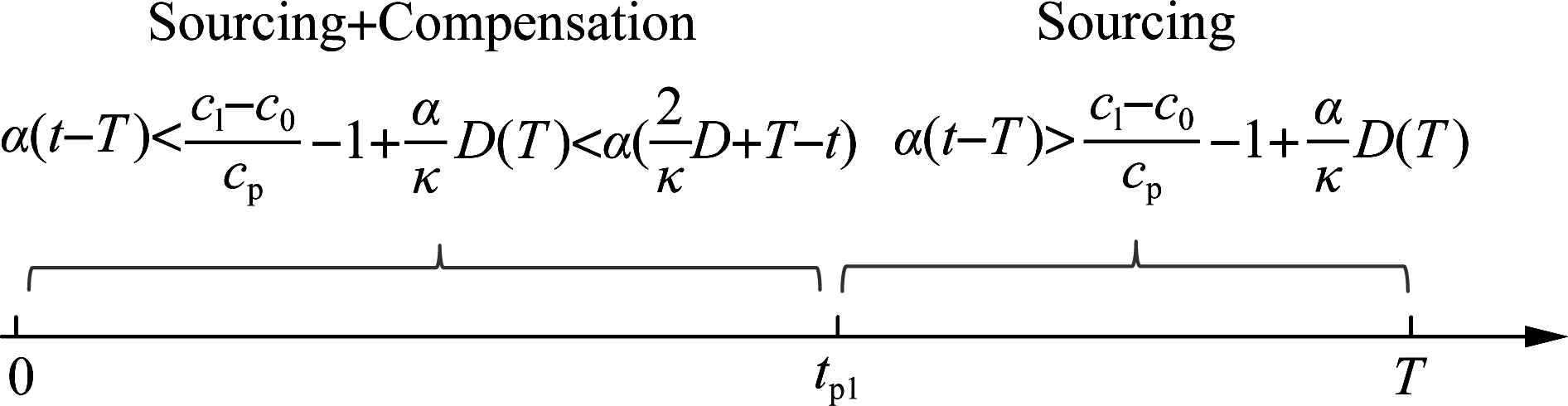
As indicated in Proposition 2, after the occurrence of the supply shortage, the optimal countermeasure of the retailer is covered in six patterns, mainly depending on the compensation cost, the length of supply disruption, and the recovery speed. If the disruption lasts a short time and the compensation cost is high, i.e., 
it is optimal that the retailer reroutes to a secondary source during the whole disruption period, that is, adopting S for all t∈(0,T). For convenience, we denote the above condition as (short T, large cp). On the contrary, if the occasion of (short T, small cp) occurs, i.e., (cl-c0)/cp-1>aT/k, strategy C that continuously compensates customers is superior over other policies. As the length of disruption becomes longer, neither pure sourcing nor pure compensation is effective. The optimal decision falls into four dynamic combined policies: CS, C-CS, CS-S, and CS-C. As stated in 3) of Proposition 2, CS that simultaneously utilizes compensation and emergency replenishments suffices to alleviate supply disruption with (medium T, small cp). The latter three strategies are advantageous to handle with long disruptions, as shown in Fig.1. C-CS represents the following decisions: purely compensating customers before using CS from time tp1. Under the adoption of CS-S and CS-C, the combined decision CS changes into pure C and S at time tps1 and tp1, respectively.
(a)
(b)
(c)Fig.1 Optimal strategies with transitions during disruption. (a) Strategy C-CS; (b) Strategy CS-S; (c) Strategy CS-C
3 Numerical Analysis
In order to visually present the optimal strategies and further shed light on the roles of the contributing factors, a numerical analysis is addressed in this section. We establish a basic set of values as follows: k=0.5, a=0.1, cl=5, c0=1, and explore how the optimal strategies change to the compensation cost cp and the disruption duration T.
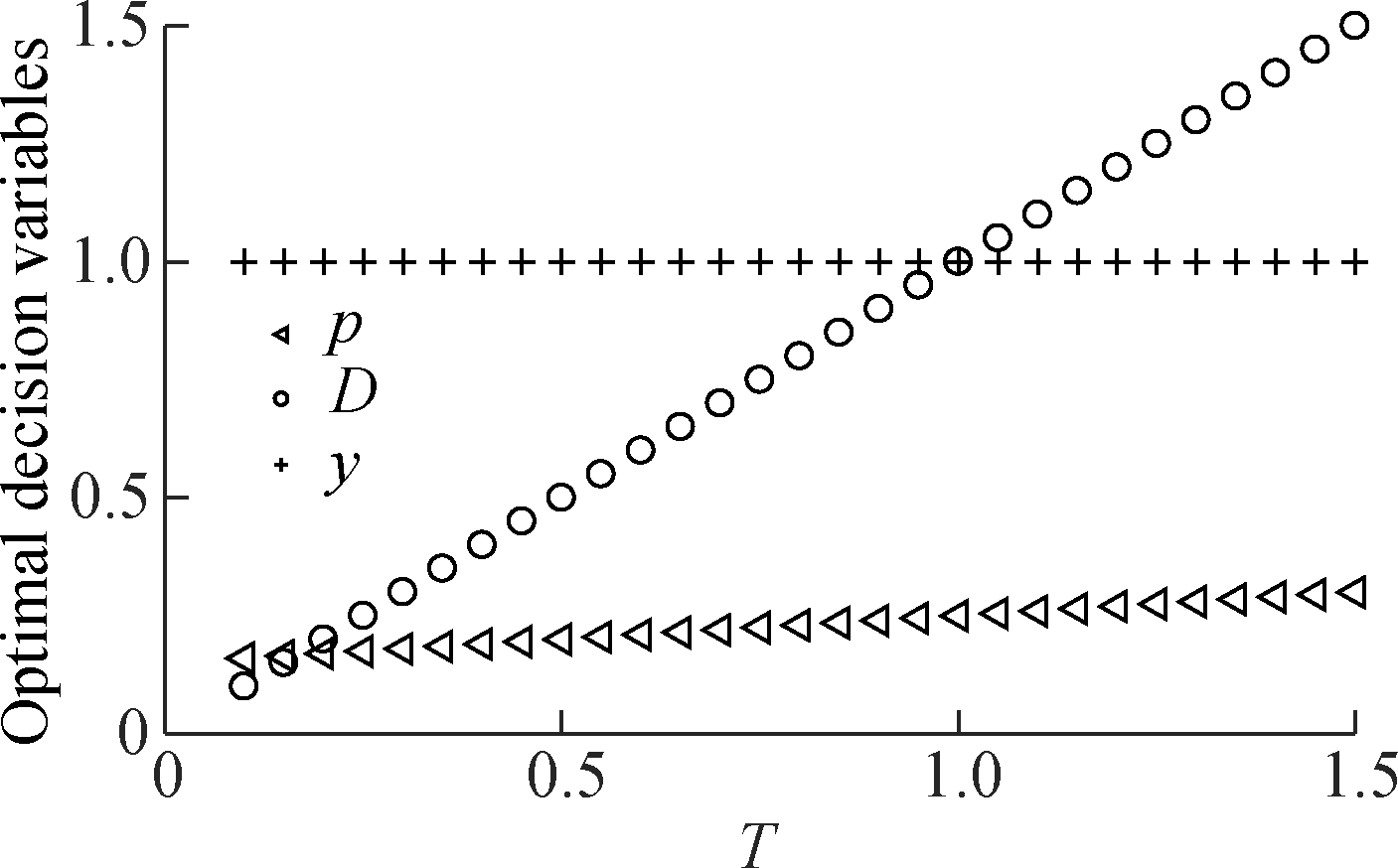
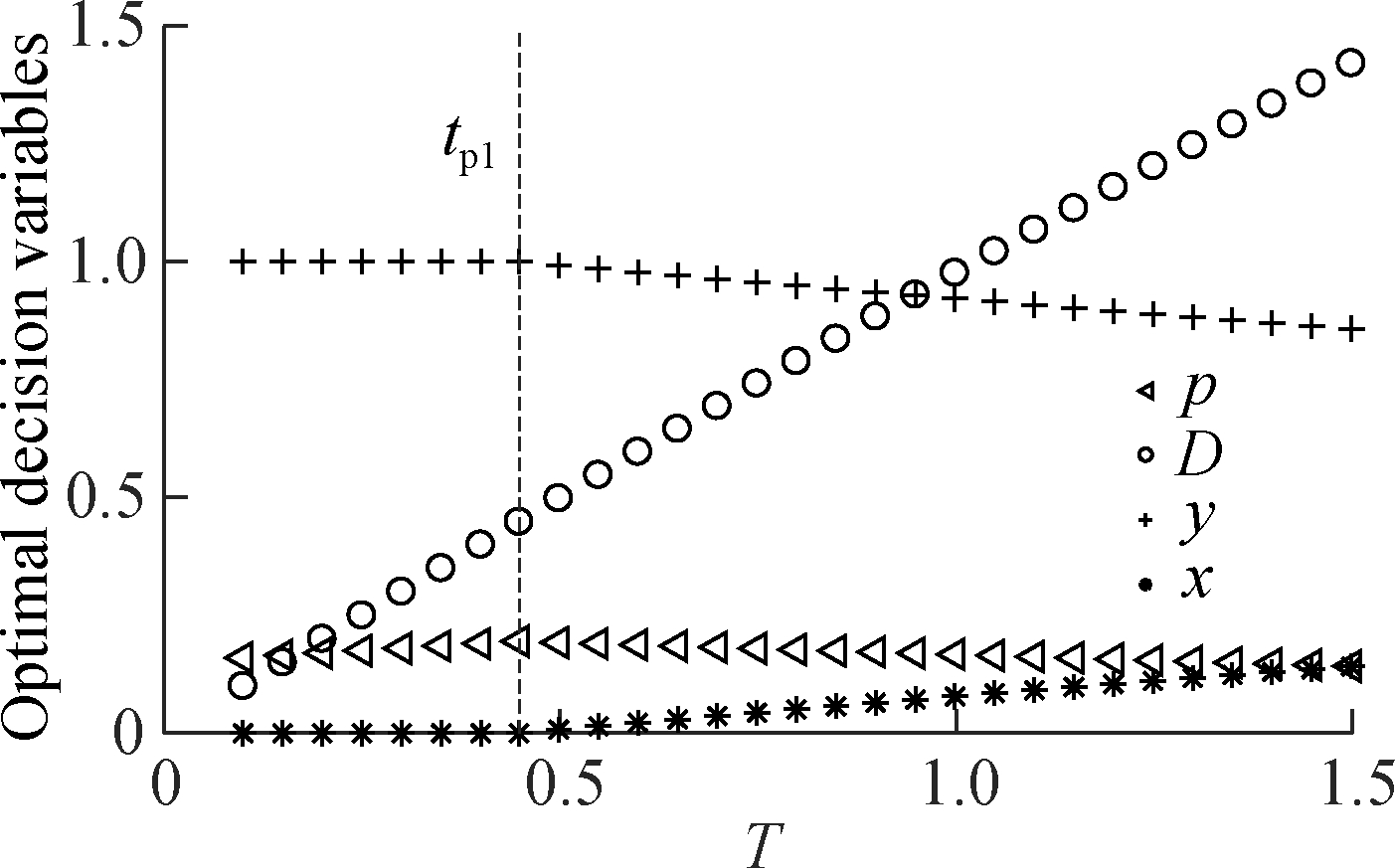
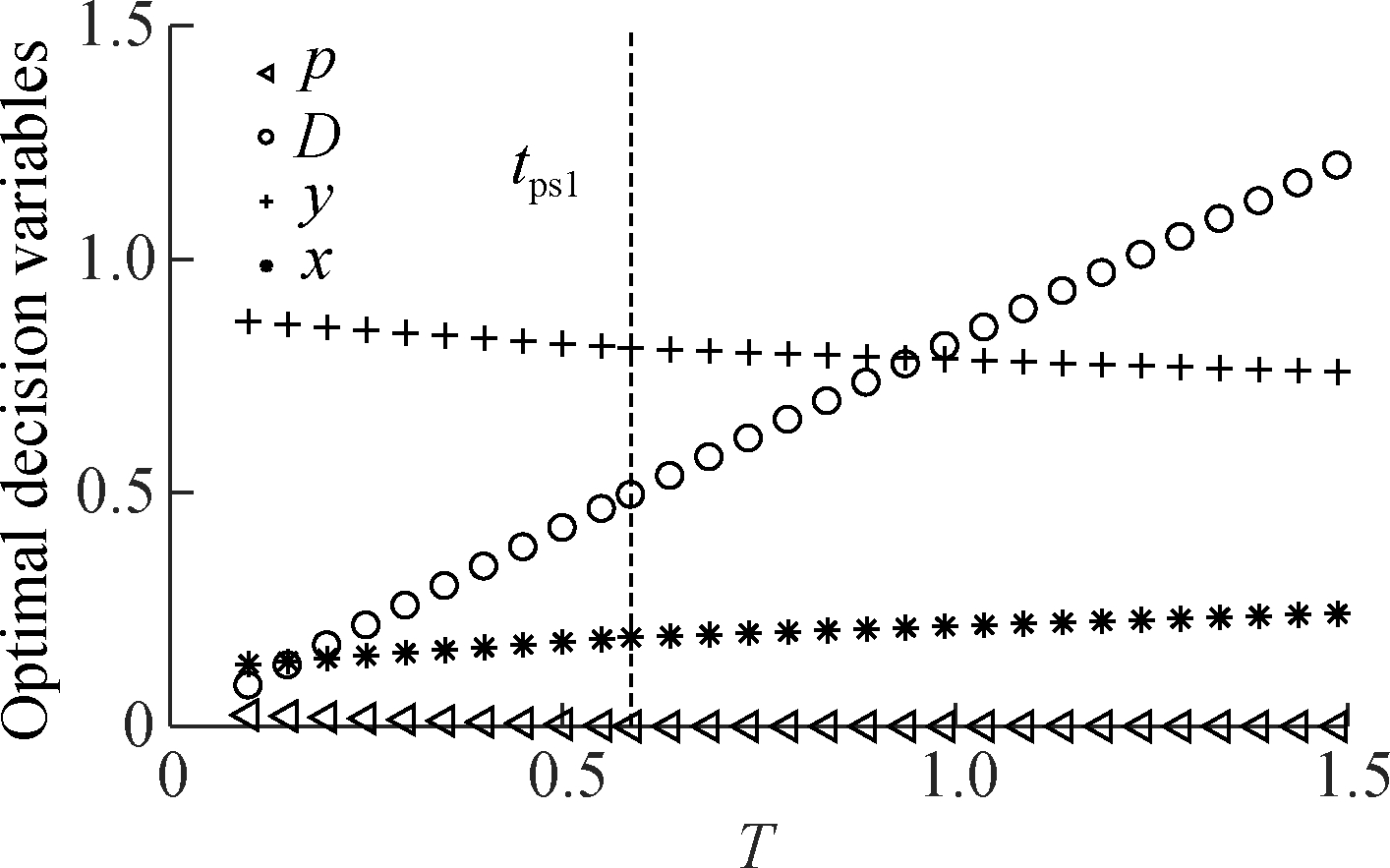
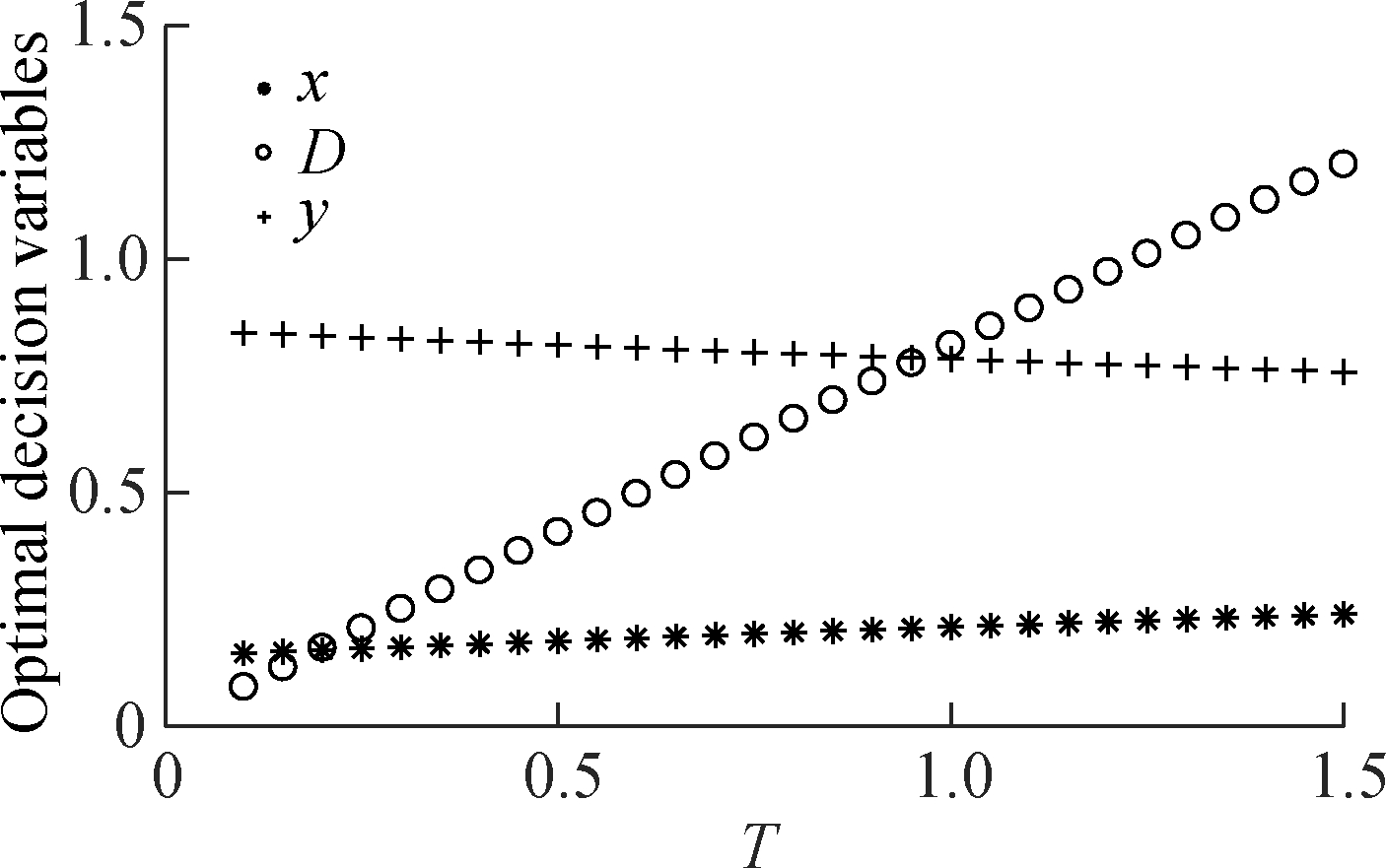
Fig.2 shows the optimal strategies for mitigating a supply shortage with the length of T=1.5, and how they change with the compensation cost cp. We observe two important managerial insights. First, after the occurrence of a short supply failure and benefitting from a favorable compensation cost (cp=2), it is optimal to provide all customers a maximum compensation p for gaining a full backorder rate, i.e., adopting a pure compensation C strategy. Note that, as the disruption continues, the maximum compensation level slightly grows over time. The reason is stated as follows. As the backlogging demand D accumulates at the rate of y=1, customers who arrive later will perceive a longer waiting time, resulting in a dropping willingness to wait automatically. In consequence, a higher compensation is required for prompting all customers to place backorders. Secondly, as cp grows, the pattern of the optimal strategies gradually evolves from C into a pure compensation-mixed policy C-CS, then a mixed policy-pure sourcing CS-C, and finally a pure sourcing S. In other words, as the advantage of compensation decreases, the time interval of implementing the alternative sourcing strategy grows. In particular, emergency procurement x should be employed to satisfy some customers from time point tp1 if cp=4, and from the beginning of the disruption if cp≥6. On the other hand, the time interval of compensation becomes shorter.
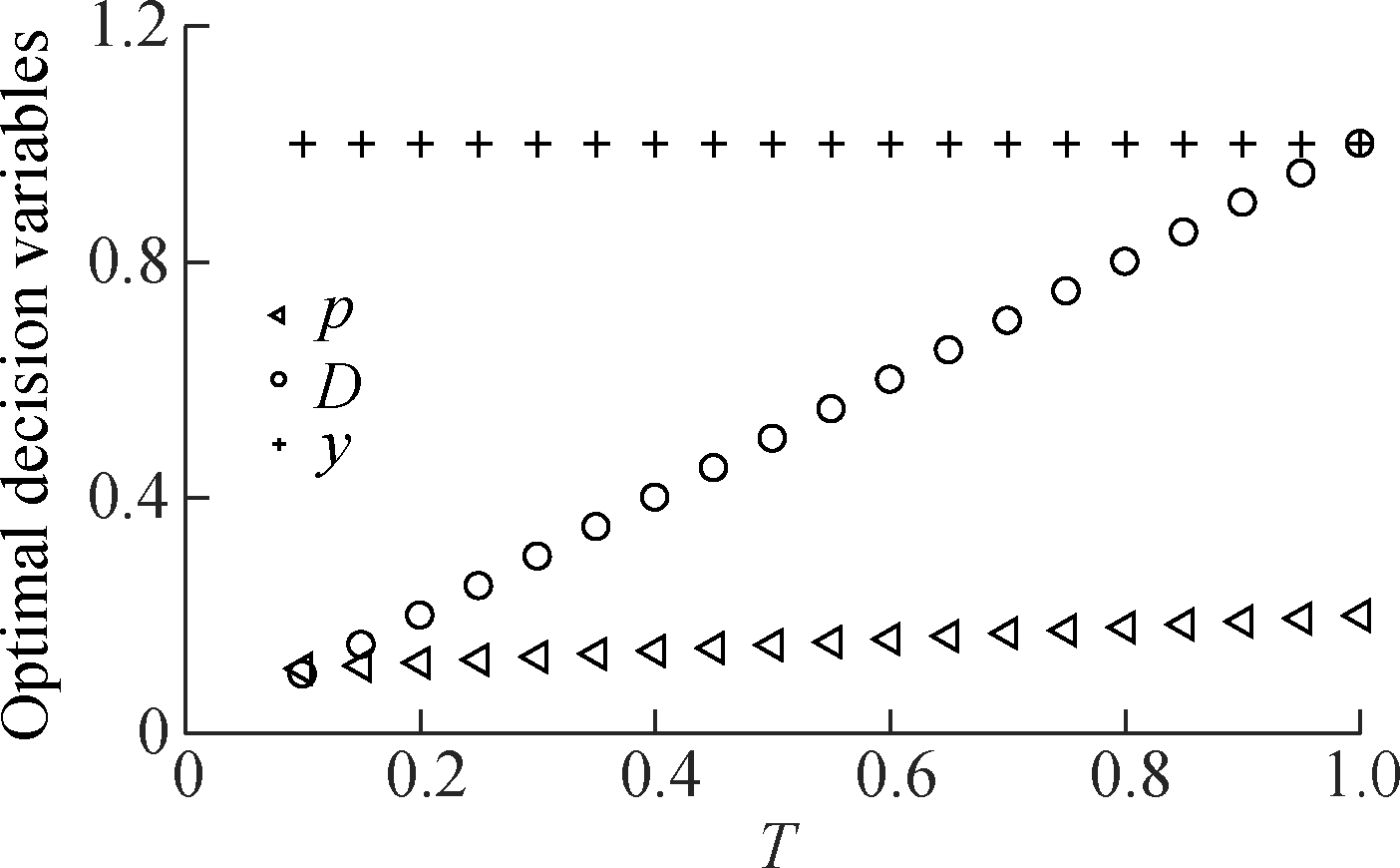
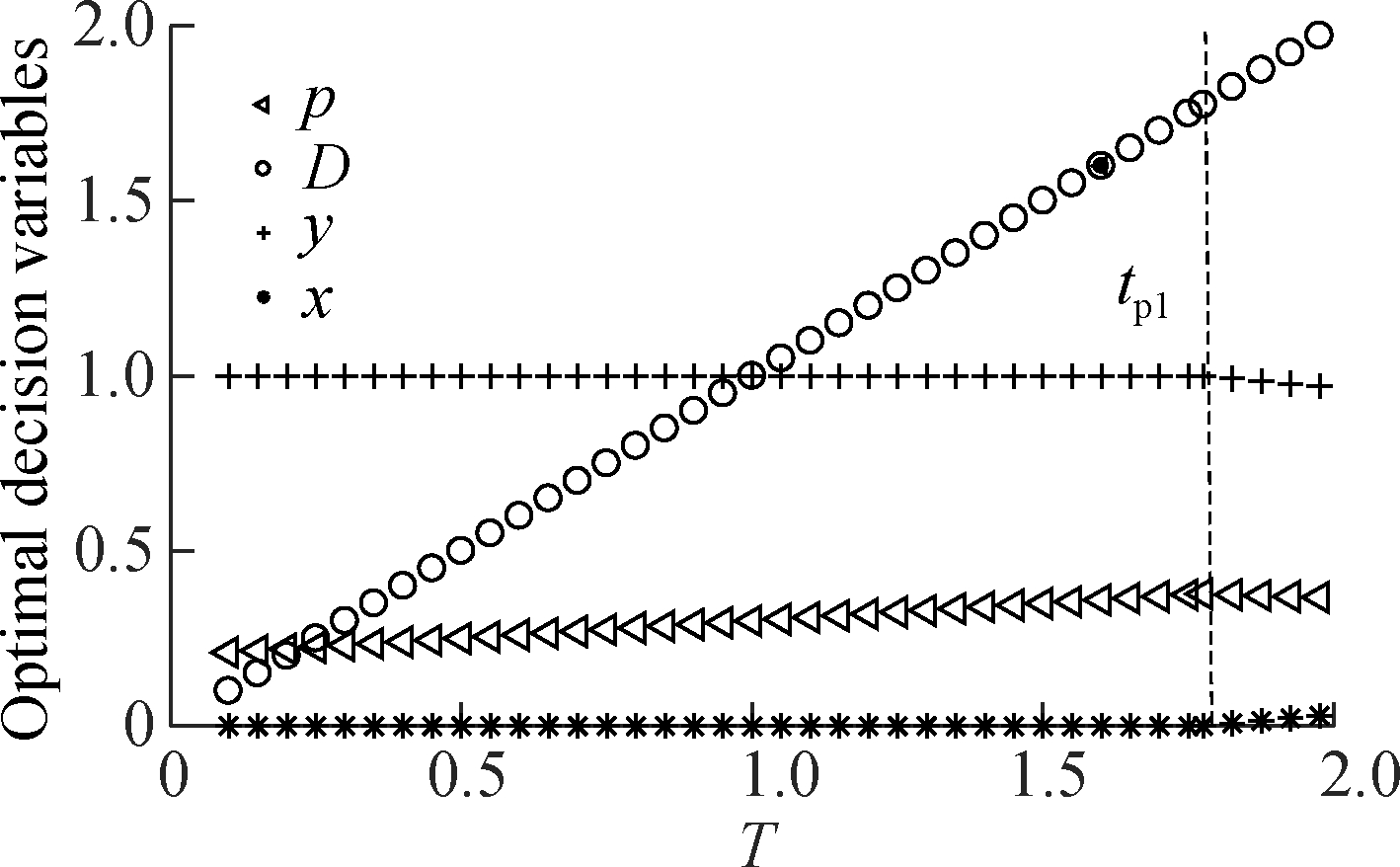
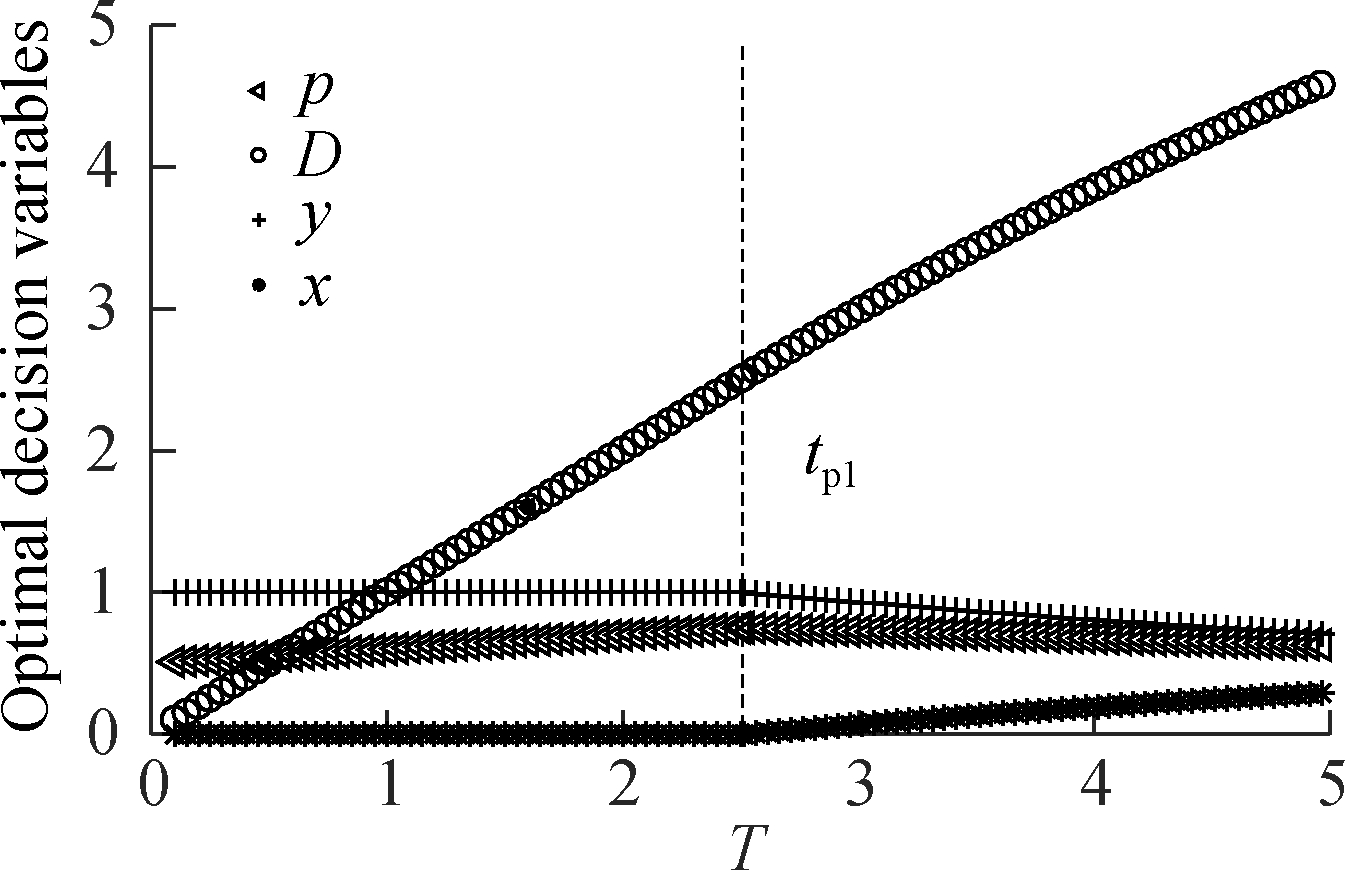
Fig.3 illustrates how optimal strategies change with the length of disruption. In the event of a low compensation cost (cp=3), purely compensating customers is sufficient to hedge against short stock-outs. However, as for long disruptions, emergency sourcing should be employed in conjunction with compensation from time tp1, i.e., taking a pure compensation-mixed policy C-CS. As the disruption becomes longer, the sourcing quantity x, as well as the corresponding time interval of using CS, are required to be longer.
(a)
(b)
(c)
(d)
Fig.2 Optimal strategies with different cp when T=1.5. (a) Strategy C under cp=2; (b) Strategy C-CS under cp=4; (c) Strategy C-CS under cp=6; (d) Strategy S under cp=8
(a)
(b)
(c)
(d)
Fig.3 Optimal strategies with different T when cp=3. (a) Strategy C under T=1; (b) Strategy C-CS under T=2; (c) Strategy C-CS under T=3.5; (d) Strategy C-CS under T=5
4 Conclusions
1) The optimal strategy to minimize the negative disruption impact during the out-of-stock period falls into six patterns: a pure sourcing, a pure compensation, a mixed policy of sourcing and compensation, a mixed policy-pure sourcing, a mixed policy-pure compensation, and a pure compensation-mixed policy. The conditions for utilizing these strategies vary from the contributing factors, e.g., compensation cost, customer sensitivity, and disruption length.
2) For short disruptions, it is sufficient to implement pure strategies during the entire out-of-stock period. If the compensation cost is small, it is preferable to purely compensate all customers for placing backorders. On the contrary, if compensation exhibits no advantage, the manufacturer should purely satisfy all the customers by seeking a secondary source along with a mark-up price, immediately after the appearance of disruption.
3) For long disruptions, the other four mixed strategies are favourable. These strategies provide practical suggestions on how to dynamically adjust the compensation level and sourcing quantity over time under different situations.
[1]Kumar M, Basu P, Avittathur B. Pricing and sourcing strategies for competing retailers in supply chains under disruption risk[J]. European Journal of Operational Research, 2018, 265(2): 533-543. DOI:10.1016/j.ejor.2017.08.019.
[2]Tang S Y, Gurnani H, Gupta D. Managing disruptions in decentralized supply chains with endogenous supply process reliability[J]. Production and Operations Management, 2014, 23(7): 1198-1211. DOI:10.1111/poms.12160.
[3]Whitney D E, Luo J, Heller D A. The benefits and constraints of temporary sourcing diversification in supply chain disruption and recovery[J]. Journal of Purchasing and Supply Management, 2014, 20(4): 238-250. DOI: 10.1016/j.pursup.2014.06.001.
[4]Su X M, Zhang F Q. On the value of commitment and availability guarantees when selling to strategic consumers[J]. Management Science, 2009, 55(5): 713-726. DOI:10.1287/mnsc.1080.0991.
[5]Tsai W C. A dynamic sourcing strategy considering supply disruption risks[J]. International Journal of Production Research, 2016, 54(7): 2170-2184. DOI:10.1080/00207543.2015.1129465.
[6]Mak H Y, Shen Z J. Risk diversification and risk pooling in supply chain design[J]. IIE Transactions, 2012, 44(8): 603-621. DOI:10.1080/0740817x.2011.635178.
[7]He B, Huang H, Yuan K F. Managing supply disruption through procurement strategy and price competition[J]. International Journal of Production Research, 2016, 54(7): 1980-1999. DOI:10.1080/00207543.2015.1074297.
[8]Chen J, Huang S, Hassin R, et al. Two backorder compensation mechanisms in inventory systems with impatient customers[J]. Production and Operations Management, 2015, 24(10): 1640-1656. DOI:10.1111/poms.12360.
[9]Snyder L V, Atan Z, Peng P, et al. OR/MS models for supply chain disruptions: A review[J]. IIE Transactions, 2016, 48(2): 89-109. DOI:10.1080/0740817x.2015.1067735.
[10]Tomlin B. On the value of mitigation and contingency strategies for managing supply chain disruption risks[J]. Management Science, 2006, 52(5): 639-657. DOI:10.1287/mnsc.1060.0515.
[11]Shao X F. Production disruption, compensation, and transshipment policies[J]. Omega, 2018, 74: 37-49. DOI:10.1016/j.omega.2017.01.004.
[12]He Y, Li S S, Xu H, et al. An in-depth analysis of contingent sourcing strategy for handling supply disruptions[J]. IEEE Transactions on Engineering Management, 2018: 1-19. DOI:10.1109/tem.2018.2868716.
[13]Ivanov D, Sokolov B. Control and system-theoretic identification of the supply chain dynamics domain for planning, analysis and adaptation of performance under uncertainty[J].European Journal of Operational Research, 2013, 224(2): 313-323. DOI:10.1016/j.ejor.2012.08.021.
[14]Li S S, He Y, Chen L J. Dynamic strategies for supply disruptions in production-inventory systems[J]. International Journal of Production Economics, 2017, 194: 88-101. DOI:10.1016/j.ijpe.2017.04.003.
[15]Shao X F, Dong M. Supply disruption and reactive strategies in an assemble-to-order supply chain with time-sensitive demand[J]. IEEE Transactions on Engineering Management, 2012, 59(2): 201-212. DOI:10.1109/tem.2010.2066280.
[16]Berkovitz L D. Optimal control theory[M]. New York: Springer Science & Business Media, 2013. DOI:10.1007/978-1-4757-6097-2.