Product upgrading accelerates greatly due to the advance in technology in many industries (e.g., mobile phones and PCs), which makes the market increasingly saturated. Many manufacturers have started to offer the trade-in program in order to encourage consumers to repeat purchasing. Under this program, consumers can get rebates when buying the new products and return the used ones. For example, the recent trade-in program that Apple provides is “Apple Trade In”. Other manufacturers, such as Huawei, Samsung and Xiaomi, have offered their own trade-in programs. At the same time, the secondhand market, especially the online market (e.g., eBay, Xianyu), grows rapidly due to the development of electronic commerce and the express industry. It becomes more convenient for consumers to sell their used products in hand through the secondhand market. Thus, when a manufacturer decides whether to implement the trade-in program, he/she should consider not only the threats from opponents’ trade-ins but also the impacts of secondhand markets. Trade-in operations therefore become more challenging.
With trade-in programs widely implemented, researchers are paying more attention to them. van Ackere and Reyniers[1] compared the effects of trade-in rebates and introductory offers on marketing durable and consumable products. Ray et al.[2] studied three pricing schemes when a monopoly manufacturer implements the trade-in program. Rao et al.[3] explored the role that trade-ins play and the motivation which drives the seller to set up a channel to facilitate trade-ins in durable goods markets. Based on two-period dynamic models with strategic consumers, Yin et al.[4-5] explored the optimal pricing decisions and characterized the conditions under which the trade-in program is beneficial without/with the up-front fee. Miao et al.[6] studied three kinds of closed-loop supply chain structures with trade-ins and analyzed the condition under which the trade-in program is beneficial to the environment. Liu et al.[7-8] investigated the optimal pricing strategy and product rollover strategy considering product innovation and strategic consumers with the trade-in program. As remanufacturing is a sustainable way to treat the collected products, the remanufacturing decision under the trade-in program is also a hot topic[9-13]. All the aforementioned studies are conducted in monopoly settings. However, only little literature focused on duopoly competition with trade-in programs, which are most related to our research. Heese et al.[14] studied the competitive advantage from taking back used products in a duopoly competition in a single period setting. Zhu et al.[15] analyzed the effect of implementing the trade-in program on the duopoly competition in a two-period setting. Both studies[14-15] did not consider product quality differentiation and they assumed that the used product has a constant salvage value for the manufacturers.
Unlike the existing research, we study the effects of the trade-in program on duopoly competition considering products quality differentiation and the secondhand market. Furthermore, the price of the used products in the secondhand market is not constant. Under the above context, we will explore the following three problems: 1) What are the impacts of trade-in programs on manufacturers? 2) What are the impacts of trade-in programs on consumers? 3) Is there any difference between the impacts when the trade-in program is implemented by different manufacturers? In order to answer these questions, we develop a game framework and analyze the impacts of the trade-in program. We find that the program shows different impacts when it is implemented by different manufacturers.
1 Problem Description and Assumptions
In the new product market, there are two manufacturers: Mh who produces high-quality product xh priced at ph, and Ml who produces low-quality product xl priced at pl. Each consumer in the new product market has a used product in hand. When purchasing a new product, the consumer will trade in the used product through manufacturers or sell it in a secondhand market. We consider that each manufacturer may or may not implement the trade-in program in the new product market. If a manufacturer implements the trade-in program, he/she will also sell the recycled used product in the same secondhand market. In our study, we will focus on four market competition scenarios:1) No manufacturer implements the trade-in program; 2) Only Mh implements it; 3) Only Ml implements it; 4) Both manufacturers implement it. Under each scenario, the decision sequence is as follows: First, Mh and Ml decide the prices of their products simultaneously, which can be seen as the Nash game; then, consumers decide whether to buy a new product (xh or xl) and trade in/sell the used product, or continue to use the used one in hand.
We make the following assumptions to describe the research problem.
Assumption 1 The size of the new product market is 1. Consumers’ willingness to pay for xh is θ and for xl is βθ (0<β<1), where θ is uniformly distributed over [0,1] and β is the value discount coefficient of the low-quality product. The marginal production costs of both products are 0.
Assumption 2 The used products of consumers in the new product market are of the same quality and each has the same perceived residual value of v (0<v<β) for its owner.
Assumption 3 The secondhand market is independent of the new product market, and the market-clearing price of used product po takes the form as po=(1-qo)v, where qo denotes the total supply of used products, similar to the assumptions in Refs.[13,16]. This price function implies that the resale price of the used product decreases in its supply and increases in residual value. This function also excludes the case that consumers just sell their used products and leave the market, because the net utility of consumers who just sells the used product is below 0. For example, consumers will not sell their smart phone unless they buy a new one.
Assumption 4 The consumer will incur a transaction cost c when a used product is sold through the secondhand market. This cost can also be thought as the hassle cost (e.g., time cost, delivery cost). For the economies of scale, we assume that the transaction cost for manufacturers to sell a used product is 0.
Assumption 5 For the existence of the transaction cost, the consumer prefers to trade in the used product when the consumer buys a new one if the manufacturer provides the trade-in program.
2 Model
In this paper, k∈{1,2,3,4} denotes four market competition scenarios. Consumers in the new product market have three options: to buy xh, buy xl or continue to use the used product. The utility of consumers buying xh is
(1)
The utility of consumers buying xl is
(2)
The utility of consumers who continue to use the used product is 
under each scenario.
Thus, the profits of Mh and Ml are
(3)
and
(4)
3 Decisions and Impacts of Trade-In Program
As each consumer in the new product market has one used product in hand, we can obtain the market-clearing price of used product 
into po=(1-qo)v, where 
Then, from Eq.(3) and Eq.(4), we have the following theorem.
Theorem 1 There exist unique equilibrium prices for Mh and Ml under the four scenarios. The expressions of the optimal prices, demands and manufacturers’ profits are given in Tab.1 and Tab.2.
Tab.1 The equilibrium prices
Scenariosp∗hp∗l1 2-c+v 1-β 4+3v-β 1-β β-2c-v 4+3v-β2 2+c-2β β+v 2-c-3β+β2 -3v2-v3 4+v-β v+β β-v 1-β -c 2+v-β 4+v-β3 2+v 1-β -c 2+v-β 4+3v-β 1+c-β β2-vβ 1-c-β -v2 4-β -3v3 4+3v-β v+β 42 1-β β+v 2-3β+β2 -3v2-v34v+v2+ 4-β β 1-β β2-v 1-β β-v2 4-β -v34v+v2+ 4-β β
Tab.2 Product demands and manufacturers’ profits
Scenariosq∗hq∗lΠ∗hΠ∗l12-c+v4+3v-β 1+v β-2c-v 4+3v-β v+β 2-c+v 2 1-β 4+3v-β 2 1+v 2c+v-β 2 1-β 4+3v-β 2 v+β 22+c-2β4+v-5β-vβ+β2 β-v 1-β -c 2+v-β 4+v-β 1-β v+β 2+c-2β 2 4+v-β 2 1-β β-v 1-β -c 2+v-β 2 4+v-β 2 1-β v+β 3 2+v 1-β -c 2+v-β 1-β 4+3v-β 1+v 1+c-β β-v 1-c-β 1-β 4+3v-β v+β 2+v 1-β -c 2+v-β 2 1-β 4+3v-β 2 1+v 1+c-β β-v 1-c-β 2 1-β 4+3v-β 2 v+β 424+v-ββ-v 4+v-β v+β 4 1-β 4+v-β 2 β-v 2 1-β 4+v-β 2 v+β
According to Heese et al.[14], we also investigate the impacts of trade-in programs from the following aspects: product demands, unit product profit margins, consumers’ net costs and manufacturers’ profits. We use 
to denote the unit profit margin of manufacturer Mi under scenario k. When Mi implements the trade in program, he/she can obtain revenue from selling the new product and the recycled used product and 
when Mi does not implement it. We use 
to denote the net costs of the consumer buying xi under scenario k. We have 
when Mi implements the trade-in program; otherwise, 
when Mi does not implement it.
Next, we assume that 
which ensures that unit profit margin and product quantity are always positive, and also guarantees that the transaction fee in the secondhand market is always below the price of the used product.
Proposition 1 The impacts of the trade-in program on product demands are: 1) 
The demand of Mh always increases when Mh implements trade-ins; and it decreases when Ml implements trade-ins. The impacts on demand of a high-quality product are similar to the results in Ref.[14]. However, the impacts on demand of a low-quality product are different. We find that the demand of xl in scenario 4 is smaller than that in scenario 1 when c is small. The reasons are as follows. First, if c is small, the saving of transaction fee will not greatly stimulate the consumption of xl when Ml implements trade-ins. When they both implement trade-in programs, Mh and Ml control the whole supply of the secondhand market since consumers prefer to trade in their used products. Since the quality of xl is lower than that of xh, Mh obtains more power than Ml to affect the secondhand market. This makes Ml become more disadvantaged in competition with Mh. Thus, if c is small, the demand of xl decreases when both manufacturers implement trade-in programs. However, when c is large, the saving of transaction fee greatly stimulates the consumption of new products due to the implementation of trade-in programs, which leads to the increase of the demand of xl in scenario 4.
Proposition 2 The impacts of the trade-in program on marginal profits of manufacturers are as follows:
The marginal profit of Mh always increases when he/she implements trade-ins and decreases when his/her rival implements trade-ins, which is similar to the result in Ref.[14]. However, for the low-quality product, we find that the unit profit margin of Ml increases when Mh implements the trade-in program if c is small, which is because the total supply of used product in the secondhand market decreases and the price of the used product increases. Under this background, when Ml does not implement trade-ins, he/she can set higher new product price as consumers can get more revenue from selling their used products; when Ml implements trade-ins, he/she can also get higher margin from selling the used products in the secondhand market. However, with the increase in c, the total supply of used product increases due to the implementation of the trade in program by Mh. Then, the used product price and the unit profit margin of Ml decrease.
Proposition 3 The impacts of the trade-in program on net costs of consumers are as follows:
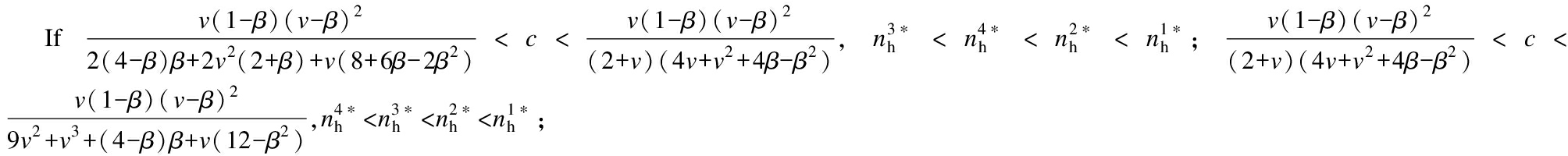
Proposition 3 shows that when Ml implements trade-ins all consumers’ net costs decrease, which is similar to the result in Ref.[14]. However, all consumers’ net costs increase when Mh implements trade-ins if c is small. The reasons are as follows. When c is small, implementing the trade-in program by Mh makes Mh have the power to affect the secondhand market since consumers prefer to trade in their used product. When Mh has more power, consumers will be more disadvantaged, and their net costs increase. With the increase in c, the saving of the transaction cost dominates the variation of consumers’ net costs and all consumers’ net costs decrease when Mh implements trade-ins. When Ml implements the trade-in program, the power he obtains to affect the secondhand market is lower than that of Mh; thus, consumers’ net costs always decrease from saving the transaction cost.
Proposition 4 The impacts of the trade-in program on manufacturers’ profits are as follows:
2) 
if 0<c<c1, 
if 0<c<c2, 
if 0<c<c3, 
Proof For the comparison between 
Since f(c) is quadratic about c, we have f(c|c=0)<0 and 
Thus, there exists unique c1 which satisfies f(c|c=c1)=0. Then, we have the result 2) of Proposition 4. Similarly, we can compare 
We omit the proofs of other results because they can be obtained by straight computation.
From Proposition 4, the profit of Mh increases when Mh implements the trade-in program; it decreases when Ml implements the program. However, the profit of Ml increases when Mh implements the trade in program if c is small. From Proposition 2, we know that the unit profit margin of Ml will increase when Mh implements trade-ins. Although the demand of xl decreases when Mh implements the trade in program, the increase of profit margin leads to the increase of the profit of Ml when c is small.
Proposition 5 For ∀k∈{1,2,3,4} and ∀i∈{l,h},
From Proposition 5, the unit product margins of both manufacturers decrease with the increase in the residual value of the used products. It is because manufacturers must lower their product prices in order to stimulate consumers to buy the new one when the used products still function well. We also find that the manufacturer’s unit marginal profit increases in the transaction cost if he/she implements the trade-in program, otherwise decreases in it. That is because consumers save the transaction cost when he/she trades in the used product for a new one. Besides, the consumers’ net cost decreases in the residual value of the used products since manufacturers set a lower new product price. We also find that consumers’ net cost increases in the transaction cost although the consumer buys the new products from the manufacturer who offers a trade-in program. We choose scenario 2 as an example. With the increase in the transaction cost, xh becomes more competitive in the competition because consumers of xh save the transaction cost. Thus, Mh can set higher price, which leads to the increase in the net costs of consumers buying xh.
4 Conclusion
In this paper, we investigate the impacts of the trade-in program on the duopoly competition considering the product quality differentiation and the existence of the secondhand market. For Mh, implementing the trade in program by Mh always benefits Mh; otherwise, implementing the trade in program by Ml always hurts the interest of Mh. However, for the low-quality manufacturer, implementing the trade-in program by Ml benefits Ml, but implementing the trade-in program by Mh can also be beneficial for Ml if the transaction cost is low enough. For the consumer, implementing the program by the low-quality manufacturer is always beneficial; however, the trade-in program implemented by the high-quality manufacturer will hurt the interest of consumers if the transaction cost is small. We also investigate the effects of the residual value and the transaction cost on the manufacturer and the consumer. The results show that the higher residual value makes the consumer incur lower net cost, but the manufacturer’s unit profit margin will decrease. With the increase in the transaction cost, the consumer will incur a higher net cost but the manufacturer who implements the trade-in program will obtain a higher unit profit margin.
[1]van Ackere A, Reyniers D J. Trade-ins and introductory offers in a monopoly[J]. The RAND Journal of Economics, 1995, 26(1): 58. DOI:10.2307/2556035.
[2] Ray S, Boyaci T, Aras N. Optimal prices and trade-in rebates for durable, remanufacturable products[J]. Manufacturing & Service Operations Management, 2005, 7(3): 208-228. DOI:10.1287/msom.1050.0080.
[3] Rao R S, Narasimhan O, John G. Understanding the role of trade-ins in durable goods markets: Theory and evidence[J]. Marketing Science, 2009, 28(5): 950-967. DOI:10.1287/mksc.1080.0461.
[4] Yin R, Tang C S. Optimal temporal customer purchasing decisions under trade-in programs with up-front fees[J]. Decision Sciences, 2014, 45(3): 373-400. DOI:10.1111/deci.12081.
[5] Yin R, Li H M, Tang C S. Optimal pricing of two successive-generation products with trade-in options under uncertainty[J]. Decision Sciences, 2015, 46(3): 565-595. DOI:10.1111/deci.12139.
[6] Miao Z W, Fu K, Xia Z Q, et al. Models for closed-loop supply chain with trade-ins[J]. Omega, 2017, 66: 308-326. DOI:10.1016/j.omega.2015.11.001.
[7] Liu J C, Zhai X, Chen L H. The interaction between product rollover strategy and pricing scheme[J]. International Journal of Production Economics, 2018, 201: 116-135. DOI:10.1016/j.ijpe.2018.03.027.
[8] Liu J C, Zhai X, Chen L H. Optimal pricing strategy under trade-in program in the presence of strategic consumers[J]. Omega, 2019, 84: 1-17. DOI:10.1016/j.omega.2018.03.005.
[9] Agrawal V V, Ferguson M, Souza G C. Trade-in rebates for price discrimination and product recovery[J]. IEEE Transactions on Engineering Management, 2016, 63(3): 326-339. DOI:10.1109/tem.2016.2574244.
[10] Shi T Q, Gu W J, Chhajed D, et al. Effects of remanufacturable product design on market segmentation and the environment[J]. Decision Sciences, 2016, 47(2): 298-332. DOI:10.1111/deci.12191.
[11] Han X H, Yang Q X, Shang J, et al. Optimal strategies for trade-old-for-remanufactured programs: Receptivity, durability, and subsidy[J]. International Journal of Production Economics, 2017, 193: 602-616. DOI:10.1016/j.ijpe.2017.07.025.
[12] Ma Z J, Zhou Q, Dai Y, et al. Optimal pricing decisions under the coexistence of “trade old for new” and “trade old for remanufactured” programs[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 106: 337-352. DOI:10.1016/j.tre.2017.08.012.
[13] Li Y J, Feng L P, Govindan K, et al. Effects of a secondary market on original equipment manufactures’ pricing, trade-in remanufacturing, and entry decisions[J]. European Journal of Operational Research, 2019, 279(3): 751-766. DOI:10.1016/j.ejor.2019.03.039.
[14] Heese H S, Cattani K, Ferrer G, et al. Competitive advantage through take-back of used products[J]. European Journal of Operational Research, 2005, 164(1): 143-157. DOI:10.1016/j.ejor.2003.11.008.
[15] Zhu X X, Wang M M, Chen G F, et al. The effect of implementing trade-in strategy on duopoly competition[J]. European Journal of Operational Research, 2016, 248(3): 856-868. DOI:10.1016/j.ejor.2015.07.053.
[16] Chang X Y, Xia H Y, Zhu H Y, et al. Production decisions in a hybrid manufacturing-remanufacturing system with carbon cap and trade mechanism[J]. International Journal of Production Economics, 2015, 162: 160-173. DOI:10.1016/j.ijpe.2015.01.020.