Abstract：The condition of an algebra to be a Hopf algebra or a Hopf (co)quasigroup can be determined by the properties of Galois linear maps. For a bialgebra H, if it is unital and associative as an algebra and counital coassociative as a coalgebra, then the Galois linear maps T1 and T2 can be defined. For such a bialgebra H, it is a Hopf algebra if and only if T1 is bijective. Moreover, 
is a right H-module map and a left H-comodule map (similar to T2). On the other hand, for a unital algebra ( no need to be associative), and a counital coassociative coalgebra A, if the coproduct and counit are both algebra morphisms, then the sufficient and necessary condition of A to be a Hopf quasigroup is that T1 is bijective, and 
at the same time (The properties are similar to T2). Furthermore, as a corollary, the quasigroups case is also considered.
An algebra (A, m) is a vector space A over a field k equipped with a map m: A⊗A→A. A unital algebra (A,m,μ) is a vector space A over a field k equipped with two maps m: A⊗A→A and μ: k→A such that m(id⊗μ)=id=m(μ⊗id), where the natural identification A⊗k≅k≅k⊗A is assumed. Generally, we write 1∈A for μ(1k).
The algebra (A,m,μ) is called associative if m(id⊗m)=m(m⊗id). It is customary to write
m(x⊗y)=xy ∀x,y∈C
A coalgebra (C,Δ) is a vector space C over a field k equipped with a map Δ:C→C⊗C. A counital coalgebra (C,Δ,ε) is a vector space C over a field k equipped with two maps Δ:C→C⊗C and ε:C→k such that (id⊗ε)Δ=id=(ε⊗id)Δ ,where the natural identification C⊗k≅k≅k⊗C is assumed.
The coalgebra (C,Δ,ε) is called coassociative if (id⊗Δ)Δ=(Δ⊗id)Δ. By using the Sweedler’s notation in Ref.[1], it is customary to write
Δ(x)=∑x(1)⊗x(2) ∀x∈C
Given acounital coalgebra (C,Δ,ε) and a unital algebra (A,m,μ), the vector space Hom(C, A) is a unital algebra with the product given by the convolution
(f*g)(x)=∑f(x(1))g(x(2))
(1)
for all x∈C, and unit element με. This algebra is denoted as C*A.
In particular, we have the algebra End(C) of endomorphisms on a given counital coalgebra (C,Δ,ε). Then, we have the convolution algebra C*End(C) with the unit element id: x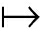
ε(x)idC. In the case that the coalgebra C is coassociative, then C*End(C) is an associative algebra.
Anonunital noncounital bialgebra (B,Δ,m) is an algebra (B,m) and a coalgebra (B,Δ) such that
Δ(xy)=Δ(x)Δ(y) ∀x,y∈B
A counital bialgebra (B,Δ,ε,m) is a counital coalgebra (B,Δ,ε) and an algebra (B,m) such that
Δ(xy)=Δ(x)Δ(y),ε(xy)=ε(x)ε(y) ∀x,y∈B
The multiplicative structure of a counital bialgebra (B,Δ,ε,m) is determined by the elements of Hom(B,End(B)):
L:B→End(B), a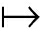La(La(x)=ax)
and
R:B→End(B), a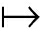Ra(Ra(x)=xa)
Obviously, it satisfies one of these maps to determine the multiplicative structure.
A unital bialgebra (B,Δ,m,μ) is a coalgebra (B,Δ) and a unital (B,m,μ) such that
Δ(xy)=Δ(x)Δ(y),Δ(1)=1 ∀x,y∈B
A unital counital bialgebra (B,Δ,ε,m,μ) is both a unital bialgebra (B,Δ,m,μ) and a counital bialgebra (B,Δ,ε,m) such that ε(1)=1.
Given aunital bialgebra (B,Δ,m,μ), we define the following two Galois linear maps[2-3]:
T1:B⊗B→B⊗B, T1(x⊗y)=Δ(x)(1⊗y)
(2)
T2:B⊗B→B⊗B, T2(x⊗y)=(x⊗1)Δ(y)
(3)
for all x,y∈B.
It is easy to check that B⊗B is a left B-module and a right B-module with the respective module structure:
a(x⊗y)=ax⊗y, (x⊗y)a=x⊗ya
for all a,x,y∈B.
Similarly, B⊗B is a left B-comodule and a right B-comodule with the respective comodule structure:
and
for all a,x,y∈B.
A Hopf algebra H is a unital associative counital coassociative bialgebra (H,Δ,ε,m,μ) equipped with a linear map S:H→H such that
∑S(h(1))h(2)=∑h(1)S(h(2))=ε(h)1
(4)
for all h,g∈H.
We have the main result of this section as follows.
Theorem 1 Let H:=(H,Δ,ε,m,μ) be a unital associative counital coassociative bialgebra.
Then, the following statements are equivalent:
1) H is a Hopf algebra;
2) There is a linear map S:H→H such that S and id are invertible to each other in the convolution algebra H*H;
3) The linear map T1:H⊗H→H⊗H is bijective, moreover, 
is a right H-module map and a left H-comodule map;
4) The linear map T2:H⊗H→H⊗H is bijective, moreover, 
is a left H-module map and a right H-comodule map;
5) The element L is invertible in the convolution algebra H*End(H);
6) The element R is invertible in the convolution algebra H*End(H).
Proof 1)⟺2). It follows Refs.[1, 4] that 1) is equivalent to 2).
2)⟺3). If 2) holds, then it follows Ref.[3] that T1 has the inverse 
defined as
for all a,b∈H.
It is not difficult to check that is a right H-module map and a left H-comodule map.
Conversely, if 2) holds, then we introduce the notation, for all a∈H.
Define a linear map S:H→H as
S(a)=(ε⊗1)∑a(1)⊗a(2)=∑ε(a(1))a(2)
That implies that, for all a∈H,
Applying (id⊗ε⊗id) to the above equation, one obtains that
Since 
is the inverse of T1 and it is a right H-module map, one can conclude that
∑a(1)⊗S(a(2))a(3)b
and
∑a(1)⊗a(2)S(a(3))b
Applying the counit to the first factor and taking b=1, we obtain Eq.(4).
Thus, S is the required antipode on H.
2)⟺4). Similarly, it follows Ref.[3] that T2 has the inverse 
given as
or all a,b∈H. Obviously, 
is a left H-module map and a right H-comodule map.
One introduces the notation, for all a∈H,
Define a linear map S′:H→H as
S′(a)=(1⊗ε)∑a[1]⊗a[2]=∑a[1]ε(a[2])
Following the program of arguments on S, we have S′ that satisfies Eq.(4).
Furthermore, we now calculate, for all a∈H,
S′(a)=∑S′(a(1))ε(a(2))=∑S′(a(1))a(2)S(a(3))=
∑ε(a(1))S(a(2))=S(a)
Therefore, we have S=S′ and they are the required antipodes on H.
1)⟺5). By hypothesis B*End(B) is an associative algebra. The element L is invertible in this algebra if and only if there exists L′:B→End(B) such that
∑L′(a(1))L(a(2))=ε(a)id=∑L(a(1))L′(a(2))
This implies that, for all a,b∈H,
∑L′(a(1))(a(2)b)=ε(a)b=∑a(1)L′(a(2))(b)
and in this case the inverse L′ is unique.
Defining S:B→B by S(a)=L′(a)(e) and taking b=1 and comparing this equation with (4), we obtain the desired result about the existence and uniqueness of S.
Similarly for 1)⟺6).
This completes the proof.
Let G be a semigroup with unit e. Then, (G,G)={(g,h)|g,h∈G} is also a semigroup with the product:
(x,y)(g,h)=(xg,yh)
for all x,y,g,h∈G.
Corollary 1 Let G be a semigroup with unit e. Then, the following statements are equivalent:
1) G is a group;
2) There is a map S:G→G such that S(g)g=e=gS(g) for all g∈G;
3) The map T1:(G,G)→(G,G),(g,h)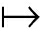(g,gh) is bijective;
4) The map T2:(G,G)→(G,G),(g,h)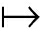(gh,h) is bijective;
5) There is a map Q:G→End(G) such that the element L:G→End(G),L(g)=Lg, for all g∈G, satisfies Q(g)(g)=e=gQ(g)(e);
6) There is a map P:G→End(G) such that the element R:G→End(G),R(g)=Rg, for all g∈G, satisfies P(g)(e)g=e=P(g)(g).
Recall from Ref.[5] that an inverse property of quasigroup (or IP loop) is defined as set G with a product, unit e and the property for each u∈G, there is u-1∈G such that
u-1(uv)=v, (vu)u-1=v ∀v∈G
A quasigroup[6] is flexible if u(vu)=(uv)u for all u,v∈G and alternative if also u(uv)=(uu)v, u(vv)=(uv)v for all u,v∈G.
It is called Moufang if u(v(uw))=((uv)u)w for all u,v,w∈G.
Recall from Ref.[7] that a Hopf quasigroup is a unital algebra H (possibly nonassociative) equipped with algebra homomorphisms Δ:H→H⊗H, ε:H→k forming a coassociative coalgebra and a map S:H→H such that
∑S(h(1))(h(2)g)=∑h(1)(S(h(2))g)=ε(h)g
(5)
∑(gS(h(1)))h(2)=∑(gh(1))S(h(2))=ε(h)g
(6)
for all h,g∈H. Furthermore, a Hopf quasigroup H is called flexible if
∑h(1)(gh(2))=∑(h(1)g)h(2) ∀h,g∈H
and Moufang if
∑h(1)(g(h(2)f))=∑((h(1)g)h(2))f ∀h,g,f∈H
Hence, a Hopf quasigroup is a Hopf algebra iff its product is associative.
Dually, we have that a Hopf coquasigroup[8] is a unital associative algebra H equipped with counital algebra homomorphisms Δ:H→H⊗H, ε:H→k and linear map S:H→H such that
∑S(h(1))h(2)(1)⊗h(2)(2)=1⊗h=
∑h(1)S(h(2)(1))⊗h(2)(2)
(7)
∑h(1)(1)⊗S(h(1)(2))h(2)=h⊗1=
∑h(1)(1)⊗h(1)(2)S(h(2))
(8)
for all h∈H. Furthermore, a Hopf coquasigroup H is called flexible if
∑h(1)h(2)(2)⊗h(2)(1)=∑h(1)(1)h(2)⊗h(1)(2) ∀h∈H
and Moufang if
∑h(1)h(2)(2)(1)⊗h(2)(1)⊗h(2)(2)(2)=
∑h(1)(1)(1)h(1)(2)⊗h(1)(1)(2)⊗h(2) ∀h∈H
Let (A,m,μ) be a unital algebra. Assume that T:A⊗A→A⊗A is a map. Then, we can define the following two coproduct maps:
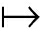T(a⊗1)
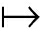T(1⊗a)
Definition 1 With the above notation, we say that T is left (resp. right) compatible with 
for all a,b∈A.
Similarly, one says that T is left (resp. right) compatible with 
for all a,b∈A.
Dually, let (C,Δ,ε) be a counital coalgebra. Let T:A⊗A→A⊗A be a map. Then, one can define the following two product maps:
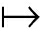(1⊗ε)T(a⊗b)
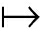(ε⊗1)T(a⊗b)
Definition 2 With the above notation, we say that T is left (resp. right) compatible with 
for all a,b∈A.
Similarly, one says that T is left (resp. right) compatible with 
(resp. 
for all a,b∈A.
We now have the main result of this section as follows.
Theorem 2 Let H:=(H,Δ,ε,m,μ) be a unital counital coassociative bialgebra. Then, the following statements are equivalent:
1) H is a Hopf quasigroup.
2) The linear map T1,T2:H⊗H→H⊗H is bijective, and 
At the same time, the map T2:H⊗H→H⊗H is bijective. Moreover, 
3) The elements L and R are invertible in the convolution algebra H*End(H).
Proof 1)⟺2). If (2) holds, similar to Theorem 1, it is easy to check whether T1 has the inverse 
for all a,b∈H. Then, we have
a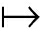
a⊗b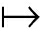
It is not difficult to check whether 
Conversely, if (2) holds, then, we define a linear map S:H→H as
Since 
one has, for all a,b∈H,
∑a(1)⊗S(a(2))b
Since is the inverse of T1, we can conclude that
∑a(1)⊗a(2)[S(a(3))b]=T1(∑a(1)⊗S(a(2))b)=
Applying the counit to the first factor, we can obtain Eq.(5). We define another linear map S′:H→H as
Similar to discussing S, we can obtain Eq.(6). By doing some calculation, we have
S(a)=∑S(a(1))ε(a(2))=∑[S(a(1))a(2)]S′(a(2))=
∑ε(a(1))S′(a(2))=S′(a)
for all a∈H.
Thus, H is a Hopf quasigroup.
1)⟺3). Similar to 1)⟺5) and 1)⟺6) in Theorem 1, it is not difficult to complete the proof.
This completes the proof.
Corollary 2 Let G be nonempty with a product and with unit e. Then, the following statements are equivalent:
1) G is a quaigroup;
2) There is a map S:G→G such that S(g)(gh)=h=(hg)S(g) for all g,v∈G;
3) The map T1:(G,G)→(G,G),(g,h)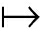(g,gh) is bijective;
4) The map T2:(G,G)→(G,G),(g,h)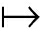(gh,h) is bijective;
5) There is a map Q:G→End(G) such that the element L:G→End(G),L(g)=Lg, for all g,h∈G, satisfies Q(g)(g)h=h=hgQ(g)(e);
6) There is a map P:G→End(G) such that the element R:G→End(G),R(g)=Rg, for all g∈G, satisfies P(g)(e)(g)h=h=P(g)(gh).
[1]Sweedler M E. Hopf algebras[M]. New York:W.A.Benjamin, 1969.
[2]Voigt C.Bornological quantum groups[J]. Pacific Journal of Mathematics, 2008, 235(1): 93-135. DOI:10.2140/pjm.2008.235.93.
[3]van Daele A. Multiplier Hopf algebras[J]. Transactions of the American Mathematical Society, 1994, 342(2): 917-932. DOI:10.1090/s0002-9947-1994-1220906-5.
[4]Montgomery S.Hopf algebras and their actions on rings[M]. Providence, Rhode Island: American Mathematical Society, 1993. DOI:10.1090/cbms/082.
[5]Albert A A. Quasigroups. Ⅰ[J]. Transaction of the American Mathematical Society, 1943,54: 507-519.
[6]Alonso 
lvarez J N, Fernández Vilaboa J M, González Rodríguez R, et al. Projections and Yetter-Drinfel’d modules over Hopf (co)quasigroups[J]. Journal of Algebra, 2015, 443: 153-199. DOI:10.1016/j.jalgebra.2015.07.007.
[7]Klim J, Majid S. Hopf quasigroups and the algebraic 7-sphere[J]. Journal of Algebra, 2010, 323(11): 3067-3110. DOI:10.1016/j.jalgebra.2010.03.011.
[8]Brzeziński T, Jiao Z M. Actions of Hopf quasigroups[J]. Communications in Algebra, 2012, 40(2): 681-696. DOI:10.1080/00927872.2010.535588.
摘要：一个代数构成Hopf代数或Hopf(余)拟群的条件可由Galois线性映射的性质来确定.对于一个双代数H, 如果其作为代数是结合有单位的, 且作为余代数是余结合有余单位的,则可以定义Galois线性映射T1和T2.对于一个结合余结合的双代数H(有单位和余单位),则H为一个Hopf代数当且仅当Galois线性映射T1是双射,且进一步地,
是右H-模和右H-余模映射.另一方面, 对于一个有单位的代数A(不一定是结合的), A作为余代数是余结合有余单位的, 如果A的余乘法和余单位均为代数同态, 则A为一个Hopf拟群当且仅当 Galois线性映射T1是双射且与右余积映射
左相容,同时与左积映射
右相容(相似的性质也适用于Galois线性映射T2).作为推论, 拟群的情形也得到了讨论.