With the standardization of web ontology language (OWL)[1] and rapid development of knowledge graphs[2], a large number of ontologies are available online and often evolve over time in many real-world applications[3]. For instance, in the fields of ontology-driven knowledge management and e-commerce, ontologies may keep growing or changing with the development of a knowledge base and the modification of productions. When new information is received, an original ontology needs to be revised for incorporating newly received information consistently. Generally, logical inconsistency consists of inconsistency and incoherence. An ontology is inconsistent if and only if it has no model; i.e., it is inconsistent in the first-order sense. An ontology is incoherent if and only if there is some unsatisfiable concept which is interpreted as an empty set. As reasoning with inconsistent ontologies produces meaningless results, handling inconsistencies in OWL ontologies is an important task. In this paper, the attention is focused on revising incoherent OWL ontologies since inconsistency is always caused by adding instances of unsatisfiable concepts or relations to an ontology.
So far, researchers have proposed various approaches for revising OWL ontologies by deleting some axioms. Qi et al.[4] proposed a kernel revision operator based on the well-known AGM framework[5] to deal with incoherence in description logic (DL) ontologies, where DL is the underlying semantics of OWL. They provided practical algorithms based on the hitting set tree algorithm by considering the weights or frequency of axioms. Similarly, Golbeck et al.[6] also adopted the kernel revision operator and incision functions, but their goal is to deal with inconsistency by considering trust information. Due to the issue of computational efficiency[7], such works often focus on theoretical work and lack efficient algorithms. To improve efficiency, Fu et al.[8] proposed a graph-based approach to revising DL-Lite ontologies by transforming an ontology to graphs and then locating incoherence. Besides, many researchers also defined fine-grained revision operators to only remove or modify part of an axiom. Qi and Du[9] proposed to revise DL terminologies through adapting the Dalal revision operator defined in propositional logic and using the notion of concept forgetting. Zhuang et al.[7,10] defined a new semantics, called type semantics, instead of standard DL semantics to revise DL-Lite TBoxes. One recent work defined a typicality-based revision of an ALC knowledge base to deal with exceptions by adding explicit exceptions to weaken inconsistencies[11].
From the claims above,it can be seen that many approaches are designed for less expressive DLs like DL-Lite and ALC, especially those fine-grained ones, while they seldom consider (partly) priority information. However, in many cases like ontology merging or user-defined priority, a partial order is usually available and these approaches cannot be applied directly[12]. For example, two source ontologies and their mappings may be generated by different tools and thus weights associated with axioms in different ontologies or mappings are incomparable. In addition, many knowledge bases have been constructed and their fusion may also face the problem of partial order[13]. More importantly, a partial order provides an easy and useful way for users to manually assign different priorities to axioms.
In this paper,a kernel revision operator for partially ordered OWL ontologies is defined and efficient algorithms based on integer linear programming (ILP) are proposed. Note that, ILP is an optimization problem of maximizing or minimizing a linear objective function. Due to their high efficiency, ILP-based models have been widely used in many tasks in the semantic web such as in fuzzy ontology reasoning[14], ontology matching[15] and knowledge base embeddings[16]. In particular, our recent work[17] applied ILP to resolve logical contradictions in single ontologies, which is different from the current work because the latter is more general and considers stratified and multiple ontologies. It is challenging to redefine ILP-based models for revising stratified ontologies. In the experiments, a comprehensive evaluation is conducted over various ontologies to show the high efficiency of applying our ILP-based model. The efficiency and effectiveness of our adapted algorithm are also analyzed for stratified ontologies.
1 Preliminaries
In this section, key notions of logical inconsistency and integer linear programming are provided and they are used to revise ontologies. The readers are assumed to be familiar with description logics (DLs)[18].
1.1 Logical inconsistency
To deal with incoherence in DL ontologies, minimal sets of axioms for explaining logical contradictions are often required to be computed first and then a solution of axioms can be generated such that removing these axioms can resolve the contradictions. In the following, the key concepts of such minimal sets are provided.
Definition 1(MUPS)[12] Let U be an unsatisfiable concept in an ontology O. A sub-ontology O′ of O is a minimal unsatisfiability-preserving sub-ontology (MUPS) w.r.t. U if U is unsatisfiable in O′ and satisfiable in every sub-ontology O″
O′.
A MUPS of O w.r.t. U is a minimal sub-ontology of O in which U is unsatisfiable. MUPS are useful to relate sets of axioms with unsatisfiability of specific concepts. We use MUPS to indicate a MUPS or multiple ones for conciseness. To relate sets of axioms to the incoherence of an ontology in general, a minimal incoherence-preserving sub-ontology is defined.
Definition 2(MIPS) Let O be an incoherent ontology. An ontology O′
O is a minimal incoherence-preserving sub-ontology (MIPS) of O if O′ is incoherent and every sub-ontology O″O′ is coherent.
A MIPS of O is a minimal incoherent sub-ontology of O. Note that a MIPS must be a MUPS, but not vice versa. In the following, both the original ontology and the newly arrived one are assumed to be individually coherent and consistent but their merging produces incoherence.
1.2 Integer linear programming
Linear programming formulates our real-life problem into a mathematical model. A linear program is an optimization problem of maximizing or minimizing a linear objective function of variables that are subject to a set of constraints expressed as linear equations or inequations[17]. An integer program forces the variables in a linear program to be integers and is referred to integer linear programming (ILP)[19].
To resolve inconsistency by deleting a set of selected axioms, pure 0-1 ILP is used and its variables can only have a value of 0 or 1. If an axiom should be deleted, its associated variable should have a value of 1, and 0 otherwise. Specifically, given n variables and m linear constraints, the problem of 0-1 ILP is to find an assignment of either 0 or 1 for the variables such that all constraints are satisfied. A 0-1 ILP optimization problem can be stated in the standard form[19]:
(1a)
(1b)
xj∈{0,1}
(1c)
where i=1,2,…,m and j=1,2,…,n. wj and aij are coefficients and b is an integer. The values of wj, aij and b are determined by specific application scenarios.
The objective function (1a) describes a criterion (or a measure) that we wish to minimize (e.g., cost) or maximize (e.g., profit). The limitations that restrict our choices for decision variables are described using mathematical constraints (1b). In many practical problems, people’s decisions are often restricted by the limitations like resource limitations and physical, strategic or economical constraints. It is noted that the complexity of solving an ILP problem is NP-complete and it depends on the number of variables[20].
2 Kernel Revision Operator
Inspired by our previous work[12], the general case of an original ontology O is considered as O=OS∪OT, where OS and OT indicate the stable part and removable part, respectively. The main difference between their stratification and ours is that axioms in OS are assumed to be more reliable than those in OT and both of them are removable. We try to remove those less reliable axioms first. In this way, users can freely assign different priorities to axioms by available or user-defined priorities.
Partially ordered ontologies can be formally defined as below.
Definition 3 (partial ordered ontologies)[12] A partially ordered ontology is a pair (O, ≼), where ≼ is a partial order over axioms in O and satisfies the condition: For any axiom φ∈OS, there exists ψ
φ for all ψ∈OT, where ψφ denotes ψ≼φ but φ≼ψ.
That is, any axiom in OS should be preferred to all axioms in OT. When ψφ, this means that φ is preferred to ψ w.r.t. ≼. In addition, ψ≃φ is used to denote ψ≼φ and φ≼ψ, which indicates that ψ is equal to φ w.r.t. ≼.
Definition 4 (conflict)[4] Let O and On be two coherent ontologies. A conflict M of O w.r.t. On is a sub-ontology of O and satisfies that M∪On is incoherent; and ∀M′M, M′∪On is coherent.
This definition is similar to the notion of a minimal axiom set consisting of a static part and a rebuttal part[21], which can be considered as a kernel. If On is empty, a conflict becomes a MUPS or MIPS as defined in Section 1.1.
Definition 5 (conflict stratification) Assume that there is a partially ordered OWL ontology (O,≼), where O=OS∪OT is incoherent w.r.t. a newcomer ontology On. Given a conflict M of O w.r.t. On, a simple stratification of M is a partition (M, 
where M={φ∈M∩OT: ∃ψ∈M, ψφ} if M∩OT≠∅ (∅ is an empty set) and M ={φ
M: ∃ψ∈M, ψφ} otherwise. Besides, 
M.
In this definition, M and 
are called the lower and upper stratum of M, respectively. If some axioms in M belong to OT, all axioms in M should belong to OT and have the least priority w.r.t. ≼. Otherwise, M consists of those axioms in M that have the least priority w.r.t. ≼. Different from the previous definition of stratification[12], M is allowed to contain axioms from OS as a general consideration. Namely, all axioms in O are removable but have different priorities. According to Definition 5, M ≠∅ can be obtained.
Inspired by the work of kernel revision[4], an incision function is defined below to select axioms from each conflict for removal.
Definition 6 (incision function) Assume that there is a partially ordered ontology (O, ≼), where O=OS∪OT is incoherent w.r.t. a newly coming ontology On. Given a set of conflicts FOn(O) of O w.r.t. On, an incision function σ for O can be defined as a function (σ: 22O→2O) such that
Condition 1 σ(FOn(O)) ∪M∈FM, F=FOn(O);
Condition 2 If M∈FOn(O), then M∩σ(FOn(O))≠∅.
This function means only axioms from a conflict can be selected (see Condition 1) and at least one axiom should be selected from each conflict (see Condition 2). Obviously, this function is an incision function defined by Qi et al[4]. Note that, if FOn(O) contains all the MIPS of O, removing the axioms in σ(FOn(O)(O)) from O can make O coherent.
Based on an incision function, a revision operator can be defined for incorporating a new ontology consistentlybased on all the MIPS.
Definition 7 (kernel revision operator)[4] Let O be an ontology to be revised and σ be an incision function for O. The kernel revision operator 
σ for O is defined as follows. For each newly received ontology On,
OσOn=(O\σ(MIPSOn(O))∪On
According to the operator, the resulting ontology becomes coherent after removing those axioms selected by the incision function.
Algorithm 1 Incision function based on ILP
Input: O=OS∪OT, On and FOn(O) w.r.t. On.
Output: A set of axioms to remove
1 Sunion=∪M∈FM, F=FOn(O)
2 X={xj|φj∈Sunion, j=1,2,…, |Sunion|}
4 for (M∈FOn(O)) {
5 if (M∩OT≠∅) then M={φ∈M∩OT: ∃ψ∈M, ψ
φ}
6 else M={φ∈M: ∃ψ∈M, ψφ}
7 Xm={xj|φj
M, xj∈X}
9 C=C∪{ci}
10 }
11 Sassi=ILP_Solver(z, C, min)
12 σ1(FOn(O))={φj|(xj=1)∈Sassi}
13 return σ1(FOn(O))
To define a specific incision function, the ILP model is applied instead of traditional methods using the hitting set tree algorithm[4]. We use the ILP model due to its high efficiency and flexible framework to select axioms and minimize the number of selected axioms. Algorithm 1 defines such an incision function based on ILP. It removes as few axioms as possible and chooses axioms from the lower stratum first. This algorithm consists of the following three parts:
First, an object function can be constructed. In Algorithm 1, a decision variable xj is first associated with each axiom φj in the union of all given conflicts (i.e., Sunion) since only axioms appearing in conflicts can be removed (see Lines 1 and 2), where j indicates the position of an axiom in Sunion. To define an objective function z (see Eq.(1a)), the coefficient of each variable is set to be 1 (see Line 3) and all axioms are assumed to be equally important. In this way, minimizing z is actually to minimize the number of axioms to be removed.
Secondly, constraints can be constructed. A constraint is constructed for each conflict (see Lines 4 to 10). Specifically, for each conflict M, M is first computed (see Lines 5 and 6) according to Definition 5. Then, the variables corresponding to axioms in M are obtained and their sum is set to be no less than 1 (see Lines 7 and 8). That is, all variables associated to axioms in M are assigned to be 0 and at least one variable in XM will be assigned to be 1. This is to ensure that at least one axiom from M can be included in the final solution.
Thirdly, a solution can be computed. Based on objective function z and constraints C, the function ILP_Solver (z, C, min) is utilized to apply a traditional ILP solver like Cplex (https://www.ibm.com/analytics/cplex-optimizer) for finding an optimal assignment to all variables under constructed constraints (see Line 11). The parameter min indicates minimizing objective function z. Finally, a solution of axioms is found and each variable of such an axiom has a value of 1 in the found assignment (see Line 12).
Proposition 1 Algorithm 1 computes an incision function σ1.
Proof We prove that σ1 is an incision function according to the conditions given in Definition 6.
From Algorithm 1, it can be seen that σ1(FOn(O)) is obtained according to the assignment Sassi, each of whose elements corresponds to an axiom in the union of FOn(O). Clearly, σ1(FOn(O))∪M∈FM, F=FOn(O).
According to the definition of M (see lines 5 and 6), we know that M is not empty if M is not empty. Besides, the constructed constraint ci requires that at least one of these variables should be assigned to be 1. If such an assignment can be found by applying an ILP solver, it means that each constraint ci has been satisfied and at least one axiom from M is selected. Namely, σ1(FOn(O))∩M≠∅.
Based on a specific incision function, a straightforward revision algorithm (see Algorithm 2) can be proposed to apply the function directly on all MIPS as shown in Definition 7. In our work, the incision function defined in Algorithm 1 is used. Besides, the commonly used method is adopted to compute MIPS based on all MUPS of all unsatisfiable concepts (see Lines 3 to 11).
Algorithm 2 Algorithm to revise a stratified ontology
Input: O=OS∪OT and On.
Output: A revised coherent ontology.
1 M=∅
2 MMIPS=∅
3 Uall =All unsatisfiable concepts in O w.r.t. On
4 for (U∈Uall) {
5 MU=All MUPS of O w.r.t. On and U
6 M=M∪MU
7 }
8 for (M1∈M) {
9 if(∃M2∈M such that M2
M1) then
10 MMIPS=MMIPS∪{M1}
11 }
Since computing MIPS is often very expensive, especially for those large ontologies or ontologies containing many conflicts, an adapted revision algorithm (see Algorithm 3) is provided to handle unsatisfiable concepts one by one. For each unsatisfiable concept U, it is necessary to check whether it is still unsatisfiable in the current ontology O which may have been changed (see Line 4). If U is still unsatisfiable, all MUPS in O w.r.t. On and U need to be computed (see Line 5) and then an incision function is used to select axioms from these MUPS. Finally, ontology O becomes coherent w.r.t. On after removing all selected axioms.
Algorithm 3 Adapted algorithm to revise a stratified ontology
Input: O=OS∪OT and On.
Output: A revised coherent ontology.
1 S=∅
2 Uall =All unsatisfiable concepts in O w.r.t. On
3 for (U∈Uall) {
4 if (O∪On
=U⊆
) then {
5 MU=All MUPS of O w.r.t. On and U
6 S=S∪σ(MU)
7 O=O\S
8 }
9 }
3 Experimental Results
Our evaluation is performed on a laptop with 2.4 GHz Intel(R) Core(TM)2 Duo CPU and 8.0 GB of RAM using 64 bit operating system Windows 7. The maximum heap space is set to be 6 GB. The relevance-based ontology debugging algorithm[22] is adopted to compute conflicts.
3.1 ILP-based algorithm vs. HST-based one
First of all, to see the efficiency of applying ILP, our ILP-based algorithm (namely Algorithm 2 with Algorithm 1 as an incision function, marked as Alg2) is compared with a commonly used algorithm based on the hitting set tree (HST)[4] (maked as Hst). Hst applies the HST algorithm directly on the conflicts to be resolved and satisfies the minimal change principle. We do not compare with some other efficient algorithms for revising OWL ontologies, such as graph-based or new semantics-based ones, since they are often designed for a specific DL ontology.
The data set consists of 6 ontologies with different numbers (i.e., from 10 to 15) of MUPS that do not share any axioms and each MUPS includes 7 axioms. Such a construction generating MUPS without overlapping axioms is more challenging to handle than those with overlapping axioms. In this way, each MUPS is also a MIPS. To concentrate on showing the efficiency of using ILP or HST, repairing single ontologies is also considered by setting On=∅ and all axioms in the ontologies are removable.
Fig.1 presents the experimental results, where the number in x-axis indicates the number of MIPS. In this figure, only the revision time is shown without the time to compute MIPS since both algorithms worked on the same sets of MIPS. From the figure, it can be observed that, Alg2 performs much better than Hst and often spends no more than 300 ms to finish each revision process. As for Hst, its revision time increases quickly when the number of MIPS increases. For example, it spends 13 and 919 s for the ontologies including 10 and 12 MIPS, respectively. For those ontologies containing more than 12 MIPS, Hst failed to finish each revision process within the limited time (i.e., 1 000 s). This is because constructing a HST is very time-consuming, especially when the MIPS are uncorrelated. ILP provides a mathematical method and can achieve very high efficiency.
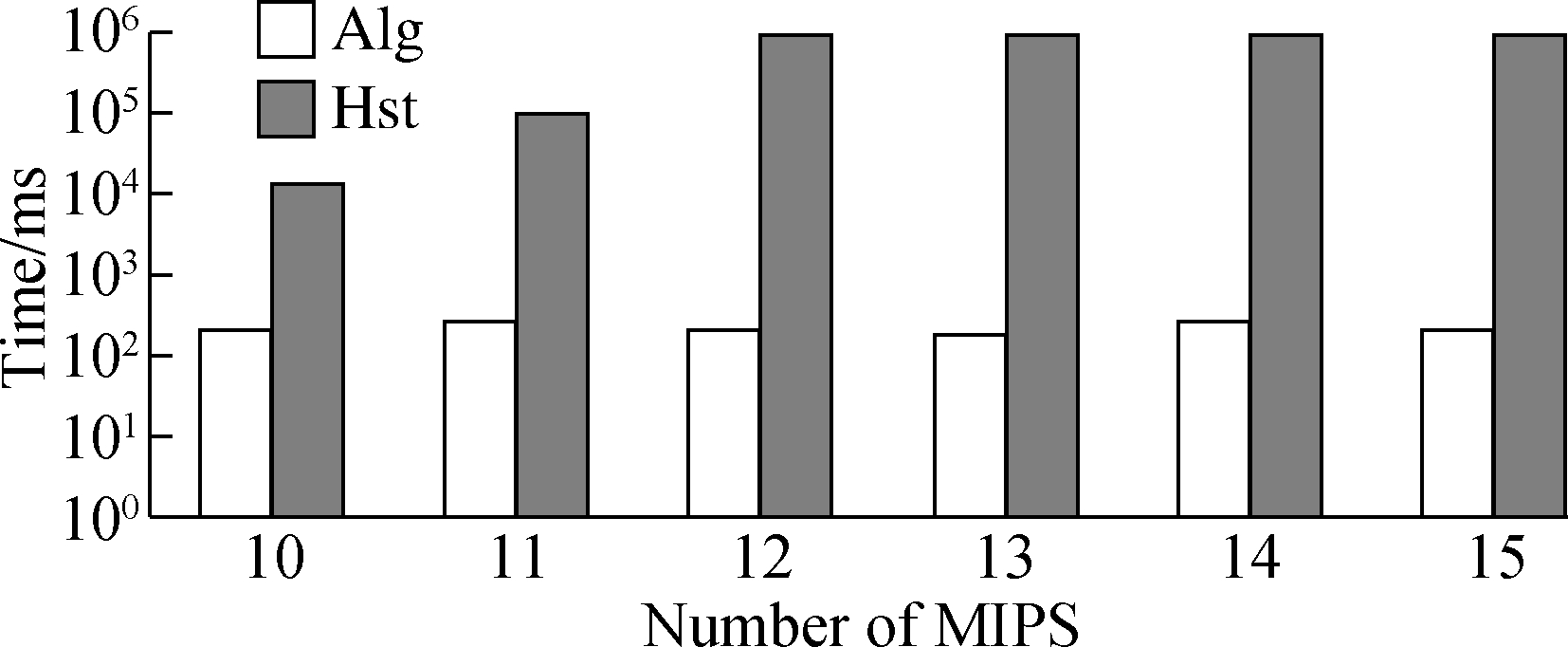
Fig.1 Time to find a solution to revise an artificial ontology
3.2 ILP-based algorithm vs. adapted one
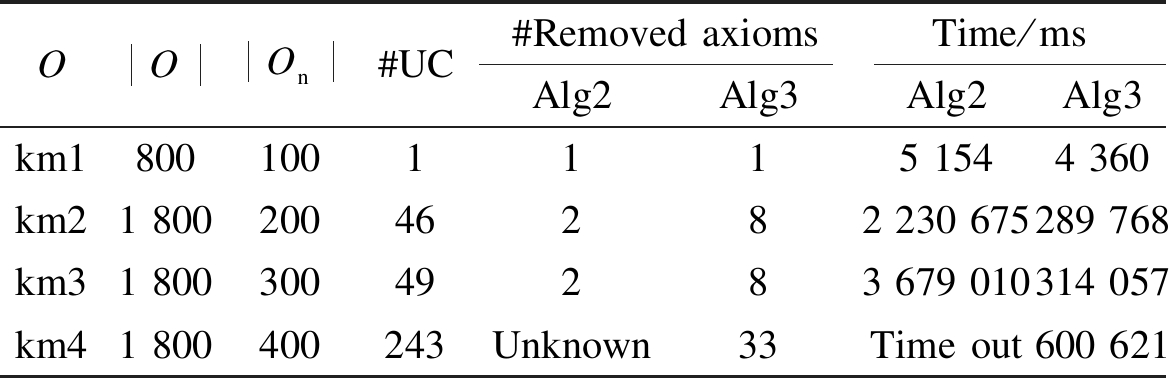
In this experiment, our two revision algorithms are evaluated based on the well-known incoherent ontologies km1, km2, km3 and km4. These ontologies were originally generated by using ontology learning algorithms. Both algorithms (namely Algorithm 2 and Algorithm 3) take Algorithm 1 as an incision function and are marked as Alg2 and Alg3, respectively. Since this ontology contains too many unsatisfiable concepts (i.e., 1 375), several sub-ontologies are extracted for testing.
Tab.1 provides the details about the extracted ontologies and the experimental results, where UC indicates unsatisfiable concepts and Time out means that a process cannot be finished within 70 min. Time in the last two columns consists of the time to compute the MUPS and the time to revise an ontology.
From Tab.1, it can be clearly observed that Alg3 is much more efficient than Alg2 since computing MIPS is very time-consuming. At the same time, it can be seen that Alg3 may remove more axioms for resolving inconsistency. Take ontology km3 as an example. It originally contained 1 800 axioms and the newly arrived ontology contained 300 axioms. The merging of the two ontologies generates 49 unsatisfiable concepts. To revise the ontology, Alg2 spent 3 679 s and removed 2 axioms while Alg3 spent 314 s and removed 8 axioms.
Tab.1 Experimental results of finding a solution for each km ontology
OOOn#UC#Removed axiomsTime/msAlg2Alg3Alg2Alg3km18001001115 1544 360km21 80020046282 230 675289 768km31 80030049283 679 010314 057km41 800400243Unknown33Time out600 621
3.3 Results over stratified ontologies
The third experiment tests the efficiency and effectiveness of our algorithm to revise stratified ontologies, where the effectiveness takes into consideration of the number of removed axioms to revise ontologies. We did this experiment by using Alg3 due to its higher efficiency and choosing km2 as a test ontology. Similar observations can be obtained by using Alg2 or choosing other ontologies. Specifically, the original ontology of km2 is stratified by randomly choosing a given number of axioms as a stable part and the remaining axioms are considered as the removable part. Tab.2 shows the number of the stable and removable parts for each test data set, where time represents the time to compute MUPS and do revision.
Tab.2 Experimental results for each stratified ontology by applying Alg3
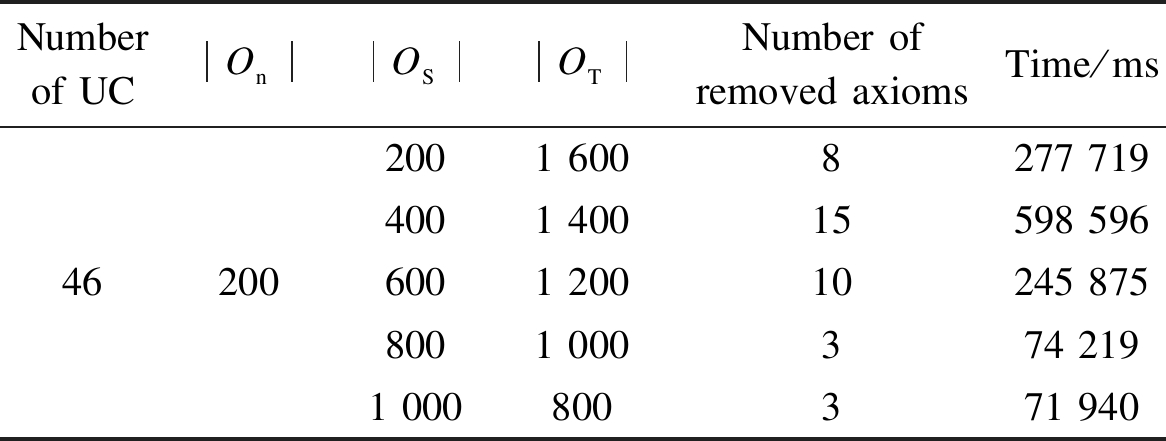
Numberof UCOnOSOTNumber ofremoved axiomsTime/ms462002001 6008277 7194001 40015598 5966001 20010245 8758001 000374 2191 000800371 940
From the table, it can be seen that, when the size of stable axioms is 800 or 1 000, Alg3 only spent about 70 s to finish the whole process and removed very few axioms (i.e., 3 axioms). In other cases, more time was spent and more axioms needed to be removed. This is caused by the axioms in the stable part (i.e., the axioms in OS). For conflict M, as our goal is to remove axioms in its removable part first, some of the axioms in the stable part will be selected for removing only if it has no intersections with the removable part. Thus, it may occur that an axiom with a high frequency in MUPS belongs to the stable part and more axioms in the removable part need to be removed for resolving inconsistency. The cases of |OS|<800 belong to such examples.
4 Conclusions
1) A novel definition of conflict stratification is provided to introduce a more general model for ontology revision, and thus users can freely assign different priorities to axioms.
2) A specific incision function based on ILP is defined for stratified ontologies and two algorithms are proposed to revise stratified ontologies.
3) To evaluate the performance of our algorithms, comprehensive experiments have been conducted to measure the efficiency and the number of removed axioms.
4) The experimental results show that the proposed ILP-based model is much more efficient than the HST-based one; and the adpated algorithm outperforms the one based on MIPS w.r.t. efficiency, while it may delete more axioms. It can also be observed that the performance of the adapted algorithm to revise stratified ontologies is influenced largely by the stratification of axioms.
[1]Grau C B, Horrocks I, Motik B, et al. OWL 2: The next step for OWL[J]. Journal of Web Semantics, 2008, 6(4): 309-322. DOI: 10.1016/j.websem.2008.05.001.
[2]Ji Q, Qi G L, Gao H, et al. Survey on schema induction from knowledge graphs [C]//China Conference of Knowledge Graph and Semantic Computing. Tianjin, China, 2018:136-142.
[3]Zablith F, Antoniou G, d’Aquin M, et al. Ontology evolution: A process-centric survey[J]. The Knowledge Engineering Review, 2015, 30(1): 45-75. DOI:10.1017/s0269888913000349.
[4]Qi G L, Haase P, Huang Z S, et al. A kernel revision operator for terminologies—algorithms and evaluation [C]// 7th International Semantic Web Conference. Karlsruhe, Germany, 2008: 419-434.
[5]Ribeiro M M, Wassermann R, Flouris G, et al. Minimal change: Relevance and recovery revisited[J]. Artificial Intelligence, 2013, 201: 59-80. DOI:10.1016/j.artint.2013.06.001.
[6]Golbeck J, Halaschek-Wiener C. Trust-based revision for expressive web syndication[J]. Journal of Logic and Computation, 2009, 19(5): 771-790. DOI:10.1093/logcom/exn045.
[7]Zhuang Z Q, Wang Z, Wang K W, et al. DL-Lite contraction and revision[J]. Journal of Artificial Intelligence Research, 2016, 56: 329-378. DOI:10.1613/jair.5050.
[8]Fu X F, Qi G L, Zhang Y, et al. Graph-based approa-ches to debugging and revision of terminologies in DL-Lite[J]. Knowledge-Based Systems, 2016, 100: 1-12. DOI:10.1016/j.knosys.2016.01.039.
[9]Qi G L, Du J F. Model-based revision operators for terminologies in description logics [C]// 21st International Joint Conference on Artificial Intelligence. Pasadena, CA, USA, 2009: 891-897.
[10]Wang Z, Wang K W, Zhuang Z Q, et al. Instance-driven ontology evolution in DL-Lite [C]// 29th AAAI Conference on Artificial Intelligence. Austin, TX, USA, 2015: 1656-1662.
[11]Micalizio R, Pozzato G L. Revision of ontologies to accommodate exceptions: A typicality-based approach[J]. Fundamenta Informaticae, 2018, 161(1/2): 163-189. DOI:10.3233/fi-2018-1699.
[12]Ji Q, Gao Z Q, Huang Z S. Conflict resolution in partially ordered OWL DL ontologies [C]// 21st European Conference on Artificial Intelligence. Prague, Czech Republic, 2014: 471-476.
[13]Dong X L, Gabrilovich E, Heitz G, et al. From data fusion to knowledge fusion[J]. Proceedings of the VLDB Endowment, 2014, 7(10): 881-892. DOI:10.14778/2732951.2732962.
[14]Bobillo F, Straccia U. Reducing the size of the optimization problems in fuzzy ontology reasoning [C]//11th International Workshop on Uncertainty Reasoning for the Semantic Web. Bethlehem, USA, 2015: 54-59.
[15]Niepert M, Meilicke C, Stuckenschmidt H. A probabilistic-logical framework for ontology matching [C]// 24th AAAI Conference on Artificial Intelligence. Atlanta, GA, USA, 2010: 1413-1418.
[16]Wang Q, Wang B, Guo L, et al. Knowledge base completion using embeddings and rules [C]// 24th International Joint Conference on Artificial Intelligence. Buenos Aires, Argentina, 2015: 1859-1866.
[17]Ji Q, Boutouhami K, Qi G L. Resolving logical contradictions in description logic ontologies based on integer linear programming[J]. IEEE Access, 2019, 7: 71500-71510. DOI:10.1109/access.2019.2919498.
[18]Baader F, Calvanese D, McGuinness D L, et al. The description logic handbook[M]. Cambridge: Cambridge University Press, 2007. DOI:10.1017/cbo9780511711787.
[19]Li H Y, Shao C P, Wang Z. Detecting fault injection attacks based on compressed sensing and integer linear programming[J]. IEEE Transactions on Dependable and Secure Computing, 2019, 16(3): 476-483. DOI:10.1109/tdsc.2018.2821140.
[20]Karp R M. Reducibility among combinatorial problems [C]// A symposium on the Complexity of Computer Computations. Yorktown Heights, NY, USA, 1972: 85-103.
[21]Baader F, Penaloza R, Suntisrivaraporn B. Pinpointing in the description logic EL+ [C]// 30th Annual German Conference on AI. Osnabrück, Germany, 2007: 52-67.
[22]Ji Q, Qi G L, Haase P. A relevance-directed algorithm for findingjustifications of DL entailments [C]// 4th Annual Asian Semantic Web Conference. Shanghai, China, 2009: 306-320.