In recent years, vehicular communications have gained attention due to their ability to improve traffic safety and efficiency, and provide abundant information services on wheels. The 802.11p networks can only provide intermittent and short-lived vehicle to infrastructure (V2I) links due to a limited radio range and lack of road side infrastructure. However, the cellular network, benefitting from wide coverage and flexibility on centralized control over network resources, guarantees the optimal performance of the network. Moreover, the vehicle to vehicle (V2V) communications have been considered to be a promising solution for alleviating the upcoming traffic pressure on core networks due to their short transmission distance between V2V pairs. The proper spectrum reuse with cellular users (CUEs) can significantly improve the spectrum efficiency. Meanwhile, non-orthogonal multiple access (NOMA) technology has become a research hotspot to further improve spectrum utilization.
Some research has been developed to investigate the potential of NOMA in boosting the performance for device to device (D2D) communications, which helps to set the base for V2V communications. Yang et al.[1] summarized three forms of NOMA and merely applied NOMA to a small scale of users, whereas the application of NOMA was not expanded on large scale of vehicular communications. Shi et al.[2] designed the user matching and power control method based on the greedy algorithm to maximize the total data transmission rate of downlink NOMA-based D2D users, yet they did not take the QoS of D2D users into consideration. Zhu et al.[3] focused on the optimization problem of NOMA downlink channel power allocation resources, considering user QoS requirements, and the maximum and minimum fairness of D2D users. Additionally, some research focused on both the QoS of the communication links and the energy efficiency simultaneously[4-7]. Li et al.[4] aimed at maximizing the energy efficiency of the D2D pairs while ensuring the QoS for the lowest data rate of the CUEs. The non-convex problem was transformed into the subtraction objective function by the Dinkelbach method. Moreover, uplink communications were also investigated. Pei et al.[5] considered that both D2D users and CUEs can obtain energy from the downlink of the hybrid relay node, and the target was maximizing the energy efficiency of the terminal equipment in an uplink transmission scenario. Pan et al.[6] solved the power control and channel allocation problems of D2D users in the context of NOMA-based CUEs, and maximized the total transmission rate of D2D users while ensuring the lower limit data transmission rate of CUEs. Moreover, the reliability of the V2V links was also taken into consideration. Xu et al.[7] focused on maximizing the packet acceptance rate in NOMA-based V2V users. However, the authors neither take into account the performance gains with NOMA in resource allocation, nor take into account the interference from NOMA-based vehicular users (VUEs) on CUEs and the data transmission rate for both CUEs and V2V users. Some research was carried out to solve the vehicular communication resource allocation by D2D schemes[8-9]. Ren et al.[8] proposed a scheme applying D2D resource allocation to the V2V scenario to solve the resource allocation of the vehicular network, and three forms of signal to interference plus noise ratio (SINR) simplification were derived. Yue et al.[9] integrated D2D and visible light communication (VLC) into V2V communications and developed the distributed resource allocation algorithm to reduce the interference between cellular links and LTE-V2V links. However, the shortcoming of applying D2D to V2V scenarios is that the traditional methods of radio resource management (RRM) for D2D communications based on full channel state information (CSI) are not feasible since it is difficult to achieve channel variations in a short time scale.
As mentioned above, most literature investigated applying NOMA to D2D communications or solving the V2V communications via D2D communications, while little literature studied the exertion of NOMA to V2V communication scenarios. V2V communication, as a promising solution to enable highly efficient and reliable vehicular communication, can be applied with NOMA to further improve the connectivity of the network and efficiency of the spectrum. Meanwhile, most of the existing literature set the hypothesis of known CSI at BS, which is impractical in vehicular communication scenarios. Therefore, we utilize the NOMA-based decentralized resource allocation method to compensate for it.
In this paper,we investigate the resource allocation in the NOMA-based V2V users underlaid V2I highway unicast vehicular communication scenario including centralized subchannel assignment and distributed power control for V2V user pairs. We aim to maximize the sum transmission rate of V2V users while satisfying the transmission rate QoS for both CUEs and VUEs. In the subchannel assignment procedures, we use the clustering algorithm for V2V transmitters (Tx) to decrease the SINR of V2V receivers in the overlapping area of VUE Txs’ transmission range. Afterwards, the Kuhn-Munkres algorithm is applied to complete the subchannel assignment, and then the verified PSO algorithm is designed during the power control procedure.
1 System Model
Consider a downlink unicast NOMA-based V2V communication network, where the base station (BS) serves CUEs through N subchannels (SCs). As shown in Fig.1, the BS is responsible for the geographic position-based subchannel assignment. The VUE Txs will take charge of the distributed power allocation in a decentralized way. Additionally, the VUE Rxs will decode the corresponding signals from the VUE Txs following the signal interference cancellation (SIC) order.
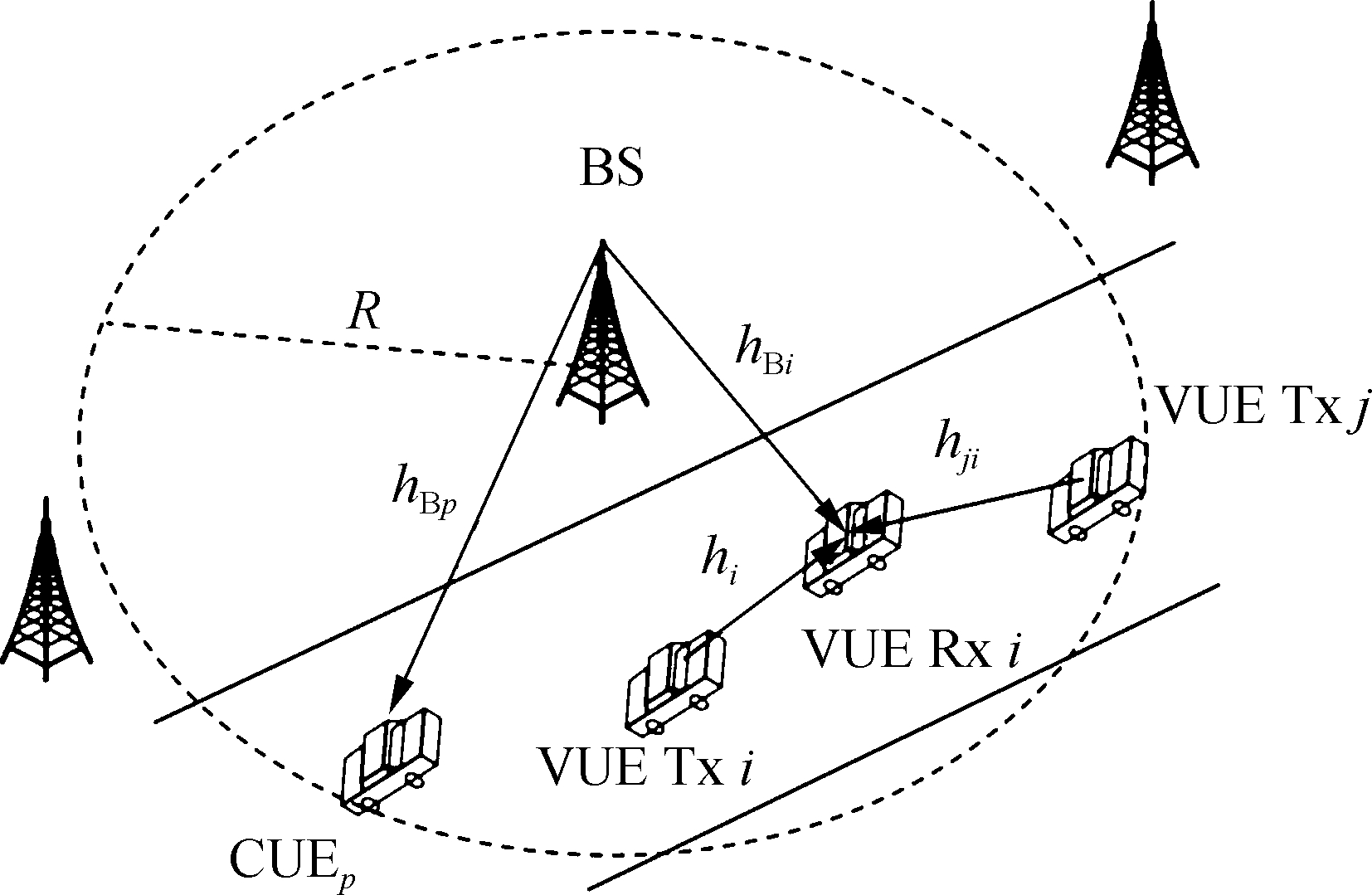
Fig.1 V2V highway scenario
In Fig.1, R is the transmission distance for the BS, and the vehicles run on the highway satisfying the Poisson process. There are CUEs, VUE Txs and their corresponding VUE receivers (Rxs) exerting NOMA to the V2V pairs. Q V2V pairs are multiplexed in the NOMA manner by splitting them in the power domain. Meanwhile, there are P(P≤N) underlaid CUEs. Denote Q={1,2,…,Q} and N={1,2,…,N} as the sets of VUEs and subchannels, respectively.
In dynamic scheduling, resource allocation for every transmission in each time slot needs the real-time CSI, which is impractical due to the fact that channels vary rapidly. However, semi-persistent scheduling (SPS) can compensate for the drawback by allocating the predefined resources to those users asking for transmission during every SPS period. Here, we set one SPS period in a one-time slot as one resource block (RB). Also, we apply SPS to our proposed resource allocation for the NOMA-based vehicular communication model.
The BS allocates spectrum resources to the VUE user pair at the beginning of the SPS period, in which the BS implements interference suppression on the frequency resource allocation according to the location information of all the vehicles. Unlike traditional orthogonal multiple access (OMA), co-channel interference needs to be considered here.
For VUE Rx i, its SINR is
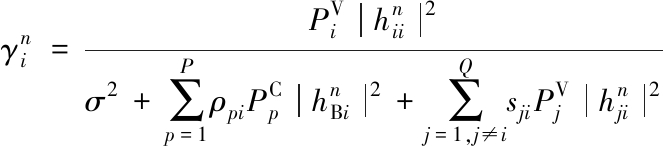
(1)
(2)
(3)
where  VUE Rx i can successfully decode and remove interference from VUE Tx j, ∀j<i.
VUE Rx i can successfully decode and remove interference from VUE Tx j, ∀j<i.
For CUE p, its SINR is

(4)
Taking the downlink transmission rate QoS for VUE Rxs and CUEs into consideration, we have
(5)
(6)
In this paper, we aim to maximize the throughput of all the V2V user pairs in one SPS period, subject to the SINR constraints and the maximum transmission power constraints for both CUEs and VUEs, as well as the V2V user pairs’ interference constraints with respect to the SIC order. Generally, our optimization problem can be expressed as
(7)
(8)
(9)
(10)
(11)
It is apparent that the optimization problem is non-convex because of the binary variable. Therefore, we decompose the optimization problem into two steps, including the subchannel assignment based on the V2V user pairs’ global position centralized in the BS and the dynamic distributed power control by VUE Txs.
2 Resource Allocation for the Vehicular System
In this section, the clustering method for V2V Txs is introduced, then the subchannel assignment via the Kuhn-Munkres algorithm is achieved, and the power control for each V2V Tx is calculated through the verified PSO. Finally, we analyze the complexity and the performance of the proposed algorithms.
2.1 Subchannel assignment
In the subchannel assignment, vehicles which keep a distance away are chosen to reuse RB in the NOMA method, which lowers the chance for the VUE Rxs to be in the overlapping area of the VUE Txs’ transmission range so that the SINR of the VUE Rxs in these areas will be influenced. Through the given τ, which is the distance threshold between different clusters, the VUE Tx can be clustered into several different clusters. In one certain VUE Tx cluster, the inter-distance of any VUE Txs is above the distance threshold τ. Each of the VUE Tx clusters reuses one subchannel with CUEs. The distance criterion can be depicted as follows:
(12)
(13)
dij≥τ
(14)
where dij is the distance between VUE Txs i and j; dki is the distance between VUE Txs k and i; and Gtris the set storing all the VUE Txs in the covering area of one BS. We introduce λ as the maximum VUE Tx cluster scale. Formula (12) is introduced to choose the VUE Tx near the cluster which has not reached the maximum scale λ. Formula (14) is the inter-distance condition in terms of the VUE Txs in the same cluster.
Repeat the search until no vehicles in the same group satisfy formulae (12), (13) and (14). Then, start grouping another group, considering the constraint that each group reuses at most one subchannel with CUEs. For fear of the excess in the number of RBs, lower the threshold τ if necessary to broaden the scale of groups as compensation.
Algorithm 1 VUE Tx clustering
Input: Set of all VUE Tx-Gtr and temporary V set to NULL, i.e., temp_Vset=∅, initialize group index t=1, max|gt|=λ.
Output: Group gt in which vehicles use the same RB.
Initialization: t=1,Gtr={all VUE Tx indice},
temp_Vset=∅
do
Choose edge VUE Txedge→gt,Gtr\{VUE Txedge}
do
for each VUE Tx∈Gtr
if VUE Tx satisfies (14)
VUE Tx→temp_Vset
end if
end for
for each VUE Tx∈temp_Vset
if VUE Tx satisfies (12)
VUE Tx→gt
VUE Tx\Gtr
end if
end for
while |gt|<λ and Gtr≠∅
t=t+1
temp_Vset=∅
while Gtr≠∅
Vehicles keep transmitting on the allocated RB until any of them changes motion states, for instance, acceleration, speed, and directions etc. Once these factors change, vehicles leave the previous groups and utilize Algorithm 1 to reallocate the RB to them, and this process is done in the BS.
Differently from Xu et al.[7], after grouping, to allocate the frequency resources appropriately, the subchannel allocation algorithm needs to be formulated. Here, we use the Kuhn-Munkres algorithm to solve it, as described in Algorithm 2.
Algorithm 2 Subchannel assignment
Input:Clustering result, CUEs’ global position, temp_dist=∅.
Output:Subchannel reuse pattern.
If t+P≤N
num(subchannel occupied)=t+P
else
for each VUE Txi∈gt
![]()
end for
dist(CUEp,gt)=mini temp_dist
Select top(t+P-N) clusters gt in
dist(CUEp,gt)
Use the Kuhn-Munkres algorithm to find the reuse pattern
end if
2.2 Distributed power control
In highway scenario, it is difficult for BS to obtain real-time CSI, therefore, distributed power control coupled with Tx-Rx selection can compensate for that. VUE Txs autonomously control their own transmission power to achieve overall improvement of transmission rate.
Note that we have downlink transmission rate QoS for both VUE Rxs and CUEs in formulae (5) and (6). The transmission rate for VUE Rx i and CUE p can be expressed as
(15)
(16)
where E[·] is the mathematical expectation.
From formulae (4) and (6), we can infer that if the sum transmission rate for all VUE Rxs needs maximizing, then formula (6) can actually be an equation, since the higher transmission rate needs a higher VUE Txs transmission power, which leads to a higher interference for CUEs sharing the same SC. Therefore,
(17)
According to formula (4), we can infer that
(18)
Here, we adopt the verified PSO algorithm to perform the calculation of power allocation and compute the sum transmission rate of all VUEs. However, differently from the PSO, we ponder the necessity of taking a time-varying summation of all VUEs’ transmission rate instead of fixed function. The whole algorithm can be expressed in Algorithm 3.
Algorithm 3 Distributed power control
Input:Initializing the particle positions with a uniformly random vector; candidate particle set Cand_set=∅; evolution velocity v; swarm scale Ψ; and the number of iteration Ω.
Output: The best particle and the corresponding sum transmission rate of all VUEs.
For each initialized particle z within the swarm scale
if z satisfies (5),(6),and (18)
Cand_set=Cand_set∪{z}
Calculate z’s sum transmission rate
end if
end for
Store best particle so far.
Store the best particles’ best known so far.
for each evolution time in iteration omega
Update particles with v in Cand_set.
for each particle in Cand_set
if z′ disagrees with (5), (6), and (18)
Cand_set\{z′}
else
Calculate sum transmission rate for z′.
end if
end for
Store best particle individually so far.
Store the particles’ best known so far.
end for
We first derive the initialized particles satisfying uniform distribution based on constraints (5), (6) and (18). We filter the eliminated particles and store the candidate particles and compute their corresponding sum rate based on the NOMA method. After the above processes, the best position of particles and the best known positions of the particles are stored. Then, the candidate particles are updated with a proper updating speed and number of iterations. Finally, the best particle is given as the optimal power control.
2.3 Complexity analysis
In the clustering section, the time complexity of clustering the VUE Txs in Algorithm 1 is O(Q2). The time complexity of subchannel assignment in Algorithm 2 is O((t+P-N)3) at most, where t is the number of VUE groups. Moreover, the time complexity of distributed power control in Algorithm 3 is ![]()
3 Simulation Results
In this section, the proposed mechanism under the highway scenario defined by IEEE [10] is evaluated. We follow the simulation setup for the freeway case detailed in Ref.[11] and model a multi-lane freeway that passes through a single cell, where the BS is located at its center, as demonstrated in Fig.1. The vehicles pass on the highway in accordance with Poisson process and the vehicle density is determined by the factor of the velocity. P CUEs and Q VUEs are randomly distributed on the highway, where V2V pairs are always formed between neighboring vehicles and CUEs are assumed to have equal shares of the total subchannels. The major parameters of simulation are listed in Tab.1, and the channel model is described in Tab.2.
Tab.1 Parameters of simulation[12]

ParametersValuesCarrier frequency/GHz2Bandwidth/MHz10Cell radius/meters500BS antenna height/meters25BS antenna gain/dBi8BS receiver noise figure/dB5Channel number4Distance from BS to highway/meters35Vehicle antenna height/meters1.5Vehicle antenna gain/dBi3Vehicle receiver noise figure/dB9Absolute vehicle speedv/(km·h-1)60 to 140Vehicle drop modelSpatial Poisson processNumber of lanes3 in each directionLane width/m4Vehicle inter-distance/m2.5Minimum rate for CUE & VUE/(bit·s-1·Hz-1)0.5Number of V2V pairs Q8Number of CUEs P4Maximum power PCmax/dBm23Maximum power PVmax/dBm23Noise power/dBm-114Swarm scale Ψ200Number of iteration500VUERxs SINR threshold γ1/dB0.45CUEs SINR threshold γ2/dB0.5
Tab.2 Channel model for V2I and V2V links[12]

ParametersV2I LinkV2V LinkPathloss model128.1+37.6log10dLOS in WINNER+B1Shadowing distributionLog-normalLog-normalShadowing standard de-viation ξ/dB83Fast fadingRayleigh fadingRayleigh fading
D2D-enabled vehicular communication[12] is introduced as a comparison with the scheme we proposed. D2D-enabled vehicular resource allocation was maximizing the sum transmission rate for all CUEs while guaranteeing the QoS for each CUE. Each CUE can share the subchannel with at most one D2D pair. In this way, the connectivity capacity is restrained and the frequency efficiency is limited as well, meanwhile, it has to calculate the reuse pattern every time slot. However, our proposed NOMA-based resource allocation can compensate for these drawbacks and does not have to calculate the reuse pattern unless VUEs in the group change their states.
Fig.2 presents the relationship between the velocity of VUEs and the sum throughput of all V2V user pairs with the comparisons of our proposed algorithm and the D2D-based V2V algorithm. The horizontal axis describes the VUEs’ velocity ranging from 60 to 140 km/h, while the vertical axis shows the sum transmission rate for all the V2V user pairs.
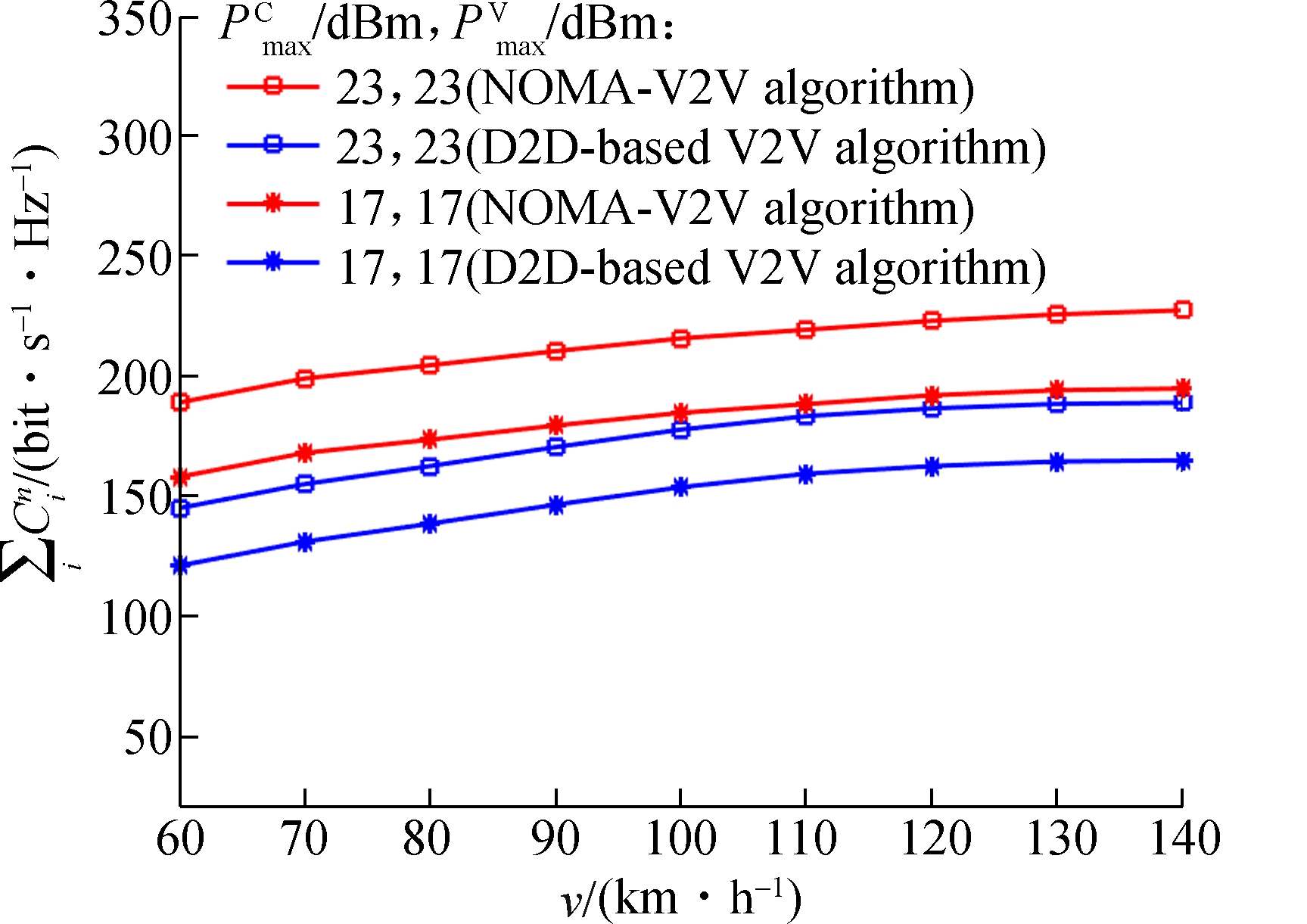
Fig.2 Sum throughput of V2V user pairs
Our proposed NOMA-V2V resource allocation outperforms D2D-based vehicular communication. It is apparent that with the increase in the speed of vehicles, the inter-vehicle distance becomes larger; therefore, the overall SINR becomes larger due to the overlapping area of VUE Txs in the same group becoming smaller. However, the growing speed slows down a little if the distance is safe enough, and the improvement of SINR becomes less. However, for the D2D-based resource allocation, the VUEs in the same group will suffer interference from each other, thus the overall rate decreases greatly.
Fig.3 illustrates the relationship between the velocity of VUEs and the sum throughput of all V2V user pairs with the influence of various values of τ. The horizontal axis describes the VUEs’ velocity ranging from 60 to 140 km/h, while the vertical axis shows the sum transmission rate for all the V2V user pairs.
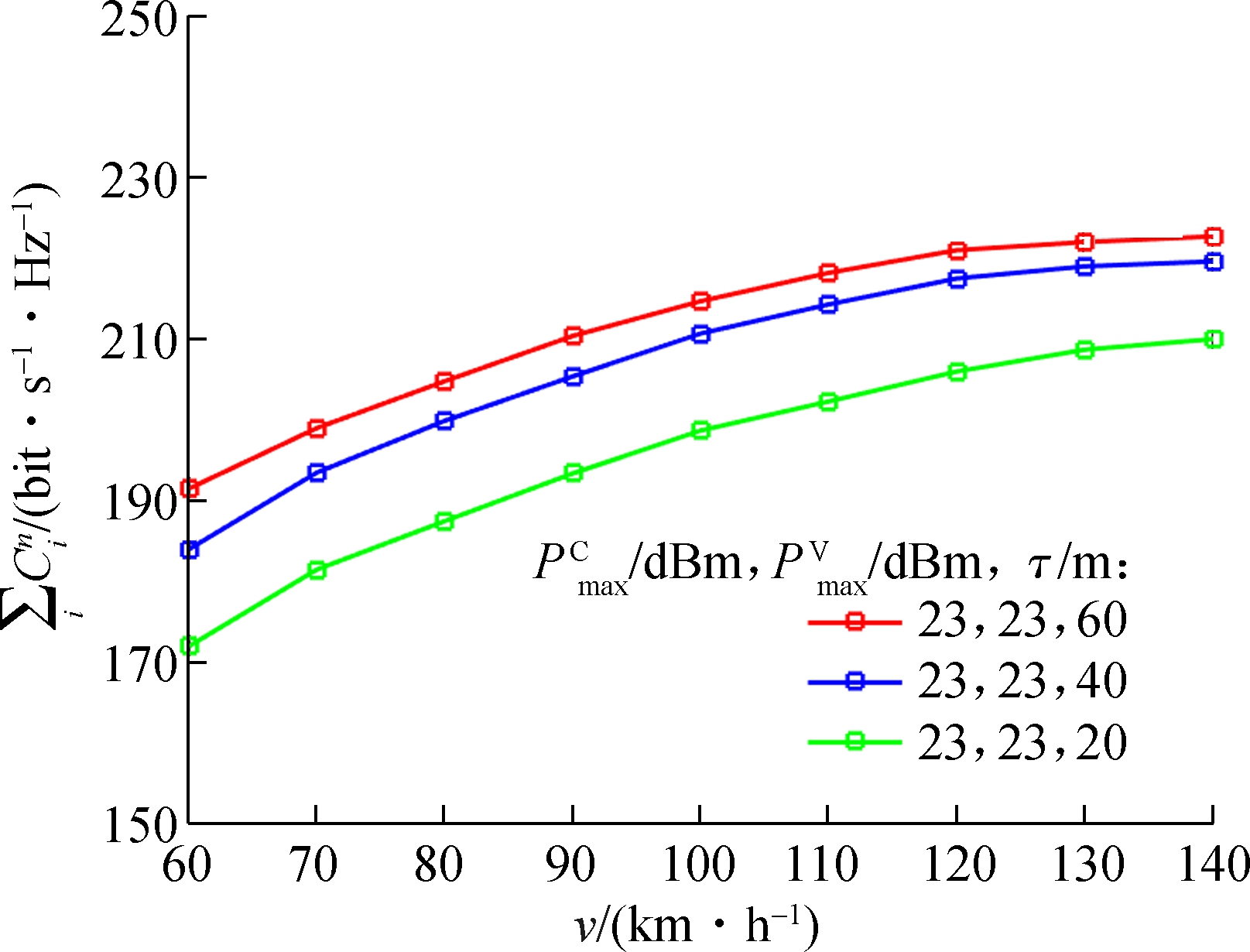
Fig.3 Sum throughput of V2V user pairs
As shown in Fig.3, with the increase in τ, the sum rate for all VUEs is improved accordingly, since the growing threshold distance can lower the chance when VUE Rx locates in the overlapping region of VUE Txs sharing the same subchannel. However, when τ becomes sufficiently large, improvement becomes less apparent. As the speed goes up, CUEs’ channel becomes worse, and CUEs need more transmission power to satisfy γ2. Consequently, the gap between the lines becomes narrower.
4 Conclusion
In this paper, a V2V resource allocation mechanism in a NOMA manner is proposed with the target of maximizing the sum transmission rate of all VUEs while guaranteeing the QoS of the transmission rate for both VUEs and CUEs. The resource allocation only occurs when vehicles change their moving status. A clustering algorithm is designed and the Kuhn Munkres algorithm is adopted to solve the subchannel assignment, then a verified PSO algorithm is designed to achieve the distributed power control. Simulation results show that the proposed scheme outperforms the D2D-based V2V resource allocation in broadening the connectivity ability of the vehicular network. The sum transmission rate for V2V pairs is improved via NOMA, and the spectrum efficiency is enhanced.
[1]Yang Z, Ding Z G, Fan P Z, et al. A general power allocation scheme to guarantee quality of service in downlink and uplink NOMA systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7244-7257. DOI:10.1109/twc.2016.2599521.
[2]Shi L J, Li B, Chen H H. Pairing and power allocation for downlink nonorthogonal multiple access systems[J].IEEE Transactions on Vehicular Technology, 2017, 66(11): 10084-10091. DOI:10.1109/tvt.2017.2748145.
[3]Zhu J Y, Wang J H, Huang Y M, et al. On optimal power allocation for downlink non-orthogonal multiple access systems[J].IEEE Journal on Selected Areas in Communications, 2017, 35(12): 2744-2757. DOI:10.1109/jsac.2017.2725618.
[4]Li B S, Zhang H L, Ji H, et al. Energy-aware resource allocation scheme for device-to-device communication based on NOMA underlaying cellular networks[C]// 2017 IEEE 17th International Conference on Communication Technology (ICCT). Chengdu, China, 2017: 513-517. DOI:10.1109/icct.2017.8359689.
[5]Pei L, Yang Z H, Pan C H, et al. Energy-efficient D2D communications underlaying NOMA-based networks with energy harvesting[J]. IEEE Communications Letters, 2018, 22(5): 914-917. DOI:10.1109/lcomm.2018.2811782.
[6]Pan Y J, Pan C H, Yang Z H, et al. Resource allocation for D2D communications underlaying a NOMA-based cellular network[J].IEEE Wireless Communications Letters, 2018, 7(1): 130-133. DOI:10.1109/lwc.2017.2759114.
[7]Xu Y Y, Gu X Y. Resource allocation for NOMA-based V2V system[C]// 2018 International Conference on Network Infrastructure and Digital Content (IC-NIDC). Guiyang, China, 2018: 239-243. DOI:10.1109/icnidc.2018.8525576.
[8]Ren Y, Liu F Q, Liu Z, et al. Power control in D2D-based vehicular communication networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(12): 5547-5562. DOI:10.1109/tvt.2015.2487365.
[9]Yue P, Wu L, Cui Z M, et al. Integrating LTE-D2D and VLC techniques to support V2V communication[C]// 2017 IEEE/CIC International Conference on Communications in China (ICCC). Qingdao, China, 2017:1-6. DOI:10.1109/iccchina.2017.8330477.
[10]Chen S Z, Hu J L, Shi Y, et al. Vehicle-to-Everything (V2X) services supported by LTE-based systems and 5G[J]. IEEE Communications Standards Magazine, 2017, 1(2): 70-76. DOI: 10.1109/mcomstd.2017.1700015.
[11]Ahmed K J, Lee M J. Secure LTE-based V2X service[J]. IEEE Internet of Things Journal, 2018, 5(5): 3724-3732. DOI: 10.1109/jiot.2017.2697949.
[12]Liang L, Li G Y, Xu W, et al. Resource allocation for D2D-enabled vehicular communications[J]. IEEE Transactions on Communications, 2017, 65(7): 3186-3197. DOI:10.1109/tcomm.2017.2699194.