Besides solving the problem of serious traffic jams in daily life[1-4], the monorail transportation has many advantages, such as a low turning radius and low noise[5-6]. There are two types of monorail: the suspended monorail with the car body suspended under the girder and the straddle monorail with the car body moving above the track beam. These two types of suspended monorail are widely used in the world. The Japanese bogie is more like the railway vehicle bogie; however, the German bogie is like an automobile. When solid tires are used in the German monorail, the suspension system is more complex. These days, China is devoted to the design of a new type of tour suspended monorail, namely the micro-suspended monorail, in which the bogie is as small as a toy.
The vehicle bridge coupling method, which is widely used in the world, can also be used in the dynamic simulation of the monorail[7-26]. Naeimi et al.[27] proved their assumption that the vehicle speed can affect the dynamic forces with the method of vehicle-bridge coupling dynamics. Meisinger et al.[28-29] studied the dynamic response of the vehicle-bridge system under the periodic excitation. As for the dynamic simulation of monorail, the dynamic deformation of the track beam is always ignored where the dynamic properties of the vehicle system are concerned[30-44]. Simulink can also be a good choice to set up the dynamic model for the advantage of manual modification[43-44]. With the method of multi-rigid body dynamics, a model of a 20 degree of the freedom micro-suspended monorail is set up in this research.
1 Tire Models
To benefit both calculation speed and accuracy, in this research, the Pacejka formula is used to construct the tire model[37] .
(1)
where Y(x) denotes the longitudinal force Fx, side force Fy or aligning moment Mz; X denotes the longitudinal creep of Fx or the sideslip of Fy and Mz; and γ is the camber angle.
The coefficients are functions of Fz and the camber angle γ.
As for the longitudinal force Fx, the coefficients of Eq.(1) is given as
C=b0,D=Fz(b1Fz+b2)![]()
Sh=b9Fz+b10,Sv=b11Fz+b12
As for the side force Fy, the coefficients of Eq.(1) is given as
C=a0,D=Fz(a1Fz+a2)![]()
E=a6Fz+a7,Sh=a8γ+a9Fz+a10
Sv=(a11Fz+a12)γFz+a13Fz+a14
As for the aligning moment Mz, the coefficients of Eq.(1) is given as
C=c0,D=Fz(c1Fz+c2)![]()
![]()
Sh=c11γ+c12Fz+c13
Sv=(c14Fz+c15)γFz+c16Fz+c17
The coefficients a0,...,a15,b0,...,b10,c0,...,c17 fitted with the test data is given as a0=1.3,a1=-22.1,a2=1 011,a3=1 078,a4=4.902,a5=0.022,a6=-0.354,a7=0.707,a8=0.029,a9=0,a10=0,a11=14.8,a12=0,a13=0,a14=0,a15=1.82;b0=1.65,b1=-21.3,b2=1144,b3=49.6,b4=226,b5=0.069,b6=-0.006,b7=0.056,b8=0.486,b9=0,b10=0;c0=2.4,c1=-2.72,c2=-2.28,c3=-1.86,c4=-2.73,c5=0.11,c6=0.03,c7=-0.07,c8=0.643,c9=-4.04,c10=0.03,c11=0.015,c12=0,c13=0,c14=-0.066,c15=0.945,c16=0,c17=0.
2 Track Irregularities
Like the traditional suspended monorail, the micro-suspended monorail’s track beam is also the box girder with an opening bottom, and the driving wheels and the guide wheels move forward along the inner wall of the box beam. In order to analyze the vehicle’s characteristics, the track beam is considered as a rigid body. The road irregularities are generated by the power spectral density S(n) according to the following equations:
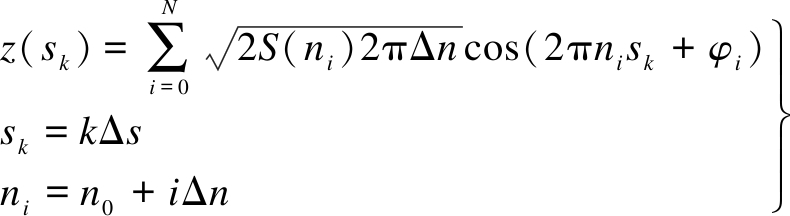
(2)
where Δs denotes the step size, m; N is the number of harmonics; n is the spatial frequency, cycles/m; Δn is the step size of frequency; n0 is the minimal frequency; φi is the stochastic phase uniform distributed in [-π,π].
S(n) is the PSD function,
S(n)=Cnw
(3)
where C and w are constants.
The road irregularities of the micro-suspended monorail can be scaled by that of the level A road:
Z(sk)=az(sk)
(4)
3 Model Establishment
The dynamic model of the micro-suspended monorail consists of the track beams, two bogies, U type suspender and a car body. As shown in Fig.1(a), the power bogie is treated as part 1; the non-power bogie, part 2; the U type suspender, part 3; and the car body, part 4. Then, a 20-degree-model is established, as shown in Fig.1(b).
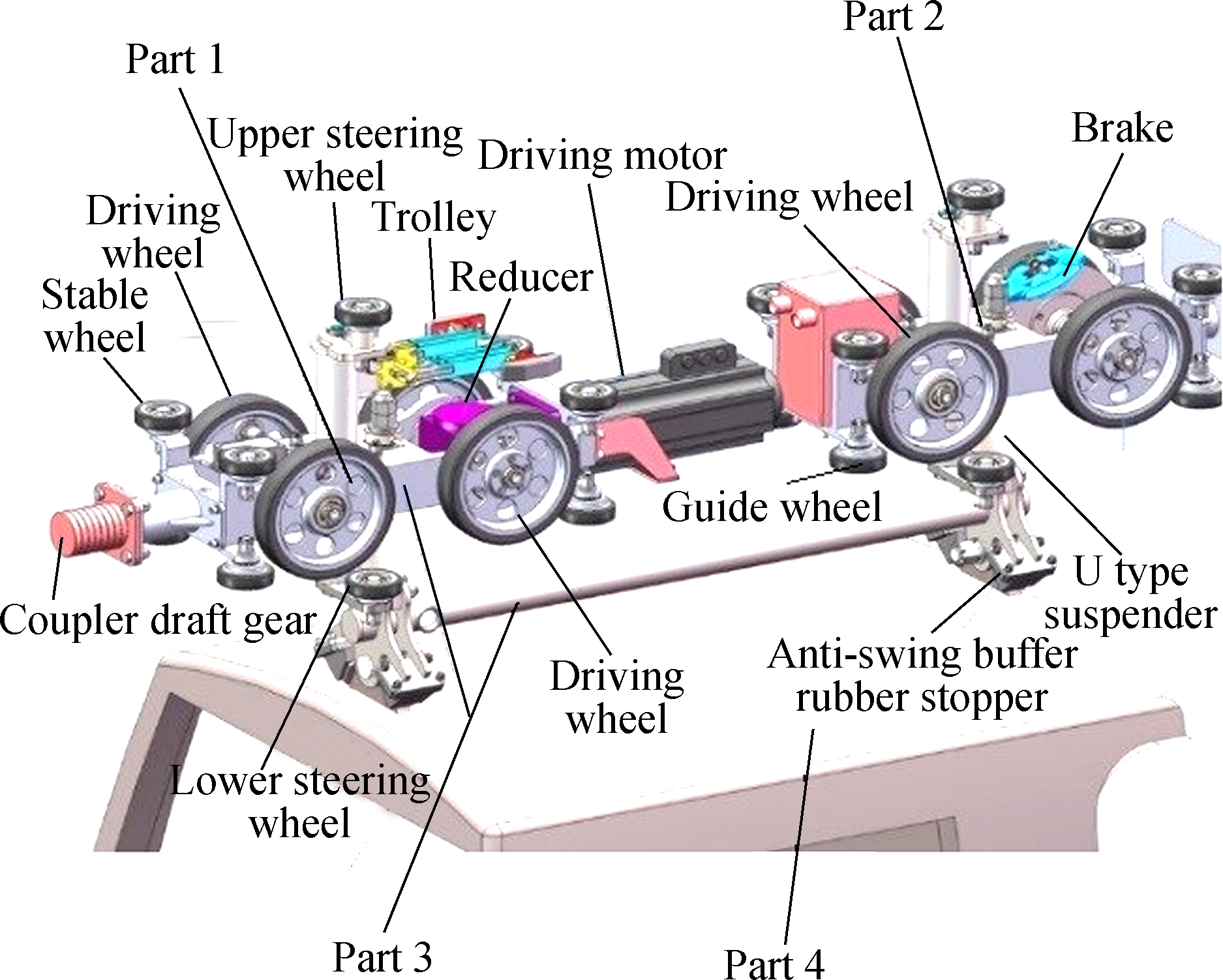
(a)
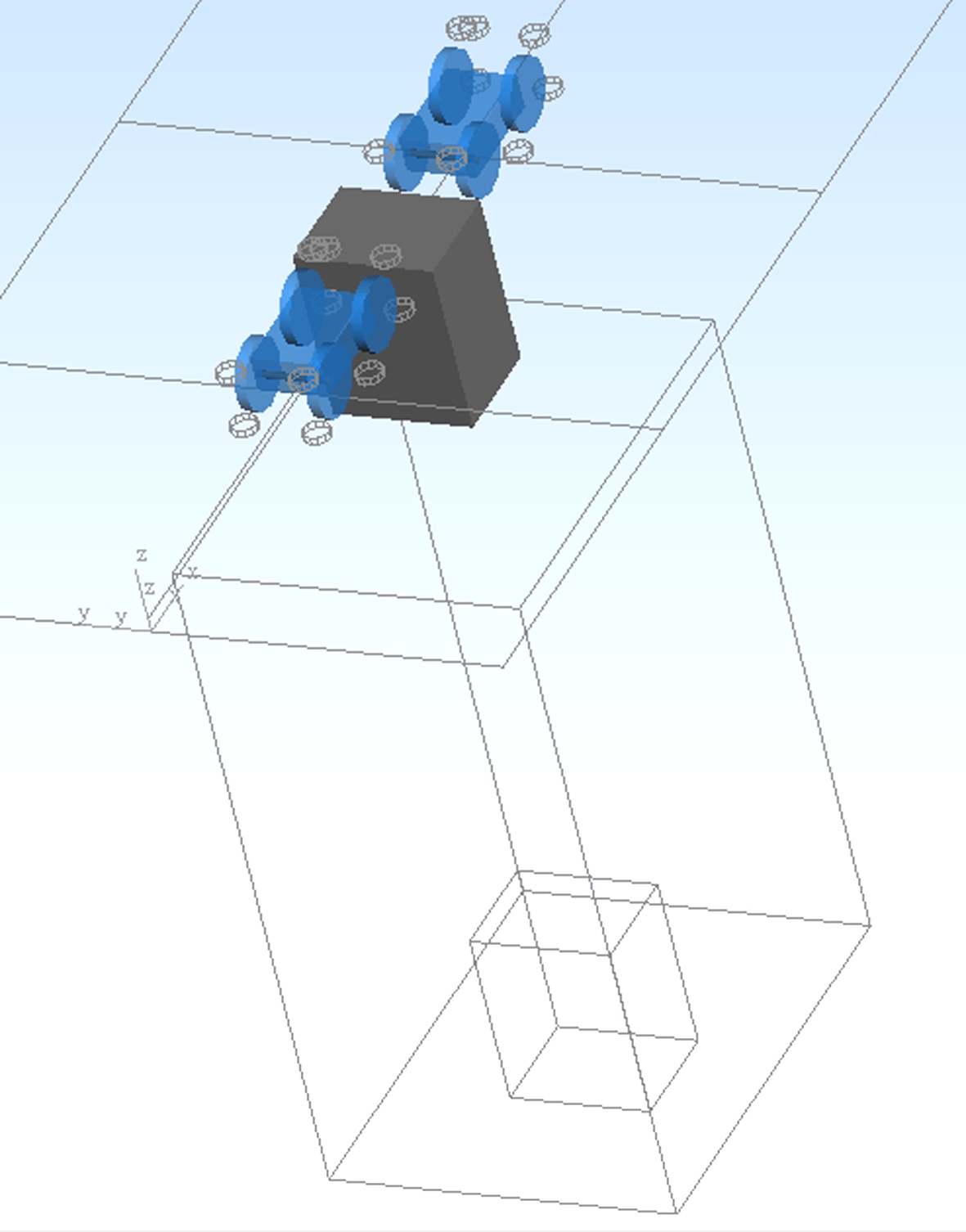
(b)
Fig.1 Structure of the vehicle.(a) Components of the vehicle; (b)Dynamic model of the vehicle system
We can only verify the model theoretically due to the fact that this vehicle is still under the process of manufacturing. Two steps are required to verify the model. First, the static equilibrium of the model is calculated. If the vibration converges rapidly, it means that there is no error in the dynamic model. Secondly, the online simulation in Simpack is carried out. No strange vibration of this vehicle means that there is no error in this model.
Our simulation result is consistent with the design of the manufacturer, which means that our simulation is precise enough.
4 Analysis of Resonance Impact
The dynamic model is linearized. By solving characteristic roots, the natural modes of the vehicle can be obtained, as shown in Tab.1.
Tab.1 Vibration modes of the vehicle system
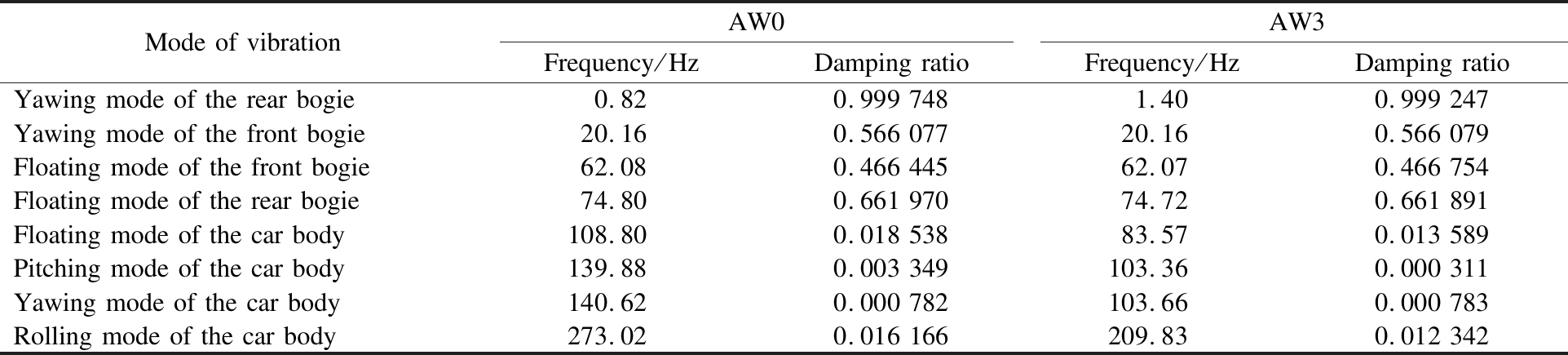
Mode of vibrationAW0AW3Frequency/HzDamping ratioFrequency/HzDamping ratioYawing mode of the rear bogie0.820.999 7481.400.999 247Yawing mode of the front bogie20.160.566 07720.160.566 079Floating mode of the front bogie62.080.466 44562.070.466 754Floating mode of the rear bogie74.800.661 97074.720.661 891Floating mode of the car body108.800.018 53883.570.013 589Pitching mode of the car body139.880.003 349103.360.000 311Yawing mode of the car body140.620.000 782103.660.000 783Rolling mode of the car body273.020.016 166209.830.012 342
According to the standard DBJ51/T099—2018[45], the Sperling index is the only index to judge the stability of the suspended monorail. The Sperling index, which is used to evaluate the vehicle’s ride comfort, can take into account vibration at different frequencies. Therefore, the Sperling index of a certain frequency fi can be obtained.
(5)
where Wi denotes the riding index; A(fi) is the vibration acceleration amplitude; fi is the vibrational frequency; and F(fi) is the weighted value of the Sperling index in the frequency domain
According to the standard[41], when the frequency is within the range of 1 to 10 Hz, the value of weight function of the Sperling index F(f)/f is large, which means that the vibration in these frequencies can greatly affect the ride comfort of the vehicle. However, the natural modal frequencies of the micro-suspended monorail are not within that range, which indicates that the resonance will not have a great effect on this vehicle.
5 Analysis of the Vehicle Motion in a Curve
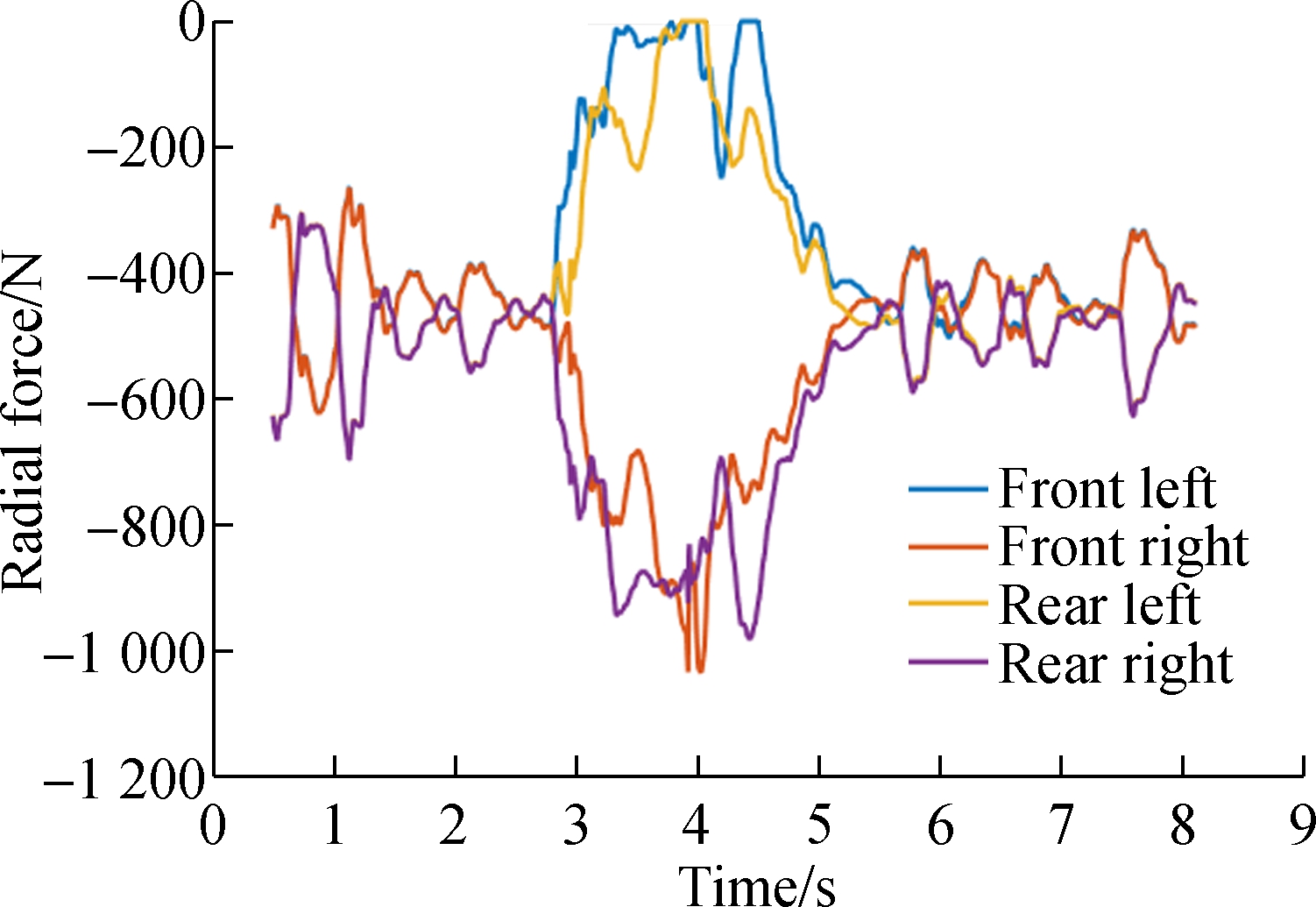
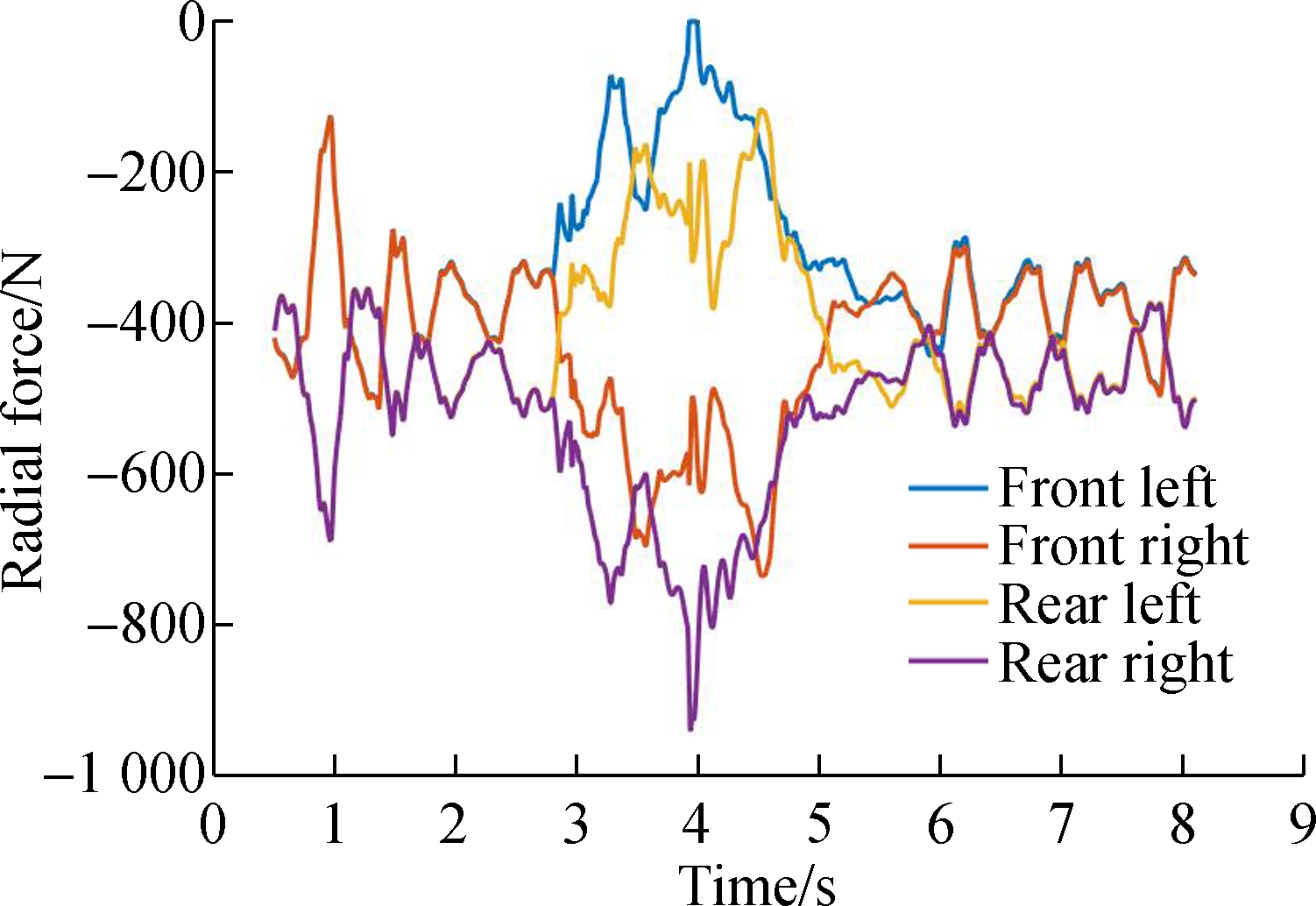
Through simulation, dynamic forces of the micro-suspended monorail can be obtained. The time domain responses of the tire forces when the vehicle passes a R12m curve at the speed of 10 and 15 km/h are shown in Figs.2 to 5, respectively. The radial maximum/minimum forces of the driving wheels are shown in Tabs.2 and 3, respectively. It is known that when the speed increases, the radial maximum force of the driving wheels also increases. As for the rear bogie, it can be noticed that, when the speed increases from 10 to 15 km/h, the maximum radial force of the driving wheels in the left of the rear bogie reduces a little and the maximum radial forces of the driving wheels in the left of the rear bogie increase.
Tab.2 Radial maximum force of the driving wheels
N

LoadAW0AW3PositionFront bogieRear bogieFront bogieRear bogie10 km/h15 km/h10 km/h15 km/h10 km/h15 km/h10 km/h15 km/hFront left619.91663.95512.24501.47933.705933.018857.830857.332Front right986.871 024.21730.12900.171 235.8101 388.940969.5411 229.350Rear left694.45735.69687.47682.311 072.9601 073.1801 089.5901 090.230Rear right979.231 093.69837.331 028.041 238.4501 447.2801 108.1601 439.730
Tab.3 Radial minimum force of the driving wheels
N

LoadAW0AW3PositionFront bogieRear bogieFront bogieRear bogie10 km/h15 km/h10 km/h15 km/h10 km/h15 km/h10 km/h15 km/hFront left000057.233 3060.492 90Front right265.078211.301126.661123.09681.063 781.081 960.722 760.668 6Rear left00103.494046.991 9066.949 60Rear right305.588301.482354.163315.07085.442 885.460 967.179 467.124 2
It can be demonstrated that, when the car passes a curve, the front bogie uplifts in the front left position and the left driving wheels derail. As for the rear bogie, the front left driving wheel hangs in the air when the vehicle speed increases from 10 to 15 km/h. However, the rear left wheel does not hang until the vehicle speed increases up to 15 km/h. It can also be learned from the figures that the forces of the right driving wheels increase but the forces of left decrease when the vehicle passes a curve, which shows that there is a rolling motion in the bogie.
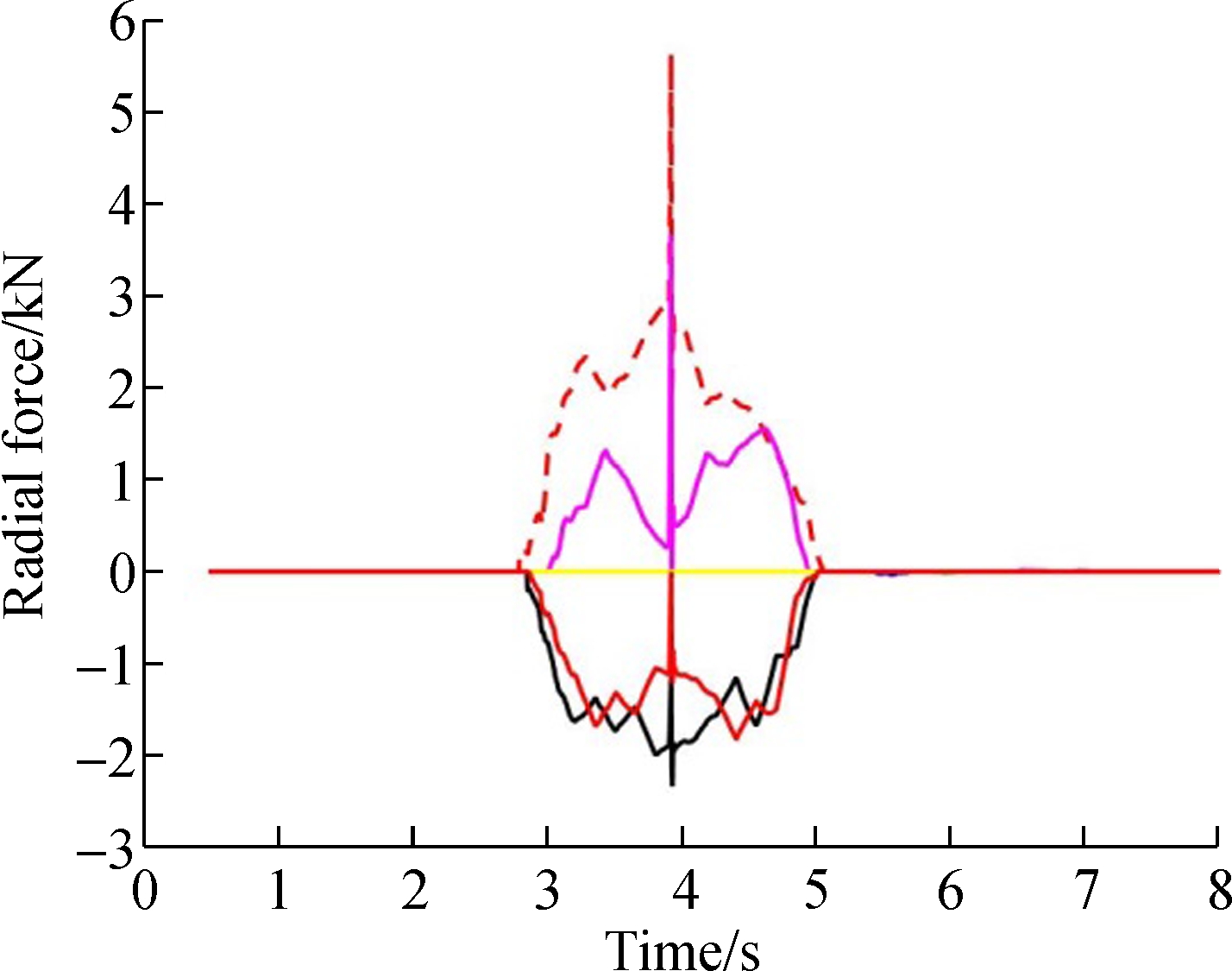
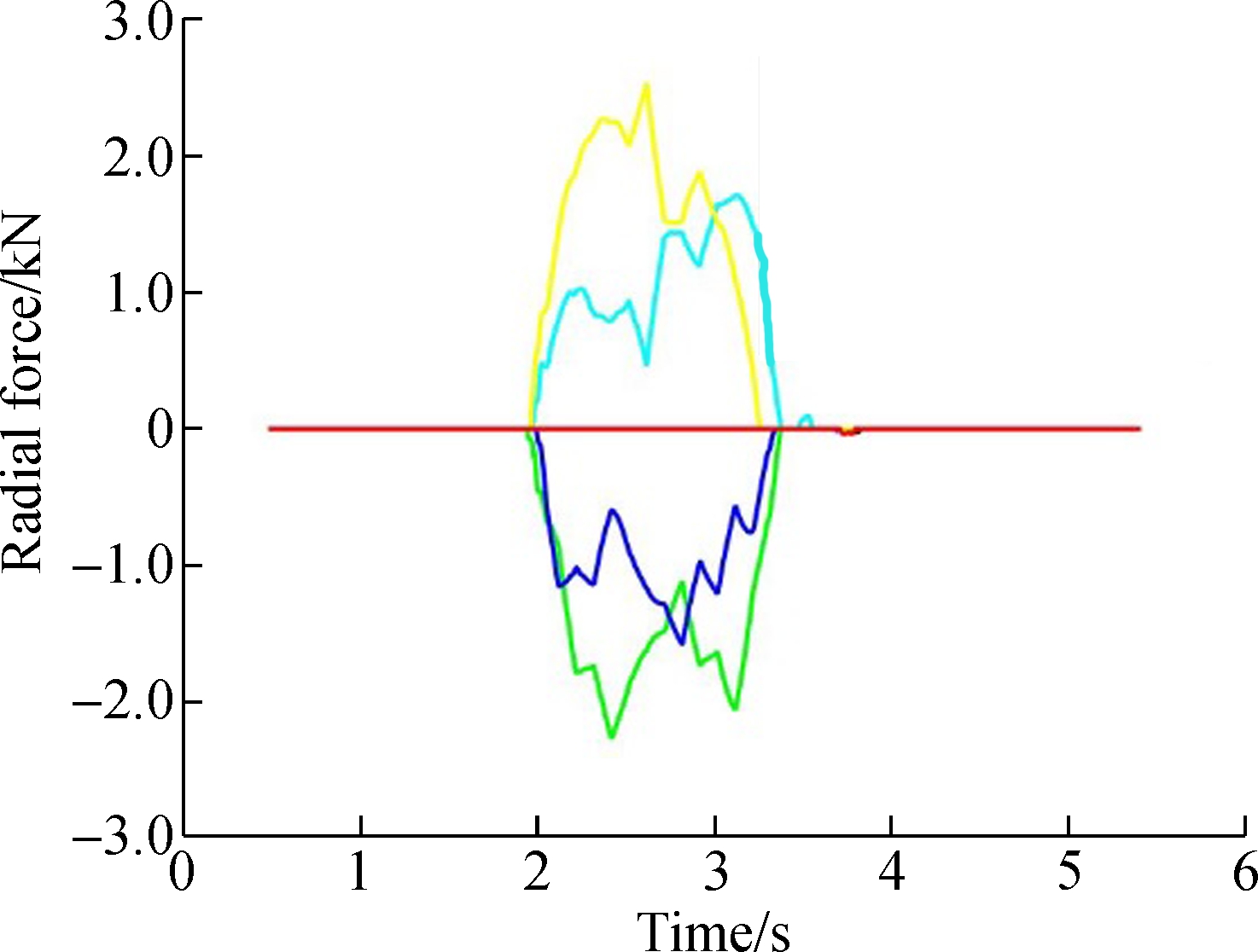
As can be seen from Figs.2 to 5, when the vehicle passes a curve, the maximum radial force of the guide wheels and stable wheels in the front left and rear right of the front bogie increases, but the maximum radial force of the guide wheels and stable wheels in the front right and rear left of the rear bogie increases. The rest of the guide wheels and the stable wheels hang in the air for a long time, which means that there is also a yawing motion of the bogies.
The working condition of AW3 is similar, as shown in Tab.2 and Tab.3. This work is carried out to ensure the tire forces under different loads are not either too strong or too weak. The variation for driving wheel forces are larger than that of AW0 which means that the rolling motion is stronger. Besides, weaker minimum forces mean that the vehicle under this condition more easily derails.
(a)

(b)
Fig.2 Radial force of the driving wheels in the front bogie at different speeds.(a) 10 km/h;(b) 15 km/h
(a)

(b)
Fig.3 Radial force of the driving wheels in the rear bogie at different speeds.(a) 10 km/h;(b) 15 km/h
(a)

(b)
![]()
Fig.4 Radial force of the guide wheels in the front bogie at different speeds.(a) 10 km/h;(b) 15 km/h

(a)
(b)
![]()
Fig.5 Radial force of the guide wheels in the rear bogie at different speeds.(a) 10 km/h;(b) 15 km/h
The stability of the vehicle when it passes through different curves is shown in Tab.4. When the radius of the curve becomes larger, the lateral stability of the vehicle improves. However, the vertical vibration of the vehicle does not change much. In order to prove the above speculation, the deflection angles of the vehicle when it passes a curve are also calculated, as shown in Fig.6. It can be learned from the figures that when the vehicle moves in and out of the curve, the yawing angle increases. When the speed increases from 10 to 15 km/h, the change of the car body’s yawing angle is not obvious. The vehicle’s rolling angle increases when the vehicle enters the curve. When the speed increases from 10 to 15 km/h, the maximum rolling angle of the car body increases greatly, which means that the car body rolls when the vehicle enters the curve. The higher the speed is, the more obvious the rolling motion is.
Tab.4 Sperling index under different working conditions

Working conditionAW0(R12m)AW3(R12m)AW3(R20m)10 km/h15 km/h10 km/h15 km/h10 km/h15 km/hLateral1.881 9593.123 2981.856 2633.131 4231.642 5012.726 874Vertical1.651 6281.162 1811.720 9581.199 3681.724 9611.152 487

(a)
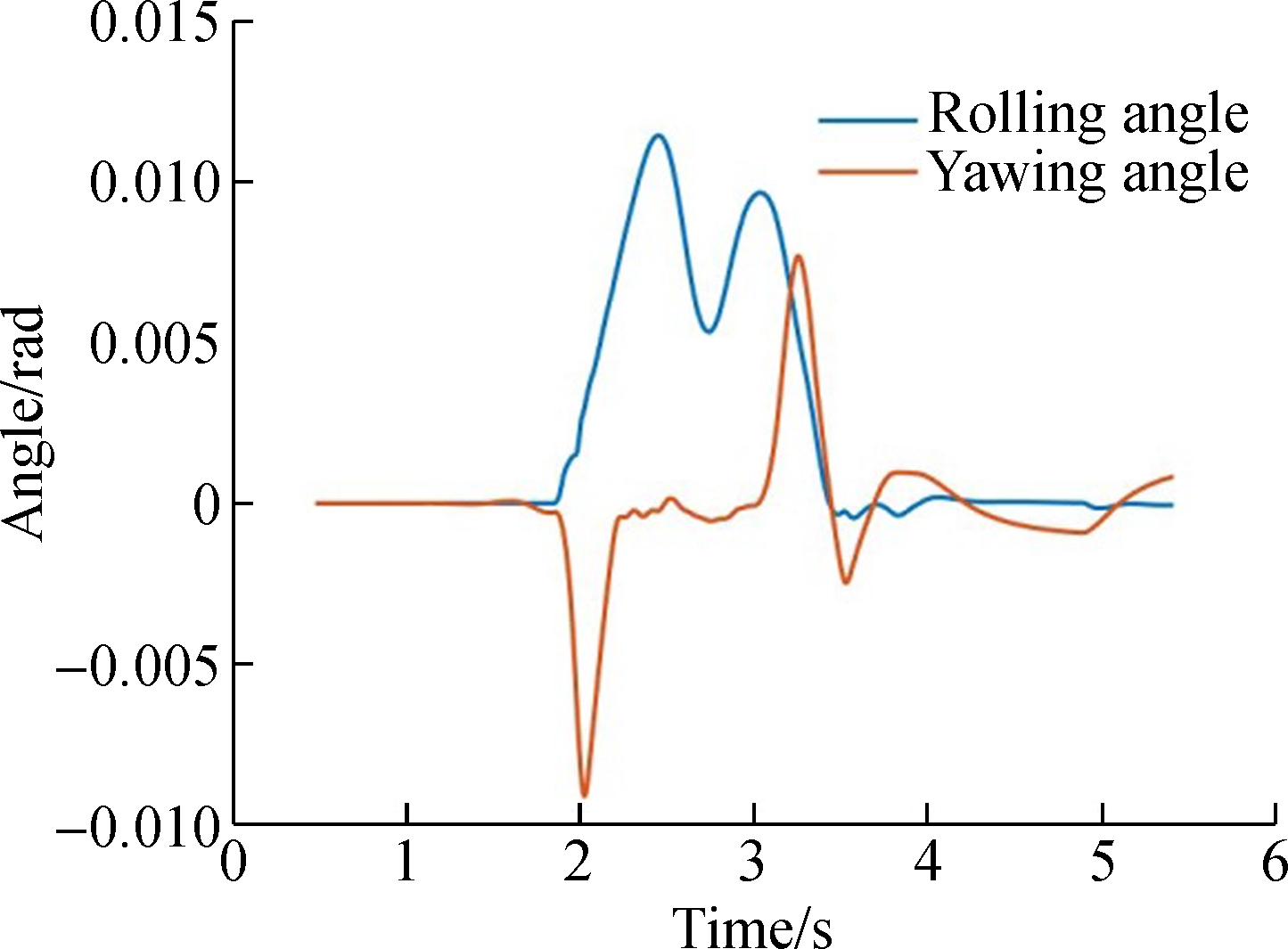
(b)
Fig.6 The rolling angle and yawing angle of the car body under different speeds. (a)10 km/h;(b)15 km/h
When the vehicle moves in a right turn curve, it yaws in the clockwise direction. Under the action of the guidewheel (stable wheel) forces, the front bogie yaws clockwise while the rear one yaws counterclockwise. Moreover, the two bogies and the car body rolls during the vehicle passing a curve. When the vehicle speed is high enough, the left drive wheel will derail and the anti-overturning moments are provided by the stable wheels. Then, the car body yaws in the counterclockwise direction when it moves out of the curve.
6 Vibration and Shock Analysis
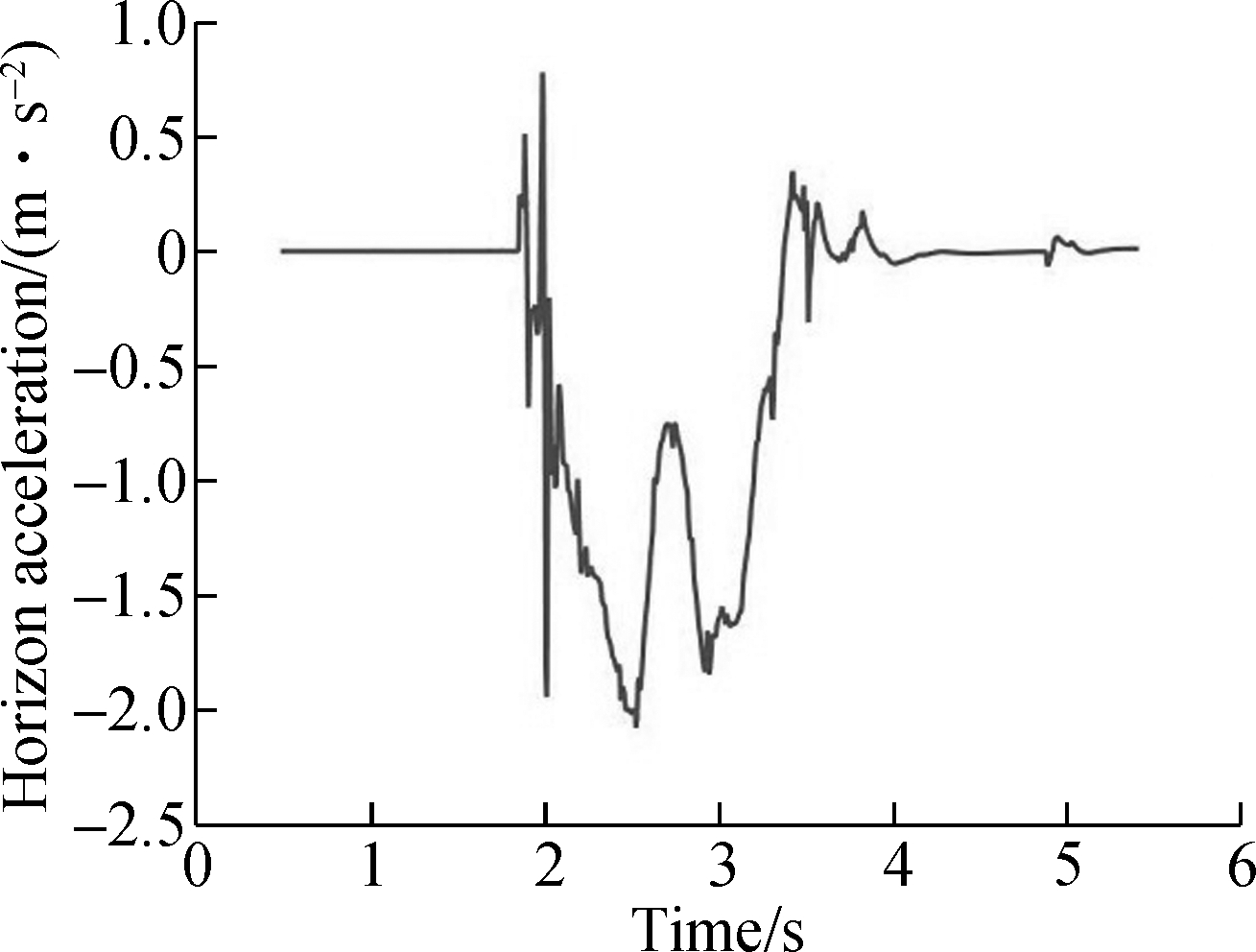
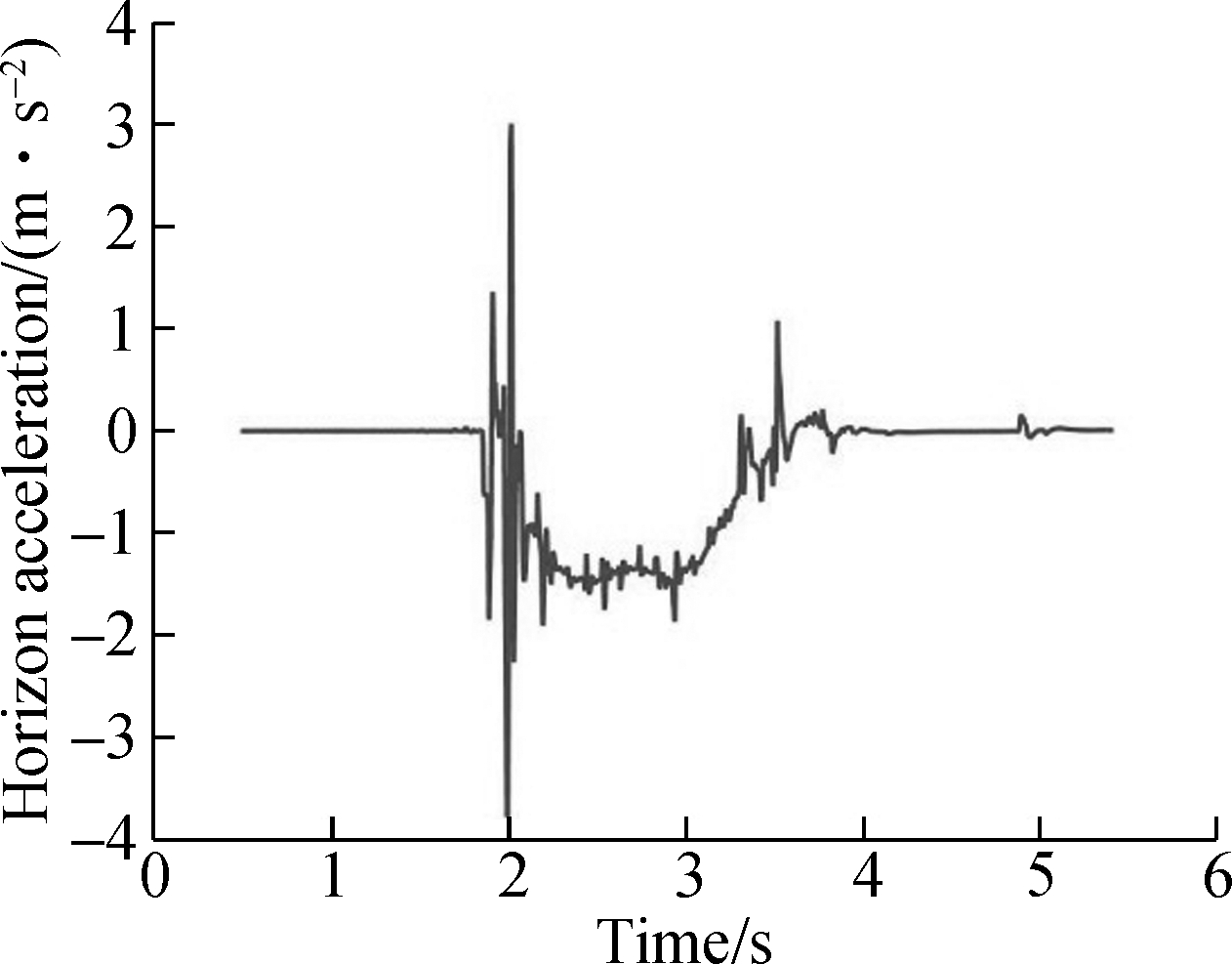
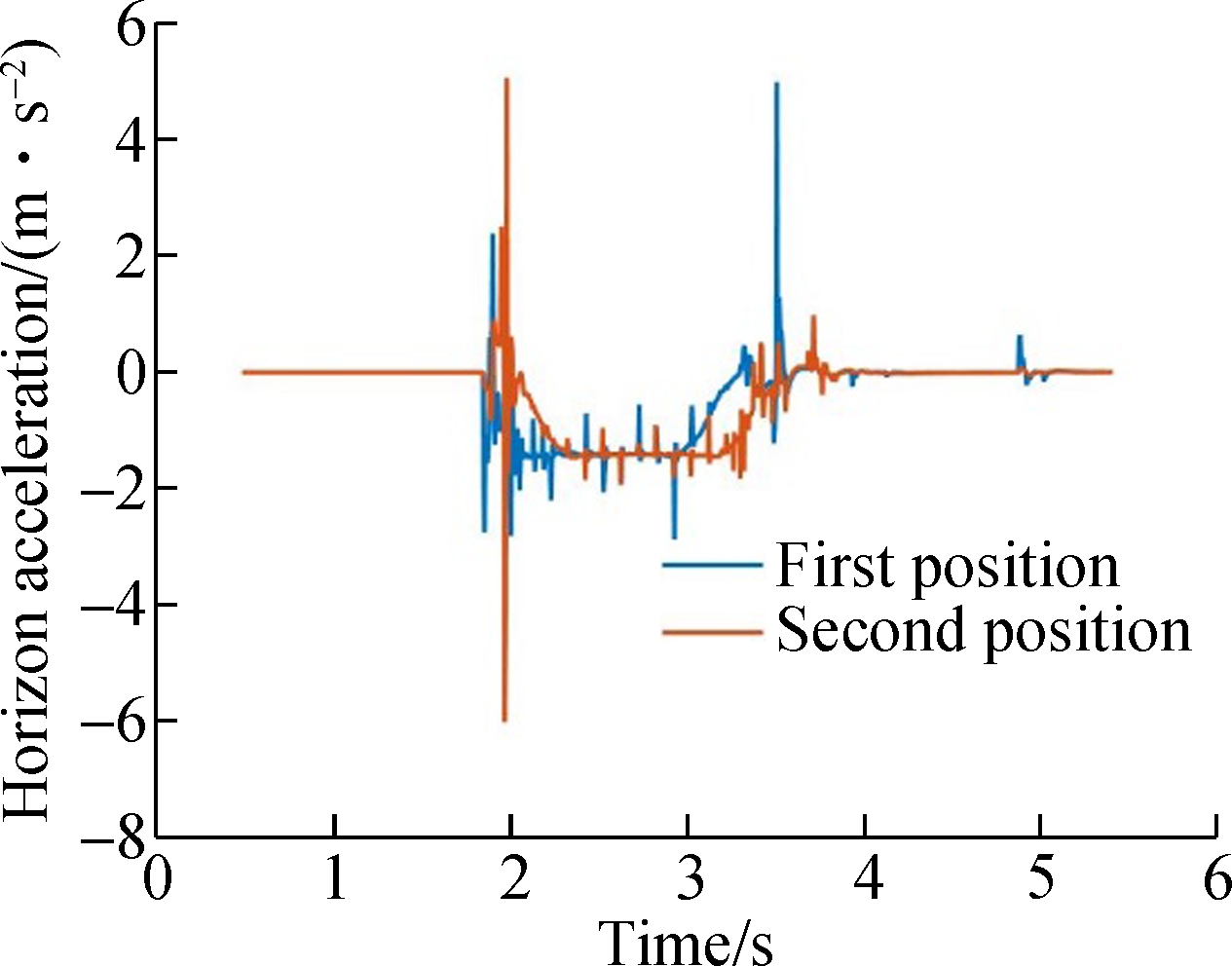
The simulation results of the accelerations are shown in Figs.7 and 8. The first/second positions denote the front/rear bogies, respectively. When the vehicle runs for about 4 s at the speed of 10 km/h, there is a lateral shock to the system. Due to the damping of the suspension system, the shock decreases when the micro suspended monorail travels from the frame to the U type suspender and then to the car body.
It can be seen from Fig.5 that the lateral acceleration increases when the vehicle speed is 15 km/h but the acceleration shock disapears.
It is known from Fig.3 that there is also a shock to the guide wheel forces when the vehicle speed is 10 km/h, which is caused by the wheel-rail collision. It is common in the running process of a traditional suspended monorail since there is a clearance between the guide wheel and guide rail surface. However, for the micro-suspended monorail, the shock will be fatal since the bogies are too light and easily overturned.
7 Detection of the Vehicle’s Crosswind Resistance
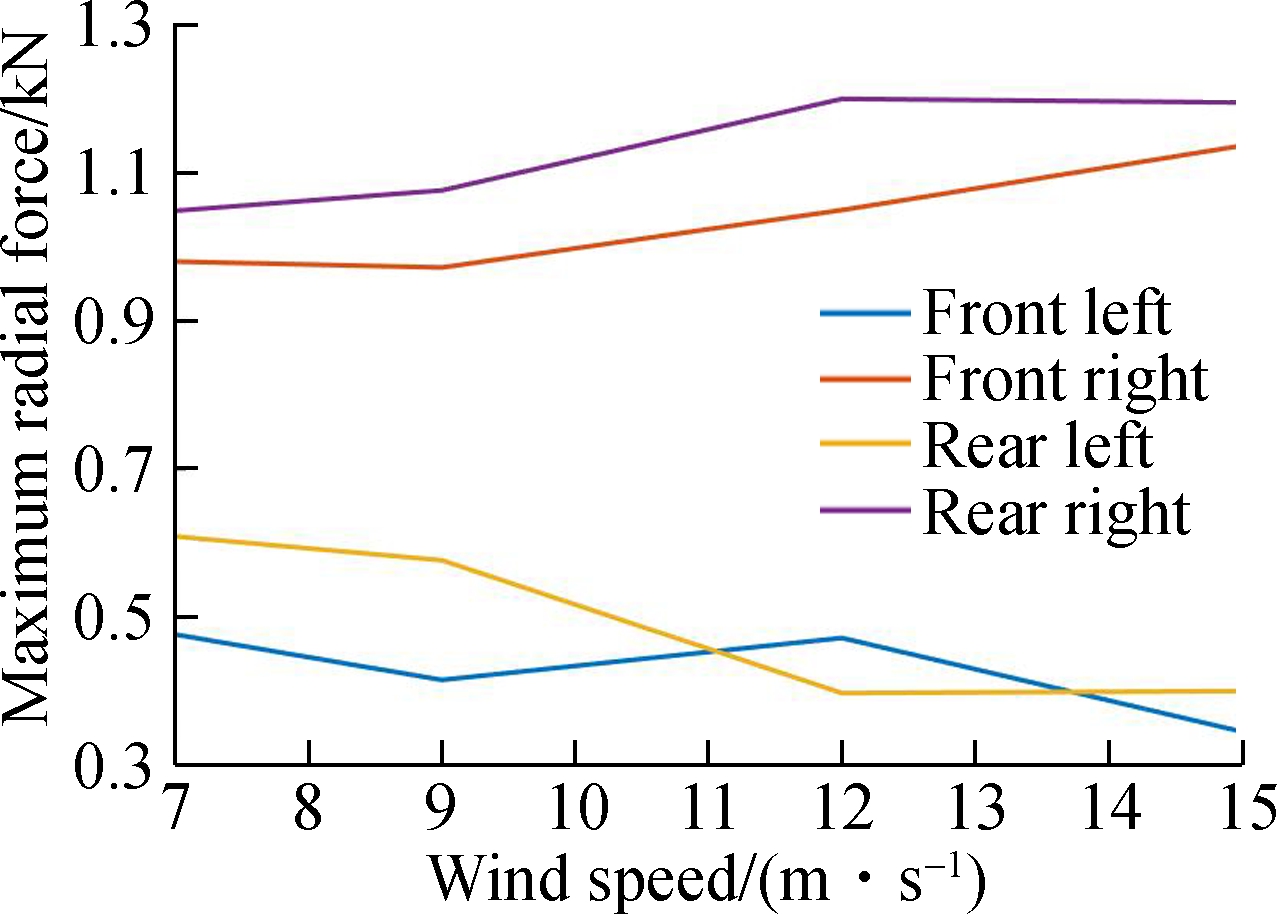
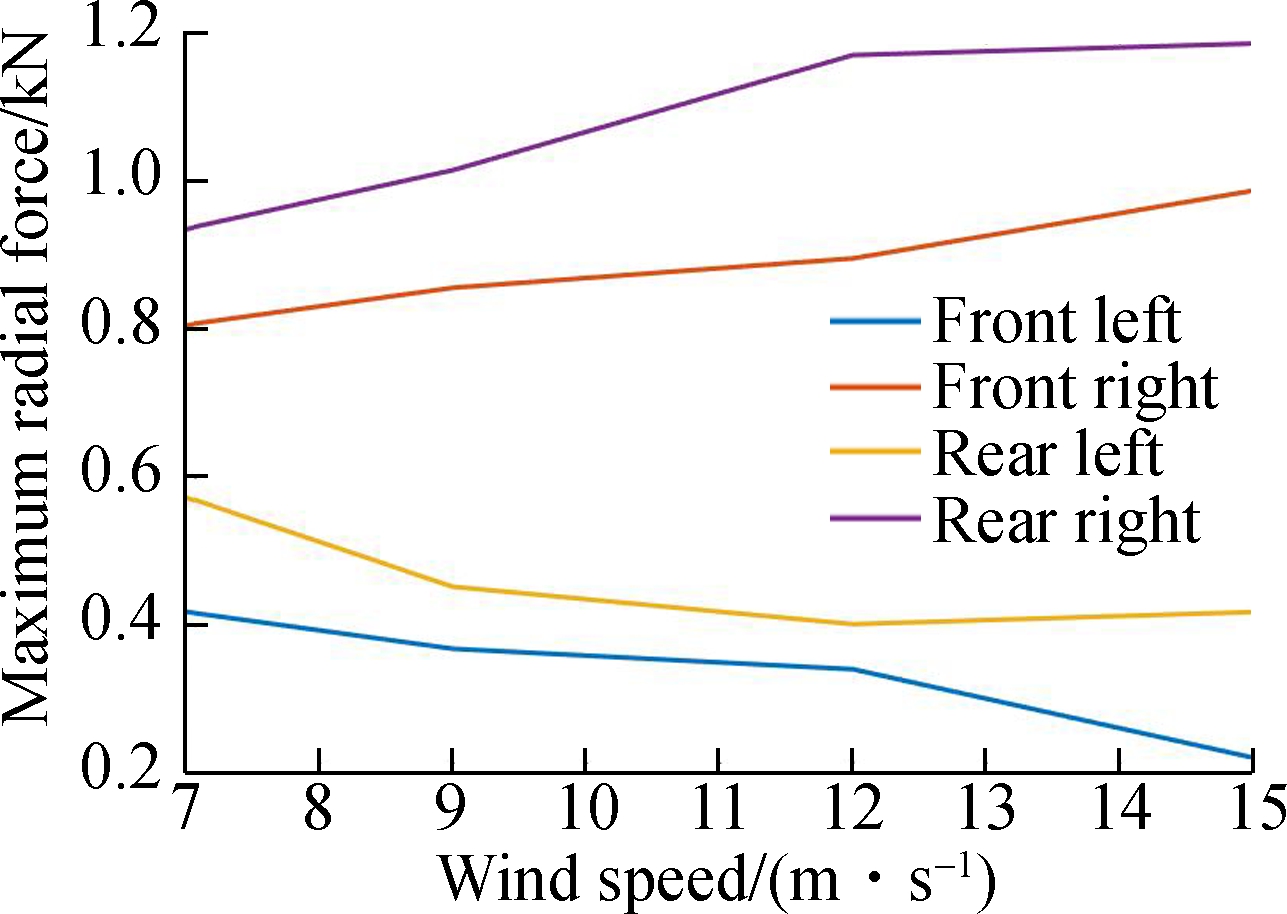
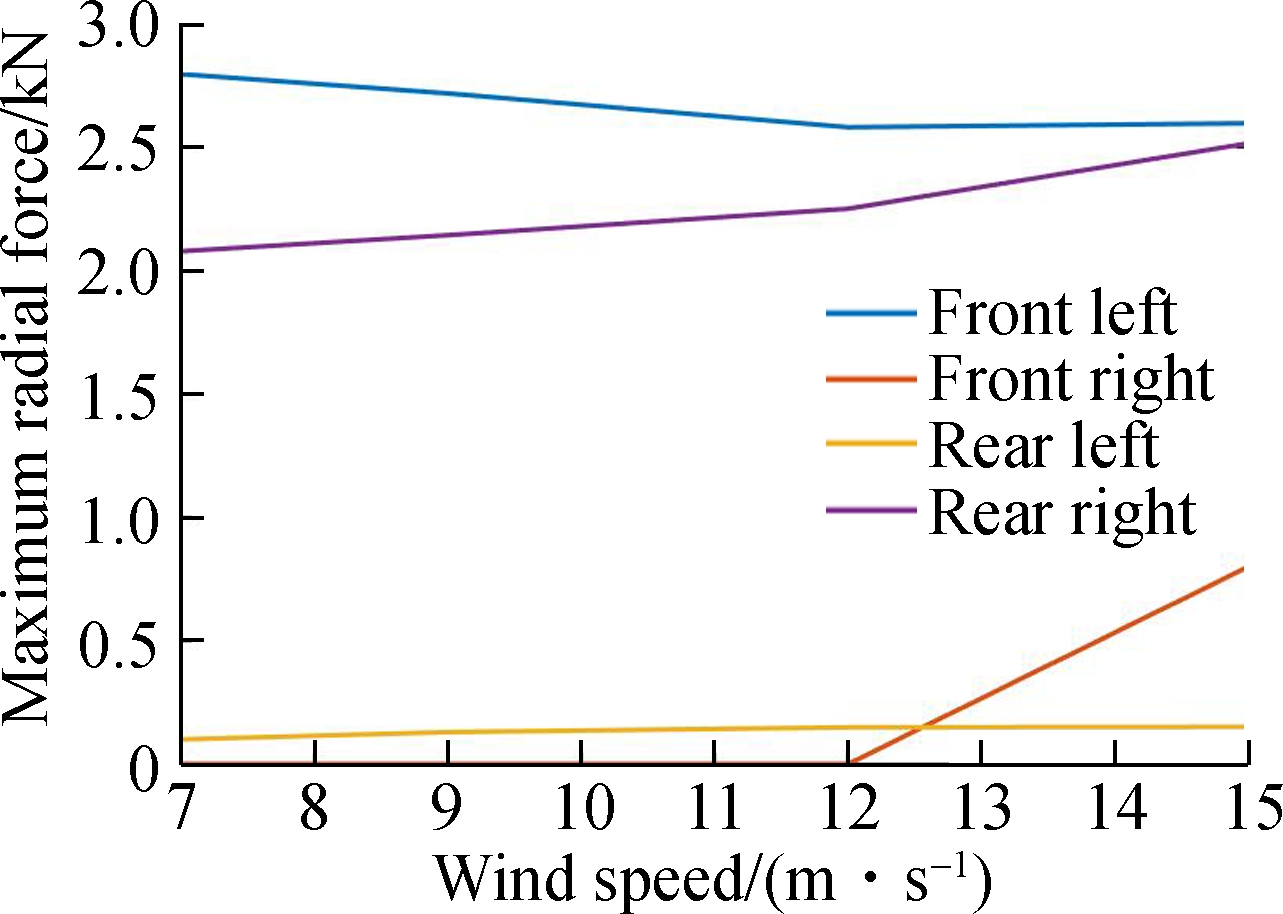
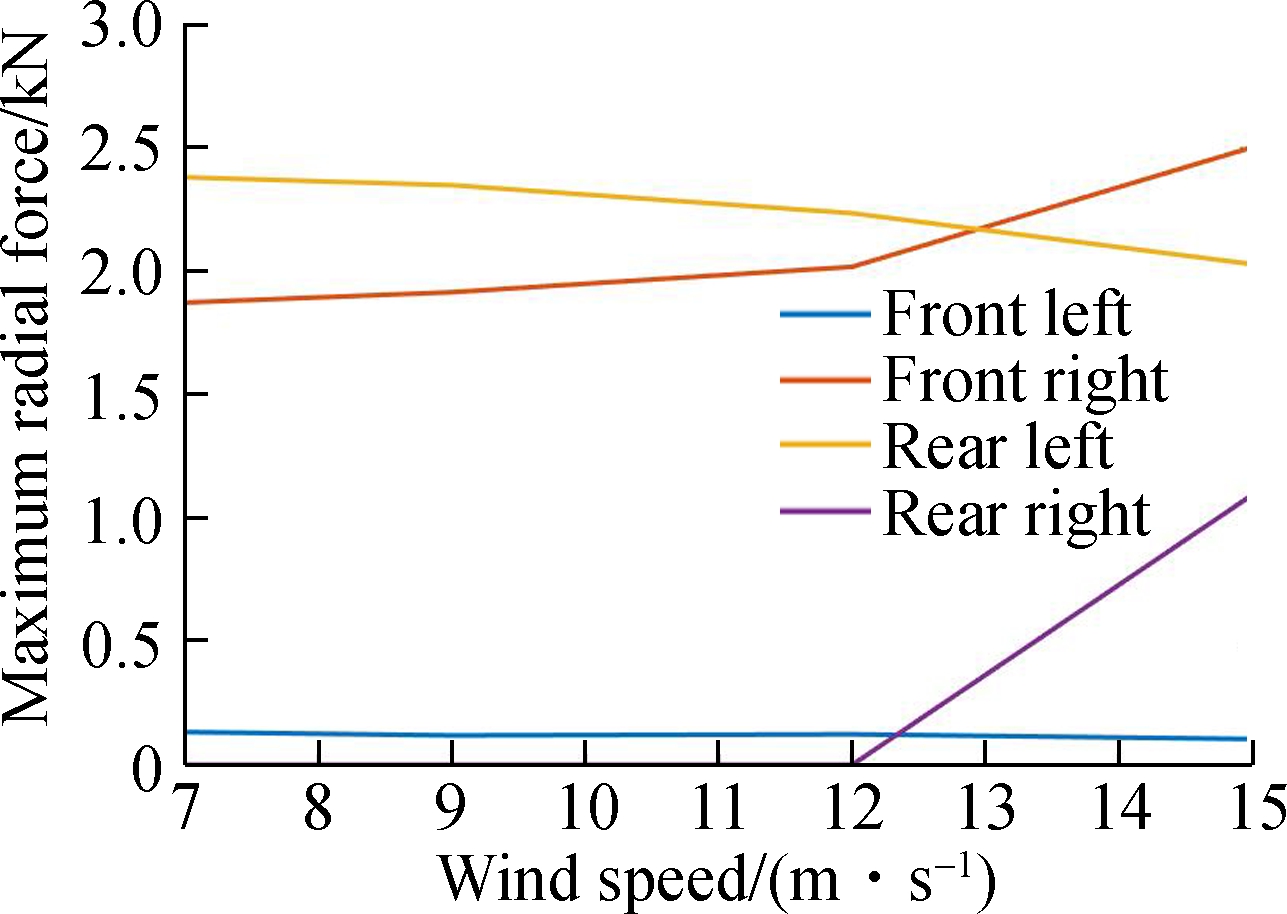
According to the Chinese standard GB 8408—2008, the micro suspended monorail vehicle cannot run when the wind speed is higher than 15 m/s. The simulation value of the crosswind wind speed ranging from 7 to 15 m/s is selected for simulation. According to the Chinese national standard CJJ96—2003, the wind load can be calculated. The maximum radial forces of tires under different wind loads can be checked when the vehicle passes the R12m curve at the speed of 15 km/h. The result is shown in Fig.9.
It can be seen from Fig.9 that the driving wheels will not derail under the action of the crosswind. It is known that the rear right guide wheel and front right stable wheel on the front bogie will make contact with the rail surface when the wind speed is above 10 km/h, but the rear right guide wheel and the front right stable wheel will derail. We also find that when the wind speed increases, the ride comfort index and the rolling angle generally increases, but the yawing angle decreases slightly. It can be known from Figs.9(c) and (d) that when the wind speed increases, the vehicle moves right and the guide wheels in the front right begin to make contact with the rail surface, resulting in some differences in ride comfort and deflection angle from previous ones. The yawing movement increases due to the new excitation from the guide wheel in the front right. It can also be learned from Fig.9(f) that when the wind speed increases, the stable wheel of the rear bogie derails due to the increase in the yawing movement.
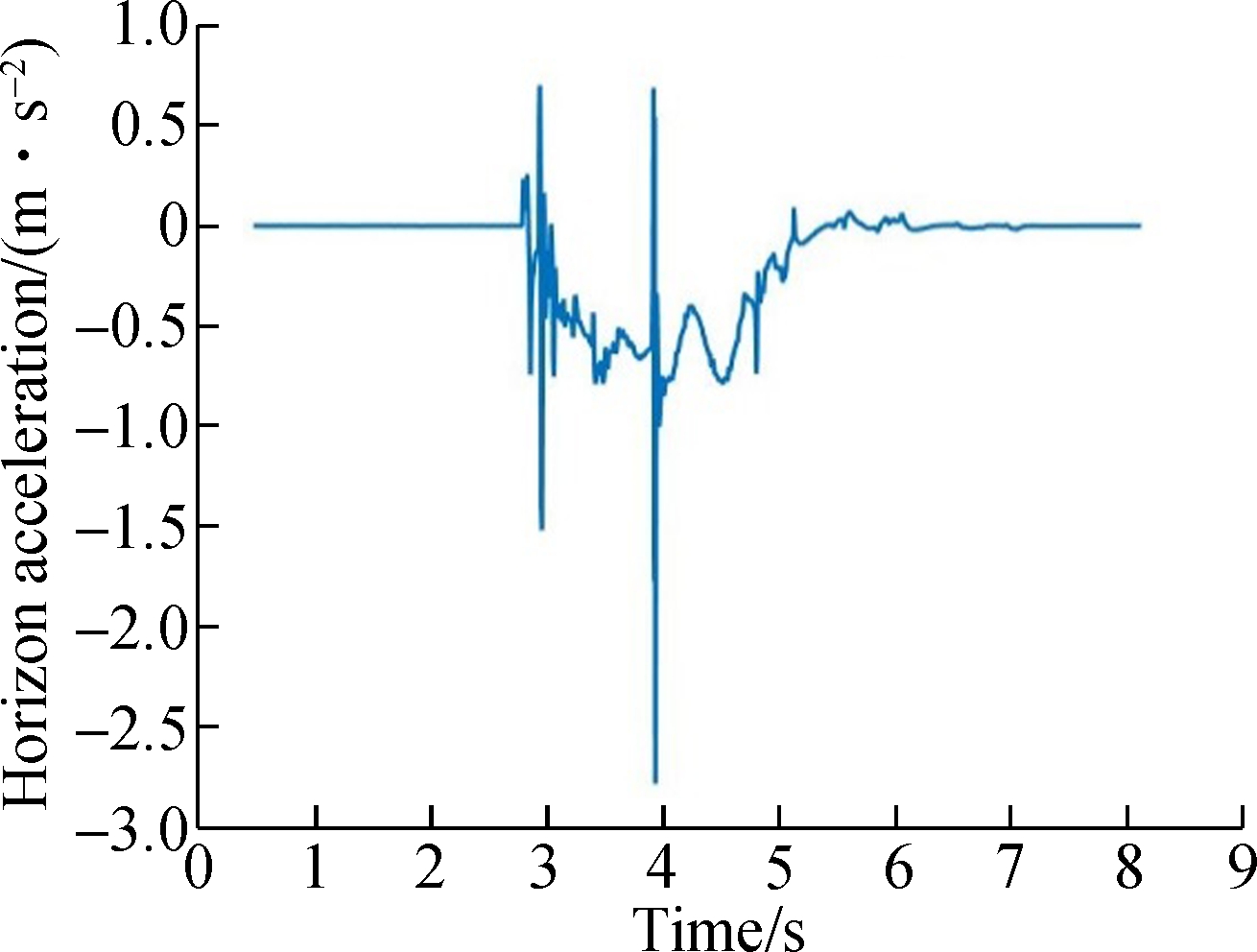
(a)
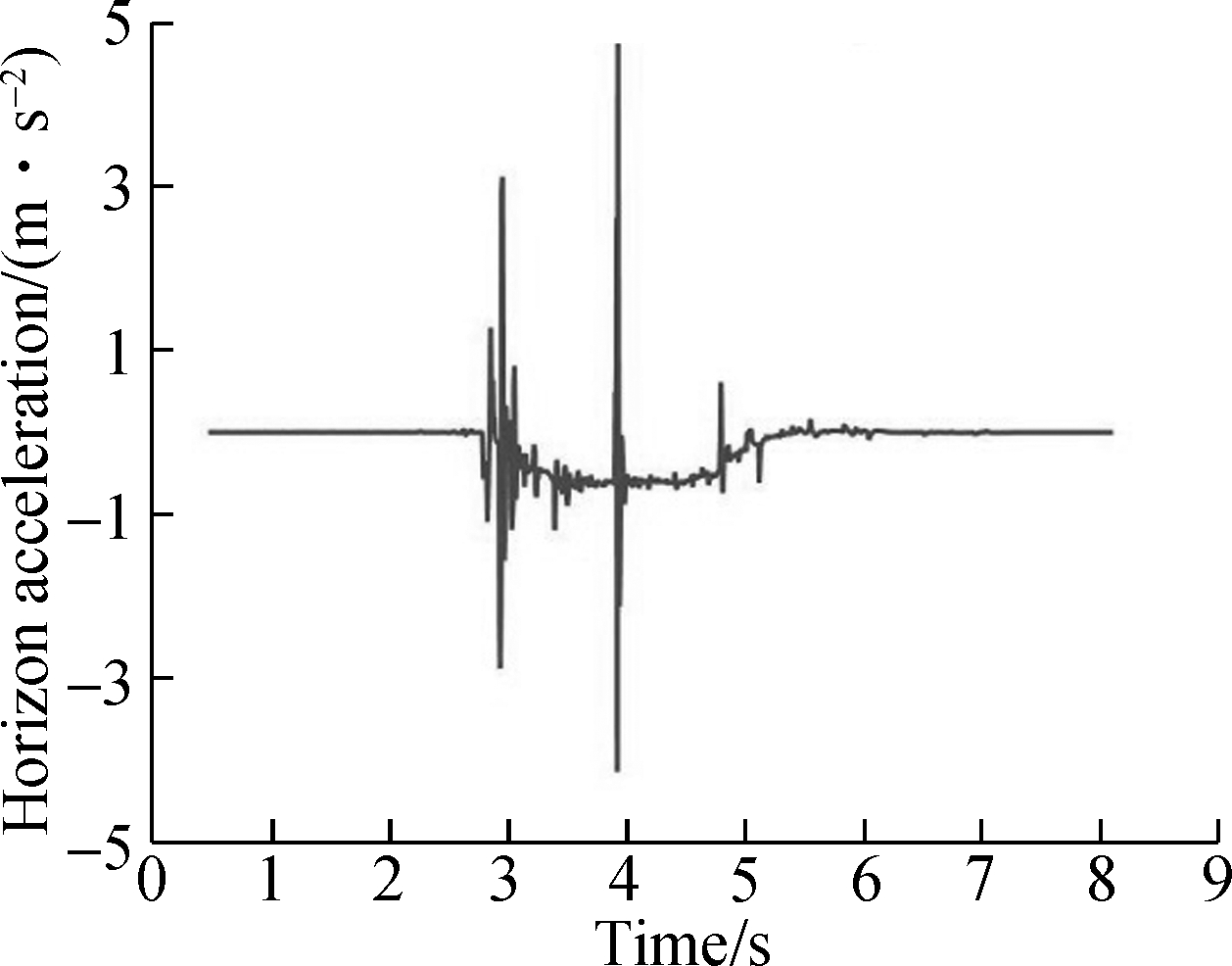
(b)
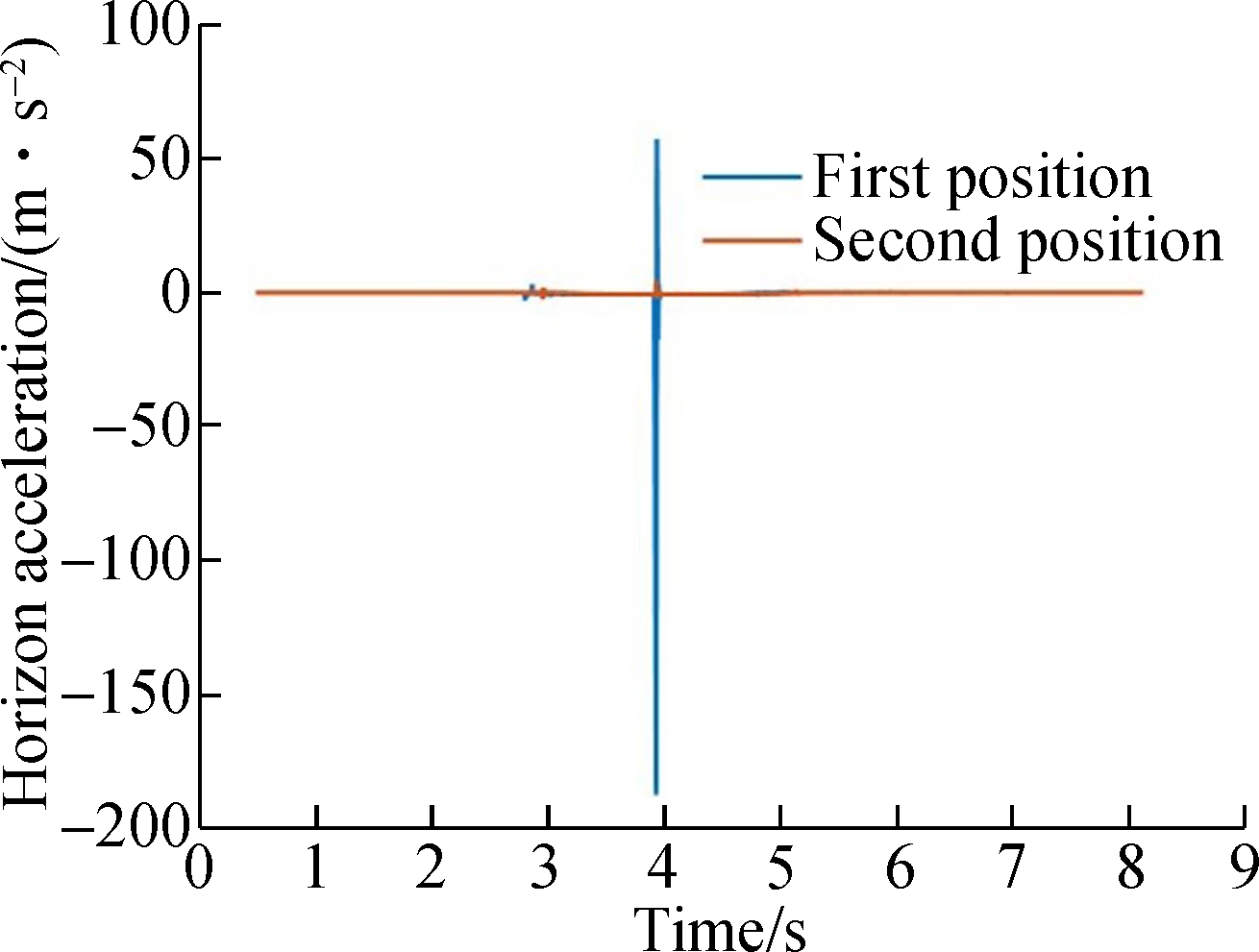
(c)
Fig.7 Acceleration of each component when the vehicle runs at 10 km/h speed.(a) Car body;(b) U type suspender;(c) Bogie
(a)
(b)
(c)
Fig.8 Acceleration of each component when the vehicle runs at 15 km/h.(a) Car body; (b) U type suspender; (c) Bogie
8 Collision Simulation Between Two Cars
In order to analyze the collision between the two vehicles, we let the front car remain stationary and let the rear car hit the front car at the speeds of 10 and 20 km/h, respectively. The impact parts are the respective couplers.
This complicated process can be simplified as a coupling model of two vehicles. It is assumed that there is a force between the two vehicles, shown as follows:
(6)
where xf denotes the longitudinal coordinate of the rear coupler joint of the front vehicle; xr is the longitudinal coordinate of the front coupler joint of the rear vehicle; and Kc is the coupler stiffness.
(a)
(b)
(c)
(d)

(e)

(f)

(g)

(h)
Fig.9 Dynamic responses of the vehicle under different wind loads.(a) Maximum radial force of the driving wheels in the front bogie;(b) Maximum radial force of the driving wheels in the rear bogie; (c) Maximum radial force of the guide wheels in the front bogie;(d) Maximum radial force of guide wheels in the rear bogie; (e) Maximum radial force of stable wheels in the front bogie;(f) Maximum radial force of stable wheels in the rear bogie; (g) Sperling index; (h) Deflection angle
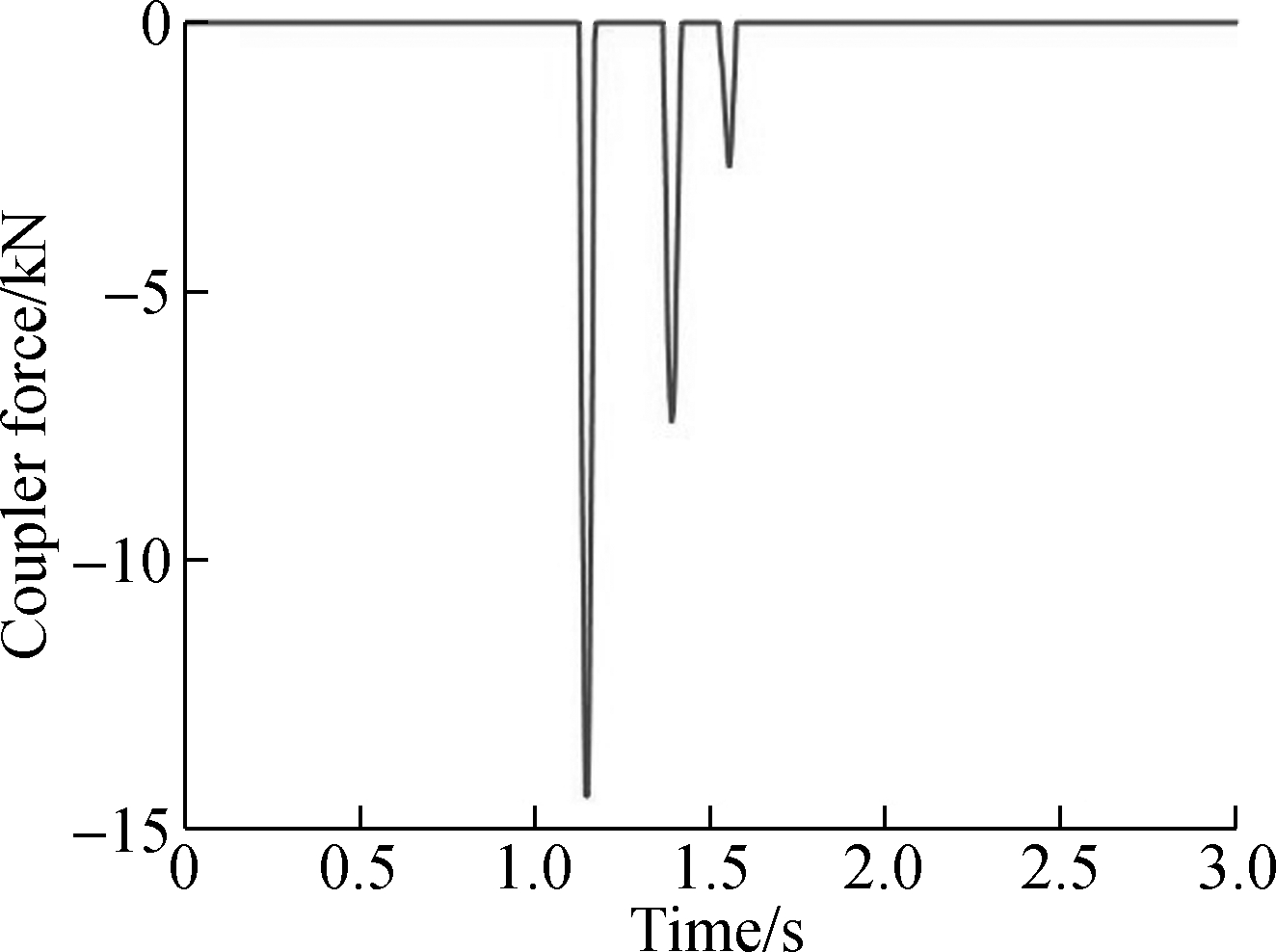
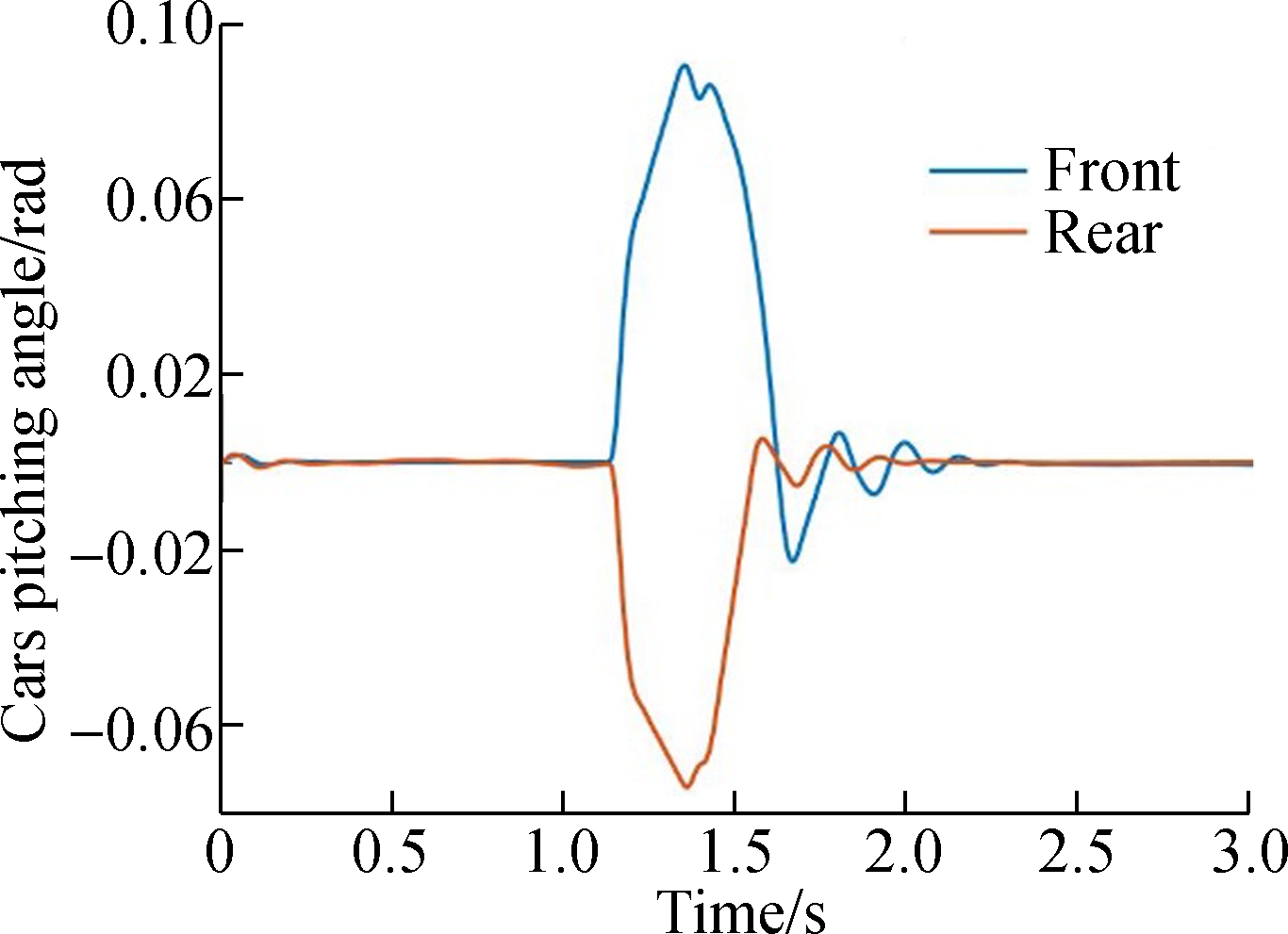
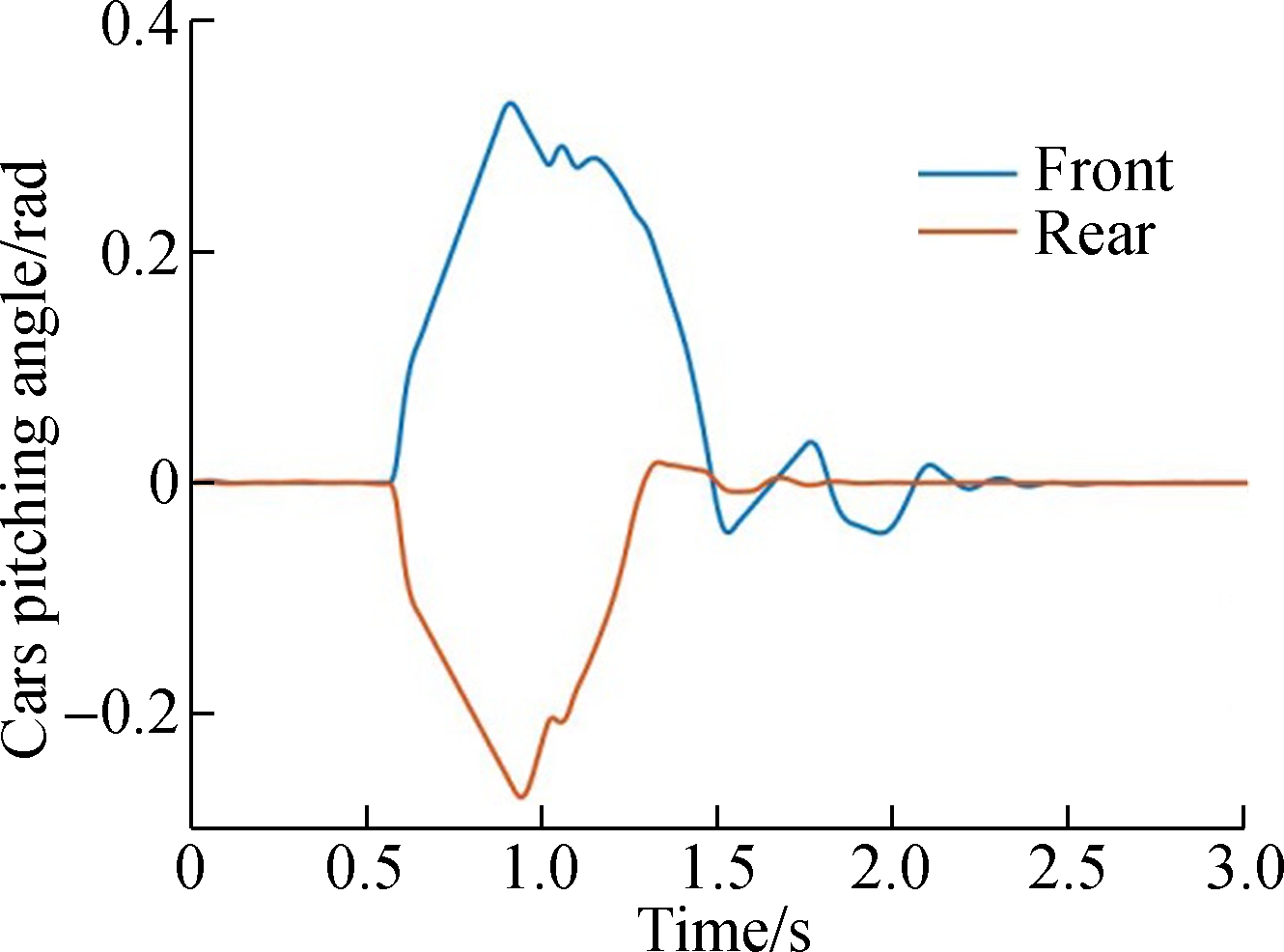
The results of the coupler force and pitching angle of the cars are shown in Fig.10.
It can be inferred from these figures that the coupler force is not a transient force but an intermittent force. When the two cars collide in one moment, pitching motion occurs in both cars. Both the rear parts of the front car and the front part of the rear car tilt up. The pitching motions of these two cars continue for a period asynchronously, making the couplers of these two cars collide several times. Then, the intermittent coupler forces are produced.
As is shown in the figures, when the rear vehicle hits the front one at the speed of 10 km/h, a 29 561 N coupler force is produced and the energy is dissipated by 3 times collisions. When the rear vehicle hits the front one at the speed of 10 km/h, a 44 474 N coupler force is produced. The pitching angle and coupler force of these two cars are much greater. Then, the energy should be dissipated by 4 times collisions.
9 Conclusions
1) Resonance can be avoided by avoiding external excitation at the main frequencies of every component. When the frequency is within the range of 1 to 10 Hz, the value of the weight function of the Sperling index F(f)/f is large, which means that the vibration in these frequencies can greatly affect the ride comfort of the vehicle. However, the natural modal frequencies of the micro-suspended monorail are not within that range, which means that the resonance will not affect the vehicle greatly.
2) When the vehicle moves in a right turn curve, it yaws in the clockwise direction. Under the action of the guidewheel (stable wheel) force, the front bogie yaws clockwise but the rear one yaws counterclockwise. Moreover, the two bogies and the car body roll during the curve passing process of the vehicle. When the vehicle speed is high enough, the left drive wheel will derail and the anti-overturning moments are provided by the stable wheels. Then, the car body yaws in the counterclockwise direction when it moves out of the curve. However, the ride comfort of the vehicle is good. It must be noticed that the shock to the guide wheel forces caused by the clearance between the guide wheel and rail surface will be fatal for this type of vehicle since the bogies are too light. However, this type of vehicle will not be easily overturned by the crosswind.
(a)

(b)
(c)
(d)
Fig.10 Dynamic responses of the car when the rear vehicle hits the front at different speeds.(a) Coupler force with the vehicle speed of 10 km/h;(b) Coupler force with the vehicle speed of 20 km/h; (c) Pitching angle of the car with the vehicle speed of 10 km/h; (d) Pitching angle of the car with the vehicle speed of 20 km/h
3) The collision simulation of two vehicles shows that there is an intermittent coupler force between two vehicles. When the two cars collide in one moment, pitching motion occurs in both cars. Both the rear parts of the front car and the front part of the rear car tilt up. The pitching motions of these two cars continue for a period of time asynchronously, making the coupler of these two cars collide several times. Then, the energy should be dissipated by the collisions.
4) This paper is merely a preliminary analysis of this kind of monorail and much research concerning the improvement of the dynamic properties of this monorail type is needed in the future.
[1]Grava S. Urban transportation systems, choices for communities [M]. New York: McGraw-Hill, 2003.
[2]Kuwabara T, Hiraishi M, Goda K, et al. New solution for urban traf c: Small-type monorail system[J] .Hitachi Review, 2001, 50(4):139-143.
c: Small-type monorail system[J] .Hitachi Review, 2001, 50(4):139-143.
[3]Kouroussis G, van Parys L, Conti C, et al. Prediction of ground vibrations induced by urban railway traffic: An analysis of the coupling assumptions between vehicle, track, soil, and buildings[J]. International Journal of Acoustics and Vibration, 2013, 18(4): 163-172. . DOI:10.20855/ijav.2013.18.4330.
[4]Sugawara M. Research on urban monorails corresponding to actual demand[J]. Journal of Japanese Monorail Association, 2000, 91: 2-26.
[5]Boehm E, Frisch H. The new operating system of the H-train in dortmund[J]. Verkehr und Technik,1994, 47: 465-470.
[6]Rahier H W, Scharf P. Sicherheitstechnische prüfung der fahrerlosen kabinenbahn des flughafens duesseldorf[J]. Signal und Draht, 2002, 94: 20-22.(in Germany)
[7]Zhang N, Xia H. Dynamic analysis of coupled vehicle-bridge system based on inter-system iteration method[J]. Computers & Structures, 2013, 114/115: 26-34. DOI:10.1016/j.compstruc.2012.10.007.
[8]Kouroussis G, Gazetas G, Anastasopoulos I, et al. Discrete modelling of vertical track-soil coupling for vehicle-track dynamics[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(12): 1711-1723. DOI:10.1016/j.soildyn.2011.07.007.
[9]Andersson A, O’Connor A, Karoumi R. Passive and adaptive damping systems for vibration mitigation and increased fatigue service life of a tied arch railway bridge[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(9): 748-757. DOI:10.1111/mice.12116.
[10]Ling L,Dhanasekar M, Thambiratnam D P. Dynamic response of the train-track-bridge system subjected to derailment impacts[J]. Vehicle System Dynamics, 2018, 56(4): 638-657. DOI:10.1080/00423114.2017.1398341.
[11]Kim J, LynchJ P. Experimental analysis of vehicle-bridge interaction using a wireless monitoring system and a two-stage system identification technique[J]. Mechanical Systems and Signal Processing, 2012, 28: 3-19. DOI:10.1016/j.ymssp.2011.12.008.
[12]Liu Y, Tan Z C, Yang C X. Refined finite element modeling of a damaged bridge with virtual distortion method coupling solid superelement[J]. Mechanical Systems and Signal Processing, 2017, 93: 559-577. DOI:10.1016/j.ymssp.2017.02.032.
[13]Wu S Q, Law S S. Evaluating the response statistics of an uncertain bridge-vehicle system[J]. Mechanical Systems and Signal Processing, 2012, 27: 576-589. DOI:10.1016/j.ymssp.2011.07.019.
[14]Chen Z,Xie Z P, Zhang J. Measurement of Vehicle-Bridge-Interaction force using dynamic tire pressure monitoring[J]. Mechanical Systems and Signal Processing, 2018, 104: 370-383. DOI:10.1016/j.ymssp.2017.11.001.
[15]Zhou S H, Song G Q, Wang R P, et al. Nonlinear dynamic analysis for coupled vehicle-bridge vibration system on nonlinear foundation[J]. Mechanical Systems and Signal Processing, 2017, 87: 259-278. DOI:10.1016/j.ymssp.2016.10.025.
[16]Jin Z B, Li G Q, Pei S L, et al. Vehicle-induced random vibration of railway bridges: A spectral approach[J]. International Journal of Rail Transportation, 2017, 5(4): 191-212. DOI:10.1080/23248378.2017.1338538.
[17]Antolín P, Zhang N, Goicolea J M, et al. Consideration of nonlinear wheel-rail contact forces for dynamic vehicle-bridge interaction in high-speed railways[J]. Journal of Sound and Vibration, 2013, 332(5): 1231-1251. DOI:10.1016/j.jsv.2012.10.022.
[18]Lei X, Noda N A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile[J]. Journal of Sound and Vibration, 2002, 258(1): 147-165. DOI:10.1006/jsvi.2002.5107.
[19]Kim C W, Kawatani M. Effect of train dynamics on seismic response of steel monorail bridges under moderate ground motion[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(10): 1225-1245. DOI:10.1002/eqe.580.
[20]Zhai W M, Xia H, Cai C B, et al. High-speed train-track-bridge dynamic interactions—Part I: Theoretical model and numerical simulation[J]. International Journal of Rail Transportation, 2013, 1(1/2): 3-24. DOI:10.1080/23248378.2013.791498.
[21]Lee C H, Kim C W, Kawatani M, et al. Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains[J]. Engineering Structures, 2005, 27(14): 1999-2013. DOI:10.1016/j.engstruct.2005.06.014.
[22]Kim Y S, Lim T K, Park S H, et al. Dynamic model for ride comfort evaluations of the rubber-tired light rail vehicle[J]. Vehicle System Dynamics, 2008, 46(11): 1061-1082. DOI:10.1080/00423110701759637.
[23]Tsunashima H. Dynamics of automated guideway transit vehicle with single-axle bogies[J]. Vehicle System Dynamics, 2003, 39(5): 365-397. DOI:10.1076/vesd.39.5.365.14146.
[24]Cai C B, He Q L, Zhu S Y, et al. Dynamic interaction of suspension-type monorail vehicle and bridge: Numerical simulation and experiment[J]. Mechanical Systems and Signal Processing, 2019, 118: 388-407. DOI:10.1016/j.ymssp.2018.08.062.
[25]Gou H Y, Zhou W, Yang C W, et al. Dynamic response of a long-span concrete-filled steel tube tied arch bridge and the riding comfort of monorail trains[J]. Applied Sciences, 2018, 8(4): 650. DOI:10.3390/app8040650.
[26]Wang H L, Zhu E Y. Dynamic response analysis of monorail steel-concrete composite beam-train interaction system considering slip effect[J]. Engineering Structures, 2018, 160: 257-269. DOI:10.1016/j.engstruct.2018.01.037.
[27]Naeimi M, Tatari M, Esmaeilzadeh A, et al. Dynamic interaction of the monorail-bridge system using a combined finite element multibody-based model[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics, 2015, 229(2): 132-151. DOI:10.1177/1464419314551189.
[28]Meisinger R. Dynamic analysis of the Dortmund University campus sky train[R].Nürnberg, Germany: Technische Hochschule Nürnberg Georg Simon Ohm, 2009-03-19.
[29]Meisinger R. Analysis of the lateral dynamics of a sky train with periodic track irregularities[C]// Proceedings of the Second International Conference on Dynamics, Vibration and Control. Beijing, China, 2006:522-534.
[30]Zhong Y M. Analysis of flexible car body of straddle monorail vehicle[J]. IOP Conference Series: Materials Science and Engineering, 2018, 324: 012071. DOI:10.1088/1757-899x/324/1/012071.
[31]Guo Q, Wang P, Chen J Y, et al. Dynamic analysis on suspended monorail vehicles passing through turnouts[J]. IOP Conference Series: Materials Science and Engineering, 2018, 439: 042078. DOI:10.1088/1757-899x/439/4/042078.
[32]Muller S. Engineering operation and state of development of the H-Bahn system[J]. Siemens Review, 1978, 45:523-527.
[33]Bao Y L, Li Y L, Ding J J. A case study of dynamic response analysis and safety assessment for a suspended monorail system[J]. International Journal of Environmental Research and Public Health, 2016, 13(11): 1121-1138.DOI:10.3390/ijerph13111121.
[34]Pu Q W, Chen X H, Tao G A, et al. Bogie of hanged-type monorail vehicle[J]. Electric Drive for Locomotives, 2015(2): 90-93. DOI:10.13890/j.issn.1000-128x.2015.02.022.(in Chinese)
[35]Xiao T, Pu Q W, Chen X H, et al. Dynamic simulation of hanged-type monorail vehicle[J]. Electric Drive for Locomotives, 2015(2): 10-13. DOI:10.13890/j.issn.1000-128x.2015.02.004. (in Chinese)
[36]Jiang Y Z, Wu P B, Zeng J, et al. Comparison of the curve negotiation properties of two different articulated monorail vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2019, 233(8): 831-843. DOI:10.1177/0954409718810946.
[37]Jiang Y Z, Wu P B, Zeng J, et al. Multi-parameter and multi-objective optimisation of articulated monorail vehicle system dynamics using genetic algorithm[J]. Vehicle System Dynamics, 2020, 58(1): 74-91. DOI:10.1080/00423114.2019.1566557.
[38]Jiang Y Z, Wu P B, Zeng J, et al. Detection and alleviation of the abnormal vibration of the monorail based on experiment and simulation[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2019, 38(2): 282-295. DOI:10.1177/1461348419825605.
[39]Jiang Y Z, Zhong W S, Wu P B, et al. Prediction of wheel wear of different types of articulated monorail based on co-simulation of MATLAB and UM software[J]. Advances in Mechanical Engineering, 2019, 11(6): 168781401985684. DOI:10.1177/1687814019856841.
[40]Jiang Y Z, Wu P B, Zeng J, et al. Simplified and relatively precise back-calculation method for the pavement excitation of the monorail[J]. International Journal of Pavement Engineering, 2019: 1-18. DOI:10.1080/10298436.2019.1623401.
[41]Jiang Y Z, Wu P B, Zeng J, et al. Researches on the resonance of a new type of suspended monorail vehicle-bridge coupling system based on modal analysis and rigid-flexible coupling dynamics[J]. Vehicle System Dynamics, 2019: 1-20. DOI:10.1080/00423114.2019.1668029.
[42]He Q L, Cai C B, Zhu S Y, et al. Key parameter selection of suspended monorail system based on vehicle-bridge dynamical interaction analysis[J]. Vehicle System Dynamics, 2020, 58(3): 339-356. DOI:10.1080/00423114.2019.1577470.
[43]Jiang Y Z, Wang Y M, Xie Q. Scheme and analysis of a kind of suspended monorail’s bogie structure[J]. Electric Drive for Locomotives, 2015(6): 56-59. DOI:10.13890/j.issn.1000-128x.2015.06.015.(in Chinese)
[44]Jiang Y Z, Wang Y M, Xie Q. Analysis of the dynamics and stationarity of suspend monorail[J]. Urban Mass Transit, 2017, 4:97-100. (in Chinese)
[45]Sichuan Engineering Construction Bureau. DBJ51/T099—2018 Design standard for suspended monorail[S].Chengdu: Sichuan Standard Press,2016. (in Chinese)