High-speed rotating structures form friction in the end, which results in an unstable operation of the system and brings frictional vibration and noise. This is a common phenomenon in engineering, for instance, brakes, clutches, compressors’ crankshafts and the train wheel-rail. The mechanical model of this end rotating friction structure is a pair of high-speed disc tribological pairs. Several physical mechanisms that attempt to explain unstable friction-induced vibration have been proposed in the literature and were reviewed in Ref.[1]: the negative friction slope[2], sprag-slip instability[3], stick-slip instability[4], and mode-coupling instability[5]. However, there has been no universal consensus of an explanation for friction phenomena and the dynamic behavior of friction-induced vibration is not fully understood.
For reducing the impact of friction on engineering and the environment, many studies have been carried out with analytical, computational and experimental techniques. To explore the frictional system, the early achievements are attributed to the dry frictional stick-slip self-excited vibration[6] and unstable structural vibration[7]. Stick-slip is often caused by the nonlinear stiffness effect[8] or nonlinear discontinuity in μ-v friction curve[9]. Hereby, the Stribeck coefficient is usually included in the stick-slip analysis to analyze the system stability and determine the critical speed of the dynamic model[10-11]. Whereas, stick-slip theory ignores the interaction between two contacting surfaces. To overcome this shortcoming, elastic or flexible discs have been adopted. Ouyang et al.[12] examined the transverse instability of an elastic disc under the action of a rotating friction slider with stick-slip vibration. Ouyang and Mottershead[13] investigated the instability of the transverse vibration of a disk excited by two co-rotating sliders on either side of it, taking into account the bending couple acting in the circumferential direction produced by the different friction forces on the two sides of the disk. Studies show that the modal coupling theory can explain most friction phenomena under different friction causes. Hoffmann and Gaul[5] studied the qualitative and quantitative aspects of the mode-coupling instability with the presence of structural damping in sliding friction systems. Kang[14] analyzed the dynamic instability induced by friction in the ball joint system and presented the conditions of the mode-coupling instability. Sui and Ding[15] established a pad-on-disc frictional model and carried out the eigenvalue analysis to evaluate the stability of the pad considering the stochastic variation of frictional coefficients and the contact effect.
The features of contact at the friction interface of the disc are ignored in most of the studies mentioned above. Actually, the contact stiffness is inevitably affected by the tribological pairs under the contact condition, causing the variety in system instability. For establishing an accurate dynamic analysis model, the contact stiffness model should be proposed in addition. As the fractal model can simulate the contact state with high precision, researchers have developed some fractal contact stiffness models and explored the influence of vital parameters on the model such as the fractal dimension D, the fractal scaling coefficient G and the applied load[16-19]. Due to the effects of friction, some scholars put forward some modified models to correct the contact stiffness[20-21]. It can be concluded that the contact stiffness is modifiable with various system characteristic parameters.
Therefore, a dynamic analysis model of the rotating tribological pair system on the circular-disc end face for determining the system stability is proposed according to the Stribeck effect and fractal contact characteristics in this paper. The dynamic differential equation of the system is modeled by the Lagrange equation. The friction torque considering the Stribeck effect is produced, and the normal contact stiffness and the tangential contact stiffness are established through the fractal theorem. The system equation is deduced and the criterion of system stability is given. The system stability is investigated and discussed by the numerical simulation analysis of the effects of applied loads, Stribeck coefficients, and fractal parameters D and G. The achievements of this work will serve as a reference and a theoretical support for the analysis of the dynamic performance of frictional systems.
1 Dynamic Model of Rotating Tribological Pair System on the End Face
The instability of the friction pair is the cause of the instability of the system. Studying the rotational freedom and axial freedom of the friction pair can accurately describe the motion state of the friction pair. The dynamic model of a non-damping system is established, as shown in Fig.1. m1and J1 represent the mass and torque of inertia of the active part, respectively; m2 and J2 represent the mass and torque of inertia of the driven part; both of them are metal parts. The displacement x1 is along the X direction; θ1 and θ2 are the rotation angles of the active and driven parts. The driven part connecting to the base is subject to the elastic constraints of k1 and k2; k1 is in the X direction and k2 is in the direction of the circumference tangent. The parameter kn is the normal contact stiffness and kt represents the tangential contact stiffness, and they are used to connect the active part and the driven part. The load p is applied along the X direction; M0 is the driving torque of the active part. r1 and r2 are the radii of the inner and outer rings of the pair on the contact surface, as shown in Fig.1(b). We assume that point B and point B′ are in the same position; point B is on the surface of the active part, but point B′ is on the driven part; there is a spring connecting two points in the circumference tangential direction, so kt is the total tangential contact stiffness on the contact surface.
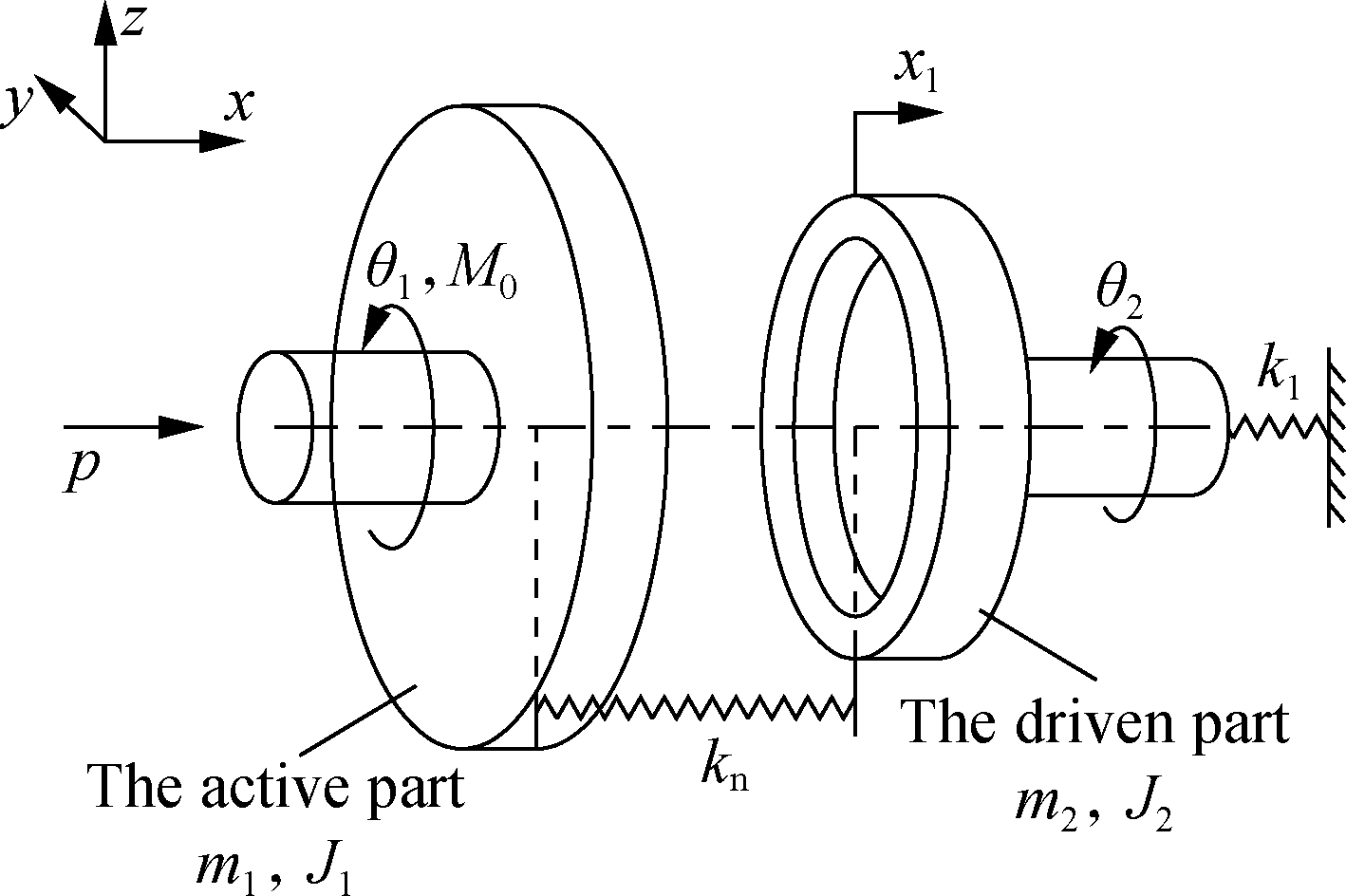
(a)

(b)
Fig.1 The rotating tribological pair system on the circular-disc end face. (a) Diagram of friction pair system; (b) The contact surface
In a system dynamics analysis, it is worth considering whether the flexibility of components affects the dynamic calculations. Generally speaking, the natural frequencies of the metal components being studied in this paper are much higher, and their thicknesses are not thin, so the flexibility of the component can be ignored. With the Lagrange system modeling method, the general form of the Lagrange second-class equation can be described as
(1)
where T is the kinetic energy of the system; V is the potential energy of the system; qi is the generalized coordinate of the system; ![]() is the generalized force of the system.
is the generalized force of the system.
Then, we have the dynamic differential equation of the system,
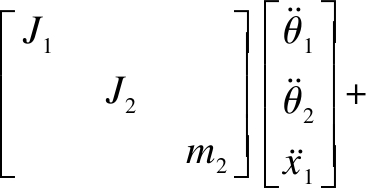
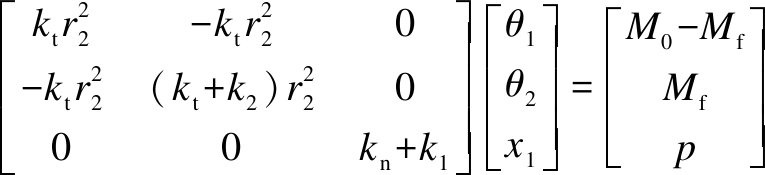
(2)
Consequently, the dynamic model of the rotating tribological pair system on the end face is set up, and it is a basic equation for exploring the system stability. The friction, a cause of system instability, can generate a negative damping in systems. Among the studies mentioned above, most of them modeled the friction force in the rotating system, which cannot describe the frictional features of the complete contact surfaces precisely; thus, the friction torque Mf taking into account the Stribeck effect is adopted in this paper. Under the consideration of the contact stiffness, the values of kn and kt are often given definitely, omitting the contact characteristics and the effect of friction. However, the contact state is also a significant factor of the system stability, which can alter the systemic stable state, so the contact stiffness should be established correctly. The specific modeling progresses are given in the following sections.
2 Friction and Contact Mathematical Model
2.1 Stribeck friction torque model
When the friction phenomenon is described by differential equations, the friction models are roughly divided into two categories: the static friction model and the dynamic friction model[22]. Armstrong-Hélouvry and Soom[23] suggested that a good static friction model could approximate the actual friction with 90% accuracy. For mathematically representing the Stribeck phenomenon, an extensively used model describing the Stribeck effect, the Gauss index model, is employed, in which the Stribeck friction coefficient dependent on the relative velocity is approximated by the following function:
fs(v)=μk+(μs-μk)e(-v/vs)2
(3)
where fs(v) is the Stribeck friction coefficient; μk is the sliding friction coefficient; μs is the maximum static friction coefficient; vs is the Stribeck coefficient.
Then, the first derivative of fs(v) is
(4)
Fig.2 exhibits the friction coefficient curves at different Stribeck coefficients with μs=0.18 and μk=0.12, which evidently illustrate the negative slope of friction-velocity. Therefore, the Stribeck coefficient should be deliberated in order to evaluate friction accurately.
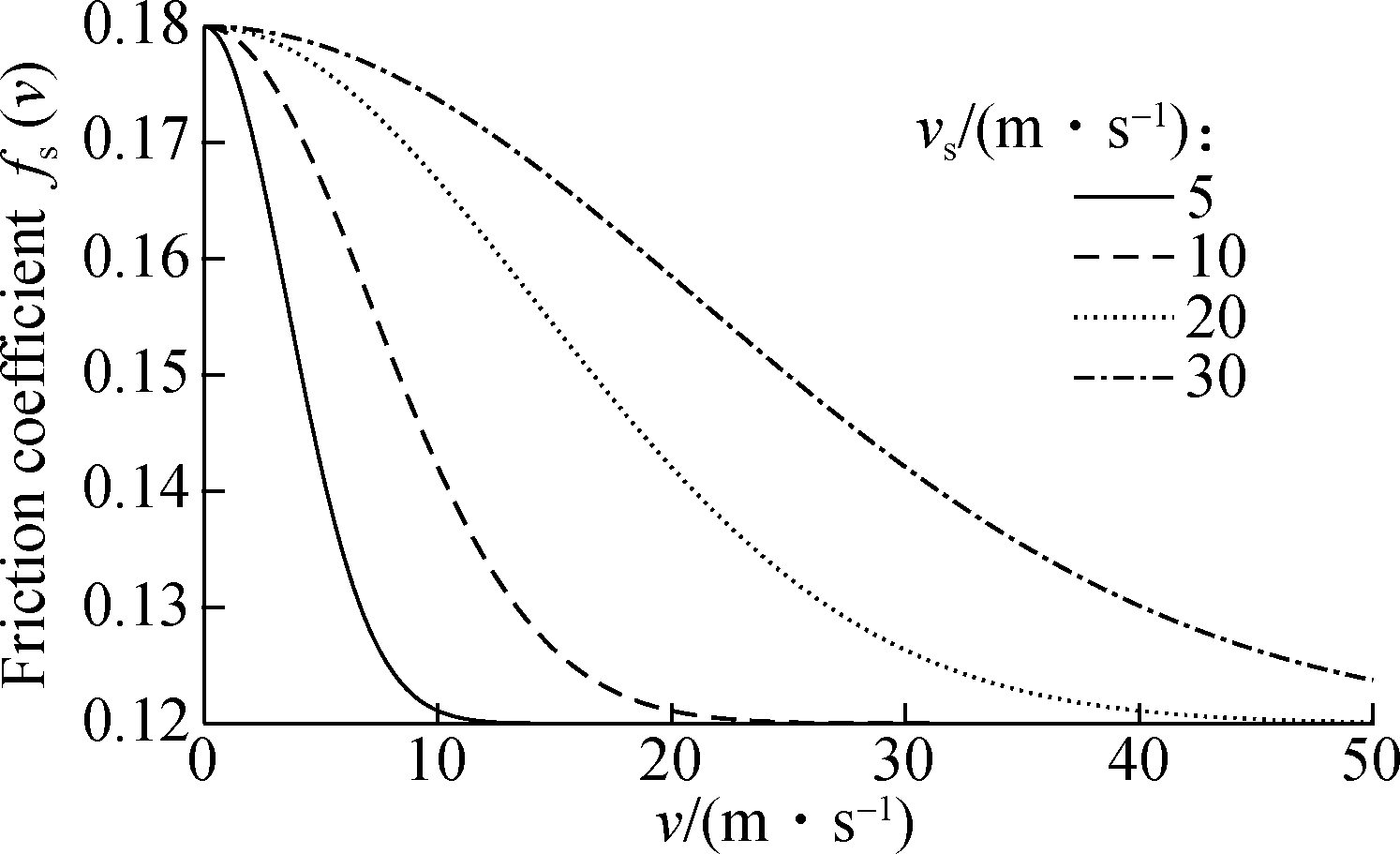
Fig.2 Stribeck friction coefficient curves
The friction force is modeled considering the Stribeck effect in most studies, while the friction torque is more suitable for presenting the rotating tribological pair system. Before modeling the friction torque, the micro-element surface on the contact surface is taken into account, as shown in Fig.1(b). At the radius ρ, the area of the micro-element is
dS=ρdθdρ
(5)
From Fig.1(a), we have the total contact load pn=knx1. Assuming that the contact load is uniformly distributed on the surface, the load on the micro-element is
(6)
where Aa is the nominal contact area; kn is the normal contact stiffness; x1 is the displacement of the contact surface.
In order to describe the Stribeck effect on the friction, we introduce the Stribeck friction coefficient fs(v) into the friction torque. The moment of friction force applied on the micro-element surface to the rotation axis is founded as
(7)
where ω is the relative rotation angular velocity, v=ωρ.
According to Eq.(7), the moment has the same expression at any angles, and then we can obtain the friction torque Mf of the entire contact surface,
(8)
where r1 and r2 are the radii of the inner and outer rings of the contact surface.
2.2 Contact stiffness fractal model
The development of the fractal theory has greatly promoted the study of surface microscopic features, which makes the contact characteristic parameters closer to the actual situation. The accurate description of the contact state is an essential prerequisite for modeling. Therefore, the establishment of kn and kt is described in the following.
The contact problem between two rough surfaces is generally equivalent to the contact problem between a rough surface and an ideal plane. Therefore, Young’s modulus E of the equivalent rough surface is given by
(9)
where E1, E2, ν1 and ν2 are the two materials’ Young’s modulus and Poisson’s ratios.
The relationship between the total dimensionless contact load p*and the dimensionless real contact area ![]() of the rough surface is provided by the M-B fractal contact model[24] under the elastic-plastic contact condition.
of the rough surface is provided by the M-B fractal contact model[24] under the elastic-plastic contact condition.
If 1<D<2 and D≠1.5, the dimensionless contact load p* is expressed as
p*=![]()
(10)
If D=1.5, the expression of p* is written as
(11)
where D is the fractal dimension; G is the fractal scaling coefficient. D and G can be obtained by the parameter identification of the surface. ac is the critical micro-contact area at the boundary point of the elastic-plastic deformation, which is described as
(12)
where K=H/σs; φ=σs/E; H and σs are the hardness and yield strength of the softer material. g1(D) and g2(D) are constants of the fractal dimension, which can be calculated as
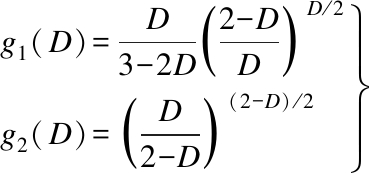
(13)
The dimensionless parameters are defined as
(14)
where Aa is the nominal contact area; Ar is the real contact area; p is the applied load.
Referring to Ref.[21] and considering the influence of friction, the critical micro-contact area is revised as
(15)
where kμ is a friction correction factor, and its expression depending on the friction coefficient μ is
(16)
Approximately regarding the micro-convex body as a sphere, the normal contact stiffness dkn depending on the contact area a of one single micro-convex body is described as
(17)
The maximum contact area al has the following relationship with the real contact area Ar,
(18)
Thus, the total normal contact stiffness kn of the rough surface is determined as

(19)
According to Ref.[17], the tangential contact stiffness kt can be modeled as
(20)
where T0 is the tangential load.
3 System Equation Deduction for the Stability Criterion
For determining the system stability, the friction torque Mf should be linearized due to the nonlinear Stribeck coefficient fs(v). According to Eq.(8), the Taylor expansion at x1=x10, ω=ω1 is written as
(21)
where x10=p/kn; ![]() and vt is the linear velocity at the radius ρ.
and vt is the linear velocity at the radius ρ.
Then, the friction torque can be expressed as
(22)
where the definitions of h1 and h2 are given by

(23)
Hence, the dynamic equation of the tribological pair system can be constructed as

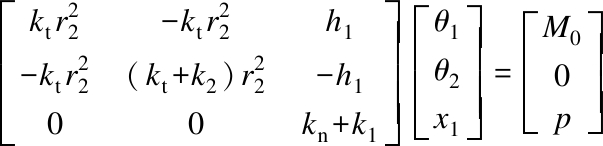
(24)
With the deliberation of the Lyapunov indirect method[25], Eq.(24) is rewritten in the state vector form:
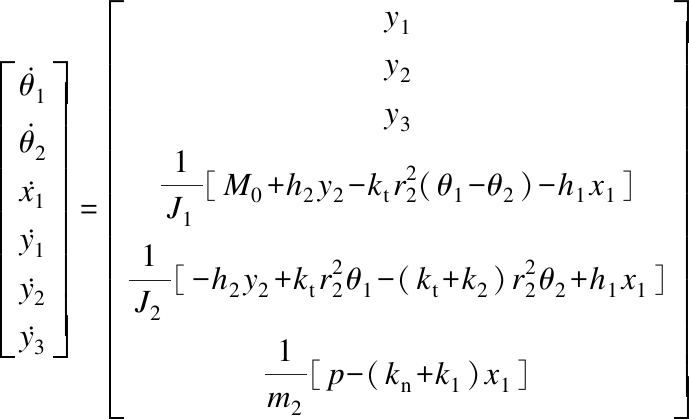
(25)
Then, the coefficient matrix A of the system can be determined from Eq.(25):
(26)
where O3×3 is the null matrix; I3×3 is the unit matrix; A1 and A2 are defined as
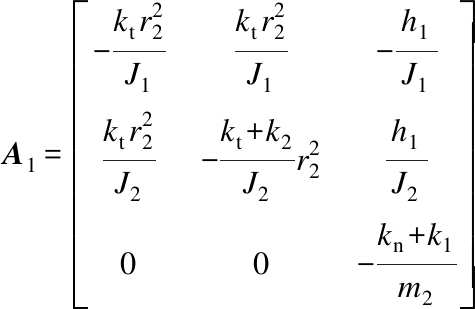
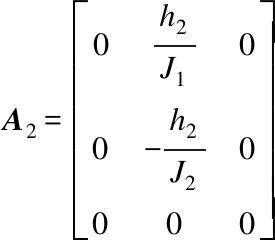
Therefore, all the parameters modeled above are substituted into Eq.(26) for computing the eigenvalues of the matrix A through MATLAB. In the light of the stability determination theorem, the eigenvalues λ of the coefficient matrix A have negative real parts on the basis of one approximation, which strongly indicates that the original nonlinear system is asymptotically stable at the equilibrium point. On the other hand, the positive real part of the eigenvalue implies the instability of the system.
4 Numerical Results and Discussion
In this paper, the stability analysis of the rotating tribological pair system on the end face is carried out with the dynamic model. The example of calculating the eigenvalues of matrix A is studied in this section with the given parameter values shown in Tab.1.
Tab.1 Model calculation parameters

ParameterValueParameterValuep/N5 000E2/GPa210k1/(MN·m-1)10ν10.27k2/(GN·m-1)10ν20.3r1/m0.03σs/MPa250r2/m0.06H/HB209m1/kg27.2vs/(m·s-1)10m2/kg16.7μs0.18J1/(kg·m2)480μk0.12J2/(kg·m2)320D1.80E1/GPa190G/nm3.6
The curves of the real part of eigenvalues Re(λ) at different speeds demonstrate that the system tends to be stable at higher speed whereas the system exhibits an unstable state at lower speed, as shown in Fig.3. Moreover, the real part of the first-order eigenvalue is invariably equivalent to zero, and the third-order shows a positive real part inferring system instability. Hence, the second- and third- order eigenvalues become the focus of this study. Due to the friction characteristics, there are many factors influencing the system stability such as the surface roughness Ra, the applied load p and the Stribeck coefficient vs, and their effects on the system stability are explored and compared as follows.
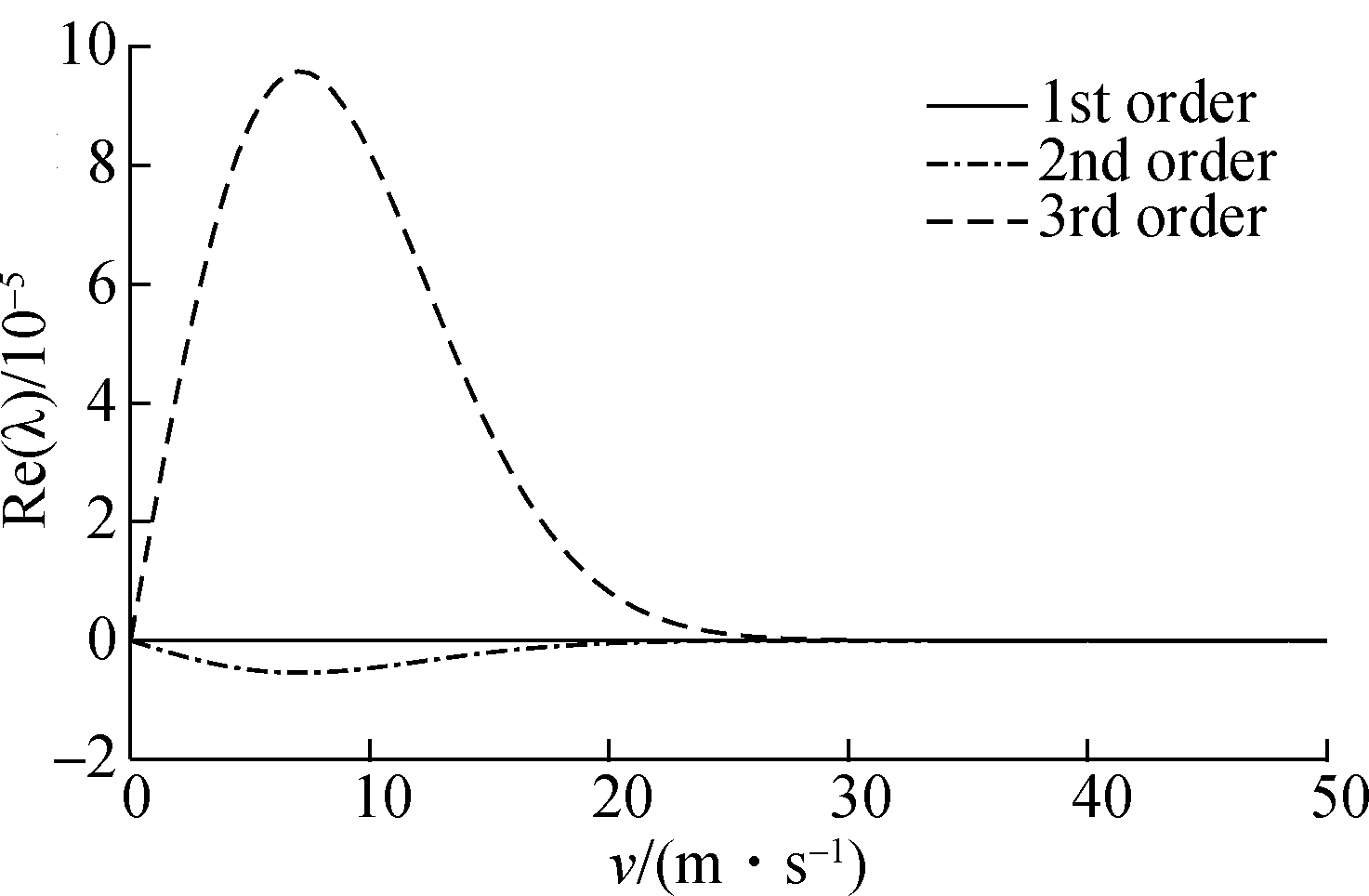
Fig.3 Real part of eigenvalue
The topography of the surface is one of the important factors affecting the state of frictional contact between surfaces. Statistical methods describe surface features through statistical parameters such as the surface roughness Ra, but the fractal theory uses fractal parameters to solve the problem of scale correlation. The surface roughness and fractal parameters are used as surface characteristics, so scholars have studied the relationship between them. Guan et al. [26] pointed out that the fractal dimensions of processed surfaces with the same manufacturing method are basically equal, and the fractal scaling coefficient changes with surface roughness. Pan et al.[27] analyzed the relationship between surface roughness and fractal parameters in details. When the fractal scaling coefficient G is small, the surface roughness Ra and the fractal dimension D have a monotonically decreasing relationship; when D value remains unchanged, the relationship between Ra and G can be expressed as
Ra∝GD-1
(27)
Therefore, the effect of surface roughness on the analysis model is indirectly reflected by studying the fractal parameters.
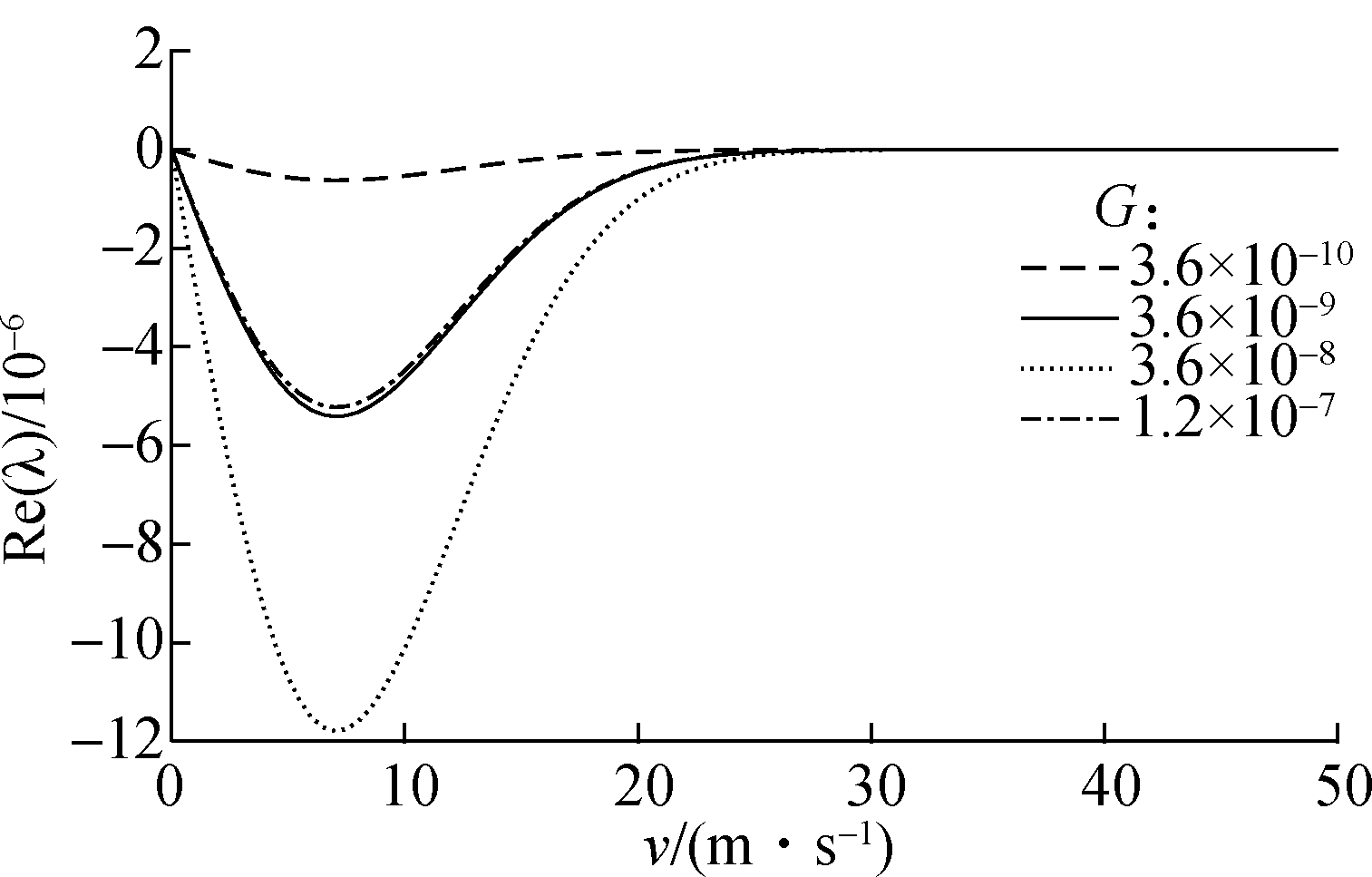
Fig.4 describes the variation of the real part of the second-order and third-order eigenvalues of the system with four fractal dimensions. It can be inferred from Fig.4(b) that the fractal dimension has little impact on the system instability, but its value at 1.75 makes the system unstable with the lowest trend. The relationship between the speed and the real part of eigenvalues at four different fractal scaling coefficients is shown in Fig.5. It obviously appears that the instability trend of the system increases first and then decreases along with the increase in the fractal scaling coefficient. Actually, when the fractal dimension D increases and the fractal scaling coefficient G decreases, the surface is smoother. The appropriate increase in surface roughness is beneficial for the system to reduce the instability phenomenon. When the surface roughness exceeds a certain value, a smoother surface is more prone to unstable friction. Most noteworthy, the peak values of curves and instability boundary values are constant. Hence, it is difficult to improve the system stability within the range of 1.65 and 1.80 of the fractal dimension.
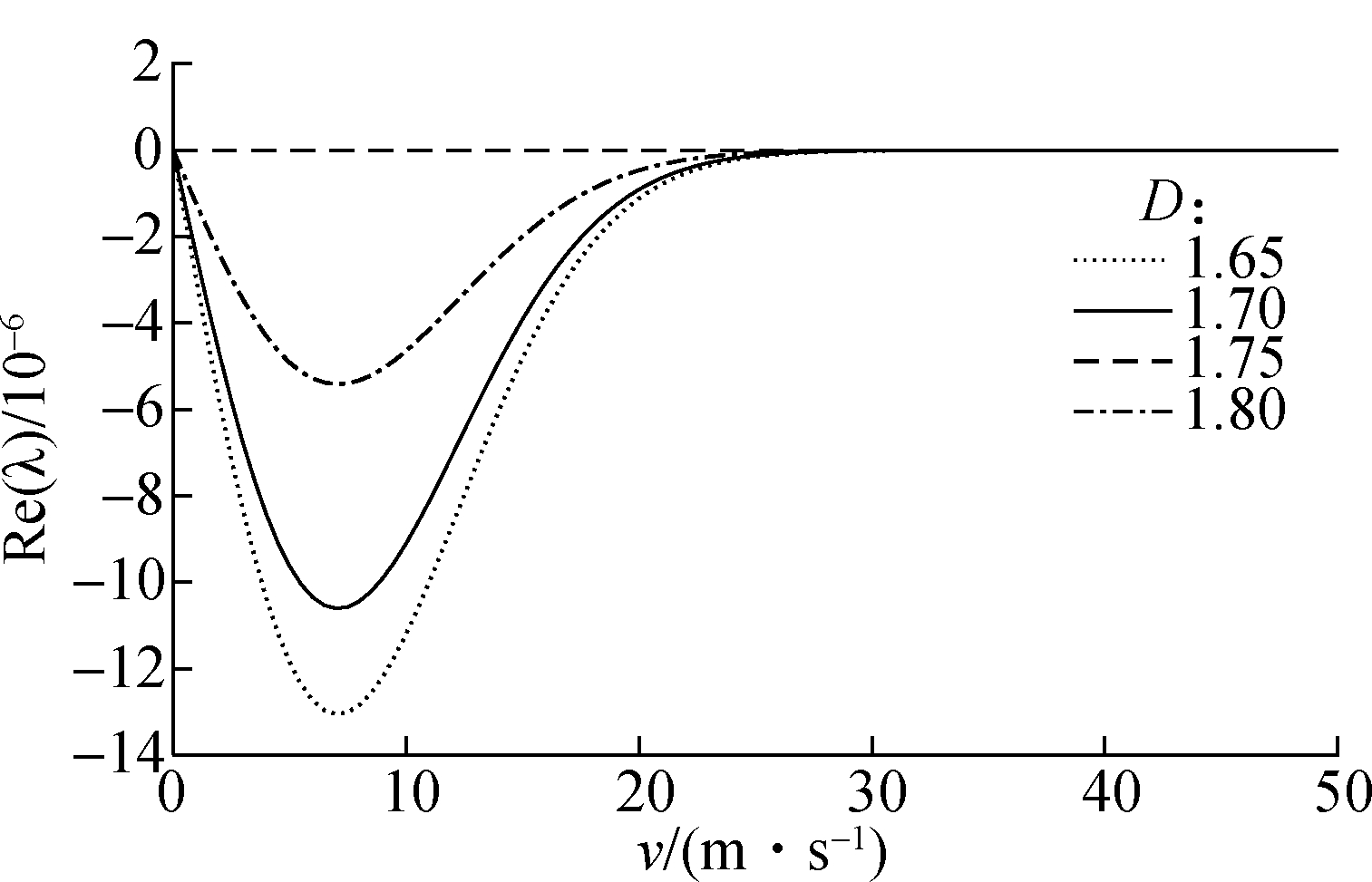
(a)
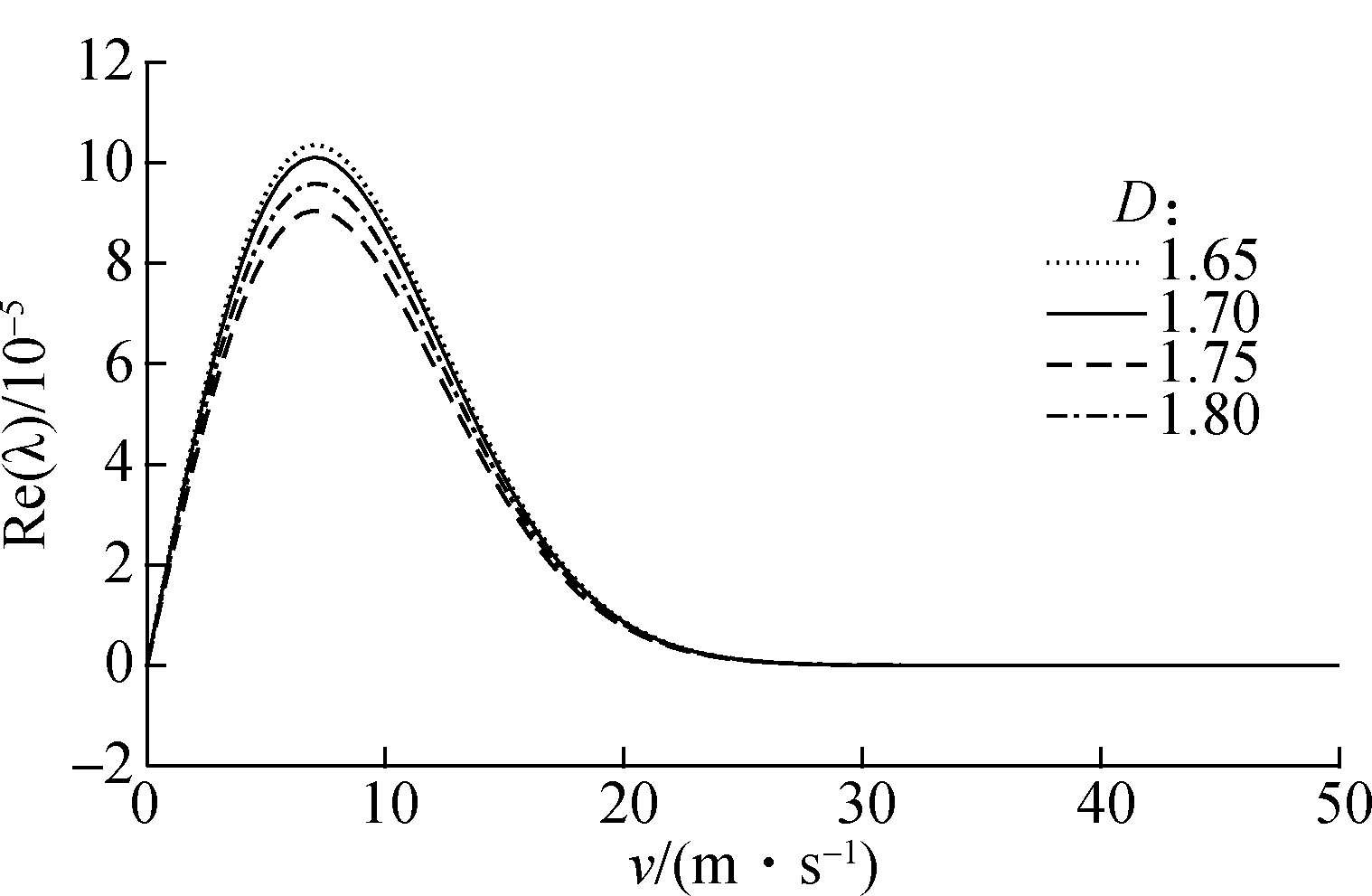
(b)
Fig.4 Effects of the fractal dimension D on the real part of eigenvalues. (a) The second-order eigenvalue;(b) The third-order eigenvalue
(a)

(b)
Fig.5 Effects of the fractal scaling coefficient G on the real part of eigenvalues.(a) The second-order eigenvalue;(b) The third-order eigenvalue
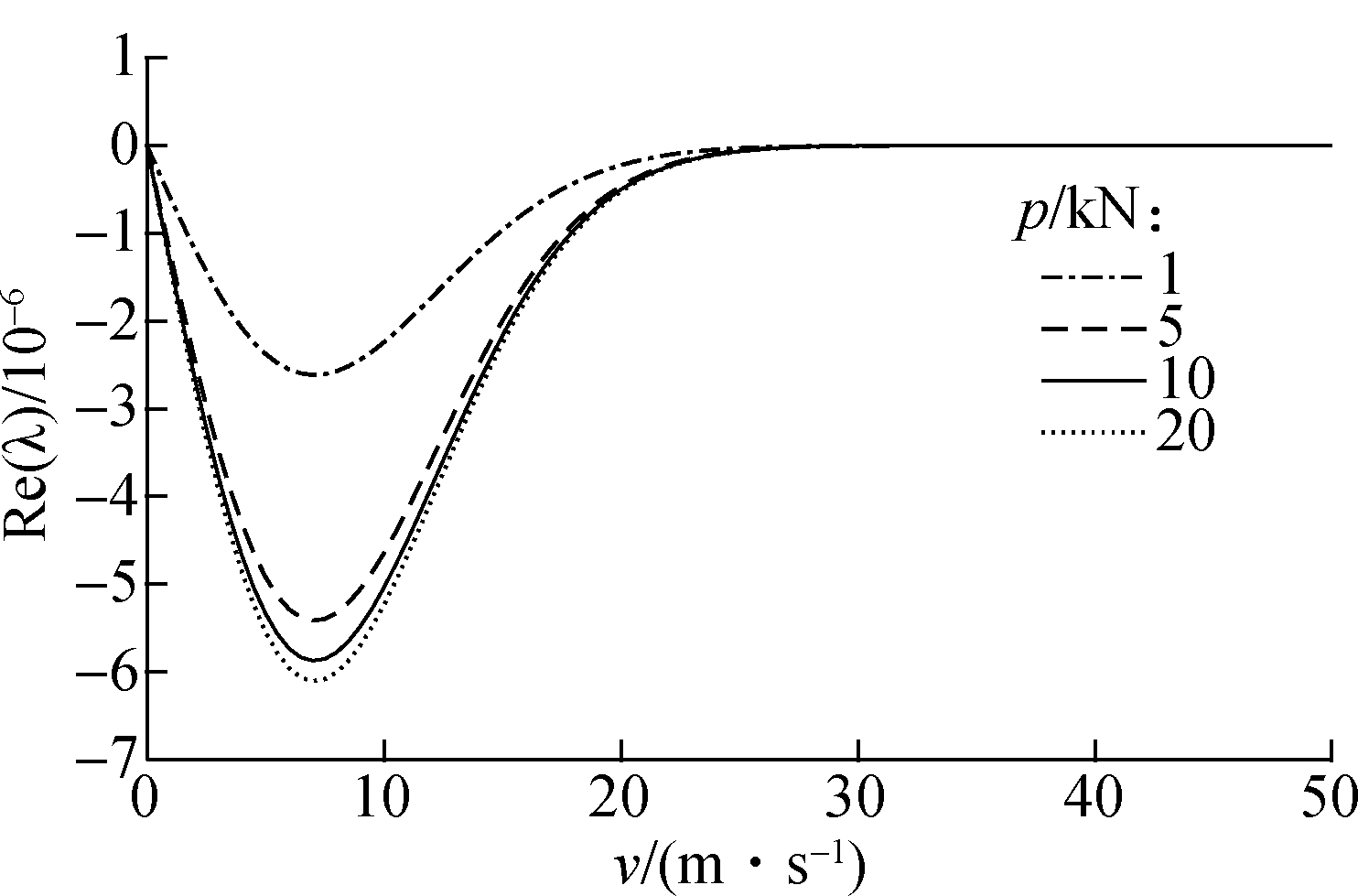
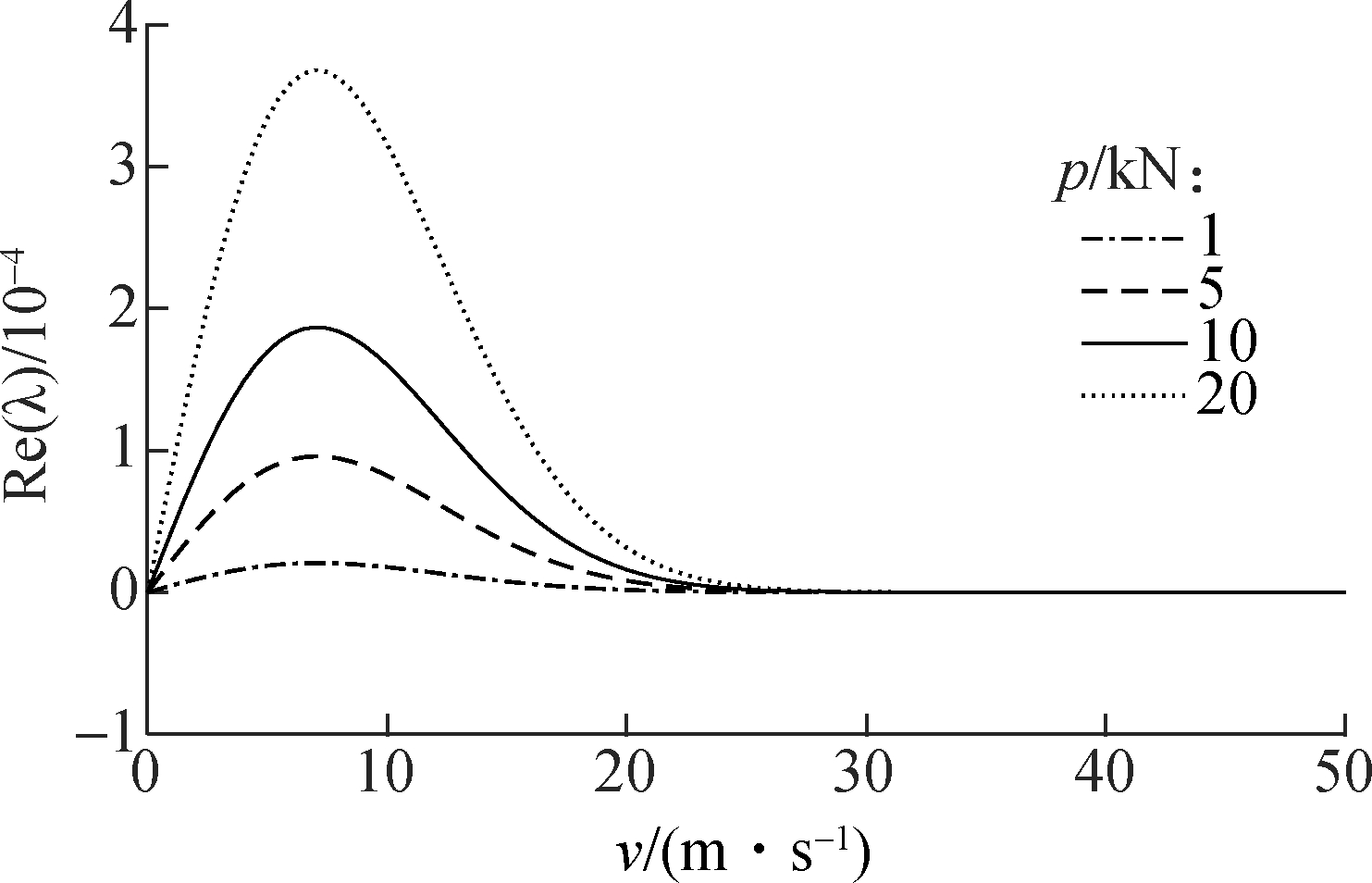
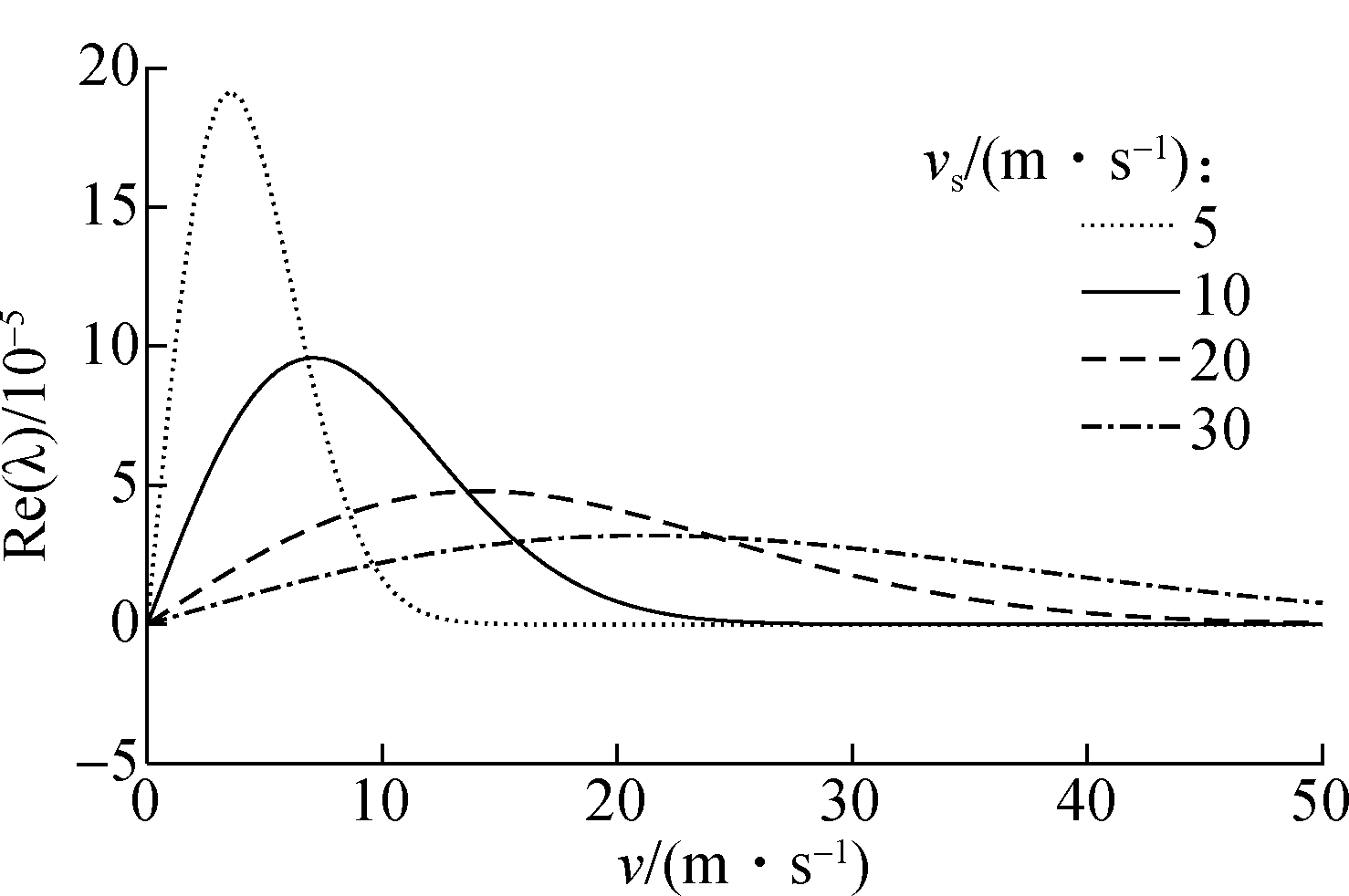
Similarly, the relationship between the speed and the real part of eigenvalues at four different loads is shown in Fig.6. It can be seen from Fig.6(b) that the instability trend of the system rises apparently with the increase in the applied load. Although the applied load has a great influence on system stability, its value should not be changed due to the index requirement in practical engineering. Fig.7 depicts the variation of system stability trends under different Stribeck coefficients. Evidently, decreasing the Stribeck coefficient makes the system more unstable, but can reduce the system instability boundary value and expand the stability interval. Actually, it is an extremely complex procedure to vary the Stribeck coefficient affected by nonlinear factors. Hence, the selection of the Stribeck coefficient should be determined according to the particular system requirements.
By comparing Fig.4 to Fig.7, it can be concluded that the instability boundary value and the speed corresponding to the peak value are not changed with the parameters of D, G or p, while they are influenced by the Stribeck coefficient. No matter how the other parameters are changed with the determined value of the Stribeck coefficient, only the trend of the system instability is changeable. Moreover, a proper surface roughness can reduce the system instability, but the smoother the surface, the more likely it is to cause friction instability.
(a)
(b)
Fig.6 Effects of the applied load p on the real part of eigenvalues.(a) The second-order eigenvalue; (b) The third-order eigenvalue

(a)
(b)
Fig.7 Effects of the Stribeck coefficient vs on the real part of eigenvalues.(a) The second-order eigenvalue;(b) The third-order eigenvalue
5 Conclusions
1) The rotating tribological pair system on the end face exhibits an unstable state at low speed and gradually enters a steady state at high speed.
2) The real part of the first-order eigenvalue of the system is always zero, and the third-order eigenvalue causes the system instability.
3) The fractal dimension and the fractal scaling coefficient have a slight impact on system stability when fractal dimensions are large, but there are optimal values for minimizing the instability trend of the system, which means that there is a best value for the surface roughness.
4) Reducing the applied load and Stribeck coefficient can improve system stability; and the instability boundary value is only altered by the Stribeck coefficient.
[1]Akay A. Acoustics of friction[J]. The Journal of the Acoustical Society of America, 2002, 111(4): 1525-1548. DOI:10.1121/1.1456514.
[2]Suzuki H, Miura R. The jerking motion in servomechanisms, considering negative slope of friction characteristics[J]. Transactions of the Institute of Electrical Engineers of Japan A, 1967, 87(Supp S1): 1321-1330.
[3]Spurr R T. A theory of brake squeal[J]. Proceedings of the Institution of Mechanical Engineers: Automobile Division, 1961, 15(1): 33-52. DOI:10.1243/pime_auto_1961_000_009_02.
[4]Popp K, Stelter P. Stick-slip vibrations and chaos[J]. Philosophical Transactions of the Royal Society of London Series A: Physical and Engineering Sciences, 1990, 332(1624): 89-105. DOI:10.1098/rsta.1990.0102.
[5]Hoffmann N, Gaul L. Effects of damping on mode-coupling instability in friction induced oscillations[J]. ZAMM, 2003, 83(8): 524-534. DOI:10.1002/zamm.200310022.
[6]Crowther A R, Singh R. Analytical investigation of stick-slip motions in coupled brake-driveline systems[J]. Nonlinear Dynamics, 2007, 50(3): 463-481. DOI:10.1007/s11071-006-9187-9.
[7]Giannini O, Massi F. Characterization of the high-frequency squeal on a laboratory brake setup[J]. Journal of Sound and Vibration, 2008, 310(1/2): 394-408. DOI:10.1016/j.jsv.2007.08.009.
[8]Devarajan K, Balaram B. Analytical approximations for stick-slip amplitudes and frequency of duffing oscillator[J]. Journal of Computational and Nonlinear Dynamics, 2017, 12(4): 044501. DOI:10.1115/1.4034734.
[9]Abdo J, Abouelsoud A A. Analytical approach to estimate amplitude of stick-slip oscillations[J]. Journal of Theoretical and Applied Mechanics, 2011, 49(4): 971-986.
[10]Niknam A, Farhang K. Vibration instability in a large motion bistable compliant mechanism due to stribeck friction[J]. Journal of Vibration and Acoustics, 2018, 140(6): 061017. DOI:10.1115/1.4040513.
[11]Xiang W, Yan S Z, Wu J N. Dynamic analysis of planar mechanical systems considering stick-slip and Stribeck effect in revolute clearance joints[J]. Nonlinear Dynamics, 2019, 95(1): 321-341. DOI:10.1007/s11071-018-4566-6.
[12]Ouyang H, Mottershead J E, Cartmell M P, et al. Friction-induced vibration of an elastic slider on a vibrating disc[J]. International Journal of Mechanical Sciences, 1999, 41(3): 325-336. DOI:10.1016/s0020-7403(98)00059-9.
[13]Ouyang H, Mottershead J E. Dynamic instability of an elastic disk under the action of a rotating friction couple[J]. Journal of Applied Mechanics, 2004, 71(6): 753-758. DOI:10.1115/1.1795815.
[14]Kang J. Theoretical model for friction-induced vibration of ball joint system under mode-coupling instability[J]. Tribology Transactions, 2015, 58(5): 807-814. DOI:10.1080/10402004.2015.1020121.
[15]Sui X, Ding Q. Instability and stochastic analyses of a pad-on-disc frictional system in moving interactions[J]. Nonlinear Dynamics, 2018, 93(3): 1619-1634. DOI:10.1007/s11071-018-4280-4.
[16]Pohrt R, Popov V L. Normal contact stiffness of elastic solids with fractal rough surfaces[J]. Physical Review Letters, 2012, 108(10): 104301. DOI:10.1103/physrevlett.108.104301.
[17]Guan D, Jing L, Hilton H H, et al. Tangential contact analysis of spherical pump based on fractal theory[J]. Tribology International, 2018, 119: 531-538. DOI:10.1016/j.triboint.2017.11.034.
[18]Sun Y Y, Xiao H F, Xu J W, et al. Study on the normal contact stiffness of the fractal rough surface in mixed lubrication[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2018, 232(12): 1604-1617. DOI:10.1177/1350650118758741.
[19]Xiao H F, Sun Y Y, Chen Z G. Fractal modeling of normal contact stiffness for rough surface contact considering the elastic-plastic deformation[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2019, 41: No.11. DOI:10.1007/s40430-018-1513-x.
[20]Liu P, Zhao H, Huang K, et al. Research on normal contact stiffness of rough surface considering friction based on fractal theory[J]. Applied Surface Science, 2015, 349: 43-48. DOI:10.1016/j.apsusc.2015.04.174.
[21]Pan W J, Li X P, Wang L L, et al. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification[J]. European Journal of Mechanics-A, 2017, 66: 94-102. DOI:10.1016/j.euromechsol.2017.06.010.
[22]Awrejcewicz J, Olejnik P. Analysis of dynamic systems with various friction laws[J]. Applied Mechanics Reviews, 2005, 58(6): 389-411. DOI:10.1115/1.2048687.
[23]Armstrong-Hélouvry B, Soom A. Control of machines with friction[J]. Journal of Tribology, 1992, 114(3): 637. DOI:10.1115/1.2920929.
[24]Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. Journal of Tribology, 1991, 113(1): 1-11. DOI:10.1115/1.2920588.
[25]Liu W J, Tang F S. Modeling a simplified regulatory system of blood glucose at molecular levels[J]. Journal of Theoretical Biology, 2008, 252(4): 608-620. DOI:10.1016/j.jtbi.2008.02.021.
[26]Guan Z Z, Ye M H, Yin X C, et al. Recognition of surface roughness based on fractal theory and the microscopic images[J]. Applied Mechanics and Materials, 2012, 241/242/243/244: 3030-3033. DOI:10.4028/www.scientific.net/amm.241-244.3030.
[27]Pan Y L, Wu L Q, Zhang Y D. Study of the relationship between fractal model parameters and roughness parameter ra[J]. Engineering Science, 2004, 6(5): 49-51.(in Chinese)