In recent years, the rapid development of vehicle-to-grid (V2G) technology has become a new way of alleviating the current energy crisis and improving the environment[1]. It is necessary to guide the charging-and-discharging behavior of large-scale electric vehicles (EVs) through electricity prices[2]. Ordered charging-and-discharging behaviors can eliminate the adverse effects of overload and power quality degradation caused by disordered charging or discharging [3]. In addition, they can also effectively support the operation of the power grid (PG), achieve peak cutting and valley filling, reduce network losses, suppress renewable energy fluctuations, and participate in frequency modulation[4], which will improve the reliability and economics of PG operation[5].
In the V2G process, the relationship between EV and PG is equal and independent. The interests of both are antagonistic and competitive, so V2G has the characteristics of game[6]. The key to realizing effective V2G is how to distribute the benefits brought by the cooperation between the two parties. The distribution of this part of benefits is mainly reflected in the formulation of the discharge price. Only by formulating a reasonable discharge price can the enthusiasm of both parties to participate in the interaction be fully utilized. If the discharge price is too low, few EV users will be attracted to participate in the interaction. Thus, the PG company will gradually increase the discharge price until the EV user’s discharge capacity meets the number of loads that PG needs to reduce. There have been many studies on the EV charging price, but less research on the price of discharging.
In existing research,Refs.[7-10] used the game theory to establish a bi-level programming model with the goal of maximizing the revenue of the PG company and minimizing the EV users’ cost. The Nash equilibrium solution of the PG company and the EV users is obtained, which is used as the basis for formulating the discharge price. In Ref.[11], the maximum benefit of PG and EV group was set as the goal, and the established Cournot model was solved by KKT condition. Refs.[12-13] considered the non-cooperation and cooperation aspects, established the interaction model between EV-users’ needs and PG company’s strategy, and studied the corresponding demand response and pricing strategy optimization. Aiming at maximizing the operating income of electric vehicles, Refs.[14-19] constructed the model of maximizing the charging-and-discharging revenue of electric vehicles. By reasonably arranging the charging-and-discharging plan and responding to the real-time electricity price, EV users can achieve good economic benefits. However, due to the diversity of demand for EV users and the uncertainty of the operating state of the power grid, it is difficult to ensure that EVs and PGs make completely rational decisions based on complete information. Unlike the traditional game theory, the evolutionary game (EG) theory does not require that both sides of the game be completely rational, nor does it require that they have all the information.
Therefore, based on the evolutionary game theory and PG with two-way smart charging piles[6], this paper will analyze the dynamic evolutionary relationship and stable evolution process of benefit distribution between EV users and PG companies, and determine the benefit distribution method that satisfies the interactive needs of both parties. The results are compared with the results obtained by the static Bayesian game. Finally, a reasonable V2G discharge price range is obtained, which can provide a reference for the formulation of V2G strategy.
1 Establishment of Evolutionary Game Model Between PG Company and EV Users
1.1 The basic theory of evolutionary game
Evolutionary game is a new theory combining the traditional game theory with dynamic evolution analysis. By assuming the possible benefits of both sides of the game, it can analyze the income trends of the two parties under different strategies and obtain the evolutionary stability strategy of the two sides in different situations. The evolutionary stable strategy (ESS) and replicator dynamics (RD) are the two core concepts of the evolutionary game theory. ESS is defined as follows: If and only if a policy satisfies the following conditions, the policy is an ESS [5].
S(v,o)≤S(o,o) ∀v
(1)
S(v,o)=S(o,o)⟹S(v,v)=S(o,k) ∀v≠s
(2)
where o is the original strategy; v is the mutation strategy; S is the expected return.
The ESS emphasizes the role of variability. Any tactical variation will lead to a smaller expected return. Therefore, the ESS is the ultimate stable solution of the evolutionary game. The RD emphasizes the role of selection. Individual decision-making in the group is achieved through dynamic processes such as learning, imitation, and variation between individuals. In the process of group dynamic adjustment, individuals in the group will choose to obtain higher-payment decisions in the previous game. Replicator dynamics can be expressed as
![]() =xv[S(v,o)-S(o,o)] v=1,2,…,V
=xv[S(v,o)-S(o,o)] v=1,2,…,V
(3)
where S(v,o) is the utility function, which represents the expected return obtained when the individual in the group adopts the pure strategy v; S(o,o) represents the average expected return; xv is the proportion of the pure strategy v selected by the group.
1.2 V2G evolutionary game model
In the V2G evolutionary game, the strategies of PG companies and EV users are shown in Tab.1, where x refers to the probability of EV users participating in cooperation, and y refers to the probability that the grid participates in cooperation.
Tab.1 The strategies for power grid companies and electric vehicle users

StrategyPG companyEV userCooperation strategySell electricity to EV users and accept EV to discharge themCharge from PG company and discharge to PG when there is a-bundant powerNon-cooperative strategyDo not accept EV dischargeDo not discharge to PG companyWillingness to cooperationyxWillingness to non-cooperation1-y1-x
Thereby, a policy set {PGx,EVy}(0≤x≤1,0≤y≤1) of V2G game is formed. For EV users, when choosing a cooperation strategy, the expected reciprocation is
SEV1=y[UEV+Edpd-Ecpc-(Ed+Ec)LB]+
(1-y)(UEV-Ecpc-EcLB-LEV)
(4)
where UEV is the normal income of EV users, mainly for the benefits brought by normal driving, and in this paper it is set to be 0.5374 yuan/(kW·h); Ed is the amount of EV-discharging energy (kW·h); pd is the discharge price of EV; Ec is the amount of charge of the EV; pc is the charging price of the EV; LB is the unit cell loss of the EV during charging or discharging; LEV is the loss that EV users may cause when EV users choose to cooperate but PG does not cooperate.
For EV users, the expected return when choosing a non-cooperative strategy is
SEV2=y(UEV-Ecpc-EcLB)+(1-y)(UEV-Ecpc-
EcLB)=UEV-Ecpc-EcLB
(5)
The average expected reciprocation for EV users is
(6)
According to Eq.(3), the dynamic equation of EV user’s replication is
(7)
For PG companies, the expected return when choosing a cooperation strategy is
SPG1=x[UPG+EdEG-Edpd-(Ed+Ec)PPG]+
(1-x)(UPG-EcPPG-LPG)
(8)
where UPG is the normal income of the PG company, mainly for normal sales revenue, and is set to be 0.498 5 yuan/(kW·h) in this paper; EG is the unit’s additional revenue brought to the PG company by cooperation, which mainly is the unit equipment investment saved by reducing the peak-to-valley difference of the power grid; PPG is the unit payment cost added by PG company when it chooses cooperation, which mainly is the construction cost of infrastructure such as charging piles; LPG is the loss that PG company may cause when it chooses cooperation and EV users do not cooperate.
For the PG company, the expected return when choosing a non-cooperative strategy is
SEV2=xUPG+(1-x)UPG=UPG
(9)
Then, the average expected return of the PG company is
(10)
PG’s replication dynamic equation is
xEdPPG-ECPPG-LPG+xLPG)
(11)
According to Eqs.(1) and (2), the stable evolution strategy of the V2G problem satisfies
S(PGx+Δx,EVy)≤S(PGx,EVy)
(12)
S(PGx,EVy+Δy)≤S(PGx,EVy)
(13)
2 V2G Evolutionary Game Equilibrium Point and Stability Analysis
Fig.1 shows the dynamic evolution phase diagram of V2G. The arrows in the figure indicate the evolution direction of the game. Let dx/dt=0, dy/dt=0. We obtain 5 points on the plane α={(x,y)|0≤x,y≤1}, i.e., O(0,0), A(1,0), B(0,1), C(1,1), and D(xD,yD).
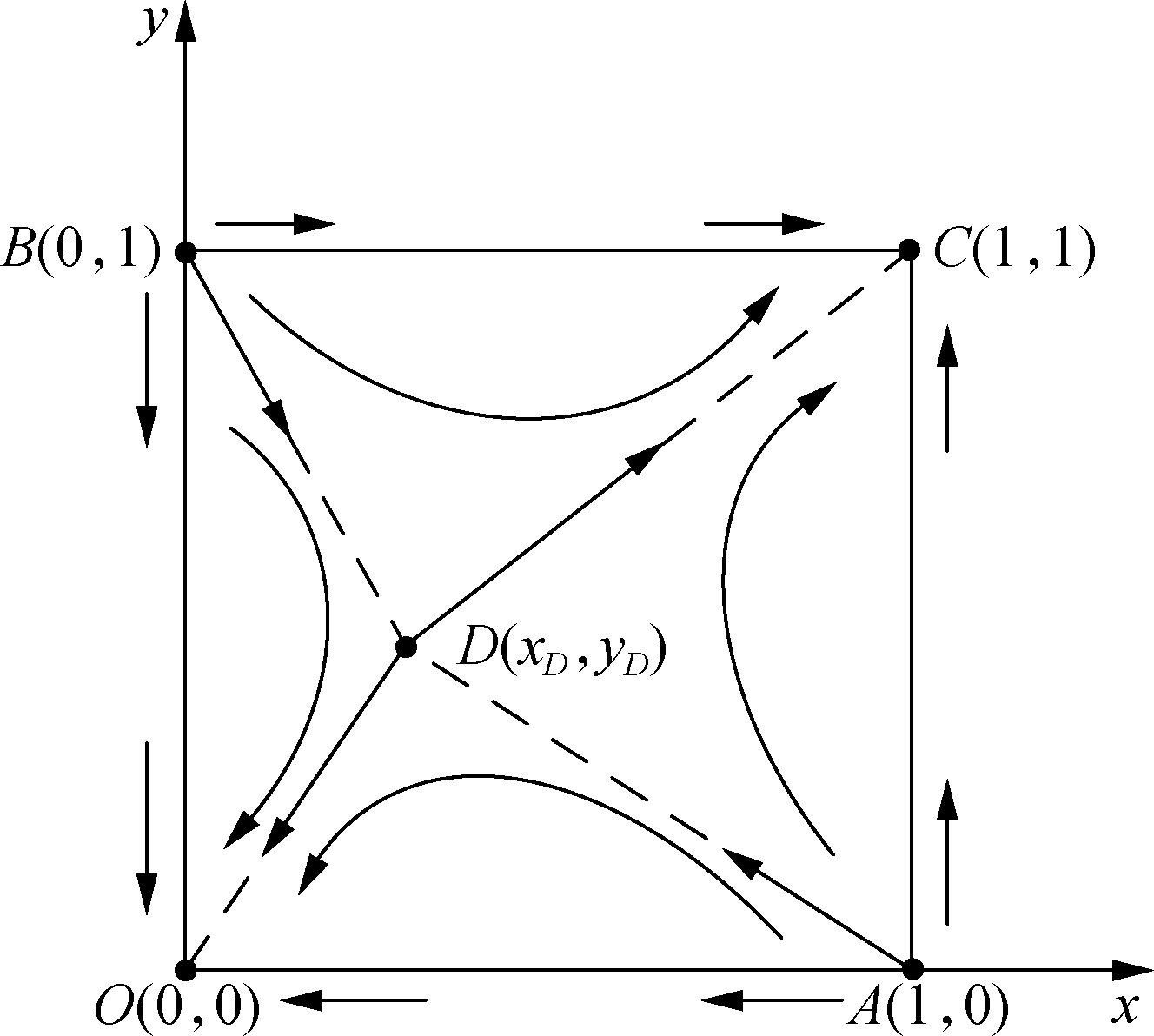
Fig.1 The dynamic evolution phase diagram of V2G
Point A in Fig.1 indicates that the EV user adopts a cooperation strategy, while PG adopts a non-cooperative strategy. Point B indicates that the PG company adopts a cooperation strategy, and EV users adopt a non-cooperation strategy. Obviously, points A and B are two unstable equilibrium points. Point C and point O are the stable strategy points of the V2G evolution game. Point C indicates that both parties participating in the game adopt a cooperation strategy, and point O indicates that both parties participating in the game adopt a non-cooperative strategy. Point D is the saddle point. When Eq.(11) is equal to 0, its abscissa xD can be calculated. Similarly, letting Eq.(7) be equal to 0, we can obtain its ordinate yD.
(14)
(15)
The saddle point D reflects the critical point of profit and loss in the V2G process. In Fig.1, the ADBO part indicates that the proportion of the two parties participating in the cooperation is too low, and the obtained income cannot compensate for the cost loss caused by this strategy. At this point, the evolutionary game will converge to point O, that is, both sides of the game will choose the non-cooperative strategy. The ADBC part indicates that the revenue from the interaction of V2G will be higher than the cost. The higher proportion of cooperation will lead to greater return. Therefore, it will eventually converge to point C, that is, both sides of the game will choose a cooperation strategy.
In the case of stabilizing strategy point C, when both parties cooperate, in order to make the income satisfy the interests of both parties and form a stable interactive relationship, the relationship to be satisfied should be
UEV+E′dpd-Ecpc-(Ec+E′d)LB>UEV
(16)
UPG+E″dEG-E″dpd-(Ec+E″d)PPG>UPG
(17)
where E′d represents the amount of discharged electricity required to ensure the profitability of the EV user; E″d represents the amount of discharged electricity required to ensure the profitability of the PG company. This means that the gains from participating in the game should be greater than the gains from not participating in the game. Solving Eqs. (16) and (17) can obtain
(18)
(19)
In a stable interactive state, the discharge electricity quantity E′d of the EV is equal to the discharge electricity quantity E″d received by the PG company, that is, Ed=E′d=E″d. According to Eqs. (18) and (19), the range of the discharge price pd can be found.
(20)
The left side of (20) reflects the unit cost paid by EV user for the game, and the right side reflects the unit revenue that the PG company can obtain from the game. Only when the discharge price satisfies (20), can both sides of the game gain advantages at the same time and continue to cooperate steadily.
3 Case Study
3.1 Assumptions
Taking the power grid with smart charging piles and electric vehicles in a city as an example, the process of the evolutionary game between them is analyzed, and the interaction implementation strategy between EVs and PG at a certain scale is obtained.
The number of EVs in the city is about 80 000. One EV battery has a capacity of 25 kW·h and a discharge depth of 0.8. The unit battery loss LB=0.41 yuan/(kW·h). Each EV charging pile is about 14 000 yuan. Its service life is 10 years. The average working time in a day is 12 h. The output power is 10 kW. The unit payment cost of the EV charging pile PPG is 0.035 5 yuan/(kW·h). The valley-period electricity price of PG is 0.285 6 yuan/(kW·h), and the peak-period electricity price is 0.491 0 yuan/(kW·h). For the convenience of analysis, the EV is charged during the valley period, and the amount of charge is the same as the battery capacity. According to Ref.[5], when the EV user cooperates with the PG company, the investment cost of the power grid unit will be reduced to approximately 14 900 yuan/kW. The service life of the unit is generally around 15 years. The time to participate in peak shaving is 3.5 h per day. The working time for one year is 200 d. Hence, the extra income of the unit brought to the PG by the EV participation interaction is EG=14 900/(15×3.2×200)=1.552 1 yuan/(kW·h).
3.2 Results and discussion
According to the foregoing analysis, the coordinates of the saddle point D are obtained as
(21)
(22)
The saddle point D is related to the cost (LEV and LPG) when the EVs or the PG cooperate unilaterally. The larger the LEV and LPG, the more the saddle point D tends to point C(1,1) in Fig.1. When LEV and LPG are known, the saddle point D will be determined by the discharge price pd and the discharge quantity Ed. The relationship between the discharge quantity and the discharge price calculated by Eqs.(18) and (19) is
(23)
(24)
Eq.(23) reflects the discharge capacity required by the EV in the case of the discharge price pd. Eq.(24) reflects the discharge capacity required by the PG in the case of the discharge price pd. If Eq.(23) is satisfied, the EV user’s requirement for the amount of discharge will be satisfied. If Eq.(24) is satisfied, the PG’s requirement for the amount of discharge will be satisfied.
The relationship between the discharge electricity price pd and the discharge electricity quantity Ed is shown in Fig.2. The coordinates of the three intersections in Fig.2 are E(1.106 0,20), F(1.481 1, 20), and G(1.463 2, 13.162 2), respectively. Curve 1 is determined by Eq. (23), reflecting the constraint relationship between discharge power and discharge price from the perspective of EV. Curve 2 is determined by Eq.(24), reflecting the constraint relationship between the discharge power received by the PG and the discharge price from the perspective of the PG company. Line 3 is the maximum discharge capacity defined by the capacity of the EV battery. There are four intervals in Fig.2. Referring to Eqs.(23) and (24), the evolutionary game relationships corresponding to each region are shown in Tab.2.
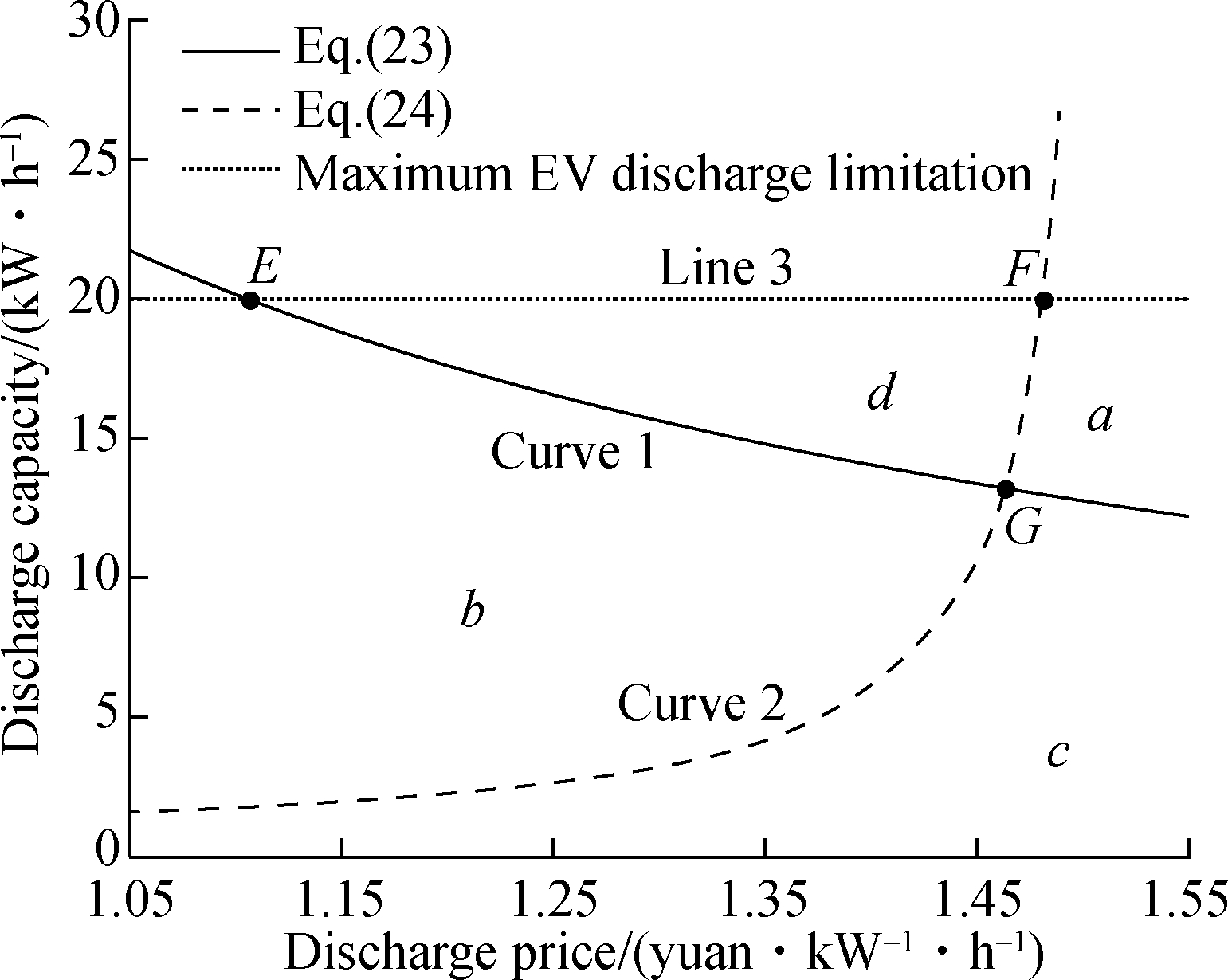
Fig.2 The dynamic evolution diagram of V2G
Tab.2 Evolutionary game relationship corresponding to each region

RegionabcdWhether to meet the EV discharge requirementsYesNoNoYesWhether to meet the PG discharge requirementsNoYesNoYesCorresponding to the point in Fig.1ABOCx1001y0101
In areas a and b, only one party can profit from V2G. This will seriously affect the enthusiasm of the non-profitable party to participate in the interaction and encourage the non-profitable party to choose the non-cooperative strategy. This will increase the cost of the originally profitable party and reduce its income. The result of the final evolution will tend to point O, making the interaction impossible. In area c, neither party can profit, and the players will not choose to interact. In area d, both the EV and the PG can benefit from the interaction, so area d is an optional range set for V2G. The interactive decision of the EV and the PG can be selected within this range.
When the discharge electricity price pd is between 1.106 0 and 1.463 2 yuan/(kW·h), the discharge electric quantity Ed is determined by curve 1 and line 3. As the discharge electricity price increases, the profit per unit of EV increases. In this case, the limitation of the discharge amount is gradually relaxed, and the adjustable range of the discharge amount is increased. When the discharge electricity price pd is between 1.463 2 and 1.481 1 yuan/(kW·h), the discharge electric quantity Ed is determined by curve 2 and line 3. As the discharge electricity price increases, the profit per unit of PG decreases. In this case, the requirement for the discharge amount is gradually increased, and the adjustable range of the discharge amount is gradually reduced. When the discharge price is 1.463 2 yuan/(kW·h), the benefits of the interaction are relatively balanced, and the dischargeable power can be adjusted to the largest extent.
Therefore, in order to achieve a benign interaction between EV and PG, the range of EV discharge price determined by PG is 1.106 0 to 1.481 1 yuan/(kW·h), and the reasonable range of discharge power determined by EV is 13.162 2 to 20 kW·h. Within the range of reasonable discharge price, the optimal discharge price should be 1.463 2 yuan/(kW·h). Within the range of the discharge price, the minimum discharge required for both parties to make a profit is 13.162 2 kW·h.
Under the optimal electricity price, the average unit energy gains of EV users and PG companies obtained by Eqs.(4) and (8) are shown in Tab.3 and compared with the returns from the static Bayesian game[20].
Tab.3 Comparison of EV and PG income under different methods yuan

MethodAverage unit discharge gain for EV usersAverage unit discharge gain for PGEvolutionary game0.487 80.490 6Static Bayesian game0.121 10.382 5
It can be seen from Tab.3 that when the optimal discharge price is adopted, the difference between the EV and PG in the evolutionary game is only 0.002 8 yuan. This value is much smaller than the result of the static Bayesian game, which is 0.261 4 yuan. At the same time, compared with the fixed strategy points determined by the static Bayesian game under the limited information, the evolutionary game is more fully used to mine the EV and PG interaction strategies, and more profits based on the optimal discharge price are gained.
4 Conclusions
1) There are four states in the interaction process, but the result of interaction evolution only has two kinds: cooperation and non-cooperation.
2) In the cooperative interaction state, as a means of participating in the interaction, there is a certain constraint relationship between the discharge price determined by PG Company and the quantity of discharging energy determined by the EV users.
3) Within a certain range of discharge rates, there is a specific response range for the discharge capacity. Only within this scope can both sides benefit from the interaction, thus achieving a benign interaction between the EV users and the PG company.
[1]Shekhar A, Prasanth V, Bauer P, et al. Economic viability study of an on-road wireless charging system with a generic driving range estimation method[J]. Energies, 2016, 9(2): 76. DOI:10.3390/en9020076.
[2]Zhang J, Gao F, Xu S Q, et al. Energy internet technological architecture and case analysis[J]. Electric Power, 2018, 51(8): 24-30. DOI: 10.11930/j.issn.1004-9649.201806128. (in Chinese)
[3]Clement-Nyns K, Haesen E, Driesen J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380. DOI:10.1109/tpwrs.2009.2036481.
[4]Rassaei F, Soh W, Chua K. Demand response for residential electric vehicles with random usage patterns in smart grids[J].IEEE Transactions on Sustainable Energy, 2015, 6(4): 1367-1376. DOI:10.1109/tste.2015.2438037.
[5]Yang X D, Zhang Y B, Zhao B, et al. Automated demand response method for electric vehicles charging and discharging to achieve supply-demand coordinated optimization[J]. Proceedings of the CSEE, 2017, 37(1):120-130. DOI: 10.13334/j.0258-8013.pcsee.151936.
[6]Zhang S X, Li L F. Management mode of integrated construction of electric vehicle charging piles and municipal LED facilities[J]. Electric Power, 2017, 50(7): 43-48. DOI: 10.11930/j.issn.1004-9649.2017.07.043.06. (in Chinese)
[7]Li C W, Liu J Y, Wei Z B. Research on electric vehicle discharge price based on game theory[J]. East China Electric Power, 2013, 41(6): 1329-1334. DOI: 1001-9529(2013)06-1329-06. (in Chinese)
[8]Li M Q, Song Y Q, Yan Z, et al. Research on game model and algorithm for electric vehicle aggregations[J]. Power System Technology, 2014, 38(6): 1512-1517. DOI:10.13335/j.1000-3673.pst.2014.06.014.(in Chinese)
[9]Yang H L, Xie X Z, Vasilakos A V. Noncooperative and cooperative optimization of electric vehicle charging under demand uncertainty: A robust stackelberg game[J].IEEE Transactions on Vehicular Technology, 2016, 65(3): 1043-1058. DOI:10.1109/tvt.2015.2490280.
[10]Zhang L, Li Y Y. A game-theoretic approach to optimal scheduling of parking-lot electric vehicle charging[J].IEEE Transactions on Vehicular Technology, 2016, 65(6): 4068-4078. DOI:10.1109/tvt.2015.2487515.
[11]Tang W R, Zhang Y J. A model predictive control approach for low-complexity electric vehicle charging scheduling: Optimality and scalability[J].IEEE Transactions on Power Systems, 2017, 32(2): 1050-1063. DOI:10.1109/tpwrs.2016.2585202.
[12]Luo C, Huang Y, Gupta V. Stochastic dynamic pricing for EV charging stations with renewable integration and energy storage[J].IEEE Transactions on Smart Grid, 2018, 9(2): 1494-1505. DOI:10.1109/tsg.2017.2696493.
[13]Bahrami S, Toulabi M, Ranjbar S, et al. A decentralized energy management framework for energy hubs in dynamic pricing markets[J].IEEE Transactions on Smart Grid, 2018, 9(6): 6780-6792. DOI:10.1109/tsg.2017.2723023.
[14]Zhan K J, Hu Z C, Song Y H, et al. Electric vehicle coordinated charging hierarchical control strategy considering renewable energy generation integration[J]. Power System Technology, 2016, 40(12):3689-3695. DOI:10.13335/j.1000-3673.pst.2016.12.009. (in Chinese)
[15]Chen J P, Piao L J, Ai Q, et al. Hierarchical optimal scheduling for electric vehicles based on distributed control[J]. Automation of Electric Power Systems, 2016, 40(18):24-31. DOI: 10.7500/AEPS20151002002. (in Chinese)
[16]Li X P, Geng G C, Jiang Q Y. A hierarchical energy management strategy for grid-connected microgrid[C]//2014 IEEE PES General Meeting. National Harbor, MD, USA, 2014:1-5. DOI:10.1109/pesgm.2014.6939515.
[17]Pan Z N, Zhang X S, Yu T, et al. Hierarchical real-time optimized dispatching for large-scale clusters of electric vehicles[J]. Automation of Electric Power Systems, 2017, 41(16): 96-104. DOI: DOI: 10.7500 /AEPS20160919012. (in Chinese)
[18]Jia L, Hu Z C, Song Y H. Considering the comprehensive planning of electric vehicle charging facilities in cities with different types of charging requirements[J]. Power System Technology, 2016, 40(9): 2579-2587. (in Chinese)
[19]Ma X F, Wang C, Hong X, et al. Optimization strategy of electric vehicle double-layer charging based on nodal blocking electricity price[J]. Power System Technology, 2016, 40(12): 3706-3716. DOI: 10. 3969 /j.issn. 1000-7229. 2018. 01. 006. (in Chinese)
[20]Sun B, Wang Z X, Zhao W H. Analysis of discharge price based on the static Bayesian game[J]. Renewable Energy Resources, 2015, 33(11): 1686-1692. DOI:10.13941/j.cnki.21-1469/tk.2015.11.015.(in Chinese)