Hinged walls or rocking cores can control the deformation pattern of the frame due to their large flexural stiffness and avoid weak story failure in frame structures. Alavi et al.[1] strengthened multi-story frame structures with hinged walls, which effectively reduced the drift demands. Wada et al.[2-4] used pin-supported walls to retrofit an existing SRC frame structure. The distributions of interstory drift ratios were improved by adding pin-supported walls. A pivoting core wall, which was supported on a friction pendulum bearing and can pivot about its base, was used to retrofit a steel moment frame building. The weak story failure was eliminated[5].
The lateral stiffness of hinged walls is zero and the structural responses cannot be reduced by adding hinged walls. Qu et al.[4] concluded that the magnitude of interstory drift ratios was not reduced by adding pin-supported walls. Makris et al.[6] showed that the pinned wall can increase the displacement response of the moment resisting frame. Therefore, dampers are added to the hinged walls to provide stiffness to them and dissipate seismic energy. Interstory drift ratios were reduced by adding dampers between the pin-supported walls and the original SRC columns[4]. BRBs were installed between the steel moment frame and the pivoting core wall to dissipate seismic energy[5]. The hinged wall contains both a steel truss and a concrete wall, which is composed of precast wall panels connected by pre-stressed tendons[7]. A steel truss which has a large stiffness can also be used as a hinged truss to control the deformation pattern of the structure. Takeuchi et al.[8-11] proposed a spine frame which rotates around the bottom middle point, and buckling restrained columns (BRCs) were used to dissipate seismic energy. A rocking steel shear wall installed with a double acting ring spring system to dissipate energy was investigated[12]. Du et al.[13] investigated the stiffness demand of a light energy dissipative rocking frame that contains self-centering energy dissipative bracing systems to dissipate seismic energy and reduce residual displacement.
Higher mode effects on the bending moment distribution of hinged walls were investigated[14-15], which showed that higher mode effects have to be considered in the design of hinged walls. The rocking wall is simplified as a flexural beam, and dampers installed at the bottom and between the rocking wall and moment frame are simplified as springs. The preliminary design method of the rocking-wall moment frame is proposed[16-18]. Nima et al.[19] proposed the equations which are used to simplify a rocking truss as a flexural beam. Wu et al.[15] proposed a simplified model for pin-supported wall structures and demonstrated that higher mode effects have to be considered when determining the strength demand of the wall. Moreover, Wiebe et al.[20] derived the vibration equations for a shear beam with a rotational spring at the bottom and a flexural beam with a rotational spring at the bottom. Yang et al.[21] proposed the seismic intensity superposition method to calculate the bending moment demand in the hinged wall considering higher mode effects.
The hinged wall with BRBs in base (HWBB) consists of a hinged wall with replaceable BRBs installed vertically at the bottom of the hinged wall. During a small earthquake, BRBs remain elastic and provide stiffness for HWBB, while BRBs yield under a large earthquake to dissipate seismic energy and provide damping for the structure. The hinged wall remains elastic while BRBs dissipate seismic energy and only BRBs need to be replaced after earthquake, avoiding the toe crushing and yielding of edge bars in conventional shear walls. BRBs provide the flexural strength while the pin bearing provides the shear strength to realize the separation of the load bearing[22]. A pseudo-dynamic test and quasi-static test on a 1:3 scale three-story hinged truss with BRBs in base (HTBB) were performed to investigate the seismic capacity and seismic performance of the specimen[23]. The hinged truss made up of steel beams, columns and braces can remain elastic during the experiment, while BRBs yielded and dissipated seismic energy. As damage is concentrated in BRBs, only BRBs need to be replaced to restore the function of the specimen. After the consecutively exciting of a minor earthquake, a design earthquake and a strong earthquake, the HTBB specimen withstood 19 cycles of displacement amplitude corresponding to 2.5% roof drift ratio with stable hysteretic performance. This test verified the excellent seismic performance of the HTBB. The hinged wall is able to remain elastic by capacity design which considers higher mode effects to control the deformation pattern of the structure.
The HWBB is applied to frame structures to improve the distribution of displacements and work as the lateral force resisting system. In this study, both the HWBB-hinged frame and HWBB-MRF (moment resisting frame) are analyzed. For the HWBB-hinged frame, as the hinged frame bears no lateral load, the derivation equations concern HWBB with mass distributed along the full height of HWBB and the hinged frame is not included in the simplified model. Vibration equations for these two simplified models are derived. Natural periods and natural modes of vibration are derived. Higher mode effects on structural responses, such as inner forces and displacements, are investigated for both the elastic structure and the plastic HWBB-hinged frame structure where BRBs yield. Parametric studies are conducted to investigate the influence of the relative stiffness ratio and the rotational stiffness ratio on the higher mode effects.
1 Derivation
The simplified model of the HWBB-hinged frame is shown in Fig.1. Shear deformation of the wall is ignored as the height of the structure is great enough. BRBs offer the whole moment resistance for the structure. BRBs are simplified as a rotational spring. The hinged wall is simplified as a flexural beam with a pinned end. The flexural stiffness of the flexural beam is EI. The rotational stiffness of the rotational spring is denoted as kb and H denotes the length of the flexural beam.

Fig.1 Simplified model of the HWBB-hinged frame structure
The moment resistance offered by the rotational spring in the simplified model is expressed as
M=kbθ
(1)
where θ denotes the interstory drift ratio of the first story, which is caused by the rotation of the hinged wall and it is calculated by the deformation of BRB as follows:
(2)
where εBRB denotes the strain in BRB ; lBRB is the length of BRB; ΔuBRB is the deformation of BRB; and B is the distance between centerlines of BRBs. Substituting Eq.(2) into Eq.(1) gives
(3)
where A denotes the area of the core plate in BRB and E is the elastic modulus of steel. Vibration equations for the simplified models of both the HWBB-hinged frame and the HWBB-MRF are derived in the following sections.
1.1 HWBB-hinged frame
As shown in Fig.1, the mass per unit length along the flexural beam is ![]() υ(x, t) is the transverse-displacement response. Physical properties are distributed evenly along the flexural beam. As the mass and stiffness are evenly distributed along the flexural beam, the partial differential equation contains only two variables, time and the distance to the bottom of the flexural beam. The partial differential equation of the flexural beam can be expressed as[24]
υ(x, t) is the transverse-displacement response. Physical properties are distributed evenly along the flexural beam. As the mass and stiffness are evenly distributed along the flexural beam, the partial differential equation contains only two variables, time and the distance to the bottom of the flexural beam. The partial differential equation of the flexural beam can be expressed as[24]
(4)
where the second part of the above equation is the inertia force.
Assume that the solution is as follows according to the separation of variables:
υ(x,t)=φ(x)Y(t)
(5)
Substituting Eq.(5) into Eq.(4) gives
(6)
where ω is the natural circular frequency of the model.
For brevity, define
(7)
The general solution of Eq.(6) is
φ(x)=A1sinax+A2cosax+A3sinhax+A4coshax
(8)
Define the following parameter for brevity:
(9)
Four boundary conditions at the ends of the flexural beam are
When x=0, M(0)=kbθ(x=0),
(10)
where M is the bending moment in the wall and θ denotes the rotation of the beam section. Therefore,
m(A1+A3)=-A2+A4
(11)
When x=0, φ(0)=0,
A2+A4=0
(12)
When x=L, M(L)=0,
-A1a2sinaL-A2a2cosaL+A3a2sinhaL+A4a2coshaL=0
(13)
When x=L, V(L)=0,
-A1a3cosaL+A2a3sinaL+A3a3coshaL+A4a3sinhaL=0
(14)
To obtain a nontrivial solution for Eqs.(11) to (14), the determinant of the matrix formed by the factors of the above four equations has to be zero.
Define
(15)
The equation for natural frequencies is
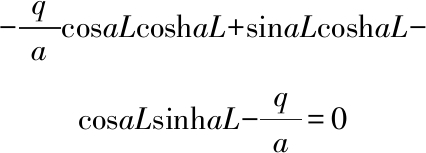
(16)
The above equation does not have analytical solutions and is solved by numerical methods. The natural vibration mode corresponding to ωn is
φn(x)=A1sinanx+A2cosanx+A3sinhanx+A4coshanx
(17)
The relationship of the four factors is derived by Eqs.(11) to (14) as follows:
A2=-A4
(18)
(19)
(20)
The external static force sn is[25]
sn=Γnmφn
(21)
where Γn is the modal participation factor; m is the mass matrix and φn represents the natural mode of the n-th mode, which is represented by the continuous function φn(x) in this paper.
The static displacement and static inner forces including the bending moment, the shear and the rotation of each beam section under sn can be derived based on the natural vibration frequencies and modes calculated.
The static displacement is
![]()
A3sinhanx+A4coshanx)
(22)
The static bending moment in the wall is
(23)
The static shear in the wall can be expressed as
(24)
The rotation of each wall section is
![]()
A3ancoshanx+A4ansinhanx)
(25)
After the BRBs yield, the rotational stiffness of the rotational spring is almost 0.02 times that of the elastic rotational stiffness. The first modal circular frequency is nearly zero as the simplified model is almost a pinned base beam.
Inner forces distribution in the HWBB-hinged frame after BRBs yield is illustrated in section 2.1.
1.2 HWBB-MRF
The simplified model of the HWBB-MRF structure is shown in Fig.2. MRF is simplified as a shear beam with its lateral stiffness denoted as K (the shear force corresponding to unit interstory drift ratio). HWBB and MRF are connected through pinned links which can transfer the horizontal forces between those two systems. The relative stiffness of the moment resisting frame and the hinged wall is defined as the relative stiffness ratio λ[15].
(26)
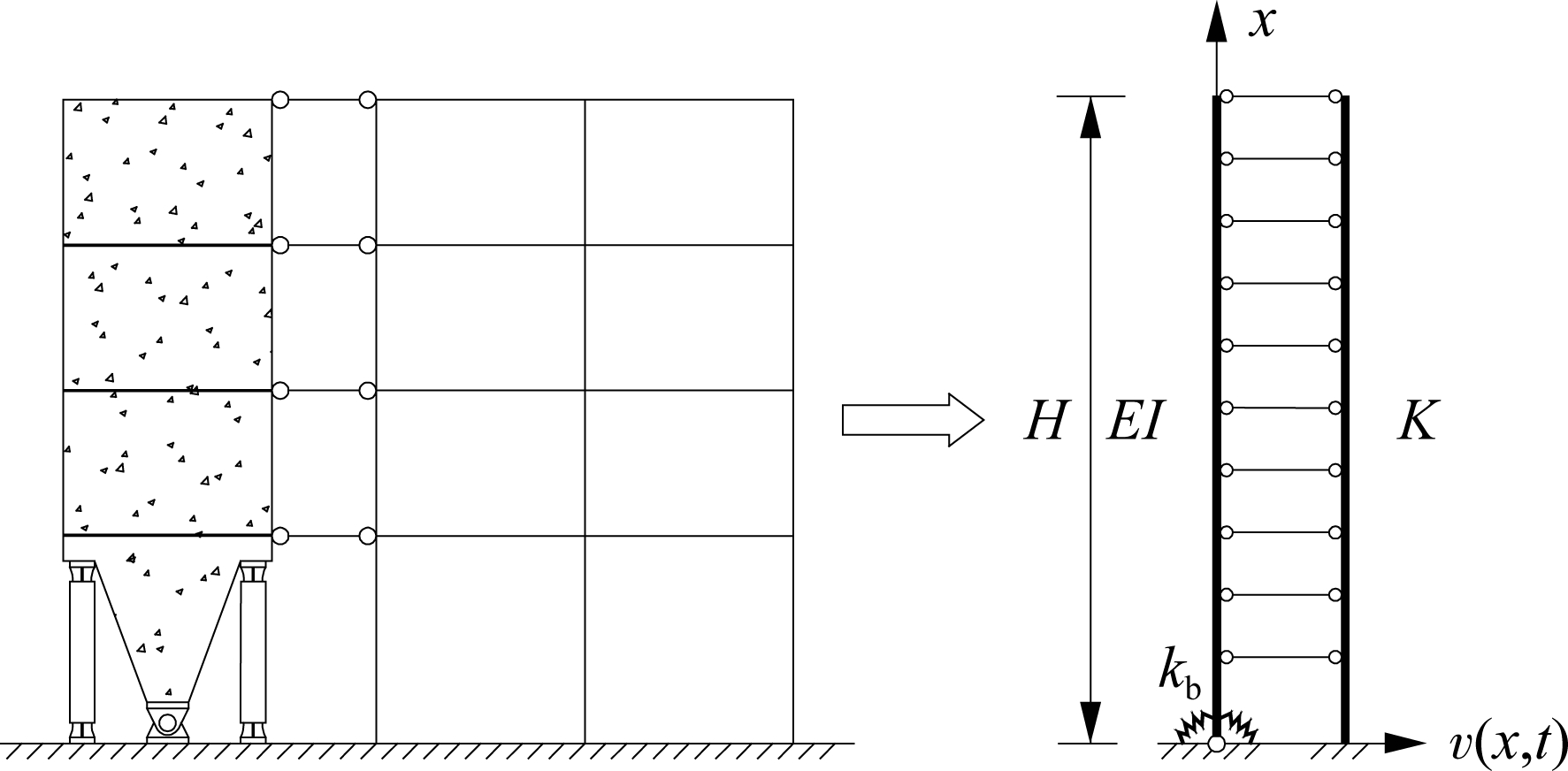
Fig.2 The simplified model of the HWBB-MRF structure
The vibration equation of the simplified model of HWBB-MRF is[15]
(27)
The definitions of α and β which are related to natural frequencies from Wu et al.[15] are as follows:
(28)
(29)
(30)
(31)
The general solution of Eq.(27) is[15]
φ(x)=C1coshαx+C2sinhαx+C3cosβx+C4sinβx
(32)
The boundary conditions are as follows:
C1α2-αkbC2-C3β2-C4kbβ=0
(33)
When x=0, φ(0)=0,
C1+C3=0
(34)
When x=H, M=0,
C1α2coshαH+C2α2sinhαH-C3β2cosβH-C4β2sinβH=0
(35)
(Kα-EIα3)C1sinhαH+(Kα-EIα3)C2coshαH-
(Kβ+EIβ3)C3sinβH+(Kβ+EIβ3)C4cosβH=0
(36)
The frequency equation can be expressed as
αkbβ2(Kβ+EIβ3)-kbβα2(Kα-EIα3)+
sinhαHcosβHα2(Kβ+Eβ3)(α2+β2)+
sinβHcoshαHβ2(Kα-EIα3)(α2+β2)+
sinhαHsinβH[kbβα2(Kβ+EIβ3)+
αkbβ2(Kα-EIα3)]+cosβHcoshαH·
[-kbβ3(Kα-EIα3)+α3kb(Kβ+EIβ3)]=0
(37)
An analytical solution cannot be obtained from this equation but numerical solutions can be obtained.
The natural vibration mode corresponding to ωn is
φn(x)=C1coshαnx+C2sinhαnx+C3cosβnx+C4sinβnx
(38)
where
(39)
C3=-C1
(40)
(41)
Based on the natural vibration frequencies and modes calculated, the static displacement and inner forces can be derived as
C3cosβnx+C4sinβnx)
(42)

(43)
![]()
C2αncosh(αnξ)-C3βnsin(βnξ)+
C4βncos(βnξ))dξ
(44)
(45)
where ![]() represents the bending moment in the wall of the HWBB.
represents the bending moment in the wall of the HWBB.
![]()
C3βnsinβnx+C4βncosβnx)
(46)
![]()
C2sinhαnξ+C3cosβnξ+C4sinβnξ)dξ
(47)
(48)
where ![]() is the total shear borne by the structure caused by the external force sn;
is the total shear borne by the structure caused by the external force sn; ![]() is the shear in the hinged wall.
is the shear in the hinged wall.
The response spectrum analysis method in Ref.[25] is used to calculate dynamic responses by multiplying the modal static responses to the pseudo acceleration corresponding to each modal period. The SRSS method can be used to combine different modal reactions according to the Chinese seismic code for structures with well-separated natural frequencies[26].
The HWBB can be simplified as a hinged wall due to the small post-yielding stiffness of BRBs. For the HWBB-hinged frame structure, the first modal period after BRBs yield is larger than 15 s due to the small post yielding stiffness of BRB. Therefore, the pseudo acceleration of the first mode is almost zero[25]. The first mode will no longer contribute to the inner forces. Higher modes have to be considered after the yielding of BRB. This is illustrated by the example in section 2.1. As displacement is not sensitive to higher modes, the whole displacement varies linearly along the height of the structure and is controlled by the first mode after the BRBs yield. For the HWBB-MRF structure, the MRF still provides the lateral stiffness for the whole structure after the BRBs yield and the first mode contribute to the inner forces after the BRBs yield[15].
2 Example Models
In this section, example models contain both the HWBB-hinged frame and HWBB-MRF. Pseudo-accelerations corresponding to different modal periods are obtained according to the design spectrum in Chinese seismic design code for frequent earthquakes with intensity 7.
2.1 HWBB-hinged frame structure
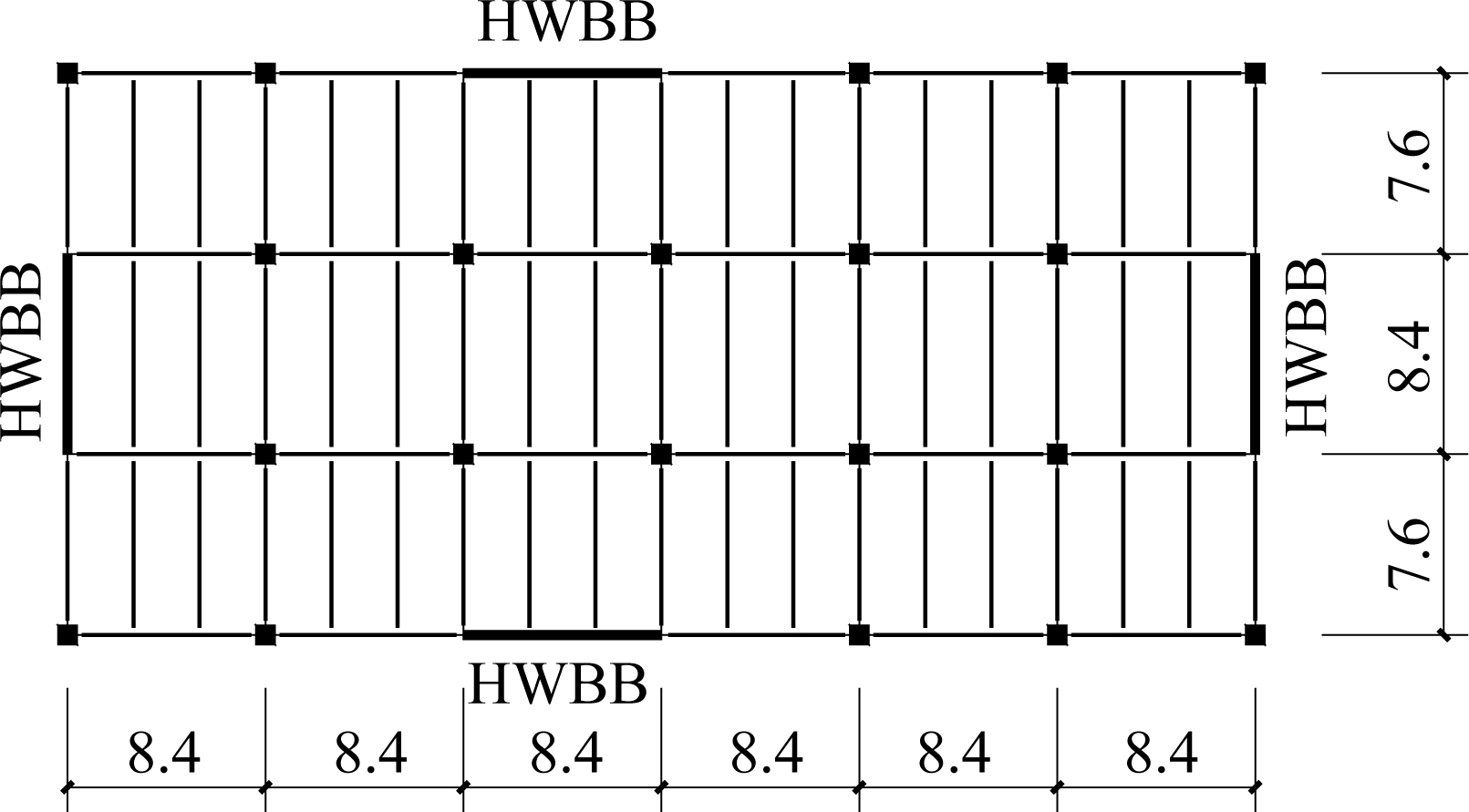
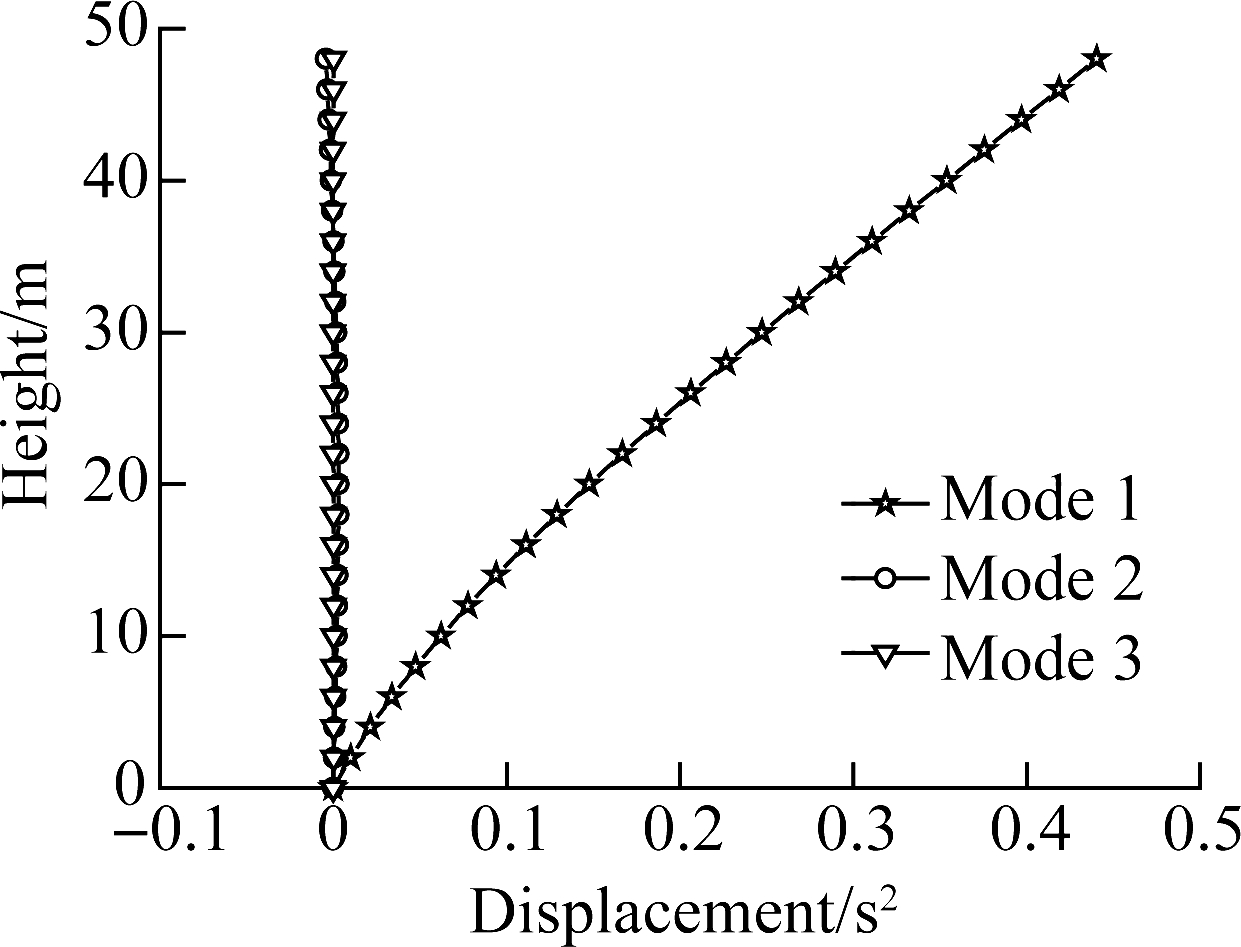
The prototype building is a twelve-story structure accompanied by two HWBBs in each direction of the building, with uniform properties over the height. Fig.3(a) depicts the floor plan, which has a footprint of 23.6 m×50.4 m with 4.0-m story heights. Concrete with 40 MPa nominal compression strength is used. Due to the symmetricity of the structure, a half structure is modeled. The seismic weight of each half of the building is 6 800 kN at each floor level. As shown in Fig.3(b), the cross section of the wall is 0.35 m×8.4 m and the flexural stiffness of the wall is EI=562 GN·m2. The area of the core plate of BRB is 22 000 mm2, the length of BRB is 3.7 m, and the distance between centerlines of two BRBs is 8.1 m, resulting in kb=40 GN·m. The frame in the prototype building bears only a vertical load and belongs to a hinged frame which does not have any lateral resistance. The first three natural periods of this structure are 3.36, 0.452 and 0.151 s, respectively. The first three natural vibration modes are shown in Fig.4.
(a)

(b)
Fig.3 Structural layout of the numerical example(unit:m).(a) Plan view; (b) Detail of HWBB

Fig.4 Natural modes of the HWBB-hinged frame
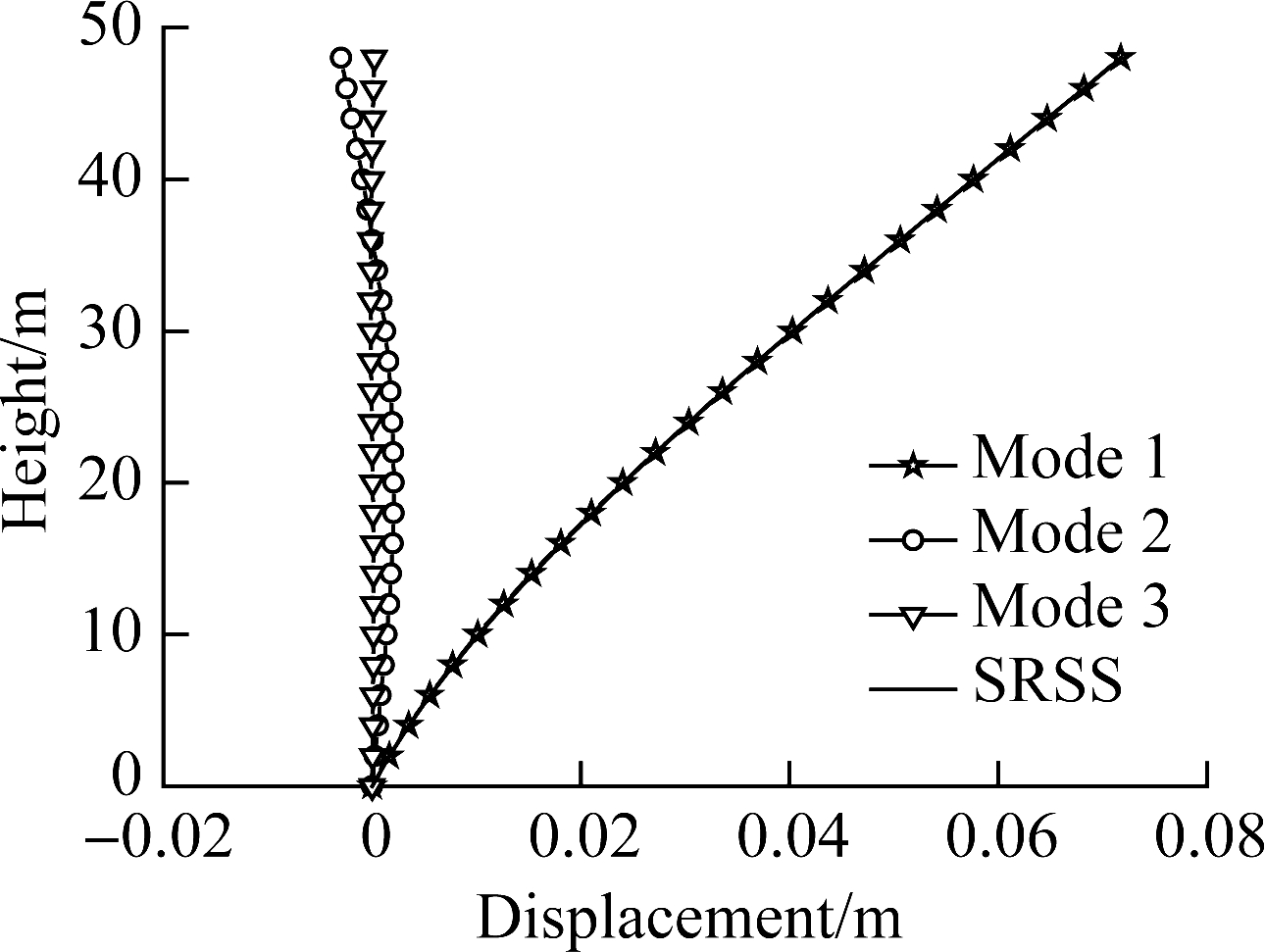
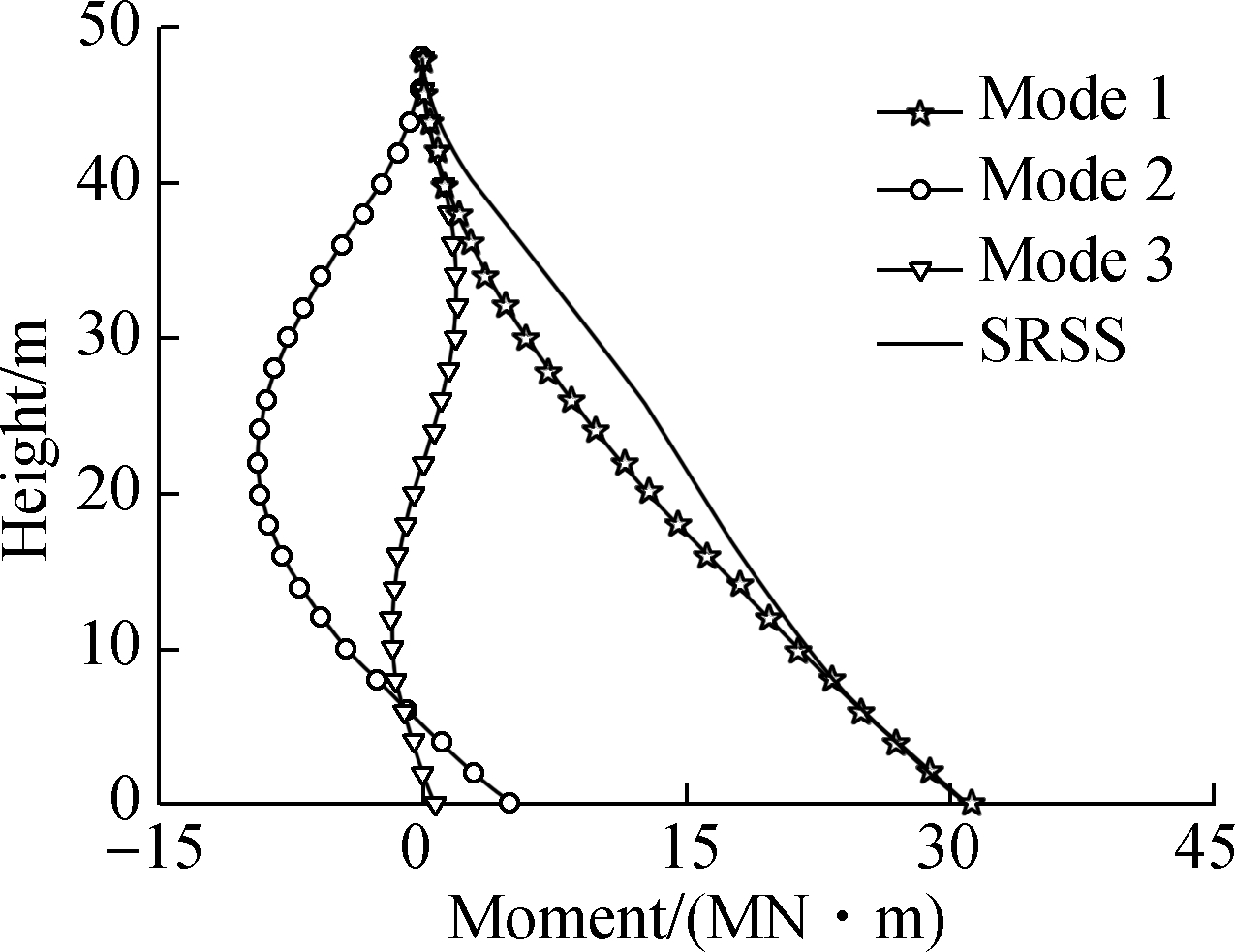
Fig.5(a) depicts the static displacement in the HWBB corresponding to the first three modes. The maximum static displacement corresponding to mode 1 is 100 times that of mode 2 and 1 600 times that of mode 3, indicating that the first mode is dominant. Fig.5(b) depicts the dynamic displacement in the HWBB along the height. The total displacement is predominantly controlled by the first mode as the maximum dynamic displacement of the first mode is 99.86% times that of the SRSS result, while contributions from the second and third modes are 4.15% and 0.283% times that of the SRSS result, respectively. It can be seen from Fig.5(c) and Fig.5(d) that higher modes have to be considered for shear and bending moment design in the HWBB. In Fig.5(c), the maximum shear in mode 1 is 65.9% that of SRSS, while the maximum shears in mode 2 and mode 3 are 71.49% and 23.3% that of SRSS, respectively. In Fig.5(d), the maximum moment in mode 1 is 98.7% that of SRSS, and the maximum moments in mode 2 and mode 3 are 30.24% and 6.31% that of SRSS, respectively.
(a)
(b)

(c)
(d)
Fig.5 Responses of HWBB.(a) Static displacement; (b) Dynamic displacement; (c) Shear in HWBB; (d) Moment in HWBB
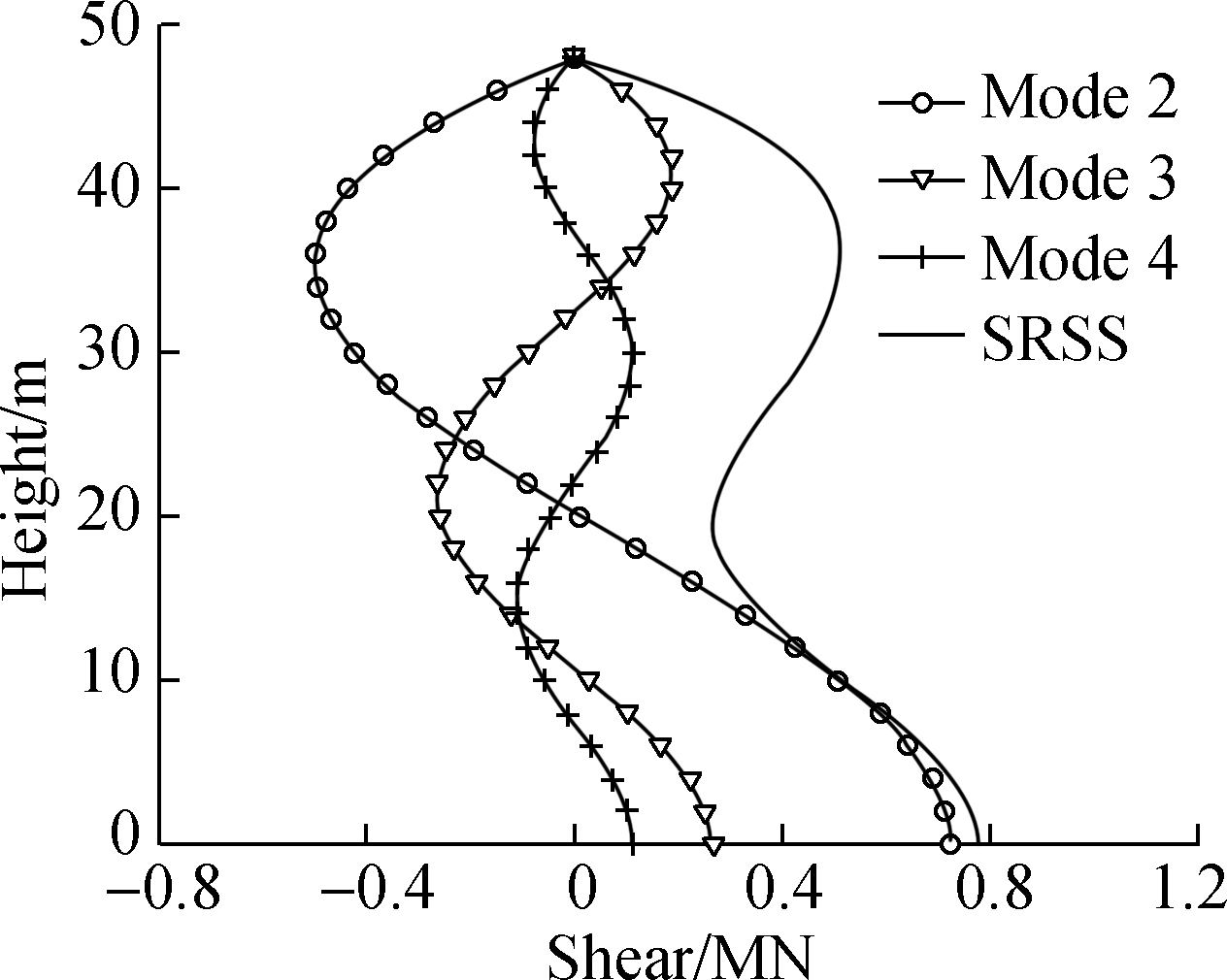
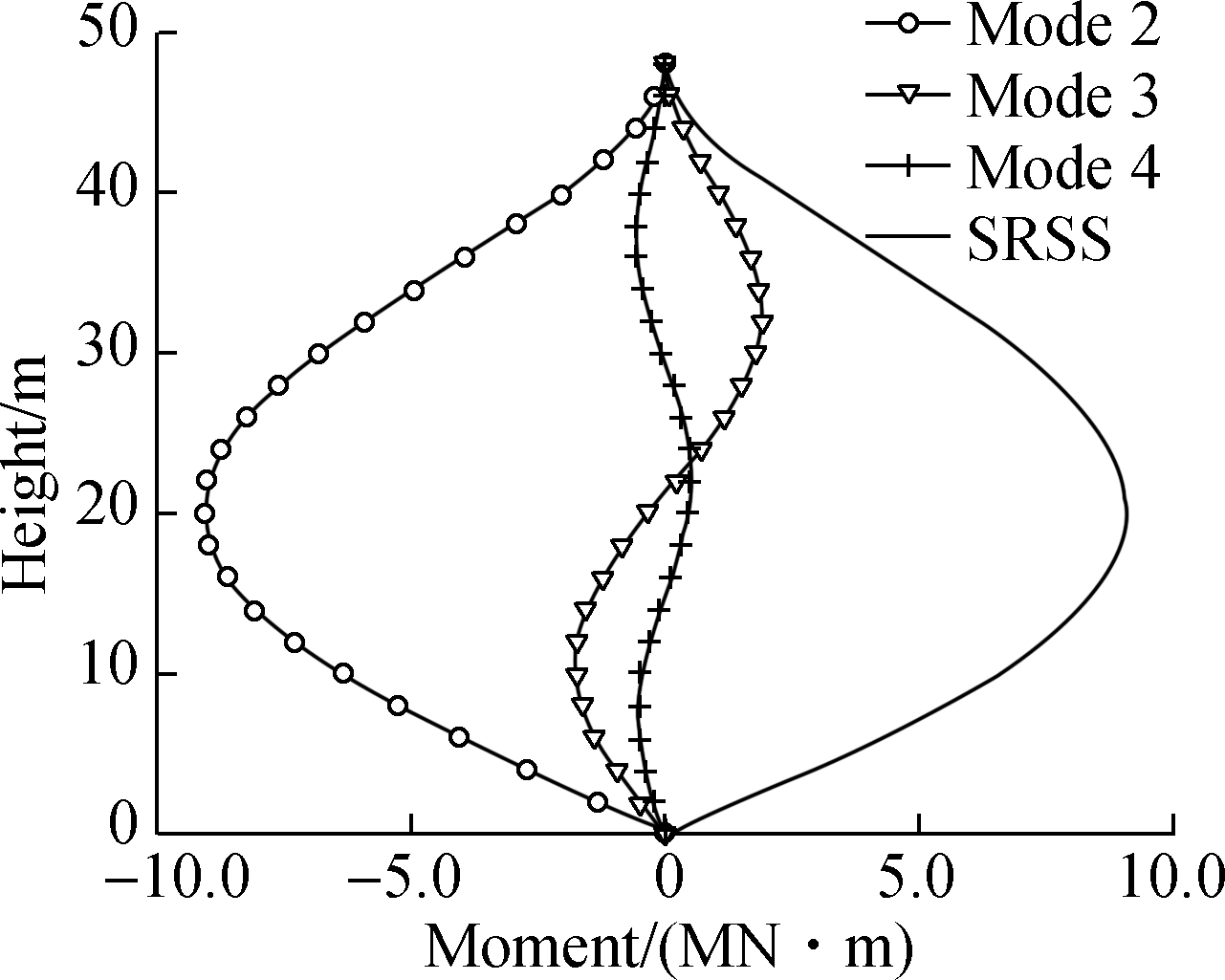
Fig.6 is the inner forces distribution in the HWBB after the BRBs yield. Due to the fact that the pseudo acceleration corresponding to the first mode almost equals zero, the first mode does not contribute to the inner forces. In Fig.6(a), the maximum shear in mode 2 is 93% that of SRSS, while the maximum shears in mode 3 and mode 4 are 33.3% and 14.4% that of SRSS, respectively. In Fig.6(b), the maximum moment in mode 2 is 98% that of SRSS, while the maximum moments in mode 3 and mode 4 are 20.5% and 6% that of SRSS, respectively. It indicates that higher modes have to be considered in the calculation of inner forces in HWBB after the BRBs yield.
(a)
(b)
Fig.6 Response of HWBB after BRBs yield.(a) Shear in HWBB; (b) Moment in HWBB
2.2 HWBB-MRF
The properties and dimensions of the HWBB are the same as the HWBB-hinged frame structure in section 2.1. The shear stiffness of the MRF is 549 MN, which corresponds to a relative stiffness ratio of 1.5. The first three natural periods are 1.69, 0.34 and 0.13 s, respectively. The natural mode shapes of the first three modes are shown in Fig.7.
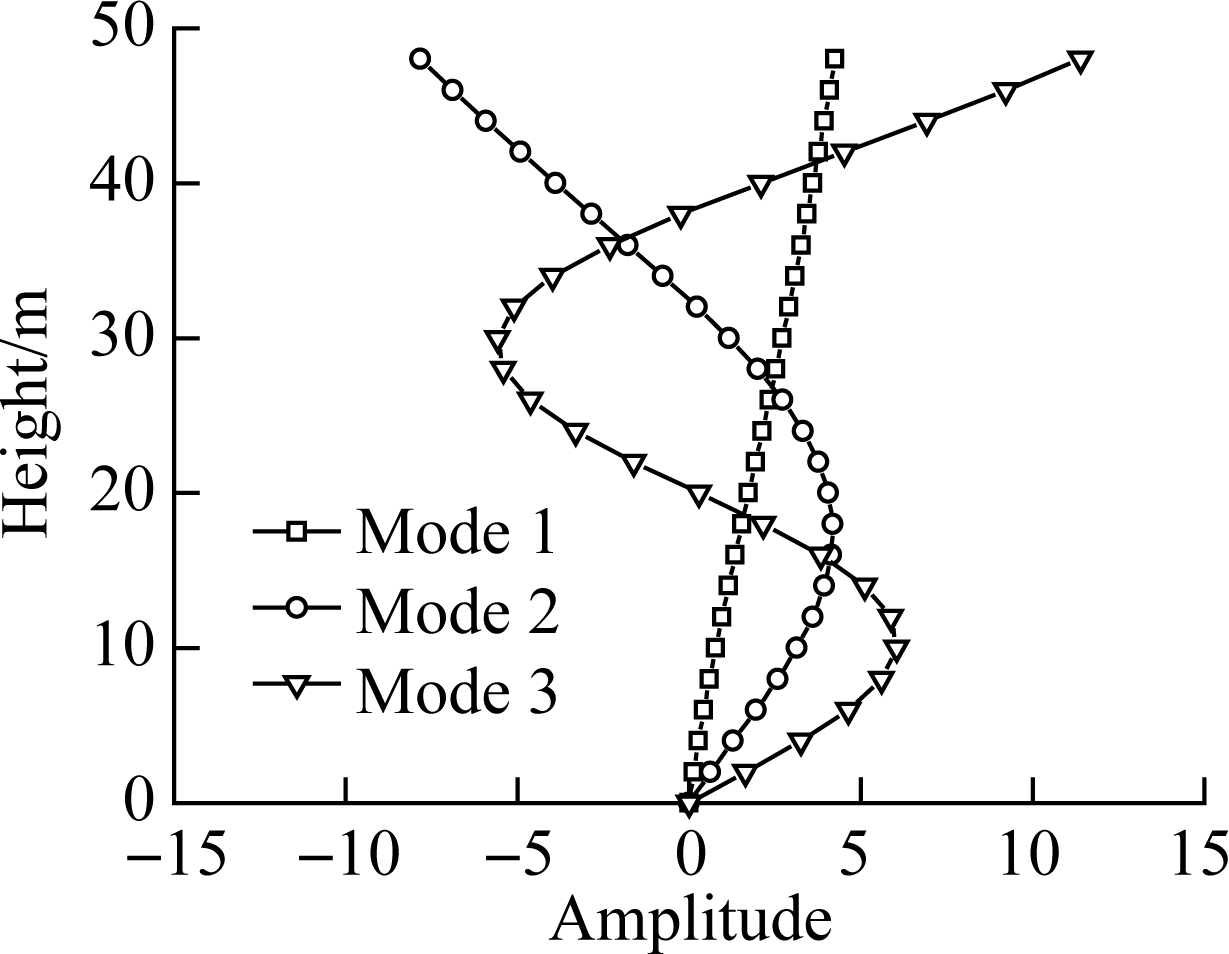
Fig.7 Natural mode shapes of the first three modes
2.2.1 Equivalent static response
The equivalent static displacement is dominantly controlled by the first mode, as shown in Fig.8.
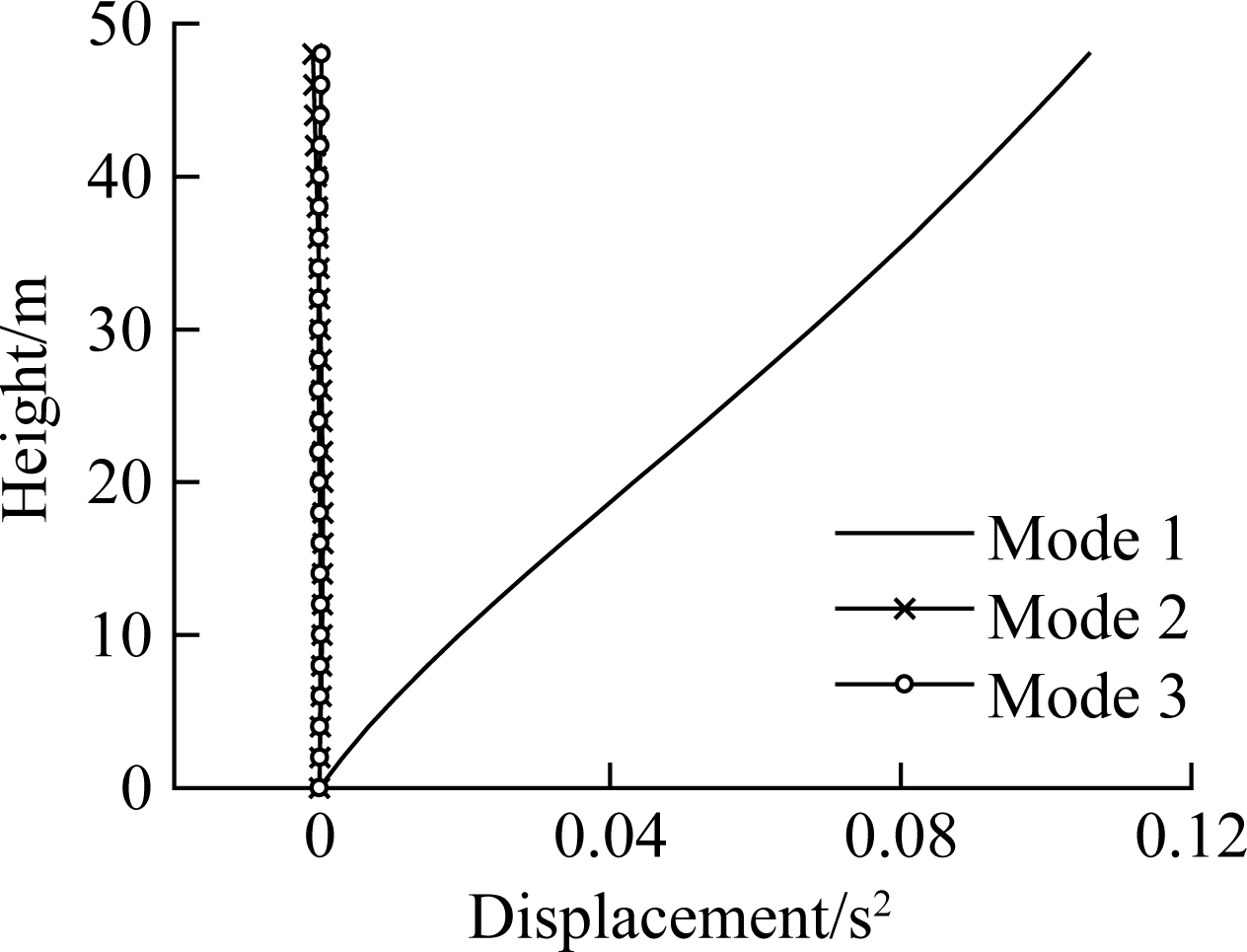
Fig.8 Static displacement distribution for the first three modes
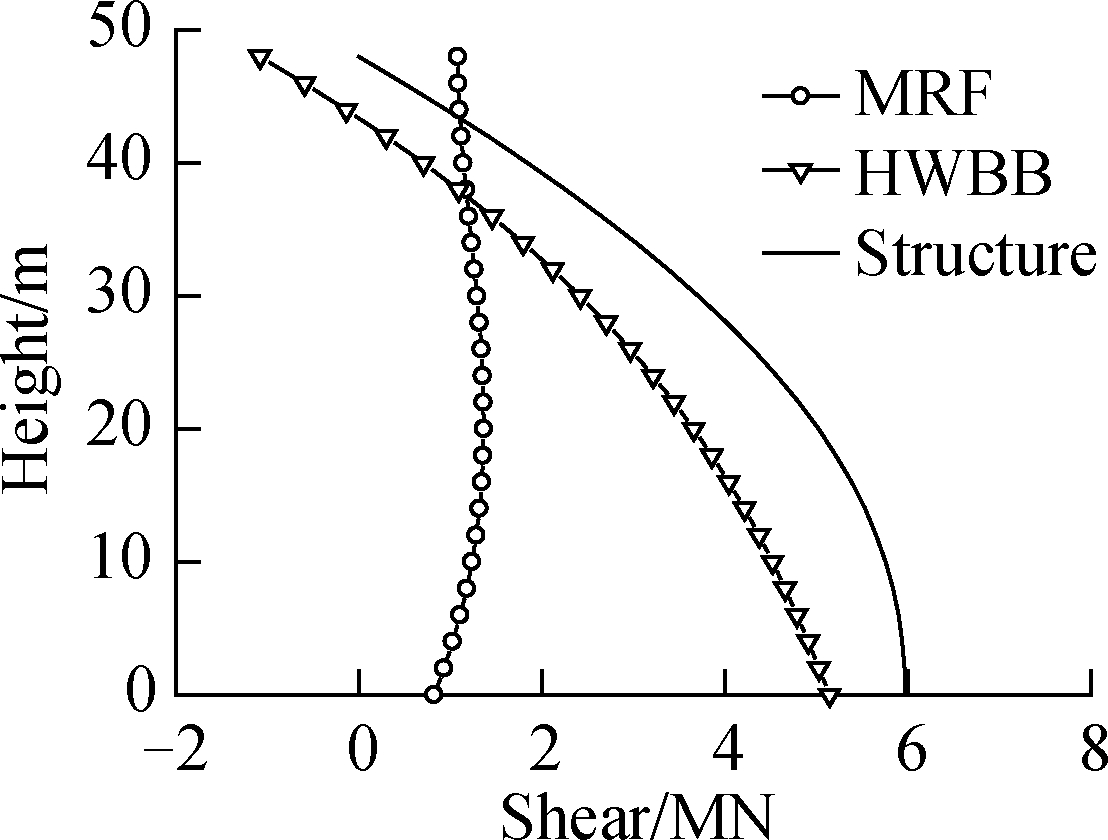
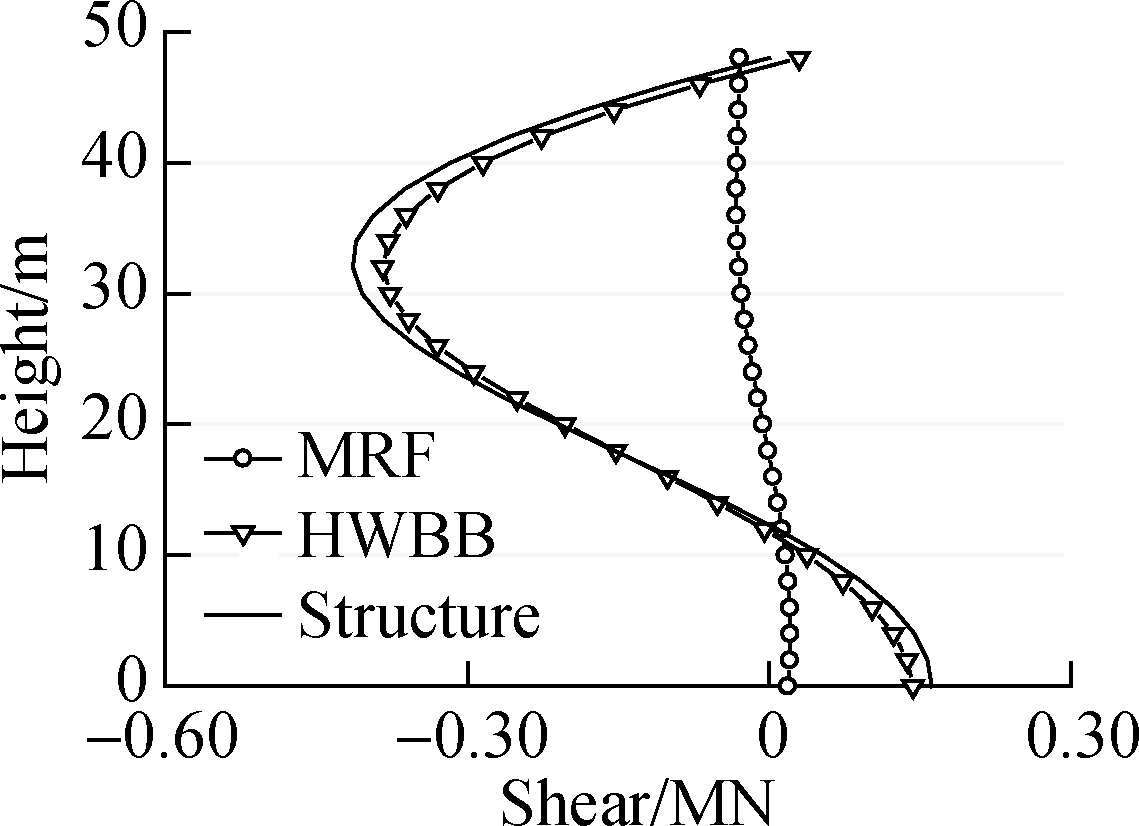
The shear distribution is depicted in Fig.9. In mode 1, both the contributions from the wall and the frame have to be considered since the maximum shear of the structure is 4.38 and 1.16 times those of the frame and HWBB. The shear borne by the MRF significantly decreases in mode 2 and mode 3.
(a)
(b)

(c)
Fig.9 Shear distribution for the first three modes.(a) Mode 1; (b) Mode 2; (c) Mode 3
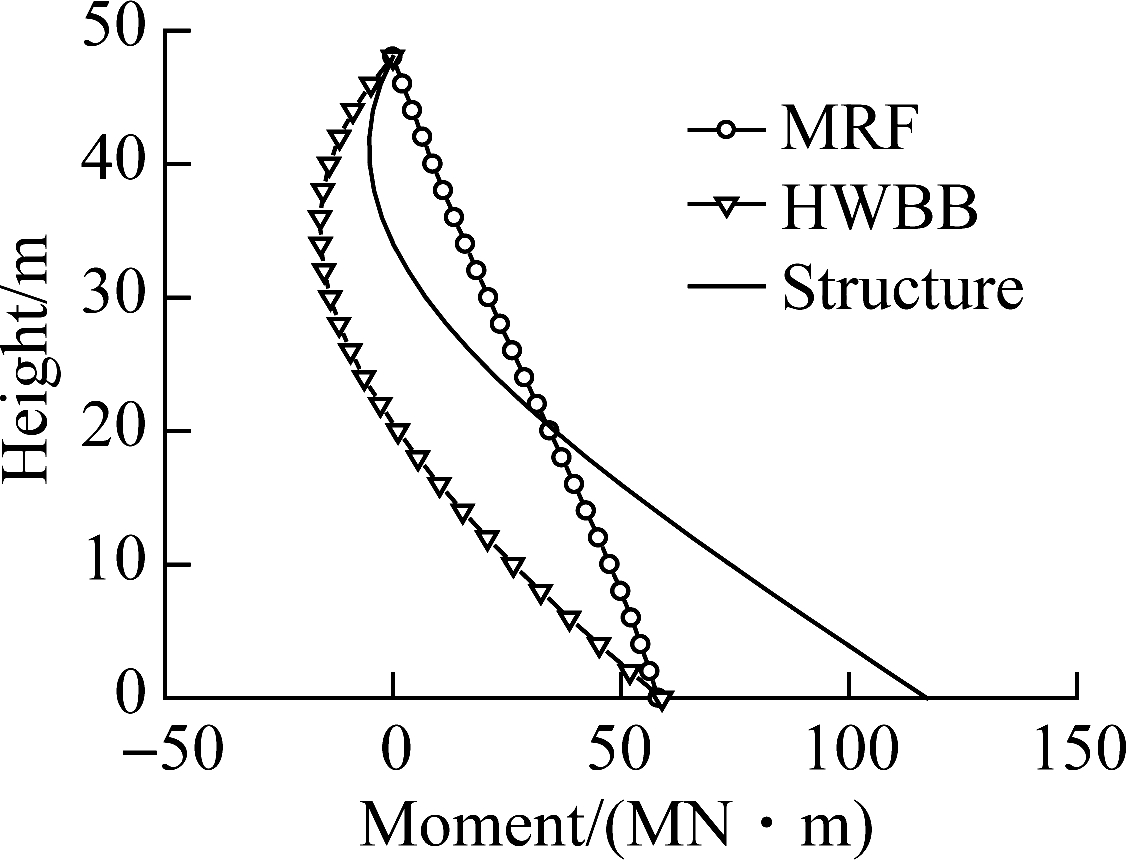
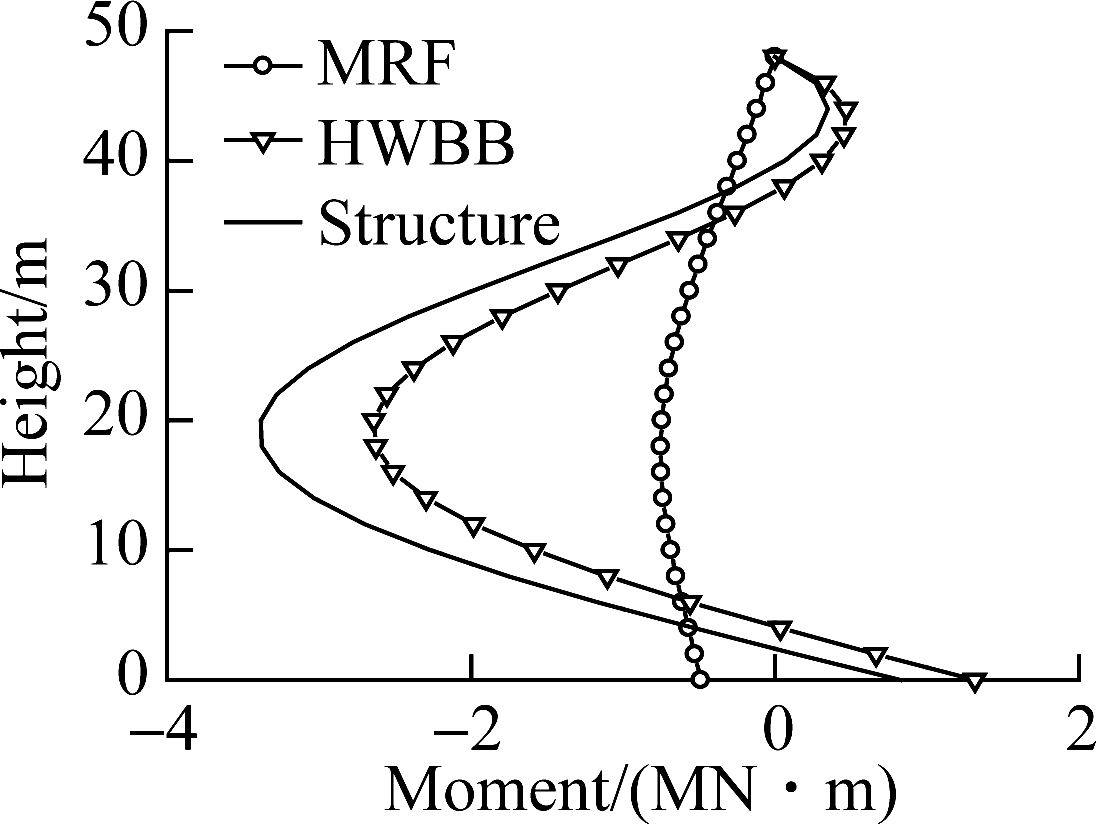
Fig.10 depicts the bending moment distribution. The contribution from the frame decreases sharply as the mode increases, especially for mode 3. The contributions from the wall are 4.514 and 10.99 times those of the frame in mode 2 and mode 3, respectively.
(a)
(b)

(c)
Fig.10 Bending moment distribution for the first three modes.(a) Mode 1; (b) Mode 2; (c) Mode 3
The static displacement is dominated by the first mode, and the frame contributes little to the shear and moment distribution in higher modes (mode 2 and mode 3). However, the wall contributes predominantly to the shear and moment in higher modes.
2.2.2 Dynamic response
Fig.11 depicts dynamic responses, which include the displacement and inner forces. Displacement is controlled by the first mode. Fig.11(a) depicts the shear in the frame. It can be seen that higher mode effects are not significant in the frame because HWBB can effectively control the deformation pattern of the frame. Therefore, the shear demand of the frame can be estimated only based on the first mode. Fig.11(a) indicates that the shear corresponding to the first mode is 99.9% that of SRSS and the shears for mode 2 and mode 3 are 8.79% and 4.62% that of SRSS, respectively.
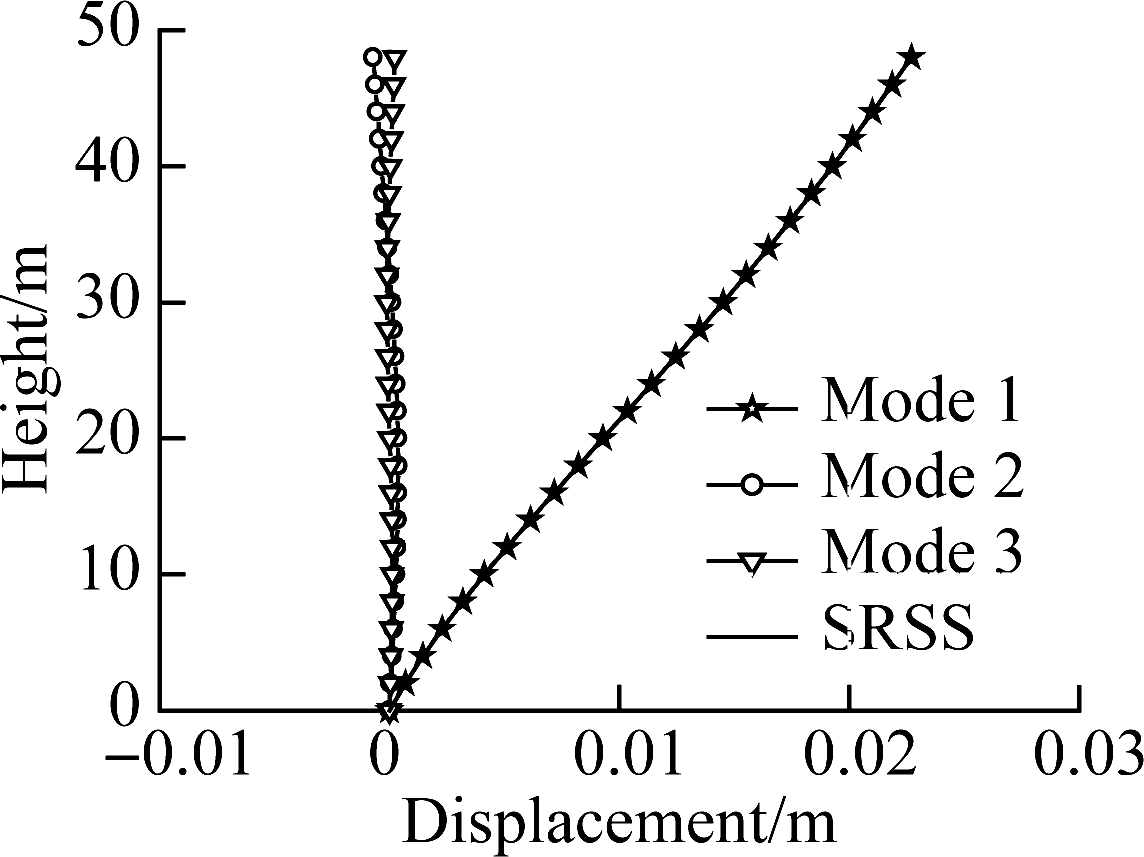
Fig.11(b) depicts the dynamic displacement response. It can be seen from the figure that the SRSS value is almost identical to the displacement of the first mode. This indicates that mode 2 and mode 3 can be ignored and mode 1 can be used to estimate the displacement demand.

(a)
(b)
(c)
(d)
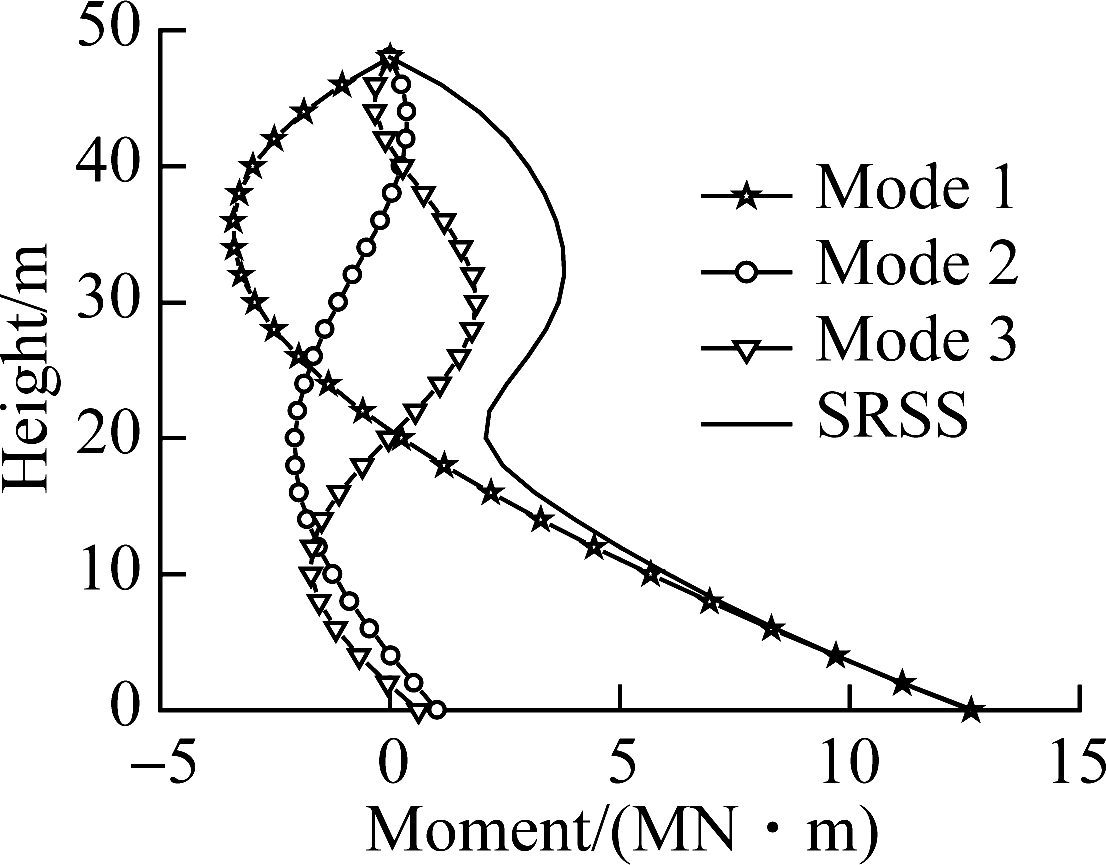
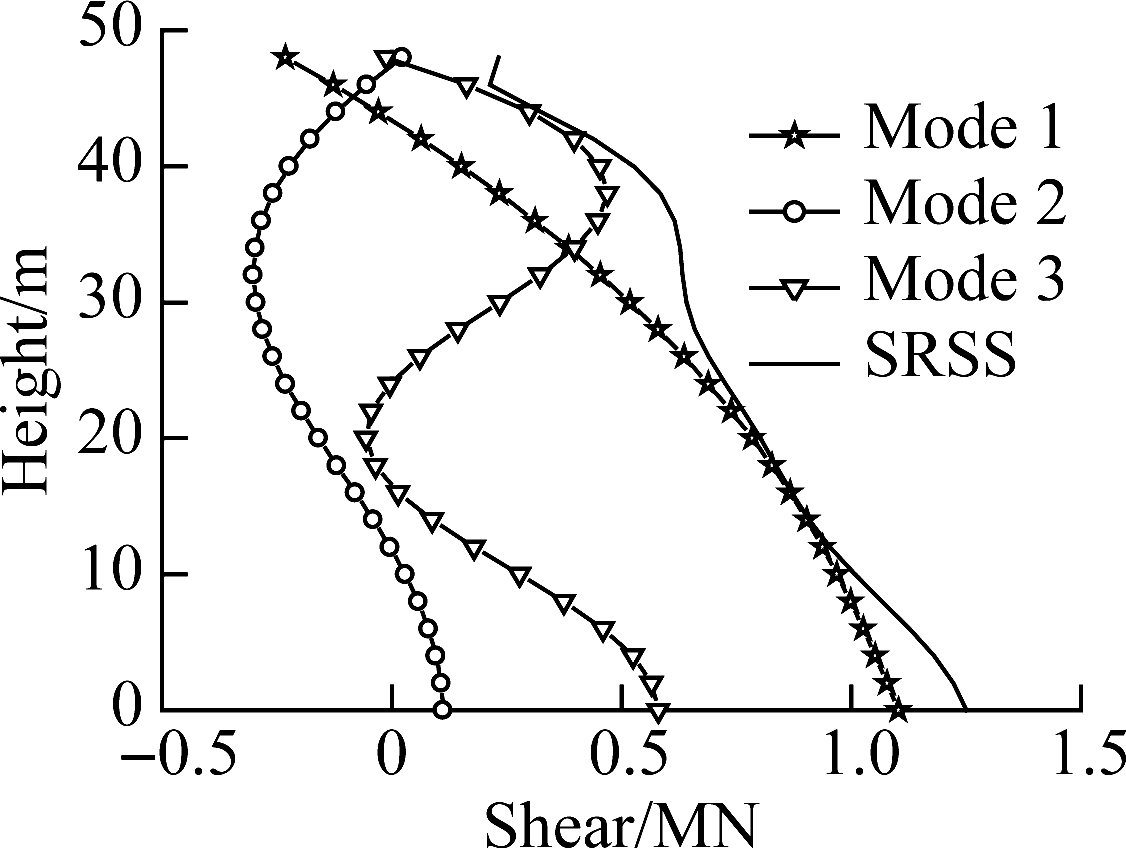
Fig.11 Dynamic response.(a) Shear in the frame; (b) Displacement; (c) Bending moment in HWBB; (d) Shear in HWBB
Fig.11(c) illustrates the bending moment distribution in HWBB. The maximum moment of mode 1 is 99.55% that of the SRSS, and the maximum moments of mode 2 and mode 3 are 16.29% and 14.79% that of the SRSS, respectively. This indicates that higher modes have a non-negligible effect on the bending moment distribution of the wall and need to be considered when determining the bending moment demand of the wall. Fig.11(d) is the shear in the hinged wall. The maximum shear of the first mode in the wall is 99.55% that obtained using the SRSS method, and the maximum values of mode 2 and mode 3 are 16.29% and 14.79% that of SRSS, respectively. This indicates that higher mode effects have to be considered when determining the shear demand in the wall.
From the above analysis, it can be seen that higher modes have a remarkable effect on the inner force distribution in the wall. Therefore, higher mode effects have to be considered during the strength design of the wall. However, the displacement and shear force in the frame are controlled by the first mode, which demonstrates that HWBB has effectively controlled the deformation pattern of the MRF.
3 Parameter Analysis
In this section, the effect on the seismic performance of two parameters, which are the relative stiffness ratio and the rotational stiffness ratio, are analyzed.
3.1 Relative stiffness ratio
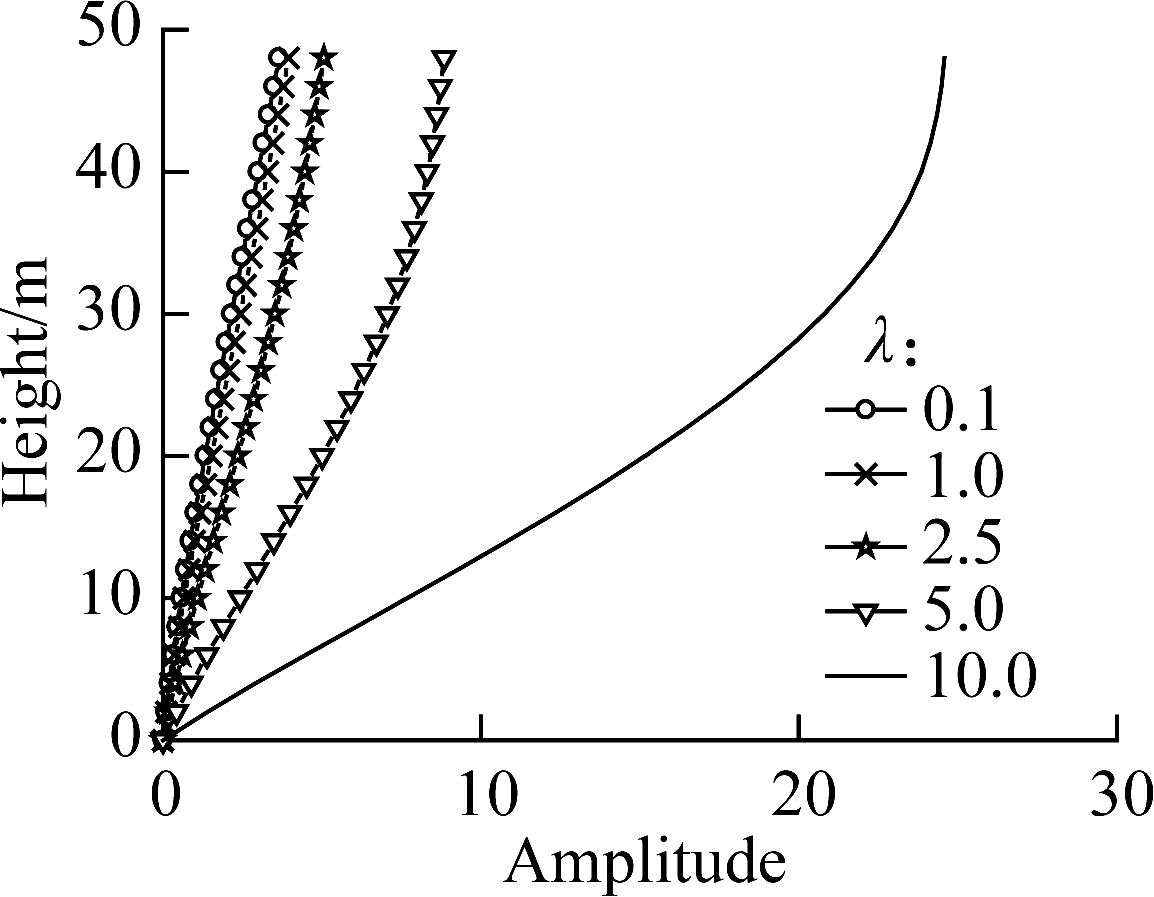
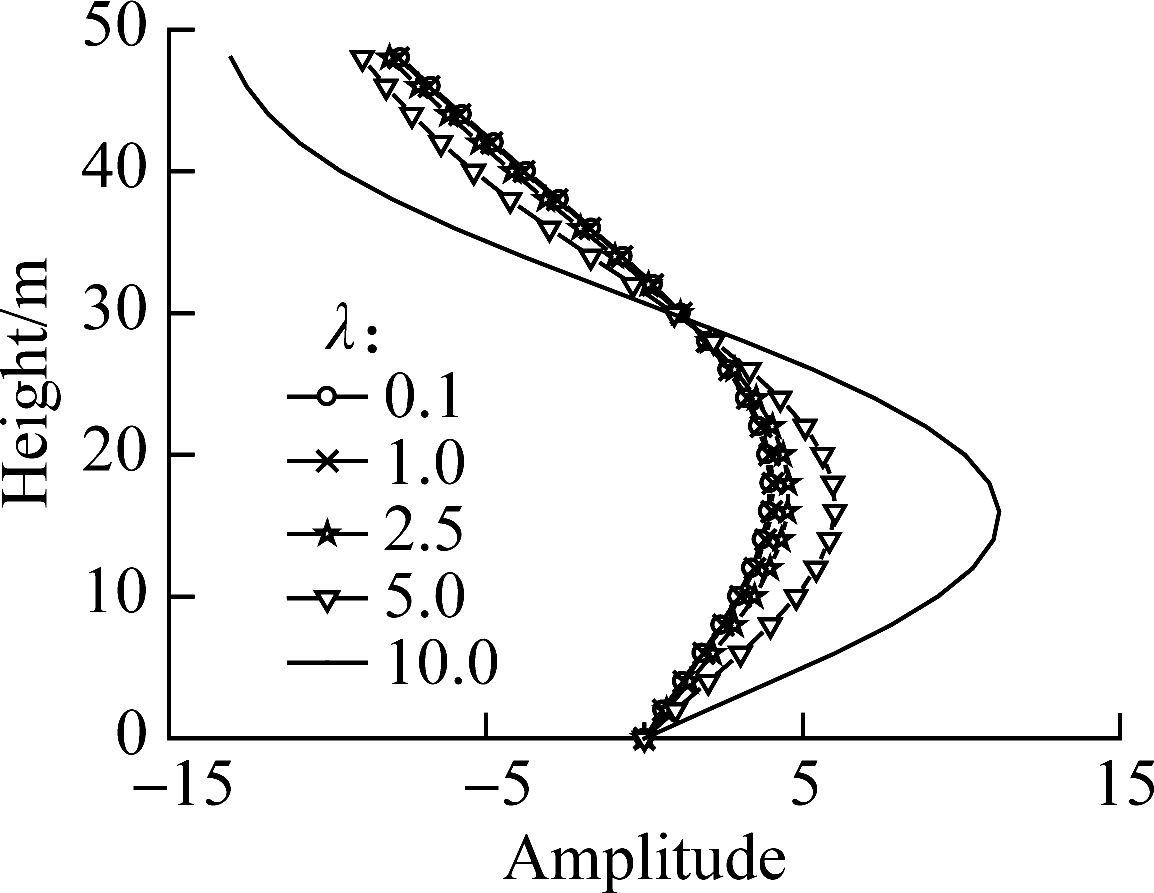
The model in section 2.2 is used in the analysis. The variation of the relative stiffness ratio is realized by the variation of the flexural stiffness of the wall, while the lateral stiffness of MRF remains constant. The effect of the relative stiffness ratio on the modal shape is illustrated in Fig.12. With the decrease in the relative stiffness ratio, the flexural stiffness of the wall increases, and the displacement amplitude corresponding to each mode decreases. The flexural stiffness of the wall reduces the displacement amplitude of mode shapes corresponding to the first three modes. However, after the relative stiffness ratio reaches a certain value, the increase in the flexural stiffness will neither effectively reduce the displacement of the mode shape nor be cost-effective.
(a)
(b)

(c)
Fig.12 Influence of the relative stiffness ratio on the modal shape.(a) Mode 1; (b) Mode 2; (c) Mode 3
Fig.13 presents the cumulative effective modal mass ratio of the first three modes. The minimum value corresponding to the first mode is larger than 70%, and the contribution from the third mode is larger than the contribution from the second mode. The effective modal mass corresponding to the first mode and second mode increases with the increase in the relative stiffness ratio, while the effective modal mass of the third mode decreases with the increase of relative stiffness. When the relative stiffness ratio is larger than or equal to 10, the cumulative effective modal mass of the first three modes will be larger than 90%, which can meet the requirement of the seismic code[26] for the minimum number of modes needed to be considered in analysis.

Fig.13 Influence of the relative stiffness ratio on the cumulative effective modal mass ratio of the first three modes
3.2 Relative stiffness of the hinged wall and rotational spring
The rotational stiffness ratio, which is the relative stiffness ratio of the rotational stiffness of the rotational spring and the flexural stiffness of the wall, is as follows:
![]()
(49)
where h is the story height, which is assumed to be the same along the height of the building for brevity.
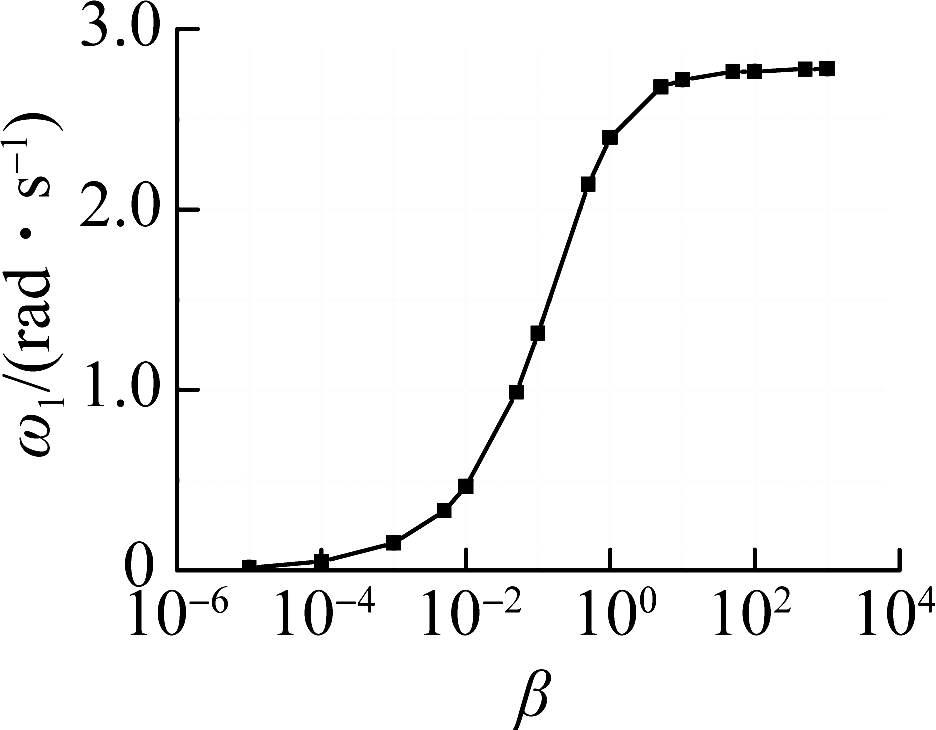
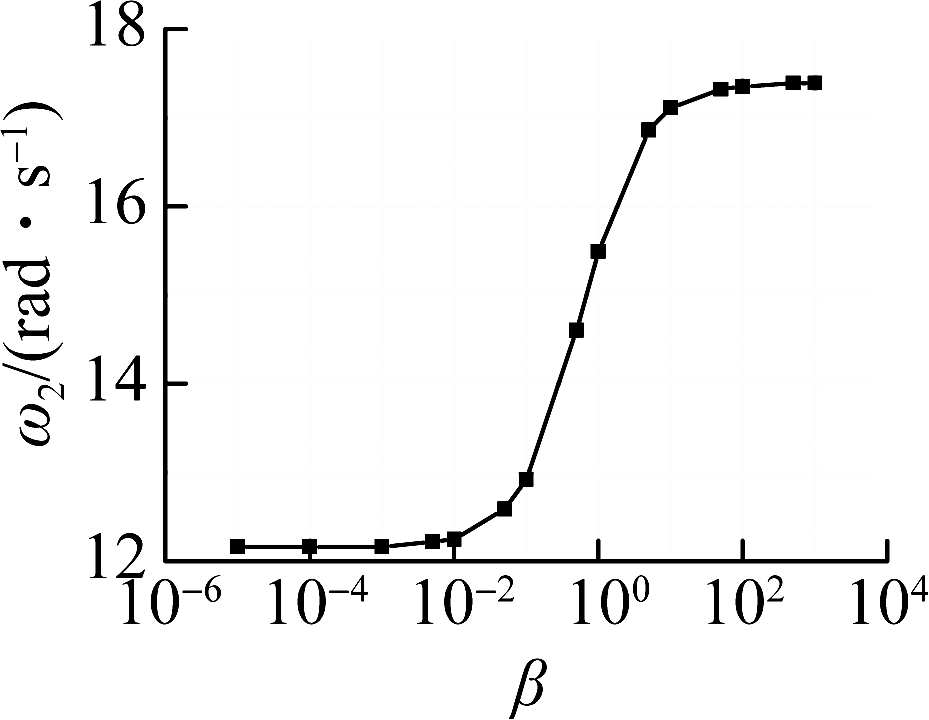
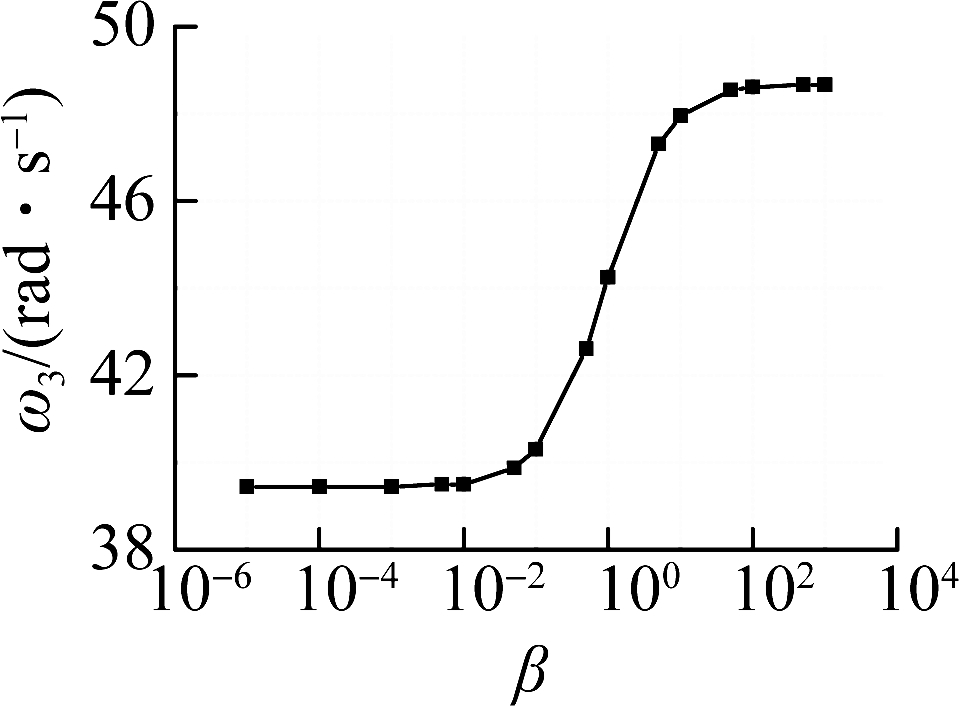
To investigate the effect of the rotational stiffness ratio, the model used is the HWBB-hinged frame structure in section 2.1. The variation of the rotational stiffness ratio is realized by the variation of the rotational stiffness of the rotational spring, while the flexural stiffness of the wall remains constant. The rotational stiffness ratio for the HWBB-hinged frame structure in section 2.1 is 0.28. Fig.14 demonstrates the effect of the rotational stiffness ratio on frequencies. The first three periods decrease with the increase in the rotational stiffness ratio. However, when the rotational stiffness becomes infinitesimal, HWBB tends towards a pin-supported wall. When the rotational stiffness becomes large enough, HWBB tends towards a cantilever beam. This is the reason why frequencies no longer vary when the rotational stiffness ratio is either too small or too large, as seen from the two flat lines in each figure.
The base shear modal contribution factor corresponding to mode n is[25]
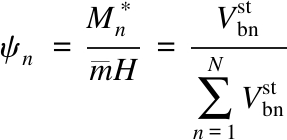
(50)
where N denotes the total number of modes and ![]() denotes the base shear effective modal mass corresponding to mode n.
denotes the base shear effective modal mass corresponding to mode n.
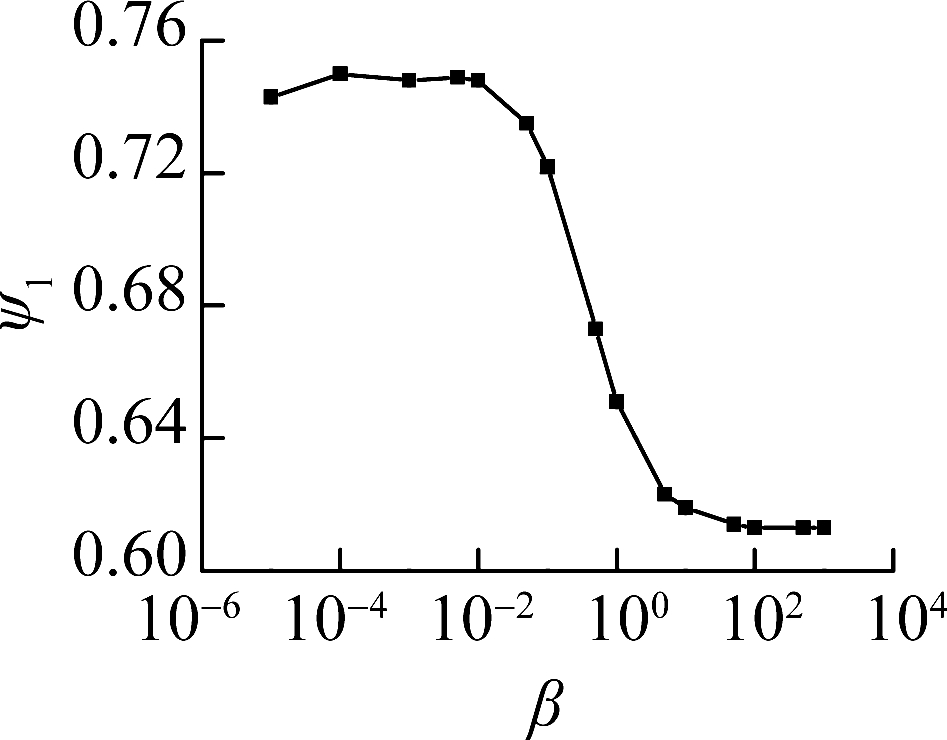
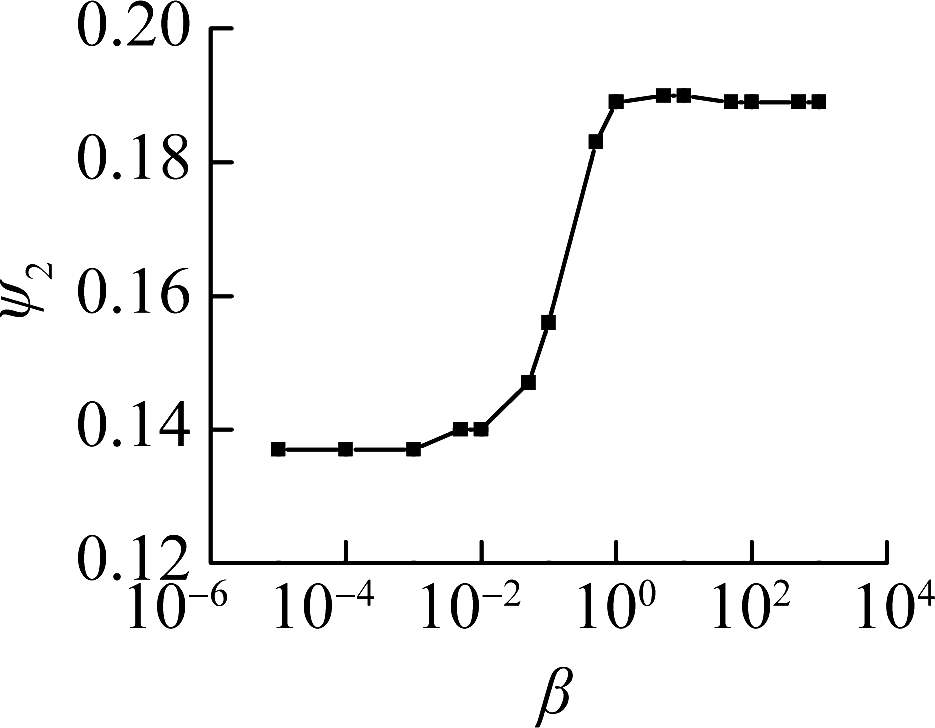
The effective modal mass is the contribution of each mode to the static base shear. As illustrated in Fig.15, the first mode effective mass decreases with the increase in the rotational stiffness ratio, while the second and third modes increase with the increase in the rotational stiffness ratio. The sum of the first three modes decreases with the increase in the rotational stiffness ratio. With the increase in the relative stiffness ratio, higher modes become more important in the contribution of the base shear.
(a)
(b)
(c)
Fig.14 Influence of the rotational stiffness ratio on the natural frequencies.(a) Mode 1;(b) Mode 2;(c) Mode 3
(a)
(b)

(c)
Fig.15 Influence of the rotational stiffness ratio on the effective modal mass.(a) Mode 1;(b) Mode 2;(c) Mode 3
4 Conclusions
1) Vibration equations are derived to investigate higher mode effects in the HWBB-frame structure. Modal analysis of the simplified models of both the HWBB-hinged frame and HWBB-MRF has been derived. Natural vibration periods and modes are derived accordingly.
2) Higher modes can influence the bending moment and shear distribution in the hinged wall, while they can be ignored in the shear distribution in MRF, which is due to the controlling function of HWBB. Moreover, the global displacement is also controlled by the fundamental mode.
3) For the HWBB-hinged frame structure, after the BRBs yield, the displacement of the HWBB-hinged frame is also controlled by the first mode. Therefore, displacement is not sensitive to higher modes. However, the first mode will no longer contribute to the inner forces. Higher modes have to be considered when determining the inner forces demand after the BRBs yield. For the HWBB-MRF structure, the first mode contributes to inner forces after the BRBs yield as MRF provides the lateral stiffness for the whole structure after the BRBs yield.
4) Parameter analysis demonstrates that the increase in the flexural stiffness wall can decrease the displacement amplitudes of the first three modes. However, after the flexural stiffness reaches a certain value, the displacement amplitude varies slowly. The first three periods all decrease with the increase in the rotational stiffness, which demonstrates that the rotational stiffness of the rotational spring can enlarge the stiffness of HWBB. With the increase in the rotational stiffness ratio, the contribution from the first mode decreases, and contributions from both the second mode and third mode increase.
[1]Alavi B, Krawinkler H. Strengthening of moment-resisting frame structures against near-fault ground motion effects [J]. Earthquake Engineering and Structural Dynamics, 2004, 33(6): 707-722. DOI:10.1002/eqe.370.
[2]Wada A, Qu Z, Ito H, et al. Seismic retrofit using rocking walls and steel dampers [C]//ATC and SEI Conference on Improving the Seismic Performance of Existing Buildings and Other Structures. San Francisco, USA, 2009: 1010-1021.
[3]Wada A, Qu Z, Sakata H. Seismic retrofit of existing SRC frames using rocking walls and steel dampers [J]. Frontiers of Architecture and Civil Engineering in China, 2011, 5(3): 259-266. DOI:10.1007/s11709-011-0114-x. (in Chinese)
[4]Qu Z, Wada A, Motoyui S, et al. Pin-supported walls for enhancing the seismic performance of building structures [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(14): 2075- 2091.DOI:10.1002/eqe.2175.
[5]Janhunen B, Tipping S, Mar T. Seismic retrofit of a 1960s steel moment-frame highrise using a pivoting spine [C]//Proceedings of the Structural Engineering Association of California 82nd Annual Convention. San Diego, USA, 2013: 320-336.
[6]Makris N, Aghagholizadeh M. The dynamics of an elastic structure coupled with a rocking wall [J]. Earthquake Engineering and Structural Dynamics, 2017, 46(6): 945-962. DOI:10.1002/eqe.2838.
[7]Kurama Y, Sause R, Pessiki S. Lateral load behavior and seismic design of unbonded post-tensioned precast concrete walls [J]. ACI Structural Journal, 1999, 96(4):622-632. DOI:10.14359/700.
[8]Takeuchi T, Suzuki K. Performance-based design for truss-frame structures using energy dissipation devices [C]//Proceedings of the 4th International Conference on Behavior of Steel Structures in Seismic Areas. Naples, Italy, 2003: 55- 61.
[9]Takeuchi T, Chen X, Matsui R. Seismic performance of controlled spine frames with energy-dissipating members [J]. Journal of Constructional Steel Research, 2015, 114: 51-65. DOI:10.1016/j.jcsr.2015.07.002.
[10]Chen X, Takeuchi T, Matsui R. Simplified design procedure for controlled spine frames with energy-dissipating members [J]. Journal of Constructional Steel Research, 2017, 135: 242-252. DOI:10.1016/j.jcsr.2017.04.017.
[11]Chen X, Takeuchi T, Matsui R. Seismic performance and evaluation of controlled spine frames applied in high-rise buildings [J]. Earthquake Spectra, 2018, 34(3): 1431-1458.DOI:10.1193/080817eqs157m.
[12]Djojo G S, Clifton G C, Henry R S, et al. Experimental testing of a double acting ring spring system for use in rocking steel shear walls [C]//8th International Conference on Behavior of Steel Structures in Seismic Areas. Shanghai, China, 2015: 1245-1252.
[13]Du Y F, Wu D Y. Performance analysis of light energy dissipative rocking frame designed on the basis of stiffness demand [J]. China Civil Engineering Journal, 2014, 47(1): 24-35. DOI:10.15951/j.tmgcxb.2014.01.006. (in Chinese)
[14]Wiebe L, Christopoulos C. Mitigation of higher mode effects in base-rocking systems by using multiple rocking sections[J]. Journal of Earthquake Engineering, 2009, 13(sup1): 83-108. DOI:10.1080/13632460902813315.
[15]Wu S J, Pan P, Zhang D B. Higher mode effects in frame pin-supported wall structure by using a distributed model [J]. Earthquake Engineering and Structural Dynamics, 2016, 45(14): 2371-2387.DOI:10.1002/eqe.2766.
[16]Grigorian C E, Grigorian M. Performance control and efficient design of rocking-wall moment frames[J]. Journal of Structural Engineering, 2016, 142(2): 04015139. DOI:10.1061/(asce)st.1943-541x.0001411.
[17]Grigorian M, Grigorian C. An introduction to the structural design of rocking wall-frames with a view to collapse prevention, self-alignment and repairability [J]. The Structural Design of Tall and Special Buildings, 2016, 25(2): 93-111.DOI:10.1002/tal.1230.
[18]Grigorian M, Grigorian C E. Sustainable earthquake-resisting system [J]. Journal of Structural Engineering, 2018, 144(2): 04017199.DOI:10.1061/(asce)st.1943-541x.0001900.
[19]Nima R, Moghadam A S, Aziminejad A. Continuum analysis approach for rocking core-moment frames [J]. Journal of Structural Engineering, 2018, 144(3): 04018006. DOI:10.1061/(asce)st.1943-541x.0001986.
[20]Wiebe L, Christopoulos C. A cantilever beam analogy for quantifying higher mode effects in multistorey buildings[J]. Earthquake Engineering & Structural Dynamics, 2015, 44: 1697-1716.DOI:10.1002/eqe.2549.
[21]Yang X Y, Wu J, Zhang J, et al. Post-yielding behavior of hinge-supported wall with buckling-restrained braces in base [J]. Journal of Earthquake and Tsunami, 2019, 13 (3/4): 1940003.DOI:10.1142/s1793431119400037.
[22]Wang X T, Wang T, Qu Z. An experimental study of a damage-controllable plastic hinge-supported wall structure [J]. Earthquake Engineering and Structural Dynamics, 2018, 47(3): 594-612. DOI:10.1002/eqe.2981.
[23]Yang X Y, Feng Y L, Wu J, et al. Experimental study on seismic performance of hinged truss with buckling-restrained braces at base [J]. Journal of Southeast University (Natural Science Edition), 2018, 48(2): 303-309. (in Chinese)
[24]Clough R W, Penzien J. Dynamics of structures[M]. 3rd eds. Berkeley, CA, USA: Computer & Structures, Inc, 1995.
[25]Chopra A K. Dynamics of structures: Theory and applications to earthquake engineering[M]. Upper Saddle River, NJ, USA: Prentice Hall, 2007.
[26]Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50011—2010 Code for seismic design of Buildings [S]. Beijing: China Architecture and Building Press, 2010. (in Chinese)