Abstract：First, an explicit representation 
for a matrix A∈Cm×n with the prescribed range T and null space S is derived, which is simpler than 
is proposed and investigated. Then, the computational complexity of the introduced algorithm is also analyzed in detail. Finally, two numerical examples are shown to illustrate that this method is correct.
Throughout this paper, the standard notations in Ref.[1] are used. The symbol 
denotes the set of all m×n complex matrices with rank r, and Cn represents the n-dimensional complex space. In represents an identity matrix of order n. For A∈Cm×n, symbols R(A), N(A), A*, A-1 and r(A) denote its range, null space, the conjugate transpose, inverse and rank, respectively. R(A)⊥ and N(A)⊥ are orthogonal complement spaces of R(A) and N(A), respectively. The index of A∈Cn×n, denoted as ind(A), is the smallest nonnegative integer k such that r(Ak)=r(Ak+1).
The {2} -inverse 
of a matrix A∈Cn×n with the prescribed range T and null space S is defined as follows:
Definition 1[1] If 
T is a subspace of Cn of dimension s≤r, and S is a subspace of Cm of dimension m-s, and then A has a {2}-inverse X such that R(X)=T and N(X)=S, if and only if AT⊕S=Cm.
In such a case, X is unique and denoted as 
proposes a unified representation for six kinds of generalized inverses, such as the Moore-Penrose inverse A†, the weighted Moore-Penrose inverse 
the group inverse Ag, the Drazin inverse Ad, the Bott-Duffin inverse 
In addition, suppose that the matrix G∈Cn×m satisfies R(G)=T and N(G)=S, then the unified treatment is as follows:
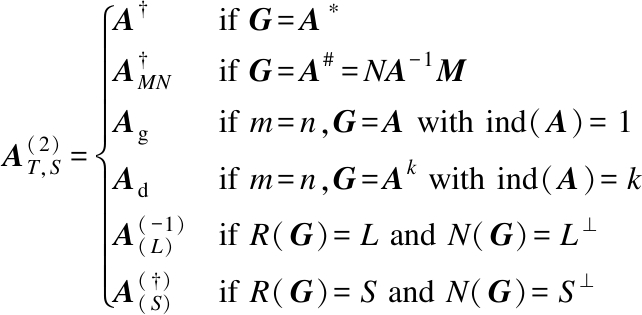
The {2} -inverse plays an important role in a stable approximation of ill-posed problems and in linear and nonlinear problems involving a rank-deficient generalized inverse[2-3]. In particular, {2} -inverse can be used in the iterative methods for solving nonlinear equations[1,4] and in statistics[5-6].
In the past thirty years, numerous experts and scholars investigated the subject of computation and representation for 
can be seen in Refs.[11-15]. Some other representations and computations can be found in Refs.[16-18]. Recently, some scholars[19-21] used Gauss-Jordan elimination methods to compute 
Moreover, the computational complexity of these Gauss-Jordan elimination methods are also analyzed in detail.
In 1998, Wei[16] provided an expression of the generalized inverse 
Lemma 1[16] Let A, T, S be the same as those in Definition 1. Suppose that G∈Cn×m such that R(G)=T and N(G)=S. If A has a {2} -inverse 
then
ind(AG)=ind(GA)=1
(1)
Furthermore, we have
(2)
Soon after, Ji[17] enhanced the results of Wei[16] and established another explicit representation of 
which is shown as follows.
Lemma 2[17] Let A, T, S and G be the same as those in Lemma 1. Let V and U* be matrices whose columns form the bases of N(GA) and N((GA)*), respectively. Define E=VU. Then, E is nonsingular, satisfying
R(E)=R(V)=R(GA), N(E)=N(U)=N(GA)
(3)
Moreover, GA+E is nonsingular and
(4)
In the following lemma, we will prove V(UV)-2UG=0.
Lemma 3 Let A, T, S and G be the same as those in Lemma 1. Let V and U* be the matrices whose columns form the bases of N(GA) and N((GA)*), respectively. Then,
V(UV)-2UG=0
(5)
Proof Since the columns of matrix U* is the basis of N((GA)*), we have (GA)*U*=0, which is also equivalent to UGA=0. This implies R(GA)⊂N(U). From Lemma 1, we know that r(G)=r(GA)=s, which means that R(GA)=R(G). Then, we have UG=0 and Eq.(5) is followed.
In this paper, we first develop the result of Ji[17] and obtain a more brief explicit representation of 
through elementary operations on an appropriate partitioned matrix is proposed and investigated. The computational complexity of the new algorithm is also analyzed in detail.
In the following theorem, we establish a new explicit expression for which is simpler than that in Ref.[17].
Theorem 1 Let A, T, S and G be the same as those in Lemma 1. Let V and U* be matrices whose columns form the bases of N(GA) and N((GA)*), respectively. Define E=VU. Then,
(6)
Proof Since V(UV)-2UG=0, we obtain Eq.(6) immediately from Eq.(4).
Following the same line of Theorem 1, another explicit representation of {2} -inverse is proposed.
Theorem 2 Let A, T, S and G be the same as those in Lemma 1. Let P and Q* be matrices whose columns form the bases of N(AG) and N((AG)*), respectively. Define F=PQ. Then,
(7)
Based on the two explicit representations (6) and (7), a method to calculate 
through elementary operations on an appropriate partitioned matrix is derived and investigated. We first give the case of m≥n.
Theorem 3 Let A, T, S and G be the same as those in Lemma 1. Then there are two nonsingular elementary matrices U and V of order n, respectively, such that
(8)
(9)
where matrix B∈Cs×nand s columns of B are the same as those of Is; furthermore,
Proof According to Lemma 1, we have r(GA)=r(G)=s, then there are two elementary matrices U and V satisfying (8) and (9). This means
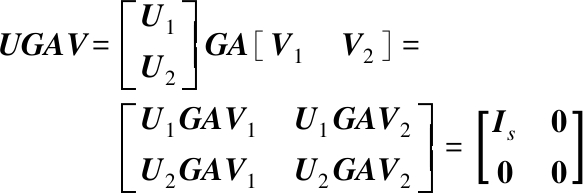
(10)
Comparing both sides of (10), we drive
(11)
We notice that matrices U2 and V2 are row full rank and column full rank matrices, respectively, and then, the above four equalities imply that
GAV2=0, U2GA=0
(12)
This implies that
(13)
According to the fact that r(U)=r(V2)=n-s=dimN((GA)*)=dimN(GA), we obtain
From Theorem 1, we derive a representation 
Theorem 4 Let A, T, S and G be the same as those in Lemma 1. Then, there exist two nonsingular elementary matrices P and Q of order m, respectively, such that
(14)
(15)
where matrix C∈Cs×m and s columns of C are those of Is; furthermore,
The proof of Theorem 4 is similar to that of Theorem 3.
2 An Algorithm to 
Based on Gaussian Elimination and the Computational Complexity
Let 
with m≥n, and Theorem 3 is summarized in the following algorithm.
Algorithm 1
Input matrices 
with s≤r and calculate GA.
Execute elementary row operations on the first n rows and the first n columns of a partitioned matrix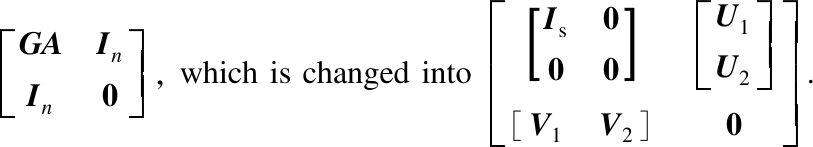 
Perform elementary row operations on matrix [GA+V2U2 G] until 
is reached.
In the following theorem, the computational complexity of Algorithm 1 is analyzed, which only focuses on multiplications and divisions.
Theorem 5 The computational complexity of Algorithm 1 to compute is
(16)
Proof It requires mn2 multiplications to form GA. s pivoting steps are needed to transform [GA In] into 
following r(GA)=s, where matrix B∈Cs×nand s columns of B are the same as those of Is. The first pivoting step involves n+1 non-zero columns in [GA In]. Thus, n divisions and n(n-1) multiplications with a total of n2 multiplications and divisions are required. For the second pivoting step, the first part of the pair reduces one column to deal with, but the second part increases one column, resulting in n+1 columns involved. This pivoting step also requires n2 operations. Continuing this way, it requires sn2 multiplications and divisions to reach the matrix 
According to the fact that s columns of B are the same as those of Is, we can directly read V1 and V2. In the third step, n2(n-s) multiplications are required to compute V2U2.
In the fourth step, n pivoting steps are needed to transform [GA+V2U2 G] into 
The first pivoting step involves n+m non-zero columns in [GA+V2U2 G]. Thus, n+m-1 divisions and (n+m-1)(n-1) multiplications are required with a total of n(n+m-1) multiplications and divisions. For the second pivoting step, There is one less non-zero column in the first part of the pair. There are n+m-1 non-zero columns to deal with. These pivoting steps require n(n+m-2) operations. Following the same idea, the i-th (1≤i≤n) pivoting step needs n(n+m-i) operations. So, it requires
n(n+m-1)+n(n+m-2)+…+n(n+m-n)=
Therefore, the total number of operations for computing is
T(m,n)=
If m≤n, the similar algorithm and computation complexities are given as follows.
Algorithm 2
Input: matrix with s≤r and calculate AG.
Execute elementary row operations on the first m rows and the first m columns of a partitioned matrix 
is reached.
Theorem 6 The computational complexity of Algorithm 2 to compute is
(17)
The Gauss-Jordan elimination is a popular method for computing the inverse of a nonsingular matrix of low order by hand. In this section, Algorithm 1 and Algorithm 2 can be used to compute some famous generalized inverses by hand if the size of matrix A is small by choosing the appropriate parameter matrix G.
Example 1[18] Use Algorithm 1 to compute the Drazin inverse Ad of matrix A,where
Solution Simple computation leads to
This implies ind(A)=2. Take G=A2 and perform elementary row and column operations on 
Thus, we have s=1 and
From U2 and V2, in view of Algorithm 1, we have
Finally, perform elementary row operations on [AG+V2U2 G]→[I3 Ad]
Therefore, we obtain
Example 2[20] Take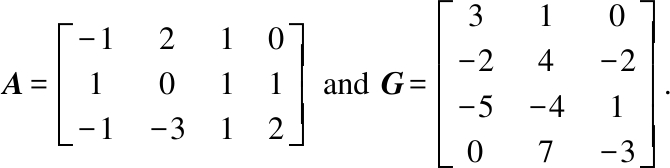 
It is easy to show that AR(G)⊕N(G)=R3, then we have 
through elementary operations.
Solution By computing, we have
AG=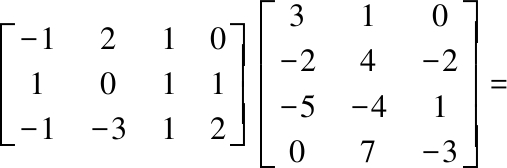
Executing elementary row operations on the first 3 rows and column operations on the first 3 columns of the following partitioned matrix:
This implies
By direct calculation, we can obtain
Then, we perform the elementary column operation transform and change 
This yields
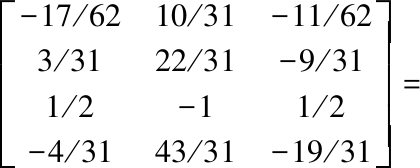
In this paper, we establish two new explicit representations for 
based on the two expressions through elementary operation on the appropriate partitioned matrices. The computation complexities of the two algorithms are also analyzed.
[1]Ben-Israel A, Greville T N E, Generalized inverse: Theory and applications [M]. 2nd eds. New York: Springer Verlag, 2003.
[2]Nashed M Z, Generalized inverse and applications [M]. New York: Academic Press, 1976.
[3]Wedin P A. Report UMINF 124.85,S-901 87 Perturbation results and condition number for outer inverses and especially for projections [R]. Umea, Sweden: Institution of Information Proceedings University of Umea, 1985.
[4]Nashed M Z, Chen X. Convergence of Newton-like methods for singular operator equations using outer inverses [J]. Numerische Mathematik, 1993,66(1): 235-257. DOI:10.1007/bf01385696.
[5]Getson A J, Hsuan F G.{2} -inverse and their statistical applications [M]//Lecture Notes in Statistics 47. Berlin: Springer, 1988.
[6]Hsuan F, Langenberg P, Getson A. The {2} -inverse with applications to statistics [J]. Linear Algebra and Its Applications, 1985,70: 241-248.DOI:10.1016/0024-3795(85)90055-2.
[7]Cai J, Chen G L. On determinantal representation for the generalized inverse and its applications [J]. Numerical Linear Algebra with Applications, 2007, 14(3):169-182.DOI:10.1002/nla.513.
[8]Sheng X P, Chen G L. Several representations of generalized inverse and their application [J]. International Journal of Computer Mathematics, 2008,85(9): 1441-1453.DOI:10.1080/00207160701532767.
[9]Sheng X P, Chen G L. New proofs of two representations and minor of generalized inverse 
Applied Mathematics and Computation, 2011, 217(13): 6309-6314.DOI:10.1016/j.amc.2011.01.003.
[10]Yu Y M, Wei Y M. Determinantal representation of the generalized inverse over integral domains and its applications [J]. Linear and Multilinear Algebra, 2009,57(6): 547-559.DOI:10.1080/03081080701871665.
[11]Chen Y L, Chen X Z. Representation and approximation of the outer inverse of a matrix A[J]. Linear Algebra and Its Applications, 2000,308(1/2/3): 85-107.DOI:10.1016/S0024-3795(99)00269-4.
[12]Djordjevic D, Stanimirovic P, Wei Y M. The representation and approximations of outer generalized inverses [J]. Acta Mathematica Hungarica, 2004,104(1/2): 1-26. DOI:10.1023/b:amhu.0000034359.98588.7b.
[13]Zheng B, Wang G R. Representation and approximation for generalized inverse [J]. Journal of Applied Mathematics and Computing, 2006,22(3):225-240.DOI:10.1007/bf02832049.
[14]Wei Y M, Wu H B. (T,S) splitting methods for computing the generalized inverse 
and rectangular systems [J].International Journal of Computer Mathematics,2001,77(3):401-424.DOI:10.1080/00207160108805075.
[15]Wei Y M, Wu H B. The representation and approximation for the generalized inverse [J]. Applied Mathematics and Computation, 2003,135(2/3):263-276.DOI:10.1016/S0096-3003(01)00327-7.
[16]Wei Y M. A characterization and representation of the generalized inverse and its application [J]. Linear Algebra and Its Applications, 1998, 280(2/3): 87-96.DOI:10.1016/s0024-3795(98)00008-1.
[17]Ji J. Explicit expressions of generalized inverses and condensed Cramer rules [ J]. Linear Algebra and Its Applications, 2005,404: 183-192. DOI:10.1016/j.laa.2005.02.025.
[18]Stanimirovi P S, Pappas D, Katsikis V N, et al. Full rank representations of outer inverse based on the QR decomposition [J]. Applied Mathematics and Computation, 2012,218(20)：10321-10333.DOI:10.1016/j.amc.2012.04.011.
[19]Ji J. Computing the outer and group inverses through elementary row operations[J]. Computers and Mathematics with Applications, 2014,68(6):655-663. DOI:10.1016/j.camwa.2014.07.016.
[20]Sheng X P, Chen G L. Innovation based on Gaussian elimination to compute generalized inverse [J]. Computers and Mathematics with Applications, 2013,65(11):1823-1829.DOI:10.1016/j.camwa.2013.03.011.
[21]Stanimirovic P S, Petkovic M D. Gauss-Jordan elimination method for computing outer inverses [J]. Applied Mathematics and Computation, 2013, 219(9): 4667-4679.DOI:10.1016/j.amc.2012.10.081.
摘要：首先给出了矩阵A∈Cm×n具有指定值域T和零空间S的外逆
的一个显示表示
该显示表示式比Ji在2005提出的表达式
要简单.然后,基于该改进的显示表示通过对一个适当的分块矩阵
使用初等变换的方法得出外逆
的一个新的算法,并且详细分析了该算法的计算量.最后,用一个数值例子检验了所提算法的正确性.