The two crucial issues, energy saving and environment conservation, have facilitated the swift growth of electric vehicles (EVs). As one important component of EVs, the battery management system (BMS) works principally in monitoring the state of cells, estimating the state of charge (SOC), balancing the voltage, and so on. To achieve these fundamental functions, one nonlinear model describing the characteristics of batteries should be established[1]. The commonly used models are the electrochemical model, the neural network model, and the equivalent circuit model. The electrochemical model establishes a nonlinear mathematical model based on the principle of internal charge transfer in batteries. It consists of a series of partial differential equations with boundary conditions. The electrochemical model is the most accurate compared with the other two, but its complexity prevents applying it to online estimation and vehicle simulation as well as its computational burden issue. The neural network is a highly nonlinear continuous-time power system with a strong self-adaptive ability. Its model can simulate the external characteristics of the battery well. However, the neural network model requires a large amount of experimental data for training and learning, and its accuracy is greatly affected by the training method. If the initial value is not chosen properly, it can easily fall into the local optimum and non-convergence[2]. Considering the internal polarization inside and easy access to online parameter identification, the equivalent circuit model is sophisticated enough to simulate the complicated charging and discharging conditions eventually, in which resistors are designed for ohmic polarization and capacitors for electrochemical polarization, respectively.
The running conditions of batteries are changeable and complex. It is remarkable that parameters of batteries are quite difficult to identify accurately. In fact, there are two sorts of approaches proverbially applied to identify them: One is the offline method and the other is the online method. Those offline methods require heavy computational resources due to their complexities, which is an issue for a real-time application such as the BMS employed in EVs. A large number of laboratory experiments may also be deployed to obtain the offline variation and sensitivity of the parameters; however, it is a demanding and time-consuming task. Apart from these, temperature, current magnitude and cycle period also have an important influence on the reactions of batteries, apparently more in the internal resistance. For the purpose of obtaining a series of parameters accurately, the online method is proposed to identify the real-time characteristics by using the multiple forgetting factors recursive least squares (MFF-RLS) method[3-5]. At the same time, these parameters are employed in the next SOC estimation.
In the model-based SOC estimation methods, the battery model that directly influences the accuracy is established and then algorithms such as the coulomb courting method, open circuit voltage method, neural network method and Kalman filter method can be taken into consideration to estimate SOC. For the coulomb courting method, a large accumulated deviation can be produced due to sensor precision and it is restricted by the initial value of SOC[6]. The open circuit voltage (OCV) is one static variable which can be measured only in idle periods. It is not suitable for the frequently running conditions of EVs[7]. The neural network method is very nonlinear and the estimation accuracy is high, but the algorithm is limited by historical data and training methods[8]. The Kalman filter method uses the statistical principle to seek the minimum mean square error and sets the state variables in estimated-corrected, and the estimation is not affected by the initial value, so it is widely used by many researchers[9-10]. However, the traditional extended Kalman filter (EKF) is to remove the high-order term after the Taylor expansion is performed at the prediction moment, and it estimates the state after the system linearization. This method reduces the accuracy and the estimation is greatly affected by the measurement noise[11]. Therefore, the covariance gradually shows morbidity during the recursive process, which can result in unstable estimation results of the filter. To avoid the morbid covariance, this paper proposes a modified covariance extended Kalman filter (MVEKF) algorithm, which recalculates the covariance in the iterative process with the modified estimation and updates the process gain to obtain a new covariance value. The value is used for the next state estimation to ensure the stability of the filter.
In this paper, an online SOC estimation algorithm was proposed by combining one online parameter identification method and the MVEKF algorithm. A second-order equivalent circuit model with dual resistors is established, in which resistors are designed for ohmic polarization and two pairs of the RC network for electrochemical polarization. Also, the multiple forgetting factor recursive least squares method is used to identify parameters online. The modified algorithm with model parameters recalculates the covariance in the iterative process with the modified estimation and updates the process gain, and this new data is used for the next state estimation to decrease errors of the filter. Finally, experiments including constant discharging, constant pulse discharging and the dynamic stress test (DST) are performed on the lithium batteries to verify the accuracy and robustness of the proposed method.
1 Battery Characteristics
1.1 Battery parameters
As a high energy storage component, the lithium battery is widely used in various fields. This paper chooses the NCR18650PF battery produced by Panasonic as the model test object. The technical parameters of the battery are shown in Tab.1.
Tab.1 Parameters of NCR18650PF battery

ParameterValueRated capacity/(mA·h)2 750Rated voltage/V3.6Standard charge voltage/V4.2Discharge cut-off voltage/V2.5Standard charging current/C0.5Maximum continuous discharge current/A10
The battery testing equipment BTS-4008, as shown in Fig.1, is selected to implement all charging and discharging experiments. This machine is equipped with eight channels to install corresponding batteries. Constant current, constant pulse current and many kinds of designed running strategies are included in the range of its working conditions. This test system communicates with the host computer through the LAN. The charging and discharging strategies are scheduled in the computer, which dominates the BTS-4008 to perform the control strategies.

Fig.1 Platform of BTS-4008
1.2 Open circuit voltage
Considering that OCV is a static variable and the self-discharge of the battery, the experiments are carried out simultaneously with multiple batteries. The average OCV is calculated to reduce the system error. The interval of 5%SOC is used in the measurement process. The measurement steps are as follows:
• Charge to 4.2 V with constant current and constant voltage, and remain stationary for 2 h;
• Start the 0.5C constant current discharge and stop after 5% of the maximum state is released;
• Record the voltage after staying for 1.5 h;
• Repeat the above steps until the discharge cut-off voltage;
• Conduct a 0.5C constant current charge and record the data at intervals of 5% SOC after staying for 1.5 h until it is charged to the nominal voltage.
Fig.2 is the relationship between OCV and SOC. The function of SOC-OCV is fitted by the polynomial fitting method. Through numerous verifications, the eight-poly-nomial is selected to match the bond to guarantee precision. The coefficients A0 to A8 of the fitting function are shown in Tab.2. It is apparent that the curves run smoothly whether under high SOC or low SOC. The OCV of charging is close to but above that of discharging on account of the features of the lithium battery. Obviously at the beginning, the two lines grow more noticeably than the remaining. When the remaining SOC is insufficient, the uncontrolled chemical reactions occur inside the battery[12].
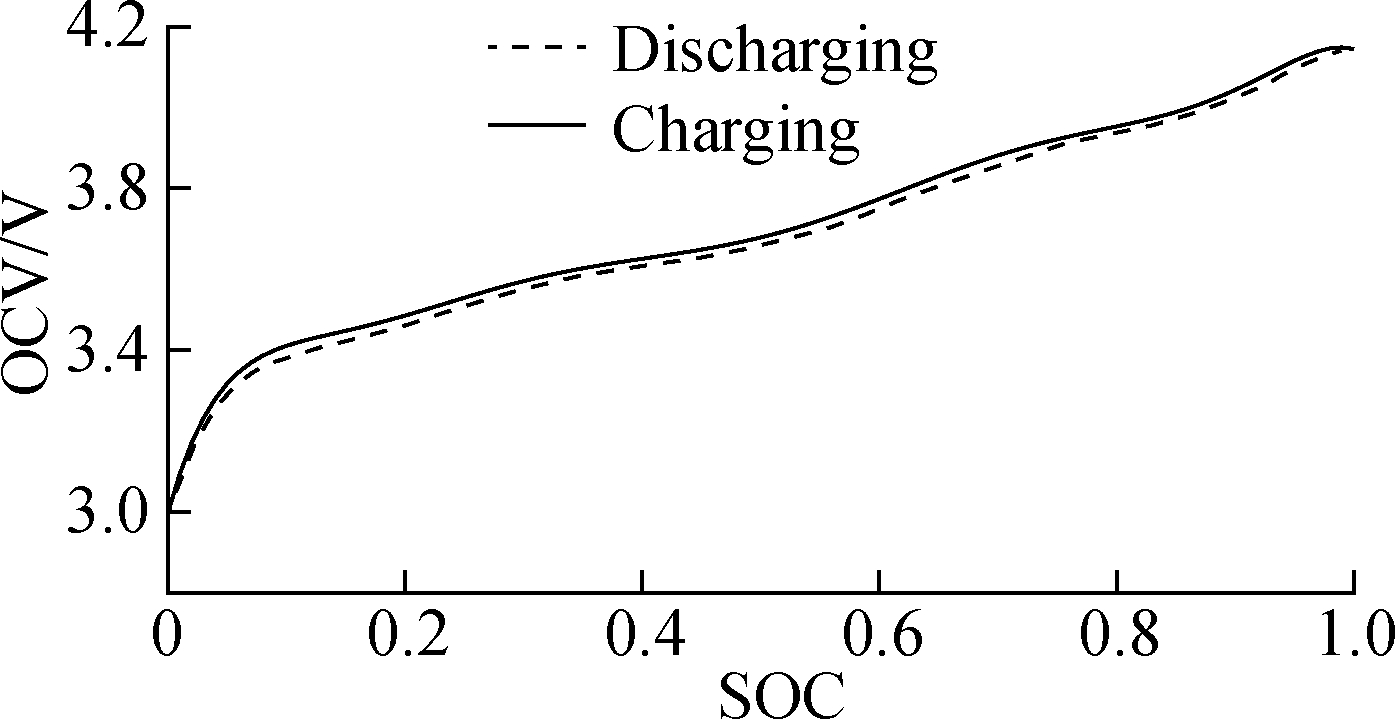
Fig.2 The relationship of SOC and OCV
Tab.2 The coefficient values of the fitting eight-polynomial in charging or discharging process
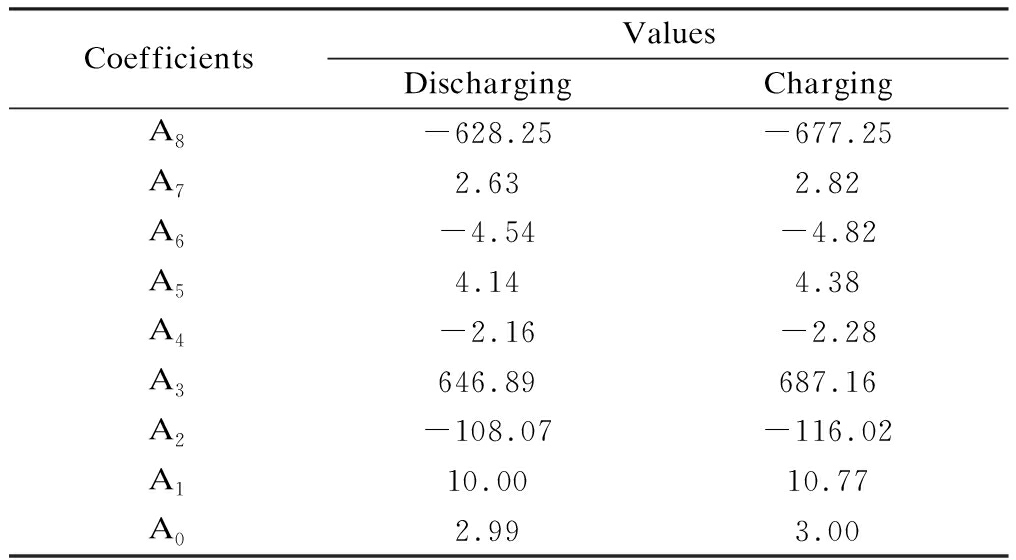
CoefficientsValuesDischargingChargingA8-628.25-677.25A72.632.82A6-4.54-4.82A54.144.38A4-2.16-2.28A3646.89687.16A2-108.07-116.02A110.0010.77A02.993.00
The fitting function error of OCV is plotted in Fig.3. From the diagram, it can be seen that the result of fitting is convincing with the maximum error of 0.03 V. The eight-polynomial functions match well with the charging and discharging curves.
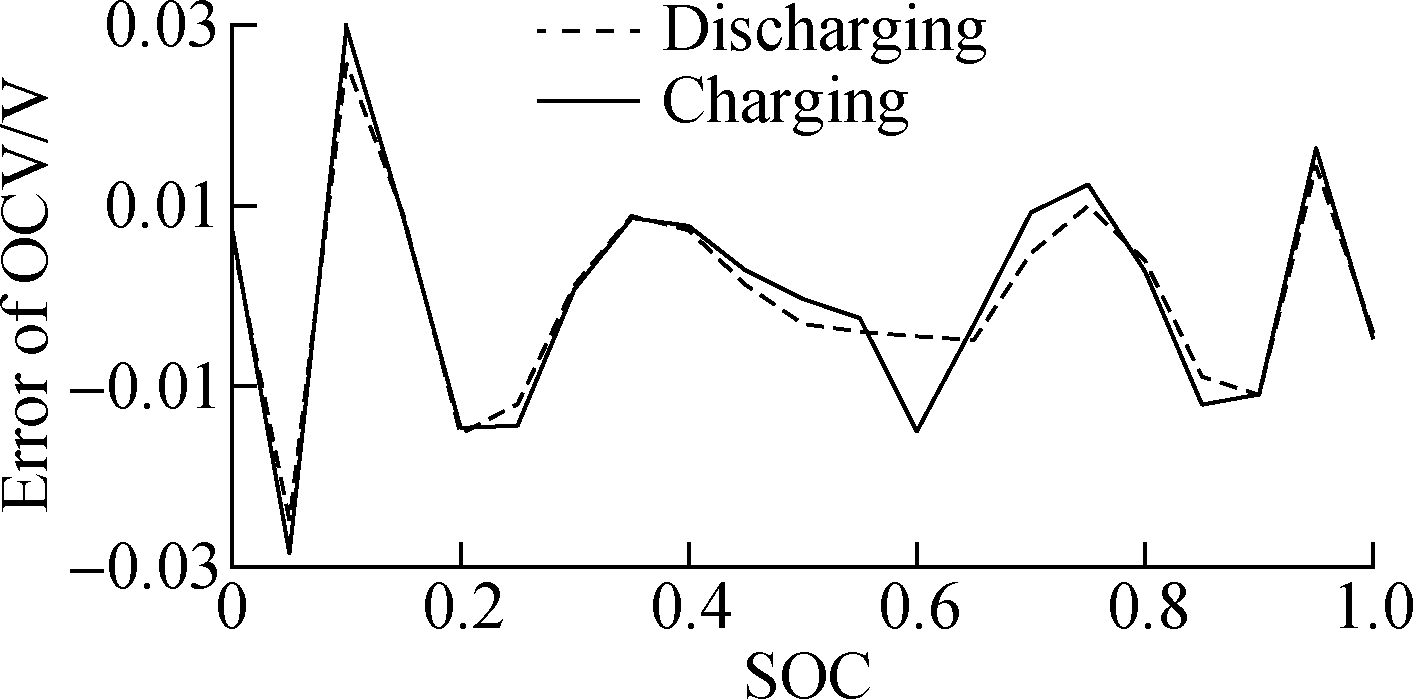
Fig.3 The fitting function error of OCV
1.3 Coulomb efficiency
Due to the resistance issues, there is a difference in the amount of electricity produced by different discharging currents. With a large current, the battery cannot export the whole amount of energy as expected, and some energy remains inside. Therefore, when estimating the SOC of the battery, the coulomb efficiency must be considered[13]. In this experiment, C means that the charge-discharge current is 2.75 A.
Wd1 is the amount of electricity discharged from the battery with 0.5C. Wc1 is the amount of electricity required to return the battery to the pre-discharge state with a specific current L. Set the charging coulomb efficiency ηc as the ratio of Wd1 to Wc1.
Wd2 is the amount of electricity discharged from the battery with a specific current L. Wc2 is the amount of electricity required to restore the battery to its pre-discharge state with 0.5C. Set the discharge coulomb efficiency ηd as the ratio of Wd2 to Wc2.
To obtain the efficiency relationship,the coulomb efficiency experiments at the rate of 0.25C, 0.375C, 0.5C, 0.75C, C, 1.25C, and 1.5C were carried out at room temperature. The charge-discharge coulomb efficiency at different rates is shown in Tab.3.
Tab.3 Coulomb efficiency at different rates
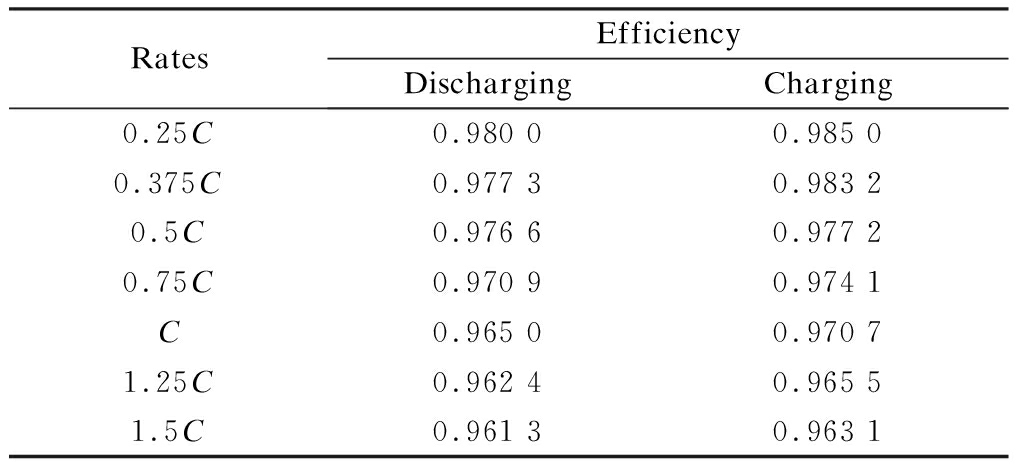
RatesEfficiencyDischargingCharging0.25C0.980 00.985 00.375C0.977 30.983 20.5C0.976 60.977 20.75C0.970 90.974 1C0.965 00.970 71.25C0.962 40.965 51.5C0.961 30.963 1
The discharging current is positive, and charging is negative. The relationship between the coulomb efficiency and the current in Fig.4 is
(1)
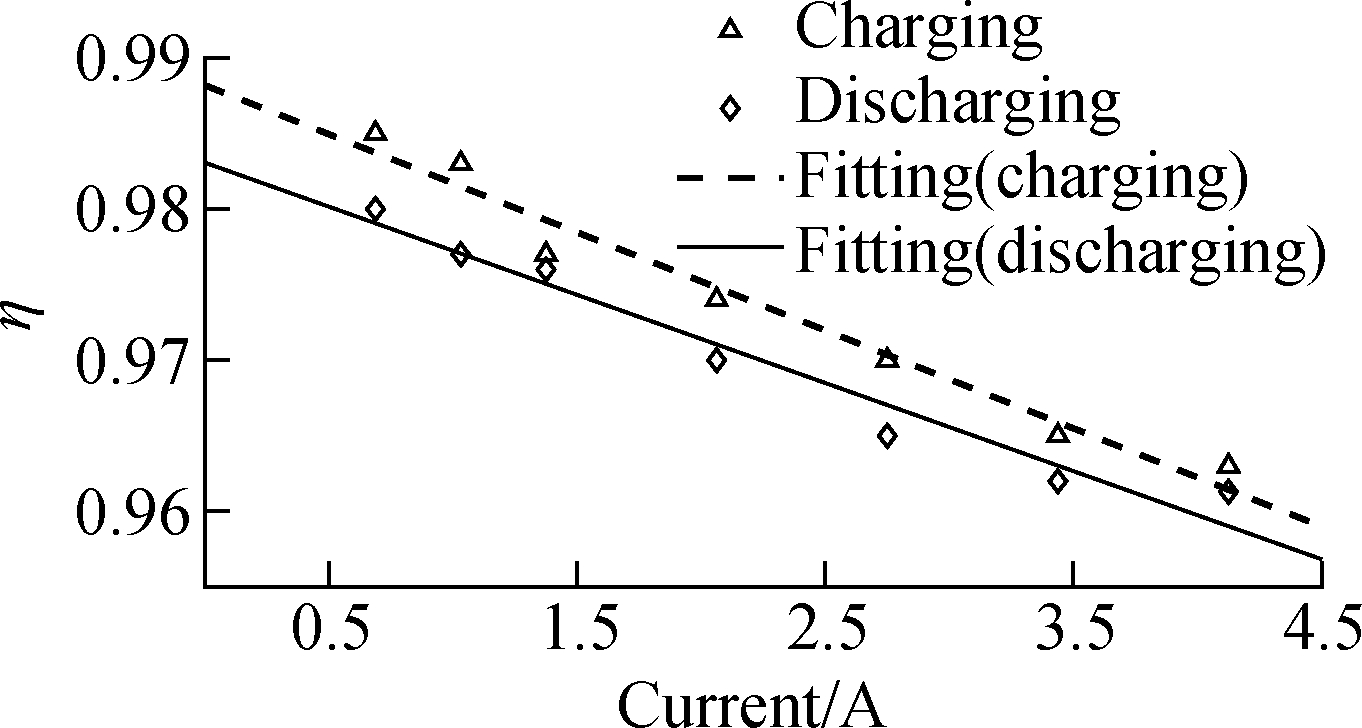
Fig.4 Fitting results between the coulomb and current efficiency
2 Model Description
The lithium battery is a complex and nonlinear system. Numerous kinds of experiments have been carried out to establish the model, which can describe it accurately. The equivalent circuit model is chosen for simplification and applicability. Based on the dynamic characteristics and working principles of the battery, the equivalent circuit model is developed by using resistors, capacitors, and voltage sources to form a circuit network[5,14]. In this work, a second-order equivalent circuit model with dual resistors is established in Fig.5. Resistors are used for ohmic polarization and the two pairs of the RC network are for electrochemical polarization.

Fig.5 Second-order equivalent circuit model
In Fig.5, the cell equivalent model includes an open circuit voltage Uocv which is used to represent the voltage source and describe the static feature of the cell. Two RC networks are composed of resistance polarization Rp and capacitance polarization Cp to describe the battery polarization phenomenon. Resistance Rchg is used to represent the cell ohmic internal resistance during charging while resistance Rdchg represents the ohmic internal resistance during discharging. A terminal voltage UL is connected to electronic load. For the sake of calculation, Rchg and Rdchg are redefined to one parameter R0.
According to the Kirchhoff law of the circuit, the model equation is

(2)
where U0 is the voltage of R0; U1 and U2 are the two pairs of RC networks; UL represents the terminal voltage. OCV is replaced by Uocv. Current I is positive during discharge while negative during charging.
After discretizing,Eq.(2) is changed into
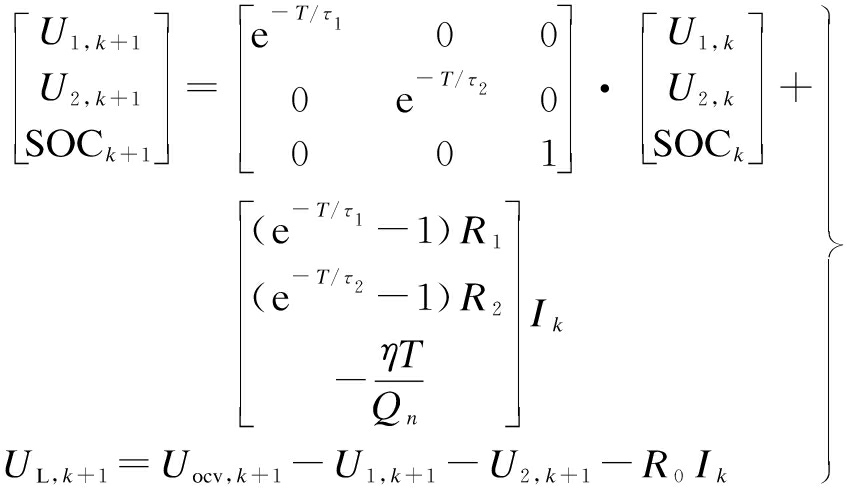
(3)
where Qn represents the rated capacity of the lithium battery; η is the coulomb efficiency; T is the sample period; τ1 and τ2 are the concentration polarization time constant and activation polarization time constant, respectively, τ1=R1C1,τ2=R2C2.
In order to apply the proposed recursive method to the simplified battery model, an auto regressive exogenous (ARX) model is required. The transfer function of the battery impedance is calculated and presented in the s-domain. After the Laplace transformation, Eq.(3) is changed from a time domain function to a frequency domain function[15]. Suppose that U(s)=Uocv(s)-UL(s), the transfer function is
(4)
Given the actual operating conditions of the lithium battery of the EV, the working current can be regarded as a linear combination of the pulse current at each sampling time. Therefore, the Z-transformation is performed using the pulse response invariant method.
The transfer function after the Z-transformation is
(5)
The difference equation after discretizing is
U(k)=a1U(k-1)+a2U(k-2)+a3I(k)+
a4I(k-1)+a5I(k-2)
(6)
a1=e-T/τ1+e-T/τ2
a2=-e-T/τ1-T/τ2![]()
![]()
a5=R0e-T/τ1-T/τ2
where a1 to a5 are the parameters to be identified.
3 Parameter Identification
3.1 Identification method
The least squares method is a simple and effective identification method. It deals with the data obtained from computational experiments. It takes the minimum square sum of errors as the calculation benchmark. The recursive least square is a widely used algorithm in different kinds of least squares methods; however, it has some shortcomings. In the process of calculation, the old correction value and the estimated value have no memory limitation. With the experiment proceeding, more and more data is collected, and the newly collected data will be easily influenced by the old data[16-17]. In order to avoid this phenomenon, it is required to increase the weight of the newly collected data in the calculation.
During the process of charging, the SOC value will increase slowly with the accumulation of time, so it is a slow time-varying parameter. For slow time-varying parameters, if the weight of historical data is not considered, the ability of new observations to modify the parameter estimation will gradually weaken.
To solve this problem, the multiple forgetting factor recursive least squares method is used in parameter identification. The multiple forgetting factor least squares method can realize on-line identification parameters method and has a strong robustness. It can weaken the influence of external environmental changes on the model and improve the identification accuracy to a certain extent. The steps of the algorithm are as follows.
Step 1 Select appropriate δ and set the initial value of P0 to ensure the convergence accuracy:
(7)
Step 2 Collect the currents and output voltages at contiguous moments and update the state variable matrix:
ηk={U(k-1),U(k-2),I(k),I(k-1),I(k-2)}T
(8)
Step 3 The output voltage is estimated by the coefficient of the previous moment and the state value of the current moment:
(9)
Step 4 Obtain the estimated error by comparing the estimated value with the actual value:
(10)
Step 5 The multiple forgetting factor is related to the state variable matrix, covariance, estimation error and noise value, and λk varies during the calculation process but not more than 1.
(11)
Step 6 The extremum principle is used to obtain the derivative, which is set to be 0 to calculate the gain matrix:
(12)
Step 7 Kk is calculated by the least square method and the estimated error is used to update the parameters:
(13)
Step 8 Update the variance matrix:
(14)
Step 9 Cycle Steps 2 to 8.
3.2 Model verification
In order to verify the accuracy of battery model and identified parameters, a few experiments are carried out at room temperature and five batteries with the same state are tested simultaneously. Referring to the hybrid pulse power characteristic (HPPC) measurement, firstly, batteries are charged to cut-off voltage at 4.2 V, then charged to a cut-off current for 0.055 A with 4.2 V, and then held for 2 h. After that, the pulse discharging process is carried out with C. The constant current discharge is performed for 6 min, and then held for 18 min. The whole process is performed 10 times. The real-time terminal voltage and current value of the charge and discharge experiments are recorded. Through the Matlab simulation, the parameters of the battery model can be identified online by the multiple forgetting factor recursive least squares method.
The concrete discharging strategy is plotted in Fig.6. The full state battery is released with 10% of SOC in constant pulse currents every time. After each discharge, the cell will be held for 18 min to calm down the OCV. As the diagram shows, the terminal voltage declines regularly under most conditions. It is clear that the voltage varies considerably when the cell is at the end of discharging. The reason why this situation occurs is that the cells in low SOC produce numerous complex chemical reactions so that they result in abnormal performances.

Fig.6 Discharging strategy
The coefficients of the recursive process are plotted in Fig.7. It performs the online identification process of the model parameters. It is apparent that parameters a1 and a2 fluctuate obviously while the trend of parameters a3, a4 and a5 vary steadily. The reason is that parameters a1 and a2 are mainly affected by the ohmic internal resistance while parameters a3, a4 and a5 are affected by the capacitance. Considering the temperature and the variable capacity, parameters a1 and a2 wave more significantly compared with the others. Parameters are deeply influenced by the ohmic internal resistance. It can also be inferred from the diagram that when the voltage approaches close to the cut-off voltage, all parameters vary dramatically, producing unexpected errors. However, as for EVs when only focusing on the valid range 10% to 90% of SOC, we can ignore the abnormal fluctuation.
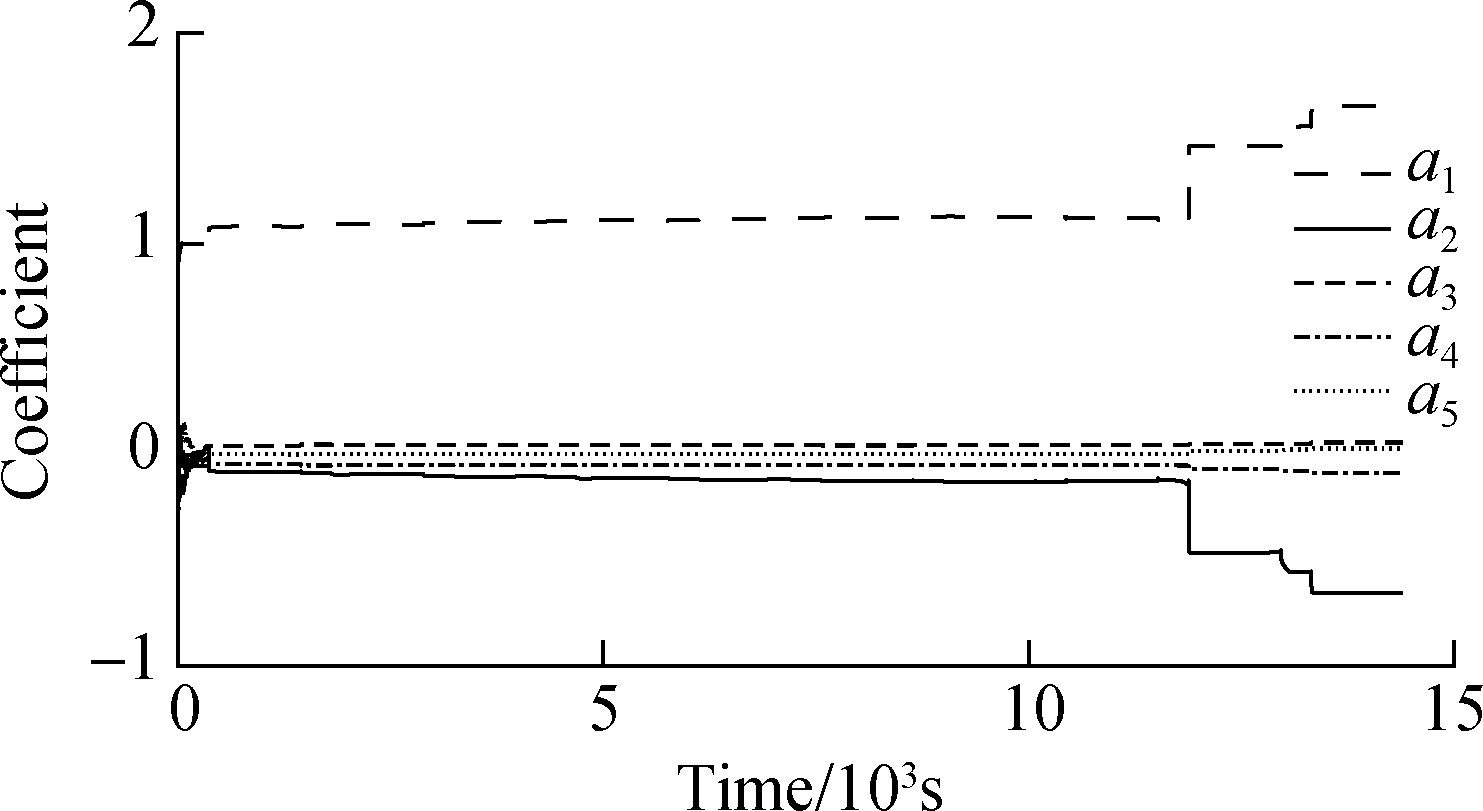
Fig.7 The change process of coefficient during the identification
From Fig.8 and Fig.9, it can be concluded from the graphs that the second-order model with the multiple forgetting factor least squares method can simulate the cells well. The estimated voltage value closely follows the terminal voltage value,which is collected by the constant pulse discharging working condition. During the entire experiment, the estimated error is within 0.3 V and the estimated error occurs at the high voltage and low voltage moments, that is, in high SOC and low SOC. When SOC is in the range of 0 to 10% and 100% to 90%, a large deviation is presented in the output voltage of the second-order model. The estimation error has a peak value above average. However, the working range of the EV lithium battery is generally 10% to 90%, so that the accuracy of the model established can meet the requirements. At the same time, it can be concluded that the fluctuation of error is synchronous with the current change, indicating that every time the current changes, an error will appear. The established second-order equivalent circuit model needs reaction time to reach the steady state, so the frequent dynamic response is not suitable for the condition.
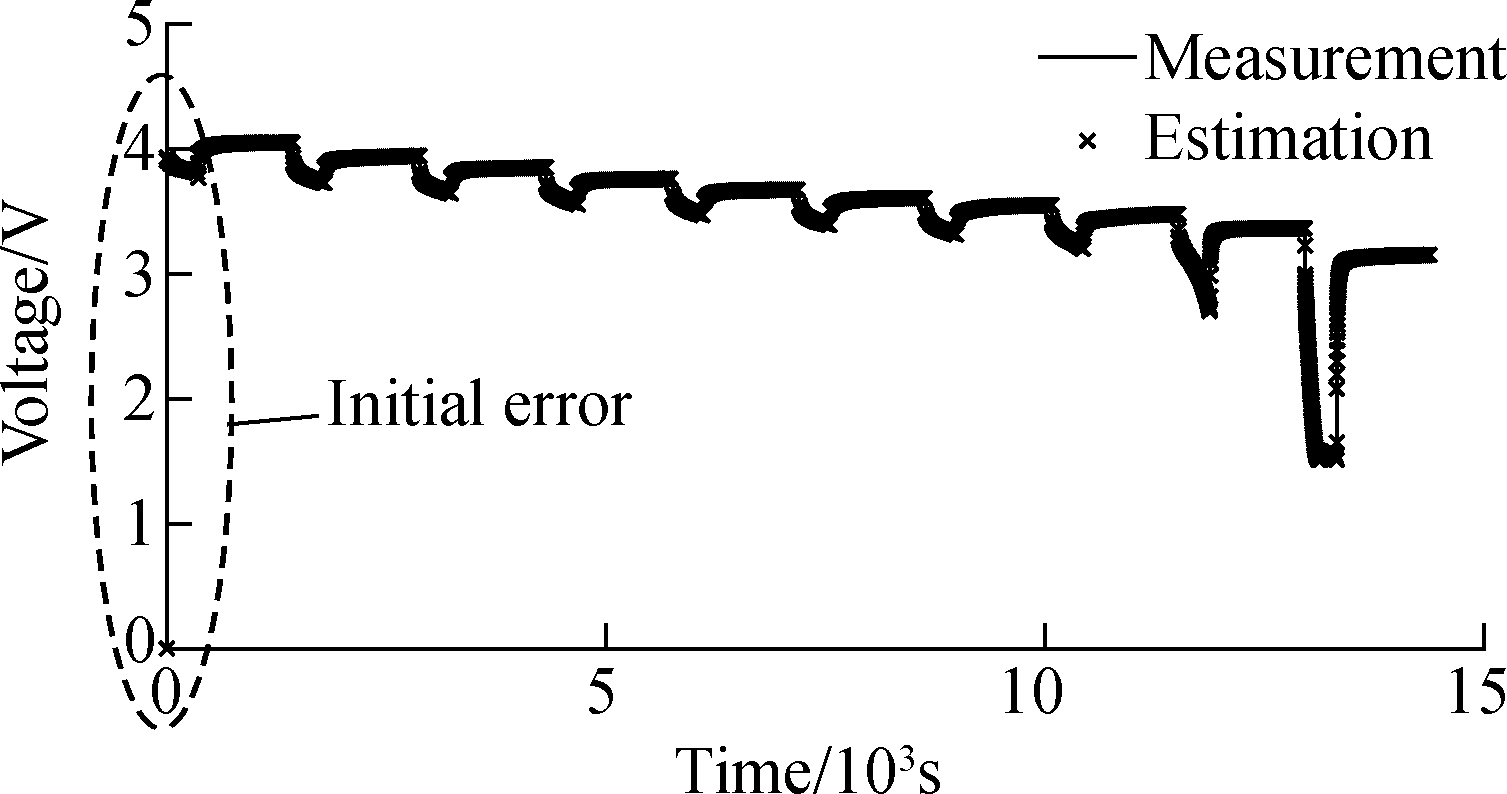
Fig.8 The estimation voltage and terminal voltage
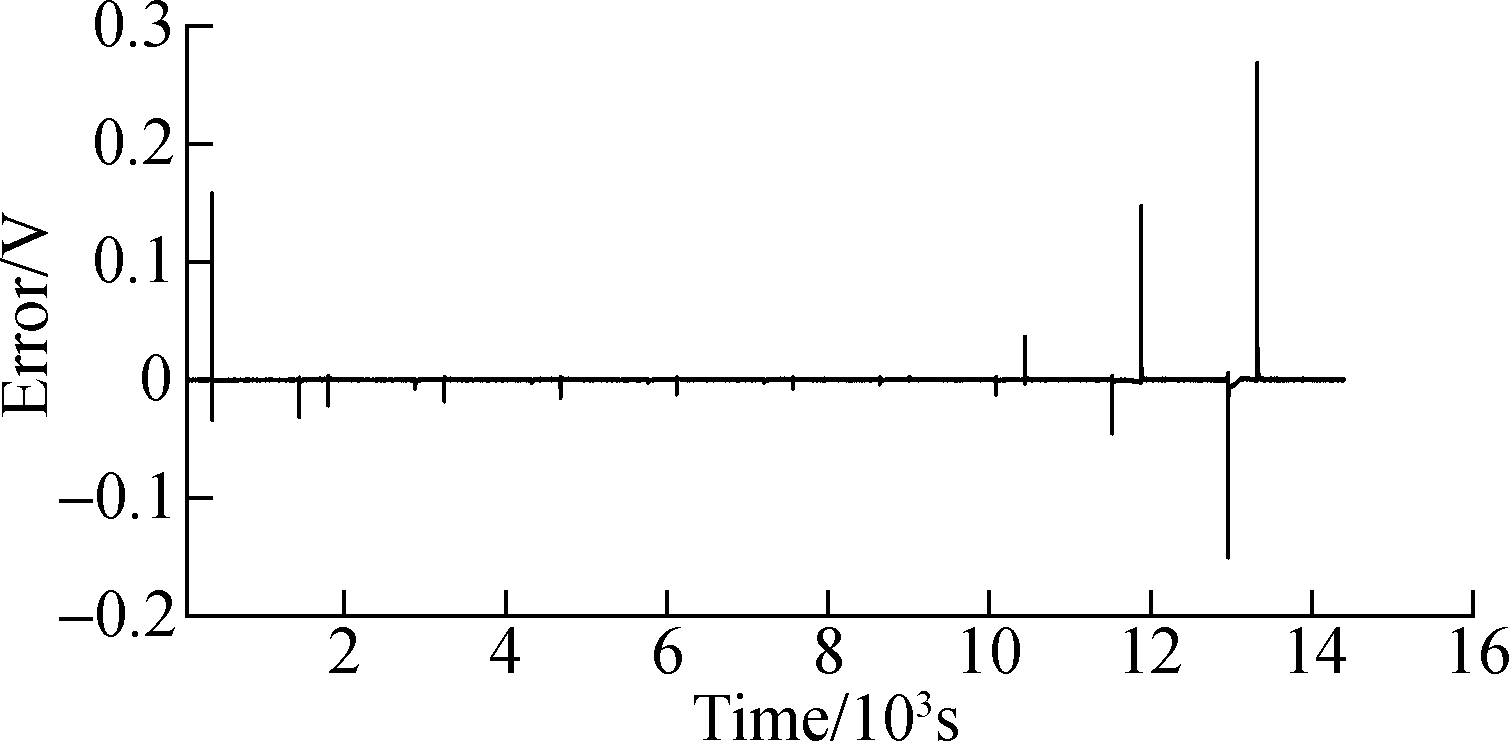
Fig.9 The error of voltages for identification
4 MVEKF Algorithm
From the above statement, the established equation of state and observation equation are
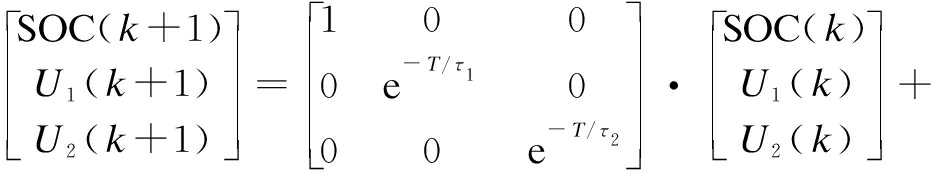
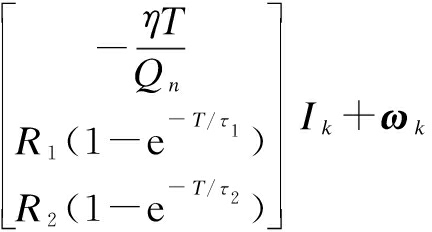
(15)
UL(k+1)=OCV(k+1)-U1(k+1)-
U2(k+1)-R0I(k+1)+vk+1
(16)
where ωk and vk+1 are mutually uncorrelated Gaussian white noise; η is the coulomb efficiency; T is the sampling period; and I(k) is the output current at k moment. In this paper, the current is positive when discharging and negative when charging.
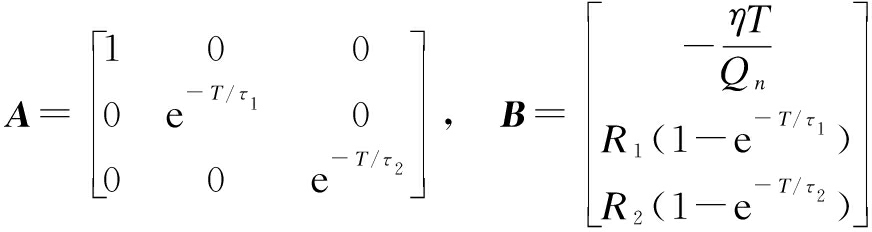

where A is the state transition matrix; B is the input control matrix; Xk is the state variable; and H is the Jacobian matrix.
The extended Kalman filter is a conventional method to deal with predictable matters. One of the fundamental situations of choosing the algorithm is the Gaussian white noise which is produced by actual problems. Therefore, several conditions are supposed as follows: ![]() is the state-filtered error. Xk is a known
is the state-filtered error. Xk is a known ![]() Pk is the state-filtered covariance of the EKF at k moment.
Pk is the state-filtered covariance of the EKF at k moment.
In the actual EKF filter, the Jacobian matrix obtained at the prediction moment also has a deviation due to a certain deviation of the predicted values[18], therefore, ![]()
The idea of the MVEKF is to recalculate the Jacobian matrix using state-filtered values in the EKF method:
The covariance matrix is updated using ![]()
The modified covariance extended Kalman filter (MVEKF) algorithm is described in the following. The OCV characteristics are firstly studied based on numerous charging and discharging experiments. From many kinds of experimental data, the empirical formula of the coulomb efficiency is built to indicate the battery capacity. According to Refs.[19-20], the second-order equivalent circuit model is established to describe the battery and the parameters are identified online with the multiple forgetting factor recursive least squares method. The MVEKF algorithm uses the imported parameters from the online identification results to calculate the battery cells. In the end, the SOC is compared with the real SOC according to the algorithm. The steps of the algorithm are as follows:
Step 1 Input off-line data(OCV, coulomb efficiency)and on-line parameters (R,C)
Step 2 Calculate the prediction process
Step 3 Calculate the Jacobian matrix at the prediction moment
Step 4 Calculate prediction covariance and Kalman gain
Pi/i-1=A·Pi-1/i-1·AT+Q
Step 5 Obtain a filtered estimate
Step 6 Recalculate the Jacobian matrix at the observation moment
Step 7 Recalculate prediction covariance and Kalman gain
Step 8 Compare data analysis and algorithm performance.
5 Experiments and Verification
In this paper,a second-order equivalent circuit model with dual resistors is established to describe the battery. The parameters of the cell are identified online by the multiple forgetting factor recursive least squares method. Based on these parameters, the MVEKF algorithm is proposed to estimate the SOC. To guarantee the the accuracy, the MVEKF as well as the EKF algorithm is written in Matlab. Constant current discharge, constant current pulse discharge and the DST condition test are carried out to verify the results.
5.1 Constant current discharge
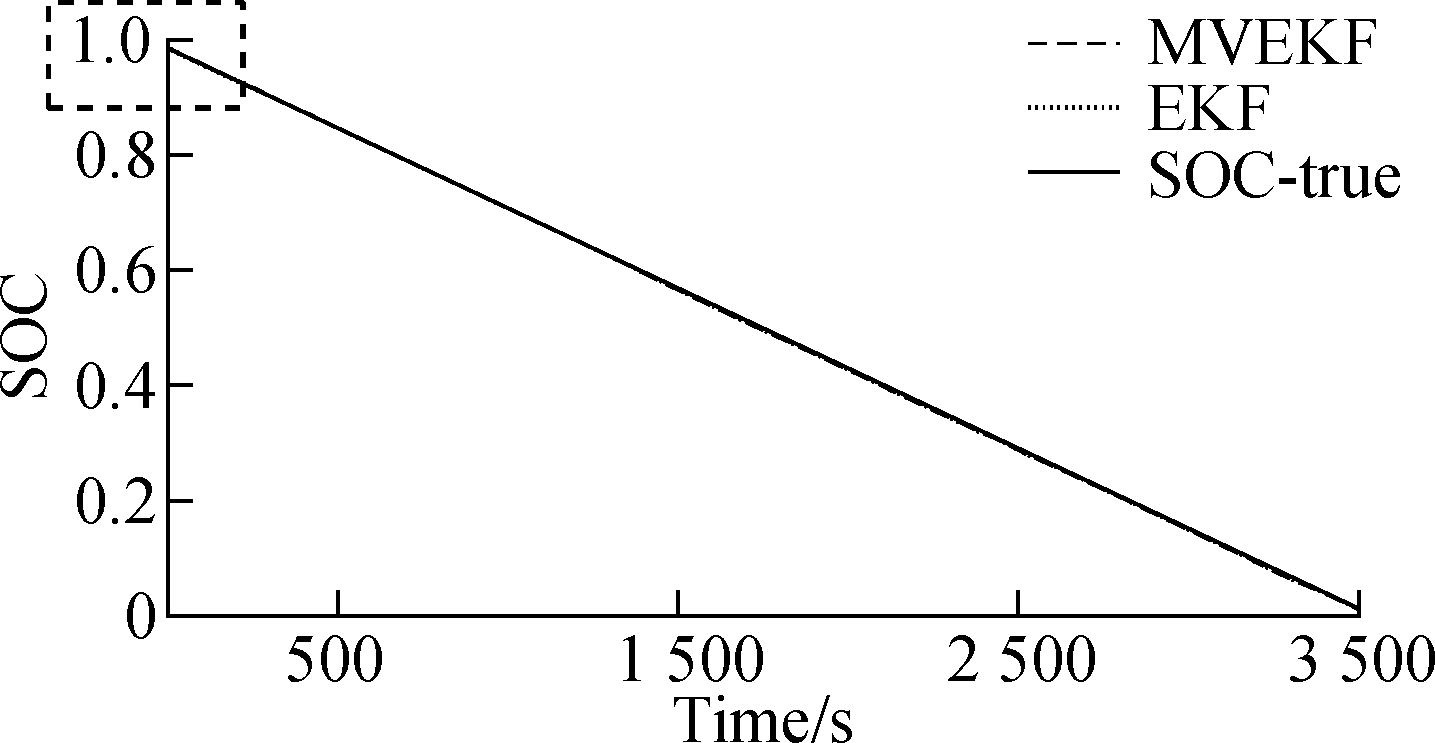
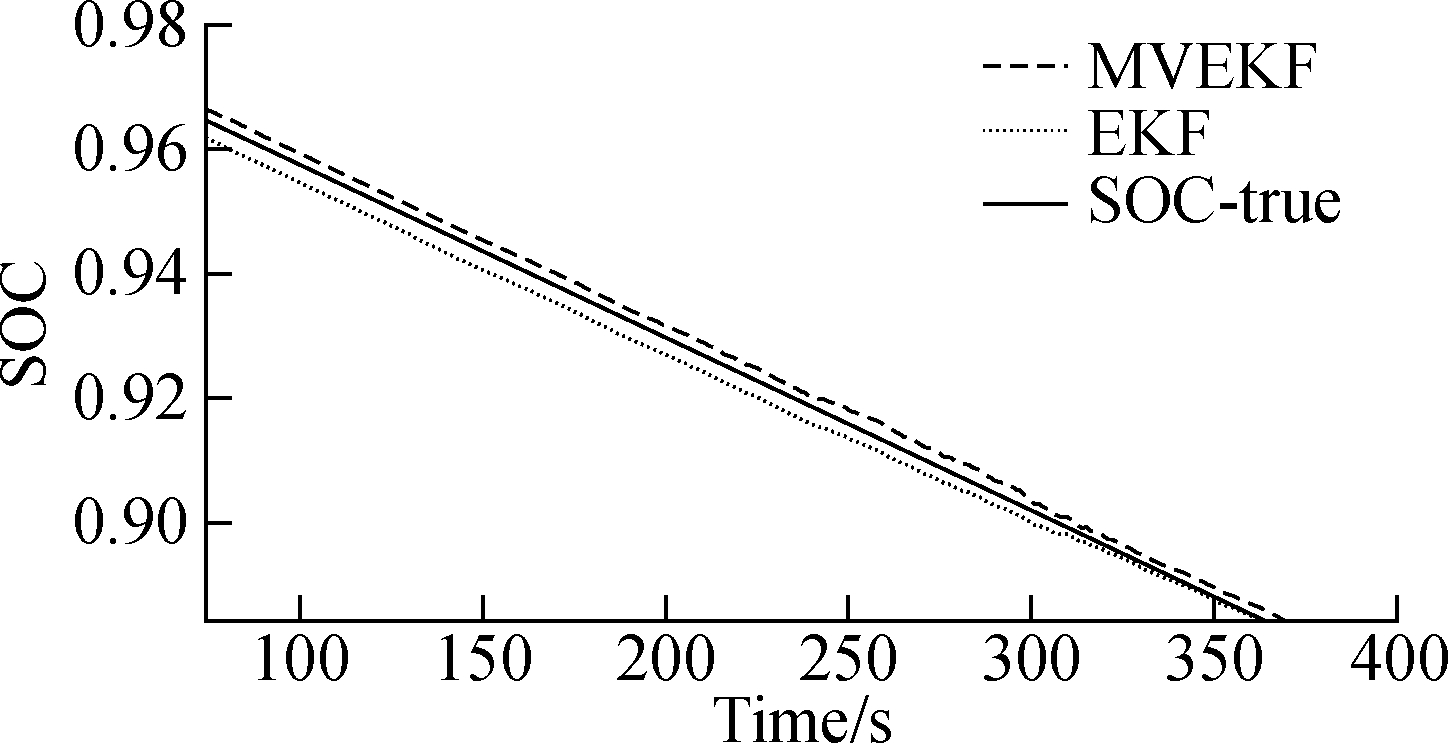
The estimation results of the constant discharge tests are plotted in Fig.10 and Fig.11 with the initial SOC values of 0.98 and 0.7, respectively. Fig.10 is an estimation result when the initial value of the SOC is known, and Fig.11 is an estimation result when the initial value of the SOC is unknown. Based on the second-order RC equivalent circuit model, it is indicated that both the EKF and MVEKF filtering algorithms can obtain accurate estimation results. The SOC estimation error of the battery model is under 2%. In this kind of discharging strategy, the current fluctuation is not large and the system noise is relatively small. According to the RC model, the EKF algorithm and the MVEKF algorithm produce pleasant filtering effects. From Fig.11, the MVEKF algorithm is more closer to the true value. It is faster to converge to the true line than the EKF algorithm, so the MVEKF is more efficient. The newly-established algorithm recalculates the covariance in the iterative process with the modified estimation and updates the process gain. The gain is used for the next state estimation to decrease errors of the filter. After every calculation, the result will be modified and the MVEKF gradually behaves better. It is concluded from the diagram that when the initial state is unknown, the convergence speeds of the EKF algorithm and the MVEKF algorithm are similar, and both have a strong robustness. However, the MVEKF algorithm is more efficient and reaches stability faster compared with the EKF.
(a)
(b)
Fig.10 The relationship between SOC and time in SOC(t=0)=0.98. (a) SOC variation with time in constant discharge tests; (b) Partial enlargement at the beginning of the simulation
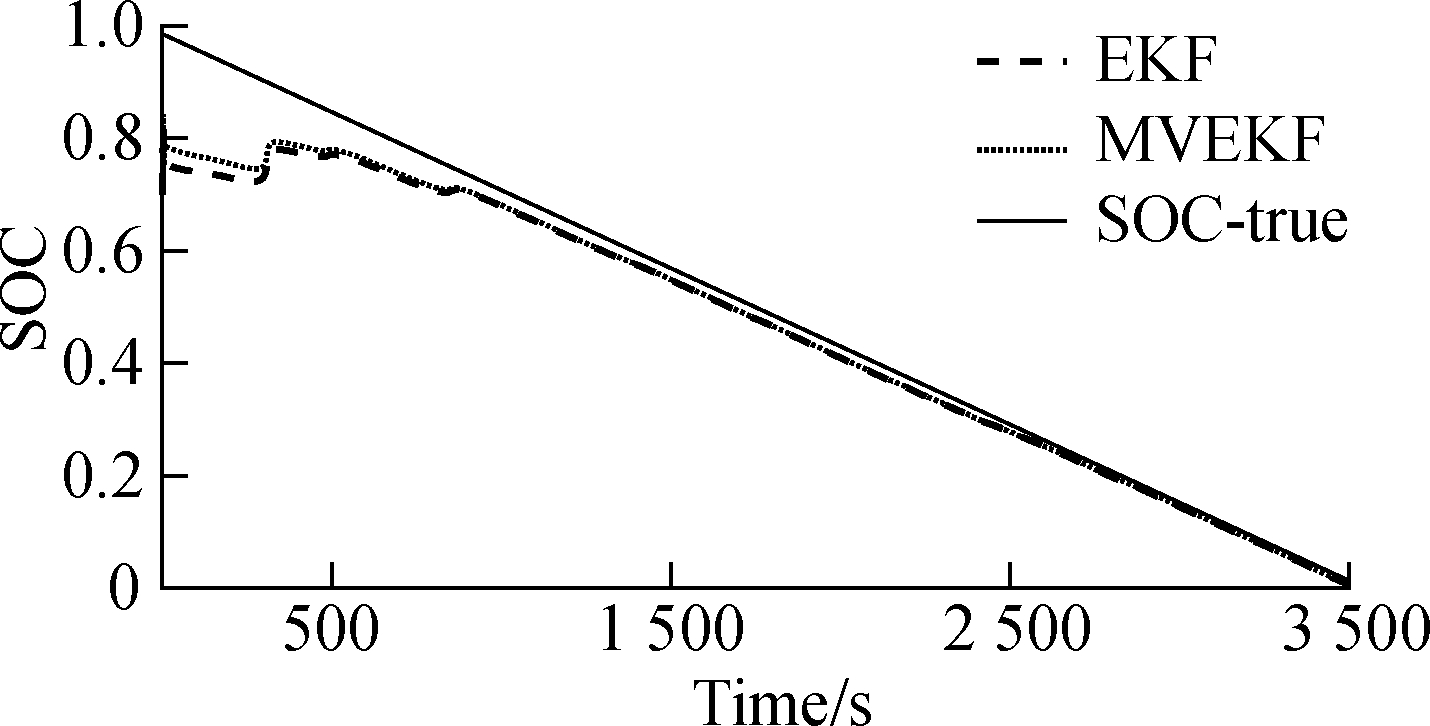
Fig.11 The relationship between SOC and time in SOC(t=0)=0.7
5.2 Pulse current discharge
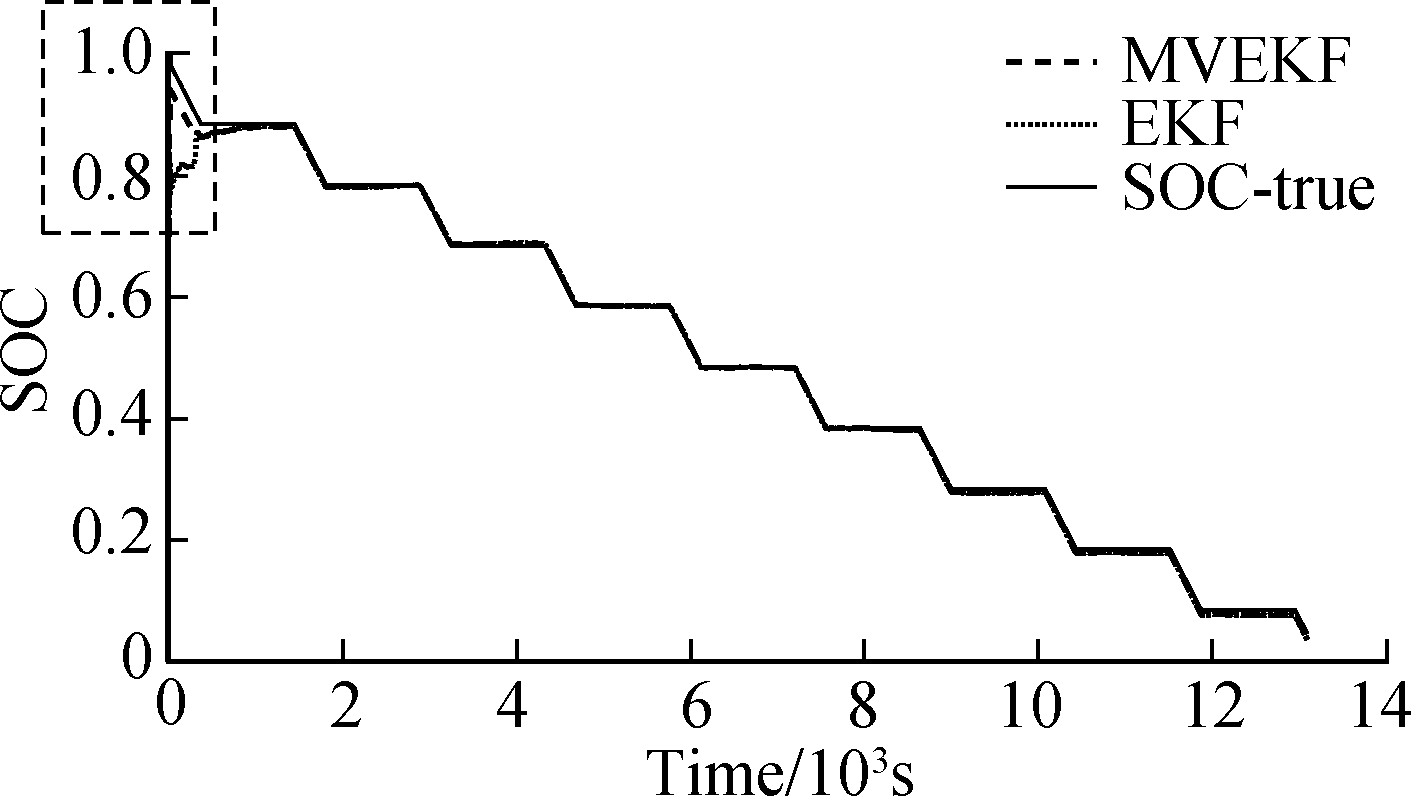
The estimation results of pulse discharge tests are plotted in Fig.12 and Fig.13 with the initial SOC values of 0.98 and 0.7, respectively.
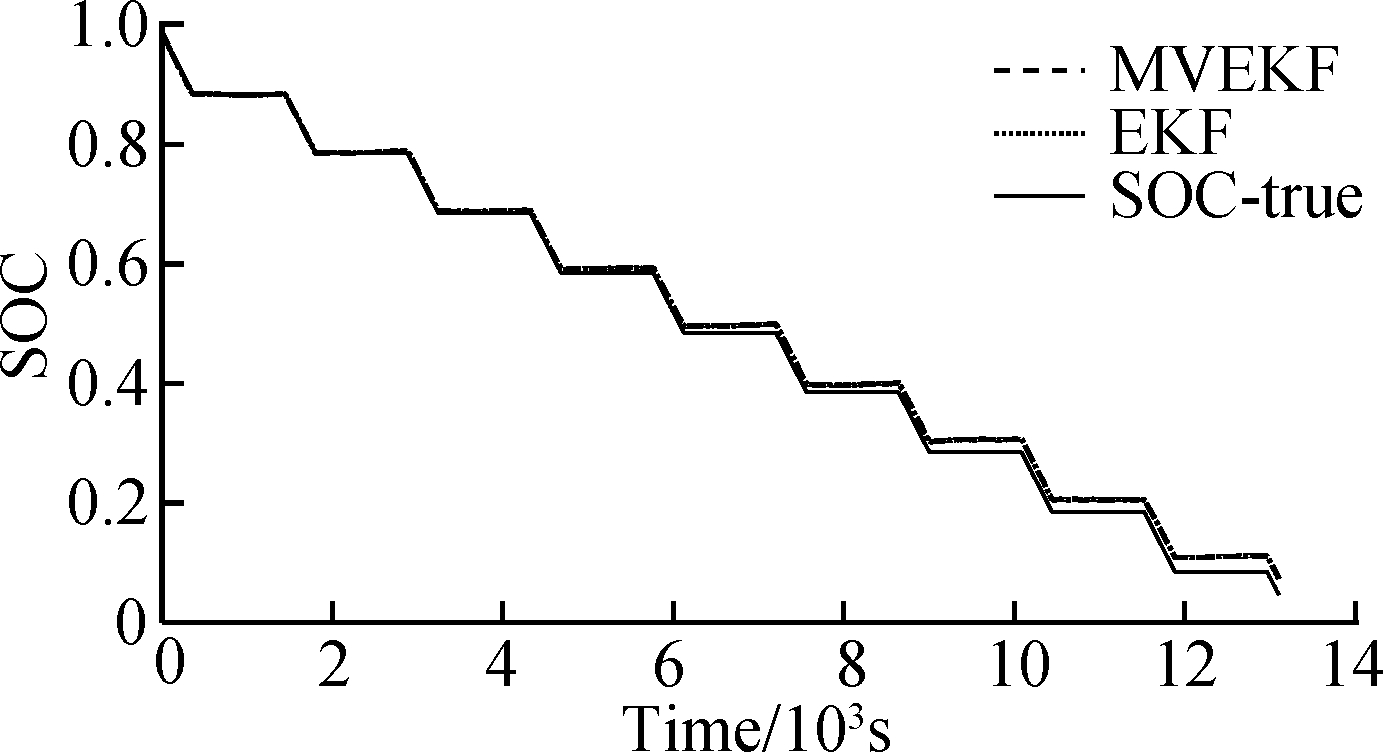
Fig.12 The relationship between SOC and time in SOC(t=0)=0.98
(a)

(b)
Fig.13 The relationship between SOC and time in SOC(t=0)=0.7. (a) SOC variation with time in pulse discharge tests; (b) Partial enlargement at the beginning of simulation
Fig.12 is an estimated result when the initial value of the SOC is known. Fig.13 is an estimated result when the initial value of the SOC is unknown. When the initial SOC is uncertain, the MVEKF algorithm converges to the real value more quickly. There are some differences between these two working conditions. The constant pulse experiments produce periodic current variation, which can test the efficiency to follow the real state. From the two diagrams, it can be seen that the MVEKF algorithm has better filtering effects and fewer estimation errors. Every time the current changes, it still performs stably and presents more precise results compared with the EKF algorithm. The online identification of parameters ensures the accuracy of the model, so that the expected results are obtained.
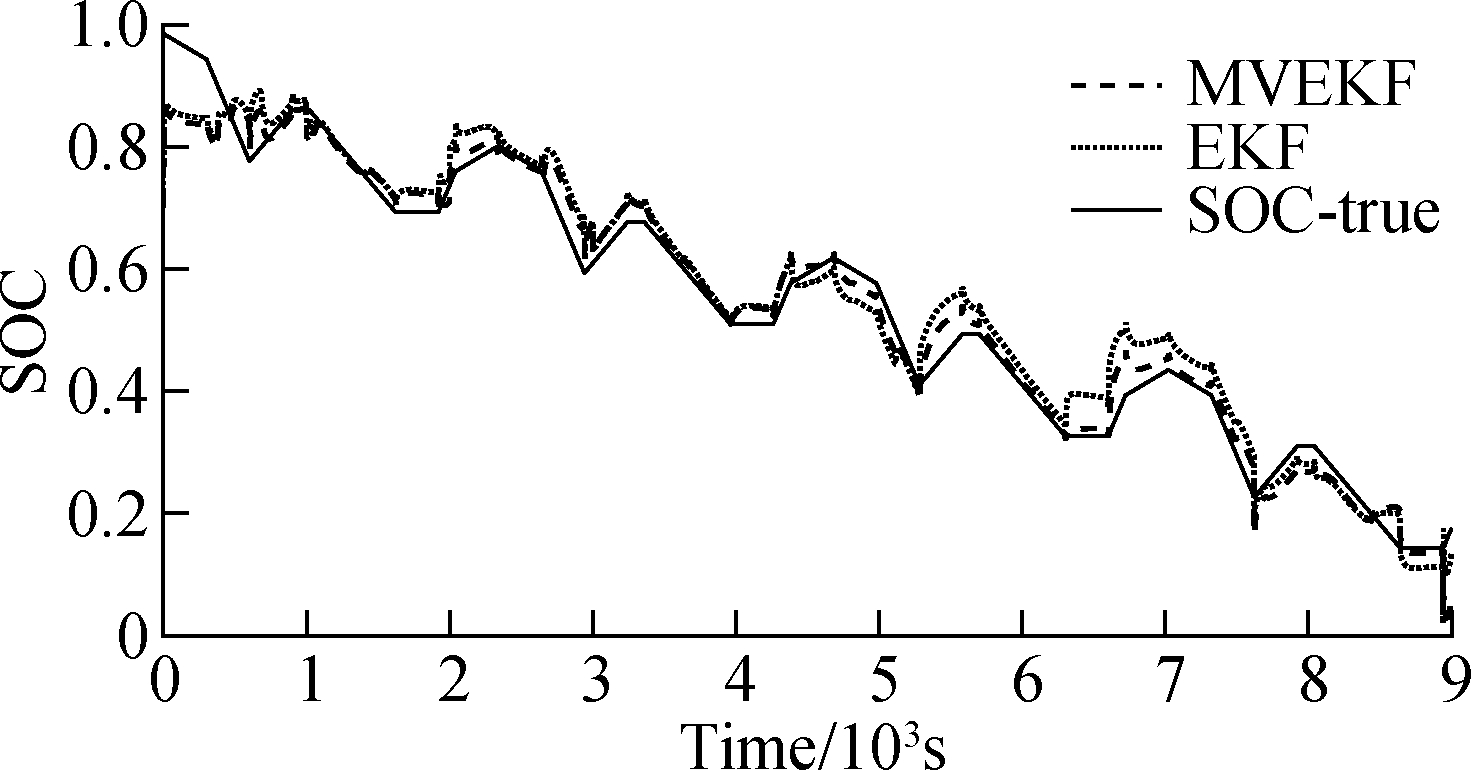
5.3 DST experiments
The estimation results of dynamic stress tests are shown in Fig.14(a) and Fig.14(b) with the initial SOC values of 0.98 and 0.7, respectively. As is known, the working environments of EV are complex and multiple. The DST experiments simulate the running situations of EV. Under DST working conditions, not only does the current vary very frequently, but the running noise is uncontrolled. The current is changeable all the time, which requires one algorithm with high efficiency as well as a high level of filtering. From the graph, the EKF algorithm results in a larger estimation error, especially, in the charging process. With numerous kinds of experimental data being updated, it is easily affected by the measurement noise. Whether in the discharging or charging process, the MVEKF produces fewer errors and follows the real SOC better than the EKF. What should be noted from the diagram is that several large errors occur in some moments. This is accounted for the uncontrolled internal resistance in abrupt current. Under most conditions, this algorithm matches well with the real condition.

(a)
(b)
Fig.14 The relationship between SOC and time in DST experiments. (a) SOC variation with time in SOC(t=0)=0.98; (b) SOC variation with time in SOC(t=0)=0.7
6 Conclusions
1) To obtain a stable and accurate SOC estimation for lithium batteries, an on-line SOC estimation algorithm was proposed by combining the online identification method and MVEKF algorithm. One accurate cell model is established based on the equivalent circuit model. The coulomb efficiency is considered as a parameter which influences the available capacity when estimating SOC.
2) The model parameters are identified on line by the multiple forgetting factor recursive least squares method. At the same time, based on these parameters, the MVEKF algorithm is selected to estimate the SOC. The second-order model can accurately estimate the terminal voltage of lithium batteries in EV, but its effect is limited to high and low voltage parts. However, considering that the effective range of EV is 10% to 90% of SOC, the model can meet the requirements.
3) Experiments including constant discharging, constant pulse discharging and the DST test are performed on the lithium batteries to verify reliability and robustness. The results indicate that the MVEKF filtering algorithm is superior to the EKF algorithm. In the complicated charging and discharging conditions of EV, the advantage of the MVEKF filtering algorithm is more obvious. Under constant current discharge and pulse current discharge conditions, both the EKF and MVEKF algorithms can estimate SOC well, but under DST conditions, the EKF has large deviations. The error is larger and unstable, especially during charging, while the MVEKF algorithm can stably estimate the SOC with high precision and a strong robustness. Therefore, the new algorithm is suitable for the complex and variable working conditions of electric vehicles.
[1] Cai L, Wang X Y, Huang L, et al. Development of battery management system for electric vehicles[J]. Electronic Quality, 2016, 10: 56-58.
[2] Liu X F, Cui B, Liu J J, et al. Real-time correction method for soc estimation of lithium ion battery based on anshimethod[J]. Journal of Automotive Safety and Energy Conservation, 2017, 8(2), 178-182.
[3] Dong G Z, Chen Z H, Wei J W,et al. An online model-based method for state of energy estimation of lithium-ion batteries using dual filters[J]. Journal of Power Sources, 2016, 301: 277-286. DOI:10.1016/j.jpowsour.2015.10.011.
[4] Duong V H,Bastawrous H A, Lim K, et al. Online state of charge and model parameters estimation of the LiFePO4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares[J]. Journal of Power Sources, 2015, 296: 215-224. DOI:10.1016/j.jpowsour.2015.07.041.
[5] Xu Z, Gao S B, Yang S F. LiFePO4 battery state of charge estimation based on the improved Thevenin equivalent circuit model and Kalman filtering[J]. Journal of Renewable and Sustainable Energy, 2016, 8(2): 024103. DOI:10.1063/1.4944335.
[6] Lin C, Tang A H, Xing J L. Evaluation of electrochemical models based battery state-of-charge estimation approaches for electric vehicles[J]. Applied Energy, 2017, 207: 394-404. DOI:10.1016/j.apenergy.2017.05.109.
[7] Ning B, Xu J, Cao B G, et al. A sliding mode observer SOC estimation method based on parameter adaptive battery model[J]. Energy Procedia, 2016, 88: 619-626. DOI:10.1016/j.egypro.2016.06.088.
[8] Lin C, Mu H,Xiong R, et al. A novel multi-model probability battery state of charge estimation approach for electric vehicles using H-infinity algorithm[J]. Applied Energy, 2016, 166: 76-83. DOI:10.1016/j.apenergy.2016.01.010.
[9] Guo Y F, Zhao Z S, Huang L M. SOC estimation of lithium battery based on AEKF algorithm[J]. Energy Procedia, 2017, 105: 4146-4152. DOI:10.1016/j.egypro.2017.03.879.
[10] Xiong R, He H W, Sun F C, et al. Evaluation on state of charge estimation of batteries with adaptive extended kalman filter by experiment approach[J]. IEEE Transactions on Vehicular Technology, 2013, 62(1): 108-117. DOI:10.1109/tvt.2012.2222684.
[11] Wang Y J, Zhang C B, Chen Z H. On-line battery state-of-charge estimation based on an integrated estimator[J]. Applied Energy, 2017, 185: 2026-2032. DOI:10.1016/j.apenergy.2015.09.015.
[12] He H W, Xiong R, Guo H Q. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles[J]. Applied Energy, 2012, 89(1): 413-420. DOI:10.1016/j.apenergy.2011.08.005.
[13] Wu Z Q, Shang M Y, Shen D D, et al. Prediction of SOC of lead-acid battery in pure electric vehicle based on BSA-RELM[J]. Journal of Renewable and Sustainable Energy, 2018, 10(5): 054103. DOI:10.1063/1.5038921.
[14] Wang Q, Feng X Y, Zhang B,et al. Power battery state of charge estimation based on extended Kalman filter[J]. Journal of Renewable and Sustainable Energy, 2019, 11(1): 014302. DOI:10.1063/1.5057894.
[15] Liu Z T, He H W. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter[J]. Applied Energy, 2017, 185: 2033-2044. DOI:10.1016/j.apenergy.2015.10.168.
[16] Ouyang Q, Chen J, Zheng J, et al.SOC estimation-based quasi-sliding mode control for cell balancing in lithium-ion battery packs[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3427-3436. DOI:10.1109/tie.2017.2750629.
[17] Huria T, Ludovici G, Lutzemberger G. State of charge estimation of high power lithium iron phosphate cells[J]. Journal of Power Sources, 2014, 249: 92-102. DOI:10.1016/j.jpowsour.2013.10.079.
[18] He H W, Xiong R, Zhang X W, et al. State-of-charge estimation of the lithium-ion battery using an adaptive extended kalman filter based on an improved thevenin model[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1461-1469. DOI:10.1109/tvt.2011.2132812.
[19] Li X Y, Wang Z P, Zhang L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles[J]. Energy, 2019, 174: 33-44. DOI:10.1016/j.energy.2019.02.147.
[20] Hannan M A,Lipu M S H, Hussain A, et al. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations[J]. Renewable and Sustainable Energy Reviews, 2017, 78: 834-854. DOI:10.1016/j.rser.2017.05.001.