The shoulder, one of the most frequently used joints, allows upper limbs to perform various daily activities, such as eating, personal hygiene management, and clothing. Rehabilitation of post-stroke shoulder disability patients requires repeated and progressive training. However, conventional treatment has limited effectiveness[1]. Thus, it is of practical significance to develop rehabilitation exoskeletons for shoulder dyskinesia, which can promote rehabilitation training at various intensity levels[2].
At the current stage, the key issue in the design of exoskeleton structures is to achieve ergonomic kinematic compatibility, thereby improving wearable comfort and efficiency of robot-assisted training[3-4]. Previous research mainly focuses on the active compensation joint and passive compensation joint. The active compensation exoskeleton guides its rotation center by referring to the experimental measurement track of a center of glenohumeral (CGH), so as to reduce the error between the exoskeleton and the human body. For example, HARMONY, designed by Kim et al.[5], compensated for the exoskeleton dynamics by setting a robot reference trajectory through active control strategies to promote the scapulohumeral rhythm. Thalagala et al.[6-7] achieved compensation by setting rails to guide the displacement of the exoskeleton rotation center. In addition, the common strategy of passive compensation joint research adds dynamic joints to the exoskeleton actuation chain and realizes the shoulder girdle fitting by passive control. For example, Yalcin et al.[8] added a passive prism joint and three parallel sliders to AssistOn-SE, to simulate the shoulder girdle. Zhang et al.[9] improved the compatibility of Co-Exos by using passive prismatic joints of four linear guides and sliders, and thus, Co-Exos can decrease the binding force due to misalignment. Li et al.[10] proposed a 3R-PU serial shoulder rehabilitation exoskeleton to realize compatibility when the unilateral humerus is lifting. They also provided a analysis basis for the PU joint motion planning and control.
Although the active compensation joint is relatively light and easy to control, its compensation effect is limited by human heterogeneity and trajectory rationality.Passive dynamic joints are controlled by tracking, which achieves a great fit with the CGH trajectory. However, they render the device complicated and cumbersome and reduce the efficiency of the driving force. In the aspect of the compensation utility, the current analysis is mainly based on static motion, such as the mobile arm support designed by Lin et al. [11] and the tendon-sheath-driven rehabilitation exoskeleton designed by Wu et al [12]. Few works have focused on the utility analysis of compensation joints considering dynamic motion.
To reduce the complexity of the mechanism and improve the universal applicability of the mechanism’s kinematics, this paper presents an unpowered and self-adaptive shoulder rehabilitation exoskeleton, which is believed to be a novel design concept, simple in structure, and widely suitable for different human physiques.
1 A Self-Adaptive Shoulder Rehabilitation Exoskeleton based on Gravity Balance
1.1 Influence factors of scapulohumeral rhythm
The glenohumeral joint of the shoulder complex has a ball-and-socket structure, and it has the largest motion range of a human joint. As the coordinated movement of humerus, scapula and clavicle leads to the floating of the glenohumeral joint, it is challenging to keep the exoskeleton axes aligned with human axes in real-time. 
et al.[13] fastened reference points M1 to M11 onto the anterior and posterior region of the shoulder girdle, as shown in Fig.1. The shoulder girdle segment as a vector between the points G and S is independent of gender, height, weight and age. It is only related to the humeral elevation methods (unilateral humeral elevation and bilateral humeral elevation), the humerus elevation φ, and the initial length of shoulder girdle d0.
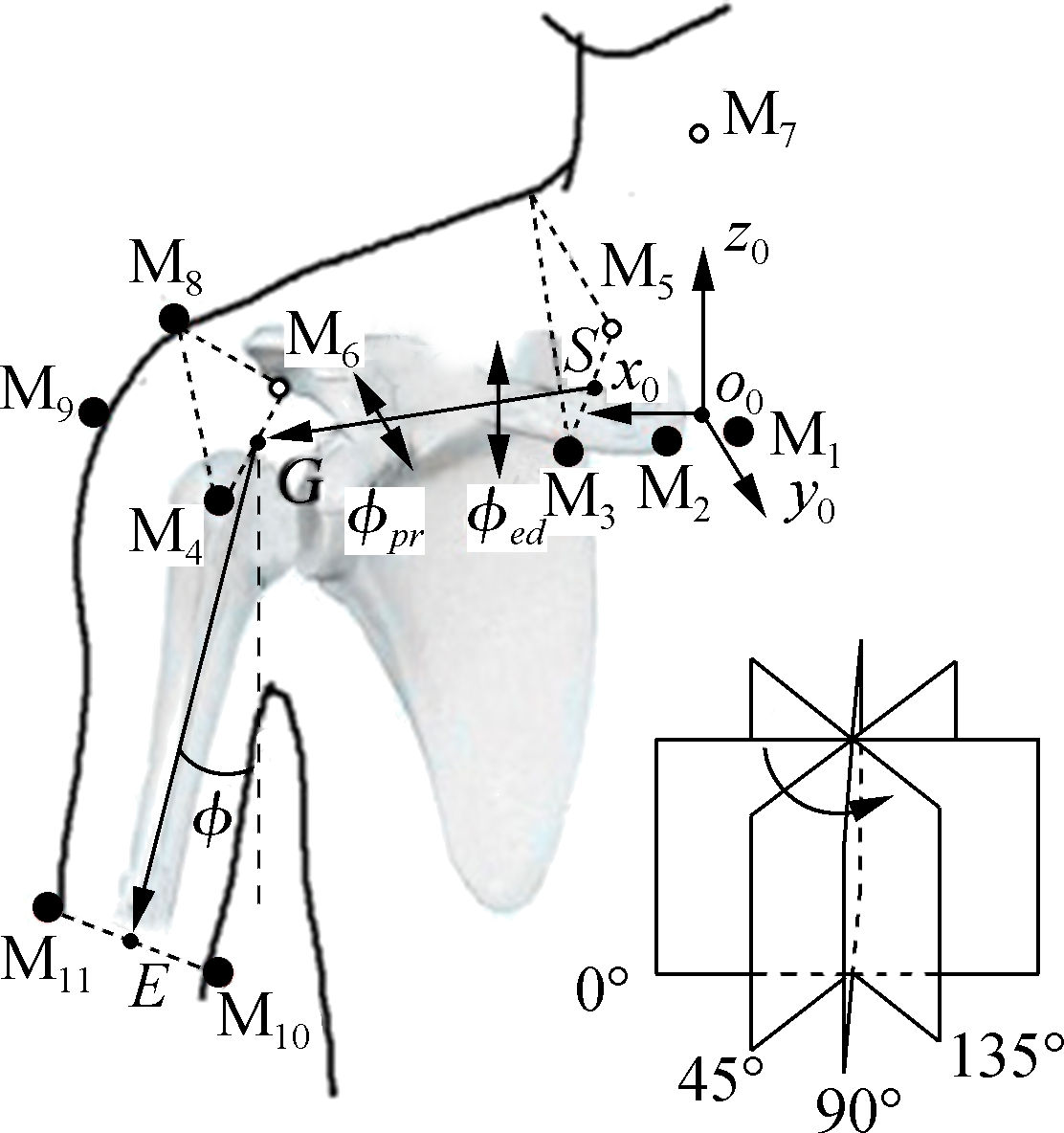
Fig.1 Reference points on the shoulder complex
et al.[13] fitted the relationship functions to obtain the shoulder girdle elevation/depression φed, shoulder girdle protraction/retraction φpr and the length of shoulder girdle dSG. Based on the functions, the spatial variation formula of a CGH is obtained as
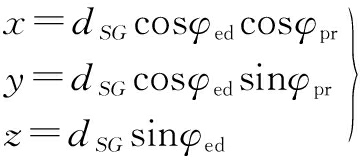
(1)
For different human bodies, the above variables will change randomly and only slightly.
1.2 Configuration synthesis of the 2R1R1P2R rehabilitation exoskeleton
Targetting the complex and cumbersome problem of passive compensation exoskeleton, this paper proposes a 2R1R1P2R serial self-adaptive shoulder rehabilitation exoskeleton. The setting of unilateral joints is shown in Fig.2, and the bilateral joints are set in symmetrical mode. Only three dynamic joints (R3, R4 and R5), whose rotating axes intersect at one point, are in the exoskeleton, which achieves the essential motor functions of the shoulder, including abduction/adduction, internal rotation/external, and flexion/extension. The height and position of the seat should be adjusted in advance to make the dynamic joint rotation center Om and the shoulder joint rotation center coincide when the upper arm naturally droops. In the independent closed-loop chain formed by the exoskeleton and the human body, there are three active joints within the exoskeleton and three biological degrees of freedom (DOFs) in the shoulder. Based on the mechanism theory, the exoskeleton still needs at least three DOFs to demonstrate human-machine compatibility. Therefore, the CGH compensation mechanism and the passive slider P1 are added to reduce the human-machine binding force caused by the floating of the glenohumeral joint in the vertical axis, coronal axis and sagittal axis.
Fig.2 The joints setting of exoskeleton
The CGH compensation mechanism is a plane 3-link mechanism consisting of two rotary joints R1 and R2. Meanwhile, in order to provide proper support while adapting the shoulder joint floating, the mechanism is designed based on gravity balance. The configuration model is shown in Fig.3. As shown in Fig.3(a), two four-bar parallelogram linkages are added to the base and vertical coupler rod L2. O3 successively connects the passive prismatic joint P1, three active joints (R3, R4 and R5) and the upper arm of the exoskeleton. k1 and k2 are the spring constants of the two ideal zero-free-length extension springs. Ai and Bi are the connection positions of both the ends of the springs.
To generally describe the plane configuration, let qi be the 2×1 unit vector on link i in the mechanism, where q1 is the ground. As shown in Fig.3(b), for the convenience of expression, a fixed coordinate system O0x0y0z0 is established at the midpoint of rod L1, where axis x0 is parallel to the coronal axis and directed outward by the sternum, axis y0 is parallel to the vertical axis and directed upward, and axis z0 is determined by right-hand rule. The coordinate systems O1x1y1z1 and O2x2y2z2 are established at the middle points of rod L1 and rod L2, where axis zi lies in the same direction as axis z0, and axis xi lies in the same direction as vector qi+1. The measurement and motion parameters of the CGH self-adaptive compensation mechanism are listed in Tab.1.
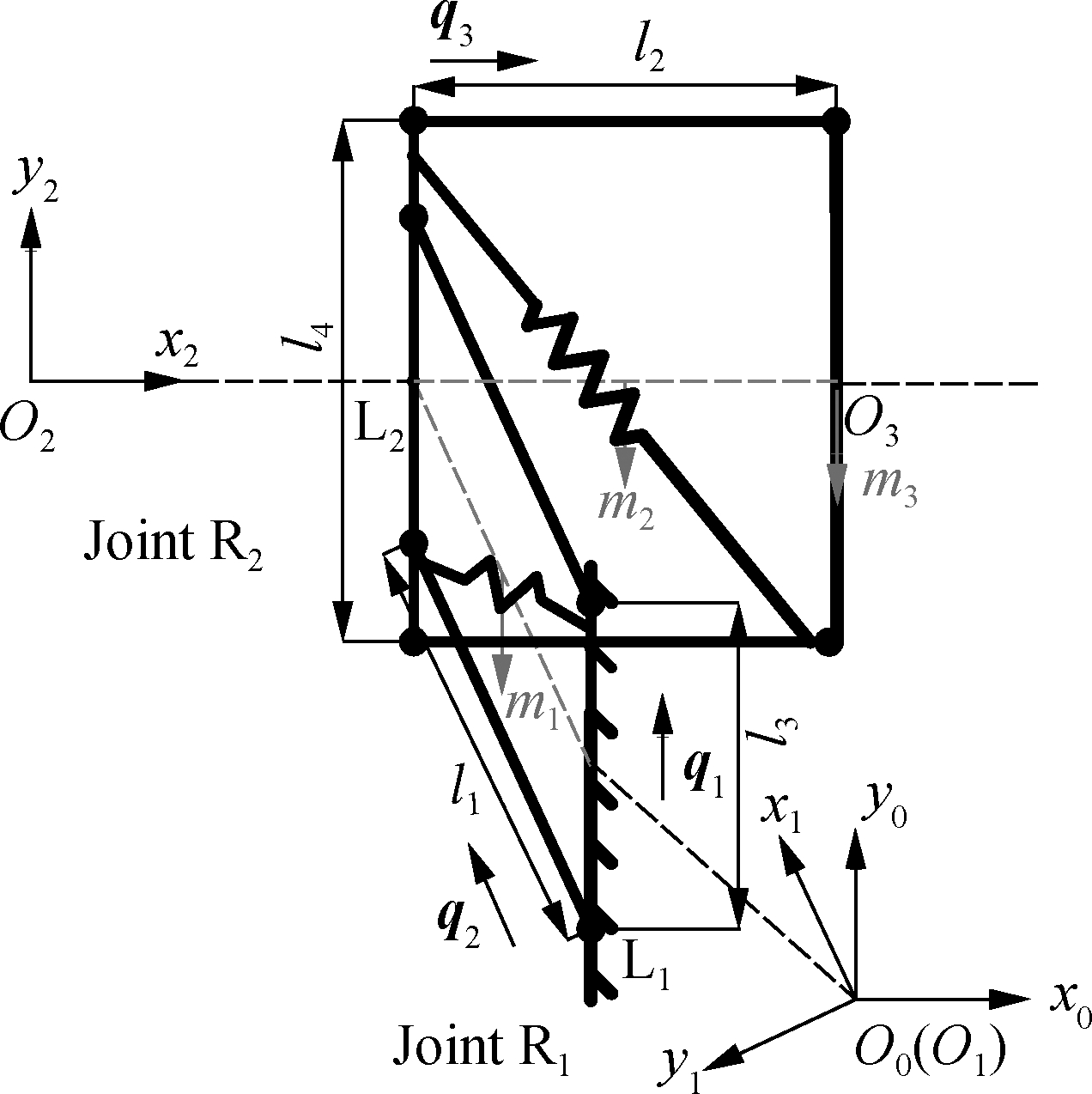
(a)
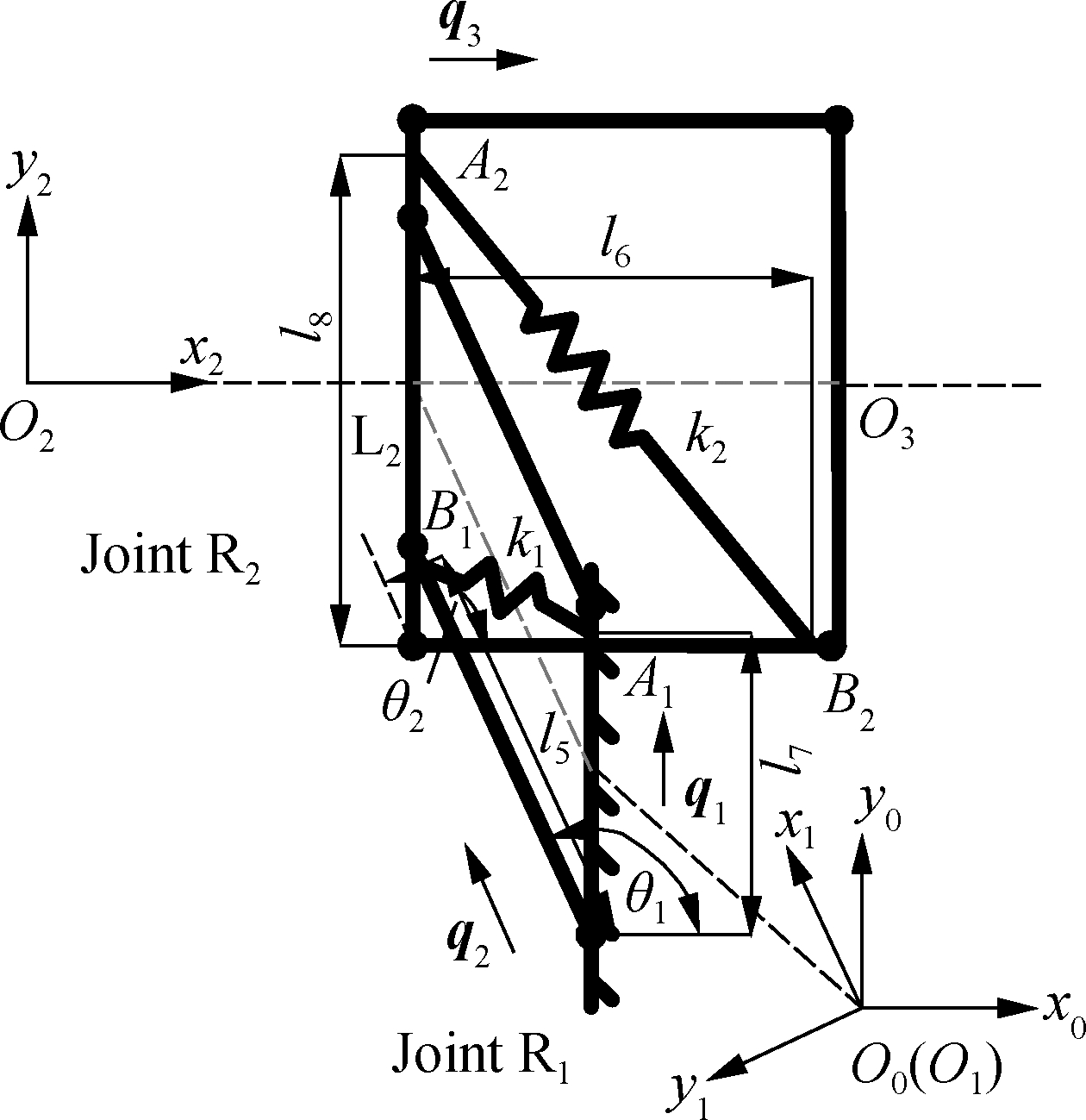
(b)
Fig.3 Model of unpowered CGH compensation mechanism. (a) The gravitational potential energy model; (b) The spring arrangement model
Tab.1 Measurement and motion parameters of the compensation mechanism
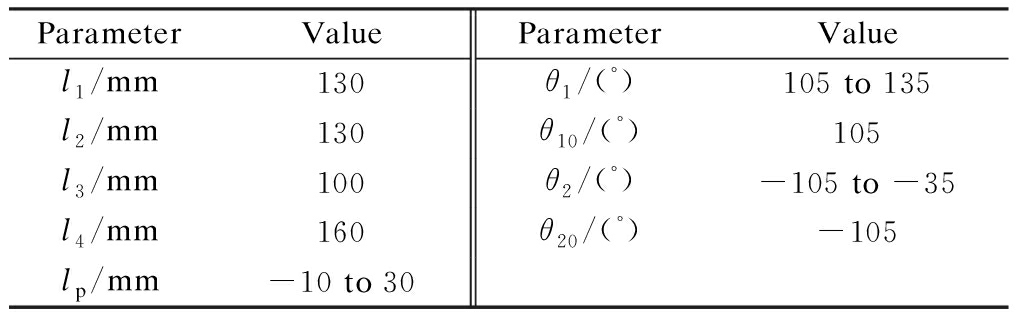
ParameterValueParameterValuel1/mm130θ1/(°)105 to 135l2/mm130θ10/(°)105l3/mm100θ2/(°)-105 to -35l4/mm160θ20/(°)-105lp/mm-10 to 30
These parameters are designed to ensure that the exoskeleton adapts to CGH floating caused by scapulohumeral rhythm. The relevant kinematic analysis is given in the next section. To ensure that the compensation joints provide stable support at any design angle without actuators, the principle of gravity balance is adopted in this design to determine the stiffness and connection position of the springs k1 and k2. Due to the slow operation of the rehabilitation joints, we only consider the gravity for the design. As shown in Fig.3(a), the stiffness matrix of the gravity of the mechanism and the arm from the reference point O1 to O3 can be obtained as
(m1+m2+m3)q
(2)
where m1 is the mass on one parallelogram and spring k1; m2 is the mass on the other parallelogram and spring k2; m3 is the mass on the arm and the exoskeleton transferred to O3.
The simplified total gravitation potential energy of the system can be written as
(3)
where g is the gravitational acceleration; μ=m1+m2+m3;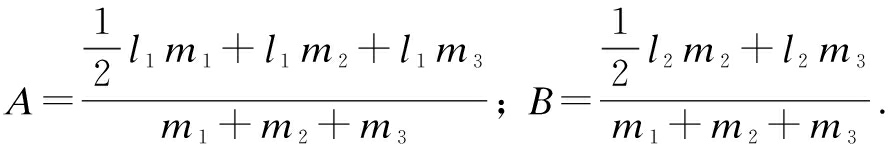 
The potential energy formula can be represented by the stiffness block matrix and configuration block matrix, which is written as
UG=QTKGQ
(4)
Therefore, the 6×6 stiffness symmetric matrix block of the system gravity can be obtained as
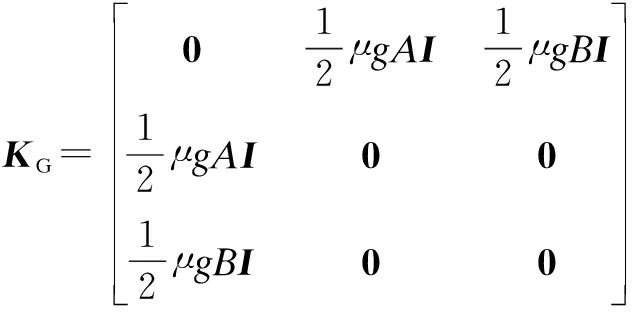
(5)
where I is the 2×2 identity matrix. Each component matrix of KG can be expressed as Kij=KijI. Kij represents the potential energy caused by links i and j and their relative angular position 
As shown in Fig.3(b), the elastic potential energy of spring k1 can be expressed as
(6)
where l5q2 and l7q1 are the vectors pointing from the rotation center to the attachment points (A1 and B1) of spring k1.
Hence, the stiffness block matrix induced by spring k1 can be obtained as
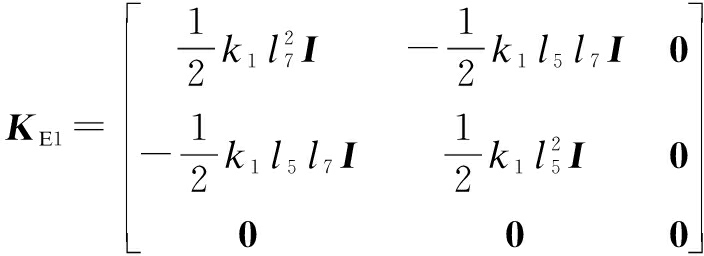
(7)
Similarly, the stiffness matrix induced by spring k2 can be obtained as
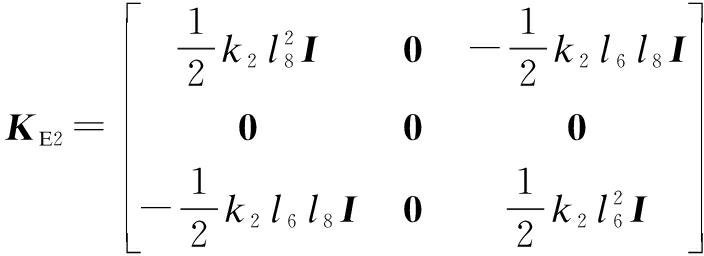
(8)
where l6 and l8 are the distances between the rotation center and two attachment points (A2 and B2) of spring k2.
According to the principle of virtual work, the necessary and sufficient condition for mechanical balance is zero virtual work performed by all external forces acting on the machine during any virtual configuration change. Hence, any component matrix related to the relative angular position θij (i≠j) in the total stiffness matrix should be a zero matrix. At this time, the potential energy is constant and is independent of the configuration change of the mechanism. The total stiffness block matrix obtained by summing Eqs.(5), (7) and (8) must be a diagonal matrix. Furthermore, the attachment points and stiffness of springs can be calculated as
(9)
(10)
At this time, it only needs to overcome the friction of the joints without considering gravity in dynamics. In the joint kinematics control, the end of the exoskeleton is fixed to the arm. Therefore, adaptive rotation can be achieved by doing the reverse leading through the arm.
The calculation advantage of the ideal spring is that the elastic potential energy can be obtained by the vectors between the spring connection points and the rotation center visually. According to Fig.4, a three-dimensional model is established, in which the ideal springs are realized by the combination of cables, pulleys and springs. The pulley is fixed at the connection point Ai of the ideal spring on the vertical rod. One end of the cable is fixed at the connection point Bi of the ideal spring on the rotating rod Li, and the other end is connected to the spring by bypassing the pulley. The other end of each spring is fixed to the vertical rod Li by the spring fixings. According to the initial distance of the ideal spring connection points Ai 0 and Bi 0, the pretensions of the two springs are k1||l5q20-l7q10||2 and k2||l8q10-l6q30||2, respectively. Since the length of the cable is a constant, the distance change of AiBi is equal to the length change of the spring. The spring elastic potential energy can still be calculated by the vector between connection points.
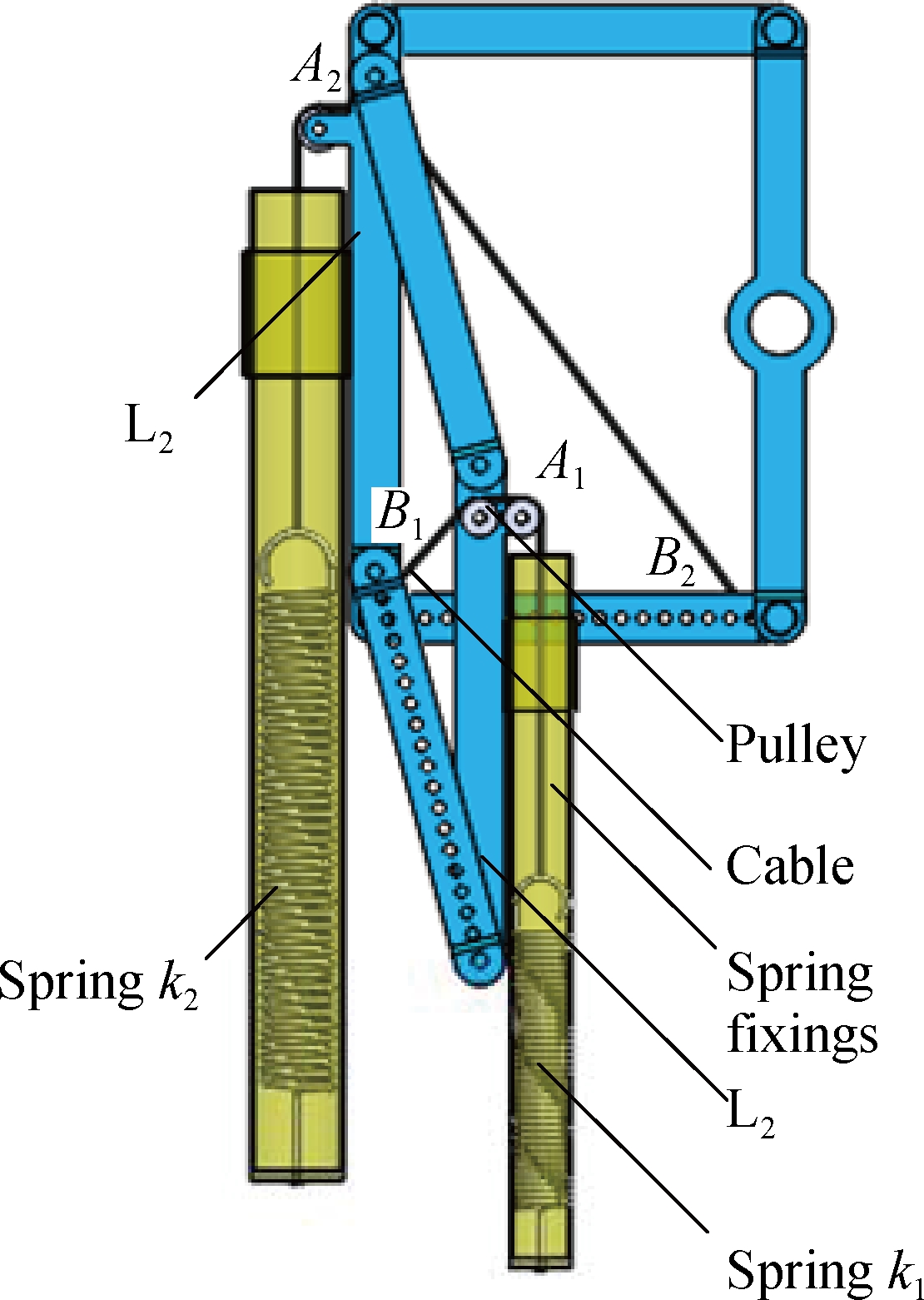
Fig.4 The 3D Model of unpowered CGH compensation
Compared with the traditional passive control exoskeleton, this exoskeleton reduces the sensor and actuator used for floating rotation fitting, and reduces the complexity and control requirements.
1.3 The adjustment strategy of springs
The rehabilitation exoskeleton should suit for different patients and training levels, which needs to deal with different quality parameters and link lengths. Accordingly, spring attachment positions and spring stiffness should be modified by Eqs.(9) and (10). Due to the difficulty in adjusting the stiffness of the metal spring, the spring stiffness is set to be a fixed value. Furthermore, fix one of the spring attachment positions Ai so that l7=l3 and l8=l4; then the design parameter formula of the other attachment point becomes a linear equation. The positions of B1 and B2 can be defined as
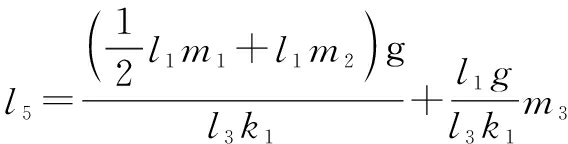
(11)
(12)
At this time, distances l5 and l6 are the remaining parameters related to the prescribed mass, and these two parameters can be independently adjusted without mutual interference. By adjusting attachment positions, the gravity balance of different weights can be realized conveniently, intuitively and quantitatively.
2 Analysis of the Human-Machine Compatibility and Dynamic Feasibility
2.1 Human-machine compatibility for the exoskeleton
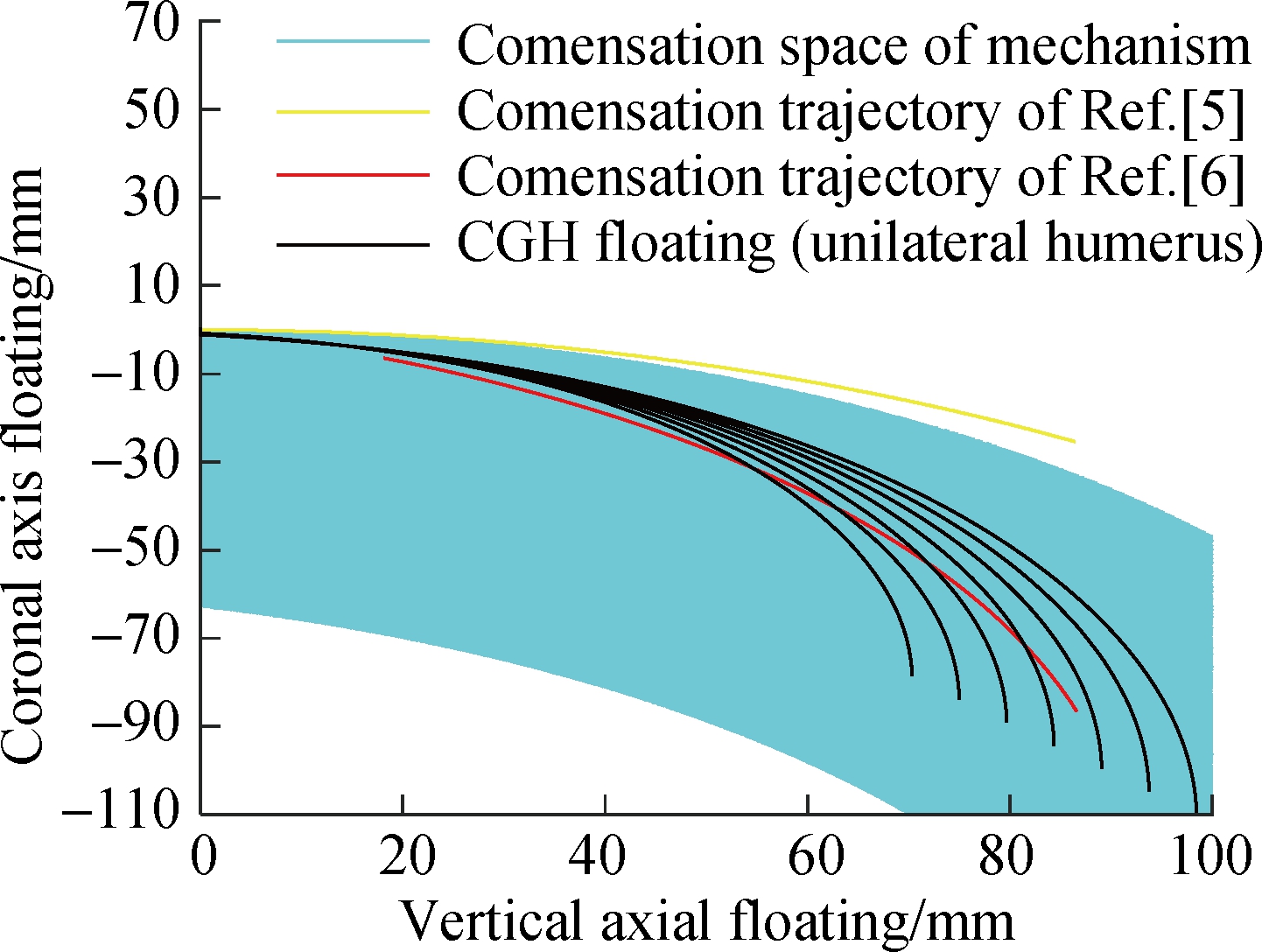
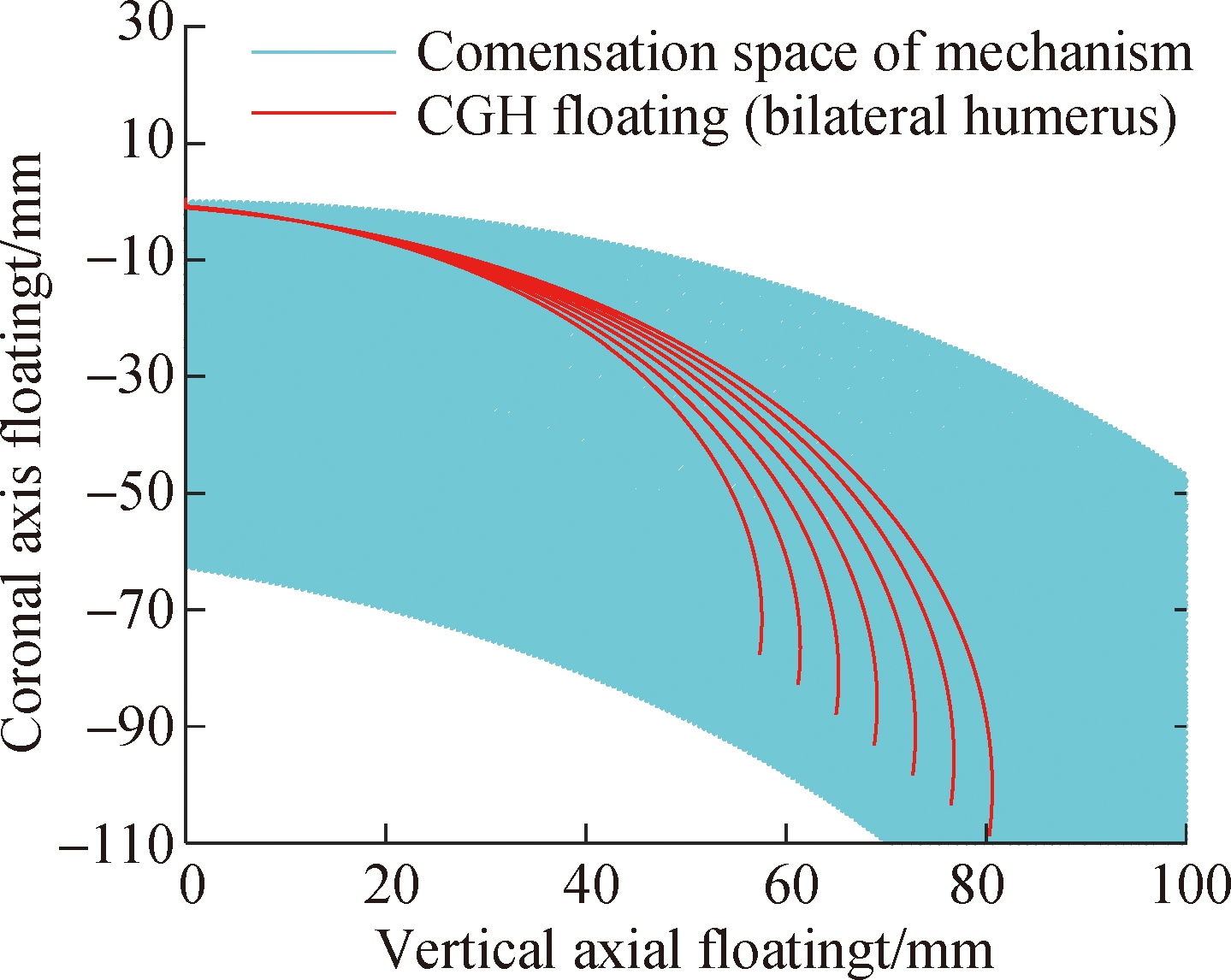
The compatibility analysis of the mechanism mainly compares the movement space of the CGH compensation mechanism with the floating space of the shoulder joint. In view of the uncertainty of the CGH floating trajectory, the design uses the coordinated motion of two rotating joints (R1 and R2). Unlike the traditional active compensation exoskeleton, this design has no specific trajectory and avoids the adjustment of the rod lengths, which results in strong universality. In rehabilitation practice, activities of daily living (ADL) are generally defined to describe the functional capacity of patients. The maximum abduction angle of the shoulder in ADL is 148.3° is based on statistical data[14], so that the maximum humerus elevation φ is set to be 150° for analysis. According to the body dimension standard of Chinese adults in GB/T 10000—1988, the 1st percentile female shoulder strap length and the 99th percentile male shoulder strap length are taken as boundary values. It can be concluded that 99% of the shoulder strap length is between 0.152 and 0.209 m, which can be divided into 7 segments (0.15, 0.16, 0.17, 0.18, 0.19, 0.2 and 0.21 m) with a 0.1 m step length. Therefore, combined with the coupling relationship of glenohumeral in Section 1.1, the vertical axis and coronal axis position of CGH of different shoulder strap lengths can be obtained, respectively, when the unilateral humerus or the bilateral humerus is elevated between 5° and 150°. Furthermore, the trajectories of CGH are compared with the movement space of mechanism. As shown in Fig.5(a), the active compensation exoskeleton proposed in Refs.[5-6] can only fit the shoulder joint floating under the single physique and single elevation method, while the CGH movement trajectories are quite different for patients. Therefore, it has a strong restriction for users. However, it can be seen from Fig.5 that the mechanism designed in this paper can completely cover the floating of the CGH, which shows strong general adaptability.
Unlike the common compensation joints, this movement space is not a simple globe, sphere, or a specific trajectory. It is roughly the same as the motion trend of CGH, which is supposed to be more reasonable. Meanwhile, due to the diversity of human joints, the motion coupling of the shoulder joint is slightly biased. The mechanism provides a redundant range of motion to accommodate this deviation.
2.2 Dynamic feasibility analysis of exoskeleton
The simulation of the exoskeleton is based on the two parallelogram models given in Fig.3. The mass and inertia parameters of the human body are obtained on the basis of anthropometric measurements and statistical data[15]. In this simulation, the masses of the upper arm, forearm, and mechanism are 2.18, 1.85 and 2.00 kg, respectively; d0=200 mm. The stiffness and attachment positions of the additional spring can be obtained by Eqs.
(a)
(b)
Fig.5 Comparison of the compensation space of the CGH joint. (a) Unilateral humerus elevation floating trajectories and the compensation trajectories of Refs.[5-6]; (b) Bilateral humerus elevation floating trajectories
(11) and (12), where k1=490 N·m, k2=380 N·m, l5=130 mm and l6=130 mm.
The simulation is implemented in ADAMS software. Considering the dynamic effect during low speed, the arm elevating process is divided into three stages: acceleration, uniform, and deceleration. At the same time, since this design is adaptively compensated, there is no specific trajectory. The analytical solutions of the inverse kinematics of R1 and R2 are used as the input driver when the unilateral humerus is elevated from 5° to 150°. It can be seen from Fig.6 that if only two rotary joints are used, it is necessary to apply the compensation drive moments from 3 to 8 N·m through the actuators. Accordingly, position control and torque control of compensation joints are crucial, which inevitably increases the difficulty and costs of control. However, the dynamic torque of the two rotary joints with gravity balance can be reduced to be less than 0.22 N·m while ensuring the human-machine compatibility. Fluctuations of the dynamic torque also significantly decrease. Note that, the patients with shoulder disabilities do not entirely lack the ability to organize limbs. With such small support provided by the patient, the shoulder joint can move freely.
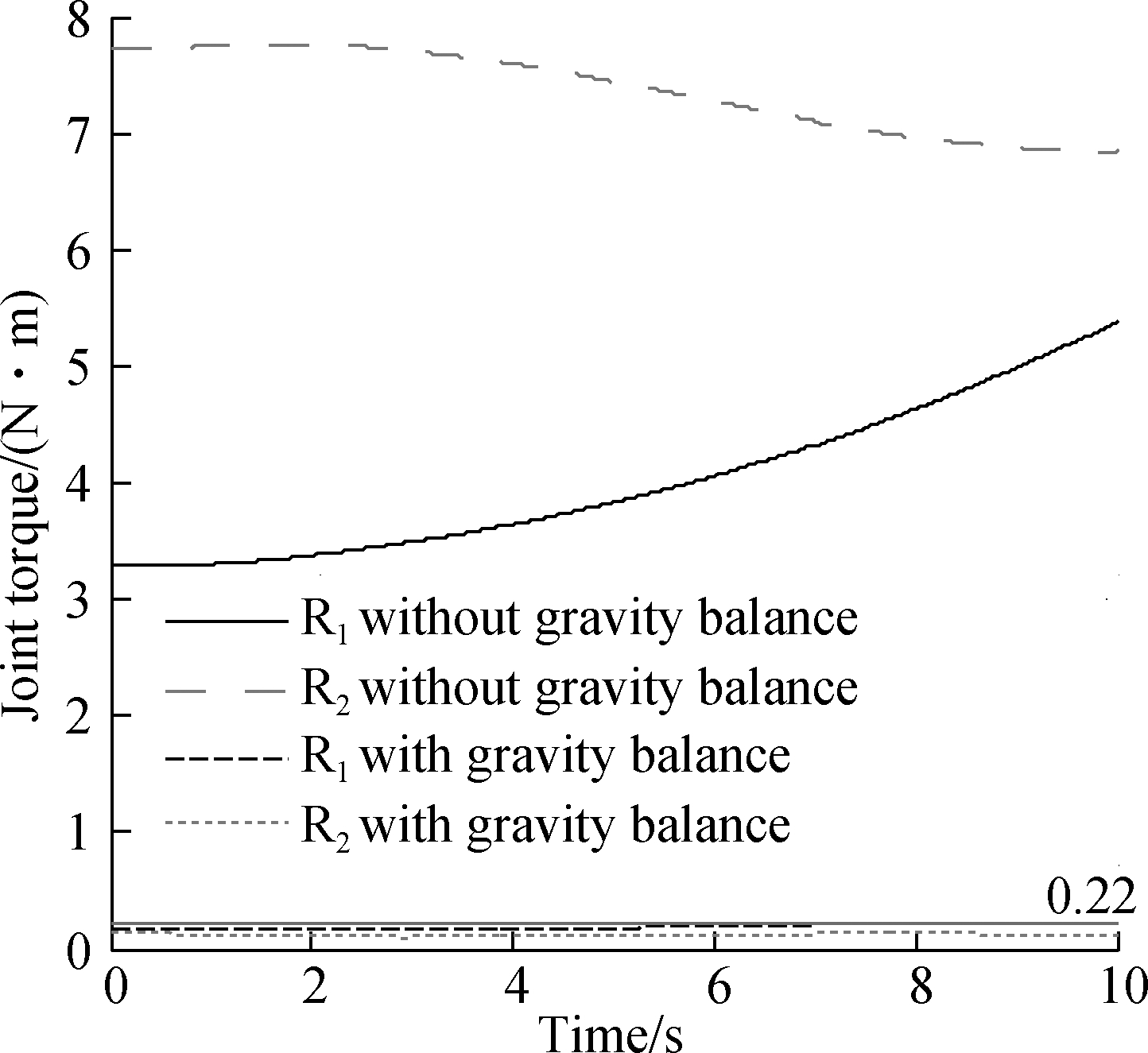
Fig.6 The change of compensation joint torque after adding gravity balance mechanism
3 Conclusions
1) This paper proposes a 2R1R1P2R serial self-adaptive shoulder rehabilitation exoskeleton, which introduces a passive slider and designs a CGH self-adaptive compensation mechanism to form the exact kinematic constraints system between the exoskeleton and upper arm. The CGH compensation mechanism based on the gravity balance performs complete weight compensation when the shoulder is floating, reducing the weight of the exoskeleton by unpowered joints. Meanwhile, it realizes shoulder joint adaptation by doing the reverse leading through the arm, without considering the passive control strategy. Furthermore, a convenient and intuitive strategy is proposed for spring adjustment.
2) Considering the influencing factors of the scapulohumeral rhythm, the exoskeleton can successfully fit the CGH movement track of 99% of the human physique, humerus elevation between 5 ° and 150 °, and different humeral elevation methods. It achieves the human-machine compatibility in various cases while meeting the requirements of shoulder rehabilitation space.
3) Through the dynamic simulation of unilateral humerus elevation, the torque of the two compensation joints is reduced from 3 to 8 N·m to less than 0.22 N·m. It verifies that the proposed CGH adaptive compensation mechanism can provide stable support when adapting to shoulder floating.
[1] van Peppen R P, Kwakkel G, Wood-Dauphinee S, et al. The impact of physical therapy on functional outcomes after stroke: What’s the evidence?[J]. Clinical Rehabilitation, 2004, 18(8): 833-862. DOI:10.1191/0269215504cr843oa.
[2] Lum P S, Burgar C G, Shor P C, et al. Robot-assisted movement training compared with conventional therapy techniques for the rehabilitation of upper-limb motor function after stroke[J]. Archives of Physical Medicine and Rehabilitation, 2002, 83(7): 952-959. DOI:10.1053/apmr.2001.33101.
[3] Crockett H C, Gross L B, Wilk K E, et al. Osseous adaptation and range of motion at the glenohumeral joint in professional baseball pitchers[J]. The American Journal of Sports Medicine, 2002, 30(1): 20-26. DOI:10.1177/03635465020300011701.
[4] Nef T, Riener R. Shoulder actuation mechanisms for arm rehabilitation exoskeletons[C]//2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics. Scottsdale, AZ, USA, 2008: 862-868. DOI:10.1109/biorob.2008.4762794.
[5] Kim B,Deshpande A D. Controls for the shoulder mechanism of an upper-body exoskeleton for promoting scapulohumeral rhythm[C]//2015 IEEE International Conference on Rehabilitation Robotics. Singapore, 2015: 538-542. DOI:10.1109/icorr.2015.7281255.
[6] Thalagala T D R G, Silva S D K C, Maduwantha L K A H, et al. A 4 DOF exoskeleton robot with a novel shoulder joint mechanism[C]//2016 IEEE/SICE International Symposium on System Integration. Sapporo, Japan, 2016: 132-137. DOI:10.1109/sii.2016.7843987.
[7] Liu C, Zhu C, Liang H B, et al. Development of a light wearable exoskeleton for upper extremity augmentation[C]//2016 23rd International Conference on Mechatronics and Machine Vision in Practice. Nanjing, China, 2016: 1-6. DOI:10.1109/m2vip.2016.7827318.
[8] Yalcin M, Patoglu V. Kinematics and design of AssistOn-SE: a self-adjusting shoulder-elbow exoskeleton[C]//2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics. Rome, Italy, 2012: 1579-1585. DOI:10.1109/biorob.2012.6290928.
[9] Zhang L Y, Li J F, Su P, et al. Improvement of human-machine compatibility of upper-limb rehabilitation exoskeleton using passive joints[J]. Robotics and Autonomous Systems, 2019, 112: 22-31. DOI:10.1016/j.robot.2018.10.012.
[10] Li J F, Liu J H, Zhang L Y, et al. Kinematics and dexterity analysis of the human-machine compatible exoskeleton mechanism for shoulder joint rehabilitation[J]. Journal of Mechanical Engineering, 2018, 54(3): 46-54. (in Chinese)
[11] Lin P Y,Shieh W B, Chen D Z. A theoretical study of weight-balanced mechanisms for design of spring assistive mobile arm support (MAS)[J]. Mechanism and Machine Theory, 2013, 61: 156-167. DOI:10.1016/j.mechmachtheory.2012.11.003.
[12] Wu Q C, Wang X S, Du F P. Development and analysis of a gravity-balanced exoskeleton for active rehabilitation training of upper limb[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016, 230(20): 3777-3790. DOI:10.1177/0954406215616415.
J. Bilateral and unilateral shoulder girdle kinematics during humeral elevation[J]. Clinical Biomechanics, 2006, 21: S20-S26. DOI:10.1016/j.clinbiomech.2005.09.009.
[14] Magermans D J, Chadwick E K J, Veeger H E J, et al. Requirements for upper extremity motions during activities of daily living[J]. Clinical Biomechanics, 2005, 20(6): 591-599. DOI:10.1016/j.clinbiomech.2005.02.006.
[15] Churchill E,Laubach L L, Mcconville J T, et al. Anthropometric source book. Volume 1: Anthropometry for Designers[M]. Houston: NASA. 1978: Ⅳ31-Ⅳ38.