In recent years, airplane crash cases all over the world have surged, one after another. Aspects on safety and reliability of aircraft systems have been investigated extensively. In particular, the importance of safety and reliability has always been a complex issue in aircraft science. The safety and reliability of aircraft have been the main focus of life cycle services, ranging from design and development to maintenance and operation. Due to the progress of technology development, civil aviation did profit from safe systems over the past years. Nevertheless, aircraft accidents and severe incidents did still occur. For example, at 08∶44 on March 10, 2019, a Boeing 737MAX belonging to Ethiopian airlines crashed, killing all 157 people, including eight crew members. It was the second Boeing 737MAX crash since October 2018. In the flight control field, the focus of the study is to develop more advanced control techniques that can prevent accidents in the future. The concept of aircraft fault tolerant control (FTC) [1-2] has been a frequently-used method in the field of aircraft research.
In this paper, we will not study the FTC of the vertical damaged aircraft. However, extensive research on FTC has been performed in both control oriented investigation and kinematics. In particular, a number of FTC-based methods have been applied in aerospace applications[3-5]. For example, Crider[6] investigated the aerodynamics of the aircraft controller design to accommodate the possible complete loss of the vertical tail. Bramesfeld et al.[7] discussed the piloting strategies for controlling a transport aircraft after loss of the vertical tail. Hitachi[8] investigated a damage-tolerant flight control system designed for propulsion-controlled aircraft (PCA). Hitachi et al.[9] developed a design of the robust PCA control system for vertical-tail-damaged aircraft by using the H∞-loop transfer recovery (H∞-LTR) technique and applied it to the Boeing-747 100/200 linearized model and nonlinear model. Li et al.[10] employed quadratic stabilization and guaranteed cost control to mitigate the damage.
In general cases, there are three primary types of faults: structural damage, actuator faults and sensor faults.However, compared with the analysis of actuator and sensor faults, there is little research on structural damage in the aerospace field[8,10-12]. The tolerant control for analyzing structural damage involves studying the engine loss, horizontal tail loss, vertical tail loss, the partial loss of wing, and so forth[6,13-14]. Various studies[3-5] were carried out tackling FTC methods for aircraft faults, where many FTCs for actuators or sensors were constructed. FTC addressed actuator faults and sensor faults[2,15].
Next, three examples are given to further understand the facts which were outlined above. The first example is the airbus A300 cargo plane, which had just taken off when Iraqi militiamen on the ground attacked it with shoulder-fired Russian SA-14 surface-to-air missiles; instantly, it lost all its hydraulics systems. The pilots managed to return to the airport, operating only with the engines[8]. The second example relates to American Airlines Flight AA191, where a McDonnell Douglas DC10 lost its left engine due to a partial loss of hydraulic system and subsequently crashed. The last incidence is the Japan Airlines Flight 123, which took off from Haneda airport in Tokyo to Itami airport in Osaka, due to the loss of its vertical tail and its hydraulics control. It crashed into the Mount Takamagahara on August 12, 1985[11].
Motivated by the above discussion,it is useful to investigate the fault-tolerant control capability related to such structural damage on control surfaces, lifting or air-frame. Sliding mode control (SMC) is a robust control method for nonlinear uncertain systems, which has attractive features to keep the systems insensitive to the uncertainties on the sliding surface. Furthermore, both the disturbances and the information of faults have been studied by using adaptive control strategies[5,16-20]. To make good use of the advantages of sliding mode control and fault tolerant control, a sliding mode fault-tolerant control method is designed for aircraft under model uncertainties[16], external disturbances and actuator faults. In finite time, they can accurately and rapidly track desired signals and stay there for all subsequent times.
Among different controller design methods, SMC is an efficient method, which is suitable for dealing with problems of incompletely modeled or uncertain systems. Numerous advantages on the basis of SMC are available for analyzing a damaged aircraft control system. Nevertheless, most of the techniques can only deal with the problems of uncertain moment inertia and external disturbances of aircraft, and few of them have explicitly addressed the damaged vertical tail faults. Therefore, it is important and necessary to develop a novel control method to handle damaged vertical tail faults during attitude maneuvers.
This paper will propose a fault-tolerant SMC strategy[21] for aircraft attitude stabilization under damaged vertical tail faults. For the first time, the novel sliding surface function is incorporated, in terms of both system states and inputs. Then, a sufficient condition, under which such type damaged aircraft system is stable, is proposed by means of the stringent linear matrix inequality (LMI) technique. By doing so, an adaptive kinematic sliding mode controller is designed for the aircraft with a damaged vertical tail, which can maintain the stability and reliability of the flight control system under different damage degrees. In order to demonstrate that the proposed schemes can guarantee the convergence of the closed-loop system’s state trajectories to the desired sliding switching in finite time and effectively weaken the chattering phenomenon for all subsequent time, the proposed control methods are applied to a conventional Boeing-747 100/200 model. Simulation results show the validity and efficiency of our proposed control methods. In other words, within the critical damage degree of the vertical tail, the aircraft still maintains stability.
1 Problem Formulation and Preliminaries
To simplify the vertical tail damage model, we need to provide the following assumption.
Hypothesis 1 In the X-Z plane as shown in Fig.1, the vertical tail damage is deemed to be symmetric. For this reason, it is hypothesized that it is negligible for the lateral center of gravity deviation caused by the damage. Simultaneously, compared with the total mass of the aircraft, we hypothesize that the mass loss caused by the vertical tail damage is ignored[10].
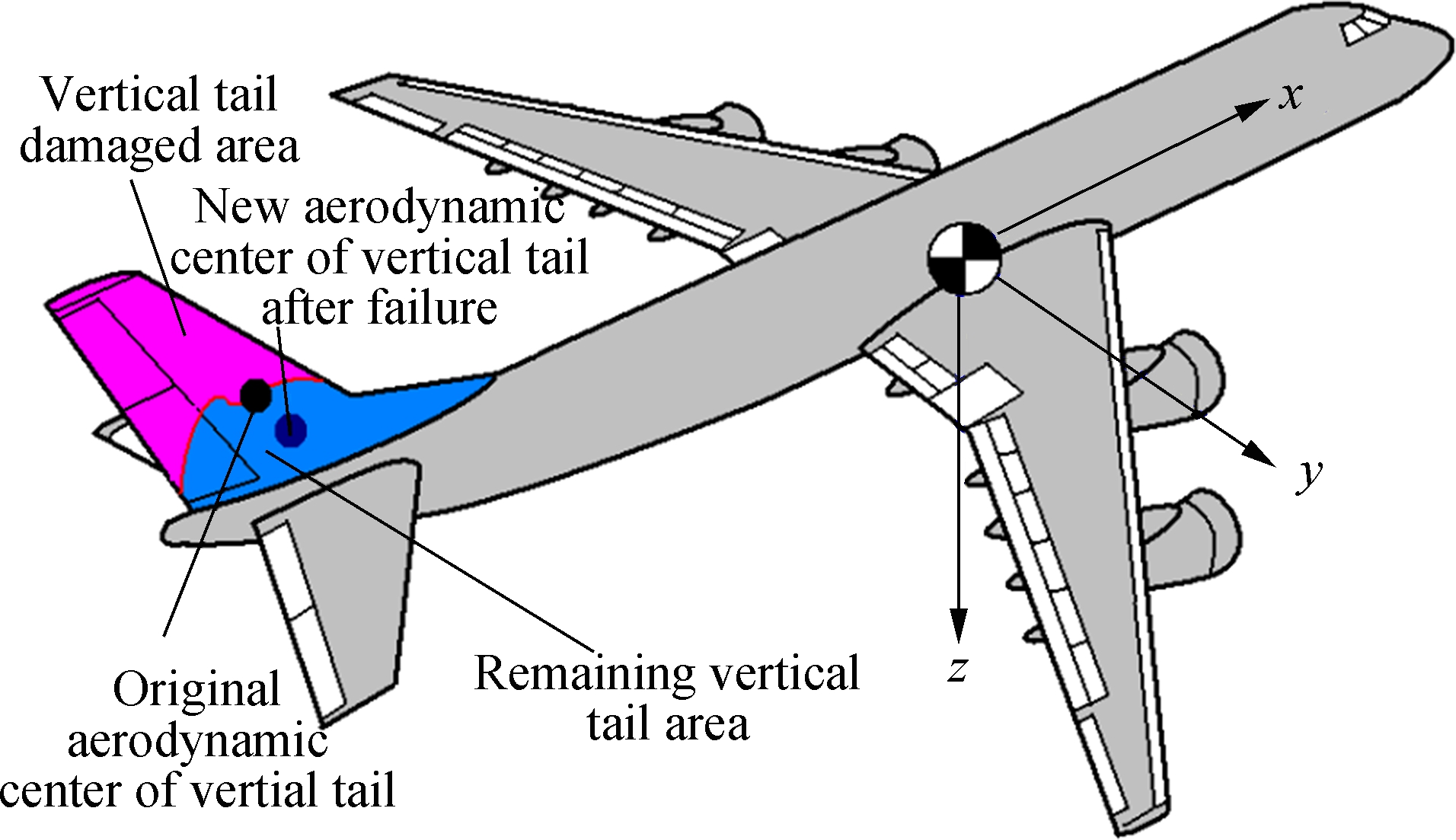
Fig.1 An aircraft with partial vertical tail loss, resulting in the aerodynamic center shift of vertical tail
1.1 Model of aircraft
In recent years, there has been excellent progress in the aircraft kinematics model. A standard method is considered a linearized model around a certain stable flight operation point. According to Ref.[22], the linearized state-space aircraft kinematics equation can be obtained:


(1)
where ![]() a14=-gcosθ0,
a14=-gcosθ0, 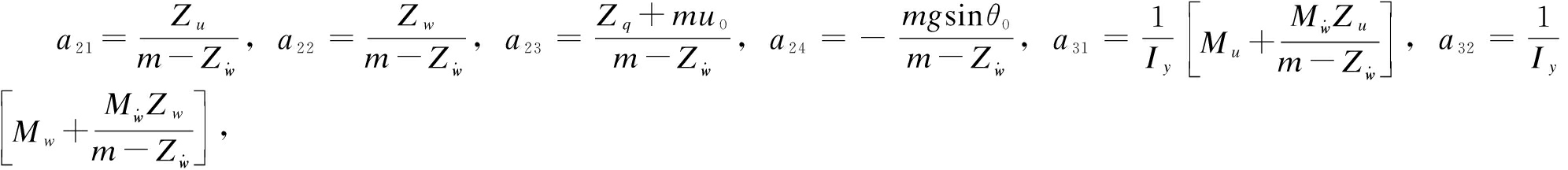 a33=
a33=![]() ,
, ![]() a58=gcosθ0,
a58=gcosθ0, 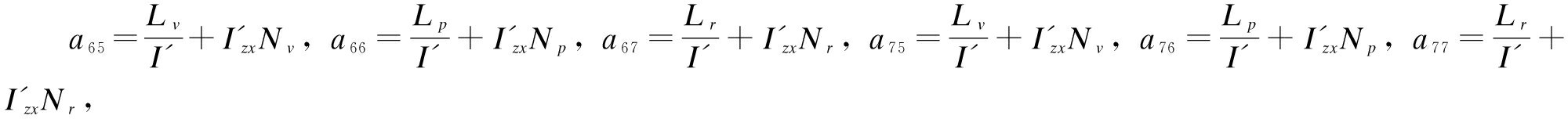 a87=tanθ0,
a87=tanθ0,  Define x(t)={u, w, q, θ, v, p, r, φ}T and u, v, w represent the longitudinal, lateral and vertical linear velocities along the axis of stability; θ, φ represent the pitch angle of aircraft and the bank angle of aircraft, respectively, and p, q, r are the body axis roll rate, pitch rate, and yaw rate, respectively. Let
Define x(t)={u, w, q, θ, v, p, r, φ}T and u, v, w represent the longitudinal, lateral and vertical linear velocities along the axis of stability; θ, φ represent the pitch angle of aircraft and the bank angle of aircraft, respectively, and p, q, r are the body axis roll rate, pitch rate, and yaw rate, respectively. Let ![]() and δe, δf, δa, δr denote the elevator, aileron, flap and rudder of the control surface deflections, respectively. Hence, the simplified form can be obtained as
and δe, δf, δa, δr denote the elevator, aileron, flap and rudder of the control surface deflections, respectively. Hence, the simplified form can be obtained as
(2)
where A and B are the homologous coefficient matrices given above.
1.2 Stability and control derivative estimation
Since aircraft is inevitably subjected to vertical tail damage, the stability and control derivatives (SACD) caused by the damage have to be studied. In the following lateral directional stability derivatives Cyβ, Cnβ, Clβ, Cyp, Cnp, Clp, Cyr, Cnr, Clr, the vertical tail damage triggers crucial parameter variations.
Let Δ express the damage-induced variation of derivatives. Consequently, a set of unknown derivative deviations can be described as ΔCyβ, ΔCnβ, ΔClβ, ΔCyp, ΔCnp, ΔClp, ΔCyr, ΔCnr, ΔClr.
The estimation of the considered SACD is rooted in an approach similar to Hitachi et al.’s work[8,10], where the deviation of the derivative value caused by the vertical tail loss, such as Cyβ, is represented as ΔCyβ. Moreover, parameter μ is introduced, which is the damage degree and it takes a value between 0 and 1. Deviation ΔCyβ is determined by vertical tail loss and it can be approximated as ![]() using the damage degree μ, where
using the damage degree μ, where ![]() represents the maximum damage case.
represents the maximum damage case.
An estimated representation of the derivative deviations with several hypotheses will be given based on Refs.[9, 23]. Above all, we hypothesize no shift in the center of gravity since the vertical tail damage/loss is deemed to be symmetric in the X-Z plane. Next, we assume that the mass loss caused by the vertical tail damage is negligible in comparison with the stability derivative deviations. The main conclusions of the estimated derivative deviation are as follows:

(3)
where μ is the parameter and it denotes the so-called degree of damage. Concretely speaking, μ=0 denotes the conventional case. 0<u<1 represents partial vertical tail loss. u=1 denotes the most serious damage on the tail loss, which means complete loss. We do not know if it is worth mentioning that the corresponding element marked with max superscript on the right side of the equation expresses the maximum derivative deviation in the case of the most severe vertical tail loss.
For illustration purposes, through the following example of the derivative deviation estimation on Clβ and Cnβ, we learn that each derivative deviation can be indicated as the maximum derivative deviation, which is factored by the percentage of vertical tail damage or the damage degree μ. In the same way, the detailed information of other stability derivatives can be obtained[8,10].
The parameter μ is introduced to denote the degree of damage: ![]() where ΔCyβ is the damage effect caused by the vertical tail loss and
where ΔCyβ is the damage effect caused by the vertical tail loss and ![]() is the maximum possible damage effect. Let b be the wing span and l and z are the horizontal and vertical positions of the aerodynamic center of the vertical tail, whose variations are denoted by Δl and Δz. Moreover, the changes of Clβ and Cnβ are accompanied by the changes of the homologous at the rolling and yawing moment, which can be described by the following equation:
is the maximum possible damage effect. Let b be the wing span and l and z are the horizontal and vertical positions of the aerodynamic center of the vertical tail, whose variations are denoted by Δl and Δz. Moreover, the changes of Clβ and Cnβ are accompanied by the changes of the homologous at the rolling and yawing moment, which can be described by the following equation:
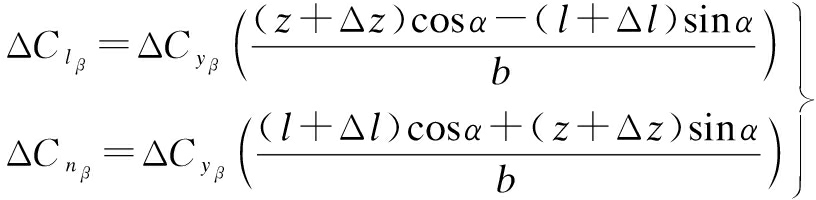
The maximum variations ![]() and
and ![]() can be defined as follows:
can be defined as follows:
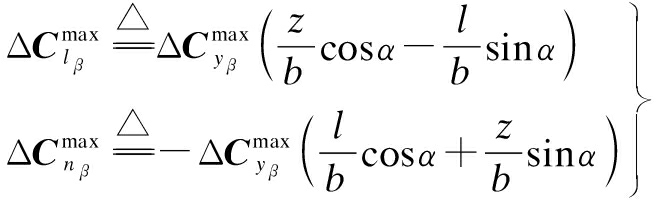
As we focus on small damage on the vertical tail in this paper, Δl and Δz are ignored in comparison with l and z, respectively. The approximations of changes of sideslip derivatives ![]() can be acquired. For the control derivatives, we assume that the rudder control actuator subsystem works normally under damage because we are concerned with the small damage to the vertical tail.
can be acquired. For the control derivatives, we assume that the rudder control actuator subsystem works normally under damage because we are concerned with the small damage to the vertical tail.
For a positive scalar ρ, ΔCyδr≈ρΔCyβ is hypothesized. Furthermore, when the vertical tail is completely damaged, i.e., Cyδr|μ=1=0, the effect of the rudder is completely lost. Hence, the following equation can be obtained:
We define
In addition,
Again, we define
and we can obtain
Through the depiction of a lateral stability derivative deviation matrix in Eq.(3), a parameterized model representation is acquired to treat the damaged aircraft kinematics. The creativity of the concept of damage degree μ allows for sliding mode FTC applications. By optimizing the damage degree value, it is possible to find the maximum allowable damage under the sliding mode FTC.
1.3 Damaged aircraft modeling
A parameterized damaged aircraft model is introduced as follows. The system (2) suffered from vertical tail damage. Simultaneously, considering disturbances and uncertainties, system (2) can be rewritten as
μ∈[0,1]
(4)
where d(t)∈R8×1 expresses the disturbance vector; A, B, ![]() D are the appropriate dimension matrices.
D are the appropriate dimension matrices. ![]() are as follows:
are as follows:
where
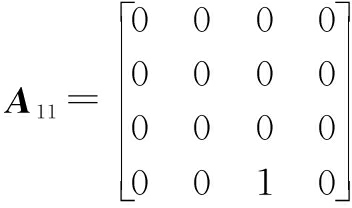
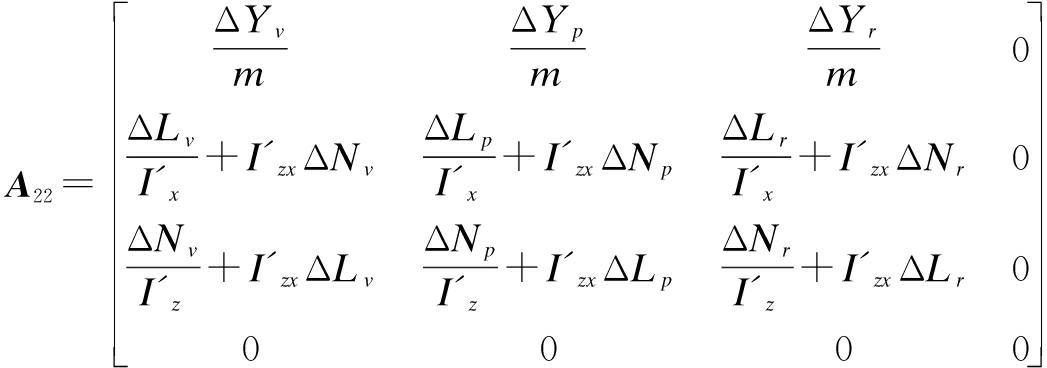
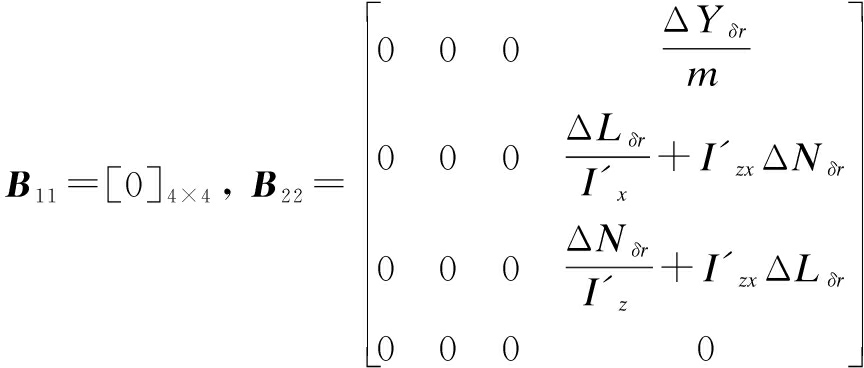
The following three equations list the maximum variations of dimensional aerodynamic derivatives[10].
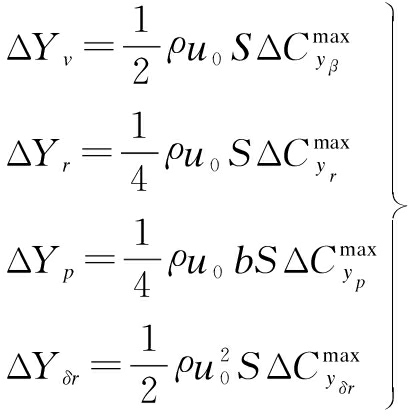


System (4) can be rewritten as the following form so as to handle the information of uncertainties and damage.
f(x,t)+Βu(t)+Dd(t)
(5)
where ![]() Here, one hypothesis needs to be provided for f(x,t).
Here, one hypothesis needs to be provided for f(x,t).
Hypothesis 2 It is hypothesized that ‖f(x,t)‖<F, where F is a constant which represents the boundlessness of disturbances and uncertainties.
Remark 1 As is known to all, lateral states are easily affected by vertical tail damage. For example, the roll rate p, pitch rate q, and yaw rate r change rapidly; hence, we choose y(t)={p,q,r}T as the tracking objective in this paper, that is
(6)
where C∈R3×8 denotes the control output distribution matrix.
2 Main Results
The purpose of FTC design is to ensure the stability of the system and maintain certain performance requirements when damage occurs. In addition, another method is to design an FTC for the flight system with structural damage under the condition of given initial attitude angular velocity, so that the attitude angular velocity can track the desired signal accurately and quickly.
2.1 Equivalent control
Regardless of disturbance and uncertainty, the controlled object is described as
(7)
The desired tracked objective is defined as yd={qd, pd, rd}T. Let e(t)=yd-y(t) be the tracking error vector and its derivative ![]() and then we design a sliding surface function as
and then we design a sliding surface function as
s(t)=Κe
(8)
where s(t)={s1(t),s2(t),s3(t),s4(t)}T; Κ∈R4×3. Based on the sliding mode control theory[24] with respect to the sliding surface, the derivative of s(t) can be obtained. Letting ![]() we obtain
we obtain
(9)
The equivalent controller is designed as
Βu(t)eq=-f(x,t)
(10)
2.2 Sliding mode control
In order to ensure that the sliding mode arrival condition is established, that is to say, ![]() (η>0), the switching control is designed,
(η>0), the switching control is designed,
Βusw=τs+σsign(s)
(11)
where τ=diag(τ1,τ2,τ3), σ=diag(σ1,σ2,σ3), ‖Dd(t)‖≤‖σ‖.
The sliding mode control law consists of the equivalent control term and switching control term,
Βu(t)=Βu(t)eq+Βu(t)sw
(12)
ΚC(-f(x,t)-τs-σsign(s)+f(x,t)-Dd(t))=
ΚC(-τs-σsign(s)-Dd(t))
(13)
Taking
(14)
then, we obtain
(15)
The Lyapunov function is chosen as ![]() s≡0. According to the LaSalle invariance principle, the closed-loop system is asymptotically stable. When t→∞, s→0.
s≡0. According to the LaSalle invariance principle, the closed-loop system is asymptotically stable. When t→∞, s→0.
Remark 2 The parameters Κ, τ, σ are introduced to improve the flexibility of the sliding surface.
Remark 3 In this paper, one novel function, namely, the hyperbolic tangent function, will take the place of the signum function in the controller, which can weaken chattering generated by sliding mode switching. Additionally, parameter ξ can adjust the speed of convergence of sliding surface, its value determines the change speed of inflexion point of hyperbolic tangent smooth function, that is, the convergence speed of the sliding surface is accelerated with the increase of ξ. Better yet, no one in the field has done that.
(16)
It is easy to prove that the state switching is faster when ξ becomes larger.
Remark 4 From Fig.2, it is easy to see that the hyperbolic tangent function curve is smooth. The nature of the hyperbolic tangent function is better than that of the signum function and saturation function. This is a simple way to weaken the chattering generated by the switch function.
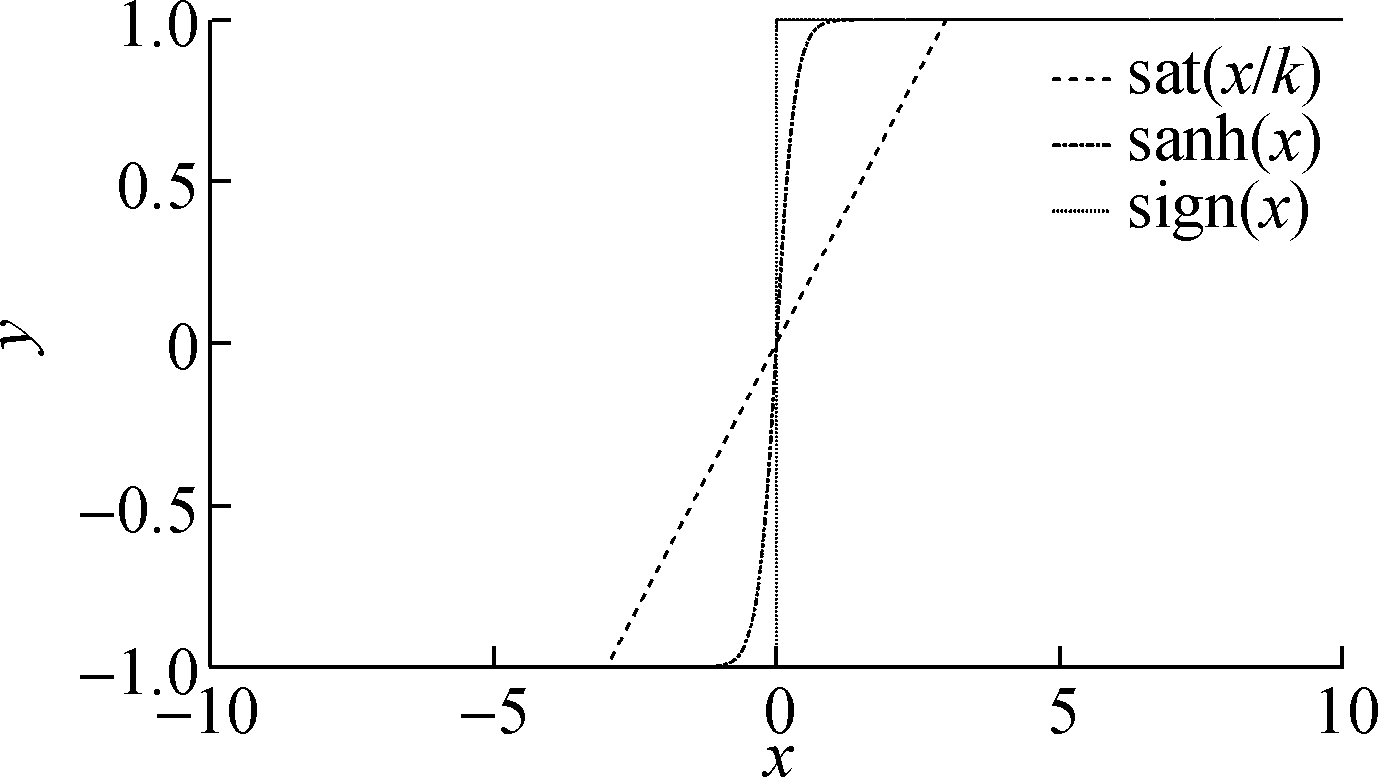
Fig.2 Comparison of three curves
Lemma 1[25] For any given s(t), there is ξ>0, and there is inequality.
(17)
Lemma 2[26] The following inequality holds for any ξ>0 and any given s(t)∈R:
(18)
where ζ is a constant satisfying ζ=e-(ζ+1)≈0.278 5.
Lemma 3[27] For V∶[0,∞)∈R, the solution of inequality equation ![]() ∀t≥t0≥0 is
∀t≥t0≥0 is
V(t)≤e-α(t-t0)V(t0)+![]() e-α(t-t0)f(τ)dτ
e-α(t-t0)f(τ)dτ
(19)
where α is an arbitrary constant.
2.3 Sliding mode control based on hyperbolic tangent function
(20)
According to Lemma 2, it can be obtained that
(21)
![]()
(22)
It is further known that
![]()
(23)
Designing
(24)
we can obtain that
(25)
where χ=τ‖ΚC‖; γ=-‖ΚC‖σηξ.
Based on Lemma 3, the solution of inequality equation ![]() is
is
(26)
Hence ![]() the sliding mode surface function and the controller are uniformly asymptotically stable.
the sliding mode surface function and the controller are uniformly asymptotically stable.
Remark 5 For the system (6) with the structural damage, the designed adaptive kinematic sliding mode fault-tolerant controller (12), (20) and (24) can not only compensate for the disturbances or uncertainties faultlessly but also have the tolerance capacity with the flight control system under a damage case.
3 Simulation
3.1 Flight conditions and data
To demonstrate the validity and effectiveness of the proposed method, we applied it on the Boeing-747 100/200 model[5,10], the kinematic model of which is described in Eq.(26). The data is listed as follows: The altitude is 6 096 m; air density is 0.653 5 kg/m3; speed is 204.59 m/s; wing area is 510.95 m2; wing span is 59.74 m; wing mean chord is 8.32 m; mass is 288 969 kg; air velocity is 204.59 m/s; thrust is 44 770 N; pressure ratio is 0.469 5; Ixx=2.859×109 kg/m2; Iyy=5.199 7×109 kg/m2; Izz=7.807×109 kg/m2; Ixz=1.523 7×108 kg/m2.
The aircraft parameters and derivatives are listed in Tab.1. The estimation of changes of stability and control derivatives are listed: ![]()
Tab.1 Aircraft parameters and derivatives
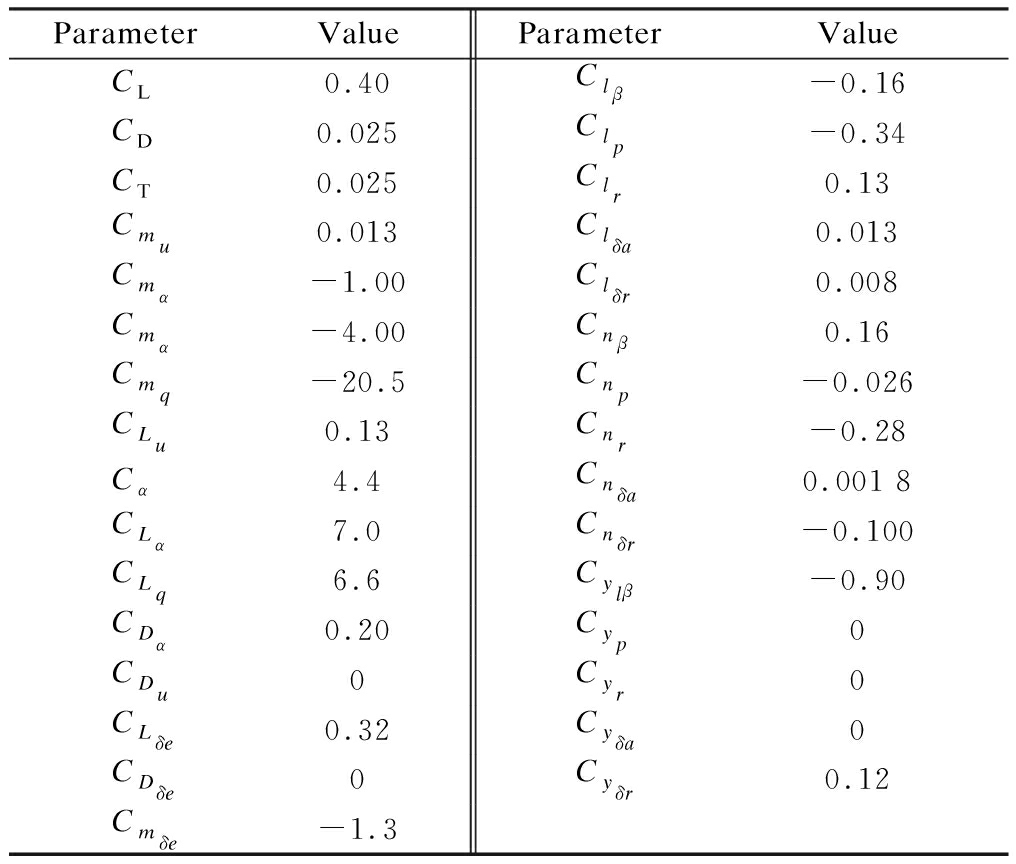
ParameterValueParameterValueCL0.40Clβ-0.16CD0.025Clp-0.34CT0.025Clr0.13Cmu0.013Clδa0.013Cmα-1.00Clδr0.008Cmα-4.00Cnβ0.16Cmq-20.5Cnp-0.026CLu0.13Cnr-0.28Cα4.4Cnδa0.001 8CLα7.0Cnδr-0.100CLq6.6Cylβ-0.90CDα0.20Cyp0CDu0Cyr0CLδe0.32Cyδa0CDδe0Cyδr0.12Cmδe-1.3
![]() The tracking objective is taken as yd=[qd, pd, rr]=[0 0 0]T rad/s and some parameters are referred to Ref.[10].
The tracking objective is taken as yd=[qd, pd, rr]=[0 0 0]T rad/s and some parameters are referred to Ref.[10].
(26)
where
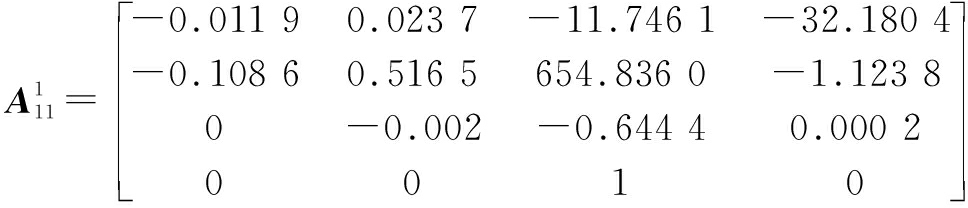
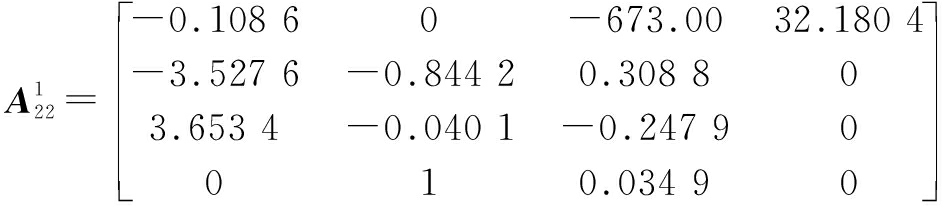





3.2 Controller design results
The kinematic sliding mode surface matrices are chosen:
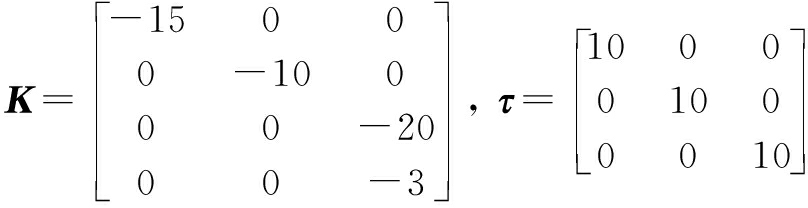

Also, the control outputs are chosen as

The state tracking trajectories and tracking error of ![]() of the closed loop system are depicted in Fig.3 and Fig.4, respectively. It is obvious that the state trajectory can track the ideal trajectory quickly at the beginning. Although there is a small error at zero point, the error decreases to zero almost immediately.
of the closed loop system are depicted in Fig.3 and Fig.4, respectively. It is obvious that the state trajectory can track the ideal trajectory quickly at the beginning. Although there is a small error at zero point, the error decreases to zero almost immediately.
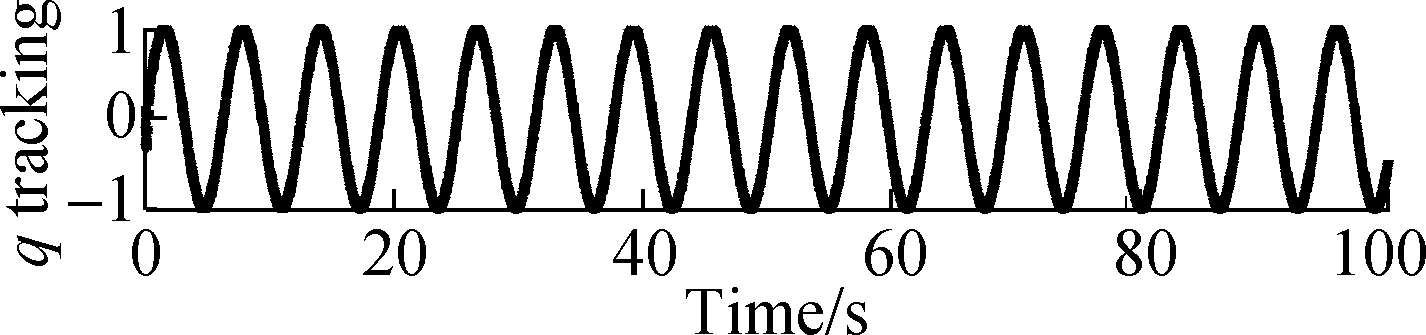
(a)
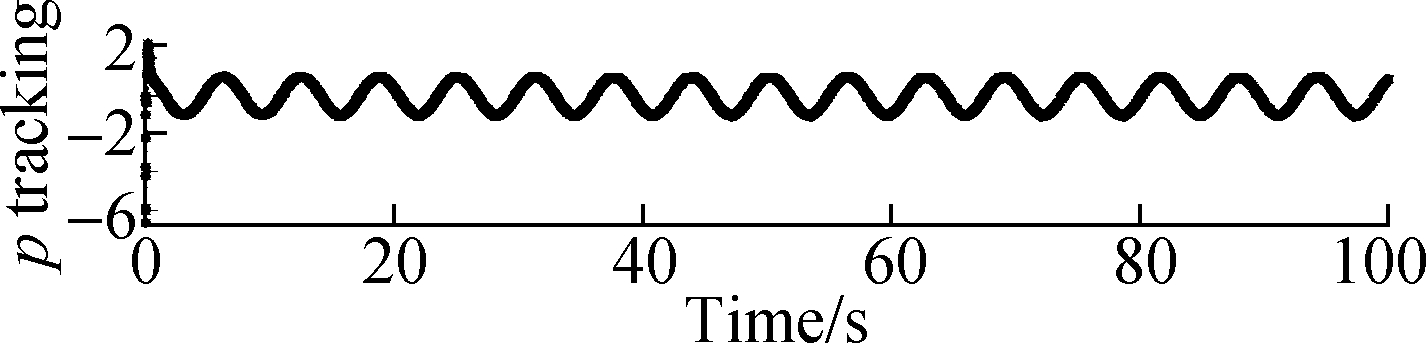
(b)
(c)
Fig.3 Tracking trajectories of a closed loop state response. (a) Tracking trajectories of roll when qd=sin(t); (b) Tracking trajectories of pitch when pd=cos(t); (c) Tracking trajectories of yaw when rd=-5
Different damage cases are considered to occur at 1 s as μ=0, 0.25, 0.35, 0.45, 0.55, 0.60, and the corresponding simulation results are depicted in Fig.5 to Fig.12, which show the time responses of attitude rates p, q and r between the cases of the free damage and different damage degrees.
It is easily seen from Fig.5 and Fig.6 that the responses of attitude roll, pitch and yaw rates can track the desired signals in the structural damage cases of μ=0 and μ=0.15, respectively. Obviously, when μ=0, that is, the convergence speed of the attitude angle of the aircraft without damage is quite instantaneous; when μ=0.15, the attitude angle tends to be stable at about 1 s, converging to 0.
(a)
(b)
(c)
Fig.4 Tracking error. (a) Tracking error of roll; (b) Tracking error of pitch; (c) Tracking error of yaw
(a)
(b)

(c)
Fig.5 Responses of roll, pitch and yaw rates when μ=0. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate

(a)
(b)
(c)
Fig.6 Responses of roll, pitch and yaw rates when μ=0.15. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
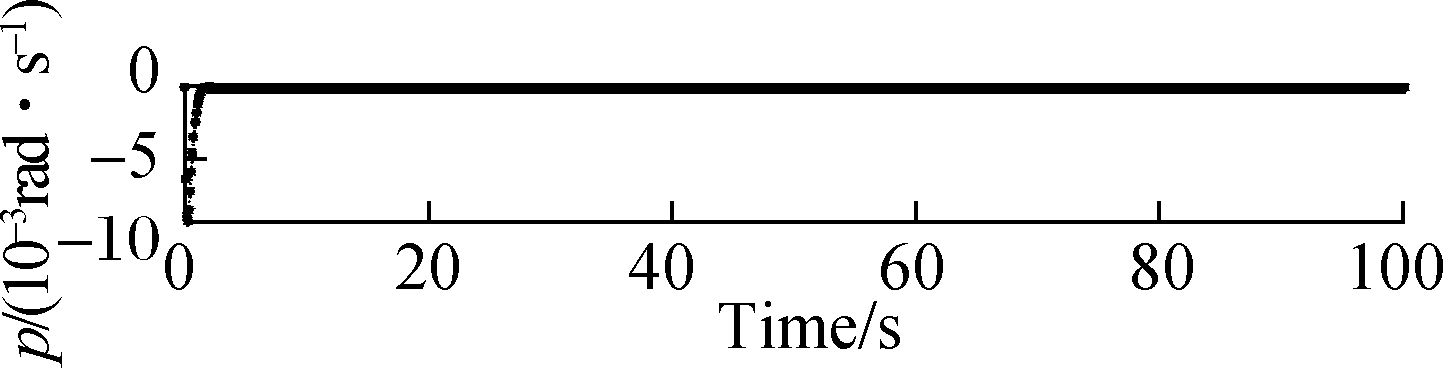
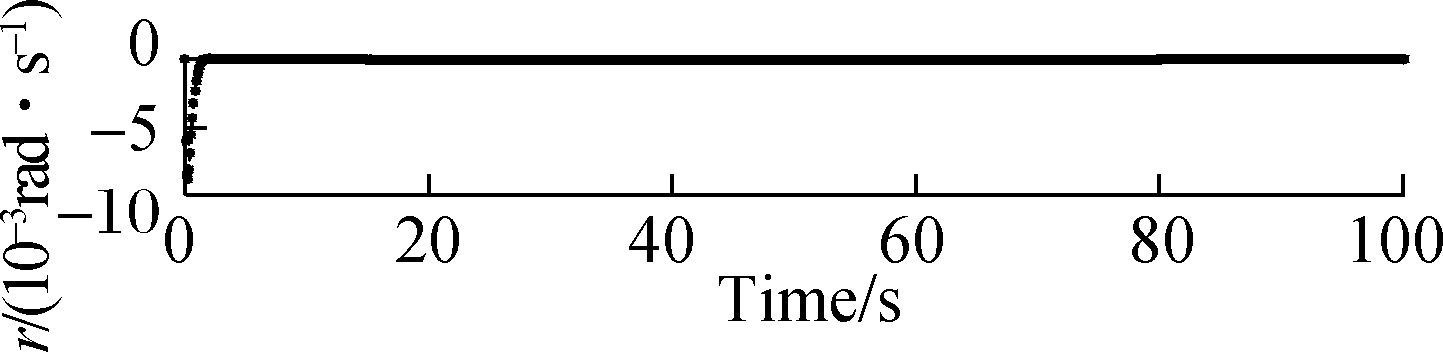
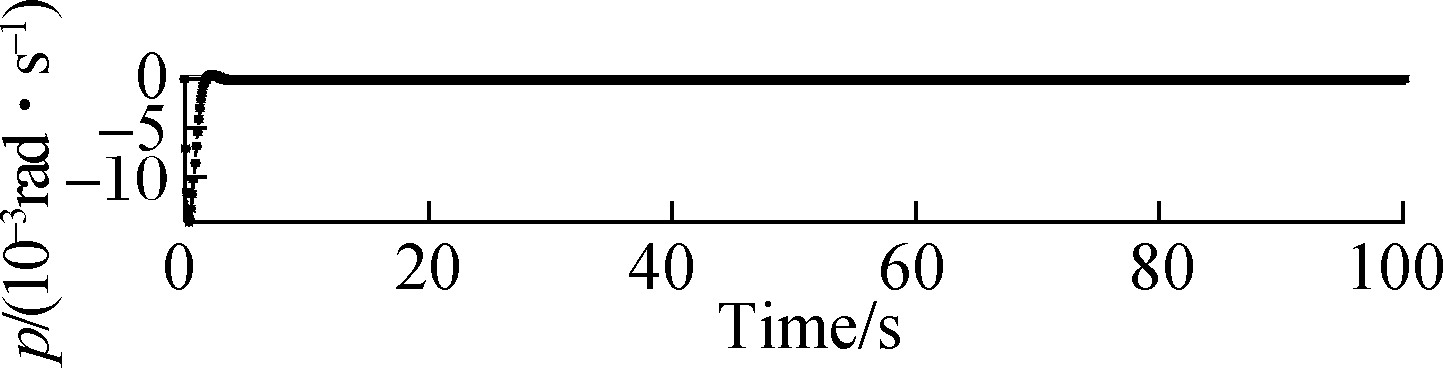
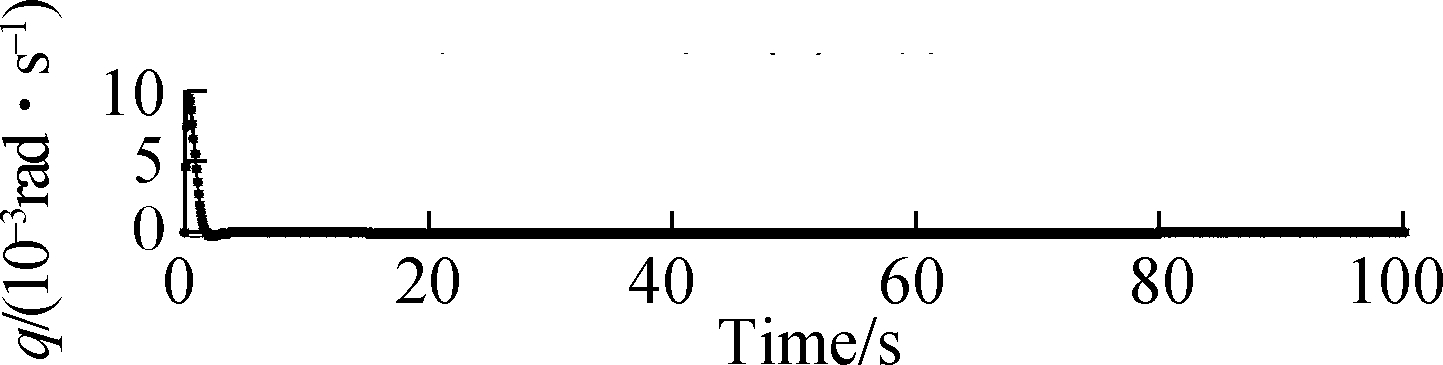
As depicted in Fig.7 and Fig.8,the attitude roll, pitch and yaw rates can be tracked preferably when the damage degree increases to μ=0.25 and μ=0.35, respectively, and the accommodation time needs 2 and 3 s. Generally speaking, the proposed method can make q, p and r track the desired signal at 2 s when μ=0.25 and at 3 s when μ=0.35. At about 3 s, the state tracking reaches the ideal state. However, as μ increases, the amplitude of the state response increases with a rate of 0.01 rad/s. It is worth mentioning that although the amplitude of the state response is increasing, it is still very small, which can be compensated for successfully based on the proposed FTC method.
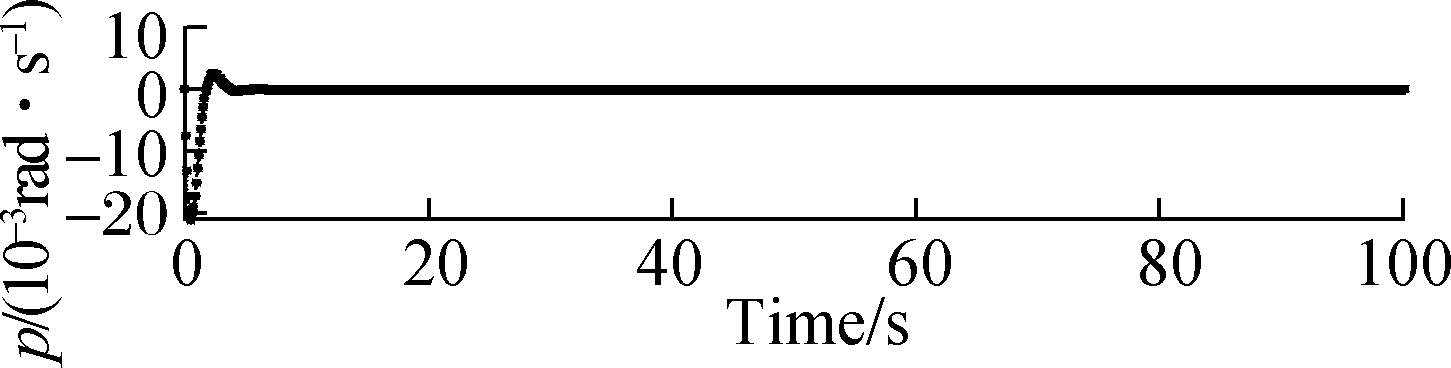
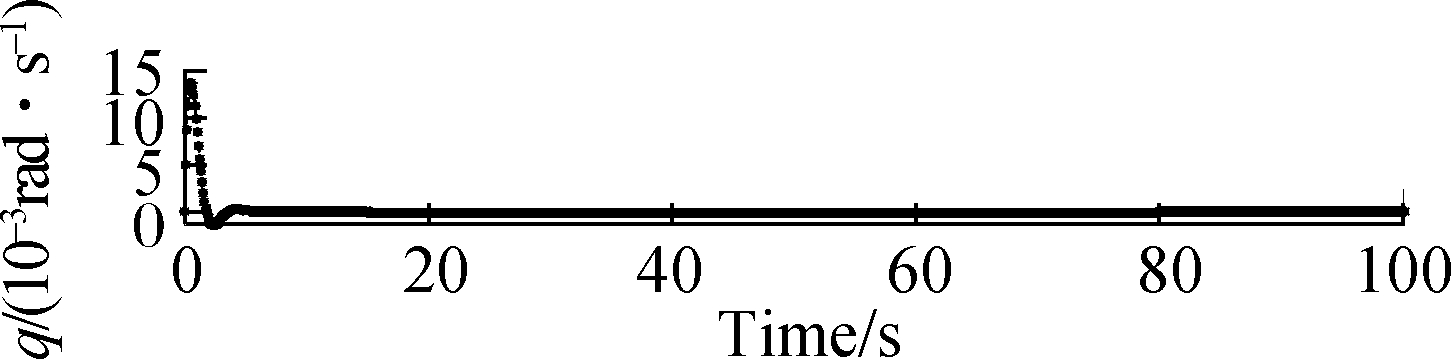
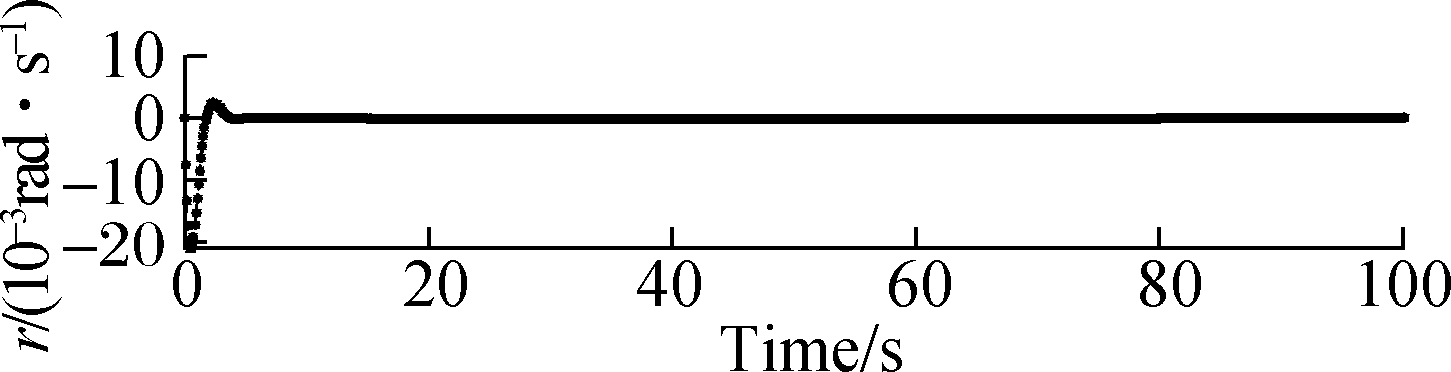
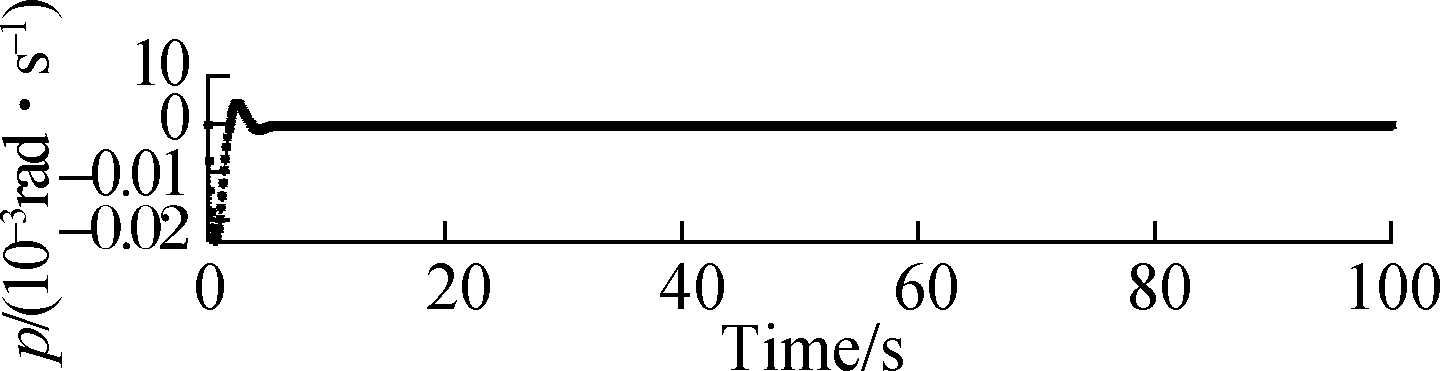
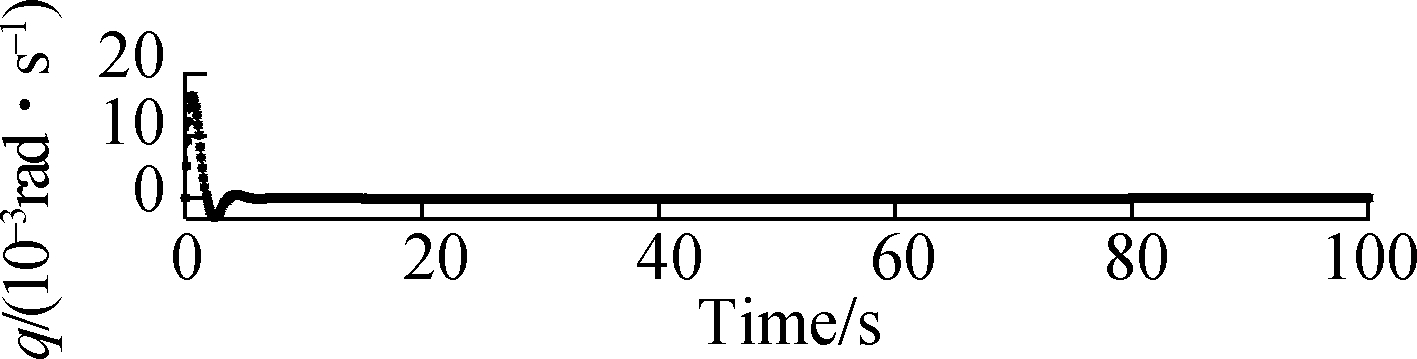
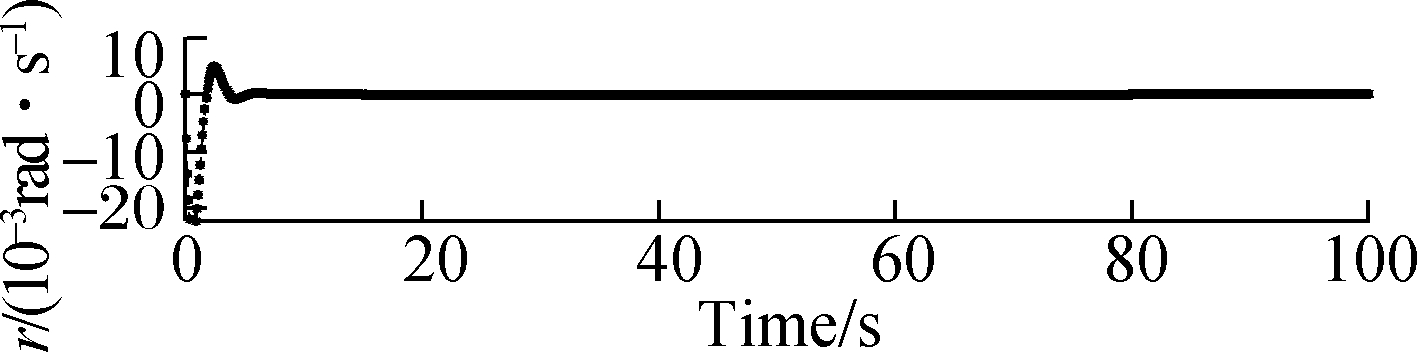
Fig.9 and Fig.10 show that the responses of the atti-tude roll, pitch and yaw rates can commendably track the desired signals in the structural damage cases of μ=0.45 and μ=0.50. When μ=0.45 and μ=0.50, the accommodation time needs 6 s, and the amplitude of the state response significantly increases by about 0.02 rad/s. Also, there is oscillation in the state trajectory.
(a)

(b)
(c)
Fig.7 Responses of roll, pitch and yaw rates when μ=0.25. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
(a)
(b)

(c)
Fig.8 Responses of roll, pitch and yaw rates when μ=0.35. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
(a)
(b)
(c)
Fig.9 Responses of roll, pitch and yaw rates when μ=0.45. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
(a)
(b)
(c)
Fig.10 Responses of roll, pitch and yaw rates when μ=0.50. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
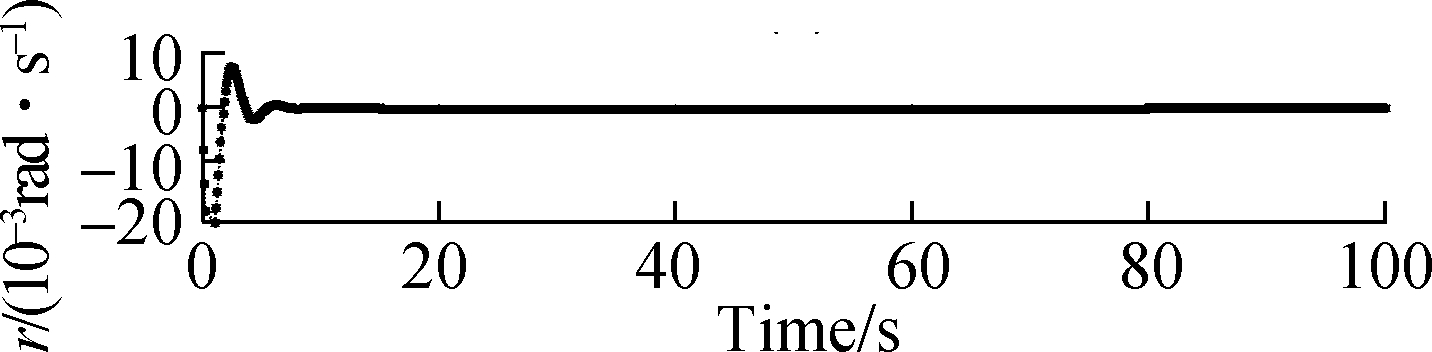
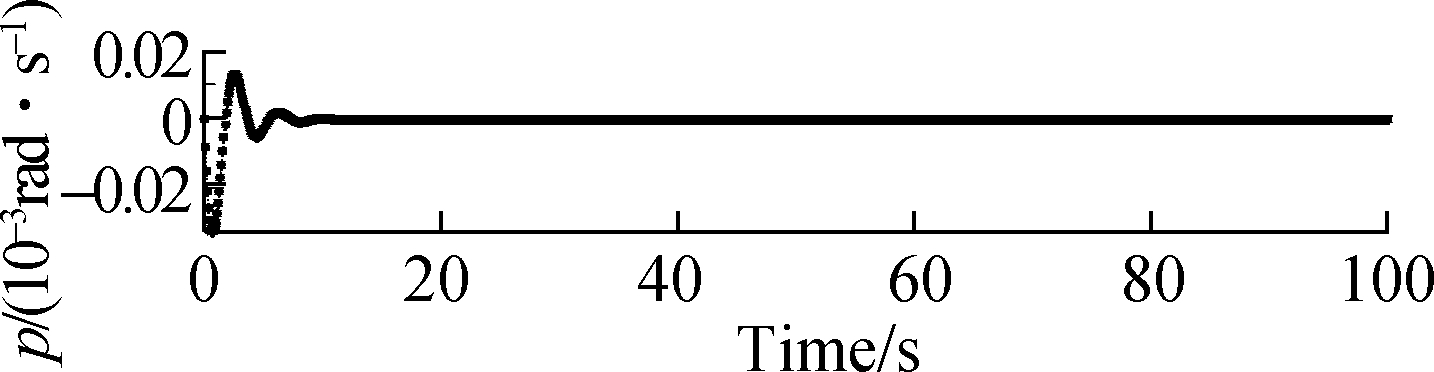
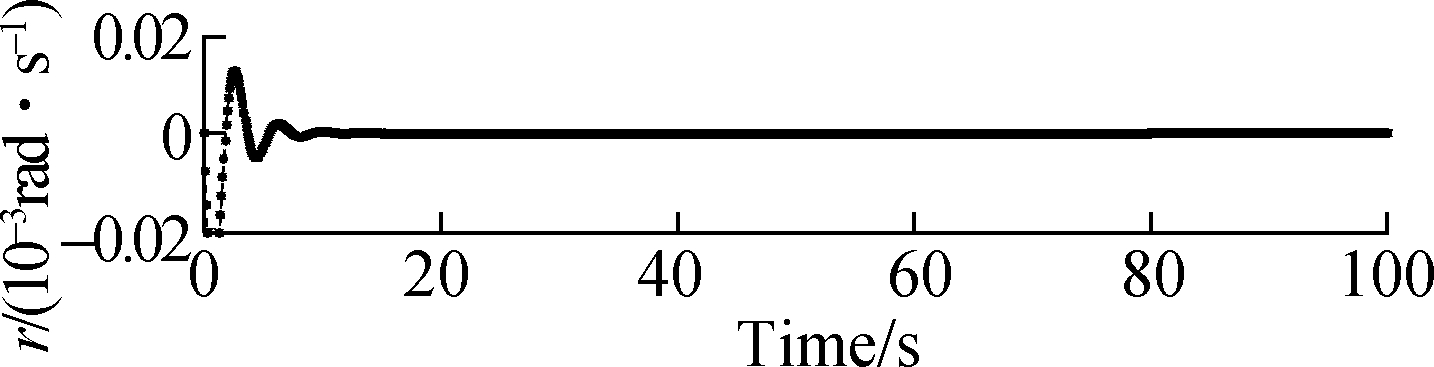
Not only more accommodated time of these two cases is needed but also the amplitude of the state response significantly increases, that is, the proposed method can still finally track the system in the cases of μ=0.55 and μ=0.60. Fig.11 and Fig.12 show that the responses of the attitude roll, pitch and yaw rates can commendably track the desired signals in the structural damage cases of μ=0.55 and μ=0.60. The accommodation time needs 10 s and the amplitude of the state response significantly increases by about 0.03 rad/s. Also, chattering occurs, which is detrimental for aircraft flight. Hence, from Fig.5 to Fig.12, we can draw the conclusion that when the damage degree is larger than 0.50 and increases to 0.60, the targets cannot be tracked well. Simultaneously, we can draw another conclusion that the proposed method can allow the target to be tracked within 1 rad/s in the case of structural damage as damage degree μ∈[0,0.5]; when damage is greater than 0.5, that is, μ∈(0.5,0.6], although the target can be finally tracked, the amplitude of the state response is rather large beyond the required range of the flight control system. Especially, when the amplitude of the roll rates is larger than 1.2 rad/s and the accommodation time is quite long when μ=0.60.
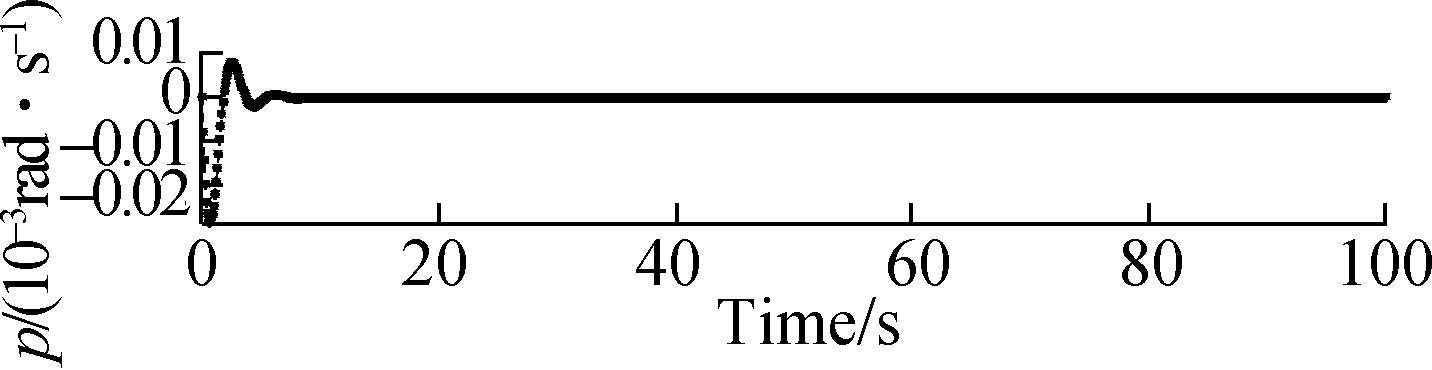
(a)

(b)
(c)
Fig.11 Responses of roll, pitch and yaw rates when μ=0.55. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
(a)

(b)
(c)
Fig.12 Responses of roll, pitch and yaw rates when μ=0.60. (a) Response of roll rate; (b) Response of pitch rate; (c) Response of yaw rate
Fig.13 depicts the dynamics of the sliding function. Fig.14 depicts the dynamics of the dynamic sliding mode controller. Through the above analysis, it is not difficult to obtain the results that as damage increases. The tracking time has not increased too much, which proves that the adaptive fault tolerant sliding mode control technology has a strong robustness and is extremely insensitive to external interference.
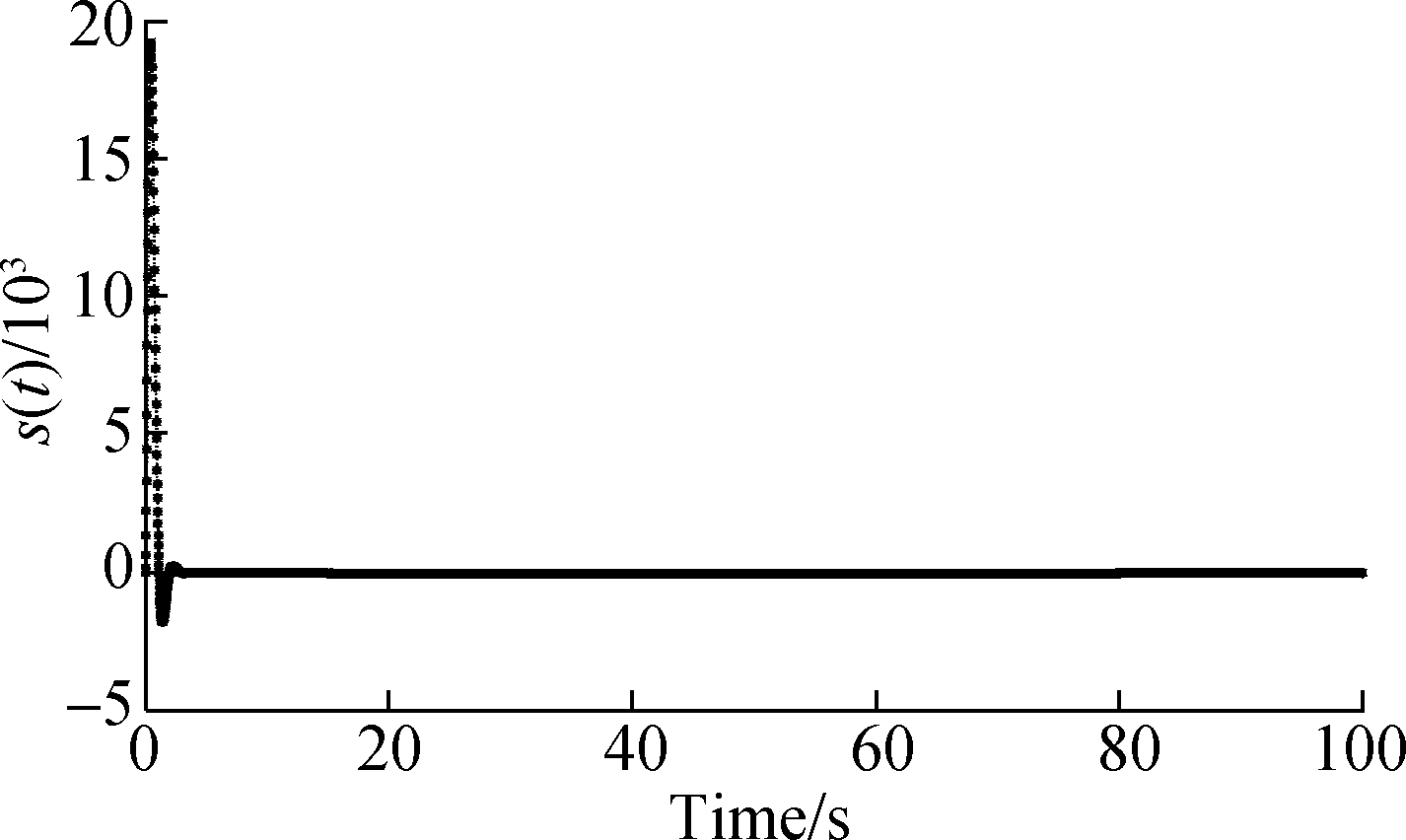
Fig.13 Sliding mode controller
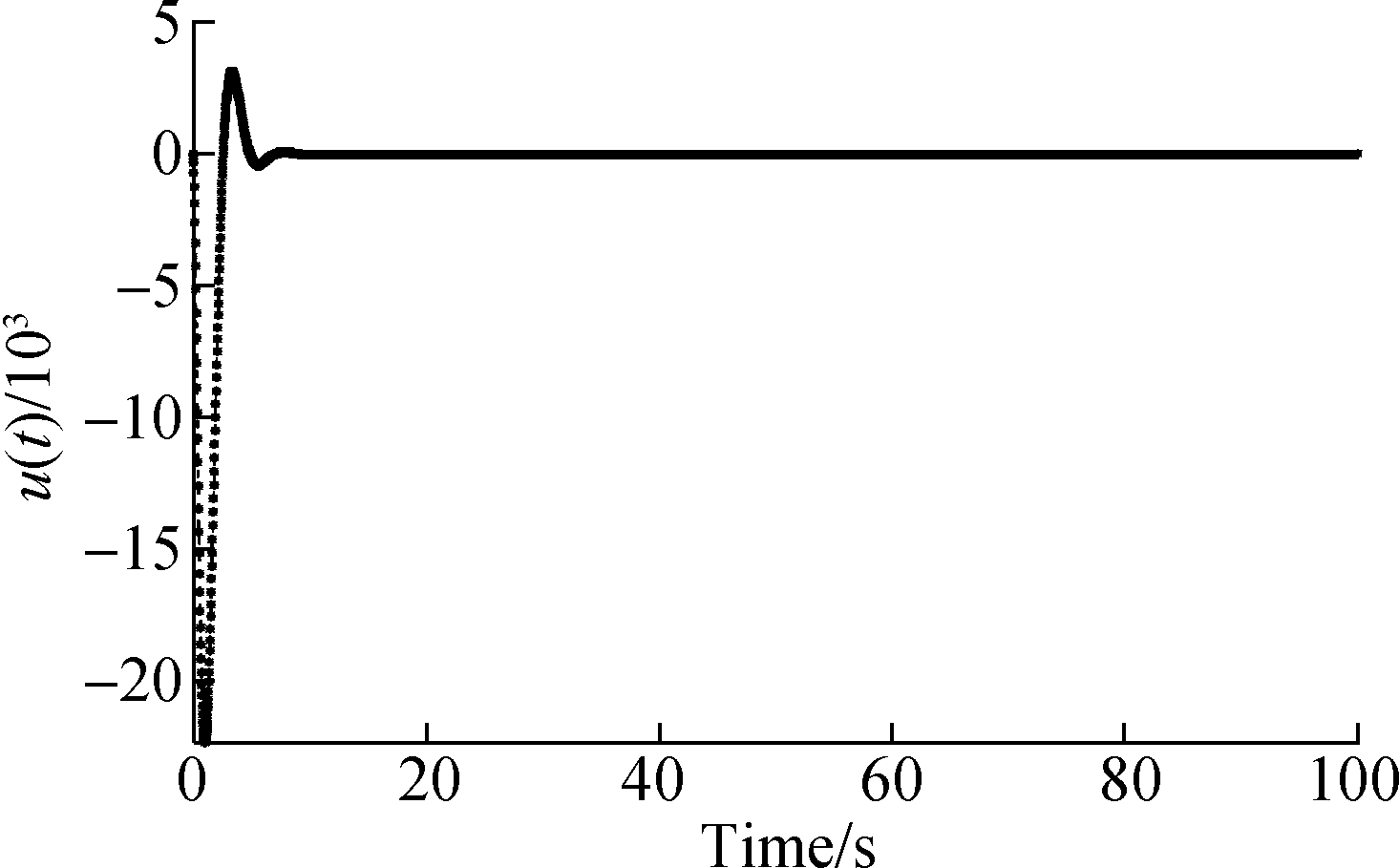
Fig.14 Sliding surface function
4 Conclusion
This paper investigates the adaptive equivalent sliding mode FTC for damaged aircraft, in particular, for the vertical tail damage or loss, based on a novel sliding surface. At the same time, the impact of external disturbances is considered. First, the damaged aircraft model is introduced, and a novel nonlinear sliding surface function is given. Then, by using the linear matrix inequality technique, a sufficient condition is proposed for the linear parameter-dependent model. Furthermore, an adaptive sliding mode FTC is designed for the damaged aircraft. In order to demonstrate the efficiency of the designed methods for the damaged system, an example of a Boeing-747 100/200 model is given. The simulation results reveal that the proposed adaptive sliding mode FTC is quite robust and can also change flight body damage cases within 10 s when the damaged degree ranges from 0 to 0.60. However, the buffeting is now weaker, but it still exists. The tolerance of the proposed methods in this paper has some limitations which need to be tackled in the future. In other words, the controller maintains stability and desired performance even when the aircraft is in trouble. In future work, we will focus on the goal of design improvement, which should aim at minimizing the chattering and enhancing tolerance of damage degree.
[1] Hu Q L, Xiao B. Fault-tolerant sliding mode attitude control for flexible spacecraft under loss of actuator effectiveness [J]. Nonlinear Dynamics, 2011, 64(1/2): 13-23. DOI:10.1007/s11071-010-9842-z.
[2] Yu X, Jiang J. Fault-tolerant flight control system design against control surface impairments [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1031-1051. DOI:10.1109/taes.2012.6178047.
[3] Li H, Wu L, Si Y,et al. Multi-objective fault-tolerant output tracking control of a flexible air-breathing hypersonic vehicle[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2010, 224(6): 647-667. DOI:10.1243/09596518jsce1002.
[4] Shen Q, Jiang B,Cocquempot V. Fault diagnosis and estimation for near-space hypersonic vehicle with sensor faults[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2012, 226(3): 302-313. DOI:10.1177/0959651811421227.
[5] Zhao J, Jiang B, Shi P,et al. Fault-tolerant control design for near-space vehicles based on a dynamic terminal sliding mode technique[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2012, 226(6): 787-794. DOI:10.1177/0959651812437624.
[6] Crider L. Control of commercial aircraft with vertical tail loss[C]//AIAA 4th Aviation Technology, Integration and Operations (ATIO) Forum. Chicago, IL, USA, 2004. DOI:10.2514/6.2004-6293.
[7] Bramesfeld G, Maughmer M D, Willits S M. Piloting strategies for controlling a transport aircraft after vertical-tail loss[J]. Journal of Aircraft, 2006, 43(1): 216-225. DOI:10.2514/1.13357.
[8] Hitachi Y. Damage-tolerant control system design for propulsion-controlled aircraft [D]. Toronto, Canada: University of Toronto, 2009.
[9] Hitachi Y, Liu H.H-infinity-LTR technique applied to robust control of propulsion-controlled aircraft[C]//AIAA Guidance, Navigation, and Control Conference. Chicago, IL, USA, 2009. DOI:10.2514/6.2009-6176.
[10] Li X B, Liu H H T. A passive fault tolerant flight control for maximum allowable vertical tail damaged aircraft[J]. Journal of Dynamic Systems, Measurement, and Control, 2012, 134(3): 031006. DOI:10.1115/1.4005512.
[11] Verhaegen M, Kanev S, Hallouzi R, et al. Fault tolerant flight control—A survey [M]. Berlin, Germany: Springer-Verlag, 2010. DOI:10.1007/978-3-642-11690-2-2.
[12] Yu X, Li P, Zhang Y M. The design of fixed-time observer and finite-time fault-tolerant control for hypersonic gliding vehicles[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4135-4144. DOI:10.1109/tie.2017.2772192.
[13] Hallouzi R, Verhaegen M. Fault-tolerant subspace predictive control applied to a Boeing 747 model[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4): 873-883. DOI:10.2514/1.33256.
[14] Hajiyev C, Caliskan F. Fault diagnosis and reconfiguration in flight control systems [M]. Boston, MA, USA: Springer-Verlag, 2003. DOI:10.1007/ 978-1-4419-9166-9.
[15] Isermann R. Fault-diagnosis systems: An introduction from fault detection to fault tolerance [M]. Berlin, Germany: Springer-Verlag, 2006. DOI: 10.1007/3-540-30368-5.
[16] Gao Z F, Jiang B, Shi P, et al. Active fault tolerant control design for reusable launch vehicle using adaptive sliding mode technique[J]. Journal of the Franklin Institute, 2012, 349(4): 1543-1560. DOI:10.1016/j.jfranklin.2011.11.003.
[17] Hu Q L. Robust adaptive sliding mode attitude maneuvering and vibration damping of three-axis-stabilized flexible spacecraft with actuator saturation limits[J]. Nonlinear Dynamics, 2009, 55(4): 301-321. DOI:10.1007/s11071-008-9363-1.
[18] Li P, Yu X, Zhang Y M, et al. Adaptive multivariable integral TSMC of a hypersonic gliding vehicle with actuator faults and model uncertainties[J]. ASME Transactions on Mechatronics, 2017, 22(6): 2723-2735. DOI:10.1109/tmech.2017.2756345.
[19] Yang H J, Xia Y Q, Fu M Y, et al. Robust adaptive sliding mode control for uncertain delta operator systems[J]. International Journal of Adaptive Control and Signal Processing, 2009, 24(8): 623-632. DOI:10.1002/acs.1154.
[20] Zhang J H, Shi P, Xia Y Q. Robust adaptive sliding-mode control for fuzzy systems with mismatched uncertainties[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(4): 700-711. DOI:10.1109/tfuzz.2010.2047506.
[21] Gao J, Shen Q, Yang P, et al. Sliding mode fault tolerant control with prescribed performance[J]. International Journal of Innovative Computing, Information and Control, 2017, 13(2): 687-694.
[22] Etkin B, Reid L D. Dynamics of flight: Stability and control [M]. New York, USA: John Wiley and Sons, Inc., 1996.
[23] Roskam J. Methods for estimating stability and control derivatives of conventional subsonic airplanes[P]. Lawrence, Kansas, USA: The University of Kansas, 1971.
[24] Utkin V I. Sliding modes in control and optimization [M]. Berlin, Germany: Springer-Verlag, 1992. DOI:10.1007/ 978-3-642-84379-2.
[25] Aghababa M P, Akbari M E. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances[J]. Applied Mathematics and Computation, 2012, 218(9): 5757-5768. DOI:10.1016/j.amc.2011.11.080.
[26] Polycarpou M M, Ioannou P A. A robust adaptive nonlinear control design[J]. Automatica, 1996, 32(3): 423-427. DOI:10.1016/0005-1098(95)00147-6.
[27] Ioannou P A, Sun J. Robust adaptive control [M]. New Jersey, NJ, USA: Prentice-Hall, 1996. DOI:10.1007/978-1-4471-5102-9-118-1.