Functionally graded (FG) materials have been encountered in a wide range of engineering applications due to the fact that their properties can vary continuously along one or two specific directions. The emerging micro-science has produced FG microstructures with various functions, which have the potential to be applied to micro electro mechanical system (MEMS) devices[1-2]. Thus, it is of practical significance to investigate the mechanical behavior and deformation characteristics of FG microstructures since their size-dependent properties have been observed from the experiments[3].
In recent years, the strain gradient elasticity[4] and modified couple stress theories (MCST)[5] have been used to deal with the real case problems of FG microstructures because the traditional mechanics theory is neither adequate to evaluate the accurate mechanical behaviors nor adequate to justify the size effect of microstructures. Accordingly, much literature has covered the linear size-dependent vibrations; i.e., bending and buckling of FG micro-beams and micro-plates. For instance, Ke et al.[6] studied the deflection, critical buckling load and natural frequencies of FG micro plates based on the MCST and Mindlin plate theory. The influences of the material length scale parameter, gradient index and inner-to-outer radius ratio on the mechanical behaviors were investigated. Lei et al.[7] developed a size-dependent FG beam model by using the strain gradient elasticity theory and sinusoidal shear deformation theory. Also, the influences of the material length scale parameter, different material compositions, and shear deformation on the bending and free vibration behavior of FG micro-beams were investigated. Thai et al.[8] investigated the static bending, buckling and free vibration behaviors of both the homogeneous core and FG skins micro-beams and the FG core and homogeneous skins microbeams. Abazid et al.[9] investigated the size-dependent bending response of the functionally graded piezoelectric micro-plate that is subjected to an external mechanical load, electric voltage and elevated temperature.
The investigations of the mechanical properties of FG microstructures covered not only the linear bending[10-11], buckling[12] or vibrations[13-15] but also the nonlinear characteristics such as the geometric-type nonlinearities and material nonlinearities. The geometric-type nonlinearities of FG microstructures were widely taken into consideration in literature[16-22] while the material nonlinearities have gradually attracted more attention. For example, Hamed[23] proposed a viscoelastic nonlinear theoretical model for the functionally gradient beam-column, and studied the redistribution of stress and strain over time and the creep buckling response. Ebrahimi et al.[24] studied the damped vibration characteristics of functionally graded viscoelastic nanobeams based on the theory of non-local strain gradient elasticity. Ghayesh[25] presented a size-dependent model for FG viscoelastic micro-beams to investigate the effects of parameters such as the gradient index, excitation frequency, the amplitude of the harmonic load and viscoelastic parameters on the nonlinear frequency of the micro-beam.
Due to their designability and excellent mechanical properties, functionally gradient micro-beams are more and more widely used in micron and nanometer devices and systems. The research on micro-beams mainly focused on the elastic micro-beam and elastic functionally gradient micro-beam under simple load, but the research on viscoelastic microbeams under arbitrary load still needs to be improved. In the present work, the aim is to develop a viscoelastic axially functionally graded (VAFG) Timoshenko micro-beams model to study the static mechanical behaviors of the VAFG micro-beam with an arbitrary type of beam section shape and arbitrary type of loads. The size effect, FG effect, Poisson effect, and the influence of the beam section shape on the mechanical behaviors of VAFG micro-beams are expected to be investigated by taking the simply supported micro-beam, which is subject to the point load, as an example. To the best of our knowledge, little literature has been published to study all of the above characteristics of a VAFG Timoshenko micro-beam. The VAFG Timoshenko micro-beam model, including the governing differential equations and boundary conditions, is established. The size effect, FG effect, Poisson effect, and the influence of the beam section shape on the mechanical behaviors of the VAFG micro-beam are studied based on the size-dependent formulations of deflection, strain, stress and couple stress of the simply supported viscoelastic FG micro-beam. This work has certain reference significance for the design of viscoelastic functionally gradient beams and their application in micro-devices.
1 Modelling VAFG Timoshenko Micro-Beam
1.1 MCST descriptions of basic variables
The traditional theory of elastic-plastic mechanics does not consider the micro-structure of materials and cannot explain the size effect of the micro-structures. Therefore, the couple stress theory and strain gradient theory, which include the characteristic size parameters related to the micro-structure of the material, were developed to investigate the size effect of the micro-structures. The couple stress theory was simplified to the modified couple stress theory to adapt to the engineering applications, which contains only one characteristic size parameter, namely the length scale parameter. Therefore, the modified couple stress theory is used to study the size effect of the VAFG micro-beam here. The strain energy density is a function of both strain and curvature according to the MCST which was first introduced by Yang et al[5]. Therefore, the strain energy of a deformed isotropic body occupying volume V is given as
(1)
where σij is the stress tensor; εij is the strain tensor; mij is the couple stress tensor; and χij is the curvature tensor. The strain and curvature tensors are formulated as
(2)
(3)
where ui are the components of the displacement vector and θi are the components of the rotation vector.
(4)
where eijk is the permutation symbol.
Based on the Kelvin-Voigt scheme, one has
(5)
where 
are the elastic stress tensor and viscous stress tensor, respectively.
(6)
where 
are the elastic couple stress tensor and viscous couple stress tensor, respectively. In Eq.(5), the elastic stress tensor is formulated as
(7a)
and the viscous stress tensor is formulated as
(7b)
where η is the viscosity coefficient. In Eq.(6), the elastic couple stress tensor is formulated as
(8a)
and the viscous couple stress tensor is formulated as
(8b)
where l is the length scale parameter; E is the elastic modulus; η is the viscosity coefficient; χij is the curvature tensors; and μ is the Poisson ratio.
In addition, the material parameter of the VAFG micro-beam altering along its longitudinal direction is
(9)
where X represents the elastic modulus E, density ρ, or viscosity coefficient η; x is the axial direction coordinate; L is the micro-beam length; Xm is the maximum of X; Xl is the value of X at the left end of beam and k is the power-law exponent. The variations of material parameters of the micro-beam under different conditions are plotted in Fig.1.
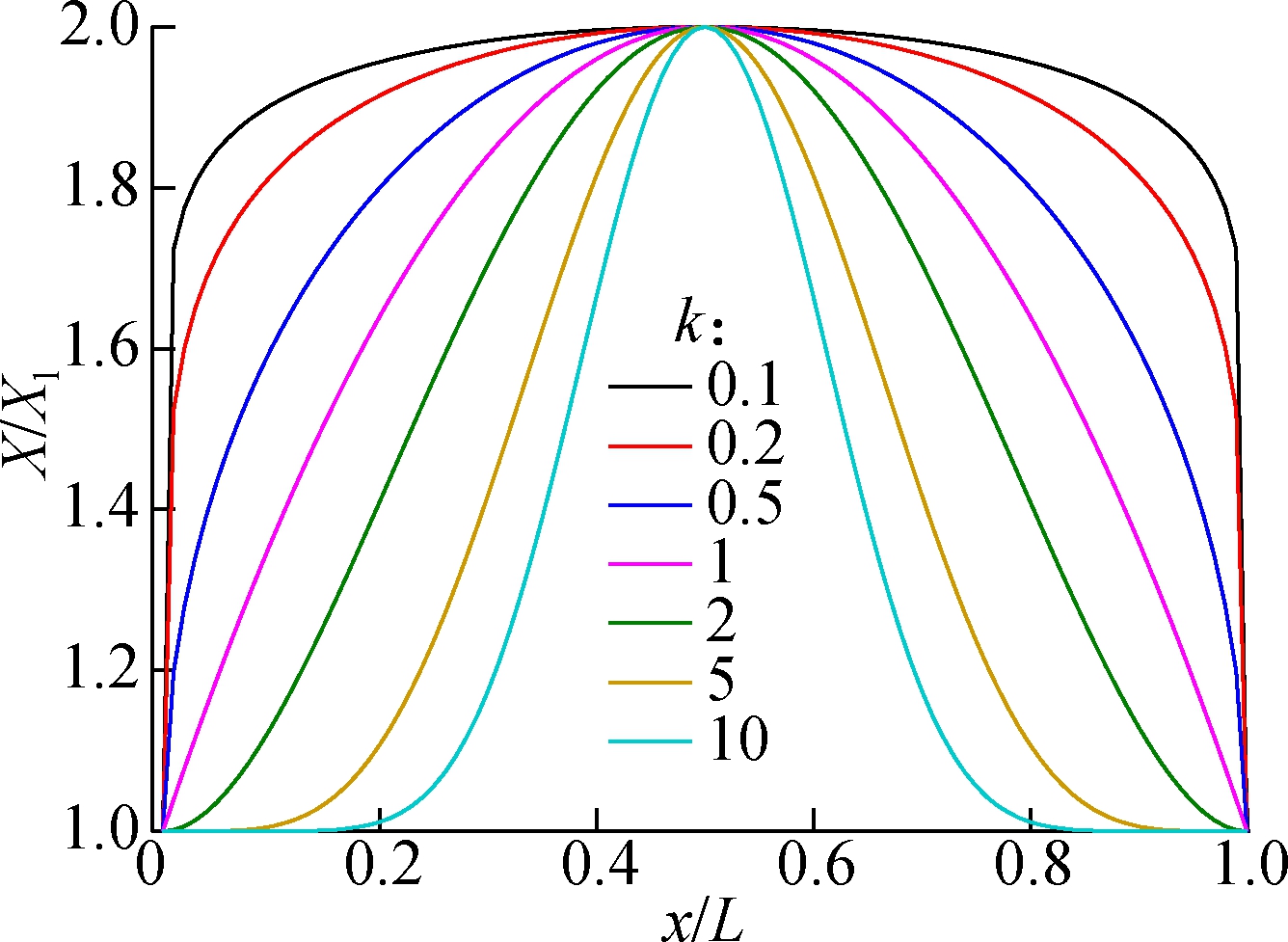
(a)
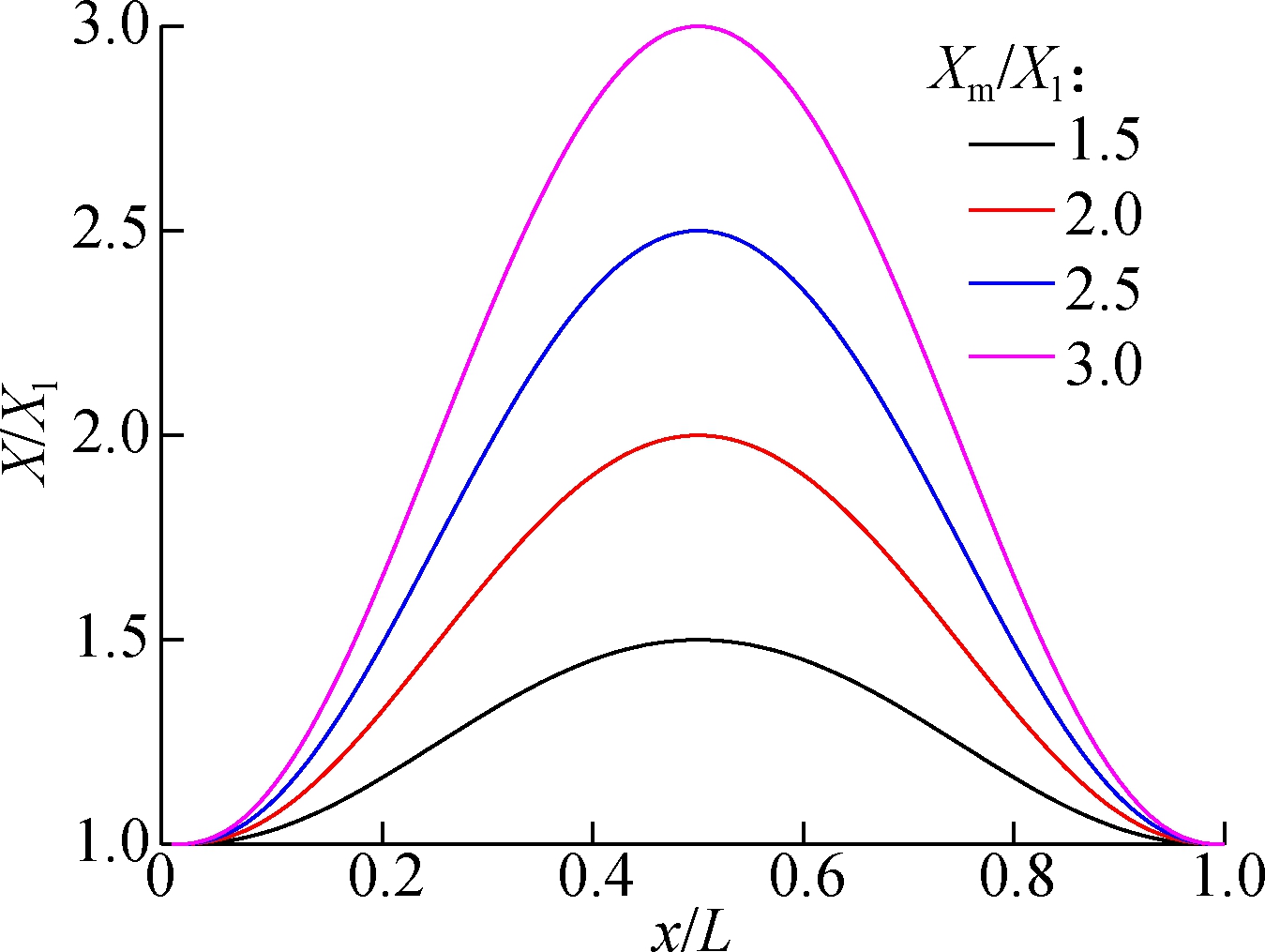
(b)
Fig.1 The variations of material parameters along axial direction of the beam. (a)The curves of material parameters and dimensionless coordinate with different power-law exponents(Xm=2Xl); (b) The curves of material parameters and dimensionless coordinate with different material parameter amplitudes (k=2.5)
According to the Timoshenko beam theory, the displacement components along x-, y- and z-directions are
u1=u(x,t)-yφ(x,t), u2=v(x,t), u3=0
(10)
where u is the axial displacement upon axial loads; v and φ are the transverse displacement and the rotation angle upon transverse loads, respectively; and t is the loading time.
Using the relationships expressed in Eqs.(2), (3), (4) and (10), the following components of the rotation angle, strain and curvature with the components of displacement and rotation angle are derived as
(11)
(12)
(13)
and the other components of the rotation, strain and curvature are zero. In view of the expressions of the rotation angle, strain and curvature as well as the stress-strain relationship, Eqs.(7a) and (7b), the following components of elastic stress and viscous stress with the components of displacement and rotation angle are expressed as
(14a)
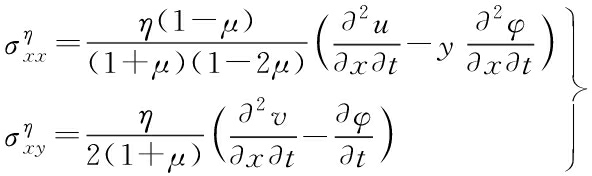
(14b)
and the other components of elastic stress and viscous stress are zero. Similarly, using the expression of curvature, Eq.(13), and the couple stress, Eqs.(8a) and (8b), the following components of the elastic couple stress and viscous couple stress with the components of displacement and rotation angle are expressed as
(15a)
(15b)
and the other components of the elastic couple stress and viscous couple stress are zero.
1.2 Governing differential equations and boundary conditions
The governing differential equations and boundary conditions can be derived by Hamilton’s principle, which reads as
δ
(Ek-Vε-Uη+Wp)dt=0
(16)
where Ek is the kinetic energy; Vε is the elastic potential energy; Uη is the viscous energy and Wp is the work done by the external force. The variation form of the kinetic energy is
(17)
where 
are the first and second derivatives of displacement with respect to time, respectively; and ui represent the displacements in the directions of x, y and z, as shown in Eq.(10).
The variation form of the elastic potential energy and the viscous energy can be written as
(18)
(19)
The variation form of the work done by the external force is
(20)
where fx and fy are the components of the body force; mz is the component of the body couple; Fx, Fy and M are the applied axial force, transverse force, and bending moment at the two ends of the micro-beam, respectively.
Inserting Eqs.(17), (18), (19) and (20) into the expression of Hamilton’s principle (Eq.(16)), the governing differential equations of the Timoshenko micro-beam are obtained as
(21a)
(21b)
(21c)
and their boundary conditions at the two ends of the micro-beam can be expressed as
(22a)
(22b)
Fy=0 or δv=0
(22c)
(22d)
where
(23a)
(23b)
(23c)
(23d)
(23e)
(23f)
(23g)
(23h)
2 Solutions of VAFG Timoshenko Micro-Beam
The static bending problems of a simply supported VAFG micro-beam with the geometry and cross-sectional shape shown in Fig.2 are solved by the above governing differential equations for a VAFG micro-beam. The results of the VAFG Timoshenko micro-beam model are the same as the traditional results of the VAFG Timoshenko beam when the terms of the couple stress are ignored in the VAFG Timoshenko micro-beam model. According to the Timoshenko beam theory and Bernoulli-Euler beam theory, the beam can be solved more accurately with a smaller ratio of the feature size to the beam length using the Timoshenko beam theory which considers the shear deformation of the beam. Based on the theory of solid mechanics, the Timoshenko beam theory has more advantage for the beam whose ratio of the feature size to beam length is below 5. Therefore, the proposed model will be used to study the mechanical behaviors of the VAFG micro-beam with the ratio of the feature size to the beam length below 5.
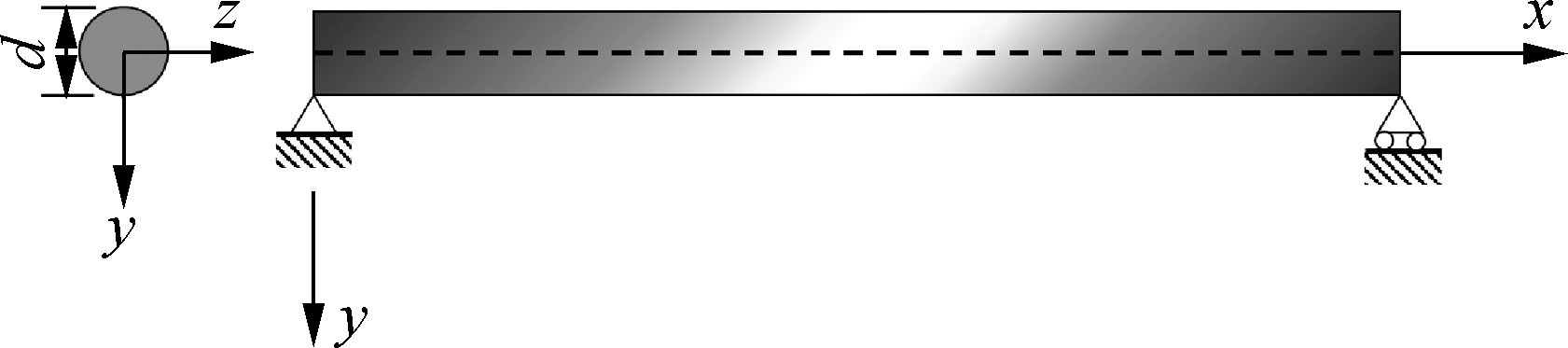
Fig.2 Schematic representation of an axially functionally graded viscoelastic micro-beam
2.1 Formula of deflection and rotation angel
In view of Eqs.(22a) to (22d), the boundary conditions of the VAFG micro-beam in Fig.2 can be identified as
v|x=0=v|x=L=0
(24)
The displacement components and rotation angle components at the mid-plane (y=0) of the micro-beam shown in Fig.2 can be expanded in a Fourier series as
(25)
(26)
(27)
where Un, Vn and Ψn are the Fourier coefficients to be determined and
(28)
The expressions of the displacement and rotation angle in Eqs.(25) to (27) satisfy the boundary conditions in Eq.(24) for any Un, Vn and Ψn. Similarly, the applied load can also be expanded in the Fourier series as
(29)
(30)
is the Fourier coefficient to be determined. Then, taking a point load as an example, the point load is expressed as
q(x)=Pδ(x-xP)
(31)
where δ(·) is the Dirac delta function; P is the magnitude of the point load; xP is the application position of the point load. Substituting Eq.(31) into Eq.(30), the Fourier coefficient of the point load can be written as
(32)
Inserting the expressions of the displacement and rotation angle (Eqs.(25), (26) and (27)) into the governing differential equations (Eqs.(21a), (21b) and (21c)), the system of algebraic equations can be obtained as
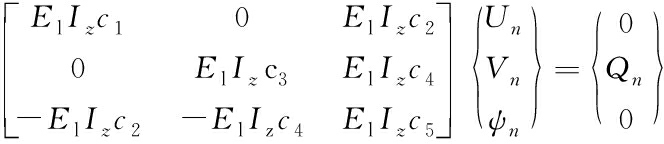
(33)
where El is the elastic modulus at the left end of the micro-beam. The moment of inertia of the cross section is
(34)
and the coefficients determined by the micro-beam size and material parameters are
(35a)
(35b)
(35c)
(35d)
(35e)
where 
is the centroid of the micro-beam section. The viscoelastic modulus is defined as
(36)
The radius of inertia for the neutral axis is
(37)
The system of the algebraic equations (Eq.(33)) can be solved as
(38)
(39)
(40)
Inserting Eqs.(38) to (40) into the displacement and rotation angle components expressions (Eqs.(25) to (27)), the displacement and rotation angle components in the normalized form are obtained as
(41)
(42)
(43)
where 
are the dimensionless axial displacement, dimensionless deflection and dimensionless rotation angle, respectively.
2.2 Formula of strain and curvature
Inserting Eqs.(38) to (40) into the strain expression Eq.(12), the strain components in the normalized form are obtained as
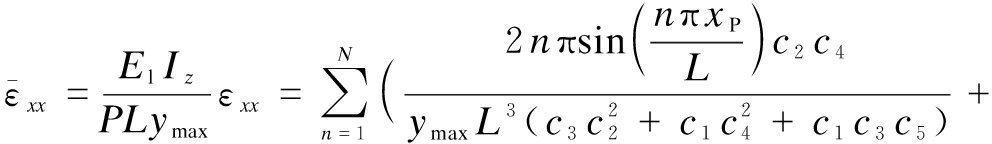
(44)
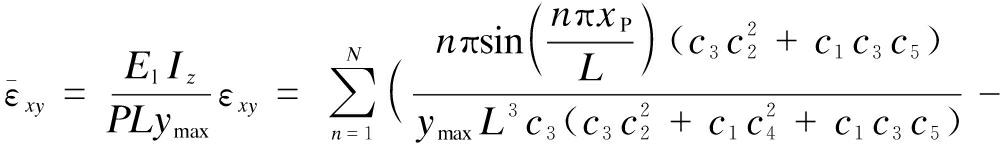
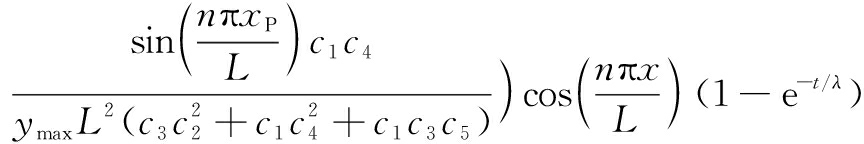
(45)
where the other components of strain are zero.
Substituting Eqs.(38) to (40) into the curvature expression (Eq.(13)), the strain components in the normalized form are obtained as
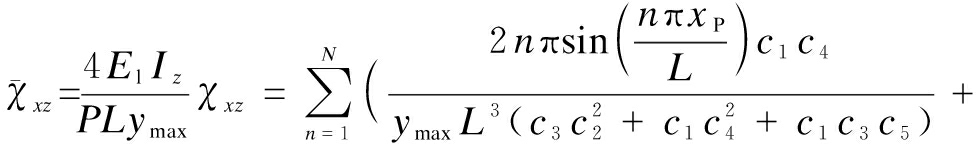
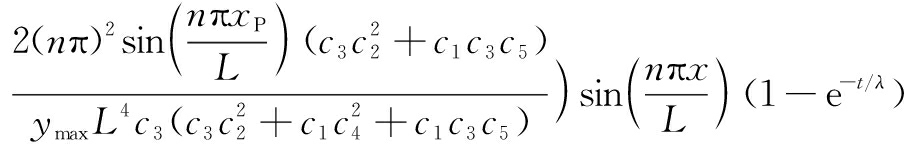
(46)
where the other components are zero. 
are the dimensionless axial strain, dimensionless tangential strain and dimensionless curvature, respectively.
2.3 Formula of stress and couple stress
Inserting Eqs.(38) to (40) into the stress expression (Eqs.(14a), (14b) and (5)), the strain components in the normalized form are obtained as
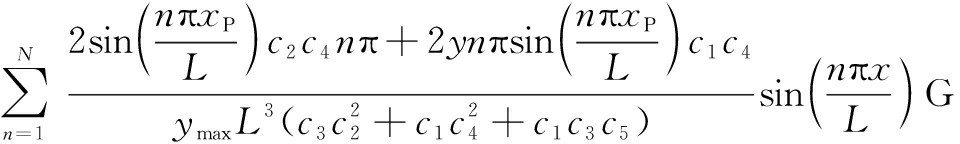
(47)
where 
is the dimensionless normal stress.
Inserting Eqs.(38) to (40) into the couple stress expression (Eqs.(15a), (15b) and (6)), the couple stress components in the normalized form are obtained as
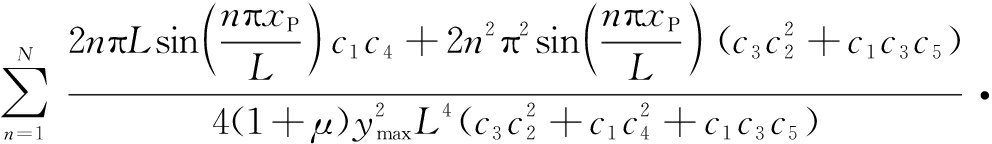
(48)
where 
is the dimensionless couple stress.
3 Numerical Calculation and Discussion
The numerical simulation for the deflection, rotation, normal stress and couple stress of the VAFG Timoshenko micro-beam is conducted as below by using the series solutions in Eqs.(42),(43),(47) and (48). The series solutions can achieve a convergence solution with terms less than 10, and we numerically simulate using 30 terms for ensuring the accuracy since the calculation method will not require too much time.
3.1 Size effects
Fig.3(a) plots the curves of the dimensionless deflection vs. dimensionless axial coordinate with different dimensionless section diameters. It is observed that each curve of dimensionless deflection forms a saddle shape whose altitude increases with the increase in the dimensionless section diameter. This illustrates that the bending stiffness declines with the increase in the dimensionless section diameter of the micro-beam, which has an obvious size effect on the bending stiffness of the micro beam. The curves are flat when the deflection reaches the maximum value, which is due to the reasonable distribution of material stiffness.
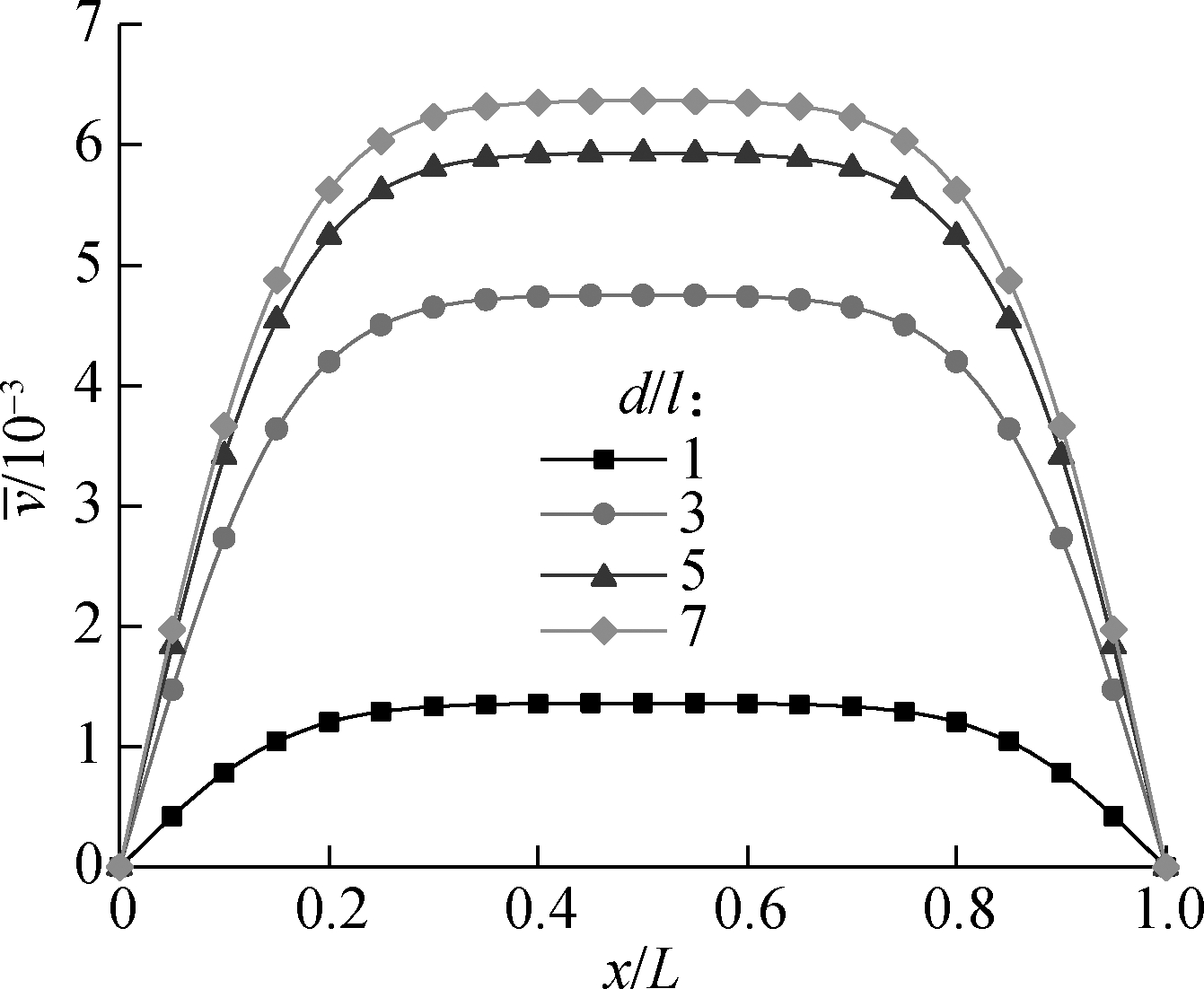
(a)
(b)
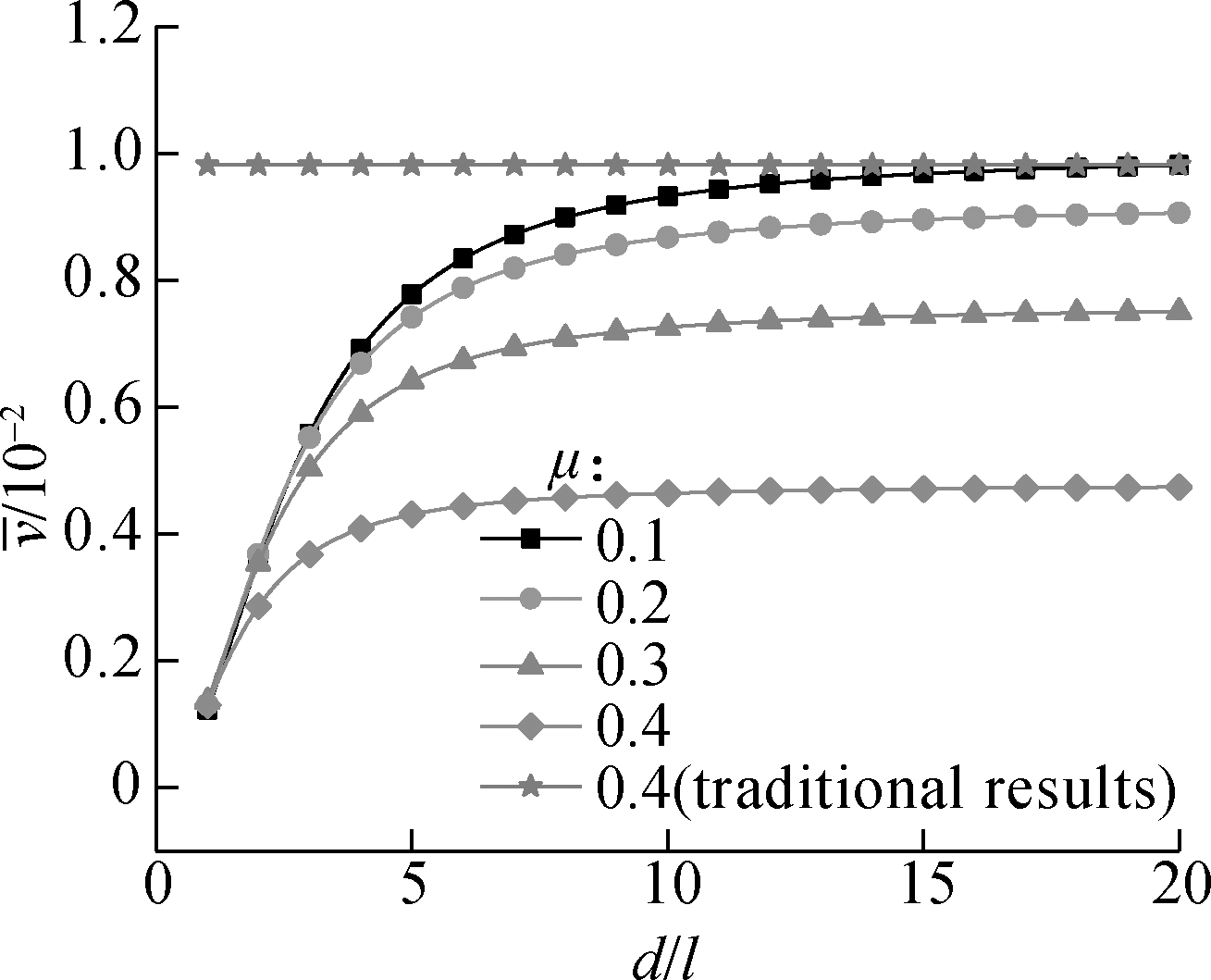
Fig.3 Curves related to the size effect on stiffness. (a) Variation of dimensionless deflection with dimensionless axial coordinate (υ=0.38,k=2.5); (b)Variation of the maximum dimensionless deflection with dimensionless diameter (x=L/2,k=2.5)
Fig.3(b) presents the variation of maximum dimensionless deflection with the dimensionless section diameter under the conditions of different Poisson ratios. It is clear that the maximum dimensionless deflection increases rapidly with the increase in the dimensionless section diameter when the dimensionless section diameter is below 5 and becomes stable when the dimensionless height is above 15. The traditional dimensionless deflection does not vary with the increase in the beam size and the size-dependent results gradually become the same as the traditional results when the beam size is large enough. This means that the size effect on bending stiffness is obvious when the dimensionless section diameter is below 5, but it can be ignored when the dimensionless section diameter is above 15. Furthermore, the initial slope of curves increases with the decrease in the Poisson ratio, which means that the smaller the value of Poisson ratio is, the more obvious the size effect on bending stiffness is.
Fig.4(a) presents the variation of the dimensionless normal stress with the dimensionless section diameter under different Poisson ratios. It is observed that the dimensionless normal stress increases rapidly when the dimensionless diameter is below 5 and tends to be a stable value when the dimensionless diameter is above 15. The traditional results do not vary with the variation of the dimensionless diameter, and the size-dependent results gradually tend to the traditional results when the dimensionless diameter is large enough. This means that the size effect on normal stress is obvious when the dimensionless section diameter is below 5, while it can be ignored when the dimensionless section diameter is above 15. Furthermore, it is clear that the initial slope of the curve of dimensionless normal stress increases with the increase in the Poisson ratio, which means that the size effect on the normal stress of the micro-beam is more obvious when the Poisson ratio increases. Fig.4(b) presents the variation of the dimensionless couple stress with the dimensionless section diameter under the conditions of different Poisson ratios. It is found that the dimensionless couple stress decreases rapidly when the dimensionless diameter is below 5 and tends to 0 when the dimensionless diameter is above 15. This indicates that the size effect of couple stress is clear when the dimensionless section diameter is below 5, while it can be ignored when the dimensionless section diameter is above 15. The phenomenon indicates that the influence of the couple stress of the micro-beam decreases with the increase in the beam size so that the mechanical behavior of the micro-beam inclines to the traditional results when the size is large enough. In addition, it is clear that the absolute value of the initial slope of the curve increases with the increase in Poisson’s ratio, which means that the size effect on couple stress of the micro-beam is more obvious when the Poisson ratio increases.
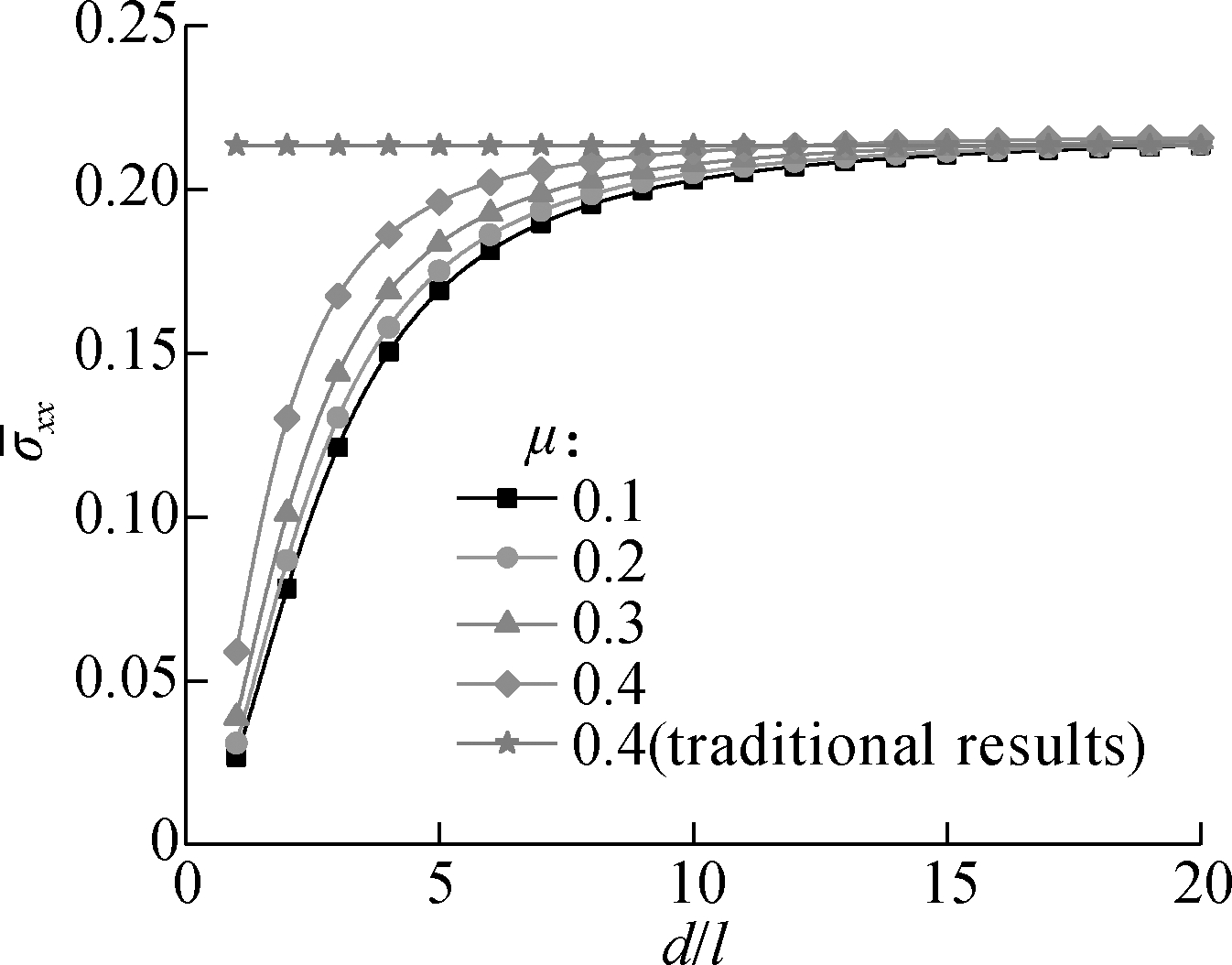
(a)
(b)
Fig.4 Curves related to the size effect on normal stress and couple stress(x=L/2, k=2.5,y=d/2). (a)Variation of dimensionless normal stress with a dimensionless diameter; (b)Variation of dimensionless couple stress with a dimensionless diameter
Fig.5(a) plots the curves of the maximum dimensionless deflection vs. the loading time with respect to different values of the Poisson ratio, which aims to study the size effect on the viscous properties of the VAFG micro-beam. It is observed that the dimensionless deflection increases with the increase in the loading time and gradually tends to become a stable value, which is due to the viscous property of the micro-beam. Moreover, the stable value decreases with the increase in the Poisson ratio and the initial slope of the curves increase with its decrease. This means that the viscous property of the micro-beam is more obvious when the value of the Poisson ratio becomes smaller.
Fig.5(b) plots the curves of the maximum dimensionless deflection vs. the loading time with respect to different values of the dimensionless section diameter. The dimensionless deflection increases with the increase in loading time and gradually tends to be a stable value due to the creep property of the VAFG micro-beam. Also, the stable value increases with the increase in the dimensionless section diameter, which illustrates that the stiffness is better with a smaller beam size. Furthermore, the initial slope of the curves increases with the increase in the dimensionless section diameter, which indicates that the viscous property of the micro-beam is more obvious when the feature size of the micro-beam becomes larger.
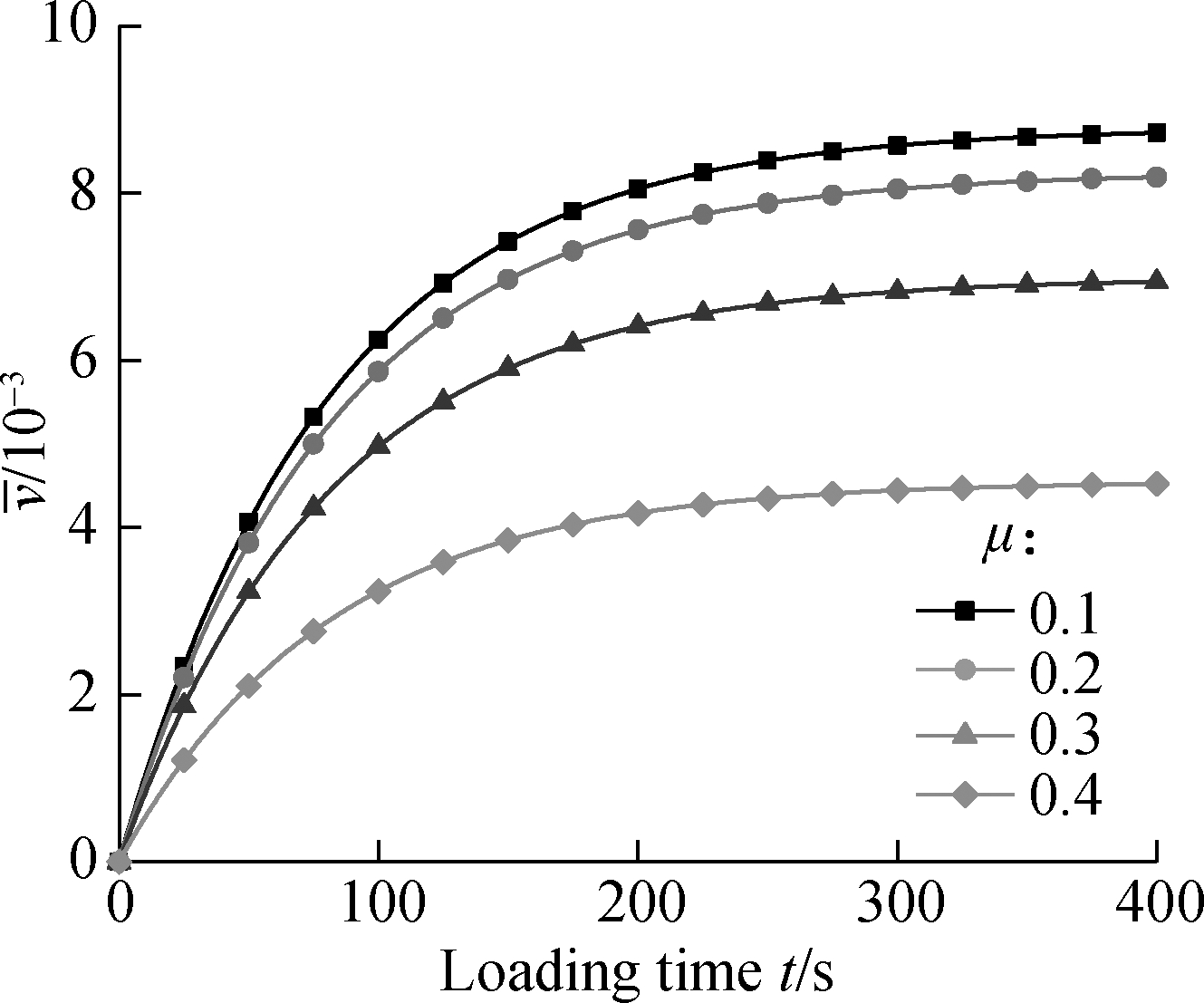
(a)
(b)
Fig.5 Curves related to the size effect on viscosity. (a)Variation of the maximum dimensionless deflection with loading time (x=L/2, k=2.5,d/l=7); (b)Variation of the maximum dimensionless deflection with loading time (x=L/2, k=2.5,υ=0.38)
3.2 Functionally graded effects
Fig.6(a) plots the curves of the dimensionless deflection vs. the dimensionless axial coordinate with different values of the power-law exponent. It is clear that the peak of the curve is flatter when the power-law exponent becomes larger, while the maximal value of deflection is constant. This means that the stiffness distribution of the micro-beam can be adjusted by changing the value of the power-law exponent of material parameter expression. Fig.6(b) plots the curves of the dimensionless deflection vs. the dimensionless axial coordinate with different variation amplitudes of material parameters. It is clear that the curve is flatter when the variation amplitude of the material parameter becomes larger, and the peak value of the dimensionless deflection decreases with the increase in the variation amplitude of the material parameter. This indicates that the larger the variation amplitude of the material parameter is, the smaller the deflection is.
Fig.7(a) plots the curves of the dimensionless deflection vs. the dimensionless diameter with different power-law exponents. The maximum dimensionless deflection increases with the increase in the value of the power-law exponent, and the increasing amplitude is insignificant when the dimensionless diameter is below 5. Also, the increasing amplitude of the maximum dimensionless deflection with the increase in the value of power-law exponent becomes obvious when the dimensionless diameter is above 10. This means that the FG effect of the power-law exponent is obvious when the dimensionless diameter is above 10, but it can be ignored when the dimensionless diameter is below 5.
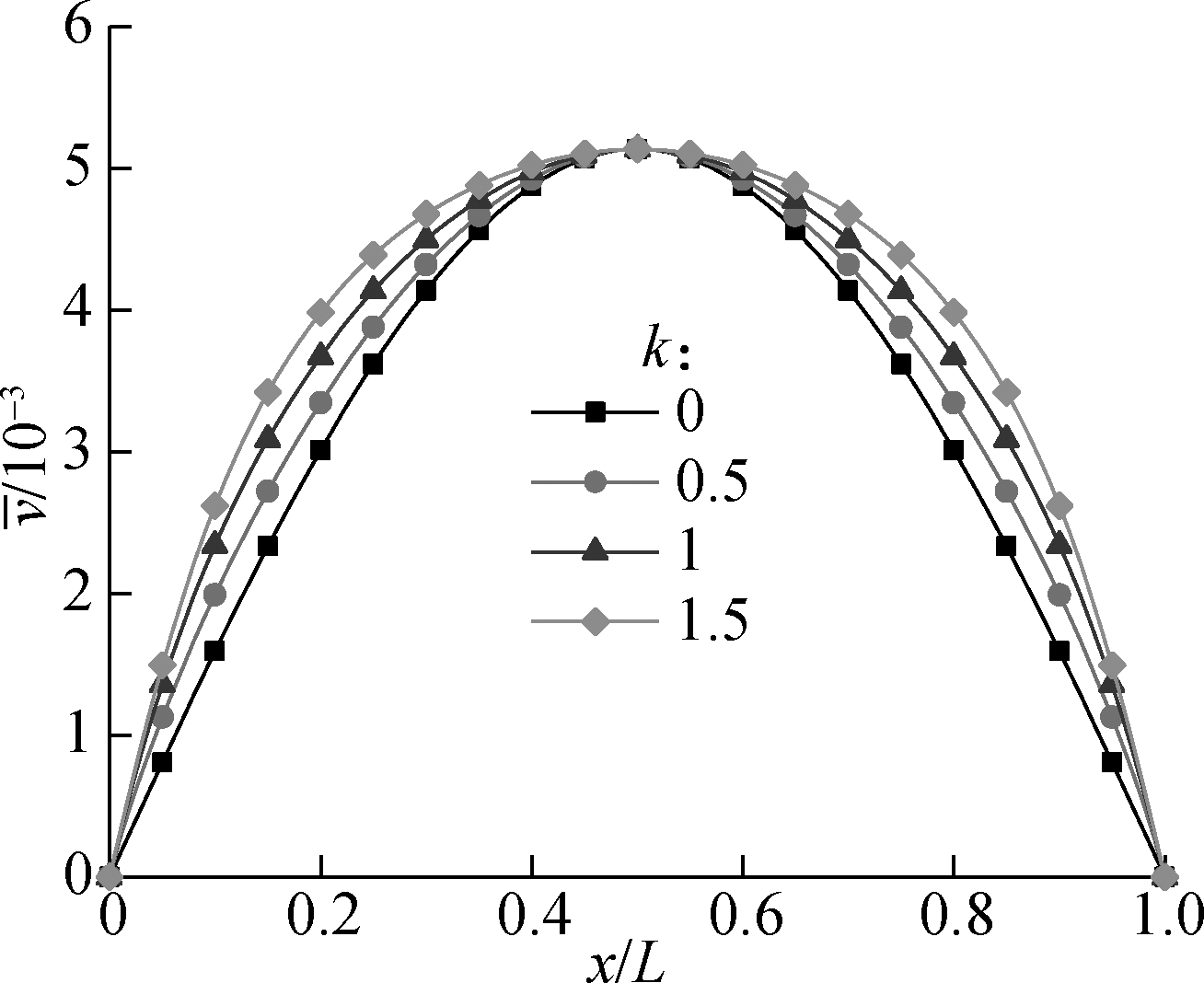
(a)
(b)
Fig.6 Curves related to the FG effect of deflection. (a) Curves of the dimensionless deflection vs. the dimensionless axial coordinate under the conditions of different power-law exponents (Xm/Xl=2, υ=0.38,d/l=7); (b) Curves of dimensionless deflection vs. dimensionless axial coordinate under the conditions of different variation amplitudes of material parameter (k=0.5,d/l=7,υ=0.38)
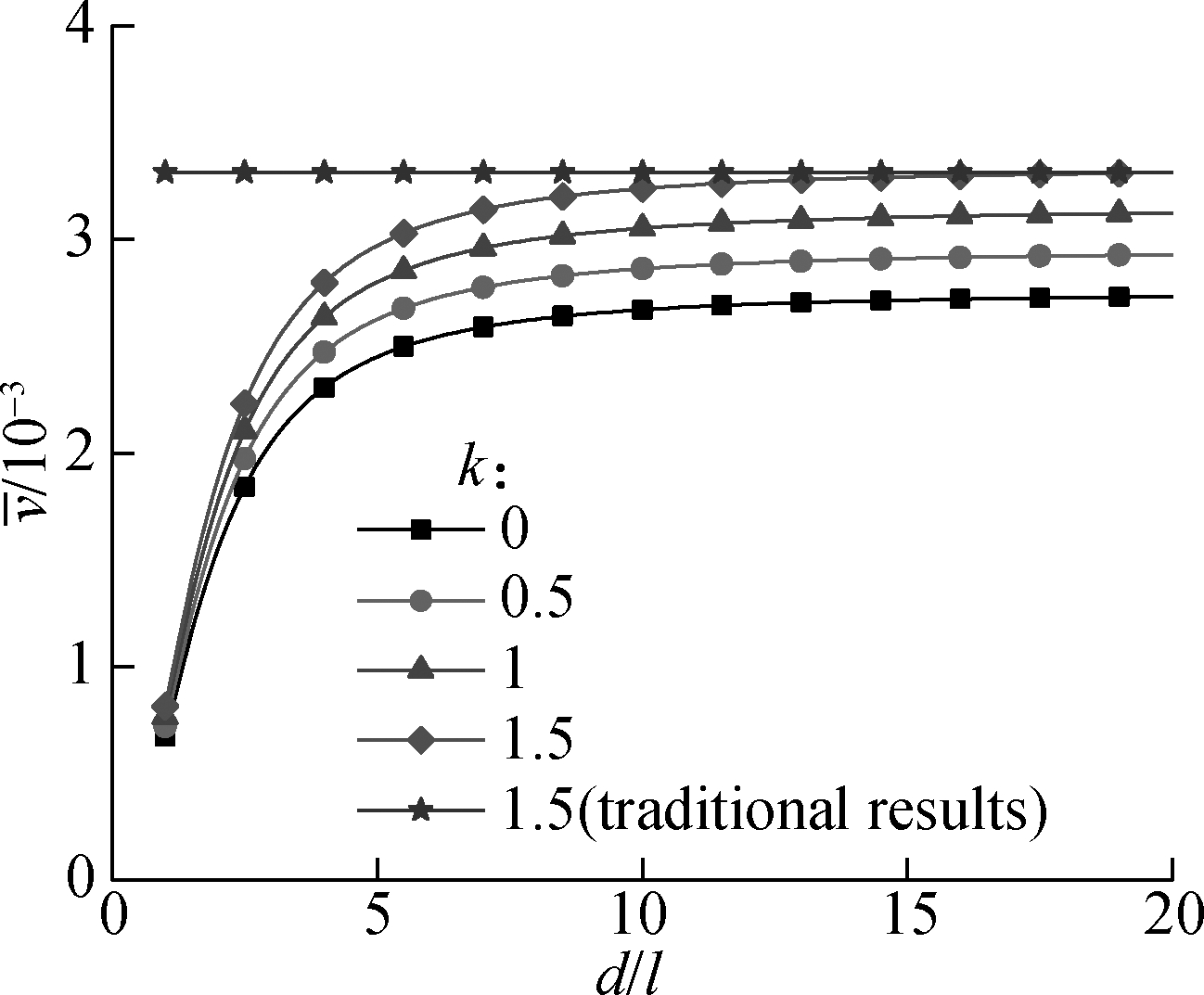
(a)
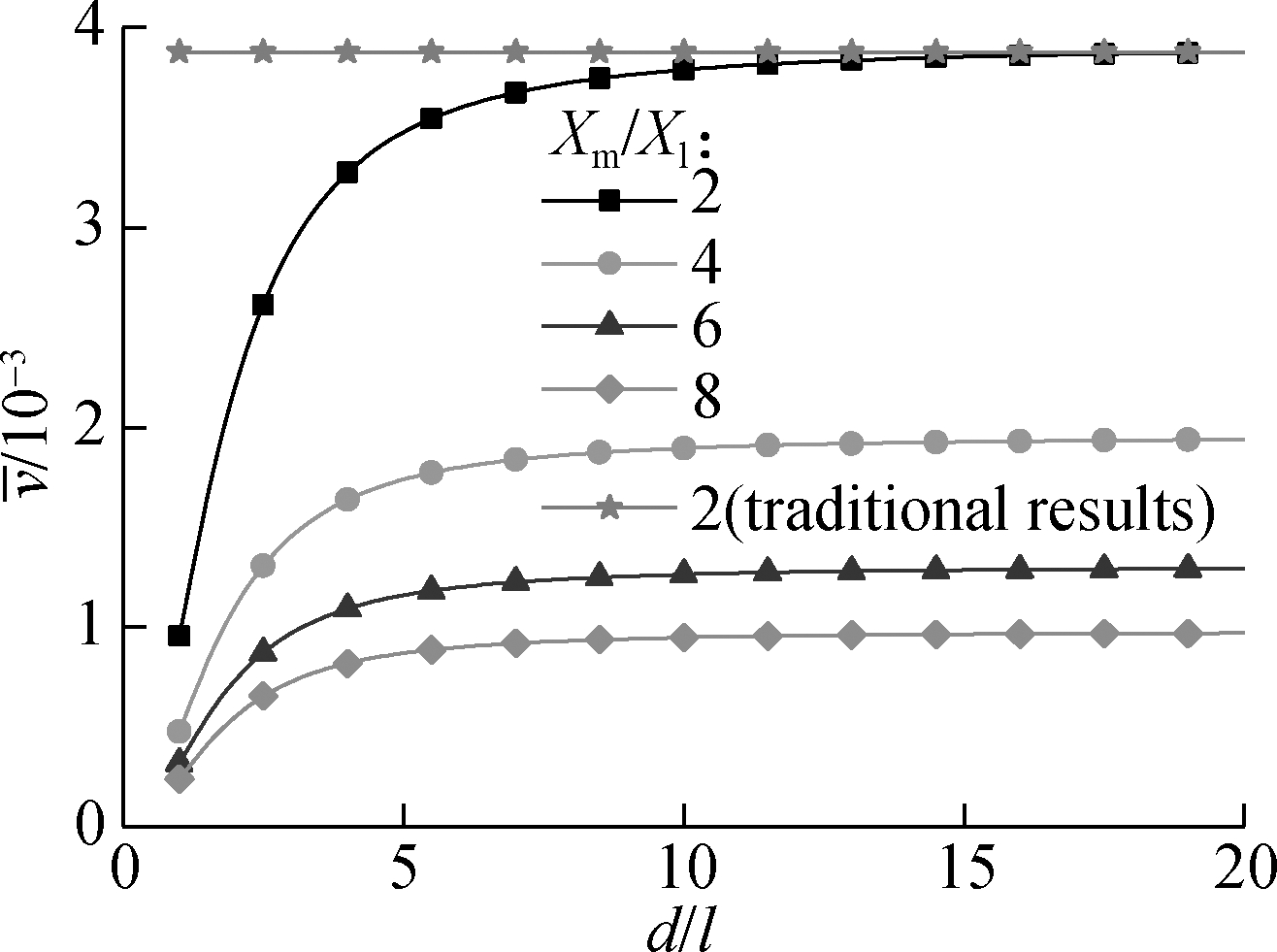
(b)
Fig.7 Curves related to the FG effect of deflection. (a) Curves of the maximum dimensionless deflection vs. the dimensionless diameter under different power-law exponents (x/L=0.25,Xm/Xl=2,υ=0.38); (b) Curves of the maximum dimensionless deflection vs. the dimensionless diameter under different variation amplitudes of material parameters (x/L=0.5,k=1.5,υ=0.38)
Fig.7(b) plots the curves of the maximum dimensionless deflection vs. the dimensionless diameter with different variation amplitudes of the material parameter. It is clear that the maximum dimensionless deflection increases with the increase in the value of variation amplitude of the material parameter, and the amplitude increases clearly when the dimensionless diameter is above 5. This means that the FG effect of the variation amplitude of the material parameter becomes more obvious with a large beam feature size.
3.3 Poisson effects
Fig.8(a) plots the curves of the dimensionless deflection vs. the Poisson ratio with different dimensionless diameters. It is clear that the maximum dimensionless deflection increases with the increase in the dimensionless diameter. The absolute value of the slope at the end point of the curve increases with the increase in the dimensionless diameter, which indicates that the larger the dimensionless diameter, the more obvious the Poisson effect of deflection. Therefore, the variation amplitude of the stiffness along with the change of the Poisson ratio is more slight with a smaller feature size. Fig.8(b) plots the curves of the dimensionless deflection vs. the Poisson ratio with different loading times. It is clear that the maximum dimensionless deflection increases with the increase in loading time. The absolute value of the slope at the end point of the curve increases with the increase in loading time, which indicates that the longer the loading time, the more obvious the Poisson effect of deflection.
3.4 Influences of inertia radius
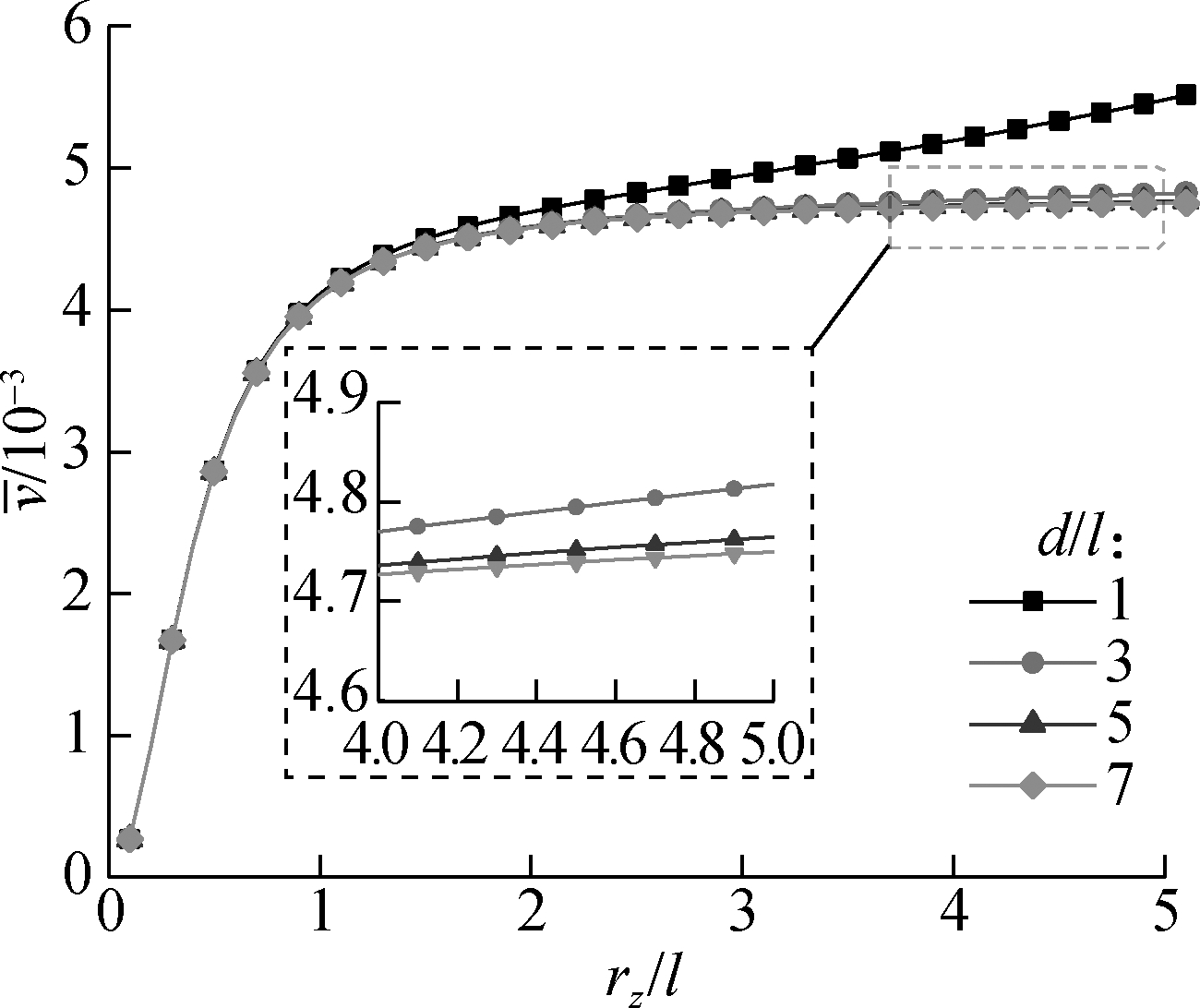
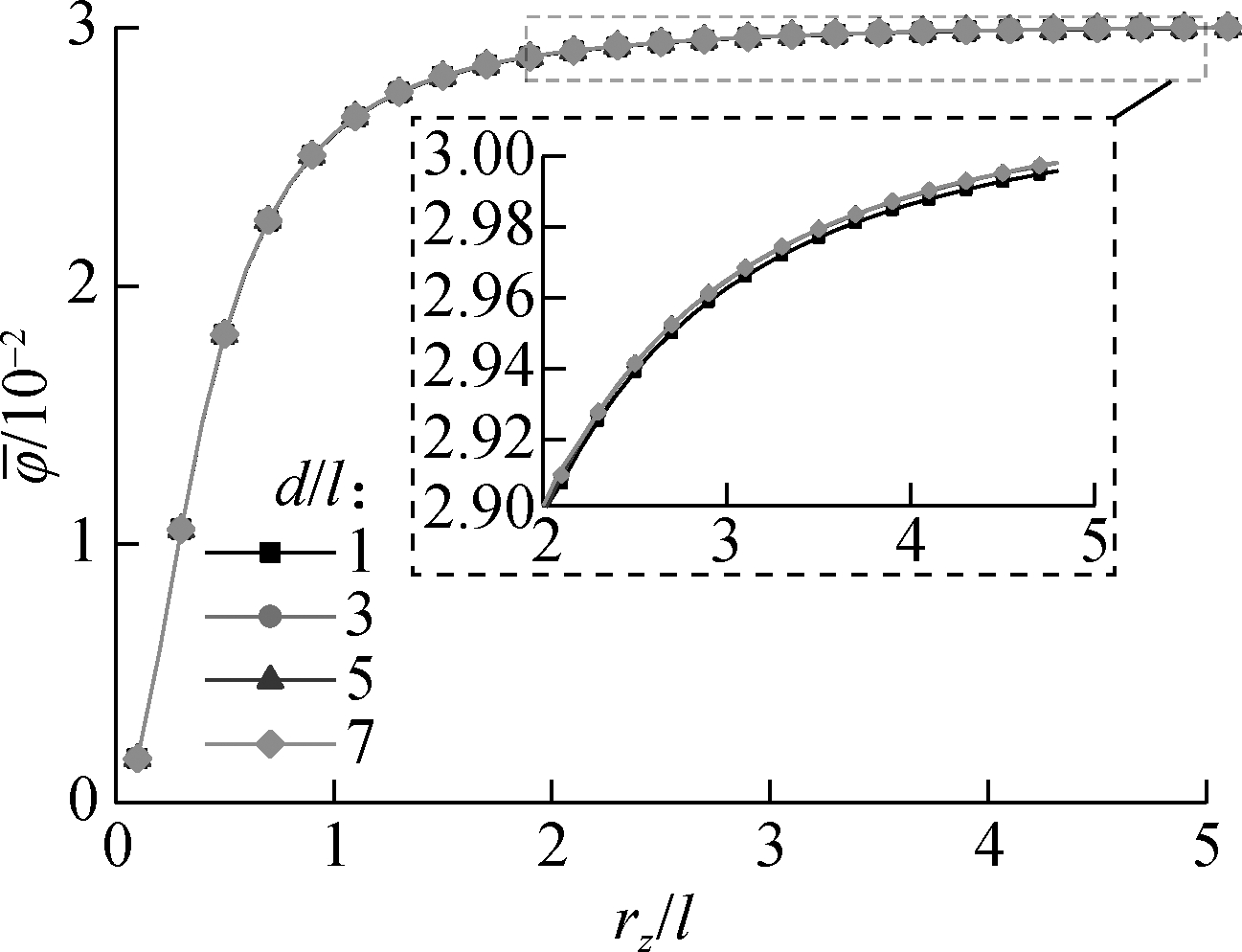
Fig.9 plots the variation of the dimensionless deflection of the beam with the dimensionless inertia radius under different dimensionless diameters. It is clear that the dimensionless deflection increases rapidly when the dimensionless inertia radius is below 1, which means that the stiffness of the beam decreases obviously with the increase in the inertia radius when rz/l<1. Also, Fig.9(a) shows that the influence of the inertia radius is more obvious with smaller dimensionless section radii, which indicates that the influence of the beam section shape on the stiffness of the beam is more obvious with a smaller beam size.
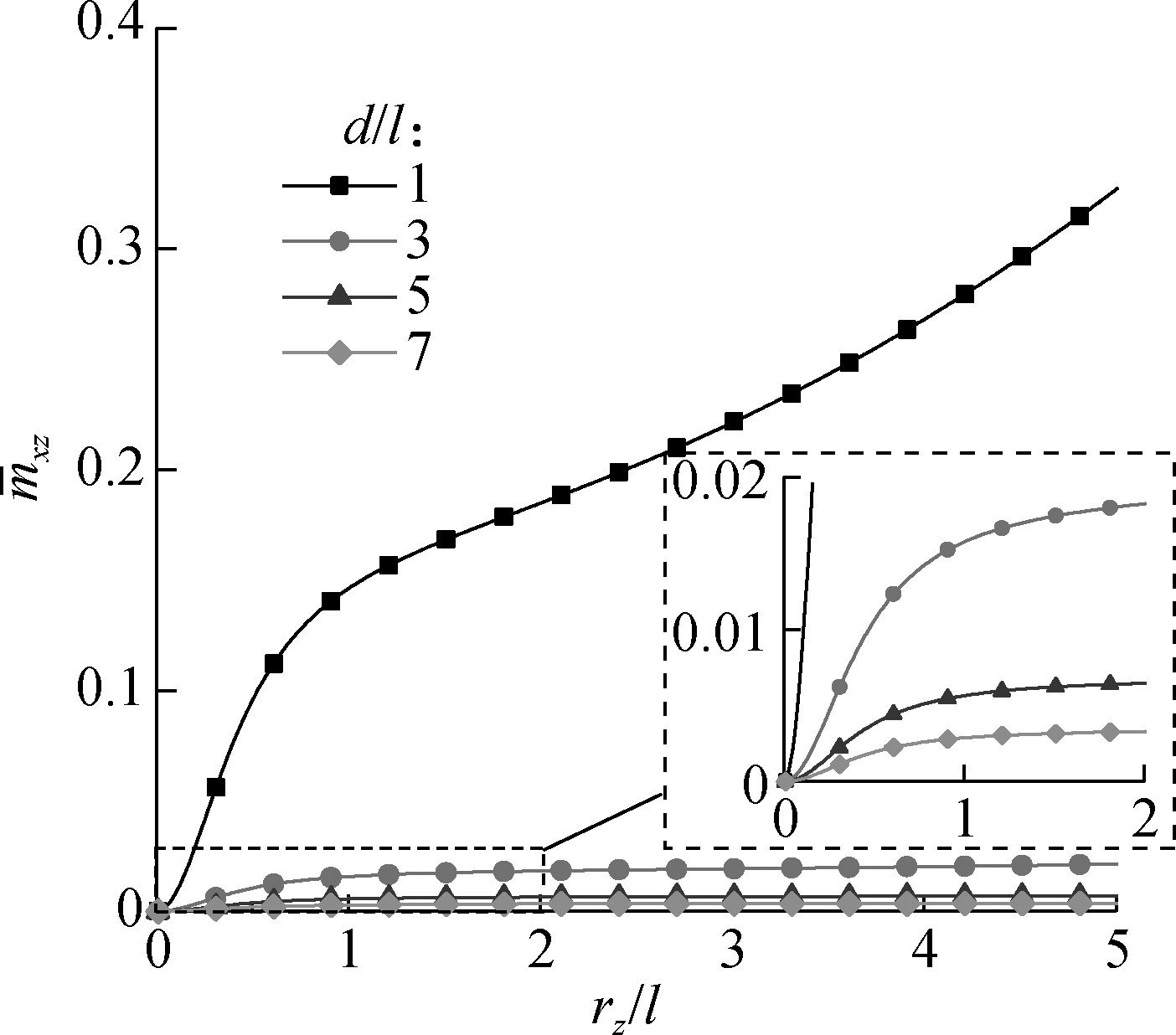
Fig.10(a) plots the variation of the dimensionless normal stress with the dimensionless inertia radius under different dimensionless diameters. It is observed that the dimensionless normal stress increases rapidly when the dimensionless inertia radius is below 1 and then gradually tends to a stable value, and the influence of the dimensionless diameter on the dimensionless normal stress is small. This means that the normal stress is influenced obviously by the micro-beam section shape when rz/l<1, and the influence of the micro-beam section shape can be ignored when rz/l>2. Fig.10(b) presents the variation of the dimensionless couple stress with the dimensionless inertia radius under different dimensionless diameters. It is observed that the dimensionless couple stress increases rapidly when the dimensionless inertia radius is below 1 and the curve becomes more flat with the increase in the dimensionless diameter. This means that the couple stress is influenced obviously by the micro-beam section shape when rz/l<1, and the larger the micro-beam size is ,the smaller the influence of the micro-beam section shape on the couple stress is.
(a)
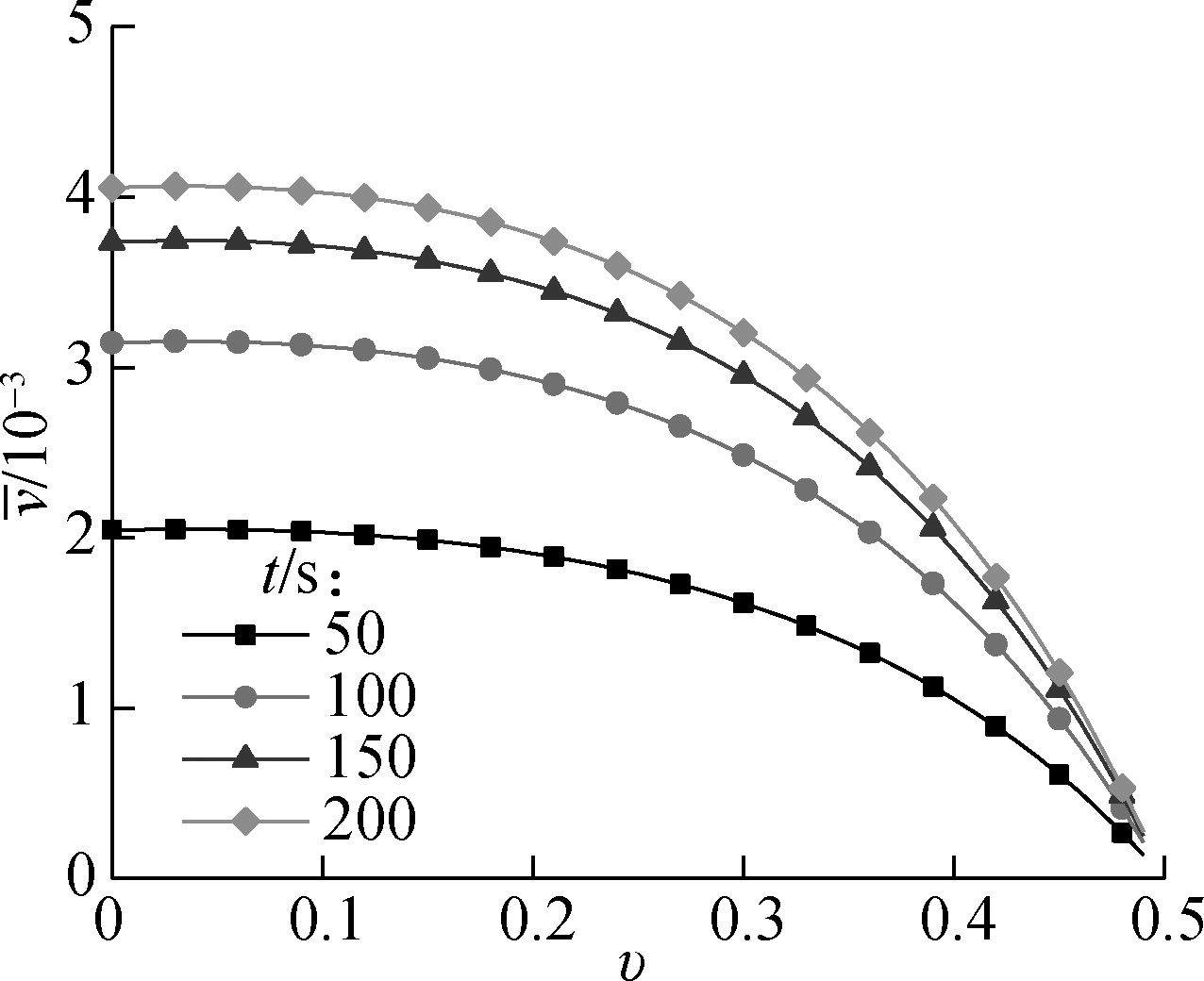
(b)
Fig.8 Curves related to the Poisson effect of deflection. (a) The curves of maximum dimensionless deflection vs. the Poisson ratio with different dimensionless diameters (k=2.5, Xm/Xl=2, t=400); (b)Curves of the maximum dimensionless deflection vs. the Poisson ratio with different loading times (k=2.5, Xm/Xl=2,d/l=7)
(a)
(b)
Fig.9 Curves related to the influences of inertia radius (x=L/2, k=2.5). (a) Variation of the dimensionless deflection with the dimensionless inertia radius; (b)Variation of dimensionless rotation angle with the dimensionless inertia radius
(a)
(b)
Fig.10 Curves related to the size effect on normal stress and couple stress(x=L/2, k=2.5,y=d/2). (a) Variation of dimensionless normal stress with dimensionless inertia radius ; (b) Variation of dimensionless couple stress with dimensionless inertia radius
4 Conclusions
1) The size effect on the deflection, normal stress and couple stress are obvious when d/l<5, and the size effect can be ignored when d/l>15. Also, the smaller the value of the Poisson ratio, the more obvious the size effect on the deflection, while the larger the value of the Poisson ratio is, the more obvious the size effect on the normal stress and couple stress is.
2) The influences of FG parameters are related to the deformation of the VAFG Timoshenko micro-beam. The FG effects caused by both the power-law exponent and the variation amplitude of material parameters are obvious and tend to be stable when the dimensionless diameter is below 5.
3) The larger the dimensionless diameters and the loading time, the more obvious the Poisson effect of the deflection.
4) The deflection, rotation angle, normal stress and couple stress increase rapidly with the increase in the dimensionless inertial radius when the dimensionless inertial radius is below 1. The rotation angle and normal stress tend to be a stable value when the dimensionless inertial radius is above 2 and the deflection and couple stress increase slower when the dimensionless inertial radius is above 2.
[1] Witvrouw A, Mehta A. The use of functionally graded poly-SiGe layers for MEMS applications[J]. Materials Science Forum, 2005, 492/493: 255-260. DOI:10.4028/www.scientific.net/msf.492-493.255.
[2] Lü C F, Lim C W, Chen W Q. Size-dependent elastic behavior of FGM ultra-thin films based on generalized refined theory[J]. International Journal of Solids and Structures, 2009, 46(5): 1176-1185. DOI:10.1016/j.ijsolstr.2008.10.012.
[3] McFarland A W, Colton J S. Role of material microstructure in plate stiffness with relevance tomicrocantilever sensors[J]. Journal of Micromechanics and Microengineering, 2005, 15(5): 1060-1067. DOI:10.1088/0960-1317/15/5/024.
[4] Lam D C C, Yang F, Chong A C M, et al. Experiments and theory in strain gradient elasticity[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(8): 1477-1508. DOI:10.1016/s0022-5096(03)00053-x.
[5] Yang F, Chong A C M, Lam D C C, et al. Couple stress based strain gradient theory for elasticity[J]. International Journal of Solids and Structures, 2002, 39(10): 2731-2743. DOI:10.1016/s0020-7683(02)00152-x.
[6] Ke L L, Yang J, Kitipornchai S, et al. Bending, buckling and vibration of size-dependent functionally graded annular microplates[J]. Composite Structures, 2012, 94(11): 3250-3257. DOI:10.1016/j.compstruct.2012.04.037.
[7] Lei J, He Y M, Zhang B, et al. Bending and vibration of functionally graded sinusoidal microbeams based on the strain gradient elasticity theory[J]. International Journal of Engineering Science, 2013, 72: 36-52. DOI:10.1016/j.ijengsci.2013.06.012.
[8] Thai H T, Vo T P, Nguyen T K, et al. Size-dependent behavior of functionally graded sandwich microbeams based on the modified couple stress theory[J]. Composite Structures, 2015, 123: 337-349. DOI:10.1016/j.compstruct.2014.11.065.
[9] Abazid M A, Sobhy M. Thermo-electro-mechanical bending of FG piezoelectric microplates on Pasternak foundation based on a four-variable plate model and the modified couple stress theory[J]. Microsystem Technologies, 2018, 24(2): 1227-1245. DOI:10.1007/s00542-017-3492-8.
[10] 
im
ek M, Reddy J N. Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory[J]. International Journal of Engineering Science, 2013, 64: 37-53. DOI:10.1016/j.ijengsci.2012.12.002.
[11] imek M, Kocatürk T, Akba D. Static bending of a functionally graded microscale Timoshenko beam based on the modified couple stress theory[J]. Composite Structures, 2013, 95: 740-747. DOI:10.1016/j.compstruct.2012.08.036.
[12] Chen X C, Li Y H. Size-dependent post-buckling behaviors of geometrically imperfect microbeams[J]. Mechanics Research Communications, 2018, 88: 25-33. DOI:10.1016/j.mechrescom.2017.12.005.
[13] Alshorbagy A E, Eltaher M A, Mahmoud F F. Free vibration characteristics of a functionally graded beam by finite element method[J]. Applied Mathematical Modelling, 2011, 35(1): 412-425. DOI:10.1016/j.apm.2010.07.006.
[14] Akgöz B, Civalek Ö. Free vibration analysis of axially functionally graded tapered Bernoulli-Euler microbeams based on the modified couple stress theory[J]. Composite Structures, 2013, 98: 314-322. DOI:10.1016/j.compstruct.2012.11.020.
[15] imek M. Size dependent nonlinear free vibration of an axially functionally graded (AFG) microbeam using He’s variational method[J]. Composite Structures, 2015, 131:207-214. DOI:10.1016/j.compstruct.2015.05.004.
[16] Shafiei N, Mirjavadi S S, Afshari B M, et al. Nonlinear thermal buckling of axially functionally graded micro and nanobeams[J]. Composite Structures, 2017, 168: 428-439. DOI:10.1016/j.compstruct.2017.02.048.
[17] Reddy J N,El-Borgi S, Romanoff J. Non-linear analysis of functionally graded microbeams using Eringen’s non-local differential model[J]. International Journal of Non-Linear Mechanics, 2014, 67: 308-318. DOI:10.1016/j.ijnonlinmec.2014.09.014.
[18] Ghayesh M H. Nonlinear dynamics of multilayered microplates[J]. Journal of Computational and Nonlinear Dynamics, 2018, 13(2): 1-12. DOI:10.1115/1.4037596.
[19] Ghayesh M H, Farokhi H. Global dynamics of imperfect axially forced microbeams[J]. International Journal of Engineering Science, 2017, 115: 102-116. DOI:10.1016/j.ijengsci.2017.01.005.
[20] Ghayesh M H, Farokhi H, Gholipour A, et al. On the nonlinear mechanics of layered microcantilevers[J]. International Journal of Engineering Science, 2017, 120: 1-14. DOI:10.1016/j.ijengsci.2017.06.012.
[21] Ghayesh M H, Farokhi H. Nonlinear mechanics of doubly curved shallow microshells[J]. International Journal of Engineering Science, 2017, 119: 288-304. DOI:10.1016/j.ijengsci.2017.06.015.
[22] Gholipour A, Farokhi H, Ghayesh M H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates[J]. Nonlinear Dynamics, 2015, 79(3): 1771-1785. DOI:10.1007/s11071-014-1773-7.
[23] Hamed E. Bending and creep buckling response of viscoelastic functionally graded beam-columns[J]. Composite Structures, 2012, 94(10): 3043-3051. DOI:10.1016/j.compstruct.2012.04.029.
[24] Ebrahimi F, Barati M R. Hygrothermal effects on vibration characteristics of viscoelastic FG nanobeams based on nonlocal strain gradient theory[J]. Composite Structures, 2017, 159: 433-444. DOI:10.1016/j.compstruct.2016.09.092.
[25] Ghayesh M H. Dynamics of functionally graded viscoelastic microbeams[J]. International Journal of Engineering Science, 2018, 124: 115-131. DOI:10.1016/j.ijengsci.2017.11.004.