Extreme climates, the reduction of natural surface retention capacity and an inadequate sewer pipe system resulted in a rapidly increasing number of urban flood disasters around the world in recent years[1]. Urban floods usually caused tremendous losses of life and property due to the high density of the population and buildings in urban areas, which has aroused increasing interest in the development of methods to simulate and predict the process of the urban floods. Various urban flood models have been widely developed and applied to simulate and assess urban floods worldwide[2-4]. With the development of one-dimensional or two-dimensional coupled urban flood models, various models considering the interaction between the one-dimensional sewer pipe system and two-dimensional surface system have been developed[5-7].
Hydrological methods were predominantly used in urban runoff models to simulate surface runoff as an input to the sewer pipe system, and the sewer flow hydraulic model was based on the numerical solution of the Saint-Venant equations[8]. Mignot et al.[9] used the two-dimensional shallow water equations to simulate the severe floods in the Richelieu urban, France. In this hydrological model, the pipes’ capacities were simply subtracted from the original input hydrographs. The urban flood model usually consisted of the distinct surface and sewer pipe system, which was called the dual drainage model, as described by Djorjevi![]() et al[10]. The interaction between two systems, which often took place in gully structures and manholes, has an important influence on the simulation accuracy of urban flood models. Schmitt et al.[11] described a detailed dual drainage simulation model and gave special consideration to the interaction between the surface and sewer pipe flow. Djorjevi
et al[10]. The interaction between two systems, which often took place in gully structures and manholes, has an important influence on the simulation accuracy of urban flood models. Schmitt et al.[11] described a detailed dual drainage simulation model and gave special consideration to the interaction between the surface and sewer pipe flow. Djorjevi![]() et al.[12] developed a new simulation model—SISPON to simulate the interaction between pipe flow and surface overland flow in networks, and the calculation method of interaction between the surface and sewer pipe system was based on the weir and orifice formula. A dual multilevel urban drainage model was proposed by Nasello and Tucciarelli[13], and the weir and orifice formula was applied to solve the interaction between upper and lower networks. Chang et al.[14] developed a novel approach to simulate the dynamic flow interaction between storm sewers and overland surface. The overflow returned from the sub-surface to the ground surface via a surcharged manhole as a point source in the two-dimensional overland flow model. Abbasizadeh et al.[15] applied a coupled overland flow model to a case and verified the capability and accuracy of the model. A coupled
et al.[12] developed a new simulation model—SISPON to simulate the interaction between pipe flow and surface overland flow in networks, and the calculation method of interaction between the surface and sewer pipe system was based on the weir and orifice formula. A dual multilevel urban drainage model was proposed by Nasello and Tucciarelli[13], and the weir and orifice formula was applied to solve the interaction between upper and lower networks. Chang et al.[14] developed a novel approach to simulate the dynamic flow interaction between storm sewers and overland surface. The overflow returned from the sub-surface to the ground surface via a surcharged manhole as a point source in the two-dimensional overland flow model. Abbasizadeh et al.[15] applied a coupled overland flow model to a case and verified the capability and accuracy of the model. A coupled  ood model based on the di
ood model based on the di usion-wave equation was proposed by Jang et al.[5] to simulate one-dimensional sewer
usion-wave equation was proposed by Jang et al.[5] to simulate one-dimensional sewer  ow and two-dimensional overland
ow and two-dimensional overland  ow simultaneously. The simulation results indicated that the inlet model has a significant impact on drainage efficiency in coupled flood simulation.
ow simultaneously. The simulation results indicated that the inlet model has a significant impact on drainage efficiency in coupled flood simulation.
The conventional overflow equations based on the weir and orifice formula have been widely used in calculating the exchange flow rate between the surface and sewer pipe system in recent years[6]. Nasello and Tucciarelli[13] applied the calculation method based on the weir and orifice formula in the dual multilevel urban drainage model, which refers to two different formulas to calculate the relationship between the street network system and the sewerage network system under different water flow conditions. Li et al.[16] presented a multi-level and modular model to simulate urban flooding. They divided the surface channel into three parts, including community areas flow, road network flow and river network flow. The control of the value of the discharge coefficient is also a key factor to improve the accuracy since the discharge coefficient in the weir and orifice formula may vary significantly with geometrical configuration[17-19].
Along with the growing need for accurate and detailed simulation of urban floods, the data quality of the exchange flow rate has become more and more important. Moreover, it is important to describe the details of the interaction between the surface and sewer pipe system clearly. Rubinato et al.[20] used the SIPSON numerical model to quantify hydraulic energy loss coefficients under surcharging and non-surcharging conditions. A series of small scale laboratory experiments were carried out by Hakiel and Szyd owski[18]. The results show that the weir and orifice formula is quite suitable for calculating the inflow rate from surface to sewer pipe for speci
owski[18]. The results show that the weir and orifice formula is quite suitable for calculating the inflow rate from surface to sewer pipe for speci c velocities of the surface water flow. The authors also indicated that the slope of surface was the key to the exchange flow rate. Rubinato et al.[21] argued that the orifice formula is suitable for representing sewer to surface flow under steady flow conditions within surcharge events.
c velocities of the surface water flow. The authors also indicated that the slope of surface was the key to the exchange flow rate. Rubinato et al.[21] argued that the orifice formula is suitable for representing sewer to surface flow under steady flow conditions within surcharge events.
With the development of computer science and mathematical theory, computational fluid dynamics (CFD)played a vital role in the development of the urban drainage model. Many investigations[22-23] indicated that CFD can be adopted as an important tool for simulating real large-scale physical experiments. Lopes et al.[24] proposed numerical simulation results of surcharge flow in a gully. The flow features including average velocities and streamlines at the center profile of the gully were also proposed. Rubinato et al.[20] used a physical scale model to quantify flow conditions through a circular inlet under shallow steady state surface flow conditions. Beg et al.[25] demonstrated the ability of the VOF model to reproduce the flow phenomena of a manhole and gully flow under different surcharge conditions. Leandro et al.[26] used the OpenFOAM to characterize the average velocity inside a gully at the center profile and discussed the qualitative air-entrainment structure for both drainage and reverse flow conditions. The growing complexity of urban flood models resulted in an equally increased data demand for the accurate exchange flow rate between the surface and sewer pipe system. The parameterization of complex models imposed a significant number of parameters to define and it needed more accurate data to solve the issue of calibration and validation. In turn, the efficient and accurate data influenced the accuracy of urban flood simulation.
This paper focuses on the interactions between the surface and sewer system in a typical real-world scale drainage system. A series of simulations are carried out to evaluate the exchange flow rate between the surface and sewer pipe system with the hydrodynamics model. The results of CFD simulation are compared with the conventional method, which can evaluate the accuracy of the weir and orifice formula. Physical experiments and CFD models can reduce the uncertainty of the weir and orifice formula and, thus, improve the accuracy of the one-dimensional or two-dimensional urban flood models. Streamlines at the center profile of the manhole under different flow conditions are also proposed, which can show the flow features of the manhole under inflow and surcharge conditions.
1 Materials and Methods
1.1 Methods
The basic governing equations are given as follows:
Continuity equation
![]() +
+![]() ·(ρu)=0
·(ρu)=0
(1)
Momentum equation
![]() +
+![]() ·(ρu⊗u)=-
·(ρu⊗u)=-![]() p+μΔu+μt(
p+μΔu+μt(![]() u+
u+![]() Tu)+ρg+F
Tu)+ρg+F
(2)
where t is the time; ρ is the density of the fluid; u is the velocity; p is the pressure; g is the gravity; F is the external body force vector; μ is the molecular viscosity coefficient; μt=Cuκ2/ε is the turbulent viscosity coefficient, which can be derived from the turbulent kinetic energy κ and turbulent dissipation rates ε, and Cu is the empirical coefficient. κ-ε equation is given as follows:
κ equation
![]()
![]() κ]+G-ρε
κ]+G-ρε
(3)
ε equation
(4)
where G is the turbulent kinetic energy source term; C is the coefficient of friction resistance; the empirical constants σk=1.0, σε=1.3, σε1=1.44, and σε2=1.92.
The VOF method is widely used to capture the free surface of water[27]. The domain is composed of two superposed fluids (water and air) in this study. The VOF model defines a volume of fluid fraction function F=F(x,y,z,t) to describe the free surface:
![]() +u·
+u·![]() αl=0
αl=0
(5)
The sum of the volume fraction of water and air is 1 in each calculation unit, namely,
(6)
where l is the phase number, and α is the phase fraction. The value of the volume fraction is equal to 1 if the cell is full with fluid, while 0 indicates that the cell contains no fluid. The cells with the values between 1 and 0 must contain the free surface. The free water surface is usually defined with a water volume fraction of 0.5.
The semi-implicit method for the pressure-linked equation (SIMPLE) algorithm proposed by Patankar and Spalding[28] is used to solve the pressure-velocity coupled field in this research. An approximation of the velocity field is obtained by solving the momentum equation. The pressure distribution from the previous iteration or an initial guess is used to calculate the pressure gradient term. The computed velocities and the estimated pressure are corrected by the pressure-correction equation.
1.2 Weir and orifice formula
The conventional weir and orifice formula is given as follows [13].
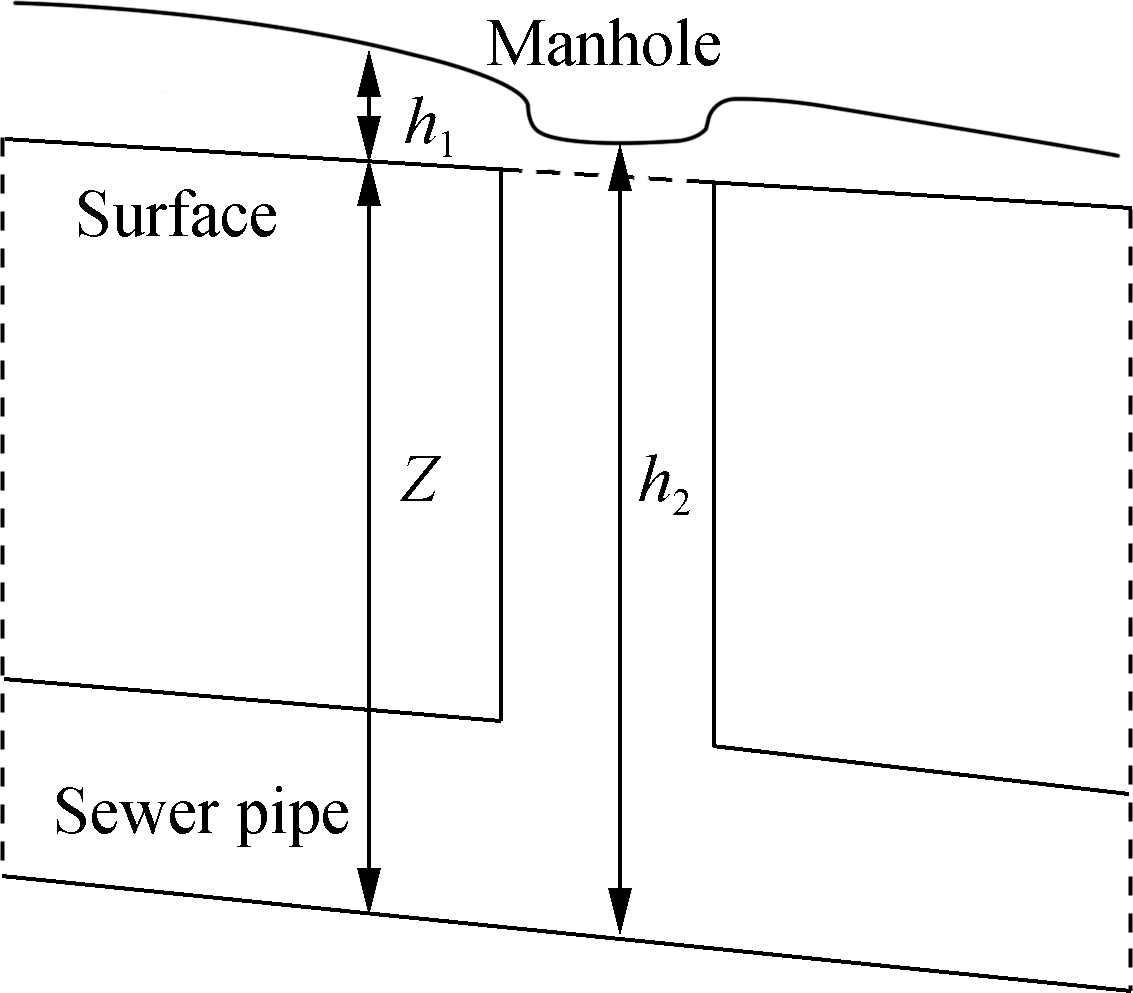
If the water level of the pipe is below ground level (see Fig.1 (a)), the flow rate Qexch from the street surface entering the sewer pipe system is
(7)
where g is the gravity; Lin is the portion of perimeter of the manhole; h1 is the water level above the ground; and Ain is the open area of the manhole.
If the piezometric head in the manhole is above ground level (see Figs.1(b) and (c)), the velocity of exchange flow between the street surface and sewer pipe system is calculated by the following orifice formula:
(8)
where h2 and Z are the water level at the manhole and crest elevation, respectively. For larger values of h1, the water surface covers all the manhole inlet open area.
1.3 Model setup
1.3.1 Computational mesh
The three-dimensional model based on the real-world street and sewer pipe system structures is built by the ANASYS Fluent, and it defines the geometrical boundary conditions. The length of the street is 20 m with a width of 10.5 m, and the diameter of the pipe is 0.6 m. The slopes of the street and the sewer pipe are set to be 0.5% in the x coordinate, and the slope of the street is 1.5% in the z coordinate. The shape of the manhole is a circle truncated cone. The height is 2 m, and the width is 1 m at the bottom and 0.6 m at the top. The model geometry and boundaries of the model are shown in Fig.2.

(a)
(b)

(c)
Fig.1 Schematic flow flux at manhole. (a) Water level of the pipe below ground level; (b) Water level of the pipe above ground level but less than h1; (c) Water level of the pipe above ground level and larger than h1
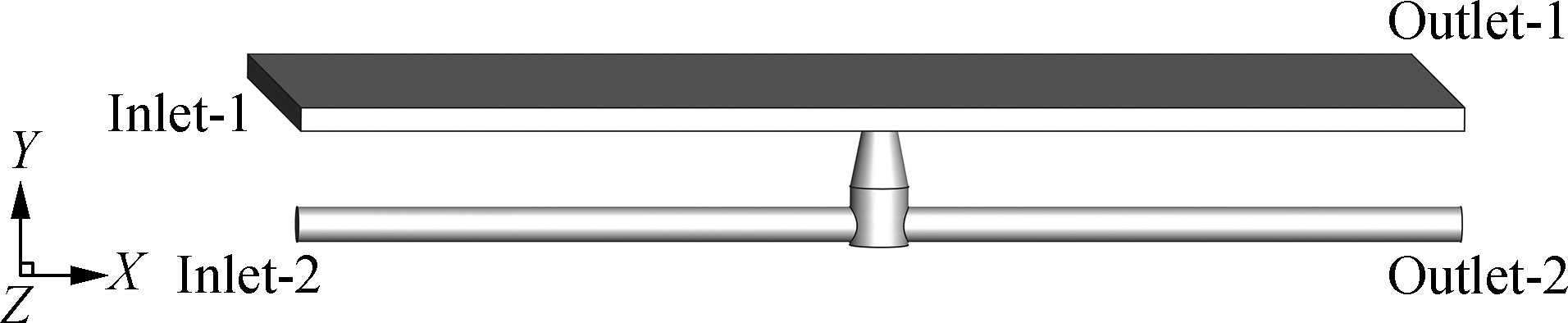
Fig.2 Structure and boundaries of the model
The mesh construction is a critical step of mathematical simulation. The mesh resolution has a significant impact on the quality of capturing the free surface of water based on the VOF method. In this research, most domains are meshed in a structured hexahedral grid with a grid spacing between 0.04 and 0.08 m. The mesh consists of about 1.2 million hexahedral cells or control volumes. The overall grid is suitable and the minimum orthogonal quality is 0.527. The finer mesh is applied to the manhole whereas the coarser mesh is applied to the main channel. Fig.3 shows the details of computational meshes.
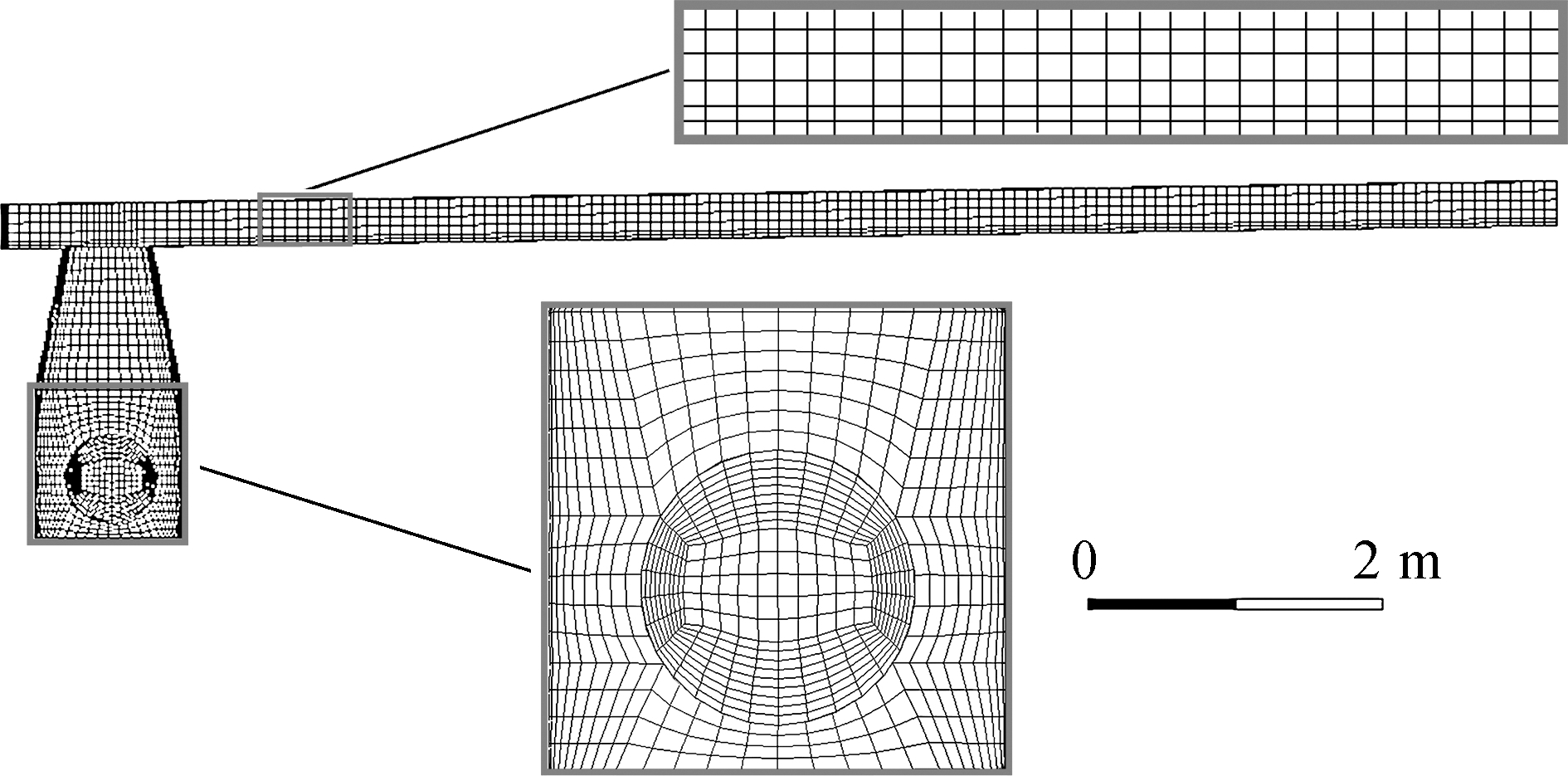
Fig.3 Details of computational mesh
1.3.2 Boundary conditions
A boundary condition mainly consists of inlet and outlet boundary conditions. The most common method to set the inlet boundary is to fix the inlet velocity. In this research, the inlet boundary condition for the case of inflow condition is set to be a predefined constant velocity across the street and pipe cross-profile (Inlet-1 and Inlet-2) (see Fig.2). Velocities under the inlet boundary conditions are calculated with different Inlet-1 water levels based on the Chézy formula. The Chézy formula describes the mean flow velocity of steady, turbulent open channel and pipe flow. Also, the street’s water level is set from 0.05 to 0.4 m (see Tab.1). Then, the flow rate of Inlet-1 can be calculated by flow velocity and the areas of Inlet-1. In this study, the sewer pipe is considered to be always filled with water, which means that the water level of the sewer pipe is set to be 0.6 m, and the velocity of the pipe is 1.545 m/s calculated by the Chézy formula. From Tab.1, it can be seen that the Froude is less than 1 when the water level is between 0.050 and 0.200 m. On all the solid boundaries, the no-slip boundary condition is applied. The dispersed type is used for the cells that lie near the interface between the two phases.
It is important that the outlet boundary condition should have a weak influence on the upstream flow and should be avoided in the regions of strong geometrical changes. The most common outlet boundary is set as the pressure outlet; the relative pressure is fixed to be 0 (Outlet-1, Outlet-2) for the case of inflow condition (see Fig.2).
Tab.1 Boundary conditions of Inlet-1 for the case of inflow condition
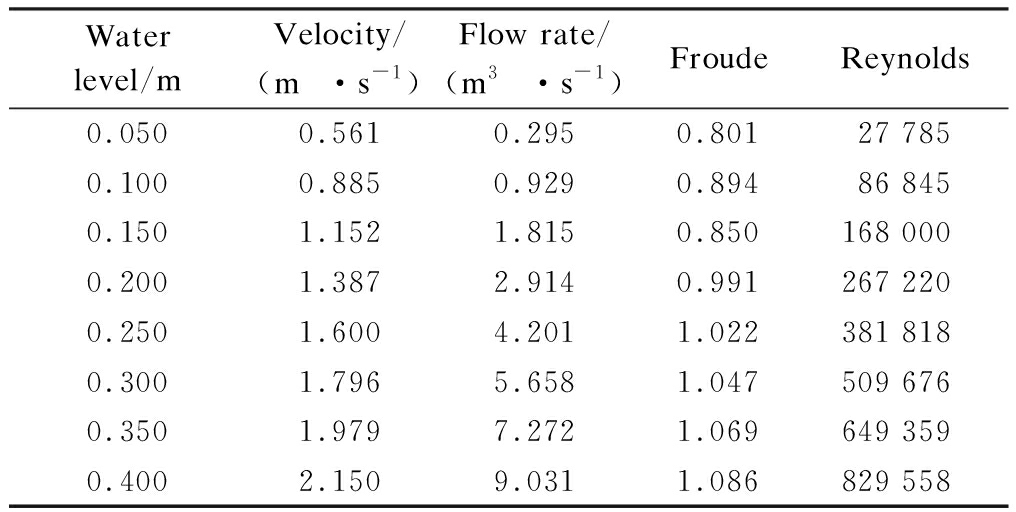
Water level/mVelocity/(m·s-1)Flow rate/(m3·s-1)FroudeReynolds0.0500.5610.2950.80127 7850.1000.8850.9290.89486 8450.1501.1521.8150.850168 0000.2001.3872.9140.991267 2200.2501.6004.2011.022381 8180.3001.7965.6581.047509 6760.3501.9797.2721.069649 3590.4002.1509.0311.086829 558
In order to simulate the overflow process, the outlet boundary conditions for the case of surcharge condition are changed to free outflow. The Inlet-1 flow rate is set to be 5.7 m3/s. The capacity of Outlet-2 is limited to be 0.437 m3/s. The flow rate of Inlet-2 in four different cases as shown in Tab.2. Then, the velocity of Inlet-2 can be calculated by the flow rate and the area of Inlet-2.
Tab.2 Boundary conditions of Inlet-2 for the case of surcharge condition
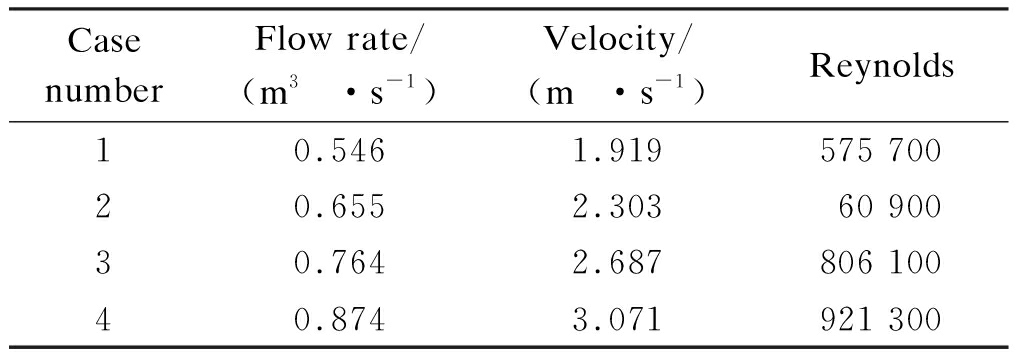
Case numberFlow rate/(m3·s-1)Velocity/(m·s-1)Reynolds10.5461.919575 70020.6552.30360 90030.7642.687806 10040.8743.071921 300
1.4 Model verification
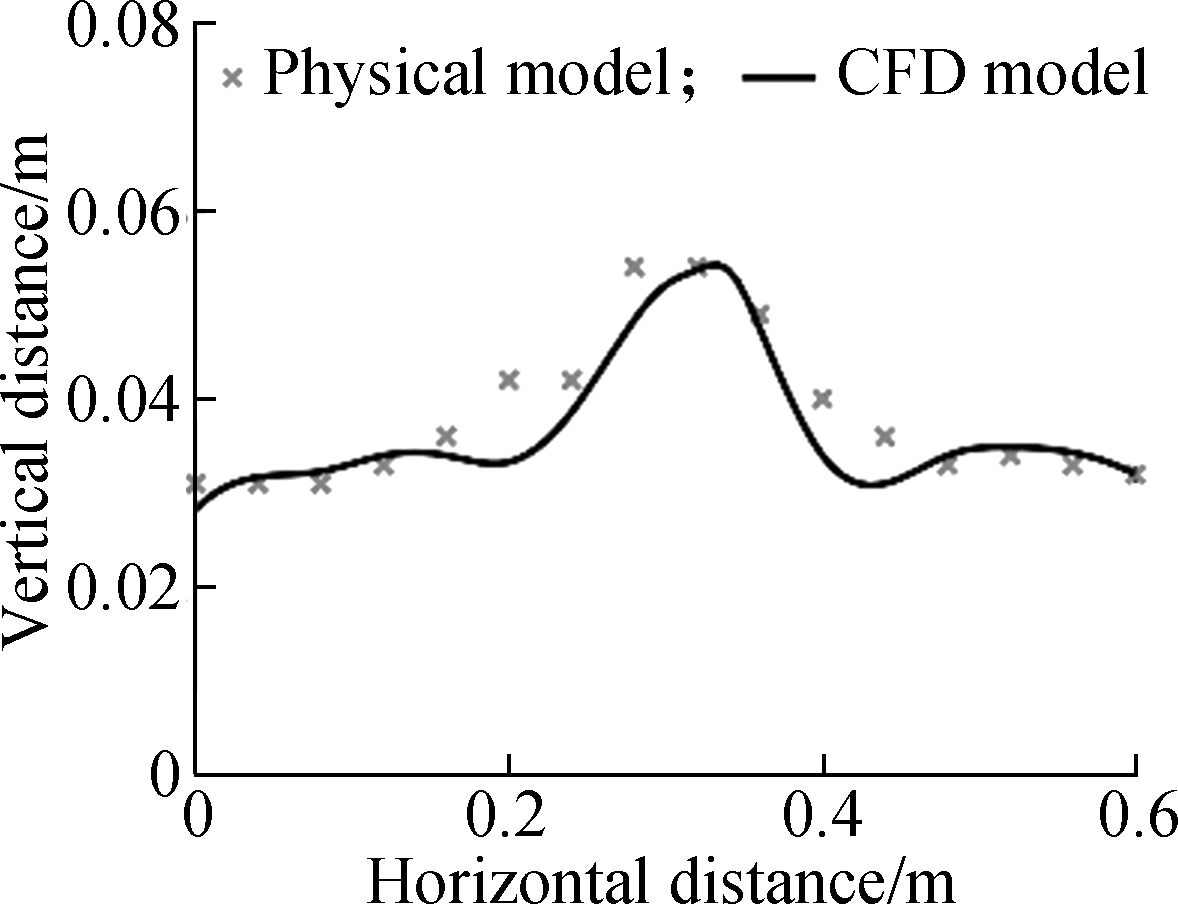
Lopes et al.[24] investigated a gully under the surcharge conditions with numerical and experimental models. The physical model data is obtained by the computational vision model.
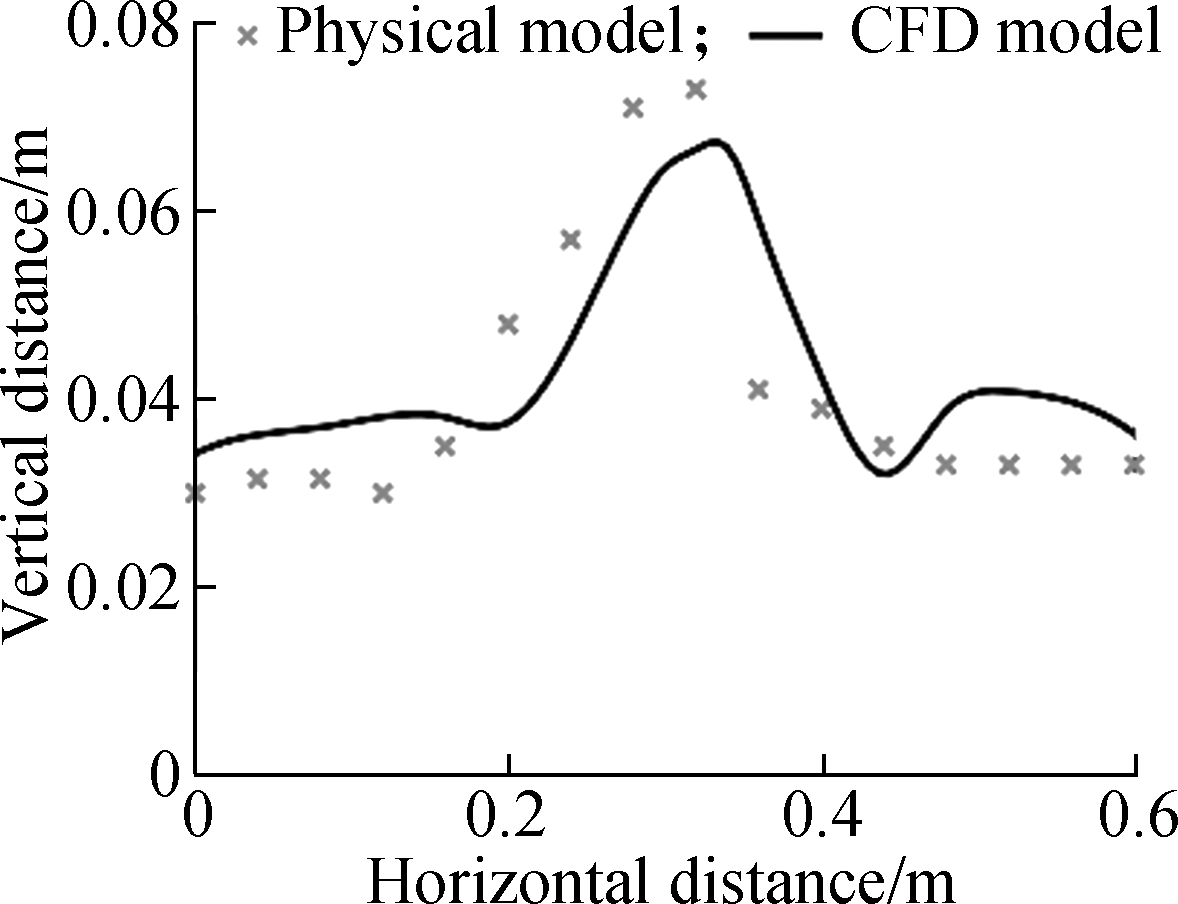
A CFD model based on the structure of Lopes et al’s experiment was created to evaluate the accuracy and efficiency of the numerical model. The numerical average contour in the central section of the gully with different inlet flow rates is shown in Fig.4. The result of Lopes et al’s physical model was compared with that of the CFD simulation. The agreement between CFD model and physical model shows that the CFD model can simulate the surcharge condition well. The maximum error is 7.12% and the minimum error is 0.52%. The numerical model can be used in further study.
2 Results and Discussion
2.1 Comparison between weir/orifice formulas and CFD simulation
The aim of this work is to assess the exchange flow rate between the surface and sewer pipe system to describe the exchange process more precisely in the urban flood model. In the first step, the simulation results are analyzed by considering the relationship between the water level above ground h1 and the exchange flow rate to assess the accuracy of the conventional method. Fig.5 shows the water and air regions at the center profile of the manhole when the Inlet-1 water level is set to be 0.35 m, which describes the water level above ground h1. The simulation results include the water level above ground h1 and the exchange flow rate between the surface and sewer pipe sys-tem calculated by the weir formula and simulation, which are listed in Tab.3. The time-step is set to be 0.02 s.

(a)
(b)
(c)
Fig.4 Comparisons of the CFD model and Lopes et al’s physical model under different inlet flow rates. (a) 4 L/s; (b) 5 L/s; (c) 6 L/s.

Fig.5 Contours of volume fraction of air (Va is the volume fraction of air)
As shown in Fig.6, the simulation results reveal that the sewer system has an extremely sensitive response to the exchange flow rate and surface inflow water levels. With the increase in the Inlet-1 water level, the water level is above ground (h1) and the exchange flow rate increases quickly. The simulation results are compared with those calculated by the conventional weir/orifice formula (Eq.(7)). The results show that CFD simulation has a high rate of similarity with the conventional method. The average difference between the conventional formula and CFD simulation is 0.025, which indicates the reliability of the conventional formula to calculate for the condition when the total inflow discharge does not exceed the design pipe’s outflow capacity. Additionally, the correlation coefficient is 0.994 and the root mean square error is 0.029. The results show that the conventional weir and orifice formula can calculate the exchange flow rate between two systems effectively in this specific case. At the same time, Rubinato et al. [20] considered that the accuracy of the weir and orifice formula depends on different conditions. When replicating experimental conditions within the numerical model, the performance of the model was found to deteriorate in the more complex surcharging flow conditions.
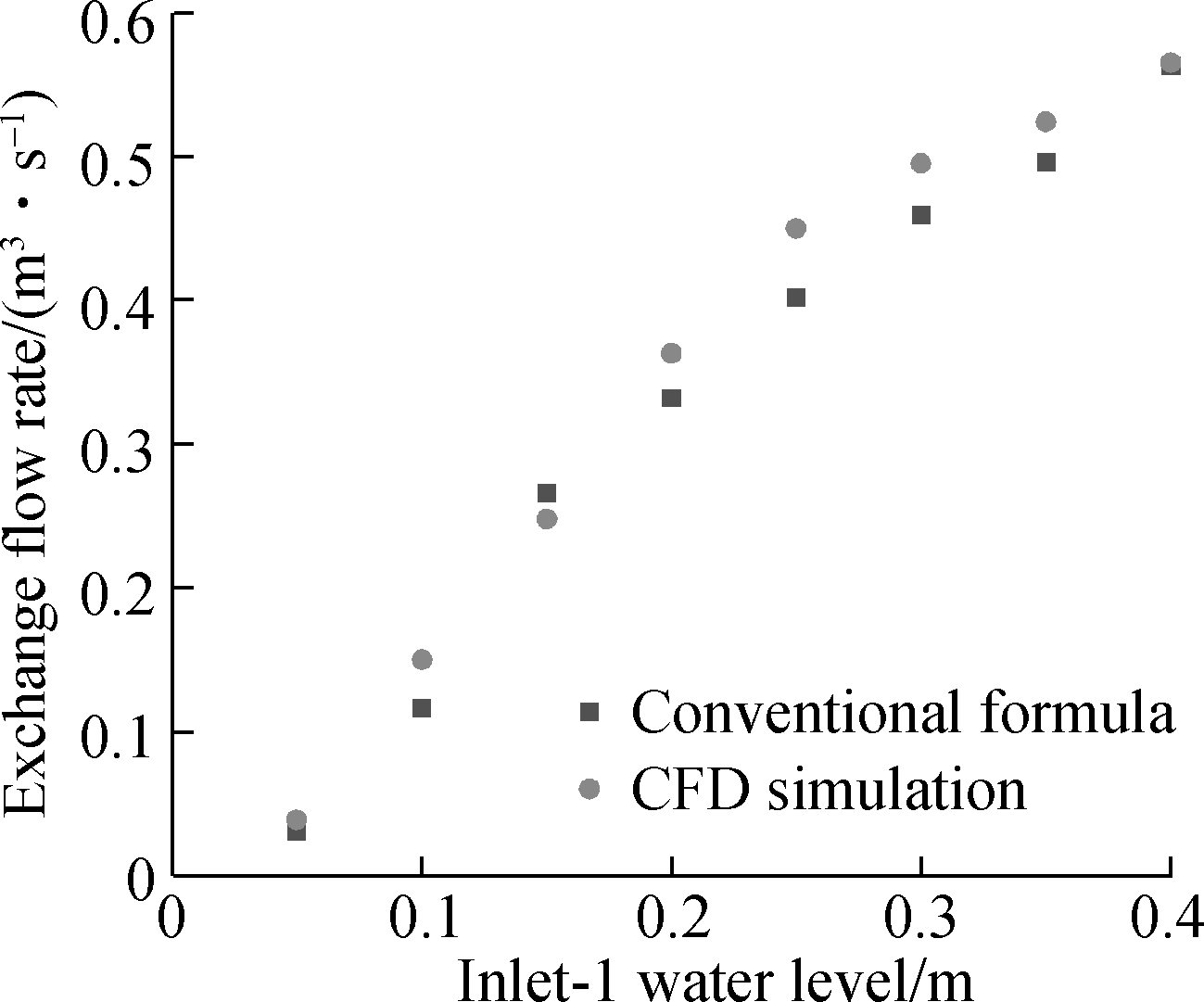
Fig.6 Comparison of CFD simulated results and weir/orifice formulas under inflow condition
With the increase in the surface flow, the sewer pipe surcharge occurs. When the inflow exceeds the outflow, the surcharges return to the surface through the manhole. The overflow process is much more complex than the inflow process. It is very difficult to set the precise boundary conditions of the real overflow process in the CFD model due to the complexity of surcharge condition. The boundary conditions of the overflow process are difficult to replicate in the CFD model with pressure or velocity boundary conditions. In this research, the outflow capacity is limited to replicate the overflow process. The boundary conditions of Inlet-2 for the case of surcharge condition are listed in Tab.2. The average exchange flow rate between the surface and sewer pipe system is also determined by the CFD simulation and conventional weir and orifice formula. The similarities of CFD simulation results and orifice formulae under the surcharge conditions are demonstrated in Fig.7. The average difference in Case 1 to Case 3 is 0.006, which indicates that the similarity between the results of CFD and the conventional formula is extremely high. The difference of the exchange flow rate in Case 4 is 0.055, which is relatively large. It may be due to the factors such as different types of inlet, which affect the flow at the manhole which becomes more complicated at higher flow rates.
The exchanged flow rates exhibit some slight fluctuations with time, which can be the result of the iterative nature of numerical computations. After about 30 s’ simulation, the simulation reaches an approximate steady state. The average exchange flow rate of the four cases from 30 to 40 s calculated respectively by the orifice formulation and CFD simulation are consistent.

Fig.7 Comparison of CFD simulated results and weir/orifice formulas under the surchage condition
2.2 Flow features of inflow conditions
Compared with the experimental model, CFD simulation can accurately and clearly present the flow features. Streamlines and velocity contours at the center manhole profile at different water levels are proposed, which can provide details of the interaction between the two systems.
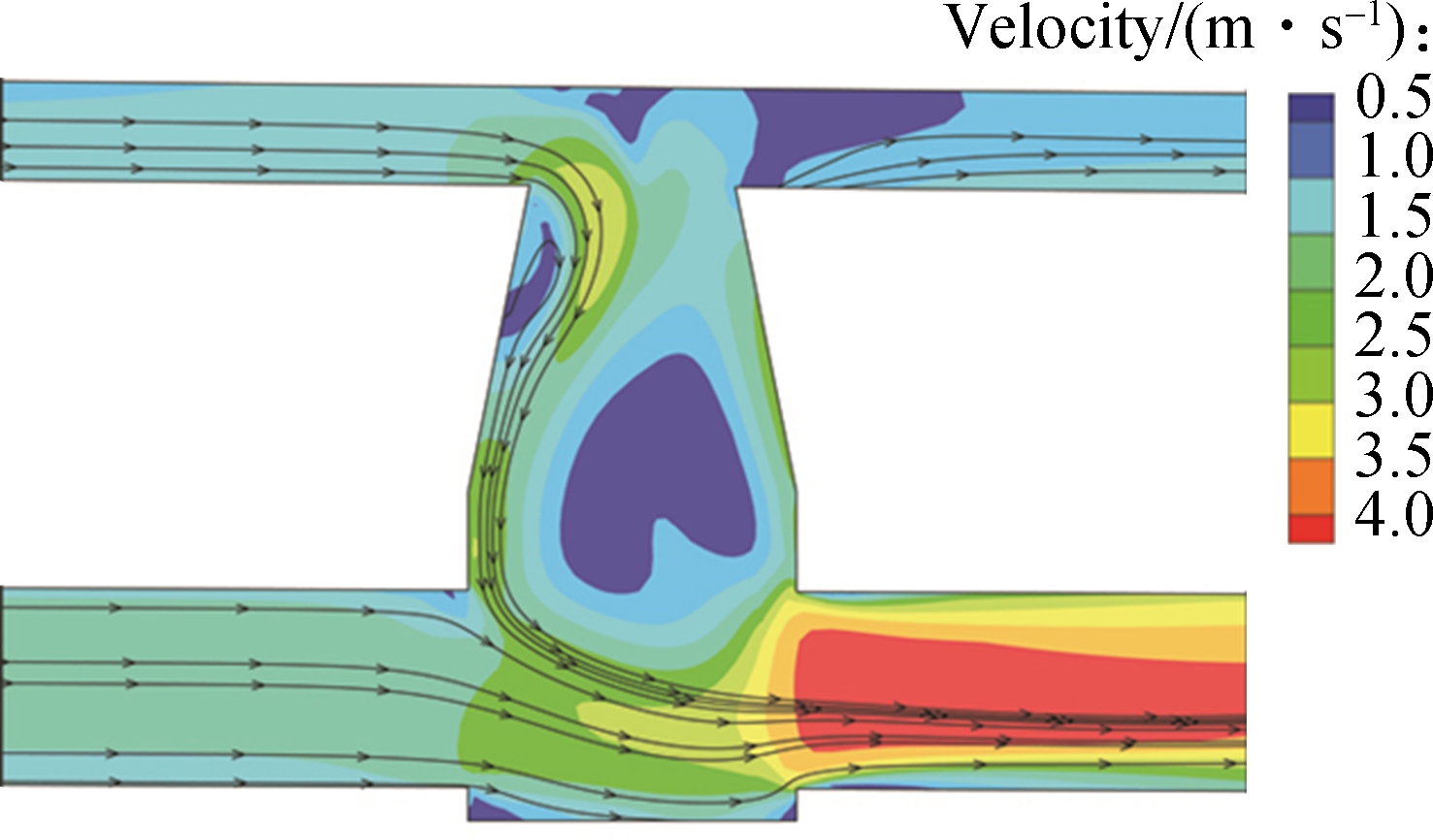
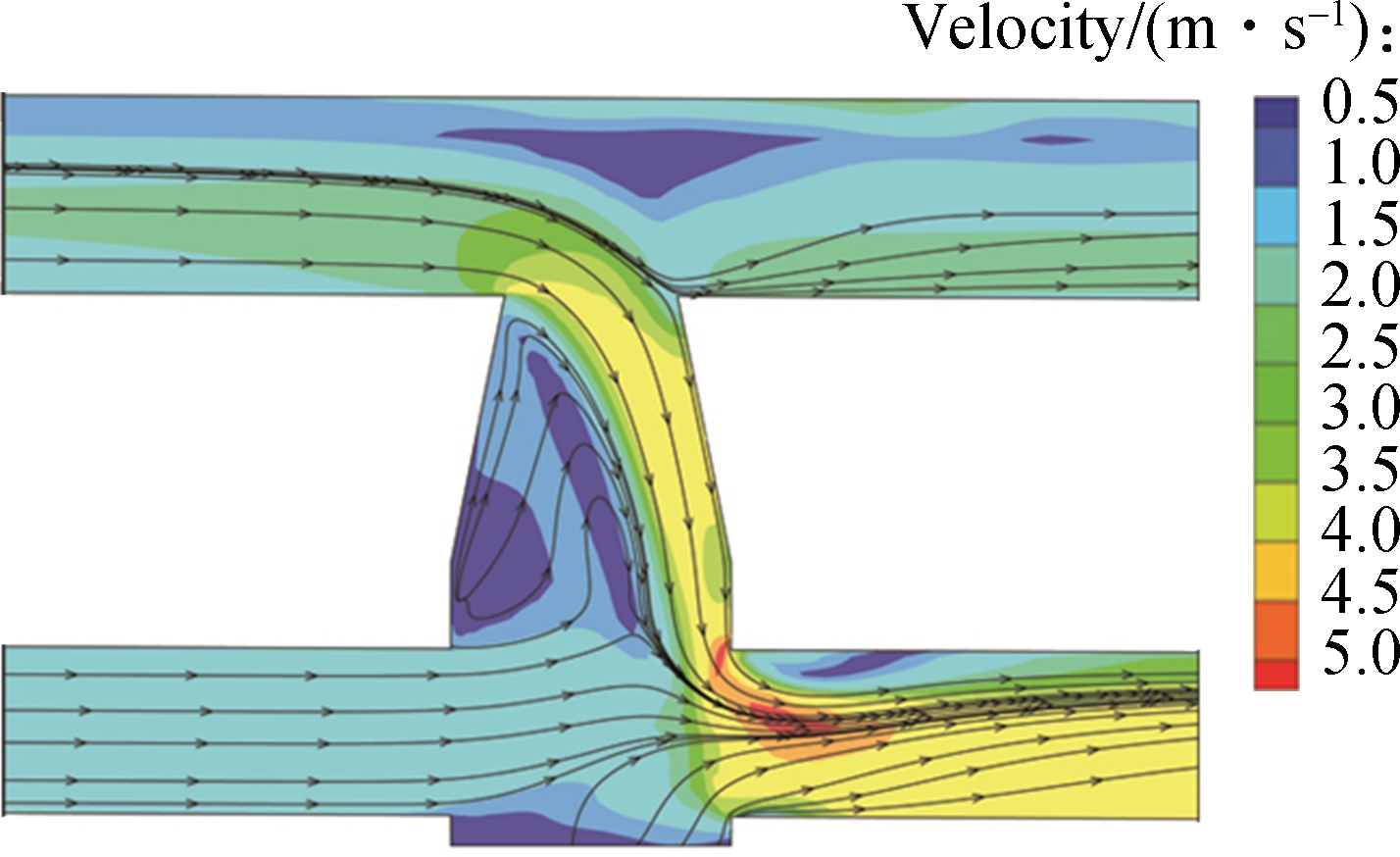
For the normal condition when the total inflow discharge from the surface does not exceed the pipe’s outflow capacity, the surface flow enters the sewer system at manholes then drains through the downstream sewer pipe without surcharge. The complex interaction between the flow from the sewer pipe system and the surface plays an important role in the exchange process. Fig.8 shows the streamlines and velocity contour at the center profile of the manhole when the flow is stable with different Inlet-1 water levels of 0.05, 0.15, 0.25 and 0.35 m. When the Inlet-1 water level is 0.05, 0.15 and 0.25 m, the flow flows through the edge of the manhole without covering all of the manhole inlet open area. With the increase in the inflow rate, the water surface covers all the open area (Inlet-1 0.35 m). It can be seen from Fig.8 that the flow from the surface and sewer pipe converges in the bottom of the manhole, and develops a complex circle flow in the left area of the manhole. The velocity of the circle flow is about 1 m/s and the velocity of inflow is about 3 m/s. The range of the circle flow enlarges with the increase in the Inlet-1 water level. The velocity of inflow increases along with the increase in Inlet-1 water level and the junction area of the manhole and the right pipe has a maximum velocity.
2.3 Flow features of surcharge conditions
The streamlines and velocity contours of the center profile under the surcharge condition are presented, which shows a qualitative analysis of overflow process.
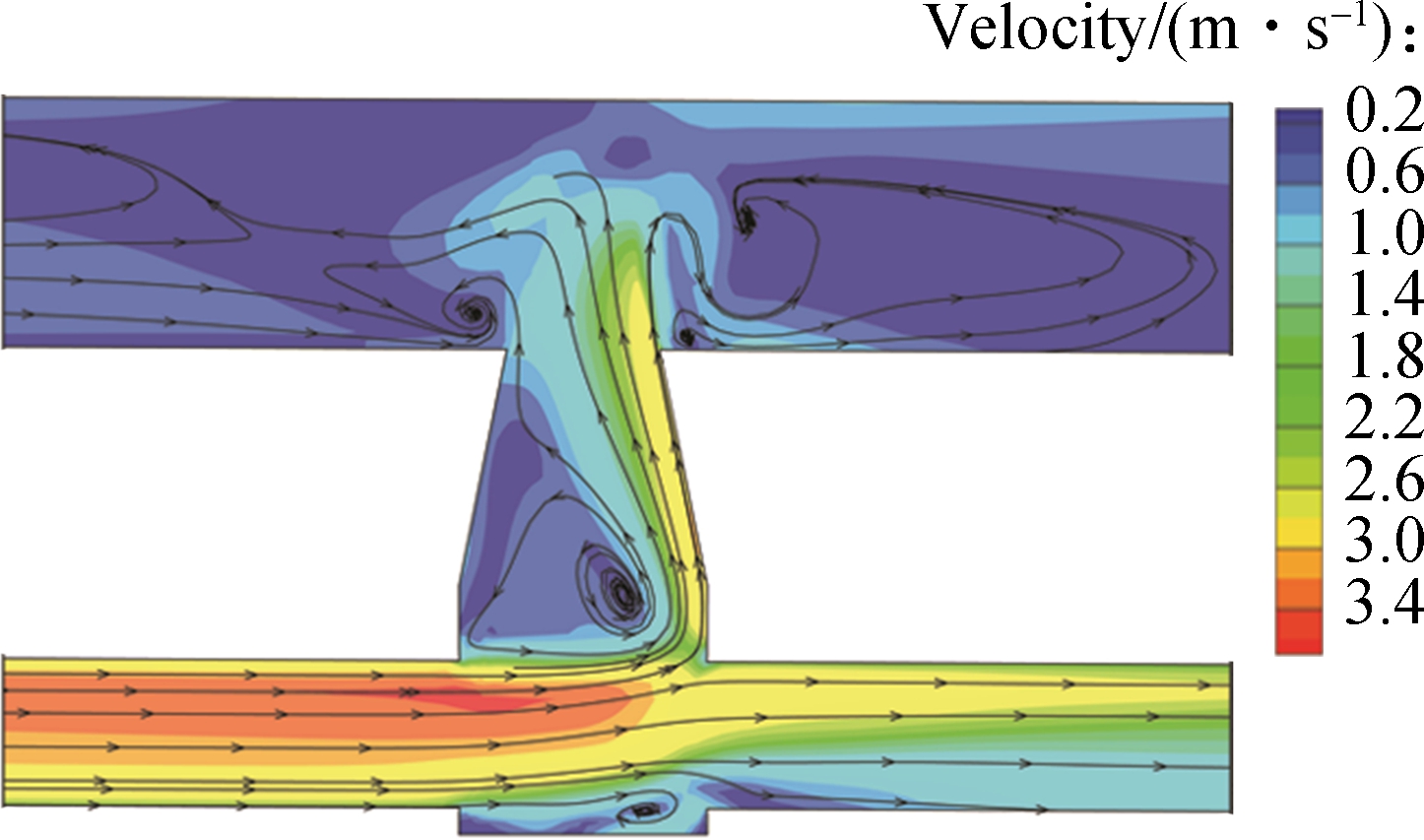
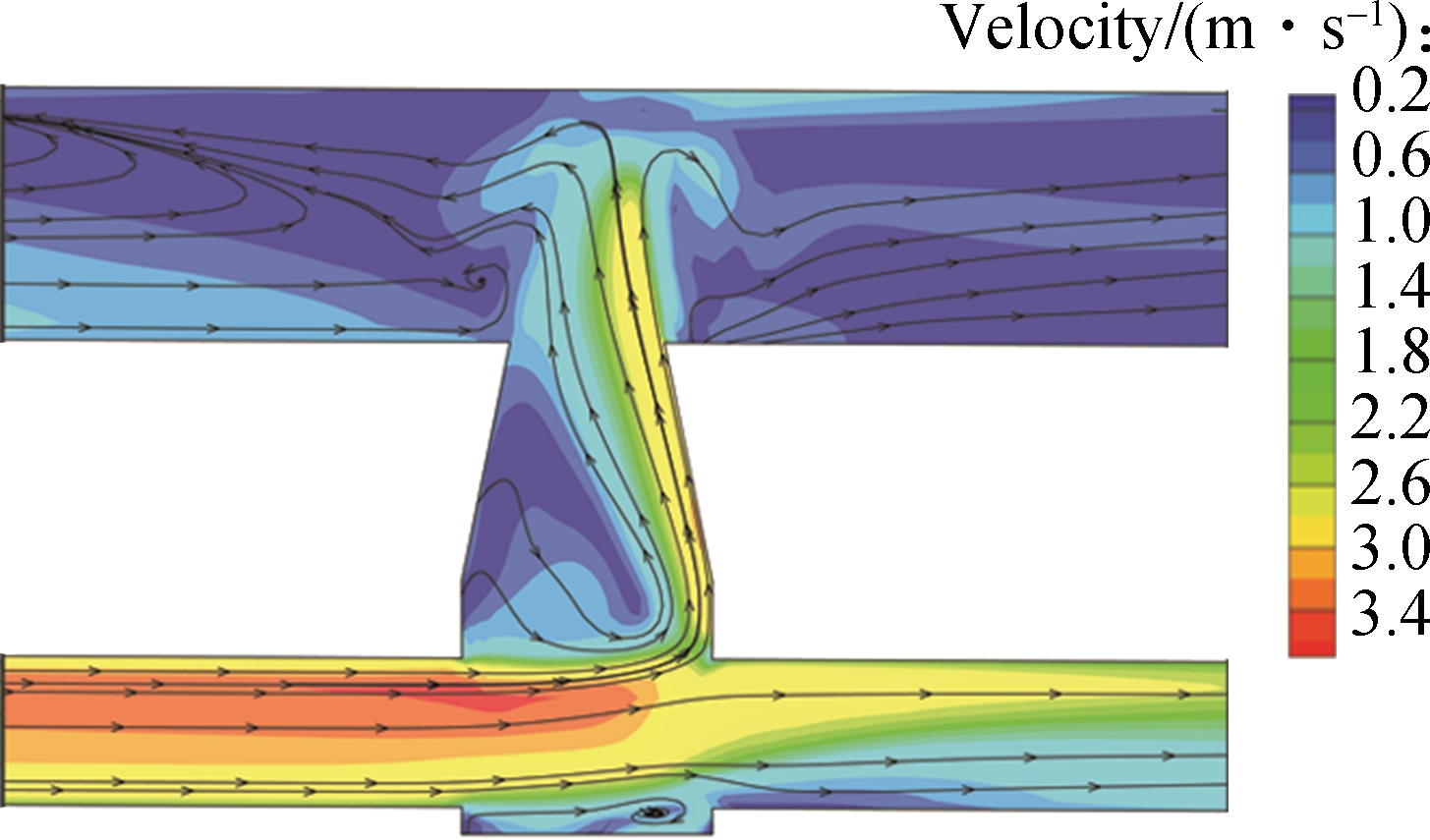
The numerical simulation under the surcharge condition lasts about 40 s. The streamlines and velocity contours of overflow at the time of 30 and 40 s of Case 3 are shown in Fig.9. As shown in Fig.9, the overflow from the sewer pipe system returns to the surface mainly through the right part of the manhole, which is similar to the research of Lopes et al[24]. When t=30 s, the left area of the manhole develops a circular flow and the velocity of the circular flow is lower compared to the right area of the manhole. Unlike the inflow process, the junction area of the manhole and left pipe has a maximum velocity. The flow features are different before and after t=30 s. Before t=30 s, the overflow only flows to the downstream with the surface flow. However, after t=30 s, the overflow flows both upstream and downstream, which has a significant effect on the surface flow. The representative overflow appears after about 30 s’ simulation.

(a)
(b)

(c)
(d)
Fig.8 Streamlines in the manhole and the pipe under different Inlet-1 water levels. (a) 0.05 m; (b) 0.15 m;(c) 0.25 m;(d) 0.35 m
(a)
(b)
Fig.9 Streamlines of overflow process at the center profile of the manhole of Case 3 under different model times. (a) t=30 s;(b) t=40 s
3 Conclusions
1) A real-world scale three-dimensional numerical model is proposed to study the exchange flow rate between the surface and sewer pipe system. The free water surface is reproduced with the three-dimensional CFD model by using the VOF model. The model can reduce uncertainty and improve the accuracy of the one-dimensional or two-dimensional urban flood models.
2) The CFD simulation results are compared with the conventional equations based on the weir and orifice formula, the agreement between CFD simulation and the weir and orifice formula is good enough in specific cases. The agreement of results verifies that the reliability of the weir and orifice formula can calculate the exchange flow rate under qualified conditions.
3) The flow features including velocity and streamlines both in normal and overflow processes are studied. Streamlines and the velocity contour at the center profile under both inflow and surcharge conditions show the flow features clearly. The variation of streamlines and contour of flow velocity indicates specific hydraulic characteristics. Under the inflow conditions, the range of the circular flow velocity enlarges with the increase of the water level on the road. The velocity of inflow is related to the water level on the surface and the junction area between the manhole and right pipe. Under the surcharge condition, overflow flows both upstream and downstream, which has a significant effect on surface flow.
4) This work demonstrates the potential application of CFD in the analysis of the interaction of urban flood flows, which can provide much clearer details of the interaction process. More realistic conditions such as the curb should be taken into account.
[1] Zhang J Y, Song X M, Wang G Q, et al. Development and challenges of urban hydrology in a changing environment: Ⅰ: Hydrological response to urbanization[J]. Advances in Water Science, 2014, 25(4): 594-605. DOI:10.14042/j.cnki.32.1309.2014.04.020.(in Chinese)
[2] Vojinovic Z, Tutulic D. On the use of 1D and coupled 1D-2D modelling approaches for assessment of flood damage in urban areas[J]. Urban Water Journal, 2009, 6(3): 183-199. DOI:10.1080/15730620802566877.
[3] Fraga I,Cea L, Puertas J. Validation of a 1D-2D dual drainage model under unsteady part-full and surcharged sewer conditions[J]. Urban Water Journal, 2017, 14(1): 74-84. DOI:10.1080/1573062x.2015.1057180.
[4] Pan A J, Hou A Z, Tian F Q, et al. Hydrologically enhanced distributed urban drainage model and its application in Beijing City[J]. Journal of Hydrologic Engineering, 2012, 17(6): 667-678. DOI:10.1061/(asce)he.1943-5584.0000491.
[5] Jang J H, Chang T H, Chen W B. Effect of inlet modelling on surface drainage in coupled urban flood simulation[J].Journal of Hydrology, 2018, 562: 168-180. DOI:10.1016/j.jhydrol.2018.05.010.
[6] Chen A S, Leandro J,Djordjevi![]() S. Modelling sewer discharge via displacement of manhole covers during flood events using 1D/2D SIPSON/P-D wave dual drainage simulations[J]. Urban Water Journal, 2016, 13(8): 830-840. DOI:10.1080/1573062x.2015.1041991.
S. Modelling sewer discharge via displacement of manhole covers during flood events using 1D/2D SIPSON/P-D wave dual drainage simulations[J]. Urban Water Journal, 2016, 13(8): 830-840. DOI:10.1080/1573062x.2015.1041991.
[7] Hsu M, Chen S, Chang T. Inundation simulation for urban drainage basin with storm sewer system[J].Journal of Hydrology, 2000, 234(1/2): 21-37. DOI:10.1016/s0022-1694(00)00237-7.
[8] Rossman L A. Storm water management model user’s manual, Version 5.0. U.S. Environ. Prot. Agency [EB/OL].(2010)[2020-03-21]. https://doi.org/PNR61.
[9] Mignot E, Paquier A, Haider S. Modeling floods in a dense urban area using 2D shallow water equations[J]. Journal of Hydrology, 2006, 327(1/2): 186-199. DOI:10.1016/j.jhydrol.2005.11.026.
[10] Djordjevi![]() S, Prodanovi
S, Prodanovi![]() D, Maksimovi
D, Maksimovi![]() . An approach to simulation of dual drainage[J]. Water Science and Technology, 1999, 39(9): 95-103. DOI:10.2166/wst.1999.0451.
. An approach to simulation of dual drainage[J]. Water Science and Technology, 1999, 39(9): 95-103. DOI:10.2166/wst.1999.0451.
[11] Schmitt T, Thomas M,Ettrich N. Analysis and modeling of flooding in urban drainage systems[J]. Journal of Hydrology, 2004, 299(3/4): 300-311. DOI:10.1016/s0022-1694(04)00374-9.
[12] Djordjevi![]() S, Prodanovi
S, Prodanovi![]() D, Maksimovi
D, Maksimovi![]() , et al. SIPSON-simulation of interaction between pipe flow and surface overland flow in networks[J]. Water Science and Technology, 2005, 52(5): 275-283. DOI:10.2166/wst.2005.0143.
, et al. SIPSON-simulation of interaction between pipe flow and surface overland flow in networks[J]. Water Science and Technology, 2005, 52(5): 275-283. DOI:10.2166/wst.2005.0143.
[13] Nasello C, Tucciarelli T. Dual multilevel urban drainage model[J]. Journal of Hydraulic Engineering, 2005, 131(9): 748-754. DOI:10.1061/(asce)0733-9429(2005)131:9(748).
[14] Chang T J, Wang C H, Chen A S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas[J].Journal of Hydrology, 2015, 524: 662-679. DOI:10.1016/j.jhydrol.2015.03.014.
[15] Abbasizadeh H, Nazif S, Hosseini S A, et al. Development of a coupled model for simulation of urban drainage process based on cellular automata approach[J]. Irrigation and Drainage, 2018, 67(2): 269-281. DOI:10.1002/ird.2186.
[16] Li D M, Wang X, Xie Y Y, et al. A multi-level and modular model for simulating the urban flooding and its application to Tianjin City[J]. Natural Hazards, 2016, 82(3): 1947-1965. DOI:10.1007/s11069-016-2279-z.
[17] Bazin P H, Nakagawa H, Kawaike K, et al. Modeling flow exchanges between a street and an underground drainage pipe during urban floods[J]. Journal of Hydraulic Engineering, 2014, 140(10): 04014051. DOI:10.1061/(asce)hy.1943-7900.0000917.
[18] Hakiel J, Szyd owski M. Interaction between storm water conduit flow and overland flow for numerical modelling of urban area inundation[M]//Hydrodynamic and Mass Transport at Freshwater Aquatic Interfaces. Cham, Switzerland: Springer International Publishing, 2016: 23-34. DOI:10.1007/978-3-319-27750-9_3.
owski M. Interaction between storm water conduit flow and overland flow for numerical modelling of urban area inundation[M]//Hydrodynamic and Mass Transport at Freshwater Aquatic Interfaces. Cham, Switzerland: Springer International Publishing, 2016: 23-34. DOI:10.1007/978-3-319-27750-9_3.
[19] Rubinato M, Shuksimth J, Saul A. Experimental investigation of flow-interactions between above and below ground drainage systems through a manhole [R/OL]. CUNY Academic Works, 2014. http://academicworks.cuny.edu/cc_conf_hic/14.
[20] Rubinato M, Lee S, Martins R, et al. Surface to sewer flow exchange through circular inlets during urban flood conditions[J]. Journal of Hydroinformatics, 2018, 20(3): 564-576. DOI:10.2166/hydro.2018.127.
[21] Rubinato M, Martins R, Kesserwani G, et al. Experimental calibration and validation of sewer/surface flow exchange equations in steady and unsteady flow conditions[J]. Journal of Hydrology, 2017, 552: 421-432. DOI:10.1016/j.jhydrol.2017.06.024.
[22] Djordjevi![]() S, Saul A J, Tabor G R, et al. Experimental and numerical investigation of interactions between above and below ground drainage systems[J]. Water Science and Technology, 2013, 67(3): 535-542. DOI:10.2166/wst.2012.570.
S, Saul A J, Tabor G R, et al. Experimental and numerical investigation of interactions between above and below ground drainage systems[J]. Water Science and Technology, 2013, 67(3): 535-542. DOI:10.2166/wst.2012.570.
[23] Fach S, Sitzenfrei R, Rauch W. Determining the spill flow discharge of combined sewer overflows using rating curves based on computational fluid dynamics instead of the standard weir equation[J]. Water Science and Technology, 2009, 60(12): 3035-3043. DOI:10.2166/wst.2009.752.
[24] Lopes P, Leandro J, Carvalho R F, et al. Numerical and experimental investigation of a gully under surcharge conditions[J]. Urban Water Journal, 2015, 12(6): 468-476. DOI:10.1080/1573062x.2013.831916.
[25] Beg M N A, Carvalho R F, Leandro J. Effect of surcharge on gully-manhole flow[J]. Journal of Hydro-Environment Research, 2018, 19: 224-236. DOI:10.1016/j.jher.2017.08.003.
[26] Leandro J, Lopes P, Carvalho R, et al. Numerical and experimental characterization of the 2D vertical average-velocity plane at the center-profile and qualitative air entrainment inside a gully for drainage and reverse flow[J]. Computers & Fluids, 2014, 102: 52-61. DOI:10.1016/j.compfluid.2014.05.032.
[27] Mohsin M, Kaushal D R. 3D CFD validation of invert trap efficiency for sewer solid management using VOF model[J]. Water Science and Engineering, 2016, 9(2): 106-114. DOI:10.1016/j.wse.2016.06.006.
[28] Patankar S, Spalding D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows[J]. International Journal of Heat and Mass Transfer, 1972, 15(10): 1787-1806. DOI:10.1016/0017-9310(72)90054-3.