The arterial of the city bears the traffic demand between the main areas, and its traffic efficiency status affects the traffic condition of the whole road network. Therefore, improving the traffic efficiency of arterial is of great significance. The existing theoretical and practical results show that by coordinating and optimizing the signal control of adjacent intersections on an arterial, the stopping time of vehicles can be reduced, and the traffic on the main road can be more efficient.
At present,the most common method to coordinate urban arterial signals is the least delay method or the maximal progression bandwidth. Closely spaced traffic signals along an arterial are typically coordinated by a typical cycle length and appropriate offsets to minimize the delay and reduce the number of stops. Such platoons of vehicles can travel along the entire arterial without stopping. The width of the band is called bandwidth. By maximizing the inbound and outbound bandwidths along an arterial, the total delay and the number of stops can usually be minimized. Many engineers favored maximizing the progression band method, which allows us to know the quality of coordination control from the space-time diagram. Several researchers have conducted some studies on bandwidth optimization for traffic progression. Little et al.[1] first proposed the MAXBAND model using the mixed-integer-linear programming model for arterial signals control. Gartner et al.[2] proposed a multi-band approach to generate a variable bandwidth progression considering the actual traffic volumes and flow capacities on each link. Li[3] proposed a two-stage method that solves the MAXBAND model controlled by a parameter and generates multiple optimal, and then the generated scenarios are evaluated and ranked according to their reliability. Moreover, some researchers[4-5] improved the classical algebraic method to adapt to different traffic scenarios. Tang et al.[6] proposed an improved multiband model, which enhanced the green band flexibility that can be adapted to the arterials with more intersections. To deal with the arterial with variable lanes, Gao et al.[7] proposed a coordinated control method of signals.
Public transportation plays an important role in improving traffic conditions due to the significant advantage of transport capacity. Although some researchers have conducted some studies on signal controls for bus priority, these studies always focused on isolated signalized intersections[8-9]. Li et al.[10] proposed a comprehensive benefit optimization model which comprehensively considers cars and buses. Wang et al.[11] proposed a two-layer optimization method for bus priority without destroying the progression band. Dai et al.[12-14] proposed the bandwidth optimization models. Xu et al.[15] proposed algorithms for signal priority treatment and recovery to meet vertical equity requirements. The algorithms based on three types of traffic detectors and time windows for the green extension, phase insertion, and early green were defined to generate and cancel priority requests conditionally. Li et al.[16] proposed a method to predict bus travel times dynamically based on the Chongqing RFID electronic license plate data.
Bandwidth-based approaches are primarily designed for fixed-time signalized arterials. Considering that the trajectory of buses is different from that of social vehicles, and passenger cars are the main components of social vehicles, this paper divided them into different progression bands according to the model. This paper uses classical MAXBAND to implement bus-relevant improvements, and proposes a new progression model for cars and buses to coordinate traffic signals along urban arterials.
1 Model Formulations
1.1 Control objective
There are many traffic parameters with a mix of buses and social vehicles along an arterial. Differently from the driving state of social vehicles alone on the main road, the bus has to dwell based on the need for passengers to get on or off the bus. The operation parameters (speed, acceleration) of the bus are also different from those of the social vehicle due to the different functions of the vehicle and its performance. Therefore, the bus trajectory is significantly different from that of social vehicles.
Considering the diversion of buses and social vehicles at links, this study develops a progression model with the major inputs of pre-set cycle length, green splits, bus dwell time, link length, and vehicle speed. The proposed model is formulated with a mixed-integer-linear programming method, which optimizes the signal offsets to yield the maximal bandwidths for both buses and social vehicles. Following the same notion as the MAXBAND signal progression model, one can formulate the objective function as follows:
(1)
where kc, kb,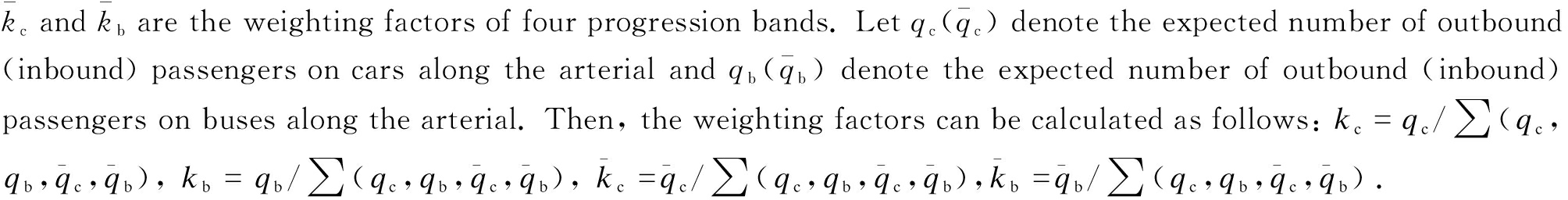 
Fig.1 shows the space-time diagram of different driving characteristics of cars and buses.
1.2 Bandwidth constraints
To ensure that the green bandwidth does not exceed the available green time, the first interference constraints are
wc,i+bc≤gi, wb,i+bb≤gi
(2)
(3)
where i is the set of intersections; wc,i(wb,i) is the time period between the start of green and the start of the car (bus) band at intersection i for an outbound intersection; 
is the time period between the end of the car (bus) band and the end of green at intersection i for
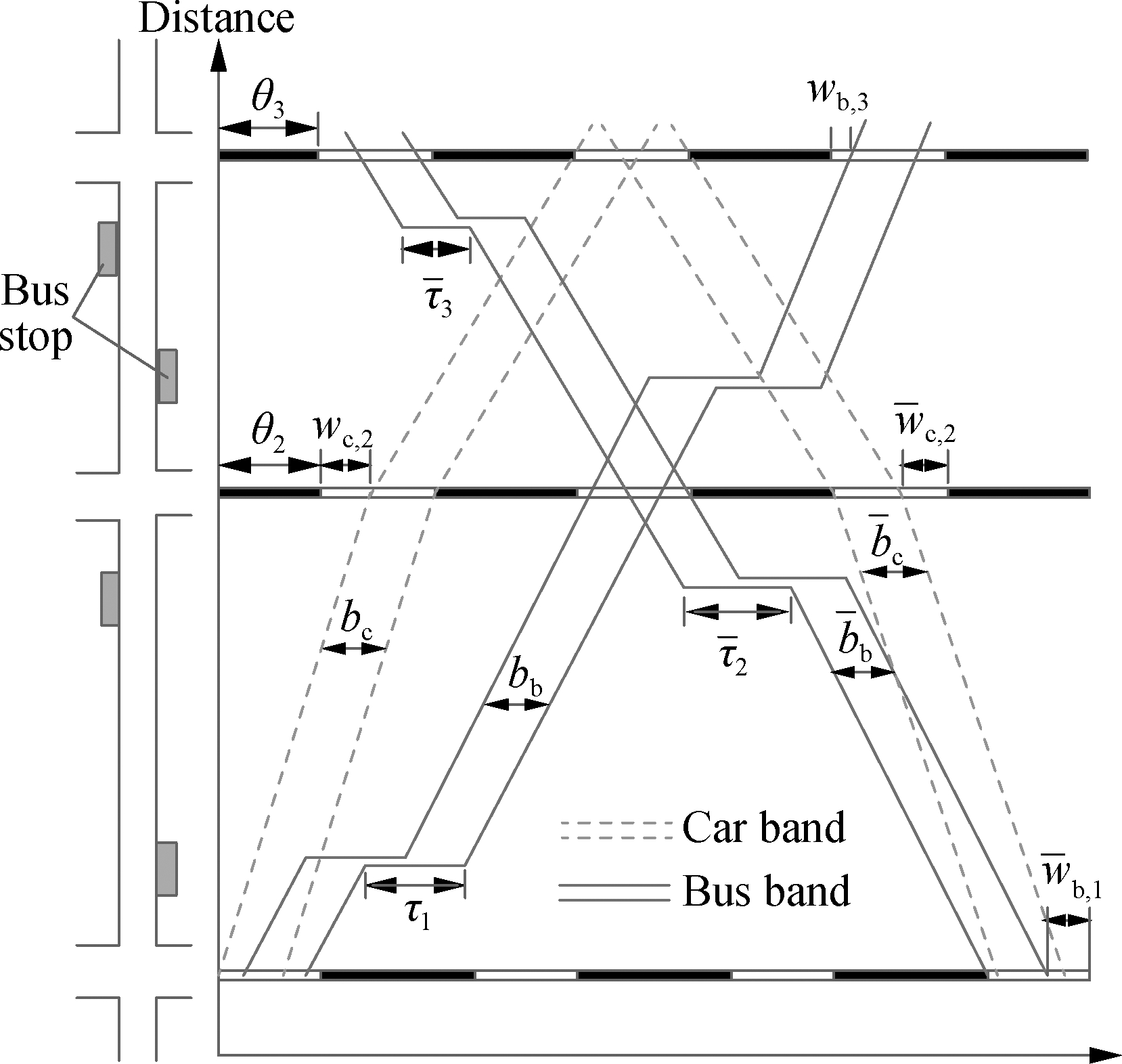
Fig.1 Space-time diagram showing green bands
an inbound intersection; bc(bb) is the outbound car (bus) bandwidth at intersection i; 
is the inbound car (bus) bandwidth at intersection i; gi is the outbound (inbound) green time at intersection i.
The second set of constraints, the progression constraints, are specified to ensure that the signals do not stop the buses and cars during the green bands. Each constraint aims to limit the differences between the centers of the inbound or outbound bands in each pair of neighboring intersections. As shown in Fig.1, the progression constraints for the links of cars can be expressed as follows:
θi+wc,i+tc,i=θi+1+wc,i+1+nC
(4)
(5)
where 
is the average outbound (inbound) travel time of cars from intersection i(i+1) to intersection i+1(i); ri is the outbound (inbound) red time at intersection i; θi is the signal offset at intersection i; C is the common cycle duration in the model; n is any integer.
Differently from the design of progression for cars, a bus may need to dwell at a bus stop for a short time when traveling between intersections. Hence, a green band designed for buses should fully reflect the impact of its dwelling time. The progression constraints for the links can be written using similar expressions:
θi+wb,i+tb,i+τi=θi+1+wb,i+1+nC
(6)
(7)
where 
is the average dwell time of buses at the outbound (inbound) bus stop after intersection i(i+1).
Also, we constrain changes of speed by putting upper and lower limits on changes in reciprocal speed.
(8)
(9)
where Li is the link length from intersection i(i+1) to intersection i+1(i); ec,i,fc,i(eb,i,fb,i) are the lower and upper limits on outbound car (bus) speed; 
are the lower and upper limits on inbound car (bus) speed.
In brief, the optimization model is summarized as follows:
s.t. Eqs.(2) to (9)
(10)
Note that the proposed model is formulated with mixed-integer-linear-programming formulations. It can be solved by existing algorithms, such as the Branch-and-band technique, or solved with software directly (such as LINGO, CPLEX).
In the model,buses’ dwelling time at a stop is a fixed value, which does not conform to the actual traffic conditions. Assuming that the dwelling time of buses at a stop follows a normal distribution, the probability of dwelling time can be expressed as
(11)
where μ and σ are the average value and variance of buses’ dwelling time at a stop, which can be obtained by field investigation. Then, considering that the bus’ dwelling time is greater than zero, as shown in Fig.2(a), the probability of dwelling time can be expressed as follows:
(12)
(13)
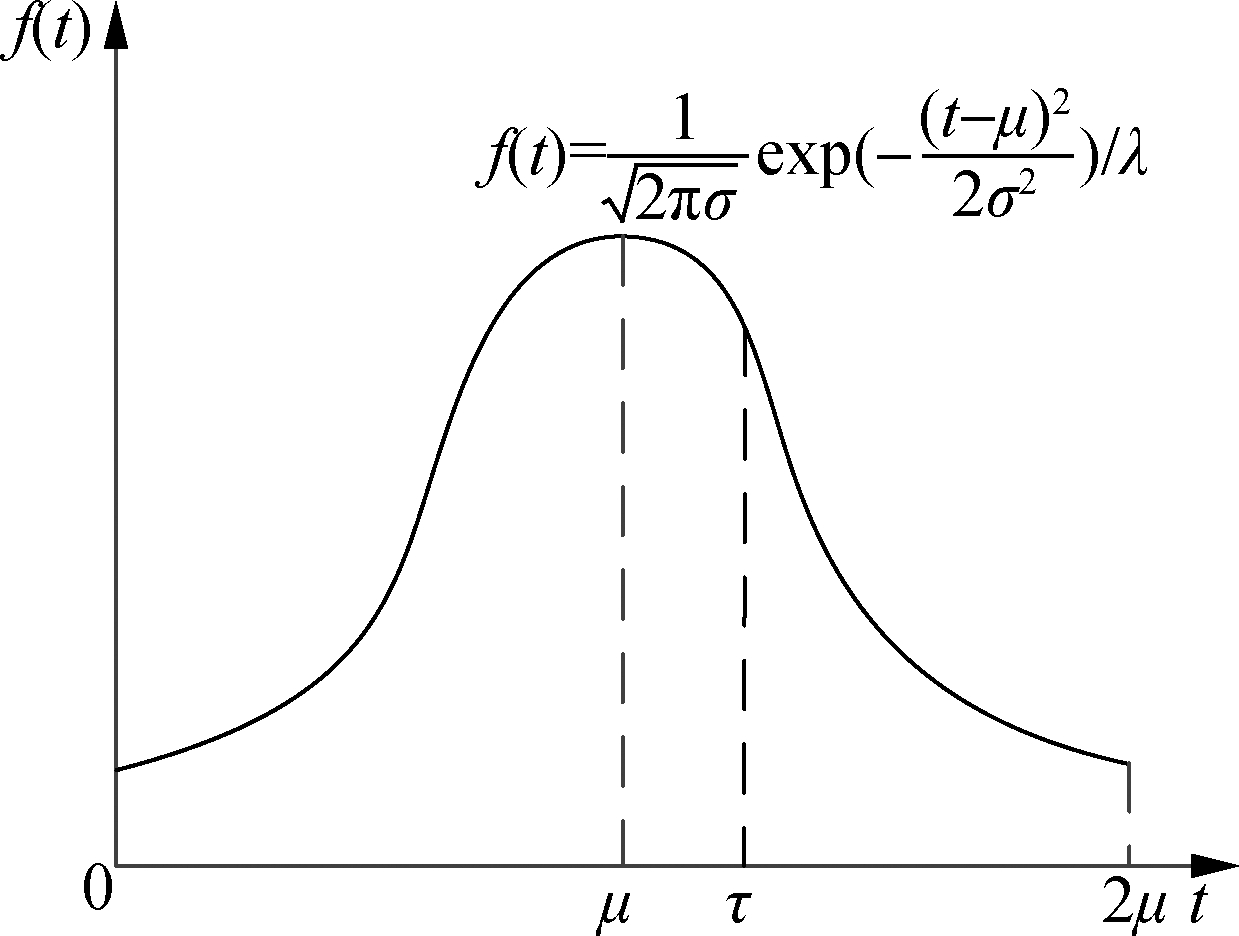
As shown in Fig.2(b), when the actual dwelling time of a bus is less than the design time, the bus will reach a downstream intersection earlier than the end of green time. The delay caused by signal control is τ-t. When the actual dwelling time of a bus is greater than the design time, the bus will miss the green time at the next intersection. The delay caused by signal control is ri+1-t+τ. Then, the average delay of buses is
(14)
(a)
(b)
Fig.2 The impact of bus dwelling time on delay. (a) Distribution function; (b) Delay of buses
where τ is an independent variable and D is a dependent variable. When D reaches the minimum value, τ is the dwelling time of the buses, which is used to design the green band. It can be solved as ∂D/∂τ=0, and the solution is
(15)
As shown in Fig.3, cars and buses pass the upstream intersection at the green time. The cars will follow their normal speed along with the link to the next intersection, but the buses will decelerate, dwell, and accelerate at the bus stop. Therefore, there will be two schemes when splitting the green progression band, as shown in Fig.4. In Scheme A, cars and buses are released at the same green time at the upstream intersection, but buses will pass the downstream intersection one cycle later than cars. The scheme is suitable for the case where the link is long or the bus dwelling time is long. In Scheme B, cars and buses pass the two intersections at the green time of the same cycle. The scheme is suitable for the case where the link is short or the bus dwelling time is short.
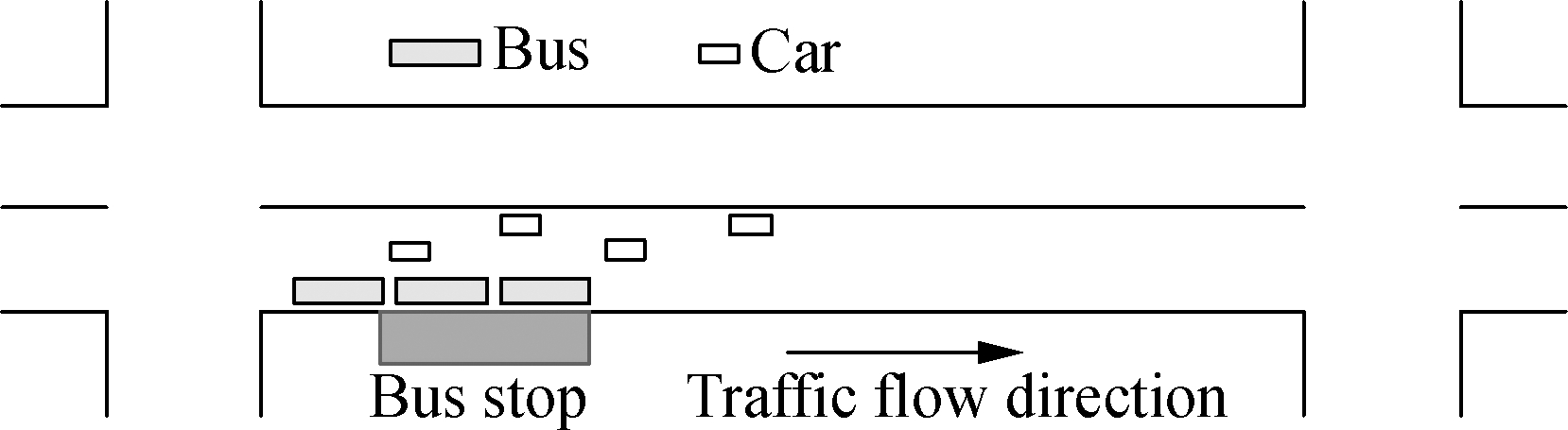
Fig.3 The difference between buses and cars in the link
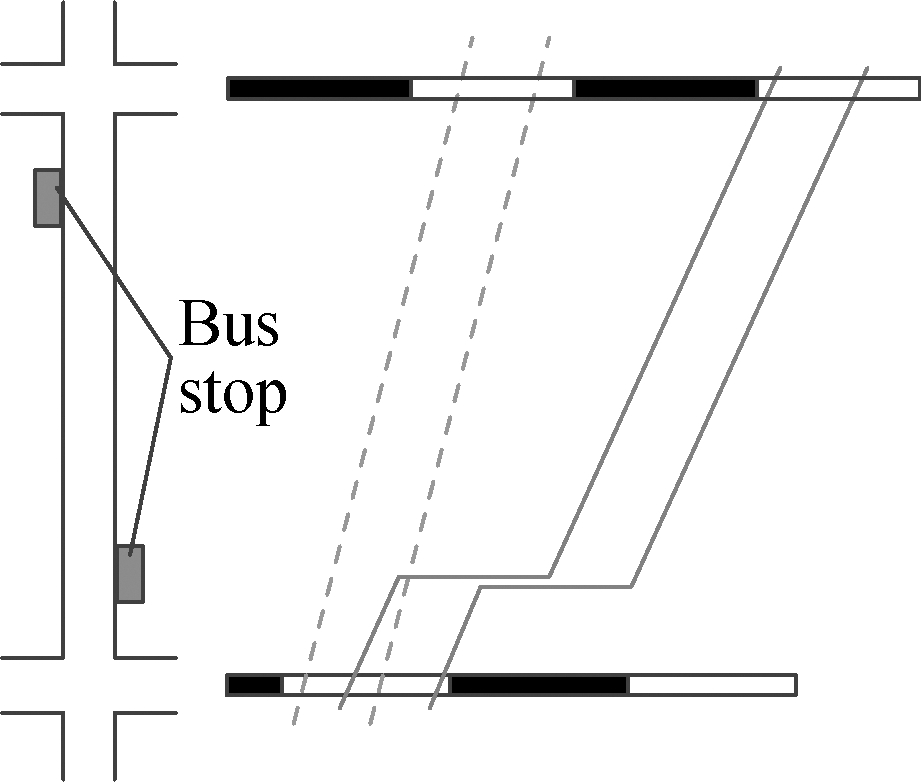
(a)
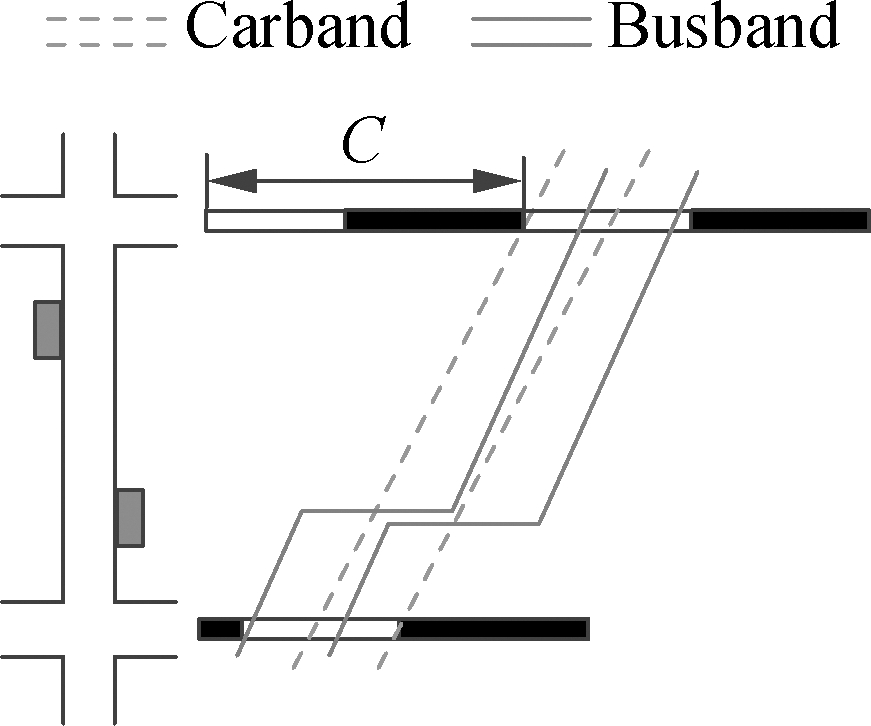
(b)
Fig.4 The two schemes for buses and cars passing downstream intersection. (a) One cycle difference; (b) At the same time
The choice of the two schemes is determined by many factors such as the length of the link, buses’ dwelling time at the stop, the speed difference between cars and buses, etc. The selection factor can be expressed as follows:
(16)
where η is the selection factor of two schemes; vc,i(vb,i) is the average speed of cars (buses) from intersection i to intersection i+1; ε is the other’s delay caused by other factors.
The traffic control engineer selects a scheme of a link that should be based on the actual traffic conditions. According to Eq.(16), the value of the scheme selection coefficient in the link can be obtained. The value of η being smaller indicates that the time difference between the two vehicles arriving at the next intersection is smaller than the period. The delay caused by the adoption of Scheme B on the road section is shorter.
The selection of a scheme should provide a basis for the limits of the two-vehicle speeds in the model. Generally, Scheme A is adopted when η is greater than 0.5, and the limits of the speeds should be satisfied:
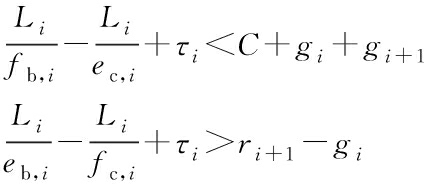
(17)
Scheme B is adopted when η is less than 0.5, and the limits of the speeds should be satisfied:
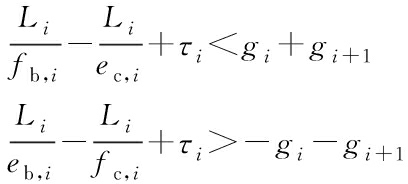
(18)
2 Numerical Examples
To illustrate the efficiency of the proposed model, this study takes an arterial segment, named as Wangjiang Road, in Hefei, for the case study. As shown in Fig.5, the experimental system for performance evaluation consists of six intersections, five connecting links, and ten bus stops. Geometry features are shown in Tab.2, and the traffic volumes at intersections of cars and buses are listed in Tabs.3 and 4.
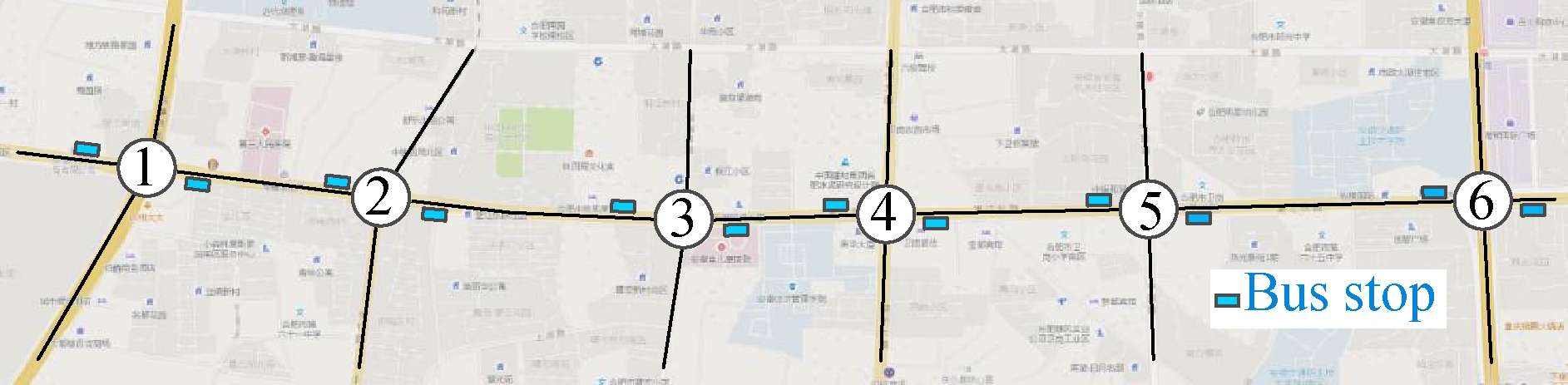
Fig.5 Scene of Wangjiang Road
Tab.2 Parameters of the studied arterial segment
Link12345Link length/m630820430700880Distribution of bus dwelling time(outbound/inbound)N(28,14)/N(34,16)N(42,14)/N(32,16)N(22,9)/N(16,12)N(25,19)/N(23,21)N(36,18)/N(33,17)
Tab.3 Traffic volumes of the car at intersections along Wangjiang Road pcu/
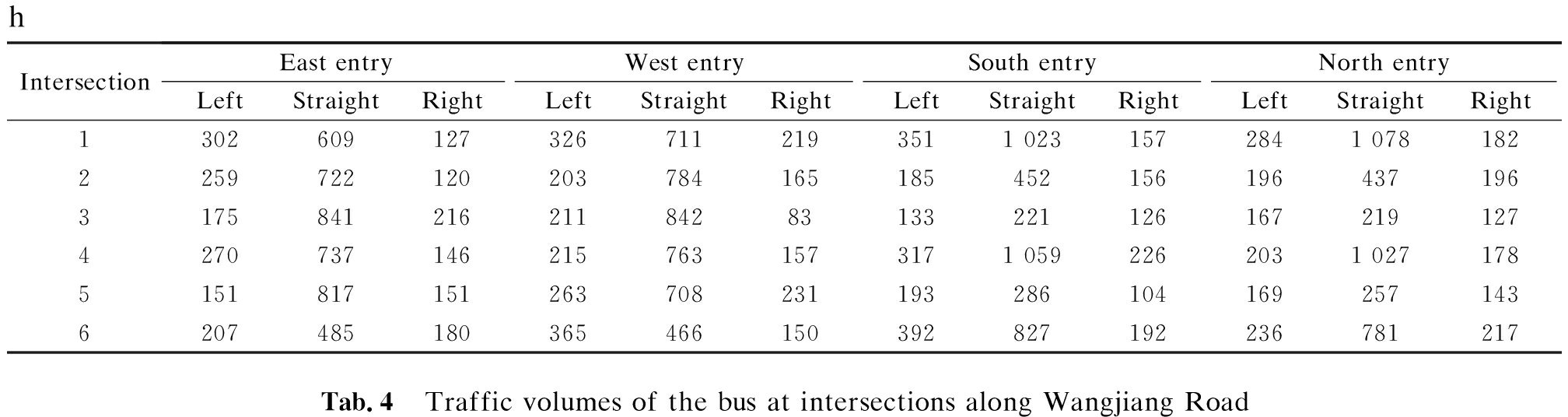
hIntersectionEast entryWest entrySouth entryNorth entryLeftStraightRightLeftStraightRightLeftStraightRightLeftStraightRight13026091273267112193511 0231572841 078182225972212020378416518545215619643719631758412162118428313322112616721912742707371462157631573171 0592262031 02717851518171512637082311932861041692571436207485180365466150392827192236781217Tab.4 Traffic volumes of the bus at intersections along Wangjiang Road
pcu/h
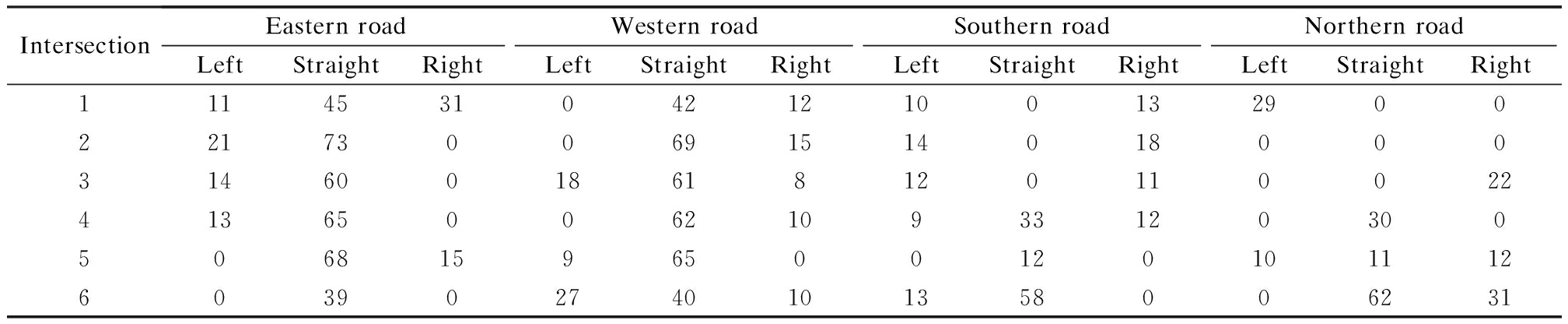
IntersectionEastern roadWestern roadSouthern roadNorthern roadLeftStraightRightLeftStraightRightLeftStraightRightLeftStraightRight1114531042121001329002217300691514018000314600186181201100224136500621093312030050681596500120101112603902740101358006231
The Webster signal equation is used to calculate the signal timing of a single intersection and the common cycle length of the six intersections is 132 s. The critical traffic patterns and critical parameters are shown in Tab.5.
Tab.5 The key parameters used in the signal control
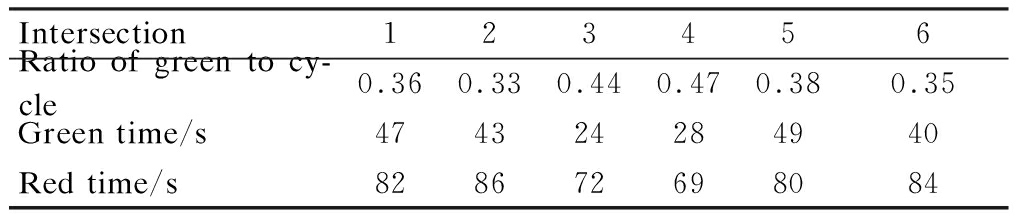
Intersection123456Ratio of green to cy-cle0.360.330.440.470.380.35Green time/s474324284940Red time/s828672698084
The hourly traffic volumes are obtained through the investigation, but how many passengers are in every vehicle is not clear. Therefore, the loading factors of passenger cars and buses are assumed to be ρc=2 and ρb=20 persons. This study conducts comparisons for the following three models, Webster, MAXBAND, and the proposed model, to evaluate the progression model’s effectiveness.
According to the survey data, the simulation sets the expected speed of cars and buses to be 40 and 35 km/h. After the selection of schemes for links, it is confirmed that links 2 and 5 adopt Scheme A; links 1, 3 and 4 adopt Scheme B. LINGO was used to solve the model, and the parameter values are shown in Tab.6.
Tab.6 The key parameters used in the signal control
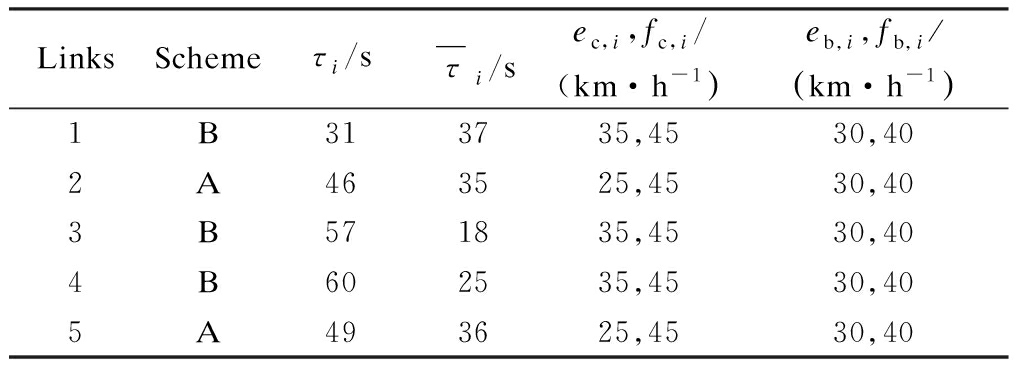
LinksSchemeτi/sτ-i/sec,i,fc,i/(km·h-1 eb i fb i km·h-1 1B313735 4530 402A463525 4530 403B571835 4530 404B602535 4530 405A493625 4530 40
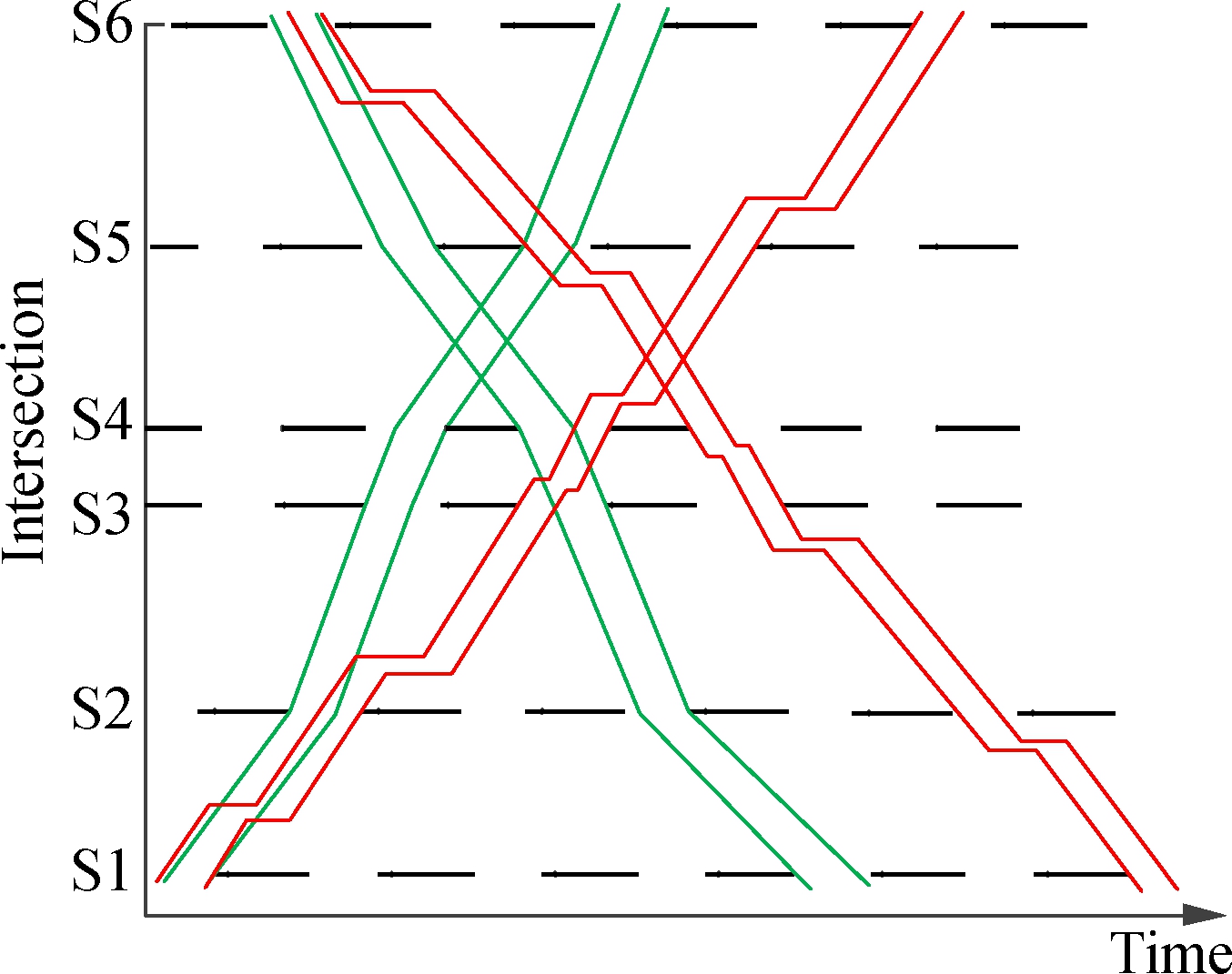
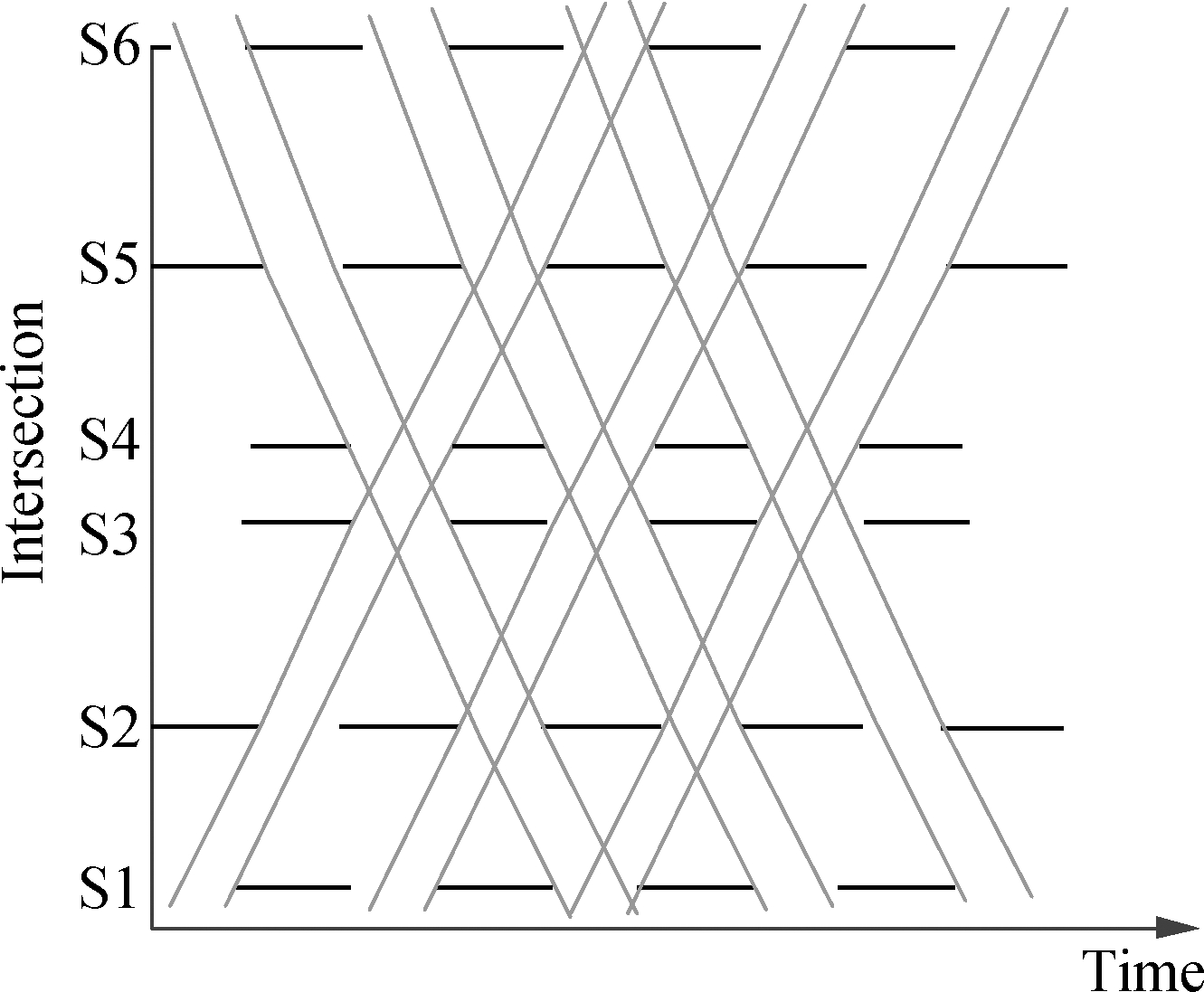
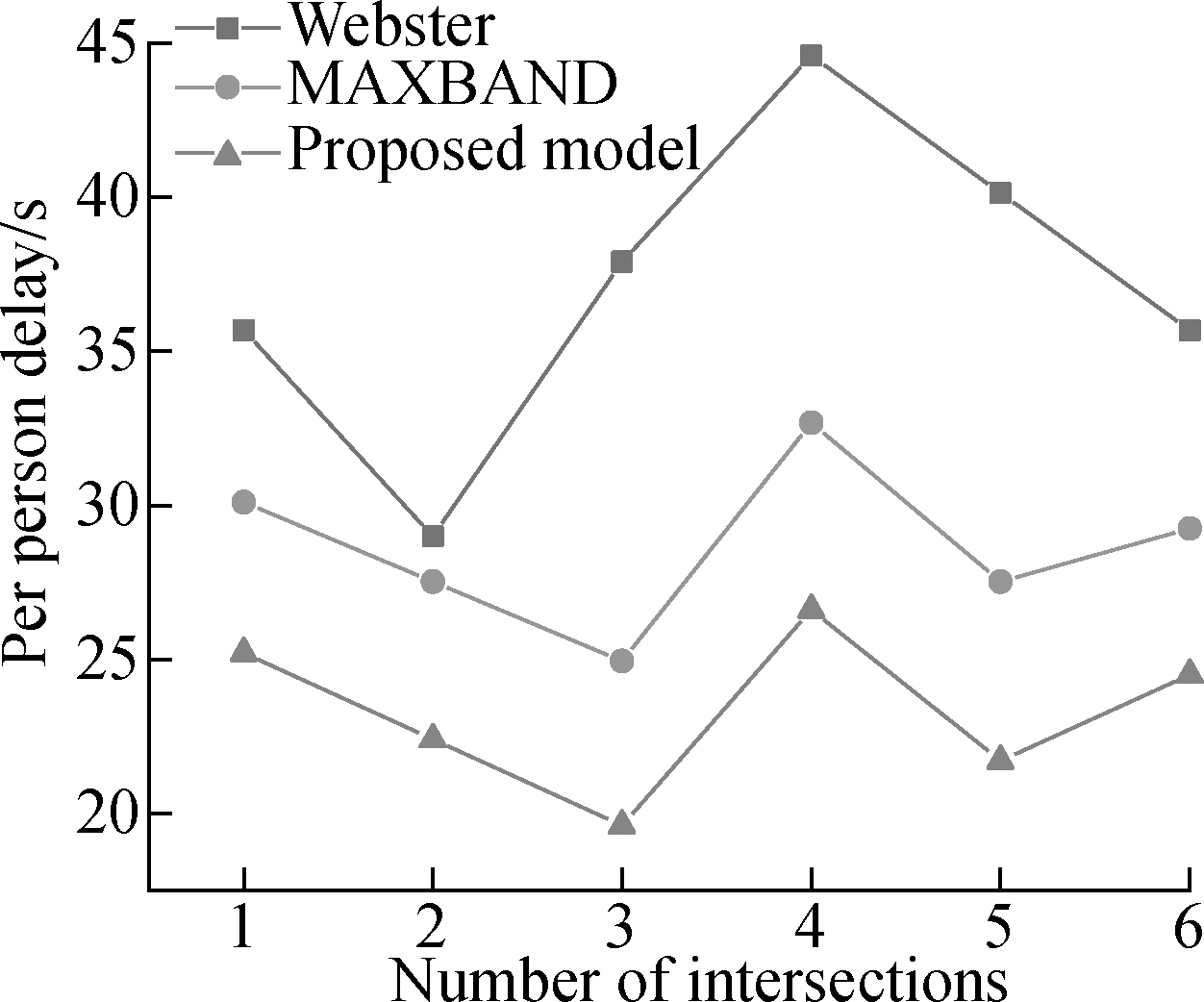
The diagrams of the proposed model and MAXBAND are shown in Fig.6. To further illustrate the applicability and efficiency of the proposed model, a one-hour length and four measures of effectiveness are selected for model assessment. The average number of bus stops, average number of car stops, average bus delay, and average car delay are analyzed by using VISSIM software. The results are shown in Fig.7 and Tab.7.
(a)
(b)
Fig.6 Time-diagram for car and bus green bands of two models. (a)Proposed model; (b) MAXBAND
Tab.7 The summary of performance under different models.
ModelNumber ofcar stopsNumber ofbus stopsNumber ofperson stops Average cardelay sAverage busdelay sAverage persondelay sWebster4 584 244 42212236223MAXBAND3 023 903 42109224162Proposed model3 302 442 90136146141
(a)
(b)
Fig.7 Performance comparison among three models. (a) Per person delay; (b) Per person stops
The simulation results show that the delay and number of stops of the vehicles will be significantly reduced after coordinated arterial control. For single intersection control, a smaller cycle length will have a lower delay for the vehicles at the intersection, but there is no significant change in the number of stops. Compared with the single intersection control, the proposed model reduces the number of stops and delay by 34.3% and 36.9%, respectively. Compared with the MAXBAND control model, the proposed model has lost the traffic efficiency of social vehicles and obviously improves the buses’ efficiency. Overall, the number of stops and per person delay in an arterial are decreased by 15.2% and 13.2%, respectively.
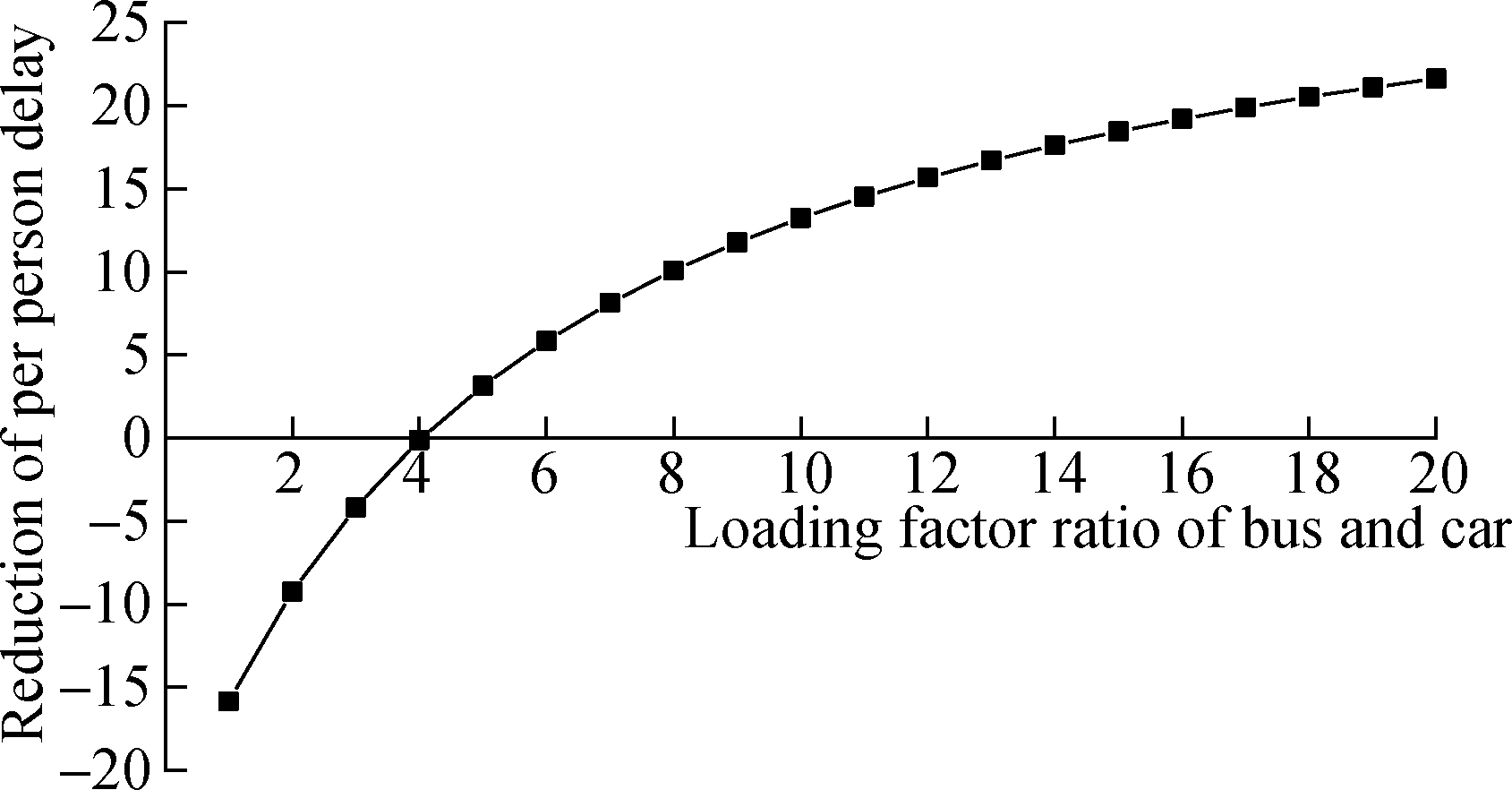
Fig.8 The reduction of average person delay by the proposed model compared to MAXBAND
To test the benefits of the proposed model over MAXBAND with respect to different values of the ratio (ρb/ρc), Fig.8 shows the reduction of average per person delay under different scenarios. Based on the data, we know that the target arterial can benefit from the proposed progression model in terms of reducing the average person delay when the ratio ρb/ρc is larger than 4. Based on the results, we can conclude that the proposed model has more advantages with the increase in the proportion of bus passengers.
3 Conclusions
1) Considering that the driving trajectory of buses is quite different from the social vehicles, this paper proposed a mixed-integer-linear programming model for arterial traffic signal coordination to obtain the green bands of the car and bus.
2) This paper takes an arterial with six intersections and ten bus stops as an example, and employs VISSIM as an unbiased tool for model evaluation. The simulation results indicate that the public transportation system can benefit significantly from this signal model. Compared to the conventional progression model for cars (MAXBAND), the proposed model can significantly reduce the number of stops and per person delay by 15.2% and 13.2%, respectively.
3) Assuming that ρc and ρb are 2 and 20, respectively, the proposed model is superior to MAXBAND.By testing different values of ρb/ρc, the results show that the target arterial can benefit from the proposed progression model in terms of reducing the average person delay when the ratio ρb/ρc is larger than 4. We can conclude that the proposed model has more advantages with the increase in the proportion of bus passengers.
[1] Little J D C, Kelson M D, Gartner N M. MAXBAND: A program for setting signals on arteries and triangular networks[J].Journal of the Transportation Research Board, 1981,795:40-46.
[2] Gartner N H,Assman S F, Lasaga F, et al. A multi-band approach to arterial traffic signal optimization[J]. Transportation Research Part B: Methodological, 1991, 25(1): 55-74. DOI:10.1016/0191-2615(91)90013-9.
[3] Li J Q. Bandwidth synchronization under progression time uncertainty[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 749-759. DOI:10.1109/tits.2013.2286098.
[4] Lu K, Xu J M, Li Y S. Algebraic method of arterial road coordinate control for bidirectional green wave under signal design mode of one-phase-one-approach[J]. China Journal of Highway and Transport, 2010, 23(3): 95-101. DOI:10.19721/j.cnki.1001-7372.2010.03.015. (in Chinese)
[5] Wang D H, Yang X R, Song X M. Improvement of classical numerical method for arterial road signal coordinate control[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(1): 29-34. DOI:10.13229/j.cnki.jdxbgxb2011.01.015.(in Chinese)
[6] Tang K S, Kong T, Wang F, et al. A modified MULTIBAND model for urban arterial coordinate control[J]. Journal of Tongji University(Natural Science), 2013, 41(7): 1002-1008.(in Chinese)
[7] Gao Y M, Zhang C B, Wei Y Y, et al. A method of coordinated control for arterial intersections with variable lanes[J]. Journal of Traffic Information and Safety, 2019(5):54-62. (in Chinese)
[8] Zhang W H, Lu H P, Shi Q, et al. Optimal signal-planning method of intersections based on bus priority[J]. Journal of Traffic and Transportation Engineering, 2004(3):49-53. DOI:10.1007/BF02911033. (in Chinese)
[9] Yu Z Y, Gayah V V, Christofa E. Person-based optimization of signal timing[J]. Transportation Research Record: Journal of the Transportation Research Board, 2017, 2620: 31-42. DOI:10.3141/2620-04.
[10] Li F, Wang J. Active transit signal priority considering overlapping phase in artery progression[C]//2010 2nd International Conference on Advanced Computer Control. Shenyang, China, 2010. DOI:10.1109/icacc.2010.5486672.
[11] Wang D H, Zhu H, Bie Y M, et al. Bus signal priority method at arterial signal progression[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(4): 859-865.(in Chinese)
[12] Dai G Y, Wang H, Wang W. A bandwidth approach to arterial signal optimisation with bus priority[J]. Transportmetrica A: Transport Science, 2015, 11(7): 579-602. DOI:10.1080/23249935.2015.1049675.
[13] Dai G Y, Wang H, Wang W. Signal optimization and coordination for bus progression based on MAXBAND[J]. KSCE Journal of Civil Engineering, 2016, 20(2): 890-898. DOI: 10.1007/s12205-015-1516-4.
[14] Cheng Y, Yang X F. Signal coordination model for local arterial with heavy bus flows[J]. Journal of Intelligent Transportation Systems, 2018, 22(5): 422-432. DOI: 10.1080/15472450.2017.1394191.
[15]Xu H F, Zheng Q M, Zhang K, et al. Signal priority technique for bus rapid transit system along an arterial based on vertical equity[J]. China Journal of Highway and Transport, 2019, 32(1):144-153. (in Chinese)
[16] Li H M, Wu J M, Sun D H, et al. Bus travel time prediction method based on RFID electronic license plate data[J]. China Journal of Highway and Transport, 2019, 32(8): 165-173,182. (in Chinese)