Owing to heavy traffic demand, it is difficult to solve the congestion problem of intersections by optimizing signal timing or adding new lanes. Therefore, researchers have been looking for unconventional management methods to increase capacities of signalized intersections. Such designs included superstreet intersections[1-2], displaced left-turn intersections[3-4], roundabouts[5], and others. In these unconventional intersection designs, the exit lanes for left turn (EFL) take full advantages of the intersection capacity, especially under the heavy left-turn traffic. The unique characteristic of the EFL intersection is its mixed-used area. The mixed-used area is used as exit-lane of opposing through vehicles or left-turn lane during different periods of a signal cycle. Also, there is a pre-signal and a median opening at the upstream of the EFL intersection. Therefore, left-turn vehicles can drive into the mixed-used area at the pre-signal and wait for the green light of the main-signal to finish their turning movements.
In the early development of lane assignment, conventional design methods of lane marking only took all the approach lanes of the signalized intersection into account. Each lane has a specific movement apart from exit lanes. In addition, the design of lane marking should consider the signal timings calculation. The conventional lane assignment considered the lane marking factor first, and then the signal setting is determined based on the lane marking. However, it may not always produce a truly optimal plan of lane markings for the EFL intersection.
Recently, a lane-based optimization model combining the design of lane marking and signal settings for isolated signal-controlled intersections was developed. The lane marking was always defined as binary variables into an optimization frame. The set of binary variables also include the common flow multiplier, cycle length, traffic flows, maximum reserve capacity as well as starts and durations of greens for traffic movements on approach lanes. In the signal control, Assi et al.[6] proposed a quick method to find the optimum lane group for 3-lane and 4-lane approaches at junctions. Yu et al.[7] proposed an optimal traffic signal control framework to minimize the total travel time. However, the importance of signal timings with lane-based allocation should not be ignored. The integrated optimization model further improved the effectiveness of traffic flows[8-12].
A lane-based optimization target model was proposed by Wong et al[13-14]. The model optimized lane attributes and signal periods based on the number of approach and exit lanes. The objective function was maximizing the intersection capacity or minimizing cycle length. The multi-objective problems were solved by the binary mixed-integer linear program (BMILP). However, once lane allocations were determined, they can only be used as approach lanes or exit lanes. Zhang et al.[15] proposed a robust optimal fixed-time signal timing and considered the environmental influence factors. However, due to the change of the inlet flow at the intersection, the characteristics of lanes and the timing of signals were not given. Wong and Heydecker[16] further studied the lane optimization problem at a single-signal intersection. They defined new lane attribute variables and introduced them into a new optimization model. However, they ignored the influence of crossing pedestrian signals, especially the phenomenon of high demand for crosswalks in China. Based on the research of Wong and Heydecker[16], Yu et al.[17] improved the single-signal intersection optimization model, in which safety islands were considered. They also proposed a multi-objective lane optimization model, which was not sensitive to traffic flow fluctuations. However, there was a lack of constraints on vehicle lanes change. Li et al.[18] proposed a multi-objective optimization method for improving traffic performance at intersections. The transportation efficiency, energy consumption and road safety were considered as the objective functions in the model. However, the EFL intersection was not considered in the model.
In order to formulate the intersection design problems into a mathematical program, this study proposes an optimization model of exit lanes for left-turn including lane schedules and signal timings. The design variables can be optimized simultaneously to obtain better intersection capacity. The objective functions are the minimization of the vehicle delay and the maximization of the left-turn capacity. Considering that the non-dominated sorting genetic algorithm-Ⅱ (NSGA-Ⅱ) has a better sorting parameter, incorporates elitism and no sharing parameter needs to be chosen a priori, we select it to solve the model. Also, a set of numerical examples is evaluated to demonstrate the effectiveness of the model.
1 Model Formulation
1.1 Optimization objective selection
In order to improve the efficiency of traffic flows, this study will be conducted from the following two aspects: lanes usage and safety impacts of the EFL design. The intersection traffic capacity and intersection vehicle delay are selected as the optimization objectives.
1.2 Input data
In order to obtain the best optimization results, this paper established a lane assignment optimization model including the traffic intersection constraints, lane attributes, signal timing and median open location.
1) Lane allocation variables
Fig.1 shows a typical intersection with four arms. If a movement from arm i to arm j is permitted on lane k, then ei,k,j=1; otherwise, ei,k,j=0.
2) Minimum permitted movement on approach lanes
Each lane must be an approach lane or an exit lane, and each approach lane must have at least one turning or through movement, which can be specified as
(1)
∀j=1,2,…,N-1;i=1,2,…,N
where N is the number of traffic arms.
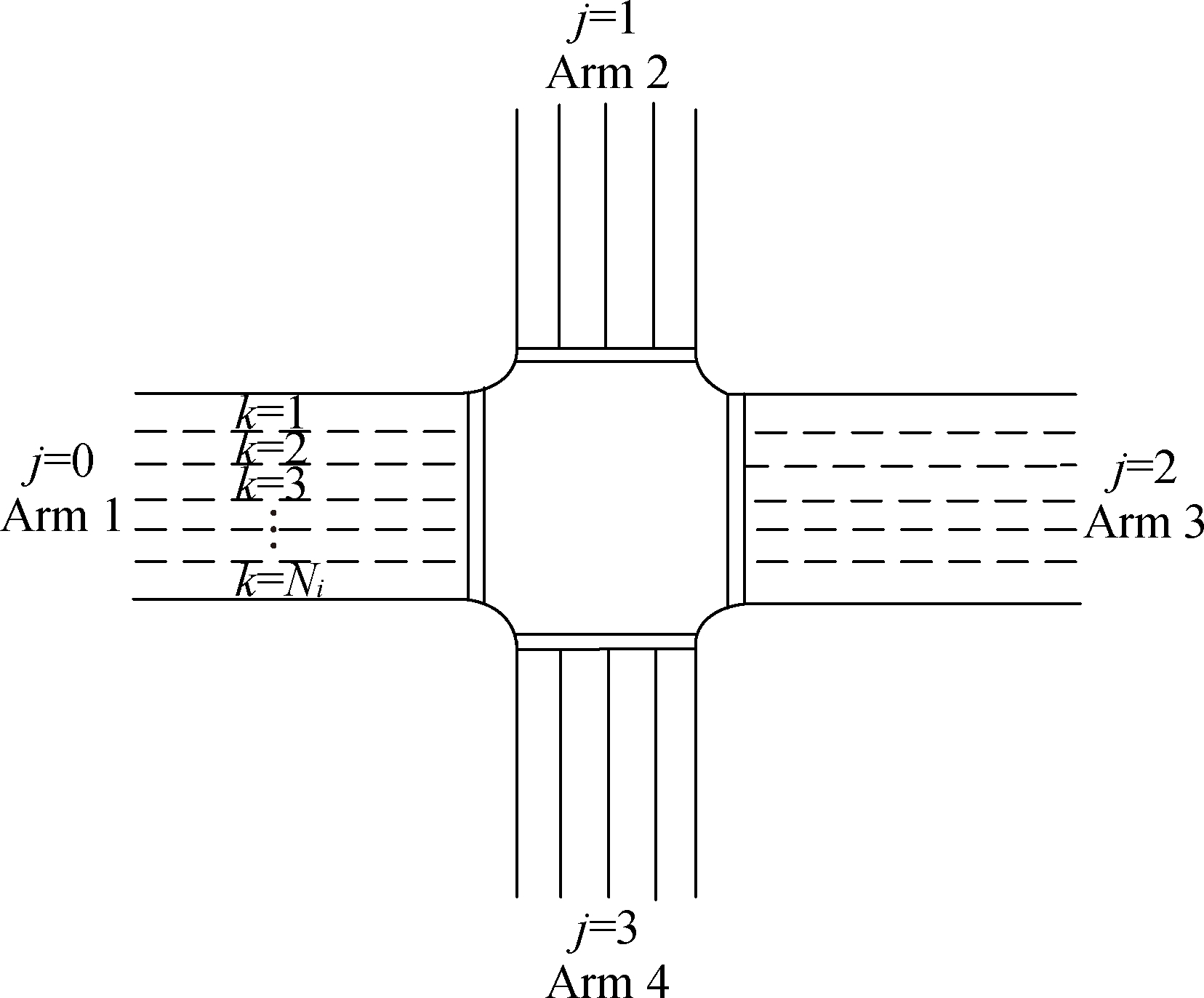
Fig.1 Numbering convention for the approach lane and exit lane in an intersection
If the traffic in the k-th lane of approach lane i is prohibited to drive towards exit lane j, its corresponding lane flow should be 0.
Mei,k,j≥qi,k,j≥0
(2)
∀i=1,2,…,N;k=1,2,…,Ni,j=1,2,…,N-1
where M is a sufficiently large positive constant and qi,k,j is the lane turning flows assigned on permitted lanes.
For each traffic flow from i to j, the number of exit lanes should not be less than that of approach lanes corresponding to this flow direction. It is to avoid impact on each traffic flow on the exit lanes.
(3)
∀j=1,2,…,N-1;i=1,2,…,N
where NE is the number of exit arms, and NT is the number of traffic lanes in arm i.
3) Cycle length
The minimum and maximum values of the intersection cycle length are denoted by Cmin and Cmax, respectively. The constraints on the cycle length can be specified as
Cmin≤C≤Cmax
(4)
4) Lane signal setting
For safety reasons, if an approach lane permits different vehicle movements, it is necessary that they receive the same signal indications, including the green duration and green start time.
M(1-ei,k,j)≥Θi,k-θi,k≥-M(1-ei,k,j)
(5)
M(1-ei,k,j)≥Φi,k-φi,k≥-M(1-ei,k,j)
(6)
∀j=1,2,…,NT-1;k=1,2,…,Ni;i=1,2,…,NT
where Θi,k is the start of green on approach traffic lanes in arm i via lane k; θi,k is the start of green for turning movements on lane k in arm i; Φi,k is the durations of green for the approach traffic lanes on lane k in arm i and φi,k is the durations of green for turning movements on lane k in arm i. If the vehicle movement (i,k,j) is allowed (ei,k,j=1), the green start time and green duration in arm i via lane k must be equal to the signal group (i,j).
5) Start of the green time setting
Since the signal period at the intersection is cyclic, the variable of the green start can take any value among a cycle as long as it satisfies other relevant constraints. However, for the convenience of calculation, this paper sets the range of all green start time variables as (0,1), namely,
1≥θi,j≥0
(7)
∀j=1,2,…,N-1;i=1,2,…,N
6) Duration of green
The green duration of each approach lane is determined by the minimum green duration of the flow direction. This can be specified by the following constraint set:
1≥φi,j≥gi,j/C
(8)
∀j=1,2,…,NT-1;k=1,2,…,Ni;i=1,2,…,NT
7) Order of signal displays
For any two conflicting phase groups (i,j) and (m,n), conflict can be avoided by releasing the sequence of the phase.
Pij,mn+Pmn,ij=1
(9)
∀(i,j),(m,n)∈ψs
A group of conflicting signal phases is represented as Pij,mn. If the green start time signal group (m,n) follows the signal group (i,j), the conflicting signal phase Pij,mn=0; otherwise Pij,mn=1. If the green start time signal group (i,j) follows the signal group (m,n), the conflicting signal phase Pmn,ij=0; otherwise Pmn,ij=1.
8) Flow conservation
The traffic demand flows Qi,j are known. Lane turning flows qi,j have been assigned on the approach lanes. The flow multiplier μ<1 indicates that the traffic volume of the intersection overloads 100(1-μ)%, and the flow multiplier μ>1 indicates that the intersection can also increase the traffic volume of 100(μ-1)%. The following set of constraints can be expressed as
(10)
where μ is the common flow multiplier and Qi,j is the demand flowing from arm i to arm j.
9) Mixed-usage-area constraint
This paper presents a lane-based optimization model combining the exit lanes for the left turn. The vehicles can turn left through the EFL under the pre-signal, indicating that the exit lane becomes a left-turn lane. All the left-turn vehicles that drive into the mixed usage area should be discharged during the green time of the pre-signal. Such design needs a good coordination between the main-signal at the intersection and the pre-signal at the median open.
For the EFL lanes, the capacity analysis of left-turn vehicles can be more complex. In practice, the vehicles in the EFL lane must be discharged during the left-turn phase of the main signal. Otherwise, the left-turn vehicles will block the traffic coming from the other direction. Thus, the capacity gains of the left-turn movements at an intersection with the EFL design can be considered as the number of left-turn vehicles that enter the EFL. The location of the upstream median opening determines the maximum number of the left-turning vehicles. The basic shockwave diagram of the EFL design is shown in Fig.2.
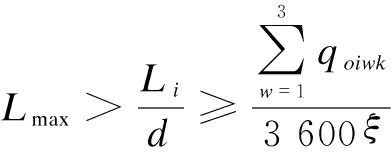
(11)
where Li is the distance between the main-signal and the pre-signal.
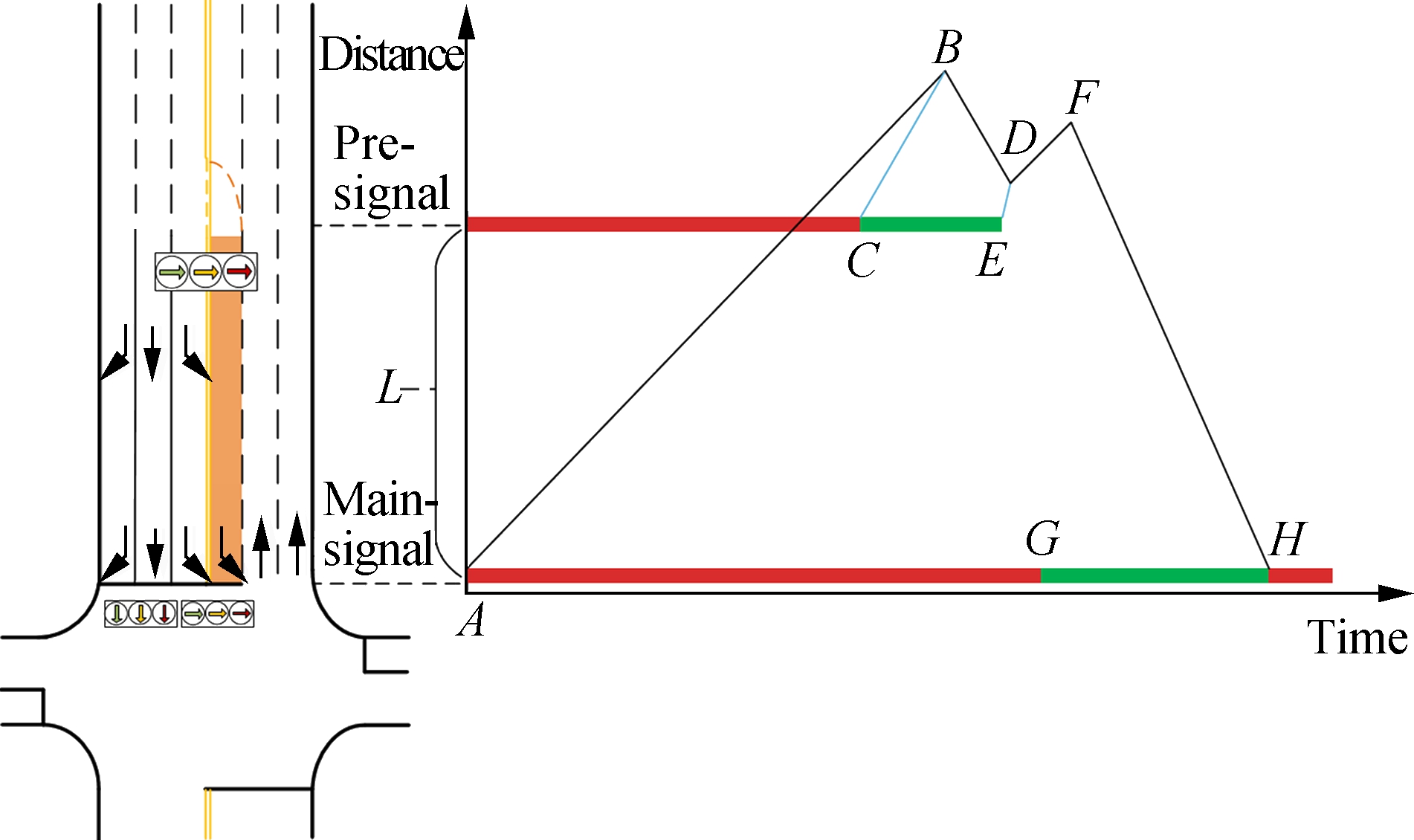
Fig.2 The basic shockwave diagram of EFL design
10) Flow factor
The saturation flow and delay on a pair of adjacent approach lanes with a common signal group must be identical. If there are multiple lanes in the same flow direction, the flow ratio of the same flow direction lanes should be consistent as follows:
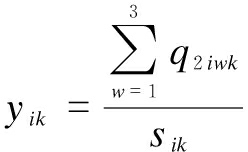
(12)
M(2-ei,k,j-ei,k+1,j)≥yi,k+1-yi,k≥-M(2-ei,k,j-ei,k+1,j)
(13)
∀j=1,2,…,NT-1;k=1,2,…,Ni;i=1,2,…,NT
11) Average delay of the vehicle
The calculation method of the average delay at intersections is calculated according to the Highway Capacity Manual HCM (2010)[19].
Di,k=D1,i,k(PF)+D2,i,k+D3,i,k
(14)
where PF is the adjustment parameter of average delay.
The calculation method of all vehicle delays in lane k of approach lane i can be expressed as
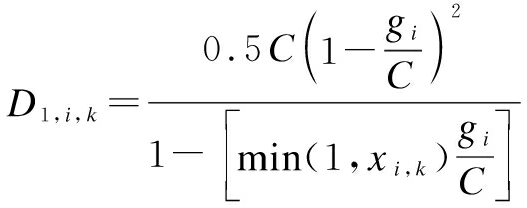
(15)
The increased delay calculation method of lane k on approach lane i can be expressed as
(16)
where T is the duration of the analysis period; kf is the incremental delay factor; i is the upstream filtering adjustment factor; ci,k is the capacity of lane k at approach i and xi,k is the volume to capacity ratio on lane k in arm i.
1.3 Optimization formulations
The maximum capacity of the left turn is an important design aspect of intersections. It should consider the requirements of geometric layout and signal timings. The objective functions are defined as the maximization of the left-turn capacity (CAP) Cleft and the minimization of the average vehicle delay D.
(17)

(18)
Subject to the linear constraints (1) to (16), in this nonlinear integer programming model, the decision variables are lane variables and signal variables.
2 Model Solution Based on Genetic Algorithm
The above optimization model is a multi-objective mixed integer nonlinear programming problem. In this model, L is the decision factor. Although it is a multi-objective model, the objective functions can be transformed into a single-objective optimization model by setting weighting parameters. Moreover, the objective functions can be solved by NSGA-Ⅱ.
The observed average traffic volume is denoted as Q′ and the specific solution steps are as follows:
Step 1 Initial population
Set the evolution counter g=0 and the maximum evolution algebra g=500. Within the range of the established region descriptor, M=100 individuals are randomly generated as the initial population P(0).
Step 2 Fitness function
The size of fitness indicates that the fitness of individuals and individuals with higher fitness are more likely to inherit to the next generation. According to the characteristics of the objective function established in this paper, the fitness function is selected as f=1/F. Then the fitness value of each individual in population P(t) is calculated. Two individuals were randomly selected from the population, and the fitness between the two was compared.
Step 3 Genetic operations
The basic genetic operations include selection, crossing and variation.
1) The selection algorithm selects individuals with a higher fitness value according to the fitness value of each individual in the current population and passes on the selected individuals into the daughter population according to the set rules.
2) The crossover operation is to randomly match pairs of each individual in the population. Each individual will exchange partial chromosomes with a certain probability to obtain a new generation of individuals. In this paper, the crossover probability is set to be 0.7.
3) The mutation operation is to generate a new individual by randomly selecting the individual to change the gene value at one or some other loci to other alleles with a certain probability, and the mutation probability is set to be 0.05.
Step 4 Algorithm stopping
If the evolutionary algebra g of the genetic algorithm is 500, the algorithm can be terminated by taking the individual with the maximum fitness.
3 Numerical Studies
In order to verify the effectiveness of the model in this paper, a four-arm junction as shown in Fig.3 is studied. From the signal timing perspective, the design of the EFL intersection needs a good coordination between the main-signal and the pre-signal as shown in Fig.4. The purpose of the studied case is to demonstrate whether the EFL will improve its efficiency or not. Relevant input data and assumptions are given as follows.
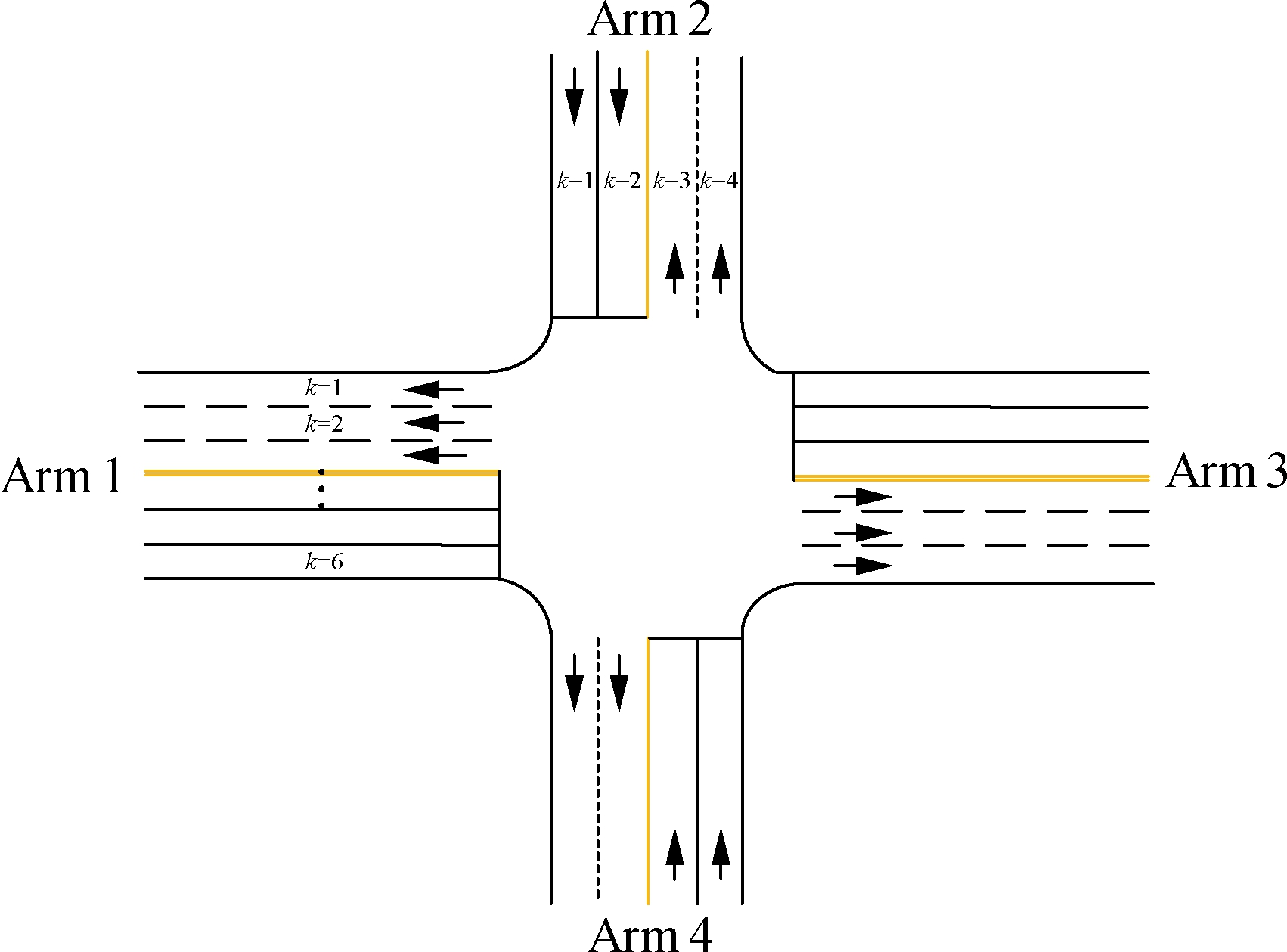
Fig.3 Layout of a four-arm junction in the example
For simplicity, the saturation flows for straight-ahead movements are 1 800 pcu/(h·lane). The maximum acceptable degrees of saturation are taken as 90% on all lanes. If the maximum acceptable degrees of saturation
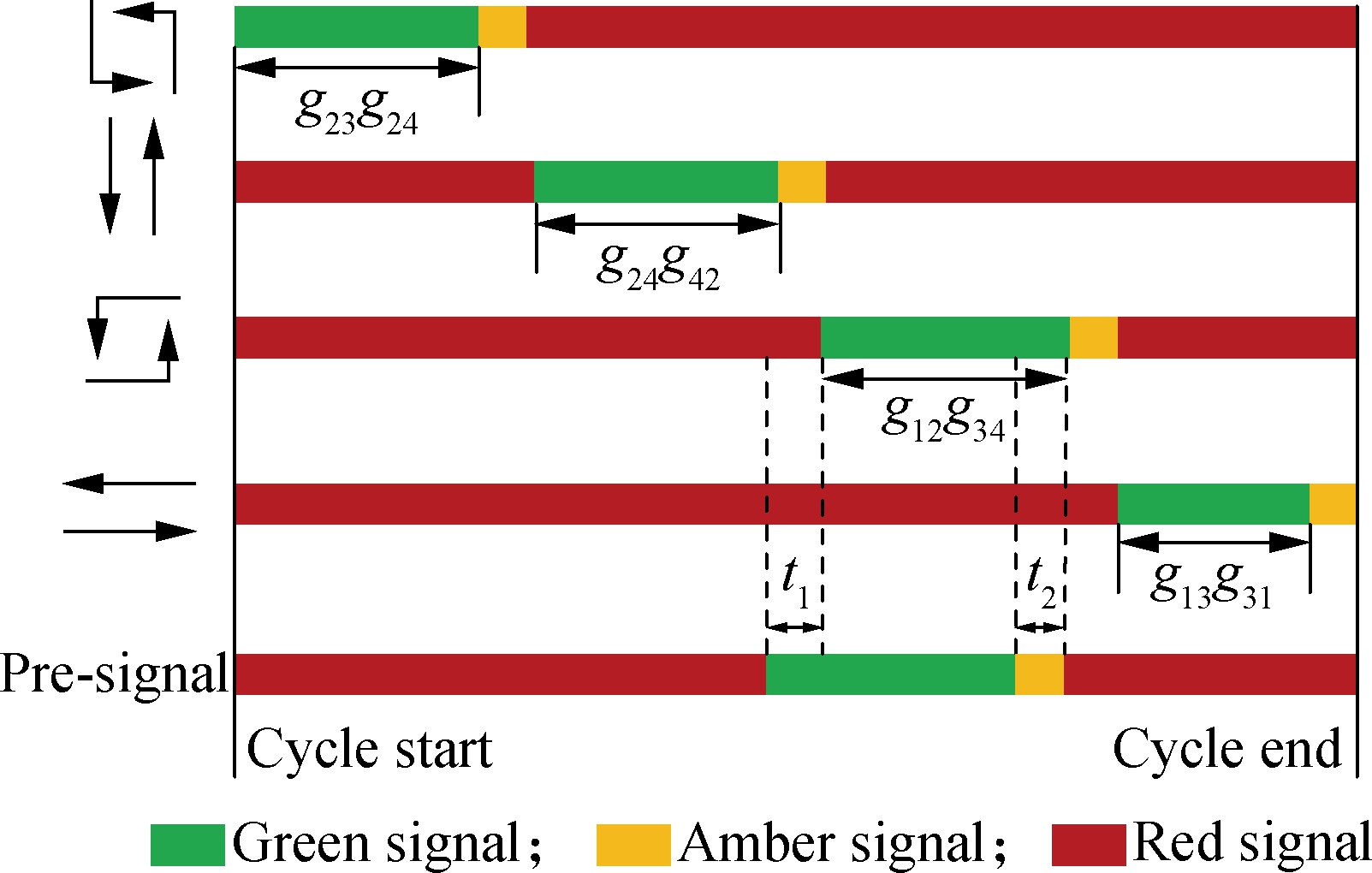
Fig.4 Signal phases
is above 90%, the optimization effect of the model is not significant. According to the HCM, the minimum cycle length is 60 s and there is no limitation on the maximum cycle length. In this study, the minimum and maximum cycle lengths are assumed to be 60 and 200 s, respectively. The minimum green durations are 5 s for all traffic movements.
The traffic demand at the intersection adopts the data during the peak hour. The left-turn phase and the straight-line phase are set to be 5 and 3 vehicles, respectively, in the last cycle. Relevant traffic demand data Qi,j is tabulated in Tab.1. The saturation degrees of all approach traffic lanes are under 0.9. NSGA-Ⅱ can solve the above nonlinear integer programming problems of the mixed usage area.
Tab.1 Traffic demands of a four-arm junction for the example

ijTraffic demands pcu·h-1)Initial vehiclequeue length/m Intersectionsaturation degree121 300538003412000.821300031 5003490050.8311 30052200041 00080.8411 300521 5008340000.8
The calculation results shown in Fig.5 show that the EFL intersection has two left-turn lanes in the west approach lanes including the mixed usage area. The flow coefficient μ=1.241 indicates that the lane allocation method can meet the requirements of the traffic demand. In the conventional intersection, it is shown that this lane allocation method can also meet traffic demands under certain saturation conditions. However, the EFL intersection has a greater traffic capacity. Using the VISSIM simulation software, the signal optimization simulation results are shown in Tab.2 and Tab.3. It can be observed from Tabs.4 and 5 that the EFL intersection has a shorter signal cycle. The left-turn effective green time from arm 1 to arm 2 of EFL intersection is shorter than that of conventional intersection. This means that the EFL intersection can not only improve the efficiency of the left turn but also reduce intersection cycle. In the simulation, the default behavior of urban road drivers in VISSIM was adopted. All the models were the cars with the expected speed of 40 to 50 km/h, and the saturation flow rate was about 1 800 veh/h.
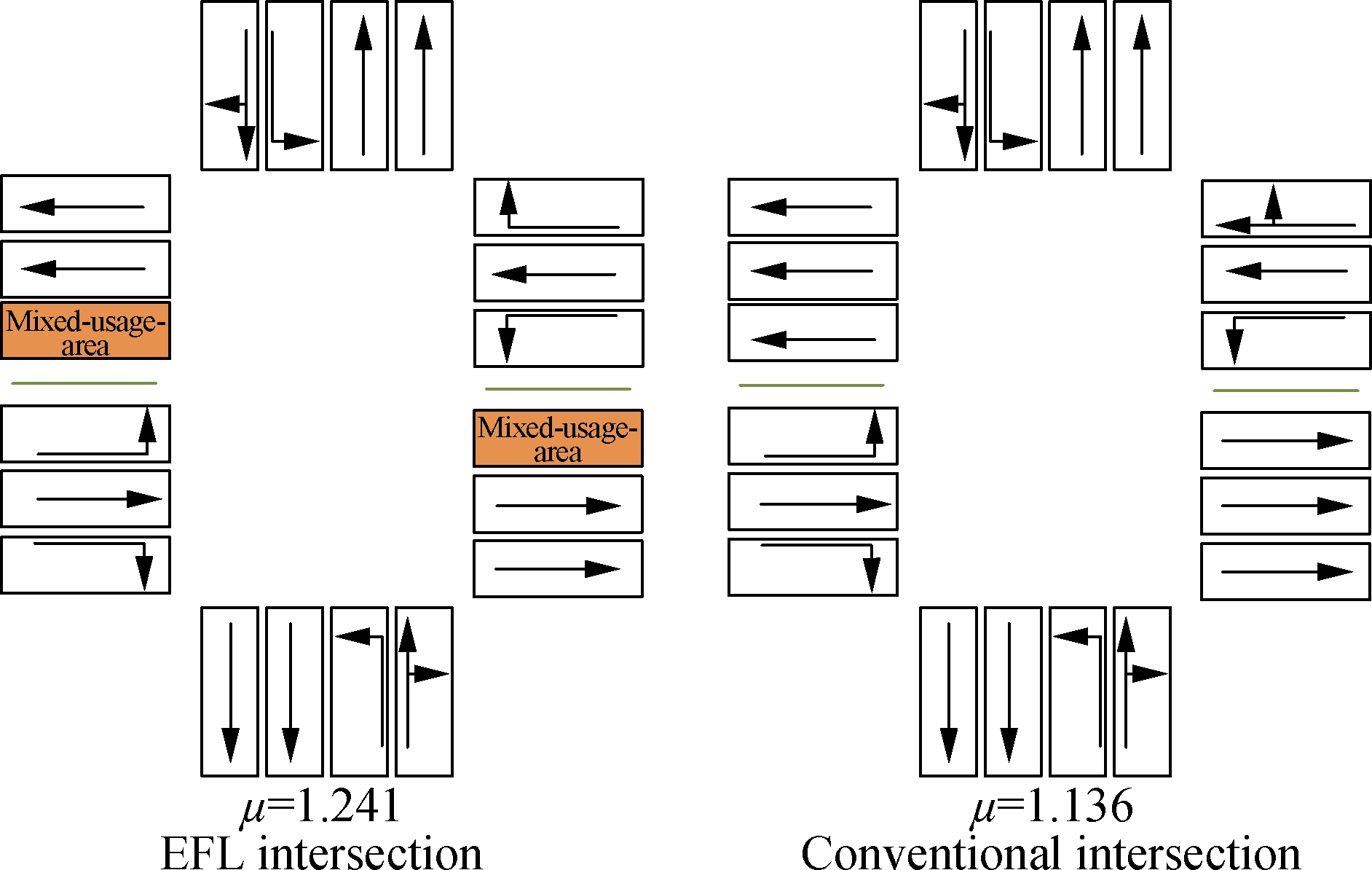
Fig.5 Optimization results of lane arrangements
Fig.6 depicts the signal control process of the EFL intersection. Also, each stage is explained as follows:
Tab.2 Signal optimization simulation results of EFL intersection

Traffic flow directionsEFL intersectionArm 1Arm 2Arm 3Arm 4234134124123Cycle length/s103103103103103103103103103103103103Start of green/s0242478517824240517878Effective green/s202323252325232320232525End of green/s2047471037410347472074103103
Tab.3 Signal optimization simulation results of conventional intersection

Traffic flow directionsConventional intersectionArm 1Arm 2Arm 3Arm 4234134124123Cycle length/s110110110110110110110110110110110110Start of green/s0343490639034340639090Effective green/s302525202320252530232020End of green/s3059591108611059593086110110
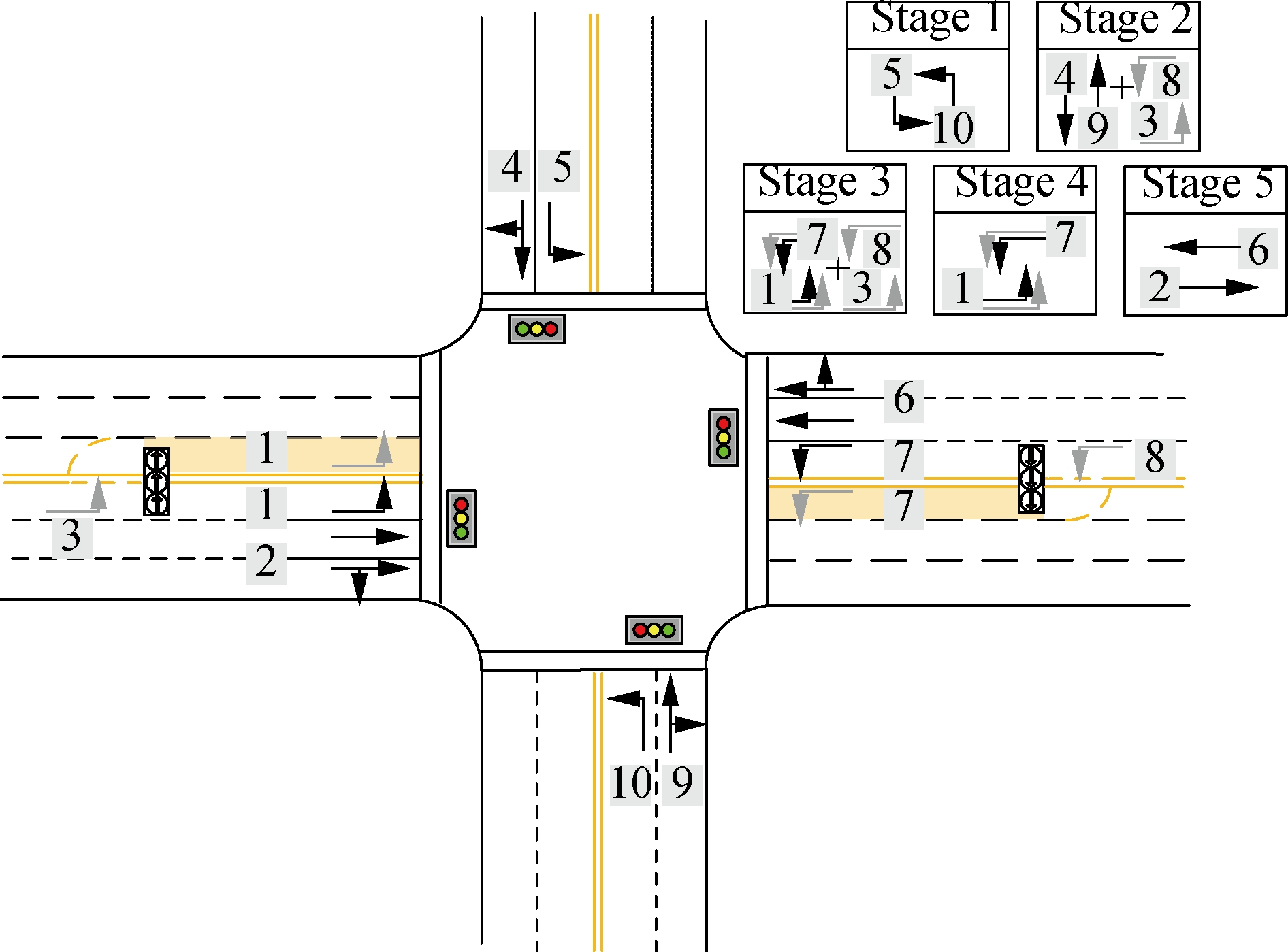
Fig.6 Signal control process of EFL intersection
Stage 1 The left-turn movements from the minor street start to be discharged (movements 5 and 10).
Stage 2 The through vehicles (movements 4 and 9) from the minor street start to be discharged. After a few seconds, the pre-signal turns green and the left-turning vehicles (movements 8 and 3) are starting to advance into the exit-lane for left-turn through the median opening.
Stage 3 The left-turn phases in the main signals turn green and all the left-turning vehicles (movements 7 and 1) are beginning to be discharged, including those in the contra ow and the conventional left-turn lanes.
ow and the conventional left-turn lanes.
Stage 4 The left-turning vehicles continue to be discharged (movements 1 and 5). The pre-signal turns red, and there are no vehicles left in the exit-lane.
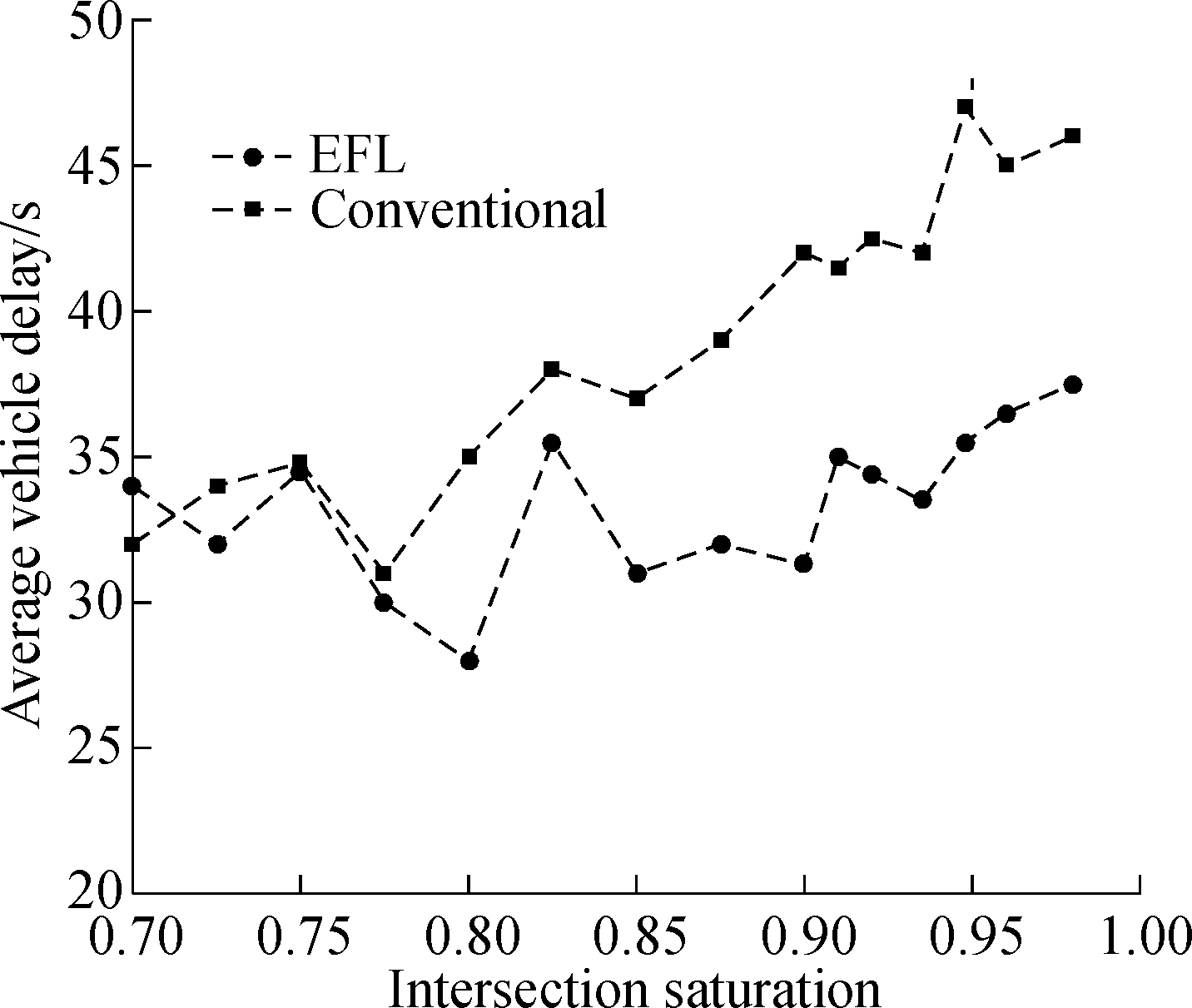
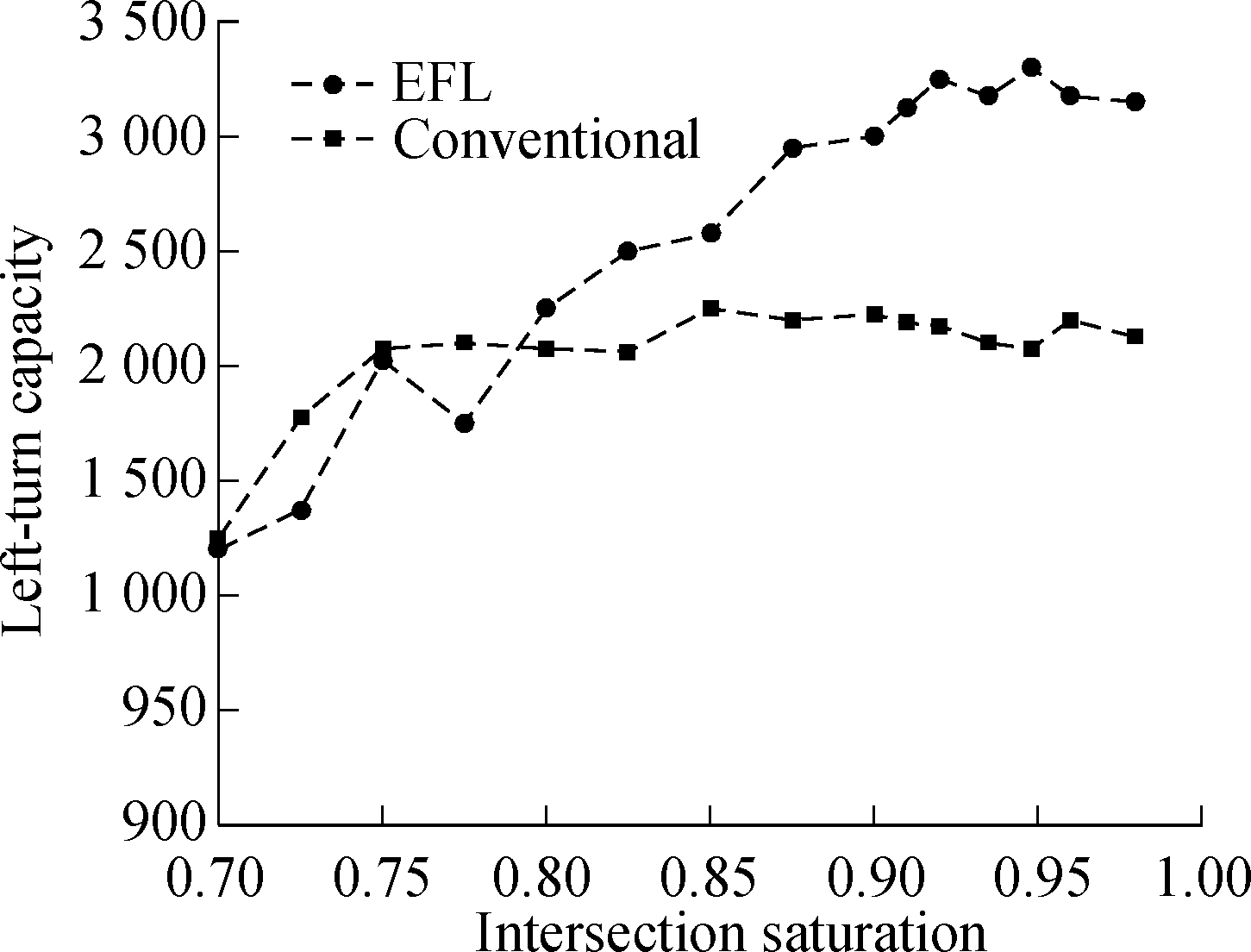
Stage 5 The through vehicles (movements 2 and 6) from the major street begin to be discharged, and the cycle is ended. The simulation results are shown in Fig.7 and Tab.4. We developed analytical models to calculate the capacity and average delay. As shown in Fig.7 and Tab.4, when intersection saturation is over 80%, the EFL design can improve the capacity and decrease the average vehicle delay of vehicles at the signal intersection. Moreover, the capacity gains mainly depend on the left-turning vehicles driving through the missed-usage-area. Therefore, the EFL design can significantly improve the capacity of intersections. When the intersection saturation is less than 80%, it needs to be determined whether the intersection needs to set EFL based on the model calculation results or not. The vehicle average delay of the EFL intersection is 14.9% lower than that of the conventional intersection (NEFL). The capacity of left turn is 9.3% higher than that of the conventional intersection. Therefore, in the optimization model, it is necessary to consider the mixed usage area on exit lanes. The EFL can reduce the average vehicle delay caused by obstruction and further improve the capacity of intersections.
4 Conclusions
1) The effectiveness of the EFL model and solution algorithms were validated through numerical studies.
(a)
(b)
Fig.7 Comparison of simulation results of average vehicle delay and traffic capacity. (a) Comparison of average vehicle delay; (b) Comparison of intersections capacity
Tab.4 Signal optimization simulation results of severe traffic demand

ModelVehicle averagedelay/sLeft-turn capacity/(pcu·h-1)Cycle/sEFL33.61163103Conventional39.51107110
The results show that both the EFL and conventional intersection can meet the traffic demand under a certain saturation condition. However, the model of EFL has a larger capacity.
2) In addition, the simulation platform was built via the VISSIM simulation for comparison. The EFL showed significant improvements in traffic operational performance. The average vehicle delays of intersection can be reduced by 14.9% and left-turn capacity can be increased by 19.3%.
3) Future research work should further pay attention to different traffic demands and ensure that it is adapting to the randomness of traffic demand in each time period. The proposed optimal model has a potential to increase the efficiency of the EFL design. However, more comprehensive research is needed to evaluate the effectiveness and safety impacts of the EFL design. The authors suggest that future studies should focus on these issues.
[1] Moon J P, Kim Y R, Kim D G,et al. The potential to implement a superstreet as an unconventional arterial intersection design in Korea[J]. KSCE Journal of Civil Engineering, 2011, 15(6): 1109-1114. DOI:10.1007/s12205-011-1157-1.
[2] Holzem A M, Hummer J E, Cunningham C M, et al. Pedestrian and bicyclist accommodations and crossings on superstreets[J]. Transportation Research Record: Journal of the Transportation Research Board, 2015, 2486: 37-44. DOI:10.3141/2486-05.
[3] Yan C W, Jiang H, Xie S Y. Capacity optimization of an isolated intersection under the phase swap sorting strategy[J]. Transportation Research Part B: Methodological, 2014, 60: 85-106. DOI:10.1016/j.trb.2013.12.001.
[4] Suh W, Hunter M P. Signal design for displaced left-turn intersection using Monte Carlo method[J]. KSCE Journal of Civil Engineering, 2014, 18(4): 1140-1149. DOI:10.1007/s12205-014-0225-8.
[5] Ma W J, Xie H Z, Liu Y, et al. Coordinated optimization of signal timings for intersection approach with presignals[J]. Transportation Research Record: Journal of the Transportation Research Board, 2013, 2355: 93-104. DOI:10.3141/2355-10.
[6] Assi K J, Ratrout N T. Proposed quick method for applying dynamic lane assignment at signalized intersections[J].IATSS Research, 2018, 42(1): 1-7. DOI:10.1016/j.iatssr.2017.03.004.
[7] Yu H, Ma R, Zhang H M. Optimal traffic signal control under dynamic user equilibrium and link constraints in a general network[J].Transportation Research Part B: Methodological, 2018, 110: 302-325. DOI:10.1016/j.trb.2018.02.009.
[8] Wolshon B, Lambert L. Reversible lane systems: Synthesis of practice[J]. Journal of Transportation Engineering, 2006, 132(12): 933-944. DOI:10.1061/(asce)0733-947x(2006)132:12(933).
[9] An K, Lo H K. Ferry service network design with stochastic demand under user equilibrium flows[J]. Transportation Research Part B: Methodological, 2014, 66: 70-89. DOI:10.1016/j.trb.2013.10.008.
[10] Yu C H, Feng Y H, Liu H X, et al. Integrated optimization of traffic signals and vehicle trajectories at isolated urban intersections[J]. Transportation Research Part B: Methodological, 2018, 112: 89-112. DOI:10.1016/j.trb.2018.04.007.
[11] Zhou Y P, Zhuang H B. The optimization of lane assignment and signal timing at the tandem intersection with pre-signal[J]. Journal of Advanced Transportation, 2014, 48(4): 362-376. DOI:10.1002/atr.1222.
[12] Sun W L, Wu X K, Wang Y P, et al. A continuous-flow-intersection-lite design and traffic control for oversaturated bottleneck intersections[J]. Transportation Research Part C: Emerging Technologies, 2015, 56: 18-33. DOI:10.1016/j.trc.2015.03.011.
[13] Wong C K, Wong S C. A lane-based optimization method for minimizing delay at isolated signal-controlled junctions[J]. Journal of Mathematical Modelling and Algorithms, 2003, 2(4): 379-406. DOI:10.1023/b:jmma.0000020424.32940.cb.
[14] Wong C K, Wong S C. Lane-based optimization of signal timings for isolated junctions[J]. Transportation Research Part B: Methodological, 2003, 37(1): 63-84. DOI:10.1016/s0191-2615(01)00045-5.
[15] Zhang L, Yin Y,Chen S. Robust signal timing optimization with environmental concerns[J]. Transportation Research Part C: Emerging Technologies, 2013, 29: 55-71. DOI:10.1016/j.trc.2013.01.003.
[16] Wong C K, Heydecker B G. Optimal allocation of turns to lanes at an isolated signal-controlled junction[J].Transportation Research Part B: Methodological, 2011, 45(4): 667-681. DOI:10.1016/j.trb.2010.12.001.
[17] Yu C H, Ma W J, Lo H K, et al. Robust optimal lane allocation for isolated intersections[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(1): 72-86. DOI:10.1111/mice.12236.
[18] Li X, Sun J Q. Intersection multi-objective optimization on signal setting and lane assignment[J].Physica A: Statistical Mechanics and Its Applications, 2019, 525: 1233-1246. DOI:10.1016/j.physa.2019.04.223.
[19] Transportation Research Board. Highway capacity manual (HCM)[S].Washington, DC: Transportation Research Board, 2010.