Warranty is a contractual obligation between the manufacturer and consumers. It can not only protect the consumers against defective items, but can also help the manufacturer to avoid customers’ unreasonable claims[1]. In addition to the basic warranty (BW), the extended warranty (EW) is also widely adopted by the manufacturer to establish a long-term relationship with the customers, and thus to gain the opportunities of product marketing and after-sale service.
Maintenance policy and the corresponding maintenance cost are of great importance for the warranty decision-making. It is reported that the warranty cost accounts for 2% to 10% of products’ operating revenues, and by optimizing the maintenance policy, the warranty cost can be reduced effectively[2]. Chien[3] proposed a periodic replacement maintenance policy for the one-dimensional (1D) warranty, which is characterized by a single variable, e.g. time (age) or usage. A two-dimensional (2D) warranty can take into account the age and usage rate concurrently, and it is more suitable for various industrial products, such as automobiles, CNC machines and engineering machinery, etc. Based on the accelerated failure time model, Shahanaghi et al.[4] proposed a model to optimize the number and degree of preventive repairs so as to minimize the EW provider’s servicing cost. From the manufacturer’s perspective, Wang et al.[5] investigated the periodic imperfect preventive maintenance (PM) for the products covered by a fixed and combined BW and EW region. Su and Shen[6] proposed two types of EW policies from the view of manufacturers, and three kinds of repair options were considered for the failed components. Based on the generalized renewal process and Stackelberg game, Santana et al.[7] designed the price for EW and on-demand maintenance to optimize the manufacturer’s profit.
In the above studies, the proposed warranty policies are rigid, and the customers are provided with the same warranty items. Actually, customers usually have different using habits, diverse operating environments and differentiated affordability, and their requirements for maintenance and warranty are personalized in nature. Moreover, the usage rate will influence product’s failure rate, maintenance policy as well as the warranty cost. Obviously, rigid warranty policies cannot satisfy customers’ personalized needs[8].
Customized warranty aims to consider various factors and meet customers’ diversified demands. Thus, it has attracted much attention in recent years. Based on the attractiveness index, He et al.[9] proposed a demand function to describe the boosted demand of extending the warranty period, and an optimal 2D BW period was obtained by maximising the expected profit. On the basis of the usage rate, Ye et al.[10] grouped the customers and provided them with differentiated EW periods. Based on the dynamic usage rate, Tong et al.[11] proposed a warranty maintenance strategy for 2D EW, a maintenance model was constructed to optimize the maintenance degree and help the service providers reduce the warranty cost. Lam et al.[12] presented an EW model including a free repair period and an EW period, where consumers had the choice to renew or not to renew the warranty period. On this basis, the long-run average cost per unit time was derived, and the optimal policies were obtained for the consumers. Su et al.[13] presented a two-stage PM optimal model and the moment that customers purchased 2D EW was considered. Jack et al.[14] put forward a repair-replace strategy for the products sold with a 2D warranty, and the accelerated failure time (AFT) model was applied to describe the effect of the usage rate on item’s degradation.
Up to now, there are still some problems with the customized warranty policies. For example, it is usually assumed that customers buy EW only when the product is sold or when the BW is expired. In fact, customers may buy EW at any time. Moreover, the proposed PM policies are usually of periodicity and iso-strength. Considering the above shortcomings, this study puts forward some improvements on the customized warranty. The main contributions include: 1) Customers can purchase EW at any time during the product’s useful life; 2) A non-equal periodic PM policy is proposed, and a more flexible warranty can be obtained; 3) The corresponding maintenance method, warranty period and warranty cost can be customized.
1 Models of Failure and Maintenance
Let Ω=(W, U) denote the total warranty period, and it includes BW and EW. A product is supposed to be sold to a customer with the usage rate r at t=0, and the manufacturer provides a 2D BW Ωb=(Wb, Ub), where Wb and Ub are the upper limits of BW’s using time and usage, respectively. When either of them reaches its upper limit, the warranty is terminated. In addition, it is supposed that for a particular customer, the usage rate r does not change within the warranty period. Thus, the end time of BW is ![]() Ub/r). Moreover, customers can buy EW Ωe=(We, Ue) at any time t(t≥0), and the end time for purchasing EW is
Ub/r). Moreover, customers can buy EW Ωe=(We, Ue) at any time t(t≥0), and the end time for purchasing EW is ![]() Ue/r). The manufacturer will bear all the maintenance cost during the warranty period.
Ue/r). The manufacturer will bear all the maintenance cost during the warranty period.
1.1 Failure modeling
Up to now, three approaches have been proposed for the failure modeling of 2D warranty, i.e., the bivariate method, composite scale method and marginal method[1,14]. Among them, the marginal method defines the failure strength as a function of product’s age and usage rate, and it considers the influence of age and usage on the times of failures simultaneously. In this study, T(t) and U(t) denote the product’s cumulative use time and usage at time t, respectively, and it is assumed that the repair time can be ignored. Thus, T(t)=t and the product’s cumulative usage is U(t)=rt.
Let λ(t|r) denote the failure strength function of the product. The mathematical expressions of λ(t|r) can be obtained by data-fitting. For details, one can refer to Refs.[5,15-16]. Therefore, the failure strength function model is
λ(t|r)=θ0+θ1r+θ2T(t)+θ3U(t)=θ0+θ1r+(θ2+θ3r)t
(1)
The extreme value of Eq.(1) is close to 0; that is, the inherent reliability of a new product is λ(0|r)=θ0+θ1r. Considering that the product’s inherent reliability is independent of its usage rate, θ1=0. In addition, the derived function of Eq.(1) is θ2+θ3r, which means that the change of failure strength is linearly related to the usage rate, regardless of the using time. This study considers the impact of age, usage as well as their interaction on the failure rate. Assuming that the product’s inherent reliability is θ0, we can obtain the improved two-dimensional warranty failure model as
λ(t|r)=θ0+θ1T(t)+θ2U(t)+θ3T(t)U(t)=
θ0+θ1t+θ2rt+θ3rt2
(2)
where θi are the constants with positive value, i=0, 1, 2, and 3, respectively.
1.2 A novel non-equal strength PM model
Up to now, three types of maintenance policies are widely applied in the warranty terms[6,17]: 1) Policy 1: Minimal repair is adopted for all the failures. 2) Policy 2: Minimal repair is adopted in BW, and minimal repair as well as periodic PM are used in EW. 3) Policy 3: Minimal repair is adopted before the customers purchase EW; and after that, minimal repair and periodic PM are adopted until the end of EW.
With the increase in cumulative usage and using time, the product’s failure rate will usually tend to increase. To make the maintenance policy more flexible, we propose a new non-equal strength periodic PM, and it is called Policy 4. Except that the maintenance strength during each period may be different, the other assumptions are the same as Policy 3.
The inspection period of PM is P(ΔT, ΔU), where ΔT and ΔU are the step sizes of the time and usage, respectively. In other words, when time reaches ΔT or the usage reaches ΔU, whichever comes first, one time of PM will be adopted. Thus, P=min(ΔT, ΔU/r). It includes three types of cases, as shown in Fig.1. The number of PMs during the warranty period is n=fix(W/P), where fix is a rounding down function. In the 2D warranty, the actual inspection time nodes are different from the change of usage rates. When the usage rate is equal to the designed usage rate r0, i.e. r0=W/U, the inspection period for PM is P(ΔT, ΔU) and the warranty period will be ended at W. When the usage rate r1>r0 and r2<r0, the maintenance inspection period is P1(ΔT1, ΔU1) and P2(ΔT2, ΔU2), respectively, where ΔT1=ΔU1/r1<ΔT, ΔU1=ΔU, ΔT2=ΔT, and ΔU2=ΔT2·r2.
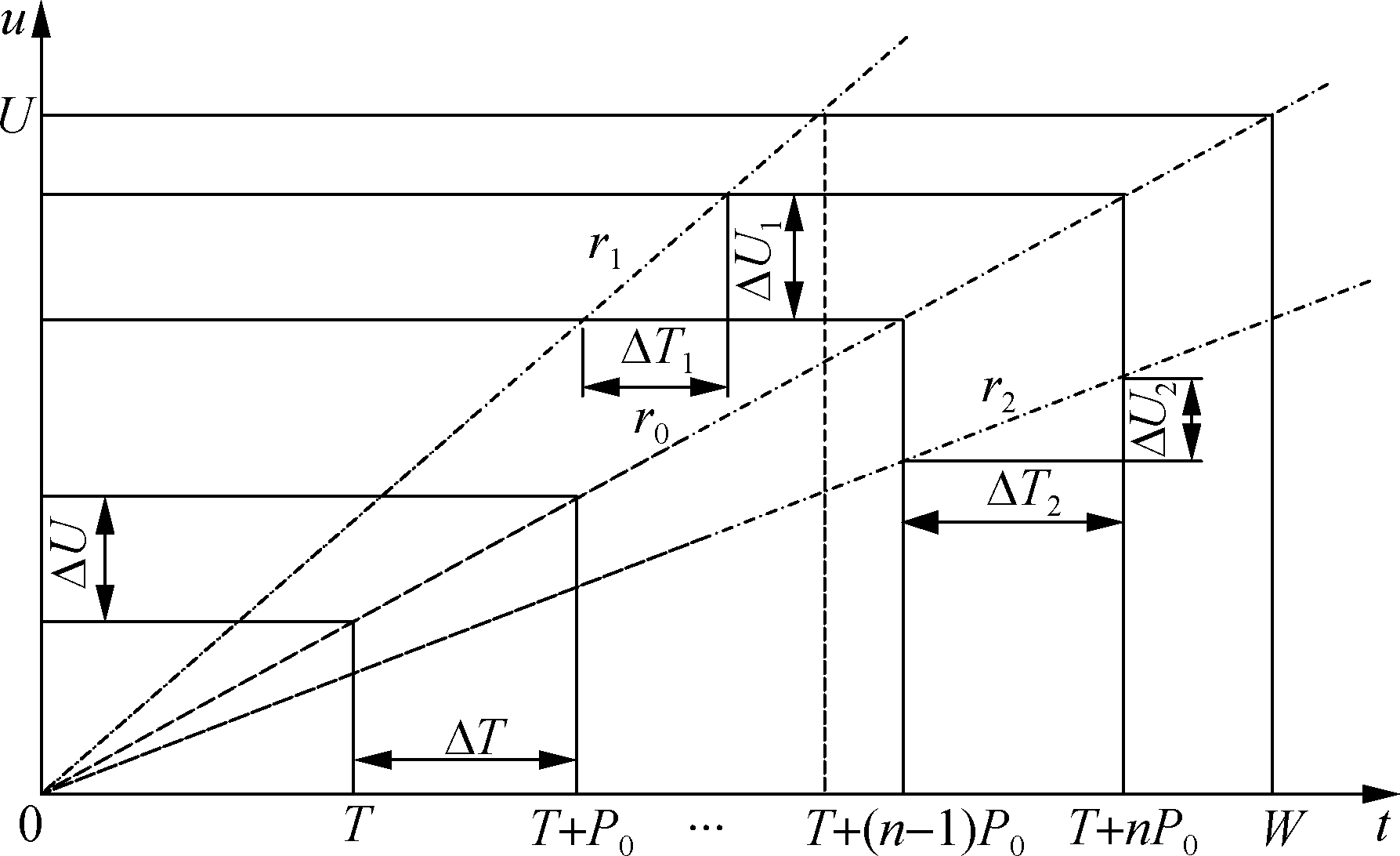
Fig.1 PM period under different usage rates
The virtual age method is used to describe the effect of PM. The virtual age factor is δ(m)=(1+m)e-m, where 0≤m≤M. Particularly, when m=0, the effect of PM is ignored; and when m=M (M is infinite), the effect of PM is the same as that of the replacement. For an incomplete PM, 0<m<M, and 0<δ(m)<1, its effect lies between the minimal repair and the replacement.
During the warranty period, the maintenance policy and failure rate’s variation tendency are shown in Fig.2, where t is the product’s using time, and λ is the product’s failure strength. At the time of T+P, the manufacturer implements the first PM with the maintenance strength of m1. The failure rate is reduced from λ2 to the failure rate, where the product’s virtual age is δ(m1)(T+P), and 0<δ(m1)<1. By analogy, after a fixed period, a PM will be performed, and the maintenance strength in each period is irrelevant. Specially, δ(mn-1)=0.
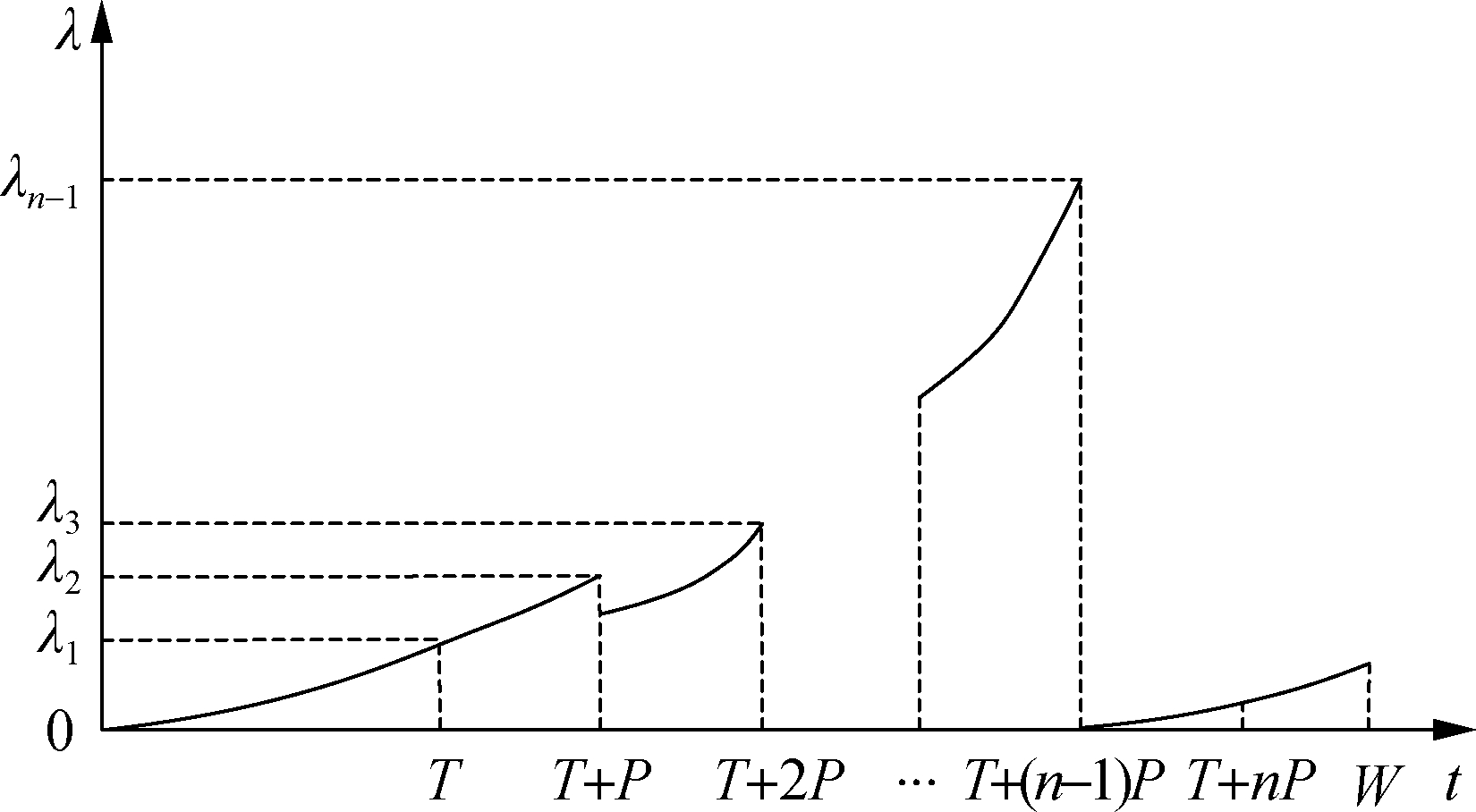
Fig.2 Failure rate’s change tendency with PM policy
The duration of a PM is W-T, then the times of PM during the warranty period is n=fix((W-T)/P). After the j-th PM, the product’s virtual age is vj (j=1, 2, …, n-1, n), then we have

(3)
For the minimal repair, the average cost is Cm, and the cost of the j-th PM is CP(mj). During the j-th PM period, the total warranty cost is Cj, which includes the cost for the minimal repair and PM. Therefore, we can obtain the warranty cost optimization model for each PM period.
min Cj=Cm![]() λ(t)dt+Cp(mj)
λ(t)dt+Cp(mj)
(4)
Let the total warranty cost during the warranty period be C. We can obtain the warranty cost optimization model during the entire warranty period as follows:
(5)
2 Modeling of Warranty Cost
In this study, two factors are considered to analyze the warranty cost, i.e., the product’s usage rate and the EW’s purchasing date. It is assumed that for a particular customer, the usage rate is subject to a random distribution G(r), and g(r) is the density distribution function. Based on the usage rate, a novel method is proposed to divide the customers into different groups, as shown in Fig.3. In Fig.3, rl and rh represent the lowest usage rate and the highest usage rate, respectively, rl≤r≤rh; k points of the usage rate are taken equally spaced during the warranty period, i.e. rl, r2, …, rh; and the customers are divided into group 1 to group k-1.
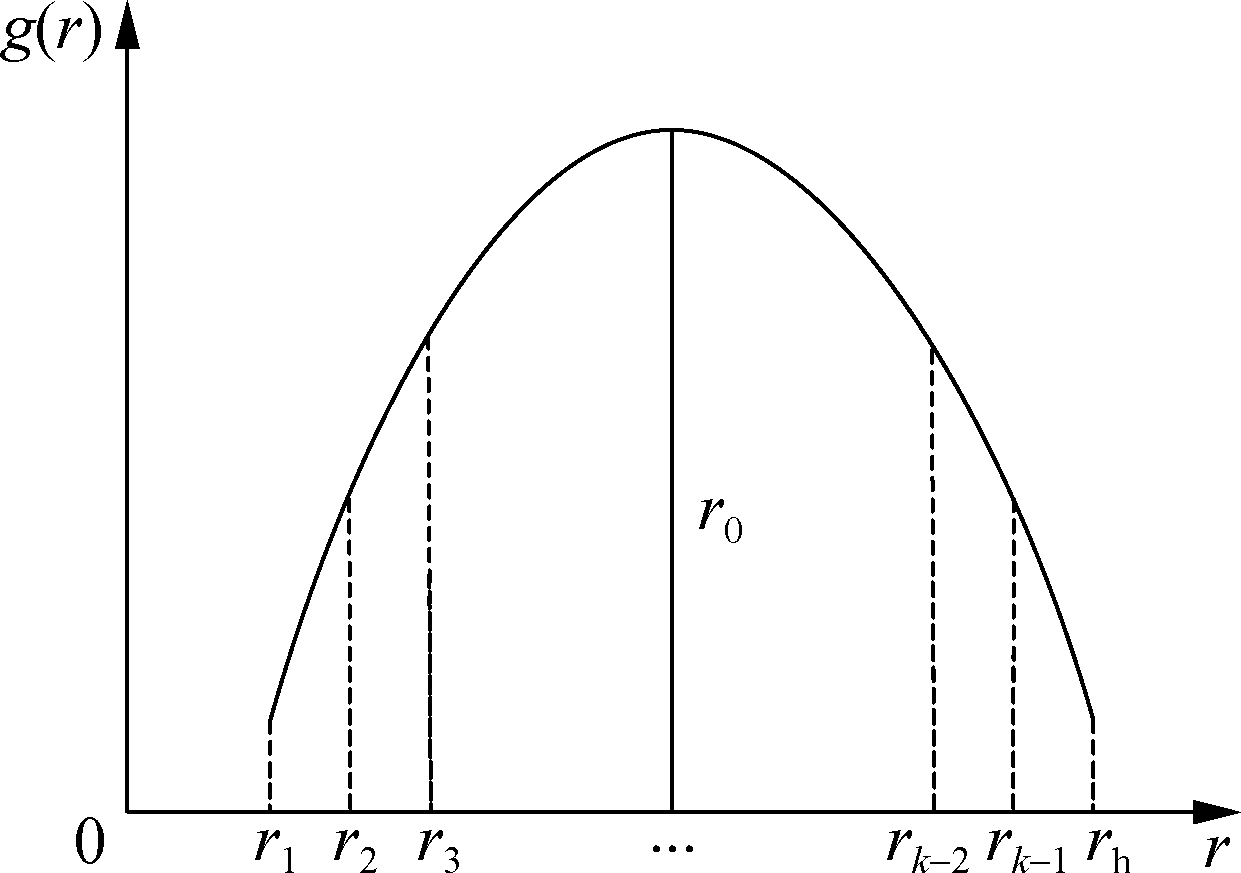
Fig.3 Customer classification based on usage rate
According to the time that the customer purchases the EW, two cases are considered.
Case 1 Customer purchases EW before the expiration of BW, i.e. 0≤T≤Wb and 0≤U≤Ub. In this case, the manufacturer provides customers with the same rectangular EW period, and determines the PM policy for the remaining BW and EW period according to the EW’s purchasing date, as shown in Fig.4.
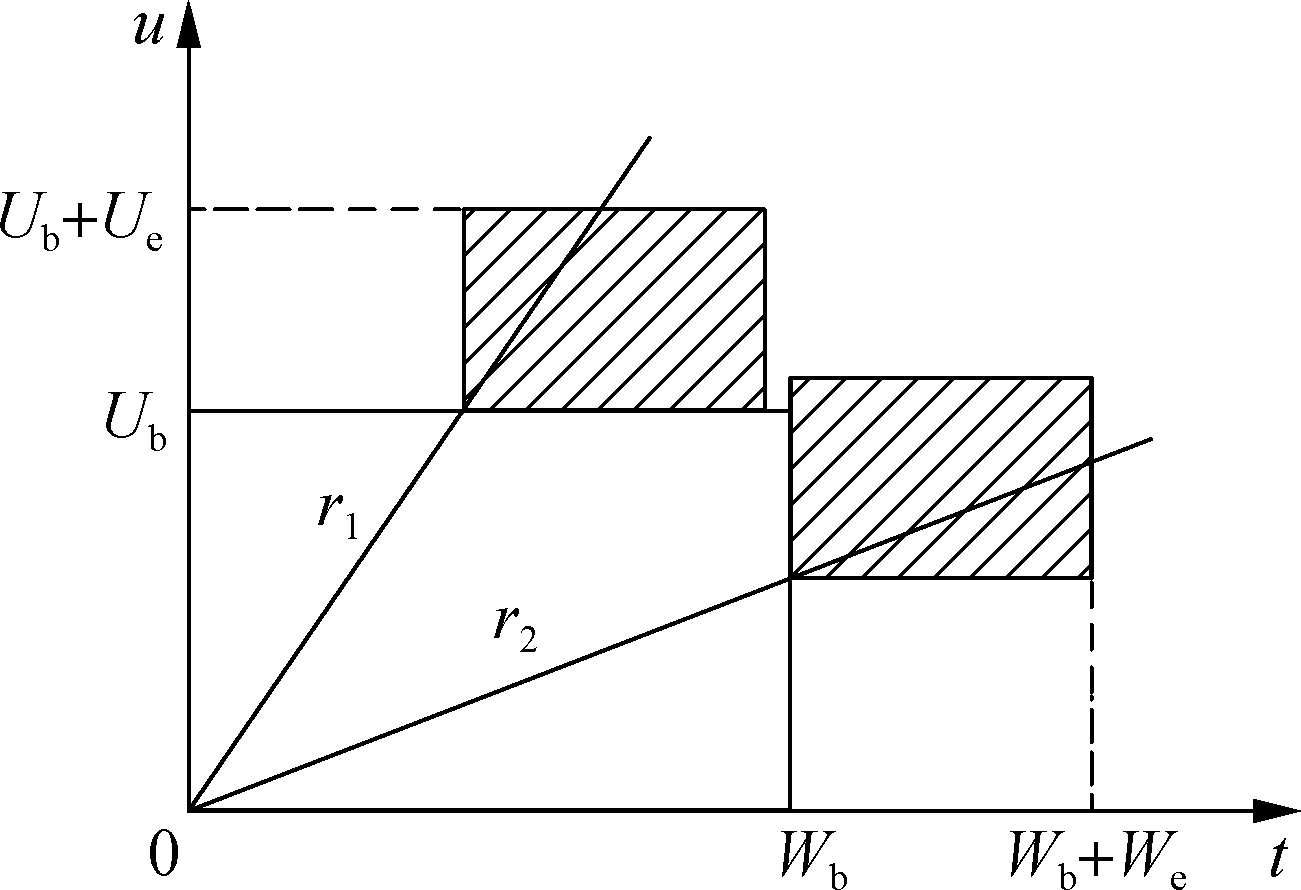
Fig.4 Purchasing EW before BW’s expiration
Case 2 Customer purchases EW at some point after the BW is expired, i.e. T>Wb or U>Ub. In this case, the manufacturer provides the customer with a customized EW period Ω′e=(W′e, U′e) as well as the maintenance polices according to the purchasing date and usage rate, as shown in Fig.5.
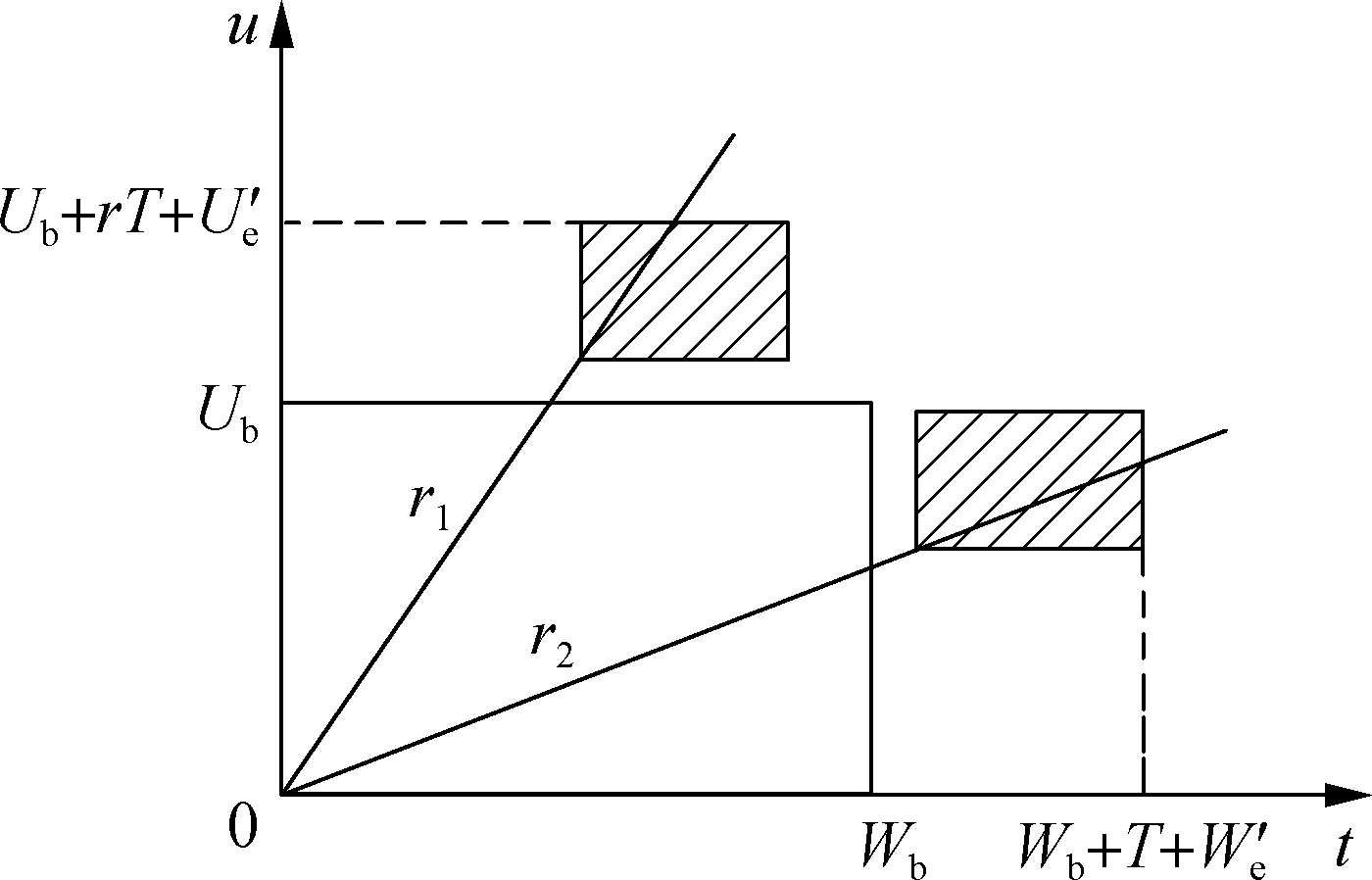
Fig.5 Purchasing EW after BW expired
In Case 1, the manufacturer needs to update the PM policy when purchasing EW. The remaining warranty period is Ω1=(Wb+We-T, Ub+Ue-Tr). Let the PM period be ![]() (Ub+Ue-Tr)/r). Therefore, the times of PM is
(Ub+Ue-Tr)/r). Therefore, the times of PM is ![]() After the j-th PM, the virtual age of the product is vj=T+
After the j-th PM, the virtual age of the product is vj=T+
![]() Therefore, during the total warranty period, the expected warranty cost is
Therefore, during the total warranty period, the expected warranty cost is
(6)
Considering the difference in customer’s usage rate, P1 and mj are the variables to be optimized, and in the total warranty period, the expected warranty cost optimization model is
![]()
s.t. Pe>0
0≤mj≤M
(7)
According to the above classification approach for the customers,the variables ![]() of group i is optimized. Thus, based on Eq.(6), the customers’ total warranty cost is
of group i is optimized. Thus, based on Eq.(6), the customers’ total warranty cost is
(8)
In Case 2, when the BW is expired and if the EW period is maintained constant with that in Case 1, the warranty cost will increase significantly. Thus, a new EW period Ω′e=(W′e, U′e) needs to be reset. Considering the profit for both the customers and manufacturers, we can obtain the EW period based on the condition that the total warranty cost is equal to the maximum total warranty cost max(C) in Case 1. When 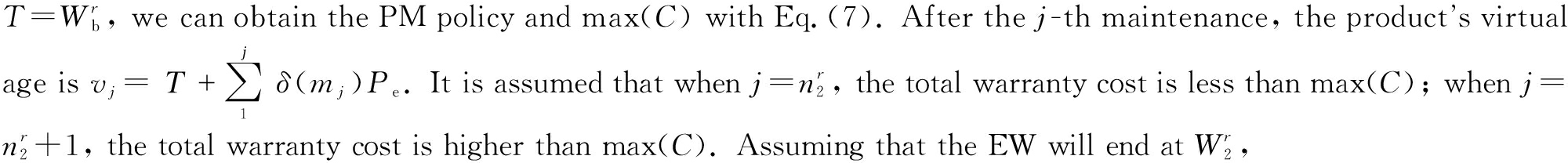 and by solving the analytical solution of the following constraint formulation, the EW period can be obtained:
and by solving the analytical solution of the following constraint formulation, the EW period can be obtained:
(9)
Based on the result of Eq.(9) and by multiplying the usage rate, the EW period can be determined. Meanwhile, the manufacturer needs to optimize the PM policy so as to minimize EW’s cost. The duration time of EW is ![]() U′e/r), and the PM period is
U′e/r), and the PM period is  The expected warranty cost during the total warranty period is
The expected warranty cost during the total warranty period is
(10)
Considering the customers’ usage rate as well as the optimizing variables of P2 and mj, we obtain the expected cost optimization model for the manufacturer as follows:
![]()
s.t. P2>0
0≤mj≤M
(11)
By optimizing ![]() the warranty policies can be customized for different customers’ groups. During the total warranty period, the manufacturer’s expected cost is
the warranty policies can be customized for different customers’ groups. During the total warranty period, the manufacturer’s expected cost is
(12)
Considering that the EW period will continue to decrease with the using time, when the using time reaches a certain threshold value, the manufacturer cannot make a profit or will even lose money by providing the warranty. Therefore, the manufacturer should set a boundary for the EW. By using Eq.(9), the deadline Td for EW’s purchasing date can be obtained.
3 Case Study
In this section, a numerical example is provided to illustrate the effectiveness of the proposed policies. Both the BW and EW periods are (3 years, 6×104 km). The parameters in the failure strength function are set as follows: θ0=0.05, θ1=0.7, θ2=0.5, and θ3=0.1. It is supposed that the customer’s usage rate is subject to a uniform distribution, rl=0.5×104 km/year, rh=3.5×104 km/year, and r0=2×104 km/year. In total, there are 6 levels of maintenance strength, i.e., m=0, 1, 2, 3, 4, 5 and M, and the corresponding PM costs are Cp= 0, 20, 50, 90, 150, 240, and 3 000 dollar, respectively. The average minimal repair cost is Cm= 250 dollar. In addition, we discretize the PM period into P(ΔT, ΔU) and ΔT and ΔU are the integers in units of month and 103 km, respectively.
According to Eq.(6), we can obtain the PM periods (i.e. ΔT and ΔU), PM strength (m) and the corresponding total warranty cost (C) when T=0. When the usage rate is r0, the comparison of different maintenance policies (presented in Section 2.2) is shown in Tab.1. Among them, Policy 4 has the lowest total warranty cost of 2 041.28 dollar. It indicates that compared with the other three policies, the proposed maintenance policy can achieve better results. The corresponding PM period is (4 months, 7×103 km). Furthermore, the strength of the first two PM periods is 0; and for the other PM periods, the strength of 2 is adopted.
Tab.1 Comparison of total warranty cost under different policies

PoliciesPolicy 1Policy 2Policy 3Policy 4ΔT/month994ΔU/103 km15157m440/2C/dollar12 225.009 891.103 013.972 041.28
Considering the maintenance policies and purchasing date of EW, the minimum warranty cost is shown in Fig.6. It can be found that Policy 1 and Policy 2 have nothing to do with the purchasing date, and the warranty cost of Policy 2 is lower than that of Policy 1. The total warranty cost of Policy 3 and Policy 4 will increase with the delay of purchasing date. At the end of BW (i.e. the 36 months), the warranty cost for Policy 3 is 9 891.10 dollar, which is the same as that of Policy 2. Furthermore, by adopting Policy 4, the minimum warranty cost is 2 030.49 dollar at 3 and 7 months, respectively. Obviously, regardless of the purchasing date of EW, the proposed maintenance policy can obtain the lowest warranty cost for the manufacturer.

Fig.6 Warranty cost for different purchases time and maintenance policies
According to Policy 4, the optimized maintenance policies for different purchasing dates are shown in Tab.2. The PM period is rounded to (4 months, 7×103 km). Additionally, the PM strength will change with the purchasing date. For example, during the first seven months, the PM strength is 2/0. It means that only the last time of PM is 0 (the last time of PM is canceled), and all the remaining maintenance strength is 2. The meaning of other PM’s strength is as follows: 3/2/0 means that the strength of the first PM is 3, the strength of the last PM is 0, and the remaining’s is 2; 3/2 means that the PM strength of the first PM is 3, and the PM strength of the remaining month is 2.
Tab.2 Optimized maintenance strategies for different purchasing dates
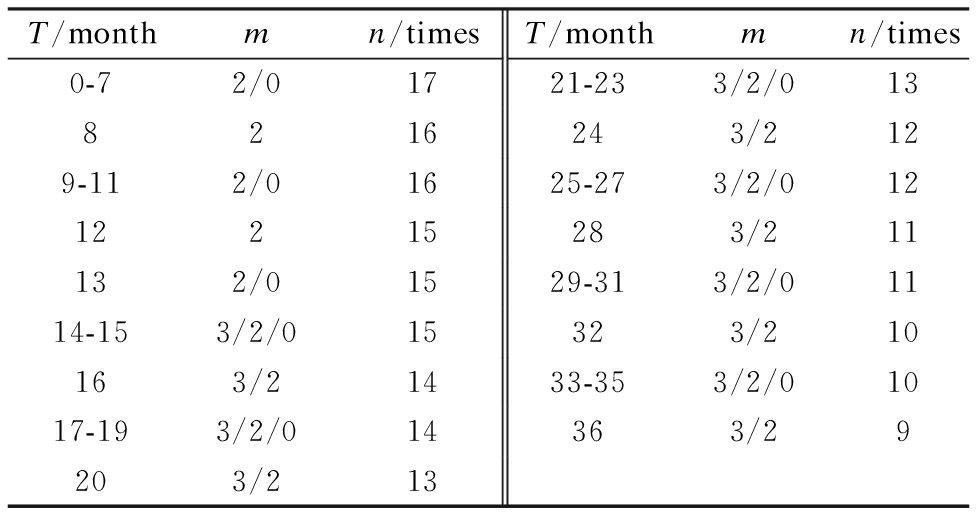
T/monthmn/timesT/monthmn/times0-72/01721-233/2/0138216243/2129-112/01625-273/2/01212215283/211132/01529-313/2/01114-153/2/015323/210163/21433-353/2/01017-193/2/014363/29203/213
According to the proposed method in Section 2, customers are divided into six groups: r1=0.75×104 km/year, r2=1.25×104 km/year, r3=1.75×104 km/year, r4=2.25×104 km/year, r5=2.75×104 km/ year, and r6=3.25×104 km/year. Based on Eqs.(7) and (8), we can obtain the average warranty cost, and the comparison of the two situations is shown in Fig.7. For the customers with a high usage rate, the BW will end earlier; while for the divided customers’ groups, the total warranty cost can be reduced in stages. The expected total warranty cost is 2 252.77 and 2 342.16 dollar for the divided and undivided usage rate strategies, respectively. Obviously, for the manufacturer it is beneficial to divide the customers into different groups based on their usage rate.
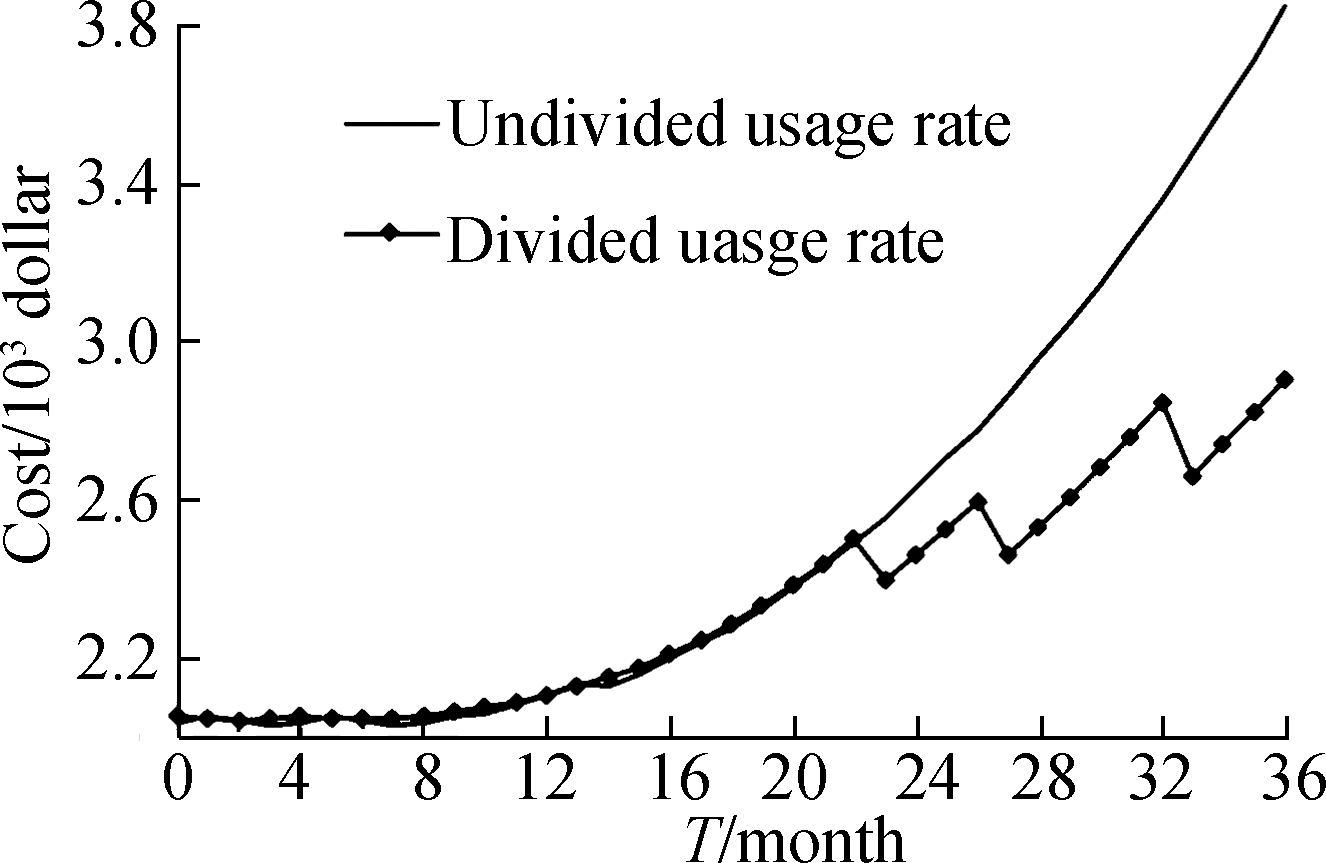
Fig.7 Comparison of warranty cost of different customer groups
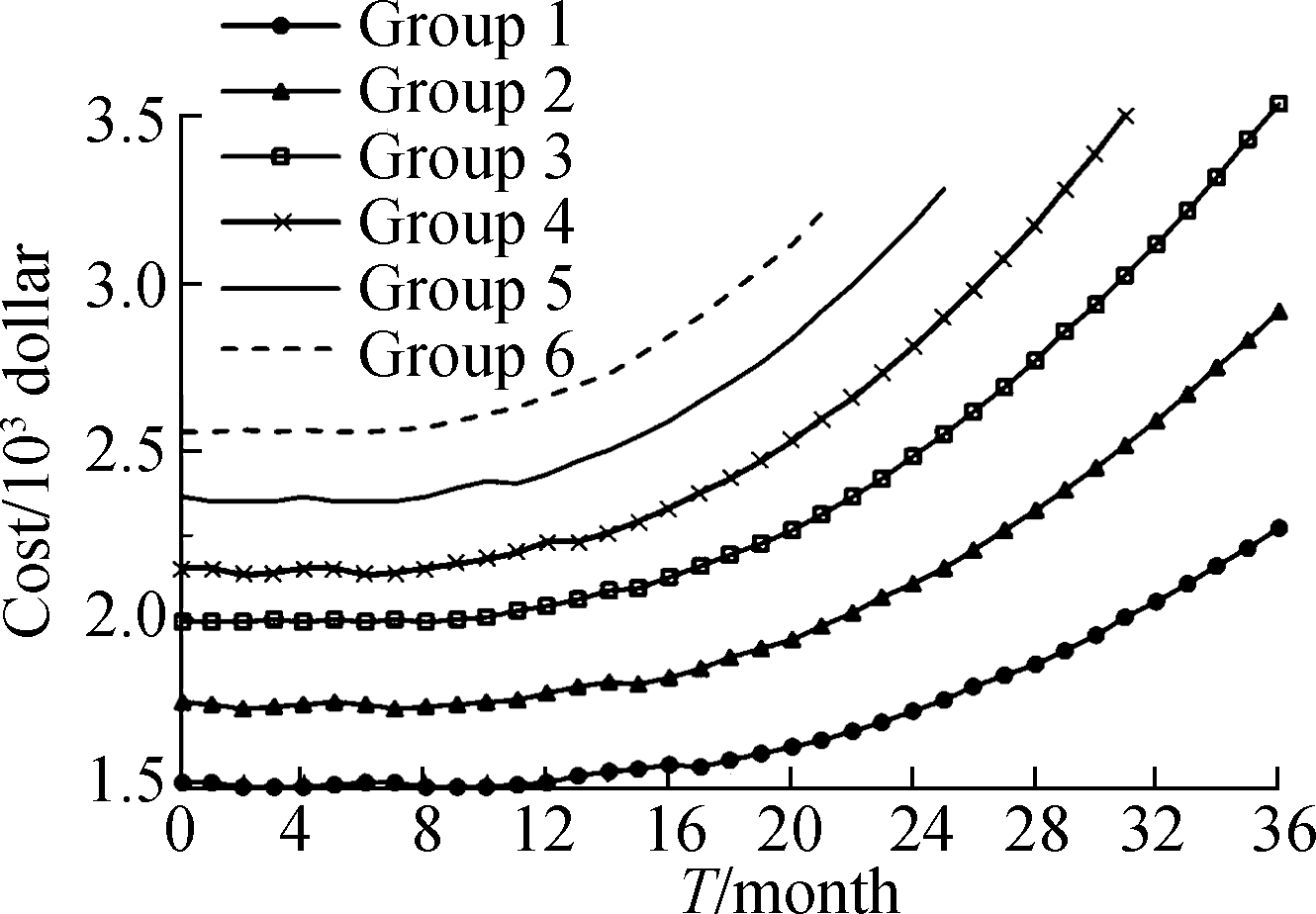
Fig.8 Warranty cost changing with purchasing date for different groups
Similarly, by minimizing the maintenance cost, we can obtain the maintenance policy for each group, as shown in Tab.3. From Tab.3, when the usage rate is low, the corresponding PM period is long, and the start time for PM will be postponed. Additionally, the PM strength may be different during each period. For instance, the PM strength for Groups 1, 2 and 4 is 2/0. It means that the strength for the last time of PM is 0 and the strength for the rest is 2. The PM strength of Group 3 are 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, respectively.
Tab.3 Optimized maintenance policy for each customer group

Customer groupGroup 1Group 2Group 3Group 4Group 5Group 6T/month978655ΔT/month654444ΔU/103km46681011m2/02/02/12/022
When BW is expired, we can obtain the EW periods for different purchasing times accordingly, as shown in Tab.4. It shows that the warranty period tends to decrease with the increase in the purchasing time, which is provided by the manufacturer. With the constraint of W′e=2, the manufacturer stops selling the EW. In the 84th month, the EW period is (24 months, 4×104 km). Therefore, the deadline for purchasing EW is set to be Td= 84 months in this case, and the optimized PM period is 4 months. At the end of BW, the PM strength is 3/2, during the EW, the PM strength becomes 4/2. It means that the PM strength for the first time is 4, and it is 2 for the rest of the time. In addition, we can also obtain the warranty cost under different maintenance policies. After optimization, the total warranty cost fluctuates around 3 700 dollar.
Tab.4 Maintenance strategies under different purchasing times

T/monthW/monthU/104 kmC/dollarT/monthW/monthU/104 kmC/dollar393263 700.26632853 634.82423263 706.94662853 641.66453263 713.64692853 648.52483263 720.36722853 655.40513263 727.10752853 662.30543263 733.86782853 669.22573263 740.64812853 676.17602853 628.00842443 563.43
Similarly, if a customer purchases EW after the BW expired, the manufacturer can also provide him/her with a customized maintenance policy. According to Eq.(9), we can obtain the optimized maintenance policy as well as the warranty cost for the customers with any usage rate. The results are similar to Fig.8 and Tab.3. Here, we do not discuss the details furthermore.
4 Conclusions
1) By combining minimal repair and PM, better maintenance effect can be obtained compared with applying only minimal repair. Furthermore, there is an appropriate time point during the BW period to update the BW maintenance policy and start the PM.
2) For the customers, the warranty cost increases if they postpone purchasing EW. Meanwhile, the corresponding warranty period is also shortened. Therefore, the manufacturer should adopt some preferential measures to encourage customers to purchase EW as early as possible.
3) Besides the purchasing date, the customer’s usage rate should be considered in a customized warranty policy. It can help the manufacturer to reduce the expected number of failures and the warranty cost during the warranty period.
4) In addition to the usage rate, in the future study, the following factors can also be integrated into the customized warranty policy, including the product’s operating environment, customer’s risk preference and their learning ability, etc.
[1] Kurvinen M, Töyrylä I, Murthy D N P. Warranty fraud management[M]. Hoboken, New Jersey, USA: John Wiley & Sons, Inc., 2016. DOI:10.1002/9781119277576.
[2] Tong P, Liu Z X, Men F, et al. Designing and pricing of two-dimensional extended warranty contracts based on usage rate[J].International Journal of Production Research, 2014, 52(21): 6362-6380. DOI:10.1080/00207543.2014.940073.
[3] Chien Y H. Optimal periodic replacement policy for a GPP repairable product under the free-repair warranty[J]. Quality Technology & Quantitative Management, 2019, 16(3): 347-354. DOI:10.1080/16843703.2017.1422218.
[4] Shahanaghi K, Noorossana R, Jalali-Naini S G, et al. Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts[J]. Engineering Failure Analysis, 2013, 28: 90-102. DOI:10.1016/j.engfailanal.2012.09.006.
[5] Wang Y K, Liu Z X, Liu Y L. Optimal preventive maintenance strategy for repairable items under two-dimensional warranty[J]. Reliability Engineering & System Safety, 2015, 142: 326-333. DOI:10.1016/j.ress.2015.06.003.
[6] Su C,Shen J Y. Analysis of extended warranty policies with different repair options[J]. Engineering Failure Analysis, 2012, 25: 49-62. DOI:10.1016/j.engfailanal.2012.04.002.
[7] Santana J M, Santiago R L V,Moura M. Extended warranty of medical equipment subject to imperfect repairs: An approach based on generalized renewal process and Stackelberg game[J]. Eksploatacja i Niezawodnosc Maintenance and Reliability, 2018, 20(4): 567-578. DOI:10.17531/ein.2018.4.8.
[8] Wang J T, Zhou Z,Peng H. Flexible decision models for a two-dimensional warranty policy with periodic preventive maintenance[J]. Reliability Engineering & System Safety, 2017, 162: 14-27. DOI:10.1016/j.ress.2017.01.012.
[9] He S G, Zhang Z M, Zhang G H, et al. Two-dimensional base warranty design based on a new demand function considering heterogeneous usage rate[J].International Journal of Production Research, 2017, 55(23): 7058-7072. DOI:10.1080/00207543.2017.1346837.
[10] Ye Z S, Murthy D N P. Warranty menu design for a two-dimensional warranty[J].Reliability Engineering & System Safety, 2016, 155: 21-29. DOI:10.1016/j.ress.2016.05.013.
[11] Tong P, Song X F, Liu Z X. A maintenance strategy for two-dimensional extended warranty based on dynamic usage rate[J].International Journal of Production Research, 2017, 55(19): 5743-5759. DOI:10.1080/00207543.2017.1330573.
[12] Lam Y,Lam P K W. An extended warranty policy with options open to consumers[J]. European Journal of Operational Research, 2001, 131(3): 514-529. DOI:10.1016/S0377-2217(00)00091-6
[13] Su C, Wang X L. A two-stage preventive maintenance optimization model incorporating two-dimensional extended warranty[J].Reliability Engineering & System Safety, 2016, 155: 169-178. DOI:10.1016/j.ress.2016.07.004.
[14] Jack N,Iskandar B P, Murthy D N P. A repair-replace strategy based on usage rate for items sold with a two-dimensional warranty[J]. Reliability Engineering & System Safety, 2009, 94(2): 611-617. DOI:10.1016/j.ress.2008.06.019.
[15] Huang Y S, Huang C D, Ho J W. A customized two-dimensional extended warranty with preventive maintenance[J].European Journal of Operational Research, 2017, 257(3): 971-978. DOI:10.1016/j.ejor.2016.07.034.
[16] Su C, Wang X L. Optimal upgrade policy for used products sold with two-dimensional warranty[J].Quality and Reliability Engineering International, 2016, 32(8): 2889-2899. DOI:10.1002/qre.1973.
[17] Bouguerra S, Chelbi A, Rezg N. A decision model for adopting an extended warranty under different maintenance policies[J]. International Journal of Production Economics, 2012, 135(2): 840-849. DOI:10.1016/j.ijpe.2011.10.022.