The vibratory roller was used to compact the deformable terrains, asphalt and other materials based on the combination of the excitation force of the drum and vehicle static load[12]. The research on vibratory rollers indicates that the operator’s ride comfort was greatly influenced by the deformable terrains, especially elastoplastic soils[25]. The vibrations generated from the tire-elastoplastic soil interaction were transmitted to the operator via the isolation systems of the seat and cab. Moreover, the vibration excitations in the low-frequency range (bellow 10 Hz) caused by the surface roughness of the deformable terrain can seriously affect the physical and mental health of the operator[6]. Consequently, the cab isolation system was one of the most important systems used to improve the vehicle’s ride quality in the low-frequency range. The cab isolation system of the vibratory rollers was mainly equipped with the rubber mounts (RM) with low-damping and high-stiffness characteristics[12, 78]. However, the stiffness property of the rubber helped suppress only noise and vibration in the high-frequency range, contrariwise, the low-damping property of the rubber generated a high-magnitude vibration which can reduce the ride quality and increase the cab shaking, especially at the low-frequency range[8]. To improve the ride quality, the influence of the design parameters of the RM on the ride quality was analyzed[2], and the TRM added by the auxiliary hydraulic mount were then optimized[1]. However, the research results show that cab shaking was still high under working conditions. Thus, it is difficult to obtain ride comfort with the RM.
The hydraulic mounts (HM) were researched for the cab of earth-moving machinery, construction equipment, and industrial vehicle to control the cab shaking as well as improve ride quality[910]. A cab model of earth-moving machinery equipped with the HM was also studied under the random excitation of the rigid road surface in a low-frequency range below 10 Hz[8]. The results show that both the power spectral density (PSD) of displacements and the root mean square (RMS) of accelerations at the cab’s mass center were significantly decreased in comparison with the RM. Besides, the pneumatic mounts (PM) of the car, passenger vehicle, commercial vehicle, and high-speed train were also applied for the cab isolation mounts to improve the ride quality[1113] and safety of the operator[1415]. The results also indicate that the operator’s ride quality was clearly improved by using the PM. Furthermore, not only did the PM show fewer resonant peaks but also the resonant peaks were lower than mechanical springs and RM with equivalent properties[12]. Both the HM and PM were then studied for the cab isolation mounts of the vibratory rollers[16]. The results show the nonlinear liquid damping and high-stiffness characteristics of HM; and that the nonlinear viscous damping and high-static/elastic stiffness characteristics of the PM can control the vibrations of the vertical operator’s seat and cab shaking in the low-frequency region. However, the research results also show that the vibration of the vertical operator’s seat and cab pitch angle was still high according to ISO 2631-1[17].
Based on the preeminent characteristics of both the PM and HM, a combined model of the hydro-pneumatic suspension (HPS) was also applied on agricultural tractors and dump trucks for enhancing the ride comfort and reducing energy[1819]. The results show that the cab’s ride comfort was greatly improved. Although the research has not yet considered deformable terrain, nonetheless, the results were obvious evidence for the study on combining both the HM and PM to improve the vibratory roller’s ride comfort. In this research, a 3D nonlinear dynamic model of the vibratory roller is established under the condition of the vehicle working on off-road soil ground. The vibration excitations of the elastic tires-deformable soil contact and rigid drum-elastoplastic soil interaction at the excitation 35 Hz of drum are applied. Experimental investigation is also used to verify the accuracy of the mathematical model. The hydro-pneumatic mounts (HPM) of the cab combined with the nonlinear adjustable damping of the HM and by the high-static stiffness and nonlinear viscous damping of the PM are studied. The effectiveness of the HPM for improving the ride comfort and the health of the operator is then assessed based on the RMS and PSD acceleration responses of the vertical operator’s seat, cab pitch and roll angles at the time and in frequency regions.
1 Modeling of Hydro-Pneumatic Mounts
The RM of the vibratory roller cab was mainly described by the linear damping Cr and stiffness coefficient Kr. Its dynamic force in the vertical direction Z is given as[12,16]
(1)
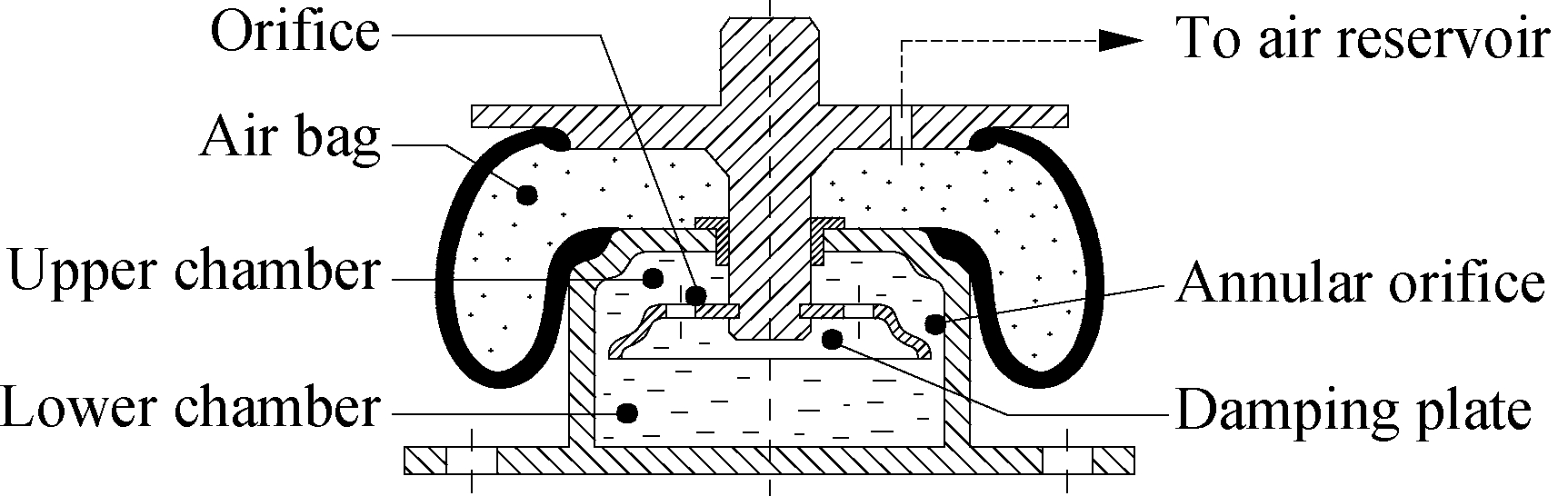
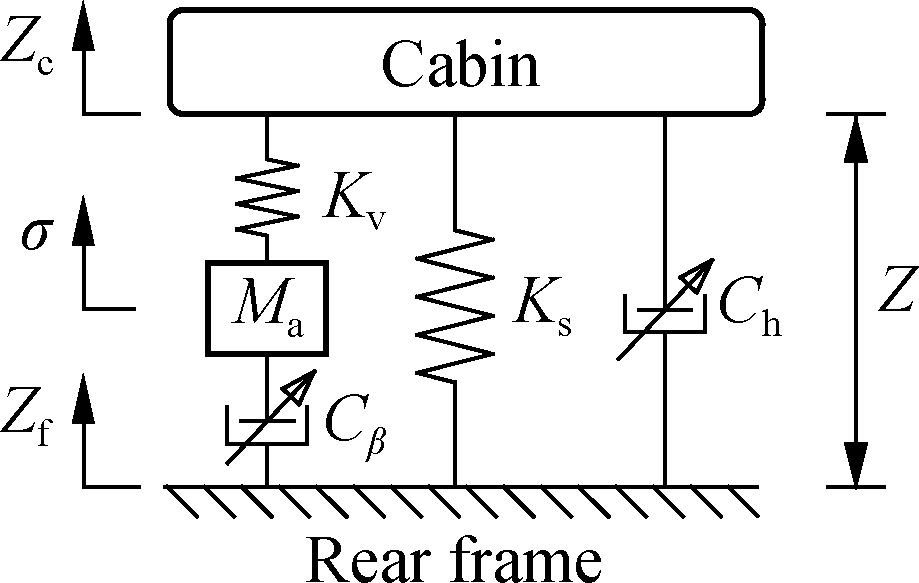
However, the RMS acceleration of the seat and cab of the vibratory rollers with RM was still high according to ISO 2631-1[17]. Thus, based on the advantages of both the HM and PM[12,14], a combined HPM for the cab of vibratory rollers is studied to further enhance the vehicle ride quality. The HPM includes an airbag connected to an air reservoir through a pipe, a damping plate driven by a bolt, and a closed chamber filled with fluid. In the upper and lower chambers of damping mounts, the fluid flow is derived by the damping plate’s transfer via the orifices and annular orifice. The structure and mathematical model of the HPM are shown in Figs.1(a) and (b).
Based on the mathematical model of the HPM in Fig.1(b), the HPM dynamic force is calculated. The dynamic response of the airbag is determined by the parameters of pressure, temperature, volume, mass, density as well as the airbag shape. The airbag is assumed to be only deformed in the Z direction. After the airbag is deformed, the new volume of reservoir and airbag are determined as[12]
(a)
(b)
Fig.1 Hydro-pneumatic mounts. (a) HPM structure; (b) HPM mathematical model
Vr=Vr0-Asaσ, Vb=Asaσ+Vb0-AiaZ
(2)
where σ is the displacement of the air in the pipe; Vr0 and Vb0 are the initial volumes of reservoir and airbag; Asa and Aia are the cross-section area of the pipeline and impact area of air in the airbag.
By applying the GENSYS model to calculate the airbag dynamic parameters in Fig.1(b), the mass Ma, the viscous and static stiffness coefficients of Kv and Ks are calculated as[12]
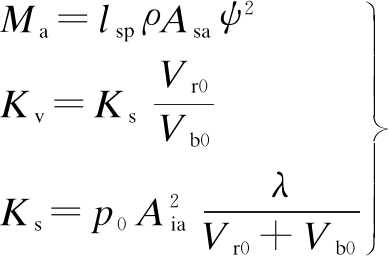
(3)
where 
lsp is the pipe length; ρ is the air density; p0 is the initial pressure of airbag; and λ is the polytropic rate of air.
The static force Fs and viscous force Fv of the airbag in the direction of Z are determined as[20]
(4)
where Cβ is the HPM’s nonlinear viscous damper coefficient.
From Eq.(4), the airbag dynamic force in the direction of Z is calculated as
(5)
It is also assumed that the inertial force of the fluid flow in the annular orifice and orifices is very small, and the dynamic response of the fluid flow via both the annular orifice and orifices is only in the direction of Z. Thus, differential pressure Δp between the upper and lower chambers is determined via the total pressure losses of the annular orifice and orifices as follows[8]:
(6)
where 
is the PHM’s relative velocity; Ca and Co are the parameters of the geometric dimensions of the annular orifice and orifices; Ac, Aa, and Ao are the areas of chamber, annular orifice, and orifices, respectively.
The damping force of the liquid generated by Δp and area Apa of the damping plate is
(7)
where Ch is the HPM’s damping coefficient, and Ch=Apa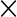
{Ca(Ac/Aa)2+Co(Ac/Ao)2}.
From Eqs.(5) and (7), the HPM dynamic force is calculated as
(8)
The dynamic forces of the cab isolation mounts are then written as
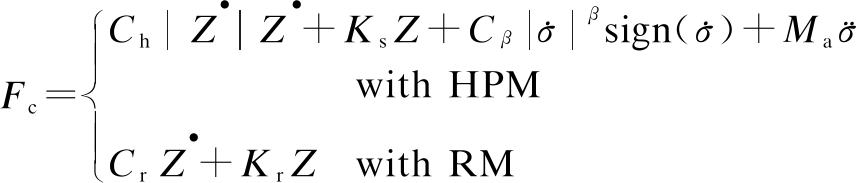
(9)
2 Vibratory Roller Dynamic Model
2.1 Vehicle dynamic model
Based on the actual structure of the vibratory roller described in Fig.2, a nonlinear dynamic model of the vibratory roller is built in Fig.3 to evaluate the HPM’s ride quality in low-frequency region.
In Fig.3, Z1-5 and M1-5 are the vertical vibration and mass of the operator’s seat, cab, front/rear frame, and drum, respectively; φ2 and φ4 are the pitch angle of the cab and rear frame; θ2-5 are the roll angle of the cab, front/rear frame, and drum, respectively; K1-4 and C1-4 are the stiffness and damping coefficients of the drum isolation mounts and tires; F, Mx and My are the vertical force and rotation moments at the articulated-frame steerage of the vehicle; la is the distance between the centre of gravity of the front frame and articulated-frame steerage while l1-7 and b1-5 are the longitudinal and transversal distances of the vehicle; and v0 is the vehicle velocity.
Fig.2 The actual structure and experimental model of the vibratory roller
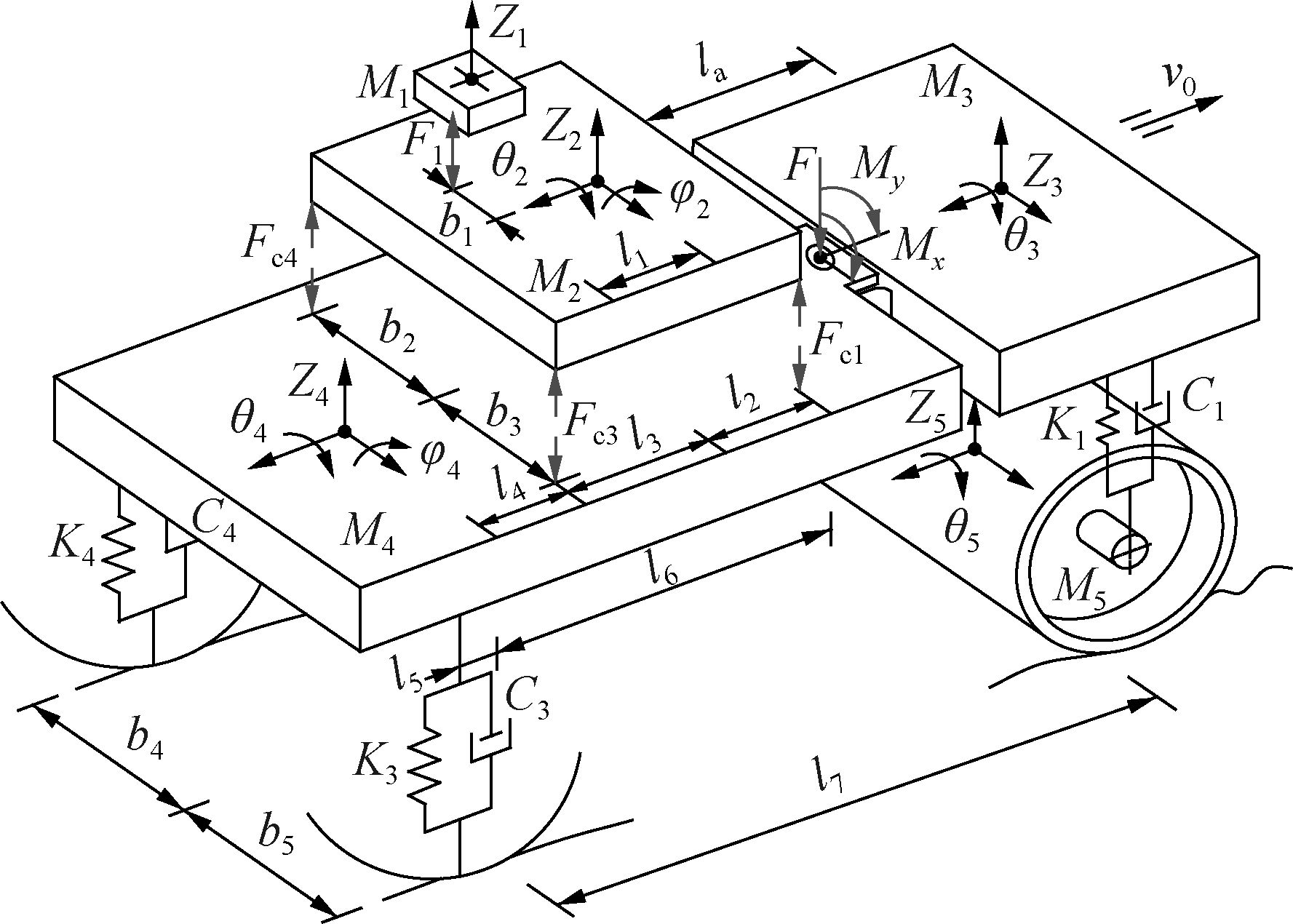
Fig.3 3D nonlinear dynamic model of the vibratory roller
Based on the vibratory roller dynamic model in Fig.3, and by using Newton’s second law of motion, the motion of the vibratory roller can be represented in the matrix form as
(10)
where Z is the displacement vector; M, C and K are the mass, damping and stiffness matrices, respectively; and F(t) is the excitation force vector.
2.2 Vibration excitation under the drum and tire
Based on the model of the rigid drum-elastoplastic soil interaction of the vibratory roller in Ref.[1], the excitation force Fdi of the drum is given as follows:
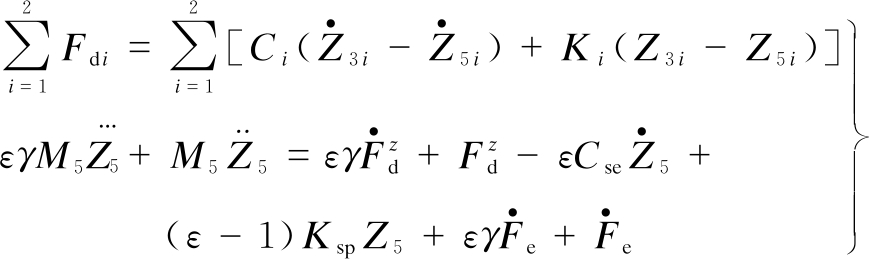
(11)
where ε and γ are the plasticity and damping factors of the deformable soil; Ksp and Cse are the coefficients of the plastic stiffness and elastic damping; and Fe is the vibration excitation force of the vibrator drum.
Moreover, the excitation force Fti of the elastic tire-deformable terrain contact is determined according to Ref.[16] as follows:
(12)
where Z4i and Zxi are the vertical vibration of the tires and sinking of the soil under the tires, i=3,4.
3 Experimental Test
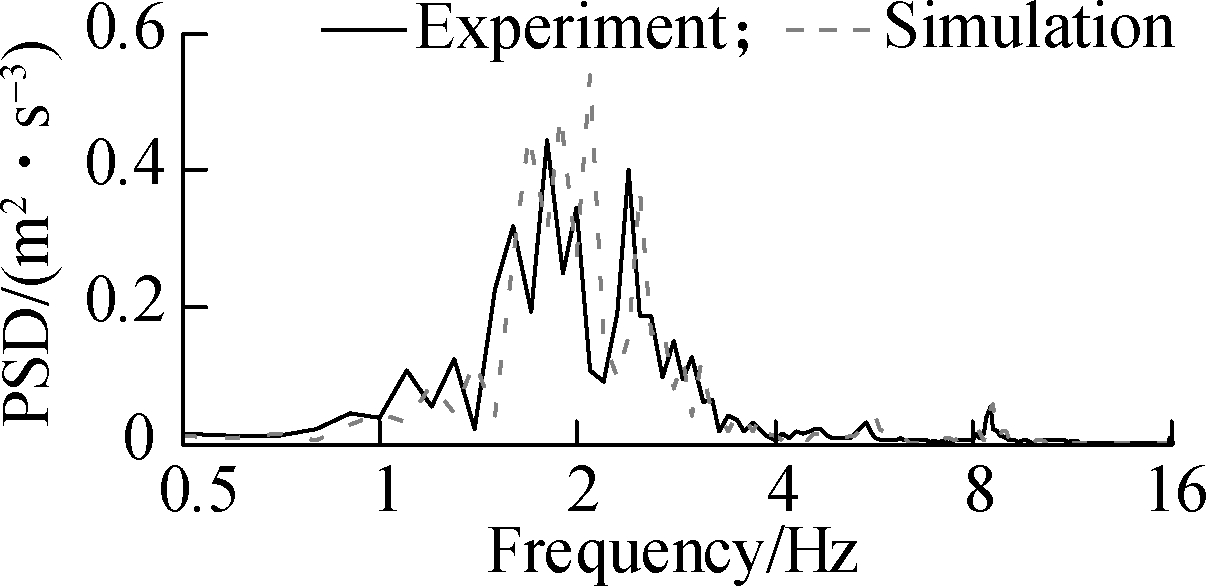
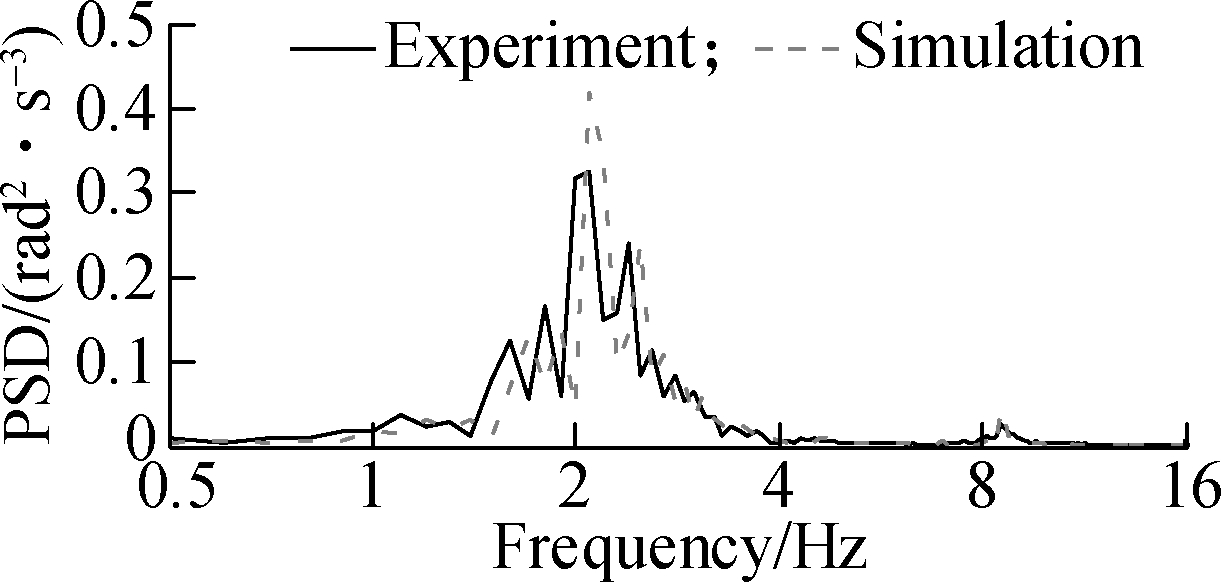
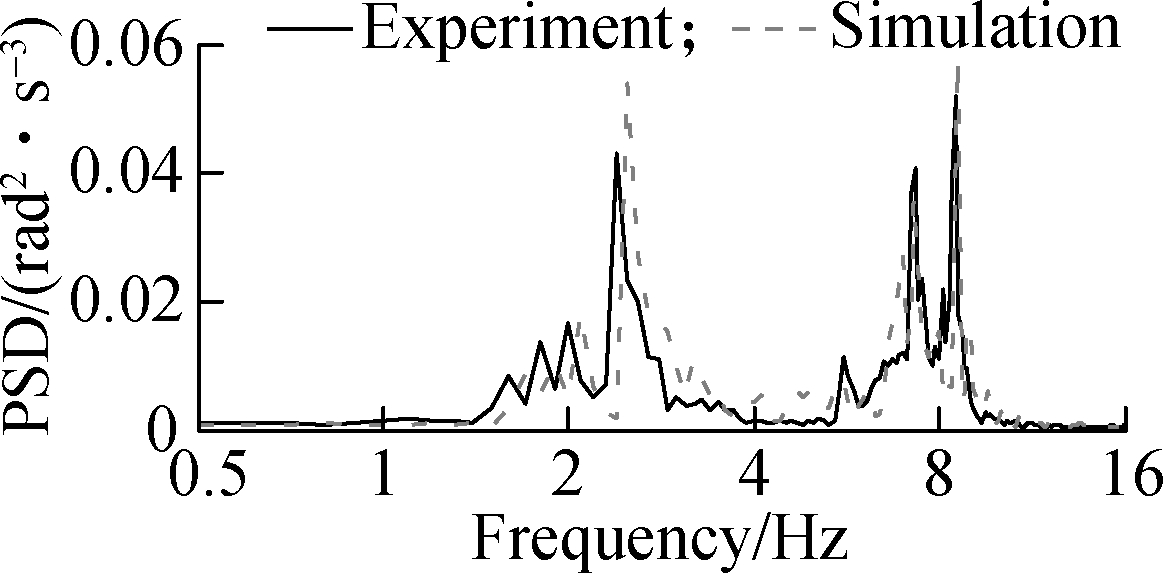
To evaluate the effectiveness of HPM based on the vibratory roller dynamic model, a vibratory roller cab equipped with the RM is tested to determine the accuracy of the dynamic model. Under the compacting condition of the vehicle on the deformable terrain, the low/high-frequency of 28/33 Hz of the excitation drum can create the maximum compaction forces due to the “double-jump” of the drum[1,4]. Based on the parameters of the vehicle[16], the experimentation and simulation of a vibratory roller are performed at a vehicle velocity of 3 km/h when the vehicle moves and compacts on the elastoplastic soil at an excitation 35 Hz of the drum. The experimental process is conducted under the same condition of the simulation, and it is described as follows: The ICP three-direction acceleration sensors, LMS dynamic test, and analysis system are used to measure the acceleration responses on the cab floor and seat, which are the same as those described in Fig.2. Through the process of measurement, the measured data of the acceleration responses of the operator’s seat and cab is then calculated and displayed. The measured results of the PSD acceleration responses of the vertical operator’s seat, cab pitch and roll angles are compared with the simulated results, as shown in Fig.4.
(a)
(b)
(b)
Fig.4 Experimental results of the vibratory roller with RM. (a) Vertical operator’s seat; (b) Cab pitch angle; (c) Cab roll angle
Figs.4(a), (b) and (c) show that the measured results of the acceleration-frequency responses of the cab and operator’s seat almost agree with the simulation results. The small error between the measured and simulated values is due to the effect of the engine vibration and error of the vehicle parameters. However, the error between the measured and simulated values is negligible. Thus, the mathematical model with the parameters of the vibratory roller is feasible and accurate. The mathematical model of the vehicle is then applied to evaluate the effectiveness of the HPM.
4 Results and Discussion
4.1 Evaluating criteria and simulating condition
The effectiveness of the vibration isolation system was assessed through the criteria of suspension deformation and the RMS acceleration response[1,8]. On the other hand, the PSD acceleration response was also used to analyze the effectiveness of the vibration isolation system in the low-frequency region[8,17]. According to the ISO 2631-1[17], the PSD acceleration response was used to assess the endurance limit of the human body under the impact of vibration in the low-frequency range. The ISO 2631-1 emphasized that the health of the operator was seriously affected by the vibration excitations below 10 Hz, especially at 0.5 to 4 Hz.
In this paper,the PSD and RMS acceleration responses of the vertical operator’s seat, cab pitch and roll angles are selected as objective functions to evaluate the effectiveness of HPM in the low-frequency region. Thus, the smaller PSD and RMS values mean that the system has the greater ability compared to the corresponding isolate mounts. The RMS acceleration response is written as
(13)
where aw(t) is the acceleration (translational and rotational) of HPM depending on the simulation time T.
To clearly emphasize the low-frequency ride comfort of the HPM, the HPM is simulated and compared with the RM when the vehicle moves and compacts at a speed of 3 km/h under an excitation of 35 Hz of the drum. The parameters of HPM and RM are listed in Tab.1. Herein, the static stiffness Ks1-4 of HPM is equivalently calculated with the static stiffness Kr1-4 of RM, other parameters of the HPM are calculated based on its structure and static stiffness, and the damping parameters of Ch1-4 are the same as that in Ref.[8].
An elastoplastic soil with its high-density and a deformable terrain of Grenville loam with a poor random surface[1,16] are used as the vibration excitations on the drum and tires in the simulation process. The dynamic model of the vibratory roller is then simulated to analyze the results.
Tab.1 Major parameters of HPM and RM
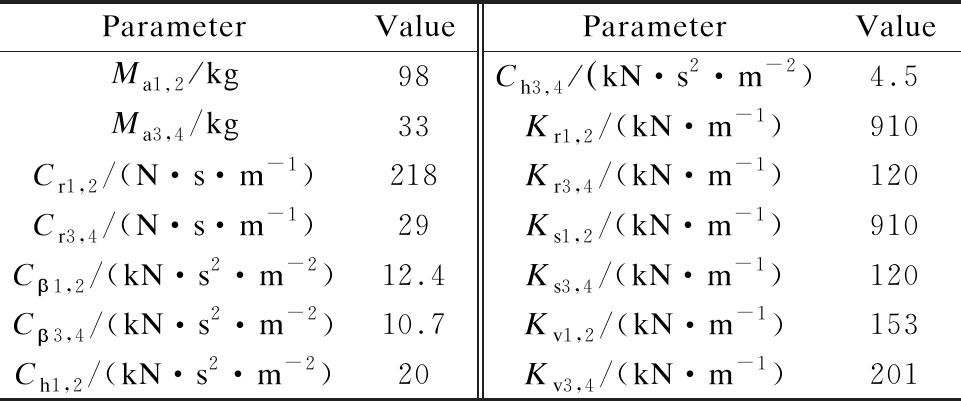
ParameterValueParameterValueMa1 2 kg98Ch3 4 kN·s2·m-2)4.5Ma3,4 /kg33Kr1,2 /(kN·m-1)910Cr1,2 /(N·s·m-1)218Kr3,4 /(kN·m-1)120Cr3,4/(N·s·m-1)29Ks1,2 /(kN·m-1)910C迳1,2 /(kN·s2·m-2)12.4Ks3,4 /(kN·m-1)120C迳3,4 /(kN·s2·m-2)10.7Kv1,2 /(kN·m-1)153Ch1,2 /(kN·s2·m-2)20Kv3,4 /(kN·m-1)201
4.2 Result of PSD acceleration responses
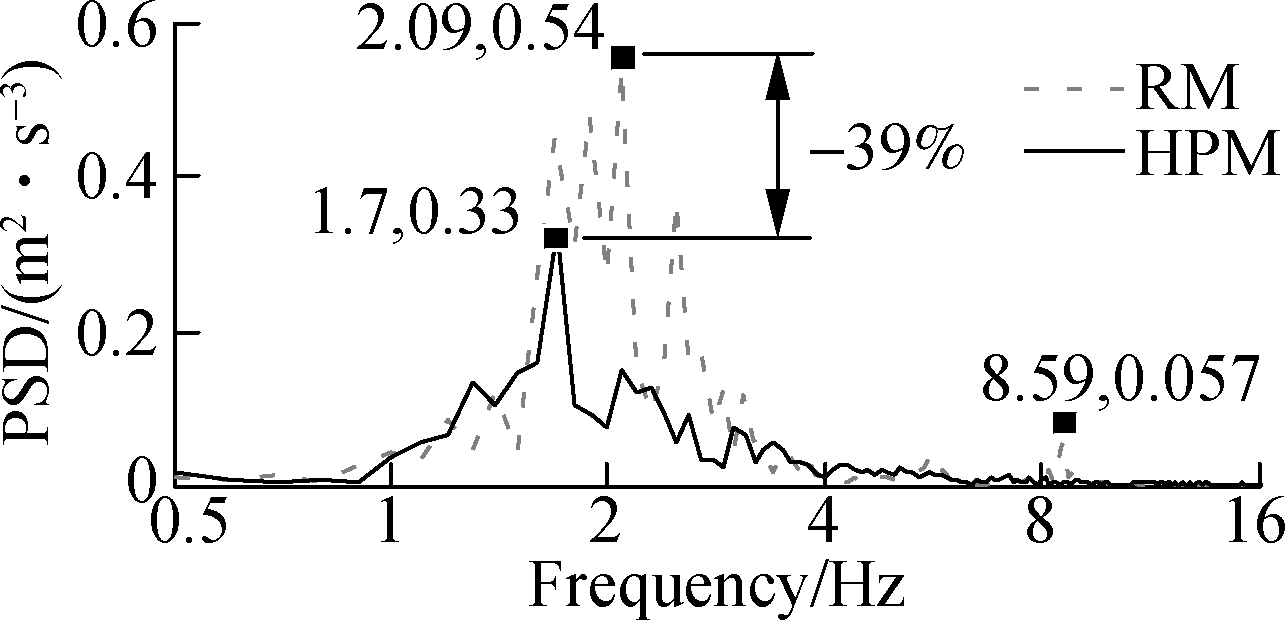
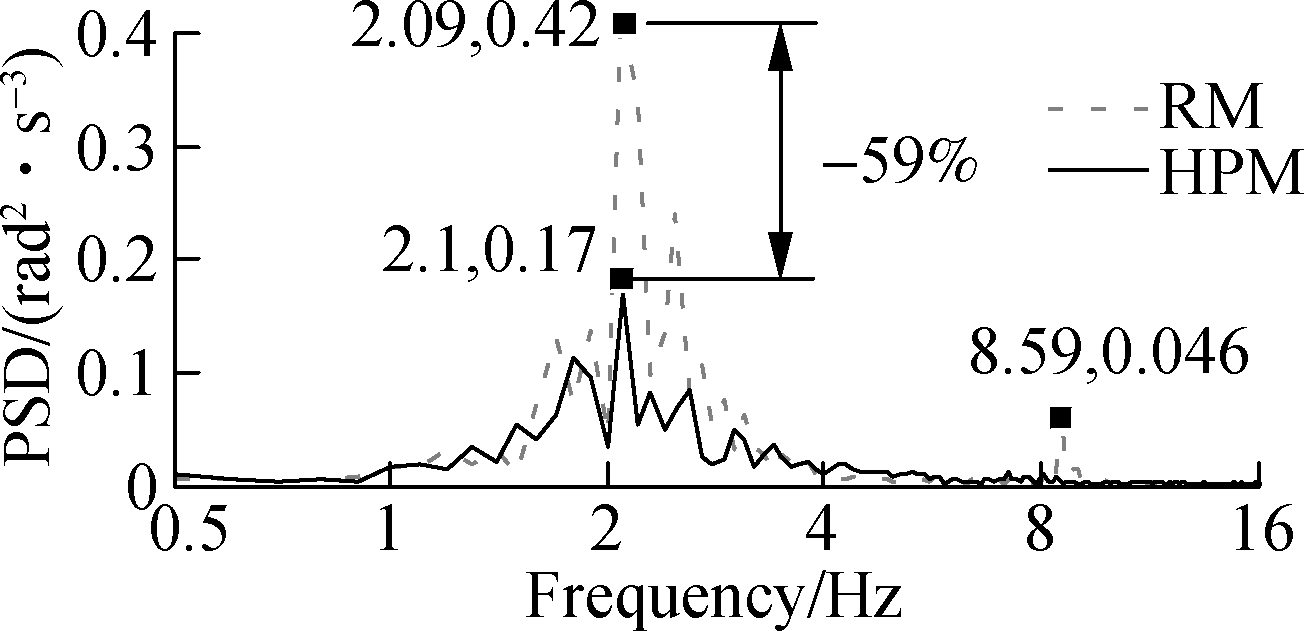
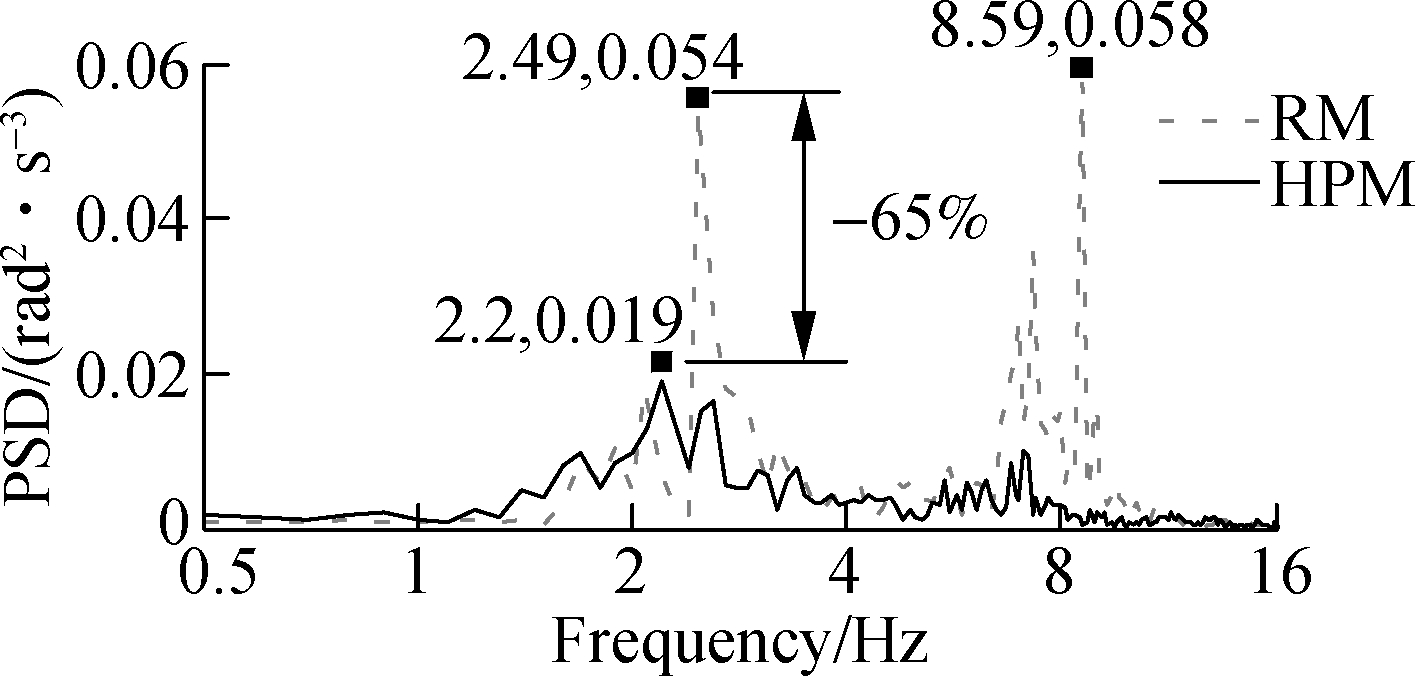
The simulation results of the PSD acceleration responses of HPM are compared with the RM, as shown in Fig.5. It can be seen from Fig.5 that the PSD values of the vertical operator’s seat, cab pitch and roll angles with RM show more resonance peaks in the low-frequency region, therefore, the operator’s health is significantly affected by the high-density of elastoplastic soil. However, the resonance peaks of the PSD accelerations with the HPM appear not only less but are also lower than that of the RM, especially at the resonance frequencies of 2.09, 2.49 and 8.59 Hz. Besides, the resonance frequencies with HPM are significantly changed in comparison with RM in all three directions, and this is due to the influence of the elastic stiffness of airbags, which changes and depends on pressure, volume, mass and density of the air in the airbags.
(a)
(b)
(b)
Fig.5 Acceleration-frequency of the cab and operator’s seat in low-frequency region.(a) Vertical operator’s seat; (b) Cab pitch angle; (c) Cab roll angle
At a low-frequency region (below 10 Hz), the resonance peak of PSD accelerations with HPM is significantly reduced in all three directions. Especially at the frequencies below 4.0 Hz, the maximum value of PSD resonance peaks of the vertical operator’s seat, cab pitch and roll angles with HPM are greatly reduced by 39%, 59% and 65% in comparison with RM. This is mainly due to the impacts of the nonlinear viscous damping force of the pneumatic damper as described in Eq.(4), and the nonlinear liquid damping force of the hydraulic damper as described in Eq.(8). The effect of the vibrations on the operator’s health is thus reduced by using the HPM. Consequently, it can be concluded that the operator’s health is remarkably improved by the HPM in the low-frequency region of the vibratory roller when working.
4.3 Result of RMS acceleration responses
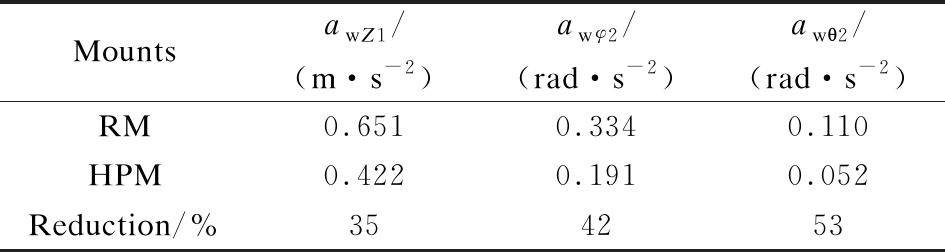
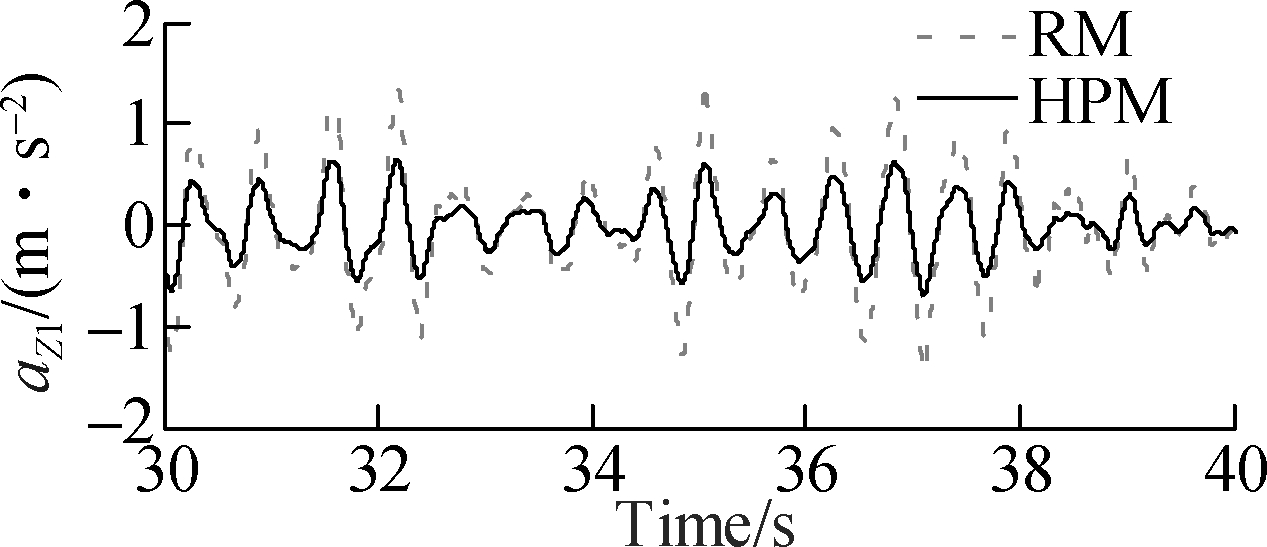
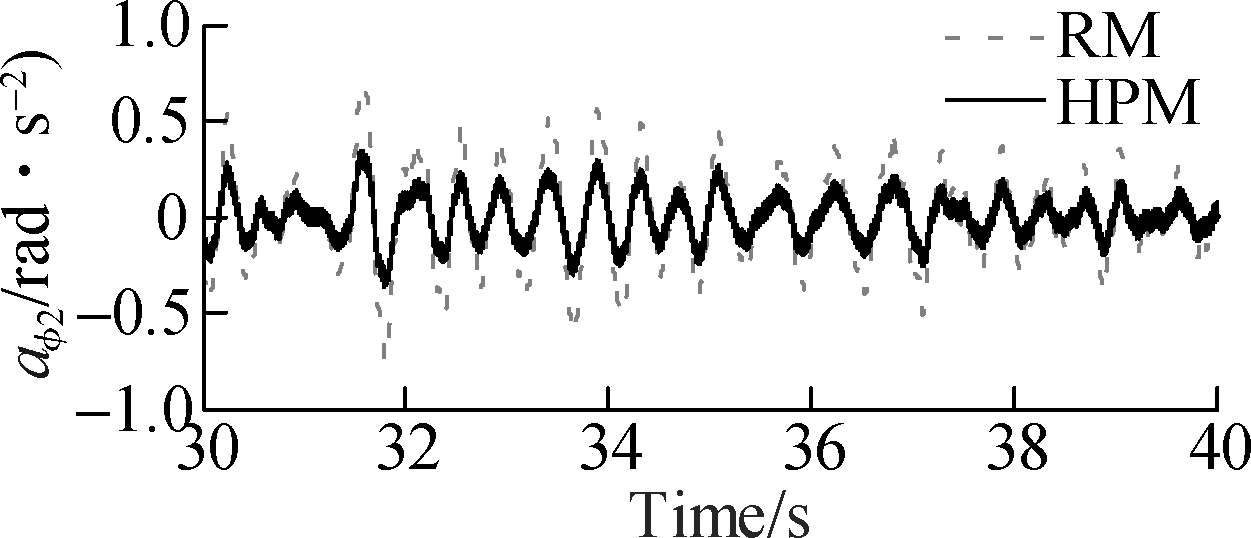
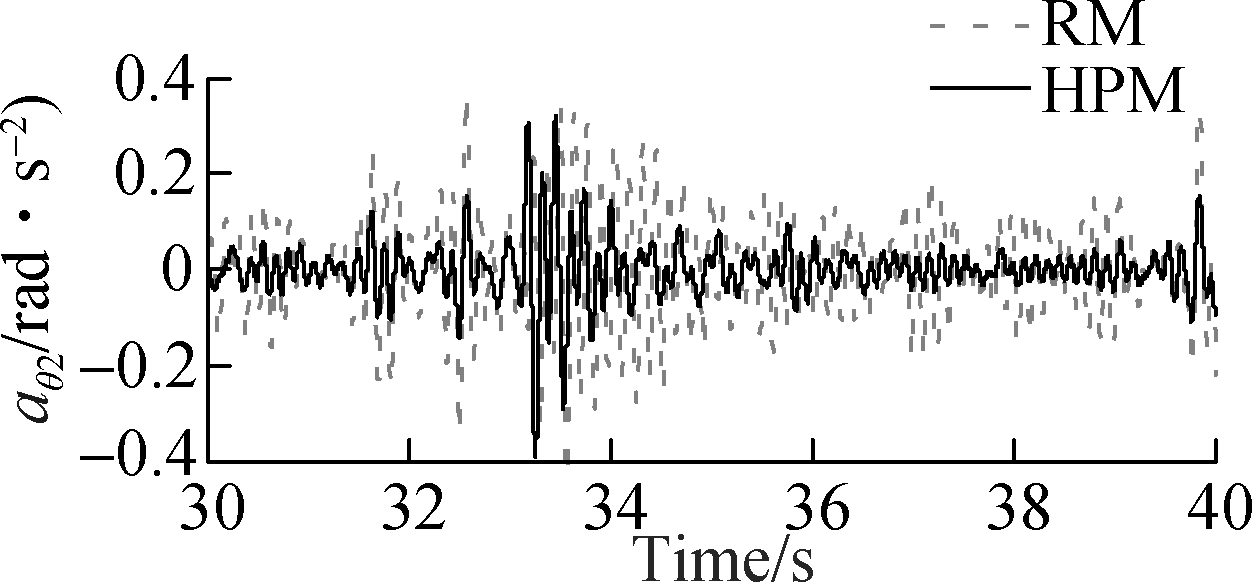
The effectiveness of HPM is not only assessed by the operator’s health through the values of PSD acceleration responses but also is evaluated by the ride comfort of the operator based on the indices of RMS acceleration values. The acceleration response of the operator’s seat, cab pitch and roll angles are depicted in Fig.6, and their RMS acceleration responses are also calculated and listed in Tab.2. The comparison results in Fig.6 show that the acceleration responses of the operator’s seat and cab with HPM are strongly reduced in comparison with RM. To highlight the effectiveness of HPM, the RMS values of the operator’s seat and cab with HPM are obviously decreased by 35%, 42% and 53%, respectively, in comparison with RM. This is also due to the impact of both the nonlinear liquid damping force and nonlinear viscous damping force of HPM. Based on the analysis results, it can be concluded that the ride comfort of the vibratory roller is clearly improved by using the HPM.
Additionally, the result of the HPM is compared with the published research results of the vibration isolation systems for the vibratory roller cab including the RM[2], PM and HM[16], and the auxiliary hydraulic mount(AHM)[1] under the same simulation conditions, as listed in Tab.3. The RMS acceleration responses of the operator’s seat and cab with HPM are less than those of the vibration isolation systems studied previously. Therefore, the HPM can improve the ride comfort for the vibratory roller cab in the low-frequency region, especially controlling the operator vibration and cab shacking.
Tab.2 RMS accelerations of the operator’s seat and cab
(a)
(b)
(b)
Fig.6 Acceleration results of the cab and operator’s seat. (a) Vertical operator’s seat; (b) Cab pitch angle; (c) Cab roll angle
Tab.3 RMS values of the cab and operator’s seat with various isolation systems for the vibratory roller cab
MountsRMPMHMAHMHPMawZ1/(m·s-2)0.6510.6340.5150.5830.422awφ2/(rad·s-2)0.3340.3250.2410.2120.191
5 Conclusions
1) Based on the experimental and numerical simulation research, the RMS and PSD accelerations of the operator’s seat and cab with HPM are strongly reduced under the elastoplastic soil at a frequency of 35 Hz of the vibrator drum when compared with RM. Especially, both the maximum values of RMS and PSD accelerations of the vertical operator’s seat, cab pitch and roll angles are remarkably reduced by 35%, 42% and 53%; and 39%, 59% and 65%, respectively.
2) Low-frequency vibration characteristics of the HPM with the high-static stiffness and nonlinear damping have an obvious effect on isolating low-frequency vibrations transmitted and controlling the cab shaking of the vibratory roller. Moreover, the nonlinear damping coefficient Ch of HPM can be optimized or controlled to further improve the low-frequency ride comfort for off-road vehicles equipped with the PHM.
[1] Nguyen V L, Zhang J R, Hua W L, et al. Ride quality evaluation of the vibratory roller cab supplemented by auxiliary hydraulic mounts via simulation and experiment [J]. Journal of Southeast University(English Edition), 2019, 35(3): 273280. DOI: 10.3969/j. issn.1003-7985. 2019. 03.001.
[2] Kordestani A, Rakheja S, Marcotte P, et al. Analysis of ride vibration environment of soil compactors[J]. SAE International Journal of Commercial Vehicles, 2010, 3(1): 259272. DOI:10.4271/2010-01-2022.
[3] Wong J Y. Data processing methodology in the characterization of the mechanical properties of terrain[J].Journal of Terramechanics, 1980, 17(1): 1341. DOI:10.1016/0022-4898(80)90014-2.
[4] Adam D, Kopf F. Theoretical analysis of dynamically loaded soils [C]//Proceedings of European Workshop Compaction of Soils and Granular Materials. Paris, France, 2000: 207220.
[5] Jiao G. Vibration simulation and optimization of cab’s vibration isolation system of vibratory roller [D]. Nanjing: Southeast University, 2010. (in Chinese)
[6] de Temmerman J, Deprez K, Hostens I, et al. Conceptual cab suspension system for a self-propelled agricultural machine: Part 2: Operator comfort optimisation[J]. Biosystems Engineering, 2005, 90(3): 271278. DOI:10.1016/j.biosystemseng.2004.08.007.
[7] Li J Q, Zhang Z F,Xu H G, et al. Dynamic characteristics of the vibratory roller test-bed vibration isolation system: Simulation and experiment[J]. Journal of Terramechanics, 2014, 56: 139156. DOI:10.1016/j.jterra.2014.10.002.
[8] Sun X J, Zhang J R. Performance of earth-moving machinery cab with hydraulic mounts in low frequency[J]. Journal of Vibration and Control, 2014, 20(5): 724735. DOI:10.1177/1077546312464260.
[9] Lee P, Vogt J, Han S Z. Application of hydraulic body mounts to reduce the freeway hop shake of pickup trucks[C]//SAE Technical Paper Series. Warrendale, PA, USA: SAE International, 2009. DOI:10.4271/2009-01-2126.
[10] Jiao S J, Wang Y, Zhang L,et al. Shock wave characteristics of a hydraulic damper for shock test machine[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 15701578. DOI:10.1016/j.ymssp.2009.12.005.
[11] Sundvall P. Comparisons between predicted and measured ride comfort in trains-a case study on modeling[R]. Stockholm, Sweden: Department of Vehicle Engineering, Royal Institute of Technology, 2001.
[12] Presthus M. Derivation of air spring model parameters for train simulation[D]. Lulea, Sweden: Lulea University of Technology, 2002.
[13] Abid H J, Chen J, Nassar A A. Equivalent air spring suspension model for quarter-passive model of passenger vehicles[J]. International Scholarly Research Notices, 2015, 2015: 16. DOI:10.1155/2015/974020.
[14] Yan J, Yin Z,Guo X X, et al. Fuzzy control of semi-active air suspension for cab based on genetic algorithms[C]//SAE Technical Paper Series. Warrendale, PA, USA: SAE International, 2008:111. DOI:10.4271/2008-01-2681.
[15] Tang G,Zhu H J, Zhang Y Q, et al. Studies of air spring mathematical model and its performance in cab suspension system of commercial vehicle[C]//SAE Technical Paper Series.Warrendale,PA,USA:SAE International, 2015: 341348. DOI:10.4271/2015-01-0608.
[16] Nguyen V, Zhang J R, Le V, et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts[J]. Shock and Vibration, 2018, 2018: 117. DOI:10.1155/2018/8527574.
[17] International Organization for Standardization. ISO 2631-1 Mechanical vibration and shock-Evaluation of human exposure to whole body vibration—Part 1: General requirements [S]. Geneve, Switzerland: International Organization for Standardization, 1997.
[18] Seo J U, Yun Y W, Park M K. Magneto-rheological accumulator for temperature compensation in hydropneumatic suspension systems[J]. Journal of Mechanical Science and Technology, 2011, 25(6): 16211625. DOI:10.1007/s12206-011-0414-z.
[19] Ali D, Frimpong S. Artificial intelligence models for predicting the performance of hydro-pneumatic suspension struts in large capacity dump trucks[J]. International Journal of Industrial Ergonomics, 2018, 67: 283295. DOI:10.1016/j.ergon.2018.06.005.
[20] Berg M. A three-dimensional airspring model with friction and orifice damping[J]. Vehicle System Dynamics, 1999, 33(sup1): 528539. DOI:10.1080/00423114.1999.12063109.