In microfluidic and nanofluidic channels, the EDL formed spontaneously as a solid surface in contact with aqueous electrolyte solutions, which in turn regulates the magnitude of the net effective surface charge[1]. The precise structure and dynamics of the EDL play a crucial role in nanofluidic transport[24]. When multivalent ions transport in the nanochannels, multivalent counterions can invert the sign of net surface charge and change the transport properties of nanofluidic devices[57]. That is, charge inversion occurred. Thoroughly understanding the fundamental mechanisms of charge inversion with multivalent ions can provide valuable insights into engineering applications, such as chemical sensors[8], microfluidic and nanofluidic devices[911], the manipulation of biomolecules[6], DNA condensation[12] and energy conversion systems[13].
The observations and underlying mechanism of charge inversion have been widely discussed in recent years. Early observations of charge inversion mainly occurred in multivalent solutions. The flows of ions transport reversed its directions in nanochannels due to the excessive adsorption of multivalent counterions on the channel walls[910]. Chou et al.[5] developed a simple experimental setup that can monitor the change of ζ-potential and the adsorption time of the charge inverting ions to the surface of the nanochannel in electrokinetic nanofluidic systems. It has been observed that charge inversion depends on the dielectric constant of solvent and charge density of the surface[14]. In our previous work[15], we found that ion-ion correlations play a great role in charge inversion and can enhance the adhesions between two surfaces. Moreover, giant charge inversion[16] can be obtained for a discretely charged surface in contact with a trivalent electrolyte solution, provided that the surface charges are localized at discrete sites and that the concentration of multivalent counterions is sufficiently high. Furthermore, charge inversion can be induced by divalent and monovalent ions. Charge inversion was observed when the divalent Mg2+ ions transport in solid-state nanofluidic nanochannels[7]. A negatively charged bacterium membrane can be inverted to be positively charged due to the strong binding of Ca2+ to the membrane’s phosphate groups[17]. A slight charge inversion[18] occurred in concentrated NaCl solutions confined between strongly charged silicon surfaces, which depends on the surface charge density, bulk concentration, and confinement.
The underlying mechanism of charge inversion has been a matter of intense debate and it is still far from being complete, although charge inversion phenomena were observed in trivalent, divalent and monovalent solutions in experiments or simulations. Previously, charge inversion was interpreted in terms of specific chemical binding between multivalent ions and the surface being screened, which is recommended in the colloid community[14]. This mechanism inevitably depends on the detailed chemical structure of the substances. However, the simulation suggests that such specific interactions are not necessary for charge inversion[19]. In biological systems, atomistic and coarse-grained simulations showed that charge inversion of peptide surface is largely dominated by electrostatic interactions, with a minor contribution of chemical specificity of salt ions. Ion solvation properties were the key to charge inversion in liposomes with multivalent ions by combining electrokinetic measurements and molecular dynamics simulations[20]. The multivalent cations and its hydrolyzed forms have great impacts on charge inversion[21]. Some new mechanisms of charge inversion, such as confinement-induced charge inversion[22], well-ordered counterions nanostructures[23], and the hydrophobic effect[24] have also been put forward. The complex interplay between the electrostatic and steric interactions should be coupled to the realistic character of surface charge to establish a faithful description of the overcharging and charge reversal at heterophase interfaces[25].
In addition to these underlying mechanisms, ion-ion correlations, which are not taken into account in the classical Poisson-Boltzmann (PB) equation, have been widely accepted, especially for multivalent ions. The extra adsorption of ions can be mainly attributed to electrostatic ion-ion correlations between multivalent ions[4]. The electrostatic ion-ion correlations theory was extensively studied[2627] and it successfully explained many experimental results[7,10,12,1415,28]. Previous research works about ion-ion correlations focused on one type of multivalent electrolyte. Mixture electrolyte surroundings are pervasive in many practical applications, such as separations and biological systems. The competition adsorption between ions with different valence, whether monovalent and divalent ions enhance or suppress charge inversion, remains challenging topics for which we still lack a deep physical understanding, although much work was done. According to the SCL theory[4], the additional screening caused by the monovalent species makes the inversion substantially stronger, because the charging energy of the macroion diminishes much more than the correlation energy of the multivalent ions. In contrast, simulations revealed that charge inversion was hindered by extra monovalent. The increasing concentration of monovalent ion can suppress charge inversion and even cause charge inversion to disappear entirely[10]. Simulation results[16] showed that the addition of monovalent ions slightly changed the magnitude of giant charge inversion. When the surface is weakly charged, the valence of coions can promote charge inversion at a moderate concentration[29], which can be further boosted by the action of polarization effects. Nevertheless, charge inversion in the presence of multivalent coions is dampened rapidly with the increasing magnitude of the surface charges.
In our previous work[15], we provided the direct force measurements between two mica surfaces in aqueous electrolyte solutions over broad ranges of LaCl3 concentrations and pH values with an SFA. The underlying mechanism of charge inversion was revealed and the ion-ion correlation forces were detected directly. However, whether the monovalent and divalent ions can enhance or suppress the charge inversion is unclear. To further clarify the effects of ion-ion correlations on charge inversion by mixture multivalent ions, in this work, we experimentally investigated the charge inversion by mixture counterions in different volume fractions of LaCl3/KCl and LaCl3/MgCl2 mixture solutions with a total ionic strength of 10-4 mol/L. The results were also analyzed based on the ion-ion correlation theory.
1 Experimental Methods
SFA, which was described in detail previously[15], was adopted to directly measure the normal forces F(D) between two molecularly smooth curved mica surfaces (mean radius R≈2 cm) at closest separation D across variable concentrations of mixture counterions. SFA is an ideal technique for studying the interactions between two charged surfaces. During the force measurements, the surface separation and interaction is monitored in real-time in situ by multiple-beam interferometry (MBI) using fringes of equal chromatic order (FECO). The interaction forces between two surfaces are measured from the deflection of a double cantilever spring, and the stiffness of which can be calibrated before or after experiments. The spring stiffness in our experiments is 950 N/m. When two surfaces are approaching or separating, at some critical point when the gradient of the force dF(D)/dD is equal to or exceeds the supporting spring stiffness, the two surfaces will jump-into adhesive contact or jump apart spontaneously from a critical point.
In this study, muscovite mica, purchased from S&J Trading Inc., was selected as the molecularly smooth charge surface. Mica can be easily cleaved to obtain large atomically smooth surfaces, allowing reproducible clean substrates to be prepared. About 1 cm2 mica sheets were cut using a hot Pt wire into pieces in a standard way[15]. A thin silver film of about 50 nm thickness was coated on one side of the cleaved thin mica sheets of a few micrometers in thickness. With the silver facing down, the mica was glued (Shell, EPON 1004F) onto a cylindrically shaped silicon disk before being loaded into the SFA chamber, facing the other one in a crossed-cylinder configuration, equivalent to the geometry of a sphere over a flat, as shown in Fig.1.
For SFA experiments, the reference distance (D=0) between two mica surfaces was firstly measured by bringing them into adhesive contact in a dry nitrogen atmosphere. Then, the SFA chamber is filled with mixture electrolyte solutions of different volume fractions of LaCl3/KCl or LaCl3/MgCl2 until the two mica surfaces are immersed. During a typical force measurement, the normal force-distance profile F(D) was obtained by an initial approach to contact and followed by separation of the two surfaces. Two approach-separation cycles were repeated in measuring the force laws between the two mica surfaces with different concentrations of multivalent ions. Ultrapure water was obtained from a water purification system produced by Millipore. Solutions were prepared with the purified water and high purity chemical reagents LaCl3, MgCl2, KCl (99.999%, 99.99%, 99.999% pure, respectively, from Sigma-Aldrich). All the solutions were degassed and filtered with a 0.2 μm membrane. Experiments were performed at a controlled temperature of (22.0±0.1)℃.
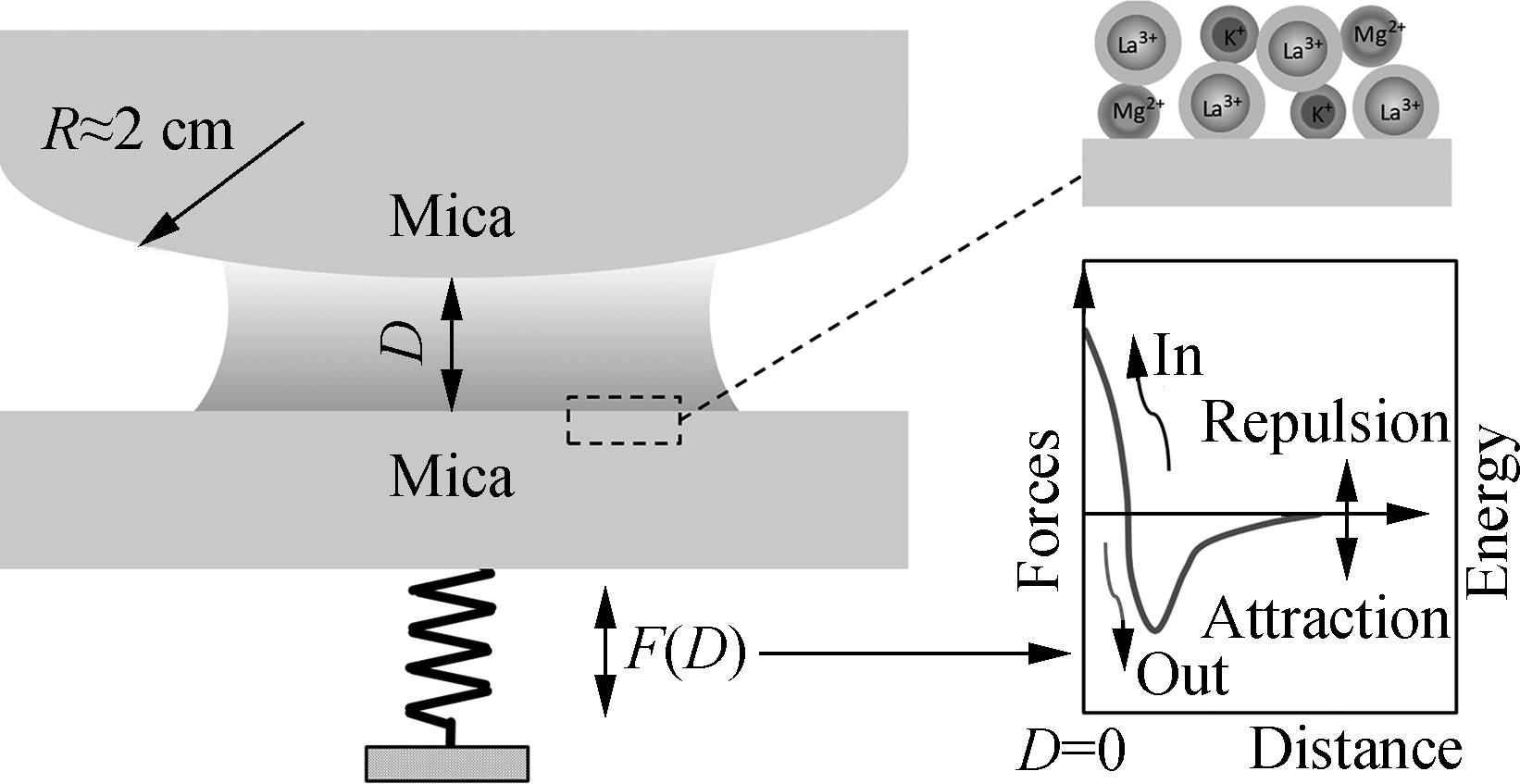
Fig.1 Schematic of the experimental setup
2 Results and Discussion
2.1 Charge inversion of surface in the mixture electrolyte solutions
In electrolyte solutions, counterions accumulate in the vicinity of solid surfaces to form EDLs due to the electrostatic attraction. Repulsion interactions arise when two such surfaces approach close due to the overlap of EDLs, which are strongly affected by the structure of EDLs and the net charges of surfaces. According to the DLVO theory, the interaction strengths between two solid surfaces in the electrolyte solutions are increased with the increase in solution concentrations.
Fig.2 presents the measured interaction F/R vs. distance D between two mica surfaces in mixture LaCl3 and KCl solutions with a total ionic strength of 10-4 mol/L, where we gradually increased the amount of La3+ ion and decreased the amount of K+ ion. The value of F/R is equal to 2πE(D) according to the Derjaguin approximation, where E(D) is the interaction energy per unit area for two flat surfaces. When there is only KCl in the solution, the long-range repulsion interaction that originated from the overlap of the EDLs of two surfaces was firstly observed with an exponential decay length of (27.8±0.6)nm. Then, the mica surfaces jump-into contact at the distance of 2.5 nm, with the maximum interaction of 2.2 mN/m. This measured interaction can be explained by the DLVO theory in monovalent solutions. When the solution was replaced by fractions of 20% LaCl3 and KCl mixture solution, the repulsion interaction decreased obviously, as shown in Fig.2(b). The decrease of the interaction is contrary to the PB prediction markedly. The distance of jump-into contact increased to 5.7 nm, with a small repulsion interaction of 0.4 mN/m.
Generally, the jump-into contact for mica surfaces in solutions results from the van der Waals attraction force exceeded the EDLs repulsion force at a short distance. The distance of the jump-into contact between mica surfaces is less than 4 nm in ultrapure water and low concentrations of electrolyte solutions. It can be speculated that the additional attraction mechanism underlies the increase of the jump-into contact distance when LaCl3 was added in the solutions. As our previous work reported[15], the cohesive energy of strongly coupled La3+ions can form laterally frozen correlation cells. The system in our experiments may be considered as a collection of laterally frozen correlation cells, each consisting of a single La3+ ion sandwiched between two mica walls with a lateral size of about half ion spacing. This sandwich structure offers additional attraction between mica surfaces and results in the jump-into contact at a larger distance.
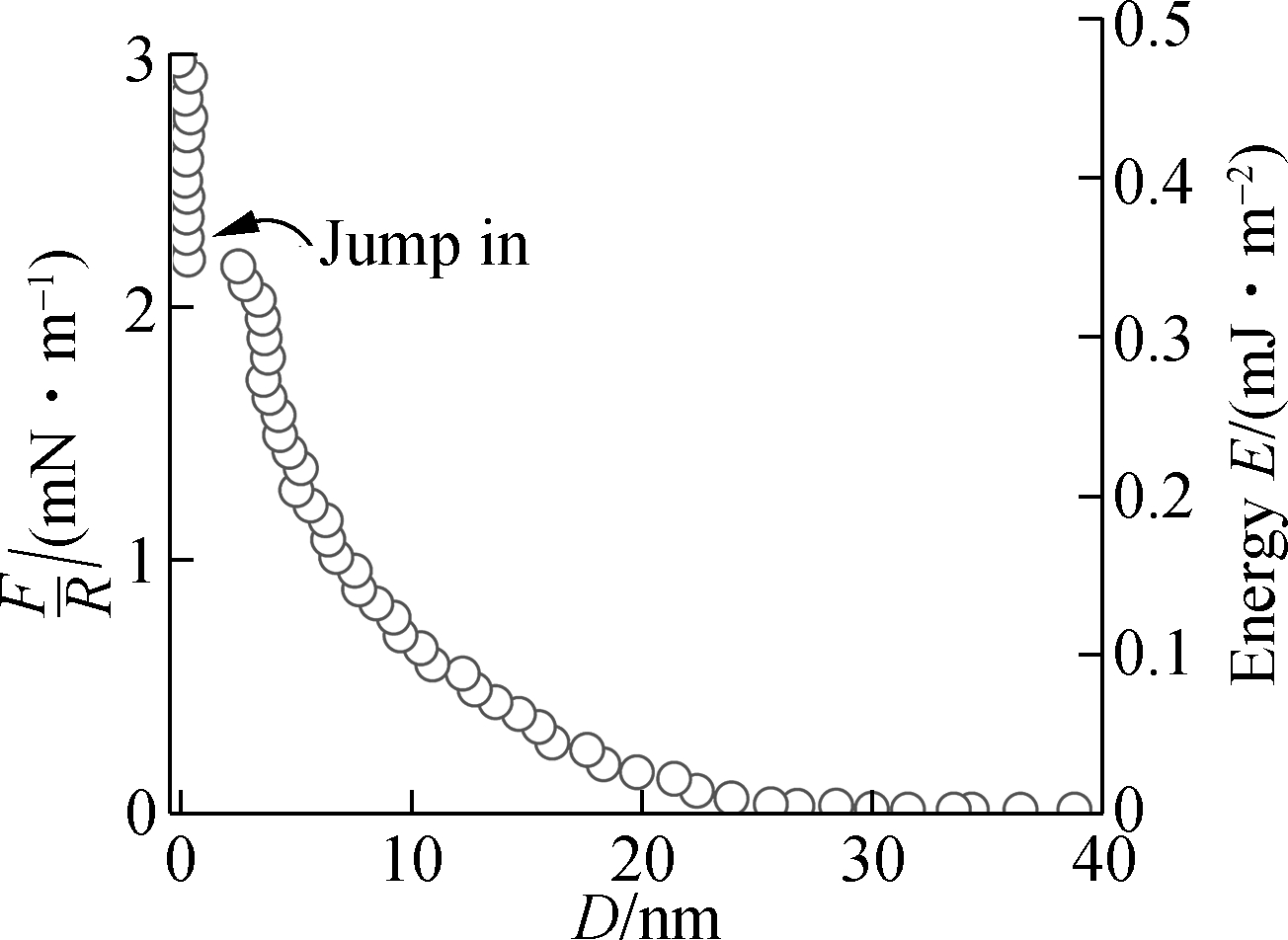
(a)
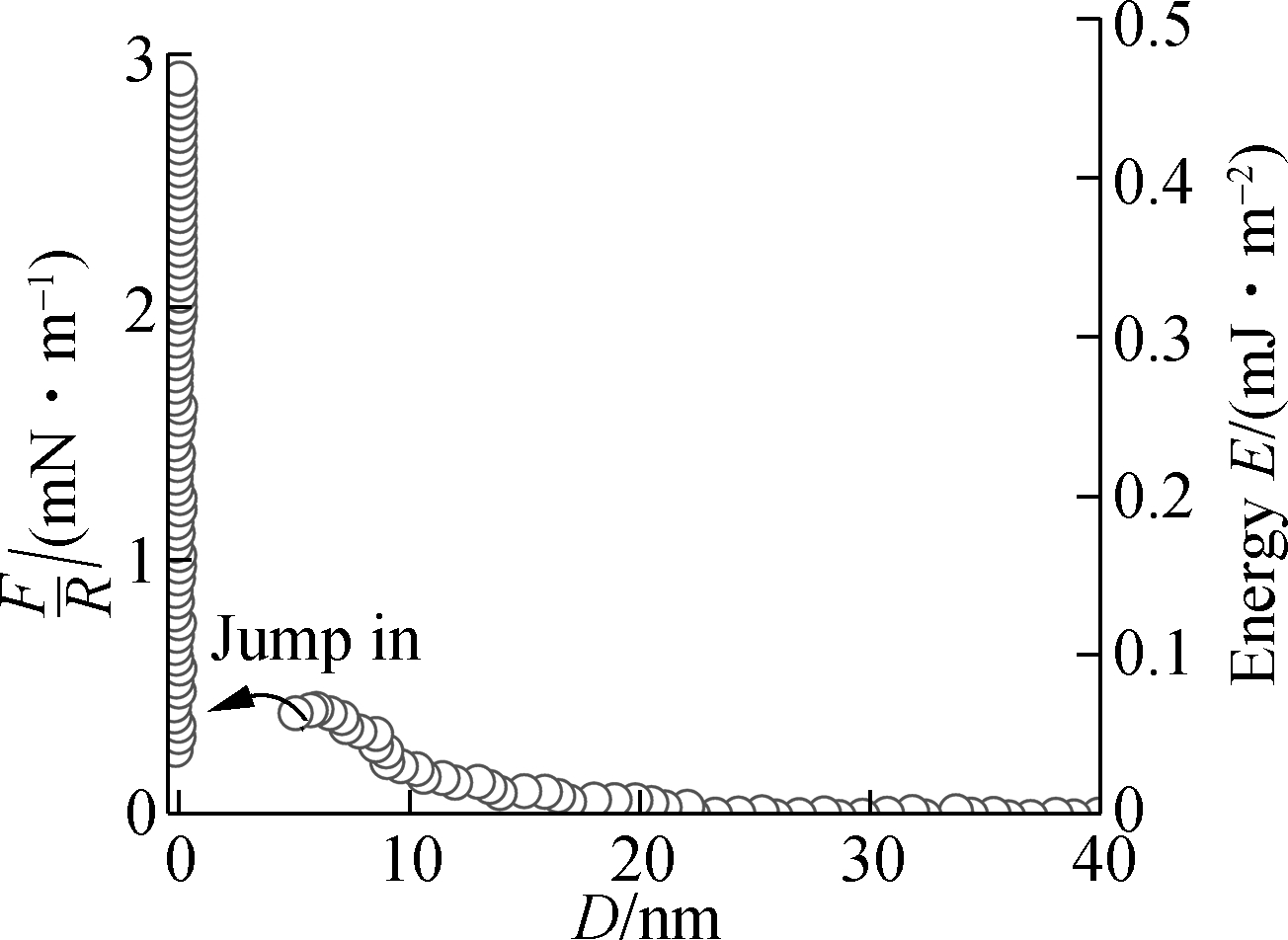
(b)
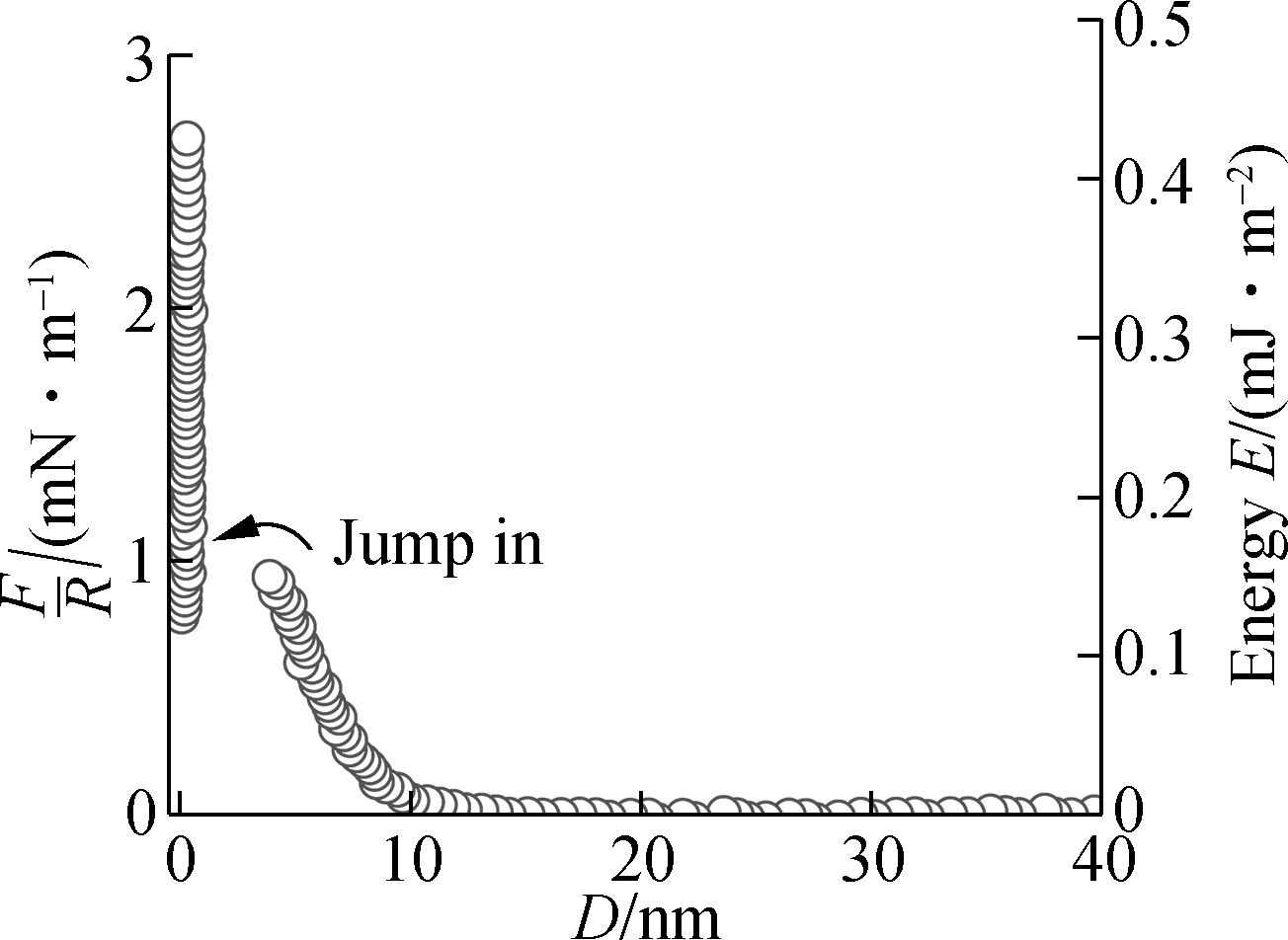
(c)
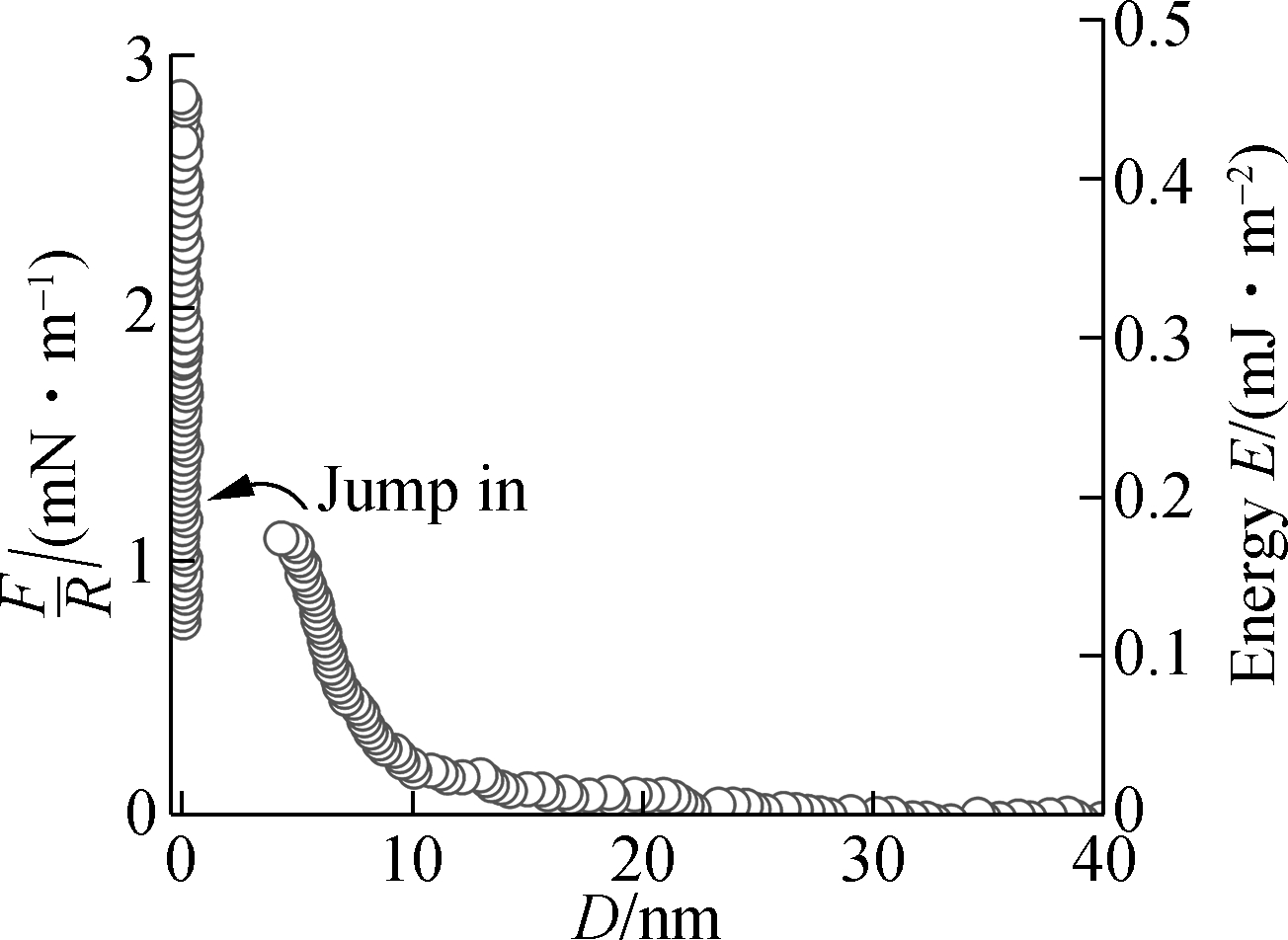
(d)
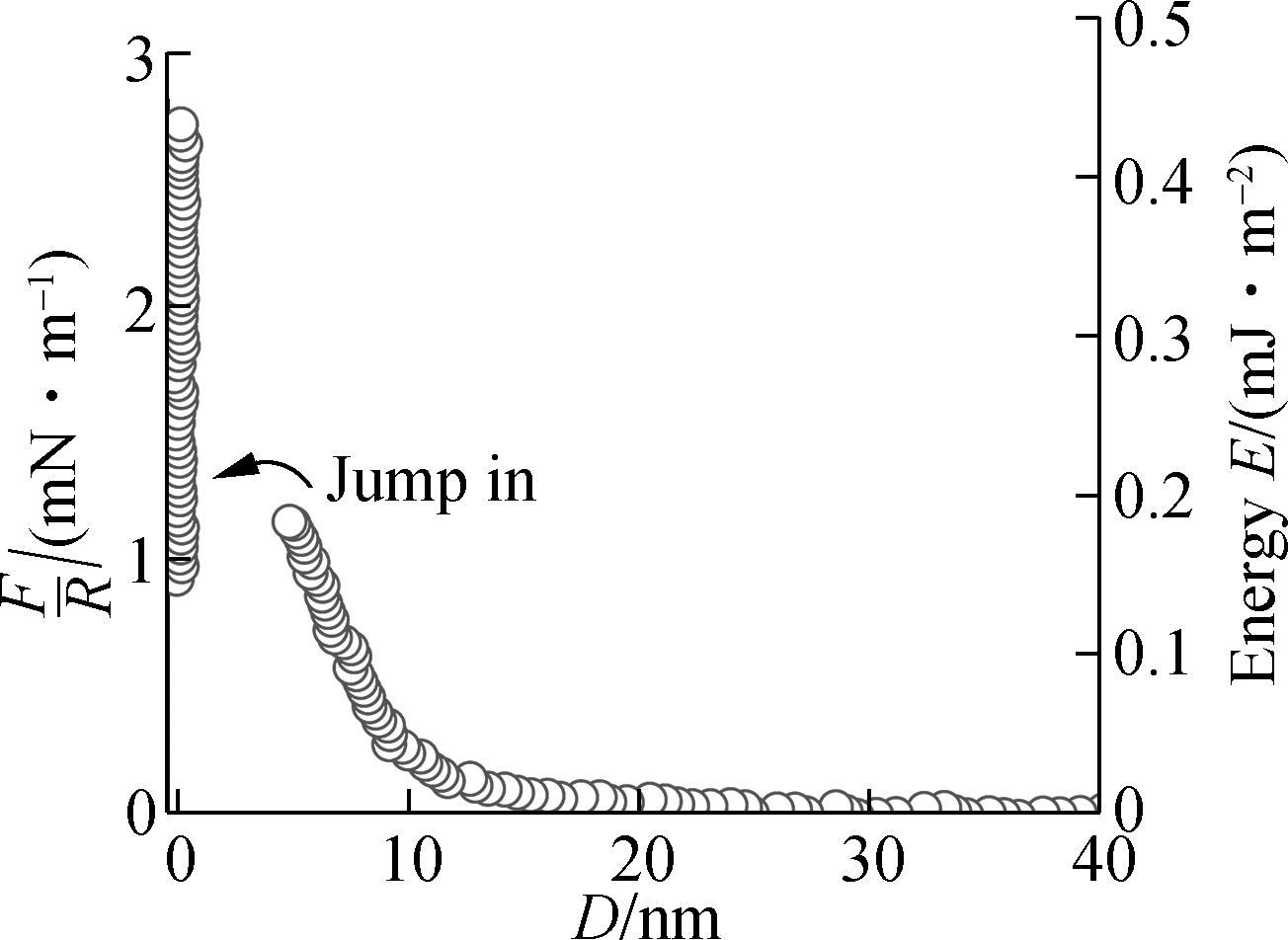
(e)
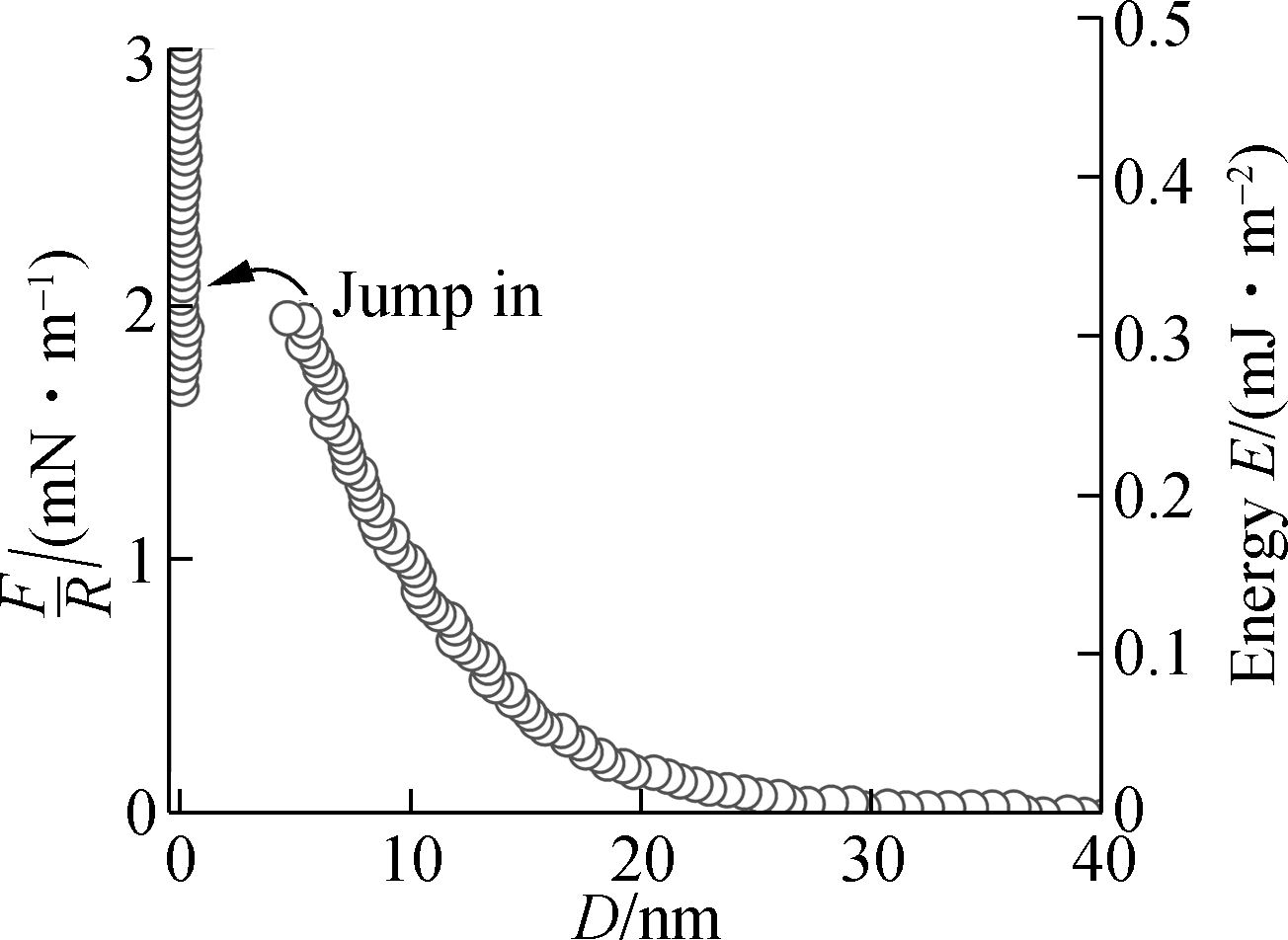
(f)
Fig.2 Interaction forces between two mica surfaces in different volume fractions of LaCl3 and KCl solutions with a total ionic strength of 10-4 mol/L.(a) 0% LaCl3; (b) 20% LaCl3; (c) 40% LaCl3; (d) 60% LaCl3; (e) 80% LaCl3; (f) 100% LaCl3
As the fractions of LaCl3 in the mixture LaCl3 and KCl solutions increase from 20% to 100%,the repulsion interactions increase again. The jump-into contact distances are between 4.2 and 4.8 nm, which is larger than that in monovalent solutions and ultrapure water. From the force-distance profiles in Fig.2, the total repulsion interaction exhibits a minimum value under the condition of around 20% normal fraction of LaCl3, above which repulsion reappeared and increased again with the increasing fraction of LaCl3 solution. That is, the charge inversion occurred on the mica surface.
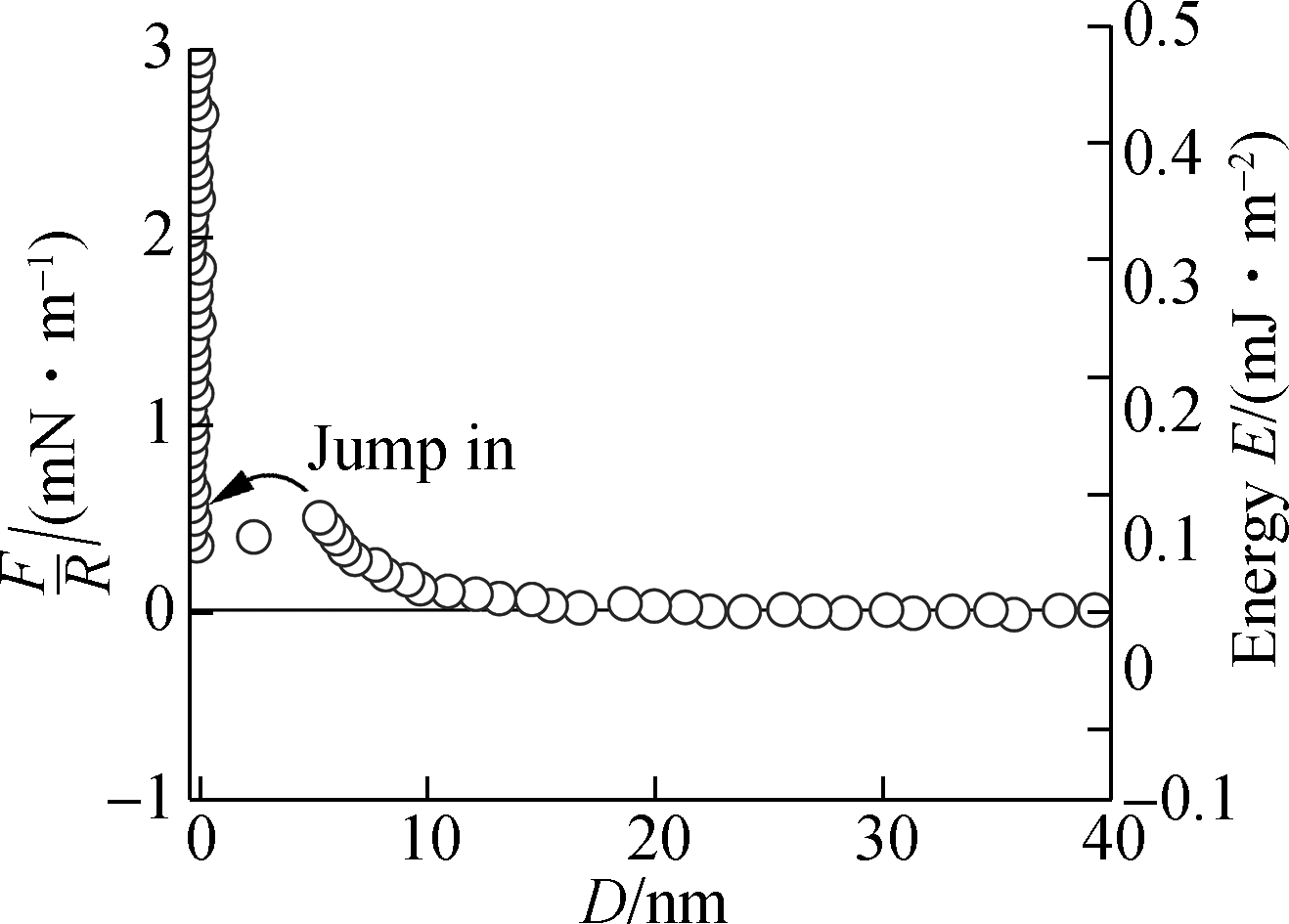
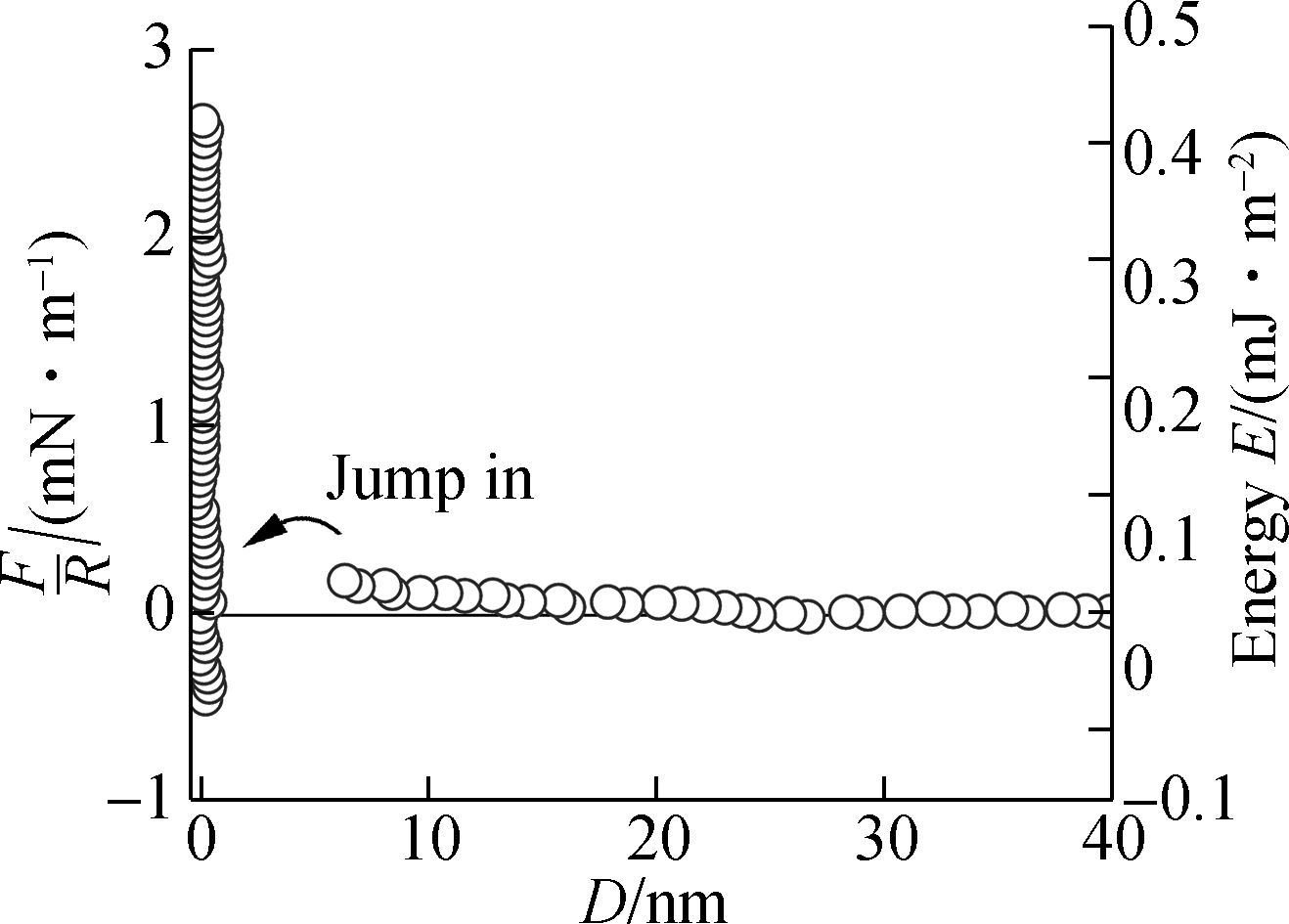
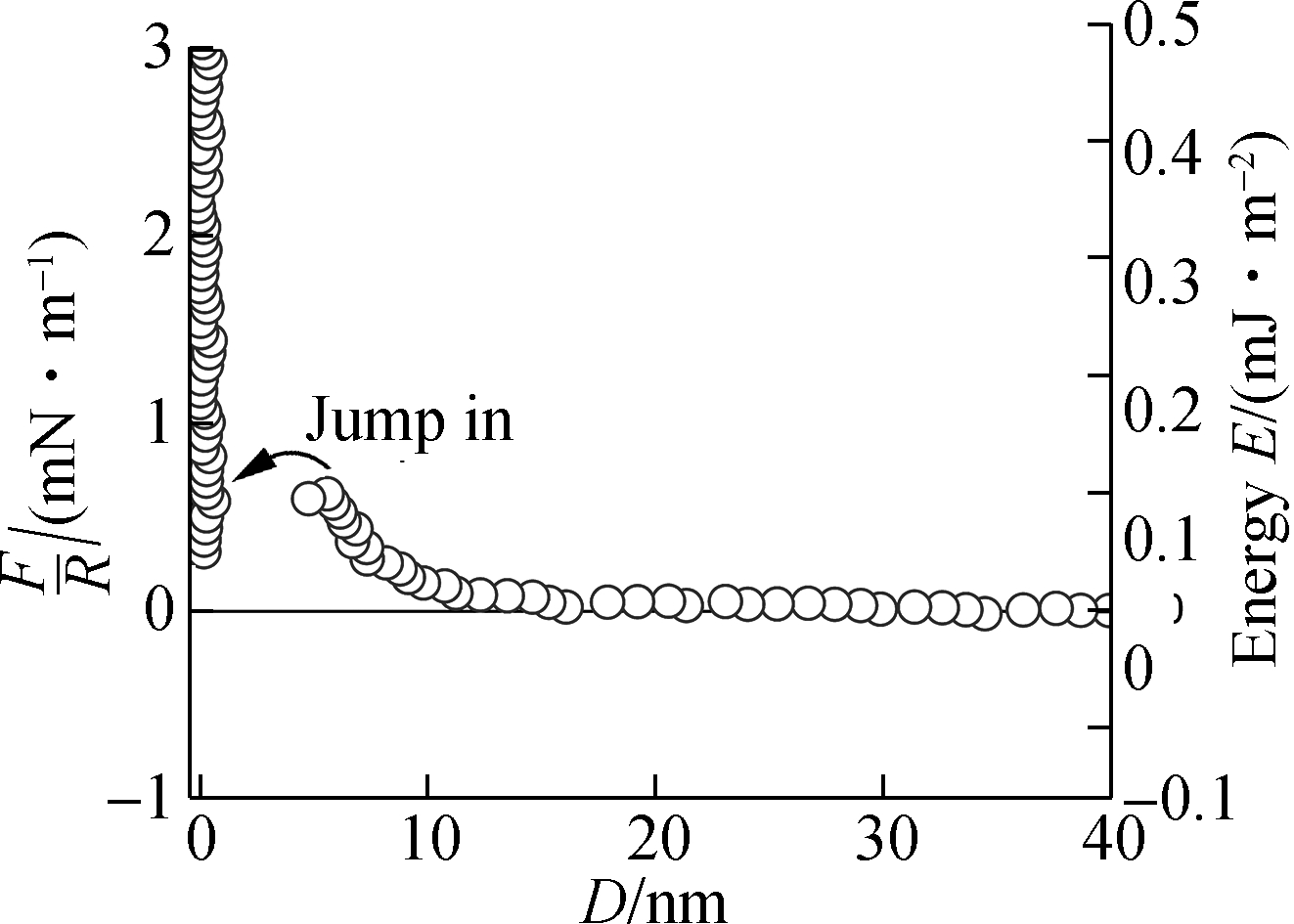
To clearly demonstrate the charge inversion of mica surface in mixture electrolytes, we performed additional experiments with a total ionic strength of 10-4 mol/L of LaCl3 and MgCl2 mixture, where we gradually increased the amount of La3+ ion and decreased the amount of Mg2+ ion. From the interaction force profiles of Fig.3, it also can be found that the interaction forces between two mica surfaces firstly decreased with the increasing fraction of LaCl3 and then increased with the increasing fraction of LaCl3. This indicates that the negatively charged mica surfaces become positive once the LaCl3 concentrations over a critical concentration ρcinv, where the surface potential of the mica surface was zero theoretically.
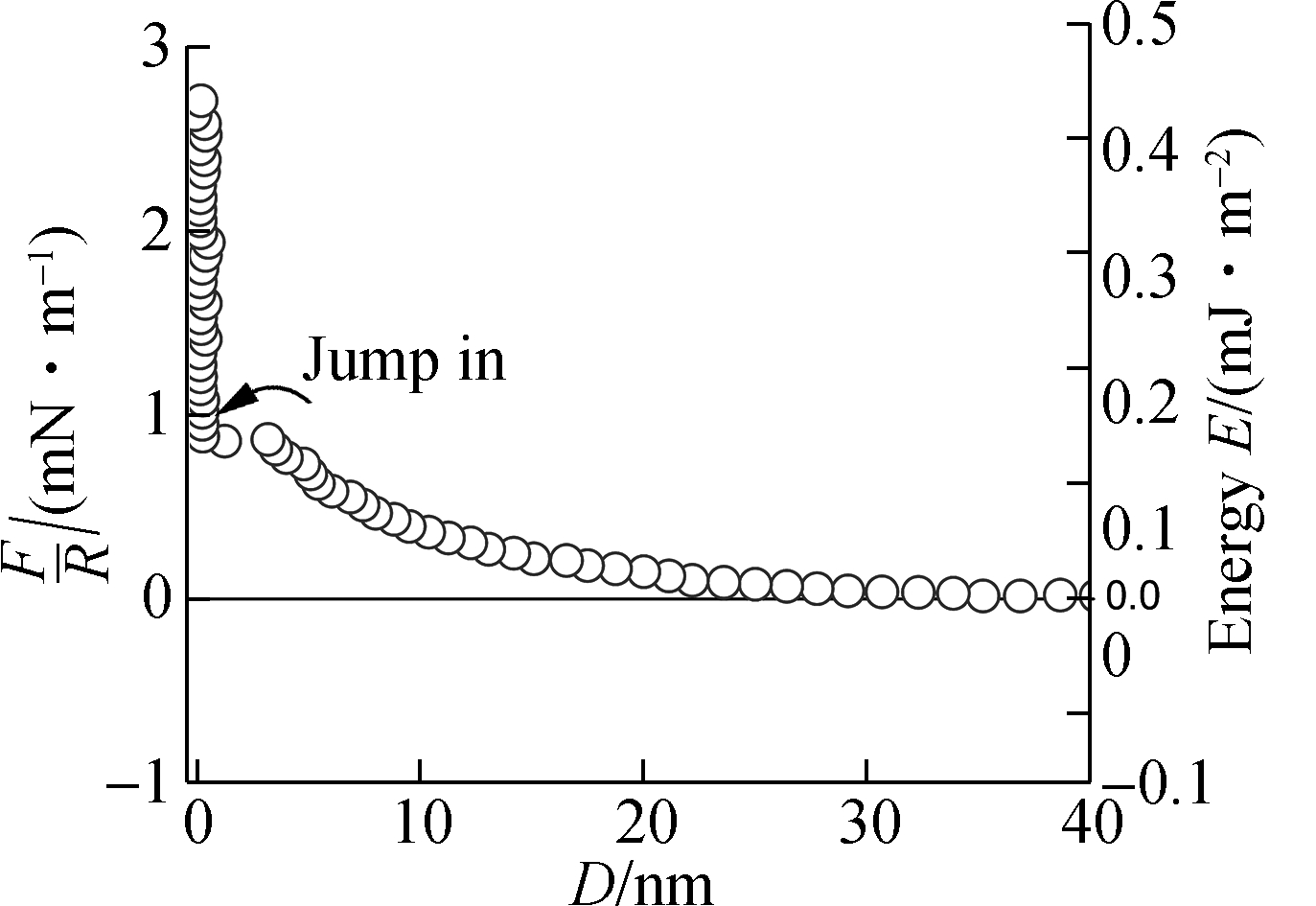
(a)

(b)
(c)
(d)
(e)

(f)
Fig.3 Interaction forces between two mica surfaces in different volume fractions of LaCl3 and MgCl2 solutions with a total ionic strength of 10-4 mol/L. (a) 0% LaCl3; (b) 20% LaCl3; (c) 40% LaCl3; (d) 60% LaCl3; (e) 80% LaCl3; (f) 100% LaCl3
The charge inversion can be viewed as the continuous adsorption of additional La3+ ions after mica surfaces are neutralized at the critical LaCl3 concentration ρcinv. The charge inversion can be also predicted from the maximum forces before the mica surfaces jump-into contact, as shown in Fig.4. We can speculate that there is a critical LaCl3 concentration ρcinv approaching 20% normal volume fraction of LaCl3 and KCl mixture solutions, where the surface potential of the mica surface becomes zero. The mica surfaces have the positive signs and their respective roles were inverted above the concentration of ρcinv. Charge inversion may occur at about 60% normal volume fraction of LaCl3 for LaCl3 and MgCl2 mixture solutions, as shown in Fig.4. The mica surface effectively behaves as if positively charged.
The repulsion between mica surfaces turns into slight attraction and then repulsion for LaCl3 and MgCl2 mixture solutions. This corresponds to a higher La3+ concentration than that of the crossover in the mixture of LaCl3 and KCl solution. This is due to the electrostatic screening effect in the mixture solution, at the same La3+ concentration, with a higher ionic strength than the pure solution. Also, the magnitude of all the repulsion interactions between mica surfaces in LaCl3 and MgCl2 mixture solutions is smaller than those in LaCl3 and KCl mixture solutions. This is because the surface potential of mica is low due to the screening effect of divalent Mg2+ ions on mica surfaces. The difference in interaction magnitudes of 100% volume fraction of LaCl3 between LaCl3/KCl and LaCl3/MgCl2 mixture solutions is attributed partly to the absorbed Mg2+ ions during the replacement of solutions, which decreased the surface charge of mica surfaces. The total surface charge became lower than that in the replacement of LaCl3/KCl solutions. It should be stressed that the concentration of monovalent or divalent counterions in the neighborhood of the mica surface might be significant although trivalent counterions are much more strongly attracted.
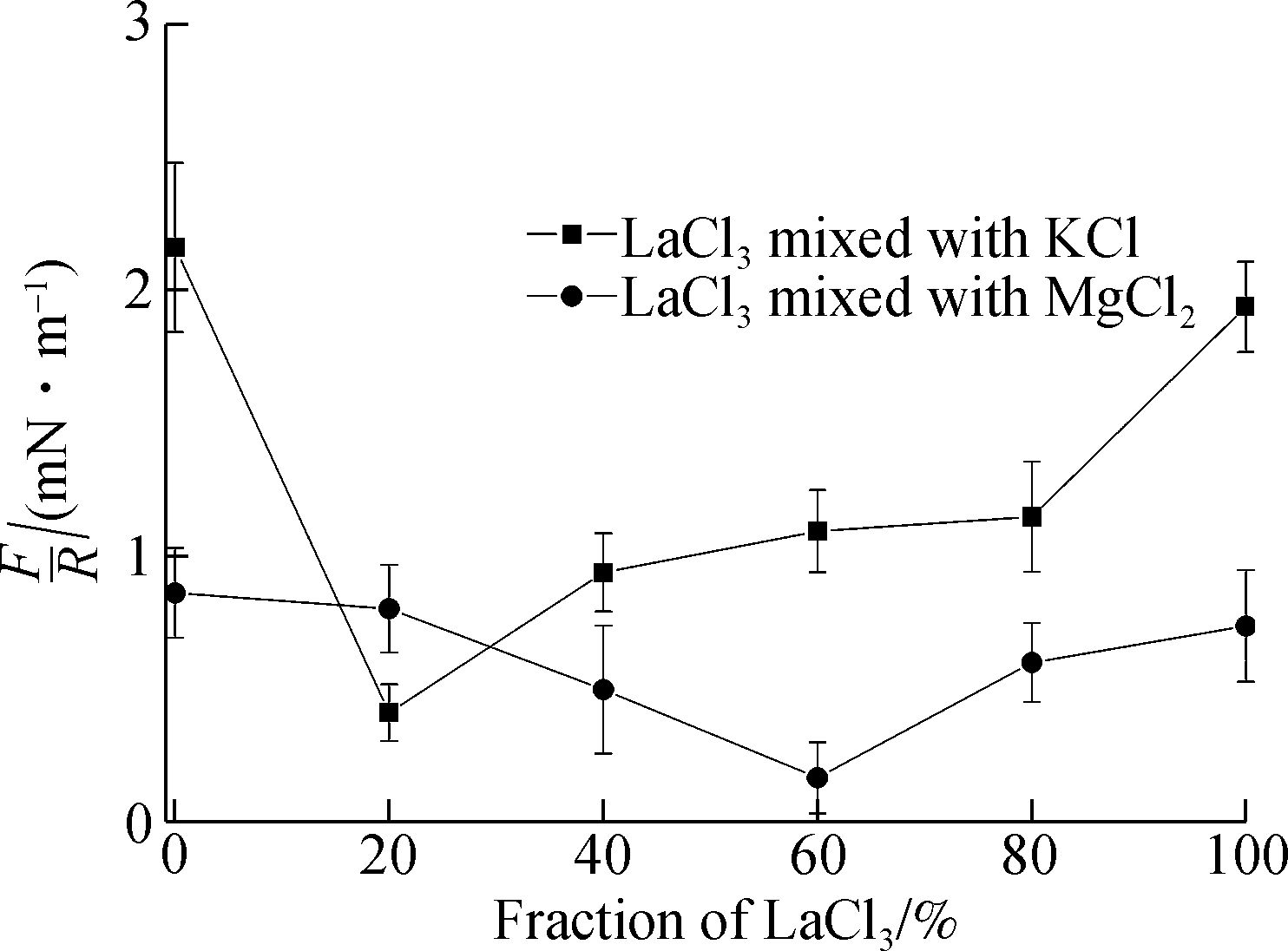
Fig.4 Maximum repulsion force before two mica surfaces jump-into contact in different volume fractions of LaCl3/KCl and LaCl3/MgCl2 solutions with a total ionic strength of 10-4 mol/L
2.2 Effects of ion-ion correlations on charge inversion
The present measurements of interactions between mica surfaces in mixture solutions provide direct evidence of charge inversion. However, they do not provide detailed information about the underlying molecular mechanisms of charge inversion. The classical PB equations fail to explain this controversial phenomenon, which treats ions as point charges and ignores inter-ion correlation effects. Also, the counterions mostly neutralize the surface charges but never overscreen the charged surface in the mean-field PB approximation. Different mechanisms of charge inversion have been put forward over the years. In this study, we employ the mean-field theory to describe the diffusion layer, while the SCL theory[4] was introduced to the Stern layer to characterize the electrostatic interactions between the multivalent ions and the surface as well as ion-ion correlations.
The adsorption of La3+ ions on mica can be included in the Stern layer via the additional energy μc due to spatial interactions between La3+ ions. According to the SCL theory, the concentration of La3+ ions in the Stern layer can be expressed as
(1)
where n is the two-dimensional concentration of La3+ ions in the Stern layer resembling Wigner crystal; rion is the hydrated ionic radius of La3+ ion; ![]() is the bulk concentration of La3+ion; e is the elementary charge; Z is the ionic valence; φs is the diffuse layer potential; kB is the Boltzmann constant; and T is the absolute temperature. The additional energy μc is given as
is the bulk concentration of La3+ion; e is the elementary charge; Z is the ionic valence; φs is the diffuse layer potential; kB is the Boltzmann constant; and T is the absolute temperature. The additional energy μc is given as
μc=-kBT(1.65Γ-2.61Γ1/4+0.26lnΓ+1.95)
(2)
where Γ is the interaction parameter defined as
(3)
where εrε0 is the dielectric constant of water; Z=3 for La3+ ions; and σb is the surface charge density of bare mica surfaces. For monovalent ions Γ≤1, and the correlation effect is negligible. However, when the ionic valence of Z≥3, the correlation effect can provide additional energy for ion adsorptions. The net surface charge density σs on the mica surface can be described as the sum of bare charge density σb of the mica and adsorbed La3+ ions as follows:
σs=σb+nZe
(4)
For the case when the bare charge is fully compensated by the multivalent ions, n=|σb/Ze| and σs is taken as zero. From Eqs.(1) to (4), a simple analytical prediction for the critical concentration of multivalent ions at which charge inversion occurs can be expressed as
(5)
For La3+ ions used in our experiment, rion=1.04 nm, σb=0.5 e/nm2, and Γ=5.4. The predicted critical concentration ρcinv is 8.78×10-6 mol/L.
Based on the SCL and PB theory, we take the SCL as a new boundary for the electrical double layer structure in the diffusion layer, and the ions away from the SCL are assumed to obey the Boltzmann equation. In this way, the effective surface potential φs can be fitted from the measured long-range interaction force laws based on the double-layer interaction forces and Grahame equation[30]. The fitted surface potential in Fig.5 shows an obvious sign changing from negative to positive. We can estimate approximately, from the guidelines in Fig.5, the critical concentrations for charge inversion in the mixture solutions are at about 12% and 45% fractions of LaCl3 with KCl and MgCl2, respectively. The correspondence concentrations of LaCl3 solution are 8.0×10-6 mol/L and 1.07×10-5 mol/L, respectively, which are slightly different from the theoretically predicted critical concentration of 8.78×10-6 mol/L.
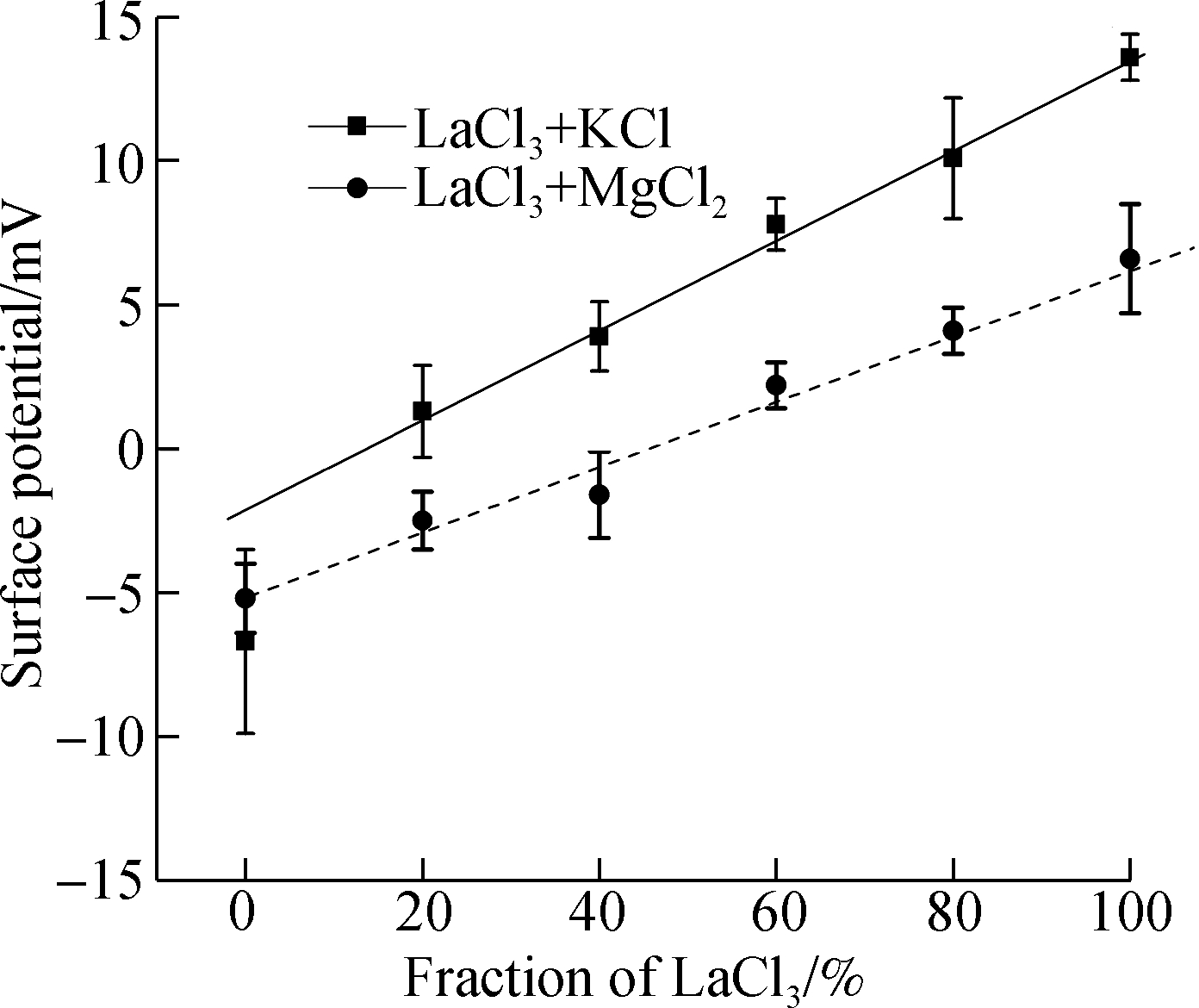
Fig.5 Fitted surface potentials of mica surfaces in different volume fractions of LaCl3/ KCl and LaCl3/MgCl2 solutions
According to the SCL theory[4], the additional screening caused by the monovalent species makes the inversion substantially stronger, because the charging energy of the macroion diminishes much more than the correlation energy of the multivalent ions the SCL layer. This occurs while the electrostatic screening is not so strong that the Wigner crystal melts. However, the experiments here reveal that the addition of monovalent ions cannot enhance the charge inversion of mica surfaces in multivalent ions solutions. The monovalent counterions in mixture solutions can replace some of the multivalent ones near the plane in our experimental systems. This replacement did not take into account in the SCL theory since charge inversion is exclusively attributed to the highly charged species. Also, although charge and excluded volume correlations act simultaneously, the ion-ion correlations effects can be dominant if the formation of the Wigner crystal is sufficient. This can justify the slight effects of monovalentions on the charge inversion in monovalent and trivalent mixture solutions. However, the charge inversion was slightly suppressed when the mica surface was immersed in the mixed solution of LaCl3 and MgCl2, which may be attributed to the competition adsorption of La3+ and Mg2+ ions. The correlations between La3+ and Mg2+ ions are comparable to those between La3+ ions. The additional energy between correlation La3+ ions can also adsorb the Mg2+ ions, then more La3+ ions are needed for compensating for the charge of mica surfaces. Hence, little more La3+ ions are needed to form laterally frozen correlation cells. This may be the reason why the critical concentration of charge inversion in LaCl3 and MgCl2 solutions is higher than that in pure LaCl3 solutions.
3 Conclusion
This paper presents experimental and modeling results aimed at understanding the effects of ion-ion correlations on charge inversion in different volume fractions of LaCl3/KCl or LaCl3/MgCl2 mixture solutions with a total ionic strength of 10-4 mol/L. The results show that charge inversion occurred in both mixture solutions. The experiments performed here reveal that the monovalent counterions cannot enhance the charge inversion in the LaCl3/KCl mixture solutions, which contrast with the SCL theory prediction of the enhancement of charge inversion by the addition of monovalentions. However, the charge inversion was slightly suppressed by introducing the divalent ions. The electrostatic correlations between divalent and trivalent ions can also be responsible for this phenomenon.
[1] Luo Z X, Xing Y Z, Ling Y C, et al. Electroneutrality breakdown and specific ion effects in nanoconfined aqueous electrolytes observed by NMR[J]. Nature Communications, 2015, 6: 6358. DOI:10.1038/ncomms7358.
[2] Sparreboom W, van den Berg A, Eijkel J C T. Principles and applications of nanofluidic transport[J]. Nature Nanotechnology, 2009, 4(11): 713720. DOI:10.1038/nnano.2009.332.
[3] Lin K B, Lin C, Polster J W, et al. Charge inversion and calcium gating in mixtures of ions in nanopores[J]. Journal of the American Chemical Society, 2020, 142(6): 29252934. DOI:10.1021/jacs.9b11537.
[4] Yu Grosberg A, Nguyen T T, Shklovskii B. Colloquium: The physics of charge inversion in chemical and biological systems[J]. Reviews of Modern Physics, 2002, 74(2): 329345. DOI:10.1103/RevModPhys.74.329.
[5] Chou K H, McCallum C, Gillespie D, et al. An experimental approach to systematically probe charge inversion in nanofluidic channels[J]. Nano Letters, 2018, 18(2): 11911195. DOI:10.1021/acs.nanolett.7b04736.
[6] Loessberg-Zahl J, Janssen K G H, McCallum C, et al. (Almost) stationary isotachophoretic concentration boundary in a nanofluidic channel using charge inversion[J]. Analytical Chemistry, 2016, 88(12): 61456150. DOI:10.1021/acs.analchem.6b01701.
[7] Li S X, Guan W H, Weiner B, et al. Direct observation of charge inversion in divalent nanofluidic devices[J]. Nano Letters, 2015, 15(8): 50465051. DOI:10.1021/acs.nanolett.5b01115.
[8] Fahad H M, Gupta N, Han R, et al. Highly sensitive bulk silicon chemical sensors with sub-5 nm thin charge inversion layers[J]. ACS Nano, 2018, 12(3): 29482954. DOI:10.1021/acsnano.8b00580.
[9] Qiao R, Aluru N R. Charge inversion and flow reversal in a nanochannel electro-osmotic flow[J]. Physical Review Letters, 2004, 92(19): 198301. DOI:10.1103/PhysRevLett.92.198301.
[10] van der Heyden F H J, Stein D, Besteman K, et al. Charge inversion at high ionic strength studied by streaming currents[J]. Physical Review Letters, 2006, 96(22): 224502. DOI:10.1103/PhysRevLett.96.224502.
[11] He Y, Gillespie D,Boda D, et al. Tuning transport properties of nanofluidic devices with local charge inversion[J]. Journal of the American Chemical Society, 2009, 131(14): 51945202. DOI:10.1021/ja808717u.
[12] Besteman K, van Eijk K, Lemay S G. Charge inversion accompanies DNA condensation by multivalent ions[J]. Nature Physics, 2007, 3(9): 641644. DOI:10.1038/nphys697.
[13] Favaro M, Jeong B, Ross P N, et al. Unravelling the electrochemical double layer by direct probing of the solid/liquid interface[J]. Nature Communications, 2016, 7: 12695. DOI:10.1038/ncomms12695.
[14] Besteman K, Zevenbergen M A G, Lemay S G. Charge inversion by multivalent ions: Dependence on dielectric constant and surface-charge density[J]. Physical Review E, 2005, 72(6): 061501. DOI:10.1103/PhysRevE.72.061501.
[15] Tan Q Y, Zhao G T, Qiu Y H, et al. Experimental observation of the ion-ion correlation effects on charge inversion and strong adhesion between mica surfaces in aqueous electrolyte solutions[J]. Langmuir, 2014, 30(36): 1084510854. DOI:10.1021/la5024357.
[16] Wang Z Y, Wu J Z. Ion association at discretely-charged dielectric interfaces: Giant charge inversion[J]. Journal of Chemical Physics, 2017, 147(2): 024703. DOI:10.1063/1.4986792.
[17] Luan B Q, Chen K L, Zhou R H. Mechanism of divalent-ion-induced charge inversion of bacterial membranes[J]. Journal of Physical Chemistry Letters, 2016, 7(13): 24342438. DOI:10.1021/acs.jpclett.6b01065.
[18] Qiu Y H, Ma J, Chen Y F. Ionic behavior in highly concentrated aqueous solutions nanoconfined between discretely charged silicon surfaces[J]. Langmuir, 2016, 32(19): 48064814. DOI:10.1021/acs.langmuir.6b01149.
[19] Rouzina I, Bloomfield V A. Macroion attraction due to electrostatic correlation between screening counterions. 1. Mobile surface-adsorbed ions and diffuse ion cloud[J]. The Journal of Physical Chemistry, 1996, 100(23): 99779989. DOI:10.1021/jp960458g.
[20] Martín-Molina A, Rodríguez-Beas C, Faraudo J. Charge reversal in anionic liposomes: Experimental demonstration and molecular origin[J]. Physical Review Letters, 2010, 104(16): 168103. DOI:10.1103/PhysRevLett.104.168103.
[21] Sugimoto T,Nishiya M, Kobayashi M. Charge reversal of sulfate latex particles in the presence of lanthanum ion[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2019, 572: 1826. DOI:10.1016/j.colsurfa.2019.03.077.
[22] Tivony R, Yaakov D B, Silbert G, et al. Direct observation of confinement-induced charge inversion at a metal surface[J]. Langmuir, 2015, 31(47): 1284512849. DOI:10.1021/acs.langmuir.5b03326.
[23] Miller M, Chu M Q, Lin B H, et al. Observation of ordered structures in counterion layers near wet charged surfaces: A potential mechanism for charge inversion[J]. Langmuir, 2016, 32(1): 7377. DOI:10.1021/acs.langmuir.5b04058.
[24] Martin-Molina A,Calero C, Faraudo J, et al. The hydrophobic effect as a driving force for charge inversion in colloids[J]. Soft Matter, 2009, 5(7): 13501353. DOI:10.1039/B820489F.
[25] Wang Z Y, Zhang P L, Ma Z W. On the physics of both surface overcharging and charge reversal at heterophase interfaces[J]. Physical Chemistry Chemical Physics, 2018, 20(6): 41184128. DOI:10.1039/C7CP08117K.
[26] Levin Y. Electrostaticcorrelations: From plasma to biology[J]. Reports on Progress in Physics, 2002, 65(11): 15771632. DOI:10.1088/00344885/65/11/201.
[27] Deng M G,Karniadakis G E. Electrostatic correlations near charged planar surfaces[J]. The Journal of Chemical Physics, 2014, 141(9): 094703. DOI:10.1063/1.4894053.
[28] Laanait N, Mihaylov M, Hou B, et al. Tuning ion correlations at an electrified soft interface[J]. PNAS, 2012, 109(50): 2032620331. DOI:10.1073/pnas.1214204109.
[29] Wang Z Y, Ma Z W, Ma Y Q. Suppression and promotion of charge inversion in the presence of multivalent coions[J]. Physical Review E—Statistical, Nonlinear and Soft Matter Physics, 2015, 92(6): 060303. DOI:10.1103/PhysRevE.92.060303.
[30] Israelachvili J N. Intermolecular and surface forces[M]. New York: Elsevier Science, 2011:293335.